八年级矩形精选复习题
浙教版八年级下册数学-矩形-练习(含解析)

浙教版八年级下册数学矩形练习一、选择题1.矩形具有而一般平行四边形不具有的性质是( )A.对角线相等B.对角相等C.对边相等D.对角线互相平分2.如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是( )A.矩形的对角线相等B.矩形的四个角是直角C.对角线相等的四边形是矩形D.对角线相等的平行四边形是矩形3.如图,在矩形ABCD中,AO=5,CD=6,则AD的长为( )A.5B.6C.7D.84.如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且DE=23,则AC的长度是( )A.25B.2C.8D.5335.如图,将矩形ABCD沿对角线AC折叠,B的对应点为E,AE与CD相交于点F.若∠FCE=40°,则∠CAB的度数为( )A.15°B.20°C.25°D.40°6.如图,在▱ ABCD中,有下列条件:①AC=BD.②∠1+∠3=90°.③OB= 1AC.④∠1=∠2.其中能判定2▱ ABCD是矩形的有( )A.①B.①②③C.②③④D.①②③④7.如图,矩形ABCD中,AB=5,AD=6,点P为平面内一点,且BP=2,点Q为CD上一个动点,则AQ+PQ的最小值为( )A.11B.52−2C.103−2D.138.已知,矩形ABCD中,AB=8,BC=6,点E是线段AB上的一个动点,将线段DE绕点D逆时针旋转90°得到DF,过F作FG⊥CD于点G,连接EF,取EF的中点H,连接DH,AH.点E在运动过程中,下列结论:①△ADE≌△GDF;②当点H和点G互相重合时,AE=6;③∠GFH=∠ADE;④32≤AH≤72.正确的有( )个.A.1B.2C.3D.4二、填空题9.如图,已知▱ABCD中对角线AC,BD相交于点O,请你添加一个适当的条件,使▱ABCD成为一个矩形.你添加的条件是__.10.已知矩形的面积是43,其中一边长为6,则对角线长为 .11.如图.将矩形ABCD沿直线DE折叠,顶点A落在BC边上F处,已知BE=3,CD=8.则BF的长是 .12.如图,已知矩形ABCD,AB=9,AD=4,E为CD边上一点,CE=6,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,连接PE,设点P运动的时间为t秒,则当t的值为 时,△PAE是以PE为腰的等腰三角形.三、解答题13.如图,在▱ABCD中,AE⊥BC于E,点F在边AD上,BE=DF,求证:四边形AECF是矩形.14.如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证∶AO=CO(2)若∠OCD=30∘,AB=3,求△AOC的面积.15.如图,在△ABC中,AC=9,AB=12,BC=15,P 为边BC上一动点,PG⊥AC 于点G,PH⊥AB 于点H.(1)求证:四边形AGPH 是矩形.(2)在点P 的运动过程中,GH 的长是否存在最小值? 若存在,请求出最小值;若不存在,请说明理由.答案解析部分1.【答案】A【解析】【分析】矩形是一个特殊的平行四边形,因此平行四边形的性质矩形都具有,而矩形的性质:①对角线相等,②四个角是直角平行四边形不具有,据此即可得到结果。
数学人教版八年级下册期末复习专项练习06矩形答案及解析

加油!有志者事竟成答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!数学人教版8年级下册期末复习真题汇编卷矩形一、单选题1.(2022秋·山东泰安·八年级校考期末)如图,以正方形ABCD 的对角线AC 为一边作菱形AEFC ,则FAB Ð=()A .20°B .30°C .50°D .22.5°2.(2023春·江苏·八年级期末)小明同学为班级设计如图所示的班徽,O 为正方形ABCD 的中心,四块全等的阴影图形均为菱形.若A ,E ,F 三点共线,则图中阴影面积与空白面积之比为()A .B .2:3C .D .1:23.(2023春·浙江·八年级期末)如图,直线l 交正方形ABCD 的对边AD 、BC 于点P 、Q ,正方形ABCD 和正方形EFGH 关于直线l 成轴对称,点H 在CD 边上,点A 在边FE 上,BC 、.HG 交于点M ,AB 、FG 交于点N .以下结论错误的是()A .EA NG AN+=B .GQM 的周长等于线段CH 的长C .BQN △的周长等于线段CM 的长D .FNA 的周长等于22DH HC+4.(2021春·浙江宁波·八年级统考期末)如图,正方形ABCD 的边长为4,E ,F ,G 分别是边AB BC AD ,,上的动点,且=AE BF ,将BEF △沿EF 向内翻折至B EF ¢,连结BB B G GC ¢¢,,,则当BB ¢最大时,B G GC ¢+的最小值为()A2B .5.6C .D .5.(2023秋·山东烟台·八年级统考期末)如图,P 为线段AB 上任意一点,分别以AP 、PB 为边在AB 同侧作正方形APCD 、PBEF ,若28CBE Ð=°,则AFP Ð的度数为()A .56°B .62°C .73°D .76°6.(2023秋·广东·八年级校联考期末)如图,在边长为5的正方形ABCD 内作45EAF а=,AE 交BC 于点E ,AF 交CD 于点F ,连接EF .若2DF =,则BE 的长为()A .157B .43C .34D .27.(2023秋·山东烟台·八年级统考期末)如图,正方形ABCD 的边长为2cm ,E 是边AD 的中点,P 为对角线BD 上一动点,连接PA 、PE ,当点P 移动到使BPA DPE Ð=Ð时,AP PE +的值为()AB C .D .8.(2022秋·内蒙古包头·九年级统考期末)如图,在正方形ABCD 中,2AB =,点E ,F 分别在边BC 和CD 上,AE AF =,60EAF Ð=°,则CF 的长是()A .2B 1C .14D 9.(2022春·山西晋城·八年级统考期末)如图,在正方形ABCD 中,点P 在边AB 上,AE DP ^于点E ,CF DP ^于点F ,若4AE =,7CF =,则EF =()A .1B .2C .3D .410.(2023秋·山东烟台·八年级统考期末)在边长为8的正方形ABCD 底座中,放置两张大小相同的正方形纸板,边EF 在AB 上,点K ,I 分别在,BC CD 上,若区域I 的周长比区域II 与区域III 的周长之和还大4,则正方形纸板的边长为()A .4B .143C .5D .16311.(2023秋·河北保定·九年级统考期末)在正方形ABCD 中,点M N ,将对角线BD 三等分,且6BD =,点E 是正方形边上的一点,对于满足ME NE a +=的点E的个数n 进行探究,结论如下.结论1:若4a =,则4n =;结论2:若a =,则4n =.下列判断正确的是()A .只有结论1正确B .只有结论2正确C .两个结论都正确D .两个结论都不正确12.(2023秋·四川宜宾·八年级统考期末)如图,直线L 上有三个正方形a ,b ,c ,若正方形a 的边长为1,正方形c 的边长为3,则正方形b 的面积为()A .4B .9C .10D .1113.(2022春·河北保定·八年级校考期末)如图,正方形ABCD 和正方形CEFG 中,点D 在CG 上,13BC CE ==,,H 是AF 的中点,那么CH 的长是()A .2.5BCD .214.(2022秋·河南郑州·九年级校联考期末)如图,正方形ABCD 中,12AB =,点E ,F 分别为,AD BC 上一点,且7AE BF ==,连接EF 交对角线BD 于点G ,点P ,Q 分别为,CE BG 的中点,则PQ 的长为()A .6B .CD .13215.(2023秋·贵州六盘水·九年级统考期末)如图,正方形ABCD 的对角线相交于点O ,Rt EOF △(两直角边长均大于AB 的长度)绕点O 旋转的过程中,与正方形重叠部分的面积()A.由小变大B.由大变小C.始终不变D.先由大变小,然后又由小变大二、填空题16.(2023秋·山西太原·九年级期末)如图,在正方形ABCD中,6AB=,点E,F分别在边,AB BC上,2==,点M在对角线AC上运动,连接EM和MF,AE BF则EM MF+的最小值等于__________.17.(2022秋·陕西榆林·九年级统考期末)如图,在正方形ABCD中,2AB=,对角线AC、BD交于点O,点E、F分别为边BC、CD上的动点(不与端点重合),且BE CF=,连接OE、OF、EF,则线段EF的最小值为________.18.(2022秋·陕西渭南·九年级统考期末)如图,正方形ABCD的对角线AC,BD 相交于点^于点F,若AC= O,点P是BC上任意一点,PE BD^于点E,PF AC则EF的长的最小值为_________.19.(2023秋·浙江湖州·九年级统考期末)如图,已知:正方形ABCD的顶点A 在矩形DEFG的边EF上,矩形DEFG的顶点G在正方形ABCD的边BC上,正方形的边长为4,DG的长为5,则DE的长为_______.20.(2022秋·河北保定·七年级校考期末)如图,在正方形ABCD 外作等边ADE ,则BED Ð=___________°.21.(2023秋·四川雅安·九年级统考期末)如图,已知正方形ABCD连接AC ,BD ,CE 平分ACD Ð交BD 于点E ,则BE =_______.22.(2022秋·湖南永州·八年级统考期末)如图,在正方形ABCD 中,P ,Q 分别为,BC CD 的中点,若40PAQ Ð=°,则APQ Ð大小为___________.23.(2023秋·陕西渭南·九年级统考期末)如图,点E 是边长为8的正方形ABCD 的对角线BD 上的一个动点(不与点B ,D 重合),连接AE ,以AE 为边向左侧作正方形AEFG ,点P 为AD 的中点,连接PG ,DG ,DG 与BA 的延长线交于点H ,在点E 运动过程中,线段PG 的最小值为______.24.(2022春·山西晋城·八年级统考期末)若点E 是BC 的中点,4CD =,将正方形ABCD 沿FH 折叠,使点D 恰好落在BC 边的中点E 处,点A 的对应点为点P ,则折痕HF 的长为________.25.(2022秋·河北石家庄·八年级校考期末)如图是“赵爽弦图”,ABH 、BCG 、CDF 和DAE 是四个全等的直角三角形,四边形ABCD 和EFGH 都是正方形.如果10AB =,6AH =,则GE =___________;此时ABCDEFGH S S 正方形正方形的值是___________.26.(2022秋·黑龙江绥化·九年级统考期末)如图,将n 个边长都为1cm 的正方形按如图所示摆放,点1A 、2A 、…、n A 分别是正方形的中心,则n 个这样的正方形重叠部分的面积和为________(用n 的代数式表示)27.(2023秋·四川乐山·八年级统考期末)欧几里得是古希腊著名数学家、欧氏几何学开创者.下面问题是欧几里得证明勾股定理的证法一小片段,同学们,让我们一起来走进欧几里得的数学王国吧!如图,分别以Rt ABC △的三边为边长,向外作正方形ABDE 、BCFG 、ACHI .(1)连接BI 、CE ,则BI 、CE 的关系是______;(2)过点B 作AC 的垂线,交AC 于点M ,交HI 于点N ,若4MN =,1NI =,则正方形BCFG 的边长是______.28.(2023秋·辽宁阜新·九年级阜新实验中学校考期末)如图,已知45MON Ð=°,在MON Ð内部作以点O 为位似中心的正方形1112A B C A ,正方形2223A B C A ,正方形3334A B C A ,…,正方形1n n n n A B C A +,其对应顶点1A ,2A ,3A ,4A …n A 都在射线ON 上,对应顶点1B ,2B ,3B ,4B …n B 都在射线OM 上,将正方形1112A B C A 的面积记作1S ;正方形2223A B C A 的面积记作2S ;正方形3334A B C A 的面积记作3S ;…,依此类推,正方形1n n n n A B C A +的面积记作n S ,若111A B =,则第n 个正方形的面积n S =______.29.(2023秋·黑龙江哈尔滨·九年级校考期末)如图,在正方形ABCD 中,点M ,N 为CD ,BC 上的点,且DM CN =,AM 与DN 交于点P ,连接AN ,点Q 为AN 中点,连接PQ ,若10AB =,4DM =,则PQ 的长为________.30.(2022秋·河南南阳·九年级统考期末)如图,正方形ABCD 的边长为6,点E ,F 分别在DC ,BC 上,4BF CE ==,连接AE 、DF ,AE 与DF 相交于点G ,连接AF ,取AF 的中点H ,连接HG ,则HG 的长为________.三、解答题31.(2023秋·山西太原·九年级期末)如图,在ABC 中,点M 和N 分别在边AB 和AC 上,MB NC =,连接,,MN BN CM ,点D ,E ,F ,G 分别是,,,MN BN BC CM 的中点.求证:四边形DEFG 是菱形.32.(2022春·江苏无锡·八年级统考期末)如图,正方形ABCD的边长为6,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB CD DA、、上,2AH=.(1)如图1,当2DG=时,求证:菱形EFGH是正方形.(2)如图2,连接CF,当△FCG的面积等于1时,求线段DG的长度.33.(2023秋·山东泰安·八年级校考期末)如图,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA PE=,PE交CD于F.(1)证明:PC PE=;(2)求CPE∠的度数;34.(2021春·广东广州·八年级校考期末)在正方形ABCD中,点E是CD边上任意一点.连接AE,过点B作BF AE^于F.交AD于H.≌;⊥于G,求证:AFB DGA(2)如图2,点E为CD的中点,连接DF,求证:FH FE+;(3)如图3,1AB=,连接EH,点P为EH的中点,在点E从点D运动到点C的过程中,点P随之运动,请直接写出点P运动的路径长.35.(2023春·广东广州·九年级广东实验中学校考期末)在正方形ABCD中,边长为2.点E是线段BC上的动点,以AE为直角边在直线BC的上方作等腰直角三角形AEF,o90Ð=,其中EF交CD于点P,AF交CD于点Q,连接CF.AEFBE=时,求线段CF的长:2Ð=Ð.②当点E在线段BC上运动时,求证:QEF FEC(2)如图2,过点B作BG AE^交EQ于点G,过点D作DH CF^所在的直线于点H,求HG的最小值.36.(2021春·湖北武汉·八年级统考期末)如图,点G是正方形ABCD对角线CA 的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.≌△△;(2)若AB=3AG=37.(2023秋·辽宁朝阳·八年级统考期末)如图,在边长为6的正方形ABCD中,E是边CD的中点.将ADEV沿AE对折至AFE△,延长EF交BC于点G,连接AG,AG平分BAFÐ.≌△△(2)求BG的长.38.(2022秋·山东烟台·八年级统考期末)如图,在正方形ABCD中,点E是BC 的中点,连接DE,过点A作AG ED^交DE于点F,交CD于点G.≌;(2)连接BF,求证:AB FB=.39.(2022秋·内蒙古包头·九年级统考期末)如图,在正方形ABCD中,6AB=,M 是对角线BD 上的一个动点102DM BD æö<<ç÷èø.连接AM ,过点M 作MN AM ^交BC 于点N .(1)如图1,求证:MA MN =;(2)如图2,过点N 作NH BD ^于H ,AM =,求MH .40.(2023秋·陕西咸阳·九年级统考期末)如图,在正方形ABCD 中,点E 为边BC 上一点,延长BC 至点G ,使得BE CG =,过点G 作FG BC ^,连接AE 、EF ,且AE EF =,求证:ABE EGF ≌.41.(2022秋·广东珠海·九年级统考期末)如图,将正方形ABCD 绕顶点A 顺时针旋转45°得到正方形A B C D ¢¢¢¢,BC 与C D ¢¢相交于点E ,连接BD ,B D ¢¢相交于点F .(1)填空:D EC ¢Ð=______度;(2)求证:四边形BED F ¢是菱形.参考答案1.D2.A3.C4.C5.B6.A7.B8.A9.C10.B11.B12.C13.B14.D15.C16.61718.119.16520.452122.70°/70度23.24.25.25n-26.1427.BI EC=28.222n -293031.证明:∵点D ,E 分别是MN ,BN 的中点,∴DE 是NMB △的中位线,∴DE MB ∥,12DE MB =,同理可得:GF MB ∥,12GF MB =,12DG NC =,∴DE GF ,DE GF =,∴四边形DEFG 是平行四边形,∵MB NC =,∴DE DG =,∴平行四边形DEFG 为菱形.32.(1)证明:∵四边形ABCD 是正方形,∴90D A Ð=Ð=°,∵四边形EFGH 是菱形,∴HG HE =,在Rt HDG △和Rt EAH △中,HG EH DG AH =ìí=î,∴()Rt Rt HL HDG EAH ≌,∴DHG AEH Ð=Ð,∵90AEH AHE Ð+Ð=°∴90DHG AHE Ð+Ð=°,∴90GHE Ð=°,∴菱形EFGH 为正方形;(2)解:过F 作FM CD ^,交DC 的延长线于点M ,连接GE ,∵在正方形ABCD 中,CD AB ∥,∴AEG MGE Ð=Ð,∵在菱形EFGH 中,GF HE ∥,HE FG =,∴HEG FGE Ð=Ð,∴AEH FGM Ð=Ð;在EHA 和GFM △中,90A M AEH MGF HE FG Ð=Ð=°ìïÐ=Ðíï=î,∴()AAS EHA GFM ≌,∴2MF AH ==,设DG x =,则6CG x =-,∴1612FCG S CG FM x =×=-=,∴5x =,即5DG =.33.(1)证明:∵四边形ABCD 是正方形,∴45AB BC ABP CBP =Ð=Ð=°,,又∵BP BP =,∴()SAS ABP CBP ≌,∴PA PC =,∵PA PE =,∴PC PE =;(2)解:由(1)知,ABP CBP △≌△,∴BAP BCP Ð=Ð,∵在正方形ABCD 中,90BAD BCD ADC CDE ===°=∠∠∠∠,∴BAD BAP BCD BCP Ð-Ð=Ð-Ð,即DAP DCP Ð=Ð,∵PA PE =,∴DAP E Ð=Ð,∴DCP E Ð=Ð,∵CFP EFD Ð=Ð(对顶角相等),∴180180PFC PCF DFE E °-Ð-Ð=°-Ð-Ð,即90CPF EDF Ð=Ð=°.34.(1)证明: 四边形ABCD 是正方形,AB AD \=,90BAD Ð=°,DG AE ^ ,BF AE ^,90AFB DGA \Ð=Ð=°,90FAB DAG \Ð+Ð=°,90DAG ADG Ð+Ð=°,BAF ADG \Ð=Ð,在AFB △和DGA △中,AFB DGA BAF ADG AB AD Ð=ÐìïÐ=Ðíï=î,(AAS)AFB DGA \≌;(2)证明:过点D 作DK AE ^于K ,DJ BF ^交BF 的延长线于J ,如图2所示: 四边形ABCD 是正方形,90BAH ADE \Ð=Ð=°,AB AD CD ==,BF AE ^ ,90AFB \Ð=°,90DAE EAB Ð+Ð=° ,90EAB ABH Ð+Ð=°,DAE ABH \Ð=Ð,在ABH 和DAE 中,BAH ADE AB DA ABH DAE Ð=Ðìï=íïÐ=Ðî,∴(ASA)ABH DAE ≌,AH DE \=,点E 为CD 的中点,12DE EC CD \==,AH DH \=,DE DH \=,DJ BJ ^ ,DK AE ^,90J DKE KFJ \Ð=Ð=Ð=°,\四边形DKFJ 是矩形,90JDK ADC \Ð=Ð=°,JDH KDE \Ð=Ð,在DJH 和DKE △中,J DKE JDH KDE DH DE Ð=ÐìïÐ=Ðíï=î,∴(AAS)DJH DKE ≌,DJ DK \=,JH EK =,\四边形DKFJ 是正方形,FK FJ DK DJ\===,DF \,2FH FE FJ HJ FK KE FJ \+=-++=;(3)解:如图3,取AD 的中点Q ,连接PQ ,延长QP 交CD 于R ,过点P 作PT CD^于T ,PK AD ^于K ,设PT b =,由(2)得:(ASA)ABH DAE ≌,AH DE \=,90EDH Ð=° ,点P 为EH 的中点,12PD EH PH PE \===,PK DH ^ ,PT DE ^,90PKD KDT PTD \Ð=Ð=Ð=°,\四边形PTDK 是矩形,PT DK b \==,PK DT =,PH PD PE == ,PK DH ^,PT DE ^,22DH DK b \==,2DE DT=,12AH DE b\==-,1122PK DE b \==-,12QK DQ DK b =-=-,PK QK \=,90PKQ Ð=° ,PKQ \是等腰直角三角形,45KQP \Ð=°,\点P 在线段QR 上运动,DQR 是等腰直角三角形,QR \==\点P 的运动的路径长为2.35.(1)解:如图,过点F 作FN BC ^于点N ,AEF 是等腰直角三角形,AE EF \=,45EAF Ð=°,90AEF ABE FNE Ð=Ð=Ð=°,90AEB BAE AEB FEN \Ð+Ð=°=Ð+Ð,=BAE FEN \ÐÐ,ABE ENF \@△△(AAS ),12BE FN \==,AB EN =,BC EN AB \==,12CN BE \==,又90N Ð=° ,CFN \△是等腰直角三角形,CF \==故答案是:2CF =;证明:如图,延长CB 至K ,使BK DQ =,连接AK ,BK DQ = ,90ABK D Ð=Ð=°,AB AD =,()SAS ABK ADQ \@,BAK DAQ Ð=Ð,AK AQ =,45EAF Ð=° ,45\Ð+Ð=°,BAE DAQ\Ð+Ð=°=Ð=Ð,45BAE BAK EAK EAD又AE AE,=()AEK AEQ\@,SAS\Ð=Ð,AEK AEQÐ=°,90AEF\Ð=Ð;FEQ FEC(2)解:如图,连接AG、GH、AH、AC,由(1)得90Ð=°,AEB AEGÐ=Ð,DCH四边形ABCD是正方形,\===,AC==,452AB AD CDÐ=°ACD,\Ð=°,90ACH,45^DH CHÐ=°,DCH\△是等腰直角三角形,DCH\=,2DC\=,CH\==AH,AEB AEGBG AE^Ð=Ð,\Ð=Ð,EBG EGB\=,BE EG又AE AE,=()\@,SASABE AGE\点G 在以点A 为圆心,AB 长为半径的圆上,当点G 在线段AH 上时,GH 有最小值,GH \2,2-.36.(1)解:∵四边形EFGA 和四边形ABCD 是正方形,∴AG AE =,AB AD =,90EAG BAD Ð=Ð=°,在GAD 和EAB 中,90GAD EAD Ð=°+Ð,90EAB EAD Ð=°+Ð,∴GAD EAB Ð=Ð,在GAD 和EAB 中,AG AE GAD EAB AD AB =ìïÐ=Ðíï=î,∴()SAS EAB GAD ≌△△;(2)解:如图,连接BD ,BD 与AC 交于点O,由(1)得:EAB GAD≌△△∴EB GD =,∵四边形ABCD是正方形,AB =∴,6BD AC AC BD ^===,∴190,32DOG OA OD BD Ð=°===,∴6OG OA AG =+=,∴EB GD ===37.(1)在正方形ABCD 中,,90AD AB BC CD D B BCD °===Ð=Ð=Ð=,∵将ADE V 沿AE 对折至AFE △,∴,,90AD AF DE EF D AFE ==Ð=Ð=°,∴,90AB AF B AFG =Ð=Ð=°,又∵AG AG =,在Rt ABG △和Rt AFG △中,AG AG AB AF=ìí=î,∴Rt Rt △≌△ABG AFG (HL ).(2)∵ABG AFG △≌△,∴BG FG =,设BG FG x ==,则6GC x =-,∵E 为CD 的中点,∴3CE EF DE ===,∴3EG x =+,∴在Rt CEG △中,2223(6)(3)x x +-=+,解得2x =,∴2BG =.38.(1)证明:∵四边形ABCD 是正方形,∴90ADG C Ð=Ð=°,AD DC =,又∵AG ED ^,∴90DAG ADF CDE ADF Ð+Ð=°=Ð+Ð,∴DAG CDE Ð=Ð,∴()ASA ADG DCE ≌△△;(2)证明:如图所示,延长DE 交AB 的延长线于H ,∵E 是BC 的中点,∴BE CE =,又∵90C HBE Ð=Ð=°,DEC HEB Ð=Ð,∴()ASA DCE HBE ≌△△,∴BH DC AB ==,即B 是AH 的中点,又∵90AFH Ð=°,∴Rt AFH △中,12BF AH AB ==.39.(1)证明:过点M 作MF AB ^于F ,作MG BC ^于G ,如图1所示:∴90AFM MFB BGM NGM Ð=Ð=Ð=Ð=°,∵四边形ABCD 是正方形,∴90ABC DAB Ð=Ð=°,AD AB =,45ABD DBC Ð=Ð=°,∵MF AB ^,MG BC ^,∴MF MG =,∵90ABC Ð=°,∴四边形FBGM 是正方形,∴90FMG Ð=°,∴90FMN NMG Ð+Ð=°,∵MN AM ^,∴90AMF FMN Ð+Ð=°,∴AMF NMG Ð=Ð,在AMF 和NMG 中,AFM NGM MF MG AMF NMG Ð=Ðìï=íïÐ=Ðî∴()ASA AMF NMG ≌,∴MA MN =;(2)解:过点A 作AF BD ^于F ,如图2所示:∴90AFM Ð=°,∴90FAM AMF Ð+Ð=°,∵MN AM ^,∴90AM N Ð=°,∴90AMF HMN Ð+Ð=°,∴FAM HMN Ð=Ð,∵NH BD ^,∴90AFM MHN Ð=Ð=°,在AFM △和MHN 中,FAM HMN AFM MHN AM MN Ð=ÐìïÐ=Ðíï=î∴()AAS AFM MHN ≌△△,∴AF MH =,在等腰直角ABD △中∵AF BD ^,∴1122AF BD ==´=∴MH =.40.证明:∵四边形ABCD 正方形,∴AB BC =,90B Ð=°,∵BE CG =,∴BC EG =,∴AB EG =,∵FG BC ^,∴90EGF Ð=°,在Rt ABE △和Rt EGF 中,AB EG =,AE EF =,∴()Rt Rt HL ABE EGF ≌,即ABE EGF ≌.41.(1)解:∵四边形ABCD 和四边形A B C D ¢¢¢¢是正方形∴90AD C ABC Ð=Ð=¢¢°∵45D AB ¢Ð=°∴18045135BED ¢°Ð=-°=°∴45D EC Ð=¢°(2)解:连接AE .∵四边形ABCD 和四边形A B C D ¢¢¢¢是正方形∴90AD C ABC Ð=Ð=¢¢°∵45D AB ¢Ð=°∴18045135BED ¢°Ð=-°=°∴45D EC Ð=¢°(方法不唯一,直接写由(1)得也可以)在正方形A B C D ¢¢¢¢中,45B D C ¢¢¢Ð=°∴D EC B D C Ð=Т¢¢¢∴D F BC ¢∥,即D F BE ¢∥.同理45DBC D EC ¢Ð=Ð=°,∴D E BF ¢∥.∴四边形BED F ¢是平行四边形在Rt AD E ¢△和Rt ABE △中AD ABAE AE=¢ìí=î∴Rt Rt AD E ABE¢△≌△∴D E BE¢=∴平行四边形BED F ¢是菱形.。
人教版初二数学8年级下册 第18章(平行四边形)矩形 专题训练(含答案)

人教版初二数学8年级下册 第18章(平行四边形)微专题3 矩形的综合训练1.如图,将矩形ABCD 沿对角线BD 折叠,点C 对应点E ,BE 交AD 于F.(1)判断△BDF 的形状并证明;(2)若AB=3,BC=4,求S △BDF2.如图,矩形ABCD 中,∠BAD 的平分线交BC 于E ,交DC 的延长线于F ,点G 是EF 的中点。
(1)求∠BDG 的度数;(2)写出AB 、AG 、AD 之间的数量关系并证明F EDCB A A B DCE FG G F EC D B A3.如图,矩形ABCD 中,E 在BC 上,CG ⊥BD 于G ,交AE 的延长线于F ,CF=BD ,求∠BAF 。
4.如图,矩形ABCD 中,E 为BC 中点,M 为DA 延长线上一点,MB 、DE 的延长线交于N ,且∠MNC=90°。
(1)求证:AD=2NE ;(2)求证:DM=DN.F GF E D C B ANMED CBA5.如图,点E 是□ABCD 中边BC 的中点,连接AE 并延长,交DC 的延长线于点F .(1) 求证:△ABE ≌△FCE(2)连接AC 、BF ,若∠AEC =2∠ABC ,求证:四边形ABFC 为矩形.6.如图,在 ABC 中,BD ⊥AC 于D ,CE ⊥AB 于E ,点M,N 分别是BC ,DE 的中点(1) 求证:MN ⊥DE(2)连接ME,MD ,若∠A =60°,求MN DE解的值. A DC B F EE DC B AN M7.如图,矩形ABCD 中,E 为CD 中点,BF 平分∠ABC ,BE ⊥EF(1) ∠AED 的度数(2)求证:GF =2DF .8.(1)如图,在矩形ABCD 中,E 是AD 的中点,将△ABE 沿BE 折叠后得到△GBE ,且点G 在矩形ABCD 内部,小明将G 延长交DC 于点F ,认为GF=DF ,你同意吗?请说明理由.(2)保持(1)中的条件不变,若DC =2DF ,求AD AB的值;(3)保持(1)中的条件不变,若DC =nDF ,直接写出AD AB 的值为 .F ED C BA G G ED C BA F微专题3 矩形的综合训练1.如图,将矩形ABCD 沿对角线BD 折叠,点C 对应点E ,BE 交AD 于F.(1)判断△BDF 的形状并证明;(2)若AB=3,BC=4,求S △BDF(1)证明:∵ AD ∥BC ∴ ∠DBC=∠ADB又 ∵ ∠DBC=∠EBD ∴ ∠EBD=∠ADB∴ △BDF 为等腰三角形(2)解:由(1)知BF=FD ,设AF=x ∴FD=BF=4-x∴ 9+x 2=(4-x )2 ∴ x=78 ∴ DF=258∴ S △ADF =12DF·AB=12×258×3=75162.如图,矩形ABCD 中,∠BAD 的平分线交BC 于E ,交DC 的延长线于F ,点G 是EF 的中点。
八年级数学下册-矩形练习及答案

矩形练习一、选择题1.如图,四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是()A. AB=CDB. AD=BCC.∠AOB=45°D.∠ABC=90°2. (辽宁东北育才中学月考)如图所示,在矩形ABCD中,对角线AC、BD相交于点O,∠ACB=30°,则∠A0B 的大小为().A.30°B.60°C.90°D.120°3.下列命题中不正确的是( ).A.直角三角形斜边中线等于斜边的一半B.矩形的对角线相等C.矩形的对角线互相垂直D.矩形是轴对称图形4.矩形邻边之比3∶4,对角线长为10cm,则周长为( ).A.14cmB.28cmC.20cmD.22cm5.(易错题)如图所示,四边形PAOB是扇形OMN的内接矩形,顶点P在MN上,且不与M,N重合,当P点在MN上移动时,矩形PAOB的形状、大小随之变化,则AB的长度()A.变大B.变小C.不变D.不能确定二、填空题6.(1)矩形的定义:__________________的平行四边形叫做矩形.(2)矩形的性质:矩形是一个特殊的平行四边形,它除了具有四边形和平行四边形所有的性质,还有:矩形的四个角______;矩形的对角线______;矩形是轴对称图形,它的对称轴是____________.(3)矩形的判定:一个角是直角的______是矩形;对角线______的平行四边形是矩形;有______个角是直角的四边形是矩形.7.在△ABC中,∠C=90°,AC=5,BC=3,则AB边上的中线CD=______.8.如图,矩形ABCD中,A B=2,BC=3,对角线AC的垂直平分线分别交AD,BC于点E、F,连结CE,则CE的长______.9. (西安铁一中月考)如图,已知 MN//PQ,EF与MN,PQ分别交于A、C两点,过A、C两点作两组内错角的平分线,分别交于点B、D,则四边形ABCD是 .10.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E,F分别是AO, AD的中点,若AB= 6 cm,BC=8 cm,则△AEF 的周长= cm.11.如图,四边形ABCD是矩形,点E在线段CB 的延长线上,连接DE交AB于点F,∠AED = 2∠CED,点G是DF的中点,若BE=1,AG=4,则 AB的长为 .三、解答题12.已知:如图,□ABCD中,AC与BD交于O点,∠OAB=∠OBA.(1)求证:四边形ABCD为矩形;(2)作BE⊥AC于E,CF⊥BD于F,求证:BE=CF.13.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.14.如图,在矩形ABCD中,AC,BD相交于点 O,AE 平分∠BAD 交 BC 于点E.若∠CAE= 15°,求∠BOE的度数.15. (重庆八中质量检测·)如图所示,AB丄AC于点A,BD丄CD于点D,O是BC的中点,若BC=6 cm,∠AOD=60°,求 AD 的长.16.如图,在ABCD中,E、F分别是AB、DC 边上的点,且AE=CF.(1)求证:△ADE≌△CBF.(2)若∠DEB=90°,求证:四边形DEBF是矩形.17.如图,在△ABC中,D是AB的中点,E是CD的中点,过点C作CF//AB交AE的延长线于点F,连接BF.(1)求证:DB=CF;(2)如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.参考答案1.D 解析 因为四边形ABCD 的对角线互相平分,所以四边形ABCD 为平行四边形,A,B 两进项为平行四形身具有的性质,C 选项添加后不能使平行四边形ABCD 变为矩形,根据矩形的定义知D 正确.2.B 解析 在矩形ABCD 中,OB=AO=CO,由∠ACB=30︒,得∠ACB=DBC=30︒ ∠AOB=∠OCB+∠OBC=60︒,故选B.3.C . 4.B .5. C 解析 连接OP,因为四边形PAOB 是矩形,所以OP=AB,OP 为扁形的半径,为定值,所以AB 的长度不变.故选C.6.(1)有一个角是直角;(2)都是直角,相等,经过对边中点的直线; (3)平行四边形;对角线相等;三个角.7.⋅234 8.⋅6139.矩形 解析首先推出∠BAC=∠DCA,继而推出AB ∥CD ;推出∠BCA=∠DAC,进而推出AD ∥BC,因此四边形ABCD 是平行四边形,易证明∠ABC=90︒,可得平行四边形ABCD 是矩形。
完整word版,八年级数学矩形基础练习题

八年级数学矩形基础练习题1.矩形具备而平行四边形不拥有的性质是()A .对角线互相均分B .邻角互补C.对角相等 D .对角线相等2.在以以下列图形性质中,矩形不用然拥有的是()A .对角线互相均分且相等B .四个角相等C.既是轴对称图形,又是中心对称图形 D .对角线互相垂直均分3.若矩形的一条对角线与一边的夹角是40°,则两条对角线订交所成的锐角是()A . 20°B. 40°C. 80°D. 100°4.直角三角形中,两条直角边边长分别为12 和 5,则斜边中线的长是()A.26B.13C.30D.6.55.以下鉴识图形不正确的选项是()A .有一个角是直角的平行四边形是矩形;B .有三个角是直角的四边形是矩形C.对角线相等的四边形是矩形D.对角线互相均分且相等的四边形是矩形6.四边形 ABCD 的对角线订交于点O,以下条件不能够判断它是矩形的是()A . AB=CD ,AB ∥ CD ,∠ BAD=90 °B. AO=CO ,BO=DO ,AC=BDC.∠ BAD= ∠ABC=90 °,∠ BCD+ ∠ ADC=180 °D.∠ BAD= ∠ BCD ,∠ ABC= ∠ADC=90 °7.如图1,矩形ABCD中, AB=8 , BC=6 ,E、 F 是AC上的三均分点,则S△BEF为()A . 8B. 12C. 16D. 24(1)8.( 2006·成都)把一张长方形的纸片按如图(2)2 所示的方式折叠,EM 、FM( 3)为折痕,折叠后的 C 点落在B′ M或B′ M的延长线上,那么∠EMF的读度为()A.85°B. 90°C. 95° D .100°9.( 2006·黑龙江)如图3,在矩形ABCD中, EF∥ AB , GH ∥ BC ,EF、 GH的交点P 在BD上,图中面积相等的四边形有()A.3 对B.4 对C.5 对D.6 对10.如图4,矩形ABCD的周长为68,它被分红7 个全等的矩形,则矩形ABCD?的面积为()A.98 B .196C. 280D.284二、填空题11.矩形 ABCD 中,对角线AC=10cm ,AB : BC=3 : 4,则它的周长是_______.12.矩形ABCD的两条对角线订交于点O ,若是矩形的周长是34cm ,又△ AOB? 的周长比△ABC的周长少7cm ,则AB=________cm , BC=________cm .13.在矩形ABCD 中,对角线AC 、 BD 订交于点O,若∠ AOB=110 °,则∠ OAB=______ .14.如图 5 所示,把两个大小圆满同样的矩形拼成“L? ”形图案, ?则∠ FAC=_______ ,∠ FCA=________ .(4)(5)(6)15.如图 6,在四边形ABCD 中, E、F、G、H 分别是 AB 、BC、 CD、DA 的中点, ?增加一个条件,使四边形EFGH 为矩形,增加的条件是:____________ .三、解答题16.已知:如图,在矩形ABCD 中, AE ⊥ BD 于 E,对角线 AC 、BD 订交于点O,?且 BE:ED=1 :3,AB=6cm ,求 AC 的长.17.已知:如图,M 为Y ABCD 的 AD 边上的中点,且MB=MC ,求证: Y ABCD是矩形.18.( 2006·泸州)如图,在矩形ABCD 中,点 E 是 BC 上一点, AE=AD , DF⊥ AE ,垂足为 F,线段 DF 与图中的哪一条线段相等?先将猜想出的结论填写在下面的横线上,今后再加以证明.即 DF=________ .(写出一条线段即可)19.如图,四边形ABCD 中,∠ ABC= ∠ ADC=90 °, M 、N 分别是 AC 、BD? 的中点,那么MN ⊥ BD 建立吗?试说明原因.20.( 2006·江苏淮安)如图,AB=CD=ED , AD=EB , BE ⊥ DE,垂足为E.(1)求证:△ ABD ≌△ EDB;( 2)只要增加一个条件,即_________,可使四边形ABCD 为矩形,加以证明.21.如图,在Y ABCD 的纸片中, AC ⊥AB , AC 与 BD 订交于点O,将△ ABC 沿对角线AC 翻转 180°,获取△ AB ′ C.( 1)求证:以 A ,C, D, B′为极点的四边形是矩形.( 2)若四边形ABCD 的面积 S=12cm 2,求翻转后纸片重叠部分的面积,即S△ACE.22.( 2006·南宁)如图 a 中的矩形ABCD ,沿对角线AC 剪开,再把△ ABC? 沿着 AD 方向平行搬动,获取图b.在图 b 中,△ADC ≌△ C′ BA ,AC ∥ A ′C′, A ′ B?∥ DC .?除△ DAC 与△ C′ BA ′外,指出有哪几对全等的三角形(不能够增加协助线和字母)?选择其中一对加以证明.( a)(b)23.以以以下列图,以△ABC 的三边在BC 的同侧分别作三个等边三角形,即:△ABD ,△ BCE,△ ACF ,回答以下问题:(1)四边形ADEF 是什么四边形?(2)当△ ABC 知足什么条件时,四边形ADEF 是矩形?(3)当△ ABC 知足什么条件时,以A, D, E, F 为极点的四边形不存在?参照答案1.D 2.D 3.C 4.D 5.C 6.C7. A 点拨: S△ABC =1×8×6=24 ,又 E、 F 是 AC 上的三均分点,21∴S△BEF =S△ABC =8 .38. B点拨:折叠中存在图形的对称形, B ′ M 与 C′ M 在同素来线上,∠EMB ′= 1∠ BMB ′,∠ FMB ′ =1∠ CMC ′,∠ EMF= ∠ EMB ′+∠ FMB ′22=1(∠ BMB ′ +∠ CMC ′) =90 °.29. C点拨: BD为对角线,P 为对角线上的点,则由题意获取面积相等的三角形:S△EPD=S△HPD,S△GBP =S△FPB.面积相等的矩形:S 矩形AGPE =S 矩形CHPF,由上述结论进行组合又获取两对面积相等的矩形和两对面积相等的直角梯形,共 5 对.10. C点拨:设小矩形宽为x,长为y.则大矩形长为5x 或2y,宽为x+y ,依题意有x+y+5x=68=34, 5x=2y ,解得x=4 , y=10 ,则大矩形长为20,宽为14,2所以大矩形面积为280.11. 28cm 12.10 7 13. 35°14. 90°45°15. AC ⊥BD答案不唯一.16. AC=12cm17.证明:∵四边形ABCD 是平行四边形.∴AB=CD .∵AM=DM , MB=MC ,∴△ ABM ≌△ DCM ,∴∠ A=∠D.∵AB ∥CD,∴∠ A+ ∠ D=180 °.∴∠ A=90 °.∴Y ABCD是矩形.18. AB (或 CD )证明:∵四边形ABCD 是矩形,∴∠B=90 °,又 DF⊥ AE ,∴∠ AFD=?90 °,∴∠ B=∠ AFD . AD ∥ BC ,∴∠ AEB= ∠DAF .∵AE=AD ,∴△ ABE ≌△ DFA .∴ AB=DF .19.点拨:连结BM 、 DM ,则 BM=DM ,又因为BN=ND ,所以 MN ⊥ BD .20.解:( 1)由“ SSS”可推出:△ ABD ≌△ EDB(2)增加 AB ∥CD 或 AD=BC 或 BE=EC 或∠ A= ∠ADC 或∠ ADC=90 °或∠ A= ∠ C 或∠ C=90°或∠ ABD= ∠ BDC 或∠ A= ∠ ABC 或∠ ADB= ∠ DBC或∠ ABC=90 °等.证明:∵ AB ∥ CD,又 AB=CD ,∴四边形 ABCD 为平行四边形,又△ABD ≌△ EDB ,∴∠ A= ∠ E=90°,∴四边形 ABCD 为矩形.21.( 1)证明:∵四边形ABCD 是平行四边形.∴AB // CD .∵△ AB ′ C 是由△ ABC 翻折获取的, AB ⊥ AC ,∴A B=AB ′,点 A 、B 、 B′在同一条直线上.∴A B ′ CD,∴四边形 ACDB ′是平行四边形.∵B ′ C=BC=AD .∴四边形 ACDB ′是矩形(2)解:由四边形 ACDB ′是矩形,得 AE=DE .∵S Y ABCD =12cm 2,∴S△ACD =6cm 2,∵△ AEC 和△ EDC 能够看作是等底等高的三角形.1∴S△AEC =S△ACD =3cm 2.222.有两对全等三角形,分别为:△AA ′ E≌△ C′ CF 和△ EBC ≌△ FDA ′,证明略.23.解:( 1)四边形ADEF 是平行四边形,△ABD 、△ BCE、△ ACF 都是等边三角形,故易证:△ DBE ≌△ ABC ≌△ FEC,可推出DE=FA , DA=FE ,∴四边形ADEF 为平行四边形(2)若四边形 ADEF 为矩形,∠ ADE=90 °,∴∠ BDE=90 ° +60 °=150°,由△ BDE ≌△ BAC ,得∠ BAC= ∠ BDE=150 °,∴当△ ABC 知足∠ BAC=150 °时,四边形 ADEF 是矩形(3)由△ BDE ≌△ BAC 得∠ BDE= ∠ BAC ,∴∠ BAC= ∠ BDE=60 ° +∠ ADE ,∴当∠ ADE=?0 °时,以 A , D, E,F 为极点的四边形不存在,此时∠BAC=60 °。
初二矩形性质及判定练习题

初二矩形性质及判定练习题
1. 矩形的定义
矩形是一个拥有四个直角的四边形。
它的特点是相邻的边相互垂直,所有的内角都是直角。
2. 矩形的性质
- 对角线相等:矩形的两条对角线相等,即AC = BD。
- 边相等:矩形的相对边相等,即AB = CD,BC = AD。
- 对角线互相平分:矩形的两条对角线都是互相平分对方的。
换句话说,AC平分BD,BD平分AC。
- 对角线垂直:矩形的两条对角线互相垂直,即∠ACD =
∠BAC = 90°,∠BCD = ∠ABD = 90°。
3. 判定矩形的条件
要判定一个四边形是否是矩形,需要满足以下条件之一:
- 四个内角都是直角。
- 对角线相等且互相平分对方。
- 两对相对边相等且平行。
4. 练题
1. 判断下列四边形是否是矩形:
- 一个有两对相对边分别相等且平行的四边形。
对角线不相等。
- 一个拥有四个直角的四边形。
对角线相等。
- 一个有两个内角不是直角的四边形。
对角线垂直且互相平分。
答案:
- 不是矩形。
- 是矩形。
- 不是矩形。
2. 画出一个矩形,标出其对角线和内角。
答案:
请自行练画图,标出对角线(AC和BD)和内角(如∠BAC
和∠BCD等)。
5. 总结
矩形是一个拥有四个直角的四边形,具有对角线相等且互相平
分对方、边相等和对角线垂直等性质。
要判定一个四边形是否是矩
形,可以根据四个内角是否都是直角、对角线的情况以及边的情况进行判断。
浙教版八年级数学初二下册:矩形习题精选(含答案)
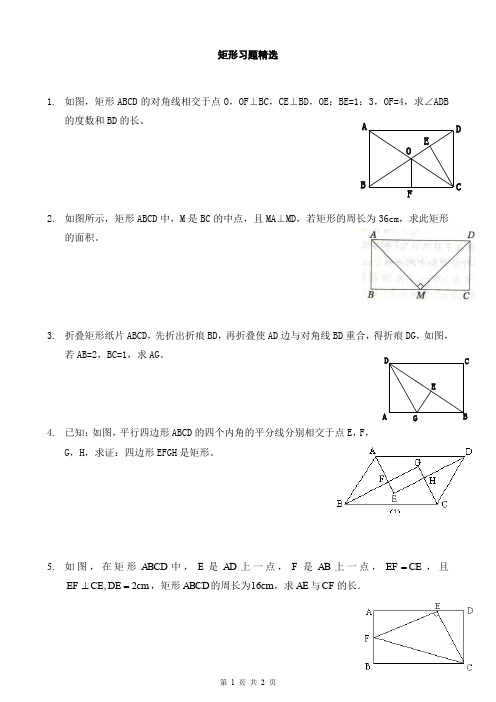
矩形习题精选1. 如图,矩形ABCD 的对角线相交于点O ,OF ⊥BC ,CE ⊥BD ,OE :BE=1:3,OF=4,求∠ADB的度数和BD 的长。
2. 如图所示,矩形ABCD 中,M 是BC 的中点,且MA ⊥MD ,若矩形的周长为36cm ,求此矩形的面积。
3. 折叠矩形纸片ABCD ,先折出折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DG ,如图,若AB=2,BC=1,求AG 。
4. 已知:如图,平行四边形ABCD 的四个内角的平分线分别相交于点E ,F ,G ,H ,求证:四边形EFGH 是矩形。
5. 如图,在矩形ABCD 中,E 是AD 上一点,F 是AB 上一点,EF CE =,且,2EF CE DE cm ⊥=,矩形ABCD 的周长为16cm ,求AE 与CF 的长.OFEDCBAGEDCBA6.已知:如图,在矩形ABCD中,E、F分别是边BC、AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.7.已知:如图所示,ABCD为菱形,通过它的对角线的交点O作AB、BC的垂线,与AB、BC,CD,DA分别相交于点E、F、G、H,求证:四边形EFGH为矩形。
参考答案1.30°,162.723.(5^1/2—1)/24.因为BG. CG AE DE 分别为四个角的角平分线,所以∠GBC+∠GCB=90°所以∠G=90°同理,可证得∠E ∠GFE ∠GHE 都为90°所以四边形FGHE为矩形5.3 √266.提示:证明△FBE和△ECD全等(ASA)于是BE=CD=BA7.△ABO △ADO △BCO △DCO 都为等全等的三角形,易证得OE=OH=OF=OD所以,∴四边形EFGH为平行四边形EG=HF故EFGH为矩形。
人教版数学八年级下册:《矩形》练习卷(含答案)
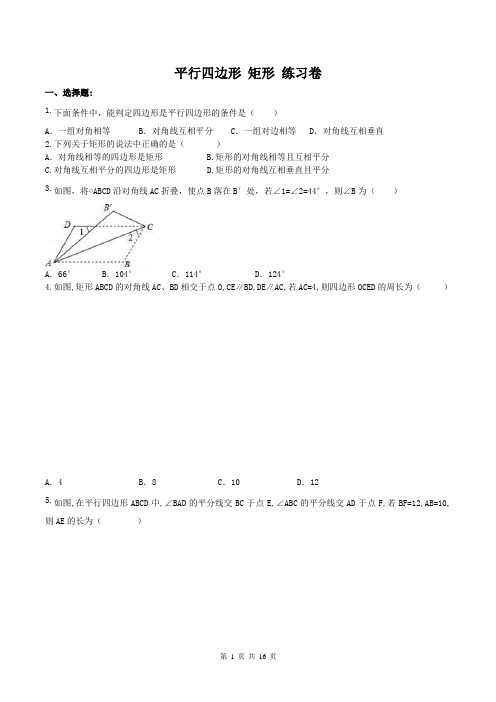
平行四边形矩形练习卷一、选择题:1.下面条件中,能判定四边形是平行四边形的条件是()A.一组对角相等B.对角线互相平分 C.一组对边相等 D.对角线互相垂直2.下列关于矩形的说法中正确的是()A.对角线相等的四边形是矩形 B.矩形的对角线相等且互相平分C.对角线互相平分的四边形是矩形D.矩形的对角线互相垂直且平分3.如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为()A.66° B.104° C.114° D.124°4.如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形OCED的周长为()A.4 B.8 C.10 D.125.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为()A.13 B.14 C.15 D.166.如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若□ABCD的周长为48,DE=5,DF=10,则□ABCD的面积等于( )A.87.5 B.80 C.75 D.72.57.下列命题中,假命题是()A.有一组对角是直角且一组对边平行的四边形是矩形B.有一组对角是直角且一组对边相等的四边形是矩形C.有两个内角是直角且一组对边平行的四边形是矩形D.有两个内角是直角且一组对边相等的四边形是矩形8.如图,P是矩形ABCD的对角线AC的中点,E是AD的中点.若AB=6,AD=8,则四边形ABPE的周长为()A.14 B.16 C.17 D.189.如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是()A.△AFD≌△DCE B.AF=ADC.AB=AFD.BE=AD﹣DF10.如图,在矩形ABCD中,AB=8.将矩形的一角折叠,使点B落在边AD上的B´点处,若AB/=4,则折痕EF 的长度为()A.8 B.C.D.1011.如图,平行四边形ABCD绕点A逆时针旋转300,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=()A.155°B.170°C.105°D.145°12.如图,已知矩形ABCD中,AB=3cm,AD=9cm,将此矩形折叠,使点D与点B重合,折痕为EF,则△ABE的面积为()A.6cm2B.8cm2C.10cm2D.12cm2二、填空题:13.如图,在矩形ABCD中,对角线AC、BD相交于点O,若DF⊥AC,∠ADF:∠FDC=3:2,则∠BDF= .14.如图,在四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别在边AB,BC上,点E,F分别为MN,DN的中点,连接EF,则EF长度的最大值为.15.如图,▱ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为.16.矩形ABCD中,AB=5,BC=4,将矩形折叠,使得点B落在线段CD的点F处,则线段BE的长为.17.如图,四边形OABC为矩形,点A,C分别在x轴和y轴上,连接AC,点B的坐标为(4,3),∠CAO的平分线与y轴相交于点D,则点D的坐标为.18.如图,△ABC中,AB=12,AC=8,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为.三、解答题:19.如图,已知在▱ABCD中,E、F是对角线BD上的两点,且BF=DE.求证:AE=CF.20.如图,已知把长方形纸片ABCD沿EF折叠后,点D与点B重合,点C落在点C′的位置上,若∠1=60°,AE=2.(1)求∠2,∠3的度数.(2)求长方形ABCD的纸片的面积S.21.如图,△ABC和△BEF都是等边三角形,点D在BC边上,点F在AB边上,且∠EAD=60°,连接ED、CF.(1)求证:△ABE≌△ACD;(2)求证:四边形EFCD是平行四边形.22.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.(1)求证:OE=OF;(2)若CE=12,CF=5,求OC的长;(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.参考答案1.B2.B.3.C4.B5.D6.B7.C.8.D9.B10.C11.A12.A13.答案为:18°14.答案为:3.15.解:分两种情况:(1)①当∠BPC=90°时,作AM⊥BC于M,如图1所示,∵∠B=60°,∴∠BAM=30°,∴BM=AB=1,∴AM=BM=,CM=BC﹣BM=4﹣1=3,∴AC==2,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∴当点P与A重合时,∠BPC=∠BAC=90°,∴BP=BA=2;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,BP===2;(2)当∠BCP=90°时,如图3所示:则CP=AM=,∴BP==;综上所述:当△PBC为直角三角形时,BP的长为 2或2或.16.答案为:2.5.17.答案为:(0,).18.答案为:2;19.证明:连接AC交BD于点O,连接AF、CE∵▱ABCD∴OA=OC,OB=OD ∵OF=BF﹣OB,OE=DE﹣OD,BF=DE∴OE=OF ∵OA=OC,OE=OF ∴四边形AECF是平行四边形∴AE=CF20.21.证明:(1)∵△ABC和△BEF都是等边三角形,∴AB=AC,∠EBF=∠ACB=∠BAC=60°,∵∠EAD=60°,∴∠EAD=∠BAC,∴∠EAB=∠CAD,在△ABE和△ACD中,∠EBA=∠ACB,AB=AC,∠EAB=∠DAC,∴△ABE≌△ACD.(2)由(1)得△ABE≌△ACD,∴BE=CD,∵△BEF、△ABC是等边三角形,∴BE=EF,∴∠EFB=∠ABC=60°,∴EF∥CD,∴BE=EF=CD,∴EF=CD,且EF∥CD,∴四边形EFCD是平行四边形.22.(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,∴∠2=∠5,∠4=∠6,∵MN∥BC,∴∠1=∠5,∠3=∠6,∴∠1=∠2,∠3=∠4,∴EO=CO,FO=CO,∴OE=OF;(2)解:∵∠2=∠5,∠4=∠6,∴∠2+∠4=∠5+∠6=90°,∵CE=12,CF=5,∴EF==13,∴OC=0.5EF=6.5;(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明:当O为AC的中点时,AO=CO,∵EO=FO,∴四边形AECF是平行四边形,∵∠ECF=90°,∴平行四边形AECF是矩形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O D C
A B
F
D C
①
②
F A D O
E B C A D
E O C
A D
E
O
C 矩形复习题
一、选择题
1. 如图,EF 过矩形ABCD 对角线的交点O ,且分别交AB 、CD 于 E 、F ,那么阴影部分的面积是矩形ABCD 的面积的
( )A 、51 B 、41
C 、31
D 、10
3
O
2.如图,矩形ABCD 的周长为20cm ,两条对角线相交于O 点,过点O 作AC 的垂线EF ,分别交AD BC ,于E F ,点,连结CE ,则CDE △的周长为( ) A .5cm B .8cm C .9cm D .10cm
3.(2009年长沙)如图,矩形ABCD 的两条对角线相交于点
O ,602AOB AB ∠==°,,则矩形的对角线AC 的长是( ) A .2 B .4 C . D .
4.如图,AC ;BD 是矩形ABCD 的对角线,过点D 作DE ∥AC 交
BC 的延长线于E ,则图中-与△ABC 全等的 三角形共有( )
A .1个
B .2个
C .3
D .4个
5.(2013四川南充)如图,把矩形ABCD 沿EF 翻折,点B 恰好落在AD 边的B ′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD 的面积是( )
A.12
B. 24
C. 123
D. 163
7.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( ).A 、3 B 、2 C 、3 D 、32
8. (2013湖南邵阳 )如图,点E 是矩形ABCD 的边AD 延长线上一点,且AD=DE,连接BE 交CD 于点O ,连接AO ,下列结论不正确的是( )
A.△AOB ≌△BOC
B.△BOC ≌△EOD
C.△AOD ≌△EOD
D.△AOD ≌△BOC
9.利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( ) A .73cm B .74cm
C .75cm
D .76cm
10.在矩形ABCD 中,1=AB ,AD AF 平分DAB ∠,过C 点作BD CE ⊥于E ,延长
AF 、EC 交于点H ,下列结论中:①FH AF =;②BF BO =;
③ CH CA =;④ED BE 3=,正确的( ) A .②③ B .③④ C .①②④
D .②③④
二、填空题
11.(2013年江西省)如图,矩形ABCD 中,点E 、F 分别是
AB 、
CD 的中点,连接DE 和BF ,分别取DE 、BF 的中点M 、N ,连接AM ,CN ,MN ,若AB =22,BC =23,则图中 阴影部分的面积为 .
12 如上中图,O 是矩形ABCD 的对角线AC 的中点,M 是AD 的中点,若AB=5,AD=12,矩形ABOM 的周长为
12.如上右矩形ABCD 中,AB =2,BC =3,对角线AC 的垂直平分线分别交AD ,BC 于点E 、F ,连接CE ,则CE 的长________.
13.有两个相邻的正方形,面积分别为4,16,那么阴影部分的面积是______.
14.如图,将左边的矩形绕点B 旋转一定角度后,位置如右边的矩形,则∠ABC=___ ___ .
16.在矩形ABCD 中,对角线AC ,BD 交于点O ,AE ⊥BD 于D ,OE:OD=1:2,AC=18,则A,B 的长为 。
17..矩形一个内角的平分线把矩形的一边分成3㎝和5㎝,则矩形的周长为 ㎝
18.如图,在平面直角坐标系中, 矩形OABC 的顶点A 、C 的坐 标分别为(10,0),(0,4),点
D 是OA 的中点,点P 在BC 上
运动,当△ODP 是腰长为5的等腰三角形时,点P 的坐标为 .
19.如图,在△ABC 中,∠ABC =90°,BD 为AC 的中线,过点C 作CE ⊥BD 于点E ,过点 A 作BD 的平行线,交CE 的延 长线于点F ,在AF 的延长线上 截取FG =BD ,连接BG 、DF . 若AG =13,CF =6,则四边形 BDFG 的周长为 .
三、解答题(证明题)
21.已知:如图,在矩形ABCD 中,E 、F 分别是边BC 、AB 上的点,且EF =ED ,EF ⊥ED . 求证:AE 平分∠BAD .
23.(2013•白银)如图,在△ABC 中,D 是BC 边上的一点,E 是AD 的中点,过A 点作BC 的平行线交CE 的延长线于点F ,且AF=BD ,连接BF .
(1)BD 与CD 有什么数量关系,并说明理由;
(2)当△ABC 满足什么条件时,四边形AFBD 是矩形?并说明理由.
24.已知:如图,在四边形ABCD 中,∠ABC=90°,CD ⊥AD ,AD 2+CD 2=2AB 2. (1)求证:AB=BC ;
(2)当BE ⊥AD 于E 时, 试证明:BE=AE+CD . 25.(2013•张家界)如图,△ABC 中,点O 是边AC 上一个动点,过O 作直线MN ∥BC .设MN 交∠ACB 的平分线于点E ,交∠ACB 的外角平分线于点F . (1)求证:OE=OF ;
(2)若CE=12,CF=5,求OC 的长;
(3)当点O 在边AC 上运动到什么位置时,四边形AECF 是矩形?并说明理由.
26. 在四边形ABCD 中,∠BAD=∠BCD=90 º,点M 是BD 的中点,点N 是AC 的中点,MN 与AC 的位置关系如何? 证明你的猜想。
27.如图,四边形ABCD 是矩形,∠EDC =∠CAB , ∠DEC =90°. (1)求证:AC ∥DE ;
(2)过点B 作BF ⊥AC 于点F ,连结EF , 试判断四边形BCEF 的形状,并说明理由.
28.在矩形ABCD 中,AB ﹦16㎝,AD ﹦6㎝,动点P 、Q 分别从A 、C 同时出发,点P 以每秒3㎝的速度向B 移动,一直达到B 止,点Q 以每秒2㎝的速度向D 移动.
⑴P 、Q 两点出发后多少秒时,为四边形PBCQ 的面积为36㎝ ⑵是否存在某一时刻,使PBCQ 为正方形,若存在,求出该时刻,若不存在说明理由.
29.在等边△ABC 中,点D 是BC 的中点,以AD 为边作等边△ADE,(1)求∠CAE 的度数
(2)点F 是AB 的中点,求证四边形AFCE 是矩形。
