锻锤基础的冲击疲劳损伤分析_张我华
锻压操作机冲击动力学分析

锻压操作机冲击动力学分析作者:刘德时李春会黄英来源:《科学家》2017年第17期摘要针对夹持棒状锻件的锻压操作机的冲击动力学行为进行分析。
采用LS-DYNA建立“锻压操作机-棒状锻件-锻造液压机”整体系统的三维有限元模型,对落锤碰撞冲击锻件的工况进行显式动力学模拟。
重点分析了冲击位置对操作机夹钳所受的最大冲击力的影响,为操作机结构设计提供理论依据。
關键词锻压操作机;冲击动力学;锻造压力机中图分类号 TG315 文献标识码 A 文章编号 2095-6363(2017)17-0206-02锻压操作机是锻造压力机重要的作业辅助装备,二者相互配合共同完成金属材料的塑性成型作业。
操作机通过其夹钳夹持锻件,对其进行翻转、提升、平移等操作,相对于以往天车与锻造操作机相互配合的作业组合方式,可以显著提高成型精度与速度,降低锻造生产过程中的能耗。
在正常的工况下,锻造压力机可以准确地控制其锻锤的运动速度与轨迹。
但是实际工况中,会出现液压系统损坏、故障以及人为操作失误或等情况,此时压力机的锻锤很可能失去有效控制,在自重的作用下,锻锤会出现自由落体运动,并与锻件发生碰撞冲击,所产生的巨大的冲击力通过锻件传导到夹钳,可能导致夹钳瞬间断裂破坏。
特别是在后期的锻压道次,锻件接近黑色的时候,此时锻件的硬度大,强度高,发生碰撞冲击后操作机夹钳被破坏的危险性大为提高。
操作机的冲击动力学行为在20世纪60年代初就引起了苏联学者米诺诺夫的注意,根据多年的现场观察以及经验总结,米诺诺夫认为操作机的动态响应过程严重滞后于锻锤与锻件的冲击过程,夹钳的最大受力不是发生在锻锤与锻件的接触变形期。
发生冲击后,锻锤在变形抗力的作用下离开锻件表面,操作机在自身惯性作用下继续下行,因为锻件的一端是放在锻造压力机的下砧上,因此,锻件对操作机夹钳的最大反作用力是竖直向上的。
米诺诺夫将操作机自身建立为一个单自由度振动模型,振动模型的刚度和质量分别是操作机的缓冲刚度和质量,在某个初速度下该单自由度系统进入自由振动过程,因为该振动系统中并没有考虑锻件,所以夹钳受力的方向与大小与均与冲击位置无关。
冲击实验报告

一、实验目的1、观察分析低碳钢材料在常温冲击下的破坏情况和断口形貌。
2、测定低碳钢材料的冲击韧度?k值。
3、了解冲击试验方法。
二、实验设备液晶全自动金属摆锤冲击试验机,游标卡尺。
三、实验材料本实验采用gb/t 229?1994标准规定的10mm?10mm?55mm u形缺口或v形缺口试件。
四、实验步骤及注意事项1、测量试件缺口处尺寸,测三次,取平均值,计算出横截面面积。
2、检查回零误差和能量损失:正式试验开始前在支座上不放试件的情况下“空打”一次:(1)取摆:按“取摆”键,摆锤逆时针转动;(2)退销:按“退销”键,保险销退销;(3)冲击:按“冲击”键,挂/脱摆机构动作,摆锤靠自重绕轴开始进行冲击;(4)放摆:按“放摆”键,保险销自动退销,当摆锤转至接近垂直位置时便自动停摆;(5)清零:按“清零”键,使摆锤角度值复位为零。
注意:必须在摆锤处于垂直静止状态时方可执行此动作。
第一次“空打”后显示屏上显示的空打冲击吸收功n1即为回零误差,此值经校正后应不大于此摆锤标称能量值的0.1%。
3、正式试验:按“取摆”键,摆锤逆时针转动上扬,触动限位开关后由挂摆机构挂住,保险销弹出,此时可在支座上放置试件(注意试件缺口对中并位于受拉边)。
然后顺序执行以上“取摆”、“退销”、“冲击”、“放摆”动作。
显示屏上将显示该试件的冲击吸收功和相应的冲击韧度。
4、摆锤抬起后,严禁在摆锤摆动范围内站立、行走和放置障碍物。
1n6n1,此值应不大于此摆锤标称能量值的10五、实验数据记录及结果处理篇二:冲击实验报告冲击实验报告一.实验目的1. 掌握常温下金属冲击试验方法;2. 了解冲击试验机结构、工作原理及正确使用方法。
二.实验设备jbw-300冲击试验机及20#钢试样和40cr试样。
三.实验原理:冲击试验是根据许多机器零件在工作时受到冲击载荷作用提出来的。
冲击载荷是动载荷,它在短时间内产生较大的力,在这种情况下往往对材料的组织缺陷反映更敏感。
锻造操作机钳臂结构疲劳分析的开题报告

锻造操作机钳臂结构疲劳分析的开题报告一、选题背景锻造操作机钳臂是锻造机械的主要部件之一,用于控制锻件的位置和方向,对于保证铸件的质量和形状具有非常重要的作用。
然而,由于长期使用和恶劣的工作环境,钳臂的材料会发生应力、疲劳和腐蚀等问题,容易出现裂纹和断裂,从而影响锻造的稳定性和安全性。
因此,对锻造操作机钳臂的结构进行疲劳分析是非常必要和重要的。
二、研究目的和意义本课题旨在探讨锻造操作机钳臂的结构疲劳问题,研究其疲劳寿命和破坏机理,为优化钳臂的设计和改进生产工艺提供科学依据。
同时,该研究还可为工程实践提供参考,提高锻造操作机的工作效率和质量,降低维护和修理成本,提升锻造行业的经济效益和社会效益。
三、研究内容和方法(一)研究内容1、锻造操作机钳臂的结构和工作原理;2、钳臂材料的物理和力学性质;3、钳臂的应力和疲劳分析;4、钳臂断裂和破坏机理的研究;5、钳臂寿命和可靠性的评估。
(二)研究方法1、理论分析法:通过理论分析方法,分析钳臂的载荷、应力和变形情况,推导出钳臂的疲劳寿命;2、有限元分析法:利用有限元分析软件,建立钳臂的三维完整模型及其支撑结构,并对其进行非线性动态分析,得出钳臂的应力分布、位移、应变能等参数;3、试验方法:通过制造钳臂试件,并进行弯曲、拉伸、扭矩等加载试验,获取钳臂的疲劳寿命和断裂形式,对研究结果进行验证和修正。
四、预期成果和进度安排(一)预期成果1、锻造操作机钳臂的结构和工作原理;2、钳臂材料的物理和力学性质;3、钳臂的应力和疲劳分析方法;4、钳臂断裂和破坏机理的研究;5、钳臂寿命和可靠性评估方法。
(二)进度安排1、文献调研:1个月;2、钳臂结构和材料特性分析:2个月;3、钳臂应力和疲劳分析:3个月;4、试验验证和成果总结:2个月;5、撰写论文、查重、终稿定稿:1个月。
五、预期的经济效益和社会效益(一)经济效益1、减少维护和修理成本;2、提高锻造操作机的工作效率和质量;3、优化钳臂的设计和改进生产工艺。
机械损伤与断裂分析

机械损伤与断裂分析机械损伤与断裂分析是现代工程领域中非常重要的一项研究内容。
在各种机械设备和结构的设计、制造和运行中,机械损伤与断裂问题经常发生,并对设备的安全性和可靠性产生重大影响。
因此,对机械损伤与断裂进行准确地分析、诊断和预测,对于保障设备的正常运行至关重要。
机械损伤通常分为两种类型:疲劳损伤和冲击损伤。
疲劳损伤是指在经过长时间反复加载和卸载的情况下,材料发生的可逆性损伤,主要表现为裂纹和裂缝的产生和扩展。
疲劳损伤是机械设备和结构断裂的主要原因之一,而且通常是不可避免的。
冲击损伤则是指在材料受到突然的高能撞击或外力作用时,发生的非可逆性损伤。
冲击损伤往往以断裂为主要表现形式,比如脆性断裂或塑性断裂。
在机械损伤与断裂分析中,其中一个重要的工具是有限元方法。
通过建立适当的数学模型,利用有限元法进行模拟和计算,可以对材料和结构进行力学行为的分析和预测。
有限元分析可以揭示材料和结构在不同加载条件下的应力、应变和位移分布,从而可以评估材料和结构的破坏潜力和安全性能。
这对于选择适当的材料和设计合理的结构具有重要指导意义。
此外,机械损伤与断裂分析也需要考虑材料的性能和特性。
不同的材料在力学行为和断裂性能方面存在着差异。
例如,金属材料通常具有较高的韧性和延展性,而陶瓷材料则较为脆弱。
因此,在进行机械损伤与断裂分析时,要注意选择合适的材料参数和模型。
除了有限元分析和材料性能的考虑,机械损伤与断裂分析还需要对设备和结构的负载条件进行全面的分析。
负载条件的不同会对机械设备和结构的破坏产生不同影响。
例如,动态负载和静态负载分别对材料和结构产生不同的应力和位移分布,进而影响裂纹和断裂的发生和扩展。
最后,机械损伤与断裂分析还需要注意考虑现实工程应用中的其他因素,如温度变化、湿度、腐蚀等。
这些因素可能会加速材料的损伤和断裂,因此需要在分析过程中进行综合考虑。
综上所述,机械损伤与断裂分析是一项复杂的工作,需要综合考虑材料性能、结构负载条件和其他现实因素。
复合材料的冲击和疲劳损伤

复合材料的冲击和疲劳损伤
麦武权
【期刊名称】《南昌航空工业学院学报》
【年(卷),期】1989(000)001
【总页数】11页(P46-56)
【作者】麦武权
【作者单位】无
【正文语种】中文
【中图分类】V257
【相关文献】
1.短纤维复合材料冲击后疲劳损伤及寿命预报 [J], 丁卫;王跃志
2.SMC—R50短纤维复合材料冲击后疲劳损伤探索 [J], 吴克安;关明星
3.短纤维复合材料冲击损伤后疲劳性能的实验研究 [J], 姜艳
4.含冲击损伤复合材料层合板疲劳试验研究 [J], 徐颖;温卫东;崔海坡
5.含冲击损伤的T300复合材料层压板的疲劳特性 [J], 程鹏飞; 李磊; 杨胜春; 谢佳卉; 熊华锋
因版权原因,仅展示原文概要,查看原文内容请购买。
比例损伤结构的两阶段损伤识别研究

比例损伤结构的两阶段损伤识别研究赵建华;张陵;孙清【期刊名称】《振动与冲击》【年(卷),期】2015(000)013【摘要】为了提高结构的多损伤识别效率,提出一种先利用归一化条件下的模态应变能变化进行结构损伤定位,然后再利用改进的频率变化法进行损伤定量的两阶段损伤识别方法。
该方法首先对损伤前后的单元模态应变能进行归一化处理,提出基于归一化条件下的模态应变能变化率的损伤定位指标并对结构进行准确的损伤定位识别;其次,在确定损伤位置的基础上,建立了只跟损伤单元数目相关的基于比例损伤模型的损伤定量方程,并用最小二乘技术进行损伤程度的求解。
为了验证所提方法的有效性,以一个单跨6节平面桁架结构为例进行数值模拟。
仿真结果表明,所提方法不但可以准确地识别出结构的损伤位置和程度,而且对测量噪声具有较强的鲁棒性。
【总页数】6页(P146-151)【作者】赵建华;张陵;孙清【作者单位】西安交通大学机械结构强度与振动国家重点实验室,西安 710049;西安交通大学机械结构强度与振动国家重点实验室,西安 710049;西安交通大学土木工程系,西安 710049【正文语种】中文【中图分类】TU311【相关文献】1.时变非线性结构两阶段损伤识别研究 [J], 吴思瑶2.一种两阶段结构损伤识别方法研究 [J], 肖辉;常军3.基于小波包能量谱的空间钢框架结构两阶段损伤识别与定位研究 [J], 胡卫兵;刘凌宇;乔冠东;文自刚4.基于改进鲸鱼算法和模态柔度的两阶段结构损伤识别 [J], 杨雨厚;成希豪;朱志刚;罗金;黄民水5.基于改进鲸鱼算法和模态柔度的两阶段结构损伤识别 [J], 杨雨厚;成希豪;朱志刚;罗金;黄民水因版权原因,仅展示原文概要,查看原文内容请购买。
冲击疗法对运动性疲劳后髌腱损伤的疗效研究

冲击疗法对运动性疲劳后髌腱损伤的疗效研究作者:刘仰斌张志花周建荣李启华来源:《科技视界》2016年第25期【摘要】目的:研究冲击疗法对髌腱损伤的治疗效果,为髌腱末端病的临床治疗提供依据。
方法:选取运动性疲劳后髌腱末端损伤患者100例,随机分为观察组与对照组各50例。
两组均在按摩、针灸的基础治疗上采用不同的治疗方案。
对照组采取保护架固定及离子电渗透疗法,观察组采取冲击疗法。
观察两组在治疗前及治疗1、3、6、12个月的VAS疼痛评分、VISA评分及角色和莫兹利评分,对比两组治疗的有效率。
结果:两组在治疗1、3、6、12个月的评分与治疗前相比,差异有统计学意义(P【关键词】冲击疗法;运动性疲劳;髌腱损伤;疗效运动性疲劳是机体在高强度或长时间运动后,导致骨骼肌细胞损伤而连续累积引起的一系列生理功能紊乱或病理状态,其发病机理及病因复杂。
研究表明,超强度长时间的运动极易导致骨骼肌细胞损伤甚至死亡,从而引起相应组织或器官的损伤[1]。
在体育运动中,由于运动性疲劳,常常致运动员诱发肌腱炎、腱鞘炎及肌腱撕裂,因此运动性疲劳被众多学者认为是引起肌腱、韧带损伤的重要因素之一,其严重影响运动员的日常训练及比赛,甚至导致运动员无法在一段时间内进行运动锻炼[2]。
冲击疗法最早出现于1985年,其主要对运动性疲劳后髌腱末端损伤有较好的治疗效果,随着医学技术的进步,在临床治疗中得到了广泛的应用。
在发达国家中,冲击疗法成为治疗运动员髌腱末端损伤的重要方法之一,但在我国相关研究较少。
为此,本文针对冲击疗法对运动性疲劳后髌腱损伤的治疗效果报道如下。
1 资料与方法1.1 一般资料选取2014年1月~2015年12月附属医院收治的运动性疲劳后髌腱末端损伤患者100例,随机分为观察组与对照组,每组50例。
两组均在按摩、针灸的基础治疗上使用不同的治疗方案,对照组采取保护架固定及离子电渗透疗法,观察组采取冲击疗法。
观察组50例中男28例,女22例;年龄20~25岁,平均(22.1±1.5)岁;病程3~6个月,平均(4.9±1.3)月。
冲击试验和疲劳强度实验
实验十三 金属材料的冲击实验一、实验目的测定和比较不同金属材料的冲击韧度,并观察破坏情况。
二、实验设备1.JB—30A 冲击试验机 2.游标卡尺 三、实验概述1.金属材料在动载荷作用下与静荷作用下所表现的性能是不同的。
在静荷下表现良好塑性的材料,在动荷下可以呈现出脆性。
因此,承受动荷作用的材料需进行冲击实验,以测定其动荷力学性能。
工程上常用冲击弯曲实验来检查产品质量,揭露在静荷实验时不能揭露的内部缺陷对力学性能的影响,以及用来揭示材料在某些条件下(如低温等)具有脆性倾向的可能性。
2.试件抵抗冲击破坏的能力通常以冲击韧度αK 表示:AE a K =(N — m/)2mm 式中,E — 冲断标准试件所消耗的能量。
A — 试件切槽削弱处之最小横截面积。
冲击韧度αK 是反映材料抵抗冲击载荷的综合性能指标,它随着试件的绝对尺寸、缺口形状,实验温度等条件的变化而不同。
为了保证实验结果能进行比较,试件的形状,尺寸及试验条件等在有关的实验标准中均有所规定。
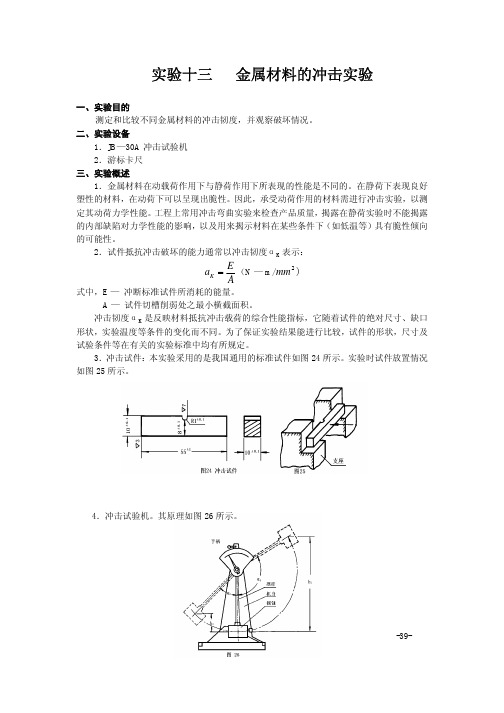
3.冲击试件:本实验采用的是我国通用的标准试件如图24所示。
实验时试件放置情况如图25所示。
-39-4.冲击试验机。
其原理如图26所示。
绕水平轴转动的摆杆下部装有摆锤,摆锤中央凹口中装有冲击刀刃。
冲击前,装好试件,将摆锤按规定抬起一角度α1,当摆锤自由下落时,将试件冲断,由于冲断试件消耗了一部分能量,因此摆锤能继续向左运动摆起一个角度α2。
所以冲断试件的能量为)(21h h Q E −=)cos (cos 12a a Ql −=此能量E 可直接在机器的度盘上读出。
四.实验步骤1.记录室温。
2.测量试件尺寸。
3.检查机器,校正零点。
检查机器运动部分和钳口座等的固结情况。
校零点用空摆实验进行。
4.安装试件。
将摆锤拉起一角度,然后将试件放入钳口座,并用样板校正位置以对准刀刃。
5.将度盘上指示副针拨至度盘左端,准备实验。
6.冲击实验。
将电器控制盒拿在手中,操作者与观察者均远离试验机一米以上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锻锤基础的冲击疲劳损伤分析X张我华,任廷鸿,邱战洪(浙江大学建筑工程学院,浙江杭州310027)摘要:用损伤力学的概念提出了一种研究由锻锤锻打引起锻锤基础系统的疲劳损伤增长和疲劳寿命估计的方法。
该方法通过定义,引入锻锤基础系统中减振垫与基础块的损伤状态寿命因子,能够估计出锻锤基础系统的减振垫和基础块的损伤疲劳寿命上、下限。
通过分析发现,长期的重复冲击载荷会引起锻锤基础系统发生疲劳微损伤积累,疲劳损伤积累的宏观损伤又引起锻锤基础的动力响应随宏观损伤发展而增大,动力响应的增大又加剧基础系统的损伤发展。
因此,为减少周围环境的振动以及保护周围环境免受锻锤冲击损伤,在锻锤基础系统设计中需考虑吸振和损伤控制。
关键词:疲劳;疲劳寿命;动态响应;损伤力学;锻锤基础系统中图分类号:T U476+.1;T G315.3文献标识码:A文章编号:1004-4523(2005)04-0506-06引 言 当结构元件受到冲击荷载时,会产生瞬时应力波并传播。
动荷载的响应会导致应力水平,特别是在损伤区域或裂缝及缺陷等周围的应力水平提高。
在损伤区域,材料的微结构由于冲击造成损伤增长将不同于非损伤区域。
由于微结构的变化,损伤结构元件的动力响应也显著不同于非损伤构件单元。
锻锤是最典型的冲击机器,并被广泛应用于机械制造业。
锻锤基础系统的疲劳寿命问题是冲击机器设计的一个重要目标之一。
目前,已有的研究大多集中于对锻锤基础系统的振动力学模型建立与参数优化、振动测试以及减振隔振措施等的研究[1~3],但同时考虑材料损伤影响的锻锤基础系统的振动及基础与减隔振材料本身的寿命预估的研究并不多见。
当考虑损伤影响问题时,需要发展新的机器基础设计方法。
本文将损伤力学概念应用于机器基础分析[4],研究了锻锤基础系统的损伤增长、损伤疲劳问题和损伤影响。
众所周知,机器基础系统在周期循环荷载下的疲劳损伤分析问题已有许多较成熟的方法,但在冲击荷载下的疲劳损伤分析问题的成熟方法尚不多见。
当锻锤基础系统受长期重复冲击荷载时,预测损伤增长对其疲劳过程的影响,无论对减少周围环境的振动以及对保护周围环境免受锻锤冲击的损伤都是很重要的。
1 锻锤基础附近土的冲击锻锤基础系统由机架、一个下落的重力锤头、砧座和基础块组成。
为了减少冲击应力在基础块和机架中的传播,在基础块和砧座之间设置了一个由橡胶、毡制品、软木塞或木料组成的弹性减振垫层。
砧座放置在减振垫上,基础块直接装置在地基土上。
其(a)机架安装在基础上(b)机架安装在砧座上图1 锻锤及其基础系统的结构形式结构形式如图1所示。
在锻锤基础的冲击动力分析过程中,冲击动力响应按集中质量阻尼系统进行数值模拟,模型简化为两个自由度的冲击振动问题,如第18卷第4期2005年12月振 动 工 程 学 报Journal of Vibratio n Eng ineeringV ol.18N o.4 Dec.2005 X收稿日期:2004-10-14;修订日期:2005-02-19基金项目:国家自然科学基金资助(50379046)和教育部博士点基金资助(A50221)图2所示。
锻锤基础系统模型的动力方程如下m 100m 2V b 1V b 2+C *1+C *2-C *2-C *2C *2V õ1V õ2+K *1+K *2-K *2-K*2K*2V 1V 2={0}(1)式中 m 1,m 2是基础块和砧座的质量;K *1是土与基础相互作用的等效刚度在损伤情况下的有效值(考虑由振动引起基础和土连接刚度的损伤8s );K *2是砧座下减振垫的有效刚度(考虑减振垫中发生损伤8p 时的有效刚度);C *1,C *2是基础系统和减振垫减振器的有效粘滞阻尼。
V 1,V 2是基础块和砧座的位移。
等效刚度K *1,K *2的数值可按弹性半空间理论求得[5]K *1=4G *r 01-v *,K *2=E *bA 2(2)式中 G *=(1-8s )2G 和v *是土的损伤剪切模量和泊松比;E *=(1-8p )2E 是减振垫的损伤杨氏模量;b 是减振垫的厚度;A 2是砧座与减振垫的接触面积;r 0是基础底面等效圆半径。
图2 锻锤基础系统的动力学分析模型锻锤基础模型自由振动的两个自然频率(X *1,X *2)可由式(1)的特征方程求得X*22,1=q 1+q 32±q 1-q 322+q 3q 212(3)式中 q 1=K *1+K *2m 1,q 2=K *2m 1,q 3=K *2m 2(4) 系统的有效粘滞阻尼比可按下式估计[6]F *1=C *1+C *2(1-A 1)22X *1(m 1+m 2a 21)F *2=C *1+C *2(1-A 2)22X *2(m 1+m 2a 22)(5) 对作用在砧座-基础-土系统上由锻锤冲击引起的自由振动,基础块和砧座的位移响应可通过损伤增长方程由初始条件求得随锻打次数变化的损伤变量8后,再由作用在砧座上的初始速度V a 来计算V 1=V a a 1-a 2e -F *1X *1t sin(X -1t )X -1-e -F *2X *2t sin(X -2t )X -2(6a)V 2=V a (a 1-a 2)e -F*1X *1t a 1sin(X -1t )X -1-e -F *2X *2t a 2sin(X -2t )X -2(6b)式中 X -i =1-F *2i X *i , (i =1,2)(7) a 2,1=1q 2q 1-q 32±(q 1-q 32)2+q 3q 212(8)V a 是砧座运动的初始速度,由锤头和砧座的冲击条件确定[5,7]。
其表达式为V a =G1+e1+w 2w 02g (w 0+p A c )hw 0(9)式中 w 0为锤头重量;w 2为砧座重量;g 为重力加速度;p 为蒸气或空气压力(kg /cm 2);A c 为活塞面积(m 2);h 为锤头落距(m );G 为下落效率;e 为弹性恢复系数。
由文献[6]知,G N =F */F (损伤阻尼比和非损伤阻尼比之比)是损伤变量8和非损伤时材料固有频率比(X 1/X 2)的函数,即G N =F *F =11-8+(1-8)X 1X 21+X 1X 2(10)由式(6)求得减振垫中的动应力解为R p =K *2(1-8p )V 1+V 2A 2+C *2V õ1+V õ2A 2(11)在冲击作用下,基础和土共同作用的动压力为p s =K *1(1-8s )V 1+C *1V õ1A 1(12)2 锻锤基础的疲劳损伤应当指出,在疲劳损伤破坏的过程中只有超过疲劳应力门槛值的那部分应力才对疲劳损伤有贡献。
通常,疲劳强度(R N )被认为是疲劳极限(R -1)的一部分,即R N =k R -1=(0.5~0.7)R -1 本文取k =0.6。
因此,在这种特定的疲劳损伤情况下,损伤增长方程可写为幂指数的形式[6]507 第4期张我华,等:锻锤基础的冲击疲劳损伤分析d 8d t=A (ûR (t )û1-8-k R -1)n 当ûR (t )û≥k (1-8)R -1其它(13)式中 k 是材料常数,可由常规的疲劳试验获得。
A >0,n >0为与载荷速率有关的材料常数。
A 和n 可用三点试测分析的实验估计出。
由于系统阻尼的影响,由冲击产生的应力幅值最初可能超过疲劳应力门槛值,随后衰减至疲劳应力门槛值以下。
因此,图3中只有阴影部分的应力区域才对疲劳损伤增长有贡献。
图3 积分域示意图为了求得第i 次锻打导致的损伤平均增量,式(13)可改写为$8i =1T∫T0A (ûR i (t )û1-8i-k R -1)n õH [ûR i (t )û-k (1-8i )R -1]d t (14)式中 H (x )为单位阶跃函数。
从图3可以看出,当t >T i 后就没有阴影面积。
T i 由应力曲线R (t )的包络线和有效疲劳应力门槛值直线ûk (1-8i )R -1û的最后一个交点求得T i =R max F *i 1X *i 1ln([k (1-8i )R -1](15) 应当指出,在每次锻打中在基础系统中引起的损伤增量可能非常微小,但长期重复锻打会引起微损伤的积累,表现为宏观损伤发展。
在重复锻打中有效疲劳应力的门槛值随着损伤增长也在发生微小的降低(材料抗疲劳能力微观劣化)。
但在一次(第i 次)锻打中,宏观损伤变量8i 的变化是非常微小的,8i 对式(13)的积分贡献可认为是一个常量,因此(1-8i )n 可从积分号中提取出来,并定义函数J (8i )如下J (8i )=1T i∫T i[ûR i (t )û-k (1-8i )R -1]n õH [ûR i (t )û-k (1-8i )R -1]d t(16)再引进一个无量纲的量,称为损伤状态寿命因子,j (8i )=J (8i )J 0(17)式中 J 0是式(16)在没有损伤情况下的初值。
损伤状态寿命因子代表了当前损伤状态和应力状态对疲劳损伤发展影响的一个无量纲因子。
这样式(14)又可改写为$8i =A J 0j (8i )(1-8i )n(18) 因为8i +1=8i +$8i ,则损伤增长的递推公式为8i +1=8i +A J 0j (8i )(1-8i )n (19) 式(19)实际上给出了材料的累积损伤。
因此,N 次锻打后的总损伤可写为A J 0∑Ni =1j (8i )(1-8i )n 。
从以上方程,可估计出疲劳寿命,即疲劳损伤失效时的打击次数。
疲劳损伤由初始损伤80开始累积,当它达到与断裂相对应的临界损伤8c 时结构疲劳破坏,这样就有∑Ni =1j (8i )(1-8i )n ≥(8c -80)AJ 0(20)应该指出,损伤状态寿命因子函数j (8i )在给定的约束条件下可求出最小值和最大值。
因此,减振垫和基础系统的疲劳寿命随损伤程度也有最小值和最大值相对应,这些最小值和最大值可根据关系式(1-8i )n ≥(1-8c )n 估计如下j s min N s ≤∑Nsi =1j s (8si )(1-8si )n s ≤N sj s max(1-8sc )n s(21a)j p min N p ≤∑Npi =1j p (8pi )(1-8pi )n p ≤N pj p max(1-8p c )n p (21b)式中 j s min ,j s max 和j p min ,j p max 分别是与基础系统和减振垫对应的损伤状态寿命因子j (8)在给定的约束条件下的的最小值和最大值。
