2018年中考数学复习第2单元方程组与不等式组第9课时一元一次不等式组及其应用检测湘教版
中考数学 精讲篇 考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

则可列方程组为
( A)
A.yx++2231xy==5500,B.xy--1223yx==5500,C.2xx++23yy==5500,D.2xx--23yy==5500,
10.(2021·成都第 26 题 8 分)为改善城市人居环境,《成都市生活垃圾 管理条例》(以下简称《条例》)于 2021 年 3 月 1 日起正式施行.某区域 原来每天需要处理生活垃圾 920 吨,刚好被 12 个 A 型和 10 个 B 型预处 置点位进行初筛、压缩等处理.已知一个 A 型点位比一个 B 型点位每天 多处理 7 吨生活垃圾. (1)求每个 B 型点位每天处理生活垃圾的吨数;
x=1,则 a+m 的值为
( C)
A.9 B.8 C.5 D.4
x=1 6.(2021·凉山州第 14 题 4 分)已知y=3,是方程 ax+y=2 的解,则 a 的值为__--11__. 7.(2020·泸州第 14 题 3 分)若 xa+1y3 与12x4y3 是同类项,则 a 的值是__33__.
3.(RJ 七下 P111 复习题 T7 改编)用 1 块 A 型钢板可制成 4 件甲种产品和 1 件乙种产品.用 1 块 B 型钢板可制成 3 件甲种产品和 2 件乙种产品;要 生产甲种产品 37 件,乙种产品 18 件,则恰好需用 A,B 两种型号的钢板 共 1 111 块.
4.(RJ 七下 P106 习题 T3 改编)一个两位数,十位数字比个位数字大 3, 若将十位数字和个位数交换位置,所得的新两位数比原两位数的13多 15, 则这个两位数是 6 633.
∵w 随 m 的增大而减小,∴费用越少,m 越大. 故方案③费用最少.
重难点 1:从实际问题中抽象一次方程(组)
我国古代数学名著《孙子算经》中记载:“今有木,不知长短.引绳
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

∴原方程组的解为y=1,将y=1 代入 2kx-3y<5 得 2×k×2-3<5,解得 k<2.
命题点 2:一次方程(组)的应用(近 3 年考查 15 次)
7.(数学文化)(2021·武汉第 7 题 3 分)我国古代数学名著《九章算术》
中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价
32 人.2 艘大船与 1 艘小船一次共可以满载游客 46 人.则 1 艘大船与 1
艘小船一次共可以满载游客的人数为
( B)
A.30
B.26
C.24
D.22
11.★(2022·武汉第 10 题 3 分)幻方是古老的数学问题,我国古代的《洛 书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要 求每一横行、 每一竖列以及两条对角线上的 3 个数之和相等,例如图① 就是一个幻方.图②是一个未完成的幻方,则 x 与 y 的和是 ( D ) A.9 B.10 C.11 D.12
14.(2020·仙桃第 12 题 3 分)篮球联赛中,每场比赛都要分出胜负,每 队胜 1 场得 2 分,负 1 场得 1 分.某队 14 场比赛得到 23 分,则该队胜 了__99__场.
15.(2020·黄冈第 19 题 6 分)为推广黄冈各县市名优农产品,市政府组 织创办了“黄冈地标馆”,一顾客在“黄冈地标馆”发现,如果购买 6 盒 羊角春牌绿茶和 4 盒九孔牌藕粉,共需 960 元,如果购买 1 盒羊角春牌 绿茶和 3 盒九孔牌藕粉共需 300 元,请问每盒羊角春牌绿茶和每盒九孔 牌藕粉分别需要多少元?
【分层分析】设购进创意文具袋 x 个,由题干信息①得购进笔记本为
((2x2+x+10)个,由题干信息②可列方程为 xx++(2(x2+x1+0)1=0)190.
中考数学复习 一元一次不等式(组)及应用

“≠”连接而成的式子.
2.解集:一般地,一个含有未知数的不等式的所有
的解,组成这个不等式的解集.
如果a>b,那么a±c>b±c
3.性质如果a>b,c>0,那么ac>bc或ac>bc
如果a>b,c<0,那么ac
①_<_bc或ac
②_<_bc
第1部分 第二单元 方程(组)与不等式(组)
二、一元一次不等式 一元一次不等式
第二单元 方程(组)与不等式(组)
课时 8 一元一次不等式(组)及应用
CONTENTS
目 录
课前自测 知识梳理 知识过关
第1部分 第二单元 方程(组)与不等式(组)
课前自测
1.已知a>b,则下列不等式中不正确的是( C )
A.4a>4b
B.a+4>b+4
C.-4a>-4b
D.a-4>b-4
第1部分 第二单元 方程(组)与不等式(组)
第1部分 第二单元 方程(组)与不等式(组)
广东中考
1.(2013广东)已知实数a,b,若a>b,则下列结论 正确的是( D )
A.a-5<b-5 B.2+a<2+b C.a3<b3 D.3a>3b
第1部分 第二单元 方程(组)与不等式(组)
2.(2018广东)不等式3x-1≥x+3的解集是( D )
(1)求商场销售A,B两种型号计算器的销售价格分别 是多少元?(利润=销售价格-进货价格)
(2)商场准备用不多于2 500元的资金购进A,B两种 型号计算器共70台,问最少需要购进A型号的计算器多 少台?
第1部分 第二单元 方程(组)与不等式(组)
解:(1)设 A 种型号计算器的销售价格是 x 元,B 种
精选-中考数学总复习第二单元方程组与不等式组第09课时一元一次不等式组及其应用课件

如果 a>b,那么 a+c③ > b+c 或 a-c④ > b-c
如果 a>b,并且 c>0,那么 ac>bc 或 > ;如果 a>b,并且 c<0,那么 ac<bc 或 <
精选中小学课件
2
课前双基巩固 考点二 一元一次不等式及其解法
不等式组的解集的求法 ② 解集
不等式组的解集情况 (假设 a<b)
������ > , ������ >
������ < , ������ <
������ > , ������ <
������ < , ������ >
x>b x<a a<x<b 无解
同大取大 同小取小 大小小大中间找 大大小小解不了
最新
精选中小学课件
7
课前双基巩固
题组二 易错题
【失分点】不等式中的等号是否取到.
[答案] C
6. [2018·雅安]
不等式组
2������-1 3
-
5������ +1 2
≤
1,
的整数解的个数是
(
)
[解析] 解2���3���-1-5������2+1≤1 得 x≥-1;解
5������-1 < 3(������ + 1)
最新
精选中小学课件
3
课前双基巩固 考点三 一元一次不等式组的概念及其解集
一元一次不等式组的概念 不等式组的解集
把几个含有同一个未知数的一次不等式联立在一起,就组成了一个一元一次不等式组
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
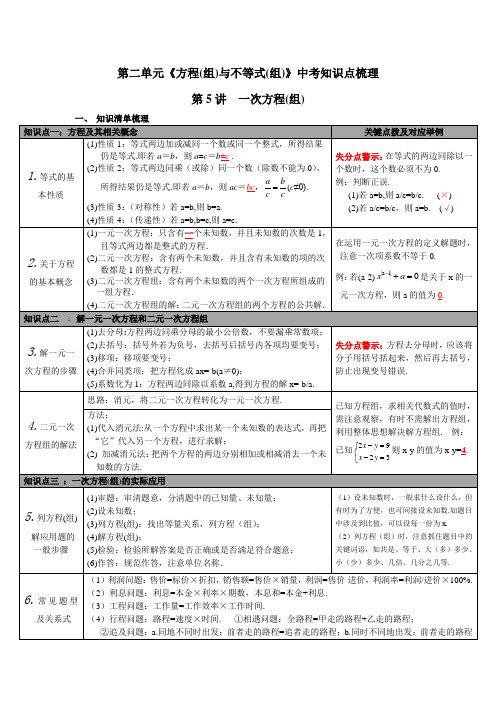
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
中考数学总复习 第二章 方程(组)与不等式(组) 第9节 一元一次不等式(组)及应用课件
8.解一元一次不等式的步骤:去分母,___去__括__号____,移项,合并同类 项,___系__数__化__为__1___(注意不等号的方向是否改变). 9.解一元一次不等式组的步骤:①先求出各个不等式的__解__集____;② 再利用数轴找它们的_公__共__部__分___;③写出不等式组的解集.
解:1≤x<4,数轴上表示略
解一元一次不等式组,先解出不等式组中的各个不等式,再根据“同 大取大,同小取小,大小、小大中间找,大大、小小找不到”准确写 出不等式组的解集.
根据不等式组的解确定字母的取值范围
x<1, 【例 4】(2015·永州)若不等式组x>m-1恰有两个整数解,则 m 的取 值范围是( A ) A.-1≤m<0 B.-1<m≤0 C.-1≤m≤0 D.-1<m<0
一元一次不等式(组)的应用
12.列不等式(组)解应用题的基本步骤为:①审题;②设未知数;③列 不等式;④解不等式;⑤检验并写出答案. 13.列不等式(组)解应用题涉及的题型常与方案设计型问题相联系,如 最大利润、最优方案等. 14.审题时应紧紧抓住“至多”、“至少”、“不大于”、“不小于 ”、“不超过”、“大于”、“小于”等关键词,注意分析题中的不 等关系,列出不等式(组),然后根据不等式(组)的解法,结合题意求解 .
_____x_>_3_3_或___x_>_-___33______________;
(2)(2015·自贡)解不等式:4x- 3 1-x>1,并把解集表示在数轴上.
解:x>4,数轴上表示略
一元一次不等式组的解法
xБайду номын сангаас1≥0, 【例 3】(2015·玉林)解不等式组x-1<34x,并把解集在数轴上表示出来.
中考数学复习 第2单元 方程(组)与不等式(组)第9课时

第9课时 一元一次不等式(组)
不等式的概 念及其解集
知识体系图 概念(不等式、解集) 不等式的性质 解不等式
一元一次 不等式
一元一次不等式的概念 一元一次不等式的解法 一元一次不等式的应用
一元一次不等式(组)
一元一次 不等式组
不等式组的概念 不等式组的解法 不等式组的应用
解集在数轴上表示
求解规律
大大取较大 小小取较小 大小小大取中间
大大小小找不到 (无解)
1.不等式:用不等号连接表示不等关系的式子叫做不等式; 2.不等式的解:类似于方程,我们把那些使不等式成立的未知数的值叫做不等式 的解; 3.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集; 4.解不等式:求不等式的解集的过程或证明不等式无解的过程,叫做解不等式.
故2不是不等式的解,所以选择D选项.
【例3】(2016年江西)将不等式3X-2<1的解集表示在数轴上正确的是(D)
【解析】此题考查了解一元一次不等式,并且将不等式的解集用数轴表示的方法.解不等 式得X<1,所以选择D选项.
【
例
4
】
(
2
0
1
6
年
达
州
)
不
等
式
组1x 3
30
x 2<x
1
的解集在数轴上表示为(A)
【解析】解该不等式组得
= 所以选择C选项,此不等式的解集为:
x 3
x>5 2Βιβλιοθήκη .-2.5<X≤3.
1.定义:含有相同未知数的若干个一元一次不等式组成的不等式组叫作一元一次 不等式组.
2.解不等式组一般先分别求出不等式组中各个不等式的解集并表示在数轴上,再 求出它们公共部分就得到不等式组的解集.
中考数学 第二章方程组与不等式组 第9讲 不等式及一元一次不等式精品课件(含11真题和12预测题)

A.a+c>b+c
B.c-a<c-b
ab C.c2>c2
D.a2>ab>b2
【解析】由于 a>b,则-a<-b,故 A、B、C 均正确;D
项中当 a=1,b=-2 时,a2<b2,故 D 不正确.
【答案】D
3.(2011中考预测题)若不等式(a+1)x>a+1的解集是x<1,则a必
须满足( )
A.a<0
4.一元一次不等式 只含有_一_个未知数,并且未知数的次数是_一__ 且系数不等于0___的不等式,叫一元一次不等式.其一般形式为ax_+__b_<__0__
或 ax+b>__0_(_a_≠_0_)___ _.
5.解不等式 求不等式 解集 的过程或证明不等式 无解 程,叫做解不等式.
的过
考点二 不等式的基本性质
(1)(2011·上海)如果 a>b,c<0,那么下列不等式成立的是( )
A.a+c>b+c
B.c-a>c-b
C.ac>bc
D.ca>cb
(2) 2010·河北 把不等式-2x<4 的解集表示在数轴上,正确的是
()
【解答】(1)A (2)A
方法总结: 1.在数轴上表示不等式的解集时,要确定边界和方向.边界:有等号 的用实心圆点,无等号的用空心圆圈.方向:大于向右,小于向左. 2.解不等式时,系数化为1时,必须明确系数的符号,当未知数的系 数为负数时,一定要改变不等号的方向.
B.a<1
C.a<-1
D.a>-1
【解析】原不等式中不等号的方向为“>”,而解集中不等号的方
向为“<”,说明系数a+1<0,解得a<-1.
【答案】C
4.(2010中考变式题)如图,a、b、c分别表示苹果、梨、桃子的质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时训练(九)一元一次不等式(组)及其应用
|夯 实 基 础| 一、选择题
1.若x>y ,则下列不等式中不一定成立的是( ) A .x +1>y +1 B .-2x<-2y C.x 2>y 2
D .x 2>y 2 2.已知点M(1-2m ,m -1)在第四象限,则m 的取值范围在数轴上表示正确的是( )
图K9-1
3.[2017·永州]模拟不等式组⎩⎪⎨⎪
⎧2x -1≤1,-12x<1的整数解的个数为( )
A .0个
B .2个
C .3个
D .无数个 4.[2016·达州]不等式组⎩⎪⎨⎪
⎧x -3≤0,
13
(x -2)<x +1的解集在数轴上表示正确的是( )
图K9-2
5.在关于x ,y 的方程组⎩
⎪⎨⎪⎧2x +y =m +7,
x +2y =8-m 中,未知数满足x≥0,y >0,那么m 的取值范围在数轴上应表示为
( )
图K9-3
6.[2016·聊城]若不等式组⎩
⎪⎨⎪
⎧x +5<5x +1,x -m >1的解集是x >1,则m 的取值范围是( )
A .m ≥1
B .m ≤1
C .m ≥0
D .m ≤0
7.对于实数x ,我们规定[x]表示不大于x 的最大整数,例如[1.2]=1,[3]=3,[-2.5]=-3.若[x +4
10]=5,
则x 的取值可以是( )
A .40
B .45
C .51
D .56
二、填空题
8.写出一个解集为x >1的一元一次不等式:________.
9.铁路部门规定旅客免费携带行李箱的长、宽、高之和不超过160 cm.某厂家生产符合该规定的行李箱,已知行李箱的高为30 cm ,长与宽的比为3∶2,则该行李箱的长的最大值为________cm.
10.[2016·邵阳]不等式组⎩
⎪⎨⎪
⎧x -1≤0,5x >3x -4的解集是________.
11.定义新运算:对于任意实数a ,b 都有:a⊕b=a(a -b)+1,其中等式右边是通常的加法、减法及乘法运算,
如:2⊕5=2×(2-5)+1=2×(-3)+1=-5,那么不等式3⊕x<13的解集为________.
三、解答题
12.[2016·连云港]解不等式1+x
3
<x -1,并将解集在数轴上表示出来.
图K9-4
13.[2017·怀化]解不等式组⎩
⎪⎨⎪⎧2x -3<x①,
3(x -1)-(x -5)≥0②,并把它的解集在数轴上表示出来.
14.[2017·日照]某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新
增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积是多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
15.[2016·湘潭]办好惠民工程,是2015年湘潭市创建全国文明城市工作重点之一,湖湘公园、杨梅洲公园、雨湖公园以及菊花塘公园四个公园免费书吧的开放,让市民朋友们毫不费劲就能阅读到自己钟爱的书籍.现免费书吧准备补充少儿读物和经典国学两个类别的书籍共20套.已知少儿读物每套100元,经典国学每套200元,若购书总费用不超过3100元,不低于2920元,且购买的经典国学如果超过10套,则经典国学全部打九折,问有哪几种购买方案?哪种购买方案费用最低?
|拓 展 提 升|
16.[2016·潍坊]运算程序如图K9-5所示,规定:从“输入一个值x”到“结果是否>95”为一次程序操作.如果程序操作进行了三次才停止,那么x 的取值范围是( )
图K9-5
A .x ≥11
B .11≤x <23
C .11<x≤23
D .x ≤23
17.自学下面材料后,解答问题.
分母中含有未知数的不等式叫分式不等式,如x -2x +1>0,2x +3
x -1<0等.那么如何求出它们的解集呢?
根据我们学过的有理数除法法则,可知两数相除,同号得正,异号得负.其字母表达式为: (1)若a>0,b>0,则a b >0;若a<0,b<0,则a
b >0.
(2)若a>0,b<0,则a b <0;若a<0,b>0,则a
b
<0.
反之:(1)若a
b >0,则⎩⎪⎨⎪⎧a>0,b>0或⎩
⎪⎨⎪⎧a<0,b<0;
(2)若a
b <0,则________或________.
根据上述规律,求不等式x -2
x +1>0的解集.
参考答案
1.D [解析] 根据不等式的性质1,不等式两边同时加上1,不等号的方向不变,A 正确;根据不等式的性质2,不等式两边同时乘负数2,不等号的方向改变,B 正确;不等式两边同时除以正数2,不等号的方向不变;当x =2,y
=-3时,x>y ,但x 2<y 2
,所以D 错误.
2.B [解析] 由点M(1-2m ,m -1)在第四象限,得1-2m >0且m -1<0,解得m <0.5.
3.C [解析] 解不等式2x -1≤1得x≤1;解不等式-1
2
x<1得x >-2,所以不等式组的解集为-2<x≤1,∴不
等式组的整数解为x =-1,0,1,共3个,故选择C.
4.A [解析] 由x -3≤0,得x≤3;由13(x -2)<x +1,得x >-52.所以,不等式组的解集为-5
2<x ≤3.
5.C [解析] 解关于x ,y 的方程组⎩⎪⎨⎪⎧2x +y =m +7,x +2y =8-m ,得⎩⎪⎨⎪⎧x =m +2,y =3-m.因为x≥0,y >0,所以⎩
⎪⎨⎪⎧m +2≥0,
3-m>0,解得-2≤m
<3,故选择C.
6.D [解析] 解不等式x +5<5x +1得x >1,解不等式x -m >1得x >m +1,由不等式组的解集为x >1可知m +1≤1,∴m ≤0.
7.C
8.x -1>0(答案不唯一)
9.78 [解析] 设该行李箱的长为3x cm ,宽为2x cm ,由题意,得5x +30≤160,解得x≤26,故行李箱的长的最大值为78 cm.
10.-2<x≤1
11.x>-1 [解析] 原不等式可化为3(3-x)+1<13,9-3x +1<13,-3x<3,x>-1,故答案为x>-1. 12.解:两边乘3得1+x <3x -3, 移项得x -3x <-3-1, 合并同类项得-2x <-4,
化系数为1,得x >2, 在数轴上表示解集:
13.解:解不等式①,得x <3.所以,不等式组的解集是-1≤x<3. 它的解集在数轴上表示如下:
14.解:(1)设原计划每年绿化面积为x 1.6x 万平方米,
根据题意,得360x -360
1.6x
=4,
解得:x =33.75,
经检验x =33.75是原分式方程的解, 则1.6×33.75=54(万平方米).
答:实际每年绿化面积为54万平方米.
(2)设平均每年绿化面积增加a 万平方米,根据题意得 54×3+2(54+a)≥360, 解得:a≥45.
答:实际平均每年绿化面积至少还要增加45万平方米.
15.解:设购买的经典国学为x 套,则少儿读物为(20-x)套,
①当购买的经典国学不超过10套时,根据题意得:⎩
⎪⎨⎪⎧200x +100(20-x )≤3100,
200x +100(20-x )≥2920,
解得:9.2≤x≤11,又∵x≤10,且x 为整数, ∴x =10,此时购买少儿读物10套. ②当购买的经典国学超过10套时,
根据题意得:⎩
⎪⎨⎪⎧200×9
10
x +100(20-x )≤3100,
200×9
10
x +100(20-x )≥2920,
解得:11.5≤x≤13.75,
又∵10<x≤20,且x 为整数, ∴x 可以取12,13,
综合①、②得出:有三种购买方案:
方案一:购买经典国学10套,少儿读物10套,共需费用:10×200+10×100=3000(元);
方案二:购买经典国学12套,少儿读物8套,共需费用:12×200×9
10+8×100=2960(元);
方案三:购买经典国学13套,少儿读物7套,共需费用:13×200×9
10
+7×100=3040(元).
∴选择方案二费用最低,即购买经典国学12套,少儿读物8套费用最低.
16.C [解析] 根据运算程序,前两次运算结果小于等于95,第三次运算结果大于95,列出不等式组:⎩⎪⎨⎪
⎧2x +1≤95,①
2(2x +1)+1≤95,②
2[2(2x +1)+1]+1>95,③
解不等式①,得x≤47,解不等式②,得x≤23,解不等式③,得x >11,所以x 的取值范围是11<x≤23.
17.解:⎩⎪⎨⎪⎧a>0,b<0 ⎩
⎪⎨⎪⎧a<0,b>0 由题中规律可知,不等式x -2
x +1>0转化为⎩⎪⎨⎪⎧x -2>0,x +1>0或⎩⎪⎨⎪⎧x -2<0,x +1<0,
所以x>2或x<-1.。
