数学:第二章二次函数单元测试(浙教版九年级上)
新浙教版九年级数学上册《二次函数》测试卷(附答案)

新浙教版九年级数学上册《二次函数》测试卷(附答案)二次函数测试卷(100分,90分钟)一、选择题(每题3分,共30分)1.下列函数中,y是x的二次函数的是()A。
y = (2x-1) - (2x+1)(2x-1)B。
y = x-1C。
y = 1/2D。
x-2y-2 = 2x-12.(2012,德阳,一题多解)在同一平面直角坐标系内,将函数图象沿x轴方向向右平移2个单位后再沿y轴向下平移1个单位,得到图象的顶点坐标是()A。
(-1,1)B。
(1,-2)C。
(2,-2)D。
(1,-1)3.(2012,滨州)抛物线y = -3x^2 - x + 4与坐标轴的交点个数是()A。
3B。
2C。
1D。
04.(2012,桂林)如图1,把抛物线y = x^2沿直线y=x平移2个单位后,其顶点在直线上的点A处,则平移后的抛物线表达式是()A。
y = (x+1)^2 - 1B。
y = (x+1)^2 + 1C。
y = (x-1)^2 + 1D。
y = (x-1)^2 - 15.设二次函数y = x^2 + bx + c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是()A。
c=3B。
c≥3C。
1≤c≤3D。
c≤36.(2013,菏泽)已知b<0,二次函数y = ax^2 + bx + a^2-1的图象为如图2所示的四个图象之一.试根据图象分析,a的值应等于()A。
-2B。
-1C。
1D。
27.(2013,内江)若抛物线y = x^2 - 2x + c与y轴的交点坐标为(0,-3),则下列说法不正确的是()A。
抛物线开口向上B。
抛物线的对称轴是直线x=1C。
当x=1时,y的最大值为-4D。
抛物线与x轴的交点坐标为(-1,0),(3,0)8.(2013,日照)如图3,已知抛物线y = -x^2 + 4x和直线y = 2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2取y1,y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有()A。
浙教版数学九年级上册二次函数单元检测二(无答案)

25.如图,抛物线y= x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
(1)求抛物线的解析式及顶点D的坐标;
18.二次函数y=a(x+k)2+k,当k取不同的实数值时,图象顶点所在直线的函数表达式是___________.
19.如图,抛物线y=ax2+bx+c的对称轴是x=-1.且过点( ,0),有下列结论:①abc>0;②a-2b+4c=0;③25a-10b+4c=0;④3b+2c>0;⑤a-b≥m(am-b);其中所有正确的结论是
12.已知抛物线顶点坐标为(4,-1),且经过点(0,3),则该抛物线的解析式为______________.
13.若抛物线y=x2-bx+9的顶点在x轴上,则b的值为________.
14.二次函数y=x2+x-6的图象与坐标轴的交点坐标为____________________________________.
15.已知点A(4,y1),B( ,y2),C(-2,y3)都在二次函数y=(x-2)2-1的图象上,则y1、y2、y3
的大小关系是_______________.
16.用一根长为32cm的铁丝围成一个矩形,则围成矩形面积的最大值是____________cm2.
17.二次函数y=(2x+1)2-2的图象的对称轴是___________________.
21.已知二次函数y=ax2+bx+c的图象与x轴交点坐标为(-1,0)、(3,0)且过(1,-2).求该二次函
数的表达式;
22.已知一次函数y=-2x+c与二次函数y=ax2+bx-4的图象都经过点A(1,-1),二次函数的对称轴
最新浙教版九年级数学上册《二次函数》单元测试题及解析-精编试题.docx

第1章自我评价一、选择题(每小题2分,共20分)1.若函数y =(2-m)xm 2-3是二次函数,且图象的开口向上,则m 的值为(B)A.± 5B.- 5C. 5D.02.若抛物线y =x 2+2x +m -1与x 轴有两个不同的交点,则m 的取值范围是(A) A. m <2 B. m >2 C. 0<m ≤2 D. m <-23.在二次函数y =x 2-2x -3中,当0≤x ≤3时,y 的最大值和最小值分别是(A) A. 0,-4 B. 0,-3 C. -3,-4 D. 0,04.对于二次函数y =-14x 2+x -4,下列说法正确的是(B)A. 当x >0时,y 随x 的增大而增大B. 当x =2时,y 有最大值-3C. 图象的顶点坐标为(-2,-7)D. 图象与x 轴有两个交点(第5题)5.已知抛物线y=x2+bx+c的部分图象如图所示.若y<0,则x的取值范围是(B)A. -1<x<4B. -1<x<3C. x<-1或x>4D. x<-1或x>36.在平面直角坐标系中,某二次函数图象的顶点坐标为(2,-1),此函数图象与x 轴相交于P,Q两点,且PQ=6.若此函数图象通过(1,a),(3,b),(-1,c),(-3,d)四点,则a,b,c,d中为正数的是(D)A. aB. bC. cD. d(第7题)7.已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=(D)A. a +bB. a -2bC. a -bD. 3a【解】 观察图象可知: 图象过原点,c =0; 抛物线开口向上,a >0;抛物线的对称轴0<-b2a<1,-2a <b <0.∴|a -b +c|=a -b ,|2a +b|=2a +b , ∴|a -b +c|+|2a +b|=a -b +2a +b =3a.8.已知抛物线y =x 2+bx +c(其中b ,c 是常数)过点A(2,6),且抛物线的对称轴与线段y =0(1≤x ≤3)有交点,则c 的值不可能是(A)A. 4B. 6C. 8D. 10【解】 ∵抛物线y =x 2+bx +c(其中b ,c 是常数)过点A(2,6),且抛物线的对称轴与线段y =0(1≤x ≤3)有交点,∴⎩⎪⎨⎪⎧4+2b +c =6,1≤-b 2×1≤3,解得6≤c ≤14.9.定义:若点P(a ,b)在函数y =1x的图象上,将以a 为二次项系数,b 为一次项系数构造的二次函数y =ax 2+bx 称为函数y =1x 的一个“派生函数”.例如:点⎝ ⎛⎭⎪⎪⎫2,12在函数y =1x 的图象上,则函数y =2x 2+12x 称为函数y =1x 的一个“派生函数”.现给出以下两个命题:(1)存在函数y =1x的一个“派生函数”,其图象的对称轴在y 轴的右侧.(2)函数y =1x的所有“派生函数”的图象都经过同一点.下列判断正确的是(C)A. 命题(1)与命题(2)都是真命题B. 命题(1)与命题(2)都是假命题C. 命题(1)是假命题,命题(2)是真命题D. 命题(1)是真命题,命题(2)是假命题 【解】 (1)∵点P(a ,b)在y =1x上,∴a ,b 同号,∴-b2a<0,即对称轴在y 轴的左侧,∴存在函数y =1x的一个“派生函数”,其图象的对称轴在y 轴的右侧是假命题.(2)∵函数y =1x的所有“派生函数”为y =ax 2+bx ,∴当x =0时,y =0,∴所有“派生函数”都经过原点,∴函数y =1x的所有“派生函数”的图象都经过同一点是真命题.10.已知二次函数y =x 2+bx +c ,当x ≤1时,总有y ≥0;当1≤x ≤3时,总有y ≤0,则c 的取值范围是(B)A. c =3B. c ≥3C. 1≤c ≤3D. c ≤3(第10题解)【解】 ∵当x ≤1时,y ≥0;当1≤x ≤3时,y ≤0, ∴当x =1时,y =0.设y =x 2+bx +c =(x -1)(x -c). ∵当1≤x ≤3时,y ≤0, ∴得草图如解图. ∴c ≥3.二、填空题(每小题3分,共30分)11.抛物线y =(x +1)2-2的顶点坐标是(-1,-2).12.写出一个二次函数的表达式,使其图象的顶点恰好在直线y =x +2上,且开口向下,则这个二次函数的表达式可写为y =-x 2+2(答案不唯一).13.已知二次函数y =ax 2+bx +c 的图象如图所示,有下列结论:①abc>0;②a-b +c<0;③2a =b ;④4a +2b +c>0;⑤若点(-2,y 1)和⎝ ⎛⎭⎪⎪⎫-13,y 2在该图象上,则y 1>y 2.其中正确的结论是②④(填序号).(第13题)14.如图,已知点D(0,1),抛物线y =-x 2+2x +3与y 轴交于点C ,P 是抛物线上的动点.若△PCD 是以CD 为底的等腰三角形,则点P 的坐标为(1±2,2).(第14题)15.如图是二次函数y 1=ax 2+bx +c 和一次函数y 2=mx +n 的图象,观察图象,写出当y 2≥y 1时x 的取值范围:-2≤x ≤1.(第15题)16.抛物线y =ax 2+bx +c 上部分点的横坐标x ,纵坐标y 的对应值如下表: x ... -2 -1 0 1 2 ... y 046 6 4 …从上表可知,下列说法中,正确的是①③④(填序号).①此抛物线与x 轴的一个交点为(3,0);②此函数的最大值为6;③此抛物线的对称轴是直线x =12;④在对称轴左侧,y 随x 的增大而增大.17.若将二次函数y =x 2+kx -12的图象向右平移4个单位后经过原点,则k 的值是__1__.(第18题)18.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连结BD ,则对角线BD 的最小值为__1__.19.已知二次函数y =ax 2+bx +c(a ≠0)和正比例函数y =23x 的图象如图所示,则方程ax 2+⎝ ⎛⎭⎪⎪⎫b -23x +c =0(a ≠0)的两根之和__>__0(填“>”“<”或“=”).(第19题)【解】 方程ax 2+⎝ ⎛⎭⎪⎪⎫b -23x +c =0可化为ax 2+bx +c =23x ,故该方程的两根即为y =ax 2+bx +c与y =23x 的图象的交点的横坐标,由图象可知两根之和大于0.20.已知关于x 的一元二次方程ax 2-3x -1=0的两个不相等的实数根都在-1和0之间(不包括-1和0),则a 的取值范围是-94<a<-2.【解】 ∵关于x 的一元二次方程ax 2-3x -1=0有两个不相等的实数根, ∴Δ=(-3)2-4·a ·(-1)>0, 解得a>-94.设二次函数y =ax 2-3x -1,当x =0时,y =-1.∵一元二次方程ax 2-3x -1=0的两个实数根都在-1和0之间, ∴易得a<0,且当x =-1时,y<0.∴a ·(-1)2-3×(-1)-1<0,解得a<-2. 综上所述,a 的取值范围是-94<a<-2.三、解答题(共50分)21.(8分)已知以x 为自变量的二次函数y =-x 2+2x +m -1的图象与y 轴交于点(0,3).(1)求出m 的值并画出这个抛物线.(2)求出它与x 轴的交点坐标和抛物线的顶点坐标. (3)当x 取什么值时,抛物线在x 轴上方? (4)当x 取什么值时,y 随x 的增大而减小?(第21题解)【解】 (1)∵抛物线y =-x 2+2x +m -1与y 轴交于点(0,3),∴m -1=3, ∴m =4.图象如解图所示.(2)令y =0,则-x 2+2x +3=0,解得x 1=-1,x 2=3. ∴与x 轴的交点坐标为(-1,0),(3,0). ∵y =-x 2+2x +3=-(x -1)2+4,∴顶点坐标为(1,4).(3)当-1<x<3时,抛物线在x轴上方.(4)当x≥1时,y随x的增大而减小.(第22题)22.(6分)如图,正方形ABCD是一张边长为12 cm的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P,Q,R三点分别在CD,AD,BC上.(1)当皮雕师傅切下△PDQ时,若DQ的长为x(cm),请用含x的式子表示此时△PDQ 的面积.(2)在(1)的条件下,当x的值为多少时,五边形PQABR的面积最大?【解】(1)设DQ=x(cm),则PD=2DQ=2x(cm),∴S△PDQ=12x·2x=x2(cm2).(2)∵PD=2x(cm),CD=12 cm,∴CR=PC=(12-2x)cm,∴S五边形PQABR=S正方形ABCD-S△PDQ-S△PCR=122-x 2-12(12-2x)2 =144-x 2-12(144-48x +4x 2) =-3(x -4)2+120,故当x =4时,五边形PQABR 的面积最大.(第23题)23.(6分)如图,正方形OABC 的边长为4,对角线OB ,AC 相交于点P ,抛物线L 经过O ,P ,A 三点,E 是正方形内的抛物线上的动点.(1)建立适当的平面直角坐标系,①直接写出O ,P ,A 三点的坐标.②求抛物线L 的函数表达式.(2)求△OAE 与△OCE 面积之和的最大值.(第23题解)【解】 (1)以O 为原点,线段OA 所在的直线为x 轴,线段OC 所在的直线为y 轴建立直角坐标系,如解图所示.①∵正方形OABC 的边长为4,对角线OB ,AC 相交于点P ,∴点O 的坐标为(0,0),点A 的坐标为(4,0),点P 的坐标为(2,2).②设抛物线L 的函数表达式为y =ax 2+bx +c.∵抛物线L 经过O ,P ,A 三点,∴⎩⎪⎨⎪⎧0=c ,0=16a +4b +c ,2=4a +2b +c ,解得⎩⎪⎨⎪⎧a =-12,b =2,c =0. ∴抛物线L 的函数表达式为y =-12x 2+2x. (2)∵E 是正方形内的抛物线上的动点,∴可设点E 的坐标为⎝ ⎛⎭⎪⎪⎫m ,-12m 2+2m (0<m <4), ∴S △OAE +S OCE =12OA ·y E +12OC ·x E =2⎝ ⎛⎭⎪⎪⎫-12m 2+2m +2m =-m 2+6m =-(m -3)2+9,∴当m =3时,△OAE 与△OCE 的面积之和最大,最大值为9.24.(8分)王大伯决定销售一批风筝,经市场调研:蝙蝠形风筝进价为10元/个,当售价为12元/个时,销售量为180个,若售价每提高1元,销售量就会减少10个.请回答以下问题:(1)求蝙蝠形风筝销售量y(个)与售价x(元/个)之间的函数表达式(12≤x≤30).(2)王大伯为了让利给顾客,并同时获得840元的利润,售价应定为多少?(3)当售价定为多少时,王大伯获得的利润最大,最大利润是多少?【解】(1)根据题意可知:y=180-10(x-12)=-10x+300(12≤x≤30).(2)设王大伯获得的利润为W,则W=(x-10)y=-10x2+400x-3000.当W=840时,-10x2+400x-3000=840,解得x1=16,x2=24.∵王大伯为了让利给顾客,∴售价应定为16元.(3)W=-10x2+400x-3000=-10(x-20)2+1000,∴当x=20时,W取最大值,最大值为1000.答:当售价定为20元时,王大伯获得的利润最大,最大利润是1000元.25.(10分)如图,在平面直角坐标系xOy中,A,B,C分别为坐标轴上的三个点,且OA=1,OB=3,OC=4.(第25题)(1)求经过A ,B ,C 三点的抛物线的函数表达式.(2)在平面直角坐标系xOy 中是否存在一点P ,使得以A ,B ,C ,P 为顶点的四边形为菱形?若存在,请求出点P 的坐标;若不存在,请说明理由.(3)若M 为该抛物线上一动点,在(2)的条件下,请求出当|PM -AM|的最大值时点M 的坐标,并直接写出|PM -AM|的最大值.【解】 (1)设抛物线的函数表达式为y =ax 2+bx +c.由题意,得点A(1,0),B(0,3),C(-4,0),∴⎩⎪⎨⎪⎧a +b +c =0,c =3,16a -4b +c =0,解得⎩⎪⎨⎪⎧a =-34,b =-94,c =3. ∴经过A ,B ,C 三点的抛物线的函数表达式为y =-34x 2-94x +3.(第25题解)(2)在平面直角坐标系xOy 中存在一点P ,使得以点A ,B ,C ,P 为顶点的四边形为菱形.理由如下:∵OB =3,OC =4,OA =1,∴BC =AC =5.如解图,当点P 在点B 的右侧,且BP 平行且等于AC 时,四边形ACBP 为菱形, 此时BP =AC =5,且点P 到x 轴的距离等于OB ,∴点P 的坐标为(5,3).当点P 在第二、三象限时,以点A ,B ,C ,P 为顶点的四边形只能是平行四边形,不可能是菱形,则当点P 的坐标为(5,3)时,以点A ,B ,C ,P 为顶点的四边形为菱形.(3)设直线PA 的函数表达式为y =kx +b(k ≠0).∵点A(1,0),P(5,3),∴⎩⎪⎨⎪⎧5k +b =3,k +b =0,解得⎩⎪⎨⎪⎧k =34,b =-34,∴直线PA 的函数表达式为y =34x -34. 当点M 与点P ,A 不在同一直线上时,根据三角形的三边关系可知|PM -AM|<PA , 当点M 与点P ,A 在同一直线上时,|PM -AM|=PA ,∴当点M 与点P ,A 在同一直线上时,|PM -AM|的值最大,即M 为直线PA 与抛物线的交点,解方程组⎩⎪⎨⎪⎧y =34x -34,y =-34x 2-94x +3, 解得⎩⎪⎨⎪⎧x 1=1,y 1=0或⎩⎪⎨⎪⎧x 2=-5,y 2=-92. ∴当点M 的坐标为⎝ ⎛⎭⎪⎪⎫-5,-92时,|PM -AM|的值最大,此时|PM -AM|的最大值为5.(第26题)26.(12分)如图,在平面直角坐标系中,直线y =-2x +10与x 轴,y 轴相交于A ,B 两点,点C 的坐标是(8,4),连结AC ,BC.(1)求过O ,A ,C 三点的抛物线的函数表达式,并判断△ABC 的形状.(2)动点P 从点O 出发,沿OB 以每秒2个单位的速度向点B 运动;同时,动点Q 从点B 出发,沿BC 以每秒1个单位的速度向点C 运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t(s),当t 为何值时,PA =QA?(3)在抛物线的对称轴上是否存在点M ,使以A ,B ,M 为顶点的三角形是等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.【解】 (1)∵直线y =-2x +10与x 轴,y 轴相交于A ,B 两点,∴点A(5,0),B(0,10).∵抛物线过原点,∴可设抛物线的函数表达式为y =ax 2+bx.∵抛物线过点A(5,0),C(8,4),∴⎩⎪⎨⎪⎧25a +5b =0,64a +8b =4,解得⎩⎪⎨⎪⎧a =16,b =-56.∴抛物线的函数表达式为y =16x 2-56x. ∵点A(5,0),B(0,10),C(8,4),∴AB 2=52+102=125,BC 2=82+(10-4)2=100,AC 2=(8-5)2+42=25, ∴AC 2+BC 2=AB 2,∴△ABC 是直角三角形.(第26题解)(2)如解图,当点P ,Q 运动t(s)时,OP =2t ,CQ =10-t. 由(1)可得AC =OA =5,∠ACQ =∠AOP =90°, 又∵PA =QA ,∴Rt △AOP ≌Rt △ACQ(HL),∴OP =CQ ,∴2t =10-t ,∴t =103, 即当t =103时,PA =QA. (3)存在.∵y =16x 2-56x =16⎝ ⎛⎭⎪⎪⎫x -522-2524, ∴抛物线的对称轴为直线x =52. ∵点A(5,0),B(0,10),∴AB =5 5.设点M ⎝ ⎛⎭⎪⎪⎫52,m , ①当BM =BA 时,⎝ ⎛⎭⎪⎪⎫522+(m -10)2=125, ∴m 1=20+5 192,m 2=20-5 192, ∴点M 1⎝ ⎛⎭⎪⎪⎫52,20+5 192,M 2⎝ ⎛⎭⎪⎪⎫52,20-5 192. ②当AM =AB 时,⎝ ⎛⎭⎪⎪⎫52-52+m 2=125, ∴m 3=5 192,m 4=-5 192,∴点M 3⎝ ⎛⎭⎪⎪⎫52, 5192,M 4⎝ ⎛⎭⎪⎪⎫52,- 5 192. ③当MA =MB 时,⎝ ⎛⎭⎪⎪⎫52-52+m 2=⎝ ⎛⎭⎪⎪⎫522+(m -10)2, ∴m =5.∵此时点M 恰好是线段AB 的中点,构不成三角形,故舍去.综上所述,点M 的坐标为M 1⎝ ⎛⎭⎪⎪⎫52,20+5 192,M 2⎝ ⎛⎭⎪⎪⎫52,20-5 192,M 3⎝ ⎛⎭⎪⎪⎫52,5 192,M 4⎝ ⎛⎭⎪⎪⎫52,- 5 192.。
最新-九年级(上)数学第二章《二次函数》单元测试卷 精品

九年级(上)数学第二章《二次函数》单元测试卷班级 姓名 学号说明:1、本卷的内容是浙教版九年级第二章:二次函数; 2、本卷考试时间70分钟;3、卷面分二部分:基础题100分(第一、二、三大题),提高题20分(第四大题)。
一、细心填一填(每小题3分,共30分)1.抛物线y=x 2+6x+8与y 轴交点坐标( ) (A )(0,8) (B )(0,-8) (C )(0,6) (D )(-2,0)(-4,0)2.抛物线y= -12(x+1)2+3的顶点坐标( ) (A )(1,3) (B )(1,-3) (C )(-1,-3) (D )(-1,3)3.把抛物线y=3x 2先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是( )(A )y=3(x+3)2 -2 (B )y=3(x+2)2+2 (C )y=3(x-3)2 -2 (D )y=3(x-3)2+2 4.下列函数中,y 随x 的增大而增大的是( ) (A )xy 1-= (B )52+-=x y (C ))0(42≥-=x x y (D )1322-+=x x y 5.抛物线y=x 2-ax+a-2与坐标轴的交点个数有( ) A.3个 B.2个 C.1个 D.0个6.若直线y=ax+b(ab ≠0)不过第三象限,则抛物线bx ax y +=2的顶点所在的象限是( ) (A )一 (B )二 (C )三 (D )四7.二次函数1422+-=x x m y 有最小值-3,则m 等于( ) (A )1 (B )-1 (C )1± (D )21±8.已知二次函数y=ax 2+bx+c 的图象如图,下列结论中,正确的结论的个数有 ( ) ① a + b + c>0 ② a - b + c <0 ③ abc < 0 ④ b =2a ⑤ b >0A. 5个B. 4个 C .3个 D. 2个9.小敏在某次投篮中,球的运动路线是抛物线的一部分(如图),若命中篮圈中心,则他与篮底的距离l 是----( ) A .3.5m B .4m C .4.5m D .4.6m10.某幢建筑物,从10米高的窗口A 用水管和向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直,(如图)如果抛物线的最高点M 离墙1米,离地面403 米,则水流下落点B 离墙距离OB 是( )(A )2米 (B )3米 (C )4米 (D )5米 二、精心选一选(每小题3分,共30分)11.二次函数=2(x - 32)2+1图象的对称轴是 。
数学九年级上浙教版第2章二次函数单元测试8

第2章 二次函数 单元测试一、选择题1. 下列各式中,y 是的二次函数的是--------------------------------------( ) A. 1y x=B. 21y x =-+C. 22y x =- D. 3y x = 2. 已知二次函数的解析式为()221y x =-+,则该二次函数图象的顶点坐标是 ( ) A. (-2,1) B. (2,1) C. (2,-1) D. (1,2)3. 抛物线y=3(x-2)2+1图象上平移2个单位,再向左平移2个单位所得的解析式为 ( )A .y=3x 2+3B .y=3x 2-1C .y=3(x-4)2+3D .y=3(x-4)2-14..二次函数221y x x =-+与x 轴的交点个数是 ( ) A .0 B .1 C .2 D .3 5.二次函数y=ax 2+bx+c 的图像如图所示, 则点A(a, c)在 ( ) A. 第一象限 B. 第二象限C. 第三象限D. 第四象限6.若y =(2-m)23mx -是二次函数,且开口向上,则m 的值为 ( )A.5±B.-5C.5D.0 7.已知二次函数y=-12x 2-3x -52,设自变量的值分别为x 1,x 2,x 3,且-3<x 1<x 2<x 3, 则对应的函数值y 1,y 2,y 3的大小关系是 ( ) A.y 1>y 2>y 3 B.y 1<y 2<y 3; C.y 2>y 3>y 1 D.y 2<y 3<y 18.小敏在今年的校运会比赛中跳出了满意一跳,函数h=3.5t -4.9t 2,可以描述他跳跃时重心高度的变化.则他跳起后到重心最高时所用的时间是 ( ) A .0.71 sB .0.70sC .0.63sD .0.36s9.如图2,已知:正方形ABCD 边长为1,E 、F 、G 、H 分别为各边上的点, 且AE =BF =CG =DH , 设小正方形EFGH 的面积为,AE 为,则关于的函数图象大致是( )A B C D10.如图,在同一直角坐标系中,一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )数学试卷及试题2xy OA xyOBx yOC xyOD二、填空题11.二次函数2(2)1y x =-+的图象的对称轴为 . 12.若二次函数y =ax 2的图象经过点(-1,2),则二次函数y =ax 2的解析式是__13.请写出一个开口向下,且函数有最大值2的二次函数的解析式是 .14.抛物线y =x 2+8x -4与直线x 轴的交点坐标是______ ___. 15.平移抛物线822-+=x x y ,使它经过原点.写出平移后抛物线的一个解析 式 . 16.如图是二次函数和一次函数的图象,观察图象,写出时x 的取值范围:____ ___。
浙教版九年级上-二次函数-单元测试

浙教版九年级上-二次函数-单元测试(总4页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--《二次函数》测试卷(满分150分;完卷时间100分钟)班级 姓名 成绩一.选择题(每题4分,共48分)1. 下列各式中,y 是x 的二次函数的是 ( )A . 21xy x +=B . 220x y +-=C . 22y ax -=-D . 2210x y -+=2.在同一坐标系中,作22y x =+2、22y x =--1、212y x =的图象,则它们 ( ) A .都是关于y 轴对称 B .顶点都在原点 C .都是抛物线开口向上 D .以上都不对3.若二次函数)2(2-++=m m x mx y 的图象经过原点,则m 的值必为 ( )A . 0或2B . 0C . 2D . 无法确定4、已知点(a ,8)在抛物线y=ax 2上,则a 的值为( )A 、±2B 、±22C 、2D 、-25.把抛物线y=3x 2先向上平移2个单位,再向右平移3个单位,所得抛物线的解析式是( )(A )y=3(x+3)2 -2 (B )y=3(x+2)2+2 (C )y=3(x-3)2 -2 (D )y=3(x-3)2+26.抛物线y=x 2+6x+8与y 轴交点坐标( )(A )(0,8) (B )(0,-8) (C )(0,6) (D )(-2,0)(-4,0)7、二次函数y=x 2+4x +a 的最大值是2,则a 的值是( )A 、4B 、5C 、6D 、78.已知原点是抛物线2(1)y m x =+的最高点,则m 的范围是 ( )A . 1-<mB . 1<mC . 1->mD . 2->m9.抛物线122+-=x x y 则图象与x 轴交点为 ( )A . 二个交点B . 一个交点C . 无交点D . 不能确定 10.)0(≠+=ab b ax y 不经过第三象限,那么bx ax y +=2的图象大致为 ( )x y y y yO x O x O x O xA B C D11.对于2)3(22+-=x y 的图象下列叙述正确的是 ( )A 顶点作标为(-3,2)B 对称轴为y=3C 当3≥x 时y 随x 增大而增大D 当3≥x 时y 随x 增大而减小12、二次函数c bx ax y ++=2的图象如图所示,则下列结论中正确的是:( )A a>0 b<0 c>0B a<0 b<0 c>0C a<0 b>0 c<0D a<0 b>0 c>0二.填空题:(每题5分,共30分)13.若132)1(--=a x a y 是关于x 的二次函数,则a= 。
数学九年级上浙教版第2章二次函数单元测试1
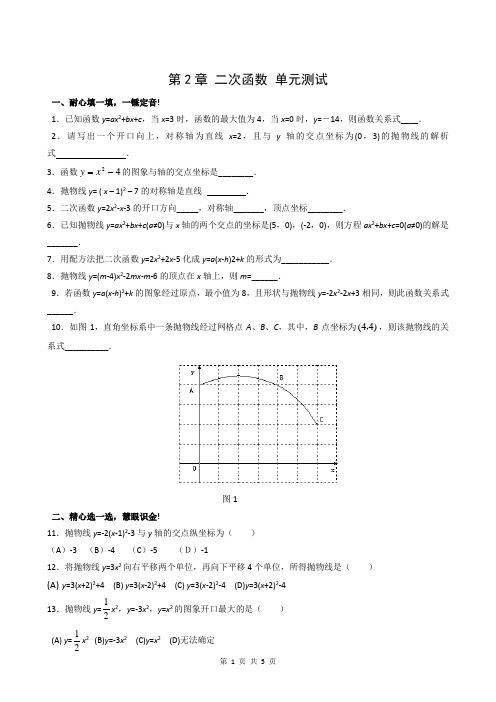
第2章 二次函数 单元测试一、耐心填一填,一锤定音!1.已知函数y =ax 2+bx +c ,当x =3时,函数的最大值为4,当x =0时,y =-14,则函数关系式____. 2.请写出一个开口向上,对称轴为直线x =2,且与y 轴的交点坐标为(0,3)的抛物线的解析式 .3.函数42-=x y 的图象与轴的交点坐标是________. 4.抛物线y = ( x – 1)2 – 7的对称轴是直线 .5.二次函数y =2x 2-x -3的开口方向_____,对称轴_______,顶点坐标________.6.已知抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点的坐标是(5,0),(-2,0),则方程ax 2+bx +c =0(a ≠0)的解是_______.7.用配方法把二次函数y =2x 2+2x -5化成y =a (x -h )2+k 的形式为___________. 8.抛物线y =(m -4)x 2-2mx -m -6的顶点在x 轴上,则m =______.9.若函数y =a (x -h )2+k 的图象经过原点,最小值为8,且形状与抛物线y =-2x 2-2x +3相同,则此函数关系式______.10.如图1,直角坐标系中一条抛物线经过网格点A 、B 、C ,其中,B 点坐标为(44),,则该抛物线的关系式__________.图1 二、精心选一选,慧眼识金!11.抛物线y =-2(x -1)2-3与y 轴的交点纵坐标为( ) (A )-3 (B )-4 (C )-5 (D)-112.将抛物线y =3x 2向右平移两个单位,再向下平移4个单位,所得抛物线是( )(A) y =3(x +2)2+4 (B) y =3(x -2)2+4 (C) y =3(x -2)2-4 (D)y =3(x +2)2-413.抛物线y =21x 2,y =-3x 2,y =x 2的图象开口最大的是( ) (A) y =21x 2(B)y =-3x 2 (C)y =x 2 (D)无法确定14.二次函数y =x 2-8x +c 的最小值是0,那么c 的值等于( ) (A)4 (B)8 (C)-4 (D)16 15.抛物线y =-2x 2+4x +3的顶点坐标是( )(A)(-1,-5) (B)(1,-5) (C)(-1,-4) (D) (-2,-7) 16.过点(1,0),B (3,0),C (-1,2)三点的抛物线的顶点坐标是( ) (A)(1,2) (B )(1,32) (C) (-1,5) (D)(2,41-) 17. 若二次函数y =ax 2+c ,当x 取x 1,x 2(x 1≠x 2)时,函数值相等,则当x 取x 1+x 2时,函数值为( ) (A )a +c (B )a -c (C )-c (D )c18. 在一定条件下,若物体运动的路程s (米)与时间t (秒)的关系式为252s t t =+,则当物体经过的路程是88米时,该物体所经过的时间为( ) (A)2秒 (B) 4秒 (C)6秒 (D) 8秒19.如图2,已知:正方形ABCD 边长为1,E 、F 、G 、H 分别为各边上的点, 且AE =BF =CG =DH , 设小正方形EFGH 的面积为,AE 为,则关于的函数图象大致是( ) 图2(A ) (B ) (C ) (D ) 20.抛物线y =ax 2+bx +c 的图角如图3,则下列结论:①abc >0;②a +b +c =2;③a >21; ④b <1.其中正确的结论是( )(A )①② (B )②③ (C )②④ (D )③④图3 三、用心做一做,马到成功!21. 已知一次函()()2322++++-=m x m x m y 的图象过点(0,5)⑴ 求m 的值,并写出二次函数的关系式; ⑵ 求出二次函数图象的顶点坐标、对称轴.22.已知抛物线2y ax bx c =++ 经过(-1,0),(0,-3),(2,-3)三点.⑴求这条抛物线的表达式;⑵写出抛物线的开口方向、对称轴和顶点坐标.23.有一个抛物线形的桥洞,桥洞离水面的最大高度BM 为3米,跨度OA 为6米,以OA 所在直线为x 轴,O 为原点建立直角坐标系(如图4所示). ⑴请你直接写出O 、A 、M 三点的坐标;⑵一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)? 图424. 甲车在弯路作刹车试验,收集到的数据如下表所示:(1y (米). (2)在一个限速为40千米/时的弯路上,甲、乙两车相向速度x (千米/时)的函数图象,并求函数的解析式.而行,同时刹车,但还是相撞了.事后测得甲、乙两车的刹车距离分别为12米和10.5米,又知乙车的刹车距离y (米)与速度x (千米/时)满足函数14y x,请你就两车的速度方面分析相撞的原因.25. 某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万.该生产线投产后, 图5 从第1年到第x 年的维修、保养费用累计为y (万元),且y =ax 2+bx ,若第1年的维修、保养费用为2万元,第2年为4万元. (1)求y 的解析式;(2)投产后,这个企业在第几年就能收回投资?第2章二次函数水平测试(八)参考答案:一、1.y =-2(x -3)2+4; 2.y =(x -2)2+3; 3.(0,-4) ; 4.x =1 ; 5.向上,x =41,(12548-,); 6.x 1=5,x 2=-2. 7.y =2(x +21)2-211; 8.-4或3; 9.y =-2x 2+8x 或y =-2x 2-8x ; 10.432612++-=x x y 二、11-15 CCADB 16-20 DDBBB .三、21. (1)将x =0,y =5代入关系式,得m +2=5,所以m =3,所以y =x 2+6x +5; (2)顶点坐标是(-3,-4),对称轴是直线x =-3.22.由已知,得30423c a b c a b c =-⎧⎪-+=⎨⎪++=-⎩,,解得a =1,b =-2,c =-3.所以y =x 2-2x -3.(2)开口向上,对称轴x =1,顶点(1,-4). 23. 解:(1)0(0,0),A (6,0),M (3,3).(2)设抛物线的关系式为y =a (x -3)2+3,因为抛物线过点(0,0),所以0=a (0-3)2+3,解得a =-31,所以y =-31(x -3)2+3=-31x 2+2x , 要使木版堆放最高,依据题意,得B 点应是木版宽C D 的中点,把x =2代入y =-31x 2+2x ,得y =38,所以这些木版最高可堆放38米. 24. 解:(1)如图,设函数的解析式为y =ax 2+bx +c .因为图象经过点(0,0)、(10,2)、(20,6), 所以c =0.所以21001006400200a b a b =++⎧⎨=++⎩,解得1100110a b ⎧=⎪⎪⎨⎪=⎪⎩.所以函数的解析式为21110010y x x =+. (2)因为y =12,所以21110010y x x =+=12, 解得x 1=30,x 2=-40(不符合题意,舍去) 又因为y 乙=10.5,所以110.54x =,x =42. 因为乙车速度为42千米/时,大于40千米/时, 所以,就速度方面原因,乙车超速,导致两车相撞.25.(1)由题意,x =1时,y =2;x =2时,y =2+4=6,分别代入y =ax 2+bx ,得a +b =2,4a +2b =6,解得,a =1,b =1,所以y =x 2+x .(2)设G =33x -100-x 2-x ,则G =-x 2+32x -100=-(x -16)2+156.由于当1≤x ≤16时,G 随x 的增大而增大,故当x =4时,即第4年可收回投资.。
浙教版九年级数学上册二次函数单元测试56

浙教版九年级数学上册二次函数单元测试56一、选择题(共10小题;共50分)1. 抛物线的顶点坐标是A. B. C.2. 抛物线可以由抛物线平移得到,则下列平移过程正确的是A. 先向左平移个单位,再向上平移个单位B. 先向左平移个单位,再向下平移个单位C. 先向右平移个单位,再向下平移个单位D. 先向右平移个单位,再向上平移个单位3. 已知函数,则当时,自变量的取值范围是A. 或C. 或4. 下列函数是二次函数的是A. B. C. D.5. 已知二次函数的图象经过,,当该二次函数的自变量分别取,时,对应的函数值是,,且,设该函数图象的对称轴是,则的取值范围是A. B. C. D.6. 已知二次函数,当取互为相反数的任意两个实数值时,对应的函数值总相等,则关于的一元二次方程的两根之积为A.7. 已知抛物线过,,,四点,则与的大小关系是A. B. C. D. 不能确定8. 函数的图象的顶点坐标是A. C. D.9. 已知函数的图象上两点,,其中,则与的大小关系为A. B. C. D. 无法判断10. 已知二次函数(为常数),在自变量的值满足的情况下,与其对应的函数值的最大值为的值为A. 或B. 或C. 或D. 或二、填空题(共6小题;共30分)11. 某种产品现在的年产量是吨,若接下来平均每年的增长率都是,写出两年后这种产品的产量与之间的关系式.12. 抛物线的对称轴是.13. 如图,在平面直角坐标系中,抛物线与交于点,过点作轴的平行线,分别交两条抛物线于点,(点与点左侧),则线段的长为.14. 如图,在平面直角坐标系中,抛物线交轴的负半轴于点.点是轴正半轴上一点,点关于点的对称点恰好落在抛物线上.过点作轴的平行线交抛物线于另一点.若点的横坐标为,则的长为.15. 定义为关于的函数的“特征数”,如:函数的“特征数”是.在平面直角坐标系中,将“特征数”是的函数的图象向下平移个单位长度,得到一个新的图象,这个新图象的函数解析式是.16. 如图,抛物线与轴相交于,两点,与轴相交于点,点在抛物线上,且,与轴相交于点,过点的直线平行于轴,与抛物线相交于,两点,则线段的长为.三、解答题(共8小题;共104分)17. 已知,是方程的两个实数根.(1)求的取值范围;(2)当时,求的值及方程的解.18. 已知关于的二次函数,当为何值时,它的图象开口向上?当为何值时,它的图象开口向下?19. 已知抛物线的对称轴是直线,求抛物线的顶点坐标.20. 如果抛物线的对称轴是直线,求的值.21. 用一根长为的木条做一个长方形框,若宽为,写出它的面积与之间的函数表达式,指出自变量的取值范围,并判断是的二次函数吗?22. 抛物线与坐标轴交于,,,求抛物线的解析式.23. 卢浦大桥拱形可以近似看作抛物线的一部分,在大桥截面的比例图上,跨度,拱高,线段表示大桥拱内桥长,,如图①在比例图上,以直线为轴,抛物线的对称轴为轴,以作为数轴的单位长度,建立平面直角坐标系,如图②.(结果精确到,参考数据:)(1)求出图②中以这一部分抛物线为图象的函数解析式,并写出函数的定义域;(2)如果与的距离,求卢浦大桥拱内实际桥长.24. 已知关于的二次函数的图象与轴交于点,,并经过点,求这个二次函数的解析式.(1)点,的横坐标分别为,点的坐标为.(2)点,的横坐标分别为,点的坐标为.(3)点,的横坐标分别为,,点是顶点,纵坐标为答案第一部分1. B2. B3. A4. C5. C【解析】当时,抛物线开口向上,则点的对称点为,,对称轴为中.6. D 【解析】二次函数,当取互为相反数的任意两个实数值时,对应的函数值总相等,可知二次函数图象的对称轴为直线,即轴,则,解得:,则关于的一元二次方程为,则两根之积为.7. A8. D9. B 【解析】函数,函数的对称轴是直线,开口向下,图象上两点,,其中,.10. C【解析】当时,随的增大而增大,当时,随的增大而减小,①若,时,取得最大值可得:,解得:或(舍);②若,当时,取得最大值可得:,解得:或(舍).综上,的值为或.第二部分11.12.【解析】由抛物线的解析式可知,其对称轴是直线.13.【解析】设抛物线的对称轴与线段交于,如图所示,由抛物线的对称性,可知:,.所以.14.【解析】当时,,解得,,则,点关于点的对称点为,点的横坐标为,点的坐标为,抛物线解析式为,当时,,则,当时,,解得,,则,的长为.15.【解析】依题意得“特征数”是的函数解析式为,其顶点坐标是,向下平移个单位后得到的顶点坐标是,所以新函数的解析式为.16.【解析】当时,,解得或,点的坐标为.当时,,点的坐标为.当时,,解得或,点的坐标为.设直线的解析式为,将,代入,得解得直线的解析式为.当时,,点的坐标为.当时,,解得,,点的坐标为,点的坐标为,.第三部分17. (1)即,,.(2),,,把代入方程得:,,.18. 当时,图象开口向上;当时,图象开口向下..20. ,解得.21. 由题意,得矩形的周长为,,.是的二次函数.22. 设抛物线的解析式为.过点,,.则则解析式为.23. (1)由于顶点在轴上,所以设以这部分抛物线为图象的函数解析式为.因为点或在抛物线上,所以,得.因此所求函数解析式为.(2)因为点,的纵坐标为,所以,得.所以点的坐标为,点的坐标为.所以.因此卢浦大桥拱内实际桥长为.24. (1).(2).(3).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 二次函数单元卷班级 姓名 成绩一、 选择题1.二次函数522-+=x x y 取最小值时,自变量x 的值是 ( ) A. 2 B. -2 C. 1 D. -1 2.函数12+-=x y 的图象大致为 ( )A B C D3.已知二次函数y=x 2+x+m ,当x 取任意实数时,都有y>0,则m 的取值范围是( ) A .m ≥14 B .m>14 C .m ≤14 D .m<144.无论m 为何实数,二次函数y=x 2-(2-m)x+m 的图象总是过定点( ):A.(1,3)B.(1,0);C.(-1,3)D.(-1,0) 5.二次函数y=mx 2-4x+1有最小值-3,则m 等于( ) A .1 B .-1 C .±1 D .±126.把抛物线1422++-=x x y 的图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是 ( )A.6)1(22+--=x y B. 6)1(22---=x yC .6)1(22++-=x y D. 6)1(22-+-=x y7.把抛物线y=2x 2 -4x-5绕顶点旋转180º,得到的新抛物线的解析式是( ) (A )y= -2x 2 -4x-5 (B )y=-2x 2+4x+5 (C )y=-2x 2+4x-9 (D )以上都不对|8.函数y=ax 2+bx+c 的图象如图所示, 那么关于x 的方程ax 2+bx+c-3=0的根的情况是( )A.有两个不相等的实数根B.有两个异号实数根C.有两个相等实数根D.无实数根9.如图,Rt △AOB 中,AB⊥OB ,且AB=OB=3,设直线x=•t 截此三角形所得阴影部分的面积为S ,则S 与t 之间的函数关系的图象为下列选项中的( )10.已知不等式x 2+px +q<0的解集是 -3<x<2,则( ) A .p=-1,q=6; B .p=1,q=6;。
C .p=-1,q=-6;D .p=1,q=-611.若函数y=mx 2+mx+m-2的值恒为负数,则m 取值范围是( ) A .m<0或m>83 B .m<0 C .m ≤0 D .m>8312.将进货单价为70元的某种商品按零售价100元一个售出时,每天能卖出20个,•若这种商品的零售价在一定范围内每降价1元,其日销量就增加1个,为了获取最大利润,则应降价( )A .5元B .10元C .15元D .20元 二填空题1.炮弹从炮口射出后飞行的高度h (m )与飞行的时间t (s )•之间的函数关系式为h=v 0tsin3xOyα-5t2,其中v0•是发射的初速度,α是炮弹的发射角,当v0=300m/s,α=30°时,炮弹飞行的最大高度为______m,该炮弹在空中运行了______s落到地面上.2.抛物线y=9x2-px+4与x轴只有一个公共点,则不等式9x2-p2<0的解集是__________.、3.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,-1),那么移动后的抛物线的关系式为__________.4.如图,用2m长的木条,做一个有横档的矩形窗子,为使透进的光线最多,那么这个窗子的面积应为_______m2.5.王翔同学在一次跳高训练中采用了背跃式,跳跃路线正好和抛物线y=2x2+3x+3相吻合,那么他能跳过的最大高度为_________ m.6.有一长方形条幅,长为a m,宽为b m,四周镶上宽度相等的花边,求剩余面积S(m2)与花边宽度x(m)之间的函数关系式为,自变量x的取值范围为。
;三、解答题1.(12分)心理学家发现,在一定的时间范围内,学生对概念的接受能力y与提出概念所用的时间x(单位:分钟)之间满足函数关系y=++43(0≤x≤30),y的值越大,表示接受能力越强.(1)若用10分钟提出概念,学生的接受能力y的值是多少(2)如果改用8分钟或15分钟来提出这一概念,那么与用10分钟相比,学生的接受能力是增强了还是减弱了通过计算来回答.^2.(创新实践题)如图,有一个抛物线的拱形立交桥,•这个桥拱的最大高度为16m,跨度为40m,现把它放在如图所示的直角坐标系里,•若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶,铁柱应取多长3.如图所示,一个运动员推铅球,铅球在点A处出手,出手时球离地面约213.铅球落地点在B处,铅球运行中在运动员前4m处(即OC=4)达到最高点,最高点高为3m.已知铅球经过的路线是抛物线,根据图示的直角坐标系,你能算出该运动员的成绩吗^y4.(应用题)(6分)如图所示,一单杠高2.2m,两立柱间的距离为1.6m,将一根绳子的两端拴于立柱与铁杠的结合处A、B,绳子自然下垂,虽抛物线状,一个身高0.7m的小孩站在距立柱0.4m处,其头部刚好触上绳子的D处,求绳子的最低点O到地面的距离.…5.我县市某蔬菜基地种植西红柿,由历年市场行情得知,从2月1日起的300天内,西红柿市场售价与上市时间的关系用图甲的一条折线表示;西红柿的种植成本与上市时间的关系用图乙表示的抛物线段表示.(1)写出图26-4甲表示的市场售价与时间的函数关系式;(2)写出图26-4乙表示的种植成本与时间的函数关系式;(3)设定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大(注:市场售价和种植成本的单位:元/102kg,时间单位:天)'答案一、DBDCA CCCDD CA二、1.125 30 2. -•4<x<4=-4x2+16x-13'4.165.158;=(a-2x)(b-2x);0<x<b/2三、1.解:(1)当x=10时,y=++43=×102+×10+43=59.(2)当x=8时,y=++43=×82+×8+43=,∴用8分钟与用10分钟相比,学生的接受能力减弱了;当x=15时,y=++43=×152+×15+43=.∴用15分钟与用10分钟相比,学生的接受能力增强了. 2.解:由题意,知抛物线的顶点坐标为(20,16),点B(40,0),∴可设抛物线的关系为y=a(x-20)2+16.)∵点B(40,0)在抛物线上,∴0=a(40-20)2+16,∴a=-1 25.∴y=-125(x-20)2+16.∵竖立柱的点为(15,0)或(25,0),∴当x=15时,y=-125(15-20)2+16=15;当x=25时,y=-125(25-20)2+16=15.∴铁柱应取15m.]3.解:能.∵OC=4,CD=3,∴顶点D坐标为(4,3),设 y=a(x-4)2+3,把A 50,3⎛⎫⎪⎝⎭代入上式,得 53=a(0-4)2+3,∴a=-112-, ∴y= -112-(x-4)2+3,即y=112-x 2+2533x +.令y=0,得112-x 2+2533x +=0,∴x 1=10,x 2=-2(舍去),故该运动员的成绩为10m4.解:如图所示,以O 为坐标原点,水平方向为x 轴,垂直方向为y 轴,建立直角坐标系,设抛物线的解析式为y=ax 2(a ≠0).设A 、B 、D 三点坐标依次为(x A ,y A ),(x B ,y B ),(x D ,y D ),由题意,得AB=,¥∴x A =,x B =,又可得x D =-(12×)=. ∴当x=时,y A =a ·()2=0.64a ; 当x=时,y D =a ·()2=0.16a . ∵y A -y D =, ∴0.64a-0.16a=,∴a=258,∴抛物线解析式为y=258x 2. (当x=时,y D =258×()2=, ∴0.2m 答:绳子的最低点距地面0.2m .5.解:(1)w 1=300(0200),2300(200300).t t t t -≤≤⎧⎨-<≤⎩(2)由图知,抛物线的顶点坐标为(150,100),可设w 2=a (t-150)2+100.又当t=50时,w 2=150,代入求得a=1200, ∴w 2=1200(t-150)2+100.(0≤t ≤300) (3)设t 时刻的纯收益为y ,依题意有y=w 1-w 2,即y=2211175(0200),20022171025(200300).20022t t t t t t ⎧-++≤≤⎪⎪⎨⎪-+-<≤⎪⎩当0≤t ≤200时,配方整理得y=-1200×(t-50)2+100, 所以,当t=50时,y 在0≤t ≤200上有最大值为100. 当200<t ≤300时,配方整理得y=-1200(t-350)2+100. 所以,当t=300时,y•在200<•t•≤300上有最大值.综上所述,由100>可知,y 在0≤t ≤300上,可以取最大值100, 此时t=50,即从2月1日开始的第50天时,上市的西红柿纯收益最大.’。
