黑龙江省双鸭山市高一数学下学期开学考试试题理无答案
黑龙江省双鸭山市高一下学期开学数学试卷

黑龙江省双鸭山市高一下学期开学数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)已知集合M={0,1,3},N={x|x=3a,a∈M},则M∪N=()A . {0}B . {0,3}C . {1,3,9}D . {0,1,3,9}2. (2分) (2019高一上·宜昌期中) 已知,且,则等于()A .B .C .D .3. (2分) (2019高三上·汉中月考) 若,,则下列不等式错误的是()A .B .C .D .4. (2分)已知函数f(x)=xn的图象过点(3,),则n=()A .B .C .D .5. (2分) (2017高二上·嘉兴月考) 已知是边长为的等边三角形,为平面内一点,则的最小值是()A .B .C .D .6. (2分)已知,则的值为()A .B .C .D .7. (2分) (2016高三上·浦东期中) 我们定义渐近线:已知曲线C,如果存在一条直线,当曲线C上任意一点M沿曲线运动时,M可无限趋近于该直线但永远达不到,那么这条直线称为这条曲线的渐近线:下列函数:①y= ;②y=2x﹣1;③y=lg(x﹣1);④y= ;其中有渐近线的函数的个数为()A . 1B . 2C . 3D . 48. (2分)(2016高一下·右玉期中) 设f(x)是定义域为R,最小正周期为的函数,若,则等于()A .B . 1C . 0D . -9. (2分)(2017·深圳模拟) 将函数的图象向左平移个周期后,所得图象对应的函数为()A .B .C .D .10. (2分) (2016高一下·钦州期末) 等腰三角形一腰上的高是,这条高与底边的夹角为60°,则底边长=()A . 2B .C . 3D . 2二、填空题 (共4题;共4分)11. (1分) (2016高一上·徐州期中) 函数f(x)= + 的定义域为________.12. (1分) (2016高三上·平罗期中) 在△ABC中,D为BC边上一点,BC=3BD,AD= ,∠ADC=45°.若AC= AB,则BD=________.13. (1分) (2016高三上·泰兴期中) 在△ABC中,sinA:sinB:sinC=2:3:4,则cosC的值为________.14. (1分) (2016高三上·天津期中) 若 =3,tan(α﹣β)=2,则tan(β﹣2α)=________.三、解答题 (共5题;共50分)15. (5分)已知函数f(x)=asinx•cosx﹣ acos2x+ a+b(a>0).(Ⅰ)写出函数的单调递增区间;(Ⅱ)设x∈[0, ],f(x)的最小值是﹣,最大值是2,求实数a,b的值.16. (10分) (2016高二上·包头期中) 在四边形ABCD中,已知∥ , =(6,1), =(x,y), =(﹣2,﹣3).(1)求用x表示y的关系式;(2)若⊥ ,求x、y值.17. (10分) (2016高三上·长宁期中) 已知 f(x)= sin2x﹣2sin2x,(1)求f(x)的最小正周期和单调递减区间;(2)若x∈[﹣, ],求f(x)的最大值及取得最大值时对应的x的取值.18. (15分) (2016高二下·茂名期末) 已知f(x)= .(1)判断函数f(x)的奇偶性并证明;(2)证明f(x)是定义域内的增函数;(3)解不等式f(1﹣m)+f(1﹣m2)>0.19. (10分)已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,<φ<)的部分图象如图所示.(1)求函数f(x)的解析式(2)如何由函数y=2sinx的图象通过适当的变换得到函数f(x)的图象,写出变换过程.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共4题;共4分)11-1、12-1、13-1、14-1、三、解答题 (共5题;共50分)15-1、16-1、16-2、17-1、17-2、18-1、18-2、18-3、19-1、19-2、。
黑龙江省高一下学期开学考试数学试题(解析版)

一、单选题1.已知集合,,那么集合( ){}52A x x =-<<{}33B x x =-<<A B = A .B . {}32x x -<<{}52x x -<<C .D . {}33x x -<<{}53x x -<<【答案】A【分析】由集合交集的定义直接运算即可得解.【详解】因为集合,,{}52A x x =-<<{}33B x x =-<<所以.{}|32B x x A -<=< 故选:A.2.设命题:,,则为( )p x ∀∈N x ∈Z p ⌝A .,B ., x ∀∈N x ∉Z x ∃∈N x ∉ZC .,D ., x ∀∉N x ∈Z x ∃∈N x ∈Z 【答案】B【分析】含有一个量词的命题的否定,既要否定结论,也要改变量词.【详解】命题:,,则为:,,故A ,C ,D 错误.p x ∀∈N x ∈Z p ⌝x ∃∈N x ∉Z 故选:B.3.设,,且,则的最小值为( )0x >0y >9xy =x y +A .18B .9C .6D .3 【答案】C【分析】根据基本不等式,即可求解.【详解】∵0,0x y >>∴,(当且仅当,取“=”)6x y +≥=3x y ==故选:C.4.若为第一象限角,则是( ) α2αA .第一象限角B .第二象限角C .第一或第二象限角D .第一或第三象限角 【答案】D【解析】写出第一象限角,得到的范围,再讨论k 的取值即可.α2α【详解】因为为第一象限角, α所以, 22,2k k k Z ππαπ<<+∈所以,,24k k k Z απππ<<+∈当时,,属于第一象限角,排除B ; 0k =024απ<<当时,,属于第三象限角,排除AC ; 1k =524αππ<<所以是第一或第三象限角2α故选:D5.已知函数,在下列区间中,包含零点的区间是 ()26log f x x x =-()f x A .B .C .D .()0,1()1,2()2,4()4,+∞【答案】C【详解】因为,,所以由根的存在性定理可知:选C. (2)310f =->3(4)202f =-<【解析】本小题主要考查函数的零点知识,正确理解零点定义及根的存在性定理是解答好本类题目的关键.6.sin 20cos 40cos 20sin140︒︒︒︒+=A . BC .D .12-12【答案】B【详解】 sin 20cos 40cos 20sin140sin 20cos 40cos 20sin 40sin(2040)sin 60︒︒+︒︒=︒︒+︒︒=︒+︒=︒故选B7.已知函数是定义在上的减函数,则当时,实数的取值范围为()f x [)0,+∞1(21)()3f a f ->a ( ) A . B . C . D . 2,3⎛⎫+∞ ⎪⎝⎭2,3⎛⎫-∞ ⎪⎝⎭1223⎡⎫⎪⎢⎣⎭,1123⎛⎫ ⎪⎝⎭,【答案】C【解析】根据函数为定义域上的减函数及定义域建立不等式组即可求解.【详解】因为函数是定义在上的减函数,且, ()f x [)0,+∞1(21)(3f a f ->所以, 1213021a a ⎧-<⎪⎨⎪≤-⎩解得, 1223a ≤<故选:C8.已知是偶函数,且在区间上是增函数,则的大小关系是()f x ()0,∞+()()()0.5,1,0f f f --( )A .B . ()()()0.501f f f -<<-()()()10.50f f f -<-<C .D .()()()00.51f f f <-<-()()()100.5f f f -<<-【答案】C【分析】利用偶函数的性质化简要比较的三个数,再根据函数在上的单调性判断出三者的()0,∞+大小关系,从而确定正确选项.【详解】∵函数为偶函数,∴,又∵在区间上是增()f x ()()()0.50.5(11),f f f f -=-=()f x ()0,∞+函数,∴,即.()()()00.51f f f <<()()()00.51f f f <-<-故选C.【点睛】本小题主要考查利用函数的奇偶性和单调性比较大小,属于基础题.二、多选题9.函数的图象过( )()log (2)(01)a f x x a =+<<A .第一象限B .第二象限C .第三象限D .第四象限【答案】BCD【分析】画出函数大致图象即可判断.【详解】的图象相当于是把的图象向左平移2个单()log (2)(01)a f x x a =+<<()log 01a y x a =<<位,作出函数的大致图象如图所示,则函数的图象过第二、三、四象限. ()()log 2a f x x =+()01a <<()f x 故选:BCD.10.下列函数中,既是奇函数,又在上单调递增的函数的是( )(0,)+∞A .B .C .D . 3y x =||1y x =+21y x =-+1y x=-【答案】AD【分析】逐个分析各项可得结果.【详解】对于A 项,设,定义域为R ,则,所以是奇函数, 3()y f x x ==3()()f x x f x -=-=-3y x =由,在上单调递增可得在上单调递增,故选项A 正确;0α>y x α=(0,)+∞3y x =(0,)+∞对于B 项,设,定义域为R ,则,所以是偶()||1y f x x ==+()||1||1()f x x x f x -=-+=+=||1y x =+函数,故选项B 错误;对于C 项,设,定义域为R ,,所以是偶函数,2()1y f x x ==-+2()1()f x x f x -=-+=21y x =-+故选项C 错误; 对于D 项,,定义域为,,所以 1()y f x x ==-(,0)(0,)-∞+∞ 1()()f x f x x-==-是奇函数,由,在上单调递减可得在上单调递减, 1y x=-0α<y x α=(0,)+∞1y x -=(0,)+∞所以在上单调递增.故选项D 正确. 1y x=-(0,)+∞故选:AD.11.函数,的图像与直线(为常数)的交点可能有( ) 1y cosx =+π,2π3x æöç÷Îç÷èøy t =t A .0个B .1个C .2个D .3个【答案】ABC 【分析】画出在的图像,即可根据图像得出. 1y cosx =+π,2π3x æöç÷Îç÷èø【详解】画出在的图像如下: 1y cosx =+π,2π3x æöç÷Îç÷èø则可得当或时,与的交点个数为0;0t <2t ≥1y cosx =+y t =当或时,与的交点个数为1; 0=t 322t ≤<1y cosx =+y t =当时,与的交点个数为2. 302t <<1y cosx =+y t =故选:ABC.12.设函数,则下列结论正确的是( )()cos2f x x x -A .的一个周期为()f x π-B .的图像关于直线对称 ()y f x =π6x =-C .的图像关于点对称 ()y f x =π,012⎛⎫ ⎪⎝⎭D .在有3个零点()y f x =[0,2π]【答案】ABC【分析】利用辅助角公式化简,再根据三角函数的性质逐个判断即可()f x【详解】, π()cos22sin 26f x x x x ⎛⎫=-=- ⎪⎝⎭对A ,最小周期为,故也为周期,故A 正确; 2ππ2T ==π-对B ,当时,为的对称轴,故B 正确; π6x =-ππ262x -=-sin y x =对C ,当时,,又为的对称点,故C 正确; π12x =26π0x -=()0,02sin y x =对D ,则, ()0f x =()ππ2sin 202π,Z 66x x k k ⎛⎫-=⇒-=∈ ⎪⎝⎭解得,故在内有共四个零点,故D 错误 ()ππ,Z 212k x k =+∈()f x [0,2π]π7π13π19π,,,12121212x =故选:ABC.三、双空题13.函数的振幅是________,初相是________. 1π3sin 36y x ⎛⎫=+ ⎪⎝⎭【答案】 3 π6【分析】根据振幅和初相的定义可得答案.【详解】振幅,3A =令则初相. 0x =π6ϕ=故答案为:3, π6四、填空题14.函数(,且)的图象必经过点的坐标________.1x y a =+0a >1a ≠【答案】()0,2【分析】利用指数函数的性质即可求解.【详解】令,得,0x =012y a =+=所以函数(,且)的图象必经过点.1x y a =+0a >1a ≠()0,2故答案为:.()0,215.等于________.2222sin 1sin 2sin 3sin 89︒+︒+︒+⋅⋅⋅+︒【答案】44.5【分析】设,由平方关系得到2222sin 1sin 2sin 3sin 89S =︒+︒+︒+⋅⋅⋅+︒求解.2222cos cos 7cos c s 888o 981S =︒+︒+︒+⋅⋅⋅+︒【详解】解:设,2222sin 1sin 2sin 3sin 89S =︒+︒+︒+⋅⋅⋅+︒因为,22222222sin 1cos 89,sin 2cos 88,sin 3cos 87,...,sin 89cos 1︒=︒︒=︒︒=︒︒=︒所以,2222cos cos 7cos c s 888o 981S =︒+︒+︒+⋅⋅⋅+︒两式相加得:,2189S =⨯所以,44.5S =故答案为:44.516.已知,且,则________. ()1sin 535α︒-=27090α-︒<<-︒()sin 37α︒+=【答案】##【分析】设,,则,,从而将所求式子转化成求的53βα︒=-37γα︒=+90βγ︒+=90γβ︒=-cos β值,利用的范围确定的符号.αcos β【详解】设,,那么,从而.53βα︒=-37γα︒=+90βγ︒+=90γβ︒=-于是.因为,()sin sin 90cos γββ︒=-=27090α︒︒-<<-所以.由,得. 143323β︒︒<<1sin 05β=>143180β︒︒<<所以cos β===所以. ()sin 37sin αγ︒+==故答案为:五、解答题17.在平面直角坐标系中,已知角α的顶点与原点重合,始边与x 轴的非负半轴重合,且角α的终边与单位圆交点为P ,,且β是第一象限角,求:和的cos 0.6β=sin()αβ-tan()αβ+值.【答案】 ,sin()αβ-=2tan()11αβ+=-【分析】先利用题给条件求得,,,再利sin αα==tan 2α=-4sin 5β=4tan 3β=用两角差的正弦公式和两角和的正切公式即可求得和的值.sin()αβ-tan()αβ+【详解】角α的终边与单位圆交点为P ,则 sin αα==tan 2α=-由,且β是第一象限角,可得, cos 0.6β=4sin 5β=4tan 3β=则 4sin()sin cos cos sin 0.65αβαβαβ-=-== ()42tan tan 23tan()41tan tan 11123αβαβαβ-+++===----⨯18.已知.求值:tan 2α=(1); sin cos sin cos αααα+-(2).2cos 2sin cos 1ααα--【答案】(1)3;(2) 85-【分析】(1)根据已知利用商数关系化弦为切即可得出答案;(2)利用平方关系和商数关系化弦为切即可得出答案.【详解】(1)∵,tan 2α=∴; sin cos tan 1213sin cos tan 121αααααα+++===---(2). 22222cos 2sin cos 12tan cos 2sin cos 1111co 1s sin ta 4n 1558αααααααααα-----=-=-=-=-++19.已知,. 0πx <<1sin cos 5x x +=(1)求的值;sin cos x x -(2)若,试比较与的大小. sin cos 1sin cos 3θθθθ+=-tan x tan θ【答案】(1) 7sin cos 5x x -=(2)tan tan x θ> 【分析】(1)将已知等式两边平方,利用完全平方公式及同角三角函数间基本关系变形,求出的值,再利用完全平方公式即可求出的值; 242sin cos 25x x =-sin cos x x -(2)根据第一问求出的值,再利用已知等式求出的值,进行比较即可.tan x tan θ【详解】(1)对于,两边平方得, 1sin cos 5x x +=221sin cos 2sin cos 25x x x x ++=所以,∵,∴,,所以, 242sin cos 25x x =-0πx <<sin 0x >cos 0x <sin cos 0x x ->∴,∴; 249(sin cos )12sin cos 25x x x x --==7sin cos 5x x -=(2)联立,解得,所以, 1sin cos 57sin cos 5x x x x ⎧+=⎪⎪⎨⎪-=⎪⎩4sin 53cos 5x x ⎧=⎪⎪⎨⎪=-⎪⎩4tan 3x =-因为,且,所以分子分母同除以有:,解得. sin cos 1sin cos 3θθθθ+=-cos 0θ≠cos θtan 11tan 13θθ+=-tan 2θ=-∴.tan tan x θ>20.已知函数f (x )=log a (x +1)-log a (1-x ),a >0且a ≠1.(1)求f (x )的定义域;(2)判断f (x )的奇偶性并予以证明;(3)当a >1时,求使f (x )>0的x 的解集.【答案】(1)(-1,1);(2)奇函数,证明见解析;(3)(0,1).【分析】(1)结合真数大于零得到关于的不等式组即可求得函数的定义域; x (2)结合(1)的结果和函数的解析式即可确定函数的奇偶性;(3)结合函数的单调性得到关于的不等式组,求解不等式组即可求得最终结果.x 【详解】(1)要使函数有意义,则, 1010x x +>⎧⎨->⎩解得,即函数的定义域为;11x -<<()f x (1,1)-(2)函数的定义域关于坐标原点对称,()log (1)log (1)[log (1)log (1)]()a a a a f x x x x x f x -=-+-+=-+--=- 是奇函数.()f x ∴(3)若时,由得,1a >()0f x >log (1)log (1)a a x x +>-则,求解关于实数的不等式可得, 1111x x x -<<⎧⎨+>-⎩x 01x <<故不等式的解集为.(0,1)21.已知函数.2()sin cos cos 2f x x x x x =+(1)求的单调递减区间;()f x (2)若函数在上有两个零点,求实数的取值范围. ()()g x f x a =-0,2π⎡⎤⎢⎥⎣⎦a 【答案】(1); 2,,63k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z (2) 31,2a ⎡⎫∈⎪⎢⎣⎭【分析】(1)先由倍角公式及辅助角公式得,再由正弦函数的单调性求解即()1sin 262f x x π⎛⎫=++ ⎪⎝⎭可;(2)将题设转化为在上有两个解,确定在上的单调性,即可求出实数()a f x =0,2π⎡⎤⎢⎥⎣⎦()f x 0,2π⎡⎤⎢⎥⎣⎦的取值范围.a【详解】(1)21cos211()sin cos cos22cos22cos2222xf x x x x x x x x x-=+=++=++,1sin262xπ⎛⎫=++⎪⎝⎭令,解得,则的单调递减区间为3222,262k x k kπππππ+≤+≤+∈Z2,63k x k kππππ+≤≤+∈Z()f x;2,,63k k kππππ⎡⎤++∈⎢⎥⎣⎦Z(2)函数在上有两个零点,可转化为在上有两个解,当()()g x f x a=-0,2π⎡⎤⎢⎥⎣⎦()a f x=0,2π⎡⎤⎢⎥⎣⎦时,0,6xπ⎡⎤∈⎢⎥⎣⎦,单增,当时,,2,662xπππ⎡⎤+∈⎢⎥⎣⎦()1sin262f x xπ⎛⎫=++⎪⎝⎭,62xππ⎡⎤∈⎢⎥⎣⎦72,626xπππ⎡⎤+∈⎢⎥⎣⎦单减,()1sin262f x xπ⎛⎫=++⎪⎝⎭又,,,要使在上有()10sin162fπ=+=13sin6222fππ⎛⎫=+=⎪⎝⎭71sin0262fππ⎛⎫=+=⎪⎝⎭()a f x=0,2π⎡⎤⎢⎥⎣⎦两个解,则.31,2a⎡⎫∈⎪⎢⎣⎭22.已知函数.1()1xf xx-=+(1)证明函数在上为减函数;()f x(1,)-+∞(2)求函数的定义域,并求其奇偶性;ln(tan)y f x=(3)若存在,使得不等式能成立,试求实数a的取值范围.(,42ππ(tan)tan0f x a x+≤【答案】(1)证明见解析;(2),奇函数;(3).,,44k k k Zππππ⎛⎫-++∈⎪⎝⎭(,3-∞-【解析】(1)利用单调性定义证明即可.(2)根据条件可得,其解集即为函数的定义域,可判断定义域关于原点对称,再根据tan1tan1xx<⎧⎨>-⎩奇偶性定义可判断函数的奇偶性.(3)令,考虑在上有解即可,参变分离后利用基本不等式可求实数的tant x=11tatt-+<+()1,+∞a取值范围.【详解】(1),,,11x∀>-21x∀>-12x x<又,()()()122212121211()()11112x xx xf x f xx x x x----=-+-=+++因为,,,故,,,11x >-21x >-12x x <110x +>210x +>120x x -<故即,所以函数在上为减函数.12())0(f x f x ->12()()f x f x >()f x (1,)-+∞(2)的满足的不等关系有:即, ((ln t )n )a y f x =x 1tan 01tan x x->+()()1tan tan 10x x +-<故,解得, tan 1tan 1x x <⎧⎨>-⎩,44k x k k Z ππππ-+<<+∈故函数的定义域为,,该定义域关于原点对称. ,44k k ππππ⎛⎫-++ ⎪⎝⎭Z k ∈令()((ln ta )n )F x f x =又 ()()()tan tan tan()tan tan 11ln ln ln 11x x x x xF x f -+--===--+,()()()tan ln x f F x =-=-故为奇函数. ln (tan )y f x =(3)令,因为,故. tan t x =(,)42x ππ∈1u >故在上不等式能成立即为 (,)42ππ(tan )tan 0f x a x +≤存在,使得,所以在上能成立, 1t >101t at t-+≤+()11t a t t -≤+()1,+∞令,则且, 1s t =-0s >()21121323t s t t s s s s-==+++++由基本不等式有2s s+≥s 所以时等号成立, ()131t t t -≤=-+1t 故的最大值为a 的取值范围为. ()11t y t t -=+3-(,3-∞-【点睛】本题考查与正切函数、对数函数有关的复合函数的性质的讨论,此类问题常用换元法把复合函数性质的讨论归结为常见函数性质的讨论,本题较综合,为难题.。
2023-2024学年黑龙江省双鸭山市高一下册开学考试数学试题(含解析)

2023-2024学年黑龙江省双鸭山市高一下册开学考试数学试题一、单选题1.命题“0(0,)x ∃∈+∞,00ln 1x x =-”的否定是A .0(0,)x ∃∈+∞,00ln 1x x ≠-B .0(0,)x ∃∉+∞,00ln 1x x =-C .(0,)x ∀∈+∞,ln 1x x ≠-D .(0,)x ∀∉+∞,ln 1x x =-【正确答案】C【详解】试题分析:特称命题的否定是全称命题,并将结论加以否定,所以命题的否定为:(0,)x ∀∈+∞,ln 1x x ≠-全称命题与特称命题2.在平面直角坐标系xOy 中,角α以x 轴的非负半轴为始边,终边与单位圆交于点122,),则sin2α=()A.2B .12C.D.2【正确答案】A【分析】直接利用任意角的三角函数定义,结合正弦二倍角公式求解即可.【详解】由任意角三角函数定义得:112sin 2α=,cos α=,1sin22sin cos 2222ααα==⨯⨯故选:A.3.若0.62a =,πlog 3b =,22πlog sin 3c =,则a 、b 、c 的大小关系为()A .a b c >>B .b a c >>C .c a b >>D .b c a>>【正确答案】A【分析】利用指数、对数的单调性,以及三角函数特殊值,即可得出结果.【详解】解:0.60221a =>= ,πππ0log 1log 3log π1=<<=,01b <<,2222log sinπlog log 103c ===,∴a b c >>,故选:A.4.函数3ln y x x=-的零点所在区间是()A .()3,4B .()2,3C .()1,2D .()0,1【正确答案】B【分析】根据解析式判断函数单调性,再应用零点存在性定理确定所在区间即可.【详解】由3,ln y y x x==-在(0,)+∞上递减,所以3ln y x x=-在(0,)+∞上递减,又3(2)ln 202f =-=>,e (3)1ln 3ln 03f =-=<,所以零点所在区间为()2,3.故选:B5.要得到函数()sin2f x x =的图象,只需将函数()sin 3g x x π⎛⎫=- ⎪⎝⎭的图象()A .所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图像向左平移3π个单位.B .所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图像向左平移6π个单位.C .所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得的图像向左平移3π个单位.D .所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得的图像向左平移6π个单位.【正确答案】D【分析】根据三角函数的图象变换,即可求解,得到答案.【详解】由题意,将函数()πg x sin x 3⎛⎫=- ⎪⎝⎭的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),可得()sin(2)3g x x π=-,再将函数()sin(2)3g x x π=-图象的各点向左平移6π个单位,可得()sin[2(sin 263f x x x ππ=+-=,所以要得到函数()f x sin2x =的图象,只需将函数()πg x sin x 3⎛⎫=- ⎪⎝⎭的图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),再将所得的图像向左平移6π个单位,故选D.本题主要考查了三角函数的图象变换,其中解答中熟记三角函数图象变换的原则,合理准确地完成平移与伸缩是解答的关键,着重考查了运算与求解能力,属于基础题.6.函数2cos sin 66y x x x ππ⎛⎫=+-≤≤ ⎪⎝⎭的最大值与最小值之和为A .32B .2C .0D .34【正确答案】A【分析】先由同角三角函数的平方关系可得22cos sin sin sin 1y x x x x =+=-++,再设sin t x =,又,66x ππ⎡⎤∈-⎢⎥⎣⎦,则11,22t ⎡⎤∈-⎢⎣⎦,再结合二次函数在闭区间上最值的求法求解即可.【详解】解:由22cos sin sin sin 1y x x x x =+=-++,又,66x ππ⎡⎤∈-⎢⎥⎣⎦,所以11sin ,22x ⎡⎤∈-⎢⎥⎣⎦,设sin t x =,则11,22t ⎡⎤∈-⎢⎥⎣⎦,则2()1f t t t =-++,11,22t ⎡⎤∈-⎢⎥⎣⎦,又函数()f t 在11,22⎡⎤-⎢⎥⎣⎦为增函数,则max 15()()24f t f ==,min 11()()24f t f =-=,则函数2cos sin 66y x x x ππ⎛⎫=+-≤≤ ⎪⎝⎭的最大值与最小值之和为513442+=,故选:A.本题考查了同角三角函数的平方关系,重点考查了二次函数最值的求法,属基础题.7.函数()13x f x a -=+(0a >,且1a ≠)的图象过一个定点P ,且点P 在直线10mx ny +-=(0m >,且0n >)图象上,则11m n+的最小值是()A .9B .8C .5D .4【正确答案】A【分析】确定函数过定点()1,4,代入直线方程得到41m n +=,变换()11114m n m n m n ⎛⎫+=++ ⎪⎝⎭,利用均值不等式计算得到答案.【详解】()13x f x a -=+过定点()1,4,故410m n +-=,即41m n +=,()111144559n m m n m n m n m n ⎛⎫+=++=++≥= ⎪⎝⎭,当4n m m n =,即13m =,16n =时等号成立.故选:A8.意大利画家达·芬奇提出:固定项链的两端,使其在重力的作用下自然下垂,那么项链所形成的曲线是什么?这就是著名的“悬链线问题”,其中双曲余弦函数就是一种特殊的悬链线函数,其函数表达式为e e cosh 2x x x -+=,相应的双曲正弦函数的表达式为e esinh 2xxx --=.设函数()sinh cosh x f x x=,若实数a 满足不等式()()232020f a f a ++-<,则a 的取值范围为()A .5,42⎛⎫- ⎪⎝⎭B .54,2⎛⎫- ⎪⎝⎭C .()5,4,2⎛⎫-∞-⋃+∞ ⎪⎝⎭D .()5,4,2⎛⎫-∞-⋃+∞ ⎪⎝⎭【正确答案】D【分析】根据题意,写出函数的解析式,由函数的奇偶性和单调性列出不等式,解之即可.【详解】由题意可知:e e ()e +ex xx x f x ---=的定义域为R ,因为e e ()()e +ex xx x f x f x ----==-,所以函数()f x 为奇函数,又因为222e e e 12()==1e +e e +1e +1x x x x x x x f x ----=-,且22()=e +1x g x 在R 上为减函数,由复合函数的单调性可知:22()1e +1x f x =-在R 上为增函数,因为()()232020f a f a ++-<,所以()()()2232022f a f a f a +<--=,所以23202a a +<,解得:4a >或52a <-,所以实数a 的取值范围为5(,(4,)2-∞-+∞ ,故选:D.二、多选题9.下列结论正确的是()A .7π6-是第三象限角B .若角α的终边过点(3,4)P -,则3cos 5α=-C .3πcos()sin(π)2A A -=+D .若圆心角为π3的扇形弧长为π,则该扇形面积为3π2【正确答案】BCD【分析】利用终边相同的角判断A ;利用任意角的三角函数的定义可判断B ;利用诱导公式求解可判断C ;利用扇形面积公式可判断D.【详解】对于A :7π5π2π66-=-,是第二象限角,故A 错误;对于B :角α的终边过点(3,4)P -,则||5r OP ==,所以cos 53x r α==-,故B 正确;对于C :π3πcos cos πcossin 222πA A A A⎡⎤⎛⎫⎛⎫⎛⎫-=+-=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,sin(π)sin A A +=-,则3πcos()sin(π)2A A -=+,故C 正确;对于D ,扇形的半径为π3π3=,面积为13ππ322⨯⨯=,D 正确;故选:BCD.10.已知()0,πθ∈,1sin cos 5θθ+=,则()A .π,π2θ⎛⎫∈ ⎪⎝⎭B .3cos 5θ=C .3tan 4θ=-D .7sin cos 5θθ-=【正确答案】AD 【分析】对1sin cos 5θθ+=两边平方得12sin cos 025θθ=-<,结合θ的范围得到π,π2θ⎛⎫∈ ⎪⎝⎭,可判断A ;再对sin cos θθ-平方将sin cos θθ代入可求出7sin cos 5θθ-=可判断D ;结合同角三角函数平方关系得到正弦和余弦值,进而求出正切值,BC 错误.【详解】1sin cos 5θθ+=,两边平方得:112sin cos 25θθ+=,解得:12sin cos 025θθ=-<①,故sin ,cos θθ异号,因为()0,πθ∈,所以π,π2θ⎛⎫∈ ⎪⎝⎭,A 正确;所以sin 0,cos 0θθ><,()22449sin cos 12sin cos 12525θθθθ-=-⋅=+=,所以7sin cos 5θθ-=②,D 正确;由①②可得43sin ,cos 55θθ==-,故4tan 3θ=-,故B ,C 不正确.故选:AD.11.函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭相邻两个最高点之间的距离为π,则以下正确的是()A .()f x 的最小正周期为πB .2π 3f x ⎛⎫- ⎪⎝⎭是奇函数C .() f x 的图象关于直线π6x =-对称D .() f x 在5ππ1212⎡⎤-⎢⎥⎣⎦,上单调递增【正确答案】ABD【分析】根据相邻两个最高点之间的距离为π得到函数的最小正周期,从而求出ω,即可得到函数解析式,再根据正弦函数的性质一一判断即可.【详解】解:因为函数π()(0)3f x x ωω⎛⎫=+> ⎪⎝⎭相邻两个最高点之间的距离为π,即函数()f x 的最小正周期为π,故A 正确;所以2ππT ω==,解得2ω=,则()π23f x x ⎛⎫=+⎪⎝⎭,所以2π2ππ22333f x x x ⎡⎤⎛⎫⎛⎫-=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦为奇函数,故B 正确;又ππ0π2sin 6036f ⎛⎫⎛⎫⎛⎫=⨯+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝-⎭-,所以函数关于点π,06⎛⎫- ⎪⎝⎭对称,即C 错误;若5ππ1212x ⎡⎤∈-⎢⎥⎣⎦,,则ππ223π2x ⎡⎤∈-⎢⎣+⎦,,因为sin y x =在ππ,22⎡⎤-⎢⎥⎣⎦上单调递增,所以()f x 在5ππ1212⎡⎤-⎢⎥⎣⎦,上单调递增,故D 正确;故选:ABD12.已知定义在R 上的函数()f x 满足(2)2()f x f x +=,且当[0,2]x ∈时,()22xf x =-,若对任(,]x m ∈-∞都有()6f x ≤,则实数m 的取值可以是()A .4B .5C .274log 2+D .275log 2+【正确答案】ABC【分析】判断函数在[]2,22k k +的单调性及值域,则可将命题转化为max ()6f m =,求解可得范围,即可判断.【详解】当[0,2]x ∈时,()22xf x =-,则在[)0,1x ∈,()f x 单调递减,[]1,2x ∈,()f x 单调递增,此时[]()0,2f x ∈.由定义在R 上的函数()f x 满足(2)2()f x f x +=得,()f x 在[0,2]的图象向右移动*2()k k ÎN 个单位时,图象纵坐标拉伸为原来的2k 倍,对应值域为0,2k⎡⎤⎣⎦;向左移动*2()k k ÎN 个单位时,图象纵坐标压缩为原来的12k 倍,对应值域为10,2k ⎡⎤⎢⎥⎣⎦.图象如图所示,若对任(,]x m ∈-∞都有()6f x ≤,由23262<<及图象可得max ()6f m =,[]max 4,6m Î,又当[]4,6x ∈时,4()422x f x -=-,故有max max max 42()4222764log m m f m -=⇒=+=-,故实数m 的取值范围为27,4log 2⎛⎤-∞+ ⎥⎝⎦.故选:ABC.三、填空题13.已知幂函数()()22321mm f x m x -+=-在()0,∞+上单调递增,则实数m 的值为______【正确答案】0由题可得()2211320m m m ⎧-=⎪⎨-+>⎪⎩,解出即可.【详解】由题可得()2211320m m m ⎧-=⎪⎨-+>⎪⎩,解得0m =.故0.14.函数()2lg 243y kx kx =--+的定义域为R ,则实数k 的取值范围是_______________.【正确答案】3,02⎛⎤- ⎥⎝⎦【分析】根据题意,将问题转化为22430kx kx --+>恒成立问题,结合二次函数的性质即可得解.【详解】由题意可知,22430kx kx --+>恒成立,当0k =时,30>恒成立,当0k ≠时,20Δ16240k k k <⎧⎨=+<⎩,解得302k -<<,综上:302k -<≤,故k 的取值范围为3,02⎛⎤- ⎥⎝⎦.故答案为.3,02⎛⎤- ⎥⎝⎦15.已知π3cos()124α+=-,则πsin(2)3α-=_________.【正确答案】18-【分析】利用诱导公式变形,再借助二倍角的余弦公式计算作答.【详解】因为π3cos 124α⎛⎫+=- ⎪⎝⎭,则ππππsin 2sin2cos 2312212ααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫-=+-=-+ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦2π118112cos 11286α⎛⎫=-+=-- ⎪⎝⎭.故答案为.18-16.函数π()2sin()(0)4f x x ωω=+>,若()f x 在区间()π,2π内无最值,则ω的取值范围是_________.【正确答案】1150,,848⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦【分析】根据正弦函数的图像与性质,可求得取最值时的自变量值,由()f x 在区间()π,2π上没有最值可知()πππ,2π4kωω+∉,进而可知πππ4k ωω+≤或ππ2π4k ωω+≥,解不等式并取k 的值,即可确定ω的取值范围.【详解】函数()()π2sin ,04f x x ωω⎛⎫=+> ⎪⎝⎭,由正弦函数的图像与性质可知,当取得最值时满足πππ,Z 42x k k ω+=+∈,解得ππ,Z 4kx k ωω=+∈,由题意可知,()f x 在区间()π,2π上没有最值,则2π2π,<1T ωω=>则()πππ,2π4kωω+∉,Z k ∈,所以πππ4k ωω+≤或ππ2π4k ωω+≥,因为0ω>,解得14k ω≥+或1182k ω≤+,当0k =时,代入可得14ω≥或18ω≤,当1k =时,代入可得54ω≥或58ω≤,当2k =时,代入可得94ω≥或98ω≤,此时无解.综上可得108ω<≤或1548ω≤≤,即ω的取值范围为1150,,848⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦.故答案为.1150,,848⎛⎤⎡⎤⋃ ⎥⎢⎥⎝⎦⎣⎦四、解答题17.{}|26A x a x a =-<<-,105x B x x ⎧⎫+=<⎨⎬-⎩⎭(1)若4a =,求R A ð;(2)若A B B ⋃=,求实数a 的取值范围.【正确答案】(1)(][),42,A =-∞-⋃+∞R ð;(2)2a ≤.【分析】(1)根据a 的值得出集合A ,再由集合的补集运算得出R A ð;(2)先求出集合B ,再由A B B ⋃=,得出A B ⊆,分集合A =∅和A ≠∅两种情况讨论可得出实数a 的取值范围.【详解】(1)若4a =,则{}()|424,2A x x =-<<=-,所以(][),42,A =-∞-⋃+∞R ð,(2)由105x x +<-得15x -<<,所以()1,5B =-,因为A B B ⋃=,所以A B ⊆,①当A =∅时,26a a -≤-,2a ∴≤;②当A ≠∅时,即2a >时,要使A B ⊆,则需1265a a -≥-⎧⎨-≤⎩,解得1112a a ≤⎧⎪⎨≤⎪⎩,解得1a ≤,所以此时a 无解.综上:实数a 的取值范围是2a ≤.本题考查集合间的子集关系和并集、补集运算,由集合的并集结果得出集合间的子集关系是本题的关键,注意需考虑子集是空集和不是空集的情况分类讨论,属于基础题.18.已知()()()()3πsin 3πtan πsin 2πcos tan 3π2f αααααα⎛⎫-+- ⎪⎝⎭=⎛⎫-- ⎪⎝⎭.(1)化简()f α;(2)若()40π(),5f αα∈=-,,求1cos 2sin 2αα+的值.【正确答案】(1)()cos f αα=(2)43-【分析】(1)利用诱导公式即可化简()f α;(2)利用同角三角函数的基本关系可求tan α的值,进而根据二倍角公式化简1cos 2sin 2αα+,即可得出答案.【详解】(1)根据诱导公式得:()()()()3πsin 3πtan πsin 2πcos tan 3π2f αααααα⎛⎫-+ ⎪⎝⎭=⎛⎫-- ⎪⎝⎭()()sin tan cos cos sin tan αααααα⋅⋅-==⋅-.(2)因为()40,π(),5f αα∈=-,所以4()cos 5f αα==-,sin 0α>,所以由22sin cos 1αα+=可得:33sin tan 54αα==-,所以21cos 22cos 14sin 22sin cos tan 3αααααα+===-.19.已知函数()sin()f x A x B ωϕ=++的一部分图象如图所示,如果0A >,0ω>,π2ϕ<.(1)求函数()f x 的解析式;(2)当ππ,66x ⎡⎤∈-⎢⎥⎣⎦时,求函数()f x 的取值范围.【正确答案】(1)()π2sin 226f x x ⎛⎫=++ ⎪⎝⎭(2)[]1,4【分析】(1)由函数的最大值和最小值求出A ,B ,由周期求出ω,由特殊点求出ϕ,即可求得函数解析式;(2)由ππ,66x ⎡⎤∈-⎢⎥⎣⎦求出π26x +的范围,再求出πsin 26⎛⎫+ ⎪⎝⎭x 的取值范围,即可求得函数的取值范围.【详解】(1)由图象可知,4022A -==,4022B +==,设()f x 最小正周期为T ,12π5πππ441264T ω=⨯=-=,∴2ω=,∴()()2sin 22f x x ϕ=++,又∵ππ2sin 22466f ϕ⎛⎫⎛⎫=⨯++= ⎪ ⎪⎝⎭⎝⎭,且π2ϕ<,∴ππ22π62k ϕ⨯+=+,k ∈Z ,∴π6ϕ=,∴函数()f x 的解析式为()π2sin 226f x x ⎛⎫=++ ⎪⎝⎭.(2)当ππ,66x ⎡⎤∈-⎢⎥⎣⎦时,πππ2662x ⎡⎤+∈-⎢⎥⎣⎦,,π1sin 2162x ⎛⎫⎡⎤+∈- ⎪⎢⎥⎝⎭⎣⎦,,∴函数()π2sin 226f x x ⎛⎫=++ ⎪⎝⎭的取值范围是[]1,4.20.已知函数()2log f x x =.(1)设函数()g x 是定义域在R 上的奇函数,当0x >时,()()g x f x =,求函数()g x 的解析式;(2)当14x ≤≤时,函数()24a x x h x f f ⎛⎫⎛⎫=⋅ ⎪ ⎝⎭⎝⎭(其中02a <≤)的最小值为14-,求实数a 的值.【正确答案】(1)()()22log ,00,0log ,0x x g x x x x ⎧>⎪==⎨⎪--<⎩(2)1【分析】(1)根据函数的奇偶性对解析式进行求解即可;(2)由题意,化简()h x 后,使用换元法进行求解即可.【详解】(1)当0x >时,()()2log g x f x x ==,当0x <时,0x ->,∴()()2log g x x -=-又∵()g x 为奇函数,∴当0x <时,()()()2log g x g x x =--=--,又∵()g x 是定义域在R 上的奇函数,∴()00g =,综上所述,函数()g x 的解析式为()()22log ,00,0log ,0x x g x x x x ⎧>⎪==⎨⎪--<⎩.(2)当14x ≤≤时,02a x >,04x>,∴()()()222222log log log log 2log log 42424aa a x x x x h x f f x x ⎛⎫⎛⎫=⋅==-- ⎪ ⎪⎝⎭⎝⎭()()22log log 2x a x =--令2log x t =,当14x ≤≤时,02t ≤≤,设()()()()2222F t t a t t a t a =--=-++,[]0,2t ∈,∵02a <≤,∴由二次函数知识知,当(]21,22a t +=∈时,()F t 最小值为22a F +⎛⎫⎪⎝⎭,令()2221244a a F -+⎛⎫=-=- ⎪⎝⎭,解得3a =(舍)或1a =,∴当14x ≤≤时,函数()24a x x h x f f ⎛⎫⎛⎫=⋅ ⎪ ⎪⎝⎭⎝⎭(其中02a <≤)的最小值为14-,则实数a 的值为1.21.已知函数2211()cos sin cos 222222x x x xf x =-(1)将函数()f x 化简成sin()A x ωϕ+的形式,并求出函数的最小正周期;(2)将函数()f x 的图象各点的横坐标缩小为原来的12(纵坐标不变),再向左平移π12个单位长度,得到函数()y g x =的图象.若方程2()1g x m -=在[0,]2x π∈上有两个不同的解1x ,2x ,求实数m 的取值范围,并求12tan()x x +的值.【正确答案】(1)()πsin 6f x x ⎛⎫=+ ⎪⎝⎭,最小正周期为2π(2)实数m 的取值范围是)1,1-,()12tan x x +【分析】(1)使用三角恒等变换和辅助角公式化简()f x ,并利用2πT ω=求出最小正周期即可.(2)先使用伸缩和平移变换得到()g x ,再将方程2()1g x m -=等价变换为1()2m g x +=,由()g x 的图象和性质求出12+m 的取值范围,即可求出实数m 的取值范围,同时,利用()g x 的对称性,可求出12tan()x x +的值.【详解】(1)2211()cos sin cos 222222x x x xf x =-221cos sin 2sin cos 222222x x x x⎛⎫=-+⨯ ⎪⎝⎭1cos 2x x =+πsin 6x ⎛⎫=+ ⎪⎝⎭,∴函数()f x 的最小正周期2π2π1T ==.(2)由(1)()πsin 6f x x ⎛⎫=+ ⎪⎝⎭,将函数()f x 的图象各点的横坐标缩小为原来的12(纵坐标不变),再向左平移π12个单位长度,得到函数()y g x =的图象,∴()πππsin 2sin 21263g x x x ⎡⎤⎛⎫⎛⎫=++=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由πππ2π22π232k x k -+≤+≤+,k ∈Z ,得5ππππ1212k x k -+≤≤+,k ∈Z ,∴()πsin 23g x x ⎛⎫=+ ⎪⎝⎭在区间5πππ,π1212k k ⎡⎤⎢⎥⎣++⎦-(k ∈Z )上单调递增,同理可求得()πsin 23g x x ⎛⎫=+ ⎪⎝⎭在区间π7ππ,π1212k k ⎛⎫++ ⎪⎝⎭(k ∈Z )上单调递减,且()g x 的图象关于直线ππ122k x =+,k ∈Z 对称,方程2()1g x m -=等价于1()2m g x +=,∴当[0,]2x π∈时,方程1()2m g x +=有两个不同的解1x ,2x ,由()g x 单调性知,()g x 在区间π0,12⎡⎤⎢⎥⎣⎦上单调递增,在区间ππ,122⎛⎤⎥⎝⎦上单调递减,且()π06g g ⎛⎫== ⎪⎝⎭,π112g ⎛⎫= ⎪⎝⎭,π2g ⎛⎫= ⎪⎝⎭112m +≤<时,方程1()2m g x +=有两个不同的解1x ,2x ,11m ≤<,实数m 的取值范围是)1,1-.又∵()g x 的图象关于直线π12x =对称,∴12π212x x +=,即12π6x x +=,∴()12tan x x +=22.函数2π()()cos()sin()3f x x x x ωϕωϕωϕ=+-+⋅++-π(0,0)2ωϕ><<同时满足下列两个条件:①()f x 图象最值点与左右相邻的两个对称中心构成等腰直角三角形;②2(,0)3是()f x 的一个对称中心;(1)当x ∈[0,2]时,求函数()f x 的单调递减区间;(2)令2511()()(),643g x f x f x m =-+-+若g (x )在53[,]62x ∈时有零点,求此时m 的取值范围.【正确答案】(1)10,6⎡⎤⎢⎥⎣⎦和7,26⎡⎤⎢⎥⎣⎦(2)171,648⎡⎤--⎢⎥⎣⎦【分析】(1)化简()f x 的解析式,根据条件①②求得,ωϕ,利用整体代入法求得()f x 的单调递减区间.(2)化简()g x 的解析式,通过分离常数法,结合三角函数的值域求得m 的取值范围.【详解】(1)2π()()cos()sin()3f x x x x ωϕωϕωϕ=+-+⋅++-()()21()cos()sin cos 224x x x x ωϕωϕωϕωϕ⎡⎤=+-+⋅+++-⎢⎥⎣⎦21sin()cos()()2x x x ωϕωϕωϕ=-+++11cos(22)sin(22)4224x x ωϕωϕ++=-++⨯-1sin(22)cos(22)44x x ωϕωϕ=-+++12πsin 2223x ωϕ⎛⎫=++ ⎝⎭.()f x 的最大值是12,由于()f x 图象最值点与左右相邻的两个对称中心构成等腰直角三角形,所以12ππ2,2,2222T T ωω=⨯===,()12πsin π223f x x ϕ⎛⎫=++ ⎪⎝⎭,由于2(,0)3是()f x 的一个对称中心,所以2π2π4πsin 2sin 20333ϕϕ⎛⎫⎛⎫++=+=⎪ ⎪⎝⎭⎝⎭,所以4ππ2π2π,,Z 323k k k ϕϕ+==-∈,由于π02ϕ<<,所以π3ϕ=,则()12π2π14πsin πsin π23323f x x x ⎛⎫⎛⎫=++=+ ⎪⎝⎭⎝⎭,由π4π3π2ππ2π232k x k +≤+≤+,解得5122,Z 66k x k k -≤≤+∈,由于[]0,2x ∈,所以()f x 的单调递减区间是10,6⎡⎤⎢⎥⎣⎦和7,26⎡⎤⎢⎥⎣⎦.(2)()515π4π1π1sin πsin πcos π6263222f x x x x⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()11π4π11sin πsin ππsin π323322f x x x x⎛⎫⎛⎫-=-+=+=- ⎪ ⎪⎝⎭⎝⎭,所以()()211cos πsin π48g x x x m =-+,依题意,()g x 在53,62x ⎡⎤∈⎢⎥⎣⎦时有零点,即方程()211cos πsin π048x x m -+=在53,62x ⎡⎤∈⎢⎥⎣⎦时有解,即()211cos πsin π48m x x =-+在53,62x ⎡⎤∈⎢⎣⎦时有解,()211cos πsin π48m x x =-+()2111sin πsin π48x x ⎡⎤=--+⎣⎦()2111sin πsin π484x x =+-()21117sin π4464x ⎡⎤=+-⎢⎥⎣⎦,()53531,,ππ,π,sin π1,62622x x x ⎡⎤⎡⎤⎡⎤∈∈∈-⎢⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,()133sin π,444x ⎡⎤+∈-⎢⎣⎦,()219sin π0,416x ⎡⎤⎡⎤+∈⎢⎥⎢⎥⎣⎦⎣⎦,所以171,648m ⎡⎤∈--⎢⎥⎣⎦.。
黑龙江省双鸭山市高一下学期开学数学试卷

黑龙江省双鸭山市高一下学期开学数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2018高一上·武汉月考) 设集合,,对于“既参加自由泳又参加蛙泳的运动员”用集合运算表示()A .B .C .D .2. (2分)已知10b1(2)=a02(3),则a+b的值为()A . 0B . 1C . 2D . 33. (2分)(2020·湛江模拟) 函数为奇函数,且在R上为减函数,若,则满足的x的取值范围是().A .B .C .D .4. (2分)某算法程序如图所示,执行该程序,若输入4,则输出的S为()A . 36B . 19C . 16D . 105. (2分)函数f(x)=lnx+2x﹣7的零点所在的区间为()A . (0,1)B . (1,2)C . (2,3)D . (3,4)6. (2分)已知实数x∈[0,8],执行如右图所示的程序框图,则输出的x不小于55的概率为()A .B .C .D .7. (2分) (2019高一下·广东期末) 已知三棱锥,侧棱两两垂直,且,则以为球心且1为半径的球与三棱锥重叠部分的体积是()A .B .C .D .8. (2分) (2019高二上·运城月考) 如图,为正方体,下面结论:① 平面;② ;③ 平面;④直线与所成的角为45°.其中正确结论的个数是()A . 1B . 2C . 3D . 49. (2分) (2016高一下·辽宁期末) 如图的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的()A . c>xB . x>aC . c>bD . b>c10. (2分)圆关于直线对称的圆的方程是()A .B .C .D .11. (2分)(2017·上高模拟) 已知函数是奇函数,则方程g(x)=2的根为()A . -B .C . 6D . ﹣612. (2分)已设是函数的反函数,若,则f(a+b)的值为()A . 1B . 2C . 3D .二、填空题: (共4题;共4分)13. (1分) (2016高二下·大庆期末) 已知函数f(x)=logax在定义域内单调递增,则函数g(x)=loga (3﹣2x﹣x2)的单调递增区间为________.14. (1分) (2019高二下·海安月考) 执行如图所示的伪代码,输出的结果是________.S←1I←3While S≤200S←S×II←I+2End WhilePrint I15. (1分)(2018·张家口期中) 已知定义在R上的函数f(x)满足f(x+1)=f(1﹣x)且在[1,+∞)上是增函数,不等式f(2a+1)≤f(a+2)成立时,求实数a的取值范围________.16. (1分)如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的体积是________三、解答题 (共6题;共60分)17. (10分) (2020高二下·张家口期中) 已知全集,若集合, B={x|x-m<0} .(1)若,求;(2)若 , 求实数的取值范围.18. (10分) (2015高二上·三明期末) 某乐园按时段收费,收费标准为:每玩一次不超过1小时收费10元,超过1小时的部分每小时收费8元(不足1小时的部分按1小时计算).现有甲、乙二人参与但都不超过4小时,甲、乙二人在每个时段离场是等可能的.为吸引顾客,每个顾客可以参加一次抽奖活动.(1)用(10,10)表示甲乙玩都不超过1小时的付费情况,求甲、乙二人付费之和为44元的概率;(2)抽奖活动的规则是:顾客通过操作按键使电脑自动产生两个[0,1]之间的均匀随机数x,y,并按如图所示的程序框图执行.若电脑显示“中奖”,则该顾客中奖;若电脑显示“谢谢”,则不中奖,求顾客中奖的概率.19. (10分) (2019高一上·咸阳期中) 已知函数,,其中,设.(1)判断的奇偶性,并说明理由;(2)若,求使成立的x的集合20. (10分) (2018高二上·芮城期中) 已知圆C过点且圆心在直线上(1)求圆C的方程(2)设直线与圆C交于A、B两点,是否存在实数a使得过点P(2,0)的直线垂直平分AB?若存在,求出a值,若不存在,说明理由。
黑龙江省双鸭山市高一数学下学期期末考试试题 理(含解析)

黑龙江省双鸭山市2016-2017学年高一数学下学期期末考试试题理(含解析)(时间:120分钟总分:150分,交答题纸)第Ⅰ卷(12题:共60分)一、选择题(包括12小题,每小题5分,共60分)1. 在中,若,则的形状是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定【答案】C【解析】,故选C.2. 已知一几何体的三视图,则它的体积为()A. B. C. D.【答案】C【解析】所求体积,故选C.3. 过两点,的直线的倾斜角是,则()A. B. C. D.【答案】D【解析】斜率,故选D.4. 若一个三角形,采用斜二测画法作出其直观图,则其直观图的面积是原三角形面积的()A. B. C. D.【答案】C5. 如果且,那么的大小关系是()A. B.C. D.【答案】B【解析】取,故选C.6. 等差数列中,已知,则数列前项和等于()A. B. C. D.【答案】B【解析】试题分析:由已知得,,所以,,,故选B.考点:等差数列的性质与求和公式.7. 已知正方体的个顶点中,有个为一侧面是等边三角形的正三棱锥的顶点,则这个正三棱锥与正方体的全面积之比为()A. B. C. D.【答案】A【解析】所求的全面积之比为:,故选A.8. 在中,已知其面积为,则= ()A. B. C. D.【答案】C【解析】或(舍),故选C.9. 若,成等差数列,成等比数列,则最小值是()A. B. C. D.【答案】D【解析】由已知可得,故选D.10. 正四棱锥的侧棱长与底面边长都相等,是的中点,则与所成角的余弦值为()A. B. C. D.【答案】D【解析】建立如图所示坐标系,令正四棱锥的棱长为,故选C.11. 已知点和,在轴上求一点,使得最小,则点的坐标为()A. B. C. D.【答案】B【解析】...............12. 如下图是一个正方体的平面展开图,在这个正方体中①②与成角③与为异面直线④以上四个命题中,正确的序号是()A. ①②③B. ②④C. ③④D. ②③④【答案】D【解析】由已知中正方体的平面展开图,得到正方体的直观图如上图所示:由正方体的几何特征可得:①不平行,不正确;②AN∥BM,所以,CN与BM所成的角就是∠ANC=60°角,正确;③与不平行、不相交,故异面直线与为异面直线,正确;④易证,故,正确;故选D.第Ⅱ卷(10题:共90分)二、填空题(包括4小题,每小题5分,共20分)13. 不等式的解集为____________________。
黑龙江省双鸭山市第一中学2023-2024学年高一下学期开学考试数学试题
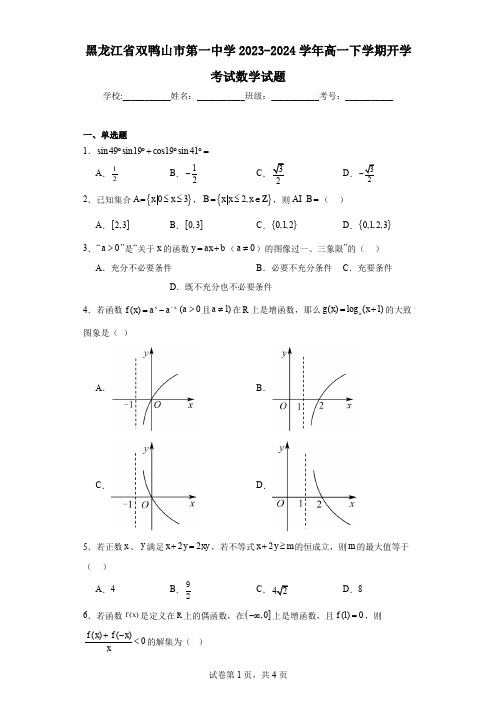
D.既不充分也不必要条件
4.若函数 f (x) ax ax (a 0 且 a 1) 在 R 上是增函数,那么 g(x) loga (x 1) 的大致 图象是( )
A.
B.
C.
D.
5.若正数 x 、 y 满足 x 2y 2xy ,若不等式 x 2y m 的恒成立,则 m 的最大值等于
B.若 ac2 bc2 ,则 a b D.若 a b , c d ,则 ac bd
11.已知 f x 是定义在 R 上的函数,且满足 f x f x 1 1,当 x 10, 时,f x x2 ,
则下列命题正确的是( )
A. f x 是周期为 2 的函数
B.当 x 1, 2 时, f x 2x x2
2
2.已知集合 A x 0 x 3 , B x x 2, x Z ,则 AI B ( )
A. 2, 3
B. 0, 3
C.0,1, 2
D.0,1, 2,3
3.“ a 0 ”是“关于 x 的函数 y ax b ( a 0 )的图像过一、三象限”的( )
A.充分不必要条件
B.必要不充分条件 C.充要条件
(1)求 f x 的解析式;
(2)若方程
af
x
sin
2x
a
1
0
在
π 4
,
π 2
上有实数解,求实数
a
的取值范围.
试卷第 4 页,共 4 页
() A.4
B.
9 2
C. 4 2
D.8
6.若函数 f (x) 是定义在 R 上的偶函数,在 , 0 上是增函数,且 f (1) 0 ,则
f (x) f (x) 0 的解集为( ) x
黑龙江省高一下学期开学数学试卷 (I)卷

黑龙江省高一下学期开学数学试卷(I)卷姓名:________ 班级:________ 成绩:________一、选择题: (共15题;共30分)1. (2分)已知集合,则的子集的个数()A . 2B . 4C . 5D . 72. (2分)一次函数y=x+3与y=-2x+6的图象的交点组成的集合是()A . {4,1}B . {1,4}C . {(4,1)}D . {(1,4)}3. (2分)已知函数,若f(x0)>1,则x0的取值范围为()A . (-1,1)B . (-1,+∞)C .D .4. (2分) (2015高三上·厦门期中) 已知函数f(x)= ,若f[f(0)]=4a,则实数a等于()A .B .C . 2D . 95. (2分) (2018高一上·南昌月考) 已知函数则()A .B .C .D .6. (2分) (2016高二上·包头期中) 利用斜二测画法得到的:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形.以上结论,正确的是()A . ①②B . ①C . ③④D . ①②③④7. (2分) (2017高一下·景德镇期末) 已知平面α及直线a,b,则下列说法正确的是()A . 若直线a,b与平面α所成角都是30°,则这两条直线平行B . 若直线a,b与平面α所成角都是30°,则这两条直线不可能垂直C . 若直线a,b平行,则这两条直线中至少有一条与平面α平行D . 若直线a,b垂直,则这两条直线与平面α不可能都垂直8. (2分) (2016高二上·怀仁期中) 如图,在三棱锥S﹣ABC中,G1 , G2分别是△SAB和△SAC的重心,则直线G1G2与BC的位置关系是()A . 相交B . 平行C . 异面D . 以上都有可能9. (2分) (2019高二上·杭州期中) 三棱锥的高为,若三条侧棱两两垂直,则为的()A . 内心B . 外心C . 垂心D . 重心10. (2分)在空间四边形ABCD中,E,F分别为边AB,AD上的点,且AE:EB=AF:FD=1:4,又H,G分别为BC,CD的中点,则()A . BD∥平面EFG,且四边形EFGH是矩形B . EF∥平面BCD,且四边形EFGH是梯形C . HG∥平面ABD,且四边形EFGH是菱形D . EH∥平面ADC,且四边形EFGH是平行四边形11. (2分) (2016高二上·桐乡期中) 已知直线m,n和平面α,满足m⊂α,n⊥α,则直线m,n的关系是()A . 平行B . 异面C . 垂直D . 平行或异面12. (2分) (2018高一上·武威期末) 设m,n是两条不同的直线,α,β是两个不同的平面.下列命题中正确的是()A . 若,,,则B . 若,,,则C . 若,,,则D . 若,,,则13. (2分) (2016高一上·天河期末) 一个几何体的三视图如图所示,则该几何体的表面积为()A . 3πB . 4πC . 2π+4D . 3π+414. (2分)直线y=﹣2x+b一定通过()A . 第一、三象限B . 第二、四象限C . 第一、二、四象限D . 第二、三、四象限15. (2分) (2015高二下·双流期中) 已知F1 , F2是双曲线的两个焦点,Q是双曲线上除顶点外的任意一点.从某一焦点引∠F1QF2的平分线的垂线,垂足为P.则P的轨迹为()A . 抛物线B . 椭圆C . 圆D . 双曲线二、填空题 (共5题;共5分)16. (1分) (2017高一上·长宁期中) 已知集合A={x|﹣2≤x≤5},B={x|m+1≤x≤2m﹣1},若B⊆A,则实数m的取值范围是________.17. (1分) (2016高三上·德州期中) 定义:f1(x)=f(x),当n≥2且x∈N*时,fn(x)=f(fn﹣1(x)),对于函数f(x)定义域内的x0 ,若正在正整数n是使得fn(x0)=x0成立的最小正整数,则称n是点x0的最小正周期,x0称为f(x)的n~周期点,已知定义在[0,1]上的函数f(x)的图象如图,对于函数f(x),下列说法正确的是________(写出所有正确命题的编号)①1是f(x)的一个3~周期点;②3是点的最小正周期;③对于任意正整数n,都有fn()= ;④若x0∈(,1],则x0是f(x)的一个2~周期点.18. (1分)已知函数(3﹣ax)(a≠0且a≠±1)在[0,2]上是减函数,则实数a的取值范围是________.19. (1分)已知某几何体的三视图如图所示(单位:cm),其中正(主)视图、侧(左)视图都是等腰直角三角形,则这个几何体的体积是________.20. (1分) (2018高二下·西宁期末) 已知曲线C:(为参数),与直线:(t 为参数),交于两点,则 ________.三、解答题 (共6题;共50分)21. (15分) (2016高一上·胶州期中) 已知函数,且.(1)求m的值;(2)判断f(x)在(0,+∞)上的单调性,并给予证明;(3)求函数f(x)在区间[﹣5,﹣1]上的最值.22. (10分) (2016高三上·绍兴期末) 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB,已知BC=2AD=2AB=2.(1)证明:BD⊥平面DEC;(2)若二面角A﹣ED﹣B的大小为30°,求EC的长度.23. (5分)方程x2+y2﹣4x+2my+2m2﹣2m+1=0表示一个圆.(1)求m的取值范围;(2)求这个圆的面积最大时圆的方程.24. (5分) (2017高二下·孝感期中) 已知四棱锥P﹣ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,.(Ⅰ)求证:平面PAM⊥平面PDM;(Ⅱ)若点E为PC中点,求二面角P﹣MD﹣E的余弦值.25. (10分) (2015高三上·锦州期中) 已知x2+y2=9的内接三角形ABC中,A点的坐标是(﹣3,0),重心G的坐标是,求:(1)直线BC的方程;(2)弦BC的长度.26. (5分)已知函数f(x)=x2﹣x﹣2a (1)若a=1,求函数f(x)的零点;(2)若f(x)有零点,求a的范围.参考答案一、选择题: (共15题;共30分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、15-1、二、填空题 (共5题;共5分) 16-1、17-1、18-1、19-1、20-1、三、解答题 (共6题;共50分) 21-1、21-2、21-3、22-1、22-2、23-1、24-1、25-1、25-2、26-1、。
黑龙江省双鸭山市高一下学期开学数学试卷

黑龙江省双鸭山市高一下学期开学数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)设f(x)=(1+)x-. 其中, t为常数;集合M={x|﹤0,},则对任意实常数t,总有()A . -3M,0MB . -3M,0MC . -3M,0MD . -3M,0M2. (2分)已知定义在上的奇函数,满足,且在区间上是增函数,若方程,在区间上有四个不同的根,则=()A . -12B . -8C . -4D . 43. (2分)函数y=的值域是()A . RB . [,+∞)C . (2,+∞)D . (0,+∞)4. (2分) (2017高一上·濉溪期末) 设函数f(x)=|logax|(0<a<1)的定义域为[m,n](m<n),值域为[0,1],若n﹣m的最小值为,则实数a的值为()A .B . 或C .D . 或5. (2分) (2016高一上·桓台期中) 方程log2x+x﹣5=0在下列哪个区间必有实数解()A . (1,2)B . (2,3)C . (3,4)D . (4,5)6. (2分)下列命题中正确的是()A . 第一象限角必是锐角B . 终边相同的角相等C . 相等的角终边必相同D . 不相等的角其终边必不相同7. (2分)设α是第二象限角,且cos=﹣,则是()A . 第一象限角B . 第二象限角C . 第三象限角D . 第四象限角8. (2分) (2018高一下·广东期中) 已知,下列向量中,与反向的单位向量是()A .B .C .D .9. (2分) (2016高一上·长春期中) 函数f(x)=πx+log2x的零点所在区间为()A . (0,)B . (,)C . (,)D . (,1)10. (2分)已知函数若关于x的方程有3个不同的实根,则实数k的取值范围为()A .B .C .D .二、填空题: (共7题;共22分)11. (1分) (2017高一上·孝感期中) 已知函数f(x)=(m2﹣m﹣5)xm﹣1是幂函数,且当x∈(0,+∞)时,f(x)是增函数,则实数m的值为________.12. (2分)(2017·金华模拟) 比较lg2,(lg2)2 , lg(lg2)的大小,其中最大的是________,最小的是________.13. (1分)关于x的不等式ax2﹣5x+b<0的解集是(2,3),则a+b的值等于________14. (1分) (2017高一上·启东期末) 求值:sin1440°=________.15. (15分) (2016高一下·益阳期中) 已知0<α<π,tanα=﹣2.(1)求sin(α+ )的值;(2)求的值;(3)2sin2α﹣sinαcosα+cos2α16. (1分)在△ABC中,若对任意t∈R,恒有| ﹣t |≥| |,则∠C=________.17. (1分) (2019高一上·北京期中) 设函数,其中表示不超过的最大整数,如:, .若函数的图象与函数的图象恰有3个交点,则实数的取值范围是________.三、三.解答题 (共5题;共35分)18. (5分) (2019高一上·长春月考) 若集合,(Ⅰ)当时,求;(Ⅱ)若,求实数的取值范围 .19. (5分) (2016高一上·包头期中) 已知4a=2a+2 ,求不等式a2x+1>ax﹣1的解集.20. (10分) (2016高三上·沙市模拟) 已知△ABC中,=λ (0<λ<1),cosC= ,cos∠ADC=.(1)若AC=5.BC=7,求AB的大小;(2)若AC=7,BD=10,求△ABC的面积.21. (10分)(2017·成都模拟) 已知函数f(x)=|2x﹣a|+|2x+3|,g(x)=|x﹣1|+2.(1)解不等式|g(x)|<5;(2)若对任意x1∈R,都有x2∈R,使得f(x1)=g(x2)成立,求实数a的取值范围.22. (5分) (2019高一上·四川期中) 已知二次函数 b是实数,,若,且方程有两个相等的实根.Ⅰ 求函数的解析式;Ⅱ 求函数在区间上的最小值.参考答案一、选择题 (共10题;共20分)1-1、2-1、3、答案:略4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题: (共7题;共22分)11-1、12-1、13-1、14-1、15-1、15-2、15-3、16-1、17-1、三、三.解答题 (共5题;共35分) 18-1、19-1、20-1、20-2、21-1、21-2、22-1、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双鸭山市第一中学2017-2018学年度下学期高一(理科)数学开学
考试试题
一、选择题(本大题共12个小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合{}1,2,4A =,{}
240x x x m B =-+=。
若{}1A B =I ,则B =( )
A.{}1,3-
B.{}1,0
C.{}1,3
D.{}1,5 2.已知正弦函数f(x)的图像过点),(m 3
7π,则m 的值为( ) A .2 B .21 C .2
3 D .1 3.已知函数⎩⎨⎧>-≤=-)
1( )23(log )1( 2)(2x x x x f x ,若4)(=a f ,则实数=a ( )
A .2-或6
B .2-或310
C .2-或2
D .2或3
10 4.已知α是第二象限角,3
4tan -=α,则αsin 的值为( ) A .54 B .54- C .5
3 D .53- 5.函数()22x f x x =+-的零点所在的一个区间是( )
A. (1,2)
B.(0,1)
C. (-1,0)
D.(-2,-1)
6.在ABC ∆中,D 为AB 边上一点,12
AD DB =u u u r u u u r ,23CD CA CB λ=+u u u r u u r u u r ,则λ=( )
A .13- B. 13
C.1-
D.2
7.函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是( )
A .[2,2]- B. [1,1]- C. [0,4] D. [1,3]
8.在矩形ABCD
中,3,3,2AB BC BE EC ===u u u v u u u v ,点F 在边CD 上,
若3AB AF ⋅=u u u v u u u v ,则AE BF ⋅u u u v u u u v 的值为( )
A .0
B .833
C .-4
D .4 9.函数()2sin 1
x f x x =+的图象大致为( )
10. 已知1
32a -=,21211log ,log 33b c ==,则( ) A . a b c >> B .a c b >> C .c a b >> D .c b a >>
11.给出下列结论:①若扇形的中心角为2,半径为1,则该扇形的面积为1; ②函数()22
cos sin y x x x R =-∈是偶函数; ③点,08π⎛⎫ ⎪⎝⎭是函数5sin 24y x π⎛⎫=+ ⎪⎝⎭
图象的一个对称中心; ④函数cos sin y x x =-在0,2π⎡⎤⎢⎥⎣⎦
上是减函数.其中正确结论的个数为( ) A. 1 B. 2 C. 3 D. 4
12.正三角形ABC 内一点M 满足,45CM mCA nCB MCA =+∠=o u u u u r u u u r u u u r ,则m n
) A .213- B .13- C .2
13+ D . 13+
二、填空题:本大题共4小题,每小题5分,共20分,请把正确的答案填写在答题卡相应的横线上.
13. 幂函数f (x )=(m 2﹣4m+4)x 8m 6m 2+-在(0,+∞)为减函数,则m 的值为
14. 将函数x x f 2sin )(=的图象沿x 轴方向向右平移6
π个单位长度,再把横坐标缩短到原
来的12
(纵坐标不变),得到函数)(x g ,则)(x g 的解析式为 15. 化简:=︒⋅︒-︒80cos 10cos 21
35sin 2 16. 已知函数()f x 的定义域为R ,对任意12x x <,有1212
()()1f x f x x x ->--,且(1)1f =, 则不等式22(log |31|)2log |31|x x f -<--的解集..
为 三、解答题:解答应写出文字说明,证明过程或演算步骤.
17.(10分)已知角α的终边在第二象限,且与单位圆交于点)4
15,
(m P . (1)求实数m 的值; (2)求1)2
3sin()sin()2sin(+--+-απαππ
α的值.
18.(12分)已知向量(1,2),(,1)a b x →→== (1)当(2)(2)a b a b +⊥-r r r r 时,求x 的值;
(2)若,a b <>r r 为锐角,求x 的范围.
19.(12分)函数()sin()f x A x ωϕ=+(0,0,||2A πωϕ>><
) 的图象的一部分如图所示.
(1)求()f x 的表达式;
(2)求()f x 在区间[0,]2
π上的值域.
20. (12分)已知5
4)sin(,31)4cos(,20=+=-<<<<βαπβπβπα
. (1)求β2sin 的值;
(2)求)4cos(
π
α+的值. 21.(12分)已知向量)sin 4,(sin ),cos 3,sin 4(x a x x x ==,函数2)(-⋅=x f ,若)(x f 的图像关于),(012π对称.
(1)求实数a ,并求出
)(x f 的单调减区间; (2)若不等式()f x m ≤在0,2π⎡⎤⎢⎥⎣⎦
上有解,求实数m 的取值范围.
22.(12分)已知:函数)(),(x x f ϕ满足关系)()()(a x f x f x +⋅=ϕ(其中a 是常数)
(1)如果12)(,1-==x x f a ,求函数)(x ϕ的值域;
(2)如果x x f a sin )(,2==π
,且对任意R x ∈,存在R x x ∈21,,
使得)()()(21x x x ϕϕϕ≤≤恒成立,求||21x x -的最小值.。
