(精品word)知识点246--对顶角、邻补角(填空题)汇总(良心出品必属精品)
《邻补角与对顶角》课件

AC O
DB
如果两个角有一个公共顶点,并且其中一个角的两边
是另一个角的两边的反向延长线,那么这两个角互为
对顶角.如图中∠1 与∠3 互为对顶角,C
∠2 与∠4 互为对顶角.
A
12
4O 3 B D
注意:对顶角是成对出现的,指两个角之间的关系,
一个角的对顶角只有一个.
.
新知探究 跟踪训练
2.下列选项中, ∠1 与∠2 互为对顶角的是( D )
对顶角的识别方法 两个角互为对顶角必须满足两个条件:①两个角有一 个公共顶点;②一个角的两边分别是另一个角的两边 的反向延长线.二者缺一不可.
新知探究 知识点2: 对顶角的性质
∠1 与∠3 在数量上有什么关系呢? C A
我猜∠1 =∠3.
12
4O 3
B
D
你能进行证明吗?
已知:直线 AB 与 CD 相交于 O 点. C
对顶角相等
有一条无公共边
两直线相交时,邻补角 有四对
邻补角互补
12
3O
B
D
互为邻补角是互为补角的特殊情况. ∠1 +∠2=180°, ∠1 +∠3 =180°.
注意: (1)邻补角是成对出现的,单独的一个角或两个以上 的角不能称为邻补角. (2)邻补角不一定都是两条直线相交形成的,一条直 线与射线(端点在直线上)相交,也可以得到一对邻 补角. (3)互为邻补角的两个角一定互补,但互补的两个角 不一定是邻补角.
新知探究 跟踪训练
1.下列各图中,∠1 与∠2 互为邻补角的是( D )
邻补角的识别方法 互为邻补角的两个角必须满足以下条件:①有一条公 共边;②另一条边互为反向延长线. 二者缺一不可.
七上19讲《余角补角对顶角》知识点大网罗

七上19讲《余⾓补⾓对顶⾓》知识点⼤⽹罗写在前⾯本讲,我们继续来研究⾓,重点对余⾓,补⾓,对顶⾓作⼀个深⼊的复习归纳,这两节的内容难度不⼤,主要在于解答题的书写和⼀些概念的判断.⼀、知识梳理1、余⾓概念:如果两个⾓的和是90°,那么这两个⾓互为余⾓,简称互余.2、补⾓概念:如果两个⾓的和是180°,那么这两个⾓互为补⾓,简称互补.3、注意点:互为余⾓、互为补⾓仅仅表明了两个⾓的数量关系,并没有限制⾓的位置关系.4、邻补⾓概念:两个⾓有⼀条公共边,它们的另⼀条边互为反向延长线,具有这种关系的两个⾓,叫做邻补⾓.5、同⼀个⾓的补⾓与余⾓的关系:同⼀个⾓的补⾓⽐它的余⾓⼤ 90°.6、余⾓补⾓的性质:同⾓的余⾓相等,同⾓的补⾓相等.等⾓的余⾓相等,等⾓的补⾓相等.7、对顶⾓概念:⼀个⾓的两边分别是另⼀个⾓两边的反向延长线,且这两个⾓有公共顶点,那么这两个⾓是对顶⾓.(对顶⾓由两条相交直线产⽣)8、对顶⾓相等.9、数对顶⾓的对数:⼆、典型例题例1:判断正误:(1)⼀个⾓⼀定⼩于它的余⾓,也⼩于它的补⾓.(2)如果两个⾓互补,那么这两个⾓是锐⾓和钝⾓.(3)如果三个⾓的和为180°,则这三个⾓互补.(4)如果两个⾓相等,那么她们的补⾓也相等.(5)若∠1=∠2,则∠1和∠2是对顶⾓.(6)互补的⾓就是平⾓.(7)互余的两个⾓⼀定都是锐⾓.(8)不相等的两个⾓不是对顶⾓.解析:(1)错误,如60°⼤于它的余⾓30°,100°⼤于它的补⾓80°.(2)错误,两个⾓可以都为直⾓.(3)错误,互补是两个⾓之间的数量关系.(4)正确.(5)错误,⽐如⼀个⾓的⾓平分线,把这个⾓分成2个相等的⼩⾓不是对顶⾓.(6)错误,两个互补的⾓的度数之和是平⾓的度数.(7)正确.(8)正确.例2解析:例3:⼀个⾓的余⾓⽐它的补⾓的⼀半还少20°,这个⾓的度数为______°.分析:这种题⽬难度不⼤,可以直接解设这个⾓的度数为x,表⽰出这个⾓的余⾓和补⾓,根据题⽬,列出⽅程.当然本题还有⼀种做法,即设这个⾓的补⾓度数为x,表⽰出这个⾓的余⾓,同时,还要利⽤⼀个隐含的数量关系,同⼀个⾓的补⾓⽐它的余⾓⼤ 90°.解答:三、思维提升1、找余⾓补⾓例1:如图,O是直线AB上⼀点,∠AOE=∠FOD=90°,OB平分∠COD,图中与∠DOE互余的⾓有哪些?与∠DOE互补的⾓有哪些?分析:找互余的⾓,⾸先要找直⾓内部的射线将直⾓分成的2个⾓,或者可以形象的称为“邻余⾓”.其次,再找有没有其他⾓和“邻余⾓”中的⼀个相等,则和另⼀个也互余.找互补的⾓,⾸先找找有没有邻补⾓.再找有没有其他⾓和邻补⾓中的⼀个相等.这⾥∠DOE相邻的余⾓有2个,∠EOF,∠DOB,再找找有没有和这两个⾓相等的⾓.∠DOE在图中没有邻补⾓,因此,只能找和它相等的⾓,不难发现是∠AOF,找∠AOF的邻补⾓,再找和∠AOF的邻补⾓相等的⾓.解答:∵∠AOE=∠FOD=90°,∴∠BOE=90°∠3+∠4=90°,∠3+∠2=90°,∴∠2=∠4,∵OB平分∠COD,∴∠4=∠5,∠2=∠5,∴∠DOE互余的是∠2、∠4、∠5;∵∠1+∠2=90°,∠3+∠2=90°,∴∠3=∠1∵∠1+∠BOF=180°,∠BOF=∠2+∠3+∠4=∠5+∠3+∠4=∠EOC,∴与∠DOE互补的⾓是∠BOF、∠EOC.例2:如下图,AOE是⼀条直线,从点O引射线OB,OC,OD,若∠AOC=∠COE=∠BOD=90°,那么图中互余的⾓有哪⼏对?互补的⾓有哪⼏对?分析:思路与例1⼀致,先找位置相邻的余⾓,找邻补⾓,然后找有没有其他⾓与其中⼀个相等的⾓,对于两个直⾓,也别忘了它们互补.解答:∵∠AOC=∠COE=∠BOD=90°∴∠1+∠2=90°∠2+∠3=90°,∠3+∠4=90°,∠1+∠4=90°,互余的⾓有4对,∠1与∠2,∠2与∠3,∠3与∠4,∠1与∠4,∴∠1=∠3,∠2=∠4∵∠1+∠DOE=180°,∴∠3+∠DOE=180°,∠4+∠AOB=180°,∴∠2+∠AOB=180°,∠AOC+∠COE=180°,∠AOC+∠DOB=180°,∠DOB+∠COE=180°,互补的⾓有7对,∠1与∠DOE,∠3与∠DOE,∠4与∠AOB,∠2与∠AOB,∠AOC与∠COE,∠AOC与∠DOB,∠DOB与∠COE.例3:如图,直线 AB与CD相交于O,OF,OD分别是∠AOE,∠BOE的平分线,(1)写出∠DOE的补⾓;(2)要若∠BOE=62°,求∠AOD和∠EOF的度数;(3)求∠DOF的度数?分析:(1)要找∠DOE的补⾓,可以找它的邻补⾓,也可以找与∠DOE相等的⾓,再找出它的补⾓.(2)要求∠AOD,不⼀定⾮要⽤⾓度之和,可以⽤180°减去∠BOD,要求∠EOF,可以求∠AOE,再求其⼀半.(3)双⾓平分线问题,找到出现两次的边OE,则∠DOF看作∠FOE+∠DOE,利⽤⼀半加⼀半可求.解答:2、⽤⽅程思想例1:如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠BOF=30°,则∠AOC=______°.分析:要求∠AOC,其实就是求∠BOD.要求∠BOD,根据⾓平分线条件,可设∠EOD为x.,然后表⽰出∠EOF,进⽽表⽰出∠COE,则∠COE+∠EOD=180°,作为⽅程的相等关系.解答:∵OE平分∠BOD,∴∠BOD=2∠BOE,∵OF平分∠COE,∴∠COF=∠FOE,∴设∠BOE=x°,则∠BOD=2x°,∵直线AB、CD相交于点O,∴∠AOC=∠BOD=2x°,∠EOF=∠COF=(x+30)°,则∠COF+∠EOF+∠DOE=2(x+30)+30=180,解得:x=40,故∠AOC=80°.2、⽤⽅程思想例2:如图,直线AB、CD、EF相交于点O,∠AOD=∠BOD,且∠DOF与∠BOF的度数之⽐为3:1,求∠COE的度数.分析:要求∠COE,其实就是求∠FOD.⽽∠DOF与∠BOD的度数⽐已知,则可以设x,利⽤它们的差是∠BOD求解,⽽∠AOD=∠BOD,它们⼜是邻补⾓,则∠BOD的度数很快可知.解答:解设∠BOF=x°,∠DOF=3x°∴∠BOD=∠DOF-∠BOF=2x°∵∠AOD=∠BOD,∠AOD+∠BOD=180°,∴∠BOD=90°,2x=90,x=45∠DOF=135°.如何关注上讲思考题答案。
人教版七年级数学下册《邻补角、对顶角的定义及性质》课件ppt

解:(1)∠AOC的邻补角是∠AOD和 ∠COB;∠BOE的邻补角是 ∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB; ∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
D E
A
O
B
F
C
5. 在下图中,花坛转角(红色标注的角)按图纸要求为135°;施工结束 后,要求你检测它是否合格?请你设计检测的方法.
思考 :剪刀剪东西的过程中,你能说说∠AOC与∠AOD,∠AOC与∠BOD这两 对角的位置保持怎样的关系吗?
A
C
O
∠AOC和∠AOD有一条公共边AO,且∠AOC的
另一边是∠AOD另一边的反向延长线.
∠AOC和∠BOD有公共顶点,且∠AOC的两边 分别是∠BOD两边的反向延长线.
DB
一、邻补角的概念 邻补角:如果两个角有一条公共边,它们的另一边互为__反__向__延__长__线__,那 么这两个角互为邻补角.图中∠1的邻补角有__∠__2_,_∠__3___.
人教版 数学 七年级 下册
理解并掌握邻补角和对顶角的概念及性质.
掌握邻补角与对顶角的性质,并能运用它们的性质 进行角的计算及解决简单实际问题..
观察下列图片,说一说直线与直线有什么样的位置关系.
观察下列图片,说一说直线与直线有什么样的位置关系.
观察下列图片,说一说直线与直线有什么样的位置关系.
角的 名称
对 顶 角
邻 补 角
特征
性质 相同点
①两条直线相 交形成的角; ②有公共顶点;
③没有公共边。
对顶 角相 等。
①两条直线相 交而成; ②有公共顶点;
③有一条公共边。
(2021年整理)邻补角与对顶角

(完整版)邻补角与对顶角编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)邻补角与对顶角)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)邻补角与对顶角的全部内容。
(完整版)邻补角与对顶角编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望 (完整版)邻补角与对顶角这篇文档能够给您的工作和学习带来便利.同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈(完整版)邻补角与对顶角> 这篇文档的全部内容。
【学习目标】:1.发展空间观念,培养识图能力,推理能力和有条理表达能力2.在具体情境中了解邻补角、对顶角,能找出图形中的一个角的邻补角和对顶角,理解对顶角相等,并能运用它解决一些简单问题【重点难点】:邻补角与对顶角的概念.对顶角性质与应用。
对顶角①两条直线相交而成的角②有一个公共顶点③没有公共边。
对顶角相等对顶角的性质:对顶角相等邻补角①两条直线相交而成的角②有一个公共顶点③有一条公共边邻补角互补相同点和不同点1。
都是两直线相交而成的角,都有一个公共顶点,它们都是成对出现。
对顶角没有公共边而邻补角有一条公共边;2。
两条直线相交时,一个角的对顶角有一个,而一个角的邻补角有两个。
1、如图,直线a,b 相交,∠1=40°,则∠2=_______∠3=_______∠4=_______2、如图直线AB 、CD 、EF 相交于点O,∠BOE 的对顶角是_______,∠COF 的邻补角是________,若∠AOE=30°,那么∠BOE=_______,∠BOF=_______3、如图,直线AB 、CD 相交于点O ,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=________.4、判断下列图中是否存在对顶角。
中考数学复习---《相交线与平行线之邻补角、对顶角》知识点总结与练习题(含答案解析)

中考数学复习---《相交线与平行线之邻补角、对顶角》知识点总结与练习题(含答案解析)知识点总结1.邻补角:①定义:两条相交之间构成的四个角中,有公共顶点且有一条公共边,另一边互为反向延长线的两个角是邻补角。
②性质:邻补角互补。
2.对顶角:①定义:有公共顶点,两边均互为反向延长线的两个角是对顶角。
②性质:对顶角相等。
练习题1.(2022•北京)如图,利用工具测量角,则∠1的大小为()A.30°B.60°C.120°D.150°【分析】根据对顶角的性质解答即可.【解答】解:根据对顶角相等的性质,可得:∠1=30°,故选:A.2.(2022•苏州)如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是()A.25°B.30°C.40°D.50°【分析】先求出∠BOD的度数,再根据角的和差关系得结论.【解答】解:∵∠AOC=75°,∴∠AOC=∠BOD=75°.∵∠1=25°,∠1+∠2=∠BOD,∴∠2=∠BOD﹣∠1=75°﹣25°=50°.故选:D.3.(2022•自贡)如图,直线AB、CD相交于点O,若∠1=30°,则∠2的度数是()A.30°B.40°C.60°D.150°【分析】根据对顶角相等可得∠2=∠1=30°.【解答】解:∵∠1=30°,∠1与∠2是对顶角,∴∠2=∠1=30°.故选:A.4.(2022•桂林)如图,直线l1,l2相交于点O,∠1=70°,则∠2=°.【分析】根据对顶角的性质解答即可.【解答】解:∵∠1和∠2是一对顶角,∴∠2=∠1=70°.故答案为:70.。
对顶角垂直同位角内错角同旁内角精品资料+同步练习

对顶角、垂线、三线八角、邻补角一、基础知识点:1.在同一平面内,两条直线的位置关系有相交和平行。
2.相交:在同一平面内,有一个公共交点的两条直线称为相交线。
3.邻补角:(1)定义:有公共顶点,且有一条公共边,另一条边互为反向延长线,具有这种位置关系的两个角,互为邻补角。
(2)性质:位置——互为邻角数量——互为补角(两角之和为180°)4.对顶角:(1)定义:有一个公共顶点,并且有一个角的两边分别是另一个角两边的反向延长线,具有这种位置关系的两个角,互为对顶角(2几何语言:∵∠1+∠2=180°∠2+∠3=180°∴∠1=∠3(同角的补角相等)5、邻补角和对顶角的区别和联系注意:⑴对顶角是成对出现的,对顶角是具有特殊位置关系的两个角;⑵如果∠α与∠β是对顶角,那么一定有∠α=∠β;反之如果∠α=∠β,那么∠α与∠β不一定是对顶角⑶如果∠α与∠β互为邻补角,则一定有∠α+∠β=180°;反之如果∠α+∠β=180°,则∠α与∠β不一定是邻补角。
(4)两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个。
1、如图,已知直线AB、CD相交于点O,∠AOC=50°,求∠BOD、∠AOD、∠BOC的度数.解:∵∠BOD与∠AOC是对顶角∴==°()∵与是邻补角∴∠AOD=180°-∠AOC=180°-50°=130°∵与是对顶角∴∠BOC=∠AOD=130°()2、如图,直线AB、CD相交于点O,OE平分∠BOC.已知∠BOE=65°,求∠AOD、∠AOC的度数.50︒OADCBE65︒OADCB【基础知识点】 6、垂线⑴定义,当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
几何语言记作: 如图所示:AB ⊥CD ,垂足为O⑵垂线性质1:过一点有且只有一条直线与已知直线垂直 (与平行公理相比较记)⑶垂线性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
知识点246 对顶角、邻补角(解答题)
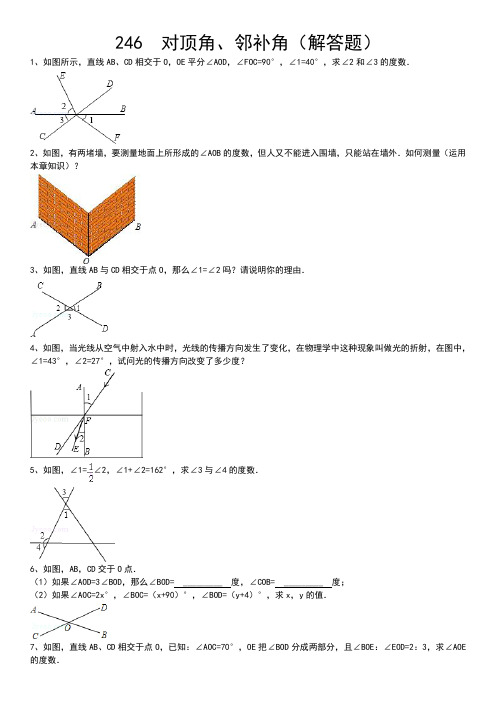
246 对顶角、邻补角(解答题)1、如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.2、如图,有两堵墙,要测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外.如何测量(运用本章知识)?3、如图,直线AB与CD相交于点O,那么∠1=∠2吗?请说明你的理由.4、如图,当光线从空气中射入水中时,光线的传播方向发生了变化,在物理学中这种现象叫做光的折射,在图中,∠1=43°,∠2=27°,试问光的传播方向改变了多少度?5、如图,∠1=∠2,∠1+∠2=162°,求∠3与∠4的度数.6、如图,AB,CD交于O点.(1)如果∠AOD=3∠BOD,那么∠BOD= _________ 度,∠COB= _________ 度;(2)如果∠AOC=2x°,∠BOC=(x+90)°,∠BOD=(y+4)°,求x,y的值.7、如图,直线AB、CD相交于点O,已知:∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,求∠AOE 的度数.8、如图(1)两条直线相交于一点,有_________ 对对顶角;如图(2)三条直线相交于一点,请写出所有对顶角;如图(3)n条直线相交于一点,有_________ 对对顶角.9、如图,直线AB、CD、EF相交于一点O,∠AOD=3∠AOF,∠AOC=120°,求∠BOE.10、如图,直线AB、CD,EF相交于点O,∠1=20°,∠BOC=80°,求∠2的度数.11、如图,直线AB与CD相交于点O,OD恰为∠BOE的角平分线.(1)图中∠AOD的补角是_________ (把符合条件的角都填出来);(2)若∠AOD=140°,求∠AOE的度数.12、(动手操作实验题)如图所示是小明自制对顶角的“小仪器”示意图:(1)将直角三角板ABC的AC边延长且使AC固定;(2)另一个三角板CDE的直角顶点与前一个三角板直角顶点重合;(3)延长DC,∠PCD与∠ACF就是一组对顶角,已知∠1=30°,∠ACF为多少?13、如图,直线a,b,c两两相交,∠1=2∠3,∠2=65°,求∠4的度数.14、如图,要测量两堵墙所形成的∠AOB的度数,但人不能进入围墙,如何测量请你写出两种不同的测量方法,并说明几何道理.15、如图,直线AB、CD相交于点0,OE平分∠AOC,∠AOD比∠AOE大75°,求∠AOD的度数.16、如图,要测量两堆围墙所形成的∠AOB的度数,但人既不能进入围墙内,又不能站在围墙上,只能站在墙外,如何测量?(要求用两种方法)17、附加题:在答题卡上相应题目的答题区域内作答.(1)计算:(﹣2)×(﹣3)= _________ .(2)已知直线AB与直线CD相交于O点,∠1=70°,则∠2= _________ 度.18、如图,把∠AOE绕点O按顺时针方向旋转一个角度,得∠COD,且使射线OC平分∠AOE的邻补角,已知∠DOE=30°,问∠AOE按顺时针方向旋转了多少度.19、如图,直线a,b,c相交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.20、如图所示,(1)是某城市古建筑群中一座古塔底部的建筑平面图,请你利用学过的知识设计如何测量出古塔外墙底部的∠ABC大小的方案,并说明理由.注:(2),(3)图备用.21、如图,三条直线AB、CD、EF相交于同一点O,若∠AOE=2∠AOC,∠COF=60°,求∠BOD的度数.22、如图∠AOD=90°,OD为∠BOC的平分线,OE为BO的延长线,若∠AOB=40°,求∠COE的度数.23、如图,直线AB与直线CD相交于点O,OE⊥AB,OF平分∠AOD,∠COE=28°.求∠AOC和∠DOF的度数.24、如图,直线AB,CD,EF交于点O,∠BOC=46°.射线OE平分∠BOC,求:(1)∠2和∠3的度数;(2)射线OF平分∠AOD吗?请说明理由.25、已知:如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠DOE=4:1.求∠AOF的度数.26、如图,一条光线AO射到墙上的镜子CD后沿OB方向反射出去,已知OM⊥CD,∠1=∠2.求证:∠2+∠3=90°.27、已知:直线AB与直线CD相交于点O,∠BOC=45°,(1)如图1,若EO⊥AB,求∠DOE的度数;(2)如图2,若EO平分∠AOC,求∠DOE的度数.28、已知直线AB、CD、EF相交于点O,∠1:∠3=3:1,∠2=20°,求∠DOE的度数.29、如图,已知直线AB、CD交于点O,且∠1:∠2=2:3,∠AOC=60°,求∠2的度数.30、如图,直线AB、CD相交于点O,OA平分∠COE,∠COE=80°,求∠BOD的度数.31、如图:AB、CD、EF相交于点O,∠1=50°,∠2=50°.求∠3的度数.32、如图,直线AB、CD交于O点,且∠BOC=80°,OE平分∠BOC,OF为OE的反向延长线.(1)求∠2和∠3的度数;(2)OF平分∠AOD吗?为什么?33、如图,AB、CD相交于点O,OB平分∠DOE,∠AOC=37°,求∠BOC,∠BOE的度数.34、小明同学认为对顶角可以这样定义:顶点公共,而且相等的角叫对顶角,你认为正确吗?如果你认为不正确请举一个反例,并对“对顶角”正确定义.答案与评分标准1、如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.考点:对顶角、邻补角;角平分线的定义。
相交线--邻补角、对顶角及性质

5.1.1(1)相交线--邻补角、对顶角及性质一.【知识要点】1.两条直线相交,可以得到四个角,我们把两条直线相交所构成的四个角中,有公共顶点但没有公共边的两个角叫做对顶角。
我们把两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角叫做邻补角。
邻补角互补,对顶角相等。
二.【经典例题】1.下面四个图形中,∠1与∠2是邻补角的是 ( )2.如图,当剪子口∠AOB 增大15°时,∠COD 增大 ,其根据是:_______________.3.对两条直线相交所得的四个角中,下面说法正确的是( )①没有公共边的两个角是对顶角 ②有公共边的两个角是对顶角 ③没有公共边的两个角是邻补角 ④有公共边的两个角是邻补角A.①②B.①③C.①④D.以上都不对4.∠1的对顶角是∠2,∠2的邻补角是∠3,若∠3=45º,则∠1的度数是( )A.45ºB.135ºC.45º和135ºD.90º三.【题库】【A 】1.如图,∠1与∠2是对顶角的是 ( )2.如下图所示,∠1与∠2是对顶角的是()A BOC D【B】1.下列说法正确的是()A.如果两个角相等,那么这两个角是对顶角B.有公共顶点的两个角是对顶角C.有公共顶点并且相等的两个角是对顶角D.如果两个角是对顶角,那么这两个角相等2.以下说法正确的是( )A.有公共顶点,并且相等的两个角是对顶角B.两条直线相交,任意两个角都是对顶角C.两角的两边互为反向延长线的两个角是对顶角D.两角的两边分别在同一直线上,这两个角互为对顶角3.下列说法中,正确的是()(A)相等的角是对顶角(B)有公共顶点,并且相等的角是对顶角(C)如果∠1与∠2是对顶角,那么∠1=∠2(D)两条直线相交所成的两个角是对顶角【C】1.如图AB、CD、EF相交于一点,∠1=50°,∠2=65°,则∠EOD=_____________度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
246 对顶角、邻补角(填空题)1、(2011•江西)一块直角三角板放在两平行直线上,如图所示,∠1+∠2=_________ 度.2、(2011•广西)如图,O是直线AB上一点,∠COB=30°,则∠1=_________ °.3、(2010•湘西州)如图,两条直线a、b相交于点O,若∠1=70°,则∠2=_________ .4、(2010•娄底)如图,直线AB、CD相交于点O.OE平分∠AOD,若∠BOD=100°,则∠AOE=_________ 度.5、(2006•宁德)用剪刀剪东西时,剪刀张开的角度如图所示,若∠1=25°,则∠2=_________ 度.6、(2002•山西)如图,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=28°,则∠EOF=_________ 度.7、(2002•宁德)如图,是用对顶角的量角器测量圆锥形零件的锥角的示意图,则此零件的锥角等于_________ 度.8、(2002•安徽)如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC 的度数是_________ 度.9、(1998•丽水)如图,直线AB与CD相交于点O,已知∠AOD=120°,则∠COB的补角是_________ 度.10、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于_________ 度.11、如图,当剪子口∠AOB增大15°时,∠COD增大_________ 度.12、如图,已知AB、CD相交于O,OE平分∠AOC,∠AOE=30°,则∠BOD=_________ 度.13、如图,已知直线AB、CD、EF相交于点O,∠1=95°,∠2=32°,则∠BOE=_________ 度.14、若∠1与∠2是对顶角,∠3与∠2互补,又知∠3=60°,则∠1=_________ .15、如图,已知直线a、b、c相交于点O,∠1=30°,∠2=70°,则∠3=_________ .16、如图,直线AB,CD相交于点O,∠AOC=54°,∠1比∠2大10°,则∠1=_________ 度;∠2=_________ 度.17、如图,a、b直线相交,∠1=36°,则∠3=_________ 度,∠2=_________度.18、如图,三条直线相交于一点,则∠1+∠2+∠3=_________ 度.19、若∠1的对顶角是∠2,∠2的邻补角是∠3,∠3=45°,则∠1的度数为_________ .20、如图,直线a,b,c两两相交,∠1=80°,∠2=2∠3,则∠4=_________ 度.21、如图,直线a与直线b相交于点O,∠1=30°,∠2=_________ .22、如图直线AB,CD,EF相交于点O,图中∠AOE的对顶角是_________ ,∠COF 的邻补角是_________ .23、如图,三条直线相交于O点,则图中相等的角(平角除外)有_________ 对.24、下列说法:①射线OA和射线AO是同一条射线;②两直线相交,只有一个交点;③相等的两个角的余角相等;④相等的两个角是对顶角.其中错误的是_________ .25、图中有_________ 对对顶角.26、如图所示,直线AB、CD交于点O,OE⊥AB且∠DOE=40°,则∠COE=_________ 度.26、如图,直线AB、CD相交于O,OE⊥OD,且∠AOC=40°,则∠BOD=_________ ,∠AOD=_________ .28、如图直线AB、CD、EF相交于同一点O,而且∠BOC=∠AOC,∠DOF=∠AOD,那么∠FOC=_________ 度.29、如图,直线AB、CD,EF相交于点O,则∠AOD的对顶角是_________ ,∠AOC 的邻补角是_________ ;若∠AOC=50°,则∠BOD=_________ ,∠COB=_________ .30、如图,若∠3+∠6=190°,则∠1+∠5=_________ ;若∠3+∠4=130°,则∠2+∠5= _________ .31、如图,直线AB,CD,EF相交于点O,若∠DOF=30°,∠AOE=20°,则∠BOC=_________ .32、如图,直线AB、CD、EF相交于点O,∠AOD=140°,∠DOE=70°,则∠AOF=_________ °.33、如图所示,当光线从空气射入水中时,光线的传播方向发生了改变,这就是光的折射现象.若∠1=42°,∠2=28°,则光的传播方向改变了_________ 度.34、如图,两条直线MN、PQ相交于点O,OG平分∠NOQ,∠1:∠2=2:5,则∠1=_________ 度,∠2=_________ 度.34、如图所示,直线a,b,c两两相交,∠1=60°,∠2=∠4,则∠3=_________ 度,∠5=_________ 度.36、三条直线两两相交于3个交点,共有_________ 对对顶角,_________ 对邻补角.37、如图,直线AB与直线CD相交于点0,E是∠AOD内一点,已知OE⊥AB,∠BOD=45°,则∠COE的度数为_________ 度.38、已知直线AB和CD相交于点O,OE平分∠BOC,已知∠BOE=65°,则∠AOC=_________ .39、如图,直线AB、CD相交于点O,∠1=50°,则∠2=_________ 度.40、如图,AB、CD相交于点O,OE平分∠BOD,∠AOC=80°,则∠BOE=_________ °.41、如图,直线AB、CD相交于O,∠1=30°,∠2=75°,则∠EOB=_________ .42、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=100°,则∠BOD的度数是_________ .43、如图对顶角有_________ 对.44、如图,AB、CD相交于点O,∠AOD+∠COB=278°,则∠AOD=_________ °,∠DOB= _________ °,若OE平分∠AOC,则∠AOE=_________ °.45、已知直线AB和CD相交于O点,OE⊥AB,∠1=55°,则∠BOD=_________ 度;若OF平分∠DOB,则∠EOF的度数是_________ 度.46、如图,∠1=15°,∠AOC=90°,点B、O、D在同一直线上,则∠2的度数为_________ .47、已知直线AB与直线CD相交于点O,∠AOD=150°,那么直线AB与直线CD的夹角为_________ 度.48、如图,三条直线交于同一点,∠1:∠2:∠3=2:3:1,则∠4=_________ .49、如图所示,直线AB、CD相交于点O,OP是∠BOD的平分线,已知∠AOC=100°,那么∠BOP=_________ .答案与评分标准1、(2011•江西)一块直角三角板放在两平行直线上,如图所示,∠1+∠2=90 度.考点:对顶角、邻补角;余角和补角。
专题:计算题。
分析:根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.解答:解:如图,∵∠1=∠3,∠2=∠4,而∠3+∠4=90°,∴∠1+∠2=90°.故答案为:90.点评:本题考查了对顶角的性质:对顶角相等.2、(2011•广西)如图,O是直线AB上一点,∠COB=30°,则∠1=150 °.考点:对顶角、邻补角。
专题:计算题。
分析:根据邻补角互补进行计算即可.解答:解:∵∠COB=30°,∴∠1=180°﹣30°=150°.故答案为:150.点评:本题考查了邻补角的定义,利用两个补角的和等于180°求解.3、(2010•湘西州)如图,两条直线a、b相交于点O,若∠1=70°,则∠2=110°.考点:对顶角、邻补角。
专题:计算题。
分析:由图可得∠1和∠2是邻补角,且∠1=70°,由邻补角的定义即可求得∠2的值.解答:解:∵∠1+∠2=180°又∠1=70°∴∠2=110°.点评:本题考查了利用邻补角的概念计算一个角的度数的能力.4、(2010•娄底)如图,直线AB、CD相交于点O.OE平分∠AOD,若∠BOD=100°,则∠AOE=40 度.考点:对顶角、邻补角;角平分线的定义。
专题:计算题。
分析:首先利用邻补角互补求出∠AOD,再利用角平分线的定义计算.解答:解:∵∠AOD与∠BOD互为邻补角,∠BOD=100°,∴∠AOD=180°﹣∠BOD=80°,又OE平分∠AOD,∴∠AOE=40°.点评:本题考查了利用邻补角和角平分线的定义,在相交线中角的度数的求解方法.5、(2006•宁德)用剪刀剪东西时,剪刀张开的角度如图所示,若∠1=25°,则∠2=25 度.考点:对顶角、邻补角。
专题:计算题。
分析:首先判断所求角与∠1的关系,然后利用对顶角的性质求解.解答:解:∵∠1与∠2是对顶角,∴∠2=∠1=25°.故答案为:25.点评:本题主要考查对顶角的性质,熟练掌握对顶角的性质是解答本题的关键.对顶角的性质:对顶角相等.6、(2002•山西)如图,直线AB、CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE,若∠AOC=28°,则∠EOF=62 度.考点:对顶角、邻补角;角平分线的定义。
分析:根据平角和角平分线的定义,以及对顶角相等求得.解答:解:∵OF平分∠AOE,∴∠AOF=∠EOF,∵∠COD为平角,∴∠AOC+∠AOF+∠EOF+∠EOD=180°,∵∠AOC与∠BOD为对顶角,∴∠AOC=∠BOD,又∵∠DOE=∠BOD,∴2∠AOC+2∠EOF=180°,又∵∠AOC=28°,∴∠EOF=62°.点评:熟记平角的特点与角平分线的性质是解决此题的关键,再者解决本题还需要利用对顶角相等与等量代换.7、(2002•宁德)如图,是用对顶角的量角器测量圆锥形零件的锥角的示意图,则此零件的锥角等于30 度.考点:对顶角、邻补角。
