2020年七年级下数学《对顶角、邻补角》练习题 (2)
人教版七年级数学下册《邻补角、对顶角的定义及性质》课件ppt
解:(1)∠AOC的邻补角是∠AOD和 ∠COB;∠BOE的邻补角是 ∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB; ∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
D E
A
O
B
F
C
5. 在下图中，花坛转角（红色标注的角）按图纸要求为135°；施工结束 后，要求你检测它是否合格？请你设计检测的方法.
思考 :剪刀剪东西的过程中,你能说说∠AOC与∠AOD,∠AOC与∠BOD这两 对角的位置保持怎样的关系吗？
A
C
O
∠AOC和∠AOD有一条公共边AO，且∠AOC的
另一边是∠AOD另一边的反向延长线.
∠AOC和∠BOD有公共顶点，且∠AOC的两边 分别是∠BOD两边的反向延长线.
DB
一、邻补角的概念 邻补角：如果两个角有一条公共边，它们的另一边互为__反__向__延__长__线__，那 么这两个角互为邻补角.图中∠1的邻补角有__∠__2_,_∠__3___.
人教版 数学 七年级 下册
理解并掌握邻补角和对顶角的概念及性质.
掌握邻补角与对顶角的性质，并能运用它们的性质 进行角的计算及解决简单实际问题..
观察下列图片，说一说直线与直线有什么样的位置关系.
观察下列图片，说一说直线与直线有什么样的位置关系.
观察下列图片，说一说直线与直线有什么样的位置关系.
角的 名称
对 顶 角
邻 补 角
特征
性质 相同点
①两条直线相 交形成的角； ②有公共顶点;
③没有公共边。
对顶 角相 等。
①两条直线相 交而成； ②有公共顶点;
③有一条公共边。
浙教版2020七年级数学下册期中综合复习培优训练题2(附答案详解)
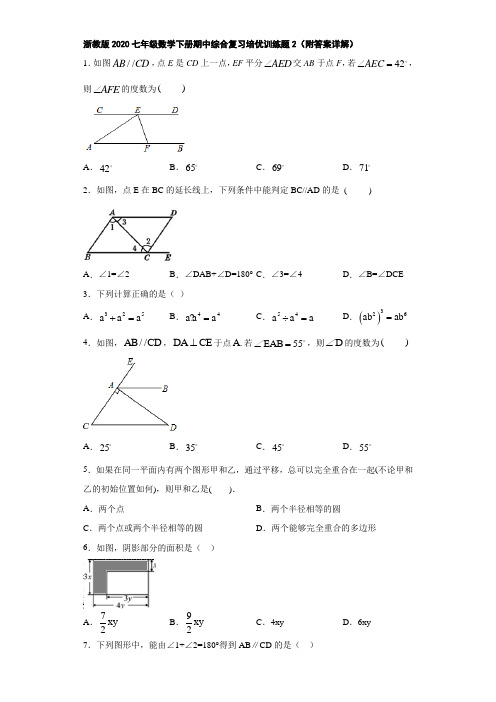
解： ，
，
由光学原理可得 ，
由三角形外角性质可得 ，
在第2次“好的发射”的条件下， ，
在第3次“好的发射”的条件下， ，
，
若最多能进行n次“好的发射”，则 ， 若 ，则反射光线 在 的左侧
解得 ，
故答案为：4．
【点睛】
本题考查了平行线的性质和图形的变化类问题，首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解 探寻规律要认真观察、仔细思考，善用联想来解决这类问题．
18．化简（2b+3a）（3a﹣2b）﹣（2b﹣3a）（2b+3a），当a=﹣1，b=2时，原式的值是_____．
19．若x＝2m，则将y＝1＋4m＋1,则用含x的代数式表示y为______________________．
20．若9x=4，3y=﹣2，则34x﹣3y的值是．
21．
22．如图，在平面直角坐标系中，小方格边长为1，点A，B，P都在格点上．
故答案为
【点睛】
考查代数式的化简求值，掌握整式的乘法法则是解题的关键.
19．
【解析】
试题分析： ，则 ．
点睛：本题主要考查的就是幂的几个公式的应用，属于中等难度的题型． ， ，解答这个问题的关键就是对这两个公式的运用要非常的熟悉，将所求的量通过公式之间的转化转化为已知的量．
20．﹣2．
【解析】试题分析：∵9x＝32x＝4，3y＝﹣2，
27．如图是一个由4条线段构成的“鱼”形图案，其中∠1=55°，∠2=55°，∠3=125°，找出图中的平行线，并说明理由．
28．计算:
（1）2(y6)2-(y4)3；（2）(ab2c)2÷（ab3c2）；
人教数学七年级下全册同步练习-初中数学七年级下册全册同步练习题(含答案,共119页)
第五章 相交线与平行线1相交线学习要求1．能从两条直线相交所形成的四个角的关系入手，理解对顶角、互为邻补角的概念，掌握对顶角的性质．2．能依据对顶角的性质、邻补角的概念等知识，进行简单的计算．课堂学习检测一、填空题1．如果两个角有一条______边，并且它们的另一边互为____________，那么具有这种关系的两个角叫做互为邻补角．2．如果两个角有______顶点，并且其中一个角的两边分别是另一个角两边的___________ ________，那么具有这种位置关系的两个角叫做对顶角． 3．对顶角的重要性质是_________________．4．如图，直线AB 、CD 相交于O 点，∠AOE ＝90°．(1)∠1和∠2叫做______角；∠1和∠4互为______角； ∠2和∠3互为_______角；∠1和∠3互为______角； ∠2和∠4互为______角．(2)若∠1＝20°，那么∠2＝______；∠3＝∠BOE －∠______＝______°－______°＝______°； ∠4＝∠______－∠1＝______°－______°＝______°． 5．如图，直线AB 与CD 相交于O 点，且∠COE ＝90°，则(1)与∠BOD 互补的角有________________________； (2)与∠BOD 互余的角有________________________； (3)与∠EOA 互余的角有________________________； (4)若∠BOD ＝42°17′，则∠AOD ＝__________； ∠EOD ＝______；∠AOE ＝______． 二、选择题6．图中是对顶角的是( )．7．如图，∠1的邻补角是( )．(A)∠BOC (B)∠BOC 和∠AOF (C)∠AOF (D)∠BOE 和∠AOF 8．如图，直线AB 与CD 相交于点O ，若AOD AOC ∠=∠31，则∠BOD 的度数为( )． (A)30° (B)45° (C)60°(D)135°9．如图所示，直线l1，l2，l3相交于一点，则下列答案中，全对的一组是( )．(A)∠1＝90°，∠2＝30°，∠3＝∠4＝60°(B)∠1＝∠3＝90°，∠2＝∠4＝30°(C)∠1＝∠3＝90°，∠2＝∠4＝60°(D)∠1＝∠3＝90°，∠2＝60°，∠4＝30°三、判断正误10．如果两个角相等，那么这两个角是对顶角．( ) 11．如果两个角有公共顶点且没有公共边，那么这两个角是对顶角．( ) 12．有一条公共边的两个角是邻补角．( ) 13．如果两个角是邻补角，那么它们一定互为补角．( ) 14．对顶角的角平分线在同一直线上．( ) 15．有一条公共边和公共顶点，且互为补角的两个角是邻补角．( )综合、运用、诊断一、解答题16．如图所示，AB，CD，EF交于点O，∠1＝20°，∠BOC＝80°，求∠2的度数．17．已知：如图，直线a，b，c两两相交，∠1＝2∠3，∠2＝86°．求∠4的度数．18．已知：如图，直线AB，CD相交于点O，OE平分∠BOD，OF平分∠COB，∠AOD∶∠DOE＝4∶1．求∠AOF的度数．19．如图，有两堵围墙，有人想测量地面上两堵围墙内所形成的∠AOB的度数，但人又不能进入围墙，只能站在墙外，请问该如何测量?拓展、探究、思考20．如图，O是直线CD上一点，射线OA，OB在直线CD的两侧，且使∠AOC＝∠BOD，试确定∠AOC与∠BOD是否为对顶角，并说明你的理由．21．回答下列问题：(1)三条直线AB，CD，EF两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(2)四条直线AB，CD，EF，GH两两相交，图形中共有几对对顶角(平角除外)?几对邻补角?(3)m条直线a1，a2，a3，…，a m－1，a m相交于点O，则图中一共有几对对顶角(平角除外)?几对邻补角?2 垂线学习要求1．理解两条直线垂直的概念，掌握垂线的性质，能过一点作已知直线的垂线．2．理解点到直线的距离的概念，并会度量点到直线的距离．课堂学习检测一、填空题1．当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线______，其中一条直线叫做另一条直线的______线，它们的交点叫做______．2．垂线的性质性质1：平面内，过一点____________与已知直线垂直．性质2：连接直线外一点与直线上各点的_________中，_________最短．3．直线外一点到这条直线的__________________叫做点到直线的距离．4．如图，直线AB，CD互相垂直，记作______；直线AB，CD互相垂直，垂足为O点，记作____________；线段PO的长度是点_________到直线_________的距离；点M到直线AB的距离是_______________．二、按要求画图5．如图，过A点作CD⊥MN，过A点作PQ⊥EF于B．图a 图b 图c6．如图，过A点作BC边所在直线的垂线EF，垂足是D，并量出A点到BC边的距离．图a 图b 图c7．如图，已知∠AOB及点P，分别画出点P到射线OA、OB的垂线段PM及PN．图a 图b 图c8．如图，小明从A村到B村去取鱼虫，将鱼虫放到河里，请作出小明经过的最短路线．综合、运用、诊断一、判断下列语句是否正确(正确的画“√”，错误的画“×”)9．两条直线相交，若有一组邻补角相等，则这两条直线互相垂直．( ) 10．若两条直线相交所构成的四个角相等，则这两条直线互相垂直． ( ) 11．一条直线的垂线只能画一条． ( ) 12．平面内，过线段AB 外一点有且只有一条直线与AB 垂直． ( ) 13．连接直线l 外一点到直线l 上各点的6个有线段中，垂线段最短． ( ) 14．点到直线的距离，是过这点画这条直线的垂线，这点与垂足的距离． ( ) 15．直线外一点到这条直线的垂线段，叫做点到直线的距离． ( ) 16．在三角形ABC 中，若∠B ＝90°，则AC ＞AB ． ( )二、选择题17．如图，若AO ⊥CO ，BO ⊥DO ，且∠BOC ＝α，则∠AOD 等于( )．(A)180°－2α (B)180°－α(C)α2190+︒ (D)2α－90°18．如图，点P 为直线m 外一点，点P 到直线m 上的三点A 、B 、C 的距离分别为P A ＝4cm ，PB ＝6cm ，PC ＝3cm ，则点P 到直线m 的距离为( )． (A)3cm (B)小于3cm (C)不大于3cm (D)以上结论都不对19．如图，BC ⊥AC ，CD ⊥AB ，AB ＝m ，CD ＝n ，则AC 的长的取值范围是( )．(A)AC ＜m (B)AC ＞n (C)n ≤AC ≤m (D)n ＜AC ＜m 20．若直线a 与直线b 相交于点A ，则直线b 上到直线a 距离等于2cm的点的个数是( )． (A)0 (B)1 (C)2 (D)3 21．如图，AC ⊥BC 于点C ，CD ⊥AB 于点D ，DE ⊥BC于点E ，能表示点到直线(或线段)的距离的线段有( )． (A)3条 (B)4条 (C)7条 (D)8条 三、解答题22．已知：OA ⊥OC ，∠AOB ∶∠AOC ＝2∶3．求∠BOC 的度数．23．已知：如图，三条直线AB ，CD ，EF 相交于O ，且CD ⊥EF ，∠AOE ＝70°，若OG 平分∠BOF ．求∠DOG ．拓展、探究、思考24．已知平面内有一条直线m 及直线外三点A ，B ，C ，分别过这三个点作直线m 的垂线，想一想有几个不同的垂足?画图说明．25．已知点M ，试在平面内作出四条直线l 1，l 2，l 3，l 4，使它们分别到点M 的距离是1.5cm ．·M26．从点O 引出四条射线OA ，OB ，OC ，OD ，且AO ⊥BO ，CO ⊥DO ，试探索∠AOC与∠BOD 的数量关系．27．一个锐角与一个钝角互为邻角，过顶点作公共边的垂线，若此垂线与锐角的另一边构成75直角，与钝角的另一边构成直73角，则此锐角与钝角的和等于直角的多少倍?3 同位角、内错角、同旁内角学习要求当两条直线被第三条直线所截时，能从所构成的八个角中识别出哪两个角是同位角、内错角及同旁内角．课堂学习检测一、填空题1．如图，若直线a，b被直线c所截，在所构成的八个角中指出，下列各对角之间是属于哪种特殊位置关系的角?(1)∠1与∠2是_______；(2)∠5与∠7是______；(3)∠1与∠5是_______；(4)∠5与∠3是______；(5)∠5与∠4是_______；(6)∠8与∠4是______；(7)∠4与∠6是_______；(8)∠6与∠3是______；(9)∠3与∠7是______；(10)∠6与∠2是______．2．如图2所示，图中用数字标出的角中，同位角有______；内错角有______；同旁内角有______．3．如图3所示，(1)∠B和∠ECD可看成是直线AB、CE被直线______所截得的_______角；(2)∠A和∠ACE可看成是直线_______、______被直线_______所截得的______角．4．如图4所示，(1)∠AED和∠ABC可看成是直线______、______被直线______所截得的_______角；(2)∠EDB和∠DBC可看成是直线______、______被直线_______所截得的______角；(3)∠EDC和∠C可看成是直线_______、______被直线______所截得的______角．综合、运用、诊断一、选择题5．已知图①～④，图①图②图③图④在上述四个图中，∠1与∠2是同位角的有( )．图2 图3 图4(A)①②③④(B)①②③(C)①③(D)①6．如图，下列结论正确的是( )．(A)∠5与∠2是对顶角(B)∠1与∠3是同位角(C)∠2与∠3是同旁内角(D)∠1与∠2是同旁内角7．如图，∠1和∠2是内错角，可看成是由直线( )．(A)AD，BC被AC所截构成(B)AB，CD被AC所截构成(C)AB，CD被AD所截构成(D)AB，CD被BC所截构成8．如图，直线AB，CD与直线EF，GH分别相交，图中的同旁内角共有( )．(A)4对(B)8对(C)12对(D)16对拓展、探究、思考一、解答题9．如图，三条直线两两相交，共有几对对顶角?几对邻补角?几对同位角?几对内错角?几对同旁内角?4 平行线及平行线的判定学习要求1．理解平行线的概念，知道在同一平面内两条直线的位置关系，掌握平行公理及其推论．2．掌握平行线的判定方法，能运用所学的“平行线的判定方法”，判定两条直线是否平行．用作图工具画平行线，从而学习如何进行简单的推理论证．课堂学习检测一、填空题1．在同一平面内，______的两条直线叫做平行线．若直线a与直线b平行，则记作______．2．在同一平面内，两条直线的位置关系只有______、______．3．平行公理是：_______________________________________________________________．4．平行公理的推论是如果两条直线都与______，那么这两条直线也______．即三条直线a，b，c，若a∥b，b∥c，则______．5．两条直线平行的条件(除平行线定义和平行公理推论外)：(1)两条直线被第三条直线所截，如果____________，那么这两条直线平行．这个判定方法1可简述为：____________，两直线平行．(2)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法2可简述为：____________，____________．(3)两条直线被第三条直线所截，如果____________，那么____________．这个判定方法3可简述为：____________，____________．二、根据已知条件推理6．已知：如图，请分别依据所给出的条件，判定相应的哪两条直线平行?并写出推理的根据．(1)如果∠2＝∠3，那么____________．(____________，____________)(2)如果∠2＝∠5，那么____________．(____________，____________)(3)如果∠2＋∠1＝180°，那么____________．(____________，____________)(4)如果∠5＝∠3，那么____________．(____________，____________)(5)如果∠4＋∠6＝180°，那么____________．(____________，____________)(6)如果∠6＝∠3，那么____________．(____________，____________)7．已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)∵∠B＝∠3(已知)，∴______∥______．(____________，____________)(2)∵∠1＝∠D(已知)，∴______∥______．(____________，____________)(3)∵∠2＝∠A(已知)，∴______∥______．(____________，____________)(4)∵∠B＋∠BCE＝180°(已知)，∴______∥______．(____________，____________)综合、运用、诊断一、依据下列语句画出图形8．已知：点P是∠AOB内一点．过点P分别作直线CD∥OA，直线EF∥OB．9．已知：三角形ABC及BC边的中点D．过D点作DF∥CA交AB于M，再过D点作DE∥AB交AC于N点．二、解答题10．已知：如图，∠1＝∠2．求证：AB∥CD．(1)分析：如图，欲证AB∥CD，只要证∠1＝______．证法1：∵∠1＝∠2，(已知)又∠3＝∠2，( )∴∠1＝_______．( )∴AB∥CD．(___________，___________)(2)分析：如图，欲证AB∥CD，只要证∠3＝∠4．证法2：∵∠4＝∠1，∠3＝∠2，( )又∠1＝∠2，(已知)从而∠3＝_______．( )∴AB∥CD．(___________，___________)11．绘图员画图时经常使用丁字尺，丁字尺分尺头、尺身两部分，尺头的里边和尺身的上边应平直，并且一般互相垂直，也有把尺头和尺身用螺栓连接起来，可以转动尺头，使它和尺身成一定的角度．用丁字尺画平行线的方法如下面的三个图所示．画直线时要按住尺身，推移丁字尺时必须使尺头靠紧图画板的边框．请你说明：利用丁字尺画平行线的理论依据是什么?拓展、探究、思考12．已知：如图，CD ⊥DA ，DA ⊥AB ，∠1＝∠2．试确定射线DF 与AE 的位置关系，并说明你的理由．(1)问题的结论：DF ______AE ．(2)证明思路分析：欲证DF ______AE ，只要证∠3＝______． (3)证明过程：证明：∵CD ⊥DA ，DA ⊥AB ，( )∴∠CDA ＝∠DAB ＝______°．(垂直定义) 又∠1＝∠2，( )从而∠CDA －∠1＝______－______，(等式的性质) 即∠3＝＿＿＿．∴DF ＿＿＿AE ．(＿＿＿＿，＿＿＿＿)13．已知：如图，∠ABC ＝∠ADC ，BF 、DE 分别平分∠ABC 与∠ADC ．且∠1＝∠3．求证：AB ∥DC ．证明：∵∠ABC ＝∠ADC ，.2121ADC ABC ∠=∠∴( ) 又∵BF 、DE 分别平分∠ABC 与∠ADC ，.212,211ADC ABC ∠=∠∠=∠∴ ( ) ∴∠______＝∠______．( )∵∠1＝∠3，( ) ∴∠2＝∠______．(等量代换) ∴______∥______．( )14．已知：如图，∠1＝∠2，∠3＋∠4＝180°．试确定直线a 与直线c 的位置关系，并说明你的理由．(1)问题的结论：a ______c ．(2)证明思路分析：欲证a ______c ，只要证______∥______且______∥______． (3)证明过程：证明：∵∠1＝∠2，( )∴a ∥______．(________，________)① ∵∠3＋∠4＝180°，( )∴c ∥______．(________，________)② 由①、②，因为a ∥______，c ∥______， ∴a ______c ．(________，________)5 平行线的性质学习要求1．掌握平行线的性质，并能依据平行线的性质进行简单的推理．2．了解平行线的判定与平行线的性质的区别．3．理解两条平行线的距离的概念．课堂学习检测一、填空题1．平行线具有如下性质：(1)性质1：______被第三条直线所截，同位角______．这个性质可简述为两直线______，同位角______．(2)性质2：两条平行线__________________，_______相等．这个性质可简述为_____________，_____________．(3)性质3：__________________，同旁内角______．这个性质可简述为_____________，__________________．2．同时______两条平行线，并且夹在这两条平行线间的______________叫做这两条平行线的距离．二、根据已知条件推理3．如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1)如果AB∥EF，那么∠2＝______．理由是____________________________________．(2)如果AB∥DC，那么∠3＝______．理由是____________________________________．(3)如果AF∥BE，那么∠1＋∠2＝______．理由是______________________________．(4)如果AF∥BE，∠4＝120°，那么∠5＝______．理由是________________________．4．已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．(1)∵DE∥AB，( )∴∠2＝______．(__________，__________)(2)∵DE∥AB，( )∴∠3＝______．(__________，__________)(3)∵DE∥AB( )，∴∠1＋______＝180°．(______，______)综合、运用、诊断一、解答题5．如图，∠1＝∠2，∠3＝110°，求∠4．解题思路分析：欲求∠4，需先证明______∥______．解：∵∠1＝∠2，( )∴______∥______．(__________，__________)∴∠4＝______＝______°．(__________，__________)6．已知：如图，∠1＋∠2＝180°．求证：∠3＝∠4．证明思路分析：欲证∠3＝∠4，只要证______∥______．证明：∵∠1＋∠2＝180°，( )∴______∥______．(__________，__________)∴∠3＝∠4．(______，______)7．已知：如图，AB∥CD，∠1＝∠B．求证：CD是∠BCE的平分线．证明思路分析：欲证CD是∠BCE的平分线，只要证______＝______．证明：∵AB∥CD，( )∴∠2＝______．(____________，____________)但∠1＝∠B，( )∴______＝______．(等量代换)即CD是________________________．8．已知：如图，AB∥CD，∠1＝∠2．求证：BE∥CF．证明思路分析：欲证BE∥CF，只要证______＝______．证明：∵AB∥CD，( )∴∠ABC＝______．(____________，____________)∵∠1＝∠2，( )∴∠ABC－∠1＝______－______，( )即______＝______．∴BE∥CF．(__________，__________)9．已知：如图，AB∥CD，∠B＝35°，∠1＝75°．求∠A的度数．解题思路分析：欲求∠A，只要求∠ACD的大小．解：∵CD∥AB，∠B＝35°，( )∴∠2＝∠______＝_______°．(____________，____________)而∠1＝75°，∴∠ACD＝∠1＋∠2＝______°．∵CD∥AB，( )∴∠A＋______＝180°．(____________，____________)∴∠A＝_______＝______．10．已知：如图，四边形ABCD 中，AB ∥CD ，AD ∥BC ，∠B ＝50°．求∠D 的度数．分析：可利用∠DCE 作为中间量过渡． 解法1：∵AB ∥CD ，∠B ＝50°，( )∴∠DCE ＝∠_______＝_______°． (____________，______) 又∵AD ∥BC ，( )∴∠D ＝∠______＝_______°．(____________，____________)想一想：如果以∠A 作为中间量，如何求解? 解法2：∵AD ∥BC ，∠B ＝50°，( )∴∠A ＋∠B ＝______．(____________，____________)即∠A ＝______－______＝______°－______°＝______°． ∵DC ∥AB ，( )∴∠D ＋∠A ＝______．(_____________，_____________) 即∠D ＝______－______＝______°－______°＝______°．11．已知：如图，AB ∥CD ，AP 平分∠BAC ，CP 平分∠ACD ，求∠APC 的度数．解：过P 点作PM ∥AB 交AC 于点M ．∵AB ∥CD ，( )∴∠BAC ＋∠______＝180°．( ) ∵PM ∥AB ，∴∠1＝∠_______，( )且PM ∥_______．(平行于同一直线的两直线也互相平行) ∴∠3＝∠______．(两直线平行，内错角相等) ∵AP 平分∠BAC ，CP 平分∠ACD ，( )∠=∠∴211______，∠=∠214______．( ) 90212141=∠+∠=∠+∠∴ACD BAC ．( )∴∠APC ＝∠2＋∠3＝∠1＋∠4＝90°．( ) 总结：两直线平行时，同旁内角的角平分线______．拓展、探究、思考12．已知：如图，AB ∥CD ，EF ⊥AB 于M 点且EF 交CD 于N 点．求证：EF ⊥CD ．13．如图，DE∥BC，∠D∶∠DBC＝2∶1，∠1＝∠2，求∠E的度数．14．问题探究：(1)如果一个角的两条边与另一个角的两条边分别平行，那么这两个角的大小有何关系?举例说明．(2)如果一个角的两边与另一个角的两边分别垂直，那么这两个角的大小有何关系?举例说明．15．如图，AB∥DE，∠1＝25°，∠2＝110°，求∠BCD的度数．16．如图，AB，CD是两根钉在木板上的平行木条，将一根橡皮筋固定在A，C两点，点E 是橡皮筋上的一点，拽动E点将橡皮筋拉紧后，请你探索∠A，∠AEC，∠C之间具有怎样的关系并说明理由．(提示：先画出示意图，再说明理由)．6 命题学习要求1．知道什么是命题，知道一个命题是由“题设”和“结论”两部分构成的．2．对于给定的命题，能找出它的题设和结论，并会把该命题写成“如果……，那么……”的形式．能判定该命题的真假．课堂学习检测一、填空题1．______一件事件的______叫做命题．2．许多命题都是由______和______两部分组成．其中题设是____________，结论是______ _____．3．命题通常写成“如果……，那么……．”的形式．这时，“如果”后接的部分是______，“那么”后接的部分是______．4．所谓真命题就是：如果题设成立，那么结论就______的命题．相反，所谓假命题就是：如果题设成立，不能保证结论______的命题．二、指出下列命题的题设和结论5．垂直于同一条直线的两条直线平行．题设是___________________________________________________________；结论是___________________________________________________________．6．同位角相等，两直线平行．题设是___________________________________________________________；结论是___________________________________________________________．7．两直线平行，同位角相等．题设是___________________________________________________________；结论是___________________________________________________________．8．对顶角相等．题设是___________________________________________________________；结论是___________________________________________________________．三、将下列命题改写成“如果……，那么……”的形式9．90°的角是直角．__________________________________________________________________．10．末位数字是零的整数能被5整除．__________________________________________________________________．11．等角的余角相等．__________________________________________________________________．12．同旁内角互补，两直线平行．__________________________________________________________________．综合、运用、诊断一、下列语句哪些是命题，哪些不是命题?13．两条直线相交，只有一个交点．( ) 14． 不是有理数．( )15．直线a与b能相交吗?( ) 16．连接AB．( )17．作AB⊥CD于E点．( ) 18．三条直线相交，有三个交点．( )二、判断下列各命题中，哪些命题是真命题?哪些是假命题?(对于真命题画“√”，对于假命题画“×”)19．0是自然数．( )20．如果两个角不相等，那么这两个角不是对顶角．( )21．相等的角是对顶角．( )22．如果AC＝BC，那么C点是AB的中点．( )23．若a∥b，b∥c，则a∥c．( )24．如果C是线段AB的中点，那么AB＝2BC．( )25．若x2＝4，则x＝2．( )26．若xy＝0，则x＝0．( )27．同一平面内既不重合也不平行的两条直线一定相交．( )28．邻补角的平分线互相垂直．( )29．同位角相等．( )30．大于直角的角是钝角．( )拓展、探究、思考31．已知：如图，在四边形ABCD中，给出下列论断：①AB∥DC；②AD∥BC；③AB＝AD；④∠A＝∠C；⑤AD＝BC．以上面论断中的两个作为题设，再从余下的论断中选一个作为结论，并用“如果……，那么……”的形式写出一个真命题．答：_____________________________________________________________________．32．求证：两条平行线被第三条直线所截，内错角的平分线互相平行．7 平移学习要求了解图形的平移变换，知道一个图形进行平移后所得的图形与原图形之间所具有的联系和性质，能用平移变换有关知识说明一些简单问题及进行图形设计．课堂学习检测一、填空题1．如图所示，线段ON是由线段______平移得到的；线段DE是由线段______平移得到的；线段FG是由线段______平移得到的．2．如图所示，线段AB在下面的三个平移中(AB→A1B1→A2B2→A3B3)，具有哪些性质．图a图b 图c(1)线段AB上所有的点都是沿______移动，并且移动的距离都________．因此，线段AB，A1B1，A2B2，A3B3的位置关系是____________________；线段AB，A1B1，A2B2，A3B3的数量关系是________________．(2)在平移变换中，连接各组对应点的线段之间的位置关系是______；数量关系是______．3．如图所示，将三角形ABC平移到△A′B′C′．图a 图b在这两个平移中：(1)三角形ABC的整体沿_______移动，得到三角形A′B′C′．三角形A′B′C′与三角形ABC的______和______完全相同．(2)连接各组对应点的线段即AA′，BB′，CC′之间的数量关系是__________________；位置关系是__________________．综合、运用、诊断一、按要求画出相应图形4．如图，AB∥DC，AD∥BC，DE⊥AB于E点．将三角形DAE平移，得到三角形CBF．5．如图，AB∥DC．将线段DB向右平移，得到线段CE．6．已知：平行四边形ABCD及A′点．将平行四边形ABCD平移，使A点移到A′点，得平行四边形A′B′C′D′．7．已知：五边形ABCDE及A′点．将五边形ABCDE平移，使A点移到A′点，得到五边形A′B′C′D′E′．拓展、探究、思考一、选择题8．如图，把边长为2的正方形的局部进行如图①～图④的变换，拼成图⑤，则图⑤的面积是( )．(A)18 (B)16 (C)12 (D)8二、解答题9．河的两岸成平行线，A，B是位于河两岸的两个车间(如图)．要在河上造一座桥，使桥垂直于河岸，并且使A，B间的路程最短．确定桥的位置的方法如下：作从A到河岸的垂线，分别交河岸PQ，MN于F，G．在AG上取AE＝FG，连接EB．EB交MN于D．在D处作到对岸的垂线DC，那么DC就是造桥的位置．试说出桥造在CD位置时路程最短的理由，也就是(AC＋CD＋DB)最短的理由．10．以直角三角形的三条边BC，AC，AB分别作正方形①、②、③，如何用①中各部分面积与②的面积，通过平移填满正方形③?你从中得到什么结论?第六章 实数6.1平方根学习要求1. 理解算术平方根和平方根的含义。
2023年春上海七年级下数学辅导讲义(沪教版)第5讲邻补角、对顶角及垂直(练习)解析版
第5讲邻补角、对顶角及垂直（练习）夯实基础1.下列语句中正确的是（）A．有一条公共边且和为180°的两个角是邻补角B．互为邻补角的两个角不等C．两边互为反向延长线的两个角是对顶角D．交于一点的三条直线形成3对对顶角【难度】★【答案】C【解析】A错误，另一边互为反向延长线；B错误，不一定，有可能相等；D错误，6对．【总结】考察邻补角，对顶角的内容．2.直线AB上有一点P和此直线外的一点Q的距离为3cm，则Q到直线AB的距离（）A．等于3cm B．大于或等于3cmC．小于或等于3cm D．都不对【难度】★【答案】C【解析】考察点到直线的距离的知识点及其运用．⊥，垂足为O．若3．（2018·上海松江区·七年级期中）如图，已知BO DE∠=︒，则AODBOC42∠=_______︒．【答案】48【分析】先根据垂直求得BOC ∠的余角EOC ∠的度数，再根据对顶角相等即可得出答案．【详解】,42BO DE BOC ⊥∠=︒90904248EOC BOC ∴∠=︒-∠=︒-︒=︒48AOD EOC ∴∠=∠=︒故答案为：48．【点睛】本题考查了余角、对顶角的计算，熟练掌握余角和对顶角的定义是解题的关键．4．（2018·上海松江区·七年级期中）如图，已知直线,a b 相交，12280∠+∠=︒，则1∠=_______︒．【答案】140【分析】根据对顶角相等可得12∠=∠，然后求解即可．【详解】12280,12∠+∠=︒∠=∠112801402∴∠=⨯︒=︒ 故答案为：140．【点睛】本题考查了对顶角，熟练掌握对顶角相等是解题的关键．5．（2018·上海杨浦区·七年级期末）已知直线AB 和直线CD 相交于点O ，200AOC BOD ∠+∠=︒，那么这两条直线的夹角等于___________度．【答案】80【分析】如下图，先根据对顶角相等求得∠AOC 的大小，再根据邻补角互补可得∠AOD 的大小，两直线的夹角用小于90°的那个角表示，据此可得夹角大小．【详解】如下图∵200AOC BOD ∠+∠=︒∴∠AOC=∠BOD=100°∴∠AOD=80°故答案为：80【点睛】本题考查对顶角和邻补角的性质，解题关键是绘制出图形，然后才好方便分析求解．6．（2016·上海奉贤区·七年级期中）如图，已知直线AB 、CD 相交于O 点，∠AOC ＋∠BOD ＝80°，那么∠BOC=_____度.【答案】140【分析】本题考查的是对顶角知识，根据∠AOC与∠BOD是对顶角，相等且和为80°解答即可【详解】∵∠AOC与∠BOD是对顶角，∴∠AOC=∠BOD；又∵∠AOC＋∠BOD＝80°，∴∠AOC=∠BOD=40°，∴∠BOC=180°-∠BOD=180°-40°=140°【点睛】本题的关键是掌握对顶角相等的知识7.直线AB与直线CD相交于点O，EO⊥AB于O，则图中∠1和∠2的关系是__________．【难度】★【答案】互余．【解析】考察对顶角的性质以及互余的意义及运用．8．（2019·上海七年级单元测试）如图所示，直线AB、CD、EF相交于点O，若∠1+∠2＝90°，∠3＝40°，求∠1的度数，并说明理由．【答案】50°【分析】根据题意已知了∠1与∠2的关系,要求∠1的角度,只要求出∠2的度数即可.观察图形,可得知∠2与∠3是对顶角,而题目中又已知了∠3的角度,计算即可得到∠1的度数. 【详解】解：因为∠2＝∠3(对顶角相等)，∠3＝40°(已知)，所以∠2＝40°(等量代换)．又因为∠1+∠2＝90°(已知)，所以∠1＝90°-∠2＝50°．【点睛】此题考查对顶角、邻补角，解题关键在于掌握其性质定义.能力提升1．（2018·上海金山区·七年级期中）如图，直线AB、CD相交于点O，∠=︒，则直线AB与直线CD的夹角是______︒．BOC135【答案】45【分析】先根据邻补角的定义求出∠AOC，再根据直线的夹角为锐角解答．【详解】解：∵∠BOC=135°，∴∠AOC=180°-∠BOC=180°-135°=45°，∴直线AB与直线CD的夹角是45°．故答案为：45．【点睛】本题考查了邻补角的定义，要注意直线的夹角是锐角．2．（2017·上海长宁区·七年级期末）如图，直线AC与直线BD交于点O，∠=∠，那么AOD2AOB BOC∠=______度．【答案】60【分析】直接利用已知结合邻补角的定义得出答案．【详解】∵直线AC 与直线BD 交于点O ，∠AOB=2∠BOC ，∴∠AOB+∠BOC=180°，∴2∠BOC+∠BOC=180°，∴∠BOC=60°，∴∠AOD=∠BOC=60°．故答案为：60．【点睛】此题考查邻补角以及对顶角，正确得出∠BOC 的度数是解题关键．3．（2018·上海嘉定区·七年级期中）如图，直线AB 与CD 相交于点O ，135BOC ∠=︒，那么它们的夹角的度数是____.【答案】45︒【分析】根据邻补角和夹角的定义，结合题意即可得到答案.【详解】因为135BOC ∠=︒，BOC ∠和AOC ∠是邻补角，则18013545AOC ∠=︒-︒=︒，则夹角的度数是45︒.【点睛】本题考查邻补角和夹角的定义，解题的关键是掌握邻补角和夹角的定义.4．（2018·上海浦东新区·七年级期中）如图，直线AB 与CD 相交于点O ，∠AOE=90°,且∠EOD=14∠COE ，∠BOD=__________°.【答案】54°【解析】解：设∠EOD=x，则∠COE=4x，∴x+4x=180°，解得：x=36°．∵∠AOE=90°，∴∠EOB=90°，∴∠BOD=90°－36°=54°．故答案为54．5．（2018·上海普陀区·七年级期中）如图，直线AB、CD相交于点O，COE∠=___________°.∠=︒，则BOE∠=︒，20140AOD【答案】120分析：观察图形可知∠AOD与∠COB是一对对顶角，根据对顶角相等可得∠COB的度数；结合图中的隐含条件∠BOE=∠COB-∠COE，即可求出∠BOE的度数.详解：∵直线AB、CD相交于点O.∴∠AOD=∠COB=140°.∵∠COE=20°，∠COB=140°，∴∠BOE=∠COB-∠COE=140°-20°=120°.点睛：本题考查了角的运算，关键是观察图形中各角之间的关系.6.从钝角∠AOB的顶点O在∠AOB内引射线OC使OC⊥OA，若∠AOC：∠COB=3：1，求∠AOB的度数．【难度】★★【答案】120︒．【解析】因为OC OA⊥（已知），所以90∠=︒（垂线的意义）AOC因为∠AOC：∠COB=3：1（已知）所以30∠=︒（等式性质）COB所以120∠=︒（等式性质）AOB【总结】考查学生画图能力，并且学会分析题目．7.如图：AO⊥BC于点O，OA平分∠DOE，∠COE=64°，求∠AOD的度数．【难度】★★【答案】26︒．【解析】因为AO BC⊥（已知）所以90∠=︒（垂直的意义）AOC因为64COE∠=︒（已知）所以26∠=︒（等式性质）AOE因为OA平分∠DOE（已知）所以26∠=∠=︒（角平分线的意义）AOD AOEQ P Q P B OAB O A 【总结】考察学生对简单几何题的分析，注意互余，角平分线等概念的理解及运用．8.作图：已知线段AB 上一点Q 及线段外一点P ．（1） 过点Q 作线段AB 的垂线；（2） 过点P 作线段AB 的垂线．【难度】★★【答案】如下图．【解析】注意标注垂直符号，以及字母的标注．【总结】画图一定要写结论．9.（1）用三角尺画一个30°的∠AOB ，在边OA 上任取一点P ，过P 作PQ ⊥OB ，垂足为Q ，量一量OP 的长，你发现点P 到OB 的距离与OP 长的关系吗?（2）若所画的∠AOB 为60°，重复上面的测量，你会发现什么?【难度】★★【答案】（1）12PQ OP =； （2）12PQ OP ≠，12OQ OP =．【解析】画图，测量，猜想结论．【总结】考察学生的作图能力，并且量出相应的长度，从而得出结论．10.如图所示，直线AB、CD、EF相交于点O，OG平分∠BOF，且CD⊥EF，∠AOE=70°，求∠DOG的度数．【难度】★★【答案】55︒．【解析】因为BOF AOE∠=∠（对顶角相等）又70AOE∠=︒（已知）所以70BOF∠=︒（等量代换）因为OG平分∠BOF（已知）所以35FOG BOG∠=∠=︒（角平分线的意义）因为CD EF⊥（已知）所以90EOD FOD∠=∠=︒（垂线的意义）所以903555DOG∠=︒-︒=︒（互余的意义）【总结】考察角平分线，垂线的意义，对顶角的内容等等．11.如图所示，O为直线AB上一点，∠AOC=13∠BOC，OC是∠AOD的平分线（1）求∠DOC的度数；（2）判断OD与AB的位置关系，并说明理由．【难度】★★【答案】（1）45︒；（2）垂直．【解析】（1）因为180AOC BOC∠+∠=︒（邻补角的意义）又∠AOC=13∠BOC（已知），所以11803BOC BOC∠+∠=︒（等量代换），所以135BOC∠=︒（等式性质），所以45AOC∠=︒（等式性质）因为OC是∠AOD的平分线（已知），所以45AOC DOC∠=∠=︒（角平分线的意义）（2）垂直．因为45AOC DOC∠=∠=︒（已知），所以90AOD∠=︒（等式性质）所以OD AB⊥（垂直的意义）．【总结】本题主要考查邻补角的意义及角平分线的意义的理解及运用．12.如图，直线AB、CD、EF相交于点O，AB⊥EF，OG平分∠FOC，OH平分∠DOG，（1）若∠AOC：∠COG=4:7，求∠DOF的度数；（2）若∠AOC：∠DOH=8:29，求∠COH的度数．【难度】★★★【答案】（1）110︒；（2）107.5︒．【解析】（1）因为OG平分∠FOC（已知）所以COG GOF∠=∠（角平分线的意义）因为∠AOC：∠COG=4:7（已知）所以设4COG x∠=，∠=，7AOC x因为AB⊥EF（已知），所以90∠=︒（垂直的意义）AOF即47790x=︒，x x x++=︒，解得：5所以20∠=︒（等式性质）COG∠=︒，35AOC因为180∠+∠=︒（邻补角的意义）COF DOF所以1803535110∠=︒-︒-︒=︒（等式性质）DOF（2）因为OG平分∠FOC（已知）所以COG GOF∠=∠（角平分线的意义）因为∠AOC：∠DOH=8:29（已知）所以设8∠=．∠=，COG xAOC kDOH k∠=，29因为AB⊥EF（已知），所以90AOF ∠=︒（垂直的意义）， 即890k x x ++=︒①因为180DOH GOH COG ∠+∠+∠=︒（平角的意义），即2929180k k x ++=︒②联立①、②，解得：35x =︒，52k =． 所以35GOC ∠=︒，52972.52HOG ∠=⨯=（等式性质） 因为COH COG GOH ∠=∠+∠（角的和差）所以3572.5107.5COH ∠=︒+︒=︒（等式性质）【总结】本题综合性较强，主要考查角平分线意义与邻补角意义的综合运用，解题时注意对题目中的条件认真分析．13.如图，直线AB 、CD 、EF 交于点O ，DOB ∠是它的余角的2倍，2AOE DOF ∠=∠，且有OG OA ⊥，求EOG ∠的度数．【难度】★★★【答案】50︒．【解析】因为DOB ∠是它的余角的2倍所以设DOB x ∠=， 则2(90)x x =-， 解得：60x =︒因为AOC BOD ∠=∠（对顶角相等），所以60AOC ∠=︒（等量代换）设DOF y ∠=，则由2AOE DOF ∠=∠，得2AOE y ∠=，因为DOF EOC ∠=∠（对顶角相等）， 所以EOC y ∠=， 即360y =︒．解得：20y =︒， 所以40AOE ∠=︒（等式性质）因为OG OA ⊥（已知）， 所以90AOG ∠=︒（垂直的意义）所以50EOG ∠=︒（等式性质）【总结】主要考察学生对基本知识点的掌握，以及对题目的分析，包括垂线的意义，对顶角的意义，设未知数解方程等等．。
七年级下数学基础训练题-2020七年级数学下册基础训练答案
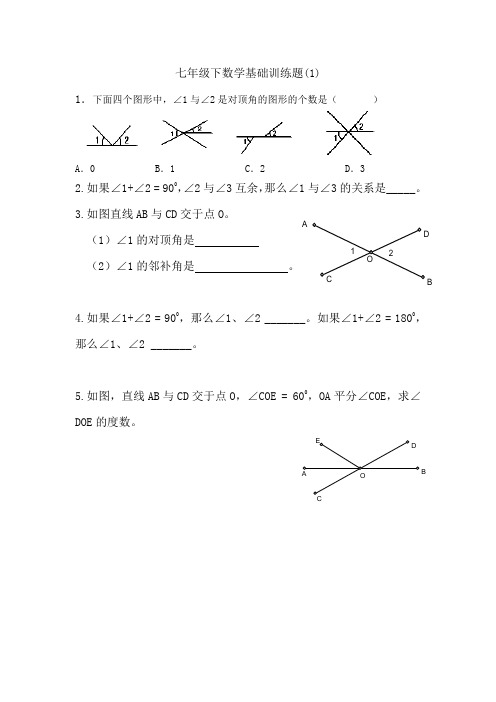
1．下面四个图形中，∠1与∠2是对顶角的图形的个数是（）A．0 B．1 C．2 D．32.如果∠1+∠2 = 900，∠2与∠3互余，那么∠1与∠3的关系是_____。
3.如图直线AB与CD交于点O。
（1）∠1的对顶角是（2）∠1的邻补角是。
4.如果∠1+∠2 = 900，那么∠1、∠2 _______。
如果∠1+∠2 = 1800，那么∠1、∠2 _______。
5.如图，直线AB与CD交于点O，∠COE = 600，OA平分∠COE，求∠DOE的度数。
BAB1.（1）指出图中∠1、∠2、∠3、∠4同位角。
∠1同位角是______。
∠2同位角是______。
∠3同位角是______。
∠4同位角是______。
（2）指出图中∠3、∠4的内错角。
∠3内错角是______。
∠4内错角是______。
（3）指出图中∠3、∠4的同旁内角。
∠3同旁内角是______。
∠4同旁内角是2.如右图，回答下列问题：(1) ∠1同位角是_____________________ (2) ∠2内错角是_____________________ (3)∠3同旁内角是_____________________ 3.找出图中的平行线，并说明理由。
4.如图∠1、∠2是 （ ）A 同位角B 内错角C 同旁内角 D5.如图，∵∠1=∠2 ∴_______‖_______.∵∠3=∠4 ∴_______‖CAL 87654321B DcHGCAB1.平行线的性质。
(1) 两直线平行，__________________________。
(2) 两直线平行，__________________________。
(3) 两直线平行，__________________________2.如图，AB ‖CD ，∠1 =630，求∠2 。
3.如图，已知∠1=∠B ，∠2=∠C ，求证：AB ‖CD4. 如图，∠1=650，∠2 =650，∠3=1000，求∠4 。
对顶角、邻补角、垂线、平移之七大题型(解析版)--2024年七年级数学下学期期中真题分类(人教版)
专题01 对顶角、邻补角、垂线、平移之七大题型题型01对顶角、领补角的定义理解1(2023上·黑龙江哈尔滨·七年级校考期中)下列各图中，∠1与∠2是对顶角的是()A. B.C. D.【答案】C【分析】本题考查了对顶角的定义，根据对顶角的定义判断即可．有一个公共点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角互为对顶角．【详解】解：A、∠1的两边不是∠2的两边的反向延长线，∠1与∠2不是对顶角，故该选项不合题意；B、∠1的两边不是∠2的两边的反向延长线，∠1与∠2不是对顶角，故该选项不符合题意；C、∠1的两边分别是∠2的两边的反向延长线，∠1与∠2是对顶角，故该选项符合题意；D、∠1的两边不是∠2的两边的反向延长线，∠1与∠2不是对顶角，故该选项不合题意．故选：C．2(2023下·福建泉州·七年级校考期中)下列图形中，∠1与∠2是邻补角的是()A. B.C. D.【答案】C【分析】邻补角是指两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角，且两个角的和为180°，由此即可求解．【详解】解：A、不是邻补角，原选项不符合题意；B、是对顶角，原选项不符合题意；C、是邻补角，原选项符合题意；D、不是邻补角，原选项不符合题意；故选：C．【点睛】本题主要考查邻补角的概念及识别，理解并掌握其概念，图形结合分析是解题的关键．3(2023下·河南郑州·七年级校考期中)下列图形中，表示∠1和∠2是对顶角的是()A. B.C. D.【答案】D【分析】两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线，这样的两个角叫做互为对顶角，由此可得出正确答案．【详解】解：根据对顶角的定义可得A,B,C都不是对顶角，只有选项D符合对顶角的定义，故选：D．【点睛】本题考查了对顶角的定义，属于基础题，要求熟练掌握对顶角的定义．4(2023下·河北唐山·七年级统考期中)下面四个图形中，∠1与∠2是邻补角的是()A. B.C. D.【答案】C【分析】根据邻补角的定义作答即可．【详解】解：由题意知，C中∠1与∠2是邻补角，故选：C．【点睛】本题考查了邻补角的定义．解题的关键在于熟练掌握两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．题型02垂线及性质、画垂线、点到直线的距离5(2023下·安徽宿州·七年级校考期中)如图，P是直线l外一点，A，B，C三点在直线l上，且PB⊥l 于点B，∠APC=90°，则下列结论中正确的是()①线段BP的长度是点P到直线l的距离；②线段AP是A点到直线PC的距离；③在PA，PB，PC三条线段中，PB最短；④线段PC的长度是点P到直线l的距离A.①②③B.③④C.①③D.①②③④【答案】C【分析】本题考查了点到直线的距离及垂线段最短等知识点．点到直线的距离，即过这一点做目标直线的垂线，由这一点至垂足的距离．熟记相关结论是解题关键．【详解】解：∵PB⊥l于点B，∴线段BP的长度是点P到直线l的距离，故①正确，④错误；∵∠APC=90°，∴线段AP的长度是A点到直线PC的距离，故②错误；根据垂线段最短，在PA，PB，PC三条线段中，PB最短，故③正确；故选：C．6(2023下·内蒙古鄂尔多斯·七年级统考期中)如图，污水处理厂要从A处把处理过的水引入排水沟PQ，做法如下：过点A作AB⊥PQ于点B，沿着AB方向铺设排水管道可用料最省．能准确解释这一现象的数学知识是．【答案】垂线段最短【分析】本题考查垂线段最短，根据垂线段最短进行判断即可．理解垂线段最短的意义是正确解答的关键．【详解】解：由题意得，解释这一现象的数学知识是“垂线段最短”，故答案为：垂线段最短．7(2023下·河南许昌·七年级校考期中)如图，网格线的交点叫格点，格点P是∠AOB的边OB上的一点(请利用三角板和直尺借助网格的格点画图)．(1)过点P画OB的垂线，交OA于点E；过点P画OA的垂线，垂足为F；(2)线段PF的长度是点P到的距离，线段的长度是点E到直线OB的距离，所以线段PE、PF、OE这三条线段大小关系是(用“<”号连接)，理由是．【答案】(1)图见解析(2)OA，PE，PF<PE<OE，垂线段最短【分析】(1)如图，找点C，连接PC，与OA交点即为E，过P点作竖直的线，与OA交点即为F；(2)根据点到直线的距离的定义、垂线段最短即可求解．【详解】(1)解：由题意作图如下，PE是OB的垂线，PF是OA的垂线．(2)解：线段PF的长度是点P到OA的距离，线段PE的长度是点E到直线OB的距离，由垂线段最短可知，PF<PE<OE，故答案为：OA，PE，PF<PE<OE，垂线段最短．【点睛】本题考查了作垂线，垂线段最短．解题的关键在于对知识的熟练掌握与灵活运用．8(2023下·河北唐山·七年级统考期中)如图，在直角三角形ABC中，∠C=90°,BC=4cm,AC=3cm．(1)点B到AC的距离是cm；点A到BC的距是cm．(2)画出表示点C到AB的距离的垂线段CD．(3)AC CD(填“>”“<”“=”)，理由是．【答案】(1)4，3(2)见解析(3)>，垂线段最短【分析】(1)根据点到直线的距离的定义求解；(2)过C点作AB的垂线，垂足为D；(3)根据垂线段最短进行判断．【详解】(1)点B到AC的距离是4cm，点A到BC的距离是3cm；故答案为4；3；(2)如图，CD为所作；(3)AC>CD，理由是垂线段最短．故答案为：>；垂线段最短．【点睛】本题考查了点到直线的距离，垂线段最短，熟练掌握点到直线距离的概念是解答本题的关键．直线外一点到这条直线的垂线段的长度，叫做这个点到这条直线的距离．题型03利用对顶角、领补角性质求角9(2023下·山西吕梁·七年级统考期中)如图，直线AB，CD相交于点O，OE⊥OF，OD平分∠BOF．(1)∠BOD的对顶角为，∠BOD的邻补角为；(2)若∠BOD=58°，求∠AOE的度数．【答案】(1)∠AOC；∠AOD，∠BOC(2)26°【分析】(1)根据对顶角的定义(有一个公共顶点，且一个角的两条边分别是另一个角的两条边的反向延长线，那么这两个角就叫做对顶角)和邻补角的定义(两个角有一条公共边，且它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角)即可得；(2)先根据角平分线的定义可得∠BOF=116°，再根据邻补角的定义可得∠AOF=64°，然后根据垂直的定义即可得．【详解】(1)解：∠BOD的对顶角为∠AOC，∠BOD的邻补角为∠AOD，∠BOC，故答案为：∠AOC；∠AOD，∠BOC．(2)解：∵OD平分∠BOF，∠BOD=58°，∴∠BOF=2∠BOD=116°，∴∠AOF=180°-∠BOF=64°，∵OE⊥OF，∴∠AOE=90°-∠AOF=90°-64°=26°．【点睛】本题考查了对顶角和邻补角的定义、与角平分线有关的计算、垂直，熟练掌握各定义和运算法则是解题关键．10(2023下·云南曲靖·七年级校考期中)如图，直线AB 、CD 相交于点O ，OE ⊥CD 于点O ，OM 平分∠BOE ，∠AOC =52°．(1)求∠BOM 的度数；(2)在∠AOM 的内部画射线ON ，若∠MON =45°，那么ON 是∠AOD 的平分线吗？请说明理由．【答案】(1)∠BOM =71°(2)ON 是∠AOD 的平分线．理由见解析【分析】(1)根据∠AOC 与∠BOD 是对顶角得到∠BOD =∠AOC =52°，再利用OE ⊥CD ，求出∠BOE ，最后利用角平分线的定义求∠BOM 即可；(2)分别求出∠DON 与∠AOD ，再根据角平分线的定义判定即可【详解】(1)解：∵∠AOC 与∠BOD 是对顶角，∴∠BOD =∠AOC =52°．∵OE ⊥CD ，∴∠DOE =90°，∴∠BOE =∠BOD +∠DOE =52°+90°=142°∵OM 平分∠BOE ，∴∠BOM =12∠BOE =12×142°=71°(2)ON 是∠AOD 的平分线．理由：根据题意，画图如下：∵∠DOM =∠BOM -∠BOD =71°-52°=19°，∠MON =45°，∴∠DON =∠DOM +∠MON =19°+45°=64°．∵∠AOC =52°，∴∠AOD =180°-∠AOC =180°-52°=128°，∴∠DON =12∠AOD ，∴ON 平分∠AOD ．【点睛】本题考查的是对顶角、邻补角的概念和性质、角平分线的定义，掌握对顶角相等、邻补角之和等于180°是解题的关键．11(2023上·黑龙江哈尔滨·七年级校考期中)已知：直线AB 、CD 相交于点O ，OE ⊥CD 于点O ，∠AOE :∠BOD =4:5．(1)如图1，求∠EOB 的度数．(2)如图2，过点O 画出直线AB 的垂线MN ，请直接写出图中所有与∠AOE 互补的角．【答案】(1)140°(2)∠EOB 、∠DON 、∠COM【分析】本题主要考查了垂线，互余和互补的性质，找出角度之间的数量关系是解题关键．(1)由平角的性质，得到∠AOE +∠BOD =90°，进而得出∠BOD =50°，即可求出∠EOB 的度数；(2)利用互余和互补的性质，分别得到∠DOM 、∠DON 、∠CON 、∠COM 的度数，再根据与∠AOE 互补的角的度数为140°，即可得到答案．【详解】(1)解：∵OE ⊥CD ，∴∠EOD =90°，∴∠AOE +∠BOD =90°，∵∠AOE :∠BOD =4:5，∴∠AOE =45∠BOD ，∴45∠BOD +∠BOD =95∠BOD =90°，∴∠BOD =50°，∴∠EOB =∠EOD +∠BOD =90°+50°=140°；(2)解：由(1)可知，∠BOD =50°，∠EOB =140°，∴∠AOE =40°，∵MN ⊥AB ，∴∠BOM =∠BON =∠AON =90°，∴∠DOM =∠BOM -∠BOD =40°，∴∠DON =∠180°-∠DOM =140°，∵∠CON =∠DOM =40°，∴∠COM =180°-∠CON =140°，∵与∠AOE 互补的角的度数为140°，∴与∠AOE 互补的角有∠EOB 、∠DON 、∠COM ．题型04 生活中的平移现象12(2023下·广西南宁·七年级校考期中)下图是德胜中学的校徽，将它通过平移可得到的图形是()A. B. C. D.【答案】C【分析】根据平移前后，图形的形状，大小，方向均不变，进行判断即可．【详解】A 、校徽左右交换位置得到，故选项错误，不符合题意；B 、向下旋转180°得到，故选项错误，不符合题意；C 、是通过平移得到，故选项正确，符合题意；D 、顺时针旋转90°故选项错误，不符合题意．故选：C ．【点睛】此题考查了图形的平移，解题的关键是熟知图形平移的性质．13(2023下·四川广元·七年级校联考期中)下面生活中的现象可以看成平移的是()①转动的指针②水平传输带上物品的运动③从楼顶自由下落的铁球(球不旋转)④随风摆动的旗帜A.①②B.③④C.②③D.②④【答案】C【分析】根据平移的定义，平移是指将一个图形上的所有点都按照某个直线方向做相同距离的移动，逐项进行判断即可．【详解】解：平移是指将一个图形上的所有点都按照某个直线方向做相同距离的移动，生活中也很多物体存在平移现象，②水平传输带上物品的运动，③从楼顶自由下落的铁球(球不旋转)是平移，①转动的指针，④随风摆动的旗帜都改变了方向，不是平移，故选：C ．【点睛】本题考查了生活中的平移现象，熟练掌握平移的定义是解答本题的关键．14(2023下·湖北武汉·七年级统考期中)如图，以下四个图标中可以看作由“基本图案”经过平移得到的是()A. B. C. D.【答案】D【分析】图形平移前后的大小，形状都不变化，据此判断即可．【详解】解：A 、不能看作由“基本图案”经过平移得到，故不符合题意；B 、不能看作由“基本图案”经过平移得到，故不符合题意；C 、不能看作由“基本图案”经过平移得到，故不符合题意；D 、能看作由“基本图案”经过平移得到，故符合题意；故选：D ．【点睛】此题考查了平移的性质，熟练掌握图形平移前后的大小，形状都不变化，只是位置变化是解题的关键．题型05 利用平移的性质求解点C 的方向平移到如图位置，已知AB =14．图中阴影部分的面积为84，DH =4，则平移距离为．【答案】7【分析】根据平移的性质可知：AB =DE ，由此可求出EH 的长．由S 阴影DHCF =S 梯形ABEH ，结合梯形的面积公式即可求出BE ．【详解】解：根据平移可得DE =AB =14，DE ∥AB ，S △ABC =S △DEF ，∴EH =14-4=10，S 阴影DHCF =S 梯形ABEH =84，∴12(EH +AB )⋅BE =84，∴12×(14+10)⋅BE =84，∴BE =7，即平移的距离为7，故答案为：7．【点睛】本题考查了平移的性质，对应点连线的长度等于平移距离，平移变化只改变图形的位置不改变图形的形状，熟记各性质并判断出阴影部分面积等于梯形ABEH 的面积是解题的关键．16(2023上·云南昆明·八年级校考期中)如图，将△ABC 沿CB 边向右平移得到△DFE ，DE 交AB 于点G ．已知∠A ：∠C ：∠ABC =1：2：3，AB =9cm ，BF =5cm ，AG =5cm ，则图中阴影部分面积为cm 2．【答案】652【分析】本题主要考查平移的性质，根据平移的性质，AB 的对应边是FD ，求出FD 的长度，∠A ：∠C ：∠ABC =1：2：3，则△ABC 是直角三角形，∠F 是直角，则BF 是梯形的高，根据AG 的长度求出BG 的长度，利用梯形的面积公式求出答案．【详解】解：∵AB =DF ，AB =9，∴DF =9，BG =AB -AG =9-5=4，又∵BF 是梯形高S 阴影=12BG +DF ⋅BF =12×4+9 ×5=652．故答案为：652．17(2023下·贵州铜仁·八年级校考期中)在一矩形花园里有两条绿化带．如图所示的阴影部分，A 1A 2∥B 1B 2、A 1A 2=B 1B 2、A 2A 3∥B 2B 3，A 2A 3=B 2B 3、A 3A 4∥B 3B 4、A 3A 4=B 3B 4、AC ∥BD ，且A 1B 1=AB ，这两【答案】S1=S2【分析】设矩形花园的宽a，根据题意可知，两条绿化地的面积都相当于长为AB，宽为a的长方形的面积．【详解】解：设矩形花园的宽a，根据题意可知，两条绿化地的面积都相当于长为AB，宽为a的长方形的面积，∴S1=S2，故答案为：S1=S2．【点睛】本题考查了生活中的平移，根据平移确定绿化带的长和宽是解题的关键．题型06利用平移解决实际问题18(2023下·河北沧州·七年级校考期中)某宾馆在重新装修后，准备在大厅主楼梯上铺设某种红色地毯，已知这种地毯每平方米售价30元，主楼梯道宽2m，其侧面如图，则购买地毯至少需要元．AI【答案】450【分析】根据题意，结合图形，先把楼梯的横竖向上向右平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．【详解】解：利用平移线段，把楼梯的横竖向上向右平移构成一个长方形，根据题意这个长方形的长与宽分别为5米，2.5米，∴地毯的长度为：5+2.5=7.5(米)，地毯的面积为：7.5×2=15(平方米)，故买地毯至少需要：15×30=450(元)．故答案为：450．【点睛】本题主要考查了生活中的平移现象，利用平移的性质，把所要求的的所有线段平移到一条直线上进行计算是解本题的关键．19(2023下·江西南昌·七年级校考期中)如图，是一块长方形的场地，长AB=52m，宽AD=41m．从A，B两处入口的小路宽都为1m，两条小路汇合处宽为2m，其余部分种植草坪，则草坪的面积为m2．【答案】2000【分析】本题要看图解答．从图中可以看出剩余部分的草坪正好可以拼成一个长方形，然后根据题意求出长和宽，最后可求出面积．【详解】解：由图片可看出，剩余部分的草坪正好可以拼成一个长方形，且这个长方形的长为52-2=50m，这个长方形的宽为：41-1=40m，因此，草坪的面积=50×40=2000平方米．故答案为：2000．【点睛】此题主要考查了平移的性质的应用，有一定的思维含量，得出草坪正好拼成长方形是解题的关键．20(2023下·黑龙江鸡西·七年级期中)春天到了，为美化环境，鸡西市儿童公园在一块长方形的空地上修两条宽一米的小路，其余部分种上不同的花卉，测得数据如图所示，求种花的面积和为．【答案】8【分析】根据图形利用平移的性质，将图中空地平移后，种花的正好组成一个长为4，宽为2的长方形，然后求出结果即可．【详解】解：根据题意可知，种花的面积和为：5-1=4×2=8．×3-1故答案为：8．【点睛】本题主要考查了平移的性质，解题的关键是根据平移得出种花的正好组成一个长为4，宽为2的长方形．题型07平移作图21(2023上·黑龙江哈尔滨·七年级校考期中)如图，△ABC的三个顶点都在每格为1个单位长度的格点上，请将△ABC先向下平移三个单位长度后再向右平移四个单位长度后得到△A1B1C1．(1)画出平移后的图形；(2)在(1)的条件下，连接BB1、CB1，直接写出三角形BCB1的面积为．【答案】(1)作图见解析；(2)△BCB1的面积为92．【分析】(1)根据平移的性质作图即可；(2)利用三角形面积公式计算即可；此题考查了作图--平移，三角形的面积，熟练掌握平移的性质是解题的关键．【详解】(1)如图，△A1B1C1即为所求；(2)如图，△BCB1的面积为12×3×3=92．22(2023上·黑龙江哈尔滨·七年级哈尔滨德强学校校考期中)如图，在每个小正方形的边长为1的方格纸中，将△ABC向上平移4个单位长度得到△DEF，使点A、B、C分别对应点D、E、F，再将△DEF平移得到△MNP，使点D、E、F分别对应点M、N、P．(1)分别画出两次平移后的三角形；(2)顺次连接点C、F、N，请直接写出△CFN的面积为．【答案】(1)见解析(2)6【分析】本题考查了作图-平移变换、三角形的面积．(1)根据平移作图即可得△DEF，再向右平移5个单位，再向下平移1个单位，画出△MNP即可得；(2)直接利用直角三角形的面积公式进行计算即可得．【详解】(1)解：分别画出两次平移后的△DEF和△MNP，如图所示．×4×3=6．(2)解：△CFN的面积为12故答案为：6．23(2023上·黑龙江哈尔滨·七年级校考期中)如图，网格中每个小正方形的边长均为1，点A、B、C均在小正方形的顶点，把三角形ABC平移得到三角形A B C ，使C点的对应点为C ．(1)请在图中画出三角形A B C ；(2)过点C 画出线段A B 的垂线，垂足为O；(3)直接写出三角形A B C 的面积为平方单位．【答案】(1)见解析(2)见解析(3)6【分析】本题考查了平移的性质，(1)根据平移的性质，找到对应的A 、B 然后画出△A B C 即可；(2)根据垂线的定义作图即可；(3)根据平移的性质即可求解．(2)解：如图线段C O为所作图形；×3×4=6，根据平移的性质，可得△A B C 的面积也是6．(3)解：△ABC的面积为12一、单选题1(2023下·山东济南·七年级统考期中)下列四个图中，∠1=∠2一定成立的是()A. B.C. D.【答案】B【分析】根据对顶角的性质、互补的定义和角在图形中的位置逐项判断即可.【详解】解：A、图形中的∠1与∠2不能判断是否相等，故本选项不符合题意；B、图形中的∠1,∠2是对顶角，所以∠1=∠2，故本选项符合题意；C、图形中的∠1与∠2不能判断是否相等，故本选项不符合题意；D、图形中的∠1与∠2是邻补角，不能判断是否相等，故本选项不符合题意；故选：B.【点睛】本题考查了对顶角的性质和互补的定义，正确识别图形、熟知对顶角相等的性质是解题关键.2(2023上·黑龙江哈尔滨·七年级校考期中)如图，AC⊥BC，CD⊥AB，则点B到CD的距离是线段( )的长度A.BDB.CDC.BCD.AD【答案】A【分析】本题考查了点到直线的距离“直线外一点到这条直线的垂线段的长度，叫做点到直线的距离”．根据点到直线的距离的定义即可得．【详解】解：∵CD⊥AB，∴点B到CD的距离是线段BD的长度，故选：A．3(2023上·河南新乡·九年级校考期中)甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，能用其中一部分平移得到的是()A.杯B.立C. 比D.曲【答案】C【分析】根据图形平移的性质解答即可．本题考查的是利用平移设计图案，熟知图形平移不变性的性质是解答此题的关键．【详解】解：由图可知A不是平移得到，B不是平移得到，D不是平移得到，C是利用图形的平移得到．故选：C．4(2023下·江西吉安·八年级校考期中)如图，将△ABC向左平移得到△DEF，连接AD，如果△ABC 的周长是16cm，四边形ACED的周长是20cm，那么平移的距离是()A.1cmB.2cmC.3cmD.4cm【答案】B【分析】根据平移的性质结合已知条件求解即可．【详解】解：∵将△ABC向左平移得到△DEF，∴AD=EB，△ABC≌△DEF，则ED=AB，EF=BC，DF=AC，∵△ABC的周长的周长是16cm，∴△DEF的周长是16cm，即DE+DF+EF=DE+AC+BC=16cm，∵四边形ACED的周长=AD+BE+BC+AC+DE=2AD+16=20(cm)，∴AD=2cm，即平移的距离是2cm；故选：B．【点睛】本题考查了平移的性质，掌握平移前后对应线段相等是解题关键．5(2023下·河南郑州·七年级校联考期中)如图，直线AB，CD相交于点O，∠EOD=90°.下列说法中错误的是()A.∠AOC=∠BODB.∠AOE和∠AOC互余C.∠AOC与∠AOD互补D.∠AOC与∠BOD互余【答案】D【分析】根据对顶角、邻补角的概念判断即可．【详解】解：A．∵∠AOC与∠BOD是对顶角，∴∠AOC=∠BOD，故本选项说法正确，不符合题意；B．∵∠EOD=90°，∴∠EOC=90°，∴∠AOE和∠AOC互余，故本选项说法正确，不符合题意；C．∵∠AOC+∠AOD=180°，∴∠AOC与∠AOD互补，故本选项说法正确，不符合题意；D．∠AOC与∠BOD相等，不一定互余，故本选项说法错误，符合题意；故选：D．【点睛】本题考查的是对顶角、邻补角，掌握对顶角的性质、邻补角的概念是解题的关键．二、填空题6(2023下·河南周口·七年级统考期中)如图，直线AB，CD相交于点O，EO⊥CD，垂足为O，若∠1 =36°，则∠2=．【答案】54°/54度【分析】根据垂线的定义，由EO⊥CD，垂足为O，得∠DOE=90°．由∠1=36°，根据对顶角的定义，得∠BOD=36°，即可求得∠2．【详解】解：∵EO⊥CD，垂足为O，∴∠DOE=90°．∵∠1=36°，∴∠BOD=36°，∴∠2=∠DOE-∠BOD=90°-36°=54°，故答案为：54°．【点睛】本题主要考查垂线、对顶角，熟练掌握垂线的定义、对顶角的定义是解决本题的关键．7(2023下·广东中山·七年级统考期中)如图，当光线从空气射入水中时，光线的传播方向发生了改变，这就是折射现象．图中∠1与∠2是不是对顶角？．(填“是”或“不是”)【答案】不是【分析】本题考查了对顶角的定义，如果两个角有公共顶点，其中一个角的两边分别是另一个角的两边的反向延长线，那么这两个角是对顶角．根据对顶角的定义直接判断即可．【详解】解：由对顶角的定义可知：∠1与∠2不是对顶角．故答案为：不是．8(2023下·河南安阳·七年级校考期中)为持续推进儿童友好公园建设，郑州市园林绿化部门计划在2023年新建绿地面积300万平方米以上．如图，在长为103米，宽为60来的长方形地块上，有纵横交错的几条小路，宽均为3米，其他部分计划种植花草，则种植花草的面积为平方米．【答案】5700【分析】可以根据平移的性质，种植花草的面积相当于一条横向长为103-3米与一条纵向长为60-3米的长方形面积，据此求解即可．【详解】解：由平移的性质可知，植花草的面积相当于一条横向长为103-3米米与一条纵向长为60-3的长方形面积，∴种植花草的面积=103-3=5700m2 ．60-3故答案为：5700．【点睛】本题考查了平移在实际中的应用，将两条小路平移至长方形的边上，使种植花草的面积等于一个长方形的面积是解决此题的关键．9(2023下·山西大同·七年级大同一中校考期中)如图，将直角三角形ABC沿边AC方向平移到三角形DEF的位置，连接BE．若AF=14，CD=6，则BE的长为【答案】4【分析】根据平移的性质，得BE=AD=CF，求出AD=CF=12AF-CD=12×14-6=4即可得出答案．【详解】解：由平移的性质，得BE=AD=CF，∴AD=CF=12AF-CD=12×14-6=4，∴BE=4．故答案为：4．【点睛】本题主要考查了平移的性质，解题的关键是熟练掌握性质，求出AD=4．10(2023下·内蒙古鄂尔多斯·七年级统考期中)如图，AB=4cm，BC=5cm，AC=2cm，将△ABC 沿BC方向平移3cm，得到△DEF，连接AD，则阴影部分的周长为cm．【答案】11【分析】本题考查平移的性质，根据平移性质得到AD=BE，AB=DE，然后计算出阴影部分周长为△ABC 的周长即可求解．利用平移的性质得到AD=BE，AB=DE是解答的关键．【详解】解：∵将△ABC沿BC方向平移3cm，得到△DEF，∴AD=BE=3cm，AB=DE=4cm，∴阴影部分的周长为AD+EC+DE+AC=BE+EC+AB+AC=BC+AB+AC=5+4+2=11cm，故答案为：11．三、解答题11(2023下·湖南永州·七年级校考期中)如图，在方格纸内将△ABC水平向右平移6个单位得到△A1 B1C1，再向上平移4个单位长度得到△A2B2C2．(1)画出△A1B1C1和△A2B2C2；(2)连接AA1、BB1，则线段AA1、BB1的位置关系是，线段AA1、BB1的数量关系是．【答案】(1)见解析(2)平行，相等【分析】(1)根据平移的性质画出点A、B、C的对应点A1、B1、C1及A2、B2、C2，再顺次连接即可得到△A1B1 C1和△A2B2C2；(2)由平移的性质即可得到答案．【详解】(1)解：如图所示，△A1B1C1和△A2B2C2即为所作；(2)解：如图，，由平移的性质可得：线段AA1、BB1的位置关系是平行，线段AA1、BB1的数量关系是相等，故答案为：平行，相等．【点睛】本题考查了作图-平移变换，平移的性质，经过平移后，对应点所连接的线段平行且相等，熟练掌握平移的性质是解题的关键．12(2023下·山东济南·七年级统考期中)如图，△ABC的三个顶点A、B、C在正方形网格中，每个小方格的边长都为1.请在方格纸上画图并回答下列问题：(1)过C点画直线AB的垂线，垂足为点E；(2)过A点画射线AF∥BC，交直线CE于点F；(3)点C到直线AB的距离为线段的长度；(4)比较大小：线段CE线段BC(填“>”、“”或“=”)．【答案】(1)见解析(2)见解析(3)CE(4)<【分析】(1)根据网格的特点作图即可；(2)根据网格的特点作图即可；(3)根据点到直线的距离的概念解答；(4)根据垂线段最短解答．【详解】(1)如图，直线CE即为所作；(2)如图，射线AF即为所作；(3)点C到直线AB的距离为线段CE的长度；故答案为：CE；(4)根据垂线段最短得：线段CE<线段BC；故答案为：<．【点睛】本题考查了利用网格作图、垂线段最短以及点到直线的距离等知识，熟练掌握相关知识是解题的关键．13(2023下·河北石家庄·七年级校考期中)作图题(1)如图，要把河中的水引到水池P，在河岸AB的什么地方开始挖渠。
优化设计七年级下册数学全部答案2
优化设计七年级下册数学全部答案25.1相交线学前温故 1、两方无2、180? 新课早知1、邻补角2、对顶角3、?BOD ?AOC 和?BOD 4、相等5、C 轻松尝试应用 1,3 CAC 4、15?5、?AOF 和?BOE 6、解:因为?AOD与?BOC是对顶角所以?AOD=?BOC 又因为?AOD+?BOC=220?所以?AOD=110?而?AOC与?AOD是邻补角则?AOC+?AOD=180? 所以?AOC=70?智能演练能力提升 1,3 CCC 4、10?5、对顶角邻补角互为余角 6、135?40?7、90?8、不是9、解:因为OE平分?AOD, ?AOE=35?, 所以?AOD=2?AOE=70?由?AOD与?AOC是邻补角，得?AOC=180?-?AOD=110?因此?COE=?AOE+?AOC=35?+110?=145? 10、2 6 12 n(n-1) 4046132 5.1.2垂线学前温故90?新课早知1、垂直垂线垂足2、D BE CD C 3、一条垂线段 4、B 5、垂线段的长度 6、D 轻松尝试应用1,3 DBD 4、?1与?2互余 5、30?6、解:由对顶角相等，可知?EOF=?BOC=35?,又因为OG?AD, ?FOG=30?,所以?DOE=90?-?FOG-?EOF=90?-30?-35?=25? 智能演练能力提升1,3 AAB 4、?? 5、解:如图.6、解:因为CD?EF, 所以?COE=?DOF=90 ? 因为?AOE=70?,所以?AOC=90?-70?=20?, ?BOD=?AOC=20?,所以?BOF=90?-?BOD=90?-20?=70?因为OG平分?BOF,所以?BOG=0.5×70?=35?, 所以?BOG=35?+20?=55?7、解(1)因为OD平分?BOE,OF平分?AOE, 所以?DOE=1/2?BOE, ?EOF=1/2?AOE,因为?BOE+?AOE=180?,所以?DOE+?EOF=1/2?BOE+1/2?AOE=90?,即?FOD=90?,所以OF?OD(2)设?AOC=x,由?AOC: ?AOD=1:5,得?AOD=5x.因为?AOC=?AOD=180?,所以x+5x=180?,所以x=30?.所以?DOE=?BOD=?AOC=30?.因为?FOD=90?,所以?EOF=90?-30?=60?8、D 9解:(1)如图所示:(2)如图所示:(3)= =(4)角平分线上的点到角两边的距离相等.5.1.3同位角、内错角、同旁内角快乐预习感知学前温故1、相等互补2、直角新课早知 1、同位角内错角同旁内角2、B 3、A 互动课堂例解:同位角有?1和?2，?3和?5; 内错角有?1和?3，?2和?5;同旁内角有?1和?4，?4和?5 轻松尝试应用1、B 2、B 3、同位同旁内内错 4、内错AB BC AC 同旁内 AC BC AB 5、解:(1)中，?1与?2是直线c、d被直线l所截得的同位角，?3与?4是直线a,b被直线l所截得的同旁内角;(2)中，?1与?2是AB,CD 被直线BC所截得的同位角，?3与?4是直线AB,CD被直线AC所截得的内错角 ;(3)中，?1与?2是直线AB,CD被直线AG所截得的同位角，?3与?4是直线AG,CE被直线CD所截得的内错角;(4)中，?1与?2是直线AD,BC被直线AC所截得的内错角，?3与?4是直线AB,CD被直线AC所截得的内错角能力升级 1,5 ADCCB 6、?B ?A ?ACB和?B 7、BD 同位 AC 内错 AC AB BC 同旁内 AB AC BD 同位 AB EF BD 同旁内 8、解:?1与?5;?1与7;?4与?39、解:因为?1与?2互补，?1=110?，所以?2=180?-110?=70?，因为?2与?3互为对顶角，所以?3=?2=70?因为?1+?4=180? 所以?4=180?-?1=180?-110?=70?、解:(1)略(2)因为?1=2?2，?2=2?3，所以?1=4?3.又因为?1+?3=180? 10所以4?3=?3=180?所以?3=36?所以?1=36?×4=144?，?2=36?×2=72?5.2.1平行线学前温故有且只有一个新课早知 1、平行2、C 3、一条4、互相平行 5、A 轻松尝试 1,3 DBB 4、AB?CD ,AD?BC 5、? ? 6、略能力升级 1,4 BCAB 5、3 A′B′, C′D,CD 6、在一条直线上过直线外一点有且只有一条直线与已知直线平行 7、解:(1)CD?MN,GH?PN.(2)略.8 解:(1)如图?示.(2)如图?所示.)平行因为PQ?AD,AD?BC, 所以PQ?BC .(2)DQ=CQ 10、解:(1)图略(2)AH=HG=GM=MC 9解:(1(3)HD:EG:FM:BC=1:2:3:45.2.2平行线的判定学前温故同一同侧之间两侧之间同侧新课早知 1、不相交平行同位角平行内错角平行同旁内角互补平行 2、C 3、A 轻松尝试1,4、ABDC 5、EF 内错角相等，两直线平行 BC 同旁内角互补，两直线平行 AD BC 平行于同一条直线的两直线平行能力提升 1,5 DCDDD 6、?FEB=100?7、内错角相等，两直线平行 8、AB EC 同位角相等地，两直线平行 AB EC 内错角相等，两直线平行 AC ED 内错角相等，两直线平行 AB EC 同旁内角互补，两直线平行 9、解:因为DE平分?BDF,AF平分?BAC, 所以2?1=?BDF,2?2=?BAC 又因为?1=?2，所以?BDF=?BAC.所以DF?AC(同位角相等，两直线平行) 10、解:(1)因为AB?EF,CD?EF,所以AB?CD. 理由:两条直线都垂直于同一条直线，这两条直线平行。
人教版七年级数学下册第五章相交线与平行线复习训练题
第五章相交线与平行线类型一邻补角与对顶角巧分辨1.如图1所示的几个图形中，能构成对顶角的是( )图12．如图2，三条直线AB，CD，EF相交于点O，则∠1的邻补角为______________．图23．如图3，直线AB，CD交于点O，射线OM平分∠AOC.若∠BOD＝76°，求∠AOM的度数．图3类型二区分同位角、内错角、同旁内角有原则4.如图4，与∠1构成内错角的是( )图4A．∠2 B．∠3 C．∠4 D．∠55．如图5，直线DE经过点C，则∠A的内错角是________，∠A的同旁内角是________________．图56．如图6，E是AB延长线上一点，指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？(1)∠A和∠D；(2)∠A和∠CBA；(3)∠C和∠CBE.图6类型三掌握相交的特殊情形——垂直7．如图7，已知AB，CD相交于点O，OE⊥CD，垂足为O，∠AOC＝30°，则∠BOE等于( )图7A ．30°B ．60°C ．120°D ．130°8.如图8所示，在直角三角形ABC 中，∠ACB＝90°，CD⊥AB 于点D ，则点A 到BC 的距离为线段______的长度；点A到CD 的距离为线段______的长度；点C 到AB 的距离为线段______的长度．图8类型四 平行线的判定和性质9.如图9，直线a ，b 被直线c 所截，下列说法正确的是( )A ．当∠1＝∠2时，一定有a∥bB ．当a∥b 时，一定有∠1＝∠2C ．当a∥b 时，一定有∠1＋∠2＝90°D ．当∠1＋∠2＝180°时，一定有a∥b10．如图10，已知AB∥CD，∠1＝60°，则∠2＝________°.图9图1011.如图11，不添加辅助线，请你写出一个能判定EB∥AC的条件：________________________．图1112．如图12，AB∥CD，直线EF交AB于点E，交CD于点F，EG平分∠BEF，交CD于点G，∠1＝50°，求∠2的度数．图1213．如图13，已知∠1＋∠2＝180°，∠DEF＝∠A，试判断∠ACB与∠DEB的大小关系，并说明理由．图1314．如图14所示，已知OP∥QR∥ST，连接PR，SR，猜想∠1，∠2，∠3三个角之间的关系，并说明理由．图14类型五命题与定理须细辨15．下列语句不是命题的是( )A．若a<0，b<0，则ab>0B．用三角板画一个60°的角C．对顶角相等D．互为相反数的两个数的和为016．下列命题中，是真命题的是( )A．对顶角相等B．同位角相等C．若a2＝b2，则a＝bD．若a>b，则－2a>－2b17．将下列命题改写成“如果……那么……”的形式．(1)直角都相等；(2)末位数字是5的整数能被5整除；(3)三角形的内角和是180°.类型六平移平移的特征：图形的平移变换中，图形的形状、大小、方向都不发生改变，只是改变了图形的位置；平移前后图形的对应点的连线平行(或在同一条直线上)且相等．18．下列现象中，不属于平移的是( )A．钟表的指针转动B．电梯的升降C．火车在笔直的铁轨上行驶D．传送带上物品的运动19．如图15，将周长为8的三角形ABC沿BC方向向右平移1个单位长度得到三角形DEF，则四边形ABFD的周长为( )图15A．6 B．8 C．10 D．12类型七方程思想在几何中的应用20．如图16，已知a∥b，∠1＝(3x＋70)°，∠2＝(5x＋22)°，求∠1的补角的度数．图16类型八开放型问题21．给出下列三个论断：①∠B＋∠D＝180°；②AB∥CD；③BC∥DE.请你以其中两个论断作为已知条件，填入“已知”栏中，以一个论断作为结论，填入“结论”栏中，使之成为一道由已知可得到结论的题目，并说明理由．已知：如图17，________________________．结论：________________________．图17类型九探究型问题22．【阅读材料】在“相交线与平行线”的学习中，有这样一道典型问题：如图18①，AB∥CD，点P在AB与CD之间，可得结论：∠BAP＋∠APC＋∠PCD＝360°.理由如下：过点P作PQ∥AB.∴∠BAP＋∠APQ＝180°.∵AB∥CD，PQ∥AB，∴PQ∥CD，∴∠PCD＋∠CPQ＝180°.∴∠BAP＋∠APC＋∠PCD＝∠BAP＋∠APQ＋∠CPQ＋∠PCD＝180°＋180°＝360°.【问题解决】(1)如图②，AB∥CD，点P在AB与CD之间，可得∠BAP，∠APC，∠PCD间的等量关系是________________________________________________________________________；(2)如图③，AB∥CD，点P ，E 在AB 与CD 之间，AE 平分∠BAP，CE 平分∠DCP，写出∠AEC 与∠APC 间的等量关系，并写出理由；(3)如图④，AB∥CD，点P ，E 在AB 与CD 之间，∠BAE＝13∠BAP，∠DCE＝13∠DCP ，可得∠AEC与∠APC 间的等量关系是________________________．图18答案1．D2.∠BOE 和∠AOF 3．解：∵∠BOD＝76°， ∴∠AOC＝∠BOD＝76°. ∵射线OM 平分∠AOC，∴∠AOM＝12∠AOC＝12×76°＝38°.4．B5.∠ACD ∠ACB，∠ACE 和∠B6．解：(1)∠A 和∠D 是直线AE ，DC 被直线AD 所截而成的同旁内角． (2)∠A 和∠CBA 是直线AD ，BC 被直线AE 所截而成的同旁内角． (3)∠C 和∠CBE 是直线DC ，AE 被直线BC 所截而成的内错角． 7．C 8.AC AD CD 9．D 10.12011．答案不唯一，如∠C＝∠EBD 12．解：∵AB∥CD，∴∠2＝∠BEG，∠BEF＋∠1＝180°. ∵∠1＝50°，∴∠BEF＝130°. ∵EG 平分∠BEF，∴∠BEG＝12∠BEF＝65°， ∴∠2＝65°.13．解：∠ACB＝∠DEB.理由：∵∠1＋∠2＝180°，∠1＋∠DFE＝180°，∴∠2＝∠DFE，∴AB∥EF，∴∠DEF＝∠BDE.∵∠DEF＝∠A，∴∠A＝∠BDE，∴AC∥DE，∴∠ACB＝∠DEB.14．解：∠2＋∠3＝180°＋∠1.理由：∵OP∥QR，∴∠2＋∠QRP＝180°，∴∠QRP＝180°－∠2.∵QR∥ST，∴∠3＝∠QRS＝∠1＋∠QRP＝∠1＋180°－∠2.∴∠2＋∠3＝180°＋∠1.15．B16. A17．解：(1)如果几个角是直角，那么它们都相等．(2)如果一个整数的末位数字是5，那么它能被5整除．(3)如果一个图形是三角形，那么它的内角和是180°.18．A19. C20．解：如图，因为a∥b，所以∠1＝∠3.又因为∠1＝(3x＋70)°，∠2＝(5x＋22)°，∠2＋∠3＝180˚，所以(3x ＋70)°＋(5x＋22)°＝180°，解得x＝11，所以∠1＝(3x＋70)°＝103°.又因为180°－103°＝77°，所以∠1的补角的度数为77°.21．解：答案不唯一，符合题意的情况有3种，即①②→③；①③→②；②③→①，任选其中一种即可．已知：如图17，∠B＋∠D＝180°，AB∥CD.结论：BC∥DE.理由：因为AB∥CD，所以∠B＝∠C(两直线平行，内错角相等)．又因为∠B＋∠D＝180°，所以∠C＋∠D＝180°，所以BC∥DE(同旁内角互补，两直线平行)．22．解：(1)如图②，作PE∥AB，得∠APE＝∠BAP.∵AB∥CD，AB∥PE，∴CD∥PE，∴∠CPE＝∠PCD，∴∠APC＝∠APE＋∠CPE＝∠BAP＋∠PCD.故答案为∠APC＝∠BAP＋∠PCD.(2)∠APC＝2∠AE C.理由：设∠EAB＝∠EAP＝x，∠ECD＝∠ECP＝y.由(1)可知：∠AEC＝x＋y，∠APC＝2x＋2y，∴∠APC＝2∠AE C.(3)设∠EAB＝a，∠DCE＝b，则∠BAP＝3a，∠DCP＝3b. 由题意得∠AEC＝a＋b，∠APC＋3a＋3b＝360°，∴∠APC＋3∠AEC＝360°.故答案为∠APC＋3∠AEC＝360°.。
精品 七年级数学下册 期末复习题2
19.把二元一次方程
x y 2 x y 3x 1 转化为用含 x 的代数式表示 y 时，应写成 y= 5 4 10
20.利用两块相同的长方形铁片测量一张桌子的高度．首先按图①方式放置，再交换两铁片的位置，按 图②方式放置．测量的数据如图，则桌子的高度是 21.已知-1<x<2,化简 x 1 x 2 = 22.使不等式 2 x
2 11 1 x 成立的最小整数解是 3 6 2
cm ．
23.不等式组
x 2a 4 2 x b 5
的解集是 0 x 2 ，那么 a b 的值等于______。
24.若不等式组
x m 的解集为 x 2 ,则 m 的取值范围是 x 6 3x 2
5.纵坐标为-8 的点一定在（ A.y 轴上
B.过（-8，0）平行于 y 轴的直线上 D.过（0，-8）平行于 x 轴的直线上 ）
C.过（0，-8）平行于 y 轴的直线上
6.已知点 P 关于 x 轴的对称点为（a，-2） ，关于 y 轴的对称点为（1，b） ，那么 P 点的坐标为（ A.(a，-b) B.（b，-a） C.（-2，1） D.（-1，2） ）
（2）
53 x 47 y 112 47 x 53 y 88
31.使得 3x-2y= a 成立的 x、y 的值，也满足方程 (2 x y 1) 2 x 3 y 0 ，其中 a a 0 ，求 a 的值。
3
32.已知
1 3m 2 n 4 m 3n 7 m n 1 m 2 n 5 是同类项，求 m、n 的值。 x y 与 x y 7 13
0
9.关于 1
3 x 0 的正整数解，下列说法正确的是（ 4
人教版七年级下数学第五章 相交线与平行线 知识点+考点+典型例题
第五章相交线与平行线【知识要点】1.两直线相交2.邻补角：有一条公共边，另一条边互为反向延长线的两个角互为邻补角。
3.对顶角（1）定义：有一个公共顶点，且一个角的两边分别是另一个角的两边的反向延长线，这样的两个角互为对顶角 (或两条直线相交形成的四个角中，不相邻的两个角叫对顶角) 。
（2）对顶角的性质：对顶角相等。
4．垂直定义：当两条直线相交所形成的四个角中，有一个角是90°那么这两条线互相垂直。
5.垂线性质：①过一点有且只有一条直线与已知直线垂直；②垂线段最短。
6．平行线的定义：在同一平面内，不相交的两条直线叫平行线，“平行”用符号“∥”表示，如直线a，b 是平行线，可记作“a∥b”7．平行公理及推论（1）平行公理：过已知直线外一点有且只有一条直线与已知直线平行。
（2）推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行。
注：（1）平行公理中的“有且只有”包含两层意思：一是存在性；二是唯一性。
（2）平行具有传递性，即如果a∥b，b∥c，则a∥c。
8．两条直线的位置关系：在同一平面内，两条直线的位置关系有相交和平行。
9．平行线的性质：（1）两直线平行，同位角相等（在同一平面内）（2）两直线平行，内错角相等（在同一平面内）（3）两直线平行，同旁内角互补（在同一平面内）10．平行线的判定（1）同位角相等，两直线平行；（在同一平面内）（2）内错角相等，两直线平行；（在同一平面内）（3）同旁内角互补，两直线平行；（在同一平面内）（4）如果两条直线都和第三条直线平行，那么这两条直线也互相平行；补充：（5）平行的定义；（在同一平面内）（6）在同一平面内．．．．．．，垂直于同一直线的两直线平行。
11.平移的定义及特征定义：将一个图形向某个方向平行移动，叫做图形的平移。
特征：①平移前后的两个图形形状、大小完全一样；②平移前与平移后两个图形的对应点连线平行且相等。
【典型例题】考点一：对相关概念的理解对顶角的性质，垂直的定义，垂线的性质，点到直线的距离，垂线性质与平行公理的区别等例1：判断下列说法的正误。
5.1 对顶角、邻补角 考点训练(含答案解析)
【考点训练】对顶角、邻补角－1一、选择题（共6小题）1．（2012•北京）如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠BOD=76°，则∠BOM等于（）38°B．104°C．142°D．144°A．(第1题) (第2题) (第3题)2．如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（）36°B．72°C．108°D．120°A．3．（2011•台湾）如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角．关于这七个角的度数关系，下列何者正确（）∠2=∠4+∠7 B．∠3=∠1+∠6 C．∠1+∠4+∠6=180°D．∠2+∠3+∠5=360°A．4．（2012•梧州）如图，直线AB和CD相交于点O，若∠AOC=125°，则∠AOD=（）50°B．55°C．60°D．65°A．(第4题) (第6题)(第7题)5．（2013•贺州）下面各图中∠1和∠2是对顶角的是（）.AB．C．D．．6．（2012•柳州）如图，直线a与直线c相交于点O，∠1的度数是（）A60°B．50°C．40°D．30°．二、填空题（共3小题）（除非特别说明，请填准确值）7．（2012•泉州）如图，在△ABC中，∠A=60°，∠B=40°，点D、E分别在BC、AC的延长线上，则∠1=_________°．8．（2013•湘西州）如图，直线a和直线b相交于点O ，∠1=50°，则∠2_________．(第8题) (第9题)9．（2013•曲靖）如图，直线AB、CD相交于点O，若∠BOD=40°，OA平分∠COE，则∠AOE=_________．三、解答题（共2小题）（选答题，不自动判卷）10．（2011•泉州）如图，直线a、b相交于点O，若∠1=30°，则∠2=_________．(第10题) (第11题)11．（2012•泉州）（2）如图，点A、O、B在同一直线上，已知∠BOC=50°，则∠AOC=_________°．参考答案与试题解析一、选择题（共6小题）1．（2012•北京）如图，直线AB，CD交于点O，射线OM平分∠AOC，若∠BOD=76°，则∠BOM等于（）A．38°B．104°C．142°D．144°考点：对顶角、邻补角；角平分线的定义．专题：常规题型．分析：根据对顶角相等求出∠AOC的度数，再根据角平分线的定义求出∠AOM的度数，然后根据平角等于180°列式计算即可得解．解答：解：∵∠BOD=76°，∴∠AOC=∠BOD=76°，∵射线OM平分∠AOC，∴∠AOM=∠AOC=×76°=38°，∴∠BOM=180°﹣∠AOM=180°﹣38°=142°．故选C．点评：本题考查了对顶角相等的性质，角平分线的定义，准确识图是解题的关键．2．如图，AB是一条直线，OC是∠AOD的平分线，OE在∠BOD内，∠DOE=∠BOD，∠COE=72°，则∠EOB=（）A．36°B．72°C．108°D．120°考点：角平分线的定义；对顶角、邻补角．专题：计算题．分析：设∠DOE=x，根据题意得到∠BOE=2x，∠AOC=∠COD=72°﹣x，再根据平角为180度，得到2×（72°﹣x）+3x=180°，解得x=36°，即可得到∠BOE的度数．解答：解：如图，设∠DOE=x，∵∠DOE=∠BOD，∴∠BOE=2x，又∵OC是∠AOD的平分线，∠COE=72°，∴∠AOC=∠COD=72°﹣x；∴2×（72°﹣x）+3x=180°，解得x=36°，∴∠BOE=2x=2×36°=72°．故选B．点评：本题考查了角的有关计算以及角平分线的性质和平角的定义，是基础知识比较简单．3．（2011•台湾）如图中有四条互相不平行的直线L1、L2、L3、L4所截出的七个角．关于这七个角的度数关系，下列何者正确（）A．∠2=∠4+∠7 B．∠3=∠1+∠6 C．∠1+∠4+∠6=180°D．∠2+∠3+∠5=360°考点：三角形内角和定理；对顶角、邻补角；三角形的外角性质．分析：根据对顶角的性质得出∠1=∠AOB，再用三角形内角和定理得出∠AOB+∠4+∠6=180°，即可得出答案．解答：解：∵四条互相不平行的直线L1、L2、L3、L4所截出的七个角，∵∠1=∠AOB，∵∠AOB+∠4+∠6=180°，∴∠1+∠4+∠6=180°．故选C．点评：此题主要考查了对顶角的性质以及三角形的内角和定理，正确的应用三角形内角和定理是解决问题的关键．4．（2012•梧州）如图，直线AB和CD相交于点O，若∠AOC=125°，则∠AOD=（）A．50°B．55°C．60°D．65°考点：对顶角、邻补角．分析：根据邻补角的和等于180°列式进行计算即可得解．解答：解：∵∠AOC=125°，∴∠AOD=180°﹣125°=55°．故选B．点评：本题考查了邻补角的两个角的和等于180°的性质，是基础题．5．（2013•贺州）下面各图中∠1和∠2是对顶角的是（）A．B．C．D．考点：对顶角、邻补角．分析：根据对顶角的定义对各选项分析判断后利用排除法求解．解答：解：A、∠1和∠2不是对顶角，故本选项错误；B、∠1和∠2是对顶角，故本选项正确；C、∠1和∠2不是对顶角，故本选项错误；D、∠1和∠2不是对顶角，是邻补角，故本选项错误．故选B．点评：本题考查了对顶角、邻补角，熟记概念并准确识图是解题的关键．6．（2012•柳州）如图，直线a与直线c相交于点O，∠1的度数是（）A．60°B．50°C．40°D．30°考点：对顶角、邻补角．分析：根据邻补角的和等于180°列式计算即可得解．解答：解：∠1=180°﹣150°=30°．故选D．点评：本题主要考查了邻补角的和等于180°，是基础题，比较简单．二、填空题（共3小题）（除非特别说明，请填准确值）7．（2012•泉州）如图，在△ABC中，∠A=60°，∠B=40°，点D、E分别在BC、AC的延长线上，则∠1=80°．考点：三角形内角和定理；对顶角、邻补角．专题：探究型．分析：先根据三角形内角和定理求出∠ACB的度数，再根据对顶角相等求出∠1的度数即可．解答：解：∵△ABC中，∠A=60°，∠B=40°，∴∠ACB=180°﹣∠A﹣∠B=180°﹣60°﹣40°=80°，∴∠1=∠ACB=80°．故答案为：80．点评：本题考查的是三角形的内角和定理，即三角形内角和是180°．8．（2013•湘西州）如图，直线a和直线b相交于点O，∠1=50°，则∠2=50°．考点：对顶角、邻补角．分析：根据对顶角相等即可求解．解答：解：∵∠2与∠1是对顶角，∴∠2=∠1=50°．故答案为=50°．点评：本题考查了对顶角的识别与对顶角的性质，牢固掌握对顶角相等的性质是解题的关键．9．（2013•曲靖）如图，直线AB、CD相交于点O，若∠BOD=40°，OA平分∠COE，则∠AOE=40°．考点：对顶角、邻补角；角平分线的定义．分析：根据对顶角相等求出∠AOC，再根据角平分线的定义解答．解答：解：∵∠BOD=40°，∴∠AOC=∠BOD=40°，∵OA平分∠COE，∴∠AOE=∠AOC=40°．故答案为：40°．点评：本题考查了对顶角相等的性质，角平分线的定义，是基础题，熟记性质并准确识图是解题的关键．三、解答题（共2小题）（选答题，不自动判卷）10．（2011•泉州）如图，直线a、b相交于点O，若∠1=30°，则∠2=30°．考点：对顶角、邻补角．专题：计算题；压轴题．分析：直接根据对顶角相等得到∠2的度数．解答：解：∵直线a、b相交于点O，∴∠1=∠2，而∠1=30°，∴∠2=30°．故答案为：30°．点评：本题考查了对顶角的性质：对顶角相等．11．（2012•泉州）（1）方程x﹣5=0的解是5．（2）如图，点A、O、B在同一直线上，已知∠BOC=50°，则∠AOC=130°．考点：对顶角、邻补角；解一元一次方程．专题：计算题；压轴题．分析：（1）观察或直接移项可得方程的解；（2）根据邻补角互补直接求出∠AOC的值．解答：解：（1）移项得，x=5；（2）∵∠BOC=50°，∴∠A0C=180°﹣50°=130°．点评：（1）本题考查了一元一次方程的解法，熟悉等式的性质是解题的关键；（2）本题考查了对顶角、邻补角，知道邻补角的和为180°是解题的关键．。
人教版七年级数学下册《相交线中求角》专项练习题-附含答案
人教版七年级数学下册《相交线中求角》专项练习题-附含答案【例题讲解】如图 直线AB CD 相交于点O OE 平分∠BOD OF 平分∠COE ．（1）若∠AOC ＝76° 求∠BOF 的度数；（2）若∠BOF ＝36° 求∠AOC 的度数；（3）请探究∠AOC 与∠BOF 的数量关系．）BOD ∠=又OE 平分180142DOE =︒-∠︒ OF 平分33EOF =∠-∠︒．）OE 平分∠COE ∠ BOE ∴∠BOE x ∠= 则2COA x ∠= EOF ∠180AOC COF +∠︒=︒ 解得：）由（1）知(180DOE ︒-∠【综合解答】1．如图 直线AB 、CD 相交于点O OE 把BOD ∠分成两部分(1)直接写出图中AOC ∠的对顶角为________ BOE ∠的邻补角为________；(2)若AOC 70∠=︒ 且BOE EOD ∠∠：=2：3 求AOE ∠的度数.2．如图 直线AB 、CD 、EF 相交于点O OG 平分∠COF ∠1=30° ∠2=45°．求∠3的度数．【答案】∠3=52.5°【详解】试题分析：先求出∠EOD的度数从而得出∠COF=105° 再根据OG平分∠COF 可得∠3的度数．试题解析：∠∠1=30° ∠2=45°∠∠EOD=180°﹣∠1﹣∠2=105°∠∠COF=∠EOD=105°又∠OG平分∠COF∠∠3=∠COF=52.5°．考点：对顶角、邻补角．3．如图直线AB、CD相交于点O∠DOE＝∠BOD OF平分∠AOE．(1)判断OF与OD的位置关系并说明理由；(2)若∠AOC：∠AOD＝1：5 求∠EOF的度数．4．如图 直线AB CD 相交于点O EO AB ⊥ 垂足为O ．（1）若35EOC ∠=︒ 求AOD ∠的度数；（2）若2BOC AOC ∠=∠ 求DOE ∠的度数．【答案】（1）125°；（2）150°【分析】(1)把COB ∠的度数计算出来 再根据对顶角的性质即可得到答案；(2)根据2BOC AOC ∠=∠ 设AOC x ∠= 2BOC x ∠=得到60BOD AOC ∠=∠=︒ 最后根据EO AB ⊥即可得到答案；【详解】解：（1）EO AB ⊥90EOB ∴∠=︒909035125COB EOC ∴∠=︒+∠=︒+︒=︒125AOD COB ∴∠=∠=︒；（2）2BOC AOC ∠=∠∴设AOC x ∠= 2BOC x ∠=又180BOC AOC ∠+∠=︒2180x x ∴+=︒60x ∴=︒60BOD AOC ∴∠=∠=︒又EO AB ⊥90EOB ∴∠=︒6090150DOE BOD EOB ∴∠=∠+∠=︒+︒=︒．【点睛】本题主要考查了对顶角的性质（对顶角相等）和邻补角的性质熟练掌握邻补角的性质和对顶角的性质是解题的关键．5．如图直线AB CD相交于O点OM平分∠AOB（1）若∠1＝∠2 求∠NOD的度数；（2）若∠BOC＝4∠1 求∠AOC与∠MOD的度数．【答案】（1）90°；（2）∠AOC＝60°；∠MOD＝150°.【分析】（1）根据角平分线的性质可得∠1+∠AOC＝90° 再利用等量代换可得∠2+∠AOC＝90° 利用邻补角互补可得答案；（2）根据条件可得90°+∠1＝4∠1 进而可得求出∠1＝30° 从而可得∠AOC的度数再利用邻补角互补可得∠MOD的度数．【详解】（1）∠OM平分∠AOB∠∠1+∠AOC＝90°．∠∠1＝∠2 ∠∠2+∠AOC＝90° ∠∠NOD＝180°﹣90°＝90°；（2）∠∠BOC＝4∠1 ∠90°+∠1＝4∠1 ∠∠1＝30° ∠∠AOC＝90°﹣30°＝60° ∠MOD＝180°﹣30°＝150°．【点睛】本题考查了角平分线和邻补角关键是掌握邻补角互补．6．如图直线AB CD EF相交于点O.(1)写出∠COE的邻补角；(2)分别写出∠COE和∠BOE的对顶角；(3)如果∠BOD＝60° ∠BOF＝90° 求∠AOF和∠FOC的度数．【答案】（1）∠COE的邻补角为∠COF和∠EOD；（2）∠COE和∠BOE的对顶角分别为∠DOF和∠AOF；（3）∠FOC=150°．【分析】（1）根据邻补角的定义（两个角有一条公共边它们的另一条边互为反向延长线具有这种关系的两个角）可得∠COE的邻补角有∠COF和∠EOD两个角；（2）根据对顶角的定义（一个角的两边分别是另一个角两边的反向延长线且这两个角有公共顶点）可得∠COE和∠BOE的对顶角分别为∠DOF和∠AOF；（3）由∠BOF=90°可得：AB∠EF 所以∠AOF=90° 由∠AOC=∠BOD可得：∠AOC =60° 由∠FOC=∠AOF+∠AOC即可求出∠FOC的度数；【详解】（1）∠COE的邻补角为∠COF和∠EOD；（2）∠COE和∠BOE的对顶角分别为∠DOF和∠AOF；（3）∠∠BOF=90°∠AB∠EF∠∠AOF=90°又∠∠AOC=∠BOD=60°∠∠FOC=∠AOF+∠AOC=90°+60°=150°．7．如图直线AB、CD相交于点O OE平分∠BOD OF平分∠COE．(1)若∠AOC=76° 求∠BOF的度数；(2)若∠BOF=36° 求∠AOC的度数；8．如图 直线AB 、CD 相交于点O OE 平分BOC ∠ 90COF ∠=．(1)若∠AOF =50° 求∠BOE 的度数；(2)若∠BOD :∠BOE =1:4 求∠AOF 的度数．【答案】（1）70BOE ∠=；（2）70AOF ∠=．【分析】（1）根据补角 余角的关系 可得∠COB 根据角平分线的定义 可得答案；（2）根据邻补角 可得关于x 的方程 根据解方程 可得∠AOC 再根据余角的定义 可得答案．【详解】(1)∠∠COF 与∠DOF 是邻补角∠∠COF =180°−∠DOF =90°．∠∠AOC 与∠AOF 互为余角∠∠AOC =90°−∠AOF =90°−50°=40°．∠∠AOC 与∠BOC 是邻补角∠∠COB =180°−∠AOC =180°−40°=140°．∠OE 平分∠BOC(2)∠BOD:∠BOE=1:4设∠BOD=∠AOC=x∠BOE=∠COE=4x．∠∠AOC与∠BOC是邻补角∠∠AOC+∠BOC=180°即x+4x+4x=180°解得x=20°．∠∠AOC与∠AOF互为余角∠∠AOF=90°−∠AOC=90°−20°=70°．【点睛】此题考查角平分线的定义对顶角、邻补角解题关键在于掌握其性质定义．9．如图∠1=∠2 ∠1+∠2=162° 求∠3与∠4的度数．【答案】∠3=54°∠4=72°【详解】试题分析：本题首先根据方程思想求出. ∠1、∠2的度数再根据对顶角、邻补角的关系求出∠3与∠4的度数．试题解析：由已知∠1=∠2 ∠1+∠2=162°解得：∠1=54° ∠2=108°．∠∠1与∠3是对顶角∠∠3=∠1=54°．∠∠2与∠4是邻补角∠∠4=180°﹣∠2=72°．考点：1二元一次方程组;2对顶角;3邻补角.10．如图直线AB CD相交于点O EO∠AB垂足为O．(1)若∠COE ＝35° 则∠AOD 的度数为_________°（直接写出结果）；(2)若∠AOD ＋∠COE ＝170° 求∠COE 的度数． 【答案】(1)125(2)40°【分析】（1）先根据两角互余求出∠AOC 的度数 再利用邻补角即可求出∠AOD 的度数；（2）设AOC x ∠= 则AOC BOD x ∠=∠= 再利用周角列出方程 解出x 的值之后再利用互余即可求出∠COE 的度数．（1）解：∠∠COE ＝35° EO ∠AB∠90AOE COE AOC ∠=∠+∠=︒∠903555AOC ∠=︒-︒=︒．又∠∠AOD 是∠AOC 的邻补角∠180125AOD AOC ∠=︒-∠=︒．（2）解：设AOC x ∠= 则AOC BOD x ∠=∠=∠360AOD COE AOC BOD BOE ∠∠+∠+∠+∠=︒＋即170902360x ︒+︒+=︒解得50x =︒．∠905040COE ∠=︒-︒=︒．【点睛】本题考查了两角互余的关系和邻补角以及周角 解题的关键是熟练掌握互余、互补的概念和对顶角相等以及周角为360︒ 互余是指两角之和为90° 互补是指两角之和为180° 并且熟知两个角有一条公共边 它们的另一边互为反向延长线 具有这种关系的两个角 叫做邻补角． 11．如图 直线AB CD 相交于点O OE 把BOD ∠分成两部分．（1）直接写出图中AOD ∠的对顶角为______ DOE ∠的邻补角为______．（2）若=90AOC ∠︒ 且:2:3BOE EOD ∠∠=．求EOC ∠的度数．【答案】（1）BOC ∠ EOC ∠；（2）126゜【分析】（1）根据对顶角和邻补角的定义直接写出即可；（2）根据对顶角相等求出∠BOD 的度数 再根据∠BOE ：∠EOD =2：3求出∠BOE 和∠EOD 的度数 即可求出∠EOC 的度数．【详解】解：（1）AOD ∠的对顶角为BOC ∠ DOE ∠的邻补角为EOC ∠．（2）∠∠BOE ：∠EOD =2：3 设2BOE x ∠= 3EOD x ∠=则590BOD AOC x ∠=∠==解得：18x =．∠354DOE x ∠==．∠180126EOC DOE ∠=-∠=．【点睛】本题主要考查了对顶角与邻补角的定义 解题的关键在于能够熟练掌握相关知识进行求解.12．如图 直线AB 和CD 相交于点O OE 把∠AOC 分成两部分且∠AOE ：∠EOC ＝3：5 OF 平分∠BOE ．（1）若∠BOD ＝80° 求∠BOE ；（2）若∠BOF ＝∠AOC +14° 求∠EOF ．【答案】（1）150°；（2）78°13．如图 直线AB CD 相交于点O OE AB ⊥ 垂足为O ．（1）直接写出图中AOC ∠的对顶角为 BOD ∠的邻补角为 ；（2）若:1:2BOD COE ∠∠= 求AOD ∠的度数．【答案】（1）BOD ∠；BOC ∠ AOD ∠；（2）150°【分析】（1）根据对顶角、邻补角的定义寻找对顶角和邻补角即可；（2）设∠BOD=x 则∠COE=2x 再根据∠BOD 与∠COE 互余可求得x 的值 从而得出∠AOC 的大小 进而得出∠AOD 的大小．【详解】（1）∠AOC 的对顶角为：∠BOD∠BOD 的邻补角为：∠BOC ∠AOD（2）∠:1:2BOD COE ∠∠=设∠BOD=x 则∠COE=2x∠OE∠AB∠∠EOB=90°∠∠COE+∠BOD=90° 即x+2x=90°解得：x=30°∠∠BOD=∠COA=30°∠∠AOD=150°【点睛】本题考查角度的简单推导 解题关键是利用对顶角相等和补角为180°转化求解．14．如图 直线MD 、CN 相交于点O OA 是∠MOC 内的一条射线 OB 是∠NOD 内的一条射线 ∠MON ＝70°．(1)若∠BOD ＝12∠COD 求∠BON 的度数；(2)若∠AOD ＝2∠BOD ∠BOC ＝3∠AOC 求∠BON 的度数． 【答案】(1)75°(2)54°【分析】（1）先由对顶角相等求出∠COD ＝70° 再由已知条件求出∠BOD 的度数 根据邻补角的定义与角的和差进行求解即可；（2）设∠AOC ＝x ° 则∠BOC ＝3x ° 利用角的和差即可解得x 进而求解．（1）∠∠MON ＝70°∠∠COD ＝∠MON ＝70°15．如图直线AB、CD相交于点O OE∠AB 且∠DOE=5∠COE 求∠AOD的度数．【答案】120°【分析】由OE∠AB可得∠EOB=90° 设∠COE=x 则∠DOE=5x 而∠COE+∠EOD=180° 即x+5x=180° 得到x=30° 则∠BOC=30°+90°=120° 利用对顶角相等即可得到∠AOD的度数．【详解】解：∠OE∠AB∠∠EOB=90°设∠COE=x 则∠DOE=5x∠∠COE+∠EOD=180°∠x+5x=180°∠x=30°∠∠BOC=∠COE+∠BOE=30°+90°=120°∠∠AOD=∠BOC=120°．。
沪教版七年级(下)数学第十三章相交线-平行线课课练及单元测试卷一和参考答案
数学七年级下第十三章相交线平行线13.1 邻补角、对顶角（1）一、选择题1、图中是对顶角的是( )A B C D2 如图，∠AOC的邻补角是( )A. ∠AODB. ∠BOCC. ∠AOD和∠BOCD. ∠AOE和∠COF第2题第4题3.下列说法中，正确的是（）A、有公共顶点，没有公共边的两个角是对顶角；B、相等的两个角是对顶角；C、如果两个角是对顶角，那么这两个角相等；D、有公共顶点且和为180°的两个角为邻补角。
4. 如图，三条直线l1、l2、l3相交于点O，则∠1+∠2+∠3= （）A、270°B、180°C、120°D、90°5、平面上三条直线两两相交最多能构成对顶角的对数是（）A、6B、8C、10D、46、已知∠1与∠2是邻补角，∠2是∠3的邻补角，那么∠1与∠3的关系是（）A、相等但不是对顶角B、邻补角C、互补但不是邻补角D、对顶角7. 三条直线相交于同一点时，对顶角有m对，相交于不同三点时，对顶角为n对，则m与n的关系是（）A、m=nB、m>nC、m<nD、m+n=10二、填空题8. 平面内两条直线相交有个交点，三条直线相交可能有个交点，四条直线相交可能有个交点，五条直线相交最多有个交点。
9、如图，直线AB、CD相交于O点，∠AOE＝90°。
∠1和∠2互为______角；∠2和∠4互为______角，∠1和∠3互为_______角。
10、如图，∠2=∠3，∠1=65°，则∠4= ，∠5= 。
11、如图，三条直线AB、CD、EF相交于点O，∠1=62°，∠2=50°，则∠COE= ，∠DOE= , ∠AOE= 。
第9题第10题第11题第12题12．如图，三条直线交于同一点，∠1：∠2：∠3=3：5：2，则∠4=___ ______．三、简答题13、如图，直线ABCDEF都经过O点，∠AOC =38°，∠COE=54°，求∠EOB、∠BOC、∠DOF、∠COF和∠FOA的度数。
沪教新版七年级下学期 中考题同步试卷：13.1 邻补角、对顶角(01)
C．140° ）
A．
B．
D．130°
C．
D．
4．已知∠α 和∠β 是对顶角，若∠α＝30°，则∠β 的度数为（
A．30°
B．60°
C．70°
5．下列图形中，∠1 与∠2 是对顶角的是（ ）
） D．150°
A．
B．
第1页（共4页）
C．
D．
6．如图，图中∠α 的度数等于（115°
第3页（共4页）
沪教新版七年级（下）中考题同步试卷：13.1 邻补角、 对顶角（01）
参考答案
一、选择题（共 8 小题） 1．B； 2．A； 3．B； 4．A； 5．C； 6．A； 7．C； 8．B； 二、填空题（共 8 小题） 9．对顶角相等； 10．50°； 11．50； 12．40°； 13．50； 14．80； 15．145； 16．20°；
度．
14．如图，直线 AB 和 OC 相交于点 O，∠AOC＝100°，则∠1＝
度．
15．如图，已知直线 AB 与 CD 交于点 O，ON 平分∠DOB，若∠BOC＝110°，则∠AON 的
度数为
度．
16．如图，直线 AB 和 CD 相交于点 O，OE 平分∠DOB，∠AOC＝40°，则∠DOE＝
度．
．
D．∠1 和∠5
10．如图，直线 a 和直线 b 相交于点 O，∠1＝50°，则∠2＝
．
第2页（共4页）
11．如图，直线 AB 与 CD 相交于点 O，∠AOD＝50°，则∠BOC＝
°．
12．如图，直线 AB、CD 相交于点 O，若∠BOD＝40°，OA 平分∠COE，则∠AOE＝
．
13．如图，直线 a、b 相交于点 O，∠1＝50°，则∠2＝
2023年春上海七年级下数学辅导讲义(沪教版)第5讲 邻补角、对顶角及垂直(讲义)解析版
第5讲邻补角、对顶角及垂直模块一：邻补角的意义和性质知识精讲1、平面上两条不重合直线的位置关系相交：两条直线有一个交点；平行：两条直线没有交点．2、邻补角的意义两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角叫做互为邻补角．3、邻补角的性质互为邻补角的两个角一定互补，但互补的两个角不一定互为邻补角．例题解析例1．（2018·上海七年级零模）已知，∠B与∠A互为邻补角，且∠B=2∠A，那么∠A为________度．【答案】60【分析】设A x ∠=，则2B x ∠=，然后根据领补角的定义进行求解即可．【详解】解：设A x ∠=，则2B x ∠=根据题意得，2180x x +=︒，解得：60x =︒，∴60A ∠=︒，故答案为：60．【点睛】本题主要考查领补角的定义及一元一次方程的解法，熟练掌握领补角的定义及一元一次方程的解法是解题的关键．例2．（2019·上海浦东新区·七年级期末）互为邻补角的两个角的大小相差60︒，这两个角的大小分别为_____________【答案】60,120︒︒【分析】设其中一个角为x ，则根据邻补角的定义得另一个角为180x ︒-，再根据两个角的大小相差60︒，列出方程，解方程即可【详解】解：设其中一个角为x ，则另一个角为180x ︒-，∵两个角的大小相差60︒，∴()18060x x ︒︒--=或()18060x x ︒︒--= ∴120x ︒=或60x ︒=，∴18060x ︒︒-=或120︒，故答案为：60,120︒︒【点睛】本题考查了邻补角的定义和解一元一次方程，熟练掌握相关知识是解题的关键 例3．（2018·上海七年级期中）如果两个角互为邻补角，其中一个角为65°，那么另一个角为______度．【答案】115【分析】根据邻补角互补即可得到结论．【详解】解：由题意得，180°-65°=115°， 答：另一个角为115°， 故答案为115．【点睛】本题考查了邻补角，熟记邻补角互补是解题的关键．例4.如图，直线AB 、CD 相交于点O ，∠AOD =35°，则∠AOC =___________；∠BOD=_________；∠BOC=______________．【难度】★【答案】145︒，145︒，35︒．【解析】AOD∠和AOC∠互为邻补角，∠，BOC∠互为邻补角．∠和BODBOD∠和AOD【总结】考察邻补角的定义．例5.经过两点可以画_______________条直线，两条直线相交，有且只有_________个交点．【难度】★【答案】1，1．【解析】考察两点确定一条直线以及相交的意义．例6.如图，∠BOF的邻补角是（）．A．∠AOE B．∠AOF和∠BOE C．∠AOB D．∠BOE和∠DOF【难度】★【答案】B【解析】考察邻补角的意义．例7.把下图中邻补角分别写出来．【难度】★【答案】AFE ∠和BFE ∠，BOD ∠和AOD ∠，BOD ∠和BOC ∠，AOC ∠和AOD ∠，AOC ∠和BOC ∠．【解析】考察邻补角的意义例8.已知∠1=∠2，∠1与∠3互余，∠2与∠4互补，则∠3___________∠4．【难度】★【答案】<．【解析】1+3=90∠∠︒（互余的意义），2+4=180∠∠︒（互补的意义），又1=2∠∠（已知）， 9031804∴︒-∠=︒-∠（等式性质）． 4390∴∠-∠=︒（等式性质）， 34∴∠<∠．【总结】考察互余，互补的概念以及利用简单的运算比较大小．例9.已知，AB 与CD 相交于O 点，若∠AOD 比∠AOC 大40°，则∠BOD =________，若∠AOD =2∠AOC ，则∠BOD =________，若∠AOD =∠AOC ，则∠BOD =________．【难度】★【答案】706090︒︒︒，，．【解析】设AOC x ∠=，则40AOD x ∠=+︒，40x x ++180=︒（邻补角的意义）， 解得：70x =︒，所以40110x +︒=︒， 所以70BOD ∠=︒（邻补角的意义）； 设AOC x ∠=，则2180x x +=︒解得：60x =︒，所以2120x=︒，所以60BOD∠=︒（邻补角的意义）；设AOC x∠=，则2180x=︒，解得：90x=︒，所以90BOD∠=︒．【总结】考察平角的意义以及邻补角的定义．例10.如图所示，O是直线AB上任意一点，以O为端点任意做一条射线OC，且OD平分∠BOC，OE平分∠AOC，求∠DOE的度数．【难度】★★【答案】90︒．【解析】因为OD平分BOC∠，OE平分AOC∠（已知）所以BOD COD∠=∠，COE AOE∠=∠（角平分线的意义）因为180BOD COD EOC AOE∠+∠+∠+∠=︒（平角的意义）所以22180EOC COD∠+∠=︒（等量代换）所以90EOC COD∠+∠=︒（等式性质）即90DOE∠=︒【总结】主要考察平角的意义，角平分线的意义的综合运用．例11.如图，射线OA、OB、OC、OD有公共端点O，且∠AOB=90°，∠COD=90°，∠AOD=5 4∠BOC，求∠BOC的度数．【难度】★★【答案】80︒．【解析】因为∠AOD=54∠BOC，所以设BOC x∠=，则54AOD x∠=．因为360AOB AOD COD BOC∠+∠+∠+∠=（周角的意义）又∠AOB=90°，∠COD=90°（已知）所以51804x x+=︒（等式性质）解得：80x=︒，即80BOC∠=．【总结】考察周角的概念，以及利用设未知数的思路求解角的度数．例12.（1）已知∠1和∠2互为邻补角，且∠1比∠2的3倍大20°，求∠1和∠2的度数；（2）一个角的补角比这个角的余角的2倍大15°，求这个角的度数．【难度】★★【答案】（1）1140∠=︒，240∠=︒；（2）15︒．【解析】（1）因为∠1和∠2互为邻补角，所以12180∠+∠=︒（邻补角的意义）．因为13220∠=∠+︒（已知），所以4220180∠+︒=︒（等量代换），所以240∠=︒，1140∠=︒（等式性质）；（2）设这个角为x，则根据题意可得：180(90)215x x-=-⨯+︒，解得：15x=︒，即这个角的度数为15︒．【总结】考察补角，余角以及邻补角的概念及其综合运用．例13.如图，直线AB 、CD 相交于点O ，且∠AOC =54°，∠1比∠2小10°，求∠1、∠2的度数．【难度】★★【答案】22︒，32︒．【解析】因为直线AB 、CD 相交于点O （已知），所以AOC BOD ∠=∠54=︒（对顶角相等）．设1x ∠=，则210x ∠=+， 故1054x x ++=︒， 解得：22x =︒，所以1032x +=︒， 即122∠=，232∠=．【总结】考察对顶角的意义及角的和差的综合运用．例14.如图，直线AB 、CD 、EF 相交于点O ，且∠AOF =3∠BOF ，∠AOC =90°，（1） 求∠COE 的度数；（2） 说明OE 、OF 分别是∠AOC 、∠BOD 的平分线的理由．【难度】★★【答案】（1）45︒；（2）略．【解析】（1）因为180AOF BOF ∠+∠=︒（邻补角的意义）又3AOF BOF ∠=∠（已知）所以4180BOF ∠=︒（等量代换）所以45∠=︒（等式性质）BOF因为直线AB、EF相交于点O（已知）所以BOF AOE∠=∠（对顶角相等）因为90∠=︒（已知）AOC所以9045∠=︒-∠=︒（等式性质）COE BOF（2）因为90COE∠=︒（已知）AOC∠=︒，45所以45AOE∠=︒（等式性质）所以AOE COE∠=∠（等量代换）因为BOF AOE∠=∠（对顶角相等）所以45∠=∠=︒（等量代换）AOE BOF同理45∠=︒DOF所以OE、OF分别是∠AOC、∠BOD的平分线（角平分线的意义）【总结】考察邻补角的意义，角平分线的意义以及相应的计算，综合性较强，注意认真分析题目中的条件．模块二：对顶角的意义和性质知识精讲1、对顶角的意义两个角有公共顶点，并且一个角的两边分别是另一个角两边的反向延长线，具有这种关系的两个角叫做互为对顶角．2、对顶角的性质对顶角相等．例题解析例1．（2019·上海浦东新区·七年级期中）下列说法：①对顶角相等；②相等的两角一定是对顶角；③如果两个角不是对顶角，那么它们一定不相等；其中正确的说法有( )A．0 B．1 C．2 D．3【答案】B【分析】根据对顶角的定义以及性质对各选项分析判断后利用排除法求解．【详解】解：①对顶角相等，正确；②相等的两个角是一定对顶角，错误；③如果两个角不是对顶角，那么它们一定不相等；错误；故选：B．【点睛】本题考查了对顶角的定义以及对顶角相等的性质，是基础题，掌握概念与性质是解题的关键．例2．（2019·上海市嘉定区震川中学七年级期中）在下列四个选项中的图形中，∠1与∠2是对顶角的图形是( ).A．B．C．D．【答案】C【分析】根据对顶角的定义，对顶角：有一个公共顶点，并且一个角的两边分别是另一个角的两边的反向延长线，具有这种位置关系的两个角，互为对顶角，据此即可判断．【详解】解：根据对顶角的定义可得，四个图形中C中∠1与∠2为对顶角．故答案为：C．【点睛】本题考查了对顶角的定义，理解定义是解题的关键.例3.下列说法中，正确的是( )A．有公共顶点的两个角是对顶角B．对顶角一定相等C．有一条公共边的两个角是邻补角D．互补的两个角一定是邻补角【难度】★【答案】B【解析】A错误，有公共顶点，并且一个角的两边分别是另一个角两边的反向延长线，具有这种关系的两个角才叫做互为对顶角；B正确；C错误，有一条公共边，且它们的另一边互为反向延长线；D错误，互补的两个角不一定是邻补角．【总结】考察邻补角和对顶角的概念．例4.把下图中对顶角分别写出来．【难度】★【答案】AOB∠和AOD∠．∠，BOC∠和COD【解析】考察对顶角的定义．例5.（1）如果以点O为端点画四条射线OA、OB、OC、OD，且OA、OC， OB、OD互为反向延长线，那么∠AOB和∠COD互为_________；（2）如果以点O为端点画三条射线OA、OB、OC，且射线OA、OC互为反向延长线，那么∠AOB 和∠COB 互为_________．【难度】★【答案】对顶角，邻补角．【解析】考察对顶角和邻补角的定义．例6.如图，共有对顶角（） A ．4对 B ．5对 C ．6对 D ．8对【难度】★【答案】D【解析】CJA ∠和KJG ∠，CJK ∠和AJG ∠，BIJ ∠和EIF ∠，BIE ∠和JIG ∠，CGB ∠和FGD ∠， CGF ∠和BGD ∠，CHF ∠和EHD ∠，CHE ∠和FHD ∠均互为对顶角．【总结】本题主要考察对顶角的概念．例7.下列说法：①对顶角相等；②相等的角是对顶角；③如果两个角不相等，那么这两个角一定不是对顶角；④如果两个角不是对顶角，那么这两个角不相等．其中正确的说法是（ ）A ．①②B ．①③C ．②③D ．②④ 【难度】★★【答案】B【解析】（1）正确；（2）错误，相等的角不一定是对顶角；（3）正确，对顶角一定是相等的，（4）错误，不是对顶角也可以相等．【总结】主要考察学生对对顶角的理解，相等的角不一定是对顶角，但对顶角一定相等，不是对顶角的两个角也可以相等．例8.a、b、c两两相交，∠1=60°，∠2：∠4=3:2，求∠3和∠5的度数．【难度】★★【答案】40︒，120︒．【解析】因为12∠=︒（已知）∠=∠（对顶角相等），160所以260∠=︒（等量代换）因为2:43:2∠=︒（等式性质）∠∠=（已知），所以440因为34∠=︒（等量代换）∠=∠（对顶角相等），所以340因为25180∠=︒（等式性质）∠+∠=︒（邻补角的意义），所以5120【总结】考察邻补角和对顶角的意义及综合运用．例9.如图，直线AB、CD交于点O，则（1）若∠2=3∠1，则∠1=__________；（2）若∠2：∠3=4：1，则∠2=__________；（3）若∠2-∠1=100°，则∠3=__________．【难度】★★【答案】45︒，144︒，40︒．【解析】（1）因为12180∠+∠=︒（邻补角的意义）， 又231∠=∠（已知）所以41180∠=︒（等量代换）， 所以145∠=︒（等式性质）；（2）因为23180∠+∠=︒（邻补角的意义），∠2：∠3=4：1（已知）所以设24x ∠=，3x ∠=， 则4180x x +=︒（等量代换），解得：36x =︒，4144x =︒（等式性质）， 即2144∠=；（3） 因为12180∠+∠=︒（邻补角的意义），∠2-∠1=100°（已知）所以2140∠=︒，140∠=︒（等式性质）， 所以340∠=︒（对顶角相等）【总结】考察学生对于邻补角知识点的掌握，同时还考察学生对于二元一次方程组的计算，设未知数列式计算等．例10.a 、b 、c 交于点O ，两条直线相交，∠2=∠1，∠3：∠1=8:1，求∠4的度数【难度】★★【答案】36︒．【解析】设12x ∠=∠=，则38x ∠=， 故8180x x x ++=︒，解得：18x =︒（等式性质）， 所以1218∠=∠=．所以436∠=︒（对顶角相等）【总结】考察学生对邻补角和对顶角的意义及综合运用．例11.已知直线AB 、CD 相交于点O ，OE 平分∠BOD ，OF 平分∠COE ，∠2：∠1=4:1，求∠AOF 的度数．【难度】★★★【答案】135︒．【解析】因为OE平分∠BOD（已知）所以1DOE∠=∠（角平分线的意义）设1x∠=，则DOE x∠=，24x∠=，因为4180x x x++=︒（平角的意义），所以30x=︒（等式性质）即30DOE∠=，所以150COE∠=︒（邻补角的意义）．因为OF平分∠COE（已知），所以COF EOF∠=∠（角平分线的意义）所以COF EOF ∠=∠12COE=∠75=︒（等式性质）因为1EOF BOF∠=∠+∠（角的和差）所以45BOF∠=︒（等式性质）因为180AOF BOF∠+∠=（邻补角的意义）所以135AOF∠=︒（等式性质）【总结】考察学生对邻补角，角平分线的意义的概念的理解以及简单的运算，综合性较强，注意认真分析条件．例12．（2020·上海市静安区实验中学七年级课时练习）观察图形，回答下列各题：（1）图A中，共有＿＿＿＿对对顶角；（2）图B中，共有＿＿＿＿对对顶角；（3）图C中，共有＿＿＿＿对对顶角；（4）探究（1）--（3）各题中直线条数与对顶角对数之间的关系，若有n条直线相交于一点，则可形成＿＿＿＿＿＿＿＿对对顶角；【答案】（1）2对；（2）6对；（3）12对；（4）n(n-1) (n≥2).试题分析：（1）图A中，共有2对对顶角；（2）图B中，共有6对对顶角；（3）图C中，共有12对对顶角；（4）找出对顶角的对数与直线的条数n之间的关系式为：n（n－1）（n ≥2）.试题解析：（1）2对；（2）6对；（3）12对；（4）2条直线相交时，对顶角对数为：1×2=2对；3条直线相交时，对顶角对数为：3×2=6对；4条直线相交时，对顶角对数为：4×3=12对；…n条直线相交时，对顶角对数为：n（n－1）（n≥2）对.点睛：本题关键在于找出直线的条数与对顶角对数的关系式.模块三：垂线(段)的意义和性质知识精讲1、垂线的意义如果两条直线的夹角为直角，那么就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．2、垂直的符号记作：“⊥”，读作：“垂直于”，如：AB⊥CD，读作“AB垂直于CD”．注：垂直是特殊的相交．3、垂直公理：在平面内，过直线上或直线外的一点作已知直线的垂线可以作一条，并且只能作一条．简记为：过一点，有且仅有一条直线与已知直线垂直4、中垂线过线段中点且垂直于这条线段的直线，叫做这条线段的垂直平分线，简称中垂线．5、垂线段的性质联结直线外一点与直线上各点的所有线段中，垂线段最短．6、点到直线的距离直线外一点到这条直线的垂线段的长度，叫做这个点到直线的距离．如果一个点在直线l上，那么就说这个点到直线l的距离为零．例题解析例1.“同一平面内，过一点有且只有一条直线与已知直线垂直”中这一点的位置（）A．在直线的上方B．在直线的下方C．在直线上D．可以任意位置【难度】★【答案】D【解析】考察对垂直公理的理解及运用．例2.如图，OA⊥OB于O，直线CD经过点O，∠AOD=35°，则∠BOC=_______．【难度】★【答案】125︒．【解析】OA OB⊥（已知）AOB∴∠=︒（垂线的意义）90AOD∠=︒（已知）35∴∠=︒（互余）BOD55∴∠=︒（邻补角的意义）125BOC【总结】考察垂线的意义以及互余的意义及综合运用．例3.下列说法中正确的是（）A．有且只有一条直线垂直于已知直线B．从直线外一点到这条直线的垂线段，叫做这点到这条直线距离C．互相垂直的两条线段一定相交D．直线c外一点A与直线c上各点连接而成的所有线段中最短线段的长是3cm，则点A 到直线c的距离是3cm【难度】★★【答案】D【解析】A错误，过一点有且只有一条直线垂直于已知直线； B错误，垂线段的长度；C错误，互相垂直的两条直线一定相交； D正确．【总结】考察垂直公理，点到直线的距离以及垂线段的性质等内容．例4.列说法正确的个数是（）①直线上或直线外一点，都能且只能画这条直线的一条垂线；②过直线l上一点A和直线l外一点B的直线，使它与直线l垂直；③从直线外一点作这条直线的垂线段，叫做这个点到这条直线的距离；④过直线外一点画这条直线的垂线段，垂线段的长度叫做这点到这条直线的距离.A．1 B．2 C．3 D．4【难度】★★【答案】C【解析】（1）错误，在同一平面内；（2）错误；（3）错误，点到直线的距离是指垂线段的长度，故选C．【总结】考察学生对基本概念的理解．∆，根据下列语句画图．例5．（2018·上海松江区·七年级期中）如图，已知ABC⊥，垂足为D；（1）过点A作AD BC（2）过点D作DE AB∥，交AC于点E；（3）点C到直线AD的距离是线段_______的长度．【答案】（1）见解析．（2）见解析．（3）CD．【分析】（1）根据垂线的定义画出直线AD即可；（2）根据平行线的定义画出直线DE即可；（3）根据点到直线的距离判断即可．【详解】（1）如图，直线AD 即为所求（2）如图，直线DE 即为所求（3）点C 到直线AD 的距离是线段CD 的长度．【点睛】本题考查了作图-复杂作图、平行线的判定及性质、点到直线的距离，熟练掌握垂线、平行线、点到直线的距离的定义是解题的关键．例6．（2019·上海市浦东新区建平中学南校七年级期中）按下列要求画图并填空：如图，（1）过点A 画直线BC 的平行线AD ；（2）过点B 画直线AD 的垂线段，垂足为点E ；（3）若点B 到直线AD 的距离为4cm ，BC=2cm ，则ABC S =________2cm ．【答案】（1）见解析（2）见解析（3）4【分析】（1）根据平行线的画法画出即可；（2）根据垂线的画法画出即可；（3）根据平行线间的距离处处相等得出三角形ABC的高为4cm，再根据三角形的面积公式即可求出．【详解】解：（1）如图:AD即为所求（2）如图: BE即为所求（3）因为BC//AD,所以三角形ABC的高为4cm；所以12442ABCS=⨯⨯=；故答案为：4【点睛】本题考查了基本作图的知识以及三角形的面积公式，正确的作出图形是解答第（3）题的关键，难度不大．例7.（2019·上海七年级单元测试）如图所示，点P是∠ABC内一点．(1)画图：①过点P画BC的垂线，垂足为D；②过点P画BC的平行线交AB于点E，过点P 画AB的平行线交BC于点F．(2)∠EPF等于∠B吗?为什么?【答案】（1）图形见解析（2）∠EPF＝∠B试题分析:（1）①过点P作BC的垂线，D是垂足；②过点P作BC的平行线交AB于E，过点P作AB的平行线交BC于F；（2）根据平行线的性质可得∠AEP＝∠B，∠EPF＝∠AEP然后利用等量代换得到结论即可．解:如图所示，(1)①直线PD即为所求；②直线PE、PF即为所求．(2)∠EPF＝∠B，理由：因为PE∥BC(已知)，所以∠AEP＝∠B(两直线平行，同位角相等)．又因为PF∥AB(已知)，所以∠EPF＝∠AEP(两直线平行，内错角相等)，∠EPF＝∠B(等量代换)．点睛:本题考查了平行线和垂线的画法及平行线的性质,熟练掌握两直线平行同位角相等,两直线平行内错角相等是解答本题的关键.例8.如图，点A到直线BC的距离是线段_______的长；线段CH的长表示点C到直线________的距离；点A到点C的距离是线段_________长．【难度】★★【答案】AE，AD，AC．【解析】考察点到直线的距离的概念的理解及运用．例9.如图,AC⊥BC，C为垂足，CD⊥AB，D为垂足，BC=8，CD=4.8，BD=6.4，AD=3.6，AC= 6，那么点C到AB的距离是_______，点A到BC的距离是________，点B到CD的距离是_____，A、B两点的距离是_________．【难度】★★【答案】4.8，6，6.4，10．【解析】点C到AB的距离是线段CD的长，即4.8；点A到BC的距离是线段AC的长，即6；点B到CD的距离是线段BD的长，即6.4；A、B两点的距离是线段AB的长，即10．【总结】考察点到直线的距离的内容．例10.作图题：过点P分别画直线a、b的垂线，垂足分别为M、N．【难度】★★【答案】【解析】考察垂线的画法例11.按下列要求画图并填空：（1）过点B画出直线AC的垂线，交直线AC于点D，那么点B到直线AC的距离是线段_________的长．（2）用直尺和圆规作出△ABC的边AB的垂直平分线EF，交边AB、AC于点M、N，联结CM．那么线段CM是△ABC的___________．（保留作图痕迹）【难度】★★【答案】（1）BD；（2）AB边上的中线【解析】考察垂线的画法．例12.一辆汽车在直线形的公路上由A向B行驶，M、N分别是位于公路AB两侧的两个学校；（1）汽车行驶时，会对公路两旁的学校都造成一定的影响，当汽车行驶到何处时，分别对两个学校影响最大?在图中标出来．（2）当汽车由A向B行驶时，在哪一段上对两个学校影响越来越大?越来越小?对M学校影响逐渐减小而对N学校影响逐渐增大?【难度】★★★【解析】（1）如下图所示，到C 点时对M 影响最大，到D 点时对N 影响最大；（2）由A 向C 时，对两学校影响逐渐增大；由D 向B 时，对两学校影响逐渐减小；由C 向D 时，对M 影响减小，对N 影响增大．【总结】本题主要考察对点到直线的距离的概念的理解及在实际问题中的运用．随堂检测1.到一条直线的距离等于2的点有（） A ．1个B ．0个C ．无数个D ．无法确定 【难度】★【答案】C【解析】到直线的距离等于2的点有无数个，这些点组成两条直线．【总结】考察点到直线的距离．2.下列说法错误的是（ ）A ．两点之间，线段最短B ．和已知直线垂直的直线有且只有一条C ．过直线外一点有且只有一条直线平行于已知直线D ．在同一平面内过一点有且只有一条直线垂直于已知直线DC N MBA【难度】★【答案】B【解析】B错误，有无数条．【总结】考察学生对垂线的意义和性质的理解．3.如图，过△ABC三个顶点A、B、C，分别作BC、AC、AB的垂线，并用“⊥”符号表示出来．【难度】★【答案】【解析】考察垂线段的作法．4.下列说法正确的个数有（）（1）直线外一点与直线上各点的所有连接线中垂线段最短；（2）画一条直线的垂线可以画无数条；（3）在同一平面内，经过一个已知点能画出一条直线和已知直线垂直；（4）从直线外一点到这条直线的垂线段叫做点到直线的距离A．1个B． 2个C． 3个D．4个【难度】★★【答案】C【解析】（4）错误，直线外一点到这条直线的垂线段的长度叫做点到直线的距离，故选C．【总结】本题主要考查点到直线的距离及垂线的相关概念等．5.若∠α=54°，∠β的两边与∠α两边互相垂直，则∠β=____________．【难度】★★【答案】54︒或126︒．【解析】∠α和∠β是相等或者互补的关系．【总结】考察垂线的意义以及两解问题，注意分类讨论．6.平面上三条直线两两相交，最多有m个交点，最少有n个交点，则m n+=____________．【难度】★★【答案】4．【解析】最多有3个交点，最少有1个交点．3+=．m nn=，4m=，1【总结】考察学生的作图分析能力．7.如图，直线AB、CD、EF相交于点O，OA平分∠COE，当∠COE=70°，求∠BOD的度数，当∠DOE=110°时，求∠BOD的度数．【难度】★★【答案】35︒，35︒．【解析】因为OA平分COE∠，∠COE=70°（已知）所以1352AOC AOE COE∠=∠=∠=︒（角平分线的意义）所以35BOD AOC∠=∠=︒（对顶角相等）同理，35BOD∠=︒【总结】考察学生对邻补角和对顶角知识点的掌握和简单应用．8.已知AB⊥l，BC⊥l，B为垂足，问：A、B、C三点共线吗?为什么? 【难度】★★【答案】共线．【解析】过直线外一点有且只有一条直线与已知直线垂直．【总结】考察垂线段意义和性质，注意对三点共线的理解．9.如图已知O是直线AC上一点，OB是一条射线，OD平分∠AOB，OE在∠BOC内，∠BOE=1 2∠EOC，∠DOE=70°，求∠EOC的度数．【难度】★★★【答案】80︒．【解析】因为OD平分∠AOB（已知）所以AOD BOD∠=∠（角平分线的意义）设BOE x∠=，BOD y∠=，则7023180x yy x+=︒⎧⎨+=︒⎩，解得：4030xy=︒⎧⎨=︒⎩，所以∠EOC =280x=︒．【总结】这一题考察学生对角平分线的内容理解，对补角的知识点的掌握以及二元一次方程组的列式和计算等．10.如图，已知∠AOB，画射线OC⊥OA，射线OD⊥OB，你能画出几种符合要求的图形?并猜想∠COD与∠AOB的数量关系，并说明理由．【难度】★★★【答案】相等或互补【解析】如图．【总结】主要考察多解问题，是对学生发散思维的要求．。
人教版七年级数学下册《识别三线八角》专项练习题-附含答案
人教版七年级数学下册《识别三线八角》专项练习题-附含答案【模型讲解】如图已知直线a b被直线c d所截直线a c d相交于点O按要求完成下列各小题．(1)在图中的∠1～∠9这9个角中同位角共有多少对？请你全部写出来；(2)∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？【分析】根据同位角、内错角和同旁内角的特征（同位角形如“F” 内错角形如“Z” 同旁内角形如“U”）判断即可.【详解】解：(1)如题图所示：同位角共有5对：分别是∠1和∠5 ∠2和∠3 ∠3和∠7 ∠4和∠6 ∠4和∠9；(2)由三线八角的判断方法∠4和∠5是由c b d三线组成并且构成“U”形图案所以∠4和∠5是同旁内角同理可得：∠6和∠8也是同旁内角故∠6和∠8之间的位置关系与∠4和∠5的相同．【模型演练】1．如图同位角共有（）对．A．6B．5C．8D．7【答案】A【分析】根据同位角的概念解答即可．【详解】解：同位角有6对∠4与∠7 ∠3与∠8 ∠1与∠7 ∠5与∠6 ∠2与∠9 ∠1与∠3故选：A．【点睛】此题考查同位角关键是根据同位角解答．2．如图下列判断中正确的个数是（）（1）∠A 与∠1是同位角；（2）∠A 和∠B 是同旁内角；（3）∠4和∠1是内错角；（4）∠3和∠1是同位角．A ．1个B ．2个C ．3个D ．4个 【答案】C【分析】准确识别同位角、内错角、同旁内角的关键 是弄清哪两条直线被哪一条线所截．也就是说 在辨别这些角之前 要弄清哪一条直线是截线 哪两条直线是被截线．【详解】解：（1）∠A 与∠1是同位角 正确 符合题意；（2）∠A 与∠B 是同旁内角．正确 符合题意；（3）∠4与∠1是内错角 正确 符合题意；（4）∠1与∠3不是同位角 错误 不符合题意．故选：C ．【点睛】此题主要考查了三线八角 在复杂的图形中识别同位角、内错角、同旁内角时 应当沿着角的边将图形补全 或者把多余的线暂时略去 找到三线八角的基本图形 进而确定这两个角的位置关系．3．如图 B ∠的内错角是（ ）A ．1∠B ．2∠C ．3∠D ．4∠【答案】A【分析】根据内错角的定义判断即可；【详解】解：A 、B ∠的内错角是1∠ 故此选项符合题意；B 、B ∠与2∠是同旁内角 故此选项不合题意；C 、B ∠与3∠是同位角 故此选项不合题意；D 、B ∠与4∠不是内错角 故此选项不合题意；答案：A．【点睛】本题主要考查了内错角的判定准确分析判断是解题的关键．4．下列所示的四个图形中∠1和∠2是同位角的是（）A．②③B．①②③C．①②④D．①④【答案】C【分析】根据同位角的定义逐一判断即得答案．【详解】图①中的∠1与∠2是同位角图②中的∠1与∠2是同位角图③中的∠1与∠2不是同位角图④中的∠1与∠2是同位角所以在如图所示的四个图形中图①②④中的∠1和∠2是同位角．故选：C．【点睛】本题考查了同位角的定义属于基础概念题型熟知概念是关键．5．如图所示下列说法不正确的是（）A．∠1和∠2是同旁内角B．∠1和∠3是对顶角C．∠3和∠4是同位角D．∠1和∠4是内错角【答案】A【分析】根据对顶角、邻补角、同位角、内错角定义判断即可．【详解】A. ∠1和∠2是邻补角故此选项错误；B. ∠1和∠3是对顶角此选项正确；C. ∠3和∠4是同位角此选项正确；D. ∠1和∠4是内错角 此选项正确；故选A.【点睛】此题考查对顶角 邻补角 同位角 内错角 同旁内角 解题关键在于掌握各性质定义.6．如图 有下列说法：其中结论正确的是（ ）①若//DE AB 则180DEF EFB ∠+∠=︒；②能与EDC ∠构成内错角的角的个数有1个③能与DEC ∠构成同位角的角的个数有2个；④能与B ∠构成同旁内角的角的个数有4个A ．①B ．①④C ．①②④D ．①③④ 【答案】B【分析】根据平行线的性质、同位角、内错角、同旁内角的定义解答即可．【详解】解：①若DE ∠AB 则∠DEF +∠EFB =180° 故①正确；②能与∠EDC 构成内错角的角的个数有2个 只有∠DEF 和∠DEA 故②错误；③能与∠DEC 构成同位角的角的个数有1个 只有∠A 故③错误；④能与∠B 构成同旁内角的角的个数有4个 分别为∠BDE 、∠BFE 、∠A 、∠C 故④正确． 故选B ．【点睛】本题主要考查了同位角、内错角、同旁内角及平行线的性质 正确理解同位角、内错角、同旁内角的定义是解答本题的关键．7．如图 直线AD BE 被直线BF 和AC 所截 则∠1的同位角和∠5的内错角分别是（ ）A．∠4 ∠2B．∠2 ∠6C．∠5 ∠4D．∠2 ∠4【答案】B【分析】同位角：两条直线a b被第三条直线c所截（或说a b相交c）在截线c的同旁被截两直线a b的同一侧的角我们把这样的两个角称为同位角；内错角：两条直线被第三条直线所截两个角分别在截线的两侧且夹在两条被截直线之间具有这样位置关系的一对角叫做内错角．根据此定义即可得出答案．【详解】解：∠直线AD BE被直线BF和AC所截∠∠1与∠2是同位角∠5与∠6是内错角故选：B．【点睛】本题考查的知识点是同位角和内错角的概念解题的关键是熟记内错角和同位角的定义．8．已知图（1）—（4）：在上述四个图中∠1与∠2是同位角的有（）.A．（1）（2）（3）（4）B．（1）（2）（3）C．（1）（3）D．（1）【答案】C【分析】根据同位角的定义；两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线（截线）的同旁则这样一对角叫做同位角进行判断即可．【详解】图①③中∠1与∠2是同位角；故选C．【点睛】此题主要考查了同位角关键是掌握同位角的边构成“F“形．9．如图直线AD、BC被直线AC所截则∠1和∠2是().A．内错角B．同位角C．同旁内角D．对顶角【答案】A【分析】根据三线八角的概念以及内错角的定义作答即可．【详解】如图所示∠1和∠2两个角都在两被截直线(直线b和直线a)异侧并且在第三条直线c（截线）的两旁故∠1和∠2是直线b、a被c所截而成的内错角．故选A．【点睛】本题考查了同位角、内错角、同旁内角的定义．在截线的同旁找同位角和同旁内角在截线的两旁找内错角．要结合图形熟记同位角、内错角、同旁内角的位置特点比较它们的区别与联系．两条直线被第三条直线所截所形成的八个角中有四对同位角两对内错角两对同旁内角．10．如图下列判断正确的是（）A．∠2与∠5是对顶角B．∠2与∠4是同位角C．∠3与∠6是同位角D．∠5与∠3是内错角【答案】A【分析】根据对顶角、同位角、同旁内角、内错角的定义分别进行分析即可．【详解】解：A、∠2与∠5是对顶角故此选项正确；B、∠2与∠4是不是同位角故此选项错误；C、∠3与∠6是同旁内角故此选项错误；D、∠5与∠3不是内错角故此选项错误；故选A．【点睛】本题考查同位角、内错角、同旁内角；对顶角、邻补角．第II卷（非选择题）请点击修改第II卷的文字说明二、填空题11．（1）如图：①所示两条水平的直线被一条倾斜的直线所截同位角有____________对内错角有__________对同旁内角有___________对；（2）如图②所示三条水平的直线被一条倾斜的直线所截同位角有_____________对内错角有__________对同旁内角有_____________对；（3）根据以上探究的结果n（n为大于1的整数）条水平直线被一条倾斜的直线所截同位角有___________对内错角有___________对同旁内角有___________对（用含n的式子表示）．根据以上探究的结果n（n为大于1的整数）条水平直线被一条竖直直线所截同位角有2n(n-1)对内错角有n(n-1)对同旁内角有n(n-1)对故答案为：2n(n-1) n(n-1) n(n-1)．【点睛】本题考查了同位角、内错角、同旁内角解答此类题确定三线八角是关键可直接从截线入手．对平面几何中概念的理解一定要紧扣概念中的关键词语要做到对它们正确理解对不同的几何语言的表达要注意理解它们所包含的意义．12．如图∠1和∠3是直线______ 和______ 被直线______ 所截而成的______ 角；图中与∠2是同旁内角的角有______ 个．【答案】AB AC DE内错3【分析】根据内错角和同旁内角的定义得出即可．【详解】解：∠1和∠3是直线AB和AC被直线DE所截而成的内错角；图中与∠2是同旁内角的角有∠6、∠5、∠7 共3个.故答案为AB；AC；DE；内错；3．【点睛】此题考查同位角、内错角、同旁内角等知识点能根据图形找出各对角是解题的关键.根据内错角和同旁内角的定义得出即可.13．如图AB、DC被BD所截得的内错角是___________ AB、CD被AC所截是的内错角是_________ AD、BC被BD所截得的内错角是_________ AD、BC被AC所截得的内错角是_____________.【答案】∠1和∠5 ∠4和∠8 ∠6和∠2 ∠3和∠7【分析】根据内错角（两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的两旁则这样一对角叫做内错角）的定义即可得.【详解】解：AB、DC被BD所截得的内错角是∠1和∠5 AB、CD被AC所截是的内错角是∠4和∠8 AD、BC被BD所截得的内错角是∠6和∠2 AD、BC被AC所截得的内错角是∠3和∠7.故答案为：∠1和∠5 ∠4和∠8 ∠6和∠2 ∠3和∠7.14．如图直线l截直线a b所得的同位角有__对它们是___；内错角有___对它们是___；同旁内角有___对 它们是___；对顶角___对 它们是___．【答案】 4 6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠ 2 4∠与8∠ 3∠与5∠ 2 4∠与5∠ 3∠与8∠ 4 1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠【分析】根据对顶角的定义 内错角的定义 同旁内角的定义 同位角的定义解答即可．【详解】直线l 截直线a b 所得的同位角有4对 分别是6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠；内错角有2对 它们是4∠与8∠ 3∠与5∠；同旁内角有2对 它们是4∠与5∠ 3∠与8∠；对顶角有4对 它们是1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠．故答案为：4；6∠与4∠ 5∠与1∠ 7∠与3∠ 8∠与2∠；2；4∠与8∠ 3∠与5∠；2；4∠与5∠ 3∠与8∠；4；1∠与3∠ 2∠与4∠ 5∠与7∠ 6∠与8∠【点睛】此题考查两直线相交所成的角 对顶角的定义 内错角的定义 同旁内角的定义 同位角的定义 熟记各定义是解题的关键．15．如图 射线DE 、DC 被直线AB 所截得的用数字表示的角中 ∠4与 ___ 是同位角 ∠4与 ___ 是内错角 ∠4与 ___ 是同旁内角．【答案】 ∠1 ∠2 ∠5、∠3【分析】根据同位角 内错角和同旁内角的定义解答即可.【详解】解：如图 射线DE 、DC 被直线AB 所截得的用数字表示的角中 ∠4与∠1是同位角 ∠4与∠2是内错角 ∠4与∠5、∠3是同旁内角．故答案为∠1 ∠2 ∠5、∠3．【点睛】本题考查了同位角、内错角、同旁内角．解答此类题确定三线八角是关键 可直接从截线入手．对平面几何中概念的理解一定要紧扣概念中的关键词语要做到对它们正确理解对不同的几何语言的表达要注意理解它们所包含的意义．16．如图标有角号的7个角中共有_____对内错角___对同位角____对同旁内角．【答案】 4 2 4.【分析】根据内错角同位角及同旁内角的定义即可求得此题．【详解】解：如图共有4对内错角：分别是∠1和∠4 ∠2和∠5 ∠6和∠1 ∠5和∠7；2对同位角：分别是∠7和∠1 ∠5和∠6；4对同旁内角：分别是∠1和∠5、∠3和∠4、∠3和∠2、∠4和∠2．故答案为(1). 4 (2). 2 (3). 4.【点睛】本题考查内错角同位角同旁内角的定义解题关键是熟练掌握定义．三、解答题17．如图∠1、∠2、∠3、∠4、∠5中哪些是同位角？哪些是内错角？哪些是同旁内角？【答案】同位角有∠1和∠5；∠4和∠3；内错角有∠2和∠3；∠1和∠4；同旁内角有∠3和∠5；∠4和∠5；∠4和∠2．【分析】同位角：两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线（截线）的同旁则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的两旁则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线（截线）的同旁则这样一对角叫做同旁内角．依此即可得出答案．【详解】解：∠∠1和∠5在截线AC同侧在被截直线BE CE同方向所成的角；∠4和∠3 在截线CE的上方被截直线DB、EB的左侧∠同位角有∠1和∠5；∠4和∠3 共2对；∠∠2和∠3在截线BD两侧被截直线AC与CE内部；∠1和∠4在截线BE两侧被截直线AC与CE 内部∠内错角有∠2和∠3；∠1和∠4 共2对；∠∠3和∠5在截线CD同侧被截直线CB与DB内部；∠4和∠5在截线CE同侧被截直线CB与EB 的内部；∠4和∠2在截线BE同侧被截直线DB与DE的内部∠同旁内角有∠3和∠5；∠4和∠5；∠4和∠2 共3对.【点睛】本题考查了同位角、内错角、同旁内角三线八角中的某两个角是不是同位角、内错角或同旁内角完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时应从角的两边入手具有上述关系的角必有两边在同一直线上此直线即为截线而另外不在同一直线上的两边它们所在的直线即为被截的线．同位角的边构成“F“形内错角的边构成“Z“形同旁内角的边构成“U”形．18．如图已知AC与EH交于点B BF与AC交于点D．问图中同位角和对顶角各有几对？并具体写出各对同位角和对顶角．【答案】同位角有7对具体见解析；对顶角有4对具体见解析【分析】根据同位角和对顶角的定义解答．【详解】同位角有7对 分别为：A ∠与HBC ∠ A ∠与FBC ∠ A ∠与GDB ∠ FBC ∠与FDG ∠ FBH ∠与FDG ∠ ABD ∠与ADF ∠ EBD ∠与ADF ∠；对顶角有4对 分别为：EBC ∠与ABH ∠ ABE ∠与HBC ∠ ADB ∠与FDG ∠ ADF ∠与GDB ∠． 【点睛】此题考查同位角和对顶角的定义 熟记定义是解题的关键．19．如图所示．①∠AED 和∠ABC 可看成是直线__________、__________被直线__________所截得的__________角； ②∠EDB 和∠DBC 可看成是直线__________、__________被直线__________所截得的__________角； ③∠EDC 和∠C 可看成是直线__________、__________被直线__________所截得的__________角．【答案】ED ；BC ；AB ；同位；ED ；BC ；BD ；内错；ED ；BC ；AC ；同旁内【详解】解：（1）∠AED 和∠ABC 可看成是直线ED 、BC 被直线AB 所截得的同位角；（2）∠EDB 和∠DBC 可看成是直线ED 、BC 被直线BD 所截得的内错角；（3）∠EDC 和∠C 可看成是直线ED 、BC 被直线AC 所截得的同旁内角．故答案为ED BC AB 同位；ED BC BD 内错；ED BC AC 同旁内．点睛：本题考查了同位角、内错角、同旁内角．两条直线被第三条直线所截形成的角中 若两个角都在两直线的同侧 并且在第三条直线（截线）的同旁 则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中 若两个角都在两直线的之间 并且在第三条直线（截线）的两旁 则这样一对角叫做内错角；两条直线被第三条直线所截形成的角中 若两个角都在两直线的之间 并且在第三条直线（截线）的同旁 则这样一对角叫做同旁内角．20．如图：（1）写出图中EDM ∠的同位角： ；（2）如果AB ∠CD 那么图中与FHC ∠相等的角有 个（FHC ∠除外）；（3）当EDM ∠=∠ 时 AB ∠CD 理由： ；（4）如果A ∠与ABD ∠互补 那么E ∠与F ∠有什么关系？说明理由．【答案】（1）EHM ∠ ACM ∠；（2）3；（3）ABD 内错角相等 两直线平行；（4）E F ∠=∠ 理由见解析．【分析】（1）根据同位角的定义即可求解； （2）先根据AB ∥CD 得到=FHC FGA ∠∠ 再根据对顶角相等得到∠FHC =∠DHE =∠FGA =∠EGB 即可求解；（3）根据内错角相等 两直线平行；确定EDM ∠的内错角即可求解；（4）根据A ∠与ABD ∠互补 得到AF ∥DE 即可得到E F ∠=∠．【详解】解：（1）因为直线EF 和ED 被直线CM 所截所以EDM ∠的同位角是EHM ∠因为直线AC 和ED 被直线CM 所截所以EDM ∠的同位角是ACM ∠故答案为：EHM ∠ ACM ∠；（2）∠AB ∥CD∠=FHC FGA ∠∠∠∠FHC 和∠DHE 互为对顶角 ∠FGA 和∠EGB 互为对顶角∠∠FHC =∠DHE =∠FGA =∠EGB故答案为：3；（3）当EDM ∠=∠ABD 时 AB ∥CD 理由：内错角相等 两直线平行；故答案为：ABD 内错角相等 两直线平行；（4）E F ∠=∠ 理由如下：因为A ∠与ABD ∠互补 （已知）所以AF ∥DE （同旁内角互补 两直线平行）所以E F ∠=∠．（两直线平行 内错角相等）【点睛】本题考查了平行线的性质与判定 对顶角相等等知识 熟知相关知识点并能结合图形灵活应用是解题关键．21．如图找出标注角中的同位角、内错角和同旁内角．【答案】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8 ∠1与∠7．【分析】根据同位角：两条直线被第三条直线所截形成的角中若两个角都在两直线的同侧并且在第三条直线(截线)的同旁则这样一对角叫做同位角；内错角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线(截线)的两旁则这样一对角叫做内错角；同旁内角：两条直线被第三条直线所截形成的角中若两个角都在两直线的之间并且在第三条直线(截线)的同旁则这样一对角叫做同旁内角结合图形进行分析即可．【详解】同位角有∠4与∠8、∠4与∠7、∠2与∠3；内错角有∠1与∠3、∠7与∠6、∠6与∠8；同旁内角有∠1与∠4、∠3与∠8 ∠1与∠7．【点睛】本题主要考查了三线八角解题关键是掌握同位角的边构成“F”形内错角的边构成“Z”形同旁内角的边构成“U”形．22．如图BE是AB的延长线指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的？它们是什么角？（1）∠A和∠D；（2）∠A和∠CBA；（3）∠C和∠CBE．【答案】见解析【详解】试题分析：（1）（2）同旁内角 “同旁”指在第三条直线的同侧；“内”指在被截两条直线之间．（3）内错角 “内”指在被截两条直线之间；“错”即交错 在第三条直线的两侧．（一个角在第三直线左侧 另一角在第三直线右侧）试题解析：（1）∠A 和∠D 是由直线AE 、CD 被直线AD 所截形成的 它们是同旁内角；（2）∠A 和∠CBA 是由直线AD 、BC 被直线AE 所截形成的 它们是同旁内角；（3）∠C 和∠CBE 是由直线CD 、AE 被直线BC 所截形成的 它们是内错角．23．已知：如图是一个跳棋棋盘 其游戏规则是一个棋子从某一个起始角开始 经过若干步跳动以后 到达终点角跳动时 每一步只能跳到它的同位角或内错角或同旁内角的位置上例如：从起始位置1∠跳到终点位置3∠有两种不同路径 路径1：193∠−−−−→∠−−−→∠同旁内角内错角；路径2：1126103∠−−−→∠−−−→∠−−−→∠−−−−→∠内错角内错角同位角同旁内角.试一试：（1）写出从起始位置1∠跳到终点位置8∠的一种路径；（2）从起始位置1∠依次按同位角、内错角、同旁内角的顺序跳 能否跳到终点位置8∠？ 【答案】（1）1128∠→∠→∠内错角同旁内角（答案不唯一）；（2）能跳到终点位置8∠.其路径为1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一） 【分析】（1）根据同旁内角、内错角和同位角的定义进行选择路径即可；（2）先判断能够到达终点位置 在根据定义给出具体路径即可.【详解】（1）可以是这样的路径：1128∠→∠→∠内错角同旁内角.（答案不唯一）（2）从起始位置1∠依次按同位角内错角同旁内角的顺序跳 能跳到终点位置8∠.其路径为 1105118∠→∠→∠→∠→∠同位角内错角同旁内角同位角（答案不唯一）. 【点睛】本题考查的是同位角、内错角和同旁内角的定义 熟知这些角的特征是解题的关键.。