北师大版七年级数学下册第二章单元测试两套含答案
七级数学下册第二章单元测试题及答案

北师大版七年级数学下册第二章 相交线与平行线单元测试卷(一)班级 姓名 学号 得分一、单选题(注释)1、如图,直线a 、b 、c 、d ,已知c ⊥a ,c ⊥b ,直线b 、c 、d 交于一点,若∠1=500,则∠2等于【 】A .600B .500C .400 D .3002、如图,AB ⊥BC ,BC ⊥CD ,∠EBC =∠BCF ,那么,∠ABE 与∠DCF 的位置与大小关系是 ( )A .是同位角且相等B .不是同位角但相等。
C .是同位角但不等D .不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( ) A .相等 B .互补 C .相等或互补 D .相等且互补4、下列说法中,为平行线特征的是( )①两条直线平行,同旁内角互补。
②同位角相等, 两条直线平行。
③内错角相等, 两条直线平行。
④垂直于同一条直线的两条直线平行. A .① B .②③ C .④ D .②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为()A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC∥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,∠1与∠2的关系是( )更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( ) A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
北师大版七年级下册数学第二单元测试卷及答案

北师大版七年级下册数学第二单元测试卷及答案单元测试(二)——相交线与平行线(B卷)一、选择题(每小题3分,共30分)1.与30度的角互为余角的角的度数是()A.30B.60C.70D.902.如图,若∠AOC增大50°,则∠BOD()A.减少50B.不变C.增大50D.增大1303.如图,直线AB与直线CD相交于点O,点E是∠AOD内一点,已知OE⊥AB,∠COE=135°,则∠BOD的度数是()A.35°B.45°C.50°D.55°4.如图,下列条件中能判定AE//CD的是()A.∠A=∠CB.∠A+∠ABC=180°C.∠C=∠XXXD.∠A=∠XXX5.如图,有三条公路,其中AC与AB垂直,XXX和XXX分别沿AC,BC同时出发骑车到C城。
若他们同时到达,则下列判断中正确的是()A.XXX骑车的速度快B.XXX骑车的速度快C.两人一样快D.因为不知道公路的长度,所以无法判断他们速度的快慢6.如图,已知a//b,直角三角板的直角顶点在直线b上。
若∠1=60°,则下列结论错误的是()A.∠5=40°B.∠2=60°C.∠3=60°D.∠4=120°7.如图,直线a,b,c,d,已知c⊥a,c⊥b,直线b,c,d交于一点。
若∠1=50°,则∠2=()A.60°B.50°C.40°D.30°8.如图,XXX,∠ABC=46°,∠CEF=154°,则∠XXX等于()A.23°B.16°C.20°D.26°9.将一条两边平行的纸带按如图所示方式折叠,若∠1=52°,则∠2等于()A.52°B.58°C.64°D.60°10.如图,直线MN分别与直线AB,CD相交于点E,F,∠XXX与∠CFE互补,∠BEF的平分线与∠DFE的平分线交于点P,与直线CD交于点G,GH//PF交MN于点H,则下列说法中错误的是()A.XXXB.∠XXX∠XXXXXXD.∠XXX∠EGD二、填空题(每小题4分,共20分)11.如图,两只手的食指和拇指在同一个平面内,它们构成的一对角可看成是__直角__角。
(完整版)北师大版七年级下学期数学第二单元测试题及答案
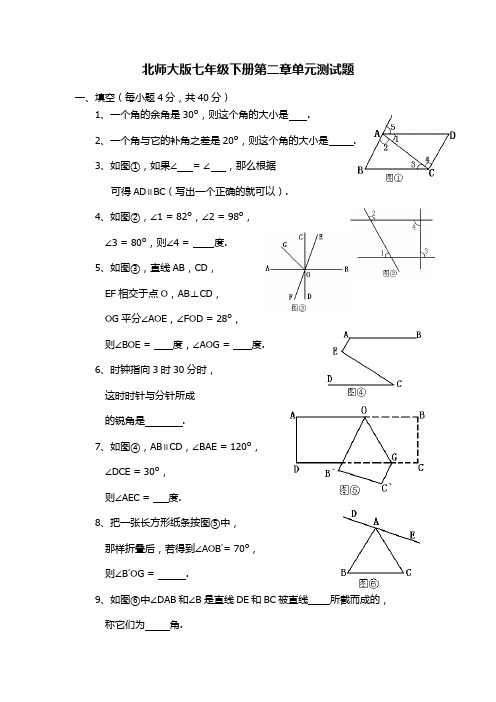
北师大版七年级下册第二章单元测试题一、填空(每小题4分,共40分)1、一个角的余角是30º,则这个角的大小是 .2、一个角与它的补角之差是20º,则这个角的大小是 .3、如图①,如果∠ = ∠ ,那么根据可得AD ∥BC (写出一个正确的就可以).4、如图②,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度.5、如图③,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE ,∠FOD = 28º,则∠BOE = 度,∠AOG = 度.6、时钟指向3时30分时,这时时针与分针所成的锐角是 .7、如图④,AB ∥CD ,∠BAE = 120º,∠DCE = 30º,则∠AEC = 度.8、把一张长方形纸条按图⑤中,那样折叠后,若得到∠AOB ′= 70º,则∠B ′OG = .9、如图⑥中∠DAB 和∠B 是直线DE 和BC 被直线 所截而成的,称它们为 角.10、如图⑦,正方形ABCD 边长为8,M 在DC 上,且DM = 2,N 是AC上一动点,则DN + MN 的最小值为 .二、选择题(每小题3分,共18分)11、下列正确说法的个数是( )①同位角相等 ②对顶角相等③等角的补角相等 ④两直线平行,同旁内角相等A . 1, B. 2, C. 3, D. 412、如图⑧,在△ABC 中,AB = AC ,∠A = 36º,BD平分∠ABC ,DE ∥BC ,那么在图中与△ABC 相似的三角形的个数是( )A. 0,B. 1,C. 2,D. 313、下列图中∠1和∠2是同位角的是( )A. ⑴、⑵、⑶,B. ⑵、⑶、⑷,C. ⑶、⑷、⑸,D.⑴、⑵、⑸14、下列说法正确的是( )A.两点之间,直线最短;B.过一点有一条直线平行于已知直线;C.和已知直线垂直的直线有且只有一条;D.在平面内过一点有且只有一条直线垂直于已知直线.15、一束光线垂直照射在水平地面,在地面上放一个平面镜,欲使这束光线经过平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为()A. 45º,B. 60º,C. 75º,D. 80º16、如图⑨,DH ∥EG ∥EF ,且DC ∥EF ,那么图中和∠1相等的角的个数是( )A. 2,B. 4,C. 5,D. 6三、解答题:17、按要求作图(不写作法,但要保留作图痕迹)(3分)已知点P 、Q 分别在∠AOB 的边OA ,OB 上(如图 ).)①作直线PQ ,②过点P 作OB 的垂线,③过点Q 作OA 的平行线.18、已知线段AB,延长AB到C,使BC∶AB=1∶3,D为AC中点,若DC = 2cm,求AB的长. (7分)分)19、如图,,已知AB∥CD,∠1 = ∠2.求证.:∠E=∠F (620、如图所示,在△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个判断:⑴ AD = CB⑵ AE = FC⑶∠B = ∠D⑷ AD∥BC请用其中三个作为已知条件,余下一个作为结论,编一道数学问题,并写出解答过程. (8分)21、如图,ABCD是一块釉面砖,居室装修时需要一块梯形APCD的釉面砖,且使∠APC=120º.请在长方形AB边上找一点P,使∠APC=120º.然后把多余部分割下来,试着叙述怎样选取P点及其选取P点的理由.(8分)22、如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E =分)140º,求∠BFD的度数. (10第二单元答案一、填空题:1.60°;2.100°;3.∠5= ∠B,同位角相等,两直线平行;4.80°;5.62°,59°;6.75°;7.90°;8.55°;9.AB,内错;10.10.二、选择题:11.B; 12.C; 13.D; 14.D; 15.A; 16.C.三、解答题:17. 略;18. AB=3cm;19.略;20. 比如:已知:⑴⑵⑷.求证:⑶;求证过程略;21. 以C为顶点,CD为一边,在∠DCB内画∠DCP=60°,交AB于P,则P点为所选取的点.证明略;22.∠BFD=70°;。
北师大版七年级数学下册第二章单元测试题及答案全套

七年级数学下册第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若∠1=500,则∠2等于【】A.600B.500C.400D.3002、如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE与∠DCF的位置与大小关系是()A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A.①B.②③C.④D.②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为()A.α+β+γ=360°B.α-β+γ=180°C.α+β-γ=180°D.α+β+γ=180°7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC∥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,∠1与∠2的关系是( )更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( ) A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是( )A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④评卷人得分二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC =___°,∠CDB=____°。
北师大版七年级数学下册第二章测试题

北师大版七年级数学下册第二章测试题(共6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--七年级(下)第二章《平行线与相交线》单元测试题(满分:100分 时间:100分钟) 望远中学 命题人: 汤艳华姓 名 班 级 得分一、填空题(每题3分,共24分)1、若,则它的余角是_________,它的补角是________.2、若∠α与∠β是对顶角,且∠α+∠β=1200 ,则∠α= ,∠β=3、如图, 和 相交, 和 是______角, 和 是______角, 和 是______角, 和 是______角.(第3题) (第4题) (第5题) 4、如图:已知: ,则5、如图:已知: ,则6、如图,,则 .(第6题) (第7题)7、如图,已知∠AOB 、∠BOC 、∠COD 的顶点是一条直线上同一点,且∠AOB=65015’, ∠BOC=78030’,则∠COD=CBADO8、一个角的补角等于这个角的余角的4倍,这个角是________.二、选择题(每题3分,共24分)9、两条直线被第三条直线所截,则().A.同位角必相等 B.内错角必相等C.同旁内角必互补 D.同位角不一定相等10、如图,与是对顶角的为()11、如图,直线a,b都与c相交,由下列条件能推出的是()①②③④A.① B.①② C.①②③ D.①②③④(第11题)(第12题)12、如图,下列条件中能判定的是()A. B.C. D.13、如图,,则下列结论中,错误的是()(第13题)(第14题)A. B.C. D.14、如图,下列推理中正确的是()A.∴ B.∴C.∴D.∴15、如图,由已知条件推出的结论,正确的是().A.由,可推出 B.由,可推出C.由,可推出D.由,可推出16、下列角的平分线中,互相垂直的是()A.平行线的同旁内角的平分线 B.平行线的同位角的平分线C.平行线的内错角的平分线 D.对顶角的平分线三、解答题(每题4分,共16分)1、如图,,求的度数.2、作图题:如图,已知∠α,∠β,求作一个角使它等于∠α+∠β3、如图,已知DE∥AB,∠EAD =∠ADE,试问AD是∠BAC的平分线吗为什么4、如图:已知:,求∠4的度数四、解答题(每题5分,共20分)1、如图:找出互相平行的直线,并说明理由.2、如图,已知AB∥CD,∠A =1000,CB平分∠ACD.回答下列问题:(1)∠ACD等于多少度为什么(2)∠ACB、∠BCD 各等于多少度为什么(3)∠ABC等于多少度为什么3、如图:已知AB∥CD,∠α =450,∠D=∠C.你能求出∠D、∠C和∠B的度数吗4、如图,完成下列推理过程已知:DE⊥AO于E, BO⊥AO,∠CFB=∠EDO证明:CF∥DO证明:∵DE⊥AO, BO⊥AO(已知)∴∠DEA=∠BOA=900()∵DE∥BO ()∴∠EDO=∠DOF ()又∵∠CFB=∠EDO()五、解答题(每题8分,共16分)1、 DE ∥BC ,CD 是∠ACB 的平分线,∠B =80,∠ACB=500 ,求∠EDC ,∠CDB新 课 标 第一网2、如图,AB ∥EF ,∠B =1350,∠C=670,则求∠1的度数.EB ADC新课标第一网。
七年级数学北师大版下册第2章《单元测试》04(含答案解析)

2
证明:如图 ② 延长 线㤰 和 ‹ 的延长线交于点 ,
因为 线∥ ‹,
所以 ∠ 线㤰 = ∠ ,
因为 线㤰∥ ‹,
所以 ∠ = ∠‹ ‹,
因为 ‹ 平分 ∠㤰 ‹,
所以 ∠㤰 ‹ = ∠‹ ‹,
所以 1 ∠㤰 ‹ = ∠ = ∠ 线㤰,
2
所以
∠
线㤰
=
1 2
∠㤰
二、填空题(共 7 小题)
10. 如图,直线 , 相交,∠2 = 3∠1,则 ∠3 =
.
11. 如果 ∠ = 35∘,那么 ∠ 的余角等于
为
.
,∠ 的补角
12. 如 图 , 直 线 ∠线 ‹ =
线与
‹ 相交于点 .
, 㤰 ⊥ 线 , ∠ 㤰 = 60∘ , 则
13. 如图,如果 ∠ 据
=∠
,那么根
(1) ‹ 与 㤰‹ 平行吗?为什么? (2)如果 ∠1 = ∠2,且 ∠3 = 105∘,求 ∠ 线 的度数. 20. 已知 线∥ ‹. (1)如图 ①,若 ∠ 线㤰 = 30∘,∠线㤰 = 148∘,求 ∠㤰 ‹ 的度数;
(2)如图 ②,若 ‹∥㤰线, ‹ 平分 ∠㤰 ‹,试探究 ∠㤰 ‹ 与 ∠ 线㤰 之 间的数量关系,并证明.
(2) 因为 㤰‹∥‹ , 所以 ∠2 = ∠线 ‹. 因为 ∠1 = ∠2, 所以 ∠1 = ∠线 ‹. 所以 ‹ ∥线 . 所以 ∠ 线 = ∠3 = 105∘. 20. (1) 如图 ①,过点 㤰 作 㤰‹∥ 线,
因为 线∥ ‹, 所以 线∥㤰‹∥ ‹, 所以 ∠ 线㤰 = ∠线㤰‹,∠‹㤰 + ∠㤰 ‹ = 180∘, 因为 ∠ 线㤰 = 30∘,∠线㤰 = 148∘, 所以 ∠‹㤰 = 118∘, 所以 ∠㤰 ‹ = 180∘ − 118∘ = 62∘;
2021-2022学年北师大版七年级数学下册《第2章相交线与平行线》单元达标测试(附答案)

2021-2022学年北师大版七年级数学下册《第2章相交线与平行线》单元达标测试(附答案)一.选择题(共10小题,满分40分)1.同一平面内,三条不同直线的交点个数可能是()个.A.1或3B.0、1或3C.0、1或2D.0、1、2或3 2.如图,在所标识的角中,互为对顶角的两个角是()A.∠1和∠2B.∠1和∠4C.∠2和∠3D.∠3和∠43.已知,OA⊥OC,且∠AOB:∠AOC=2:3,则∠BOC的度数为()A.30°B.150°C.30°或150°D.90°4.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是()A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短5.下列图形中,线段AD的长表示点A到直线BC距离的是()A.B.C.D.6.如图,直线l与∠BAC的两边分别相交于点D、E,则图中是同旁内角的有()A.2对B.3对C.4对D.5对7.如图,直线DE截AB,AC,其中内错角有()对.A.1B.2C.3D.48.下列说法正确的是()A.不相交的两条线段是平行线B.不相交的两条直线是平行线C.不相交的两条射线是平行线D.在同一平面内,不相交的两条直线是平行线9.在同一平面内两条不重合的直线的位置关系是()A.相交或垂直B.平行或垂直C.相交或平行D.以上都不对10.下列说法正确的有()①同位角相等;②若∠A+∠B+∠C=180°,则∠A、∠B、∠C互补;③同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交;④同一平面内两条直线的位置关系可能是平行或垂直;⑤有公共顶点并且相等的角是对顶角.A.1个B.2个C.3个D.4个二.填空题(共8小题,满分32分)11.下列说法中,①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.不正确的是(填序号)12.已知直线a∥b,b∥c,则直线a、c的位置关系是.13.如图所示,请你填写一个适当的条件:,使AD∥BC.14.如图,点E是AD延长线上一点,如果添加一个条件,使BC∥AD,则可添加的条件为.(任意添加一个符合题意的条件即可)15.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是.16.如图,AB∥CD,点P为CD上一点,∠EBA、∠EPC的角平分线于点F,已知∠F=40°,则∠E=度.17.已知直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,则点P到b的距离是.18.已知直线l1∥l2,BC=3cm,S△ABC=3cm2,则S△A1BC的高是.三.解答题(共9小题,满分48分)19.如图,平原上有A,B,C,D四个村庄,为解决当地缺水问题,政府准备投资修建一个蓄水池.(1)不考虑其他因素,请你画图确定蓄水池H点的位置,使它到四个村庄距离之和最小;(2)计划把河水引入蓄水池H中,怎样开渠最短并说明根据.20.画图题:(1)在如图所示的方格纸中(单位长度为1),经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线EF和平行线GH.(2)判断EF、GH的位置关系是.(3)连接AC和BC,则三角形ABC的面积是.21.作图并写出结论:如图,点P是∠AOB的边OA上一点,请过点P画出OA,OB的垂线,分别交BO的延长线于M、N,线段的长表示点P到直线BO的距离;线段的长表示点M 到直线AO的距离;线段ON的长表示点O到直线的距离;点P到直线OA的距离为.22.看图填空,并在括号内注明说理依据.如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF 平行吗?解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以∥().又因为AC⊥AE(已知),所以∠EAC=90°.()所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2=°.所以∠EAB=∠FBG().所以∥(同位角相等,两直线平行).23.如图,∠ACD=2∠B,CE平分∠ACD,求证:CE∥AB.24.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;(1)直接写出图中∠AOC的对顶角为,∠BOE的邻补角为;(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.25.(1)如图1,已知AB∥CD,那么图1中∠P AB、∠APC、∠PCD之间有什么数量关系?并说明理由.(2)如图2,已知∠BAC=80°,点D是线段AC上一点,CE∥BD,∠ABD和∠ACE 的平分线交于点F,请利用(1)的结论求图2中∠F的度数.26.如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB、CD的位置关系如何?并说明理由.27.如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM 时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过秒后边OC与边ON互相垂直.(直接写出答案)参考答案一.选择题(共10小题,满分40分)1.解:如图,三条直线的交点个数可能是0或1或2或3.故选:D.2.解:观察图形可知,互为对顶角的两个角是∠3和∠4.故选:D.3.解:∵OA⊥OC,∴∠AOC=90°,∵∠AOB:∠AOC=2:3,∴∠AOB=60°.因为∠AOB的位置有两种:一种是在∠AOC内,一种是在∠AOC外.①当在∠AOC内时,∠BOC=90°﹣60°=30°;②当在∠AOC外时,∠B′OC=90°+60°=150°.故选:C.4.解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,故选:D.5.解:线段AD的长表示点A到直线BC距离的是图D,故选:D.6.解:直线AC与直线AB被直线l所截形成的同旁内角有:∠ADE与∠AED、∠CDE与∠BED;直线AC与直线DE被直线AB所截形成的同旁内角有:∠DAE与∠DEA;直线AB与直线DE被直线AC所截形成的同旁内角有:∠EAD与∠EDA;故选:C.7.解:直线DE截AB、AC,形成两对内错角,直线AB截AC,DE,形成一对内错角;直线AC截AB,DE,形成一对内错角.综上,共形成4对内错角.故选:D.8.解:根据平行线的定义:在同一平面内,不相交的两条直线是平行线.A,B,C错误;D正确;故选:D.9.解:在同一平面内两条不重合的直线的位置关系是平行和相交.故选:C.10.解:∵同位角不一定相等,∴①错误;∵互补或互余是两个角之间的关系,∴说∠A+∠B+∠C=180°,则∠A、∠B、∠C互补错误,∴②错误;∵同一平面内的三条直线a、b、c,若a∥b,c与a相交,则c与b相交,∴③正确;∵同一平面内两条直线的位置关系可能是平行或相交,∴④错误;∵如图,∠ABC=∠ABD,∠ABC和∠ABD有公共顶点并且相等的角,但不是对顶角,∴⑤错误;即正确的个数是1个,二.填空题(共8小题,满分32分)11.解:①在同一平面内,不相交的两条线段叫做平行线,正确;②过一点,有且只有一条直线平行于已知直线,正确;③两条平行直线被第三条直线所截,当两直线平行,同位角相等,故原命题错误;④同旁内角相等,两直线平行,正确.故答案为:①②④.12.解:若直线直线a∥b,b∥c,则直线a、c的位置关系是平行,故答案为:平行.13.解:添加∠F AD=∠FBC,或∠ADB=∠DBC,或∠DAB+∠ABC=180°.∵∠F AD=∠FBC∴AD∥BC(同位角相等两直线平行);∵∠ADB=∠DBC∴AD∥BC(内错角相等两直线平行);∵∠DAB+∠ABC=180°∴AD∥BC(同旁内角互补两直线平行).14.解:若∠A+∠ABC=180°,则BC∥AD;若∠C+∠ADC=180°,则BC∥AD;若∠CBD=∠ADB,则BC∥AD;若∠C=∠CDE,则BC∥AD;故答案为:∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.(答案不唯一)15.解:用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是同位角相等,两直线平行;故答案为:同位角相等,两直线平行.16.解:设∠EPC=2x,∠EBA=2y,∵∠EBA、∠EPC的角平分线交于点F∴∠CPF=∠EPF=x,∠EBF=∠FBA=y,∵∠1=∠F+∠ABF=40°+y,∠2=∠EBA+∠E=2y+∠E,∴∠1=∠CPF=x,∠2=∠EPC=2x,∴∠2=2∠1,∴2y+∠E=2(40°+y),∴∠E=80°.故答案为:80.17.解:∵直线a∥b,a与b之间的距离为5,a与b之间有一点P,点P到a的距离是2,∴点P到b的距离是5﹣2=3,故答案为:3.18.解:过点A作AD⊥l2,过A1作A1E⊥l2,∵l1∥l2,∴AD=A1E,∴S△ABC=S△A1BC=3cm2,即BC•AD=BC•A1E=3,∵BC=3cm,∴A1E=2cm,则S△A1BC的高是2cm,故答案为:2cm三.解答题(共9小题,满分48分)19.解:(1)∵两点之间线段最短,∴连接AD,BC交于H,则H为蓄水池位置,它到四个村庄距离之和最小.(2)过H作HG⊥EF,垂足为G.“过直线外一点与直线上各点的连线中,垂线段最短”是把河水引入蓄水池H中开渠最短的根据.20.解:(1)如图(2)EF与GH的位置关系是:垂直;(3)设小方格的边长是1,则AB=2,CH=2,∴S△ABC=×2×2=10.21.解:如图所示:线段PN的长表示点P到直线BO的距离;线段PM的长表示点M到直线AO的距离;线段ON的长表示点O到直线PN的距离;点P到直线OA的距离为0,故答案为:PN,PM,PN,0.22.解:因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以AC∥BD(同位角相等,两直线平行).又因为AC⊥AE(已知),所以∠EAC=90°.(垂直的定义)所以∠EAB=∠EAC+∠1=125°.同理可得,∠FBG=∠FBD+∠2=125°.所以∠EAB=∠FBG(等量代换).所以AE∥BF(同位角相等,两直线平行).故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.23.证明:∵CE平分∠ACD,∴∠ACD=2∠DCE,∵∠ACD=2∠B,∴∠DCE=∠B,∴AB∥CE.24.解:(1)∠AOC的对顶角为∠BOD,∠BOE的邻补角为∠AOE;故答案为:∠BOD,∠AOE;(2)∵∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD,∠BOE:∠EOD=2:3,∴,∴,∴∠BOE=28°,∴∠AOE=180°﹣∠BOE=152°.25.解:(1)结论:∠P=∠PCD﹣∠P AB.理由:如图1中,设AB交PC于H.∵AB∥CD,∴∠PCD=∠AHC,∵∠AHC=∠P AB+∠P,∴∠P=∠AHC﹣∠P AB,∴∠P=∠PCD﹣∠P AB.(2)如图2中,设∠ABF=∠FBD=y,∠ACF=∠FCE=x,由(1)可知:∠F=x﹣y,∵BD∥CE,∴∠BDC=∠DCE=2x,∵∠BDC=∠ABD+∠A,∴2x=2y+80°,∴x﹣y=40°,∴∠F=40°.26.证明:直线AB、CD的位置关系为:AB∥CD,理由如下:∵BE是∠ABD的平分线,DE是∠BDC的平分线,∴∠1=∠ABD,∠2=∠BDC.∵∠1+∠2=90°,∴∠ABD+∠BDC=2(∠1+∠2)=2×90°=180°,∴AB∥CD.27.解:(1)在△CEN中,∠CEN=180°﹣30°﹣45°=105°;(2)如图②,∵∠CON=5∠DOM∴180°﹣∠DOM=5∠DOM,∴∠DOM=30°∵∠OMN=60°,∴MN⊥OD,∴MN∥BC,∴∠CEN=180°﹣∠DCO=180°﹣45°=135°;(3)如图③,MN∥CD时,旋转角为90°﹣(60°﹣45°)=75°,或270°﹣(60°﹣45°)=255°,所以,t=75°÷5°=15秒,或t=255°÷5°=51秒;所以,在旋转的过程中,三角板MON运动15秒或51秒后直线MN恰好与直线CD平行.(4)MN⊥CD时,旋转角的角度差上90°,所以90°÷(20°﹣10°)=9秒,故答案为:9.。
北师大版七年级数学下册第二章单元测试卷

第二章评估测试卷(时间:120分钟满分:120分)一、选择题(下列各题的备选答案中,只有一个答案是正确的,每小题2分,共20分)1.如图,有一个破损的扇形零件,小明利用图中的量角器量出这个扇形零件的圆心角度数为50°,你认为小明测量的依据是(B)A.垂线段最短B.对顶角相等C.圆的定义D.三角形内角和等于180°2.如图,直线AD,BE被直线BF和AC所截,则∠1的同位角和∠5的内错角分别是(B)A.∠4,∠2 B.∠2,∠6 C.∠5,∠4 D.∠2,∠43.如图,∠1=∠2=∠3=55°,则∠4的度数为(C)A.115° B.120° C.125° D.135°4.如图,下列条件中,不能判定直线l1∥l2的是(D)A.∠1=∠3 B.∠2+∠4=180°C.∠4=∠5 D.∠2=∠35.如图,将直角三角尺的直角顶点落在直尺上,且斜边与直尺平行,那么在形成的这个图中与∠α互余的角共有(C)A.4个B.3个C.2个D.1个6.如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是(B)A.∠1=∠3 B.∠2=∠4C.∠C=∠CBE D.∠C+∠ABC=180°7.如图,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15.5°,则下列结论不正确的是(D)A.∠2=45° B.∠1=∠3C.∠AOD与∠1互为补角D.∠1的余角等于75.5°8.如图是赛车跑道的一段示意图,其中AB∥DE,测得∠B=140°,∠D=120°,则∠C的度数为(B)A.120° B.100° C.140° D.90°9.如图,AB∥CD,EF平分∠AEG,若∠FGE=40°,那么∠EFG 的度数为(C)A.35° B.40° C.70° D.140°10.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能(C)A.相等B.互补C.相等或互补D.相等且互补二、填空题(每小题3分,共18分)11.如图,计划把河水引到水池A中,先作AB⊥CD,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是直线外一点与直线上各点连接的所有线段中,垂线段最短.12.如图,已知直线AB与CD交于点O,ON平分∠DOB,若∠BOC=110°,则∠AON的度数为145度.13.如图,∠BDE的同位角是∠BGC,∠BDE的内错角是∠FGD,∠BDE的同旁内角是∠DGC,∠ADE与∠DGC是两条直线ED和CF 被直线AB所截成的同位角.14.如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的大小是50°.15.如图是我们常用的折叠式小刀,刀柄外形是一个矩形挖去一个小半圆,其中刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成∠1与∠2,若∠1=75°,则∠2的度数为15°.16.如图所示,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯的∠A是120°,第二次拐弯的∠B是150°,第三次拐弯的角是∠C,这时的道路恰好与拐弯前的道路平行,则∠C等于150°.三、解答题(第17小题6分,第18、19小题各8分,共22分)17.完成下列证明:如图所示,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.证明:因为AD⊥BC,EF⊥BC(已知),所以∠EFB=90°,∠ADB=90°(垂直的定义),所以∠EFB=∠ADB(等量代换),所以EF∥AD(同位角相等,两直线平行),所以∠1=∠BAD(两直线平行,同位角相等),又∠1=∠2(已知),所以∠BAD=∠2(等量代换),所以DG∥BA(内错角相等,两直线平行).18.如图,a ∥b ∥c ,∠1=40°,∠2=100°,BD 平分∠ABC ,求∠DBE 的度数.解:因为a ∥b ,所以∠ABE =∠1=40°.因为b ∥c ,所以∠EBC +∠2=180°.因为∠2=100°,所以∠EBC =80°.所以∠ABC =∠ABE +∠EBC =40°+80°=120°.因为BD 平分∠ABC ,所以∠DBC =12∠ABC =60°,所以∠DBE =∠EBC -∠DBC =80°-60°=20°.19.如图,已知AD ⊥BC ,EF ⊥BC ,∠3=∠C ,求证:∠1=∠2.证明:因为AD ⊥BC ,EF ⊥BC (已知),所以∠BDA =90°,∠BFE =90°,所以∠BDA =∠BFE ,所以AD ∥EF (同位角相等,两直线平行),所以∠1=∠4(两直线平行,同位角相等),又∠3=∠C (已知),所以AC ∥DG (同位角相等,两直线平行),所以∠2=∠4(两直线平行,内错角相等),所以∠1=∠2(等量代换).四、(每小题8分,共16分)20.如图,直线AB,CD相交于点O,OE⊥AB于点O,且∠DOE =3∠COE,求∠AOD的度数.解:因为∠DOE+∠COE=180°,且∠DOE=3∠COE,所以∠COE=45°,所以∠BOC=90°+45°=135°,所以∠AOD=∠BOC=135°(对顶角相等).21.(2020·四平模拟)如图,AB∥CD,∠ADC=∠ABC.求证:∠E =∠F.证明:因为AB∥CD,所以∠ABC=∠DCF.又因为∠ADC=∠ABC,所以∠ADC=∠DCF.所以DE∥BF.所以∠E=∠F.五、(本题10分)22.已知,如图,AB∥CD,BD平分∠ABC,CE平分∠DCF,∠ACE=90°.(1)判断BD和CE的位置关系并说明理由;(2)判断AC和BD是否垂直并说明理由.解:(1)BD ∥CE .理由:因为AB ∥CD ,所以∠ABC =∠DCF ,所以BD 平分∠ABC ,CE 平分∠DCF ,所以∠2=12∠ABC ,∠4=12∠DCF ,所以∠2=∠4,所以BD ∥CE (同位角相等,两直线平行).(2)AC ⊥BD ,理由:由(1)知BD ∥CE ,所以∠DGC +∠ACE =180°, 因为∠ACE =90°,所以∠DGC =180°-90°=90°,即AC ⊥BD .六、(本题10分)23.如图,已知∠ABC =63°,∠ECB =117°,∠P =∠Q .(1)AB 与ED 平行吗?为什么?(2)∠1与∠2是否相等?说说你的理由.解:(1)平行.理由:因为∠ABC =63°,∠ECB =117°, 所以∠ABC +∠ECB =180°,所以AB ∥ED (同旁内角互补,两直线平行).(2)相等.理由:因为∠P=∠Q(已知),所以PB∥CQ(内错角相等,两直线平行),所以∠PBC=∠QCB(两直线平行,内错角相等).因为AB∥CD(已证),所以∠ABC=∠DCB(两直线平行,内错角相等),所以∠ABC-∠PBC=∠DCB-∠QCB(等式的性质),即∠1=∠2.七、(本题12分)24.如图,AB∥CD,BF平分∠ABE,DF平分∠CDE,∠BFD =55°,求∠BED的度数.题图解:如图,过点E,F分别作EG∥AB,FH∥AB,答图则有∠5=∠ABE,∠3=∠1.又因为AB∥CD,所以EG∥CD,FH∥CD,所以∠6=∠CDE,∠4=∠2,所以∠1+∠2=∠3+∠4=∠BFD=55°.因为BF 平分∠ABE ,DF 平分∠CDE ,所以∠ABE =2∠1,∠CDE =2∠2,所以∠BED =∠5+∠6=2∠1+2∠2=2(∠1+∠2)=2×55°=110°.八、(本题12分)25.如图,直线AB ,CD 相交于点O ,OE 平分∠BOD .(1)若∠AOC =70°,∠DOF =90°,求∠EOF 的度数;(2)若OF 平分∠COE ,∠BOF =15°,求∠AOC 的度数.解:(1)因为∠DOB 与∠AOC 互为对顶角,所以∠DOB =∠AOC =70°,因为OE 平分∠BOD ,所以∠DOE =12∠BOD =35°,所以∠EOF =∠DOF -∠DOE =55°.(2)设∠AOC =x ,则∠DOB =∠AOC =x .因为OE 平分∠BOD ,所以∠DOE =∠EOB =12∠BOD =12x ,所以∠EOC =180°-∠DOE =180°-x 2,因为∠EOF =∠EOB +∠BOF ,所以∠EOF =x 2+15°.因为OF 平分∠COE ,所以∠EOC =2∠EOF ,所以180°-x 2=2⎝ ⎛⎭⎪⎫x 2+15°, 解得x =100°,即∠AOC =100°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版七年级数学下册第二章相交线与平行线单元测试卷(一)班级姓名学号得分评卷人得分一、单选题(注释)1、如图,直线a、b、c、d,已知c⊥a,c⊥b,直线b、c、d交于一点,若⊥1=500,则⊥2等于【】A.600B.500C.400D.3002、如图,AB⊥BC,BC⊥CD,⊥EBC=⊥BCF,那么,⊥ABE与⊥DCF的位置与大小关系是()A.是同位角且相等B.不是同位角但相等;C.是同位角但不等D.不是同位角也不等3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能()A.相等B.互补C.相等或互补D.相等且互补4、下列说法中,为平行线特征的是()⊥两条直线平行,同旁内角互补; ⊥同位角相等, 两条直线平行;⊥内错角相等, 两条直线平行; ⊥垂直于同一条直线的两条直线平行.A.⊥B.⊥⊥C.⊥D.⊥和⊥5、如图,AB⊥CD⊥EF,若⊥ABC=50°,⊥CEF=150°,则⊥BCE=()A.60°B.50°C.30°D.20°6、如图,如果AB⊥CD,则角α、β、γ之间的关系为()=180°=360°B.α-β+γA.α+β+γ=180°C.α+β-γ=180°D.α+β+γ7、如图,由A到B 的方向是()A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°8、如图,由AC⊥ED,可知相等的角有()A.6对B.5对C.4对D.3对9、如图,直线AB、CD交于O,EO⊥AB于O,⊥1与⊥2的关系是()更多功能介绍/zt/A.互余B.对顶角C.互补D.相等10、若⊥1和⊥2互余,⊥1与⊥3互补,⊥3=120°,则⊥1与⊥2的度数分别为() A.50°、40°B.60°、30°C.50°、130°D.60°、120°11、下列语句正确的是()A.一个角小于它的补角B.相等的角是对顶角C.同位角互补,两直线平行D.同旁内角互补,两直线平行12、图中与⊥1是内错角的角的个数是()A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,⊥AOD和⊥BOC的和为202°,那么⊥AOC的度数为()A.89°B.101°C.79°D.110°14、如图,⊥1和⊥2是对顶角的图形的个数有()A.1个B.2个C.3个D.0个,⊥⊥4=⊥7,,⊥⊥1=⊥7,⊥⊥2+⊥3=180°15、如图,直线a、b被直线c所截,现给出下列四个条件:⊥⊥1=⊥5其中能判定a⊥b的条件的序号是()A.⊥⊥B.⊥⊥C.⊥⊥D.⊥⊥评卷人得分二、填空题(注释)16、如图,⊥ACD=⊥BCD,DE⊥BC交AC于E,若⊥ACB=60°,⊥B=74°,则⊥EDC=___°,⊥CDB=____°。
17、如图,BA⊥DE,⊥B=150°,⊥D=130°,则⊥C的度数是__________。
18、如图,AD⊥BC,⊥A是⊥ABC的2倍,(1)⊥A=____度;(2)若BD平分⊥ABC,则⊥ADB=____。
19、如图,DH⊥EG⊥BC,DC⊥EF,图中与⊥1相等的角有________________________。
20、如图,AB⊥CD,直线EF分别交AB、CD于E、F,EG平分⊥BEF,若⊥1=72°,则⊥2=_________。
21、如图,AB⊥EF,CD⊥EF,⊥1=⊥F=45°,那么与⊥FCD相等的角有___个,它们分别是____。
22、如图,AB⊥CD,AF分别交AB、CD于A、C,CE平分⊥DCF,⊥1=100 °,则⊥2=_____.23、如图,⊥1与⊥4是_____角,⊥1与⊥3是_____角,⊥3与⊥5是_____角,⊥3与⊥4是_____角.24、如图,⊥1的同旁内角是_____,⊥2的内错角是_____.25、如图,已知⊥2=⊥3,那么_____⊥_____,若⊥1=⊥4,则_____⊥_____.26、如图,若⊥1=⊥2,则_____⊥_____.若⊥3+⊥4=180°,则_____⊥_____.,⊥1=65°,则⊥3=_____.27、如图,已知直线AB、CD交于点O,OE为射线,若⊥1+⊥2=90°28、看图填空:⊥直线AB、CD相交于点O,⊥⊥1与_____是对顶角,⊥2与_____是对顶角,⊥⊥1=_____,⊥2=_____.理由是:29、如图,直线a,b相交,⊥1=55°,则⊥2=_____,⊥3=_____,⊥4=_____.30、若⊥A与⊥B互余,则⊥A+⊥B=_____;若⊥A与⊥B互补,则⊥A+⊥B=_____.31、如图,三条直线交于同一点,则⊥1+⊥2+⊥3=_____.,则⊥β=_____.32、如果⊥α与⊥β是对顶角,⊥α=30°评卷人得分三、解答题(注释)33、如图,已知⊥1+⊥2=180°,⊥3=⊥B,试判断⊥AED与⊥C的关系。
34、如图,AB⊥CD,⊥1=⊥2,⊥BDF与⊥EFC相等吗?为什么?35、如图,⊥1=⊥2,⊥C=⊥D,那么⊥A=⊥F,为什么?36、如图,DE⊥CB,试证明⊥AED=⊥A+⊥B。
37、如图,⊥CAB=100°,⊥ABF=130°,AC⊥MD,BF⊥ME,求⊥DME 的度数.38、已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,⊥GQC=120°,求⊥EGB和⊥HGQ的度数。
,CD与EF平行吗?为什39、如图,⊥ABD= 90°,⊥BDC=90°,⊥1+⊥2=180°么?40、如图,EF交AD于O,AB交AD于A,CD交AD于D,⊥1=⊥2,⊥3=⊥4,试判AB和CD的位置关系,并说明为什么.41、已知直线a、b、c两两相交,⊥1=2⊥3,⊥2=40°,求⊥4.单元测试卷(一)参考答案,c⊥b,⊥a⊥b。
1.【解析】⊥c⊥a⊥⊥1=500,⊥⊥2=⊥1=500。
故选B。
2.【解析】试题分析:由AB⊥BC,BC⊥CD,⊥EBC=⊥BCF,即可判断⊥ABE与⊥DCF的大小关系,根据同位角的特征即可判断⊥ABE与⊥DCF的位置关系,从而得到结论.⊥AB⊥BC,BC⊥CD,⊥EBC=⊥BCF,⊥⊥ABE=⊥DCF,⊥⊥ABE与⊥DCF的位置与大小关系是不是同位角但相等,故选 B.考点:本题考查的是同位角点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.3.【解析】试题分析:根据平行线的性质即可得到结果.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角相等或互补,故选 C.考点:本题考查的是平行线的性质点评:解答本题的关键是熟记如果两个角的一边在同一直线上,另一边互相平行,那么这两个角相等或互补.4.【解析】试题分析:根据平行线的性质依次分析各小题即可.为平行线特征的是⊥两条直线平行,同旁内角互补,⊥同位角相等,两条直线平行;⊥内错角相等,两条直线平行;⊥垂直于同一条直线的两条直线平行,均为平行线的判定,故选 A.考点:本题考查的是平行线的性质点评:解答本题的关键是熟练掌握平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两条直线平行,同旁内角互补.5.【解析】试题分析:根据两直线平行,内错角相等求出⊥BCD等于55°;两直线平行,同旁内角互补求出⊥ECD等于30°,⊥BCE的度数即可求出.⊥AB⊥CD,⊥ABC=50°,⊥⊥BCD=⊥ABC=50°,⊥EF⊥CD,⊥⊥ECD+⊥CEF=180°,⊥⊥CEF=150°,,⊥⊥ECD=180°-⊥CEF=180°-150°=30°.⊥⊥BCE=⊥BCD-⊥ECD=50°-30°=20°考点:此题考查了平行线的性质点评:解题的关键是注意掌握两直线平行,同旁内角互补,两直线平行,内错角相等.6.【解析】试题分析:首先过点E作EF⊥AB,由AB⊥CD,即可得EF⊥AB⊥CD,根据两直线平行,同旁内角互补与两直线平行,内错角相等,即可求得⊥α+⊥1=180°,⊥2=⊥γ,继而求得α+β-γ=180°.过点E作EF⊥AB,⊥AB⊥CD,⊥EF⊥AB⊥CD,,⊥2=⊥γ,⊥⊥α+⊥1=180°,-⊥α+⊥γ⊥⊥β=⊥1+⊥2=180°.-γ=180°⊥α+β故选C.考点:此题考查了平行线的性质点评:解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,注意辅助线的作法.7.【解析】试题分析:根据方位角的概念和三角形的内角和即可得到结果.根据方位角的概念,由A测B的方向是南偏东90°-30°=60°,故选 B.考点:本题考查的是方位角,三角形的内角和点评:解答本题的关键是要求同学们熟练掌握方位角的概念,再结合三角形的角的关系求解.8.【解析】试题分析:根据平行线的性质,对顶角相等即可判断.根据平行线的性质,对顶角相等可知相等的角有5对,故选 B.考点:本题考查的是平行线的性质,对顶角相等点评:解答本题的关键是熟练掌握两直线平行,同位角相等;两直线平行,内错角相等.9.【解析】试题分析:根据EO⊥AB结合平角的定义即可得到结果.⊥EO⊥AB,,⊥⊥1+⊥2=90°故选 A.考点:本题考查的是平角的定义,互余的定义点评:解答本题的关键是熟记和为90°的两个角互余,平角等于180°.10.【解析】试题分析:先根据互补的定义求得⊥1,再根据互余的定义求得⊥2.⊥⊥1与⊥3互补,⊥3=120°,-⊥3=60°,⊥⊥1=180°⊥⊥1和⊥2互余,-⊥1=30°,⊥⊥2=90°故选 B.若⊥A与⊥B互余,则⊥A+⊥B=90°;若⊥A与⊥B互补,则⊥A+⊥B=180°.考点:本题考查的是互余,互补点评:解答本题的关键是熟记和为90°的两个角互余,和为180°的两个角互补.11.【解析】试题分析:根据补角的性质,对顶角的性质,平行线的判定定理依次分析各项即可.A、直角的补角是直角,故本选项错误;B、直角都相等,但不一定是对顶角,故本选项错误;C、同位角相等,两直线平行,故本选项错误;D、同旁内角互补,两直线平行,本选项正确;故选 D.考点:本题考查的是补角,对顶角,平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.12.【解析】试题分析:根据同内错角的概念即可判断.与⊥1是内错角的角的个数是3个,故选 B.考点:本题考查的是内错角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.13.【解析】试题分析:根据对顶角相等及⊥AOD和⊥BOC的和为202°,即可求得结果.由图可知⊥AOD=⊥BOC,而⊥AOD+⊥BOC=202°,⊥⊥AOD=101°,⊥⊥AOC=180°-⊥AOD=79°,故选 C.考点:本题考查的是对顶角,邻补角点评:解答本题的关键是熟练掌握对顶角相等,邻补角之和等于180°.14.【解析】试题分析:根据对顶角的定义依次分析各个图形即可求得结果.是对顶角的图形只有⊥,故选 A.考点:本题考查的是对顶角点评:解答本题的关键是熟练掌握对顶角的定义:两条直线相交形成的没有公共边的一对角叫对顶角.15.【解析】试题分析:根据平行线的判定定理即可得到结果.能判定a⊥b的条件是⊥⊥1=⊥5,⊥⊥1=⊥7,故选 A.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.16.【解析】试题分析:由⊥ACD=⊥BCD,⊥ACB=60°,根据DE⊥BC,即可求得⊥EDC的度数,再根据三角形的内角和定理即可求得⊥BDC的度数.⊥⊥ACD=⊥BCD,⊥ACB=60°,⊥⊥ACD=⊥BCD=30°,⊥DE⊥BC,⊥⊥EDC=⊥BCD=30°,⊥⊥CDB=180°-⊥BCD-⊥B=76°.考点:此题考查了平行线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等,三角形的内角和为180°.17.【解析】试题分析:过C作CF⊥AB,把⊥C分成两个角,根据平行线的性质即可求出两个角,相加就可以得到所求值.如图:过C作CF⊥AB,则AB⊥DE⊥CF,⊥1=180°-⊥B=180°-150°=30°,⊥2=180°-⊥D=180°-130°=50°⊥⊥BCD=⊥1+⊥2=30°+50°=80°.考点:本题考查的是平行线的性质点评:通过作辅助线,找出⊥B、⊥D与⊥C的关系是解答本题的关键.18.【解析】试题分析:根据平行线的性质,角平分线的性质即可得到结果.⊥AD⊥BC,⊥⊥A+⊥ABC=180°;⊥⊥A:⊥ABC=2:1,⊥⊥A=120°,⊥ABC=60°;⊥BD平分⊥ABC,⊥⊥DBC=30°,⊥AD⊥BC,⊥⊥ADB=30°.考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等;两直线平行,同旁内角互补.19.【解析】试题分析:根据两直线平行,同位角相等,内错角相等,找出⊥1的同位角与内错角以及与⊥1相等的角的同位角与内错角,从而得解.根据平行线的性质,与⊥1相等的角有⊥FEK,⊥DCF,⊥CKG,⊥EKD,⊥KDH.考点:本题考查的是平行线的性质点评:解答本题的关键是熟练掌握两直线平行,同位角相等;两直线平行,内错角相等;在图中标注上角更形象直观.20.【解析】试题分析:两直线平行,同旁内角互补,可求出⊥FEB,再根据角平分线的性质,可得到⊥BEG,然后用两直线平行,内错角相等求出⊥2.⊥AB⊥CD,,⊥2=⊥BEG,⊥⊥BEF=180°-⊥1=180°-72°=108°又⊥EG平分⊥BEF,⊥⊥BEG=⊥BEF=54°,⊥⊥2=⊥BEG=54°.考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,内错角相等;两直线平行,同旁内角互补.21.【解析】试题分析:由AB⊥EF,CD⊥EF,⊥1=⊥F=45°,根据三角形的内角和为180°,平角的定义即可得到结果.⊥AB⊥EF,CD⊥EF,⊥1=⊥F=45°,⊥⊥A=⊥ABG=⊥FCD=45°,⊥与⊥FCD相等的角有4个,它们分别是⊥F,⊥1,⊥FAB,⊥ABG.考点:本题考查的是三角形的内角和点评:解答本题的关键是熟练掌握三角形的内角和为180°,平角等于180°.22.【解析】试题分析:先根据平行线的性质求得⊥DCF的度数,再根据角平分线的性质即可求得结果.⊥AB⊥CD,⊥⊥DCF=⊥1=100 °,⊥CE平分⊥DCF,⊥⊥2=50°.考点:本题考查的是平行线的性质,角平分线的性质点评:解答本题的关键是熟练掌握两直线平行,同位角相等.23.【解析】试题分析:根据同位角、内错角、同旁内角的概念即可判断.⊥1与⊥4是同位角,⊥1与⊥3是对顶角,⊥3与⊥5是同旁内角,⊥3与⊥4是内错角.考点:本题考查的是同位角、内错角、同旁内角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.24.【解析】试题分析:根据同旁内角、内错角的特征即可判断.⊥1的同旁内角是⊥B、⊥C,⊥2的内错角是⊥C.考点:本题考查的是同位角、内错角、同旁内角的概念点评:准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线.25.【解析】试题分析:根据平行线的判定定理即可得到结果.若⊥2=⊥3,则AB⊥CD;若⊥1=⊥4,则AD⊥BC.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记内错角相等,两直线平行.26.【解析】试题分析:根据平行线的判定定理即可得到结果.若⊥1=⊥2,则DE⊥BC;若⊥3+⊥4=180°,则DE⊥BC.考点:本题考查的是平行线的判定点评:解答本题的关键是熟记同位角相等,两直线平行;同旁内角互补,两直线平行.27.【解析】试题分析:先求出⊥2的度数,再根据对顶角相等即可得到结果.,⊥1=65°,⊥⊥1+⊥2=90°,⊥⊥2=25°⊥⊥3=⊥2=25°.考点:本题考查的是对顶角点评:解答本题的关键是熟练掌握对顶角相等.28.【解析】试题分析:根据对顶角的定义及对顶角相等即可求得结果.⊥直线AB、CD相交于点O,⊥⊥1与⊥BOD是对顶角,⊥2与⊥AOD是对顶角,⊥⊥1=⊥BOD,⊥2=⊥AOD,理由是:对顶角相等.考点:本题考查的是对顶角点评:解答本题的关键是熟练掌握对顶角的定义:两条直线相交形成的没有公共边的一对角叫对顶角,同时熟记对顶角相等.29.【解析】试题分析:根据对顶角相等及平角的定义即可得到结果.,⊥3=55°,⊥4=125°.⊥⊥1=55°,⊥⊥2=125°考点:本题考查的是对顶角,平角的定义点评:解答本题的关键是熟练掌握对顶角相等,平角等于180°.30.【解析】试题分析:根据互余,互补的定义即可得到结果.若⊥A与⊥B互余,则⊥A+⊥B=90°;若⊥A与⊥B互补,则⊥A+⊥B=180°.考点:本题考查的是互余,互补点评:解答本题的关键是熟记和为90°的两个角互余,和为180°的两个角互补.31.【解析】试题分析:根据对顶角相等及平角的定义即可得到结果.由图可知⊥1+⊥2+⊥3=180°.考点:本题考查的是对顶角,平角的定义点评:解答本题的关键是熟练掌握对顶角相等,平角等于180°.32.【解析】试题分析:根据对顶角相等即可得到结果。
