2011湖北高考数学(理)word版、可编辑、高清无水印
2011全国一高考数学(理)word版、可编辑、高清无水印

2011年普通高等学校招生全国统一考试理科数学(必修+选修II)第Ⅰ卷第Ⅰ卷共l2小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题(1)复数1z i =+,z 为z 的共轭复数,则1zz z --= (A )2i - (B )i - (C )i (D )2i(2)函数2(0)y x x =≥的反函数为(A )2()4x y x R =∈ (B )2(0)4x y x =≥(C )24y x =()x R ∈ (D )24(0)y x x =≥(3)下面四个条件中,使a b >成立的充分而不必要的条件是 (A )1a b +> (B )1a b -> (C )22a b > (D )33a b >(4)设n S 为等差数列{}n a 的前n 项和,若11a =,公差2d =,224A n S S +-=,则k =(A )8 (B )7 (C )6 (D )5(5)设函数()cos (0)f x x ωω=>,将()y f x =的图像向右平移3π个单位长度后,所得的图像与原图像重合,则ω的最小值等于(A)13(B)3(C)6(D)9(6)已知直二面角α− ι−β,点A∈α,AC⊥ι,C为垂足,B∈β,BD⊥ι,D 为垂足.若AB=2,AC=BD=1,则D到平面ABC的距离等于(A)23(B)33(C)63(D) 1(7)某同学有同样的画册2本,同样的集邮册3本,从中取出4本赠送给4位朋友每位朋友1本,则不同的赠送方法共有(A)4种(B)10种(C)18种(D)20种(8)曲线y=2xe-+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为(A)13(B)12(C)23(D)1(9)设()f x是周期为2的奇函数,当0≤x≤1时,()f x=2(1)x x-,则5 ()2f-=(A) -12(B)14-(C)14(D)12(10)已知抛物线C:24y x=的焦点为F,直线24y x=-与C交于A,B两点.则cos AFB∠=(A)45 (B)35 (C)35- (D)45-(11)已知平面α截一球面得圆M ,过圆心M 且与α成060二面角的平面β截该球面得圆N.若该球面的半径为4,圆M 的面积为4π,则圆N 的面积为 (A)7π (B)9π (C)11π (D)13π(12)设向量a ,b ,c 满足a =b =1,a b =12-,,a c b c --=060,则c 的最大值等于(A)2 (B)3 (c)2 (D)1绝密★启用前2011年普通高等学校招生全国统一考试 理科数学(必修+选修II) 第Ⅱ卷 注意事项:1答题前,考生先在答题卡上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考 证号填写清楚,然后贴好条形码。
2011年湖北高考数学试题及答案(理科)
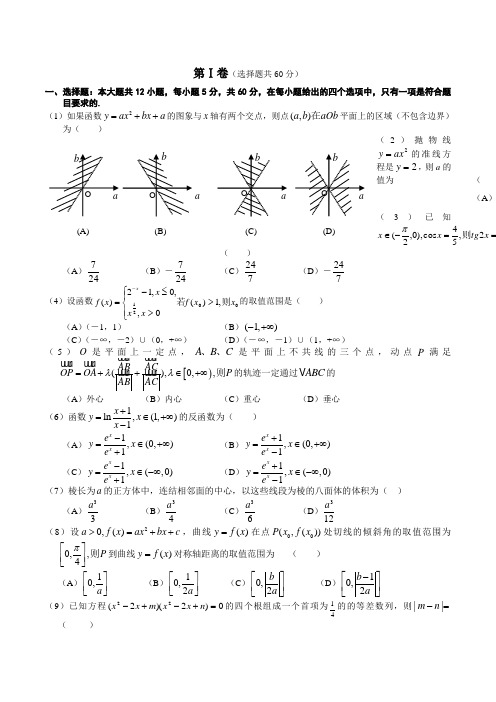
第Ⅰ卷(选择题共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)如果函数2y ax bx a =++的图象与x 轴有两个交点,则点(,)a b aOb 在平面上的区域(不包含边界)为( )(2)抛物线2ax y =的准线方程是2=y ,则a 的值为((A )(3)已知==-∈x tg x x 2,54cos ),0,2(则π( )(A )247 (B )-247 (C )724 (D )-724 (4)设函数0021,1)(0,,0,12)(x x f x x x x f x 则若>⎪⎩⎪⎨⎧>≤-=-的取值范围是( ) (A )(-1,1) (B )(1,)-+∞(C )(-∞,-2)∪(0,+∞) (D )(-∞,-1)∪(1,+∞)(5)O 是平面上一定点,A B C 、、是平面上不共线的三个点,动点P 满足[)(),0,,A B A CO P O A P A B A Cλλ=++∈+∞则的轨迹一定通过ABC 的 (A )外心(B )内心(C )重心(D )垂心(6)函数1ln,(1,)1x y x x +=∈+∞-的反函数为( ) (A )1,(0,)1x x e y x e -=∈+∞+ (B )1,(0,)1x xe y x e +=∈+∞- (C )1,(,0)1x x e y x e -=∈-∞+ (D )1,(,0)1x xe y x e +=∈-∞- (7)棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为( )(A )33a (B )34a (C )36a (D )312a(8)设20,()a f x ax bx c >=++,曲线()y f x =在点00(,())P x f x 处切线的倾斜角的取值范围为0,,4P π⎡⎤⎢⎥⎣⎦则到曲线()y f x =对称轴距离的取值范围为 ( ) (A )10,a ⎡⎤⎢⎥⎣⎦ (B )10,2a ⎡⎤⎢⎥⎣⎦ (C )0,2b a ⎡⎤⎢⎥⎣⎦ (D )10,2b a ⎡-⎤⎢⎥⎣⎦(9)已知方程0)2)(2(22=+-+-n x x m x x 的四个根组成一个首项为41的的等差数列,则=-||n m ( )aa a abbbbOOOO(A) (B) (C) (D)263451 (A )1 (B )43 (C )21 (D )83 (10)已知双曲线中心在原点且一个焦点为F (7,0),直线1-=x y 与其相交于M 、N 两点,MN 中点的横坐标为32-,则此双曲线的方程是 ( ) (A )14322=-y x (B )13422=-y x (C )12522=-y x (D )15222=-y x (11)已知长方形的四个顶点A (0,0),B (2,0),C (2,1)和D (0,1),一质点从AB 的中点0P 沿与AB 的夹角θ的方向射到BC 上的点1P 后,依次反射到CD 、DA 和AB 上的点2P 、3P 和4P (入射角等于反射角),设4P 的坐标为(4x ,0),若214<<x ,则tg θ的取值范围是 ( )(A )(31,1) (B )(31,32) (C )(52,21) (D )(52,32)(12)一个四面体的所有棱长都为2,四个顶点在同一球面上,则此球的表面积为( )(A )π3(B )4π(C )π33(D )π62003年普通高等学校招生全国统一考试(江苏卷)数 学(理工农医类)第Ⅱ卷(非选择题共90分)二.填空题:本大题共4小题,每小题4分,共16分把答案填在题中横线上(13)92)21(xx -的展开式中9x 系数是(14)某公司生产三种型号的轿车,产量分别为1200辆,6000辆和2000辆为检验该公司的产品质量,现用分层抽样的方法抽取46辆进行检验,这三种型号的轿车依次应抽取___________,__________,___________辆(15)某城市在中心广场建造一个花圃,花圃分为6个部分(如图)现要栽种4种不同颜色的花,每部分栽种一种且相邻部分不能栽种同样颜色的花,不同的栽种方法有___________________种(以数字作答)(16)对于四面体ABCD ,给出下列四个命题①,,AB AC BD CD BC AD ==⊥若则②,,AB CD AC BD BC AD ==⊥若则③,,AB AC BD CD BC AD ⊥⊥⊥若则④,,AB CD AC BD BC AD ⊥⊥⊥若则 其中真命题的序号是__________________.(写出所有真命题的序号)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或或演算步骤(17)(本小题满分12分)有三种产品,合格率分别为0.90,0.95和0.95,各抽取一件进行检验(Ⅰ)求恰有一件不合格的概率;(Ⅱ)求至少有两件不合格的概率(精确到0.001)(18)(本小题满分12分)已知函数()sin()(0,0)f x x R ωϕωϕπ=+>≤≤是上的偶函数,其图象关于点3(,0)4M π对称,且在区间0,2π⎡⎤⎢⎥⎣⎦上是单调函数求ωϕ和的值(19)(本小题满分12分)如图,在直三棱柱111C B A ABC -中,底面是等腰直角三角形,︒=∠90ACB ,侧棱21=AA ,D 、E 分别是1CC 与B A 1的中点,点E 在平面ABD 上的射影是△ABD 的重心G (Ⅰ)求B A 1与平面ABD 所成角的大小(结果用反三角函数值表示)(Ⅱ)求点1A 到平面AED 的距离E GD CBAC 1B 1A 1(20)(本小题满分12分)已知常数0,(0,),(1,0)a c a i >==向量经过原点O 以c i λ+ 为方向向量的直线与经过定点(0,)2A a i c λ-以为方向向量的直线相交于P ,其中R λ∈试问:是否存在两个定点E 、F ,使得PE PF+为定值若存在,求出E 、F 的坐标;若不存在,说明理由(21)(本小题满分12分)已知0,a n >为正整数(Ⅰ)设()n y x a =-,证明1'()n y n x a -=-;(Ⅱ)设()()nnn f x x x a =--,对任意n a ≥,证明1'(1)(1)'()n n f n n f n ++>+(22)(本小题满分14分)设0a >,如图,已知直线:l y ax =及曲线2:,C y x C =上的点1Q 的横坐标为11(0).(1)n a a a C Q n <<≥从上的点作直线平行于x 轴,交直线11n n l P P ++于点,再从点作直线平行于y 轴,交曲线1.(1,2,3,n n C Q Q n +=于点 …)的横坐标构成数列{}n a(Ⅰ)试求1n n a a +与的关系,并求{}n a 的通项公式; (Ⅱ)当111,2a a =≤时,证明1211()32n k k k k a a a ++=-<∑ (Ⅲ)当1a =时,证明1211()3nk k k k a a a ++=-<∑Oc ylxQ 1Q 2Q 3 1a 2a 3a r 2 r 12003年普通高等学校招生全国统一考试数 学 试 题(江苏卷)答案一、选择题:本题考查基本知识和基本运算,每小题5分,满分60分.1.C 2.B 3.D 4.D 5.B 6.B 7.C 8.B 9.C 10.D 11.C 12.A 二、填空题:本题考查基本知识和基本运算,每小题4分,满分16分. 13.221- 14.6,30,10 15.120 16.①④三、解答题17.本小题要主考查相互独立事件概率的计算,运用数学知识解决问题的能力,满分12分. 解:设三种产品各抽取一件,抽到合格产品的事件分别为A 、B 和C. (Ⅰ)95.0)()(,90.0)(===C P B P A P , .50.0)()(,10.0)(===C P B P A P因为事件A ,B ,C 相互独立,恰有一件不合格的概率为176.095.095.010.005.095.090.02)()()()()()()()()()()()(=⨯⨯+⨯⨯⨯=⋅⋅+⋅⋅+⋅⋅=⋅⋅+⋅⋅+⋅⋅C P B P A P C P B P A P C P B P A P C B A P C B A P C B A P 答:恰有一件不合格的概率为0.176. 解法一:至少有两件不合格的概率为)()()()(C B A P C B A P C B A P C B A P ⋅⋅+⋅⋅+⋅⋅+⋅⋅012.005.010.095.005.010.0205.090.022=⨯+⨯⨯⨯+⨯= 解法二:三件产品都合格的概率为812.095.090.0)()()()(2=⨯=⋅⋅=⋅⋅C P B P A P C B A P由(Ⅰ)知,恰有一件不合格的概率为0.176,所以至有两件不合格的概率为.012.0)176.0812.0(1]176.0)([1=+-=+⋅⋅-C B A P答:至少有两件不合的概率为0.012.(18)在小题主要考查三角函数的图象和单调性、奇偶性等基本知识,以及分析问题和推理计算能力,满12分分。
2011年湖北高考数学试题

(湖北卷)数学(理工类)一、选择题:1. i 为虚数单位,则201111i i +⎛⎫⎪-⎝⎭=A.- iB.-1C. iD.12.已知{}21|log ,1,|,2U y y x x P y y x x ⎧⎫==>==>⎨⎬⎩⎭,则U C P =A. 1[,)2+∞B. 10,2⎛⎫⎪⎝⎭C. ()0,+∞D. 1(,0][,)2-∞+∞3.已知函数11()3sin cos ,f x x R θθ--=-∈,若()1f x ≥,则x 的取值范围为A. |,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭B. |22,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭C. 5{|,}66x k x k k Z ππππ+≤≤+∈ D. 5{|22,}66x k x k k Z ππππ+≤≤+∈ 4.将两个顶点在抛物线22(0)y px p =>上,另一个顶点是此抛物线焦点的正三角形个数记为n ,则A. n=0B. n=1C. n=2D. n ≥35.已知随机变量ξ服从正态分布()22N ,a ,且P(ξ<4)=0.8,则P(0<ξ<2)= A.0.6 B.0.4 C.0.3 D.0.26.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()222f x g x a a -+=-+(a >0,且0a ≠).若()2g a =,则()2f =A .2 B.154 C. 174D. 2a 7.如图,用K 、1A 、2A 三类不同的元件连接成一个系统。
当K 正常工作且1A 、2A 至少有一个正常工作时,系统正常工作,已知K 、1A 、2A 正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为A .0.960 B.0.864 C.0.720 D.0.5768.已知向量a=(x+z,3),b=(2,y-z),且a ⊥ b.若x,y 满足不等式1x y +≤,则z 的取值范围为A..[-2,2]B.[-2,3]C.[-3,2]D.[-3,3]9.若实数a,b 满足0,0,a b ≥≥且0ab =,则称a 与b 互补,记,那么(),0a b ϕ=是a 与b 互补的A.必要而不充分的条件B.充分而不必要的条件C.充要条件D.即不充分也不必要的条件 10.放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变。
2011年高考数学试卷 湖北理

2011年普通高等学校招生全国统一考试湖北卷(理类)【选择题】【1】.i 为虚数单位,则2011i 1i 1⎪⎭⎫⎝⎛-+=( ).(A )-i (B )-1 (C )i (D )1 【2】.已知{}1,log |2>==x x y y U,⎭⎬⎫⎩⎨⎧>==2,1|x x y y P ,则U P =ð( ).(A)⎪⎭⎫⎢⎣⎡+∞,21 (B) ⎪⎭⎫ ⎝⎛21,0 (C) ()+∞,0 (D) (]⎪⎭⎫⎢⎣⎡+∞⋃∞-,210,【3】.已知函数()cos ,f x x x x =-∈R .若()1f x ≥,则x 的取值范围为( ).(A) π|π+π+π,3x k x k k ⎧⎫≤≤∈⎨⎬⎩⎭Z (B) π|2π+2π+π,3x k x k k ⎧⎫≤≤∈⎨⎬⎩⎭Z (C) π5π|π+π+,66x k x k k ⎧⎫≤≤∈⎨⎬⎩⎭Z (D) π5π|2π+2π+,66x k x k k ⎧⎫≤≤∈⎨⎬⎩⎭Z 【4】.将两个顶点在抛物线22(0)y px p =>上,另一个顶点是此抛物线焦点的正三角形个数记为n ,则( ).(A )n =0 (B )n =1 (C )n =2 (D )n ≥3【5】.已知随机变量ξ服从正态分布2(2,)N σ,且(4)0.8P ξ<=,则(02)P ξ<<=( ).(A)0.6 (B)0.4 (C)0.3 (D)0.2 【6】.已知定义在R上的奇函数()f x 和偶函数()g x 满足()()20,x x f x g x a a a a -+=-+>≠()且.若(2)g a =,则(2)f =( ).(A)2 (B)154 (C) 174(D) 2a 【7】.如图,用12,,K A A 三类不同的元件连接成一个系统.当K 正常工作且12,A A 至少有一个正常工作时,系统正常工作,已知12,,K A A 正常工作的概率依次是0.9,0.8,0.8,则系统正常工作的概率为( ).(A)0.960 (B)0.864 (C)0.720 (D)0.576【8】.已知向量(,3)x z =+a ,(2,)y z =-b ,且⊥a b .若x,y 满足不等式1x +y ≤,则z 的取值范围为( ). (A)[]2,2- (B) []2,3- (C) []3,2- (D) []3,3-【9】.若实数,a b 满足0,0a b ≥≥且0ab =,则称a 与b 互补,记(,)a b a b ϕ=-,那么(,)0a b ϕ=是a 与b 互补的( ).(A)必要而不充分的条件 (B)充分而不必要的条件 (C)充要条件 (D)既不充分也不必要的条件【10】.放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变.假设在放射性同位素铯137的衰变过程中,其含量M (单位:太贝克)与时间t (单位:年)满足函数关系:300()2tM t M -=,其中0M 为0t =时铯137的含量.已知30t =时,铯137含量的变化率是10ln 2-(太贝克/年),则(60)M =( ). (A) 5太贝克 (B) 75ln 2太贝克 (C) 150ln 2太贝克 (D) 150太贝克 【填空题】【11】.18x ⎛ ⎝的展开式中含15x 的项的系数为 .(结果用数值表示) 【12】.在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到1瓶已过保质期的概率为 .(结果用最简分数表示)【13】.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为 升.【14】.如图,直角坐标系xOy 所在平面为α,直角坐标系x Oy ''(其中y '轴与y 轴重合)所在的平面为β,45xOx '∠=.(Ⅰ)已知平面β内有一点P ',则点P '在平面α内的射影P 的坐标为 ;(Ⅱ)已知平面β内的曲线C '的方程是22(220x y ''+-=,则曲线C '在平面α内的射影C 的方程是 .【15】.给n 个自上而下相连的正方形着黑色或白色.当4n ≤时,在所有不同的着色方案中,黑色正方形互不相...邻.的着色方案如下图所示:由此推断,当6n =时,黑色正方形互不相...邻.的着色方案共有 种,至少有两个黑色正方形相.邻.的着色方案共有 种.(结果用数值表示) 【解答题】【16】.设ABC ∆的内角,,A B C 所对的边分别为,,a b c .已知11,2,cos 4a b C ===. (Ⅰ)求ABC ∆的周长; (Ⅱ)求cos()A C -的值.【17】.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当20200x ≤≤时,车流速度v 是车流密度x 的一次函数. (Ⅰ)当0200x ≤≤时,求函数()v x 的表达式;(Ⅱ)当车流密度x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)()()f x x v x =⋅可以达到最大,并求最大值.(精确到1辆/小时)【18】.如下图,已知正三棱柱111ABC A B C -的各棱长都是4,E 是BC 的中点,动点F 在侧棱1CC 上,且不与点C 重合.(Ⅰ)当1CF =时,求证:1EFAC ⊥;(Ⅱ)设二面角C AF E --的大小为θ,求tan θ的最小值. 【19】.已知数列{}n a 的前n项和为n S ,且满足:11(0),(,,1)n n a a a a rS n r r *+=≠=∈∈≠-N R .(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若存在k *∈N ,使得12,,k k k S S S ++成等差数列,试判断:对于任意的m *∈N ,且2m ≥,12,,m m m a a a ++是否成等差数列,并证明你的结论.【20】.平面内与两定点12(,0),(,0)(0)A a A a a ->连续的斜率之积等于非零常数m 的点的轨迹,加上12,A A 两点所成的曲线C 可以是圆、椭圆或双曲线. (Ⅰ)求曲线C 的方程,并讨论C 的形状与m 值的关系;(Ⅱ)当1m =-时,对应的曲线为1C ;对给定的(1,0)(0,)m ∈-⋃+∞,对应的曲线为2C .设12,F F 是2C 的两个焦点.试问:在1C 上,是否存在点N ,使得△12F NF 的面积2S m a =.若存在,求12tan F NF ∠的值;若不存在,请说明理由.【21】.(Ⅰ)已知函数()ln 1,(0,)f x x x x =-+∈+∞,求函数()f x 的最大值; (Ⅱ)设,(1,2,k k a b k=…)n 均为正数,证明:(1)若1122a b a b ++…+12n n a b b b ≤++…+n b ,则1212b b a a …1n b n a ≤;(2)若12b b ++…1n b +=,则12121b b b b n≤…2212n b n b b b ≤++…+2n b .。
2011年高考数学湖北卷(理科)-带答案

2011年高考数学湖北卷(理科)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是满足题目要求的。
1.i 为虚数单位,则201111i i +⎛⎫= ⎪-⎝⎭( )(A) -1 (B) -i (C) 1 (D) i 2. 已知{}21log ,1,,2U y y x x P y y x x ⎧⎫==>==>⎨⎬⎩⎭,则U P =ð( ) (A)(]1,0,2⎡⎫-∞+∞⎪⎢⎣⎭ (B) 10,2⎛⎫⎪⎝⎭ (C) ()0,+∞ (D) 1,2⎡⎫+∞⎪⎢⎣⎭3.已知函数()3sin cos ,f x x x x R =-∈,若()1f x ≥,则x 的取值范围为( ) (A) 22,3P x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭(B) 522,66P x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭(C),3P x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭(D) 5,66P x k x k k Z ππππ⎧⎫=+≤≤+∈⎨⎬⎩⎭4.将两个顶点在抛物线22y px =()0p >上,另一个顶点是抛物线焦点的正三角形个数记为n ,则( )(A)0n = (B) 1n = (C) 2n = (D) 3n ≥ 5.已知随机变量ξ服从正态分布()22,N σ,且()40.8P ξ<=,则()02P ξ<<=( )(A) 0.2 (B) 0.3 (C) 0.4 (D) 0.6 6.已知定义在R上的奇函数()f x 和偶函数()g x 满足()()()20,1x x f x g x a a a a -+=-+>≠且,若()2g a =,则()2f =( ) (A)2a (B) 2 (C)154 (D) 1747.如图,用K 、12A A 、三类不同的原件连接成一个系统,当K 正常工作且12A A 、至少有一个正常工作时,系统正常工作,已知K 、12A A 、正常工作的概率依次为0.9、0.8、0.8,则系统正常工作的概率为( )(A)0.960 (B) 0.864 (C) 0.720 (D) 0.5768.已知向量()(),3,2,a x z b y z a b =+=-⊥,且,若x ,y 满足不等式1x y +≤,则z的取值范围为:(A) []3,3- (B)[]3,2- (C)[]2,2- (D) []2,3- 9.若实数a ,b 满足0,0,0a b ab ≥≥=且,则称a 与b 互补,记()22,a b a b a b ϕ=+--,那么(),0a b ϕ=是a 与b 互补的(A)充分而不必要条件 (B)必要而不充分条件(C) 充要条件 (D)既不充分也不必要条件10.放射性元素由于不断有原子放射出微粒子而变成其它元素,其含量不断减少,这种现象称为衰变。
2011湖北高考数学试题及答案(理科)

试卷类型:A2010年普通咼等学校招生全国统一考试(湖北卷)数学(理工类)本试卷共4页,三大题21小题,全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1 •答卷前,考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡 上。
并将准考证号条形码横贴在答题卡的指定位置。
在用 2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2 •选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目选项 的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答在试 题卷、草稿纸上无效。
3. 填空题和解答题的作答:用0.5毫米黑色签字笔直接在答题卡上对应的答 题区域内。
答在试题卷、草稿纸上无效。
4. 考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选 项中,只有一项是符合题目要求的。
A.- iB.-1C. iD.12.已知 U = : y | y = log 2 x, x 1,P= y|y= —, x 2 ,则C U P = L x J3.已知函数f (x )z ;3s in r-cosf,x ・R ,若f (x )_1,则x 的取值范围为{ Tl l JI lA. x|k 二 _x _k 「?,k ZB. x 12 k 二 _ x _ 2k 二:k ZI3J I 3Ji5 ii5 iC. {x|kx_k ,k = Z} D. {x|2k x_2k ,k ^ Z}6 6 6 61. i 为虚数单位,贝U(-二 A.[丄,::) B.2 C. 0, ::D.1 ,0][^^::)11-14.将两个顶点在抛物线y2=2px(p . 0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则A. n=0B. n=1C. n=2D. n _3试卷类型:A5 •已知随机变量■服从正态分布N 2, a2,且P( <4)= 0.8,则P( 0 V < 2)=A .0.6 B.0.4 C.0.3 D.0.26. 已知定义在R上的奇函数fx和偶函数g x满足f xg x =a2 - a22( a >0,且a = 0).若g 2 = a,则f 2 =A. 2B. 15C. 17D. a24 47. 如图,用K、A“ A2三类不同的元件连接成一个系统。
2011年湖北高考数学试题及答案(理科)

一、第一天:指定时间地点集合.乘火车赴广州开始轻松愉快的香港.澳门之旅不含餐.住火车上第二天:早上抵达广州,汽车赴深圳:团友在领队的带领下从皇岗进入香港,前往维多利亚两岸游览:参观会展中心,金紫荆广场(游览30分钟)。
赴香港海洋公园(游览3小时),后乘室外观光电梯前往大树湾参观古建筑群“集古村”等,前往香港的风水宝地----浅水湾,祈求正财神保佑,游览完毕后乘车登太平山,俯瞰“东方之珠”---香港的美丽夜景,乘船游览维多利亚港观两岸夜景(游览约45分钟);在此可近距离观赏九龙及香港岛幻美的灯光.(含中晚餐)住:香港第三天:早餐后,游览香港神庙----黄大仙庙(游览30分钟),随后参观珠宝展示中心(90分钟)、百货商场(90分钟),欣赏不同款式的珠宝钻石的制作过程,更可随心购买心爱的首饰及纪念品,参观香港的免税商店,体验香港购物天堂的乐趣,后参观尖沙咀落成在海滨长廊上的“星光大道”,以香港电影业发展史及旨在表扬幕前巨星和幕后电影工作者成就为主题的星光大道设于尖沙咀海滨长廊。
后前往国际著名DFS免税店。
香港市区酒楼用晚餐;(含早中晚餐)住:香港第四天:早餐后,前往码头乘船前往澳门(乘船约50分钟),游览澳门标志性建筑物圣保罗教堂遗迹大三巴牌坊、异国情调的澳督府,参观澳门起源及最古老庙宇妈祖庙,后车游望海观音,澳门大桥,观澳门九九回归广场标志莲花台,珠宝店,手信店,可自费前往著名的威尼斯人度假酒店游览观光(门票160元/人自理,)晚上10:30分经拱北关口抵珠海;(含早中晚餐)住:珠海第五天:早餐后,外观九州城,百货店(45分钟),珠宝店(60分钟)游情侣路(车游),珠海标志----渔女像(车游),中餐后乘车返回广州,晚上乘火车返程。
(含早中餐)住火车上第六天:上午抵达,结束愉快的行程回到温暧的家。
二、接待标准1、交通:,株州至广州往返为非空调硬卧,景区间空调旅游汽车,香港至澳门海上飞船2、住宿、珠海,二星酒店,香港三星酒店双标间(有彩电、空调、独卫;产生单男单女的情况下,由我社安排三人间,如果客人不愿意住三人间,则由客人自行补足房差)3、用餐:全程含3早7正(内地段正餐10人一桌,8菜1汤;港澳段正餐10人一桌,7菜1汤,均不含酒水。
2011年高考湖北省数学试卷-理科(含详细答案)

试卷类型:A2011年普通高等学校招生全国统一考试(湖北卷)数 学(理工农医类解析)本试题卷共4页,三大题21小题。
全卷满分150分。
考试用时120分钟。
注意事项:1答题前,考生务必将自己的姓名、准考证号填写在试题卷和答题卡上.并将准考证 号条形码粘贴在答题卡上的指定位置,用2B 铅笔将答题卡上试卷类型B 后的方框涂黑。
2选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
咎在试题卷、草稿纸上无效。
3填空题和解答题用0.5毫米黑色墨水箍字笔将答案直接答在答题卡上对应的答题区 域内。
答在试题卷、草稿纸上无效。
4考生必须保持答题卡的整洁。
考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只 有一项是满足题目要求的.1.i 为虚数单位,则=⎪⎭⎫⎝⎛-+201111i iA.i -B.1-C.iD.1【答案】A解析:因为()i i i i i =-+=-+221111,所以i i i i i i -====⎪⎭⎫⎝⎛-++⨯3350242011201111,故选A .2.已知{}1,log 2>==x x y y U ,⎭⎬⎫⎩⎨⎧>==2,1x x y y P ,则=P C U A. ⎪⎭⎫⎢⎣⎡+∞,21 B.⎪⎭⎫⎝⎛21,0 C.()+∞,0 D. ()⎪⎭⎫⎢⎣⎡+∞∞-,210,【答案】A解析:由已知()+∞=,0U .⎪⎭⎫ ⎝⎛=21,0P ,所以⎪⎭⎫⎢⎣⎡+∞=,21P C U ,故选A .3.已知函数()x x x f cos sin 3-=,R x ∈,若()1≥x f ,则x 的取值范围为A. ⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k x k x ,3ππππ B . ⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k x k x ,232ππππC. ⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k x k x ,656ππππ D. ⎭⎬⎫⎩⎨⎧∈+≤≤+Z k k x k x ,65262ππππ 【答案】B解析:由条件1cos sin 3≥-x x 得216sin ≥⎪⎭⎫⎝⎛-πx ,则 652662πππππ+≤-≤+k x k ,解得ππππ+≤≤+k x k 232,Z k ∈,所以选B . 4.将两个顶点在抛物线()022>=p px y 上,另一个顶点是此抛物线焦点的正三角形的个数记为n ,则A. 0=n B . 1=n C. 2=n D. 3≥n 【答案】C解析:根据抛物线的对称性,正三角形的两个 顶点一定关于x 轴对称,且过焦点的两条直线 倾斜角分别为030和0150,这时过焦点的直线 与抛物线最多只有两个交点,如图所以正三角形 的个数记为n ,2=n ,所以选C.5.已知随机变量ξ服从正态分布()2,2σN ,且()8.04=<ξP ,则()=<<20ξPA. 6.0 B . 4.0 C. 3.0 D. 2.0 【答案】C 解析:如图,正态分布的密度函数示意图所示,函数关于 直线2=x 对称,所以()5.02=<ξP ,并且()()4220<<=<<ξξP P则()()()2420<-<=<<ξξξP P P3.05.08.0=-=所以选C.6.已知定义在R 上的奇函数()x f 和偶函数()x g 满足()()2+-=+-xxaa x g x f()1,0≠>a a 且,若()a g =2,则()=2fA. 2 B . 415 C. 417 D. 2a 【答案】B解析:由条件()()22222+-=+-aa g f ,()()22222+-=-+--a a g f ,即()()22222+-=+--a a g f ,由此解得()22=g ,()222--=a a f ,所以2=a ,()41522222=-=-f ,所以选B . 7.如图,用21A A K 、、三类不同的元件连接成一个系统,K 正常工作且21A A 、至少有一个正常工作时,系统正常工作.已知21A A K 、、正常工作的概率依次为9.0、8.0、8.0,则系统正常工作的概率为A. 960.0 B . 864.0 C. 720.0 D. 576.0 【答案】B解析:21A A 、至少有一个正常工作的概率为()()211A P A P -()()94.004.018.018.011=-=-⨯--=,系统正常工作概率为()()()()864.096.09.0121=⨯=-A P A P K P ,所以选B .8.已知向量a ()3,z x +=,b ()z y -=,2,且a ⊥b .若y x ,满足不等式1≤+y x ,则z 的取值范围为A. []2,2- B . []3,2- C. []2,3- D. []3,3- 【答案】D解析:因为a ⊥b ,()()032=-++z y z x , 则y x z 32+=,y x ,满足不等式1≤+y x ,则点()y x ,的可行域如图所示,当y x z 32+=经过点()1,0A 时,y x z 32+=当y x z 32+=经过点()1,0-C 时,y x z 32+=取得最小值-3 所以选D .9.若实数b a ,满足0,0≥≥b a ,且0=ab ,则称a 与b 互补,记()b a b a b a --+=22,ϕ,那么()0,=b a ϕ是a 与b 互补A . 必要而不充分条件B . 充分而不必要条件C. 充要条件D. 既不充分也不必要的条件 【答案】C解析:若实数b a ,满足0,0≥≥b a ,且0=ab ,则a 与b 至少有一个为0,不妨设0=b ,则K A 1A 2()0,2=-=-=a a a a b a ϕ;反之,若()0,22=--+=b a b a b a ϕ,022≥+=+b a b a两边平方得ab b a b a 22222++=+0=⇔ab ,则a 与b 互补,故选C.10.放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯137的衰变过程中,其含量M (单位:太贝克)与时间t (单位:年)满足函数关系:()3002t M t M -=,其中0M 为0=t 时铯137的含量,已知30=t 时,铯137的含量的变化率...是2ln 10-(太贝克/年),则()=60M A . 5太贝克 B . 2ln 75太贝克 C . 2ln 150太贝克 D . 150太贝克 【答案】D解析:因为()300/22ln 301tM t M -⨯-=,则()2ln 1022ln 3013030300/-=⨯-=-M M ,解得6000=M ,所以()302600tt M -⨯=,那么()150416002600603060=⨯=⨯=-M (太贝克),所以选D .二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上,一题两空的题,其答案按先后次序填写.答错位置,书写不清,模棱两可均不得分11.在1831⎪⎪⎭⎫ ⎝⎛-x x 展开式中含15x 的项的系数为 .(结果用数值表示)【答案】17【解析】二项式展开式的通项公式为rr r r x x C T ⎪⎪⎭⎫ ⎝⎛-=-+3118181rr r r x C ⎪⎭⎫ ⎝⎛-=--31211818,令2152118=⇒=--r r r ,含15x 的项的系数为17312218=⎪⎭⎫ ⎝⎛-C ,故填17.12.在30瓶饮料中,有3瓶已过了保质期.从这30瓶饮料中任取2瓶,则至少取到1瓶已过了保质期饮料的概率为 .(结果用最简分数表示) 【答案】14528 解析:从这30瓶饮料中任取2瓶,设至少取到1瓶已过了保质期饮料为事件A ,从这30瓶饮料中任取2瓶,没有取到1瓶已过了保质期饮料为事件B ,则A 与B 是对立事件,因为()291513272302527⨯⨯==C C B P ,所以()()145282915132711=⨯⨯-=-=B P A P ,所以填14528. 12.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为 升. 【答案】6667解析:设该数列{}n a 的首项为1a ,公差为d ,依题意⎩⎨⎧=++=+++439874321a a a a a a a ,即⎩⎨⎧=+=+421336411d a d a ,解得⎪⎪⎩⎪⎪⎨⎧==+6673471d d a , 则d d a d a a 374115-+=+=6667662134=-=,所以应该填6667. 14.如图,直角坐标系xOy 所在的平面为α,直角坐标系//Oy x (其中/y 轴与y 轴重合)所在的平面为β,0/45=∠xOx .(Ⅰ)已知平面β内有一点()2,22/P ,则点/P 在平面α内的射影P 的坐标为 ; (Ⅱ)已知平面β内的曲线/C 的方程是()02222/2/=-+-y x,则曲线/C 在平面α内的射影C 的方程是 .【答案】()2,2,()1122=+-y x解析:(Ⅰ)设点/P 在平面α内的射影P 的坐标为()y x ,,则点P 的纵坐标和()2,22/P 纵坐标相同,所以2=y ,过点/P 作Oy H P ⊥/,垂足为H ,连结PH ,则0/45=∠HP P ,P 横坐标0/45cos H P PH x ==2222245cos 0/=⨯==x , 所以点/P 在平面α内的射影P 的坐标为()2,2;(Ⅱ)由(Ⅰ)得2245cos //⨯==x x x ,y y =/,所以⎪⎩⎪⎨⎧==yy x x //2代入曲线/C 的方程()02222/2/=-+-y x,得()⇒=-+-0222222y x ()1122=+-y x ,所以射影C 的方程填()1122=+-y x .15.给n 个则上而下相连的正方形着黑色或白色.当4≤n 时,在所有不同的着色方案中,黑色正方形互不相邻....的着色方案如下图所示:由此推断,当6=n 时,黑色正方形互不相邻....着色方案共有 种,至少有两个黑色正方形相邻..着色方案共有 种.(结果用数值表示) 【答案】43,21解析:设n 个正方形时黑色正方形互不相邻....的着色方案数为n a ,由图可知, 21=a ,32=a , 213325a a a +=+==, 324538a a a +=+==,由此推断1365435=+=+=a a a ,21138546=+=+=a a a ,故黑色正方形互不相邻....着色方案共有21种;由于给6个正方形着黑色或白色,每一个小正方形有2种方法,所以一共有6422222226==⨯⨯⨯⨯⨯种方法,由于黑色正方形互不相邻....着色方案共有21种,所以至少有两个黑色正方形相邻..着色方案共有432164=-种着色方案,故分别填43,21. 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分10分) 设ABC ∆的内角C B A 、、所对的边分别为c b a 、、.已知1=a ,2=b ,41cos =C . (Ⅰ)求ABC ∆的周长; (Ⅱ)求()C A -cos 的值.本小题主要考查三角函数的基本公式和解斜三角形的基础知识,同时考查基本运算能力 解析:(Ⅰ)∵441441cos 2222=⨯-+=-+=C ab b a c ∴2=cn=1 n=2n=3n=4∴ABC ∆的周长为5221=++=++c b a .(Ⅱ)∵41cos =C ,∴415411cos 1sin 22=⎪⎭⎫ ⎝⎛-=-=C C ,∴8152415sin sin ===cCa A ∵c a <,∴C A <,故A 为锐角,∴878151sin 1cos 22=⎪⎪⎭⎫ ⎝⎛-=-=A A ∴()C A -cos C A C A sin sin cos cos +=16114158154187=⨯+⨯=. 17.(本小题满分12分)提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v (单位:千米/小时)是车流密度x (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当20020≤≤x 时,车流速度v 是车流密度x 的一次函数. (Ⅰ)当2000≤≤x 时,求函数()x v 的表达式;(Ⅱ)当车流密度x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)()()x v x x f ⋅=可以达到最大,并求出最大值.(精确到1辆/小时)本题主要考查函数、最值等基础知识,同时考查运用数学知识解决实际问题的能力.解析:(Ⅰ)由题意:当200≤≤x 时,()60=x v ;当20020≤≤x 时,设()b ax x v +=,显然()b ax x v +=在[]200,20是减函数,由已知得⎩⎨⎧=+=+60200200b a b a ,解得⎪⎪⎩⎪⎪⎨⎧=-=320031b a故函数()x v 的表达式为()x v =()⎪⎩⎪⎨⎧≤≤-<≤.20020,20031,200,60x x x(Ⅱ)依题意并由(Ⅰ)可得()=x f ()⎪⎩⎪⎨⎧≤≤-<≤.20020,20031,200,60x x x x x当200≤≤x 时,()x f 为增函数,故当20=x 时,其最大值为12002060=⨯;当20020≤≤x 时,()()()310000220031200312=⎥⎦⎤⎢⎣⎡-+≤-=x x x x x f , 当且仅当x x -=200,即100=x 时,等号成立.所以,当100=x 时,()x f 在区间[]200,20上取得最大值310000. 综上,当100=x 时,()x f 在区间[]200,0上取得最大值3333310000≈,即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时. 18.(本小题满分12分)如图,已知正三棱柱111C B A ABC -的各棱长都是4,E 是BC 的中点,动点F 在侧棱1CC 上,且不与点C 重合.(Ⅰ)当1=CF 时,求证C A EF 1⊥;(Ⅱ)设二面角E AF C --的大小为θ,θtan 的最小值. 本题主要考查空间直线与平面的位置关系和二面角等基础 知识,同时考查空间想象能力、推理论证能力和运算求解 能力. 解析:ABCEA 1C 1B 119.(本小题满分13分)已知数列{}n a 的前n 项和为n S ,且满足:1a a =(0)a ≠,n n rS a =+1 (n ∈N *,,1)r R r ∈≠-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若存在k ∈ N *,使得1+k S ,k S ,2+k S 成等差数列,试判断:对于任意的m ∈N *,且2m ≥,1+m a ,m a ,2+m a 是否成等差数列,并证明你的结论.20. (本小题满分14分)平面内与两定点1(,0)A a -,2(,0)A a (0)a >连续的斜率之积等于非零常数m 的点的轨迹,加上1A 、2A 两点所成的曲线C 可以是圆、椭圆或双曲线. (Ⅰ)求曲线C 的方程,并讨论C 的形状与m 值得关系;(Ⅱ)当1m =-时,对应的曲线为1C ;对给定的(1,0)(0,)m U ∈-+∞,对应的曲线为2C ,设1F 、2F 是2C 的两个焦点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试卷类型:A
2010年普通高等学校招生全国统一考试(湖北卷)
数学(理工类)
本试卷共4页,三大题21小题,全卷满分150分。
考试用时120分钟。
★祝考试顺利★
注意事项:
1.答卷前,考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡上。
并将准考证号条形码横贴在答题卡的指定位置。
在用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答在试题卷、草稿纸上无效。
3.填空题和解答题的作答:用0.5毫米黑色签字笔直接在答题卡上对应的答题区域内。
答在试题卷、草稿纸上无效。
4.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. i 为虚数单位,则2011
11i i +⎛⎫
⎪
-⎝⎭
=
A.- i
B.-1
C. i
D.1
2.已知{}21|log ,1,|,2U y y x x P y y x x ⎧⎫
==>==>⎨⎬⎩⎭
,则U C P =
A. 1
[,)2+∞ B.
10,2⎛⎫
⎪⎝⎭
C. ()0,+∞
D. 1
(,0][,)2
-∞+∞
3.已知函数11()cos ,f x x R θθ---∈,若()1f x ≥,则x 的取值范围为
A. |,3x k x k k Z ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭
B. |22,3x k x k k Z ππππ⎧⎫
+≤≤+∈⎨⎬⎩⎭
C. 5{|,}6
6x k x k k Z π
πππ+
≤≤+
∈ D. 5{|22,}66
x k x k k Z ππ
ππ+≤≤+∈
4.将两个顶点在抛物线22(0)y px p =>上,另一个顶点是此抛物线焦点的正三角形个数记为n ,则
A. n=0
B. n=1
C. n=2
D. n ≥3
试卷类型:A
5.已知随机变量ξ服从正态分布()22N ,a ,且P(ξ<4)=0.8,则P(0<ξ<2)=
A.0.6 B.0.4 C.0.3 D.0.2
6.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()222f x g x a a -+=-+(a >0,且0a ≠).若()2g a =,则()2f =
A .2 B.
154 C. 17
4
D. 2a 7.如图,用K 、1A 、2A 三类不同的元件连接成一个系统。
当K 正常工作且1A 、2A 至少有一个正常工作时,系统正常工作,已知K 、1A 、2A 正常工作的概率依次是0.9、0.8、0.8,则系统正常工作的概率为
A .0.960 B.0.864 C.0.720 D.0.576
8.已知向量a=(x+z,3),b=(2,y-z),且a ⊥ b.若x,y 满足不等式1x y +≤,则z 的取值范围为
A..[-2,2]
B.[-2,3]
C.[-3,2]
D.[-3,3] 9.若实数a,b 满足0,0,a b ≥≥且0ab =,则称a 与b 互补,记,
那么(),0a b ϕ=是a 与b 互补的
A.必要而不充分的条件
B.充分而不必要的条件
C.充要条件
D.即不充分也不必要的条件
10.放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,
这种现象称为衰变。
假设在放射性同位素铯137的衰变过程中,其含量M (单位:太贝克)与时间t (单位:年)满足函数关系:30
0()2
t M t M -=,其中M 0为t=0时铯137的含
量。
已知t=30时,铯137含量的变化率是-10In2(太贝克/年),则M (60)=
A.5太贝克
B.75In2太贝克
C.150In2太贝克
D.150太贝克
二、填空题:本大题共5小题,每小题5分,共25分。
请将答案填在答题卡对应题号的位置上,一题两空的题,其中答案按先后次序填写。
答错位置,书写不清,模棱俩可均不给分。
11. 18
x ⎛- ⎝
的展开式中含15
x 的项的系数为
12.在30瓶饮料中,有3瓶已过了保质期。
从这30瓶饮料中任取2瓶,则至少取到一瓶已过保质期的概率为 。
(结果用最简分数表示)
13.《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共为3升,下面3节的容积共4升,则第5节的容积为 升。
试卷类型A
14.如图,直角坐标系xOy 所在平面为α,直角坐标系''x Oy (其中'y 与y 轴重合)所在的平面为β,'45xOx ∠=︒。
(Ⅰ)已知平面β内有一点'P ,则点'P 在平面α内的射影P 的坐标为 ;
(Ⅱ)已知平面β内的曲线'C 的方程是'2'2(220x y +-=,则曲线'C 在平面α内的射影C 的方程是 。
15. 给n 个自上而下相连的正方形着黑色或白色。
当4n ≤时,在所有不同的着色方案中,黑色正方形互不相连....
的着色方案如下图所示:
由此推断,当6n =时,黑色正方形互不相连....的着色方案共有 种,至少有两个黑色正方形相连..
的着色方案共有 种,(结果用数值表示) 三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分10分)
设ABC 的内角..A B C 所对的边分别为..a b c ,已知11. 2.cos .4
a b C ===
(Ⅰ)求ABC 的周长 (Ⅱ)求()cos A C -的值 17. (本小题满分12分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况。
在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流速度x 的函数。
当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当20200x ≤≤时,车流速度v 是车流密度x 的一次函数. (Ⅰ)当0200x ≤≤时,求函数()v x 的表达式;
(Ⅱ)当车流密度x 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)()().f x x v x =可以达到最大,并求最大值(精确到1辆/每小时)
18. (本小题满分12分)
如图,已知正三棱柱111ABC A B C -的各棱长都是4,E 是BC 的中点,动点F 在侧棱1CC 上,且不与点C 重合.
(Ⅰ)当CF =1时,求证:EF ⊥1A C ;
(Ⅱ)设二面角C AF E --的大小为θ,求tan θ的最小值.
19.(本小题满分13分)
已知数列{}n a 的前n 项和为n S ,且满足:1a a =(0)a ≠,1n n a rS += (n ∈N *,,1)r R r ∈≠-. (Ⅰ)求数列{}n a 的通项公式;
(Ⅱ)若存在k ∈ N *,使得1k S +,k S ,2k S +成等差数列,是判断:对于任意的m ∈N *,且2m ≥,1m a +,m a ,2m a +是否成等差数列,并证明你的结论. 20. (本小题满分14分)
平面内与两定点1(,0)A a -,2(,0)A a (0)a >连续的斜率之积等于非零常数m 的点的轨迹,加上1A 、2A 两点所成的曲线C 可以是圆、椭圆成双曲线. (Ⅰ)求曲线C 的方程,并讨论C 的形状与m 值得关系;
(Ⅱ)当1m =-时,对应的曲线为1C ;对给定的(1,0)(0,)m U ∈-+∞,对应的曲线为2C ,设1F 、2F 是2C 的两个焦点。
试问:在1C 撒谎个,是否存在点N ,使得△1F N 2F 的面积2||S m a =。
若存在,求tan 1F N 2F 的值;若不存在,请说明理由。
21.(本小题满分14分)
(Ⅰ)已知函数()1f x Inx x =-+,(0,)x ∈+∞,求函数()f x 的最大值; (Ⅱ)设11,a b (1,2k =…,)n 均为正数,证明:
(1)若1122a b a b ++…n n a b ≤12b b ++…n b ,则`1
1b a 2
2b a …n
b n a 1≤; (2)若12b b ++…n b =1,则
1
n
≤11a b 22a b …n a n b ≤21b +22b …2n b 。
