山西省2014届高三高考考前质量监测数学理试题(WORD版)
2014年高考真题——理科数学(全国大纲卷)解析版 Word版含解析

第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1.设103i z i=+,则z 的共轭复数为 ( )A .13i -+B .13i --C .13i +D .13i -2.设集合2{|340}M x x x =--<,{|05}N x x =≤≤,则M N =I ( )A .(0,4]B .[0,4)C .[1,0)-D .(1,0]-3.设sin 33,cos55,tan 35,a b c =︒=︒=︒则 ( )A .a b c >>B .b c a >>C .c b a >>D .c a b >>4.若向量,a b r r 满足:()()1,,2,a a b a a b b =+⊥+⊥r r r r r r r 则b =r ( )A .2B .2C .1D .225.有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )A .60种B .70种C .75种D .150种6.已知椭圆C :22221x y a b +=(0)a b >>的左、右焦点为1F 、2F 3,过2F 的直线l 交C 于A 、B 两点,若1AF B ∆的周长为43C 的方程为 ( )A .22132x y +=B .2213x y +=C .221128x y +=D .221124x y +=7.曲线1x y xe-=在点(1, 1)处切线的斜率等于( ) A .2e B .e C .2 D .18.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )A .814πB .16πC .9πD .274π 【答案】A .【解析】考点:1.球的内接正四棱锥问题;2. 球的表面积的计算.9.已知双曲线C 的离心率为2,焦点为1F 、2F ,点A 在C 上,若122F A F A =,则21cos AF F ∠=( )A .14B .13C .24D .23 10.等比数列{}n a 中,452,5a a ==,则数列{lg }n a 的前8项和等于 ( )图2A .6B .5C .4D .311.已知二面角l αβ--为60︒,AB α⊂,AB l ⊥,A 为垂足,CD β⊂,C l ∈,135ACD ∠=︒,则异面直线AB 与CD 所成角的余弦值为 ( )A .14B 2C 3D .12【答案】B.【解析】12.函数()y f x =的图象与函数()y g x =的图象关于直线0x y +=对称,则()y f x =的反函数是( )A .()y g x =B .()y g x =-C .()y g x =-D .()y g x =--第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 8y x 的展开式中22x y 的系数为 . 【答案】70.14.设,x y 满足约束条件02321x y x y x y -≥⎧⎪+≤⎨⎪-≤⎩,则4z x y =+的最大值为.15.直线1l 和2l 是圆222x y +=的两条切线,若1l 与2l 的交点为()1,3,则1l 与2l 的夹角的正切值等于 .2l的夹角的正切值:12124 tan13k kk kθ-==+.考点:1.直线与圆的位置关系(相切);2.两直线的夹角公式.16.若函数()cos2sinf x x a x=+在区间(,)62ππ是减函数,则a的取值范围是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)ABC∆的内角A,B,C的对边分别为a,b,c,已知3cos2cosa C c A=,1tan3A=,求B.18. (本小题满分12分)等差数列{}na的前n项和为nS,已知110a=,2a为整数,且4nS S≤.(I )求{}n a 的通项公式; (II )设11n n n b a a +=,求数列{}n b 的前n 项和n T . 19. (本小题满分12分) 如图,三棱柱111ABC A B C -中,点1A 在平面ABC 内的射影D 在AC 上,090ACB ∠=,11,2BC AC CC ===. (I )证明:11AC A B ⊥; (II )设直线1AA 与平面11BCC B 31A AB C --的大小.20. (本小题满分12分)设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为0.6,0.5,0.5,0.4,各人是否需使用设备相互独立.(I)求同一工作日至少3人需使用设备的概率;(II)X表示同一工作日需使用设备的人数,求X的数学期望.21.(本小题满分12分)已知抛物线C :22(0)y px p =>的焦点为F ,直线4y =与y 轴的交点为P ,与C 的交点为Q ,且5||||4QF PQ =. (I )求C 的方程;(II )过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l '与C 相较于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【答案】(I )24y x =;(II )直线l 的方程为10x y --=或10x y +-=.22. (本小题满分12分)函数()()()ln 11ax f x x a x a=+->+. (I )讨论()f x 的单调性;(II )设111,ln(1)n n a a a +==+,证明:23+22n a n n <≤+. 【答案】(I )(i )当12a <<时,()f x 在()21,2a a --上是增函数,在()22,0a a -上是减函数,在()0,+∞上是增函数;(ii )当2a =时,()f x 在()1,-+?上是增函数;(iii )当2a >时,()f x 在是()1,0-上是增函数,在()20,2a a -上是减函数,在()22,a a -+∞上是增函数;(II)详见试题分析.1n k=+时有2333kak k<?++,结论成立.根据(i)、(ii)知对任何n N*Î结论都成立.考点:1.利用导数研究函数的单调性;2.利用数学归纳法证明数列不等式.。
山西省运城市2014~2015学年第一学期期末高三调研测试理科数学试题
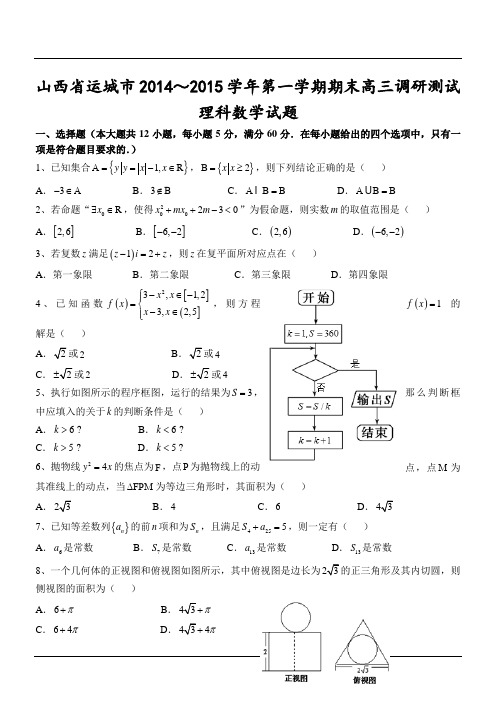
山西省运城市2014~2015学年第一学期期末高三调研测试理科数学试题一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}1,R y y x x A ==-∈,{}2x x B =≥,则下列结论正确的是( ) A .3-∈A B .3∉B C .A B =B D .A B =B2、若命题“0R x ∃∈,使得200230x mx m ++-<”为假命题,则实数m 的取值范围是( )A .[]2,6B .[]6,2--C .()2,6D .()6,2-- 3、若复数z 满足()12z i z -=+,则z 在复平面所对应点在( ) A .第一象限 B .第二象限 C .第三象限D .第四象限4、已知函数()[](]23,1,23,2,5x x f x x x ⎧-∈-⎪=⎨-∈⎪⎩,则方程()1f x =的解是( )A2 B或4 C.或2 D.或4 5、执行如图所示的程序框图,运行的结果为3S =,那么判断框中应填入的关于k 的判断条件是( ) A .6k >? B .6k <? C .5k >? D .5k <?6、抛物线24y x =的焦点为F ,点P 为抛物线上的动点,点M 为其准线上的动点,当F ∆PM 为等边三角形时,其面积为( )A. B .4 C .6 D. 7、已知等差数列{}n a 的前n 项和为n S ,且满足4255S a +=,则一定有( ) A .6a 是常数 B .7S 是常数 C .13a 是常数 D .13S 是常数8、一个几何体的正视图和俯视图如图所示,其中俯视图是边长为的正三角形及其内切圆,则侧视图的面积为( )A .6π+ B.π C .64π+ D.4π 9、已知三棱锥C S -AB 的四个顶点都在一个半径为r 的球面上,球心O 在AB 上,S O ⊥底面C AB,C A =,则球的体积与三棱锥体积之比是( )A .πB .2πC .3πD .4π10、已知不等式组3410043x y x y +-≥⎧⎪≤⎨⎪≤⎩表示区域D ,过区域D 中任意一点P 作圆221x y +=的两条切线且切点分别为A 、B ,当∠APB 最大时,cos ∠APB =( ) A.B .12 C. D .12- 11、已知函数()sin cos f x a x b x =+(R x ∈),若0x x =是函数()f x 的一条对称轴,且0tan 2x =,则点(),a b 所在的直线为( )A .20x y -=B .20x y +=C .20x y -=D .20x y += 12、设函数()sin x f x e x =+,()2g x x =-,设()()11,x f x P ,()()22Q ,x g x (10x ≥,20x >),若直线Q//P x 轴,则P ,Q 两点间最短距离为( )A .2B .3C .4D .5 二、填空题(本大题共4小题,每小题5分,共20分.) 13、已知1a =,2b =,3a b +=,则a 与b 的夹角为 . 14、如图所示,在矩形C OAB 内任取一点P ,则点P 恰落在图中阴影部分中的概率为 .15、若正数a ,b 满足1a b +=,则11a ba b +++的最大值为 . 16、已知双曲线22221x y a b-=(0a >,0b >)上一点C ,过双曲线中心的直线交双曲线于A ,B 两点,记直线C A ,C B 的斜率分别为1k ,2k ,当12122ln ln k k k k ++最小时,双曲线离心率为 . 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17、(本小题满分10分)设C ∆AB 的内角A ,B ,C 所对边的长分别为a ,b ,c ,且cos C sin a b =+B . ()1求B ;()2若1c =,3a =,C A 的中点为D ,求D B 的长.18、(本小题满分12分)如图,已知四棱锥CD P -AB ,底面CD AB 为菱形,PA ⊥平面CD AB ,C 60∠AB =,E ,F 分别是C B ,C P 的中点.()1证明:D AE ⊥P ;()2若2AB =,2PA =,求二面角F C E -A -的余弦值.19、(本小题满分12分)2014年11月10日C APE 会议在北京召开,某服务部需从大学生中招收志愿者,被招收的志愿者需参加笔试和面试两部分,把参加笔试的40名大学生的成绩分组:第组[)75,80,第2组[)80,85,第3组[)85,90,第4组[)90,95,第5组[)95,100,得到的频率分布直方图如图所示:()1分别求出成绩在第3,4,5组的人数;()2现决定在笔试成绩较高的第3、4、5组中用分层抽样抽取6人进行面试.①已知甲和乙的成绩均在第3组,求甲或乙进入面试的概率;②若从这6名学生中随机抽取2名学生接受考官D 的面试,设第4组中有X 名学生被考官D 面试,求X 的分布列和数学期望.20、(本小题满分12分)设数列{}n a 的前n 项和为n S ,且首项13a ≠,13n n n a S +=+(n *∈N ).()1求证:{}3n n S -是等比数列;()2若{}n a 为递增数列,求1a 的取值范围.21、(本小题满分12分)已知椭圆:E 22221x y a b+=(0a b >>)过点()2,1M ,焦距为.()1求椭圆E 的方程;()2若直线平行于OM ,且与椭圆E 交于A 、B 两个不同的点(与M 不重合),连接MA 、MB ,MA 、MB 所在直线分别与x 轴交于P 、Q 两点,设P 、Q 两点的横坐标分别为s ,,探求s t +是否为定值?若是,求出该定值;若不是,请说明理由.22、(本小题满分12分)设函数()2ln f x x bx a x =+-.()1若2x =是函数()f x 的极值点,和0x 是函数()f x 的两个不同零点,且()0,1x n n ∈+,n ∈N ,求n ;()2若对任意[]2,1b ∈--,都存在()1,x e ∈(e 为自然对数的底数),使得()0f x <成立,求实数a 的取值范围.运城市2014~2015学年第一学期期末高三调研测试试题理科数学参考答案。
2014年山西省高考数学{理}试卷及答案

2014年普通高等学校招生全国统一考试理科数学注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答第Ⅰ卷时,选出每个小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮搽干净后,再选涂其他答案标号,写在本试卷上无效.3. 回答第Ⅱ卷时,将答案写在答题卡上,答在本试题上无效.4. 考试结束,将本试题和答题卡一并交回.第Ⅰ卷一.选择题:共12小题,每小题5分,共60分。
在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.已知集合A={x |2230x x --≥},B={x |-2≤x <2=,则A B ⋂=A .[-2,-1]B .[-1,2)C .[-1,1]D .[1,2)2.32(1)(1)i i +-=A .1i +B .1i -C .1i -+D .1i --3.设函数()f x ,()g x 的定义域都为R ,且()f x 时奇函数,()g x 是偶函数,则下列结论正确的是A .()f x ()g x 是偶函数B .|()f x |()g x 是奇函数C .()f x |()g x |是奇函数D .|()f x ()g x |是奇函数4.已知F 是双曲线C :223(0)x my m m -=>的一个焦点,则点F 到C 的一条渐近线的距离为A B .3 C D .3m5.4位同学各自在周六、周日两天中任选一天参加公益活动,则周六、周日都有同学参加公益活动的概率A .18B .38C .58D .786.如图,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示为x 的函数()f x ,则y =()f x 在[0,π]上的图像大致为7.执行下图的程序框图,若输入的,,a b k 分别为1,2,3,则输出的M =A .203 B .165 C .72 D .1588.设(0,)2πα∈,(0,)2πβ∈,且1sin tan cos βαβ+=,则A .32παβ-=B .22παβ-=C .32παβ+=D .22παβ+=9.不等式组124x y x y +≥⎧⎨-≤⎩的解集记为D .有下面四个命题:1p :(,),22x y D x y ∀∈+≥-,2p :(,),22x y D x y ∃∈+≥,3P :(,),23x y D x y ∀∈+≤,4p :(,),21x y D x y ∃∈+≤-.其中真命题是A .2p ,3PB .1p ,4pC .1p ,2pD .1p ,3P10.已知抛物线C :28y x =的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个焦点,若4FP FQ =,则||QF =A .72B .52C .3D .211.已知函数()f x =3231ax x -+,若()f x 存在唯一的零点0x ,且0x >0,则a 的取值范围为A .(2,+∞)B .(-∞,-2)C .(1,+∞)D .(-∞,-1)12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A .B .C .6D .4第Ⅱ卷本卷包括必考题和选考题两个部分。
【恒心】山西省2014-2015年度高三第三次诊断考试数学(理科)试题及参考答案【超清版】

' # ཞ Lz8{|' }~ , ! ! ! " $ D' $& " ( ' " ' # ' ' $ !% }~ }~ / "*N- #1 2 3 *4&槡 &$ " " $ &槡 & (! /! ! % ! % # ) ./*' F0" 1" ! ) ! ## , 7 8 3 # L#,$ [Z(, * #0 0 ' ## , < 0 # -' " ) ' . 'L' Q$n '& #EF ' 0 *' ! ) ## )r`s' &')$ 1" m24 m24 -! $ < .! < m234< m234< /! 0 ! (! " 0 &槡 & -! $ ! % " 0 &槡 & .! ! %
4
# @ #0
#, 4#@
!
' ' ÄÚ`a9cd& eA0A' #A0 A/ e ' ! (!ØÙdq' A/A [Z*/ A ' ' / #A eA0[Z. #A *0A' 0A/ A/A 0[Z. A/[Z- eA0 A' #[ZÄ/-fcd' 0A' D[Z/A WÄ´! ! '# - ' * - %' * *e! # " ¾eÛ¾- ,' ! % ! /! *0 ," *0 0 , ! % 0" 0 # ! % 0 ) , ! + ! 0 ) * * * * - *
新课标I(第03期)-2014届高三名校数学(理)试题分省分项汇编 专题03 导数解析版Word版含解析

一.基础题组1. 【河南省郑州市2014届高中毕业年级第一次质量预测试题】已知曲线23ln 4x y x =-的一条切线的斜率为12-,则切点的横坐标为( ) A .3 B .2 C .1 D .122. 【山西省忻州一中、康杰中学、临汾一中、长治二中四校2014届高三第二次联考】定积分=-⎰-dx x x 2222( ) A.5B.6C.7D.83. 【山西省太原市太远五中2014届高三12月月考】已知函数xe xx f cos )(=,则函数)(x f 在点))0(,0(f 处切线方程为 . 【答案】10x y +-= 【解析】试题分析:∵'2sin cos ()()x xx xe xe f x e --=,∴1k =-,(0)1f =,∴1y x -=-,即10x y +-=. 考点:利用导数求曲线的切线.4. 【唐山市2013-2014学年度高三年级第一学期期末考试】已知0a >,函数32f(x)x ax bx c =+++在区间[2,2]-单调递减,则4a b +的最大值为 .5. 【河北省衡水中学2014届高三上学期四调考试】设()ln af x x x x=+, 32()3g x x x =--.(Ⅰ)当2a =时,求曲线()y f x =在1x =处的切线的方程;(Ⅱ)如果存在12,[0,2]x x ∈,使得12()()g x g x M -≥成立,求满足上述条件的最大整数M ;(Ⅲ)如果对任意的1,[,2]2s t ∈,都有()()f s g t ≥成立,求实数a 的取值范围.6. 【河北省唐山市一中2014届高三12月月考】(本小题满分12分)某地区注重生态环境建设,每年用于改造生态环境总费用为x 亿元,其中用于风景区改造为y 亿元。
该市决定制定生态环境改造投资方案,该方案要求同时具备下列三个条件:①每年用于风景区改造费用随每年改造生态环境总费用增加而增加;②每年改造生态环境总费用至少a 亿元,至多b 亿元;③每年用于风景区改造费用不得低于每年改造生态环境总费用的15%,但不得高于每年改造生态环境总费用的25%.若1=a ,4=b ,请你分析能否采用函数模型y =31(416)100x x ++作为生态环境改造投资方案.二.能力题组1. 【河北省唐山市一中2014届高三12月月考】已知函数()f x 对于一切实数x,y 均有()()()21f x y f y x x y +-=++成立,且()()110,0,21g 2a f x f x o x ⎛⎫=∈+ ⎪⎝⎭则当,不等式< 恒成立时,实数a 的取值范围是 .2. 【山西省太原市太远五中2014届高三12月月考】由曲线sin ,cos y x y x ==与直线0,2x x π==所围成的平面图形(图中的阴影部分)的面积是 .【答案】2 【解析】3. 【山西省忻州一中、康杰中学、临汾一中、长治二中四校2014届高三第二次联考】(本小题满分12分) 已知函数ln(1)()2x x f x x -=-.(Ⅰ)讨论函数()f x 的单调性;(Ⅱ)设2()23g x x x =++,证明:对任意1(1,2)(2,)x ∈+∞ ,总存在2x R ∈,使得12()()f x g x >.试题解析:(1)''2212ln(1)1[ln(1)]ln(1)1()(2)(2)x x x x x x x f x x x --+------==-- .................1分设1()2ln(1)11h x x x x =--+---, 22'22(1)2(1)1(2)()0(1)(1)x x x h x x x ---+-==≥--∴()h x 在(1,)+∞是增函数,又(2)0h = ………………3分 ∴当(1,2)x ∈时, ()0h x < ,则'()0f x <,()f x 是单调递减函数; 当(2,)x ∈+∞时, ()0h x > ,则'()0f x >,()f x 是单调递增函数. 综上知:()f x 在(1,2)单调递减函数,()f x 在(2,)+∞单调递增函数 ……………………6分三.拔高题组1. 【山西省忻州一中、康杰中学、临汾一中、长治二中四校2014届高三第二次联考】0.50.521log log 1(1)(7)x mx x x +>---对任意x ∈[2,4]恒成立,则m 的取值范围为 .∴当4x =时,max 45y =,∴45m >.考点:1.对数函数的单调性;2.恒成立问题;3.利用导数求函数最值.2. 【唐山市2013-2014学年度高三年级第一学期期末考试】(本题满分12分)已知函数(x)1x x e f xe =+.(1)证明:0(x)1f <≤; (2)当0x >时,21(x)1f ax >+,求a 的取值范围.试题解析:(Ⅰ)设(x)xe 1x g =+,则'(x)(x 1)e xg =+.当(,1)x ∈-∞-时,'(x)0g <,(x)g 单调递减; 当(1,)x ∈-+∞时,'(x)0g >,(x)g 单调递增. 所以1(x)g(1)1e0g -≥-=->.又0xe >,故(x)0f >.…2分'2(1e )(x)(xe 1)x x x e f -=+ 当(,0)x ∈-∞时,'(x)0f >,(x)f 单调递增; 当(0,)x ∈+∞时,'(x)0f <,(x)f 单调递减. 所以(x)f(0)1f ≤=. 综上,有0(x)1f <≤.…5分3. 【河北省唐山市一中2014届高三12月月考】(本小题满分12分)已知)0()(>-=a e x x f ax.(1)曲线y=f (x )在x=0处的切线恰与直线012=+-y x 垂直,求a 的值;(2)若x ∈[a ,2a]求f (x )的最大值; (3)若f (x 1)=f (x 2)=0(x 1<x 2),求证:.【答案】(1)13a =;(2)当ln a a a >,即a e <时,max ()()f x f a a e ==-,当ln 2a a a a ≤≤,即2e a e ≤≤时,max ()(ln )ln f x f a a a a a ==-,当2ln a a a <,即2a e >时,2max ()(2)2f x f a a e ==-;(3)证明过程详见解析. 【解析】试题分析:本题主要考查导数的运算,利用导数研究函数的单调性、最值、切线方程以及不等式的证明等基础知识,考查分类讨论思想,综合分析和解决问题的能力.第一问,对()f x 求导,将0x =代入得到切线的斜率,由已知切线与直线210x y -+=垂直得出方程,解出a 的值;第二问,先对()f x 求导,利用导数的正负判断出函数的单调区间,再讨论已知[,2]x a a ∈和单调区间的关系来决定最值的位置;第三问,利用第二问的结论,得出max ()ln f x a a a =-,因为12()()0f x f x ==,所以数形结合,得max ()0f x >,解得a e >,数形结合得出两组点的横坐标的关系21ln x x a a a ->-,又利用12()()0f x f x ==,得出11x a x e =,22x ax e =,进行转换得到所求证的不等式.(3)由(2)知,max ()(ln )ln f x f a a a a a ==-,∵12()()0f x f x ==,∴max ()(ln )ln 0f x f a a a a a ==->, ∴ln 1a >,得a e >,∴()0f a a e =->,且(ln )0f a a >. 得21ln x x a a a ->-,又11x a x e =,22x ax e =,∴1211()(ln )12x x a a a a a x e e e x a--=<=. 考点:1.利用导数求切线的斜率;2.两条直线垂直的充要条件;3.利用导数判断函数的单调性;4.利用导数求函数的最值.4. 【河南省郑州市2014届高中毕业年级第一次质量预测试题】(本小题满分12分)已知函数()ln f x x x =,()(1)g x k x =-.(1)若()()f x g x ≥恒成立,求实数k 的值;(2)若方程()()f x g x =有一根为11(1)x x >,方程''()()f x g x =的根为0x ,是否存在实数k ,使1x k x =?若存在,求出所有满足条件的k 值;若不存在,说明理由. 试题解析:⑴解:注意到函数()f x 的定义域为(0,)+∞, 所以()()f x g x ≥恒成立()()f xg x x x⇔≥恒成立, 设(1)()ln (0)k x h x x x x-=->, 则221()k x kh x x x x -'=-=, ------------2分当0k ≤时,()0h x '>对0x >恒成立,所以()h x 是(0,)+∞上的增函数, 注意到(1)0h =,所以01x <<时,()0h x <不合题意.-------4分5. 【山西省曲沃中学2014届高三上学期期中考试】已知函数()e x f x =,点(,0)A a 为一定点,直线()x t t a =≠分别与函数()f x 的图象和x 轴交于点M ,N ,记AMN ∆的面积为()S t . (1)当0a =时,求函数()S t 的单调区间;(2)当2a >时, 若0[0,2]t ∃∈,使得0()e S t ≥, 求实数a 的取值范围.(II )因为1()||e 2t S t t a =-,其中t a ≠ 当2a >,[0,2]t ∈时,1()()e 2tS t a t =-因为0[0,2]t ∃∈,使得0()e S t ≥,所以()S t 在[0,2]上的最大值一定大于等于e1'()[(1)]e 2t S t t a =---,令'()0S t =,得1t a =- …………………8分6. 【山西省太原市太远五中2014届高三12月月考】已知函数ln 1af x x a x =+∈+R ()(). (1)当92a =时,如果函数g x f x k =-()()仅有一个零点,求实数k 的取值范围; (2)当2a =时,试比较f x ()与1的大小; (3)求证:1111ln 135721n n +>+++++ ()n ∈*N ()一个交点,所以关键是()y f x =的图像,对()f x 求导,令'()0f x >和'()0f x <判断函数的单调性,确定函数的极值和最值所在位置,求出具体的数值,便可以描绘出函数图像,来决定k 的位置;第二问,先将2=a 代入,得到()f x 解析式,作差法比较大小,得到新函数()h x ,判断()h x 的正负即可,通过对()h x 求导,可以看出()h x 在(0,)+∞上是增函数且(1)0h =,所以分情况会出现3种大小关系;第三问,法一:利用第二问的结论,得到表达式1211ln+>+k k k ,再利用不等式的性质得到所证表达式的右边,左边是利用对数的运算性质化简,得证;法二,用数学归纳法证明,先证明当1n =时不等式成立,再假设当n k =时不等式成立,然后利用假设的结论证明当1n k =+时不等式成立即可.①当1>x 时,0)1()(=>h x h ,即1)(>x f ; ②当10<<x 时,0)1()(=<h x h ,即1)(<x f ;③当1=x 时,0)1()(==h x h ,即1)(=x f . ……………………………8分(3)(法一)根据(2)的结论,当1>x 时,112ln >++x x ,即11ln +->x x x . 令k k x 1+=,则有1211ln +>+k k k , ∑∑==+>+∴n k nk k k k 111211ln . ∑=+=+nk k k n 11ln )1ln( , 1215131)1ln(++++>+∴n n . …………………………………12分。
山西省山大附中2014届高三5月模拟 数学理 Word版含答案.

O 510 15 20频率组距重量0.060.1 山西大学附中2013—2014学年高三第二学期5月下数学试题(理科考试时间:120分钟满分: 150分一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项符合题目要求 1.已知集合{2,0,1,4}A =,集合{04,R}=<≤∈B x x x ,集合C A B =.则集合C可表示为 A .{2,0,1,4}B . {1,2,3,4}C .{1,2,4}D . {04,R}x x x <≤∈2.复数5(3z i i i =-+(i 为虚数单位,则复数z 的共轭复数为A .2i -B .2i +C .4i -D .4i + 3. 设γβα,,为平面,n m ,为直线,则β⊥m 的一个充分条件是 A .n m n ⊥=⋂⊥,,βαβα B .γβγαγα⊥⊥=⋂,,m C .αγββα⊥⊥⊥m ,, D .αβα⊥⊥⊥m n n ,,4.阅读如下程序框图,如果输出4i =,那么空白的判断框中应填人的条件是A .?10≤SB .?12≤SC .?14≤SD .?16≤S5.220sin2x dx π=⎰ A .0 B .142π- C .144π- D .12π-6.右图是一容量为100的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为A .11B .11.5C .12D .12.5 7.(9a b c ++的展开式中,432a b c 项的系数为A .126B .420C .630D .12608.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为A .23πB .3πC .29πD .169π 9.过抛物线24y x =焦点F 的直线交其于,A B 两点,O 为坐标原点.若||3AF =,则AOB ∆的面积为A .22B .2C .322D .2210.由(y f x =的图象向左平移3π个单位,再把所得图象上所有点的横坐标伸长到原来的2倍得到12sin(36y x π=-的图象,则(f x 为A .312sin(26x π+B .12sin(66x π-C .312sin(23x π+D .12sin(63x π+ 11.现有四个函数:①sin y x x =⋅;②cos y x x =⋅;③|cos |y x x =⋅;④2x y x =⋅的图象(部分如下:则按照从左到右图象对应的函数序号安排正确的一组是A .①④③②B .①④②③C .④①②③D .③④②①12.定义在R 上的函数(f x 满足:((1,(04,f x f x f '+>=则不等式(3x xe f x e >+(其中e 为自然对数的底数的解集为A .(0,+∞B .((,03,-∞+∞C .((,00,-∞+∞D .(3,+∞二、填空题:(本大题共4小题,每小题5分,共20分13.已知向量1,(z x a -=,,2(z y b +=,且b a ⊥,若变量,x y 满足约束条件⎪⎩⎪⎨⎧≤+≥-≥5231y x xy x ,则z 的最大值为 . 14.正四面体ABCD 的棱长为4,E 为棱BC 的中点,过E 作其外接球的截面,则截面面积的最小值为______.15.有4张分别标有数字1,2,3,4的红色卡片和4张分别标有数字1,2,3,4的蓝色卡片,从这8张卡片中取出4张卡片排成一行,则这一行的4张卡片所标数字之和等于10的概率为 .16.设O 是ABC ∆的三边中垂线的交点,,,a b c 分别为角,,A B C 对应的边,已知2220b b c -+=,则BC AO ⋅uu u r uuu r的范围是___________________.三、解答题: 17.(本小题满分12分已知数列}{n a 中,51=a 且1221n n n a a -=+-(2n ≥且*n N ∈.(Ⅰ证明:数列12n n a -⎧⎫⎨⎬⎩⎭为等差数列; (Ⅱ求数列}{n a 的前n 项和n S .o X xxy x y x y x y公安部最新修订的《机动车驾驶证申领和使用规定》于2013年1月1日起正式实施,新规实施后,获取驾照要经过三个科目的考试,先考科目一(理论一,科目一过关后才能再考科目二(桩考和路考,科目二过关后还要考科目三(理论二.只有三个科目都过关后才能拿到驾驶证.某驾校现有100名新学员,第一批参加考试的20人各科目通过的人数情况如下表:参考人数通过科目一人数通过科目二人数通过科目三人数201242请你根据表中的数据:(Ⅰ估计该驾校这100名新学员有多少人一次性(不补考获取驾驶证;(Ⅱ第一批参加考试的20人中某一学员已经通过科目一的考试,求他能通过科目二却不能通过科目三的概率;(Ⅲ该驾校为调动教官的工作积极性,规定若所教学员每通过一个科目的考试,则学校奖励教官100元.现从这20人中随机抽取1人,记X 为学校因为该学员而奖励教官的金额数,求X 的数学期望. 19.(本小题满分12分如图,在四棱锥P ABCD -中,,//,,22,,PA AD AB CD CD AD AD CD AB E F ⊥⊥===分别为,PC CD 的中点, DE EC =(Ⅰ求证:平面ABE ⊥平面BEF ;(Ⅱ设PA a =,若平面EBD 与平面ABCD 所成锐二面角[,]43ππθ∈,求a 的取值范围.20.(本小题满分12分已知椭圆1C 的中心为原点O ,离心率e 2=2,其一个焦点在抛物线2:C 22y px =的准线上,若抛物线2C 与直线: 20l x y -+=相切.(Ⅰ求该椭圆的标准方程;(Ⅱ当点(,Q u v 在椭圆1C 上运动时,设动点(,P v u u v 2-+的运动轨迹为3C .若点T 满足:OT MN OM ON =+2+uu u r uuu r uuu r uuu r,其中,M N 是3C 上的点,直线OM 与ON 的斜率之积为1-2,试说明:是否存在两个定点,F F 12,使得TF TF 12+为定值?若存在,求,F F 12的坐标;若不存在,说明理由.已知函数((1xf x x e-=+(e 为自然对数的底数。
山西省2014~2015学年度高三第四次诊断考试数学(理)试卷

山西省2014~2015学年度高三第四次诊断考试数学(理)试卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、设集合{}215x x A =-≥,集合x y ⎧B ==⎨⎩,则A B 等于( )A .()3,7B .[]3,7C .(]3,7D .[)3,7 2、已知向量()2,1a m =,向量()1,8b =-,若a b ⊥,则实数m 的值是( ) A .4- B .4 C .43 D .14 3、设sin 20156a ππ⎛⎫=- ⎪⎝⎭,函数()(),0,0xa x f x f x x ⎧>⎪=⎨-<⎪⎩,则21log 6f ⎛⎫ ⎪⎝⎭的值等于( )A .14 B .4 C .16D .6 4、若R m ∈,则“6log 1m =-”是“直线1:l 210x my +-=与2:l ()3110m x my ---=平行”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件5、若等比数列{}n a 的各项均为正数,且510119122a a a a e +=,则1220ln ln ln a a a ++⋅⋅⋅+等于( ) A .50 B .25 C .75 D .1006、函数()2cos xf x x π=的图象大致是( )A .B .C .D .7、为得到函数sin 3y x π⎛⎫=+ ⎪⎝⎭的图象,可将函数sin y x =的图象向左平移m 个单位长度,或向右平移n 个单位长度(m ,n 均为正数),则m n -的最小值是( ) A .3π B .23π C .43π D .53π8、设636e a =,749e b =,864e c =,则a ,b ,c 的大小关系为( )A .a b c >>B .b a c >>C .c b a >>D .c a b >>9、在C ∆AB 中,角A 、B 、C 所对的边分别为a 、b 、c,若222b c a +-=,且b =,则下列关系一定不成立的是( )A .a c =B .b c =C .2a c =D .222a b c +=10、已知点E 、F 、G 分别是正方体1111CD C D AB -A B 的棱1AA 、1CC 、1DD 的中点,点M 、N 、Q 、P 分别在线段DF 、G A 、BE 、11C B 上,则以M 、N 、Q 、P 为顶点的三棱锥Q P -MN 的俯视图不可能是( )A .B .C .D .11、已知O 为原点,双曲线2221x y a -=(0a >)上有一点P ,过P 作两条渐近线的平行线,且与两渐近线的交点分别为A ,B ,平行四边形OBPA 的面积为,则双曲线的离心率为( ) AB. CD12、已知函数()(](]1,112,1,3x f x x x ⎧∈-⎪=⎨--∈⎪⎩,其中0m >,且函数()f x 满足()()4f x f x +=.若方程()30f x x -=恰有5个根,则实数m 的取值范围是( )A. B.83⎫⎪⎪⎭ C.43⎛ ⎝ D .48,33⎛⎫⎪⎝⎭ 二、填空题(本大题共4小题,每小题5分,共20分.)13、若圆C 的半径为,圆心在第一象限,且与直线430x y -=和x轴都相切,则该圆的标准方程是 .14、设0α=⎰,tan 3β=,则()tan αβ+= .15、点A ,B ,C ,D 在同一球面上,C AB =B =,C 2A =,若球的表面积为254π,则四面体CD AB 体积的最大值为 .16、设C n n n ∆A B 的三边长分别为n a ,n b ,n c ,1n =,2,3,⋅⋅⋅,若11b c >,1112b c a +=,1n n a a +=,12n n n a c b ++=,12n n n a bc ++=,则n ∠A 的最大值是 . 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17、(本小题满分10分)在C ∆AB 中,已知()sin sin sin A +B =A +B .()1求角B ;()2若4tan 3A =,求sin C 的值.18、(本小题满分12分)已知命题:p 方程22121x y m m -=-表示焦点在y 轴上的椭圆;命题:q 双曲线2215y x m -=的离心率()1,2e ∈,若p 、q 有且只有一个为真命题,求实数m 的取值范围.19、(本小题满分12分)数列{}n a 满足11a =,()()111n n na n a n n -=---,2n ≥且n *∈N .()1证明:数列n a n ⎧⎫⎨⎬是等差数列; ()2设13n n b -=,求数列{}n b 的前n 项和n S .20、(本小题满分12分)已知四棱柱1111CD C D AB -A B ,侧棱1AA ⊥底面CD AB ,底面CD AB 中,D AB ⊥A ,C//D B A ,2AB =,D 4A =,C 1B =,侧棱14AA =.()1若E 是1AA 上一点,试确定E 点位置使//EB 平面1CD A ;()2在()1的条件下,求平面D BE 与平面D AB 所成角的余弦值.21、(本小题满分12分)如图,分别过椭圆:E 22221x y a b+=(0a b >>)左、右焦点1F 、2F 的动直线1l ,2l 相交于P 点,与椭圆E 分别交于A 、B 与C 、D 不同四点,直线OA 、OB 、C O 、D O 的斜率1k 、2k 、3k 、4k 满足1234k k k k +=+.已知当1l 与x 轴重合时,AB =. ()1求椭圆E 的方程;()2是否存在定点M 、N ,使得PM +PN 为定值?若存在,求出M 、N 点坐标并求出此定值;若不存在,请说明理由.22、(本小题满分12分)已知函数()ln f x ax x x =+的图象在点x e =(e 为自然对数的底数)处的切线的斜率为3. ()1求实数a 的值;()2若()2f x kx ≤对任意0x >成立,求实数k 的取值范围;()3当1n m >>(m ,n *∈Nm n>.。
山西省太原五中2014届高三2月月考数学理试卷Word版含答案

山西省太原五中2013—2014学年度第二学期月考(2月)高三数学(理)第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知命题:,2lg P x R x x ∃∈->,命题2:,0q x R x ∀∈>,则( ) A.命题q p ∨是假命题 B.命题q p ∧是真命题 C.命题)(q p ⌝∧是真命题 D.命题)(q p ⌝∨是假命题2.设集合A =B ={(,),}x y x R y R ∈∈,从A 到B 的映射),(),(:y x y x y x f -+→在映射下,B 中的元素为(4,2)对应的A 中元素为 ( )A .(4,2).(3,1) 329,,则5( )项.A.19B.20C.21D.22 4.复数ii+12(i 是虚数单位)的虚部是( ) A .i B.i - C .1 D.1- 5.一个几何体按比例绘制的三视图如图所示(单位:m ),则该几何体的体积为( )3m . A .37 B.29 C .27D.496.某流程图如图所示,现输入如下四个函数,则可以输出的函A C7展开式中的常数项是( )A .180B .120C .90D .458.在△ABC 中,若2AB AB AC BA BC CA CB =⋅+⋅+⋅,则△ABC 是( ) A.等边三角形 B.锐角三角形 C.钝角三角形 D.直角三角形9像如图示,则将()y f x =的图像向右平移 )A .x y 2sin = B.x y 2cos =10.已知双曲线2222:1x y C a b-=的左、右焦点分别是12,F F ,正三角形12AF F 的一边1AF 与双曲线左支交于点B ,且114AF BF =,则双曲线C 的离心率的值是( ) A .123+ B.1313+ D11.已知函数()2014sin (01)(),log 1x x f x x x π⎧≤≤⎪=⎨>⎪⎩若a 、b 、c 互不相等,且)()()(c f b f a f ==,则a +b +c 的取值范围是( )A .(1,2014)B .(1,2015)C .(2,2015)D .[2,2015]12.设x ,y ∈R ,且满足33(2)2sin(2)2,(2)2sin(2)6,x x x y y y ⎧-++-=⎪⎨-++-=⎪⎩则x y +=( ) A .1 B .2 C .3 D .4第Ⅱ卷本卷包括必考题和选考题两部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
及对应的直线 l 的方程;若没有,请说明理由.
3
21.(本小题满分 12 分) 已知函数 f ( x) x a ln x 1, a R . (Ⅰ)求函数 f ( x ) 的单调区间; (Ⅱ)若 2 f ( x )
ln x 0 对于任意 x [1, ) 恒成立,求 a 的取值范围. x
A'
A
D
E
D
2
M
E
N
B
C
B
C
19.(本小题满分 12 分) 某电视台举办猜歌曲的娱乐节目:随机播放歌曲片段,选手猜出歌曲名称可以赢取奖金. 曲库中歌曲 足够多,不重复抽取. 比赛共分 7 关:前 4 关播放常见歌曲;第 5,6 关播放常见或罕见歌曲,曲库中常见 歌曲与罕见歌曲数量比为 1:4;第 7 关播放罕见歌曲.通过关卡与对应的奖金如右表所示.选手在通过每一 关(最后一关除外)之后可以自主决定退出比赛或继续闯关;若退出比赛,则可获得已经通过关卡对应奖 金之和;若继续闯关但闯关失败,则不获得任何奖金. 关卡 关卡奖金 / 元 累计奖金 / 元 1 1000 1000 (Ⅰ) 选手甲准备参赛, 在家进行自我测试: 50 首常见歌曲, 2 2000 3000 甲能猜对 40 首;40 首罕见歌曲,甲只 3 3000 6000 能猜对 2 首,以他猜对常见歌曲与罕见歌曲的频率最为概率. 4 4000 10000 ①若比赛中,甲已顺利通过前 5 关,求他闯过第 6 关的概 5 8000 18000 率是多少? 6 12000 30000 ②在比赛前, 甲计划若能通过第 1,2,3 关的任意一关, 则继 7 20000 50000 续;若能通过第 4 关,则退出,求这种情况下甲获得奖金的数学 期望; (Ⅱ)设选手乙猜对罕见歌曲的概率为 p,且他已经顺利通过前 6 关,当 p 满足什么条件时,他选择 继续闯第 7 关更有利?.
正视图 2 2 2
侧视图
C. 2 3
D. 4 3
2 10. 若锐角满足 2sin+2 3cos=3, 则 tan(2+ )的值是 3
1
A.-3 7
B.3 7
3 7 C.7
3 7 D. 7
11.定义在 R 上的函数 f ( x ) 的图象既关于点(1, 1)对称,又关于点(3, 2)对称,则 f (0) f (2) f (4)
*
.
18.(本小题满分 12 分) 如图,在 RtA BC 中,A B=BC=2,D, E 分别是 A B,A C 的中点,将 A DE 沿线段 DE 折起到
′ ′ ′ ′ ′
ADE, 使平面 ADE⊥平面 DBCE. (Ⅰ)当 M 是 DE 的中点时,证明 BM⊥平面 ACD; (Ⅱ)设 BE 与 DC 相交于点 N, 求二面角 B-AN-C 的余弦值.
y≥0 5. 若实数 x, y 满足约束条件x-y≥0 ,则 z x 2 y 的取值范围是 2x-y-2≤0
A. [0, 1] B. [1, 6] C. [0, 6] D. [2, 6] 6. 若抛物线 y 2 2 px( p 0) 与直线 x y 1 0 相交于 A,B 两点, 且 OA · OB =-1,则 p= A. 1 B. 2 C. 4 D. 8 7. 执行如图所示的程序框图,输出的 S 值是 A. – C. 0 3 2 B. D. 3 2 3
山西省 2014 届高三高考考前质量监测 理科数学
一、选择题:本大题共 1 2 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1+i 1.复数 的实部是 1-i A. -2 B. ―1 C. 0 2. 集合 A,B 满足 A∪B={1, 2}, 则不同的有序集合对(A, B)共有 A. 4 个 B. 7 个 C. 8 个 3. 若平面向量 a , b 满足| a + b |=1,| a - b |=3,则 a · b = A. 1
20.(本小题满分 12 分)
x2 2 过椭圆 E: y 1的右焦点且垂直于 x 轴的直线与椭圆 E 相交于 A, B 两点, 直线 l :y mx n 2
与椭圆 E 交于 C,D 两点,与线段 AB 相交于点 P(与 A,B 不重合). (Ⅰ)当 m=1 时,四边形 ACBD 能否成为平行四边形,请说明理由; (Ⅱ)当直线 l 与圆 x y 1相切时,四边形 ACBD 的面积是否有最大值,若有,求出其最大值,
G
C
D
A
P F
O
B
E
23. (本小题满分 10 分)选修 4―4,坐标系与参数方程 已知曲线 C1 的参数方程为
x 2 cos y 2 sin
( 为参数), 以坐标原点为极点, x 轴的非负半轴为极轴建
立极坐标系,曲线 C2 的极坐标方程为 cos sin 0( 0,0 2 ). (Ⅰ)求曲线 C1 与 C2 交点的极坐标; (Ⅱ)设曲线 C1 与 C2 的交点为 A,B , 线段 AB 上两点 C,D,且|AC|=|BD|= 求|PC|+|PD|的最大值. 2 ,P 为曲线 C1 上的点, 2
2
D. 1 D. 9 个
→ →
→ →
→
→
→
→
B. -1
C. 2
D. -2
4. 已知 a R , 设 p: a 3a 2 0 ; q:关于 x 的方程 x2 2x log2a 0 有实数根. 则 p 是 q 的 A. 充分不必要条件 C. 充要条件 B. 必要不充分条件 D. 既不充分也不必要条件
选做题:请考生在第 22、23、24 三题中任选一题做答,如果多做,则按所做的第一题记分。做答时, 用 2B 铅笔在答题卡上把所选题目对应的题号涂黑. 22. (本小题满分 10 分)选修 4—1:几何证明选讲 如图,AB 为⊙O 的直径,点 D 是⊙O 上的一点,点 C 是弧 AD 的中点,弦 CE⊥AB 于 F. GD 是⊙O 的切线,且与 EC 的延长线相交于点 G, 连接 AD,交 CE 于点 P. (Ⅰ)证明:ACD∽APC; (Ⅱ)若 GD= 2+1,GC=1,求 PE 的长.
1 x m
emx2 的图像与函数 g ( x) x 1 图像有公共点,则正实数 m 的取值范围是
_____________ 三、解答题:本大题共 6 小题,共 70 分。解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分 12 分) 已知数列 {an } 的前 n 项和为 Sn =3n-n2, n N (Ⅰ)求通项公式 an ; (Ⅱ) 设 bn 2n ,求数列{ anbn }的前 n 项和 Tn .
f (14)
A. 16 2 4 B. 24 2 2 C. 32 3 3 D. 48
12. 在四边形 ABCD 中,AB=CD,∠CAB=3∠CAD, ∠ACD=∠CBD,则 tan∠ACD= A. B. C. D. 3
二、填空题:本大题共 4 小题,每小题 5 分。 13.某学校共有教师 300 人,其中中级教师有 192 人,高级教师与初级教师的人数比为 5:4. 为了解教师专 业发展需求,现采用分层抽样方法进行调查,在抽取的样本中有中级教师 64 人,则该样本中的高级教 师人数为___________. 14. 5 名工人分别要在某 3 天中选择 1 天休息,且每天至少有一人休息,则不同的安排方式有_________种 (用数字填写). 15. 已知三棱锥 P-ABC 中, ABC 是边长为 6 的正三角形, PA⊥平面 ABC , 且三棱锥外接球的表面积为 64, 则 PA= 16. 若函数 f ( x) e .
→ →
8. 已知双曲线
x2 y 2 x2 y 2 1( a 0, b 0) 1(a 0, b 0) 的四个 与曲线 a 2 b2 3a 2 b2
2
顶点,则双曲线的离心率是 A. 2 B. 2 C. 3 9. 某几何体的三视图如图所示,则该几何体的体积是 A. 2 3 3 B. 4 3 3 D. 3
5
6
7
8
9
10
24. (本小题满分 10 分)选修 4-5:不等式选讲 已知函数 f ( x) x a 2x, a R . (Ⅰ)当 a 2 时,解不等式 f ( x) 4 x 2 的解集;
(Ⅱ)若存在 x 使 f ( x) x 2 2x 1 成立,求 a 的取值范围.
