2018-2019年眉山市初中分班数学模拟试题(49)附详细答案
2019届四川省眉山市中考适应性考试数学试卷【含答案及解析】

2019届四川省眉山市中考适应性考试数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、单选题1. 的相反数是( )A. B. C. D.2. 下列等式一定成立的是( )A.B.C.D.3. 某种生物细菌的直径为0.0000382cm,把0.0000382用科学计数法表示为( )A. B. C. D.4. 如图,直线a,b被直线c所截,若a∥b,∠1=40°,∠2=70°则∠3=( )A. 70°B. 100°C. 110°D. 120°5. 甲、乙、丙三家超市为了促销一种定价均m元的商品,甲超市连续两次降价20%;乙超市一次性降价40%;丙超市第一次降价30%,第二次降价10%,此时顾客要购买这种商品,最划算的超市是( )超市.A. 甲B. 乙C. 丙D. 甲乙丙都一样6. 一次数学测试,某小组五名同学的成绩如下表所示(有两个数据被遮盖)7. 同学ABCDE方差平均成绩得分8179808280td8. 设,是方程的两个实数根,则 ( ) .A. 2016B. 2017C. 2018D. 20199. 将一个有45°角的三角尺的直角顶点C放在一张宽为3cm的纸带边沿上,另一个顶点A 在纸带的另一边沿上,测得三角尺的一边AC与纸带的一边所在的直线成30°角,如图,则三角尺的最长边的长为( )A. 6B.C. D.10. 如图AB是⊙0的直径,弦CD⊥AB于E,连结OC、AD,且,则( )A. B.C. D.11. 关于的分式方程的解为正数,则的取值范围是( )A. B.C. 且D. 且12. 如图,在边长为2m的正方形ABCD中,M为AD的中点,延长MD至点E,使ME=MC,连接EC,则tan ( )A. B.C. D.13. 两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥轴于点C,交的图象于点A,PC⊥轴于点D,交的图象于点B. 当点P在的图象上运动时,以下结论:①②的值不会发生变化③PA与PB始终相等④当点A是PC的中点时,点B一定是PD的中点.其中一定不正确的是( )A. ①B. ②C. ③D. ④二、填空题14. 因式分【解析】-x= .15. 已知关于x的一元二次方程有实数根,则m的取值范围是.16. 将抛物线向右平行移动2个单位,再向下平行移动1个单位长度得抛物线的解析式为,则比抛物线的解析式为___________.17. 圆锥底面圆的半径为1cm,母线长为6cm,则圆锥侧面展开图的圆心角是_____.18. 如果关于的不等式的正整数解是1,2,3那么的取值范围是____.19. 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,使点B落在点E处,连结DE,若DE:AC=3:5,则的值为___.三、解答题20. 计算:.21. 先化简,再求值:,其中.22. 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.23. 如图是某货站传送货物的平面示意图,为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4m.(1)求新传送带AC的长度;(2)如果需要在货物着地点C的左侧留出2m的通道,试判断距离B点4m的货物MNQP是否需要挪走,并说明理由.(结果精确到0.01m,已知)24. 甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行了有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会. 在一个纸盒里装有2个红求和2个白球,除颜色外其他都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表)甲超市25. 球两红一红一白两白礼金券5105td26. 球两红一红一白两白礼金券10510td27. 四川某特产专卖店销售核桃,其进价为每千克40元,按每千克60元销售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销量可增加20千克.若该专卖店销售这种核桃想要平均每天获利2240元,请回答:(1)每千克核桃应降价多少元?(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折销售?(3)若该专卖店想获得最大利润W,核桃的单价应定为多少元?最大利润是多少?28. 在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.(1)如图1,若AC:AB=1:2,EF⊥CB,求证:EF=CD;(2)如图2,若AC:AB=1: ,EF⊥CE,求EF: EG的值.29. 如图,已知抛物线经过A(-1,0),B(3,0),C(0,3)三点,直线是抛物线的对称轴.(1)求抛物线的函数解析式及顶点D的坐标;(2)设点P是直线上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)在直线上是否存在点M,使△MAC为等腰三角形?若存在,求出所有符合条件的点M 的坐标,若不存在,请说明理由.参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】第23题【答案】第24题【答案】第25题【答案】第26题【答案】。
2019年四川省眉山市中考数学试卷及答案
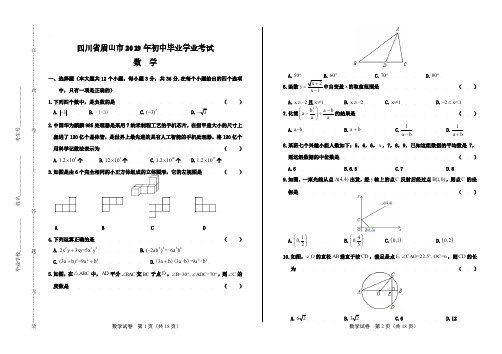
数学试卷 第1页(共18页) 数学试卷 第2页(共18页)四川省眉山市2019年初中毕业学业考试数 学一、选择题(本大题共12个小题,每小题3分,共36分.在每个小题给出的四个选项中,只有一项是正确的) 1.下列四个数中,是负数的是( )A.3-B.-(-3)C.2(3)-D.2.中国华为麒麟985处理器是采用7纳米制程工艺的手机芯片,在指甲盖大小的尺寸上塞进了120亿个晶体管,是世界上最先进的具有人工智能的手机处理器,将120亿个用科学记数法表示为( )A.91.210⨯个B.91210⨯个C.101.210⨯个D.111.210⨯个3.如图是由6个完全相同的小正方体组成的立体图形,它的左视图是( )ABC D 4.下列运算正确的是( )A.232235x y xy x y +=B.2336(2)6ab a b ﹣=- C.222(39)a b a b ++=D.22339a b a b a b +()(-)=-5.如图,在ABC △中,AD 平分BAC ∠交BC 于点D ,3070B ADC ∠︒∠︒=,=,则C ∠的度数是( )A.50︒B.60︒C.70︒D.80︒ 6.函数y =x 的取值范围是( )A.2x ≥-且1x ≠B.2x ≥-C.1x ≠D.21x ≤-< 7.化简2b a b a a a ⎛⎫--÷ ⎪⎝⎭的结果是( )A.a b -B.a b +C.1-a bD.1+a b8.某班七个兴趣小组人数如下:5,6,6,x ,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是( )A.6B.6.5C.7D.89.如图,一束光线从点(4,4)A 出发,经y 轴上的点C 反射后经过点(1,0)B ,则点C 的坐标是( )A.10,2⎛⎫⎪⎝⎭B.0,45⎛⎫ ⎪⎝⎭C.()0,1D.()0,210.如图,O e 的直径AB 垂直于弦CD ,垂足是点22.56E CAO OC ∠︒,=,=,则CD 的长为( )A.B.C.6D.12-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无-----------------效----------------毕业学校_____________ 姓名________________ 考生号________________ ________________ ___________数学试卷 第3页(共18页) 数学试卷 第4页(共18页)11.如图,在矩形ABCD 中,68AB BC =,=,过对角线交点O 作EF AC ⊥交AD 于点E ,交BC 于点F ,则DE 的长是( )A.1B.74C.2D.12512.如图,在菱形ABCD 中,已知46060AB ABC EAF ∠︒∠︒=,=,=,点E 在CB 的延长线上,点F 在DC 的延长线上,有下列结论:;BE CF EAB CEF ABE EFC ∠∠①=②=;③△∽△;④若=15BAE ∠︒,则点F 到BC 的距离为2.则其中正确结论的个数是( )A.1个B.2个C.3个D.4个二、填空题(本大题共6个小题,每小题3分,共18分) 13.分解因式:32363=a a a +- .14.设a b 、是方程22019=0x x +-的两个实数根,则()()1a b b --的值为 .15.已知关于x y ,的方程组21254x y k x y k +=-⎧⎨+=+⎩的解满足5x y +=,则k 的值为 .16.如图,在Rt ABC △中,90512B AB BC ∠︒=,=,=,将ABC △绕点A 逆时针旋转得到ADE △,使得点D 落在AC 上,则tan ECD ∠的值为 .17.如图,在Rt AOB △中,OA OB ==.O e 的半径为2,点P 是AB 边上的动点,过点P 作O e 的一条切线PQ (点Q 为切点),则线段PQ 长的最小值为 .18.如图,反比例函数(0)ky x x=>的图象经过矩形OABC 对角线的交点M ,分别交AB ,BC 于点D E 、.若四边形ODBE 的面积为12,则k 的值为 .三、解答题(本大题共6个小题,共46分)19.(6分)计算:201(46sin 453-︒⎛⎫--+ ⎪⎝⎭.20.(6分)解不等式组:275(1).532x x x x +-⎧⎪⎨->⎪⎩…数学试卷 第5页(共18页) 数学试卷 第6页(共18页)21.(8分)如图,在四边形ABCD 中,AB DC ∥,点E 是CD 的中点,=AE BE .求证:=D C ∠∠.22.(8分)如图,在岷江的右岸边有一高楼AB ,左岸边有一坡度=1:2i 的山坡CF ,点C 与点B 在同一水平面上,CF 与AB 在同一平面内.某数学兴趣小组为了测量楼AB 的高度,在坡底C 处测得楼顶A 的仰角为45︒,然后沿坡面CF上行了到达点D 处,此时在D 处测得楼顶A 的仰角为30︒,求楼AB 的高度.23.(9分)某中学举行钢笔书法大赛,对各年级同学的获奖情况进行了统计,并绘制了如下两幅不完整的统计图.请结合图中相关信息解答下列问题:(1)扇形统计图中三等奖所在扇形的圆心角的度数是 度; (2)请将条形统计图补全;(3)获得一等奖的同学中有14来自七年级,有14来自九年级,其他同学均来自八年级.现准备从获得一等奖的同学中任选2人参加市级钢笔书法大赛,请通过列表或画树状图的方法求所选出的2人中既有八年级同学又有九年级同学的概率.24.(9分)在我市“青山绿水”行动中,某社区计划对面积为23 600 m 的区域进行绿化,经投标由甲、乙两个工程队来完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,如果两队各自独立完成面积为2600m 区域的绿化时,甲队比乙队少用6天.(1)求甲、乙两工程队每天各能完成多少面积的绿化;(2)若甲队每天绿化费用是1.2万元,乙队每天绿化费用为0.5万元,社区要使这次绿化的总费用不超过40万元,则至少应安排乙工程队绿化多少天?-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无-----------------效----------------毕业学校_____________ 姓名________________ 考生号________________________________ ___________四、解答题(本大题共2个小题,共20分)25.(9分)如图1,在正方形ABCD中,AE平分CAB∠,交BC于点E,过点C作CF AE⊥,交AE的延长线于点G,交AB的延长线于点F.(1)求证:BE BF=;(2)如图2,连接BG BD、,求证:BG平分DBF∠;(3)如图3,连接DG交AC于点M,求AEDM的值.26.(11分)如图1,在平面直角坐标系中,抛物线249y x bx c=-++经过点(5,0)A-和点(1,0)B.(1)求抛物线的解析式及顶点D的坐标;(2)点P是抛物线上A D、之间的一点,过点P作PE x⊥轴于点E,PG y⊥轴,交抛物线于点G,过点G作GF x⊥轴于点F,当矩形PEFG的周长最大时,求点P的横坐标;(3)如图2,连接AD BD、,点M在线段AB上(不与A B、重合),作DMN DBA∠∠=,MN交线段AD于点N,是否存在这样点M,使得DMN△为等腰三角形?若存在,求出AN的长;若不存在,请说明理由.数学试卷第7页(共18页)数学试卷第8页(共18页)数学试卷 第9页(共18页) 数学试卷 第10页(共18页)四川省眉山市2019年初中毕业学业考试数学答案解析一、选择题 1.【答案】D【解析】2333||3,(3)9∴-=,-(-)=-=,四个数中,负数是【考点】正数和负数 2.【答案】C【解析】120亿个用科学记数法可表示为:101.210⨯个. 【考点】科学记数法的表示方法 3.【答案】D【解析】左视图有2层3列,第一层有3个正方形,第二层有一个正方形;每列上正方形的分布从左到右分别是2,1,1个. 【考点】三视图 4.【答案】D【解析】A.22x y 和3xy 不是同类项,故不能合并,故选项A 不合题意; B.()323628aba b -=-,故选项B 不合题意;C.222(3)96a b a ab b +=++,故选项C 不合题意;D.22(3)(3)9a b a b a b +-=-,故选项D 符合题意. 【考点】合并同类项的法则、幂的运算性质以及乘法公式 5.【答案】C【解析】30,70,703040B ADC BAD ADC B ︒︒︒︒︒∠=∠=∴∠=∠-∠=-=QAD Q 平分280BAC BAC BAD ∠∴∠∠︒,==, 180180308070.C B BAC ∴∠︒∠∠︒︒︒︒=--=--=【考点】三角形的外角性质定理、角平分线的定义以及三角形的内角和定理 6.【答案】A【解析】根据二次根式有意义,分式有意义得:20x +≥且10x -≠, 得:2x ≥﹣且1x ≠.【考点】分式有意义,分母不为0,二次根式的被开方数 7.【答案】B【解析】原式22()()a b a a b a b aa b a a b a a b-+-=⨯=⨯=+--.【考点】分式的混合运算 8.【答案】C【解析】566789x Q ,,,,,,,这组数据的平均数是7,775667899x ∴⨯+++++∴=-()=,这组数据从小到大排列为:5,6,6,7,8,9,9则最中间为7,即这组数据的中位数是7. 【考点】中位数 9.【答案】B【解析】如图所示,延长AC 交x 轴于点D .Q 这束光线从点(4,4)A 出发,经y 轴上的点C 反射后经过点(1,0)B , ∴设(,)C O C ,由反射定律可知,1OCD OCB OCD ∠∠∴∠∠=,=,CO DB ⊥Q 于O COD BOC ∴∠∠∴,=,在COD △和COB △中:OCD OCB OC OCCOD COB ∠=∠⎧⎪=⎨⎪∠=∠⎩, (),1,(1,0)COD COB ASA OD OB D ∴≅∴==∴-△△,设直线AD 的解析式为y kx b +=,则将点(4,4)A ,点(1,0)D -代入得444505,4k k b k b b ⎧⎧=⎪⎪=+⎪⎪∴⎨⎨=-+⎪⎪=⎪⎪⎩⎩∴直线AD 为4455y x =+,∴点C 坐标为40,5⎛⎫⎪⎝⎭.【考点】反射定律、全等三角形的判定与性质、待定系数法求一次函数解析式 10.【答案】A【解析】=CD AB CE DE ⊥∴Q ,,=2=222.5=45BOC A OCE ∠∠⨯︒︒∴Q ,△为等腰直角三角形,数学试卷 第11页(共18页) 数学试卷 第12页(共18页)62CE CD CE ∴===∴==【考点】圆周角定理 11.【答案】B【解析】连接CE ,如图所示:Q 四边形ABCD 是菱形,=90==6==8=ADC CD AB AD BC OA OC ∴∠︒,,,, EF AC AE CE ⊥∴Q ,=,设DE x =,则8CE AE x ==-,在Rt CDE △中,由勾股定理得:2226(8)x x +=-,解得:74x =,即7.4DE =【考点】矩形的性质、线段垂直平分线的性质、勾股定理 12.【答案】B【解析】Q 四边形ABCD 是菱形,AB BC ACB ACD ∴∠∠=,=,60BAC EAF BAE CAF ABC ∠∠︒∴∠∠Q ==,=,△是等边三角形, 6060ABC ACB ACD ACB ABE ACF ∴∠∠︒∴∠∠︒∴∠∠==,==,=,在BAE △和CAF △中,BAE CAF AB ACABE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()BAE CAF SAS AE AF BE CF ∴∴△≌△,=,=.故①正确;60EAF AEF ∠︒∴Q =,△是等边三角形,60AEF ∴∠︒=,60AEB CEF AEB EAB EAB CEF ∠+∠∠+∠︒∴∠∠Q ==,=,故②正确;6060ACD ACB ECF ∠∠︒∴∠︒Q ==,=,60AEB ABE ∠︒∴Q <,△和EFC △不会相似,故③不正确;过点A 作AG BC ⊥于点G ,过点F 作FH EC ⊥于点H ,156045EAB ABC AEB ∠︒∠︒∴∠︒Q =,=,=,在Rt AGB △中,60,4,2,ABC AB BG AG ︒∠==∴==Q 在Rt AEG △中,45,AEG EAG AG GE ︒∠=∠=∴==Q ,2EB EG BG ∴=-=,,120,2AEB AFC ABE ACF EB CF ︒≅∴∠=∠===Q △△,60FCE ∴∠︒=,在Rt CHF △中,30,2,1CFH CF CH ︒∠==∴=Q.1)3FH ∴=-=-∴点F 到BC的距离为3.综上,正确结论的个数是2个.【考点】四边形综合、菱形的性质、等边三角形的判定、全等三角形的判定和性质 二、填空题13.【答案】23(1)a a -【解析】()32223633213(1)a a a a a a a a -+=-+=-. 【考点】提公因式法、公式法分解因式 14.【答案】2017﹣【解析】a b Q 、是方程220190x x +-=的两个实数根,12019a b ab ∴+=-,=-,(1)(1)()12019112017a b ab a b ∴--=-++=-++=-.【考点】根与系数的关系 15.【答案】2【解析】210254x y k x y k +=-⎧⎨+=+⎩①②,2⨯-②①,得3=99x k +,解得=33x k +,把=33x k +代入①,得332=1k y k ++-,解得=2y k --,=5332=5x y k k +∴+Q ,--,解得=2k .【考点】二元一次方程组解的定义数学试卷 第13页(共18页) 数学试卷 第14页(共18页)16.【答案】32【解析】在Rt ABC △中,由勾股定理可得=13AC . 根据旋转性质可得=13,=5=12=8AE AD DE CD ∴,,. 在Rt CED △中,123tan 82DE ECD DC ∠===. 【考点】旋转的性质以及解直角三角形 17.【答案】 【解析】连接OQPQ Q 是O e 的切线,OQ PQ ∴⊥;根据勾股定理知222PQ OP OQ ∴=-,当PO AB ⊥时,线段PQ 最短, Q 在Rt AOB △中,8OA OB AB ====,4,OA OBOP PQ AB∴==∴==g 【考点】切线的性质、等腰直角三角形的性质以及勾股定理 18.【答案】4【解析】由题意得:E M D 、、位于反比例函数图象上,则11||,||22OCE OAD S k S k ∆∆==, 过点M 作MG y ⊥轴于点G ,作MN x ⊥轴于点N ,则ONMG S k Y =,又M Q 为矩形ABCO 对角线的交点,则S 矩形44ONMG ABCO S k Y ==, 由于函数图象在第一象限,0k ∴>,则124,422k kk k ++=∴=. 【考点】反比例函数系数k 的几何意义 三、解答题19.【答案】原式916918=-+=-+=. 【考点】实数运算20.(6分)【答案】275(1)532x x x x +-⎧⎪⎨->⎪⎩①②…,解①得:4x ≤,解②得1x >-, 则不等式组的解集为14x ≤-<. 【考点】解一元一次不等式组21.【答案】证明:==AE BE EAB EBA ∴∠∠Q ,,===AB DC DEA EAB CEB EBA DEA CEB ∴∠∠∠∠∴∠∠Q ∥,,,,Q 点E 是CD 的中点,=DE CE ∴,在ADE △和BCE △中,,(),DE CE DEA CEB ADE BCE SAS D C AE BE =⎧⎪∠=∠∴≅∴∠=∠⎨⎪=⎩△△.【考点】全等三角形的判定与性质、等腰三角形的性质、平行线的性质、等腰三角形的性质22.【答案】在Rt DEC △中,2221,,2DE i DE EC CD CD FC ==+==Q222(2)DE DE ∴+=,解得:20m 40m DE EC ∴=,=,过点D 作DG AB ⊥于G ,过点C 作CH DG ⊥于H ,如图所示:则四边形DEBG 、四边形DECH 、四边形BCHG 都是矩形,45ACB AB BC AB BC ∠︒⊥∴Q =,,=,设m (20)m (40)m AB BC x AG x DG x -=+==,=,, 在Rt ADG △中,20tan ,40AG x ADG DG x -=∠∴+Q,解得:50x =+答:楼AB的高度为(50+)米. 【考点】解直角三角形的应用数学试卷 第15页(共18页) 数学试卷 第16页(共18页)23.【答案】(1)108 (2)如图所示(3)一等奖中七年级人数为1414⨯=(人),九年级人数为1414⨯=(人),则八年级的有2人,画树状图如下:由树状图知,共有12种等可能结果,其中所选出的2人中既有八年级同学又有九年级同学的有4种结果,所以所选出的2人中既有八年级同学又有九年级同学的概率为13. 【解析】(1)Q 被调查的总人数为1640%40÷=(人),∴扇形统计图中三等奖所在扇形的圆心角的度数是1236010840︒︒⨯=. (2)一等奖人数为40812164++-()=(人), 补全图形如下:【考点】列表法或树状图法求概率24.【答案】(1)设乙工程队每天能完成绿化的面积是2m x , 根据题意得:60060062x x-=,解得:50x =, 经检验,50x =是原方程的解,则甲工程队每天能完成绿化的面积是2502200(m )⨯=, 答:甲、乙两工程队每天能完成绿化的面积分别是22100m 50m 、. (2)设甲工程队施工a 天,乙工程队施工b 天刚好完成绿化任务, 由题意得:100503600a b +=,则7213622b a b -==-+, 根据题意得:721.20.5402bb -⨯+…,解得:32b ≥, 答:至少应安排乙工程队绿化32天. 【考点】分式方程和一元一次不等式的应用四、解答题25.【答案】(1)证明:Q 四边形ABCD 是正方形,90,90ABC AB BC EAB AEB ∴∠︒∴∠+︒==,=, 90AG CF FCB CEG ⊥∴∠+∠︒Q ,=,AEB CEG EAB FCB ∠∠∴∠∠Q =,=,在ABE △和CBF △中,90EAB FCB AB BC ABE CBF ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,()ABE CBF ASA BE BF ∴∴△≌△,=;(2)证明:Q 四边形ABCD 是正方形,45ABD CAB ∴∠=∠=︒,AE Q 平分22.5CAB CAG FAG ∠∴∠∠︒,==,在AGC △和AGF △中,90CAG FAG AG AG AGC AGF ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,()AGC AGF ASA CG GF ∴∴△≌△,=,90CBF GB GC GF ∠︒∴Q =,==,90909022.567.5GBF GFB FCB GAF ∴∠∠︒-∠︒∠︒︒︒===-=-=, 1801804567.567.5DBG ABD GBF ∴∠︒∠∠︒︒︒︒=--=--=,DBG GBF BG ∴∠∠∴=,平分DBF ∠;(3)连接BG ,如图3所示:数学试卷 第17页(共18页) 数学试卷 第18页(共18页)Q 四边形ABCD 是正方形,,45,90,DC AB DCA ACB DCB AC ︒︒∴=∠=∠=∠=∴,9022.5112.5DCG DCB BCF DCB GAF ∠∠+∠∠+∠︒+︒︒Q ====, 18018067.5112.5ABG GBF DCG ABG ∠︒∠︒︒︒∴∠∠=-=-=,=,在DCG △和..中,,()DC AB DCG ABG DCG ABG SAS CG BG =⎧⎪∠=∠∴≅⎨⎪=⎩△△,22.5CDG GAB CDG CAG ∴∠∠︒∴∠∠==,=,45,~,AE ACDCM ACE DCM ACE DM DC︒∠=∠=∴∴==Q △△. 【考点】相似三角形的判定与性质、正方形的性质、角平分线定义、等腰直角三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质 26.【答案】(1)抛物线的表达式为:2441620(5)(1)9999y x x x x =-+-=--+, 则点(-2,4)D ;(2)设点241620,999P m m m ⎛⎫--+ ⎪⎝⎭,则241620,2(2)42999PE m m PG m m =--+=--=--, 矩形PEFG 的周长2416202()242999PE PG m m m ⎛⎫=+=--+-- ⎪⎝⎭28172259418m ⎛⎫=-++ ⎪⎝⎭,809-<Q ,故当174m =-时,矩形PEFG 周长最大,此时,点P 的横坐标为174-;(3),180DMN DBA BMD BDM ADB ∠∠∠+∠︒-∠Q ==,180NMA DMB DMN ∠+∠︒-∠=,,~,AN AMNMA MDB BDM AM BM BD∴∠=∠∴=△△, 而6,5AB AD BD ===,①当MN DM =时,BDM AMN ∴△≌△, 即:5AM BD ==,则1AN MB ==;②当NM DN =时,则2NDM NMD AMD ADB AD AB AM ∠∠∴∴⨯=,△∽△,=,即:256AM =⨯,则256AM =, 而AN AM BM BD =,即25625566AN =-,解得:5536AN =; ③当DN DM =时,DMN DAB ∠∠Q >,而DAB DMN DNM DMN ∠∠∴∠∠=,>,DN DM ∴≠,故1AN =或5536.【考点】二次函数综合运用。
眉山市2018年初中学业水平暨高中阶段学校招生考试数学试卷参考解答

眉山市2018年高中招生考试数学试题参考解答1.C 2.D 3.D 4.B 5.C 6.A 7.B 8.C 9.A 10.C 11.A 12.12.D 点拔:∵CD =2AD ,又F 为CD 中点,∴CD =2CF ,于是CF =CD , 在□ABCD 中,BC =AD ,∴CF =BC ,∴∠CFB =∠CBF ,又CD ∥AB ,∴∠CFB =∠ABF , ∴∠CBF =∠ABF ,故∠ABC=2∠ABF ,①正确;取AB 的中点G ,连结FG ,可得DFGA 为平行四边形,∴FG ∥AD ,由平行线等分线段定理,可得FG 平分BE ,易得FG ⊥BE ,∴FG 为BE 的垂直平分线,因而有FE =FB ;②正确;延长EF 交BC 的延长线于G ,易证△DEF ≌△CHF ,S △EFB =S △BFH =S △BFC +S △CFH =S △BFC +S △DEF ,于是EF =FH ,S 四边形DEBC=2S △EFB 成立;③正确;(现在的数学教材真是怪物,三角形中位线定理本应按原全日制教材应在平行四边形一章讲,结果放到相似形再讲,没有原安排科学合理。
在讲三角形中位线定理后,按理应讲梯形中位线定理,而目前华东师大版教材将梯形中位线定理彻底枪毙了。
此题第③结论判断,若用梯形中位线定理,令FG 交BE 于I ,则FI =21(DE +BC ), ∴S 梯形DEBC =21(DE +BC )·BE =FI ·BE =2S △EFB 很容易得出.) ③的正确性的又一说明:S △DEF =21S △DFA =41S □DFGA =81S □ABCD ,S △AEB =21S △ABD =41S □ABCD ,S △BCF =21S △BCD =41S □ABCD ,S △EFB =S □ABCD ―S △DEF ―S △AEB ―S △BCF =S □ABCD ―81S □ABCD -41S □ABCD -41S □ABCD =83S □ABCD , ∴S 梯形DEBC =S □ABCD -41S □ABCD =43S □ABCD ,∴S 梯形DEBC =2 S △EFB .由□ADFG 可知∠DEF =∠DFG ,由EF =FB 及FG ⊥BE ,可得∠DFG =∠BFG ,不难知□BCFG 是菱形,所以∠GFB =∠CFB ,于是∠CFE =3∠DEF .④正确.二、13.)3)(3(-+x x x 14.1y >2y15.6<k 且3≠k .解:两边同乘)3(-x ,得:k x x =--)3(2,解得:k x -=6,∵原分式方程有一个正数解,所以0>x ,且3≠x , 于是⎩⎨⎧≠->-3606k k ,解得6<k 且3≠k .16.21π 解:∵AC=BC=2,∴AB =8222222=+=+BC AC .S 阴影BB ′C =S 扇形ABB ′-SRt △ABC =BC AC AB ∙-21360452π 2421)8(812-=⨯-=ππ. 由旋转特征知:AC =AC ′=2,S △ABC =S △AB ′C ′=2,S 阴影B ′C ′C =S △AB ′C ′-S 扇形ACC ′=2360452AC π-=2-21π ∴S 阴影=S 阴影BB ′C +S 阴影B ′C ′C =π-2+2-21π=21π.17.2如图,连结BE 、AE .∵BE ∥DC ,∴∠AOD=∠ABE . 在Rt △ABE 中,有BE =2,AE =22,tan ∠ABE=2=BEAE,∴tan ∠AOD=2. 另解:解:如图,连接BE ,∵四边形BCEK 是正方形, ∴KF=CF=21CK ,BF= 21BE ,CK=BE ,BE ⊥CK ,∴BF=CF ,根据题意得:AC ∥BK ,∴△ACO ∽△BKO ,∴KO :CO=BK :AC=1:3,∴KO :KF=1:2,∴KO=OF=21CF=21BF , 在Rt △PBF 中,tan ∠BOF= BF : OF =2, ∵∠AOD=∠BOF , ∴tan ∠AOD=2. 故答案为:218.51 解:∵AC ·OB =160,∴S 菱形=21AC ·OB =80.∴S △OAB =40 在菱形OABC 中,AC ⊥OB ,AC =2AD ,OB =2OD ,∴2AD ·2OD =160, ∴AD ·OD =40,作DF ⊥OA 于F ,延长FD 交BE 于G , ∴AD ·OD =OA ·DF .G∵A (-10,0),∴OA =10,∴40=10DF ,解得DF =4.不难证明△DAF ≌△DCG ,∴DG =DF =4,于是GF =8,∴EH =8 又△ADF ∽△DOF ,∴OFDFDF AF =,∴DF 2=AF ·OF , 设AF =x ,则OF =OA -AF =10-x ,∴x (10-x )=16,解得x =2或x =8(舍去)∴AF =GC =2,OF =8,∴S △DFO =21OF ·DF =16,∴k =2 S △DFO =32, ∴k =-32,则双曲线的解析式为xy 32-=∴S △EHO =21OH ·EH =21OH ·8=21k =16,∴OH =4∴GE =HF =OF -OH =8-4=4,又GC =AF =2,∴CE =GE -GC =2. ∴S △CEO =21CE ·EH =21×2×8=8,∴S △OCE ∶S △O AB =8∶40=51. 三、19.解:原式=1+4×23-23-4=-3. 20.解:原式=)12()1()1()2()1()1)(1(2-+⋅⎪⎪⎭⎫ ⎝⎛+--++-x x x x x x x x x x x=)12()1()1(2)1(1222-+⋅⎪⎪⎭⎫ ⎝⎛+--+-x x x x x x x x x x =)12()1()1(21222-+⋅++--x x x x x x x x =)12()1()1(122-+⋅+-x x x x x x =21x x +. ∵0222=--x x ,∴222+=x xD∴原式=21)1(21221=++=++x x x x .21.解:(1)如图所示,C 1(-1,2); (2)如图所示,C 2(-3,-2); (3)直线l 的函数解析式为x y -=.22.解:向左延长点B 处的水平线与AC 交于点D ,显然BD ⊥AC . 设BD =x ,在Rt △BDA 中,tan60°=AD BD ,∴AD =x BD BD 333360tan =︒=. 在Rt △BDC 中,∠DBC =90°-37°=53°, tan53°=BDCD,∴CD =BD tan53°=x tan53° 又∵AD +DC =AC =13∴x 33+x tan53°=13,解得︒+=53tan 3313x ,在Rt △BDC 中,cos53°=BCBD, ∴BC ==︒53cos BD︒+53tan 3313·︒53cos 1≈343313+·35=20-53(千米).23.解:(1)该班总人数=6÷15%=40(人) ∴m =40×40%=16,40×n%=8解得:n =20;(2)羽毛球的百分比是:6÷40=15%,所以该校参加羽毛球的人数大约为 1000×15%=150(人) (3)树状图如图D D D C CCC BBB D AA AP(一男一女)=21126=. 24. 解:(1)设李明第x 天生产的粽子数量为280只,根据题意得:8020+x =280,解得:10=x ,所以李明第10天生产的粽子数量为280只; (2)由图象知,当100≤≤x 时,2=p ;当2010≤<x 时,设b kx p +=,将点(10,2)、(20,3)代入得:⎩⎨⎧=+=+320210b k b k ,解得⎩⎨⎧==11.0b k ,所以11.0+=x p , ①当60≤≤x 时,W =(4-2)·34x =72x ,当6=x 时,W 最大=432(元)②当106≤<x 时,W =(4-2)(20x +80),当10=x 时,W 最大=560(元)③当2010≤<x 时,W =(4-11.0-x )(20x +80)=2405222++-x x∵02<-=a ,∴当132=-=abx 时(在2010≤<x 内),W 最大=578(元) 综上所述,第13天利润最大,最大利润为578元.四、25.证明:(1)∵AC =AB ,M 为BC 的中点, ∴∠CAM =∠BAM ,AM ⊥BC ,在Rt △ACM 中,∠CAH =90°-∠ACB ,又∵AC ⊥BD ,∴在Rt △CBE 中,∠CBE =90°-∠ACB , ∴∠CAM =∠CBE ∴∠BAM =∠CBE又∵MB=MN.∴∠MNB =∠MBN ,∴∠BAM +∠ABN =∠CBE +∠DBN ∴∠ABN =∠DBN∴BN 平分∠ABE ;(2)在□DNBC 中,BN =CD ,BN ∥CD ,∴∠CDB =∠DBN ,由(1)知∠ABN =∠DBN ∴∠CDB =∠ABN ,又AB =BD , ∴△ABN ≌△BCD ,∴BC =AN设BM =MC =a ,则BM =MN =a ,AN =BC =2a , ∴AM =AN +MN =3a在Rt △ABN 中,AB =BD =1,由勾股定理,得222AB BM AM =+,代入得:1922=+a a ,解得:1010=a . 故BC =2×5101010=. (3)由F 为AB 的中点,M 为BC 的中点,知FM 为△ABC 的中位线,∴21=AC FM ,又AC =BD ,∴21=BD FM . ∵21==BC BM BC MN ,∴=BC MN BDFM 又FM 是Rt △ABM 斜边上的中线,∴FM =AF ,∴∠FMN =∠BAM ,由(1)的证明知:∠BAM =∠CBD ,因而有:∠FMN =∠CBD ∴△MFN ∽△BDC.26.解:(1)∵抛物线c bx ax y ++=2过点A (0,3),∴c =3,∵抛物线对称轴为2=x , ∴22=-ab.∴a b 4-=又B (1,0)在抛物线上,∴0=++c b a ,解得1=a ,4-=b . ∴抛物线解析式为342+-=x x y .(2)令与OE 平行且与抛物线相切于P 的直线为l , 由于△AOE 的面积是定值为29,∴△OPE 的面积最大时,四边形AOPE 面积最大.令与OE 平行且与抛物线相切于P 的直线为l ′,此时位置的P 能使四边形AOPE 面积最大 ∵∠AOE 的平分线为OE ,所以直线OE 的解析式为x y =,设直线的l ′的解析式为d x y +=,∴d x x x +=+-342有两个相等的实根,∴0)3(425=--d ,解得413-=d . ∴OQ =413,OH =OQsin45°=2813∴413342-=+-x x x ,解得225=x ,∴225=m .在Rt △AOE 中,OE =︒45sin OA=23,∴S △OPE =OH OE ⋅21=83928132321=⨯⨯, ∴四边形AOPE 面积最大面积=S △AOE +S △OPE =29+839=875,(3)如图3,过P 作MN ⊥y 轴,交y 轴于M ,交l 于N , ∵△OPF 是等腰直角三角形,且OP=PF , 易得△OMP ≌△PNF , ∴OM=PN ,∵P (m ,m 2-4m+3),则-m 2+4m-3=2-m , 解得:m=255+ 或255- ,∴P 的坐标为(255+ ,215+ )或(255-,251-); 如图4,过P 作MN ⊥x 轴于N ,过F 作FM ⊥MN 于M , 同理得△ONP ≌△PMF , ∴PN=FM , 则-m 2+4m-3=m-2, 解得:x=253+或253- ; P 的坐标为(253+,251- )或(253- ,251+); 综上所述,点P 的坐标是:(255+ ,215+ )或(255-,251-)或(253+,251- )或(253- ,251+).。
2019年四川省眉山市中考数学试卷-答案

四川省眉山市2019年初中毕业学业考试数学答案解析一、选择题1.【答案】D【解析】2333||3,(3)9∴-=,-(-)=-=,四个数中,负数是【考点】正数和负数2.【答案】C【解析】120亿个用科学记数法可表示为:101.210⨯个.【考点】科学记数法的表示方法3.【答案】D【解析】左视图有2层3列,第一层有3个正方形,第二层有一个正方形;每列上正方形的分布从左到右分别是2,1,1个.【考点】三视图4.【答案】D【解析】A .22x y 和3xy 不是同类项,故不能合并,故选项A 不合题意;B .()323628ab a b -=-,故选项B 不合题意;C .222(3)96a b a ab b +=++,故选项C 不合题意;D .22(3)(3)9a b a b a b +-=-,故选项D 符合题意.【考点】合并同类项的法则、幂的运算性质以及乘法公式5.【答案】C【解析】30,70,703040B ADC BAD ADC B ︒︒︒︒︒∠=∠=∴∠=∠-∠=-= AD 平分280BAC BAC BAD ∠∴∠∠︒,==,180180308070.C B BAC ∴∠︒∠∠︒︒︒︒=--=--=【考点】三角形的外角性质定理、角平分线的定义以及三角形的内角和定理6.【答案】A【解析】根据二次根式有意义,分式有意义得:20x +≥且10x -≠,得:2x ≥﹣且1x ≠.【考点】分式有意义,分母不为0,二次根式的被开方数7.【答案】B 【解析】原式22()()a b a a b a b a a b a a b a a b-+-=⨯=⨯=+--. 【考点】分式的混合运算8.【答案】C【解析】566789x ,,,,,,,这组数据的平均数是7, 775667899x ∴⨯+++++∴=-()=,这组数据从小到大排列为:5,6,6,7,8,9,9 则最中间为7,即这组数据的中位数是7.【考点】中位数9.【答案】B【解析】如图所示,延长AC 交x 轴于点D .这束光线从点(4,4)A 出发,经y 轴上的点C 反射后经过点(1,0)B ,∴设(,)C O C ,由反射定律可知,1OCD OCB OCD ∠∠∴∠∠=,=, CO DB ⊥于O COD BOC ∴∠∠∴,=,在COD △和COB △中:OCD OCB OC OCCOD COB ∠=∠⎧⎪=⎨⎪∠=∠⎩, (),1,(1,0)COD COB ASA OD OB D ∴≅∴==∴-△△,设直线AD 的解析式为y kx b +=,则将点(4,4)A ,点(1,0)D -代入得444505,4k k b k b b ⎧⎧=⎪⎪=+⎪⎪∴⎨⎨=-+⎪⎪=⎪⎪⎩⎩∴直线AD 为4455y x =+,∴点C 坐标为40,5⎛⎫ ⎪⎝⎭. 【考点】反射定律、全等三角形的判定与性质、待定系数法求一次函数解析式10.【答案】A【解析】=CD AB CE DE ⊥∴,,=2=222.5=45BOC A OCE ∠∠⨯︒︒∴,△为等腰直角三角形,62CE CD CE ∴====【考点】圆周角定理11.【答案】B【解析】连接CE ,如图所示:四边形ABCD 是菱形,=90==6==8=ADC CD AB AD BC OA OC ∴∠︒,,,,EF AC AE CE ⊥∴,=,设DE x =,则8CE AE x ==-,在Rt CDE △中,由勾股定理得:2226(8)x x +=-, 解得:74x =,即7.4DE = 【考点】矩形的性质、线段垂直平分线的性质、勾股定理12.【答案】B 【解析】四边形ABCD 是菱形,AB BC ACB ACD ∴∠∠=,=,60BAC EAF BAE CAF ABC ∠∠︒∴∠∠==,=,△是等边三角形,6060ABC ACB ACD ACB ABE ACF ∴∠∠︒∴∠∠︒∴∠∠==,==,=,在BAE △和CAF △中,BAE CAF AB ACABE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()BAE CAF SAS AE AF BE CF ∴∴△≌△,=,=.故①正确;60EAF AEF ∠︒∴=,△是等边三角形,60AEF ∴∠︒=,60AEB CEF AEB EAB EAB CEF ∠+∠∠+∠︒∴∠∠==,=,故②正确;6060ACD ACB ECF ∠∠︒∴∠︒==,=,60AEB ABE ∠︒∴<,△和EFC △不会相似,故③不正确;过点A 作AG BC ⊥于点G ,过点F 作FH EC ⊥于点H ,156045EAB ABC AEB ∠︒∠︒∴∠︒=,=,=,在Rt AGB △中,60,4,2,ABC AB BG AG ︒∠==∴==,在Rt AEG △中,45,AEG EAG AG GE ︒∠=∠=∴==2EB EG BG ∴=-=,,120,2AEB AFC ABE ACF EB CF ︒≅∴∠=∠===△△,60FCE ∴∠︒=,在Rt CHF △中,30,2,1CFH CF CH ︒∠==∴.1)3FH ∴==∴点F 到BC的距离为3.综上,正确结论的个数是2个.【考点】四边形综合、菱形的性质、等边三角形的判定、全等三角形的判定和性质二、填空题13.【答案】23(1)a a -【解析】()32223633213(1)a a a a a a a a -+=-+=-.【考点】提公因式法、公式法分解因式14.【答案】2017﹣【解析】a b 、是方程220190x x +-=的两个实数根,12019a b ab ∴+=-,=-,(1)(1)()12019112017a b ab a b ∴--=-++=-++=-.【考点】根与系数的关系15.【答案】2【解析】210254x y k x y k +=-⎧⎨+=+⎩①②, 2⨯-②①,得3=99x k +,解得=33x k +,把=33x k +代入①,得332=1k y k ++-,解得=2y k --,=5332=5x y k k +∴+,--,解得=2k .【考点】二元一次方程组解的定义16.【答案】32【解析】在Rt ABC △中,由勾股定理可得=13AC .根据旋转性质可得=13,=5=12=8AE AD DE CD ∴,,. 在Rt CED △中,123tan 82DE ECD DC ∠===. 【考点】旋转的性质以及解直角三角形17.【答案】【解析】连接OQPQ 是O 的切线,OQ PQ ∴⊥;根据勾股定理知222PQ OP OQ ∴=-,当PO AB ⊥时,线段PQ 最短,在Rt AOB △中,8OA OB AB ====,4,OA OB OP PQ AB∴==∴【考点】切线的性质、等腰直角三角形的性质以及勾股定理18.【答案】4【解析】由题意得:E M D 、、位于反比例函数图象上,则11||,||22OCE OAD S k S k ∆∆==, 过点M 作MG y ⊥轴于点G ,作MN x ⊥轴于点N , 则ONMG S k =, 又M 为矩形ABCO 对角线的交点,则S 矩形44ONMG ABCO S k ==,由于函数图象在第一象限,0k ∴>,则124,422k k k k ++=∴=. 【考点】反比例函数系数k 的几何意义三、解答题19.【答案】原式916918=-+-+=. 【考点】实数运算 20.(6分)【答案】275(1)532x x x x +-⎧⎪⎨->⎪⎩①②,解①得:4x ≤,解②得1x >-, 则不等式组的解集为14x ≤-<.【考点】解一元一次不等式组21.【答案】证明:==AE BE EAB EBA ∴∠∠,,===AB DC DEA EAB CEB EBA DEA CEB ∴∠∠∠∠∴∠∠∥,,,,点E 是CD 的中点,=DE CE ∴,在ADE △和BCE △中,,(),DE CE DEA CEB ADE BCE SAS D C AE BE =⎧⎪∠=∠∴≅∴∠=∠⎨⎪=⎩△△.【考点】全等三角形的判定与性质、等腰三角形的性质、平行线的性质、等腰三角形的性质22.【答案】在Rt DEC △中,2221,,2DE i DE EC CD CD FC ==+== 222(2)DE DE ∴+=,解得:20m 40m DE EC ∴=,=,过点D 作DG AB ⊥于G ,过点C 作CH DG ⊥于H ,如图所示:则四边形DEBG 、四边形DECH 、四边形BCHG 都是矩形,45ACB AB BC AB BC ∠︒⊥∴=,,=,设m (20)m (40)m AB BC x AG x DG x -=+==,=,,在Rt ADG △中,20tan ,40AG x ADG DG x -=∠∴=+,解得:50x =+答:楼AB 的高度为(50+)米.【考点】解直角三角形的应用23.【答案】(1)108(2)如图所示(3)一等奖中七年级人数为1414⨯=(人),九年级人数为1414⨯=(人),则八年级的有2人,画树状图如下:由树状图知,共有12种等可能结果,其中所选出的2人中既有八年级同学又有九年级同学的有4种结果,所以所选出的2人中既有八年级同学又有九年级同学的概率为13.【解析】(1)被调查的总人数为1640%40÷=(人), ∴扇形统计图中三等奖所在扇形的圆心角的度数是1236010840︒︒⨯=. (2)一等奖人数为40812164++-()=(人),补全图形如下:【考点】列表法或树状图法求概率 24.【答案】(1)设乙工程队每天能完成绿化的面积是2m x ,根据题意得:60060062x x-=,解得:50x =, 经检验,50x =是原方程的解,则甲工程队每天能完成绿化的面积是2502200(m )⨯=,答:甲、乙两工程队每天能完成绿化的面积分别是22100m 50m 、. (2)设甲工程队施工a 天,乙工程队施工b 天刚好完成绿化任务,由题意得:100503600a b +=,则7213622b a b -==-+, 根据题意得:721.20.5402b b -⨯+,解得:32b ≥, 答:至少应安排乙工程队绿化32天.【考点】分式方程和一元一次不等式的应用四、解答题25.【答案】(1)证明:四边形ABCD 是正方形,90,90ABC AB BC EAB AEB ∴∠︒∴∠+︒==,=,90AG CF FCB CEG ⊥∴∠+∠︒,=,AEB CEG EAB FCB ∠∠∴∠∠=,=,在ABE △和CBF △中,90EAB FCB AB BC ABE CBF ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,()ABE CBF ASA BE BF ∴∴△≌△,=;(2)证明:四边形ABCD 是正方形,45ABD CAB ∴∠=∠=︒, AE 平分22.5CAB CAG FAG ∠∴∠∠︒,==,在AGC △和AGF △中,90CAG FAG AG AG AGC AGF ︒∠=∠⎧⎪=⎨⎪∠=∠=⎩,()AGC AGF ASA CG GF ∴∴△≌△,=,90CBF GB GC GF ∠︒∴=,==,90909022.567.5GBF GFB FCB GAF ∴∠∠︒-∠︒∠︒︒︒===-=-=,1801804567.567.5DBG ABD GBF ∴∠︒∠∠︒︒︒︒=--=--=,DBG GBF BG ∴∠∠∴=,平分DBF ∠;(3)连接BG ,如图3所示:四边形ABCD 是正方形,,45,90,DC AB DCA ACB DCB AC ︒︒∴=∠=∠=∠=∴,9022.5112.5DCG DCB BCF DCB GAF ∠∠+∠∠+∠︒+︒︒====,18018067.5112.5ABG GBF DCG ABG ∠︒∠︒︒︒∴∠∠=-=-=,=,在DCG △和..中,,()DC AB DCG ABG DCG ABG SAS CG BG =⎧⎪∠=∠∴≅⎨⎪=⎩△△,22.5CDG GAB CDG CAG ∴∠∠︒∴∠∠==,=,45,~,AE AC DCM ACE DCM ACE DM DC︒∠=∠=∴∴=△△【考点】相似三角形的判定与性质、正方形的性质、角平分线定义、等腰直角三角形的判定与性质、等腰三角形的判定与性质、全等三角形的判定与性质26.【答案】(1)抛物线的表达式为:2441620(5)(1)9999y x x x x =-+-=--+, 则点(-2,4)D ; (2)设点241620,999P m m m ⎛⎫--+ ⎪⎝⎭, 则241620,2(2)42999PE m m PG m m =--+=--=--, 矩形PEFG 的周长2416202()242999PE PG m m m ⎛⎫=+=--+-- ⎪⎝⎭ 28172259418m ⎛⎫=-++ ⎪⎝⎭, 809-<,故当174m =-时,矩形PEFG 周长最大, 此时,点P 的横坐标为174-; (3),180DMN DBA BMD BDM ADB ∠∠∠+∠︒-∠==, 180NMA DMB DMN ∠+∠︒-∠=,,~,AN AM NMA MDB BDM AM BM BD∴∠=∠∴=△△, 而6,5AB AD BD ===, ①当MN DM =时,BDM AMN ∴△≌△,即:5AM BD ==,则1AN MB ==;②当NM DN =时,则2NDM NMD AMD ADB AD AB AM ∠∠∴∴⨯=,△∽△,=, 即:256AM =⨯,则256AM =, 而AN AM BM BD =,即25625566AN =-,解得:5536AN =; ③当DN DM =时,DMN DAB ∠∠>,而DAB DMN DNM DMN ∠∠∴∠∠=,>,DN DM≠,故1AN=或55 36.【考点】二次函数综合运用。
2018眉山市中考数学试题(含答案及部分解析)

数学试卷第1页(共6页)眉山市2018年初中学业水平暨高中阶段学校招生考试数 学 试 卷注意事项:1。
本试卷分A 卷和B 卷两部分,A 卷共100分,B 卷共20分,满分120分,考试时间120分钟.2. 答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
3。
答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号;答非选择题时,必须使用05毫米黑色签字笔,将答案书写在答题卡规定的位置上;所有题目必须在答题卡上作答,在试题卷上答题无效.4。
不允许使用计算器进行运算,凡无精确度要求的题目,结果均保留准确值。
5.凡作图题或辅助线均用签字笔画图。
A 卷(共100分) 第Ⅰ卷(选择题共36分)1.绝对值为1的实数共有 A .0个 B .1个 C .2个 D .4个答案:C2.据相关报道,开展精准扶贫工作以来,我国约有65000000人摆脱贫困,将65000000用科学记数法表示为 A .65×106B .0。
65×108C .6。
5×106D .6。
5×107答案:D3.下列计算正确的是 A .(x +y )2=x 2+y 2 B .(-21xy 2)3=-16x 3y 6 C .x 6÷x 3=x 2D .22)( =2答案:D4.下列立体图形中,主视图是三角形的是数学试卷第2页(共6页)答案:B5.将一副直角三角板按如图所示的位置放置,使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是 A .45° B .60° C .75°D .85°答案:C6.如图所示,AB 是⊙O 的直径,P A 切⊙O 于点A ,线段PO 交⊙O 于点C ,连结BC ,若∠P =36°,则∠B 等于 A .27° B .32°C .36°D .54°答案:A7.某校有35名同学参加眉山市的三苏文化知识竞赛,预赛分数各不相同,取前18名同学参加决赛。
2019年四川省眉山市中考适应性考试数学试题及答案

眉山市初中2019届中考适应性考试数 学 试 卷本试卷分A 卷和B 卷两部分. A 卷共100分,B 卷共20分, 满分120分,考试时间120分钟.注意事项:1、答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上.2、答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.答非选择题时,必须使用0.5毫米黑色签字笔,将答案书写在答题卡规定的位置上.3、不允许使用计算器进行运算,凡无精确度要求的题目,结果均保留准确值.4、所有题目必须在答题卡上作答,在试题卷上答题无效.5、考试结束后,将答题卡交回.A 卷(共100分) 第Ⅰ卷(选择题,共36分)一、选择题:本大题共12个小题,每小题3分,共36分,在每小题给出的四个选项中,只有一项是正确的,请将正确答案填涂在答题卡相应位置.1、如果a 的相反数是13-,那么a 的值是 A .3- B .3 C .13- D .132、能使x有意义的x 的取值范围是A .x >-2B .x≥-2C .x≥-2且x≠0D .x >0 3、下列各式运算正确的是A .235()a a =B .236a a a ⋅=C .32a a a -= D .235a a a +=4、在“百度”搜索引擎中输入“初中数学教育”,能搜索到与之相关的网页约为 8 680 000个,将这个数用科学记数法表示为A .51068.8⨯ B .6108.86⨯ C .61068.8⨯ D .71068.8⨯5、如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是A .B .C .D . 6、在下列命题中,正确的是A .一组对边平行的四边形是平行四边形B .有一个角是直角的四边形是矩形C .有一组邻边相等的平行四边形是菱形D .对角线互相垂直平分的四边形是正方形 7、两实数根的和是3的一元二次方程为 A .x 2+3x ﹣5=0 B .x 2﹣5x+3=0C .2x 2﹣6x+3=0D .3x 2﹣6x+8=08、如右图,CD 是⊙0的直径,A ,B 是⊙0上的两点,若70ADC ∠=,则ABD ∠ 的度数为A .50B .40C .30D .209、若关于x 的一元二次方程kx 2﹣2x ﹣1=0有实数根,则k 的取值 范围是A .k ≥-1且k ≠0B .k ≥-1C .k ≤1D .k ≤1且k ≠010、某车间5名工人日加工零件数分别为6,10,4,5,4,则这组数据的中位数和众数分别是 A .4,5 B .5,4 C .6,4 D .10,6 11、如图,在三角形纸片ABC 中,90ACB ∠=,3BC =,6AB =,在AC 上取一点E ,以BE 为折痕,使AB 的一部分与BC 重合,A 与BC 延长线上的点D 重合,则CE 的长度为AB .6 C. D .312、函数y =4x 和y =1x 在第一象限内的图象如图,点P 是y =4x 的图象上一动点,PC ⊥x 轴于点C ,交y =1x 的图象于点A . PD ⊥y 轴于点D ,交y =1x 的图象于点B 。
2018年全国初中数学联赛模拟试题(含答案)

2018年全国初中数学联赛模拟试题第一试一、选择题(每小题7分,共42分)1.已知a 、b 、c 是两两不相等的实数.则方程(x-a )(x-b )+(x-b )(x-c )+(x-c )(x-a )=0根的情况为( ).(A )必有两个不相等的实根 (B )没有实根(C )必有两个相等的实根 (D )方程的根有可能取值a 、b 、c2.在半径为1的圆内,自点A 出发的所有长度不小于该圆的内接正△ABC•的边长a 的弦,所组成的图形的面积为( ) (A )2π+23 (B )3π+22 (C )2π+33 (D )3π+323.已知a 、b 为实数,设b-a=2 006,如果关于x 的一元二次方程x 2+ax+b=0的根都是整数,则该方程的根共有( )组.(A )4 (B )6 (C )8 (D )104.如图是一个三角形数表,从上到下依次称作第一行、第二行、…….•已知该三角形数表中每个“”中的数均为正整数的倒数,且等于与其相连的两脚下数之和.如果第一行中的那个数是11,则第三行中的数从左至右的填法有( ).(A )恰有一种 (B )恰有两种 (C )恰有三种 (D )有无数多种5.在△ABC 中,AB<BC<CA ,且AC-AB=2,AD 为∠BAC 的平分线,E 为边AC 上的一点,•联结BE 交AD 于点G ,且2,AC AE AGCD BD GD===2 007,则边BC 的长为( ). (A )2 008 (B )2 007 (C )2 006 (D )2 0056.某次数学竞赛设选择题(含6个小题)、填空题(含4个小题)、解答题(含3个小题)分类,其中,选择题、填空题均每小题7分,解答题中第1小题20分、第2、3小题每小题25分,满分140分.评分标准是:选择题、填空题做对得7分,不做或做错得0分;解答题设0分,5分,10分,15分,20分,25分共6档.那么,这次考试所得的不同分数最多有( )种.(A )141 (B )129 (C )105 (D )117二、填空题(每小题7分,共28分) 1.已知a 、b 、c 均为非零实数,满足:b c a c a b a b c a b c +-+-+-==,则()()()a b b c c a abc+++的值为_________. 2.点G 是△ABC 的重心,过点G 的直线与边AB 、AC 分别交于点M 、N .已知,AM ANm AB AC==n .则一次函数y=-nmx+n 与x 轴、y 轴所围成的三角形的面积的最小值为______.3.把n 个大小均不相同的正方形互不重叠地拼在一起,•所得的图形的面积恰为2006,则n 的最小值为______.4.如图,两个全等的边长为正整数的正△A 1B 1C 1和正△A 2B 2C 2的中心重合,•且满足A 1B 1⊥A 2C 2,若六边形ABCDEF 的面积为S=13m n-,其中,m 、n 为有理数,则mn的值为_______.第二试一、(20分)求证:面积和周长分别对应相等的两个直角三角形全等.二、(25分)已知k、a都是正整数,2 004k+a、2 004(k+1)+a都是完全平方数.(1)请问这样的有序正整数(k,a)共有多少组?(2)试指出a的最小值,并说明理由.三、(25分)如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M•在对角线BD 上,且满足∠BAM=∠DAN,∠BCM=∠DCN.求证:(1)M为BD的中点;(2)AN AM CN CM.参考答案第一试 一、1.A .原方程可化为3x 2-2(a+b+c )x+ab+bc+ca=0. 其判别式为△=4(a+b+c )2-4×3(ab+bc+ca ) =2[(a-b )2+(b-c )2+(c-a )2].因为a 、b 、c 两两不相等,则△>0,所以,方程必有两个不相等的实根. 2.D .由题给条件易知,这些弦组成的图形恰为正△ABC 及其所对的弓形. 设△ABC 的中心为O ,则小扇形BOC 的面积为3π.而S △AOB =S △AOC =12×12×sin120°.故所求的图形的面积为2+3π. 3.B .由韦达定理得x 1+x 2=-a ,x 1x 2=b ,则x 1+x 2+x 1x 2=2 006. 所以,(x 1+1)(x 2+1)=2 007=9×223=-9×(-223)=3×669=-3×(-669)=1×2 007=(-1)×(-2 007). 易知方程有6组解. 4.C .设第二行的两个数为m 、n ,则11m n+=1(m 、n ∈N +). 于是,m=1111n n n =+--,解得n-1=1.从而,n=2,且n=2, 即第二行的数只能为12,12. 设第三行中12脚下的两个数为12=11m n+(m 、n ∈N +). 则m=24222n n n =+--.故(n-2)│4,知n-2=1,2,4.于是,6,4,3,34, 6.m m m n n n ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩或或 故第三行的数由左到右是13,16,13或16,13,16或14,14,14. 5.B .如图,过点E 作EF ∥AD 交CD 于点F ,设AB=x ,则AC CD CDAE DF BD==. 有BD=DF .所以,DG 为△BEF 的中位线,则BG=GE . 又∠BAG=∠EAG ,所以,AB=AE=x . 得CE=AC-AE=AC-AB=2. 又因EF ∥AD ,所以AE CE ACDF CF CD===2. 故DF=2x,CF=1. 而222EF CE AD AC AE CE x ===++ 及22220081EF GD AG AD AG GD GD===++,故x=2 006. 因此,BC=2 007. 6.D(1)选择题及填空题的得分有0,7,14,…,70共11种可能,解答题得分有0,5,10,•…,70共有15种可能,故产生11×15=165种结果.(2)下列23个分数0,5,7,10,12,14,15,17,19,20,21,22,24,25,26,27,•28,•29,30,31,32,33,34可以得到且只有一种获得方法;又35=7×5=5×7,即35•分可表示为做对5个7分或7个5分的题,故前面23个分数相应分别加上35•所得的分数均有两种获得方法.于是,这新的23个分数各有两种获得方法,且均小于70.根据对称性,用140减去新的23个分数所得的数也均有两种表示方法,这些数恰为71到140之间的能够取到的分数.前后共计2×23=46个数.(3)由70=7×10=5×14=7×5+5×7,知共有三种获取方法. 故满足不重复的要求的不同分数共165-46-2=117(种).二、1.-1或8.令b c a c a b a b ca b c+-+-+-===k,则b+c=(k+1)a,c+a=(k+1)b,a+b=(k+1)c.于是,2(a+b+c)=(k+1)(a+b+c).故a+b+c=0或b+c=2a,c+a=2b,a+b=2c.所以()()()a b b c c aabc+++=-1或8.2.29如图,在△ABD中,应用梅涅劳斯定理得AM BE DGMB ED GA=1,即12MB EDAM BE=.在△ADC中,应用梅涅劳斯定理得AG DE CNGD EC NA=1,即12DE CNEC NA=.则1122BM CN BE EC DEAM AN ED DE DE+=+==1.故BA CAAM AN+=3,即11m n+=3.所以,3mn=m+n≥mn mn≥49.而一次函数y=-nmx+n与x轴、y轴的交点坐标为(m,0),(0,n),故所求的三角形的面积S=12mn≥29,且当且仅当m=n时,等号成立.注:本题也可以用特殊值法求解.3.3.设n个正方形的边长分别为x1,x2,…x n,则x12+x22+…+x n=2006.由于x i2≡0或1(mod 4),而2 006≡2(mod 4),故x i中至少有两个奇数。
2018-2019年眉山市初中分班数学模拟试卷(48)附详细答案

小升初数学综合模拟试卷48一、填空题:1.4321+3214+2143+1432=_______.3.如图,阴影部分的面积是______.4.用四则运算符号把1、9、9、7四个数连成一个算式(允许添括号),使这个算式的结果等于79,那么这样的算式是______(可能有多种写法,只要求写出一个).5.找出四个互不相同的自然数,使得对于其中任何两个数,它们的和总可以被它们的差整除.如果要求这四个数中最大的数与最小的数的和尽可能的小,那么这四个数里,中间两个数的和是______.某服装商店出售服装,去年按定价的85%出售,能获得25%的盈利,由于今年买入价降低,按同样定价的75%出售,却能获得30%的盈利,那7.有一类自然数,每一个数各位数字之和都是奇数,而且都是两位数的乘积(例如10×10=100),且其乘积都小于200,那么这一类自然数中,第五大的数是______.8.某工程由甲单独做25天后,再由乙单独做60天即可完成.如果甲、乙两人合作,需40天完成,现在甲先单独做34天,然后再由乙来单独完成,还需要做______天.9.某商店以5元3斤苹果的价格买进苹果若干,又以2.5元1斤的价格将苹果卖出.如果商店要赚100元钱利润,那么商店必须卖出苹果_______斤.10.足球比赛10∶00开始,9∶30允许观众入场,但早有人来排队等候入场.从第一个观众来到时起,每分钟来的观众人数一样多,如果开4个入场口,9∶45时就不再有人排队;如果开6个入场口,9∶37就没有人排队,那么第一个观众到达的时间是9点______分______秒.二、解答题:1.某钟表,在6月29日零点比标准时间慢5分,它一直走到7月6日上午6时,比标准时间快5分,那么这只表所指时间是正确的时刻应该是在哪月哪日哪时?(“零点”和“7时”都指的是标准时间)2.某出版社出版某种书,今年每册书的成本比去年增加10%,但售价不变,因此每本利润下降了40%,那么今年这种书的成本在售价中所占的百分数是多少?3.两个整数A、B的最大公约数是C,最小公倍数是D,并且已知C不等于1,也不等于A或B,C+D=187,那么A+B等于多少?4.某列火车通过长为82米的铁桥用了22秒,如果火车的速度加快一倍,它通过706米的铁桥就用50秒,那么火车的长度是多少米?答案,仅供参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小升初数学综合模拟试卷49
一、填空题:
1.1997+1996-1995—1994+1993+1992—1991—1990+…+9+8—7—6+5+4—3—2+
1=______.
3.在图中的七个圆圈内各填一个数,要求每一条直线上的三个数中,当中的数是两边两个数的平均数,现在已经填好两个数,那么,x=______
4.把1、2、3、4、5填入下面算式的方格内,使得运算结果最大:
□+□-□×□÷□那么这个最大结果是_______.
5.设上题答数为a,a的个位数字为b,2×b的个位数字为c.如图,
积的比是______.
6.要把A、B、C、D四本书放到书架上,但是,A不能放在第一层,B不能放在第二层,C不能放在第三层,D不能放在第四层,那么,不同的放法共有______种.
7.从一张长2109毫米,宽627毫米的长方形纸片上,剪下一个边长尽可能大的正方形,如果剩下的部分不是正方形,那么在剩下的纸片上再剪下一个边长尽可能大的正方形,按照上面的过程,不断地重复,最后剪得的正方形的边长是______毫米.
8.龟兔赛跑,全程5.4千米.兔子每小时跑25千米,乌龟每小时跑4千米,乌龟不停地跑,但兔子却边跑边玩,它先跑1分,然后玩15分,又跑2分,玩15分.再跑3分,玩15分,……,那么先到达终点的比后到达终点的快______分.
9.从1,2,3,4,5中选出四个数,填入图中的方格内,使得右边的数比左边的数大,下面的数比上面的数大,那么,共有______种填法.
比女生少人.
二、解答题:
1.小明从甲地到乙地,去时每小时走5千米,回来时每小时走7千米,来回共用4小时,小明去时用了多长时间?
2.有一个长方体,它的正面和上面的面积之和是119,如果它的长、宽、高都是质数,那么这个长方体的体积是多少?
3.在400米环形跑道上,A、B两点相距100米(如图),甲、乙两人分别从A、B两点同时出发,按逆时针方向跑步,甲每秒跑7米,乙每秒跑5米,他们每人跑100米都停5秒.那么,甲追上乙需要多少秒?
4.五年级三班有26个男生,某次考试全班有30人超过85分,那么女生中超过85分的比男生中未超过85分的多几人?
答案,仅供参考。
一、填空题:
1.1997
原式=(1997—1995)+(1996—1994)+(1993—1991)+(1992—1990)+…+(9—7)+(8—6)+(5—3)+(4—2)+1=2+2+…+2+2+
因为从1至1997共1997个数,所以从2至1997共1996个数,这
1996
2.
一定相等,所以,9A+5B=23,A和B都是自然数,先试A=1,B=1或B=2或B=3,均不成立;再试A=2,B=1.因此,只有A=2,B=1时,成立,即:A+B=3.
3.14.
如图,余下的四个圆圈分别用A、B、C、D四个字母来表示,
由每一条直线上三个数的关系可知:
从①式中知,B比D大2,那么②式可写成:D=(8+D+2)÷2,故D=10,所以,C=(10+12)÷2=11,于是,(8+x)÷2=11,x=14.
最大圆面积为:π×32=9π,所以阴影部分面积与最大圆面积之比为:
6.9
A不能放在第一层,那么A只能放在第二、三、四层,有3种可能情况.如果第一层放B,不论第二、三、四哪一层放A、C、D也就可以确定3了.因此,当第一层放B时,所有可能摆放情况有以下三种:
第一层第二层第三层第四层
B A D C
B D A C
B C D A
(注意:C不能在第三层,D不能在第四层).
当第一个位置放C或D时,也各有3种可能的摆放方法,因此,不同的放法共有3×3=9种.7.57
由于627的3倍比2109小,因此,开始时的长方形纸片上,可以连剪3个边长为627的正方形:2109=627×3+228,剩下的部分是长、宽分别为627和228的长方形,依此类推,有627=228×2+171
228=171×1+57
也就是说,当剩下长171,宽57的长方形时,可以刚好剪成三个边长为57的正方形,所以,最后剪得的正方形边长是57毫米.
8.8.04
兔子跑完全程(不包括玩的时间),需要:
12.96=1+2+3+4+2.96
12.96分钟分成五段跑完,中间兔子玩了4次,每次15分,共玩了15×4=60(分),兔子跑完全程共需要12.96+60=72.96(分).而乌龟跑完
81—72.96=8.04(分).
9.10
先看左上角,它是所填四个数中最小的一个,所以,只能取1或2.如果取1,它右边一个空可填2,3或4,当填2时,下面两空有三种情况(3,4),(3,5),(4,5);当填3时,下面两空可填(2,4),(2,5),(4,5);当填4时,下面两空可填(2,5),(3,5).如果左上角取2,右下角一定取5,3和4可交换,便得到另外两种情况,综上所述,共有10种填法.10.15
(人),男生比女生少240—225=15人.
二、解答题:
1.2小时20分.
去时速度∶回来速度=5∶7,所以,去时时间∶回来时间= 7∶5,因此,
所以,去时用2小时20分.
2.170
如图,长方体的正面和上面的面积之和=长×宽+长×高=长×(宽+高)=119=7×17,那么,有两种可能:
(1)长=7,宽+高=17
(2)长=17,宽+高=7
宽和高必是一个奇质数与一个偶质数2,7=2+5,符合要求;17=2+15不符合要求,所以长=17,长方体体积=2×5×17=170.
3.65秒
甲、乙不停留,甲追上乙需要多少时间?两人同时出发,相差100米,甲每秒比乙快2米,所以100÷2=50(秒)就可以追上乙,甲跑50×7=350(米),在100米, 200米, 300米处共停留5×3=15(秒),所以甲追上乙需要50+15=65(秒).
4.4人.
设女生中超过85分的有x人,则男生中超过85分的有(30—x)人,那么男生中未超过85分的有26-(30-x)=(x-4)(人),所以女生中超过85分的比男生中未超过85分的多x-(x-4)=4(人).。
