【附加15套高考模拟试卷】重庆市三峡名校联盟2020届高三5月联考数学(文)试题含答案
重庆市名校联盟2023-2024学年高三下学期第一次联考数学试题

重庆市名校联盟2023-2024学年高三下学期第一次联考数学试题学校:___________姓名:___________班级:___________考号:___________由④⑤得()()24-+-=g x g x ,则()()24++=g x g x ,所以()()424+++=g x g x ,得到()()4g x g x +=,()g x 周期为4,因为()()24-+-=g x g x ,令1x =,则()()114g g +-=,又因为()g x 为偶函数,则()()11g g =-,则()241=g ,所以()12g =,()()()20254506112=´+==g g g ,故选项B 错误;因为()()422f x g x -+-=, 得()()22f x g x +-=,()()22f x g x -+=,又因为()()24-+=g x g x ,所以()()20f x f x +-=,又因为()()4f x f x =-,所以()()420-+-=f x f x ,所以()()20f x f x ++=,则()()42()f x f x f x +=-+=,所以()f x 周期为4,由③知,()()()4f x f x f x =-=-,所以()f x 是R 上的偶函数,故选项C 正确;由选项B 知,()()22f x g x +-=,()()4f x f x =-,()()24-+=g x g x ,对三个式子分别关于x 求导可得,()()20¢¢--=f x g x ⑥,()()4f x f x ¢¢=--⑦,()()20¢¢--=g x g x ⑧,由⑥得()()20¢¢--=f x g x ⑨,⑥-⑨结合⑧可得()()2f x f x ¢¢=-,又因为()()4f x f x ¢¢=--,则()()()22¢¢¢+=--=-f x f x f x ,即()()2f x f x ¢¢+=-,则()()()42f x f x f x ¢¢¢+=-+=,()f x ¢周期为4,由()()4f x f x ¢¢=--知,()()22¢¢=-f f ,()20f ¢=,所以DM AD^,因为AP^平面ABCD,且DMÌ平面ABCD,,所以AP DM^因为AP AD AAP ADÌ平面PAD,Ç=,,所以DM^平面PAD,且ANÌ平面PAD,所以DM AN^,因为AP AD=,且点N是线段PD的中点,所以AN PD^,又因为DM PD DDM PDÌ平面PDM,I,,=所以AN^平面PDM,(2)因为AP^平面ABCD,且90Ð=°,BAD所以直线,,AB AD AP两两垂直,以A为原点,分别以直线,,AB AD AP为x轴,y轴,z轴,建立空间直角坐标系,如图所示:由2224====得,BC AB AP AD利用切合函数得到两个关键等式;三是把多变量转化为单变量,构造函数,利用单调性证明不等式.。
重庆市2023届高三五月第二次联考数学试题

重庆市2023届高三五月第二次联考数学试题学校:___________姓名:___________班级:___________考号:___________二、多选题9.甲同学投掷骰子5次,并请乙同学将向上的点数记录下来,计算出平均数和方差.由于记录遗失,乙同学只记得这五个点数的平均数为2,方差在区间[1.2,2.4]内,则这五个点数()A.众数可能为1B.中位数可能为3C.一定不会出现6D.出现2的次数不会超过两次10.设m,n为不同的直线,a,b为不同的平面,则下列结论中正确的是()三、填空题13.已知向量a r 与b r 为一组基底,若4ma b ®+r与2a b®+r 平行,则实数m =________.14.命题:“()1,x "Î+¥,210x ->”的否定是________.15.某市第一中学校为了做好疫情防控工作,组织了6名教师组成志愿服务小组,分配到东门、西门、中门3个楼门进行志愿服务.由于中门学生出入量较大,要求中门志愿者人数不少于另两个门志愿者人数,若每个楼门至少分配1个志愿服务小组,每个志愿服务小组只能在1个楼门进行服务,则不同的分配方法种数为________.五、解答题17.在ABCV 中,内角A ,B 2p<.(1)求角A 的大小;(2)()f x 的所有极值点为1x ,2x ,…,n x ,若()()()120n f x f x f x +++=L ,求m 的值.在正方体1111ABCD A B C D -中,1CC ^面由ABCD 为正方形,所以AC BD ^.又1CC AC C =I ,所以BD ^面1ACC ,所因为1BD BA B =I ,所以1AC ^平面1A BD 设1AC 与平面1A BD 交于点1P ,由等体积法11113111222322AP ´´´´=´´´´´。
2020年5月重庆市渝西九校联考联盟2020届高三毕业班高考模拟联考数学(文)试题(解析版)

绝密★启用前重庆市渝西九校联考联盟2020届高三毕业班下学期高考模拟联合考试数学(文)试题 (解析版)2020年5月一、选择题:本大题共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|26A x x x =>-,{}0,2,4,6B =,则A B =( ) A. {}0 B. {}0,2C. {}2,4D. {}4,6【答案】D 【解析】 【分析】先化简集合A ,再求交集,即可得出结果.【详解】因为{}{}|26|2A x x x x x =>-=>,{}0,2,4,6B =, 所以{}4,6A B =. 故选:D.【点睛】本题考查集合的交集运算,熟记概念即可,属于基础题型. 2.若z 1=2﹣3i ,z 2=3+2i ,则( ) A. z 1+z 2的实部为1 B. z 2=iz 1 C. z 1+z 2的虚部为1 D. z 2=﹣iz 1【答案】B 【解析】 【分析】采用逐一验证法,根据复数的四则运算,分别计算z 1+z 2,iz 1,简单判断可得结果.【详解】由题可知:z 1=2﹣3i ,z 2=3+2i所以z 1+z 2=5- i ,故z 1+z 2的实部为5,虚部为-1,排除A,B()1212332,=-=+∴=iz i i i z iz ,排除D,则B 正确 故选:B【点睛】本题考查复数的四则运算,重在于计算,属基础题.3.若双曲线22:13x y C m-=则C 的虚轴长为( )A. 4B.C. D. 2【答案】C 【解析】 【分析】利用离心率得到关于m 的方程,求出其解后可得虚轴长.【详解】因为双曲线22:13x y C m -==, 解得6m =,所以虚轴长为故选:C.【点睛】本题考查双曲线的离心率及虚轴长,注意双曲线()2222:10,0x y C a b a b-=>>中各几何量计算公式的正确应用,如虚轴长指2b ,本题属于基础题. 4.已知函数()6log f x x =,则()222f -=( ) A. ()4f B. ()6fC. ()9fD. ()12f【答案】C 【解析】 【分析】根据对数的运算法则,直接计算,即可得出结果. 【详解】因为()6log f x x =,。
2020届高三数学5月联合考试试题文

2020届高三数学5月联合考试试题文本试卷4页。
总分150分。
考试时间120分钟。
注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上相应的位置。
2.全部答案在答题卡上完成,答在本试卷上无效。
3.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案用0.5mm黑色笔迹签字笔写在答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x∈Z|-1≤x≤2},B={x|y=ln(x-1)},则A∩B=A.{-1,0,1,2}B.{0,1,2}C.{1,2}D.{2}2.已知(m,n∈R),则复数z=m+ni在复平面内对应的点位于A.第一象限B.第二象限C.第三象限D.第四象限3.书籍是人类的智慧结晶和进步阶梯,阅读是一个国家的文化根基和创造源泉。
2014年以来,“全民阅读”连续6年被写人政府工作报告。
某高中为了解学生假期自主阅读书籍类型,在全校范围内随机抽取了部分学生进行调查。
学生选择的书籍大致分为以下四类:A历史类、B文学类、C科学类、D哲学类。
根据调查的结果,将数据整理成如下的两幅不完整的统计图,其中a-b=10。
根据上述信息,可知本次随机抽查的学生中选择A历史类的人数为A.45B.30C.25D.224.某几何体的三视图如图所示,则该几何体的表面积为A.18+6B.24C.13D.185.“李生素数猜想”是数学史上著名的未解难题,早在1900年国际数学家大会上,由德国数学家希尔伯特提出。
所谓“孪生素数”是指相差为2的“素数对”,例如3和5。
从不超过20的素数中,找到这样的“孪生素数”,将每对素数作和。
从得到的结果中选择恰当的数,构成一个等差数列,则该等差数列的所有项之和为A.72B.68C.56D.446.函数f(x)=的部分图象大致为7.某校甲、乙、丙、丁四位同学参加了第34届全国青少年科技创新大赛,老师告知只有一位同学获奖,四人据此做出猜测:甲说:“丙获奖”;乙说:“我没获奖”;丙说:“我没获奖”;丁说:“我获奖了”若四人中只有一人判断正确,则判断正确的是A.甲B.乙C.丙D.丁8.已知△ABC的内角A,B,C的对边分别为a,b,c,且满足a=6,c=2,tanA+tanB=,则S△ABC=A.3B.9C.9D.3y.在矩形ABCD中,AB=1,AD=,点M在对角线AC 上,点N在边CD上,且,,则=A. B.4 C. D.10.已知x1=,x2=分别是函数f(x)=2cos(ωx+φ)(ω>0,|φ|<)相邻的极大值点与零点。
重庆市三峡名校联盟2022-2023学年高一上学期联考数学试题及参考答案

重庆市三峡名校联盟2022-2023学年高一上学期联考数学试题及参考答案一、单项选择题(本大题共8题,每小题5分,共计40分,每小题列出的四个选项中只有一项是最符合题目要求的.)1、已知命题x x R x p 2,:2>∈∃,则p ⌝为()A.x x R x 2,2>∈∀B.x x R x 2,2≤∈∀C.xx R x 2,2>∉∃D.xx R x 2,2≤∈∃2、已知函数1222)1()(--⋅--=m m x m m x f 是幂函数,且在),(∞+0上递减,则实数m =()A.-1B.2或-1C.4D.23、0sin :>θp ,θ:q 是第一象限角或第二象限角,则p 是q 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4、下列散点图中,估计有可能用函数)0(lg >+=b x b a y 来模拟的是()A .B .C .D .5、设,25sin a = 则= 205tan 115cos 65sin ()A.221a a -B.221a a --C.2a -D.2a 6、已知函数,x x x f --+-=+1122)1(则)(x f ()A.是偶函数,且在R 是单调递增B.是奇函数,且在R 是单调递增C.是偶函数,且在R 是单调递减D.是奇函数,且在R 是单调递减7、若)(x f 为奇函数,且0x 是x e x f y 2)(-=的一个零点,则0x -是下列哪个函数的零点()A.2)(--=-x e x f y B.2)(+=x e x f y C.2)(-=x e x f y D.2)(+-=x e x f y8、高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,用其名字命名的“高斯函数”为:设,R x ∈用][x 表示不超过x 的最大整数,则][x y =称为高斯函数,例如:,1]5.0[-=-,1]5.1[=已知函数⎪⎪⎩⎪⎪⎨⎧∈++-∈+=)3,65(,1376)65,0(,1)sin(2)(x x x x x x f π,则函数)]([x f y =的值域为()A.{-2,-1,0,1,2,3}B.{-1,0,1,2,3}C.{-1,0,2,3}D.{-2,-1,0,1,2}二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9、下列函数中,定义域为),(∞+0的函数是()A.xy lg =B.x y =C.21-=xy D.xe y =10、下列说法正确的是()A.若22bc ac >,则ba > B.若d cb a >>,,则d bc a ->-C.若,0,0>>>c a b 则abc a c b >++ D.若,0>>b a 则ab b a 11+>+11、已知函数2+2,<1()=+3,1x x f x x x -≥⎧⎨⎩,则()A.2)]3([=f f B.若32,1)(-==-=x x x f 或则C.),1[02)(+∞∞-< ),的解集为(x f D.3),(,≥>∈∀a x f a R x 则12、已知3632==y x ,则下列说法正确的是()A.)(2y x xy +=B.16>xy C.9<+y x D.3222<+y x 三、填空题(本题共4小题,每小题5分,共20分.其中15题第一空2分,第二空3分.)13、请写出同时满足下列两个条件的函数()=x f ____________.(1))(x f 在定义域内单调递增,(2))()()(y f x f y x f ⋅=+14、求81log 2721325log 32⨯-+的值为____________.15、设时钟时针长5cm ,时间经过4小时30分钟。
重庆市三峡名校联盟2020年秋高二数学上学期联考试题答案解析卷

重庆市三峡名校联盟2020年秋高二数学上学期联考试题答案解析卷一、单选题1.已知集合{}2,1,0,1,2A =--,{B y Ry =∈=∣,则A B =( )A .{}0,1 B .{}0,1,2C .{}1,2 D .{}1【答案】B【分析】首先求出集合B ,再根据交集的定义计算可得;【详解】解:因为{B y Ry =∈=∣,所以{}|0B y y =≥,因为{}2,1,0,1,2A =--所以{}0,1,2A B =故选:B【点睛】本题考查交集的计算,属于基础题.2.斜率为2,且过直线4y x =-和直线2y x =+交点的直线方程为( ) A .21y x =+ B .21y x =-C .22y x =-D .22y x =+【答案】A【分析】求出两直线的交点坐标,根据点斜式可得结果.【详解】联立42y x y x =-⎧⎨=+⎩,解得13x y =⎧⎨=⎩,所以两直线的交点坐标为()1,3,所求直线方程为()321y x -=-.整理为21y x =+.故选:A【点睛】本题考查了求两直线的交点,考查了直线方程的点斜式,属于基础题. 3.设0a b <<,则下列不等式中不成立的是( )A .11a b> B .11a b a>- C .||a b >-D .>【答案】B【分析】对于A ,C ,D 利用不等式的性质分析即可,对于B 举反例即可 【详解】对于A ,因为0a b <<,所以0ab >,所以0a bab ab<<,即11a b >,所以A 成立;对于B ,若2a =-,1b =-,则11a b =--,112a =-,此时11a a b>-,所以B 不成立; 对于C ,因为0a b <<,所以||||a b b >=-,所以C 成立;对于D ,因为0a b <<,所以0a b ->->>D 成立,故选:B.【点睛】本题考查不等式的性质的应用,属于基础题.4.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB = A .3144AB AC -B .1344AB AC -C .3144+AB AC D .1344+AB AC 【答案】A【分析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得1122BE BA BC =+,之后应用向量的加法运算法则-------三角形法则,得到BC BA AC =+,之后将其合并,得到3144BE BA AC =+,下一步应用相反向量,求得3144EB AB AC =-,从而求得结果.【详解】根据向量的运算法则,可得()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC =++=+, 所以3144EB AB AC =-,故选A. 【点睛】该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.5.函数()x xe ef x x--=的图象大致是( )A .B .C .D .【答案】A【分析】先根据函数的奇偶性排除部分选项,再利用特殊值判断.【详解】因为函数()x x e e f x x --=的定义域为:{}|0x x ≠,且()()x x x xe e e ef x f x x x-----===-,所以()f x 是偶函数,排除BD ,又因为1(0)f x e e -=->,排除C ,故选:A6.若直线1:220l ax y +-=与直线()22:(1)10l x a y a +-++=平行,则a 的值为( ) A .1a=- B .2a = C .2a =-或1a = D .2a =或1a =-【答案】B【分析】利用直线平行的充要条件知:(1)20a a --=,求a 值,注意验证所得a 值是否符合题意,即可确定a 值.【详解】由题意知:(1)20a a --=,解得2a =或1a =-,当1a =-时,1:220l x y -+=,2:220l x y -+=两线重合,故不合题意; 当2a =时,1:10l x y +-=,2:50l x y ++=两线平行; ∴2a=.故选:B.7.张衡(78年~139年)是中国东汉时期伟大的天文学家、文学家、数学家.他的数学著作有《算罔论》,他曾经得出结论:圆周率的平方除以十六等于八分之五.已知正方体的外接球与内切球上各有一个动点A ,B ,若线段AB 的最小值为)A .9B .9.42C D .【答案】D【分析】由正方体性质,确定线段AB 最小时两点与球心的位置关系及数量关系R r AB -=,若正方体棱长为a ,内切球半径2a r =,外接球半径R =,求a ,结合已知条件以及球的表面积公式,求外接球表面积.【详解】由正方体的性质知:其外接球与内切球的球心重合,所以两球的球面上两点A ,B 的距离最小时,球心与A ,B 共线,且在球心的同侧,若正方体棱长为a ,内切球半径2a r =,外接球半径R =,∴1122R r a -==,即1a =,则R =∴外接球的表面积243S R ππ==,而25168π=,有π=∴S=故选:D.8.设椭圆22221(0)x y a b a b +=>>的左、右焦点分别为1F ,2F ,P 是椭圆上的一点,()1213PF PF λλ=≤≤,122F PF π∠=,则椭圆离心率的取值范围为( )A.⎛ ⎝⎦B.⎣⎦C.⎣⎦D.⎫⎪⎪⎣⎭【答案】C【分析】利用椭圆定义和勾股定理可表示出2,a c ,得到()22211e λλ+=+,利用换元法将()2211λλ++转化为二次函数的形式,求得二次函数的值域即为2e 的范围,解不等式可求得结果. 【详解】设()1,0F c -,()2,0F c , 由椭圆定义知:()1222212PF PF PF PF PF a λλ+=+=+=…∴,122F PF π∠=,()222222221222214PF PF PF PF PF c λλ∴+=+=+=…∴,由∴∴可得:()()2222222114114c e a λλλλ++===++, 设1t λ=+,[]1,3λ∈,[]2,4t ∴∈,则()22222221122221111222t t t e t t t t t -+-+⎛⎫===-+=-+ ⎪⎝⎭,当112t =时,()2min12e =;当114t =时,()2max58e=; 21528e ∴≤≤,解得:e ∈⎣⎦.故选:C.【点睛】关键点点睛:本题考查椭圆离心率取值范围的求解问题,解题关键是能够将离心率表示为关于λ的函数的形式,进而通过函数值域的求解方法来求得离心率的取值范围.9.已知,αβ是两个不重合的平面,,m n 是两条不重合的直线,则下列命题不正确的是( ) A .若,,//m n m n αβ⊥⊥,则αβ⊥ B .若,//m n αα⊥,则m n ⊥ C .若//,m αβα⊂,则//m βD .//,//m n αβ,则m 与α所成的角和n 与β所成的角相等 【答案】A【分析】根据线、面垂直平行的判断定理性质,逐一进行判断. 【详解】选项A :若,m n m α⊥⊥,则n ⊂α或//n α,又//n β,并不能得到αβ⊥这一结论,故选项A 错误; 选项B :若,//m n αα⊥,则由线面垂直的性质定理和线面平行的 性质定理可得m n ⊥,故选项B 正确;选项C :若//,m αβα⊂,则有面面平行的性质定理可知//m β, 故选项C 正确;选项D :若//,//m n αβ,则由线面角的定义和等角定理知,m 与α 所成的角和n 与β所成的角相等,故选项D 正确. 故选:A【点睛】本题考查了线面垂直的性质定理,线面平行的性质定理,面面平行的性质定理,以及线面角的定义和等角定理等基础知识,需要对每个选项逐一进行判断,属于中档题.二、多选题10.已知实数,x y 满足方程22410x y x +-+=,则下列说法正确的是( ) A .y x -2-B .22xy +的最大值为7+C .y xD .x y +的最大值为2【答案】AB【分析】设2x θ=,y θ=,将ABD 中的式子化为三角函数的形式,根据三角函数的最值可求得结果;根据y x 的几何意义,利用圆的切线的求解方法可求得yx的取值范围,由此确定C 的正误.【详解】由22410x y x +-+=得:()2223x y -+=,可设2x θ=,y θ;对于A,224y x πθθθ⎛⎫-=-=-- ⎪⎝⎭,当sin 14πθ⎛⎫-= ⎪⎝⎭时,()max 2y x -=,A 正确; 对于B,222243cos 3sin 7x y θθθθ+=+++=+,当cos 1θ=时,()22max7x y +=+B 正确;对于C ,y x表示圆()2223x y -+=上的点与坐标原点连线的斜率, 设过坐标原点的圆的切线方程为y kx ==k =,y x ⎡∴∈⎣,maxy x ⎛⎫∴= ⎪⎝⎭C 错误; 对于D,224x y πθθθ⎛⎫+==++ ⎪⎝⎭,当sin 14πθ⎛⎫+= ⎪⎝⎭时,()max 2x y +=,D 错误. 故选:AB.【点睛】关键点点睛:本题考查与圆上的点的坐标有关的最值问题的求解,解题关键是能够利用换元法,结合三角恒等变换的公式将问题转化为三角函数值域的求解.11.设1F ,2F 是双曲线2222:1(0,0)x y C a bb-=>>的左、右焦点,O 是坐标原点,过2F 作C 的一条渐近线的垂线,垂足为P .若1|PFOP =,则下列说法正确的是( )A.2F P b =BC .点P 在直线x a =上 D .双曲线的渐近线方程为y =【答案】ABC【分析】利用点到直线的距离公式可判断A;求出OP,由12cos OP FOP OF ∠=-,得到1PF ==,根据余弦定理可知1cos FOP ∠=ac-,可判断B ;由点P 在直线y =上,可设()()0P x x >,由OP a =可判断C ;由e = D.【详解】由双曲线的性质可知,双曲线的一条渐近线方程为by x a=,即0bx ay -=, 焦点()1,0F c -,()2,0F c ,()0,0,0a bc >>>因为过2F 作C 的一条渐近线的垂线,垂足为P , 所以2bcF Pb c===,故A 正确; 因为OP a ===,则()1222cos cos 180cos OPaFOP F OP FOP OF c∠=-∠=-∠=-=-, 所以1PF ==,在三角形1OPF 中,根据余弦定理可知2221111cos 2OP OF F PFOP OP OF +-∠==⋅ 22262a c a aac c+-=-,解得223a c =,即离心率e =e =B 正确;因为点P 在直线y =上,可设()()0P x x >,由OP a =可知,OP a ===,解得x a =,故C 正确;因为e ==b a =y =,故D 错误. 故选:ABC.【点睛】本题考查双曲线的几何性质以及渐近线方程、离心率的求法,关键点是熟练掌握双曲线的几何性质,考查综合分析问题、解决问题能力及运算能力,属于中档题. 12.如图,直三棱柱11,ABC A B C -,ABC 为等腰直角三角形,AB BC ⊥,且12AC AA ==,E ,F 分别是AC ,11AC 的中点,D ,M 分别是1AA ,1BB 上的两个动点,则( )A .FM 与BD 一定是异面直线B .三棱锥D MEF -的体积为定值14C .直线11B C 与BD 所成角为2πD .若D 为1AA 中点,则四棱锥1D BB FE -【答案】CD【分析】A 当特殊情况M 与B 重合有FM 与BD 相交且共面;B 根据线面垂直、面面垂直判定可证面1BEFB ⊥面11ACC A ,可知EMFS 、D 到面1BEFB 的距离,可求D EMF V -;C 根据线面垂直的判定及性质即可确定11B C 与BD 所成角;D 由面面垂直、勾股、矩形性质等确定外接球半径,进而求体积,即可判断各项的正误.【详解】A :当M 与B 重合时,FM 与BD 相交且共面,错误; B :由题意知:BEAC ⊥,AC EF ⊥且BE EF E =,则AC ⊥面1BEFB ,又AC ⊂面11ACC A ,面1BEFB ⋂面11ACC A EF =,所以面1BEFB ⊥面11ACC A ,又1121122EMFSEF BE =⋅⋅=⨯⨯=,D 到面1BEFB 的距离为1h =,所以1133D EMF EMFV h S-=⋅⋅=,错误; C :由AB BC ⊥,1BCB B ⊥,1B B AB B =,所以BC ⊥面11ABB A ,又11//BC B C ,即11B C ⊥面11ABB A ,而BD ⊂面11ABB A ,则11BD B C ⊥,正确;D :由B 中,面1BEFB ⊥面11ACC A ,即面DEF ⊥面1BEFB ,则D 到面1BEFB 的距离为1h =,又D 为1AA中点,若1,BF EB 交点为O ,G 为EF 中点,连接,,OG GD OD ,则OG GD ⊥,故OD ==,由矩形的性质知:1OB OEOF OB ====,令四棱锥1D BB FE -的外接球半径为R ,则R =,所以四棱锥1D BB FE -的外接球体积为3436V R π==,正确.故选:CD.【点睛】关键点点睛:利用线面、面面关系确定几何体的高,结合棱锥体积公式求体积,根据线面垂直、勾股定理及矩形性质确定外接球半径,结合球体体积公式求体积. 三、填空题13.为了了解某社区居民的2019年家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程,则___________________.【答案】9【分析】计算样本点中心,代入回归方程得出t 的值. 【详解】8.28.61011.311.9105x ++++==,0.76100.48y =⨯+=6.27.189.785t ++++∴=,解得9t =故答案为:914.已知,0()απ∈-,4cos 5α=-,则tan 4πα⎛⎫+= ⎪⎝⎭_________________.【答案】7【分析】根据,0()απ∈-,4cos 5α=-,利用三角函数的基本关系求得tan α,再利用两角和的正切公式求解.【详解】因为,0()απ∈-,4cos 5α=-,所以3sin 5α=-,3tan 4α=, 所以3tan tan144tan 7341tan tan 144παπαπα++⎛⎫+=== ⎪⎝⎭-⋅-, 故答案为:715.在三棱锥P ABC -中,PA ⊥平面ABC ,90BAC ∠=︒,D ,E ,F 分别是AB ,BC ,CP 的中点,2AB AC PA ===,则直线PA 与平面DEF 所成角为_________弧度. 【答案】4π 【分析】根据题意作出示意图,取AC 中点G ,作GH EF ⊥,根据条件证明GFH ∠即为线面角,由此求解出线面角.【详解】如图所示,取AC 中点G ,连接,FG GE ,作GH EF ⊥交EF 于H 点, 因为,F G 为,PC AC 中点,所以//FG PA所以PA 与平面DEF 所成角即为FG 与平面DEF 所成角 又因为PA ⊥平面ABC ,所以FG 平面ABC ,所以FG DE ⊥ 又因为,D E 为,BA BC 中点,所以//DE AG ,同理可知//GE AD 又因为90BAC∠=︒,所以90DEG ∠=︒,所以DE GE ⊥,且GEFG G =所以DE ⊥平面EFG ,所以DE GH ⊥且,GH EF EFDE E ⊥=所以GH ⊥平面EFD ,所以FG 与平面DEF 所成角为GFH ∠ 又因为111,122FG PA EG AB ====,所以==EF所以sin 2EG GFHEF ∠==0,2GFH π⎛⎫∠∈ ⎪⎝⎭,所以4GFH π∠= 故答案为:4π.【点睛】关键点睛:本题考查利用几何方法求解线面角,解答问题的关键在于能否准确的找到线面角,难度一般,本题还可以利用向量方法求解线面角.四、双空题16.已知动点P 到定点(2,0)F 的距离比到定直线3x =-的距离小1,则点P 的轨迹M 的标准方程为________;A 、B 、C 为该轨迹M 上的三点,若0FA FB FC ++=,则||||||FA FB FC ++=________. 【答案】28y x = 12【分析】根据条件知动点P 到定点(2,0)F 的距离和到定直线2x =-的距离相等,再由抛物线的定义求解;根据0FA FB FC ++=,得到点(2,0)F 是三角形的重心,得到6A BB x x x ++=,再利用抛物线的定义求解.【详解】因为动点P 到定点(2,0)F 的距离比到定直线3x =-的距离小1, 所以动点P 到定点(2,0)F 的距离和到定直线2x =-的距离相等, 所以动点P 的轨迹是以(2,0)F 的为焦点的抛物线, 则22p=,解得4p =, 所以点P 的轨迹M 的标准方程为28y x =;因为A 、B 、C 为M 上的三点,且0FA FB FC ++=, 所以点(2,0)F 是三角形的重心, 则6A BB x x x ++=,所以||||||22212A B C FA FB FC x x x ++=+++++=故答案为:28y x =,12五、解答题 17.已知等差数列{}n a 的公差2d =,且126a a +=.(1)求数列{}n a 的通项公式;(2)若等比数列{}n b 满足11ba =,22b a =,求数列{}n n a b +的前n 项的和n S .【答案】(1)2n a n =;(2)2122n n S n n +=++-.【分析】(1)结合等差数列的通项公式和已知条件即可求出首项,进而可求出通项公式. (2)求出{}n b 的通项公式,根据数列求和的定义写出n S 的表达式,结合等差数列、等比数列前n 项和的公式即可求出n S .【详解】(1)由126a a +=,得126a d +=,又2d =,所以12a =,所以()2212n a n n =+-=.(2)设{}n b 公比为q ,由题意12b =,224b q ==,即2q,所以2n n b =,于是22n nn a b n +=+,故()()22124222222n n n S n n n +=++⋅⋅⋅++++⋅⋅⋅+=++-.【点睛】本题考查了等差数列的通项公式,考查了等比数列的通项公式,考查了数列的求和,属于基础题.18.设ABC 的内角,,A B C 的对边分别为,,a b c .已知b =3c =,1cos 6B =-.(1)求sin C 的值; (2)求ABC 的面积.【答案】(1)6;(2. 【分析】(1)根据同角三角函数关系求得sin B ,利用正弦定理求得结果; (2)利用余弦定理构造方程求得a ,由三角形面积公式求得结果.【详解】(1)1cos 06B =-<且()0,B π∈,,2B ππ⎛⎫∴∈ ⎪⎝⎭,sin 6B ∴==由正弦定理得:sin sin6c B C b ===. (2)由余弦定理得:222261cos 266a cb a B ac a +--===-,解得:2a =或3a =-(舍),11sin 222ABCSab C ∴==⨯=.【点睛】本题考查正余弦定理解三角形的问题,考查学生对于正弦定理、余弦定理和三角形面积公式掌握的熟练程度,属于基础题.19.如图,四边形ABCD 为正方形,PD ⊥平面ABCD ,2PD DC ==,点E ,F 分别为AD ,PC 的中点.(△)证明://DF 平面PBE ;(△)求点F 到平面PBE 的距离.【答案】(∴)见解析;(∴ 【详解】试题分析:(∴)取PB 的中点G ,连接EG 、FG ,由已知结合三角形中位线定理可得//DE FG 且DE FG =,得四边形DEGF 为平行四边形,从而可得//DF EG ,再由线面平行的判定可得//DF 平面PBE ;(∴)利用等积法可得:D PBEP BDE V V =﹣﹣,代入棱锥体积公式可得点F 到平面PBE 的距离.试题解析:(∴)证明:取点G 是PB 的中点,连接EG ,FG ,则//FG BC ,且12FG BC =, ∴//DE BC 且12DE BC =,∴//DE FG 且DE FG =, ∴四边形DEGF 为平行四边形,∴//DF EG ,∴//DF 平面PBE .(∴)解:由(∴)知//DF 平面PBE ,所以点D 到平面PBE 的距离与F 到平面PBE 的距离是相等的,故转化为求点D 到平面PBE 的距离,设为d . 利用等体积法:D PBEP BDE V V --=,即1133PBE BDE S d S PD ∆∆⋅=⋅,112BDE S DE AB ∆=⨯⨯=,∴PE BE ==,PB =∴PBE S ∆=∴d =.点睛:本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题;在证明线面平行的过程中,常见的方法有:1、构造三角形的中位线;2、构造平行四边形;3、利用面面平行;在该题中利用的是构造平行四边形.求点到面的距离主要是利用等体积法.20.一个圆经过点()2,0F,且和直线20x +=相切.(1)求动圆圆心的轨迹C 的方程; (2)已知点()1,0B-,设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P Q 、,若x 轴是PBQ ∠的角平分线,证明直线l 过定点. 【答案】(1)28y x =;(2)证明见解析【分析】(1)圆心到定点()2,0F 与到定直线2x =-的距离相等,可知圆心的轨迹是以点F 为焦点的抛物线,求出方程即可;(2)易知直线l 斜率存在且不为零,可设直线():0l my x n m =+≠,设()11,Px y ,()22,Q x y ,联立直线l与抛物线方程,可得关于y 的一元二次方程,由x 轴是PBQ ∠的角平分线,可得121211y y x x -=++,整理可求得128y y =-,再结合韦达定理128y y n =,从而可求得n 的值,进而可求得直线l 过定点.【详解】(1)由题意,圆心到定点()2,0F与到定直线2x =-的距离相等,根据抛物线的定义可知,圆心的轨迹是以点F 为焦点的抛物线,其方程为28y x =.(2)由题可知,直线l 与C 有两个交点且不垂于于x 轴, 所以直线l 斜率存在且不为零,设直线():0l my x n m =+≠,()11,Px y ,()22,Q x y ,联立28my x ny x=+⎧⎨=⎩,可得2880y my n -+=, 则264320m n ∆=->,且1280y y m +=≠,128y y n =,又2118y x =,2228y x =,x 轴是PBQ ∠的角平分线,所以12122212121188y y y y x x y y --=⇒=++++,整理可得128y y =-, 所以1288y y n ==-,即1n =-,此时满足0∆>,故l :1my x =-,所以,直线PQ 过定点()1,0.【点睛】本题考查抛物线的定义,考查直线与抛物线位置关系的应用,考查直线恒过定点问题,考查学生的计算求解能力,属于中档题.21.如图,四棱锥P ABCD -中,PA ⊥平 面ABCD ,平面ABCD 是直角梯形,90ADC ∠=︒,//AD BC ,AB AC ⊥,AB AC ==E 在AD 上,且2AE ED =.(1)已知点F 在BC 上,且2=CF FB ,求证:平面PEF ⊥平面PAC ; (2)若直线PC 与平面PAB 所成的角为45︒,求二面角--A PB E 的余弦值.【答案】(1)证明见解析;(2). 【分析】(1)先证明四边形ABFE 为平行四边形,得//AB EF ,则AC EF ⊥,又可得PA EF ⊥,即可证明EF ⊥平面PAC ,进而证得平面PEF ⊥平面PAC ;(2)根据线面角定义找出PC 与平面PAB 所成角,得PA 的长度,建立空间直角坐标系,分别求出平面PAB 与平面PBE 的法向量,再利用向量法求出二面角--A PB E 的余弦值. 【详解】(1)∴AB AC ⊥,AB AC =,∴45ACB ∠=︒,∴底面ABCD 是直角梯形,90ADC ∠=︒,//AD BC ,∴45ACD ∠=︒,即AD CD =,则2==BC AD ,∴2AE ED =,2=CF FB ,∴23==AE BF AD , ∴四边形ABFE 是平行四边形,则//AB EF ,∴AC EF ⊥, ∴PA ⊥底面ABCD ,∴PA EF ⊥, ∴PAAC A =,∴EF ⊥平面PAC .又∴EF ⊂平面PEF ,∴平面PEF ⊥平面PAC . (2)∴PA AC ⊥,AC AB ⊥,∴AC ⊥平面PAB , 则APC ∠为直线PC 与平面PAB 所成的角,所以tan 1∠==ACAPC PA,即==PA AC , 取BC 的中点为G ,连接AG ,则AG BC ⊥,以A 为坐标原点建立如图所示的空间直角坐标系A xyz -,则(1,1,0)B -,(1,1,0)C ,20,,03⎛⎫⎪⎝⎭E ,P ,∴51,,03⎛⎫=-⎪⎝⎭EB ,20,3⎛=- ⎝EP ,设平面PBE 的法向量(,,)n x y z =,则503203n EB x y n EP y ⎧⋅=-=⎪⎪⎨⎪⋅=-+=⎪⎩,令3y =,则(5,3,2)n=∴(1,1,0)AC=是平面P AB 的一个法向量,∴cos ,32n AC n AC n AC⋅〈〉===⋅,即二面角--A PB E .【点睛】方法点睛:本题考查线面垂直,及面面角的求法,利用空间向量求立体几何常考查的夹角:设直线,l m 的方向向量分别为,a b ,平面,αβ的法向量分别为,u v ,则∴两直线,l m 所成的角为θ(02πθ<≤),cos a b a bθ⋅=;∴直线l 与平面α所成的角为θ(02πθ≤≤),sin a u a uθ⋅=;∴二面角l αβ--的大小为θ(0θπ≤≤),cos .u v u vθ⋅=22.已知椭圆2222:1(0)x y E a b a b+=>>的左焦点为(1,0)F -,其四个顶点围成的四边形面积为(1)求曲线E 的方程;(2)过点F 的直线l与曲线E 交于A ,B 两点,设AB 的中点为M ,C 、D 两点为曲线E 上关于原点O 对称的两点,且(0)CO OM λλ=>,求四边形ACBD 面积的取值范围.【答案】(1)22132x y +=;(2).【分析】(1)将椭圆四个顶点围成的四边形面积表示为2ab ,结合焦点坐标,联立方程组,求解即可; (2)设出直线l 的方程,利用弦长公式求AB ,再利用0()CO OM λλ>= ,建立直线l 方程中参数,m λ的关系,再利用点到直线的距离,以及面积公式,将四边形面积表示为函数形式,求该函数的取值范围即可. 【详解】(1)根据题意得2ab =226a b =,又因为2221c a b ==-,解得23a =,22b =,所以椭圆E 的方程为22132x y +=;(2)∴当直线l 的斜率为0时,点M 与O 重合,不满足0()CO OM λλ>=,故不成立; ∴当直线l 斜率不为0时,设:1AB x my =-, 代入E 得222(1)360my y -+-=整理得22(23)440m y my +--=, 设11(,)A x y ,22(,)B x y ,则12122244,2323m y y y y m m -+==++,所以21|AB y y =-== 212122246()22,2323m x x m y y m m -+=+-=-=++ 所以2232(,)2323mM m m -++,因为0()CO OM λλ>=,所以2232(,)2323mC m m λλ-++,又因为C 在曲线E 上,代入得222222294(23)(23)132m m m λλ+++=, 整理得2223m λ=+因为点O 到直线AB的距离d=设四边形ACBD 面积为S ,ABO 的面积为1S ,则11122S AB d =⋅==所以1112(1)(1)223ABC ABDS S S S S Smλλλ=+=++-==⋅+,将2223mλ=+代入得S==,m R∈,20m∴≥,21011m∴<≤+,211113221m∴≤<++4S∴≤<故四边形的取值范围为.【点睛】本题考查椭圆方程的求解,以及椭圆中四边形面积的最值,涉及弦长公式的应用,考查学生的逻辑推理能力与运算能力,属于较难题.。
2020年重庆市高考数学模拟试卷(文科)(5月份)(有答案解析)
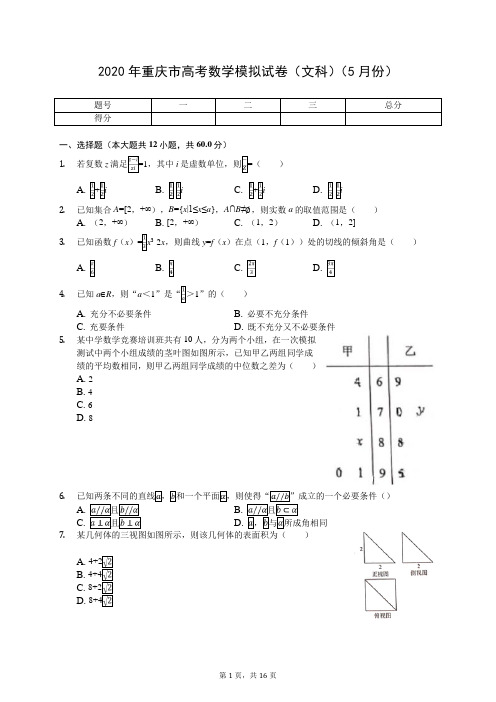
解析:【分析】 本题考查利用导数分析切线的方程,关键是掌握导数的几何意义,属于基础题. 设切线的斜率为 k,其倾斜角是 θ,求出函数 f(x)的导数,利用导数的几何意义可得 k=f′(1), 即 tanθ,结合 θ 的范围,分析可得答案. 【解答】
解:根据题意,函数 f(x)= x3-2x,设切线的斜率为 k,其倾斜角是 θ,
9.答案:B
解析:解:∵等腰梯形 ABCD 中, =2 ,E,F 分别为 AD,BC 的中点,G 为 EF 的中点,
∴
=
=
=
=
,
∵ =, =,
第 8 页,共 16 页
∴
=
,
故选 B. 利用向量的共线定理、平行四边形法则即可得出. 本题考查了平面向量加减混合运算,熟练掌握向量的共线定理、平行四边形法则是解题的关键,属 基础题.
函数 f(x)= x3-2x,则 f′(x)=x2-2,
则有 k=f′(1)=-1, 则 tanθ=-1,
又由 0≤θ<π,则 θ= ,
故选:D.
4.答案:B
解析:【分析】 本题考查充分条件、必要条件是一
第 6 页,共 16 页
种简单有效的方法,属于基础题. 根据 a<1,不一定能得到 (如 a=-1 时);但当 【解答】 解:由 a<1,不一定能得到 (如 a =-1 时);
解得 y=4+x, 甲组同学的中位数为:80+x,乙同学的中位数为 70+y ∴甲乙两组同学成绩的中位数之差为|(80+x)-(70+y)|=|10+x-y|=|10+x-4-x|=6. 故选:C. 甲乙两组同学成绩的平均数相同,得 y=4+x,甲组同学的中位数为:80+x,乙同学的中位数为 70+y, 由此能求出甲乙两组同学成绩的中位数之差. 本题考查平均数、方差、中位数的求法,考查茎叶图的性质等基础知识,考查运算求解能力,是基 础题.
重庆市三峡名校联盟2020-2021学年高一数学下学期5月联考试题数学答案

数 学 答 案一、单选题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)二、多选题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多项是符合题目要求,全部选对得5分,部分选对得3分,选错不得分)三、填空题(本大题共4小题,每小题5分,共20分)13、3 15、6π 16、⎣ 四、解答题(本大题共6小题,共70分,解答题应写出文字说明、证明过程或演算步骤) 17、(本小题10分,每小问各5分)解:(1)由题意,c os 9a b a bθ⋅===+因为[0,π]θ∈,故3π4θ=. ........................5分 (2)(3,12)a kb k k +=-+-,因为()c a kb ⊥+,所以()0c a kb ⋅+=,即3120k k -++-=,解得2k =-. ...........................10分18、(本小题12分,每小问各6分)解:(1)因为2sin 3sin C B =,所以23c b =,因为3A π=,ABC 的面积为331133sin 222b bc A b ==⨯⨯⨯,...................4分所以解得2b =,可得3c = ..............................6分(2)法1.(向量法)因为D 为BC 边的中点,可得2AD AB AC =+, .....................8分两边平方,可得22242AD AB AC AB AC =++⋅222cos 94619c b bc A =++=++=,...........10分所以线段AD 长为192...............................12分说明:法2.计算7a =,利用两角互补cos cos 0ADB ADC ∠+∠=计算AD 长。
法3.延长AD 至E ,使D 为AE 中点,在三角形ABE 中余弦定理计算AE 长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的面积为______.
14.一个几何体的三视图如图所示,其中正视图是边长为 2 的等边三角形,俯视图是半圆.现有一只蚂蚁
从点 A 出发沿该几何体的侧面环绕一周回到点 A ,则蚂蚁所经过路程的最小值为__________.
x y 4 0 x 2 0 15.若 x, y 满足约束条件 x y 2 0 ,则 z=x 2y 的最大值为__________.
A.4 B.8 C.16 D.32
4.已知实轴长为 2
2
的双曲线
C: x2 a2
y2 b2
1(a
b
0) 的左、右焦点分别为
F1(﹣2,0),F2(2,0),
点 B 为双曲线 C 虚轴上的一个端点,则△BF1F2 的重心到双曲线 C 的渐近线的距离为( )
1
2
32
A. 3 B. 3 C. 3 D. 3
( 是参数).求 的直角坐标方程和 的普通
22.(10 分)如图,在直四棱柱 P ABCD 中, ADB 90 , CB CD .点 E 为棱 PB的中点.
若 PB PD ,求证: PC BD ;求证: CE //平面 PAD .
参考答案
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目 要求的。 1.A 2.A 3.B 4.A 5.C 6.B 7.B 8.A 9.B 10.C 11.B 12.D
2 1 A. 2 B. 2 1 C. 2 2 D. 2 4
11.已知△ABC 的三个内角 A、B、C 所对边长分别为 a、b、c,向量 =(a+c,a-b), =(b,a-c),若
∥ ,则∠C=(
)
A. B. C. D.
12.在如图所示的 ABC 中,点 D ,E 分别在边 AB ,CD 上,且 BD 2AD ,CE 2ED ,则 BE ( )
5.已知集合 A 1,0,1, B x N | x 1,则 A B ( )
A.0 B.1,0 C.{1, 0,1} D. ,1
6.4 张卡片上分别写有数字 1,2,3,4,从这 4 张卡片中随机抽取 2 张,则取出的 2 张卡片上的数学之 和为偶数的概率是( )
1
1
2
3
A. 2 B. 3 C. 3 D. 4
7.如图, 一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为( )
A.1 B.2 C.3 D.4
8.已知函数 f (x) (ax 1)(x b) ,如果不等式 f (x) 0 的解集为 (1,3) ,那么不等式 f (2x) 0 的解集
为( )
A. (, 3) (1 , ) 22
小;若 b 8, a c ,且 ABC 的面积为 3 3 ,求 a .
18.(12 分)已知椭圆 C : x2 2y2 4 .求椭圆 C 的离心率;设 O 为原点,若点 A 在直线 y 2 上,点 B 在
椭圆 C 上,且 OA OB ,求线段 AB 长度的最小值.
19.(12 分)已知 f x ln x a1 x .讨论 f x 的单调性;当 f x 有最大值,且最大值大于 2a 2 时,
A.4 B.2 C.1 D.0
2.若直线 2ax by 2 0(a 0,b 0) 被圆 x2 y2 2x 4 y 1 0 截得弦长为 4,则 4 1 的最小值 ab
是( )
A.9
B.4
1
1
C. 2 D. 4
3.已知集合 A {x N | 2 x<4},B {x | x 1 0} ,则集合 A ∩ B 中子集的个数是( ) 3 x
重庆市三峡名校联盟 2020 届高三 5 月联考数学(文)试题
一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目 要求的。
1.已知函数 f x x2 2x sin x 1 x 1在区间1,3 的最大值为 M,最小值为 m,则 M m
(2)由题意结合面积公式和余弦定理得到关于 a,c 的方程组,求解方程组即可求得 a 的值.
【详解】
求 a 的取值范围.
20.(12 分)如图,等边三角形 所在平面与梯形
所在平面互相垂直,且有
,
,
.
证明:
平面 ;求点 到平面 的距离.
21.(12 分)极坐标系与直角坐标系 有相同的长度单位,以原点 为极点,以 轴正半轴为极轴,曲线
的极坐标方程为
,曲线 的参数方程为
方程;若 与 有两个不同的公共点 , ,求 .
(, 1) (3 , ) ( 1 , 3)
C.
2 2 D. 2 2
B. ( 3 , 1) 22
9.已知 (1 x) (1 x)2 (1 x)n a0 a1x a2 x2 an xn ,若 a1 a2 an1 29 n ,那
么自然数 n ( )
A.3 B.4 C.5 D.6 10.一个组合体的三视图如图所示(图中网格小正方形的边长为 1),则该几何体的体积是( )
x 3y 3 0
16.已知实数 x, y 满足
x y 1 0 x y 1 0
z
,则
2x y 8 2x y 的最小值为______.
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。
17.(12 分) ABC 的内角 A, B,C 所对的边分别为 a,b, c ,已知 (a c)2 b2 2 3ab sin C .求 B 的大
A. 1 AC 2 AB 33
B. 2 AC 1 AB 33
3 AC 5 AB
C. 4
9
1 AC 7 AB
D. 3
9
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
13.如图,平面四边形 ABCD 中, BAD 45 ,CB AB ,CD AD ,CD 2 2 ,CB 1.则 ABD
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
15 13. 2
14. 6 2
15.14 16.2
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。1Βιβλιοθήκη .(1)3;(2)
5
13 .
【解析】
【分析】
(1)由题意结合余弦定理计算可得 cosB 1 3sinB ,据此讨论计算可得 B . 3
