重庆市名校联盟2019~2020学年度第一次联合考试 数学试题(高2021级)
重庆市名校联盟2023-2024学年高三下学期第一次联考数学试题

重庆市名校联盟2023-2024学年高三下学期第一次联考数学试题学校:___________姓名:___________班级:___________考号:___________由④⑤得()()24-+-=g x g x ,则()()24++=g x g x ,所以()()424+++=g x g x ,得到()()4g x g x +=,()g x 周期为4,因为()()24-+-=g x g x ,令1x =,则()()114g g +-=,又因为()g x 为偶函数,则()()11g g =-,则()241=g ,所以()12g =,()()()20254506112=´+==g g g ,故选项B 错误;因为()()422f x g x -+-=, 得()()22f x g x +-=,()()22f x g x -+=,又因为()()24-+=g x g x ,所以()()20f x f x +-=,又因为()()4f x f x =-,所以()()420-+-=f x f x ,所以()()20f x f x ++=,则()()42()f x f x f x +=-+=,所以()f x 周期为4,由③知,()()()4f x f x f x =-=-,所以()f x 是R 上的偶函数,故选项C 正确;由选项B 知,()()22f x g x +-=,()()4f x f x =-,()()24-+=g x g x ,对三个式子分别关于x 求导可得,()()20¢¢--=f x g x ⑥,()()4f x f x ¢¢=--⑦,()()20¢¢--=g x g x ⑧,由⑥得()()20¢¢--=f x g x ⑨,⑥-⑨结合⑧可得()()2f x f x ¢¢=-,又因为()()4f x f x ¢¢=--,则()()()22¢¢¢+=--=-f x f x f x ,即()()2f x f x ¢¢+=-,则()()()42f x f x f x ¢¢¢+=-+=,()f x ¢周期为4,由()()4f x f x ¢¢=--知,()()22¢¢=-f f ,()20f ¢=,所以DM AD^,因为AP^平面ABCD,且DMÌ平面ABCD,,所以AP DM^因为AP AD AAP ADÌ平面PAD,Ç=,,所以DM^平面PAD,且ANÌ平面PAD,所以DM AN^,因为AP AD=,且点N是线段PD的中点,所以AN PD^,又因为DM PD DDM PDÌ平面PDM,I,,=所以AN^平面PDM,(2)因为AP^平面ABCD,且90Ð=°,BAD所以直线,,AB AD AP两两垂直,以A为原点,分别以直线,,AB AD AP为x轴,y轴,z轴,建立空间直角坐标系,如图所示:由2224====得,BC AB AP AD利用切合函数得到两个关键等式;三是把多变量转化为单变量,构造函数,利用单调性证明不等式.。
重庆市2019-2020学年下学期高一(期末)联合检测试卷数学试题

学习资料分享[公司地址]高一(下)联合检测试卷(数学)参考答案第1页共3页2020年春高一(下)联合检测试卷数学参考答案一、选择题1~6CBDCBA 7~12DCBCBB 第7题提示:从四个字母中取2个有6种取法,其中两个字母不同的有5种,所求概率为56.第8题提示:12a q =,43211123a q a q a q =+,解得3q =,462162a a q ==.第9题提示:画出不等式表示的区域,使得直线122z y x =-经过可行域且截距最小时的解为22()33, ,z 的最大值为23-.第10题提示:不妨设小正方形边长为1,所求概率为15.第11题提示:2222222221()212cos 22442a b a b a b c a b ab C ab ab ab ab +-++-+===≥≥,角C 的最大值为3π,此时ABC ∆为等边三角形.第12题提示:∵2BP PC = ,∴1233QP QB QC =+ ,∴(2)33||||QA QB QC QA QP QA QP ⋅+=⋅=-⋅ 设||[04]QA m =∈ , ,2(2)3(4)31212QA QB QC m m m m ⋅+=--=-- ≥.二、填空题13.3214.1415.916.2224333n n n ⋅-+-第15题:18162(2)(2)()281018x y x y x y x y y x +=++=++++≥,∴29x y +≥,等号成立时32x =,6y =.第16题:由题知2121123(21)14642n n n n b a n n --==--+=-+,前n 项和为214(14)(1)226443214233n n n n n n n -+⋅-⋅+=⋅-+--.三、解答题17.(10分)解:(1)直线AB 的斜率为13221-=--,……2分直线AB 的方程为:12(2)y x -=--,25y x =-+;……4分(2)点C 到直线AB的距离d ==,……6分高一(下)联合检测试卷(数学)参考答案第2页共3页||AB =,……8分故ABC ∆的面积17||22S AB d =⋅=.……10分18.(12分)解:(1)当1a =时,2320x x -+≤,(1)(2)0x x --≤,故解集为[12], ;……6分(2)由题知22(21)4(1)430a a a ∆=+-+=-≤,解得33[]22a ∈-, .……12分19.(12分)解:(1)由题知(2)b λλ=- ,,|||b λ== 2λ=-,故(24)b =- ,;……6分(2)22222()(2)22||||cos 3a b a b a a b b a a b b π-⋅+=-⋅-=-⋅110()2052=--=-.……12分20.(12分)解:(1)设前4组的频率分别为1234a a a a , , , ,公差为d ,由题知210.016100.16a a d =+=⨯=故123414610.016100.84a a a a a d +++=+=-⨯=,……3分联立解得10.06a =,0.1d =;……4分又1230.48a a a ++=,∴中位数为40.50.4845550109a -+⨯=;……6分(2)10x =,56y =,……8分121()ˆ(n i i i n i i x x y y b x x ==--∑=-∑22222(610)(4056)(810)(5556)(1210)(6056)(1010)(6056)(1410)(6556)(610)(810)(1210)(1010)(1410)--+--+--+--+--=-+-+-+-+-114=故1157ˆˆ561042a y bx =-=-⋅=,回归直线为1157ˆ42y x =+,……10分当18x =时,ˆ78y=,估计该车间某位有18年工龄的工人的生产速度为78件/小时.……12分21.(12分)解:(1)设AD m =,在ADC ∆中由余弦定理22232cos 4m CD m CD AC π+-⋅⋅=……3分高一(下)联合检测试卷(数学)参考答案第3页共3页即22()102m +-⋅-=,解得2m AD ==;……6分(2)在BDC ∆、ADC ∆中由正弦定理sin sin BD DCB BC BDC∠=∠ (9)分sin sin 5DCA AD ADC AC ∠===∠.……12分22.(12分)解:(1)设公差为d ,则1172(2)3a d a d +-+=,1132362a d a d ⋅+=+,解得13a =,2d =,……3分∴1(1)21n a a n d n =+-=+,21(1)22n n n S na d n n -=+=+;……6分(2)1111()(21)(23)22123n b n n n n ==-++++,1111111[()()()]2355721233(23)n n T n n n =-+-++-=+++ ,……8分又15139T =,由题得2219(23)93(23)m n m n =⋅++,即223(23)23m n m n =++,∴222694129m n m m n mn n +=++,即2291292m n m m =+-(*)由题知2291292m m m m>+-且*m N ∈,故37m <<,……10分故只需考虑456m =, , ,4m =时14425n =,5m =时22519n =,6m =时36n =,又*n N ∈,故满足条件的m n ,只有一组:636m n =⎧⎨=⎩.……12分。
2024-2025学年重庆市“名校联盟”高一上学期第一次联合考试数学试题(含答案)

2024-2025学年重庆市“名校联盟”高一上学期第一次联合考试数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.下列命题中正确的A. ⌀与{0}表示同一个集合;B. 方程{x|(x−2)2(x−3)=0}的所有解的集合可表示为{2,2,3};C. 由3,4,5组成的集合可表示为{3,4,5}或{4,5,3};D. 很小的实数可以构成集合.2.已知命题p:∀x<1,x2<1,命题q:∃x≤0,x3+2≥0,则A. ¬p:∀x≥1,x2≥1B. ¬p:∃x<1,x2≥1C. ¬q:∀x≥0,x3+2<0D. ¬q:∃x≥0,x3+2<03.设M=2a2+5a+3,N=(a+1)(a+2),则M与N的大小关系为A. M>NB. M<NC. M≤ND. M≥N4.设集合U={x∈N∗|x≤5},A={3,4},B={2,3},则(C U A)∪B=A. {1,2,3}B. {1,2,3,4}C. {1,2,3,5}D. {2,3,4,5}5.“2≤x≤3”是“x2−x−12≤0”的A. 必要不充分条件B. 充分必要条件C. 充分不必要条件D. 既不充分也不必要条件6.若t>1,则关于x的不等式(t−x)(x−1t)>0的解集为A. (t,1t)B. (−∞,1t)∪(t,+∞)C. (1t,t)D. (−∞,t)∪(1t,+∞)7.若对任意x<0,不等式x+1x≤m2+3m恒成立.则实数m的取值范围是A. −2≤m≤−1B. m≤−2或m≥−1C. m≤1或m≥2D. 1≤m≤28.若a、b、c是三个不全相等的实数,且不等式ab+3bc≤t(a2+b2+c2)恒成立,则实数t的最小值为A. 102B. 52C. 22D. 32二、多选题:本题共3小题,共18分。
2019-2020学年重庆市六校联考高一上期末数学试卷((有答案))

2019-2020 学年重庆市六校联考高一(上)期末数学试卷一、选择题:本大题共12 小题,每题 5 分,共 60 分 .在每题给出的四个备选项中,只有一项为哪一项切合题目要求的.1.(5 分)=()A.B.C.D.2.(5 分)已知会合 M={ 1,2} , N={ 2, 3, 4} ,若 P=M∪ N,则 P 的子集个数为()A.14 B.15 C.16 D.323.(5 分)已知函数 f(x)=,若f(﹣1)=f(1),则实数a的值为()A.1 B.2C.0D.﹣ 14.(5 分)若函数 f( x) =ax2﹣bx+1(a≠0)是定义在 R 上的偶函数,则函数g(x)=ax3+bx2+x (x∈R)是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数.(分)设2,b=()3,c=3,则()5 5a=logA. c< b< a B. a<b< c C.c<a<b D.b<a<c6.(5分)已知 tan(α﹣β)= ,tan(﹣β)=,则 tan(α﹣)等于()A.B.C.D.7.(5 分)方程 x﹣ log x=3 和 x﹣log x=3 的根分别为α,β,则有()A.α<βB.α>βC.α =βD.没法确立α与β大小8.(5 分)函数 f( x)=2sin( 2x+)的图象为M,则以下结论中正确的选项是()A.图象 M 对于直线 x=﹣对称B.由 y=2sin2x的图象向左平移获得MC.图象 M 对于点(﹣,0)对称D. f(x)在区间(﹣,)上递加.(分)函数2( x﹣)的图象沿 x 轴向右平移 m 个单位( m>0),所得图象对于 y 95y=sin轴对称,则 m 的最小值为()A.π B.C.D.10.(5 分)已知 f(x)是定义在 R 上的偶函数,且在区间(﹣∞,0)上单一递减,若实数 a知足f(3| 2a+1|)>f(﹣),则 a 的取值范围是()A.(﹣∞,﹣)∪(﹣,+∞) B.(﹣∞,﹣)C.(﹣,+∞) D.(﹣,﹣).(分)已知α∈332,5[,] ,β∈ [ ﹣,0] ,且(α﹣)﹣sin α﹣ 2=0,8β+2cos β11+1=0则 sin(+β)的值为()A.0 B.C.D. 112.(5 分)若区间 [ x1, x2] 的长度定义为| x2﹣x1| ,函数 f(x) =( m∈R,m ≠0)的定义域和值域都是 [ a,b] ,则区间 [ a,b] 的最大长度为()A.B.C.D.3二、填空题:本大题共 4 小题,每题 5 分,共 20 分 .把答案填写在答题卡相应地点上 .13.(5分)计算: log3+lg4+lg25+(﹣)0=..(分)已知扇形的面积为4cm 2,扇形的圆心角为 2 弧度,则扇形的弧长为.14 515.(5分)若α∈( 0,π),且cos2 α =sin(+α),则 sin2 α的值为..(分)已知正实数x,y,且 x 2+y2,若(,),则(,)的值域为.16 5=1f x y = f x y三、解答题:本大题共 6 小题,共 70 分 .解答应写出文字说明、证明过程或演算步骤. 17.(10 分)已知全集 U=R,函数的定义域为会合A,会合 B={ x| 5≤x<7}(1)求会合 A;(2)求( ?U B)∩ A.18.( 12 分)在平面直角坐标系xOy 中,若角α的始边为 x 轴的非负半轴,其终边经过点 P( 2,4).(1)求 tan α的值;(2)求的值.19.(12 分)已知二次函数f (x)=mx2+4x+1,且知足 f (﹣ 1) =f(3).(1)求函数 f (x)的分析式;(2)若函数 f (x)的定义域为(﹣ 2,2),求 f (x)的值域.20.(12 分)已知函数 f (x)=sin2ωx+2 cos ω xsin ωx+sin(ωx+)sin(ωx ﹣)(ω>0),且 f (x)的最小正周期为π.(1)求ω的值;(2)求函数 f (x)在区间( 0,π)上的单一增区间.21.(12 分)已知函数 f( x)=log2()﹣x(m为常数)是奇函数.(1)判断函数 f (x)在 x∈(,+∞)上的单一性,并用定义法证明你的结论;(2)若对于区间 [ 2,5] 上的随意 x 值,使得不等式 f( x)≤ 2x+m 恒建立,务实数 m 的取值范围.22.(12 分)已知函数f( x)=a(| sinx|+| cosx| )﹣sin2x﹣1,若f() =﹣.(1)求 a 的值,并写出函数f(x)的最小正周期(不需证明);(2)能否存在正整数 k,使得函数 f(x)在区间 [ 0,kπ] 内恰有 2017 个零点?若存在,求出k的值,若不存在,请说明原因.2019-2020 学年重庆市六校联考高一(上)期末数学试卷参照答案与试题分析一、选择题:本大题共12 小题,每题 5 分,共60 分 .在每题给出的四个备选项中,只有.一项为哪一项切合题目要求的1.(5 分)=()A.B.C.D.【解答】解: cos=cos(π+)=﹣cos=﹣应选 D.P=M∪ N,则P 的子集个数为()2.(5 分)已知会合 M={ 1,2} , N={ 2, 3, 4} ,若A.14 B.15 C.16 D.32【解答】解:会合 M={ 1, 2} , N={ 2, 3, 4} ,则 P=M∪N={ 1,2,3,4} ,∴P 的子集有 24=16 个.故答案为: C.3.(5 分)已知函数 f(x)=,若f(﹣1)=f(1),则实数a的值为()A.1 B.2C.0D.﹣ 1【解答】解:∵函数 f( x)=,f(﹣1)=f(1),∴f(﹣ 1)=1﹣(﹣ 1)=2, f( 1)=a,∵f(﹣ 1)=f(1),∴a=2.应选: B.4.(5 分)若函数 f( x) =ax2﹣bx+1(a≠0)是定义在 R 上的偶函数,则函数g(x)=ax3+bx2+x (x∈R)是()A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数【解答】解: f (x)为偶函数,则 b=0;∴g(x) =ax3+x;∴g(﹣ x)=a(﹣ x)3﹣ x=﹣( ax3+x) =﹣ g(x);∴g(x)是奇函数.应选 A..(分)设2,b=()3,c=3,则()5 5a=logA. c< b< a B. a<b< c C.c<a<b D.b<a<c【解答】解: a=log2<,b=()3∈( 0,1),c=3>1.∴c>b>a.应选: B.6.(5 分)已知 tan(α﹣β)=,tan(﹣β)=,则tan(α﹣)等于()A.B.C.D.【解答】解:∵ tan (α﹣β)=,tan(﹣β)=,∴tan (α﹣)=tan[(α﹣β)﹣(﹣β)] ===.应选: C.7.(5 分)方程 x﹣ log x=3 和 x﹣log x=3 的根分别为α,β,则有()A.α<βB.α>βC.α =βD.没法确立α与β大小【解答】解:方程 x﹣log x=3 和x﹣log x=3,分别化为: log2x=3﹣x,log3x=3﹣ x.作出函数图象: y=log2x,y=3﹣x,y=log3x.则α<β.应选: A.8.(5 分)函数 f( x)=2sin( 2x+)的图象为M,则以下结论中正确的选项是()A.图象 M 对于直线 x=﹣对称B.由 y=2sin2x的图象向左平移获得MC.图象 M 对于点(﹣,0)对称D. f(x)在区间(﹣,)上递加【解答】解:∵函数 f( x)=2sin(2x+ )的图象为 M ,令 x=﹣,可得 f(x)=0,可得图象 M 对于点(﹣,0)对称,故图象 M 不对于直线 x=﹣对称,故 C 正确且 A 不正确;把 y=2sin2x的图象向左平移获得函数 y=2sin2(x+ )=2sin(2x+)的图象,故 B 不正确;在区间(﹣,)上,2x+∈(0,π),函数 f(x)=2sin( 2x+)在区间(﹣,)上没有单一性,故 D 错误,应选: C..(分)函数2( x﹣)的图象沿 x 轴向右平移 m 个单位( m>0),所得图象对于 y 9 5y=sin轴对称,则 m 的最小值为()A.π B.C.D.【解答】解:函数 y=sin2(x﹣)==的图象沿x轴向右平移m个单位( m> 0),可得 y=的图象,再依据所得图象对于 y 轴对称,可得 2m=( 2k+1)? ,k ∈Z ,即 m ═( 2k+1)? ,则 m 的最小值为,应选: D .10.(5 分)已知 f (x )是定义在 R 上的偶函数,且在区间(﹣∞, 0)上单一递减,若实数 a知足f (3|2a +1|)>f (﹣),则 a 的取值范围是( ) A .(﹣∞,﹣ )∪(﹣ ,+∞) B .(﹣∞,﹣)C .(﹣ ,+∞)D .(﹣ ,﹣ )【解答】 解:∵函数 f ( x )是偶函数,∴f ( 3| 2a +1| )> f (﹣),等价为 f (3| 2a +1| )> f (),∵偶函数 f (x )在区间(﹣∞, 0)上单一递减, ∴f ( x )在区间 [ 0,+∞)上单一递加,∴3| 2a +1| > ,即 2a+1<﹣ 或 2a+1> ,解得 a <﹣ 或 a >﹣,应选 A ..( 分)已知 α∈3 32,[ , ] ,β∈ [ ﹣ ,0] ,且(α﹣ ) ﹣sin α﹣ 2=0,8β+2cos β11 5+1=0则 sin ( +β)的值为( )A .0B .C .D . 1【解答】 解:∵( α﹣ )3﹣sin α﹣ 2=0,可得:(α﹣)3﹣cos ( )﹣ 2=0,即(﹣ α) 3+cos ()+2=0由 8β3+2cos 2β+1=0,得( 2β)3+cos2β+2=0,∴可得 f ( x )=x 3+cosx+2=0,其,x 2=2β.∵α∈[ , ] ,β∈[ ﹣,0] ,∴∈[ ﹣π,0] , 2β∈[ ﹣π,0]可知函数 f (x)在 x∈[ ﹣π,0] 是单一增函数,方程x3+cosx+2=0 只有一个解,可得,即,∴,那么 sin(+β) =sin =.应选: B.12.(5 分)若区间 [ x1, x2] 的长度定义为| x2﹣x1| ,函数 f(x) =(m∈R,m ≠0)的定义域和值域都是 [ a,b] ,则区间 [ a,b] 的最大长度为()A.B.C.D.3【解答】解:函数f(x)=(m∈R,m≠ 0)的定义域是{ x| x≠0},则[ m,n]是其定义域的子集,∴[ m,n] ? (﹣∞, 0)或( 0,+∞).f (x)==﹣在区间[ a,b]上时增函数,则有:,故 a,b 是方程 f (x)=﹣=x 的同号相异的实数根,即 a,b 是方程( mx)2﹣( m2+m)x+1=0 同号相异的实数根.那么 ab=,a+b=,只要要△>0,即( m2+m)2﹣ 4m2>0,解得: m>1 或 m<﹣ 3.那么: n﹣ m==,故 b﹣a 的最大值为,应选:A.二、填空题:本大题共 4 小题,每题 5 分,共 20 分 .把答案填写在答题卡相应地点上.13.(5 分)计算: log3+lg4+lg25+(﹣)0=.【解答】解:原式 = +lg102+1= +2+1=.故答案为:..(分)已知扇形的面积为4cm 2,扇形的圆心角为 2 弧度,则扇形的弧长为4cm.14 5【解答】解:设扇形的弧长为 l,圆心角大小为α(rad),半径为 r,扇形的面积为 S,则: r 2.解得,===4r=2∴扇形的弧长为l=r α=2×2=4cm,故答案为: 4cm.15.(5 分)若α∈( 0,π),且cos2 α =sin(+α),则 sin2 α的值为﹣1.【解答】解:∵α∈( 0,π),且cos2α=sin(+α),∴cos2α=2sin(+α),∴( cosα+sin α)?(cosα﹣ sin α)=(cosα+sinα),∴cosα+sin α=0,或 cosα﹣sin α=(不合题意,舍去),∴α=,∴ 2α=,∴ sin2α=sin=﹣ 1,故答案为:﹣ 1..(分)已知正实数x ,,且2+y2,若(,)=,则(,)的值域为[,16 5y x=1f x y f x y 1).【解答】解: x2+y2=1;∴=====;∵1=x2+y2≥2xy,且 x,y>0;∴;∴1<1+2xy≤2;∴;∴;∴f( x, y)的值域为.故答案为: [,1).三、解答题:本大题共 6 小题,共 70 分 .解答应写出文字说明、证明过程或演算步骤.17.(10 分)已知全集 U=R,函数的定义域为会合A,会合 B={ x| 5≤x<7}(1)求会合 A;(2)求( ?U B)∩ A.【解答】解:(1)由题意可得:;解得 3≤ x<10;∴A={ x| 3≤x<10} ;(2)C U B={ x| x<5 或 x≥7} ;∴( C U B)∩ A={ x| 3≤x<5 或 7≤ x< 10} .18.( 12 分)在平面直角坐标系xOy 中,若角α的始边为 x 轴的非负半轴,其终边经过点 P( 2,4).(1)求 tan α的值;(2)求的.【解答】解:(1)由随意角三角函数的定可得:.(2)==.19.(12 分)已知二次函数 f (x)=mx2+4x+1,且足 f ( 1) =f(3).(1)求函数 f (x)的分析式;(2)若函数 f (x)的定域( 2,2),求 f (x)的域.【解答】解:(1)由 f( 1) =f(3)可得二次函数的称x=1⋯(2 分)即进而得 m= 2⋯(4 分)所以二次函数的分析式f(x)= 2x2+4x+1⋯(6 分)(2)由( 1)可得 f (x)= 2(x 1)2+3⋯(9 分)所以 f(x)在( 2,2] 上的域( 15,3] ⋯( 12 分)20.(12 分)已知函数 f (x)=sin2ωx+2 cos ω xsin ωx+sin(ωx+)sin(ωx )(ω>0),且 f (x)的最小正周期π.(1)求ω的;(2)求函数 f (x)在区( 0,π)上的增区.【解答】解:(1)f(x) =sin2 ωx+2 cosωxsin ωx+sin(ωx+)sin(ωx ),=+ sin2 ωx (cos2ωx sin2ωx),=;⋯(5 分)由意得,即可得ω=1⋯(6 分)(2)由( 1)知由函数增性可知:整理得:⋯(9 分)∴f( x)在( 0,π)上的增区,⋯(12分)21.(12 分)已知函数f( x)=log2() x(m 常数)是奇函数.(1)判断函数 f (x)在 x∈(,+∞)上的性,并用定法明你的;(2)若于区 [ 2,5] 上的随意 x ,使得不等式 f( x)≤ 2x+m 恒建立,求数 m 的取范.【解答】解:(1)由条件可得 f( x)+f(x)=0,即,化得 1 m2 22,进而得 m=±2;由意 m= 2 舍去,x =14x所以 m=2,即,上减函数;明以下:, f(x1)(2)2() 12()+x 2,f x=log x log因<x1<x2,所以x2x1>0,2x11> 0,2x21> 0;所以 f(x1) f( x2)> 0,即 f( x1)> f(x2);所以函数 f (x)在 x∈(,+∞)上减函数;(2) g( x)=f( x) 2x,由( 1)得 f(x)在 x∈(,+∞)上减函数,所以 g(x)=f( x) 2x在 [ 2,5] 上减;所以 g(x)=f( x) 2x在 [ 2,5] 上的最大,由意知 n≥g(x)在 [ 2,5] 上的最大,所以.22.(12 分)已知函数 f( x)=a(| sinx|+| cosx| ) sin2x 1,若 f() =.(1)求 a 的,并写出函数 f(x)的最小正周期(不需明);(2)能否存在正整数 k,使得函数 f(x)在区 [ 0,kπ] 内恰有 2017 个零点?若存在,求出 k 的,若不存在,明原因.【解答】解:(1)函数 f (x) =a(| sinx|+| cosx| )sin2x 1,∵f() =﹣.∴a(sin +cos)﹣ sin﹣1=﹣.解得: a=1,函数 f(x)的最小正周期 T=π,(2)存在 n=504,知足题意:原因以下:当时,,设 t=sinx+cosx,则,sin2x=t2﹣ 1,则,可得 t=1 或,由 t=sinx+cosx 图象可知, x 在上有 4 个零点知足题意.当时,,t=sinx﹣cosx,则,sin2x=1﹣t 2,,,t=1 或,∵,∴x 在上不存在零点.综上议论知:函数 f (x)在 [ 0,π)上有 4 个零点,而 2017=4×504+1,所以函数在 [ 0,504π] 有 2017 个零点,所以存在正整数 k=504 知足题意.。
重庆市九校联盟2019_2020学年高二数学上学期联考试题文
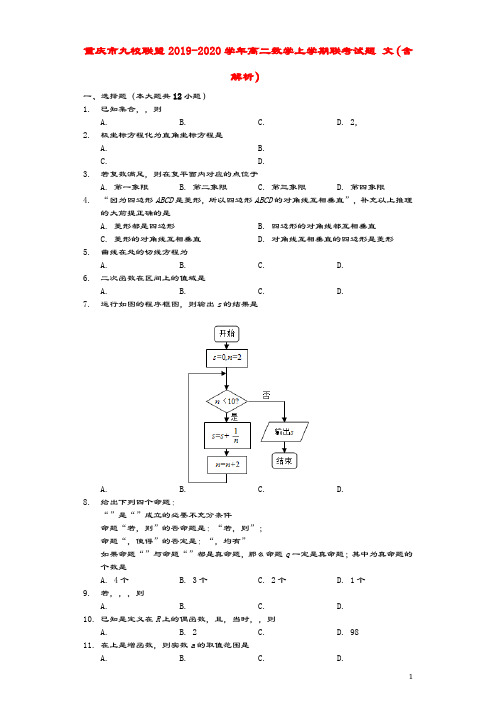
,
解得也可分离变量解.
,
令 得,
,是的极值点,
,,
解得:,
,
则,
在上单调递减,
当时,
的最大值为.
【解析】因为函数在处的切线l与直线平行,所以.
函数,令,求导,列表格分析函数的单调性极值,若函数在上恰有两个零点,,进而得出结果.
因为,是函数的两个极值点,所以令 得,的两个根是,,,,,因为,所以解得:,,求出它的最小值,就可得出答案.
4.【答案】C
【解析】解:用三段论形式推导一个结论成立,
大前提应该是结论成立的依据,
由四边形ABCD是菱形,所以四边形ABCD的对角线互相垂直的结论,
大前提一定是菱形的对角线互相垂直,
故选:C.
用三段论形式推导一个结论成立,大前提应该是结论成立的依据,由四边形ABCD为菱形,得到四边形ABCD的对角线互相垂直的结论,得到大前提.
9.【答案】A
【解析】解:,,,
则.
故选:A.
利用对数函数和指数函数的单调性求解.
本题考查三个数的大小的比较,是基础题..
10.【答案】A
【解析】解:是定义在R上的偶函数,且,
,即周期为6,
当时,,
则.
故选:A.
由已知可得,,即周期为6,从而有,代入即可求解.
本题主要考查了利用偶函数的性质及周期求解函数值,体现了转化思想的应用
本题考查用三段论形式推导一个命题成立,要求我们填写大前提,这是常见的一种考查形式,属于基础题.
5.【答案】A
【解析】解:的导数为,
可得曲线在处的切线斜率为,
且切点为,
则切线方程为,
即.
故选:A.
重庆市“名校联盟”2025届高三上学期第一次联合考试数学试题(含答案)

重庆市“名校联盟”2025届高三上学期第一次联合考试数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.若集合A ={x ∈N|x⩽ 10},a =22,则下面结论中正确的是( )A. {a }⊆AB. a ⊆AC. {a }∈AD. a ∉A2.记S n 为数列{a n }的前n 项和.“任意正整数n ,均有a n >0”是“{S n }是递增数列”的( )A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3.已知向量OA =(1,−3),OB =(2,−1),OC =(m +1,m−2),若点A ,B ,C 能构成三角形,则实数m 不可以是( )A. −2B. 12C. 1D. −14.已知cos(75∘+α)=13,则sin (α−15∘)+cos(105∘−α)的值是( )A. 13B. −13C. 23D. −235.已知函数f(x)=ln x−1x 在点(1,−1)处的切线与曲线y =ax 2+(a−1)x−2只有一个公共点,则实数a 的取值范围为( )A. {1,9}B. {0,1,9}C. {−1,−9}D. {0,−1,−9}6.数学活动小组由12名同学组成,现将这12名同学平均分成四组分别研究四个不同课题,且每组只研究一个课题,并要求每组随机选出一名组长,则不同的分配方案有( )种.A. C 312C 39C 36A 33A 44B. C 312C 39C 36A 4443 C. C 312C 39C 3634D. C 312C 39C 36437.血氧饱和度是呼吸循环的重要生理参数。
人体的血氧饱和度正常范围是95%∼100%,当血氧饱和度低于90%时,需要吸氧治疗,在环境模拟实验室的某段时间内,可以用指数模型S(t)=S 0e kt 描述血氧饱和度S(t)随着给氧时间t(单位,小时)的变化而变化的规律,其中S 0为初始血氧饱和度,K 为参数。
重庆市名校联盟2021-2022学年高二下学期第一次联合考试数学试题(解析版)

【3题答案】
【答案】A
【解析】
【分析】观察导函数的符号,确定原函数的单调性即可.
【详解】由导函数的图象可知,原函数在 的右侧有两个单调区间,先增后减,A正确.
故选:A.
4.高二某班共有50名学生,其中女生有20名,“三好学生”人数是全班人数的 ,且“三好学生”中女生占一半,现从该班学生中任选1人参加座谈会,则在已知没有选上女生的条件下,选上的学生是“三好学生”的概率为()
故选:BC.
第Ⅱ卷(非选择题,共90分)
三、填空题(本大题共4小题,每小题5分,共20分)
13.已知随机变量X的分布列如下表,则 =______.
X
0
1
P
a
3a
【13题答案】
【答案】
【解析】
【分析】先利用分布列的性质求出 ,再求 得解.
【详解】解:由随机变量X的分布列得 解得 ,
∴ , .
故答案为:
③若所有偶数项的二项式系数的和为128,则 ,
解得 ,得 ,
所以 ,
所以展开式中二项式系数最大的项为 .
【小问2详解】
由(1)可知, ,
则 ,
其展开式的通项为 ,
令 ,得 ,
所以常数项 .
19.某校从学生文艺部7名成员(4男3女)中,挑选2人参加学校举办的文艺汇演活动.
(1)求男生甲被选中的概率;
(2)在已知男生甲被选中的条件下,女生乙被选中的概率;
9.将甲,乙,丙,丁4个志愿者分别安排到学校的图书馆、食堂、实验室帮忙,要求每个地方至少安排一个志愿者帮忙,则下列选项正确的是()
A.总共有12种分配方法
B.总共有36种分配方法
C.若甲、乙安排在同一个地方帮忙,则有6种分配方法
2019-2020学年人教A版重庆市九校联盟高三上学期联考数学试卷(文科) 含解析

2019-2020学年高三第一学期联考数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|0<x<3},B={x|x≤1},则A∪B=()A.(﹣∞,1] B.(﹣∞,3)C.(0,1] D.(1,3)2.的实部为()A.﹣2 B.﹣1 C.1 D.23.设函数f(x)=,若f(x)是奇函数,则g(1)=()A.﹣4 B.﹣2 C.2 D.44.某地有两个国家AAAA级旅游景区﹣﹣甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的月客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的月客流量,以下结论错误的是()A.甲景区月客流量的中位数为12950人B.乙景区月客流量的中位数为12450人C.甲景区月客流量的极差为3200人D.乙景区月客流量的极差为3100人5.若tanα=4,sinβ=2cosβ,则tan(a+β)=()A.B.6 C.D.6.某人午觉醒来,发现表停了,他打开收音机,想听电台整点报时,则他等待时间不少于20分钟的概率为()A.B.C.D.7.执行如图的程序框图,若输入的x的值为5,则输出的n的值为()A.2 B.3 C.4 D.58.已知M是抛物线C:y2=2px(p>0)上一点,F是C的焦点,过M作C的准线的垂线,垂足为N,若∠MFO=120°(O为坐标原点),△MNF的周长为12,则|NF|=()A.4 B.C.D.59.最早发现勾股定理的人应是我国西周时期的数学家商高,根据记载,商高曾经和周公讨论过“勾3股4弦5”的问题,我国的《九章算术》也有记载.所以,商高比毕达哥拉斯早500多年发现勾股定理.现有△ABC满足“勾3股4弦5”,如图所示,其中AB=4,D为弦BC上一点(不含端点),且△ABD满足勾股定理,则=()A.B.C.D.10.已知命题p:在△ABC中,若A>B,则cos A+cos B>0,命题q:在等比数列{a n}中,若a2a6=16,则a4=4.下列命题是真命题的是()A.p∧(¬q)B.(¬p)∨q C.(¬p)∧(¬q)D.p∧q11.已知函数,则f(x)的图象的对称中心为()A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)12.若函数f(x)=log a(x2﹣2ax+a2+4)(a>0,且a≠1)有最大值,且最大值不小于﹣1,则a的取值范围为()A.B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.不等式组,表示的可行域的面积为.14.若等差数列{a n}的前10项和为100,且a3=5,则a12=.15.若函数f(x)=e x﹣mx在[﹣2,0]上为减函数,则m的取值范围为.16.过双曲线C:=1(a>0,b>0)的右焦点F作双曲线C的一条弦AB,且有=,若以AB为直径的圆经过双曲线C的左顶点,则双曲线C的离心率为.三、解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.(一)必考题:共60分.17.在等比数列{a n}中,a1+a2=5,且a2+a3=20.(1)求{a n}的通项公式;(2)求数列的前n项和S n.18.设a,b,c分别为△ABC内角A,B,C的对边.已知,b=2.(1)若,求B;(2)若a=2c,求△ABC的面积.19.某公司为确定下一年度投入某种产品的宜传费,需了解年宣传费对年销售量(单位:t)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费x(万元)和年销售量y(单位:t)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.(1)根据表中数据建立年销售量y关于年宣传费x的回归方程.(2)已知这种产品的年利润x(万元)与x,y的关系为z=y﹣0.05x2﹣1.85根据(1)中的结果回答下列问题:①当年宣传费为10万元时,预测该产品的年销售量及年利润;②估计该产品的年利润与年宣传费的比值的最大值.附:回归方程中的斜率和截距的最小二乘估计公式分别为==,=.参考数据:,.20.已知函数的图象在点(1,f(1))处的切线方程为10x+y+b =0.(1)求a,b的值;(2)若对x∈(0,+∞)恒成立,求m的取值范围.21.已知椭圆C:=1(a>b>0)的离心率e=,且圆x2+y2=1经过椭圆C的上、下顶点.(1)求椭圆C的方程;(2)若直线l与椭圆C相切,且与椭圆C1:=1相交于M,N两点,证明:△OMN的面积为定值(O为坐标原点).(二)选考题:共10分.请考生从第22,23两题中任选一题作答.如果多做,则按所做的第一个题目计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,直线l的参数方程为(t为参数),曲线C的参数方程为(m>0,n>0,α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,且曲线C的极坐标方程为ρ=8sinθ.(1)求a,m,n的值;(2)已知点P的直角坐标为(0,1),l与曲线C交于A,B两点,求|PA|+|PB|.[选修4-5:不等式选讲]23.已知函数f(x)=3|x+1|﹣|2x﹣4|.(1)求不等式f(x)>3的解集;(2)若对任意x∈R,不等式f(x)﹣|x﹣2|≤t2﹣8t恒成立,求t的取值范围.参考答案一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若集合A={x|0<x<3},B={x|x≤1},则A∪B=()A.(﹣∞,1] B.(﹣∞,3)C.(0,1] D.(1,3)解:∵A={x|0<x<3},B={x|x≤1},∴A∪B=(﹣∞,3).故选:B.2.的实部为()A.﹣2 B.﹣1 C.1 D.2解:∵.∴的实部为﹣1.故选:B.3.设函数f(x)=,若f(x)是奇函数,则g(1)=()A.﹣4 B.﹣2 C.2 D.4解:根据题意,函数f(x)=,则f(﹣1)=3﹣(﹣1)=4,又由g(x)为奇函数,则f(1)=﹣f(﹣1)=﹣4,则有2g(1)=﹣4,则有g(1)=﹣2;故选:B.4.某地有两个国家AAAA级旅游景区﹣﹣甲景区和乙景区.相关部门统计了这两个景区2019年1月至6月的月客流量(单位:百人),得到如图所示的茎叶图.关于2019年1月至6月这两个景区的月客流量,以下结论错误的是()A.甲景区月客流量的中位数为12950人B.乙景区月客流量的中位数为12450人C.甲景区月客流量的极差为3200人D.乙景区月客流量的极差为3100人解:甲景区月客流量的中位数为12950人,乙景区月客流量的中位数为12450人.根据茎叶图的数据,可知甲景区月客流量的极差为3200人,乙景区月客流量的极差为3000人,故选:D.5.若tanα=4,sinβ=2cosβ,则tan(a+β)=()A.B.6 C.D.解:∵∵sinβ=2cosβ,∴tanβ=2,∴tan(α+β)===﹣,故选:C.6.某人午觉醒来,发现表停了,他打开收音机,想听电台整点报时,则他等待时间不少于20分钟的概率为()A.B.C.D.解:由题意知这是一个几何概型,∵电台整点报时,∴事件总数包含的时间长度是60,∵满足他等待的时间少于20分钟的事件包含的时间长度是20,故所求的概率值为P=1﹣=.故选:C.7.执行如图的程序框图,若输入的x的值为5,则输出的n的值为()A.2 B.3 C.4 D.5解:执行程序框图,可得(x,n)依次为:(5,0),(7,1),(9,2),(11,13),(13,4),∵132+13>132,∴输出的n的值为4.故选:C.8.已知M是抛物线C:y2=2px(p>0)上一点,F是C的焦点,过M作C的准线的垂线,垂足为N,若∠MFO=120°(O为坐标原点),△MNF的周长为12,则|NF|=()A.4 B.C.D.5解:因为∠MFO=120°,所以∠FMN=60°.又M是抛物线C上一点,所以|FM|=|MN|,则△FMN是等边三角形,则.故选:A.9.最早发现勾股定理的人应是我国西周时期的数学家商高,根据记载,商高曾经和周公讨论过“勾3股4弦5”的问题,我国的《九章算术》也有记载.所以,商高比毕达哥拉斯早500多年发现勾股定理.现有△ABC满足“勾3股4弦5”,如图所示,其中AB=4,D为弦BC上一点(不含端点),且△ABD满足勾股定理,则=()A.B.C.D.解:由等面积法可得,依题意可得,AD⊥BC,所以.故选:A.10.已知命题p:在△ABC中,若A>B,则cos A+cos B>0,命题q:在等比数列{a n}中,若a2a6=16,则a4=4.下列命题是真命题的是()A.p∧(¬q)B.(¬p)∨q C.(¬p)∧(¬q)D.p∧q解:设A+B'=π,则cos A=﹣cos B',因为A+B<π,所以0<B<B'<π,所以cos B>cos B',则cos B>﹣cos A,即cos A+cos B>0,故命题p是真命题.因为a2a6=16,所以,所以a4=±4,则命题q是假命题.∴p∧(¬q)是真命题.故选:A.11.已知函数,则f(x)的图象的对称中心为()A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)解:因为===,令(k∈Z),得(k∈Z),f(x)=,则f(x)的图象的对称中心为(k∈Z),故选:D.12.若函数f(x)=log a(x2﹣2ax+a2+4)(a>0,且a≠1)有最大值,且最大值不小于﹣1,则a的取值范围为()A.B.C.D.解:因为g(x)=x2﹣2ax+a2+4=(x﹣a)2+4有最小值,函数f(x)=log a(x2﹣2ax+a2+4)=log a g(x)(a>0,且a≠1)有最大值,且最大值不小于﹣1所以,0<a<1,所以,f(x)max=log a4≥﹣1,∴.因为a>0,所以,故选:A.二、填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡中的横线上. 13.不等式组,表示的可行域的面积为 3 .解:作出可行域,如图所示,可行域的面积为.故答案为:314.若等差数列{a n}的前10项和为100,且a3=5,则a12=23 .解:根据题意,等差数列{a n}的前10项和为100,则S10=,变形可得a1+a10=2a1+9d=20,又a3=a1+2d=5,则有d=2,故a12=a3+9d=23;故答案为:23.15.若函数f(x)=e x﹣mx在[﹣2,0]上为减函数,则m的取值范围为[1,+∞).解:∵函数f(x)=e x﹣mx在[﹣2,0]上为减函数,∴f'(x)=e x﹣m≤0在[﹣2,0]上恒成立,即m≥e x对x∈[﹣2,0]恒成立,∴m≥e0=1.∴m的取值范围为[1,+∞).故答案为:[1,+∞).16.过双曲线C:=1(a>0,b>0)的右焦点F作双曲线C的一条弦AB,且有=,若以AB为直径的圆经过双曲线C的左顶点,则双曲线C的离心率为 2 .解:因为=,所以F是弦AB的中点,且AB垂直于x轴.因为以AB为直径的圆经过双曲线C的左顶点,所以,即,则c﹣a=a,故.故答案为:2.三、解答题:本大题共5小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17~21题为必考题,每个试题考生都必须作答.第22,23题为选考题,考生根据要求作答.(一)必考题:共60分.17.在等比数列{a n}中,a1+a2=5,且a2+a3=20.(1)求{a n}的通项公式;(2)求数列的前n项和S n.【解答】解.(1)因为公比,所以a1+a2=5a1=5,即a1=1,故.(2)因为,所以=4n+2n﹣2.18.设a,b,c分别为△ABC内角A,B,C的对边.已知,b=2.(1)若,求B;(2)若a=2c,求△ABC的面积.【解答】解.(1)因为,所以由A∈(0,π),可得.因为,所以=,所以或,又b<a,所以;(2)由余弦定理,可得,即3c2+2c﹣4=0,解得(负根舍去),故△ABC的面积为是=.19.某公司为确定下一年度投入某种产品的宜传费,需了解年宣传费对年销售量(单位:t)的影响.该公司对近5年的年宣传费和年销售量数据进行了研究,发现年宣传费x(万元)和年销售量y(单位:t)具有线性相关关系,并对数据作了初步处理,得到下面的一些统计量的值.(1)根据表中数据建立年销售量y关于年宣传费x的回归方程.(2)已知这种产品的年利润x(万元)与x,y的关系为z=y﹣0.05x2﹣1.85根据(1)中的结果回答下列问题:①当年宣传费为10万元时,预测该产品的年销售量及年利润;②估计该产品的年利润与年宣传费的比值的最大值.附:回归方程中的斜率和截距的最小二乘估计公式分别为==,=.参考数据:,.解:(1),.设y关于x的线性回归方程为,则,,故y关于x的线性回归方程为;(2)①由(1)知,当x=10时,,则该产品的年销售量约为9.1t,z=9.1﹣0.05×100﹣1.85=2.25,则该产品的年利润约为22.5万元;②z=0.85x+0.6﹣0.05x2﹣1.85=﹣0.05x2+0.85x﹣1.25,∴.∵=0.5,当且仅当,即x=5时取等号,∴,∴该产品的年利润与年宣传费的比值的最大值为0.35.20.已知函数的图象在点(1,f(1))处的切线方程为10x+y+b =0.(1)求a,b的值;(2)若对x∈(0,+∞)恒成立,求m的取值范围.解:(1),则,解得.所以,解得.(2)由(1)知,,设函数g(x)=x3+3x﹣14(x>0),g'(x)=3x2+3>0,所以g(x)为增函数,而g(2)=0,令g'(x)<0,得0<x<2;令g'(x)>0,得x>2.所以当0<x<2时,f'(x)<0;当x>2时,f'(x)>0.所以,从而,即m<26﹣42ln2.21.已知椭圆C:=1(a>b>0)的离心率e=,且圆x2+y2=1经过椭圆C的上、下顶点.(1)求椭圆C的方程;(2)若直线l与椭圆C相切,且与椭圆C1:=1相交于M,N两点,证明:△OMN的面积为定值(O为坐标原点).解:(1)因为圆x2+y2=1过椭圆C的上、下顶点,所以b=1.又离心率,所以,则a2=4.故椭圆C的方程为.(2)证明:椭圆,当直线l的斜率不存在时,这时直线l的方程为x=±2,联立,得,即,则.当直线l的斜率存在时,设l:y=kx+m,联立,得(4k2+1)x2+8kmx+4(m2﹣1)=0,由△=0,可得m2=4k2+1.联立,得(4k2+1)x2+8kmx+4(m2﹣4)=0.设M(x1,y1),N(x2,y2),所以,,则=.因为原点到直线l的距离,所以.综上所述,△OMN的面积为定值.(二)选考题:共10分.请考生从第22,23两题中任选一题作答.如果多做,则按所做的第一个题目计分.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy中,直线l的参数方程为(t为参数),曲线C的参数方程为(m>0,n>0,α为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,且曲线C的极坐标方程为ρ=8sinθ.(1)求a,m,n的值;(2)已知点P的直角坐标为(0,1),l与曲线C交于A,B两点,求|PA|+|PB|.解:(1)曲线C的极坐标方程为ρ=8sinθ.转换为ρ2=8ρsinθ,则x2+y2=8y,即x2+(y﹣4)2=16.因为m>0,n>0,所以a=m=n=4.(2)将直线l的参数方程为(t为参数),代入x2+(y﹣4)2=16,得.设A,B两点对应的参数分别为t1,t2,则,t1t2=﹣7<0.所以.[选修4-5:不等式选讲]23.已知函数f(x)=3|x+1|﹣|2x﹣4|.(1)求不等式f(x)>3的解集;(2)若对任意x∈R,不等式f(x)﹣|x﹣2|≤t2﹣8t恒成立,求t的取值范围.解:(1)当x<﹣1时,f(x)=﹣3(x+1)+(2x﹣4)>3,解得x<﹣10;当﹣1≤x≤2时,f(x)=3(x+1)+(2x﹣4)>3,解得,则;当x>2时,f(x)=3(x+1)﹣(2x﹣4)>3,解得x>﹣4,则x>2;综上知,不等式f(x)>3的解集为(﹣∞,﹣10)∪(,+∞);(2)由f(x)﹣|x﹣2|=3|x+1|﹣|2x﹣4|﹣|x﹣2|=3|x+1|﹣3|x﹣2|=|3x+3|﹣|3x ﹣6|≤|3x+3﹣(3x﹣6)|=9,若对任意x∈一、选择题,不等式f(x)﹣|x﹣2|≤t2﹣8t恒成立,则t2﹣8t≥9,解得t≤﹣1或t≥9;则t的取值范围是(﹣∞,﹣1]∪[9,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
秘密★启用前 【考试时间:2019年11月14日 15:00—17:00】重庆市名校联盟2019~2020学年度第一次联合考试数学试题(高2021级)(本试卷共2页,总分150分,考试时间120分钟)注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,并认真核对条形码上的姓名、准考证号、座位号及科类名称。
2.请将准考证条形码粘贴在右侧的[考生条形码粘贴处]的方框内。
3.选择题必须使用2B 铅笔填涂;非选择题必须用0.5毫米黑色字迹的签字笔填写,字体工整、笔迹清楚。
4.请按题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效,在草稿纸、试题卷上答题无效。
5.保持答题卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、刮纸刀。
第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个备选项中,只有一项是符合题目要求的) 1.抛物线y x 212-=的焦点坐标是( ) A .(0,14-) B .(0,18-) C .108-(,)D .104-(,)2.圆(x -2)2+(y +3)2=2的圆心和半径分别是( )A .(-2,3),2B .(2,-3),2C .(-2,3),2D .(2,-3),23.如图,△A 'B 'C '是△ABC 的直观图,其中A ′B ′=A ′C ′,A ′B ′∥x ′轴,A ′C ′∥y ′轴,那么△ABC 是( )A .等腰三角形B .钝角三角形C .等腰直角三角形D .直角三角形 4.下列命题正确的是( ) A .三点确定一个平面B .如果两个平面有三个不共线的公共点,则两个平面重合C .若b a ,是两条直线,βα,是两个平面,且βα⊂⊂b a ,,则a 与b 异面D .若两条直线与第三条直线垂直,则这两条直线平行5.若圆C :046422=+--+y x y x 与圆M 关于y 轴对称,则圆M 的方程为( ) A .(x +2)2+(y -3)2=9B .(x -2)2+(y +3)2=9C .(x +2)2+(y -3)2=3D .(x -2)2+(y +3)2=36.已知圆锥的高为1,侧面积为π52,则这个圆锥的体积等于( ) A .34π B .38π C .4π D .8π7.若直线x -y +m =0被圆(x -1)2+y 2=5截得的弦长为m 的值为( ) A .1B .-3C .1或-3D .28.如图,在长方体ABCD -A 1B 1C 1D 1中,AA 1=1,AB =AD =2,E ,F 分别是BC ,DC 的中点,则异面直线AD 1与EF 所成角的余弦值为( ) A.5B.5C .35D .459.已知P 、Q 是椭圆15322=+y x 上的两动点,且满足OQ OP ⊥(O 为坐标原点),则2211OQOP+为( ) A .81 B .158 C .8D .无法确定10.已知双曲线12222=-by a x (a >0,b >0)的左、右焦点分别为F 1、F 2,过F 1作垂直于x 轴的直线交双曲线的两条渐近线于M ,N 两点,若∆MF 2N 是钝角三角形,则该双曲线离心率的范围是( ) A .(2,+∞)B.+∞)C .(1+2,∞+)D.(11+,11.设区域G ={(x ,y )| x 2+y 2-4y +2≤0},P (x ,y )是区域G 内的任意一点,则2222y x y x ++的取值范围是( )A .[0,2] B .[2,1] C .[0,1] D .[1,2]12.已知椭圆C :22198x y +=的左、右顶点分别为A 、B ,F 为椭圆C 的右焦点,圆x 2+y 2=9上有一动点P (P 不同于A ,B 两点),直线P A 与椭圆C 交于点Q ,k 1,k 2分别为直线BP ,QF 的斜率,则12k k 的取值范围是( ) A .(-∞,98) B .(-∞,-1)(-1,0) C .34∞(-,)D .(-∞,0)3(0,)4第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分)13.已知圆x 2+y 2=1与圆x 2+y 2-6x -8y +m =0外切,则m 的值为 . 14.以y =± x 为渐近线且经过点(2,0)的双曲线方程为 . 15.已知直线l 过点P (2,1),且与双曲线x 2-24y=1相交于A 、B 两点,若P 为AB 的中点,则直线l 的方程为 .16.在四棱锥S -ABCD 中,底面ABCD 是矩形,平面SABBC =4,当四棱锥S -ABCD 体积最大时,该四棱锥外接球的表面积等于 .三、解答题(本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分10分)如图,正方体ABCD A B C D ''''-的棱长为a ,连接A C '',,,,,,A D A B BD BC C D '''' 得到一个三棱锥,求:(1)三棱锥A BC D ''-的表面积与正方体表面积的比值; (2)三棱锥A BC D ''-的体积. 18.(本小题满分12分)已知圆C 经过点A (0,0),B (7,7),圆心在直线43y x =上. (1)求圆C 的标准方程;(2)若直线l 与圆C 相切且在x ,y 轴的截距相等,求直线l 的方程. 19.(本小题满分12分)已知双曲线C 过点(3,-2)和点(1)2. (1)求双曲线C 的标准方程;(2)若点M 在双曲线C 上,F 1,F 2为双曲线的左、右焦点,且|MF 1|=2|MF 2|,求∆F 1MF 2的面积。
20.(本小题满分12分)如图,四棱锥P -ABCD 中,⊥PA AC ,⊥PA AD ,AD//BC ,AB=AD=AC=3,PA=4,CD=6,2=,N 是PC 中点,E 为PB 中点. (1)证明:MN//AE ;(2)求AN 与PM 所成角的余弦值. 21.(本小题满分12分)已知抛物线M :y 2=2px (p >0)上一点()a A ,1,且FA =2(F 为抛物线M 的焦点)。
(1)若⎪⎭⎫⎝⎛b B ,21,⎪⎭⎫⎝⎛c C ,35是M 上的两点,证明:|FB |,|F A |,|FC |依次成等比数列; (2)若直线y =kx -3(k ≠0)与M 交于P (x 1,y 1),Q (x 2,y 2)两点,且OP OQ ⋅=-4,求线段PQ 的垂直平分线在x 轴上的截距.22.(本小题满分12分)已知椭圆C :=1(a >b >0),短轴长为P (异于左右顶点)与左右顶点连线的斜率之积为43-。
(1)求椭圆C 的标准方程;(2)设直线L 与椭圆C 相切于点A ,过点A 作关于原点O 的对称点B ,过点B 作BM ⊥L ,垂足为M ,求△ABM 面积的最大值.重庆市名校联盟2019~2020学年度第一次联合考试数学试题参考答案(高2021级)1—5 BDDBA 6—10 ACACB 11—12 CD13. 9 14.14422=-y x 15.0158=--y x 16.20π17.解:(1)正方体ABCD -A ′B ′C ′D ′的棱长为a ,则三棱锥A ′-BC ′D 的棱长为a ,表面积为4××(a )2=2a 2,正方体表面积为6a 2,…………………………………(4分)∴三棱锥A ′-BC ′D………………………………(5分) (2)三棱锥A ′-BC ′D 的体积为a 3-4××a 3=a 3.………………………………………(10分) 18.解:(1)根据题意,设圆C 的圆心为(a ,b ),半径为r ,则其标准方程为(x -a )2+(y -b )2=r 2,………………………………………………………(2分)圆C 经过点A (0,0),B (7,7),圆心在直线上,则有,解可得,…………………………………………………(5分)则圆C 的标准方程为(x -3)2+(y -4)2=25,………………………………………………(6分) (2)若直线l 与圆C 相切且与x ,y 轴截距相等,分2种情况讨论:①,直线l经过原点,设直线l的方程为y=kx ,则有=5,解可得:k =-,此时直线l的方程为y =-x;……………………………………………(8分)②,直线l不经过原点,设直线l的方程为x+y-m=0,则有=5,解可得m=7+5或7-5,此时直线l的方程为x+y +5-7=0或x+y-5-7=0;…………………………………(10分)综合可得:直线l的方程为y =-x或x+y +5-7=0或x+y-5-7=0.……………(12分)19.解:(1)若双曲线焦点在x轴上,设双曲线C 的标准方程为:=1,则,解得a2=3,b2=2,∴双曲线C 的标准方程是:.………………………………………………………(3分)若双曲线焦点在y轴上,设双曲线C 的标准方程为:,则,解得a2=-2,b2=-3(舍去).综上,双曲线C 的标准方程是:.…………………………………………………(6分)(2)因为点M在双曲线上,且|MF1|=2|MF2|,所以点M在双曲线的右支上,则有,故,,又,因此在△MF1F2中,cos∠F1MF2==.所以12sin6∠=F MF,………………………(10分)112sin21212121=∠=∆MFFMFMFSMFF....................................................................(12分)20.(1)证明:取BC中点F,连接AF,连接EN.因为AM2=,所以M是线段AD的三等分点且AM=2MD在ACD∆中, AC=3,AD=3,CD=632c o s=∠∴C A D在ABC∆中,CADACB∠=∠,AC=3 故CF=2,BC=4……………………………………(4分)又E,N是PB,PC的中点,所以:EN//BC且EN=2又因为:AD//BC,AM=2 所以,EN//AD且EN=AM,故四边形AENM是平行四边形所以:MN//AE………………………………………………………………………………………(6分)(2)取MC中点G,连接AG,连接MC因为N,G分别是PC,MC的中点,所以NG//PM,故ANG∠或其补角是异面直线AN,PM所成角………………………………………………(8分)易得:AN=25,NG=5,AG=221……………………………………………………………(10分)在ANG∆中,222cos225AN NG AGANGAN NG+-∠==⋅12分)21.证明:(1)由题意得:221=+p∴p=2,∴y2=4x,…………………………………………………………………………………(2分)根据题意可得:|FB|=+1=,|F A|=1+1=2,|FC|=+1=,……………………………(5分)∵22=×=4,∴|FB|,|F A|,|FC|依次成等比数列…………………………………………………………………(6分)(2)由,消x可得ky2-4y-12=0 ①∴y1+y2=,y1y2=-,2219.kxx=∵4.-=→→OQ OP ,即4..2121-=+yy x x∴k =23………………………………………………………………………………………………(8分) 将k=23代入①式,0>∆满足条件。
