最新整理小学几何图形知识点汇总
小学五年级数学解析:几何图形的分类与性质

小学五年级数学解析:几何图形的分类与性质一、几何图形的分类1. 三角形的分类按边分类:等边三角形、等腰三角形、不等边三角形。
按角分类:锐角三角形、直角三角形、钝角三角形。
例题解析:例题1:识别并分类下列三角形:一个等边三角形、一个直角三角形、一个钝角三角形。
解答:按边分类,等边三角形的三边相等;按角分类,直角三角形有一个角为90度,钝角三角形有一个角大于90度。
2. 四边形的分类类型:正方形、长方形、平行四边形、梯形、菱形。
例题解析:例题2:识别并分类下列四边形:一个正方形、一个长方形、一个平行四边形。
解答:正方形的四边相等且四个角都是直角,长方形的对边相等且四个角都是直角,平行四边形的对边平行。
3. 多边形的分类定义:多边形是由多条线段组成的封闭图形。
常见的有五边形、六边形等。
例题解析:例题3:识别并分类下列多边形:一个五边形、一个六边形。
解答:五边形有五条边,六边形有六条边。
二、几何图形的性质1. 三角形的性质三角形内角和:任何三角形的内角和都是180度。
例题解析:例题4:已知一个三角形的两个角分别为50度和60度,求第三个角的度数。
解答:第三个角的度数 = 180度 - 50度 - 60度 = 70度。
2. 四边形的性质四边形内角和:任何四边形的内角和都是360度。
例题解析:例题5:已知一个四边形的三个角分别为90度、85度和95度,求第四个角的度数。
解答:第四个角的度数 = 360度 - 90度 - 85度 - 95度 = 90度。
3. 多边形的性质多边形的内角和:多边形的内角和 = (n - 2) × 180度,其中n为边的数量。
例题解析:例题6:求一个五边形的内角和。
解答:五边形的内角和 = (5 - 2) × 180度 = 540度。
三、几何图形的实际应用1. 建筑设计中的几何图形例题解析:题目:设计一个正方形花坛,要求每边长为5米,问花坛的面积是多少?解答:正方形的面积 = 边长×边长 = 5米× 5米 = 25平方米。
图形知识点总结五年级

图形知识点总结五年级在小学五年级的数学课程中,图形知识是一个重要的组成部分,它帮助学生建立空间观念,理解图形的基本属性以及它们之间的关系。
以下是对五年级图形知识点的总结:一、平面图形1. 直线与射线:直线是无限延伸的,射线有一个端点,从端点向一个方向无限延伸。
2. 线段:线段有起点和终点,长度有限。
3. 角:角由两条射线组成,它们的端点重合形成角的顶点。
角的大小可以通过度量器测量。
4. 平行线:在同一平面内,不相交的两条直线称为平行线。
5. 垂直线:当两条直线相交,形成90度的角时,它们是垂直的。
二、几何图形1. 三角形:由三条线段围成的图形,内角和为180度。
三角形可以分为等边三角形、等腰三角形和一般三角形。
2. 四边形:由四条线段围成的图形,包括正方形、长方形、平行四边形、梯形等。
3. 圆:所有点到中心点的距离相等的平面图形,圆心是圆的中心,半径是圆心到圆上任意一点的距离。
三、图形的属性1. 周长:图形边缘的长度总和。
2. 面积:图形内部的区域大小。
3. 对称性:图形的对称轴可以是一条直线或一个点。
四、图形的变换1. 平移:图形在平面内沿着某一方向移动,不改变其形状和大小。
2. 旋转:图形绕某一点旋转一定角度,不改变其形状和大小。
3. 反射:图形沿某一条直线翻转,形成镜像。
五、图形的组合1. 组合图形:将多个基本图形组合在一起,形成新的图形。
2. 分割图形:将一个图形分割成几个部分,每个部分可以是基本图形。
六、图形的测量1. 长度测量:使用直尺测量线段的长度。
2. 角度测量:使用量角器测量角的大小。
3. 面积测量:计算图形的面积,常用的公式包括三角形面积公式、四边形面积公式等。
七、图形的应用1. 日常生活:在日常生活中,我们经常需要用到图形知识,比如测量房间的面积,计算材料的用量等。
2. 艺术设计:在艺术和设计领域,图形知识是构图和创造美的基础。
通过这些知识点的学习,学生不仅能够理解平面图形的基本性质,还能够将这些知识应用到实际生活中,提高解决问题的能力。
小学生必背几何知识点总结

小学生必背几何知识点总结一、基本概念1. 点、线、面:点是没有长度、宽度和高度的;线是由无限多个点连在一起形成的;面是由无限多条线连在一起形成的。
2. 直线、射线、线段:直线是没有端点的;射线是一个端点发散而出的,另一个方向无限延伸的部分;线段是由两个端点确定的部分。
3. 角:由两条射线的公共端点所围成的图形称为角,公共端点称为角的顶点,两条射线称为角的两边。
4. 三角形:由三条线段所围成的图形称为三角形。
5. 四边形:由四条线段所围成的图形称为四边形。
二、基本图形的性质1. 三角形的内角和:所有内角和为180°。
2. 三角形的外角和:所有外角和为360°。
3. 直角三角形:一个角为90°的三角形称为直角三角形。
4. 等边三角形:三条边相等的三角形称为等边三角形。
5. 等腰三角形:两条边相等的三角形称为等腰三角形。
6. 直线上的角:直线上的两个相邻角互为补角,补角的和为180°。
三、平行线和垂直线1. 平行线:在同一平面内,不相交且方向相同的两条直线称为平行线。
2. 垂直线:在同一平面内,相交且相交角为90°的两条直线称为垂直线。
3. 平行线交叉:平行线交叉时,所得的对应角相等、内错角相加为180°、外错角相加为180°。
4. 垂直线交叉:垂直线交叉时,所得的相邻角相加为180°。
四、长方形、正方形、菱形和梯形1. 长方形:对角线相等、相对边相等且两两平行的四边形称为长方形。
2. 正方形:对角线相等、四个边相等且四个角为90°的四边形称为正方形。
3. 菱形:对角线相等、四个边相等的四边形称为菱形。
4. 梯形:有两边平行的四边形称为梯形。
五、圆的基本性质1. 圆心和半径:圆心是圆的中心点,半径是圆心到圆上任意一点的距离。
2. 圆的周长:圆的周长等于直径乘以π,即C=πd。
3. 圆的面积:圆的面积等于半径平方乘以π,即A=πr²。
(完整)小学几何图形必考知识点汇总,
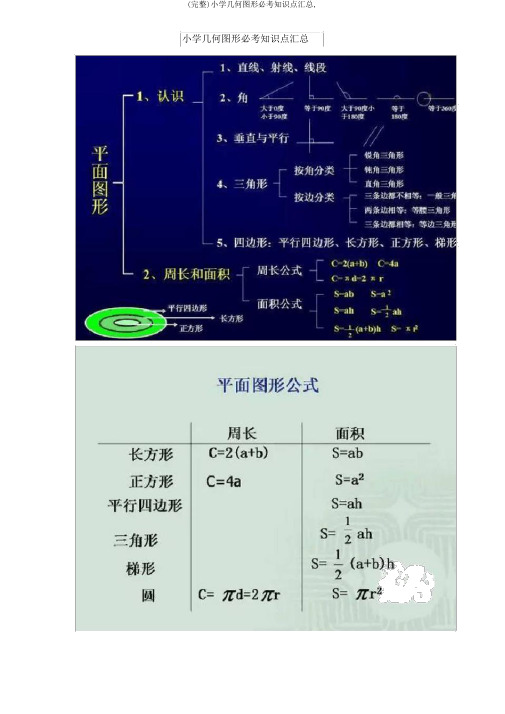
小学几何图形必考知识点汇总小学阶段常考的几何易错知识点1线、角1.直线没有端点,没有长度,可以无限延伸。
2.射线只有一个端点,没有长度,射线可以无限延伸,并且射线有方向。
3.在一条直线上的一个点可以引出两条射线。
4.线段有两个端点,可以测量长度。
圆的半径、直径都是线段。
5.角的两边是射线,角的大小与射线的长度没有关系,而是跟角的两边叉开的大小有关,叉得越大角就越大。
6.几个易错的角边关系:(1 〕平角的两边是射线,平角不是直线。
(2 〕三角形、四边形中的角的两边是线段。
(3 〕圆心角的两边是线段。
7.两条直线相交成直角时,这两条直线叫做互相垂直。
其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
8.从直线外一点到这条直线所画的垂直线段的长度叫做点到直线的距离。
9.在同一个平面上不相交的两条直线叫做平行线。
2三角形1.任何三角形内角和都是 18 0 度。
2.三角形具有稳定的特性,三角形两边之和大于第三边,三角形两边之差小于第三边。
3.任何三角形都有三条高。
4.直角三角形两个锐角的和是 90 度。
5.两个三角形等底等高,那么它们面积相等。
6.面积相等的两个三角形,形状不一定相同。
3正方形面积1.正方形面积:边长×边长2.正方形面积:两条对角线长度的积÷24三角形、四边形的关系1.两个完全一样的三角形能组成一个平行四边形。
2.两个完全一样的直角三角形能组成一个长方形。
3.两个完全一样的等腰直角三角形能组成一个正方形。
4.两个完全一样的梯形能组成一个平行四边形。
5圆1.把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径。
那么长方形的面积等于圆的面积,长方形的周长比圆的周长增加 r ×2。
2.半圆的周长等于圆的周长的一半加直径。
3.半圆的周长公式:C= pd?2+ d 或C= pr +2 r4.在同一个圆里,半径扩大或缩小多少倍,直径和周长也扩大或缩小相同的倍数。
小学生必背几何知识点总结

小学生必背几何知识点总结小学生在学习几何时,需要掌握一些基础的几何知识点,这不仅有助于他们更好地理解数学概念,还能培养他们的空间想象力。
以下是小学生必背的几何知识点总结:1. 点、线、面:点是几何图形的基本元素,没有大小只有位置;线是由无数个点组成的,有长度但没有宽度;面是由无数条线组成的,有长度和宽度但没有厚度。
2. 平面图形:平面图形是指所有点都在同一个平面上的图形。
常见的平面图形有三角形、四边形、圆形等。
3. 三角形:三角形是由三条线段首尾相连形成的封闭图形。
根据边和角的不同,三角形可以分为等边三角形、等腰三角形、直角三角形和不等边三角形。
4. 四边形:四边形是由四条线段首尾相连形成的封闭图形。
常见的四边形有正方形、长方形、平行四边形、梯形和菱形。
5. 圆:圆是由一个中心点和所有与中心点等距离的点组成的平面图形。
圆的周长称为圆周,圆的面积可以通过公式 \( A = \pi r^2 \) 计算,其中 \( r \) 是圆的半径。
6. 立体图形:立体图形是指具有长度、宽度和高度的三维图形。
常见的立体图形有立方体、长方体、圆柱体、圆锥体和球体。
7. 立方体和长方体:立方体是所有边长相等的长方体,而长方体的长、宽、高可以不同。
它们的表面积和体积可以通过特定的公式计算。
8. 圆柱体和圆锥体:圆柱体由两个平行且相等的圆面和连接它们的侧面组成。
圆锥体是一个圆面和一个顶点组成,侧面收缩到一个点。
9. 球体:球体是由所有与中心点等距离的点组成的三维图形。
球体的表面积和体积也可以通过公式计算。
10. 对称性:许多几何图形具有对称性,例如轴对称和中心对称。
轴对称图形可以沿一条直线(称为对称轴)对折后两部分完全重合,中心对称图形则是围绕一个中心点旋转180度后与原图形重合。
11. 角度:角度是用来描述两条射线(或线段)的夹角大小的度量。
角度的单位是度(°),直角是90°,平角是180°,周角是360°。
小学三年级数学几何的初步认识知识点

1.几何图形的认识:-点:没有大小和形状的位置。
-线段:由两个端点和之间的所有点组成,没有曲线。
-直线:在平面上的无限延伸得两个方向上的点组成。
-尖角:小于90度的角。
-钝角:大于90度但小于180度的角。
-直角:等于90度的角。
-平行线:永远不会相交的线。
-垂直线:相交的角度为90度的线。
2.几何图形的识别和分类:-三角形:有三条边的图形。
-矩形:有四个直角的四边形。
-正方形:四个边相等且四个直角的四边形。
-平行四边形:有两组对边平行的四边形。
-圆形:由一个圆心和一条半径相等的弧线组成。
-弧:圆形的一部分。
-曲线:线条在不同点上的变向。
3.几何图形的特征:-边:图形的边缘。
-角:两条线相交所形成的区域。
-顶点:两条边或多条边的交点。
-对称性:图形左右或上下对折后完全相同。
-线对称:通过中心线对折后完全一样。
-中心对称:图形可通过其中一点为中心旋转180度后重合。
4.几何图形的关系和组合:-图形的包含和相交关系:一个图形是否被另一个图形包围或相交。
-集合:一个或多个物体的组合。
-二维几何体:平面上的图形。
-三维几何体:有长度、宽度和高度的立体图形。
-分解和组合:将复杂的图形分解成简单的图形,并将简单的图形组合成复杂的图形。
以上是小学三年级数学几何初步认识的一些重要知识点。
随着学习的深入,孩子们还将学习到更多有关几何的概念和技能,如相似、等边、等腰三角形等。
这些基础知识为孩子打下了坚实的几何基础,为将来更深入的数学学习奠定了基础。
小学平面几何重点总结

小学平面几何重点总结
1. 直线、线段和射线
- 直线是由无数个点连成的轨迹,没有起点和终点。
- 线段是直线上的两个点及其之间的部分,有起点和终点。
- 射线是直线上的一个点及其之后的部分,有一个起点但没有终点。
2. 角
- 角是由两条射线共享一个端点组成的图形。
- 角的大小可用角度来量度,角度的单位可以是度或弧度。
- 锐角是小于90度的角,直角是90度的角,而钝角是大于90度但小于180度的角。
3. 三角形
- 三角形是由三条线段组成的图形。
- 三角形的三条边和三个内角的关系:任意两边之和大于第三边,任意两角之和小于180度。
- 常见的三角形类型包括等边三角形、等腰三角形和直角三角形。
4. 矩形
- 矩形是一个有四个直角(90度)的四边形。
- 矩形的特点:对角线相等,相对边相等,相邻边互相垂直。
5. 正方形
- 正方形是一个具有四条相等边和四个直角的矩形。
- 正方形的特点:对角线相等,所有边相等,所有角均为直角。
6. 圆
- 圆是由与一个固定点的距离相等的点构成的图形。
- 圆的特征:半径是从圆心到圆上的任意一点的距离,直径是
通过圆心的两个点的距离,圆周是圆的边界。
以上是小学平面几何的一些重点总结,请您参考。
小学图形与几何知识点

小学图形与几何知识点在小学阶段,图形与几何是数学学习中的重要组成部分。
它不仅能帮助孩子们建立空间观念,还能培养他们的逻辑思维和解决实际问题的能力。
接下来,咱们就一起梳理一下小学图形与几何的主要知识点。
一、平面图形1、线段、射线和直线线段有两个端点,可以度量长度;射线有一个端点,一端可以无限延伸;直线没有端点,两端都可以无限延伸。
2、角从一点引出两条射线所组成的图形叫做角。
角通常用符号“∠”来表示。
角的大小与两条边张开的程度有关,与边的长短无关。
角可以分为锐角、直角、钝角、平角和周角。
锐角小于 90 度,直角等于 90 度,钝角大于 90 度小于 180 度,平角等于 180 度,周角等于 360 度。
3、三角形由三条线段围成的图形叫做三角形。
三角形具有稳定性。
三角形按角可以分为锐角三角形、直角三角形和钝角三角形;按边可以分为等边三角形、等腰三角形和不等边三角形。
三角形的内角和是 180 度。
4、四边形由四条线段围成的封闭图形叫做四边形。
常见的四边形有平行四边形、长方形、正方形和梯形。
平行四边形两组对边分别平行且相等。
长方形对边平行且相等,四个角都是直角。
正方形四条边都相等,四个角都是直角。
梯形只有一组对边平行。
5、圆圆是一种曲线图形。
圆心用字母 O 表示,半径用字母 r 表示,直径用字母 d 表示。
在同一个圆中,直径是半径的 2 倍,即 d = 2r。
圆的周长计算公式是 C =2πr 或 C =πd,圆的面积计算公式是 S =πr²。
二、立体图形1、长方体长方体有 6 个面,相对的面完全相同;有 12 条棱,相对的棱长度相等;有 8 个顶点。
长方体的棱长总和=(长+宽+高)× 4长方体的表面积=(长×宽+长×高+宽×高)× 2长方体的体积=长×宽×高2、正方体正方体有 6 个面,每个面都是正方形,6 个面完全相同;有 12 条棱,12 条棱长度都相等;有 8 个顶点。
