第7章2 水跃
第七章 水跃

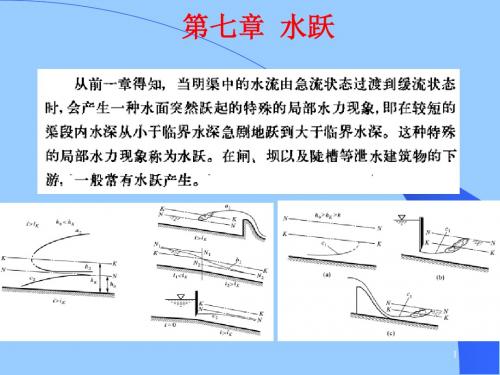
第七章 水跃考点一 水跃的基本概念1、水跃现象在明渠中水流由急流过渡到缓流时,会产生一种水面突然跃起的特殊局部水流现象,即在较短的渠段内水深从小于临界水深急剧的跃到大于临界水深,这种特殊的局部水流现象称为水跃。
2、相关概念(1)跃前断面、跃后断面(2)跃前水深、跃后水深、共轭水深 (3)跃高、跃长 3、.水跃的分类水跃可以按其位置和跃前断面的弗劳德数进行分类。
(1)按水跃跃首所处的位置,可以将水跃分为远驱水跃、临界水跃和淹没水跃。
其分类标准以坝址(或闸后收缩断面)处收缩断面水深'c h 的共轭水深"c h (即跃后水深)与下游水深t h 相比较:当t c h h >"为远驱水跃t c h h ="为临界水跃t c h h <"为淹没水跃。
(2)按跃前断面的弗劳德数Fr 可以将水跃分为波状水跃、弱水跃、不稳定水跃、稳定水跃和强水跃。
当7.11<<Fr 为波状水跃; 当5.27.1<<Fr 为弱水跃;当5.45.2<<Fr 为不稳定水跃,也叫颤动水跃; 当95.4<<Fr 为稳定水跃; 当9>Fr 为强水跃。
或当7.11<<Fr 为波状水跃; 当7.1>Fr 为完全水跃。
考点二 棱柱体水平明渠的水跃方程在水平明渠中,水跃的基本方程为22221112c c h A gA Q h A gA Q +=+ 式中Q 为流量;21A A 、分别表示水跃前、后断面的面积;21c c h h 、分别表示水跃前、后断面形心距水面的距离。
当明渠断面的形状、尺寸以及渠中的流量一定时,水跃方程的左右两边都是水深的函数。
此函数称为水跃函数,以符号c Ah gAQ h J +=2)(表示,则有 )()("'c c h J h J =上式表明,在棱柱体水平明渠中,跃前水深'c h 与跃后水深"c h 之间具有相同的水跃函数值,所以也叫这两个水深为共轭水深。
《水力学》第七章 水跃
上式与临界水深的条件相同。因此,与 J (h)
相应的水深即是临界水深。
15
Q( 2 v2 1v1 ) Fp1 Fp 2 Ff
Q2 Q2 A1 hc1 A2 hc 2 gA gA 1 2
16
17
18
19
20
二、梯形明渠共轭水深的计算方法
梯形明渠共轭水深不易由水跃方程直接解出.在计算其 共轭水深时,除了可以采用前述的试算法或图解法外,为了
当h>hk时(相当于曲线的 上半支);J(h)随着h即随 着跃后水深的减小而减小;
当h<hk时(相当于曲线 的下半支); J(h)随着h即随
着跃前水深的减小而增大。
12
当已知h1欲求h2时只须绘出曲线的上半支有关部 分。通过横坐标轴上J(h)= J(h1)= J(h2)的已知点A作一 与纵坐标轴h相平行的直线,该直线与曲线相交于B点。 显然,此B点的纵坐标值即是欲求值的h2。其图解示 意图见图 a 。当已知h2求h1时。则只须绘出曲线的下 半支的有关部分,其图解示意图如图 b 所示。
Q2 Q2 A1 hc1 A2 hc 2 gA gA2 1
将以上诸关系式代入水跃方程,则得到棱柱体矩形 水平明渠的水跃方程如下:
2 q 2 h12 q 2 h2 gh1 2 gh2 2
2 h2 h12 q 2 q2 2 2 gh1 gh2
h h q (h2 h1 ) 2 gh1h2
2、设摩阻力Ff=0。 3、设β1=β2=1 Q 将连续性方程 v1 A 1 代入动量方程,得:
Q2 Q2 A1hc1 A2 hc 2 gA1 gA2
Q v2 A2
棱柱体水平明渠的水跃方程 8
水力学第7章明渠非均匀流

水面曲线定性分析的理论基础:明渠恒定渐变流的基本微分方程
对于正底坡渠道i>0
对于平底坡渠道i=0
对于反底坡渠道i<0
dh/ds取不同值时的几何意义
dh/ds>0时,水深沿程增加,产生雍水曲线;
dh/ds<0时,水深沿程减少,产生降水曲线;
dh/ds→0时,水深趋于正常水深,即水面线与均匀流水面线渐近相切;
水跃稳定,消能效率高,跃后水面也较平稳。
由缓流向急流过渡时一定经过临界水深hcr,此时会产生水面降落的局部水力现象,此现象称为水跌或跌水。
水跌
缓坡接陡坡的渠道会产生水跌现象
图a中前段渠道i1<icr,后一段渠道i2>icr;
图b中缓坡渠道末端有一跌坎;可以将跌坎看作为i→∞的陡坡渠道;
因J>0,故在平坡i=0和逆坡i<0时:
;在顺坡i>0时:
则要看J和i的大小来决定了。
断面比能函数的特点
当流量、断面形状及尺寸一定时,断面比能Es只是水深h的函数
当h→0时A→0,于是e→∞,即断面比能函数曲线与水平轴渐近相切;
当h→∞时A→∞,于是e→∞,即断面比能曲线与过坐标原点的45°线渐近相切。
是一个无量纲的数,称为弗劳德数,用Fr表示。
流动是临界流时,弗劳德数等于1。所以液体在明渠中的流动 状态也可用弗劳德数来进行判别。
定义弗劳德(Froude)数
当 时,水流为缓流,
当 时,水流为急流,
当 时,水流为临界流,
vw
vw’
将石子投入等速运动的水流中,则波传播速度是水流流速与波速向量和。当水流流速小于波速(v < vw)时,微波向下游传播的绝对速度为(v + vw),向上游传播的绝对速度为( vw- v)。
水力学第7章-1水跃

依据共轭水深方程,由一个共轭水深求另一个共 轭水深。
hc1 A1
1Q2
gA1
hc2 A2
2Q2
gA2
由于共轭水深方程是一个关于共轭水深的高次 方程,不便直接计算,常用的方法为试算法。
11
12
13
例7.2 棱柱形平底明渠,断面形状、尺寸、跃 前水深给定。问:水跃段中底槛的存在对跃后水 深有何影响?
效率越高。 通过实验资料分析,可知:
1 Fr1 1.7 ,为波状水跃,消能效果最差; 1.7 Fr1 2.5 ,为弱水跃, K j 20% ; 2.5 Fr1 4.5 ,为不稳定水跃,K j 20 45% ;
4.5 Fr1 9 ,为稳定水跃,K j 45 70% ; Fr1 9 ,为强水跃,K j 85% 。
b
q2 h12 q2 h22 gh1 2 gh2 2
17
q2 h12 q2 h22 gh1 2 gh2 2
2q 2 g
h1h22 h2h12
h1
h2 2
18 q2 gh23
1
h2 2
1 8Fr22 1
同样地
h2
h1 2
q2 1 8 gh13
1
h1 2
1 8Fr12 1
A1hc1
Q2 gA2
A2hc2
T
h
即
J
(h1 )
J
(h2
)
T
h2
可见,h1不变,有底槛时,
h1
h2 会减小。
J (h2) J (h1) J (h)
16
二、矩形明渠共轭水深的计算
共轭水深方程
Q2 gA1
A1hc1
第七章 明渠流

第七章明渠流【教学基本要求】1、了解明槽水流的分类和特征,了解棱柱体渠道的概念,掌握明槽底坡的概念和梯形断面明渠的几何特征和水力要素。
2、了解明槽均匀流的特点和形成条件,熟练掌握明槽均匀流公式,并能应用它来进行明渠均匀流水力计算。
3、理解水力最佳断面和允许流速的概念,掌握水力最佳断面的条件和允许流速的确定方法,学会正确选择明渠的糙率n值。
4、掌握明槽均匀流水力设计的类型和计算方法,能进行过流能力和正常水深的计算,能设计渠道的断面尺寸。
5、掌握明渠水流三种流态(急流、缓流、临界流)的运动特征和判别明渠水流流态的方法,理解佛汝德数Fr的物理意义。
6、理解断面比能、临界水深、临界底坡的概念和特性,掌握矩形断面明渠临界水深h k 的计算公式和其它形状断面临界水深的计算方法。
7、了解水跃和水跌现象,掌握共轭水深的计算,特别是矩形断明渠面共轭水深计算。
8、能进行水跃能量损失和水跃长度的计算。
9、掌握棱柱体渠道水面曲线的分类、分区和变化规律,能正确进行水面线定性分析,了解水面线衔接的控制条件。
10、能进行水面线定量计算。
【学习重点】• 1. 明渠均匀流水力计算;• 2. 明渠水流三种流态的判别;• 3. 明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;• 4. 水跃的特性。
【内容提要和学习指导】这一章是工程水力学部分内容最丰富也是实际应用最广泛的一章。
本章有4个重点:明渠均匀流水力计算;明渠水流三种流态的判别;明渠恒定非均匀渐变流水面曲线分析和计算,这部分也是本章的难点;水跃的特性和共轭水深计算。
学习中应围绕这4个重点,掌握相关的基本概念和计算公式。
§7-1 概 述人工渠道,天然河道及水流未充满全断面的管道等统称为明渠。
明渠水流是一种具有自由液面的水流,水流的表面压强为大气压强,即相对压强为零。
因此,明渠水流也称为无压流,而管流中的水流充满全断面,没有自由表面。
在研究明渠水流运动规律之前,必须对明渠的几何特性有所了解。
水力学第七章

渐近线 1: h 0, A 0, Es 横坐标为渐近线
渐近线 2: h , A , Es 坐标轴成 45°直线
Es m in
d Es dh
d dh
h
aQ2 2gA2
1
aQ2 d A gA3 d h
B
d A B(水面宽) dh
d
d Es 1 aQ2B 1 av2 1 Fr2
6
dh d Q2 dh dh Q2dA dh Q2dA dh v2B ds dh 2gA2 ds ds (1 A3gdh ) = ds (1 A3gdh ) ds (1 gA ) dEs dh (1 Fr2 ) ds ds
第三节 临界底坡、缓坡和陡坡
给定 Q、n、渠道断面形状尺 b /m 4.0
Fr
F G
1
2
L2 v 2 gL3
1
2
v
gL
<1 =1 >1
Fr 是流态判别的准数
二、缓流和急流的能量分析
(一) 断面单位能量(断面比能) 1. 断面比能定义
右图为一明渠非均匀流,以渠 底为基准面,过水断面单位液重的 总能量为
Es
h cos
av2 2g
h cos
aQ2 2gA2
顺水波: vw ' v vw v gh (微波传播方向和水流方向一致) 式中, vw ' 顺水波传
播波速。
逆水波: vw ' v vw v gh (微波传播方向和水流方向相反) 式中,vw ' 逆水波传播
波速.
(二)明渠水流流态判别的标准——佛劳德数
佛劳德数:流速与波速之比,以 Fr 表示 Fr v v vw gh
第七章明渠恒定非均匀流
水力学第七章课件 水跃

棱柱体水平明渠中,跃前和跃后水深不相等,但其水
跃函数值相等,h1 h2 互称为共轭水深 h1
h2
当断面形状尺寸、流量Q一定时,绘h J(h)曲线
h
J(h)
当h→0,J
h
Q2 gA
hc
A
当趋近于∞时, J h 也趋近于∞
当h∈[0,∞],J(h)有J(h)min
J (h)min
d[J (h)] dh
Ahc
Q2B gA2
d( Ahc dh
)
0
d(Ahc ) lim Δ(Ahc ) lim (A B Δ h) A
dh
Δh0 Δ h
Δ h0
2
Q 2 A3 Fr 1 gB
临界流方程
h
hk J min
J(h)
d[J (h)] dh
d dh
Q2 gA
Ahc
Q2B gA2
A
A(1
Q2B gA3
gA
hc A
J h1 J h2
1
2
a K
h1 FP1
v1
Ff i = 0
v2 FP2
K h2
x
1
Lj
2
Q2v2 1v1 P1 P2 Ff g hc1A1 g hc2 A2 0
式中,A过水断面的面积;
hc 相应于A上形心点水深 ; 1 ,2 对应跃前和跃后断面
Q2v2 1v1 P1 P2 Ff g hc1A1 g hc2 A2
)
A(1
Fr
2)
h
hk
:
d[J (h)] dh
A(1
Fr 2 )
0
h
hhk
:
《水力学》第七章 水跃
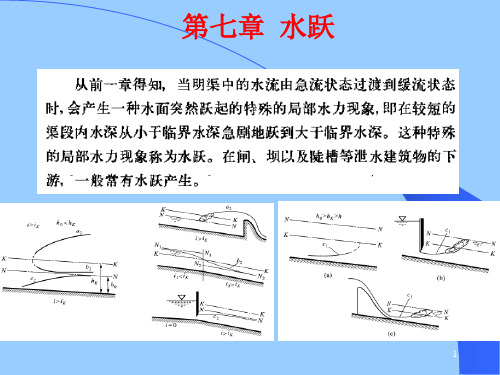
上式表明,在棱柱体水平明渠中 , 跃前水深 在棱柱体水平明渠中, 在棱柱体水平明渠中 h1与跃后水深 2具有相同的水跃函数值, 与跃后水深h 具有相同的水跃函数值, 两个水深为共轭水深。 两个水深为共轭水深。 共轭水深
9
J ( h1 ) = J ( h2 )
第七章 水跃
1
1.水跃分区 水跃分区
2
2. 水跃的特性参数
表面旋滚起点过水断面1-1称为跃前断面 跃前断面,该断面处 跃前断面 水深h1称为跃前水深 跃前水深。 跃前水深 跃后断面,该断面处 表面旋滚末端的过水断面2-2称为跃后断面 跃后断面 的水深h2称为跃后水深 跃后水深。 跃后水深 跃前、后水深之差a= h2-h1称为跃高 跃前断面和跃后断 跃高,跃前断面和跃后断 跃高 面之间的距离称为跃长 j。 跃长L 跃长
11
水跃函数存在J(h)min,与J(h)min 相应的水深即是临界水深hk; 当h>hk时(相当于曲线的 上半支);J(h)随着h即随 着跃后水深的减小而减小; 当h<hk时(相当于曲线 的下半支); J(h)随着h即随 着跃前水深的减小而增大。
12
当已知h1欲求h2时只须绘出曲线的上半支有关部 分。通过横坐标轴上J(h)= J(h1)= J(h2)的已知点A作一 与纵坐标轴h相平行的直线,该直线与曲线相交于B点。 显然,此B点的纵坐标值即是欲求值的h2。其图解示 意图见图 a 。当已知h2求h1时。则只须绘出曲线的下 半支的有关部分,其图解示意图如图 b 所示。
32
二、棱柱体水平明渠中水跃的能量损失计算
2.水跃段水头损失的计算 水跃段水头损失的计算
2 a1v12 a2v2 E j = (h1 + ) − (h2 + ) (7.16) 2g 2g
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
α 2 = 0.85Fr1 + 0.25 > 1
2 3
跃后段水头损失的计算
2 2 a3 v3 a2 v2 E jj = (h2 + ) − (h3 + ) 2g 2g
E jj =
h1 [(α 2 − 1)(η + 1)] 4η
化简计算
( h2 − h1 ) 3 hw = 4 h1h2
3、水跃的消能效率 、
水力学B 水力学
第7章 水跃
能源与机械工程系
由急流向缓流过渡产生 的水力突变现象
1
K
2
K
h1
h
h2
k
1
Lj
2
一、水跃概述 1、水跃现象: 水跃现象:
2、相关概念: 相关概念:
3、主要内容: 主要内容: 1)确定水跃运动的基本规律;ห้องสมุดไป่ตู้)确定水跃运动的基本规律; 2)共轭水深h1和h2的计算; 共轭水深 的计算; 3)水跃跃长 Lj 的计算; 的计算; 的计算; 4)能量损失 Ej 的计算;
[ 1 + 8Fr −1] [ 1 + 8Fr −1]
2 1 2 2
2、共轭水深的一般计算 、
1、试算法 2、图解法(利用水跃函数曲线) 图解法(利用水跃函数曲线)
7.3 棱柱体水平明渠中水跃的能量损失
1、 能量损失机理: 、 能量损失机理:
2、水跃能量损失计算 、
水跃段水头损失的计算
2 a1v12 a2 v2 E j = (h1 + ) − (h2 + ) E j = h1 [(η − 1) 3 − (α 2 − 1)(η + 1)] 2g 2g 4η
7.1
棱柱体水平明渠的水跃方程 棱柱体水平明渠的水跃方程
1、方程推导: 方程推导:
Q2 Q2 + A1hc1 = + A2 hc 2 gA1 gA2
水跃方程
2、水跃函数曲线及其特点: 水跃函数曲线及其特点:
Q J (h) = + Ah c gA
2
水跃函数曲线及断面比能曲线
7.2 棱柱体水平明渠共轭水深的计算 1、矩形断面共轭水深的计算 、
Q = bq , h A = bh , hC = 2
代入水跃方程可得: 代入水跃方程可得:
h1 h2 = 2
h h1 = 2 2
q2 − 1 1+ 8 3 gh 1
q2 − 1 1+ 8 3 gh 2
或
h1 h2 = 2 h2 h1 = 2
2 v12 v2 E = E j + E jj = (h1 + ) − (h2 + ) 2g 2g
E (水跃总水头损失) Kj = E1 (跃前断面比能)
消能系数K 越大则水跃的消能效率越高。 消能系数 j越大则水跃的消能效率越高。 可以写成关于Fr 的形式: 可以写成关于 1的形式:
h1 (η − 1) 3 2 ( 1 + 8 Fr1 − 3) 3 E 4η Kj = = = = f ( Fr1 ) 2 2 2 E1 V 8( 1 + 8 Fr1 − 1)(2 + Fr1 ) h1 + 1 2g
4、水跃的分类 、
波状水跃 1 < Fr1 < 1.7
波状水跃
弱水跃 1.7 ≤ Fr1 < 2.5 不稳定水跃 2.5 ≤ Fr1 < 4.5 稳定水跃 4.5 ≤ Fr1 ≤ 9.0 强水跃 Fr1 > 9.0
7.4
棱柱体水平明渠跃长的计算
一、矩形明渠跃长经验公式:(仅作估算用) 矩形明渠跃长经验公式:(仅作估算用) :(仅作估算用 ①成科大公式 Lj=10.8h1 (Fr1-1)0.93 Fr1=1.72~19.55 ~ ② Elevatorski(欧勒佛托斯基) 公式 Lj= 6.9 ( h2- h1) ③陈椿庭公式 Lj=9.4h1 (Fr1-1) ④ 切尔托乌索夫公式 Lj=10.3h1 (Fr1-1)0.81
二、梯形明渠的跃长的经验公式为: 梯形明渠的跃长的经验公式为:
B2 − B1 L j = 5h2 1 + 4 B1
式中B 为水跃前后断面处的水面宽度。 式中B1及B2为水跃前后断面处的水面宽度。
