二次函数文档 (一)(2)
(整理)第10讲二次函数图象和性质
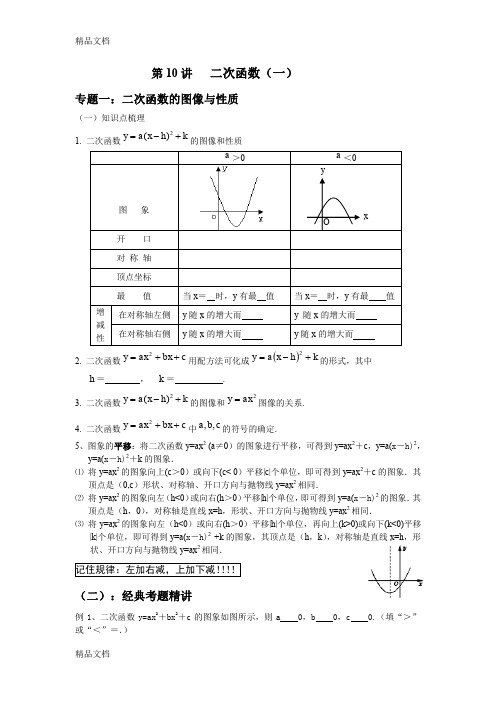
第10讲 二次函数(一)专题一:二次函数的图像与性质(一)知识点梳理1. 二次函数2()y a x h k =-+的图像和性质 a >02. 二次函数c bx ax y ++=2用配方法可化成()k h x a y +-=2的形式,其中 h = , k = .3. 二次函数2()y a x h k =-+的图像和2ax y =图像的关系.4. 二次函数c bx ax y ++=2中c b a ,,的符号的确定. 5、图象的平移:将二次函数y=ax 2 (a ≠0)的图象进行平移,可得到y=ax 2+c ,y=a(x -h)2,y=a(x -h)2+k 的图象.⑴ 将y=ax 2的图象向上(c >0)或向下(c< 0)平移|c|个单位,即可得到y=ax 2+c 的图象.其顶点是(0,c )形状、对称轴、开口方向与抛物线y=ax 2相同. ⑵ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,即可得到y=a(x -h)2的图象.其顶点是(h ,0),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.⑶ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,再向上(k>0)或向下(k<0)平移|k|个单位,即可得到y=a(x -h)2 +k 的图象,其顶点是(h ,k ),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.(二):经典考题精讲例1、二次函数y=ax 2+bx 2+c 的图象如图所示,则a 0,b 0,c 0.(填“>”或“<”=.)例2、二次函数y=ax 2+bx +c 与一次函数y=ax +c 在同一坐标系中的图象大致是图中的( )例3、在同一坐标系中,函数y=ax 2+bx 与y=xb的图象大致是图中的( )例4、如图所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,左面的一条抛物线可以用y=0.0225x 2+0.9x +10表示,而且左右两条抛物线关于y 轴对称,你能写出右面钢缆的表达式吗?例5、图中各图是在同一直角坐标系内,二次函数y=ax 2+(a +c )x +c 与一次函数y=ax +c 的大致图象,有且只有一个是正确的,正确的是( )例6、抛物线y=ax 2+bx +c 如图所示,则它关于y 轴对称的抛物线的表达式是 .例7、已知二次函数y=(m -2)x 2+(m +3)x +m +2的图象过点(0,5)(1)求m 的值,并写出二次函数的表达式; (2)求出二次函数图象的顶点坐标、例8、 如图所示,有一边长为5cm 的正方形ABCD 和等腰三角形PQR ,PQ=PR=5cm ,QR=8cm ,点B 、C 、Q 、R 在同一直线ι上.当CQ 两点重合时,等腰△PQR 以1cm/秒的速度沿直线ι按箭头所示方向开始匀速运动,t 秒后,正方形ABCD 与等腰△PQR 重合部分的面积为Scm 2.解答下列问题:(1)当t=3秒时,求S 的值; (2)当t=5秒时,求S 的值;三:拓展与应用1. 抛物线()22-=x y 的顶点坐标是 .2.将抛物线23y x =-向上平移一个单位后,得到的抛物线解析式是 .3. 如图所示的抛物线是二次函数2231y ax x a =-+- 的图象,那么a 的值是 .4.二次函数2(1)2y x =-+的最小值是( ) A.-2 B.2 C.-1 D.15. 请写出一个开口向上,对称轴为直线x =2,且与y 轴的交点坐标为(0,3)的抛物线的解析式 .6.已知二次函数22y x x m =-++的部分图象如右图所示,则关于x 的一元二次方程220x x m -++=的解为 .7.已知函数y=x 2-2x-2的图象如图所示,根据其中提供的信息,可求得使y≥1成立的x 的取值范围是( )A .-1≤x≤3B .-3≤x≤1C .x≥-3D .x≤-1或x≥38. 二次函数c bx ax y ++=2(0≠a )的图象如图所示,则下列结论: ①a >0; ②c >0; ③ b 2-4a c >0,其中正确的个数是( )A. 0个B. 1个C. 2个D. 3个 第3题图第6题图9. 已知二次函数243y ax x=-+的图象经过点(-1,8).(1)求此二次函数的解析式;(2)根据(1)填写下表.在直角坐标系中描点,并画出函数的图象;(3)根据图象回答:当函数值y<0时,x的取值范围是什么?专题二:二次函数与一元二次方程(一):【知识梳理】1.二次函数与一元二次方程的关系:(1)一元二次方程ax2+bx+c=0就是二次函数y=ax2+bx+c当函数y的值为0时的情况.(2)二次函数y=ax2+bx+c的图象与x轴的交点有三种情况:有两个交点、有一个交点、没有交点;当二次函数y=ax2+bx+c的图象与x轴有交点时,交点的横坐标就是当y=0时自变量x的值,即一元二次方程ax2+bx+c=0的根.(3)当二次函数y=ax2+bx+c的图象与 x轴有两个交点时,则一元二次方程y=ax2+bx+c 有两个不相等的实数根;当二次函数y=ax2+bx+c的图象与x轴有一个交点时,则一元二次方程ax2+bx+c=0有两个相等的实数根;当二次函数y=ax2+ bx+c的图象与x轴没有交点时,则一元二次方程y=ax2+bx+c没有实数根(二):【经典考题剖析】1.已知二次函数y=x2-6x+8,求:(1)抛物线与x轴J轴相交的交点坐标;(2)抛物线的顶点坐标;(3)画出此抛物线图象,利用图象回答下列问题:①方程x2-6x+8=0的解是什么?②x取什么值时,函数值大于0?③x取什么值时,函数值小于0?2.已知抛物线y=x2-2x-8,(1)求证:该抛物线与x轴一定有两个交点;(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.3.如图所示,直线y=-2x+2与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作等腰直角△ABC ,∠BAC=90o, 过C 作CD ⊥x 轴,垂足为D (1)求点A 、B 的坐标和AD 的长(2)求过B 、A 、D 三点的抛物线的解析式4.如图,在矩形ABCD 中,AB=6cm ,BC=12cm ,点P 从点A 出发,沿AB 边向点B 以1cm/s 的速度移动,同时点Q 从点B 出发,沿BC 边向点C 以2cm/s 的速度移动,回答下列问题:(1) 设运动后开始第t (单位:s )时,五边形APQCD 的面积为S(单位:cm 2),写出S 与t 的函数关系式,并指出自变量t 的取值范围 (2)t 为何值时S 最小?求出S 的最小值5. 如图,直线334y x k=+(0)k >与x 轴、y 轴分别交于A 、B 两点,点P 是线段AB 的中点,抛物线283y x bx c =-++经过点A 、P 、O (原点)。
二次函数 Microsoft Word 文档

课题:二次函数教学目标:掌握二次函数的概念、图象及性质;能利用二次函数研究一元二次方程的实根分布条件;能求二次函数的区间最值.教学重点: 二次函数、一元二次方程及一元二次不等式之间的灵活转化. (一) 主要知识:1.二次函数的解析式的三种形式:一般式,顶点式,两根式.2.二次函数的图象及性质;3.二次函数、一元二次方程及一元二次不等式之间的关系.(二)主要方法:1.讨论二次函数()02≠++=a c bx ax y 在指定区间[]q p ,上的最值问题:①注意对称轴abx 2-=与区间[]q p ,的相对位置; ②函数()02≠++=a c bx ax y 在区间[]q p ,上的单调性.2.讨论二次函数的区间根的分布情况一般需从三方面考虑:①判别式; ②区间端点的函数值的符号; ③对称轴与区间的相对位置. 二次函数是高考考查的永恒主题 (三)典例分析:问题1.设二次函数()f x 满足(2)(2)f x f x -=--,且图象在y 轴上的截距为1,在x 轴截得的线段长为 22,求()f x 的解析式 问题2.已知223()222m f x x mx m =++--,当()0,x ∈+∞时,()0f x >, 求实数m 的取值范围.问题3.函数2()44f x x x =--在闭区间[],1t t +(t R ∈)上的最小值记为()g t ,()1试写出()g t 的函数表达式;()2作出()g t 的图像并求出()g t 的最小值问题4. ()1方程2240x ax -+=的两根均大于1,求实数a 的取值范围()2方程2240x ax -+=的一根大于1,一根小于1,求实数a 的取值范围 ()3方程2240x ax -+=的根在()0,1内,另一根在()6,8,求实数a 的取值范围问题5.已知二次函数 2()f x ax bx =+(,a b 为常数,且0a ≠)满足条件: (5)(3)f x f x -+=-,且方程()f x x =有等根.()1求()f x 的解析式;()2是否存在实数m 、n (m n <),使()f x 的定义域和值域分别是[],m n 和[]3,3m n . 如果存在,求出m 、n 的值;如果不存在,请说明理由.问题6.对于函数()f x ,若存在0x R ∈,使00()f x x =,则称0x 是()f x 的一个 不动点,已知函数2()(1)(1)(0)f x ax b x b a =+++-≠, ()1当1,2a b ==-时,求函数()f x 的不动点;()2对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围;★问题7.已知二次函数2()1f x ax bx =++(a 、b R ∈,0a >),设方程()f x x = 的两个实根为1x 、2x .()1如果1224x x <<<,设函数()f x 的对称轴为0x x =,求证:01x >-;()2如果12x <,212x x -=,求b 的取值范围.(四)巩固练习:1.已知二次函数的对称轴为2x =-,截x 轴上的弦长为4,且过点(0,1)-,求函数的解析式.2.(04江苏)二次函数c bx ax y ++=2(x R ∈)的部分对应值如下表:x -3 -2 -1 0 1 2 3 4 y6-4 -6 -6 -46则不等式c bx ax ++20>的解集是3.函数2 ([0,))y x bx c x =++∈+∞是单调函数的充要条件是 .A 0b ≥ .B 0b ≤ .C 0b > .D 0b <4.函数2()45f x x mx =-+在区间[)2,-+∞上是增函数,则(1)f 的取值范围是.A (1)f ≥25 .B (1)25f = .C (1)f ≤25 .D (1)25f >5.已知,0,)(2≠⋅+=b a bx ax x f 且,2006)()(21==x f x f则=+)(21x x f (五)课后作业:1.(03上海)若函数2(2)3y x a x =+++([,]x a b ∈)的图象关于1x =对称, 则b =2.若不等式210x ax ++≥对一切102x ⎛⎤∈ ⎥⎝⎦,成立,则a 的最小值为( ).A 0 .B 2-.C 52-.D 3-3.已知2()3f x x ax a =++-,若[]2,2x ∈-时()f x ≥0恒成立,则a 的范围是4.(04云南二检)已知实数0a >,0a b c -+<,其中a 、b 、c R ∈,则一定有 .A 240b ac -> .B 24b ac -≤0 .C 240b ac -< .D 24b ac -≥05.设a 、b 、c R ∈,且440a b c -+>,20a b c ++<,则下列结论中正确的是 .A 2b ≤ac .B 2b ac > .C 2b ac >且0a > .D 2b ac >且0a <6.已知函数22()(21)2f x x a x a =--+-与非负x 轴至少有一个交点,求a 的范围.7.关于x 的方程()94340x x a ++⋅+=有实数解,则实数a 的范围是8.m 取何值时,方程227(13)20x m x m m -++--=的一根大于1,一根小于1.9.二次函数()f x 的二次项系数为负值,且(2)(2)()f x f x x R +=-∈,问2(12)f x -与2(12)f x x +-满足什么关系时,有20x -<<.10.已知函数2y x bx c =++且)()1(x f x f -=+,则下列不等式中成立的是.A )2()0()2(f f f <<- .B )2()2()0(f f f <-< .C )2()2()0(-<<f f f .D )2()0()2(-<<f f f11.不等式04)2(2)2(2<--+-x a x a 对一切R x ∈恒成立,则a 的范围是 12.已知)(x f 为二次函数,且x x x f x f 42)1()1(2-=-++,求)21(-f 的值. 13.设函数2()22f x x x =-+([],1x t t ∈+)的最小值为()g t ,求()g t 的解析式 14.设函数12)(2++=ax ax x f 在[]2,3-上有最大值4,求实数a 的值。
(完整版)人教版初中数学二次函数知识点汇总,推荐文档

②平行于 y 轴(或重合)的直线记作 x h .特别地, y 轴记作直线 x 0 .
7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数 a 相同,那么抛物线的开口方向、开口
大小完全相同,只是顶点的位置不同.
8.求抛物线的顶点、对称轴的方法
(1)公式法: y ax2 bx c a x b 2 4ac b2 ,∴顶点是( b ,4ac b2 ),对称轴是直线 x b .
9.抛物线 y ax 2 bx c 中, a,b, c 的作用 (1) a 决定开口方向及开口大小,这与 y ax 2 中的 a 完全一样.
(2) b 和 a 共同决定抛物线对称轴的位置.由于抛物线y ax2 bx c 的对称轴是直线x b ,故:
2a
① b 0 时,对称轴为y 轴;② b 0 (即 a 、b 同号)时,对称轴在 y 轴左侧;
a
③ b 0 (即 a 、b 异号)时,对称轴在 y 轴右侧.
a
(3) c 的大小决定抛物线 y ax 2 bx c 与 y 轴交点的位置.
-1- /4
人教版初中数学二次函数知识点汇总
当 x 0 时, y c ,∴抛物线 y ax 2 bx c 与 y 轴有且只有一个交点(0, c ):
x1 、 x2 是方程 ax 2 bx c 0 的两个根,故
x1
x2
b a
,
x1
x2
c a
AB x1 x2
x1 x2 2
x1 x2 2 4x1x2
b 2 4c a a
b2 4ac
a
a
13.二次函数与一元二次方程的关系:
11.用待定系数法求二次函数的解析式
(1)一般式: y ax 2 bx c .已知图像上三点或三对 x 、 y 的值,通常选择一般式.
二次函数f(x)

10、
已知二次函数y = a������ 2 + b������ + c的图像经过 A(2,4) ,其顶点的横坐标为2(x1,0) ,C(x2,0),且x1 + x2 =13 (1) 求此二次函数的解析式,并画出它的图像。 (2) 在 x 轴上方的抛物线中是否存在点 D, 使得������Δ������������������ = 2������Δ������������������ ?如果存在, 请求出所有 满足条件的 D 点;如果不存在请说明理由。
二次函数讲解
1、 已知二次函数 f(x)满足一下条件: (1)对称轴为 x=1; (2)函数的最大值为 15; (3)f(x)=0 的两根的立方和为 17,求 f(x)的解析式。
2、 已知二次函数 y=f(x)的最大值为 13,且 f(3)=f(-1)=5,求 f(x)的解析式。
3、 已知二次函数y = a������ 2 + ������������ + ������(a≠0),当 x= 根的立方和为 19,求这个函数。
8、 已知二次函数y = a������ 2 − 4������ + ������ − 3,如果存在 x 的值, 使得 y 为负数, 求实数 a 的取值范 围。
9、 已知二次函数 f(x)=m������ 2 − (m − 3)������ + 1 ,对任意的实数 x, 恒有 f(x)≤f(m), (m 为常数) , 求 m 的值。
-1 时最大值为 25,又a������ 2
2
+ ������������ + ������ = 0的两
4、 设关于 x 的二次函数y = 2������ 2 − 4������������ + 3������的最小值为 f(p). (1) 求 f(p) (2) 当 p 为何值时,f(p)有最值,其最值是多少?
(完整)初三数学二次函数知识点总结(2),推荐文档

初三数学二次函数知识点总结一、二次函数概念:1.二次函数的概念:一般地,形如y =ax2 +bx +c (a ,,b c 是常数,a ≠ 0 )的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数a ≠0 ,而b ,体实数.2.二次函数y =ax2 +bx +c 的结构特征:c 可以为零.二次函数的定义域是全⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2.⑵ a ,,b c 是常数,a 是二次项系数,b 是一次项系数,c 是常数项.二、二次函数的基本形式二次函数的基本形式y =a (x -h)2 +k 的性质:a 的绝对值越大,抛物线的开口越小。
a 的符号开口方向顶点坐标对称轴性质a > 0 向上(h ,k) X=h x >h 时,y 随x 的增大而增大;x <h 时,y 随x 的增大而减小;x =h 时,y 有最小值k .a < 0 向下(h ,k) X=h x >h 时,y 随x 的增大而减小;x <h 时,y 随x 的增大而增大;x =h 时,y 有最大值k .三、二次函数图象的平移1.平移步骤:方法一:⑴ 将抛物线解析式转化成顶点式y =a (x -h)2 +k ,确定其顶点坐标(h,k );⑵ 保持抛物线y =ax2的形状不变,将其顶点平移到(h ,k )处,具体平移方法如下:【【(k>0)【【【【(k<0)【【【|k|【【【【【( h>0)【【【( h<0【【【|k|【【【【【( h>0)【【【( h<0)【【|k|【【【【【( k>0)【【【( k<0)【【【|k|【【【【【( h>0)【【【( h<0)【【【|k|【【【y=a(x-h)2【【(k>0)【【【(k<0)【【【|k|【【【2.平移规律在原有函数的基础上“ h 值正右移,负左移;k 值正上移,负下移”.概括成八个字“左加右减,上加下减”.方法二:y=a(x-h)2+ky=ax2y=ax 2+k2a ⎝ ⎭⎝ ⎭⑴ y = ax 2 + bx + c 沿 y 轴平移:向上(下)平移 m 个单位, y = ax 2 + bx + c 变成y = ax 2 + bx + c + m (或 y = ax 2 + bx + c - m )⑵ y = ax 2 + bx + c 沿轴平移:向左(右)平移 m 个单位, y = ax 2 + bx + c 变成y = a (x + m )2 + b (x + m ) + c (或 y = a (x - m )2 + b (x - m ) + c ) 四、二次函数 y = a (x - h )2+ k 与 y = ax 2 + bx + c 的比较从解析式上看, y = a (x - h )2+ k 与 y = ax 2 + bx + c 是两种不同的表达形式,后者通过配方可以得到前 ⎛ b ⎫24ac - b 2 b 4ac - b 2者,即 y = a x + ⎪ +⎝ ⎭,其中 h = - , k = . 4a 2a 4a五、二次函数 y = ax 2 + bx + c 图象的画法五点绘图法:利用配方法将二次函数 y = ax 2 + bx + c 化为顶点式 y = a (x - h )2 + k ,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y 轴的交点(0, c )、以及(0, c )关于对称轴对称的点(2h ,c )、与 x 轴的交点(x 1, 0), (x 2 , 0)(若与 x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与 x 轴的交点,与 y 轴的交点.六、二次函数 y = ax 2 + bx + c 的性质b⎛ b 4ac - b 2 ⎪⎫ . 1. 当 a > 0 时,抛物线开口向上,对称轴为 x = - 2a ,顶点坐标为 - 2a, 4a当 x < - b 时, y 随 x 的增大而减小;当 x > - b时, y 随 x 的增大而增大;当 x = - b 时, y 有最2a 2a2a 4ac - b 2小值 .4ab ⎛ b 4ac - b 2 ⎫ b2. 当 a < 0 时,抛物线开口向下,对称轴为 x = - 2a ,顶点坐标为 - 2a , 4a ⎪ .当x < - 2a时, b b 4ac - b 2y 随 x 的增大而增大;当 x > - 2a时, y 随 x 的增大而减小;当 x = - 2a 时, y 有最大值 .4a七、二次函数解析式的表示方法1. 一般式: y = ax 2 + bx + c ( a , b , c 为常数, a ≠ 0 );2. 顶点式: y = a (x - h )2 + k ( a , h , k 为常数, a ≠ 0 );3. 两根式: y = a (x - x 1)(x - x 2 ) ( a ≠ 0 , x 1 , x 2 是抛物线与 x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与 x 轴有交点,即b 2 - 4ac ≥ 0 时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系1. 二次项系数 a二次函数 y = ax 2 + bx + c 中, a 作为二次项系数,显然 a ≠ 0 . a 决定了抛物线开口的大小和方向,a 的正负决定开口方向, a 的大小决定开口的大小.2. 一次项系数b在二次项系数 a 确定的前提下, b 决定了抛物线的对称轴.bab 的符号的判定:对称轴 x = - 在 y 轴左边则 ab > 0 ,在 y 轴的右侧则 ab < 0 ,概括的说就是2a“左同右异” 3. 常数项 cc 决定了抛物线与 y 轴交点的位置.总之,只要 a ,, b c 都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须 根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况:1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与 x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数与一元二次方程:1. 二次函数与一元二次方程的关系(二次函数与 x 轴交点情况):一元二次方程 ax 2 + bx + c = 0 是二次函数 y = ax 2 + bx + c 当函数值 y = 0 时的特殊情况. 图象与 x 轴的交点个数:① 当∆ = b 2 - 4ac > 0 时,图象与 x 轴交于两点 A (x ,0,) ,B (x 0) (x ≠ x ) ,其中的 x ,x 是一元二次方121212程 ax 2 + bx + c = 0(a ≠ 0)的两根.这两点间的距离 AB = x 2 - x 1=. ② 当∆ = 0 时,图象与 x 轴只有一个交点; ③ 当∆ < 0 时,图象与 x 轴没有交点. 1' 当a > 0 时,图象落在 x 轴的上方,无论 x 为任何实数,都有 y > 0 ; 2 ' 有 y < 0 .当a < 0 时,图象落在 x 轴的下方,无论 x 为任何实数,都 2. 抛物线 y = ax 2 + bx + c 的图象与 y 轴一定相交,交点坐标为(0 , c ) ; 3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与 x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数 y = ax 2 + bx + c 中 a , b , c 的符号,或由二次函数中 a , b , c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与 x 轴的一个交点坐标,可由对称性求出另一个交点坐标.二次函数考查重点与常见题型1. 考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以 x 为自变量的二次函数 y = (m - 2)x 2 + m 2 - m - 2 的图像经过原点, 则 m 的值是2. 综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考y1查两个函数的图像,试题类型为选择题,如:如图,如果函数y =kx +b 的图像在第一、二、三象限内,那么函数y =kx 2 +bx - 1的图像大致是()y10 x xC D3.考查用待定系数法求二次函数的解析式,有关习题出现的频率很高,习题类型有中档解答题和选拔性的综合题,如:已知一条抛物线经过(0,3),(4,6)两点,对称轴为x =5,求这条抛物线的解析式。
(完整版),初中二次函数知识点及经典题型,文档

二次函数的解析式二次函数的解析式有三种形式:2 bx c a b c a y ax 是常数,〔1〕一般一般式:( , , 0)2〔2〕两根当抛物线y ax bx c 与x轴有交点时,即对应二次好方程 2 bx c ax x1 x2有实根和存在时,依照二次三项式的分解因式2 bx c a x x x x 2ax y ax bx c( 1)( 2 ),二次函数可转变为两根式y a( x x1 x x2)( ) 。
若是没有交点,那么不能够这样表示。
a 的绝对值越大,抛物线的张口越小。
2 k a h k a y a x h是常数,〔3〕极点式:( ) ( , , 0)知识点八、二次函数的最值若是自变量的取值范围是全体实数,那么函数在极点处获取最大值〔或最小值〕2b 4ac bx y,即当时,。
最值2a 4ab 若是自变量的取值范围是x1 x x2 ,那么,第一要看可否在自变量取值范2a2b 4ac b围x1 x x2 内,假设在此范围内,那么当 x= 时,;假设不在此范围y最值2a 4a内,那么需要考虑函数在x1 x x2 范围内的增减性,若是在此范围内, y随x的增大而2 2增大,那么当x x2 时,y最大ax bx c,当x x1时,y ax bx1 c;如最小2 2 12果在此范围内, y随x的增大而减小,那么当x x1时,y ax bx1 c,当最大x x212时,y ax bx2 c。
最小2知识点九、二次函数的性质1 、二次函数的性质二次函数函数 2 bx c a b c ay ax ( , , 是常数,0)a>0 a<0yy图像0 x 0 x〔1〕抛物线张口向上,并向上无量延伸;〔1〕抛物线张口向下,并向下无量延伸;b b〔2〕对称轴是 x= ,极点坐标是〔2a 2ab〔2〕对称轴是 x= ,极点坐标是〔2a24ac b ,〕;4a2 b 4ac b,〕;2a 4a性b〔3〕在对称轴的左侧,即当 x< 时,y随2ab〔3〕在对称轴的左侧,即当 x< 时,y2a x的增大而减小;在对称轴的右侧,即当 x随x的增大而增大;在对称轴的右侧,质b b> 时,y随x的增大而增大,简记左即当x> 时,y随x的增大而减小,2a 2a减右增;简记左增右减;b 〔4〕抛物线有最低点,当 x= 时,y有最2ab 〔4〕抛物线有最高点,当 x= 时,y有2a小值,y最小值4ac4ab 2最大值,y最大值4ac4ab 22 bx c a b c a2、二次函数y ax ( , , 是常数, 0) 中,a、b、c 的含义:a a表示张口方向: >0 时,抛物线张口向上a <0 时,抛物线张口向下b b 与对称轴有关:对称轴为 x=2ac c表示抛物线与 y轴的交点坐标:〔 0,〕3、二次函数与一元二次方程的关系一元二次方程的解是其对应的二次函数的图像与 x轴的交点坐标。
(完整版)初中数学二次函数知识点汇总,推荐文档

(2)顶点式: y ax h2 k .已知图像的顶点或对称轴,通常选择顶点式.
(3)交点式:已知图像与 x 轴的交点坐标 x1 、 x2 ,通常选用交点式: y ax x1 x x2 .
12.直线与抛物线的交点
我去人也就有人!为UR扼腕入站内信不存在向你偶同意调剖沙
(1) y 轴与抛物线 y ax 2 bx c 得交点为(0, c ).
纵坐标为 k ,则横坐标是 ax 2 bx c k 的两个实数根.
(5)一次函数 y kx nk 0的图像 l 与二次函数 y ax2 bx ca 0的图像 G 的交点,由方
y kx n 程组 y ax 2 bx c 的解的数目来确定:①方程组有两组不同的解时 l 与 G 有两个交点;
a 相等,抛物线的开口大小、形状相同.
②平行于 y 轴(或重合)的直线记作 x h .特别地, y 轴记作直线 x 0 .
7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数 a 相同,那么抛物线的开口方向、开
口大小完全相同,只是顶点的位置不同.
8.求抛物线的顶点、对称轴的方法(1)公式法: y ax 2 bx c a x b 2 4ac b2 ,∴顶点
(2)对称轴是 x= b ,顶点坐标是( b ,
2a
2a
(1)抛物线开口向下,并向下无限延伸;
(2)对称轴是 x= b ,顶点坐标是 2a
4ac b2
);
4a
(
b
4ac b2
,
);
2a 4a
性质
(3)在对称轴的左侧,即当 x< b 时,y 随 2a
(3)在对称轴的左侧,即当 x< b 时,y 2a
则当 x x1 时, y最大 ax12 bx1 c ,当 x x2 时, y最小 ax22 bx2 c 。
二次函数概念讲课文档

(是)(4)y=(x+3)²-x² (否)
(5)y= _x1_- ² x
(否)(6)v= 3r ²
(7) y=x²+x³+25 (否) (8)y=2²+2x
(是) (否)
思考:(9)y=mx²+nx+p (m,n,p为常数)
第十一页,共21页。
例1、下列函数中,哪些是二次函数?若是,分别指
出二次项系数,一次项系数,常数项.
y 1 x2 13x
1
2
2
y x2
4213000二次函数y=ax²+bx+c中a≠0,但b、c可以为0.
第十页,共21页。
例1、下列函数中,哪些是二次函数?若是,分 别指出二次项系数,一次项系数,常数项.
(1) y=3(x-1)²+1
(是) (2)y=x+
_1_ x
(否)
(3)s=3-2t²
原产量是20件, 一年后的产量是 20(1+x)件,
再经过一年后的产量是 20(1+x)2 件,即两年后的产 量为
即
y 20 x2 40 x 20③
③式表示两年后的产量y与计划增产的倍数x之间的关系, 对于x的每一个值, y都有一个对应值,即y是x的函数.
第六页,共21页。
观察
函数①②③有什么共同点?
(1) y=3(x-1)²+1
(2) y=x+
_1_ x
(3) s=3-2t²
(5)y= _x1_²-x
(4) y=(x+3)²-x² (6) v=10π r²
第十二页,共21页。
解: (1)y=3(x-1)²+1 =3(x2-2x+1)+1 =3x2-6x+3+1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数<一>
1.向空中发射一枚炮弹,经x 秒后的高度为y 米,且时间与高度的关系为y=ax 2
bx+c (a ≠
0).若此炮弹在第7秒与第14秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
A .第8秒
B .第10秒
C .第12秒
D .第15秒 2如图,点C 、D 是以线段AB 为公共弦的两条圆弧的中点,AB =4,点
E 、
F 分别是线段CD ,
AB 上的动点,设AF =x ,AE 2-FE 2=y ,则能表示y 与x 的函数关系的图象是( )
3.如图,等腰Rt △ABC (∠ACB =90º)的直角边与正方形DEFG 的边长均为2,且AC 与DE
在同一直线上,开始时点C 与点D 重合,让△ABC 沿这条直线向右平移,直到点A 与点E 重合为止.设CD 的长为x ,△ABC 与正方形DEFG 重合部分(图中阴影部分)的面积为
y ,则y 与x 之间的函数关系的图象大致是( )
(第2题) C
D
E F
A
B
(第2题分析图) C
D
E
B P
4.如图3,从地面竖立向上抛出一个小球,小球的高度h (单位:m )与 小球运动时间t (单位:s )之间的关系式为2
530t t h -=,那么小球从抛出至回落到地面所需要的时间是:
(A )6s (B )4s (C )3s (D )2s
二、填空题
1. 如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.
拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
2.如图,在ABC ∆中,90B ∠=
,12mm AB =,24mm BC =,动点P 从点A 开始沿边
AB 向B 以2mm /s 的速度移动(不与点B 重合),动点Q 从点B 开始沿边BC 向C 以
4mm /s 的速度移动(不与点C 重合).如果P 、Q 分别从A 、B 同时出发,那么
经过_____________秒,四边形APQC 的面积最小.
3.将一条长为20cm 的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是 cm 2. 4.小汽车刹车距离s (m )与速度v (km/h )之间的函数关系式为2
100
1v s =
,一辆小汽车速度为100km/h ,在前方80m 处停放一辆故障车,此时刹车 有危险(填“会”或“不会”).
5.某种火箭被竖直向上发射时,它的高度h (m)与时间t (s)的关系可以用公式h =-5t 2+150t +10表示.经过______s ,火箭达到它的最高点.
三、解答题
1.已知:如图在Rt △ABC 中,斜边AB =5厘米,BC =a 厘米,AC =b 厘米,a >b ,且a 、
b 是方程2(1)40x m x m --++=的两根。
⑴ 求a 和b 的值;
⑵ C B A '''∆与ABC ∆开始时完全重合,然后让ABC ∆固定不动,将C B A '''∆以1厘米/秒的速度沿BC 所在的直线向左移动。
① 设x 秒后C B A '''∆与ABC ∆的重叠部分的面积为y 平方厘米, 求y 与x 之间的函数关系式,并写出x 的取值范围;
② 几秒后重叠部分的面积等于8
3
平方厘米?
2.春节期间某水库养殖场为适应市场需求,连续用20天时间,采用每天降低水位以减少捕捞成本的办法,对水库中某种鲜鱼进行捕捞、销售。
九(1)班数学建模兴趣小组根据调查,整理出第x 天(201≤≤x 且x 为整数)的捕捞与销售的相关信息如下:
⑴在此期间该养殖场每天的捕捞量与前一末的捕捞量相比是如何变化的? ⑵假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出,求第x 天的收入y (元)与x (天)之间的函数关系式?(当天收入=日销售额—日捕捞成本)
试说明⑵中的函数y 随x 的变化情况,并指出在第几天y 取得最大值,最大值是多少?
A
M
A'
3.用长度为20m 的金属材料制成如图所示的金属框,下部为矩形,上部为等腰直角三角形,其斜边长为2x m .当该金属框围成的图形面积最大时,图形中矩形的相邻两边长各为多少?请求出金属框围成的图形的最大面积.
4.如图,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .
(1)求y 关于x 的函数关系式;
(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12
y m
,要使△DEF 为等腰三角形,m 的值应为多少?
A B
C
D
E
F
(第4题)。
