实验五牛顿迭代法
关于牛顿迭代法的课程设计实验指导
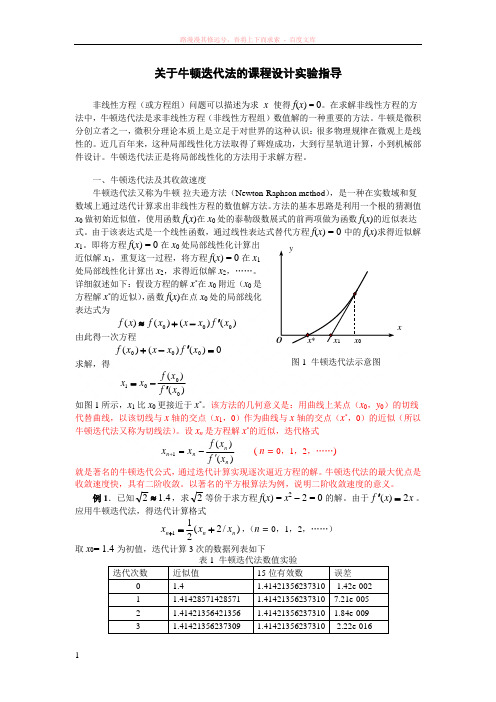
yx O x * x 1 x 0关于牛顿迭代法的课程设计实验指导非线性方程(或方程组)问题可以描述为求 x 使得f (x ) = 0。
在求解非线性方程的方法中,牛顿迭代法是求非线性方程(非线性方程组)数值解的一种重要的方法。
牛顿是微积分创立者之一,微积分理论本质上是立足于对世界的这种认识:很多物理规律在微观上是线性的。
近几百年来,这种局部线性化方法取得了辉煌成功,大到行星轨道计算,小到机械部件设计。
牛顿迭代法正是将局部线性化的方法用于求解方程。
一、牛顿迭代法及其收敛速度牛顿迭代法又称为牛顿-拉夫逊方法(Newton-Raphson method ),是一种在实数域和复数域上通过迭代计算求出非线性方程的数值解方法。
方法的基本思路是利用一个根的猜测值x 0做初始近似值,使用函数f (x )在x 0处的泰勒级数展式的前两项做为函数f (x )的近似表达式。
由于该表达式是一个线性函数,通过线性表达式替代方程中的求得近似解x 1。
即将方程f (x ) = 0在x 0处局部线性化计算出近似解x 1,重复这一过程,将方程f (x ) = 0在x 1处局部线性化计算出x 2,求得近似解x 2,……。
详细叙述如下:假设方程的解x *在x 0附近(x 0是方程解x *的近似),函数f (x )在点x 0处的局部线化表达式为)()()()(000x f x x x f x f '-+≈由此得一次方程 0)()()(000='-+x f x x x f求解,得 )()(0001x f x f x x '-= 如图1所示,x 1比x 0更接近于x *。
该方法的几何意义是:用曲线上某点(x 0,y 0)的切线代替曲线,以该切线与x 轴的交点(x 1,0)作为曲线与x 轴的交点(x *,0)的近似(所以牛顿迭代法又称为切线法)。
设x n 是方程解x *的近似,迭代格式)()(1n n n n x f x f x x '-=+ ( n = 0,1,2,……) 就是著名的牛顿迭代公式,通过迭代计算实现逐次逼近方程的解。
数学数学实验Newton迭代法

数学实验题目4 Newton 迭代法摘要0x 为初始猜测,则由递推关系产生逼近解*x 的迭代序列{}k x ,这个递推公式就是Newton 法。
当0x 距*x 较近时,{}k x 很快收敛于*x 。
但当0x 选择不当时,会导致{}k x 发散。
故我们事先规定迭代的最多次数。
若超过这个次数,还不收敛,则停止迭代另选初值。
前言利用牛顿迭代法求的根程序设计流程问题1(1 程序运行如下:r = NewtSolveOne('fun1_1',pi/4,1e-6,1e-4,10) r = 0.7391(2 程序运行如下:r = NewtSolveOne('fun1_2',0.6,1e-6,1e-4,10) r = 0.5885问题2(1 程序运行如下:否 是否是是定义()f x输入012,,,x N εε开 始1k =01()f x ε<0100()()f x x x f x =-'102||x x ε-<k N =输出迭代失败标志输出1x输出奇 异标志结 束01x x = 1k k =+ 否r = NewtSolveOne('fun2_1',0.5,1e-6,1e-4,10)r = 0.5671(2)程序运行如下:r = NewtSolveOne('fun2_2',0.5,1e-6,1e-4,20)r = 0.5669问题3(1)程序运行如下:①p = LegendreIter(2)p = 1.0000 0 -0.3333p = LegendreIter(3)p = 1.0000 0 -0.6000 0p = LegendreIter(4)p =1.0000 0 -0.8571 0 0.0857p = LegendreIter(5)p = 1.0000 0 -1.1111 0 0.2381 0②p = LegendreIter(6)p = 1.0000 0 -1.3636 0 0.4545 0 -0.0216r = roots(p)'r= -0.932469514203150 -0.6612 0.9324695142031530.6612 -0.238619186083197 0.238619186083197用二分法求根为:r = BinSolve('LegendreP6',-1,1,1e-6)r = -0.932470204878826 -0.661212531887755 -0.2386200573979590.2386 0.661192602040816 0.932467713647959(2)程序运行如下:①p = ChebyshevIter(2)p = 1.0000 0 -0.5000p = ChebyshevIter(3)p = 1.0000 0 -0.7500 0p = ChebyshevIter(4)p = 1.0000 0 -1.0000 0 0.1250p = ChebyshevIter(5)p = 1.0000 0 -1.2500 0 0.3125 0②p = ChebyshevIter(6)p = 1.0000 0 -1.5000 0 0.5625 0 -0.0313r = roots(p)'r = -0.965925826289067 -0.7548 0.9659258262890680.7547 -0.258819045102521 0.258819045102521用二分法求根为:r = BinSolve('ChebyshevT6',-1,1,1e-6)r = -0.965929926658163 -0.7755 -0.2588289221938780.2588 0.7020 0.965924944196429与下列代码结果基本一致,只是元素顺序稍有不同:j = 0:5;x = cos((2*j+1)*pi/2/(5+1))x =0.965925826289068 0.7548 0.258819045102521-0.258819045102521 -0.7547 -0.965925826289068(3)程序运行如下:①p = LaguerreIter(2)p = 1 -4 2p = LaguerreIter(3)p = 1 -9 18 -6p = LaguerreIter(4)p = 1 -16 72 -96 24p = LaguerreIter(5)p =1.0000 -25.0000 200.0000 -600.0000 600.0000 -120.000②p = LaguerreIter(5)p =1.0000 -25.0000 200.0000 -600.0000 600.0000 -120.000r = roots(p)'r =12.6432 7.8891 3.5964257710407111.4520 0.263560319718141用二分法求根为:r = BinSolve('LaguerreL5',0,13,1e-6)r = 0.263560314567722 1.4789 3.5964257656311507.0720 12.6490(4)程序运行如下:①p = HermiteIter(2)p = 1.0000 0 -0.5000p = HermiteIter(3)p = 1.0000 0 -1.5000 0p = HermiteIter(4)p = 1.0000 0 -3.0000 0 0.7500p = HermiteIter(5)p = 1.0000 0 -5.0000 0 3.7500 0②p = HermiteIter(6)p = 1.0000 0 -7.5000 0 11.2500 0 -1.8750r = roots(p)'r =-2.3587 2.3588 -1.3358490740136961.335849074013698 -0.4367 0.4366用二分法求根为:r = BinSolve('HermiteH6',-3,3,1e-6)r =-2.3516 -1.335849********* -0.43630.4366 1.335848983453244 2.3504所用到的函数function r = NewtSolveOne(fun, x0, ftol, dftol, maxit)% NewtSolveOne 用Newton法解方程f(x)=0在x0附近的一个根%% Synopsis: r = NewtSolveOne(fun, x0)% r = NewtSolveOne(fun, x0, ftol, dftol)%% Input: fun = (string) 需要求根的函数及其导数% x0 = 猜测根,Newton法迭代初始值% ftol = (optional)误差,默认为5e-9% dftol = (optional)导数容忍最小值,小于它表明Newton法失败,默认为5e-9 % maxit = (optional)迭代次数,默认为25%% Output: r = 在寻根区间内的根或奇点if nargin < 3ftol = 5e-9;endif nargin < 4dftol = 5e-9;endif nargin < 5maxit = 25;endx = x0; %设置初始迭代位置为x0k = 0; %初始化迭代次数为0while k <= maxitk = k + 1;[f,dfdx] = feval(fun,x); %fun返回f(x)和f'(x)的值if abs(dfdx) < dftol %如果导数小于dftol,Newton法失败,返回空值r = [];warning('dfdx is too small!');return;enddx = f/dfdx; %x(n+1) = x(n) - f( x(n) )/f'( x(n) ),这里设dx = f( x(n) )/f'( x(n) )x = x - dx;if abs(f) < ftol %如果误差小于ftol,返回当前x为根r = x;return;endendr = []; %如果牛顿法未收敛,返回空值function p = LegendreIter(n)% LegendreIter 用递推的方法计算n次勒让德多项式的系数向量Pn+2(x) = (2*i+3)/(i+2) * x*Pn+1(x) - (i+1)/(i+2) * Pn(x)%% Synopsis: p = LegendreIter(n)%% Input: n = 勒让德多项式的次数%% Output: p = n次勒让德多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %P0(x) = 1p = 1;return;elseif n == 1 %P1(x) = xp = [1 0];return;endpBk = 1; %初始化三项递推公式后项为P0pMid = [1 0]; %初始化三项递推公式中项为P1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Pn+1pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的PnpBkCal(3:i+3) = pBk;pFwd = (2*i+3)/(i+2) * pMidCal - (i+1)/(i+2) * pBkCal; %勒让德多项式三项递推公式Pn+2(x) = (2*i+3)/(i+2) * x*Pn+1(x) - (i+1)/(i+2) * Pn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把勒让德多项式最高次项系数归一化function p = ChebyshevIter(n)% ChebyshevIter 用递推的方法计算n次勒让德-切比雪夫多项式的系数向量Tn+2(x) = 2*x*Tn+1(x) - Tn(x)%% Synopsis: p = ChebyshevIter(n)%% Input: n = 勒让德-切比雪夫多项式的次数%% Output: p = n次勒让德-切比雪夫多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %T0(x) = 1p = 1;return;elseif n == 1 %T1(x) = xp = [1 0];return;endpBk = 1; %初始化三项递推公式后项为T0pMid = [1 0]; %初始化三项递推公式中项为T1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Tn+1pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的PnpBkCal(3:i+3) = pBk;pFwd = 2*pMidCal - pBkCal; %勒让德-切比雪夫多项式三项递推公式Tn+2(x) = 2*x*Tn+1(x) - Tn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把勒让德-切比雪夫多项式最高次项系数归一化function p = LaguerreIter(n)% LaguerreIter 用递推的方法计算n次拉盖尔多项式的系数向量Ln+2(x) = (2*n+3-x)*Ln+1(x) - (n+1)*Ln(x)%% Synopsis: p = LaguerreIter(n)%% Input: n = 拉盖尔多项式的次数%% Output: p = n次拉盖尔多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %L0(x) = 1p = 1;return;elseif n == 1 %L1(x) = -x+1p = [-1 1];return;endpBk = 1; %初始化三项递推公式后项为L0pMid = [-1 1]; %初始化三项递推公式中项为L1for i = 0:n-2pMidCal1 = zeros(1,i+3); %构造用于计算的x*Ln+1(x)pMidCal1(1:i+2) = pMid;pMidCal2 = zeros(1,i+3); %构造用于计算的Ln+1(x)pMidCal2(2:i+3) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的Ln(x)pBkCal(3:i+3) = pBk;pFwd =( (2*i+3)*pMidCal2 - pMidCal1 - (i+1)*pBkCal )/ (i+2); %拉盖尔多项式三项递推公式Ln+2(x) = (2*n+3-x)*Ln+1(x) - (n+1)^2*Ln(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把拉盖尔多项式最高次项系数归一化function p = HermiteIter(n)% HermiteIter 用递推的方法计算n次埃尔米特多项式的系数向量Hn+2(x) = 2*x*Hn+1(x) - 2*(n+1)*Hn(x)%% Synopsis: p = HermiteIter(n)%% Input: n = 埃尔米特多项式的次数%% Output: p = n次埃尔米特多项式的系数向量if round(n) ~= n | n < 0error('n必须是一个非负整数');endif n == 0 %H0(x) = 1p = 1;return;elseif n == 1 %H1(x) = 2*xp = [2 0];return;endpBk = 1; %初始化三项递推公式后项为L0pMid = [2 0]; %初始化三项递推公式中项为L1for i = 0:n-2pMidCal = zeros(1,i+3); %构造用于计算的x*Hn+1(x)pMidCal(1:i+2) = pMid;pBkCal = zeros(1,i+3); %构造用于计算的Hn(x)pBkCal(3:i+3) = pBk;pFwd =2*pMidCal - 2*(i+1)*pBkCal; %埃尔米特多项式三项递推公式Hn+2(x) = 2*x*Hn+1(x) - 2*(n+1)*Hn(x)pBk = pMid; %把中项变为后项进行下次迭代pMid = pFwd; %把前项变为中项进行下次迭代endp = pFwd/pFwd(1); %把拉盖尔多项式最高次项系数归一化function r = BinSolve(fun, a, b, tol)% BinSolve 用二分法解方程f(x)=0在区间[a,b]的根%% Synopsis: r = BinSolve(fun, a, b)% r = BinSolve(fun, a, b, tol)%% Input: fun = (string) 需要求根的函数% a,b = 寻根区间上下限% tol = (optional)误差,默认为5e-9%% Output: r = 在寻根区间内的根if nargin < 4tol = 5e-9;endXb = RootBracket(fun, a, b); %粗略寻找含根区间[m,n] = size(Xb);r = [];nr = 1; %初始化找到的根的个数为1maxit = 50; %最大二分迭代次数为50for i = 1:ma = Xb(i,1); %初始化第i个寻根区间下限b = Xb(i,2); %初始化第i个寻根区间上限err = 1; %初始化误差k = 0;while k < maxitfa = feval(fun, a); %计算下限函数值fb = feval(fun, b); %计算上限函数值m = (a+b)/2;fm = feval(fun, m);err = abs(fm);if sign(fm) == sign(fb) %若中点处与右端点函数值同号,右端点赋值为中点b = m;else %若中点处与左端点函数值同号或为0,左端点赋值为中点a = m;endif err < tol %如果在a处函数值小于tolr(nr) = a; %一般奇点不符合该条件,这样可以去除奇点nr = nr + 1; %找到根的个数递增k = maxit; %改变k值跳出循环endk = k + 1; %二分迭代次数递增endendfunction X = powerX(x,a,b)% powerX 对给定向量(x1, x2,..., xn)返回增幂矩阵(x1^a, x2^a,..., xn^a; x1^a+1, x2^a+1,..., xn^a+1; ...; x1^b, x2^b,..., xn^b;)%% Synopsis: X = powerX(x,a,b)%% Input: x = 需要返回增幂矩阵的向量% a,b = 寻根区间上下限%% Output: X = 增幂矩阵(x1^a, x2^a,..., xn^a; x1^a+1, x2^a+1,..., xn^a+1; ...; x1^b, x2^b,..., xn^b;)if round(a) ~= a | round(b) ~= berror('a,b must be integers');elseif a >= berror('a must be smaller than b!');endx = x(:)';row = b-a+1;col = length(x);X = zeros(row, col);for i = b:-1:aX(b-i+1,:) = x.^i;Endfunction [f, dfdx] = fun1_1(x)f = cos(x) - x;dfdx = -sin(x) - 1;function [f, dfdx] = fun1_2(x)f = exp(-x) - sin(x);dfdx = -exp(-x) - cos(x);function [f, dfdx] = fun2_1(x)f = x - exp(-x);dfdx = 1 + exp(-x);function [f, dfdx] = fun2_2(x)f = x.^2 - 2*x*exp(-x) + exp(-2*x);dfdx = 2*x - 2*exp(-x) + 2*x*exp(-x) - 2*exp(-2*x);function y = LegendreP6(x)p = LegendreIter(6);X = powerX(x,0,6);y = p*X;function y = ChebyshevT6(x)p = ChebyshevIter(6);X = powerX(x,0,6);y = p*X;function y = LaguerreL5(x)p = LaguerreIter(5);X = powerX(x,0,5);y = p*X;function y = HermiteH6(x)p = HermiteIter(6);X = powerX(x,0,6);y = p*X;思考题(1)由于Newton法具有局部收敛性,所以在实际问题中,当实际问题本身能提供接近于根的初始近似值时,就可保证迭代序列收敛,但当初值难以确定时,迭代序列就不一定收敛。
牛顿迭代法(Newton‘s Method)

牛顿迭代法(Newton’s Method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson Method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
与一阶方法相比,二阶方法使用二阶导数改进了优化,其中最广泛使用的二阶方法是牛顿法。
考虑无约束最优化问题:其中 \theta^{\ast} 为目标函数的极小点,假设 f\left( \theta \right) 具有二阶连续偏导数,若第 k 次迭代值为 \theta^{k} ,则可将f\left( \theta \right)在\theta^{k}近进行二阶泰勒展开:这里,g_{k}=x^{\left( \theta^{k} \right)}=∇f\left( \theta^{k} \right)是f\left( \theta \right) 的梯度向量在点 \theta^{k}的值, H\left( \theta^{k} \right) 是 f\left( \theta \right) 的Hessian矩阵:在点 \theta^{\left( k \right)}的值。
函数 f\left( \theta \right) 有极值的必要条件是在极值点处一阶导数为0,即梯度向量为0,特别是当H\left( \theta\right) 是正定矩阵时,函数 f\left( \theta \right) 的极值为极小值。
牛顿法利用极小点的必要条件:这就是牛顿迭代法。
迭代过程可参考下图:在深度学习中,目标函数的表面通常非凸(有很多特征),如鞍点。
因此使用牛顿法是有问题的。
如果Hessian矩阵的特征值并不都是正的,例如,靠近鞍点处,牛顿法实际上会导致更新朝错误的方向移动。
这种情况可以通过正则化Hessian矩阵来避免。
常用的正则化策略包括在Hessian矩阵对角线上增加常数α 。
正则化更新变为:这个正则化策略用于牛顿法的近似,例如Levenberg-Marquardt算,只要Hessian矩阵的负特征值仍然相对接近零,效果就会很好。
实验五 用Newton法计算方程的根

五. 讨论分析当初始值选取离零点较远时将导致算法无法使用,例如第三题,将初始值改为2就无法计算出结果了,显示如下例如求020sin 35=-+-x x e x 的根,其中控制精度1010-=eps ,最大迭代次数40=M ,在steffensen 加速迭代方法的程序中,我们只需改动:it_max=40; ep=1e-10, 其余不变 。
利用以上程序,我们只需输入:phi=inline('exp(5*x)-sin(x)+(x)^3-20');[x_star,index,it]=steffensen(phi,0.5)可得:x_star = 0.637246094753909index = 0it = 41观察上述结果,index = 0,it = 41表明迭代失败,所以使用以上方法估计的时候,应该尽量估计出解的范围,偏离不应过大,距离增加迭代次数增加,也有可能迭代失败六. 改进实验建议根据上述分析,我认为,应该先对函数作一个简图,方便知道解的大概位置,然后我们才将这个大概值代入Newton 法或者Steffensen 中进行求解。
当然,我们可以用其他数学软件实现Newton 迭代法,我们可以用z-z 超级画板,其操作流程为:牛顿迭代法的公式是:x n+1=x n-f(x n)/f'(x n)。
下面我们就用牛顿迭代法设计程序求方程f(x)=ln(x)+2*x-6的近似解。
(一)观察方程f(x)=0的零点位置(1)显示坐标系的坐标刻度。
(2)作出函数y=ln(x)+2*x-6的图像,如下图所示:可以观察到方程的根在区间[2,3]上,我们可以设定近似解的初始值为2。
(二)设计求方程近似解的程序(1)在程序工作区中输入:f(x){ln(x)+2*x-6;}执行后,返回结果为:>> f(x) #这表示在计算机已经完成了函数f(x)的定义。
(2)定义f(x)的导函数g(x),在程序工作区中输入:Diff(f(x),x);执行后,返回结果为:>> 2+1/x #得到了f(x)的导函数。
牛顿迭代法及其应用

牛顿迭代法及其应用牛顿迭代法是求解非线性方程的一种常用方法,其基本思想是利用泰勒公式,将原方程式化为近似的一次方程,不断迭代,直到获得满足要求的精度值为止。
在数学、物理、化学等领域,牛顿迭代法被广泛应用。
1. 原理与步骤给定一个函数 f(x),我们希望求出它的一个根,即使得 f(x) = 0 的 x 的值。
考虑到非线性函数的复杂性,我们采用牛顿迭代法来解决。
假设已经猜测出一个近似值 x0,通过泰勒公式将 f(x) 在 x0 处展开:f(x) ≈ f(x0) + f'(x0)(x - x0)为了简化计算,我们令上式等于0,即:f(x0) + f'(x0)(x - x0) = 0将 x 化简可得:x = x0 - f(x0) / f'(x0)将上式作为下一次迭代的初始值,即可不断迭代求解,直到满足要求的精度值。
2. 牛顿迭代法的应用2.1 偏微分方程偏微分方程是现代科学和工程所涉及的许多领域的基础,而牛顿迭代法可用于求解非线性偏微分方程。
由于牛顿迭代法依赖于初始值的选择,因此需要根据实际问题来选择初始值,从而得到精确的解。
2.2 统计学在统计学中,牛顿迭代法被广泛应用于最大似然估计。
最大似然估计是在给定数据集的前提下,寻找一种参数估计方法,使得似然函数(即给定数据集下模型参数的条件下,该数据集出现的概率)最大。
通过牛顿迭代法,可以快速求解似然函数的最大值,从而获得最优的参数估计结果。
2.3 非线性优化在优化问题中,如果目标函数为非线性函数,则无法通过简单的线性规划来解决,需要借助于牛顿迭代法。
通过迭代求解逼近目标函数的零点,可以实现非线性规划问题的求解。
3. 注意事项在使用牛顿迭代法时,需要注意以下几点:3.1 初始值的选择初始值的选择会直接影响到迭代的次数和迭代结果的精度。
一般来说,我们选择敏感度较高的点作为初始值,例如驻点或函数导数为零的点。
3.2 解存在性和唯一性使用牛顿迭代法求解方程时,需要保证解的存在性和唯一性。
牛顿迭代法——精选推荐

⽜顿迭代法⽜顿(Newton's method)⼜称为⽜顿-拉夫逊(拉弗森)⽅法(Newton-Raphson method),它是在17世纪提出的⼀种在域和域上近似求解⽅程的⽅法。
⽜顿迭代公式设r是\(f(x)=0\)的根,选取\(x_0\)作为r的初始近似值,过点\((x_0,f(x_0))\) ,做曲线 \(y=f(x)\)的切线L,L的⽅程为\(y=f(x_0)+f’(x_0)(x-x_0)\) ,求出L与x轴交点的横坐标\[x_1=x_0-\frac{f(x_0)}{f’(x_0)}\]称\(x_1\)为r的⼀次近似值。
过点\((x_1,f(x_1))\) 做曲线 \(y=f(x)\)的切线,并求该切线与x轴交点的横坐标\[x_2=x_1-\frac{f(x_1)}{f’(x_1)}\]称\(x_2\)为r的⼆次近似值。
重复以上过程,得r的近似值序列,其中,\[x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}\]称为r的\(n+1\)次近似值,上式称为⽜顿迭代公式。
⽤⽜顿迭代法解⾮线性⽅程,是把⾮线性⽅程\(f(x)=0\)线性化的⼀种近似⽅法。
把 \(f(x)\)在点 \(x_0\)的某邻域内展开成泰勒级数\[f(x)=f(x_0)+f’(x_0)(x-x_0)+\frac{f’’(x_0)(x-x_0)^2}{2!}+…+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!}+R_n(x)\]取其线性部分(即泰勒展开的前两项),并令其等于0,即 \(f(x_0)+f’(x_0)(x-x_0)=0\),以此作为⾮线性⽅程 \(f(x)=0\)的近似⽅程,若\ (f’(x_0)\neq0\),则其解为\[x_1=x_0-\frac{f(x_0)}{f’(x_0)}\]这样,得到⽜顿迭代法的⼀个迭代关系式:\[x_{n+1}=x_n-\frac{f(x_n)}{f’(x_n)}\]从下⾯的图中,我们可以看到⽜顿迭代的⼏何意义,每次迭代,都会更加逼近\(f(x)=0\)的解。
牛顿迭代法实验
100
1000 10000
6.00
7.10 6.11
27.00
29.70 30.84
31.00
29.10 30.06
36.00
34.10 32.99
13/16
实验结论:方程 z3 – 1 = 0 在复平面上有三个根
z1 1
取正方形区域 {( x, y ) | 2 x 2, 2 y 2} 内任意点确定复数 z0 x iy 为牛顿迭代法初值
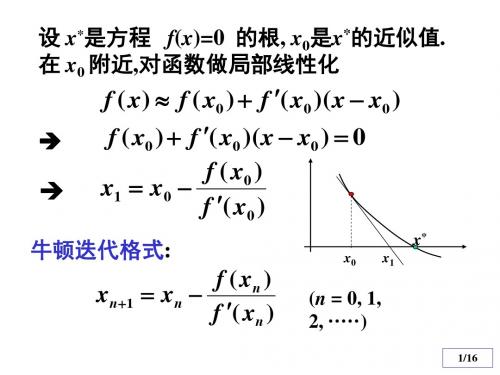
设 x*是方程 f(x)=0 的根, x0是x*的近似值. 在 x0 附近,对函数做局部线性化
f ( x) f ( x0 ) f ( x0 )( x x0 ) f ( x0 ) f ( x0 )( x x0 ) 0 f ( x0 ) x1 x0 f ( x0 )
8/16
实验绘图主程序 function A0=Newtonlab(n) if nargin==0,n=101;end t=linspace(-2,2,n); [x,y]=meshgrid(t); X=roots([1,0,0,-1]); [A0,A1,A2,A3]=Nlab(x,y,X); A=A0+2*A1+3*A2+4*A3; figure(1),pcolor(x,y,A),shading interp figure(2),pcolor(x,y,A0), shading interp
10/16
利用矩阵统计各区域百分比程序
[m,n]=size(A0); N=m*n; II=find(A0==1);N0=length(II); II=find(A1==1);N1=length(II); II=find(A2==1);N2=length(II); II=find(A3==1);N3=length(II); format bank results=100*[N0,N1,N2,N3]/N
牛顿迭代法的基本原理知识点

牛顿迭代法的基本原理知识点牛顿迭代法是一种求解方程近似解的数值计算方法,通过不断逼近方程的根,以获得方程的解。
它基于牛顿法则和泰勒级数展开,被广泛应用于科学和工程领域。
本文将介绍牛顿迭代法的基本原理和相关知识点。
一、牛顿迭代法的基本原理牛顿迭代法的基本原理可以总结为以下几个步骤:1. 假设要求解的方程为 f(x) = 0,给定一个初始近似解 x0。
2. 利用泰勒级数展开,将方程 f(x) = 0 在 x0 处进行二阶近似,得到近似方程:f(x) ≈ f(x0) + f'(x0)(x - x0) + 1/2 f''(x0)(x - x0)^23. 忽略近似方程中的高阶无穷小,并令f(x) ≈ 0,得到近似解 x1:0 ≈ f(x0) + f'(x0)(x1 - x0) + 1/2 f''(x0)(x1 - x0)^2求解上述方程,得到近似解 x1 = x0 - f(x0)/f'(x0)。
4. 通过反复迭代的方式,不断更新近似解,直到满足精度要求或收敛于方程的解。
二、牛顿迭代法的收敛性与收敛速度牛顿迭代法的收敛性与收敛速度与初始近似解 x0 的选择和方程本身的性质有关。
1. 收敛性:对于某些方程,牛顿迭代法可能无法收敛或者收敛到错误的解。
当方程的导数为零或者初始近似解离根太远时,迭代可能会发散。
因此,在应用牛顿迭代法时,需要对方程和初始近似解进行合理的选择和判断。
2. 收敛速度:牛顿迭代法的收敛速度通常较快,二阶收敛的特点使其在数值计算中得到广泛应用。
在满足收敛条件的情况下,经过每一次迭代,近似解的有效数字将至少加倍,迭代次数的增加会大幅提高精度。
三、牛顿迭代法的优点与局限性1. 优点:1) 收敛速度快:牛顿迭代法的二阶收敛特性决定了它在求解方程时的高效性和快速性。
2) 广泛适用:牛顿迭代法可以用于求解非线性方程、方程组和最优化问题等,具有广泛的应用领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)实验目的
•熟悉Matlab编程;
•学习非线性方程求根的方法及程序设计算法
2)实验题目
1、迭代函数对收敛性的影响
实验题目
用迭代法求方程的根。
方案1:化方程为等价方程
取初值,迭代10次。
方案2:化为等价方程
取初值,迭代10次,观察其计算值,并加以分析。
实验程序:
实验结果:
方案一收敛很快,偏差和偏差的相对误差几乎为零;方案二不收敛
由此可见,迭代序列的敛散性与迭代公式有关,也与相邻两次迭代的偏差和偏差的相对误差有关,他们的值越小,迭代序列的收敛速度越快。
2、初值的选取对迭代法的影响
实验题目
用牛顿法求方程在x=1.5 附近的根。
方案1:使用牛顿法并取,由
得
迭代10次。
方案2:取,使用同样的公式
迭代10次,观察比较并分析原因。
实验程序:
实验结果:
3.收敛性与收敛速度的比较
实验题目
求方程的全部实根,
方案1:用牛顿法求解;
方案2:用简单迭代法;
取相同迭代初值,比较各方法的收敛速度。
实验程序:
1.普通迭代,选用初值0.5
2.牛顿迭代法
实验结果:
实验结果分析与小结
通过本次试验:
1:迭代函数会影响到迭代的收敛性,所以得到方程的近似解,迭代时必须选择收敛的迭代函数。
2只要迭代收敛,迭代初值的选取不会影响迭代的最终结果,不过如果初值越接近准确解,所需迭代次数越少。
