复合材料盒段结构稳定性分析
复合材料的力学性能与结构设计

复合材料的力学性能与结构设计复合材料是由两种或两种以上的材料组合而成的材料,具有优异的力学性能和结构设计潜力。
在本文中,将探讨复合材料的力学性能以及如何进行结构设计。
一、复合材料的力学性能复合材料由于多种材料的组合,具有独特的力学性能。
以下将讨论复合材料在强度、刚度和韧性方面的性能。
1. 强度由于不同材料之间的协同作用,复合材料通常具有很高的强度。
这是由于各个组成材料的优点相互弥补,从而提高整体强度。
例如,纤维增强复合材料中的纤维可以提供很高的强度,而基体材料可以增加韧性。
2. 刚度复合材料具有很高的刚度,这是由于组成材料之间的相互作用。
纤维增强复合材料中的纤维可以提供很高的刚度,而基体材料可以提供弹性和柔韧性。
因此,复合材料在受力时可以保持其形状和结构的稳定性。
3. 韧性复合材料通常具有较高的韧性,这是由于材料的组合结构所致。
纤维增强复合材料中的纤维可以分散和吸收能量,从而提高材料的韧性。
相反,在单一材料中,这种能量分散效应很少出现。
二、复合材料的结构设计复合材料的结构设计是为了实现所需的力学性能和功能。
以下将介绍复合材料结构设计的关键因素。
1. 材料选择合理的材料选择是进行复合材料结构设计的关键因素。
不同材料具有不同的力学性能和化学特性,因此需要根据应用需求选择合适的材料组合。
例如,在需要高强度和刚度的应用中,可以选择纤维增强复合材料。
2. 界面控制复合材料中不同材料之间的界面是其力学性能的重要因素。
界面的控制可以通过界面处理和表面改性来实现。
例如,通过添加粘合剂或增加表面处理剂,可以增强纤维与基体之间的结合,提高界面的力学性能。
3. 结构设计结构设计是为了实现所需的功能和性能。
在复合材料结构设计中,需要考虑材料的排布方式、层压顺序和几何形状等因素。
通过合理设计复合材料的结构,可以充分发挥其力学性能,同时满足应用需求。
三、结论复合材料具有优异的力学性能和结构设计潜力。
通过合理选择材料、控制界面以及进行结构设计,可以充分发挥复合材料的力学性能。
复合材料盒段结构优化设计实用技术研究

偏置 前
图 2两种方案 比对 由于在 H pr s y eMeh软件里只能设置 梁元 的初始偏置 ,因此从 Hy — pr e 软件里导 出. f eM s h b 文件 ,在. f d b 文件里添加 以下 N s a 语 言, d ar tn 让 梁元 的 形 心 位 置 跟 随 变 量 而 变 化 :
科技信息
工 程 技 术
复 合 村 料 量 段 结 构 优 化 设 计 实 用 技 术 研 穷
上 海飞机 设计 研 究 院结 构设 计研 究部 罗腾腾
[ 摘 要 ] 中充分利用复合材料 的可设 计性 , 文 设计 出ห้องสมุดไป่ตู้足结构 刚度 强度以及稳定性 等性 能指标要 求且使 结构重量更轻的飞行 器结 构。本文的重点是将 粱单元结构 的位 置参数引入 优化设计技术 中, 较传统 的元件参数优化技 术更 具工程 实用性 , 大大提 高了优化 工 作 效 率 , 由此 而 产 生 两 个 优 化 方案 ( 别 在 于 粱 元 是 否 偏 置 ) 通 过 两 个优 化 方案 的论 证 , 置 方案 算例 较 好 的数 值 优 化 结果 充 分 并 区 。 偏 证明 了梁元偏置的有效性和 工程设计 的 实用性 , 明 了在优化设计 工作 中对 梁元进行偏 置设计的优越性 和必要 性。论文工作对复 表
变量
… …
式 中 , 表 示 目标 函 数 ;l2 ,n 设 计 变 量 ; 变 量 的 维 数 ; x) x, , x 为 x… n为
&X 和 h X为不等式约束和等式约束 。 () , ) ( 对于 复杂 的复合材料 结构 , 构的优化设计在每个 区域里进行 。 结 可 以根据结构 承受载荷状态 , 材料 , 单元类 型 , 层层数等不 同 , 铺 对结构进 行相应 的优化 区域划分 , 文优化分析采取如下技术 : 本 ( 在划分的区域里进行优化设计 ; 1 ) ( 复合材料采用经 典的铺层角度 O ±4 /0 按 照一定 的铺 层 比例 2 ) / 59 , 对称铺层 , 只优化铺层 厚度 , 不考虑铺 层顺序 ; ( 将梁元结 构的位 置参数引入 优化设计技 术 中, 中梁元 的形心 3 ) 文 位 置跟随层合板 的厚度 变量而变化。
复合材料结构特点

复合材料结构特点
复合材料结构的特点主要包括以下几点:
1.各向异性:复合材料由多种材料组成,其结构在不同方向上呈现出不同的性质
和性能,因此具有各向异性的特点。
2.层合板状结构:复合材料通常采用层合板状结构,各层之间相互垂直,以提高
材料的强度和稳定性。
3.材料成分可调:复合材料的组成材料可以根据需要进行调整,以达到所需的性
能要求。
4.耐疲劳性好:复合材料具有较好的耐疲劳性能,能够在多次循环载荷下保持其
性能。
5.便于加工:复合材料可以方便地进行切割、成型和加工,适用于各种制造和应
用场景。
6.具有可设计性:复合材料的性能可以通过设计和优化其组成和结构来调节,以
满足不同的应用需求。
7.物理非线性和几何非线性:复合材料的结构和性能可能表现出非线性的特点,
如弹性模量、泊松比等参数随应变的变化而变化。
8.结构形状、边界条件和加载状况复杂:复合材料的结构形状、边界条件和加载
状况可能非常复杂,需要仔细设计和分析。
这些特点使得复合材料在许多领域中得到了广泛应用,如航空航天、汽车、建筑、体育器材等。
复合材料多墙盒段的有限元分析
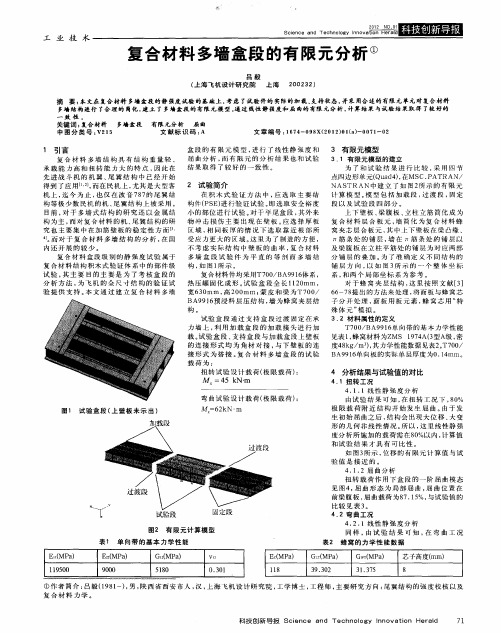
2 试验简 介
在 积 木 式 验 证 方 法 中 , 选 取 主 要 结 应 构 件( S 进 行 验 证 试验 。 P E) 即选 取 安 全 裕 度 小 的 部 位进 行试 验 。 对于 平 尾盒 段 , 外 来 其 物 冲 击 损 伤 主 要 出 现 在 壁 板 。 选 择 厚 板 应 区 域 , 同 板 厚 的 情 况 下 选 取 靠 近 根 部 所 相 受应力更大的区域。 这里 为 了 制造 的 方 便 , 不 考 虑 实 际 结 构 中 壁 板 的 曲 率 , 合 材 料 复 多 墙 盒 段 试 验 件 为 平 直 的 等 剖 面 多 墙 结 构 , 图1 示 。 如 所 复合材 料 件均 采用T7 0 0 /BA9 6 系 , 91 体 热 压 罐 固化 成 形 。 验 盒 段 全 长 1 0 m , 试 1 r 2a 宽6 0 3 mm , 2 0 高 0 mm ; 皮 和 粱 为 T7 0 蒙 0/ B 9 6 浸 料 层 压 结 构 , 为 蜂 窝夹 层 结 A9 1 预 墙
M , 4 k ・ = 5 N m
上 下 壁 板 、 腹 板 、 柱 立 筋 简 化 成 为 梁 立 复 合 材 料 层合 板 元 , 简 化 为 复 合 材料 蜂 墙 窝夹 芯 层合 板 元 , 中 上 下 壁板 在 梁 凸缘 、 其 筋 条 处 的 铺 层 , 在 筋 条 处 的 铺 层 以 墙 及 梁 腹 板 在 立 柱 平 筋 处 的 铺 层 为 对 应 两 部 分 铺 层 的 叠加 。 了 准 确 定 义 不 同 结 构 的 为 铺 层 方 向 , 如 图3所 示 的 一 个 整 体 坐 标 以 系 , 两 个 局 部 坐 标 系 为参 考 。 和 对 于 蜂 窝 夹 层结 构 , 里 按 照文 献 【 】 这 3 6 —7 提 出的 方 法 来处 理 , 面 板 与 蜂窝 芯 6 8 将 子分开处理 , 板用板元 素, 窝芯用 “ 面 蜂 特 殊 体元” 拟 。 模 3 2 材料 属性 的定义 . T7 0 BA9 6 向带 的基 本 力 学 性 能 0/ 9l 单 见表 1 蜂窝材 料 为z 1 7 A(型 A , , MS 9 4 3 级 密 度4 k / )其 力学性 能 数据 见表 2 T7 0 8 g m , 。 0/ B 9 6 向板 的实 际单 层 厚度 为0 1 rm。 A9 1 单 .4 a
基于子模型的大型复合材料飞机结构屈曲稳定性数值分析及优化技术研究

{ms tdtaipasr p ms nac o gbt{ }cg,snneecyv.to udg ol ptiset m hcvg el eIet ioego sw j o bli m ir si e h i e n mi nuc udt i a t s le n m k g Ys i sa e n d n s 0 f r e e i 舭to , 舭w utschlnierm hy l 打uo n b ra e t qe i幻 p c e hi i eh e r 舭 i g l or m z f o e f cp t i r s nade c ny H h r r i t e t o m u t npeio n f i c. e tee o l ii st o o ao ci f e i r m s %, n em dl i l n s eo i adt oe wt e m t i h h e z f e
维普资讯
机 械 设 计 与 制 造
一
第 2期 20 0 7年 2月
4一
Ma hn r De in & Ma ua tr c iev sc n fcu e
文章编号 : 0 — 9 7 2 0 )2 O O — 3 1 139(070一040 0
( e a me t f c a ia E gn eig N n h n ntueo eo a t a T cn lg, a c a g3 0 3 , hn ) D p r n o h ncl n ie r , a c a gIs tt f rn ui l eh ooy N n h n 3 0 4 C ia t Me n i A c
} 【 要】 摘 随着计算机科学和有限元技术的发展, 屈曲稳定性问 题有限元数值求解技术已经比较成熟, } j 但是在大型复杂结构工程应用中 还是由于计算量大、 收敛困难而受到限制, 特别是在需要反复迭代计算的优 j
复合材料结构特点、设计要点以及成型方法

复合材料是一种由两种或两种以上的材料组合而成的材料,具有强度高、重量轻、耐腐蚀等优点。
复合材料在航空航天、汽车制造、建筑工程等领域有着广泛的应用。
本文将重点探讨复合材料的结构特点、设计要点以及成型方法。
一、复合材料的结构特点1.1 高强度:复合材料由于是由不同材料组合而成,可以充分发挥各种材料的优点,因此具有很高的强度。
比如碳纤维复合材料的强度是钢的几倍。
1.2 轻质:由于复合材料多为聚合物基体和增强材料组成,因此具有较低的密度,重量轻,适合用于要求重量轻的场合,比如航空航天领域。
1.3 耐腐蚀性好:复合材料多数是无机非金属材料与有机高分子材料的复合,因此具有良好的耐腐蚀性,可以在恶劣环境下长期使用。
1.4 难以加工:复合材料的工艺性和加工性较差,需要采用特殊的加工技术和工艺流程。
二、复合材料的设计要点2.1 结构设计:在设计复合材料结构时,需要充分考虑材料的性能和特点,合理设计结构,提高材料的使用效率。
2.2 成型工艺设计:不同的复合材料有不同的成型工艺,需要根据具体的材料性能和工艺流程来设计成型工艺,以保证产品质量。
2.3 自动化设计:现代复合材料加工已经向着自动化方向发展,因此设计时需要考虑如何实现自动化生产。
2.4 环境友好设计:在设计复合材料产品时,需要充分考虑材料的回收性和再利用性,采用环保的材料和工艺。
三、复合材料的成型方法3.1 手工层叠成型:手工层叠成型是一种常见的复合材料成型方法,通过人工将增强纤维层叠在一起,再浸渍树脂,最后经过固化得到成品。
3.2 压模成型:在压模成型中,复合材料预先放置于模具中,然后通过压力和温度的作用,使树脂固化,最终得到成品。
3.3 真空吸塑成型:真空吸塑成型是将复合材料覆盖在模具表面,然后利用真空负压使其贴紧模具表面,并通过加热固化得到成品。
3.4 自动化制备:随着自动化技术的发展,复合材料成型也越来越多地采用自动化制备技术,如自动化层叠机、自动化压模机等。
复合材料结构的力学性能分析与优化设计

复合材料结构的力学性能分析与优化设计复合材料在现代工程领域中得到广泛应用,其独特的力学性能使其成为许多领域的首选材料。
为了确保使用复合材料结构的稳定性和安全性,对其力学性能进行准确的分析与优化设计是必不可少的。
复合材料的力学性能分析需要考虑以下几个方面:材料属性、构件设计和力学行为。
首先,复合材料的力学性能是由其材料属性决定的。
复合材料由纤维和基体组成,纤维负责承载载荷,而基体则起到连接纤维的作用。
在分析复合材料的力学性能时,需要了解纤维的类型、方向和体积分数,以及基体的特性。
这些信息可以通过材料测试和实验获得,例如拉伸测试、弯曲测试和压缩测试等。
通过这些测试可以获得复合材料的弹性模量、屈服强度和断裂韧性等力学特性。
其次,构件设计是影响复合材料力学性能的关键因素。
复合材料可以通过不同的构件设计来适应不同的工程要求。
构件的几何形状、层数、层序和连接方式等都会对复合材料的力学性能产生影响。
在进行力学性能分析时,需要根据构件的实际情况建立有限元模型。
有限元分析是一种常用的数值模拟方法,通过将复合材料结构划分为小块进行离散建模,然后通过求解有限元方程得到应力、应变和变形等信息。
通过有限元分析,可以评估不同构件设计对复合材料力学性能的影响,为优化设计提供依据。
最后,力学行为是评价复合材料力学性能的关键。
复合材料的力学行为通常包括线弹性、非线性、破坏和疲劳等。
线弹性是指在小应变范围内,复合材料的应力和应变呈线性关系。
非线性行为包括塑性变形、集中变形和层间剪切等,这些行为会导致驰豫和刚度退化。
破坏行为是复合材料在超出其极限时发生的,通常包括纤维断裂、基体剥离和界面开裂。
疲劳行为是复合材料在长期受到循环载荷作用下发生的。
优化设计是通过改变材料和结构参数来增强复合材料的力学性能。
在复合材料结构的力学性能分析中,通过在有限元模型中改变材料的属性和构件的设计来优化设计。
优化设计的目标可以是最小化构件的重量、最大化构件的刚度、最大化构件的承载能力等。
考虑稳定性的复合材料机翼盒段优化分析

Op i z t n a ay i n b x o omp st n a e n sa i y t mia i n lss o o f o c o i wig b s d o t b l e i t
s utr e h h igw i iya nt nTef r es de o ayi ei une d - t cuaw i tfte n ,hc s s los a thn ut rt i na l n t f ec i r l g o w haf l c r . t i h u s n zg h n l f o f frn ri ge addwl e et os anv u nte pi zdrshso a e osr n o I eetos na l i a m n nt ta e t e u wtt t nt tf托r t o n s n c c r l o h o mi e i h h hc i a _ s nagehs ra i uneo e pi zdw ihp r ie yteds n e e osr n eod i l a e f e nt t e e t emtdb i . nt nt ts yn on gt n c l h o mi g t h e g Wh h c i a ib te ag r n e e , en une d pae etos a t nh t i dw i tse ue. h eic t dg bt fe c i l m n nt n o teo i z e h ird d r n n ea i r hi l f o s c c r i pm e g c
s nd i t i i gri e a m t dfr t l k a ds i l,a d uk n i e t o i z o b r a n t r e r i e o s ei v a es i a cl g g w h p m a n ye d ghp a eo f nb c t f e s n r g a b tn n b i fc ra os an cnio. e pi zn ew i tl ee eti ovosb eui . % o te at cnt it odtn f rot igt e h o f c biu yrdcn 9 6 f h os r i A t mi h g s f s g 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[暲45/暲45]
[暲45/02/暲45/02/90]s [45/03/-45/02/45/03/-45/90/45/
03/-45/02/45/03/-45]
注 :下 标 2 表 示 连 续 铺 2 层 ;90表 示 90曘方 向 只 铺 1 层 。
· 2056 ·
暋暋试验 件 两 端 分 别 与 支 持 盒 段 和 加 载 盒 段 连 接,试 验 件 通 过 支 持 盒 段 过 渡 固 定 在 承 力 墙 上。 通 过 对 加 载 盒 段 的 加 载 ,将 载 荷 传 递 到 试 验 件 上 。 分别对试验件进行扭转载荷和弯曲载荷的稳定性 试 验 。 扭 转 加 载 试 验 中 ,试 验 件 一 侧 固 定 ,另 一 侧 受 扭 矩 载 荷 作 用 ;弯 曲 加 载 试 验 中 ,试 验 件 一 侧 固 定 ,另 一 侧 受 弯 矩 载 荷 作 用 。 整 个 试 验 过 程 中 ,试 验 装 置 缓 慢 、均 匀 地 进 行 加 载 。
鉴于复合材料 盒 段 结 构 组 成 构 件 较 多,各 个 组成部件对其他 部 件 的 网 格 有 影 响,故 先 在 边 界 生成一维单元,再 由 一 维 单 元 拓 展 生 成 二 维 壳 单 元。实际构件之 间 的 胶 接 或 螺 栓 连 接,如 蒙 皮 与 梁 缘 条 之 间 的 连 接 等 ,简 化 为 无 缝 连 接 ,即 将 相 接 触的两板建立成 1 个 有 限 单 元,将 两 板 的 复 合 材 料铺层全部赋给1个有限元单元。金属材料也采 用 这 种 方 法 ,将 金 属 材 料 叠 加 到 复 合 材 料 铺 层 中 , 使连接的多个板成为一个整体。复合材料盒段结 构 的 有 限 元 模 型 如 图 2 所 示 ,模 型 共 有 8332 个 有 限 元 单 元 、8532 个 节 点 。
矩阵,是关于 应 力 水 平 的 矩 阵;KG 为 几 何 非 线 性 刚 度 矩
阵 ,由 结 构 的 大 位 移 引 起 。
1.1暋 线性失稳 线性稳 定 性 理 论 以 小 位 移、小 应 变 的 线 弹 性
理 论 为 基 础 ,不 考 虑 加 载 过 程 中 结 构 位 形 的 变 化 ,
其临界失稳载荷的线性广义特征值方程为
· 2055 ·
中 国 机 械 工 程 第 20 卷 第 17 期 2009 年 9 月 上 半 月
在增量 加 载 过 程 中,第i 个 增 量 步 迭 代 收 敛
后,将线性失稳 特 征 值 的 刚 度 矩 阵 作 为 第i 个 增
量 步 开 始 时 的 切 向 刚 度 矩 阵 。加 载 过 程 包 含 了 第i
误差较大的原因。
关 键 词 :复 合 材 料 ;盒 段 结 构 ;稳 定 性 ;有 限 元
中 图 分 类 号 :V214.4暋 暋 暋 文 章 编 号 :1004—1ห้องสมุดไป่ตู้2X(2009)17—2055—05
StudyonBucklingofCompositeBoxStructure LuBinghe暋WanXiaopeng暋Zhao Meiying
试验件上布置 应 变 测 量 片,随 着 载 荷 的 逐 渐 增大,试验测量装 置 自 动 收 集 试 验 的 载 荷 值 和 应 变值等信息。通过对收集的载荷值和应变值等信 息 的 处 理 ,生 成 载 荷 - 应 变 曲 线 ,用 于 判 断 复 合 材 料盒段结构是否失稳。扭转失稳试验得到的失稳 临 界 扭 矩 为 28灡0kN·m,弯 曲 失 稳 试 验 得 到 的 临 界 失 稳 弯 矩 为 55灡5kN·m。 2.2暋 盒 段 有 限 元 分 析
图 2暋 复 合 材 料 盒 段 结 构 的 模 型
复 合 材 料 盒 段 结 构 稳 定 性 分 析 ——— 卢 秉 贺 暋 万 小 朋 暋 赵 美 英
2.2.2暋 扭 转 稳 定 性 分 析 扭矩的加载方 式:固 定 盒 段 沿 长 度 方 向 一 侧
固定端部节点的 6 个 自 由 度,扭 矩 是 通 过 对 另 一 侧端部节点施加载荷实现的。
1暋 稳 定 性 分 析 的 有 限 元 方 法
结构的稳定性 主 要 取 决 于 刚 度,即 结 构 自 身
的刚度和对它的支持刚度。采用增量形式的总体
Lagrange方法,由虚功原 理 可 得 到 单 元 的 切 线 刚 度矩阵 : [7]
K = KL +K氁 +KG
(1)
式中,KL 为线性 刚 度 矩 阵;K氁 为 初 应 力 矩 阵 或 几 何 刚 度
使用有 限 元 前 后 置 分 析 处 理 程 序 MSC.Pat灢 ran/Nastran对 复 合 材 料 试 验 盒 段 结 构 进 行 稳 定 性 分析。 2.2.1暋 有 限 元 建 模
根 据 复 合 材 料 盒 段 模 型 的 规 模,采 用 二 维 shell单 元 进 行 建 模。 使 用 shell单 元,可 以 利 用 MSC.Patran程序 自 有 的 复 合 材 料 铺 层 工 具,方 便地进行复合材料结构建模。
0暋 引 言
复合材料具有 比 强 度 高、比 刚 度 高 和 可 设 计 性 等 优 点 ,因 此 ,采 用 先 进 复 合 材 料 已 经 成 为 减 轻 飞机结构 重 量 和 满 足 飞 机 新 功 能 要 求 的 重 要 途 径 。 [1] 减轻重量 和 提 高 结 构 效 率 的 双 重 要 求,使 得飞机 广 泛 使 用 薄 壁 结 构[2]。 这 些 由 蒙 皮、梁、 墙、肋和长桁构成 的 空 间 盒 段 结 构 是 飞 机 的 机 翼 和尾翼上常见的结构形式。薄壁结构在承受载荷 作 用 时 ,最 常 见 的 失 效 模 式 是 强 度 破 坏 和 失 稳 (屈 曲 )。 为 了 保 证 飞 机 的 使 用 安 全 ,需 要 进 行 相 应 的 强度校核和稳定性分析 。 [3]
(KL +毸K氁)q = 0
(2)
式中,毸 为载荷比例因子;q 为横向位移向量。
1.2暋 非线性失稳
非线性失稳理论考虑结构受载过程中不断变
化 的 结 构 位 形 ,建 立 的 平 衡 方 程 为
[KL +K氁(氁)+KG(u)+毸(K氁(殼氁)+KG(殼u))]殼q = 殼P (3)
式中,殼q 为结构当前的位移 增 量;殼P 为 结 构 当 前 的 载 荷 增量。
(1)线性 稳 定 性 分 析。线 性 分 析 方 法 可 以 计 算得 到 多 阶 失 稳 模 态,前 3 阶 失 稳 扭 矩 分 别 为 29灡6kN·m、29灡7kN·m、30灡1kN·m。1 阶 和 3 阶失稳模态中,前梁孔边节点 失 稳 特 征 明 显,2 阶 失 稳 模 态 中 ,后 梁 孔 边 节 点 失 稳 特 征 明 显 ,说 明 在 扭转条件作用下,前 后 梁 因 为 开 孔 容 易 发 生 失 稳 现象。图3为 1 阶 失 稳 模 态 示 意 图,1 阶 失 稳 模 态对 应 的 失 稳 扭 矩 即 临 界 失 稳 扭 矩 为 29灡6 kN·m。
随着计算机技 术 的 迅 猛 发 展,有 限 元 方 法 得 到了广泛的应用。稳定性分析的有限元方法主要 有线性分析方法和非线性分析方法。线性分析方 法 是 以 小 位 移 、小 应 变 的 线 弹 性 理 论 为 基 础 的 ;非 线性分 析 方 法[4]考 虑 以 往 加 载 历 史 的 非 线 性 影 响,非线性 弧 长 法 可 用 于 计 算 急 速 通 过 (snapthrough)等后屈曲问题 。 [5飊6]
定性进行了计算,并将计算结果与试验结果进行了对比分析。扭转载荷 下 线 性 和 非 线 性 的 计 算 结 果 都
与 试 验 数 据 接 近 ;弯 曲 载 荷 下 的 非 线 性 计 算 的 结 果 比 较 接 近 试 验 结 果 ,线 性 计 算 的 结 果 与 试 验 结 果 误 差
较大。分析表明非线性方法适合复合材料盒段结构的稳定性计算。最 后,进 一 步 分 析 了 导 致 线 性 计 算
复 合 材 料 盒 段 结 构 稳 定 性 分 析 ——— 卢 秉 贺 暋 万 小 朋 暋 赵 美 英
复合材料盒段结构稳定性分析
卢秉贺暋万小朋暋赵美英
西 北 工 业 大 学 ,西 安 ,710072
摘 要 :分 别 采 用 线 性 和 非 线 性 的 有 限 元 方 法 ,对 复 合 材 料 加 筋 壁 板 盒 段 结 构 的 扭 转 稳 定 性 和 弯 曲 稳
本文分别使用线性分析方法和非线性分析方 法计算复合材料 盒 段 结 构 的 稳 定 性,得 到 失 稳 载 荷 比 例 因 子 、临 界 失 稳 载 荷 、最 大 位 移 值 和 失 稳 位 置,并将其与复合 材 料 盒 段 结 构 的 稳 定 性 试 验 结
收 稿 日 期 :2008—11—05
果进行对比。
个增量步以前所有加载过程中各种非线性因素对
刚度矩阵的影响。屈曲失稳载荷Pcr 为
Pcr = Pi-1 +毸殼Pi-1
(4)
非线性失稳理论体现了初始位移和初始应力
的 影 响 ,考 虑 到 了 位 移 增 量 和 应 力 增 量 的 影 响 。
2暋 复 合 材 料 盒 段 结 构 稳 定 性 分 析
2.1暋 稳 定 性 试 验 复 合 材 料 试 验 盒 段 (图1)长 约1500mm,宽 约
为金属材料外,试 验 件 结 构 其 余 部 件 均 使 用 复 合
