八年级数学竞赛讲座四边形
初中数学竞赛辅导：平行四边形
新课标八年级数学竞赛培训第15讲：平行四边形1.在矩形ABCD中，已知两邻边AD=12, AB=5, P是AD边上异于A和D的任意一点，且PE_LBD, PF±AC, E、F分别是垂足，那么PE+PF= θɔ .则S AAOD=-×OD×AG, SΔAOP+SΔPOD=-×AO×PF+-×DO×PE^L×DO× (PE+PF), 2 2 2 2*∙*SΔAOD=SΔAOP+SΔPOD »∙*∙ PE+PF=AG,・・・等腰三角形底边上的任意一点到两腰距离的和等于腰上的高，PE+PF=AG. VAD=12, AB =5, ΛBD=λ^2^2=B, .∙. A g-12)<5=60, .∙.pg+pjr zz-θθ. ɪ 313 13点评：本题考查矩形的性质、等腰三角形的性质、三角形的面积计算.解决本题的关键是明白等腰三角形底边上的任意一点到两腰距离的和等于腰上的高.2. (2003・宁波)如图，BD是平行四边形ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需要增加的一个条件是BE=DF .(填一个即可)解答：解：使四边形AECF也是平行四边形，则要证四边形的两组对边相等，或两组对边分别平行，如果BE=DF, 则有：∖"AD//BC：.ZDAF= ZBCE, VAD=BC, BE=DF, Λ∆ADF^∆BCE,ΛCE=AF,同理，Z∖ABE丝Z∖CFD, .∙.CF=AE,四边形AECF是平行四边形.故答案为：BE=DF.点评：本题考查了平行四边形的判定，是开放题，答案不唯一，本题利用了平行四边形和性质，通过证△ ADF^ ΔBCE, △ ABE^ ACFD,得到CE=AF, CF=AE利用两组对边分别相等来判定平行四边形.3.如图，已知矩形ABCD中，对角线AC、BD相交于O, AE_LBD于E,若AB=6, AD=8, 解答：解：矩形各内角为直角，；.AABD为直角三角形，在直角AABD中，AB=6, AD=8则AE= 4.8 .则BD=V AB2+AD2=10, MABD 的面积S」AB・AD」BD・AE, AE=AB的=4.8.BD点评：本题考查了勾股定理在直角三角形中的运用，考查了三角形面积的计算，本题中根据勾股定理求BD的值是解题的关键.4.如图，以AABC的三边为边在BC的同一侧分别作三个等边三角形，即^ABD∖∆BCEΛ∆ACF. (1)四边形ADEF是平行四边形；(2)当Z∖ABC满足条件AB=AC 时,四边形ADEF为菱形；(3)当ZiABC满足条件AB=AC=BC 时,四边形ADEF不存在. 解答：解(1)四边形ADEF是个平行四边形在AABC和ADBE中，VBC=BE, BA=BD, ZDBE=ZABC (与/ABE 之和都等于60。
初中数学竞赛专题-第九章完全四边形的性质及应用1
第九章完全四边形的性质及应用【基础知识】我们把两两相交又没有三线共点的四条直线及它们的六个交点所构成的图形,叫做完全四边形．六个点可分成三对相对的顶点,它们的连线是三条对角线．如图91-,直线ABC 、BDE 、CDF 、AFE 两两相交于A 、B 、C 、D 、E 、F 六点,即为完全四边形ABCDEF ．线段AD 、BF 、CE 为其三条对角线．完全四边形中既有凸四边形、凹四边形,还有折四边形以及四个三角形．如图91-中有凸四形ABDF ,凹四边形ACDE ,折四边形BCFE ,四个三角形ACF △、BCD △、DEF △、ABE △．在完全四边形ABCDEF 中,对四个三角可以写出梅涅劳斯定理的4个式子（见图11-后说明）；若直线AD 交BF 于H ,交CE 于G ,则可以写出塞瓦定理的7个式子（见图23-）；利用空全四边形及其对角线的相交可以讨论梅涅劳斯定理与塞瓦定理的互推（图22-）；完全四边形的四个三角形的外接圆共点（即完全四边形的密克尔点及西姆松线（见图67-））等．这是我们已介绍的完全四边形的性质,完全四边形还有一系列有趣的性质,下面我们介绍其中的几条： 性质1设M 为完全四边形ABCDEF 的密克尔点．（1）若B 、C 、E 、F 四点共圆于O ,则M 点在对角线AD 所在直线上,且OM AD ⊥； （2）若A 、B 、D 、F 四点共圆于O ,则M 点在对角线CE 上,且OM CE ⊥． 注此性质还可参见例10（9）,例11（3）、（5）．O B KC(a)MD FEOBMC F 图9-2(b)D证明（1）如图92- （a ）．设过B 、C 、D 三点的圆交直线于点M ',则AD AM AB AC AE AF '⋅=⋅=⋅,即知点M '在DEF △的外接圆上,亦即知点M '就是完全四边形ABCDEF 的密克尔点M ．设K 为AM 延长线上一点,由2CME CMK KME CBE CFE CFE COE ∠=∠+∠=∠+∠=∠=∠,知C 、E 、O 、M 四点共圆．于是1902OMK OME EMK OCE COE ∠=∠+∠=∠+∠=︒,即证．（2）如图92- （b ）．同（1）可证过B 、C 、D 三点的圆与CE 的交点即为完全四边形ABCDEF 的密克尔点M ．由圆幂定理（即点对O 的幂）有 222CO CD CF R CM CE R =⋅+=⋅+,222ED ED ED R EM EC R =⋅+=⋅+（其中R 为O 半径）．上述两式相减,有()2222CO EO CE CM ME CM ME -=-=-．由定差幂线定理,知OM CE ⊥．推论1在完全四边形ABCDEF 中,凸四边形ABDF 内接于O ,AD 与BF 交于点G ,则CDB 、CFA 、EFD 、EAB 、OAD 、OBF 六圆共点；CFB 、CDA 、GAB 、GDF 、OBD 、 OFA 六圆共点；EFB 、EAD 、GBD 、GFA 、OAB 、ODF 六圆共点．事实上,可设M 为完全四边形ABCDEF 的密克尔点,则由性质1（2）,知M 在CE 上,且OM CE ⊥．于是,知C 、M 、D 、B 及M 、E 、F 、D 分别四点共圆,有9090BMO BMC BDC ∠=︒-∠=︒-∠()9018090BDF BDF =︒-︒-∠=∠-︒=11(180)909022BOF BOF BFO ︒-∠-︒=︒-∠=∠．从而知,点M 在OBF 上．同理,知点M 在OAD 上．由密克尔点的性质知,CDB 、CFA 、EFD 、EAB 四圆共点于M ．故以上六圆共点M ．同理,设N 为完全四边形CDFGAB 的密克尔点,则CFB 、CDA 、GAB 、GDF 、OBD ,OFA 六圆共点于N ．设L 为完全四边形EFAGBD 的密克尔点,则EFB 、EAD 、GBD 、GFA 、OAB 、ODF 六圆共点于L ．图9-3l 6l 5l 4l 1BDCGMFE N L推论2如图93-,在完全四边形ABCDEF 中,凸四边形ABDF 内接于O ,AD 与BF 交于点G ．CDB 与CFA 、CDA 与CFB 、OBD 与OFA 、ODA 与OBF 、EAB 与EFD 、EAD 与EFB 、OAB 与ODF 、GAB 与GDF 、GBD 与GFA 共九对圆的连心线分别记为1l ,2l ,3l ,⋯,9l ,则1l 、2l 、3l 、4l 、OC 五线共点于OC 的中点；4l 、5l 、6l 、7l 、OE 五线共点于OE 的中点；3l 、7l 、 8l 、9l 、OG 五线共点于OG 的中点．事实上,可设M 、L 、N 分别为完全四边形ABCDEF 、EFAGBD 、CDFGAB 的密克尔点,则OM CE ⊥于M ,OL EG ⊥于L ,ON CG ⊥于N ．注意到OM 是ODA 与OBF 的公共弦,则4l 是OM 的中垂线,从而知4l 过OC 的中点,4l 也过OE 的中点．因CN 是CDA 与CFB 的公共弦,则2l 是CN 的中垂线,而ON CN ⊥,从而2l 过OC 的中点；又注意到CM 是CDB 与CFA 的公共弦,则1l 是CM 的中垂线,又OM CM ⊥,则1l 过OC 的中点,ON 是OBD与OFA 的公共弦,则3l 是ON 的中垂线．而ON CN ⊥,3l 过OC 的中点．故1l 、2l ,3l 、4l 、OC 五线共点于OC 的中点．同理,注意到LE 、ME 、OL 分别是EAD 与EFB ．EFD 与EAB 、OAB 与ODF 的公共弦,推知4l 、5l 、6l 、7l 、OE 五线共点于OE 的中点．注意到GN 、LG 、OL 、ON 分别是GAB 与GDF 、GBD 与GFA 、OAB 与ODF 、OBD 与OFA 的公共弦,推知,3l 、7l 、8l 、9l 、OG 五线共点于OG 的中点．注 由上述推论,即知下列竞赛题即为其特殊情形： （1）（1990年全国高中联赛题）四边形ABCD 内接于圆,对角线AC 与BD 交于点P ,PAB △、PBC △、PCD △、PDA △的外心分别为1O 、2O 、3O 、4O ．求证：13O O 、24O O 与OP 三线共点．（2）（2006年国家集训队测试题）四边形ABCD 内接于O ,且圆心O 不在四边形的边上,对角线AC 与BD 交于点P ,OAB △、DBC △、OCD △、ODA △的外心分别为1O 、2O 、3O 、4O ．求证：13O O 、24O O 与OP 三线共点．性质2完全四边形ABCDEF 的三条对角线AD 、BF 、CE 的中点M 、N 、P 共线（即牛顿线）．图9-4证明如图94-,分别取CD 、BD 、BC 的中点Q 、R 、S ,于是,在ACD △中,M 、R 、Q 三点共线；在BCF △中,S 、R 、N 三点共线；在BCE △中,S 、Q 、P 三点共线．由平行线性质,有MQ AC MR AB =,HR FD NS FC =,PS EBPQ ED =． 对BCD △及截线AFE 应用梅涅劳斯定理,有1CA BE DEAB ED EC⋅⋅=,即有1QM RN SP MR NS PQ ⋅⋅=． 再对QRS △应用梅涅劳斯定理的逆定理,知M 、N 、P 三点共线．注此性质中的线称为牛顿线,其证明还有10多种．性质3完全四边形的一条对角线被其他两条对角线调和分割（两点内分与外分同一线段成同一比值,称这两点调和分割这一线段）． 证明如图95- （a ）、（b ）,在完全四边形ABCDEF 中,对角线AD 所在直线交BF 于M ,交CE 于N ,需证AM MDAN ND=（此式表明点M 、N 调和分割AD ）． NPBDCFAEBDCFANE (b)(a)图9-5MM若BF CE ∥,如图95- （a ）,则由AM BF MDAN CE ND==,即证． 若BF CE ≠,可设直线BF 与CE 交于点P ． 对ADF △及点B 应用塞瓦定理,有1AM DC FEMD CF EA⋅⋅=． 对ADF △及截线CNE 应用梅涅劳斯定理,有1AN DC FEND CF EA⋅⋅=． 上述两式相除,即得AM MDAN ND=． 对于图95- （b ）,类似地可证明有BM MF BP NF =（M 、P 调和分割BF ）,CN NECP PE=（N 、P 调和分割CE ）；对于图95- （a ）,也可看作直线BF 、CE 相交于无穷远点,也有这两式．性质4完全四边形的三条对角线为直径的圆共轴,且完全四边形的四个三角形的垂心在这条轴上．C图9-6证明如图96-,在完全四边形ABCDEF 中,分别以对角线AD 、BF 、CE 为直径作圆,这三个圆 的圆心就是三条对角线的中点M 、N 、P ．设1H 、2H 、3H 、4H 分别为DEF △、ACF △、ABE △、BCD △的垂心,注意到三角形垂心的性质：三角形的垂心是所有过任一条高的两个端点的圆的根心（见根轴的性质3及垂心的性质4）． 在完全四边形ABCDEF 中,显然1H 、2H 、3H 、4H 不重合,由于DEF △的垂心1H 是三个圆两 两根轴的根心,而对于DEF △,在它的边所在直线上的高C 、B 、A ,点1H 关于以CE 、BF 、AD 为直径的圆的幂相等,即点1H 在这三个圆两两的根轴上．同样,对于ACF △,在它的边所在直线上的点B 、D 、E ,其垂心2H 关于以CE 、BF 、AD 为直径的圆的幂相等,以及点3H 、4H 均关于以CE 、BF 、AD 为直径的圆的幂相等．故1H 、2H 、3H 、4H 均在这三个圆的两两的根轴上,即这三个圆两两的根轴重合,亦即共轴,且四个三角形的垂心在这条根轴上．注 证明1H 、2H 、3H 、4H 四点共线,也可以这样证：由于完全四边形ABCDEF 的四个DEF △、ACF △、ABE △、BCD △的外接圆交于一点M ,且点M 关于这四个三角形的西姆松线为同一条直线l ,根据西姆松线的性质：点P 的西姆松线平分点P 与三角形垂心的连线（西姆松定理及应用中例5）,则知l 过1MH 、2MH 、3MH 、4MH 的中点,从而点1H 、2H 、3H 、4H 共线．推论3完全四边形的垂足线与牛顿线垂直（两圆连心线垂直于公共弦）．性质5完全四边形的四个三角形的外接圆圆心共圆,这四个圆心每三个构成的三角形的垂心分别在构成完全四边形的四条直线上,且这四个垂心为顶点构成的四边形与四个圆心为顶点构成的四边形全等． 上述性质即指在完全四边形ABCDEF 中,1O 、2O 、3O 、4O 分别为ACF △、BCD △、DEF △、ABE △的外心,1H 、2H 、3H 、4H 分别为423O O O △、413O O O △、241O O O △、123O O O △的垂心,则 （1）1O 、2O 、3O 、4O 四点共圆（斯坦纳圆）；（2）423O O O ACF △∽△,123O O O ABE △∽△,241O O O DEF △∽△,413O O O BCD △∽△；（3）1H 、2H 、3H 、4H 分别在BE 、AE 、AC 、CF 上,且四边形1234H H H H ≌四边形2143O O O O ． 证明设M 为完全四边形ABCDEF 的密克尔点,连接BM 、2CO 、2O M 、3MO 、DM ,则（l ）12211801802O O M CO M CDM ∠=︒-∠=︒-∠．同理,13180O O M FDM ∠=︒-∠．从而()1213360180O O M O O M CDM FDM ∠+∠=︒-∠+∠=︒．因此,1O 、2O 、3O 、M 四点共圆．同理,3O 、4O 、2O 、M 四点共圆．故1O 、2O 、3O 、4O 四点共圆．图9-7(a)（2）由BM 为2O 与4O 的公共弦,则知24O O BM ⊥．同理23O O DM ⊥． 于是423O O O BMD BCD ACF ∠=∠=∠=∠．同理,24323180O O O O MO BAF CAF ∠=︒-∠=∠=∠,故423O O O ACF △∽△． 同理,123O O O ABE △△∽． 于是241O O O BEA DEF ∠=∠=∠．又214213314213324O O O O O O O O O O O O O O O ∠=∠+∠=∠+∠ CAF ACF DFE =∠+∠=∠．从而241O O O DEF △∽△． 同理,413O O O BCD △∽△．（3）自2O 作34O O 的垂线交BE 于1H '点,连4BO 、2BO 、41O H ',由4O 为ABE △的外心,有1490H BO BAE '=︒-∠及1242439090H O O O O O BAE '∠=︒-∠=︒-∠,知14124H BO H O O ''∠=∠,从而1H '、2O 、B 、4O 四点共圆,于是14212H O O H BO ''∠=∠．又2O 为BCD △的外心,知12290H BO O BE BCD '∠=∠=︒-∠． 于是1424239090H O O BCD O O O '∠=︒-∠=︒-∠,即14242390H O O O O O '∠+∠=︒．这表明41O H '也垂直于23O O ,即知1H '为423O O O △的垂心,故1H '与1H 重合．过3O 过14O O 的垂线交AE 于2H ',连4O E 、3O E 、42O H ',则4290O EF ABE '∠=︒-∠,()4321431439018090=18090=90O O H OO O OO O CBD ABE ABE '∠=︒-︒-∠=∠-︒=∠-90︒︒-∠-︒︒-∠,从而2H '、4O 、3O 、E 四点共圆,则有42343O H O O EO '∠=∠．又132134432429090OO H OO O O O H BDC O EH BDC ABE ACF '''∠=∠+∠=∠+∠=∠+︒-∠=︒-∠, ()()42343334290O H O O FO DEO DEO DEF DEF O EH ''∠=∠=∠+∠=∠-︒+∠-∠()()9090180180DEF DEF ABE ABE EDF ACF =∠-︒+∠-︒-∠=∠+︒-∠-︒=∠,即13242390OO H O H O ''∠+∠=︒,这说明2H '为134O O O △的垂心,故2H '与2H 重合． 过点2O 作14O O 的垂线交AC 与点3H ',连1CO 、2CO 、31H O ',则()32121432132118018090H O O O OO H O O DEF H O O AFC '''∠+︒-∠=∠+︒-∠=∠+∠=︒,3190H CO AFC '∠=︒-∠．于是32131H O O H CO ''∠=∠,即知3H '、C 、2O 、1O 四点共圆,有23121O H O O CO '∠=∠．又3243211243112490H O O H O O OO O H CO OO O AFC FDE '''∠=∠+∠=∠+∠=︒-∠-∠ ()9090FDE FED FDE FED=︒-∠++∠=︒-∠,()231121290O H O OCO ACF ACO FCO ACF AFC '∠=∠=∠-∠+∠=∠-︒-∠()90180180CBD CAF CBD CAF FED CAF FED +∠-︒=︒-∠+∠-︒=∠+∠-∠=∠．即32423190H O O O H O ''∠+∠=︒,由此知3H '为124O O O △的垂心,故3H '与3H 重合．OMH 1H 2H 3H 4O 4O 1O 3O 2图9-8过点3O 作12O O 的垂线交CF 于点4H ',连1O F 、14O H '、3O F ,由1O 为ACF △的外心,有490H FQ FAC '∠=︒-∠及4312139090H O O O OO FAC '∠=︒-∠=︒-∠,知41431H FO H O O ''∠=∠,从而4H '、3O 、F 、1O 四点共圆,于是41343H O O H FO ''∠=∠．又3O 为DEF △的外心,知43390H FO DFO FED '∠=∠=︒-∠ 于是4131329090H OO FED OO O '∠=︒-∠=︒-∠,即41313290H O O O O O '∠+∠=︒．这表明14O H '也垂直于23O O ,即知4H '为123O O O △的垂心,故4H '与4H 重合． 综上可知,1H 、2H 、3H 、4H 分别在BE 、AE 、AC 、CF 上． 下面,我们证明四边形1234H H H H ≌四边形2143O O O O ．由于1O 、2O ．3O ．4O 共圆,设该圆圆心为O ,设M 为23O O 的中点．由垂心的性质（即Servois 定理）：三角形任一顶点至该三角形垂心的距离,等于外心至其对边的距离的两倍．于是412O H OM =且41O H OM ∥,142O H OM =且14O H OM ∥,故1441O H O H ∥,即1414O H H O 为平行四边形,从而有4114H H O O ∥．同理1221H H O O ∥,2332H H O O ∥,3443H H O O ∥． 从而四边形12342143H H H H O O O O ≌．推论4在完全四边形ABCDEF 中,A 、B 、D 、F 四点共圆于O ,1O 、2O ．3O ．4O 分别为BCD △、DEF △、ABE △、ACF △的外心,1H 、2H 、3H 、4H 分别为234O O O △、134O O O △、124O O O △、123O O O △的垂心,M 为完全四边形ABCDEF 的密克尔点,1K ,2K ,3K ,4K ,5K ,6K 分别34AO O △、13BO O △、14CO O △、12DO O △、23EO O △、24FO O △的外心,24O O 与13O O 所在直线交于点1P ,直线21O O 与43O O 交于点2P ,1J 、2J 分别为14O O 、23O O 的中点,直线12I H 与34H H 交于点1Q ,直线13H H 与24H H 交于点2Q ,直线12O O 与34H H 交于点L ,直线43O O 与12H H 交于点N ,124O O O △的外心为X ,123H H H △的外心为Y ,X 与Y 交于点S 、T 则（1）O 在X ,且12ACE OO O △∽△；（2）14231423O O O O OM ST H H H H ∥∥∥∥∥； （3）14231423H O H O O H O H XY CE ∥∥∥∥∥；（4）1243OO O MO O △△≌；（5）点1J 、2J 、1P 、2P 、1Q 、2Q 在直线XY 上,N 、L 在直线ST 上；（6）点1K 、2K 、4K 、6K 在直线ST 上,3K 、5K 在直线XY 上且它们关于直线XY 对称； （7）1J 、2J 分别OMC △、OME △的外心； （8）1P 、2P 分别BOF △、AOD △的外心．证明如图99-,（1）联结1OO 、2OO 、1O M 、2O M 、AD 、MD 、DO 、OB 、OF 、1O D 、2O D ,则()1111180902O MD O DM DO M DCM ∠=∠=︒-∠=︒-∠． P 2K 5L J 2J 1Q 2Q 1P 1XY K K 1K 2K 3K 4N H 1H 2H 3H 4S OO 4O 1O 3O 2B D M F AT图9-9同理,290O MD DEM ∠=︒-∠．从而()12180180180O MO DCM DEM BDC BAF ∠=︒-∠+∠=︒-∠=︒-∠．① 又1O 为BDC △的外心,知1OO 为BD 的中垂线,于是,112O OD BOD BAD ∠=∠=∠,212O OD FOD FAD ∠=∠=∠,则1212O OO O OD O OD BAD FAD BAF ∠=∠+∠=∠+∠=∠．② 由①、②知,点O 在X 上,注意到12121OO O OO D O O D BCD MCD BCE ∠=∠+∠=∠+∠=∠．③ 由②、③知,12OO O ACE △∽△．（2）注意到14O O 是公共弦CM 的中垂线,23O O 是EK 的中垂线,以及OM CE ⊥,则知1423O O O O OM ∥∥．设此三线段的中垂线为l ,则知点X 在l 上．由性质5（3）知,1414H H O O ∥,2323H H O O ∥,故1423H H H H OM ∥∥．又注意到四边形1414H H O O 为平行四边形,则由1H 为234O O O △的垂心,知四边形1414H H O O 为矩形,即知14H H 与14O O 的中垂线共线,即知点Y 也在直线l 上,亦即知l 为ST 的中垂线,故为ST OM ∥．（3）由性知5（3）知,X 与Y 为等圆,知ST 垂直平分XY ,且41XO YH =,即知四边形14XYH O 为等腰梯形,亦知ST 为14H O 的中垂线,同理ST 为23O H 的中垂线．于是14231423H O H O O H O H XY CE ∥∥∥∥∥,且其前五条线段的中垂线为ST ．（4）由上即知1243OO O MO O △≌．（5）由（2）、（3）即知,1J ．2J 、1P 、2P 、1Q 、2Q 均在直线XY 上,N 、L 在直线ST 上．（6）由性质5（3）知,12H H 在1K 上,即知1K 在14H O 的中垂线ST 上,同理,2K 、4K 、6K 亦在ST 所在的直线上．又3K 在14O O 的中垂线上,则3K 在XY 所在的直线上． 同理,5K 也在直线XY 上．注意到1K X 垂直平分34O O ,4K Y 垂直平分34H H ,则有14K X K Y ∥． 同理41K X K Y ∥由此知1K 与4K 关于XY 对称． 同理5K 与3K 、2K 与6K 也关于XY 对称．（7）注意到四边形14O O OM 为等腰梯形,1J 为14O O 的中点,14O O 为CM 的中垂线,则111OJ J M J C ==,即1J ,为OMC △的外心,由此知1J 在OC 上,且1J 为OC 的中点．同理,2J 在OE 上,且2J 为OE 的中点．（8）注意到1802180BMF BAF BOF ∠=︒-∠=︒-∠,知M 在OBF △的外接圆上,又1O 、3O 分别是四边形BCMD 、ABM E 的外接圆圆心,知13O O 为公共弦BM 的中垂线,同理,42O O 为FM 的中垂线．于是13O O 与42O O 的交点1P 为BOF △的外心． 同理,43O O 与12O O 的交点2P 为AOD △的外心 注以上推论由山东济南刘世军给出．性质6在完全四边形ABCDEF 中,点G 是对角线AD 所在直线上异于点A 的任意一点,则cot cot cot cot AGC AGF AGB AGE ∠+∠=∠+∠证明如图910-,点G 可以在对角线AD 上或其延长线上,连CE 与直线AD 相交于点K ．在ACE △及点D 应用塞瓦定理,有1AB CK EF BC KE FA⋅⋅=．① AED KBCGAFE D KBCGBDCFAK GE图9-10(c)(b)(a)注意到sin sin GAB GBC S AB AG AGBBC S CG BGC⋅∠==⋅∠△△, sin sin GCK GKE S CK CG AGCKE S EG AGE ⋅∠==⋅∠△△, sin sin GEF GFA S EF EG EGAFA S AG AGF⋅∠==⋅∠△△ 将上述三式代入①式,得sin sin sin sin sin sin BGC EGFAGC AGB AEG AGF∠∠=∠⋅∠∠⋅∠．② 而()sin sin ?sin cos cos sin BGC AGC AGB AGC AGB AGC AGB ∠=∠-∠=∠⋅∠-∠⋅∠, ()sin sin cos EGF AGE AGF ∠=∠-∠=sin cos cos sin AGE AGF AGE AGF ∠⋅∠-∠⋅∠．将上述两式代入②式,得cot cot cot cot AGB AGC AGF AGE ∠-∠=∠-∠．故cot cot cot cot AGC AGF AGB AGE ∠+∠=∠+∠．性质7在完全四边形ABCDEF 中,过B 、F 作与对角线AD 平行的直线分别交对角线CE 于G 、H ,连结BH 、FG 相交于点P ,则点P 在直线AD 上．GQHBDCFAPE图9-11证明延长AD 交CE 于点Q ．对ACE △及点D 应用塞瓦定理,有1CQ EF ABQE FA BC⋅⋅=．()* 由BG AD FH ∥∥,有AB GQ BC CG =,AQCQ CG BG=⋅,FH EF EA AQ =⋅． 将上述三式代入()*式得1GQ EA EHQE AF BG⋅⋅= 又由BG FH ∥,有FH FPBG PG=．于是上式变为1GQ EA EP QE AF PG ⋅⋅=． 对EFG △应用梅涅劳斯定理的逆定理,知A 、P 、Q 共线,故点P 在直线AD 上．性质8在完全四边形ABCDEF 中,四边形ABDF 有内切圆的充分必要条件是下述三条件之一：（1）BC BE FC FE +=+；（2）AC DE AE CD +=+: （3）AB DF BD AF +=+．证明（1）充分性：如图912-,在CF 上截取CG CB =,在EA 上截取EH EB =,连BG 、GH 、BH ,则FH EH EF EB EF =-==．又BC BE FC FE +=+,则BE FE FC BC -=-． 故FH FC BC FC CG GF =-=-=．分别作BCG ∠、BEH ∠、GFH ∠的平分线．由CB CG =、EB EH =、FG FH =,知上述三个角的平分线所在直线是BGH △三边的垂直平分线,从而这三个角平分线交于一点．设该点为I ,由角平分线的性质,知I 到CB 与CF 、到EB 与EF ,到FC 与EA 的距离均相等,即I 到四边形ABDF 四边的距离相等,所以,四边形ABDF 有内切圆．必要性：设内切圆分别交AB 、BD 、DF 、FA 于点P 、Q 、R 、S ,则CP CR =、BP BQ =, EQ ES =,RF FS =．于是()()BC BE CP BP BQ QE +=-++=CP QE CR ES CR +=+=+()()RF FS ES CR RF ES FS FC FE -+=++-=+．（2）充分性：在AC 上截取CM CD =,在AE 上截取EN ED =,则AM AC CM AC CD AE D E =-=-=- （已知条件）AE EN AN =-=,则DCM ∠、DEN ∠、MAN ∠的平分线就是MDN △的三边的中垂线,由此即知四边形ABDF 有内切圆． 必要性：同（1）可证（略）． （3）由切线长定理即证．性质9在完全四边形ABCDEF 中,四边形ABDF （在BAF ∠内）有旁切圆（或折四边形BCFE 有下切圆）的充分必要条件是下述三条件之一：图9-13A（1）AB BD AF FD +=+；（2）AC CD AE ED +=+；（3）BC CF BE EF +=+．证明（1）充分性：在射线AB 上取点K ,使BK BD =,在射线AF 上取点L ,使得FL FD =,连DK 、DL 、KL ．由AB BK AB BD AF FD AF FL AL +=+=+=+=,知BDK △、FDL △、DLK △均为等腰三角形,设点A I 为DKL △的外心,易知A I B 、A I F 、A I A 分别为DKL △的三边DK 、DL 、KL 的中垂线,即它们分别是DBC ∠、DFE ∠、EAC ∠的平分线,则点A I 到四边形ABDF 各边的距离相等,即知四边形ABDF （在BAF ∠内）有旁切圆,圆心即为A I ．必要性：（略）．（2）必要性：设旁切圆与四边形分别相切于点M 、P 、Q 、N ,则AM AN =、CP CM =、EQ EN =、DP DQ =,从而AC CD AC CP PD AM PD AN DQ AE EN +=++=+=+=++ DQ AE EQ QD AE ED =++=+．充分性：（略）．（3）类似（2）而证．【典型例题与基本方法】例1在凸四边形ABCD 中,对角线AC 平分BAD ∠,E 是CD 边上一点,BE 交AC 于G ,DG 交BC 于F ．求证FAC EAC ∠=∠．（1999年全国高中联赛题）证明如图914-,在完全四边形CFBGDE 中,点A 为对角线CG 所在直线上一点,由题设知BAC CAD ∠=∠．由性质6,即知FAC EAC ∠=∠．例2已知圆1S 与圆2S 交于P 、Q 两点,1A 、1B 为圆1S 上不同于P 、Q 的两个点,直线1A P 、1B P 分别交圆2S 于2A 、2B ,直线11A B 和22A B 交于点C ．证明：当点1A 和1B 变化时,12A A C △的外心总在一个定圆上．（IMO 43-预选题,2003年国家队集训测试题）B S 2S 1QO 1O 2PA 2B 1CA 1O 图9-15证明如图915-,当点1A 和1B 变化时,点C 、1B 、1A 、P 、2B 、2A 组成完全四边形的六个顶点．由性质5知点Q 恰为全四边形的密克尔点,由此即知12A A C △的外心O 在完全四边形四个三角形的外接圆圆心所在的圆（即斯坦纳圆）上,例3如图916-,四边形ABCD 的两条对角线交于点O ,两组对边的延长线分别相交于E 、F ,过O 作EF 的平行线交BC 、AD 于I 、J ．求证：OI OJ =．（《数学教学》2006年第10期问题681号）IOB DMCFANGEJ 图9-16证明延长AC 交EF 于点G ,在完全四边形ABECFD 中,由性质3,有AO OCAG GC=． 又IJ EF ∥,则OI OC AO OJAG GC AG GF===． 故OI OJ =．注类似地,在完全四边形ABECFD 中,直线IJ 交AE 于M ,交直线ED 于N ,则有ON OC AO OMEG GC AG EG ===,故OM ON =． 由此,我们可推证得：过完全四边形对角线的交点作另一条对角线的平行线,所作直线与平行对角线的同一端点所在边（或延长线）相交,所得线段被对角线交点平分． 【解题思维策略分析】1．灵活应用完全四边形的优美性质解题例4以ABC △的边BC 为直径作半圆,与AB 、AC 分别交于点D 、E ．过D 、E 作BC 的垂线,垂足分别是F 、G ．线段DE 、EF 交于点M ．求证：AM BC ⊥．（1996年第37届IMO 中国国家队选拔赛试题）A 图9-17证明如图917-,连结BE 与CD ,设它们相交于点O ,因BE AC ⊥,CD AB ⊥, 则O 为ABC △的垂心,于是AO BC ⊥．又DF BC ⊥,EG BC ⊥,则DF AO EG ∥∥． 由性质7,得点M 在AO 上,于是AM BC ⊥．例5如图918-,在ABC △中,90BAC ∠=︒,G 为AB 上给定的一点(G 不是线段AB 的中点),设D 为直线CG 上与C 、G 都不相同的任意一点,并且直线AD 、BC 交于E ,直线BD 、AC 交于F ,直线EF 、AB 交于H ．试证明交点H 与D 在直线CG 上的位置无关．（1990年苏州市高中竞赛题）GP N BDMCFAHE图9-18证明作BM CG AN ∥∥,点M 、N 均在直线EF 上．连结AM 、BN ．对CEF △,由性质7,知AM 与BN的交点P 在CG 上．则HB BM PB GBHA AN PN GA===． 这说明点H 由G 唯一确定．即点H 与D 在直线CG 上的位置无关． 注 例5中条件90BAC ∠=︒是多余的．例6如图919-,任意五角星形12345A A A A A 12345C C C C C 的五个小三角形的外接圆分别交于星形外的五个点1B 、2B 、3B 、4B 、5B ．求证：1B 、2B 、3B 、4B 、5B 五点共圆．DA 5A 1A 2A 3A 4B 5B 1B 2B 3B 4C 5C 1C 2C 3C 4图9-19证明由于五角星可看做是由五个完全四边形所组成,由密克尔性质知每一个完全四边形有一个密克尔点,此题即证五个密克尔点1B 、2B 、3B 、4B 、5B 共圆． 设22B A 的延长线与14C B 的延长线交于点D ,令141B B D ∠=∠,1432B C A ∠=∠,1253B B A ∠=∠,4D ∠=∠,2335B B A ∠=∠,3346A B B ∠=∠,523 7A A A ∠=∠,314 8A C B ∠=∠．注意到对完全四边形124135C A C AC A 及完全四边形452413C A C A C A 分别应用密克尔点性质知514A C C △的外接圆要过1B 及4B ,因此1B 、4B 、1C 、4C 四点共圆．又2A 、2B 、4C 、1B 共圆,则123∠=∠=∠,从而1B 、2B 、4B 、D 共圆．再由2A 、2B 、3A 、3B 共圆,知57∠=∠．又由3A 、3B 、1C 、4B 共圆,知68∠=∠．因此3456478180D B ∠+∠=∠+∠+∠=∠+∠+∠=︒,故2B 、3B 、4B 、D 共圆,即1B 、2B 、3B 、4B 、D 五点共圆．同样可证2B 、3B 、4B 、5B 共圆,故五个密克尔点共圆．例7如图920-,设H 是锐角ABC △的高线CP 上的任一点,直线AH 、BH 分别交BC 、AC 于点M 、N ,MN 与CP 交点O ,过O 的直线交CM 于D ,交NH 于点E ．求证：EPC DPC ∠=∠．(2003年保加利亚奥林匹克试题)EHG O BD CLAM NPQ 图9-20证明如图917-,连结PM 、PN ,则由完全四边形的性质5,知MPC NPC ∠=,并令其大小为ϕ,再令EPC x ∠=,DPC y ∠=．欲证x y =,只须证明cot cot cos sin sin cos sin cos sin sin sin cos x y x y x y x y x y ϕϕ=⇔=⇔=⇔ ()()sin sin sin cos sin cos sin sin sin sin cos cos sin sin sin sin x y x y x y x y x y xyϕϕϕϕϕϕ---=-⇔=．由()sin sin NEP EHP NP x S NE EH S PH x ϕ+==△△, 有()sin sin x NE PHxEH NPϕ-=⋅． 同理()sin sin y DM CPyCD PMϕ-=⋅． 注意到PM MO PN NO =,只须证1NE CD PH MOEH DM CP NO⋅⋅⋅=．设MOD δ∠=,EOP ϕ∠=,又因sin sin NEO EHO S NE HO EH S OH δϕ==△,sin sin CDO DMO S CD CO DM S OM ϕδ==△△． 于是,又只须证1OC PHOH PC⋅=, 即OC PCOH PH=． 而此式,由完全四边形CNAHBM 应用其对角线调和分割性质即证,故EPC DPC ∠=∠． 2．发掘有约束条件的完全四边形问题制作竞赛题的背景 例8如图921-,在完全四边形ABCDEF 中,AB AE =．图9-21(1)若BC EF =,则CD DF =,反之若CD DF =,则BC EF =．(2)若BC EF = (或CD DF =),M 为完全四边形的密克尔点,则MD CF ⊥或ACF △的外心1O ,在直线MD 上．(3)若BC EF = (或CD DF =),点A 在CF 上的射影为H ,ABE △的外心为2O ,则2O 为AM 的中点,且22O D O H =．(4)若BC EF =（或CD DF =）,M 为完全四边形的密克尔点,则MB ME =,且MB AC ⊥,ME AE ⊥． 证明(1)可由完全四边形中含有的比例乘积式（或对ACF △及截线BDE 应用梅涅劳斯定理）有1AB CD FE BC DF EA⋅⋅= 因AB AE =,则由上式,知CD DF BC EF =⇔=．(2)由(1)知,BCD △和DEF △的外接圆是等圆（或由正弦定理计算推证得）．又由A 、B 、M 、E 四点共圆,有CBM AEM FEM ∠=∠=∠,从而CM MF =,于是DCM DFM △△≌,有CDM FDM ∠=∠．故MD CF ⊥．由于DM 是CF 的中垂线,而1O 在CF 的中垂线上,故ACF △的外心1O 在直线MD 上．(3)由(2)知,BCD △和DEF △外接圆是等圆,从而BCM EFM △△≌,即有BM EM =,即知点M 在BAE ∠的平分线上,亦即A 、2O 、M 共线,从而知2O 为AM 的中点． 或者直接计算得2O 为AM 的中点,在ABE △中,由正弦定理,知 22211sin 2cos 2sin 9022ABAB AC AEAO AEBAA +⋅===∠⎛⎫︒- ⎪⎝⎭． 设圆1O 的半径为1R ,流意到1O 、D 、M 共线,则 11112cos 2sin 2sin 2A AM R O MA R MCA R C ⎛⎫=∠=∠=+ ⎪⎝⎭．于是122cos 2sin cos2222sin sin 2cos2A A A R C C AM AC AE AO AFC CA ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭==+⋅∠+ 而22sin cos 2sin cos cos sin cos sin 2cos 222222A A A A A A C C C C ⎛⎫⎛⎫+=+=⋅+ ⎪ ⎪⎝⎭⎝⎭()cos sin sin 1cos cos sin sin sin cos cos sin sin sin C A C A C A C C A C A C AFC =++=++=+∠．故22AM AO =,即2O 为AM 的中点．注意到MD CF ⊥,AH CF ⊥,所以2O 在线段DH 的中垂线上,故22O D O H =．(4)由(3)知,BE EM =．又2O 为AM 的中点,而2O 为圆心即AM 为直径,则MB AC ⊥,ME AE ⊥．或注意到AB AE =,从而MB ME =．以例8为背景,则可得到如下竞赛题．试题1已知锐角ABC △,CD 是过点C 的高线,M 是边AB 的中点,过M 的直线分别交射线CA 、CB 于点K 、L ,且CK CL =．若CKL △的外心为S ．证明：SD SM =．（2003年第54届波兰奥林匹克题）证明事实上,如图922-,此题即为在完全四边形CKAMLB 中,C ∠为锐角,顶点在边AB 上的射影为D ,且CK CL =,AM M B =,S 为CKL △的外心,此即为例8中的(3),过M 与AB 垂直的线与CS 延长线交为M ．图9-22BDMCAGEKS试题2设AM 、AN 分别是ABC △的中线和内角平分线,过点N 作AN 的垂线分别交AM 、AB 于点Q 、P ,过P 作AB 的垂线交AN 于O ．求证：QO BC ⊥．（2000年亚太地区奥林匹克题）O 'P'N 'BO CMAQ N EP图9-23证明事实上,如图923-,过M 作PQ 的平行线交AB 于P ',交AN 于N ',过P '与AB 垂直的直线交直线AN 于O ',则由Rt P O N '''△与Rt PON △是以A 为位似中心的位似形,知MO QO '∥．设P N ''的延长线与AC 的延长线交于点E ,则为完全四边形AP BMEC '的密克尔点,于是由例8中的(2),知O M BC '⊥．从而OQ BC ⊥．以具有相等的边（含边上的线段）的完全四边形为背景的竞赛题还有如下的2003年日本奥林匹克题． 试题3 P 是ABC △内的一点,直线AC 、BP 相交于Q ,直线AB 、CP 相交于R ,已知 AR RB CP ==,CQ PQ =．求BRC ∠．事实上,可在CR 上取点S ,使RS CP =,则由ACS QPC BPR ∠=∠=∠,可推证得SC RP =．由完全四边形中的比例乘积式（即对ABQ △及截线RPC 应用梅涅劳斯定理）知AC BP =． 又由ACS BRP △△≌,得AD BR =．由此推得AS AR RS ==,即60ARS ∠=︒,从而120BRC ∠=︒． 例9如图924-,完全四边形ABCDEF 中,AC BE ⊥,AE CF ⊥．图9-24A(1)若顶点C 、E 在对角线BF 所在直线上的射影分别为G 、H ,则GB FH =．(2)若对角线AD 的延长线交对角线CE 于P ,BPF △的外接圆交AD 于1A ,交CD 于1C ,交DE 于1E ,则111=2ACE A BC PE F S S △,且4ACE BPF S S △△≥．证明(1)由题设知C 、E 、F 、B 、四点共圆,且CE 的中点为其圆心,过O 作OM BF ⊥于M ,则由弦心距性质知BM M F =．又CG OM EH ∥∥,CO OE =,从而GM MH =．故 GB GM BM MH MF FH =-=-=．(2)在ACE △中,由题设知BPF △的外接圆为ACE △的九点圆,从而知1A 、1C 、1E 分别为AD 、CD 、ED 的中点．于是1112BCC PCC BCPD S S S +=△△1112PEE FEE DPEF S S s +=△△1112BAA FAA ABDF S S S +=△△从而1112ACE A BC PE F S S =．由完全四边形的性质,即知4ACE BPE S S △△≥．以例9为背景,则可得到如下竞赛题．试题4锐角ABC △中,BD 和CE 是其相应边上的高．分别过顶点B 和C 引直线ED 的垂线BF 和CG ,垂足为F 、G ．求证：EF DG =． （1998年第22届独联体奥林匹克题） 试题5锐角ABC △中,A ∠的平分线与三角形外接圆交于另一点1A ．点1B 、1C 与此类似．直线1AA 与B ∠、C ∠两角的外角平分线相交于点0A ,点0B 、0C 与此类似,求证：(1)000A B C △的面积是六边形111AC BACB 面积的两倍．(2) 000A B C △的面积至少是ABC △面积的四倍．（1989年第30届IMO 试题）试题6已知圆1O 与圆2O 交于A 、B 两点,过点A 作12O O 的平行线,分别与圆1O 、圆2O 交于C 、D 两点,以CD 为直径的圆3O 分别与圆1O 、圆2O 交于P 、Q 两点．证明：CP 、DQ 、AB 三线共点．（2004年第54届白俄罗斯奥林匹克题）事实上,由12CD O O ∥,且12AB O O ⊥,知CD AB ⊥．又可推得CP 、DQ 、AB 是BCD △的三条高线,故共点．例10在完全四边形ABCDEF 中,顶点A 、B 、D 、F 四点共圆O ,其对角线AD 与BF 交于点G ．A图9-25(1)若顶点角C ∠、E ∠的平分线相交于点K ,则CK EK ⊥．(2)BGD ∠的角平分线与CK 平行,DGF ∠的角平分线与EK 平行．(3)从C 、E 分别引圆O 的切线,若记切点分别为P 、Q ．则222CE CP EQ =+；此题设条件下的完全四边形ABCDEF 的密克尔点在对角线CE 上；若分别以C 、E 为圆心,以CP 、EQ 为半径作圆弧交于点T ,则CT ET ⊥．(4)若从C (或E )引圆O 的两条切线,切点为R 、Q ,则E (或C )、R 、G 、Q 四点共圆． (5)过C 、E 、G 三点中任意两点的直线,分别是另一点关于圆O 的极线． (6)点O 是GCE △的垂心．(7)过对角线BF (或BF ∥CE 时的AD )两端点处的圆O 的切线的交点在对角线CE 所在直线上． (8)设1O 、2O 分别是ACF △、ABE △的外心,则12OO O DCE △△∽．(9)设点M 是完全四边形ABCDEF 的密克尔点,则OM CE ⊥,且O 、G 、M 共线,OM 平分AMD ∠,OM 平分BMF ∠．(10)过点E (或C )的圆的割线交圆O 于R 、P ,直线PC (或PE )交圆O 于点S ,则R 、G , S 三点共线． (ii)设对角线AD 的延长线交对角线CE 于W ,则WC WE =的充要条件是2WA WD WC ⋅=．(12)设对角线CF 的中点为Z ,连结AZ 交圆O 于N ,则C 、D 、N 、E 四点共圆． 证明(1)如图925-,连结CE ,令1DEC ∠=∠,2DCE ∠=∠,则 ()1221)180BCD DEF ABD AFD ∠+∠+∠+∠+∠+∠=∠+∠=︒（, 即知1()12902BCD DEF ∠+∠+∠+∠=︒,从而()1180[12]902CKE BCD DEF ∠=︒-∠+∠+∠+∠=︒, 故CK EK ⊥．(2)设DGF ∠的平分线交DE 于X ,KE 交GF 于l ,则()1122FGX DGF GFA GAF ∠=∠=∠+∠,()111()222FIE GFA AED GFA ADB GAF GFA GAF ∠=∠-∠=∠-∠-∠=∠+∠．故CX KE∥．同理,BGD ∠的平分线与CK 平行．(3)设过点B 、C 、D 的圆交CE 于点M ,连结DM ,则AFD CBD DME ∠=∠=∠,从而D 、M 、E 、F 四点共圆,于是CM CE CD CF ⋅=⋅,EM EC ED EB ⋅=⋅． 此两式相加,得2CE CD CF ED EB =⋅+⋅．又CP 、EQ 分别是圆O 的切线,有2CD CF CP ⋅=,2ED EB EQ ⋅=． 放223CE CP EQ =+．显然,M 是圆BCD 与圆DEF 的另一个交点,此即为密克尔点,即题设条件下的完全四边形的密克尔点在CE 上．由于CT CP =,ET EQ =,故222CT ET CE +=,即CT ET ⊥． (4)如图926-,连结CQ 交圆O 于R ',过E 作EH CQ ⊥于H ,X DR'R YZ H C MEAP QO B FG图9-26过点C 作圆的切线CP ,切点为P ,则()222CE EQ CP CR CQ CH HR CQ ''-===-． 又()()222222CE EQ CH HE HE HQ -=+-+()()22CH HQ CH HQ CH QH =-=-+ ()CH Ho CO =-．从而HR HQ '=,由此即可证 Rt Rt EHR EHQ '△△≌．于是EQ ER '=,而EQ ER =,则ER ER '=．又R '、R 均在圆O 上,故R '与R 重合,即C 、R 、Q 三点共线． 或者,设CE 上的点M 是密克尔点,则2EQ ED EB EM EC =⋅=⋅． 从而222CE EQ CE EM EC CE CM CD CF -=-⋅=⋅=⋅()()22CO OQ CO OQ CO OQ =-+=-由此,知CQ OE ⊥．而RQ OE ⊥,故C 、R 、Q 三点共线．为证R 、G 、Q 共线,连结AR 交BF 于点X ,连结RF 交AD 于点Y ,设RQ 与AF 交于点Z ,连结AQ 、QF ．于是sin sin QAZ QZF S AZ QA AQZZF S QF ZQF∠==∠△△． 同理sin sin FY DF FDY YR DR YDR ∠=∠,sin sin RX BR RBXXA BA XBA∠=∠． 由EAQ EQF △△≌,有RX EBQF ER =． 同理,有DF DE DR DB =,RX EBXA ER=． 而AQZ YDR ∠=∠,ZQF RBX ∠=∠,FDY XBA ∠=∠,EQ ER =． 于是1AZ FY RX ZF YE XA⋅⋅=对ARF △应用塞瓦定理的逆定理,知AY 、FX 、RZ 共点于G ,故R 、G 、Q 共线． 综上可知,C 、R 、G 、Q 四点共线．(5)由(4)即证．(6)由于OE RQ ⊥,即OE CG ⊥．同样OC EG ⊥．由此即知,O 为GCE △的垂心,亦可知OG CE ⊥． (7)由(5)知,直线CE 是点G 关于圆O 的极线,从而过点G 的弦的两端点处的切线的交点在直线CE 上． (8)若点O 在AD 上,则1O 、2O 分别为AC 、AE 的中点,此时,显然12OO O DCE △∽△． 若点O 不在AD 上,如图927-所示,则1O 、2O 不在AC 、AE 上．O O 1O 2BDCFAE图9-27连结1AO 、1CO 、AD 、AO 、OD 、2AO 、2O E 、BF ． 由22(180)2AO E ABE AFD AOD ∠=︒-∠=∠=∠, 及22O A O E =．OA OD =, 知2AO E AOD △△∽． 即有2AO AEAO AD=． 又2O AE OAD ∠=∠, 则2AOO ADE △△≌．同理1AO C AOD △∽△,1AOO ACD △△≌． 于是12O O OO AO CD AD DE==． 由12AO C AO E △∽△,知12O O AC AOCE AE AD==, 从而12OO O DCE △∽△．(9)如图928-,过点D 和M 作圆O 的割线MD 交圆O 于点T ,连结AM 、AO 、TO ．由A 、B 、D 、F及A 、B 、M 、E 分别共圆,知EFD ABE AM E ∠=∠=∠．TOBD C FAME图9-28又由D 、F 、A 、T 共圆,知EFD ATD ATM ∠=∠=∠,因AE 、TM 是过两相交圆交点F 、D 的割线,从而EM AT ∥．于是TAM AM E ATM ∠=∠=∠,即知MA MT =．又OA OT =,从而MO AT ⊥,故OM ME ⊥．而M 在CE 上,故OM CE ⊥,又由(6)知,OG CM ⊥,故O 、G 、M 三点共线． (此题为2002年中国国家队选拔赛题的特殊情形,故OM 平分AMD ∠,OM 平分BMF ∠) (10)如图929-,连结PA 、PB 、SD 、DR 、RF 、PF ．S BDCFARG EP 图9-29由EFR FPA △∽△,CPA CSB △∽△,有FR FE PA PE =,AP CPSB CB=． 从而FR FE CPSB PE CB=⋅． 由ERD EBP △∽△,CBP CSA △∽△,亦有 RD ED CPAS EP CA=⋅． 由上述两式相除,得 ER AS FE CASB RD ED CB ⋅=⋅． 用BDAF乘上式两边,应用完全四边形性质1中式①（即对ABE △及截线CDF 应用梅涅劳斯定理）．知 1EF AC BDFA CB DE ⋅⋅= 从而1FR DB SARD BS AF⋅⋅=．。
8年级数学竞赛专题辅导之平行四边形
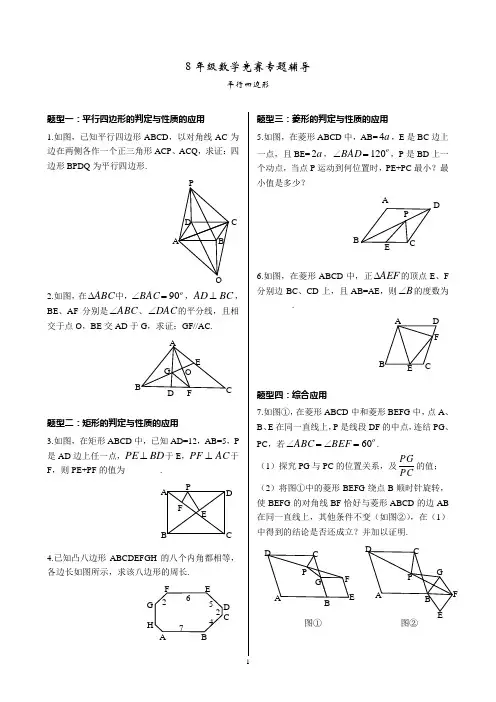
18年级数学竞赛专题辅导平行四边形题型一：平行四边形的判定与性质的应用 1.如图，已知平行四边形ABCD ，以对角线AC 为边在两侧各作一个正三角形ACP 、ACQ ，求证：四边形BPDQ 为平行四边形.2.如图，在ABC ∆中，oBAC 90=∠，BC AD ⊥，BE 、AF 分别是ABC ∠、DAC ∠的平分线，且相交于点O ，BE 交AD 于G ，求证：GF//AC.题型二：矩形的判定与性质的应用3.如图，在矩形ABCD 中，已知AD=12，AB=5，P 是AD 边上任一点，BD PE ⊥于E ，AC PF ⊥于F ，则PE+PF 的值为________.4.已知凸八边形ABCDEFGH 的八个内角都相等，各边长如图所示，求该八边形的周长.题型三：菱形的判定与性质的应用5.如图，在菱形ABCD 中，AB=a 4，E 是BC 边上一点，且BE=a 2，o BAD 120=∠，P 是BD 上一个动点，当点P 运动到何位置时，PE+PC 最小？最小值是多少？6.如图，在菱形ABCD 中，正AEF ∆的顶点E 、F 分别边BC 、CD 上，且AB=AE ，则B ∠的度数为________.题型四：综合应用7.如图①，在菱形ABCD 中和菱形BEFG 中，点A 、B 、E 在同一直线上，P 是线段DF 的中点，连结PG 、PC ，若oBEF ABC 60=∠=∠. （1）探究PG 与PC 的位置关系，及PCPG的值； （2）将图①中的菱形BEFG 绕点B 顺时针旋转，使BEFG 的对角线BF 恰好与菱形ABCD 的边AB 在同一直线上，其他条件不变（如图②），在（1）中得到的结论是否还成立？并加以证明.CABEF C DPDA图① 图②2专题演练一、选择题1.周长为68的长方形ABCD 被分成7个全等的长方形，如图所示，则长方形ABCD 的面积为（ ）A. 98B. 196C. 280D. 2842.如图，菱形花坛ABCD 的边长为6m ，∠A=120°，其中由两个正六边形组成的图形部分种花，则种花部分图形的周长为（ ）A.12mB.20mC.22m D24m 二、填空题3.如图，矩形ABCD中，AC 、BD 相交于点O ，AE 平分∠BAD ，交BC 于E ，若∠EAO=15°，则∠BOE 的度数为________.4.如图，以△ABC 的三边为边在BC 的同一侧分别作三个等边三角形，即△ABD 、△BCE 、△ACF. （1）四边形ADEF 的形状是________； （2）当△ABC 满足条件 ________时，四边形ADEF 为菱形；（3）当△ABC 满足条件________时，四边形ADEF不存在.三、解答题5.如图，在锐角△ABC 中，AD 、CE 分别是BC 、AB边上的高，AD 、CE 相交于F ，BF 的中点为P ，AC 的中点为Q ，连接PQ 、DE.（1）求证：直线PQ 是线段DE 的垂直平分线； （2）如果△ABC 是钝角三角形，∠BAC ＞90°，那么上述结论是否成立？并加以证明.6.在矩形纸片ABCD 中，AB=a ，BC=ka ，将纸片折叠一次，使顶点A 与C 重合，如果纸片中不重合部分的面积为23a ，求k 的值.。
八年级数学竞赛培训第26讲：四边形
新课标八年级数学竞赛培训第26讲：面积问题一、填空题（共9小题，每小题4分，满分36分）1．（4分）在梯形ABCD中，AB∥CD，AC、BD相交于点O，若AC=5，BD=12，中位线长为，△AOB的面积为S 1，△COD的面积为S2，则=_________．2．（4分）如图，是一个圆形花坛，中间的鲜花构成一个菱形图案（单位：米），若每平方米种植鲜花20株，那么这个菱形图案中共有鲜花_________株．3．（4分）如图，矩形内有两个相邻的正方形面积分别为4和2，那么阴影部分的面积为_________．4．（4分）如图，在△ABC中，∠B=∠CAD，，则=_________．5．（4分）如图，梯形ABCD中，AB∥CD，AB=a，CD=b（a＜b），对角线AC与BD相交于O，△BOC的面积为梯形ABCD的面积的，则=_________．6．（4分）如图，△ABC中，AD与BE相交于F，已知S△AFB=12cm2，S△BFD=9cm2，S△AFE=6cm2，那么四边形CDFE的面积为_________cm2．7．（4分）如图，分别延长△ABC的三边AB、BC、CA至A′、B′、C′，使得AA′=3AB，BB′=3BC，CC′=3AC，若S△ABC=1，则S△A'B'C‘=_________．8．（4分）如图，设△ABC的面积是1，D是边BC上一点，且，若在边AC上取一点，使四边形ABDE的面积为，则的值为_________．9．（4分）如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1、3、5，则这个等边三角形的边长为_________．二、选择题（共9小题，每小题5分，满分45分）10．（5分）如图，点E，F分别是矩形ABCD的边AB，BC的中点，连AF，CE，设AF，CE交于点G，则等于（）B11．（5分）（2007•玉溪）如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）12．（5分）如图，在△ADC中，EF∥BC，S△AEF=S四边形BCEF，则AE：AB等于（）B13．（5分）已知菱形ABCD的两条对角线AC、BD的乘积等于菱形的一条边长的平方，则14．（5分）（2001•荆州）如图，四边形ABCD中，∠A=135°，∠B=∠D=90°，BC=2，AD=2，则四边形ABCD的面积是（）415．（5分）ABCD是边长为1的正方形，△BPC是等边三角形，则△BPD的面积为（）B16．（5分）如图，在△ABC中，∠ACB=90°，分别以AC，AB为边，在△ABC外作正方形ACEF和正方形AGHB，作CK⊥AB，分别交AB和GH于D和K，则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是（）不能确定，与17．（5分）（2003•广州）有一块缺角矩形地皮ABCDE（如图），其中AB=110m，BC=80m，CD=90m，∠EDC=135°，现准备用此块地建一座地基为长方形（图中用阴影部分表示）的教学大楼，以下四个方案中，地基面积最大的是（）B18．（5分）在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，新课标八年级数学竞赛培训第26讲：面积问题参考答案与试题解析一、填空题（共9小题，每小题4分，满分36分）1．（4分）在梯形ABCD中，AB∥CD，AC、BD相交于点O，若AC=5，BD=12，中位线长为，△AOB的面积为S 1，△COD的面积为S2，则=．=×=30=．2．（4分）如图，是一个圆形花坛，中间的鲜花构成一个菱形图案（单位：米），若每平方米种植鲜花20株，那么这个菱形图案中共有鲜花480株．AC BD=3．（4分）如图，矩形内有两个相邻的正方形面积分别为4和2，那么阴影部分的面积为．，∴两个正方形的边长分别是）﹣24．（4分）如图，在△ABC中，∠B=∠CAD，，则=3：1．=，即=，即===，====35．（4分）如图，梯形ABCD中，AB∥CD，AB=a，CD=b（a＜b），对角线AC与BD相交于O，△BOC的面积为梯形ABCD的面积的，则=．．=，==，∴，即==．，即．6．（4分）如图，△ABC中，AD与BE相交于F，已知S△AFB=12cm2，S△BFD=9cm2，S△AFE=6cm2，那么四边形CDFE的面积为23.4cm2．====，7．（4分）如图，分别延长△ABC的三边AB、BC、CA至A′、B′、C′，使得AA′=3AB，BB′=3BC，CC′=3AC，若S△ABC=1，则S△A'B'C‘=19．式可得==，，易知：===8．（4分）如图，设△ABC的面积是1，D是边BC上一点，且，若在边AC上取一点，使四边形ABDE的面积为，则的值为．上的高相同，==，，，的面积为，即，，，上的高相同，由面积公式得：===故答案为：．9．（4分）如图，从等边三角形内一点向三边作垂线，已知这三条垂线段的长分别为1、3、5，则这个等边三角形的边长为．BC AM===9×=66二、选择题（共9小题，每小题5分，满分45分）10．（5分）如图，点E，F分别是矩形ABCD的边AB，BC的中点，连AF，CE，设AF，CE交于点G，则等于（）EF=BN=MN=BMPG=PQ=MN=MB（）=11．（5分）（2007•玉溪）如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S是（）（12．（5分）如图，在△ADC中，EF∥BC，S△AEF=S四边形BCEF，则AE：AB等于（）．可以求得，根据S 即可得S×AB===．等的性质，本题中根据求值是解题的关键．13．（5分）已知菱形ABCD的两条对角线AC、BD的乘积等于菱形的一条边长的平方，则ACACACABAB14．（5分）（2001•荆州）如图，四边形ABCD中，∠A=135°，∠B=∠D=90°，BC=2，AD=2，则四边形ABCD的面积是（），=﹣×2×15．（5分）ABCD是边长为1的正方形，△BPC是等边三角形，则△BPD的面积为（）B=，×1=+﹣16．（5分）如图，在△ABC中，∠ACB=90°，分别以AC，AB为边，在△ABC外作正方形ACEF和正方形AGHB，作CK⊥AB，分别交AB和GH于D和K，则正方形ACEF的面积S1与矩形AGKD的面积S2的大小关系是（）不能确定，与，即可得17．（5分）（2003•广州）有一块缺角矩形地皮ABCDE（如图），其中AB=110m，BC=80m，CD=90m，∠EDC=135°，现准备用此块地建一座地基为长方形（图中用阴影部分表示）的教学大楼，以下四个方案中，地基面积最大的是（）．．18．（5分）在△ABC中，已知BD和CE分别是两边上的中线，并且BD⊥CE，BD=4，CE=6，BDDB BD DB BD =×。
八年级数学竞赛讲座平行四边形附答案
第十五讲平行四边形平行四边形是一类特殊的四边形，它的特殊性体现在边、角、对角线上，矩形、菱形是特殊的平行四边形，矩形的特殊性体现在有一个角是直角，菱形的特殊性体现在邻边相等，所以，它们既有平行四边形的性质，又有各自特殊的性质．对角线是解决四边形问题的常用线段，对角线本身的特征又可以决定四边形的形状、大小，连对角线后，平行四边形就产生特殊三角形，因此解平行四边形相关问题时，既用到全等三角形法，特殊三角形性质，又要善于在乎行四边形的背景下探索问题，利用平行四边形丰富的性质为解题服务．熟悉以下基本图形、基本结论：例题求解【例1】如图，在矩形ABCD中，已知AD=12，AB=5，P是AD边上任意一点，PE⊥BD于E，PF⊥AC于F，那么PE+PF的值为．(全国初中数学联赛试题)思路点拨分别求出PE、PF困难，△AOD为等腰三角形，若联想“到等腰三角形底边上任一点到两腰距离的和等于腰上的高”这一性质，则问题迎刃而解．注特殊与一般是对立统一的，在一定条件下可以互相转化，相对于一般而言，特殊的事物往往更简单、更直观、更具体．因而人们常常通过特殊去认识一般；另一方面，一般概括了特殊，一般比特殊更为深刻地反映着事物的本质，所以人们也往往通过一般去了解特殊．一般与特殊，是知识之间联系的一种重要形式，知识常常在一般到特殊或特殊到一般的变化过程中，不斩地得到延伸与拓展．【例2】已知四边形ABCD，从下列条件中：(1)AB∠CD，(2)BC∥AD；(3)AB=CD；（4）BC=AD；(5)∠A=∠C；(6)∠B=∠D．任取其中两个，可以得出“四边形ABCD是平行四边形”这一结论的情况有（）A．4种 B．9种 C．13种 D． 15种(山东省竞赛题)思路点拨根据平行四边形的判定方法及新的组合方式判定．【例3】】如图，在△ADC中，∠DAC=90°，AD⊥BC，DC、AF分别是∠ABC、∠DAC的平分线，BE和AD交于G，求证：GF∥AC．(湖北省荆州市中考题)思路点拨从角的角度证明困难，连结CF，在四边形AGFE的背景下思考问题，证明四边形AGFE为特殊平行四边形，证题的关键是能分解出直角三角形中的基本图形．【例4】如图，设P为等腰直角三角形ACB斜边AB上任意一点，PE⊥AC于点E，PF⊥BC于点F，PG ⊥EF于G点，延长GP并在其延长线上取一点D，使得PD＝PC，求证：BC⊥BD，且BC=BD．(全国初中数学联赛试题)思路点拨尽管图形复杂，但证明目标明确，只需证明△CPB≌△DPB，应从图中分离出特殊三角形、特殊四边形，充分运用它们的性质为证题服务．【例5】如图，在等腰三角形ABC中，延长边AB到点D，延长边CA到点E，连结DE，恰有AD=BC=CE=DE．求∠BAC的度数．(北京市竞赛题)思路点拨 题设条件给出的是线段的等量关系，要求的却是角的度数，相等的线段可得到全等三角形、特殊三角形，为此需通过构造平行四边形改变它们的位置．注 课本中平行四边形的判定定理是从边、角、对角线三个方面探讨的，一般情况是，从四边形边、角、对角线三类元素任意选取两类，任意组合就产生许多判定平行四边形的命题．其中有真命题与假命题，对于假命题，要善于并熟悉构造反例．构造反例是学习数学的一种重要技能，可以帮助我们理解概念．培养推理能力，数学史上就曾有许多著名的论断被一个巧妙的反例推翻的实例．若题设条件中有彼此平行的线段或造成平行的因素，则通过作平行线，构造平行四边形，这是解四边形问题的常用技巧，这是由于平行四边形能使角的位置更理想，送线段到恰当的地方，使线段比良性传递．学力训练1．如图，BD 是平行四边形ABCD 的对角线，点E 、F 在BD 上，要使四边形AECF 是平行 四边形，还需要增加的一个条件是 (填上你认为正确的一个即可，不必考 虑所有可能情形) (宁波市中考题)2．(1)如图，已知矩形ABCD 中，对角线AC 、BD 相交于O ，AE ⊥BD 于E ，若∠DAE ：∠BAE ＝3：1，则∠CAC ＝ ； (河南省中考题)(2)矩形的一个角的平分线分矩形一边为lcm 和3cm 两部分，则这个矩形的面积 为 cm 2． (武汉市中考题)3．如图，以△ABC 的三边为边在BC 的同一侧分别作三个等边三角形，即△ABD 、△BCE 、△ACF ． (1)四边形ADEF 是 ；(2)当△ABC 满足条件 时，四边形ADEF 为矩形；(3)当△ABC 满足条件 时，四边形ADEF 不存在． (2000年贵州省中考题)4．已知一个三角形的一边长为2，这边上的中线为1，另两边之和为1+3，则这两边之积为 ． (2001年天津市选拔赛试题)5．四边形的四条边长分别是a 、b 、c 、d ，其中a 、c 为对边，且满足cd ab d c b a 222222+=+++，则这个四边形一定是( )A．平行四边形 B．两组对角分别相等的四边形C．对角线互相垂直的四边形 D．对角线相等的四边形6．如图，周长为68的矩形ABCD被分成7个全等的矩形，则矩形ABCD的面积为( )A．98 B．196 C．280 D． 284(湖北省荆州市中考题)7．如图，菱形花坛ABCD的边长为6m，∠B＝60°，其中由两个正六边形组成的图形部分种花，则种花部分的图形的周长(粗线部分)为( )A．123 m B．20m C． 22m D．24m(吉林省中考题)8．在凸四边形ABCD中，AB∥CD，且AB+BC=CD+DA，则( )A．AD>BC B．AD<BCC．AD=BC D．AD与BC的大小关系不能确定(“希望杯”邀请赛试题)9．如图，△ABC为等边三角形，D、F分别是BC、AB上的点，且CD=BF，以AD为边作等边△ADC．(1)求证：△ACD≌△CNBF；(2)当D在线段BC上何处时，四边形CDEF为平行四边形，且∠DEF=30°?证明你的结论． (南通市中考题)10．如图，在Rt△ABC中，AB=AC，∠A=90°，点D为BC上任一点，DF⊥AB于F，DE⊥AC于C，M为BC的中点，试判断△MEF是什么形状的三角形，并证明你的结论．(黑龙江省中考题)11．如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．(1)求证：CO＝FO；(2)当点O运动到何处时，四边形AECF是矩形?并证明你的结论．(3)当△ABC满足什么条件时，四边形AECF是正方形?12．如图，在平行四边形ABCD中，EF∥BC，GH∥AB，EF、GH的交点P在BD上，图中有对四边形面积相等，它们是．(常州市中考题)13．如图，菱形ABCD的对角线AC、BD相交于O，△AOB的周长为3+3，∠ABC＝60°，则菱形ABCD的面积为．14．如图，矩形ABCD的对角线相交于O，AE平分∠BAD交BC于E，∠CAE=15°，则∠BOE= ．15．如图，矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为． (山东省竞赛题)16．如图，平行四边形ABCD中，∠ABC=75°，AF⊥BC于F，AF交BD于E，若DE=2AB，则∠AED的大小是( )A．60° B．65° C．70° D．75° (“希望杯”邀请赛试题)17．如图，正△AEF 的边长与菱形ABCD 的边长相等，点E 、F 分别在BC 、CD 上，则∠B 的度数是( ) A ．70° B ．75° C ．80° D ．95° (重庆市竞赛题)18．如图，正方形ABCD 外有一点P ，P 在BC 外侧，并在平行线AB 与CD 之间，若PA=17，PB=2，PC=5，则PD=( )A ．25B ．19C ．32D ．17 (“五羊杯”竞赛题)19．如图，在平行四边形ABCD 中，BC=2AB ，CZ ⊥AB 于E ，F 为AD 的中点，若∠AEF=54°，则∠B=( )A ．54°B ．60°C ．66°D ．72° (武汉市选拔赛试题)20．如图，在Rt △ABC 中，∠ABC ＝90°，∠C=60°，BC ＝2，D 是AC 的中点，以D 作DE ⊥AC 与CB 的延长线交于E ，以AB 、BE 为邻边作长方形ABEF ，连结DF ，求DF 的长．21．如图，菱形的对角线AC 与BD 交于点O ，延长BA 到E ，使AE=21AB ，连结OE ，延长DE 交CA 的延长线于F ．求证：OE=21DF ． 22．阅读下面短文：如图1，△ABC 是直角三角形，∠C=90°，现将△ABC 补成矩形，使△ABC 的两个顶点为矩形一边的两个端点，第三个便点落在矩形这一边的对边上，那么符合要求的矩形可以画出两个：矩形ACBD 和矩形AEFB(如图2)．解答问题；(1)设图2中矩形ACBD和矩形AEFB的面积分别为S l、S2，则S1 S2(填“>”，“=”或“<”)；(2)如图3，△ABC是钝角三角形，按短文中的要求把它补成矩形，那么符合要求的矩形可以画出个，利用图3把它画出来；(3)如图4，△ABC是锐角三角形且三边满足BC>AC>AB，按短文中的要求把它补成矩形，则符合要求的矩形可以画出个，利用图4把它画出来；(4)在(3)中所画出的矩形中，哪一个的周长最小?为什么?(陕西省中考题)23．如图，在△ABC中，∠C=90°，点M在BC上，且BM＝AC，N在AC上，且AN=MC，AM与BN相交于P，求证：∠BPM=45°．(杭州市“求是杯”竞赛题)24．如图，在锐角△ABC中，AD、CZ分别是BC、AB边上的高，AD、CE相交于F，BF的中点为P，AC的中点为Q，连结PQ、DE．(1)求证；直线PQ是线段DE的垂直平分线；(2)如果△ABC是钝角三角形，∠BAC>90°，那么上述结论是否成立?请按钝角三角形改写原题，画出相应的图形，并给予必要的说明．(“希望杯”邀请赛试题)。
初中数学专题讲座精编中考系列复习(四边形)
中考复习(四边形)一、中考要求1、了解四边形和多边形的有关概念；掌握四边形及多边形的内角和、外角和定理；知道四边形的不稳定性及其应用；2、熟练掌握平行四边形、矩形、菱形、正方形的概念、性质和判定，并能运用相关知识进行有关论证及计算，知道这些图形之间的区别和联系；3、了解中心对称和中心对称图形的概念，掌握中心对称的性质，能判定一个图形是否中心对称图形，找出对称中心，能画出与已知图形成中心对称的图形；4、熟练掌握梯形、等腰梯形、直角梯形的概念，掌握等腰梯形的性质和判定，并能熟练运用它们进行有关的论证和计算；5、熟练掌握平行线等分线段定理，三角形、梯形中位线定理，并能运用这些定理进行有关的论证和计算，会按要求等分已知线段；6、会用割补等方法计算特殊四边形的面积和不规则图形的面积；7、能综合运用上述知识解决具体的实际应用问题。
二、点击重、难点1、重点内容为平行四边形的定义、性质和判定，它是学习特殊平行四边形、梯形、平行线等分线段定理等相关知识的基础，是这些图形转化的“归宿”，是学好本单元知识的关键。
2、难点有两个：一是各种特殊平行四边形的性质与判定很多，可以从边（邻边、对边）、角、对角线三个主要方面比较，不可混淆；二是中心对称，渗透了旋转变化的思想。
三、中考热点分析与预测四边形知识是中考的重点内容，题型涉及填空、选择、解答题等各种形式，尤其值得重视的是与四边形相关的开放探索性问题，以及与相似形、三角函数、圆、函数等知识构建起的综合题。
在2003年的中考中，四边形知识的题量大约占全卷试题总量的14%，平均分值一般占到10%左右，有些地区比例更高，比如河北分值占到18.3%.估计今后有关四边形试题将保持综合性，加大开放性，增强探索性，体现应用性。
四、知识要点聚焦1、四边形的内角和等于1800，n边形的内角和等于(n-2)·1800，任意多边形的外角和等于3600，n边形的对角线条数为n(n-3)/2.2、平行四边形性质：（1）平行四边形的对边平行且相等、对角相等、对角线互相平分；（2）平行四边形是中心对称图形.判定：（1）定义判定；（2）两组对边分别相等的四边形是平行四边形；（3）两组对角分别相等的四边形是平行四边形；（4）对角线互相平分的四边形是平行四边形；（5）一组对边平行且相等的四边形是平行四边形.3、矩形性质：（1）具有平行四边形的所有性质；（2）四个角都是直角；（3）对角线相等（推论：直角三角斜边上的中线等于斜边的一半）；（4）既是中心对称图形，又是轴对称图形；（5）其面积等于两条邻边的乘积.判定：（1）定义判定；（2）有三个角是直角的四边形；（3）对角线相等的平行四边形.4、菱形性质：（1）具有平行四边形的所有性质；（2）四条边相等；（3）对角线互相垂直平分，且每一条对角线平分一组对角；（4）既是中心对称图形，又是轴对称图形；（5）其面积等于两条对角线长乘积的一半（适用于所有对角线互相垂直的四边形）.判定：（1）定义判定；（2）四条边相等的四边形；（3）对角线互相垂直的平行四边形.5、正方形性质：具有矩形、菱形的一切性质.判定：（1）定义判定；（2）先判定四边形为矩形，再判定它也是菱形；（3）先判定四边形为菱形，再判定它也是矩形.6、等腰梯形性质：（1）两腰相等；（2）两条对角线相等；（3）同一底上的两个底角相等；（4）是轴对称图形.判定：（1）在同一底上的两个角相等的梯形是等腰梯形；（2）对角线相等的梯形是等腰梯形.7、平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰。
人教版数学八年级培优竞赛 四边形的面积问题 专题课件
D
E
F C
G
A
B
第7题图
AE
F
PN
QM
D m1
H m2 m3
B
G C m4
l1 l2 l3 l4 第8题图
A
D
F E
B 第9题图 C
8.如图，已知直线 l1、l2、l3、l4 及 m1、m2、m3、m4 分别互相平行，且 S 四边形 ABCD＝100，S 四边形 EFGH＝60.则 S 四边形 PQMN ＝ ___2_0____.
11.如图，在四边形 ABCD 中，设∠BAD＋∠ADC＝270°，且 E、F 分别为 AD、BC 的中点，EF＝4，以 AB、CD 为直径作半圆，求这两个半圆面积的和.
AE D
B
F
C
连接 BD，取 BD 中点 G，连接 GE，GF，则 GE＝ 1 AB，GF＝ 1 CD，GE⊥GF，
2
2
故两个半圆面积之和为 1 GE2 GF2 8 . 2
关系如图 2 中折线段 OEFGHI 所示.
（1）求 A、B 两点的坐标；
（2）若直线 PD 将五边形 OABCD 分成面积相等的两部分，确定此时点 P 的
位置。
y(cm)
D
y GH
C
B
4
F
O
A
x(cm) O 3 E 6 11 12
I t(s)
m n 6
（1）设
OD＝m，OP＝n，显然
m＞3，则
取 G（6，2），作 GH⊥x 轴，则四边形 GHOC 是矩形且与四边形 OABC 的面积 相等，则 EF 必定过点 Q（3，1），于是 C 到直线 l 的最大距离为 CQ＝ 10 .
素养提升
八年级数学四边形讲义完整版(共6讲)
八年级数学四边形讲义全面完整版（全六讲）第一讲平行四边形的性质一、【基础知识精讲】1.平行四边形的定义：两组对边分别平行的四边形是平行四边形．用符号“”表示．2．平行四边形的性质：(1) 平行四边形的对边平行且相等．(2) 平行四边形的对角相等，邻角互补。
(3) 平行四边形的对角线互相平分．3．两条平行线间的距离：(1) 定义：两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线间的距离．(2) 两平行线间的距离处处相等．(3)平行线间的平行线段相等．4．平行四边形的面积：(1) 如图12-1-2①，．(（2）同底(等底)同高(等高)的平行四边形面积相等．如图12-1-2②，有公共边BC，则．二、【例题精讲】例1（1）已知中，∠A比∠B小20°，那么∠C的度数是_______．（2）在中，周长为28，两邻边之比为3︰4，则各边长为_______ _．（3）一个平行四边形的一边长是8，一条对角线长是6，则它的另一条对角线x的取值范围为__________ ．（4）平行四边形邻边长是4 cm和8cm，较短边上的高是5 cm，则另一边上的高是____________．例2．已知：在□ABCD中，过AC与BD的交点O作直线，与BA、DC的两条延长线交于M、N两点，求证：OM＝ON．例3．如图，在□ABCD中，E、F分别是BC、AD上的点，且AE∥CF，AE与CF相等吗？说明理由.【练一练】1. 已知□ABCD中，∠B=70°，则∠A=_____，∠C=_____，∠D=______．2．在ABCD中：①∠A: ∠B=5:4，则∠A=_______；②∠A+∠C=200°，则∠A=______，∠B=______；3．在□ABCD中，AB=3cm，BC=4cm，则□ABCD的周长等于_______．4. 若平行四边形周长为54，两邻边之比为4:5，则这两边长度分别______________；5. 已知ABCD对角线交点为O，AC=24mm,BD=26mm, 若AD=22mm，则△OBC的周长为_________；【探究与拓展】例1、如图，已知ABCD中，若AD=2AB，AB=BF=AE，则EC与FD垂直，试说明其理由。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
八年级数学竞赛讲座四
边形
集团标准化工作小组 #Q8QGGQT-GX8G08Q8-GNQGJ8-
八年级数学竞赛讲座 四边形（2）
一、 知识要点：
1、梯形的定义、判定；
2、等腰梯形的定义、性质、判定；
3、三角形、梯形的中位线定理；
二、 例题：
1、用长为1，4，4，5的线段为边作梯形，求其中面积最小的那个梯形的两条对角线的长度之和；
2、已知：如图，等腰梯形ABCD 中，AB ∥DC ，且AB ＞CD ，两对角线AC 、BD 相互垂直，若BC=213，AB+CD=34，求AB ，CD 的长；
3、如图：在梯形ABCD 中，AD ∥BC ，∠BAC=90°，AB=AC ，BD=BC ，AC 与BD 相交于点E ，求∠DCE 的度数；
4、已知：如图，在四边形ABCD 中，AB=CD ，E 、F 分别
是BC 、AD 的中点，BA 、CD 的延长线分别与EF 的延长线交于点M 、N
求证：∠AMF=∠CNE
5、已知：如图，梯形ABCD 中，AD ∥BC ，E 、F 分别是
两底AD 、BC 的中点，且EF=2
1（BC －AD ）， 求证：∠B+∠C=90°；
6、已知：如图，在△ABC 中，∠ACB=90°，D 为BC 的中点， G 为AD 的中点，CG 的延长线交AB 于点E ，EF ∥AC 交AD 于
点F ，求证：BE=2CF ；
7、已知：如图，M 是AB 的中点，C 是AB 上任意一点，N 、P 分别是DC 、DB 的中点，Q 是MN 的中点，PQ 的延长线交AC 于点E ，
求证：E 是AC 的中点；
8、如图：四边形ABCD 中，∠BAD=∠BCD ，∠ABC ≠∠ADC ，
∠ABC ，∠BCD ，∠CDA ，∠DAB 的平分线两两相交于E 、F 、G 、H ，
求证：四边形EFGH 为等腰梯形；
9、已知：梯形ABCD 中，AD ∥BC ，AD ＜BC ，E 为AB 的中点，DE ⊥CE ，求证：AD+BC=DC ；
10、已知，如图，梯形ABCD 中，AD ∥BC ，E 为CD 中点，
EF ⊥AB 于F ， 求证：AB EF S ABCD ⋅=梯形
11、在直角梯形ABCD 中，AB ⊥AD ，CD ⊥AD ，将BC 按逆时针方向绕点B 旋转90°，得到线段BE ，连接AE 、CE ，（如图（1））。
①若AB=2厘米，DC=3厘米，求证：1=∆ABE S 平方厘米；
A D F E
B C
②在图（1
）中，将线段
DC向上平行移动（其他条件不变），梯形ABCD和△ABE 的形状就会变化，如图（2）所示，如果DC一直移动到AB的上方，得到图（3），请你在上图的基础上将图（3）画完整（不需画出表示BC旋转方向的虚线）
12、如图：在直角梯形ABCD中，∠B=∠C=90°，AB=BC，M为BC上的一点，且∠DMC=45°，求证：AD=AM
13、如图：在四边形ABCD中，AD∥BC，AD=BC，BD=DC，AC⊥BD于M，
求证：)
(
2
1
DC
AB
CM+
=
14、在梯形ABCD中，AB∥CD，记
2
1
,
,S
S
S
S
S
S
DOC
AOB
BCD
=
=
=
∆
∆
∆
，
试判断
2
1
S
S+与S的大小，并说明理由；
15、如图，在△ABC中，BE平分∠ABC，CD平分∠ACB，P是DE的中点，过P向AB、BC、CA作垂线，垂足分别为B、M、Q、N，求证：PQ=PM+PN；
C D
M
B A
A B
M
D C
EA
N
D P E
作业题：
1、如图：在△ABC 中，AD 、BE 都是中线，MN 平分BE 且平行于AD ，已知AD 、BE 、MN 将△ABC 分成六部分的面积依次记为a 、b 、c 、d 、e 、f ，当f=18时，求a 、b 、c 、d 、e 的值；
2、在梯形ABCD 中，已知AC=BC ，M 是底边AB 的中点，
L 是DA 延长线上一点直线LM 交BD 于点N ，
求证：∠ACL=∠BCN
3、在梯形ABCD 中，AB ∥CD ，且AB=2CD ，M 、N 分别是对角线AC 、BD 的中点，设梯形ABCD 的周长为1l ，四边形CDMN 的周长为2l ，求1l 与2l 满足的关系式；
4、在梯形ABCD 中，AB ∥CD ，AB=a ，CD=b(a>b)，M 是DC 延长线上一点，如果AM 把梯形分成面积相等的两部分，求CM 的长；
5、△ABC 中，M 是AB 的中点，P 是AC 的中点，D 是MB 的中点，N 是CD 的中点，Q 是MN 的中点，直线PQ 交MB 于K ，求证：KB=KD ；
6、直角梯形ABCD 中，AB ∥CD ，E 是AD 上一点，△BCE 是等腰直角三角形，∠CEB=90°，M 是BC 的中点，求证：△ADM 是等腰直角三角形； D C M N A B D C
M
E
A B。