高等数学上 函数 教案 初等函数
基本初等函数 教案

基本初等函数教案教案标题:基本初等函数教案目标:1. 理解基本初等函数的概念和特征;2. 掌握基本初等函数的图像、定义域、值域和性质;3. 能够应用基本初等函数解决实际问题。
教学内容:1. 基本初等函数的定义和分类;2. 基本初等函数的图像和性质;3. 基本初等函数的定义域和值域;4. 基本初等函数的应用。
教学步骤:一、导入(5分钟)1. 引入基本初等函数的概念,让学生了解初等函数与常数函数、线性函数的区别;2. 通过举例,引导学生思考基本初等函数在生活中的应用。
二、概念讲解与示例分析(15分钟)1. 介绍基本初等函数的定义和分类,如常数函数、幂函数、指数函数、对数函数、三角函数等;2. 分别讲解每种基本初等函数的图像和性质,并通过图像展示和实例分析来加深学生的理解。
三、定义域和值域的讨论(15分钟)1. 解释基本初等函数的定义域和值域的概念;2. 以各种基本初等函数为例,引导学生求解其定义域和值域,并进行讨论和总结。
四、应用实例分析(15分钟)1. 提供一些实际问题,让学生应用基本初等函数解决;2. 引导学生分析问题,选择合适的基本初等函数进行建模,并求解问题。
五、练习与拓展(15分钟)1. 给学生一些练习题,巩固基本初等函数的概念和运用能力;2. 鼓励学生拓展思维,尝试解决更复杂的问题。
六、总结与反思(5分钟)1. 对本节课学习的内容进行总结;2. 鼓励学生提出问题或反思,以便进一步完善教学。
教学资源:1. 教材:包含基本初等函数的相关知识点和例题;2. 幻灯片:用于呈现基本初等函数的图像和性质;3. 实例题库:包含基本初等函数的应用实例。
教学评估:1. 课堂练习:通过练习题,检查学生对基本初等函数的理解和应用能力;2. 问题解答:通过学生的提问和回答,评估学生对基本初等函数的掌握程度;3. 实际问题解决:观察学生在应用实例中的解决能力,评估其综合运用能力。
教学延伸:1. 探索更多基本初等函数的性质和应用;2. 引导学生进行实际调研,了解基本初等函数在不同领域的应用案例;3. 鼓励学生自主学习和探索,拓展基本初等函数的应用范围。
基本初等函数优秀教案

基本初等函数优秀教案介绍:本教案旨在帮助学生理解和掌握基本初等函数的性质、图像和变化规律。
通过多种活动和案例分析,学生将能够深入了解函数的定义、性质和应用。
教学目标:1. 理解基本初等函数的定义和性质;2. 掌握函数图像的绘制方法;3. 分析函数的变化规律和应用实例。
教学重点:1. 函数的定义和性质;2. 函数图像的绘制方法。
教学难点:1. 函数性质的理解和应用;2. 函数图像的多样性和变化规律。
教学准备:1. 教师备课资料:基本初等函数的性质、定义和应用实例;2. 学生学习资料:教材教辅及图表练习册。
教学过程:Step 1:引入(10分钟)教师通过简单的问题引起学生对函数的认知,例如:“什么是函数?”“你能举出几个函数的例子?”然后教师可介绍函数的定义和概念。
Step 2:认识基本初等函数(20分钟)教师将基本初等函数的种类和性质呈现给学生,如常数函数、线性函数、二次函数、指数函数、对数函数等。
学生可以观察并分析这些函数的特点和图像。
Step 3:讨论函数性质(30分钟)学生分小组进行讨论,探究基本初等函数的性质。
教师可提供一些引导性问题,如“常数函数的图像是什么样的?”、“线性函数和二次函数的图像有什么区别?”等。
学生通过分析和讨论,总结出函数的性质。
Step 4:绘制函数图像(30分钟)学生根据教师提供的函数表达式,利用图表练习册上的坐标纸和绘图工具,绘制基本初等函数的图像。
教师可以带领学生一起绘制,同时解答学生在绘图过程中的问题。
Step 5:探索函数变化规律(30分钟)学生通过观察和分析绘制的函数图像,总结出函数的变化规律和特点。
教师可以给学生提供一些实际问题,引导学生应用函数进行解决。
Step 6:应用实例分析(20分钟)教师给学生提供一些实际生活中的问题,要求学生分析并应用基本初等函数进行解决。
学生可以通过函数的图像和变化规律,找到问题的合理解决方法。
Step 7:总结与延伸(10分钟)教师对本节课的重点内容进行总结,并对学生的学习情况进行评价。
高中数学初等函数性质教案

高中数学初等函数性质教案主题:初等函数性质教学目标:1. 理解初等函数的定义和性质。
2. 运用初等函数的性质解决实际问题。
3. 掌握初等函数的图像和性质。
4. 熟练运用初等函数进行函数运算。
教学内容:1. 初等函数的定义2. 初等函数的性质:奇偶性、周期性、对称性等3. 初等函数的图像表示4. 初等函数的运算教学重点:1. 理解初等函数的性质。
2. 掌握初等函数的运算方法。
教学难点:1. 运用初等函数性质解决复杂问题。
2. 绘制初等函数的图像。
教学方法:1. 讲授结合实例分析。
2. 课堂练习巩固。
3. 个别辅导解决疑难问题。
教学流程:一、导入(5分钟)教师引导学生回顾初等函数的基本概念,并提出本节课的学习目标。
二、讲解初等函数的性质(15分钟)1. 介绍初等函数的奇偶性、周期性和对称性等基本性质。
2. 分析不同类型的初等函数,并让学生讨论其性质。
三、练习巩固(20分钟)1. 针对初等函数的性质进行练习,检验学生理解程度。
2. 学生互相交流解题思路,相互学习。
四、讲解初等函数的图像表示(15分钟)1. 介绍如何绘制初等函数的图像。
2. 示范绘制不同类型初等函数的图像。
五、课堂练习(20分钟)1. 让学生绘制初等函数的图像,并分析其性质。
2. 出示实际问题,让学生运用初等函数解决问题。
六、总结(5分钟)回顾本节课的重点内容,强调初等函数的性质对解决问题的重要性。
七、作业布置(5分钟)布置相关作业,巩固学生对初等函数性质的理解。
教学资源:1. 教材相关内容2. 小白板、彩色笔3. 练习册、作业纸教学反思:通过本堂课的教学,学生对初等函数的性质有了更深入的理解,能够熟练运用初等函数解决实际问题。
但在绘制初等函数的图像时,部分学生仍存在困难,需要多给予指导和练习机会。
下节课需要注重图像的绘制方法,提高学生的图像表达能力。
高等数学教案第一章

第一章函数与极限一、教学内容1.函数:常量与变量、函数的定义;2.函数的表示方法:解析法、图示法、表格法;函数的性质:单调性、奇偶性、有界性和周期性;3.初等函数:基本初等函数、反函数、复合函数、初等函数、分段表示的函数,并会建立函数关系;4.极限:数列极限、函数极限、左右极限、极限四则运算法则、两个重要极限、无穷小量、无穷大量、无穷小量的性质;5.连续:连续、间断、初等函数的连续性、闭区间上连续函数的性质。
二、教学目的1.理解函数的概念及其性质,熟练掌握求函数定义域和函数值的方法;2.掌握基本初等函数的解析表达式、定义域、主要性质和图形;3.了解反函数的概念及互为反函数的函数图象之间的关系;理解复合函数、分段函数的概念;了解初等函数的概念;会建立函数关系;4.了解数列极限与函数极限的概念(描述性定义);会求左右极限;5.掌握极限四则运算法则;掌握用两个重要极限求极限的方法;能熟练进行极限运算;6.理解无穷小量、无穷大量的概念及相互关系;7.理解函数连续概念;掌握由初等函数的连续性求极限的方法;了解闭区间上连续函数的性质。
三、教学重点1.函数的概念及其性质、基本初等函数、复合函数;2.极限的运算。
3.无穷小量、无穷大量的概念及相互关系;4.函数连续概念、闭区间上连续函数的性质。
四、教学难点1.极限的概念;2.无穷小量、无穷大量的概念及相互关系; 3.函数连续概念。
第一节 函数一、集合 1、集合概念具有某种特定性质的事物的总体叫做集合。
组成这个集合的事物称为该集合的元素。
表示方法:用A ,B ,C ,D 表示集合;用a ,b ,c ,d 表示集合中的元素1)},,,{321 a a a A = 2)}{P x x A 的性质=元素与集合的关系:A a ∉ A a ∈一个集合,若它只含有有限个元素,则称为有限集;不是有限集的集合称为无限集。
常见的数集:N ,Z ,Q ,R ,N + 元素与集合的关系:A 、B 是两个集合,如果集合A 的元素都是集合B 的元素,则称A 是B 的子集,记作B A ⊂。
高等数学第二节初等函数

余弦函数: y=cos x
函数图象关于 y 轴对称,是偶函数;
是周期函数,周期为2 ;
cos x 1,是有界函数。
正切函数: y=tan x
y
y=tan x
-
2
O
2
函数图象关于原点对称,是奇函数;
是周期函数,周期为 ;
当 x (k - , k ), k Z 时,
则它们构成的复合函数为 y=f [(x)] = lgsinx.
例2.设y=f (u)=lg(u–2), u=(x)=sinx,能否构成
复合函数?
因u=sinx的值中,不能使y=lg(u-2)有意义, 所以 它们不能构成复合函数
例3. 指出下列复合函数的结构
(1) y cos2 x
(2) y
反正切函数 y arctan x
反正切函数图象关于原点对称, 是奇函数; 是单调增函数; arctan x , 是有界函数。
2
反余切函数 y arccot x
是单调减函数; 0 arccot x ,是有界函数。
二、复合函数
在实际问题中,因变量与自变量的关系不是直接的,
y 1- x2
定义: 设函数 y f (u),其中u ( x), 且(x) 的
值的全部或部分落在 f(u)的定义域内, 则称函数
y f [( x)]为 x的复合函数,而 u 为中间变量
x u f y
自变量
中间变量 因变量
例1.设y=f (u)=lgu, 而u=(x)=sinx.
解
y y 设通话x分钟,中国联通收费 1 元,中国移动收费 2 元
则
y1 36 0.4x, y2 0.6x
高一数学上册《函数的基本性质》教案、教学设计

3.学生在小组合作学习中的参与度有待提高。教师应关注学生的个体差异,调动每个学生的积极性,使他们在合作交流中发挥自己的优势,共同进步。
4.学生对于数学知识在实际生活中的应用认识不足,教师可通过引入实际问题,让学生体会数学知识的价值,激发学生学习数学的兴趣。
6.教学评价,关注成长
在教学过程中,教师应关注学生的成长和发展,采用多元化的评价方式,如课堂表现、作业完成情况、小组合作交流等,全面评估学生的学习效果。
7.创设互动氛围,激发学生学习兴趣
8.融入信息技术,提高教学质量
利用多媒体、网络等信息技术手段,丰富教学资源,提高教学质量。如通过数学软件绘制函数图像,让学生更直观地感受函数性质。
3.结合所学函数性质,尝试解决以下拓展性问题:
(1)已知函数f(x) = x^3 - 6x^2 + 9x + 1,判断其奇偶性,并求单调区间。
(2)已知函数g(x) = 3cos(2x) + 4sin(x),求最小正周期及一个周期内的单调区间。
4.请同学们预习下一节课内容,了解函数的极值及其在实际问题中的应用。
3.鼓励学生积极参与课堂讨论,勇于表达自己的观点,培养学生自信、勇敢的品质。
4.通过解决实际问题,让学生认识到数学知识在生活中的重要作用,增强学生应用数学知识解决实际问题的意识,提高学生的社会责任感。
在本章节的教学过程中,教师应以学生为主体,关注学生的个体差异,充分调动学生的积极性、主动性和创造性。通过讲解、示范、讨论等多种教学手段,使学生在掌握函数基本性质的基础上,提高自身的数学素养和综合素质。同时,注重培养学生的团队合作精神,使其在合作交流中相互学习、共同成长。
初等函数教案模板高中

课时:2课时年级:高一年级教材:《高中数学》人教版教学目标:1. 理解初等函数的概念,掌握基本初等函数的种类及其性质。
2. 能够运用初等函数解决实际问题,提高学生的数学应用能力。
3. 培养学生的逻辑思维能力和数学素养。
教学重难点:1. 重点:掌握基本初等函数的概念和性质,能够区分不同类型的基本初等函数。
2. 难点:理解初等函数在解决实际问题中的应用,提高学生的数学应用能力。
教学过程:第一课时一、导入1. 复习初中阶段函数的概念,回顾函数的定义、定义域、值域等概念。
2. 通过生活中的实例,如温度与时间的关系、路程与时间的关系等,引导学生理解函数在生活中的应用。
二、新课讲解1. 介绍基本初等函数的概念,包括常数函数、幂函数、指数函数、对数函数和三角函数等。
2. 讲解每种基本初等函数的定义、性质和图像特点,引导学生通过观察图像来理解函数的性质。
三、课堂练习1. 学生独立完成教材中的例题,巩固对基本初等函数的理解。
2. 教师巡视指导,解答学生在练习过程中遇到的问题。
四、课堂小结1. 总结本节课所学内容,强调基本初等函数的概念和性质。
2. 强调函数在解决实际问题中的重要性。
第二课时一、复习导入1. 回顾上一节课所学的基本初等函数的概念和性质。
2. 通过提问的方式,检查学生对基本初等函数的理解程度。
二、新课讲解1. 介绍初等函数的运算,包括函数的加、减、乘、除和复合运算。
2. 讲解函数的图像变换,如平移、伸缩、对称等,引导学生通过变换图像来理解函数的性质。
三、课堂练习1. 学生独立完成教材中的例题,巩固对初等函数运算和图像变换的理解。
2. 教师巡视指导,解答学生在练习过程中遇到的问题。
四、实际问题应用1. 引导学生运用所学知识解决实际问题,如计算物体的运动速度、求解物体的高度等。
2. 学生分组讨论,共同解决问题,教师巡视指导。
五、课堂小结1. 总结本节课所学内容,强调初等函数的运算和图像变换。
2. 强调初等函数在解决实际问题中的重要性。
1 函数的概念、性质、初等函数
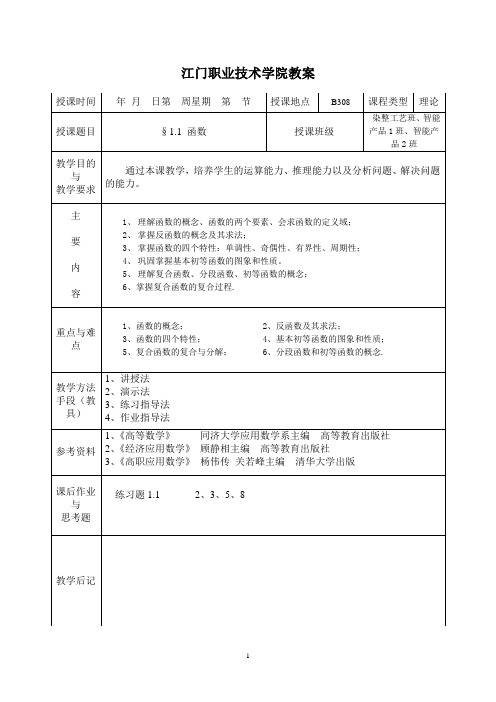
江门职业技术学院教案授课时间年月日第周星期第节授课地点B308 课程类型理论授课题目§1.1 函数授课班级染整工艺班、智能产品1班、智能产品2班教学目的与教学要求通过本课教学,培养学生的运算能力、推理能力以及分析问题、解决问题的能力。
主要内容1、理解函数的概念、函数的两个要素、会求函数的定义域;2、掌握反函数的概念及其求法;3、掌握函数的四个特性:单调性、奇偶性、有界性、周期性;4、巩固掌握基本初等函数的图象和性质。
5、理解复合函数、分段函数、初等函数的概念;6、掌握复合函数的复合过程.重点与难点1、函数的概念; 2、反函数及其求法;3、函数的四个特性;4、基本初等函数的图象和性质;5、复合函数的复合与分解;6、分段函数和初等函数的概念.教学方法手段(教具)1、讲授法2、演示法3、练习指导法4、作业指导法参考资料1、《高等数学》同济大学应用数学系主编高等教育出版社2、《经济应用数学》顾静相主编高等教育出版社3、《高职应用数学》杨伟传关若峰主编清华大学出版课后作业与思考题练习题1.1 2、3、5、8 教学后记教学过程设计§1.1 函 数一、函数的概念1.定义:设D 与B 是两个非空实数集,如果对D 中的每一个数x ,按照某种对应法则f ,B 中存在惟一的数y 与之对应,则对应法则f 是定义在数集D 上的函数。
记作)(x f y =。
在点0x 处的函数值记为0|x x y =或)(0x f 。
2、两个要素:在函数定义中,定义域与对应法则是函数概念的两个要素。
两个函数,如果定义域和对应法则都相同,它们就是同一函数,否则就不是同一函数。
函数的定义域是使函数解析式有意义的自变量的取值范围。
求函数的定义域应遵守以下原则:(1)分式中分母不能为零;(2)偶次根式内被开方数非负;(3)对数的真数大于0,底数大于0且不等于1;(4)在反三角函数中,要符合反三角函数的定义域。
(5)如果函数表达式中含有分式、根式、对数式或反三角函数式,应该取各部分定义域的交集;(6)对于表示实际问题的解析式,还应该保证符合实际意义.例 求函数y =)12arcsin(312-+-x x 的定义域. 二、反函数的求解步骤−−−−→−=的方程解x x f y )1()(−−−→−=-互换、y x y f x )2(1)()(1x f y -= (注明其定义域)三、函数的特性1、奇偶性:若函数)(x f 的定义域D 关于原点对称,则(1),D x ∈∀)(x f -)()(x f x f ⇒-=是奇函数(图象关于原点对称)(2),D x ∈∀)(x f -)()(x f x f ⇒=是偶函数(图象关于y 轴对称)补例: 判定下列函数的奇偶性:1、)1ln(2++=x x y (奇函数)2、12)(2-=x x f (偶函数)3、12)(2-=x x f )1,1[-∈x (非奇非偶函数)4、)cos lg(sin )(22x x x f += (既是奇函数,又是偶函数)2、单调性:设函数)(x f 的定义域为D ,区间D I ⊂,如果I x x ∈∀21,,当21x x <时,有(1))()()(21x f x f x f ⇒<在I 上单调增加;(2))()()(21x f x f x f ⇒>在I 上单调减少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教师:接下来,我们学习第一节映射与函数中的函数。
一、函数 (板书)
1. 函数的概念 (板书) 定义 设数集D ⊂R , 则称映射f : D →R 为定义在D 上的函数, 通常简记为
y =f (x ), x ∈D ,
其中x 称为自变量, y 称为因变量, D 称为定义域, 记作D f , 即D f =D 。
函数值f (x )的全体构成的集合称为函数f 的值域,记作R f = f (D )={y| y =f (x ), x ∈D }.
2. 函数的两要素 (板书)
构成函数的两个重要因素:定义域及对应法则 .
如果两个函数的定义域相同, 对应法则也相同, 那么这两个函数就是相同的, 否则就是不同的.(熟记)
3. 常见函数 (板书)
(1) 函数 2y = 定义域D =(-∞, +∞),值域W ={2}
(2) 绝对值函数:⎩⎨⎧<-≥==0
0 ||x x x x x y 其定义域为D =(-∞, +∞), 值域为R f =[0, +∞)。
(3) 符号函数:⎪⎩
⎪⎨⎧<-=>==01000 1sgn x x x x y 其定义域为D =(-∞, +∞), 值域为R f ={-1, 0, 1}。
(4) 取整函数:设x 为任一实数,不超过x 的最大整数,称为x 的整数部 分, 记作[ x ],例如0]7
5[=, 1]2[=, [π]=3。
把x 看作变量,函数
y = [ x ]
即为取整函数。
其定义域为D =(-∞, +∞), 值域为R f =Z 。
(5) 分段函数:
老师:在自变量的不同变化范围中, 对应法则用不同式子来表示的函数称为分段函数。
符号函数和取整函数都是分段函数。
例:狄利克雷函数
1()0x y D x x ⎧==⎨⎩
当是有理数时当是无理数时 4. 函数的几种特性 (板书)
(1) 函数的有界性
设函数f (x )的定义域为D , 数集X ⊂D . 如果存在数K 1, 使得
f (x )≤K 1
对任一x ∈X 都成立, 那么称函数f (x )在X 上有上界,K 1称为函数f (x )在X 上的一个上界。
如果存在数K 2, 使得
f (x )≥ K 2
对任一x ∈X 都成立,那么称函数f (x )在X 上有下界,K 2称为函数f (x )在X 上的一个下界。
如果存在正数M , 使得
| f (x ) |≤M
对任一x ∈X 都成立,那么称函数f (x )在X 上有界; 如果这样的M 不存在, 则称函数f (x )在X 上无界。
例如
1) f (x )=sin x 在(-∞, +∞)上是有界的: |sin x |≤1.
2) 函数x
x f 1)(=在开区间(0, 1)内有下界, 无上界. (2) 函数的单调性
设函数y = f (x )的定义域为D , 区间I ⊂D . 若12x I x ∀∈,
, 当x 1<x 2时, 恒有 f (x 1)< f (x 2)
则称函数f (x )在区间I 上是单调增加的.
若12x I x ∀∈,
, 当x 1<x 2时, 恒有 f (x 1)> f (x 2),
则称函数f (x )在区间I 上是单调减少的.
单调增加和单调减少的函数统称为单调函数.
(3) 函数的奇偶性
设函数f (x )的定义域D 关于原点对称(若x ∈D , 则-x ∈D ). 如果对于∀ x ∈D , 有
f (-x ) = f (x )
则称f (x )为偶函数.
如果对于∀x ∈D , 有
f (-x ) = -f (x ),
则称f (x )为奇函数.
奇函数和偶函数的图像最大的特点:奇函数关于原点对称,偶函数关于Y 轴对称。
(4) 函数的周期性
设函数f (x )的定义域为D . 如果存在一个正数l , 使得对于∀x ∈D 有(x ±l )∈D , 且
f (x +l ) = f (x )
则称f (x )为周期函数, l 称为f (x )的周期,一般要求是最小正周期。
例: f (x )=sin2x 周期为π
例1:狄利克雷函数
1()0x y D x x ⎧==⎨⎩当是有理数时当是无理数时
1) 是奇函数 ( X )
2) 是偶函数 ( √ )
3) 是单增函数 ( X )
4) 是有界函数 ( √ )
5) 是周期函数 ( √ )
r 是有理数,D (x+r )= D (x ),有理数加有理数等于有理数,无理数加有理数等于无理数,任何一个有理数都是周期,故无最小正周期。
