复变函数第2章
复变函数第2章
By 宋朝红2.1 复变函数的极限2.2 复变函数的连续性2.3 导数2.4 解析函数2.5 调和函数Math HZAU第二章导数zz f z z f z Δ)()Δ(lim 000Δ−+→1 导数与微分定义：设函数w=f(z)在包含z 0的某邻域D 内有定义，点z 0+⊿z ∈D. 如果极限存在, 则称f (z )在z 0可导, 此极限值就称为f (z )在z 0的导数, 记作0000Δ0(Δ)()d ()lim .d Δ|z z z f z z f z w f z z z=→+−′==如果f (z )在区域D 内处处可导, 则称f(z)在Ｄ内可导.例1求f (z )=z 2的导数例3讨论函数f (z )=|z|2的可导性函数可导一定连续，但连续却不一定可导例2问：函数f (z )=x +2yi 是否可导？求导公式与法则①常数的导数c ′=(a+ib )′=0.②(z n )′=nz n-1(n 是自然数).③设函数f (z ),g (z ) 均可导，则[f (z )±g (z )]′=f ′(z )±g ′(z )，[f (z )g (z )]′= f ′(z )g (z )+ f (z )g ′(z )----实函数中求导法则的推广)0)((,)()(')()()('')()(2≠−=⎥⎦⎤⎢⎣⎡z g z g z g z f z g z f z g z f④复合函数的导数( f [g (z )])′=f ′(w )g ′(z )，其中w=g (z )。
.0)()()()(10处可导点外）处在复平面上（除分母为导；在整个复平面上处处可由以上讨论z Q z P z R z a z a a z P nn =+++=⇒"⑤反函数的导数，其中: w=f (z )与z=ϕ(w )互为单值的反函数，且ϕ′(w )≠0。
)('1)('w z f ϕ=例3求f (z )=Arcsinz=-iLn (iz+ ）的导数。
复变函数-第2章
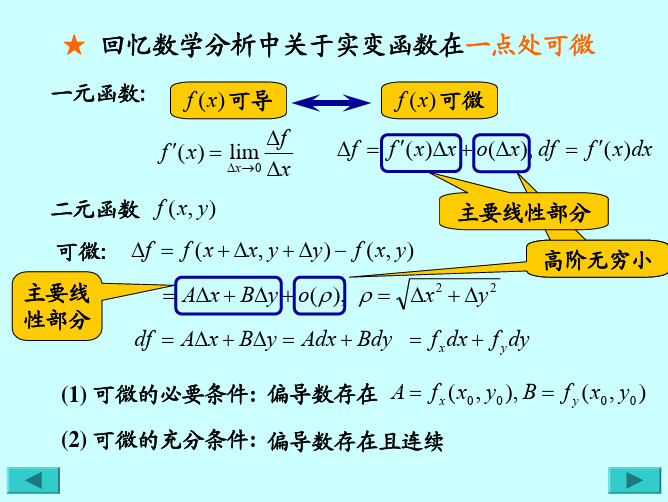
(1) 若 Δz 沿实轴趋于0, 即 Δz = Δx,
f ′( z0 ) = lim u ( x0 + Δx, y0 ) + iv( x0 + Δx, y0 ) − u ( x0 , y0 ) − iv( x0 , y0 ) Δx →0 Δx u ( x0 + Δx, y0 ) − u ( x0 , y0 ) v( x0 + Δx, y0 ) − v( x0 , y0 ) = lim + i lim Δx → 0 Δx → 0 Δx Δx ∂u ∂v = ( x0 , y0 ) + i ( x0 , y0 ) ∂x ∂x
∀ z0 ∈ C,
f ( z0 + Δz ) − f ( z0 ) z0 + Δz − z0 Δz = = Δz Δz Δz Δx − iΔy ⎧ 1, Δy = 0 = →⎨ 差商的极限不存在！ Δx + iΔy ⎩− 1, Δx = 0
所以, 与 z 有关的函数不可微. 比如, x, y作为一元或者二元实函数都是可微的, z+z z−z 但作为复函数则不可微! x= ,y= 2 2i
但是,
| ΔxΔy | f (0 + Δz ) − f (0) = Δz Δx + iΔy
取 Δy = kΔx
Δx → 0 +
|k| 1 + ik
差商极限不存在, 故不可微. ★ 想一想问题出在哪里? 注意到, 实函数 u ( x, y ) = | xy | 在(0,0)不可微!
反证, 若实函数 u ( x, y ) = | xy | 在(0,0)可微, 则
2. 柯西-黎曼(Cauchy-Riemann)方程
若函数 f ( z ) = u ( x, y ) + iv( x, y ) 在 z0 = x0 + iy0 可导, 则
复变函数复变函数2
z0
)或
dw dz
z z0
.
应该注意：上述定义中z 0的方式是任意的。
容易证明： 可导
可微 ；可导
连续。
如果 f (z) 在区域D内处处可导, 就说 f (z) 在Ｄ内可导.
例1 求 f (z) = z2 的导数。
[解] 因为 lim f (z Δ z) f (z) lim (z Δ z)2 z2
§2.2 解析函数和调和函数的关系
定义1 实函数u(x, y)为区域D内的调和函数：
u(x, y)在区域D内有二阶连续偏导数，
且满足u uxx uyy 0
(称为调和方程或Laplace方程)
定理1：f (z) u(x, y) iv(x, y)是区域D内的解析函数
u与v是区域D内的调和函数
f (z)在区域D内解析：f (z)在D内处处解析.
函数在一点解析 在该点可导。反之不一定成立。
在区域内： 解析 可导 .
例如 f (z) = z2 在整个复平面上解析；w f (z) z 2
仅在原点可导，故在整个复平面上不解析；
f (z) = x +2yi 在整个复平面上不解析。
例4 讨论函数 f (z)=1/z 的解析性.
是区域内的正交 曲线族。
(正交：两曲线在交点处的切线垂直 )
证：u ( x,
y)
C1在( x,
y)处切线的斜率ku
ux uy
，
v(x,
y)
C2在(x,
y)处切线的斜率kv
vx vy
ku kv
ux uy
vx vy
C
R
vy uy
uy vy
1,
得证。
例如 f z z2 x2 y2 i2xy, f z 2z 0z 0.
复变函数第二章 解析函数
第 一 节 解 析 函 数 的 概 念
( 5)
f ( z ) ′ g ( z ) f ′ ( z ) − f ( z ) g ′ ( z ) , g (z) ≠ 0 = 2 g ( z) g ( z)
( 6)
{
f g ( z )
}
′
= f ′ ( w ) g ′ ( z ) , 其中w = g ( z )
dw 可见：可导 ⇔ 可微， f ′ ( z0 ) = 且 dz
z = z0
如果f ( z ) 在区域D内每一点可微，
则称f ( z ) 在D内可微.
记作 dw = f ′ ( z ) dz
第 一 节 解 析 函 数 的 概 念
二、解析函数 定义 1o 如果f ( z ) 在z0 及z0的某邻域内处处可导，
设w = f ( z ) 定义于区域D, z0 ∈ D , z0 + ∆ z ∈ D
f ( z0 + ∆ z ) − f ( z0 ) 如果 lim 存在 ∆ z →0 ∆z 则 称 f ( z ) 在 z0点 可 导 ， 而 极 限 值 为 f ( z ) 在 z0点 dw 的导数，记作 f ′ ( z0 ) 或 dz z = z0
∴ ∆ u = a ∆ x − b ∆ y + o1 ∆ v = b∆ x + a ∆ y + o2
反之，不成立。
( 2)
( 3)
f ( z ) 在区域D内解析
⇔ f ( z ) 在 区 域 D内 可 导 。
f ( z ) 在 z0 解析 ⇔
f ( z ) 在 z0的某邻域 N δ ( z0 )内解析。
第 一 节 解 析 函 数 的 概 念
复变函数第二章
2连续、可导、解析的关系
f ( z ) 在D内解析
f ( z ) 在D内可导
f ( z ) 在z0解析
f ( z ) 在z0可导
f ( z ) 在z0连续
3 复变函数与二元实函数的关系
设f ( z ) = u ( x, y ) + iv( x, y ), A = u0 + iv0 , z0 = x0 + y0i
例5
求出下列各函数的解析区域,并求出导数.
1）f ( z ) =
z
2
2
z +1
,
x+ y x− y 2) f ( z ) = 2 +i 2 2 2 x +y x +y
f ( z )在z 2 + 1 ≠ 0，即z ≠ ±i外处处可导，因此 解: 1) 其解析区域为复平面内除去z ≠ ±i两点.且
2z 2 z ( z 2 + 1) − z 2 2 z = 2 f ′( z ) = 2 2 ( z + 1) 2 ( z + 1)
则称f ( z )在z 0 可导.这个极限值称为f ( z )在z 0的导数.
dω 记作f ′( z0 ) = dz
z = z0
f ( z 0 + ∆z ) − f ( z 0 ) = lim . ∆z → 0 ∆z
在定义中应注意: 在定义中应注意
z0 + ∆z → z0 (即∆z → 0)的方式是任意的 .
∂u ∂u ∂x ∂u ∂y ∂u ∂u 则 = + = cos θ + sin θ ∂r ∂x ∂r ∂y ∂r ∂x ∂y
导数公式的其它形式 导数公式
∂u ∂v f ′( z ) = +i ∂x ∂x
复变函数第2章(钟玉泉)
容易看出, 这四个偏导数处处连续, 但仅当 x=y=0时, 它们才满足柯西-黎曼方程, 因而函 数仅在z=0可导, 但在复平面内任何地方都不 解析.
例2 设函数f(z)=x2+axy+by2+i(cx2+dxy+y2). 问常 数a,b,c,d取何值时, f(z)在复平面内处处解析? [解] 由于 ux=2x+ay, uy=ax+2by, vx=2cx+dy, vy=dx+2y 要使ux=vy, uy=-vx, 只需2x+ay=dx+2y, 2cx+dy=-ax-2by. 因此, 当a=2, b=-1, c=-1, d=2时, 此函数在复 平面内处处解析, 这时 f(z)=x2+2xy-y2+i(-x2+2xy+y2) =(1-i)(x+iy)2=(1-i)z2
定理二 函数f(z)=u(x,y)+iv(x,y)在其定义域D内 解析的充要条件是u(x,y)与v(x,y)在D内可微, 并满足柯西-黎曼方程。
例1 判断下列函数在何处可导, 在何处解析:
1)w z ; 2) f ( z ) e (cos y i sin y); 3)w z Re( z )
f ( z0 Δ z ) f ( z0 ) f ( z0 ) e Δz
应当注意, 定义中z0+Dzz0(即Dz0)的方式 是任意的, 定义中极限值存在的要求与 z0+Dzz0的方式无关, 也就是说, 当z0+Dz在区 域D内以任何方式趋于z0时, 比值
f ( z0 Δ z ) f ( z0 ) 都趋于同一个数. Δz
【复变函数】第二章 解析函数(工科2版)
2 2 2 解: f ( z ) = | z | = x + y
∴ u( x , y ) = x 2 + y 2 , v ( x , y ) = 0
∂u ∂u ∂v ∂v = 2 x, = 2 y, = 0, =0 ∂x ∂y ∂x ∂y
条件, 由C-R条件 x=0, y=0 , 条件 所以在z=0处可导 处处不解析. 所以在 处可导, 处处不解析 处可导
目录
上页
下页
返回
结束
【例3】讨论下列函数的解析性 可导性 . 】讨论下列函数的解析性, (1). f ( z ) = x + 2 yi 在复平面上处处不可导, 解：f (z) 在复平面上处处不可导,处处不解析
( 2 ). f ( z ) = z 2
在复平面上处处可导, 解：f (z) 在复平面上处处可导,处处解析 1 ( 3 ). f ( z ) = z 1 解：f ′( z ) = − 2 除 z = 0 外处处可导,处处解析. 外处处可导,处处解析. z 1+ z ( 4 ). f ( z ) = 1− z 2 解：f ′( z ) = 外处处可导,处处解析. 2 除 z = 1 外处处可导,处处解析. (1 − z )
返回 结束
目录
上页
下页
内处处为0, 内为一个常数. 【例6】若f'(x)在D内处处为 则f(x)在D内为一个常数 】 在 内处处为 在 内为一个常数 Proof: 由导数的计算公式
∂u ∂v ∂u ∂v f ′( z ) = +i =0 ⇔ = 0, = 0, ∂x ∂x ∂x ∂x
∂u ∂v ∂v ∂u = 0, = 0, f ′( z ) = −i =0 ⇔ ∂y ∂y ∂y ∂y
第2章 复变函数
( x, y ) Î E .
(1)
其中 u = u ( x, y ) 和 v = v( x, y ) 是一对二元实函数, 它们分别称为 f ( z ) 的实部和虚部, 分别记 为 Re f ( z ) 和 Im f ( z ). 这说明一个复函数等价于一对二元实变量的实函数. 复函数的形如(1)式的表示形式对应于复数的代数形式. 对应于复数的指数形式, 相应地可 以将复函数表示为指数形式:
f ( z) > M ,
则称当 z 0 时, f ( z ) 趋近于无穷大 记为 lim f ( z ) = ¥.
z z0
(2) 设 w = f ( z ) 是定义在 E 上的复函数, 无穷远点 ¥ 是 E 的聚点(即对任意 r > 0, ¥ 的
r 邻域 { z : z > r } 中包含 E 中的点), 是一复数. 若对任意 > 0, 存在 r > 0, 使得当 z Î E 并且 z > r 时, 有
复变函数的连续性
定是 E 的聚点. 若
z z0
lim f ( z ) = f ( z0 ),
则称 f ( z ) 在点 z0 处(相对于集 E )连续. 若 f ( z ) 在 E 上的每一点处都连续, 则称 f ( z ) 在 E 上连 续. 例6 例 5(2)的结论表明多项式函数在复平面上处处连续. 设 f ( z ) = u ( x, y ) + iv( x, y ) 是定义在 E 上的复函数, z0 = x0 + iy0 是 E 的聚 定理 2.1.2
于是 f ( z ) f ( z0 ) f ( z ) f ( z0 )
1 f ( z0 ) . 2
1 f ( z0 ) . 即 2
复变函数第二章(第三讲)
∂u ∂v 1 ∂u ∂v iii) 求导数： f '(z) = ∂x + i ∂x = i ∂y + ∂y 求导数：
前面我们常把复变函数看成是两个实函数拼成的, 前面我们常把复变函数看成是两个实函数拼成的, 但是求复变函数的导数时要注意, 但是求复变函数的导数时要注意, 并不是两个实函 数分别关于x, 求导简单拼凑成的 求导简单拼凑成的. 数分别关于 ,y求导简单拼凑成的.实可微与复可微 是完全不同的概念。 是完全不同的概念。
§2.2 解析函数的充要条件
Cauchy-Riemann定理 1. Cauchy-Riemann定理 2. 举例
Cauchy-Riemann定理 1. Cauchy-Riemann定理
定理 设f (z)= u + i v, z= x +i y, z0=x0+i y0, 则f (z)在 在
(1) u( x, y), v( x, y)在( x0 , y0 )可微, ∂u ∂v ∂u ∂v z0处可导⇔ . (2) = , = − 在( x0 , y0 )成立 ∂x ∂y ∂y ∂x 定义 方程
∂u ∂v = ∂x ∂y
∂v ∂u =− ∂x ∂y
称为Cauchy-Riemann方程(简称C-R方程).
֠
由此可以看出可导函数的实部与虚部有密切 的联系. 的联系.
֠ 利用该定理可以判断那些函数是不可导的. 利用该定理可以判断那些函数是不可导的.
基本步骤: 偏导数的连续性， 基本步骤 i) 判别 u(x, y)，v (x, y) 偏导数的连续性， ， ii) 验证 验证C-R条件 条件. 条件
由以上讨论得 函数； P ( z ) = a 0 + a1 z + L + a n z n 是整个复平面上的解析 函数； P(z) R( z ) = 是复平面上 ( 除分母为 0点外 )的解析函数 . Q( z)
第二章复变函数
v( x, y) = xy
∂u =0 ∂y ∂v =x ∂y
Q 都是初等函数，在复平面内处处连续；
∂u ∂v ∂x = ∂y 针对柯西 − 黎曼方程 仅在 z = 0处成立 ∂u = − ∂v ∂y ∂x
∂u ∂v 导数： f ' ( z = 0 ) = [ + i ] | z = 0 = ( 2 x + iy ) | x = 0, y = 0 = 0 ∂x ∂x
∂u ∂v |( x, y ) +i |( x, y ) ∂x ∂x
（）∆z 0 2 →
沿虚轴
∆ z = i∆ y
{u ( x, y + ∆y ) + iv ( x, y + ∆y )} − {u ( x, y ) + iv ( x, y )} lim i∆ y ∆y → 0 1 u ( x, y + ∆y ) − u ( x, y ) v ( x , y + ∆y ) − v ( x , y ) + lim lim ∆y i ∆y →0 ∆y ∆y → 0
f 例: f ( z ) = u + iv为解析函数， ' ( z ) ≠ 0, 则曲线u ( x, y) = c1
v( x, y ) = c2必互相正交。
证： ux 曲线 u ( x , y ) = c1 斜率为 k1 = − uy vx 曲线 v ( x , y ) = c 2 斜率为 k 2 = − vy
w = f ( z) = z
2
的可导性。
2 2 ∆ w f ( z + ∆z ) − f ( z ) z + ∆z − z = = ∆z ∆z ∆z
第二章 复变函数
第二章 复变函数:第二节：初等函数1、指数函数：我们要把实指数函数的定义扩充到整个复平面上，使得复变数z=x+iy 的函数f (z )满足下列条件：（1）x e x f R x =∈∀)(,；（2）f (z )在整个复平面C 上解析；（3）C ,21∈∀z z ，有)()()(2121z f z f z z f =+； 则可以证明，)sin (cos )(y i y e z f x +=，事实上，由(3)及(1)有)()()(iy f e iy x f z f x =+=令 ),()()(y iB y A iy f +=其中A (y )及B (y )是实值函数，所以)()()(y B ie y A e z f x x +=显然，y y A cos )(=及y y B sin )(=满足上面的条件。
若,,222111iy x z iy x z +=+=则有)()]sin()[cos()sin (cos )sin (cos )()(2121212211212121z z f y y i y y e y i y e y i y ez f z f x x x x +=+++=++=+ 因此，定义复指数函数，为)sin (cos exp y i y e z e w x z +==由此有Euler 公式：y i y e iy sin cos +=；指数函数的基本性质：（4）C ∈∀z ，0≠z e ；（5）指数函数z e w =在整个复平面内有定义并且解析，z z e e =)'(，指数函数z e w =是实指数函数在复平面上的解析推广；（6）Euler 公式：y i y e iy sin cos +=；（7）从定义得||x z e e =， ,2,1,02±±=+=k k y Arge z ，π利用Euler 公式，得到复数的指数表示式：若复数z 的模为r ，幅角为θ，则有θθθi re i r z =+=)sin (cos ；（8）指数函数是周期i π2为得周期函数；（9）指数函数的几何映射性质：由于指数函数有周期i π2，所以研究当z 在带形}2Im 0C,|{π<<∈=z z z B 中变化时，函数z e w =的映射性质。
《复变函数论》第二章
第二章 复变函数第一节 解析函数的概念及C.-R.方程1、导数、解析函数定义2.1：设()w f z =是在区域D 内确定的单值函数，并且0z D ∈。
如果极限00,0()()limz z z Df z f z z z →∈--存在，为复数a ，则称)(z f 在0z 处可导或可微，极限a 称为)(z f 在0z 处的导数，记作0'()fz ，或z z dw dz=。
定义2.2：如果()f z 在0z 及0z 的某个邻域内处处可导，则称()f z 在0z 处解析；如果()f z 在区域D 内处处解析，则我们称()f z 在D 内解析，也称()f z 是D 的解析函数。
解析函数的导（函）数一般记为'()f z 或d ()d f z z。
注解1、εδ-语言，如果任给0ε>，可以找到一个与ε有关的正数()0δδε=>，使得当z E ∈，并且0||z z δ-<时，00()()||f z f z a z z ε--<-，则称)(z f 在0z 处可导。
注解2、解析性与连续性：在一个点的可导的函数必然是这个点的连续函数；反之不一定成立；注解3、解析性与可导性：在一个点的可导性是一个局部概念，而解析性是一个整体概念；注解4、函数在一个点解析，是指在这个点的某个邻域内解析，因此在此点可导；反之，在一个点的可导性不能得到在这个点解析。
解析函数的四则运算：()f z 和()g z 在区域D 内解析，那么()()f z g z ±，()()f z g z ，()/()f z g z （分母不为零）也在区域D内解析，并且有下面的导数的四则运算法则：(()())''()'()[()()]''()()()'()f zg z f z g z f z g z f z g z f z g z ±=±=+2()'()()()'()()[()]'f z f z g z f z g z g z g z -⎡⎤=⎣⎦。
复变函数论第二章总结
复变函数论第二章总结一、思维导图二、分类1.与积分路径无关：定理1 如果函数f(z)在单连通域内处处解析，F(z)为f(z)的一个原函数，那么：其中为单连通域内的两个点。
2.与积分路径有关：①无奇点：定理2（柯西积分定理）设f(z)在单连通域E内解析，C为E 内任一简单闭曲线，则：例题：②有一个奇点：定理3（柯西积分公式）如果函数f(z)在区域D内处处解析，C为D内的任何一条正向简单闭曲线，它的内部完全含于D，为C 内任意一点，那么例题：定理4（高阶导数公式）解析函数的导数仍然为解析函数，它的n阶导数为：例题：③有两个及以上奇点：定理5（复合闭路定理）设C为多连通域D内的一条简单闭曲线，是在C内部的简单闭曲线，它们互不包含也互不相交，并且以为边界的区域全含于D，如果f(z)在D内解析，则： (1) ，例题：2.解析函数与调和函数的关系1.调和函数的定义：若u(x,y)在区域E内具有连续的二阶偏导数，且在E内满足，则称函数u(x,y)为区域E的调和函数。
方程称为调和方程。
定理1 任何一个在区域E上解析的函数f(z)=u(x,y)+iv(x,y)，其实部与虚部都是该区域上的调和函数。
（该定理的逆定理不成立！要使u+iv解析，还需要满足C-R条件才可以）2.对于给定的调和函数u(x,y)，把使u+iv构成解析函数的调和函数v(x,y)称为u(x,y)的共轭调和函数。
3.求共轭调和函数的两种方法：①偏积分法（最常用，且不容易出错）如果已知一个调和函数u，那么就可以利用柯西－黎曼方程求得它的共轭调和函数v,从而构成一个解析函数u+vi。
这种方法称为偏积分法。
例题：②偏积分法：例题：（这里的积分路径一般从原点(0,0)开始选取，选任意的也可以）。
复变函数论第2章
返回
下页
结束
18
铃
例5 研 究 函 数 f ( z ) z 2 ,g ( z ) x 2 y i 和 h ( z ) z 2 的 解 析 性 .
答案： f(z)z2 在复平面内是解; 析的
g(z)x2yi处处不 ; 解析
下面h 讨 (z)论 z2的解,析性
h(z0z)h(z0) z0 z2 z02
首页
上页
返回
下页
结束
15
铃
2、解析函数及其简单性质
(1) 解析函数的定义 定义 如 果 函 数 f(z)在 z0及 z0的 邻 域 内 处 处 可 导 ,那 么
称 f(z)在 z0解 析 .A n a ly sis
如果函数 f (z)在区域 D内每一点可微(解析), 则称 f (z)在区域 D内解析. 或称 f (z)是 区域 D 内 的 一 个 解 析 函 数 (全 纯 函 数 或 正 则 函 数 ).
z 0
f ( z 0 ) z 是 函 数 w f ( z ) 的 改 变 量 w 的 线 性 部 分 .
f(z0) z称为 w 函 f(z)在 数 z0点 的,微分
记作 d w f(z0) z.
如 果z0函 的数 微,则 在 分称 存 f(z)函 在数
在 z0可. 微 14
首页
上页
返回
y
x y
x
1 ik 1 ik
首页
上页
返回
下页
结束
20
铃
由于 k的任意, 性
z 1ki不趋于一个确定 . 的值 z 1ki
lim h(z0z)h(z0)不存 . 在
z 0
z
因此 h(z)z2仅在 z0处可,而 导在其他点都 不可,根 导据定 ,它义在复平面内析 处. 处不解
复变函数：第2章 解析函数
• 知 zlim f ( z ) = f ( z 0 )，故 →z
0
f (z )在点 z 0 处连续.
• 2.1.3 复变函数的微分 • 定义2 称函数 f (z)的改变量 ∆w的线性部分 定义 f ′( z0 )∆z 为函数 f (z)在点 z 0 处的微分，记作
n
k ( z + ∆z ) n = ∑ C n z k ( ∆ z ) n − k = n k =0
1 2 n ( ∆z ) n + C n (∆z ) n −1 z + C n ( ∆z ) n − 2 z 2 + ⋯ + C n ( ∆z ) n − n z n
所以，由导数定义有
n
( z + ∆z ) − z f ′( z ) = ( z )′ = lim ∆z →0 ∆z
n
n
= lim [(∆z )
∆z →0
n −1
+ C (∆z )
1 n
n−2
z +⋯+ C
n −1 n −1 n
z
]
= nz
n −1
• 例2 求 f ( z ) = • 解 由例1
z 的导数.
2
df f ′( z ) = = 2z dz
• 2.1.2 可导与连续的关系 • 若函数 w = f (z )在点 z 0处可导，则 点 z 0 处必连续. • 证 因为
dw 或 dz
，即
z = z0
dw f ′( z0 ) = dz
z = z0
f ( z0 + ∆z ) − f ( z0 ) = lim ∆z →0 ∆z
复变函数-第二章-解析函数
23
(3.4)当为无理数或 Im 0时：
z e
Lnz
e
(ln z i arg z 2 k i )
e
ln z
e
i arg z
e
2 k i
---- 无穷多值函数
(3.5)当 0, z 0 e0Lnz e0 1
在除原点和负实轴复平面内主值支及各分支解析，且 1 Ln z Ln z z e e z 1 z
e e
1 z
1 x yi
1 z
1 z
e
x y i x2 y2 x2 y2
,
Re(e ) e
x x2 y2
y cos 2 . 2 x y
16
2、 对数函数 定义 指数函数的反函数称为对数函数.即
把满 足 e w z( z 0)的函 数 w f (z) 称为 对数 函数 , 记作w Lnz.
10
推论1 函数f (z)=u(x, y)+iv(x, y),如果u(x, y)
和 v(x, y)的四个偏导数 :
u u v v , , , x y x y
在点(x,y)处连续 且满足 方程，则 f(z)在点 u , v v C-R u
x y z=x+iy处可导。 , x y .
给定一复数 z，如何计算 Lnz ？
令w u iv , z re i , 那 么 e u iv re i u ln r , v 2k ( k为 整 数).
w Lnz ln r i ( 2k ) ( k 0,1,) 每个确 定的k 或 Lnz ln z iArg z ln z i (arg z 2k ) 对应一
复变函数第2章解析函数
当 f (z) z时，dw= dz ，z 所以 f 在(z)点
z 0处的微分又可记为
dw zz0 f (z0 ) d z
亦即
dw
dz zz0
f (z0 )
由此可知，函数 w f (z)在点 z处0 可导与可微 是等价的.
复变函数的求导法则与高数完全类似：
则称 gx, y为 D内的调和函数
定理2.3 设 f z u i，v 若 f 在z 区域 内D 解
析，则 与u 均v 为 内D的调和函数.
定义2.4 若在区域 D内， u与 v均为调和函数
且满足C-R条件
ux vy , uy vx 则称 u 为 v的共轭调和函数
定理2.4 设 ux, y在区域 D内为调和函数，则
z0
)
lim
zz0
f (z) f (z0) z z0
0 f (z0 ) 0
知
lim
zz0
f (z)
f (z0 )，故
f在(z)点 处z 0连续.
同高数一样，称函数 f (z) 的改变量 w的线性部 分 f (z0 )z为函数 f (z在) 点 z处0 的微分，记作 dw 或 zz0 df(z) z，z0 即
2.1 复变函数的导数
定义2.1 设函数 w f z定义在区域 D
内，z0 D ，（z0 z） D ，若极限
lim f z0 z f z0
z0
z
存在，则称此极限为函数 f z在点 z0处的导数，
记作 f z0 或
df ，即
dz zz0
f
z0
df dz
z z0
lim
z0
f
z0
第02章_复变函数的积分
Re zdz
l
y
i
A
O
l
(2) (1)
B (1, i)
1
分别沿路径(1)和(2)，如图 解：
1 (1) I1 xdx ixdy i 0 0 2
1 1
1 1
Re zdz xd(x iy) xdx ixdy
l l
x
1 (2) I 2 0 id y x d x 0 0 2
k 1
n
k
x
当 n 而且每一个 z k 0时， 若该和的极限存在，并且其值与 各 k的选取无关，则该和的极限 称为 f ( z )沿曲线 l从 A到 B的路积分
z0
O
记作 l f ( z )dz ，即：
l
f ( z )d z
max z k 0
lim
f (
k 1
l l
复变函数的路积分可以归结为两个实变函数的线积分, 它 们分别是路积分的实部和虚部。 因此, 实变函数线积分的许多性质对复变函数的路积分也 成立。复变函数的路积分满足如下6条性质： 1. 常数因子可以移到积分号之外； 2. 函数的和的积分等于各个函数的积分之和； 3. 反转积分路径，积分变号； 4. 全路径上的积分等于各段上积分之和； 5. 积分不等式1：
l1
B' A'
f (z)dz f (z)dz
CD
l2
f ( z)dz
l1
D 'C '
f ( z)dz 0
其中沿同一割线两边缘上的积分值相互抵消，于是有
f (z)dz
l
l
f ( z )dz f ( z )dz 0
复变函数课件第二章
记作
dw f ( z 0 z ) f ( z0 ) f ( z0 ) lim . dz z z0 z 0 z
复变函数与积分变换
Complex Analysis and Integral Transform
复变函数与积分变换
Complex Analysis and Integral Transform
y 1 0 当 z 0(x 0, y 0) 时， lim z 0 x iy i y lim ∴ z 0 不存在，即处处不可导。 x iy
y lim 0 当 z 0(x 0, y 0) 时， z 0 x iy
复变函数与积分变换
复变函数与积分变换
在定义中应注意: z0 z z0 (即z 0)的方式是任意的.
Complex Analysis and Integral Transform
即z0 z在区域D内以任意方式趋于 0时, z f ( z0 z ) f ( z0 ) 比值 都趋于同一个数 . z
y 1 f f ( z z ) f ( z ) lim , lim lim y 0 x i y z 0 z z 0 i z x 0
当点沿不同的方向使z 0时, 极限值不同 ,
故f ( z ) Im z在复平面上处处不可导.
复变函数与积分变换
例2
Complex Analysis and Integral Transform
2
研究函数 f ( z ) z 2 , g( z ) x 2 yi 和
h( z ) z 的解析性.
解 由本节例1和例3知:
f ( z ) z 2 在复平面内是解析的 ;
魏雅薇复变函数论第二章
令 r(z)
f (z0 z) z
f (z0 )
f (z0 ).
南开大学 魏雅薇
r f ( z 0 z ) f ( z 0 ) f ( z 0 ) z ( z ) z ,
再由 limr(z)0, 所以 z0
lim
z0
f
(z0
z)
f (z0),
即 f ( z ) 在 z 0 处连续.
(2) 若 f ( z ) 在区域D内每一点都解析，则称 f ( z ) 在区域D内解析, 或者称 f ( z ) 是区域D内的 解析函数.
南开大学 魏雅薇
(3) 设G是一个区域，若闭区域 D G ,
且 f ( z ) 在G内解析，则称 f ( z ) 在闭区域 D 上
解析.
函数 f ( z ) 在 z 0 处解析和在 z 0 处可导意义
极限limf 不存在． z0 z
故f(z)Imz在复平面上处处.不可导
南开大学 魏雅薇
可导与连续的关系 函数f (z)在z0处可导，则在z0处一定连续, 但
函数f (z)在z0处连续不一定在z0处可导. 事实上,由 f (z)在z0点可导, 必有 lizm 0f(z0 zz )f(z0)f(z0)0 ,
南开大学 魏雅薇
故 f(zz) zf0(z0)(zz0)zz02zz zz0 0.
虽然 lzi m z0(zz0)z2z0z02z02,但是当
z z分别从平行于x, y轴方向趋于z0时，z
z0 z0
分别
以1和-1为极限，因此 l i m z z0
z z
z0 z0
不存在. 又因为
z0 0,
所以
lim
(5 ) g f( (z z ) ) f(z)g (z g )2 (z f )(z)g (z), (g (z) 0 ).
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章 解析函数1. 复变函数：()w f z =w =f (z )又常写成w =u (x ,y )+iv (x ,y )，从而对复变函数f (z )的讨论可相应地 转化为对两个实函数u (x ,y )和v (x ,y )的讨论.2.复变函数的极限与连续：定义2.2 设函数w =f (z )定义在z 0的去心邻域0<|z -z 0|<r 内，若存在常数A ，对于任意给定的0ε>,都存在一正数(0)r δδ<≤,使得当0<|z -z 0|<δ时,有()f z A ε<-,则称函数f (z )当0z z →时的极限存在，常数A 为其极限值.记作0lim ()z z f z A →=或 0()()f z A z z →→.定理2.1 设f (z )=u (x ,y )+iv (x ,y ),z 0=x 0+iy 0,A =a +ib ，则000(,)(,)lim ()lim (,),z z x y x y f z A u x y a →→=⇔= (2.1) 00(,)(,)lim (,).x y x y v x y b →= (2.2)定义 2.3 若00lim ()()z z f z f z →=，则我们就说函数 f (z ) 在点 z 0 处连续. 如果函数f (z )在区域D 内每一点都连续，那么称函数f (z )在区域D 内连续.定理2.5 设函数000()(,)(,),f z u x y iv x y z x iy =+=+,则f (z )在点z 0连续的充分必要条件是u (x ,y )、v (x ,y ) 均在点(x 0,y 0)连续.3.复变函数的导数定义2.4 （导数的定义）设函数w =f (z )定义在z 平面上区域D 内，点z 0、z 0+Δz D ∈, 00Δ(Δ)()w f z z f z ∈=+-,若极限00Δ0Δ0(Δ)()Δlimlim ΔΔz z f z z f z w z z →→+- 存在,则称函数f (z ) 在 z 0可导,这个极限值称为f (z )在z 0的导数,记作00000Δ0(Δ)()d ()d lim ().d d Δz z z z z f z z f z f z w f z z z z==→+-='== (2.3) 由于复变函数导数的定义在形式上和一元实函数的导数定义一致，并且复变函数中的极限运算法则与实函数中一样，所以微积分中几乎所有的关于函数导数的计算规则都可以不加更改地推广到复变函数中来.4.解析函数的概念定义2.6 若函数f (z )在点z 0及z 0的邻域内处处可导，则称函数f (z )在点z 0解析.若函数f (z )在区域D 内每一点都解析，则称函数f (z )在区域D 内解析，或称f (z )是D 内的解析函数.若f (z )在点z 0不解析，但在z 0的任一邻域内总有f (z )的解析点，则称z 0为f (z )的奇点.5.函数可导与解析的充要条件定义2.6 对于二元实函数u (x ,y )和v (x ,y )，方程,.u v u v x y y x∂∂∂∂==-∂∂∂∂ (2.5) 称为柯西-黎曼方程（简记为C-R 方程）.定理2.7 设函数f (z )=u (x ,y )+iv (x ,y )在区域D 内有定义，则f (z )在区域D 内一点z =x +iy 可导的充要条件是(1) 二元实函数u (x ,y )和v (x ,y )在点(x ,y )可微；(2) u (x ,y ),v (x ,y )在点(x ,y )满足柯西-黎曼方程.6.初等函数（1）指数函数定义2.7 对于复变数z =x +iy ，定义指数函数为:e e e (cos sin ).z x iy x y i y +==+e z 又用记号exp(z )表示.（2）对数函数定义2.8 规定对数函数是指数函数的反函数，即若e (0)w z z =≠则称函数w =f (z )为z 的对数函数，记作w =Ln z .令w =u +iv ,则w =u +iv =ln|z |+i Arg z ∆Ln z .注意到Arg z 是多值函数，所以对数函数w =f (z )也是多值函数.上式中Arg z 取主值arg z (-π<arg z ≤π)时对应的w 值称为Ln z 的主值，并记作ln z =ln|z |+i arg z .这样对数函数可表示为:w =ln z =ln z +2k πi =ln|z |+i arg z +2k πi , k =0,±1, ±2,….上式中对于每一个确定的k ,对应的w 为一单值函数，称为Ln z 的一个分支.（3）幂函数定义2.9 函数w =z a =e a Ln z （z≠0,a 为复常数）称为z 的一般幂函数.当一般的幂函数aw z =的底数z 为一确定复常数b (b≠0)时，则b a =e a Ln b 称为乘幂.由于Ln b =ln|b |+i arg b +2k πi ，所以乘幂b a 也是多值的.（4）三角函数与反三角函数定义2.10 规定e e e e sin , cos .22iz iz iz izz z i ---+== 其它三角函数定义如下:sin cos 11tan , cot , sec , csc .cos sin cos sin z z z z z z z z z z==== （5）双曲函数与反双曲函数我们用指数函数来定义双曲函数.定义2.11 规定e e e e sh , ch 22z z z zz z ---+== 小 结复变函数及其极限、连续、导数等概念是微积分学中相应概念的推广.复变函数的定义在形式上只是将一元实函数的定义域与值域由“实数集”扩大为“复数集”，但要注意实函数是单值函数，而复变函数有单值函数与多值函数之分.一个复变函数f (z )=u (x ,y )+iv (x ,y )对应着两个二元实函数u (x ,y )和v (x ,y )，所以对复变函数的研究可以转化为对它的实部和虚部两个二元实函数的研究.另外将复变函数看成复平面上两个点集之间的映射，有时可以将问题直观化、几何化.复变函数极限的定义在形式上与一元实函数极限的定义相似，因此复变函数具有与实函数类似的极限运算法则.但实质上复变函数的极限与二元实函数的极限是等价的.一元实函数的极限00lim (),x x f x x x →→是指x 在x 轴上从x 0的左右两侧以任何方式趋向于x 0，而在复变函数的极限0lim ()z z f z →中，0z z →是指z 在z 0的邻域内以任何方式趋于z 0.如果z 沿两条不同路径趋于z 0, f (z )不趋于同一复数，那么f (z )在z 0处的极限不存在.复变函数的连续定义是依赖于极限定义的，若00lim ()()z z f z f z →=,则我们说f (z )在z 0处连续.复变函数w =f (z )=u (x ,y )+iv (x ,y )极限存在与连续的充要条件是其实部u (x ,y )和虚部v (x ,y )极限存在与连续.复变函数的导数定义在形式上与一元实函数导数的定义相似，因此复变函数具有与实函数类似的求导法则.复变函数导数为函数的改变量Δw 与自变量Δz 的比0(+Δ)()ΔΔΔf z z f z w z z-=当Δ0z →的极限，该极限值与Δ0z →的方式无关，也就是说如果当Δz 沿某一路径趋于0时，ΔΔw z 的极限不存在,或沿两条不同路径趋于0时，ΔΔw z趋于不同的数，则f (z )在z 0处不可导.由此可见复变函数在一点可导要比一元实函数可导条件更强.解析函数是复变函数的主要研究对象，它有着一元实函数所没有的好性质，如解析函数的导数仍是解析函数，解析函数的虚部为实部的共轭调和函数以及解析函数可以展开为幂级数等，这些性质在后面就会学到.应当注意的是解析与可导的区别与联系.对于一个区域而言， 函数解析与可导是一回事；但对于一个点，解析就比可导要求高得多.函数在某点解析不仅要求在该点可导而且要求在该点的某邻域内可导.判断函数可导与解析的方法主要有以下三种：(1)利用可导与解析的定义.(2)利用可导(解析)函数的和、差、积、商及其复合仍为可导(解析)函数这一性质.(3)利用可导与解析的充要条件(即定理2.7和定理2.8).定理2.7给出了函数f (z )在一点z D ∈处可导的充要条件，由于z 的任意性，从而可以得到函数在区域D 内可导与解析的充要条件，即定理2.8.复初等函数是实初等函数在复数域的推广，它既保持了实初等函数的一些性质，又有一些不同的性质.指数函数e z =e x (cos y +i sin y )在z 平面上处处解析，并且(e z )'=e z ,它具有实指数函数相同的某些性质如加法定理.但周期为2πi 这与实指数函数不同，实指数函数e x 可以看成数e 的x 次幂，但在复变函数中e z 仅仅是一个记号，而不再有幂的含义.对数函数Ln z =ln z +i Arg z 是一多值函数，它在除去原点与负实轴的复平面上处处解析,且有(l nz )' =1z.它保持了实对数函数的如下性质： 11212122ln()ln ln ,ln ln ln .z z z z z z z z ⎛⎫=+=- ⎪⎝⎭应当注意的是，等式1ln ln ln n z n z z n== 不再成立，其中2n ≥,为正整数.幂函数w =z a =e a L n z , 除了整幂函数z n (z 为正整数)外都是多值函数，在除去原点与负实轴的复平面上处处解析,且有(z a )'=az a -1.而整幂函数z n (z 为正整数)是单值函数，在复平面上处处解析，且(z n )'=nz n -1.当底数z 为一确定的常数b (b ≠0)时，b a =e a L nb 为乘幂.三角正弦函数与三角余弦函数e e e e sin , cos 22iz iz iz izz z i ---+== 在复平面上处处解析，并且(sin z )'=cos z ,(cos z )'=-sin z .它保持了对应的实函数的奇偶性、周期性，类似的三角恒等式成立，但是不再具有有界性，即|sin z |≤1,|cos z |≤1不成立.其它三角函数与反三角函数、双曲函数与反双曲函数读者可以自己小结它们的性质.1.讨论函数(1) f (z )= Im(z ) ;(2) f (z )=|z |2z .的可导性，并在可导点处求其导数.。