很好的数控车圆弧编程技巧
数控编程圆弧计算方法(一)

数控编程圆弧计算方法(一)数控编程圆弧计算方法在数控机床上,圆弧是常见的加工形式之一。
然而,要正确地编写圆弧的数控程序,需要掌握圆弧的计算方法,包括圆弧的起点、终点、半径等参数的计算。
下面将详细介绍数控编程中的圆弧计算方法。
圆弧的定义圆弧是一个弧线形状,由圆锥曲线或球面曲线的一部分组成。
圆弧有起点、终点、圆心和半径等参数。
圆弧的表示方法在数控编程时,圆弧可以用多种方式来表示。
其中一种常用的方式是用圆心坐标及起点、终点的位置坐标来表示。
假设圆弧的起点为P1,终点为P2,圆心为C,半径为R,则圆心坐标可以用以下公式计算:C=(P1+P2)/2+(P1−P2)⊥∗R/(2∗|P1−P2|)其中“+”表示向量加法,“⊥”表示向量垂直,“|.|”表示向量的模。
通过圆心坐标及起点、终点的位置坐标,可以计算出圆弧的圆心角度数、圆弧的弧长等参数。
圆弧的程序调用格式在数控编程中,圆弧通常使用G02或G03指令来表示。
以G02指令为例,其格式为:G02 X_ Y_ I_ J_ R_其中X、Y表示终点坐标,I、J表示圆心坐标与起点的相对距离,R表示圆弧半径。
需要注意的是,只有当起点与当前点之间没有直线段时才能使用I、J参数。
圆弧的误差分析在数控加工中,为了保证加工精度,需要对圆弧误差进行分析。
圆弧误差包括位置误差和形状误差。
位置误差是由起点到圆心、圆心到终点的直线段引起的误差,可以通过适当调整I、J参数来补偿。
形状误差是由数控机床控制系统、加工刀具等因素引起的误差,可以通过加工补偿、精度提高等措施来减小。
总结圆弧计算方法是数控编程中的核心内容之一,正确地编写圆弧程序可以提高加工效率、保证加工精度。
需要掌握圆弧的定义、表示方法、程序调用格式以及误差分析等方面的知识,才能编写出高质量的数控程序。
圆弧计算方法示例以下是一组示例,展示如何通过已知起点、终点和圆弧半径来计算圆心坐标和其他相关参数。
假设起点坐标为(0, 0),终点坐标为(2, 2),圆弧半径为1,则可按如下方法计算圆心坐标:C=(P1+P2)/2+(P1−P2)⊥∗R/(2∗|P1−P2|)=(0+2)/2+(0−2,0−2)⊥∗1/(2∗√2)=(1,1)由此可得圆心坐标为(1, 1)。
数控编程圆弧计算方法

数控编程圆弧计算方法数控编程是现代加工工业中不可或缺的一部分。
在数控编程中,圆弧是一种常见的曲线形状,用于许多零件的制造。
编写数控程序时,计算和定义圆弧是非常重要的,因为它们决定了工件将如何加工。
在本文中,我们将介绍数控编程圆弧计算的方法和技巧。
1. 圆弧定义在数控编程中,圆弧由其半径,圆心和起点和终点角度定义。
通常使用G02和G03代码定义圆弧方向,其中G02表示顺时针方向,而G03表示逆时针方向。
为了编写正确的程序,您需要知道圆弧的所有参数。
2. 圆弧半径计算在圆弧定义中,半径是最基本的参数之一。
如果您知道圆弧的直径,可以将其除以2来计算半径。
但是,如果您只知道起点和终点的坐标,则需要使用勾股定理来计算半径。
例如,如果您知道起点(X1,Y1)和终点(X2,Y2),则可以使用以下公式计算半径:半径 = sqrt((X2-X1)^ 2 +(Y2-Y1)^ 2)/ 2此公式基于圆弧是一个四分之一的圆的假设。
请记住,如果您有关于圆心的信息,则可以直接使用半径。
3. 圆心计算在数控编程中,圆心是定义圆弧的另一个重要参数。
如果您知道圆弧的起点,终点和半径,则可以使用以下公式计算圆心(XC,YC):XC = (X1 + X2)/ 2 + R *(Y1-Y2)/ LYC = (Y1 + Y2)/ 2 + R *(X2-X1)/ L其中L是起点和终点之间的距离。
4. 圆弧角度计算圆弧的起点和终点角度也是定义圆弧的重要参数之一。
在数控编程中,起点和终点之间的角度称为圆弧角度。
该值可以使用以下公式计算:角度 = arctan2(Y2-YC,X2-XC)- arctan2(Y1-YC,X1-XC)其中arctan2是反正切函数,返回的值是弧度制。
请注意,在计算角度时,您需要验证圆弧方向是顺时针还是逆时针。
5. 圆弧编程示例下面是一个简单的圆弧编程示例:N10 G90 G01 X0 Y0N20 G02 X30 Y0 I30 J0N30 G03 X0 Y0 I-30 J0这个程序将在XY平面上创建一个四分之一的圆。
数控车床圆弧编程实例

数控车床圆弧编程实例
《数控车床圆弧编程实例》
一、编程前准备工作
1.确定加工材料的材质、尺寸,材料的图形,加工位置,刀具尺寸。
2.确定加工程序:加工方式,用刀方式,切削深度等,以及终点、起点等。
3.确定刀具的位置:刀具的位置要与原点一致,否则,程序就会出现偏差。
4.确定工件的定位:工件的定位应与终点保持一致,避免出现误差。
二、编程过程
1.圆弧程序的起点和终点的坐标要确定好。
2.确定刀具切入点和切出点,以及切入速度。
3.根据定位点,确定切削参数,如切削深度、切削宽度、切削速度等。
4.根据定位点坐标,计算各点的刀具坐标、移动速度等,并依次加以编写程序代码。
5.将程序中的相关参数赋值,程序完成后,将程序上传到数控车床上,检查程序中是否有误。
三、编程实例
// 圆弧程序示例
Contact1 M4;
M6;
G17;
G40;
G50;
G61;
G90;
//设定初始坐标
G00 X0.0 Y0.0;
//设定刀具参数
G54;
T1;
M7;
//设定切削参数
S1000;
F100;
//开始循环加工
G01 Z-20.0;
M3;
G02 X50.0 Y50.0 I20.0; G01 Z0.0;
M5;
G00 X0.0 Y0.0;
M30;
//刀具回零
G00 X0.0 Y0.0;
M30;
四、程序检测
通过模拟运行程序,查看程序中是否存在误差或遗漏,检查各参数是否达到要求,确保程序准确无误。
数控车g92圆弧编程滚花实例

数控车g92圆弧编程滚花实例引言在数控车床(数控车)加工中,g92圆弧编程滚花是一种常见的加工方法。
通过合理编程,可以在工件表面制作出各种精美的花纹和图案。
本文将介绍g92圆弧编程滚花的相关知识和实例,帮助读者了解和掌握这一加工技术。
什么是g92圆弧编程滚花?g92圆弧编程滚花是一种数控车床加工方法,通过在工件表面上连续切削一系列相同的圆弧,从而形成滚花效果。
g92表示用于定义程序坐标系的g代码,它指定了圆弧的半径、切削方向和旋转角度等参数,使得数控车床能够按照设定的轨迹进行自动加工。
实例演示:制作一个圆形花纹下面以制作一个圆形花纹为例,详细介绍g92圆弧编程滚花的具体步骤和实施方法:步骤1:确定工件和加工参数首先确定要加工的工件和相关的加工参数,包括工件直径、加工深度、切削速度等。
在本例中,我们将以直径为50mm的圆盘为例进行演示。
步骤2:准备g代码编写数控程序,用于告诉数控车床如何进行g92圆弧编程滚花。
以下是一个示例的g代码:N10 G20 G90 G98 G54N20 T01 M06N30 G00 X0. Y0. S2000 M03N40 G43 Z0.1 H01N50 G92 S2300N60 G01 Z-5. F0.15N70 G02 X0. Y0. R2.N80 G01 Z0.N90 G00 X0. Y0. Z10.步骤3:解析g代码将g代码逐行解析,以便理解每条指令的含义和作用。
1.N10 G20 G90 G98 G54: 设置工作单位为英寸,切换到绝对坐标系,选择工作坐标系为G54。
2.N20 T01 M06: 切换到工具1,并进行刀具更换。
3.N30 G00 X0. Y0. S2000 M03: 将刀具快速移到X轴和Y轴的0位置,并设置主轴速度为2000转/分钟,打开主轴。
4.N40 G43 Z0.1 H01: 启用刀具长度补偿,在Z轴方向上偏移0.1mm,选择刀具长度补偿号为1。
数控车床圆弧螺纹怎么编程【技巧】

通常采用宏程序进行编制。
原理很简单,就是把圆弧上每一个点的坐标依次求出来,可以采用勾股定理或三角函数,每求出一个坐标(x,z)就采用螺纹加工指令G32或G92加工一遍,一直把这个完整的圆弧走完即可!如果圆弧比较大,可以再添加一个循环指令,进行分层加工即可!大概的思路就是这样的。
比如以一个简单图为例!参考程序如下:仿真效果如图所示扩展资料:加工圆弧螺纹,通常采用宏程序进行编制。
原理很简单,就是把圆弧上每一个点的坐标依次求出来,可以采用勾股定理或三角函数,每求出一个坐标(x,z)就采用螺纹加工指令G32或G92加工一遍,一直把这个完整的圆弧走完即可!如果圆弧比较大,可以再添加一个循环指令,进行分层加工即可!在数控车床上可以车削米制、英寸制、模数和径节制四种标准螺纹,无论车削哪一种螺纹,车床主轴与刀具之间必须保持严格的运动关系:即主轴每转一转(即工件转一转),刀具应均匀地移动一个(工件的)导程的距离。
以下通过对普通螺纹的分析,加强对普通螺纹的了解,以便更好的加工普通螺纹。
数控车床对普通螺纹的加工需要一系列尺寸,普通螺纹加工所需的尺寸计算分析主要包括以下两个方面:1、螺纹加工前工件直径考虑螺纹加工牙型的膨胀量,螺纹加工前工件直径D/d-0.1P,即螺纹大径减0.1螺距,一般根据材料变形能力小取比螺纹大径小0.1到0.5。
2、螺纹加工进刀量螺纹加进刀量可以参考螺纹底径,即螺纹刀最终进刀位置。
螺纹小径为:大径-2倍牙高;牙高=0.54P(P为螺距)螺纹加工的进刀量应不断减少,具体进刀量根据刀具及工作材料进行选择。
在数控车床中,螺纹切削一般有三种加工方法:G32直进式切削方法、G92直进式切削方法和G76斜进式切削方法,由于切削方法的不同,编程方法不同,造成加工误差也不同。
我们在操作使用上要仔细分析,争取加工出精度高的零件。
1、G32直进式切削方法,由于两侧刃同时工作,切削力较大,而且排削困难,因此在切削时,两切削刃容易磨损。
数控编程圆弧计算方法

数控编程圆弧计算方法
数控编程是机械加工中非常重要的一部分,它可以通过编程来控制机床进行加工。
其中圆弧计算是数控编程中的一个重要内容,因为很多零件都包含有圆弧形状,准确计算圆弧可以保证零件的精度和质量。
数控编程圆弧计算方法主要包括以下几个方面:
1. 圆弧的半径计算:在圆弧加工中,半径是一个非常重要的参数,需要根据零件图纸中给出的半径进行计算。
计算方法是:半径=圆弧的直径÷2。
2. 圆弧的圆心计算:圆弧的圆心是计算圆弧路径的重要参数,需要根据零件图纸中给出的圆心坐标进行计算。
计算方法是:圆心坐标=起点坐标+向量1+向量2,其中向量1和向量2可以根据起点、终点和半径计算得出。
3. 圆弧的切线方向计算:圆弧的切线方向是计算进给速度和刀具路径的重要参数,需要根据圆心坐标和半径计算得出。
计算方法是:切线方向=圆心坐标-起点坐标或终点坐标-圆心坐标,这两个向量都是在圆弧平面内的向量。
4. 圆弧的角度计算:圆弧的角度是计算圆弧路径长度和编程精度的重要参数,需要根据圆弧的半径和圆心角度计算。
计算方法是:角度=圆心角度×π÷180,其中π是圆周率,180是角度制和弧度制之间的转换因子。
数控编程圆弧计算方法是数控编程中的基础知识之一,掌握了这些计算方法可以提高圆弧加工的精度和效率。
同时,在数控编程中,还有很多其他的计算方法和技巧需要掌握,只有不断学习和实践才能成为一名优秀的数控编程工程师。
数控车床圆弧零件编程实例
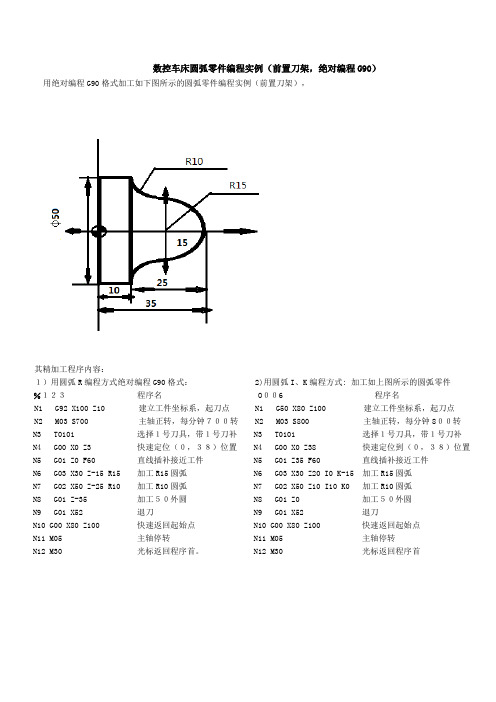
数控车床圆弧零件编程实例(前置刀架,绝对编程G90)用绝对编程G90格式加工如下图所示的圆弧零件编程实例(前置刀架),
其精加工程序内容:
1)用圆弧R编程方式绝对编程G90格式: 2)用圆弧I、K编程方式: 加工如上图所示的圆弧零件
%123程序名 O006 程序名
N1 G92 X100 Z10 建立工件坐标系,起刀点 N1 G50 X80 Z100 建立工件坐标系,起刀点
N2 M03 S700 主轴正转,每分钟700转 N2 M03 S800 主轴正转,每分钟800转
N3 T0101 选择1号刀具,带1号刀补 N3 T0101 选择1号刀具,带1号刀补
N4 G00 X0 Z3 快速定位(0,38)位置 N4 G00 X0 Z38 快速定位到(0,38)位置N5 G01 Z0 F60 直线插补接近工件 N5 G01 Z35 F60 直线插补接近工件
N6 G03 X30 Z-15 R15 加工R15圆弧 N6 G03 X30 Z20 I0 K-15 加工R15圆弧
N7 G02 X50 Z-25 R10 加工R10圆弧 N7 G02 X50 Z10 I10 K0 加工R10圆弧
N8 G01 Z-35 加工50外圆 N8 G01 Z0 加工50外圆
N9 G01 X52 退刀 N9 G01 X52 退刀
N10 G00 X80 Z100 快速返回起始点 N10 G00 X80 Z100 快速返回起始点
N11 M05 主轴停转 N11 M05 主轴停转
N12 M30 光标返回程序首。
N12 M30 光标返回程序首。
数控r圆弧算法和编程

数控r圆弧算法和编程
数控(Numerical Control,简称NC)是一种自动化控制技术,用于控制机械设备的运动。
在数控加工中,圆弧是常见的几何形状之一,因此掌握数控圆弧算法和编程对于实现精确的加工操作非常重要。
数控圆弧算法主要包括圆弧插补算法和圆弧拟合算法。
圆弧插补算法是指在给定的起点、终点和半径条件下,计算出一系列离散点,以实现平滑的圆弧路径。
常见的插补算法包括线性插补、二次插补和三次插补等。
线性插补是最简单的插补算法,通过在起点和终点之间均匀分布的加工点来逼近圆弧,但是精度较低。
而二次插补和三次插补则通过更高次的插值函数来提高加工精度。
圆弧拟合算法是指根据一系列给定的点,找到最佳的圆弧来拟合这些点。
这些点通常是由CAD/CAM系统生成的,而拟合算法的目标是找到与给定点最接近的圆弧。
常用的拟合算法包括最小二乘法、最小二乘圆、B样条曲线等。
这些算法可以根据具体的应用需求选择,以实现最佳的加工效果。
在数控编程中,圆弧的描述通常使用指令来完成。
常见的指令包括
G02和G03,分别用于顺时针和逆时针的圆弧插补。
这些指令需要提
供起点、终点、半径和平面信息,以实现对圆弧路径的控制。
此外,还有一些辅助指令用于定义圆弧的特征,如I和J指令用于定义圆心相对于起点的偏移量,K指令用于定义圆弧所在平面的偏移量等。
这些指令的正确使用对于实现预期的加工效果至关重要。
总之,数控圆弧算法和编程是数控加工过程中的重要组成部分。
掌握这些算法和编程技术,能够实现精确的圆弧加工路径,提高加工效率和加工质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、圆弧分层切削法
1.圆弧始点、终点均不变,只改变半径R
如图a所示,在零件加工一个凸圆弧,根据过两点作圆弧,半径越小曲率越大的原则,因此在切
削凸圆弧时,可以固定始点和终点把半径R由小逐渐变
大至规定尺寸。
但要注意,圆弧半径最小不得小于成品
圆弧弦长的一半。
N10 G01 X40 -5 F;
N20 G03 X40 Z-25 10.2 F;
N30 G00 X53;
N40 Z-5;
N50 G01 40 F;
N60 G03 X40 Z-25 12 F;
N70 G00 X53;
N80 Z-5;
N90 G01 40 F;
N100 G03 X40 Z-25 16 F :
2.圆弧始点、终点坐标变化,半径R不变
如图b所示,在零件上加工一个凹圆弧,为了合理分配吃刀量,保证加工质量,采用等半径圆弧
递进切削,编程思路简单。
N10 G01 X54 Z-30 F0 .3;
N20 G02 X60 Z-33 R10 F0 .2;
N30 G00 X54 Z-30;
N40 G01 48 F ;
N50 G02 X60 Z-36 10 F;
N60 G00 X48 Z-30;
N70 G01 42 F ;
N80 G02 X60 Z-39 10 F;
N90 G00 X42 Z-30;
N100 G01 40 F;
N110 G02 X60 Z-40 10 F;
3.圆弧始点、终点坐标,半径R均变化
如图c所示,在零件一端加工一个半球,在该种情况下,走刀轨迹的半径R等于上次走刀半径R
与Z(或X)方向的变化量∆Z(∆X)之差。
N10 G01 X0 10 F;
N20 G03 X60 Z-20 30 F ;
N30 G00 Z6;
N40 X0;
N50 G03 X60 Z-20 26 F;
N60 G00 Z2;
N70 X0;
N80 G03 X60 Z-20 22 F ,
N90 G00 Z0;
N100 X0;
N110 G03 X60 Z-20 20 F;
二、先锥后圆弧法
1.该方法是先把过多的切削余量用车锥的方法切除掉,最后一刀走圆弧的路线切削圆弧成型,如图
d所示。
N10 G01 X102 -30 F;
N20 G90 X100 Z-50 -5 F;
N30 I-10;
N40 I-15;
N50 I-20;
N60 G01 X60 -30 F;
N70 G02 X100 Z-50 20 F;
2.当是凸圆弧时,可根据几何知识算出ab段的长度,然后再车锥,最后车弧,如图e所示。
db=+R=
ab=*db=
留取一部分精加工余量,则ab取,
ab=bc
根据1中的方法先加工出锥形,然后再精车圆弧。
三、结束语
在数控加工中,往往机床操作者也是零件切削程序的编制者,这就要求编制的程序工艺简单,调整方便,加工精度高等。
在操作现场没有CAD制图软件、计算机等辅助计算工具时,采用上述方法编程切削圆弧可大大减少计算量。
思路简单,工艺得体,延长刀具的使用寿命,加工出来的零件精度高,为圆弧类零件的加工带来方便。
