(完整版)多元回归分析中变量的选择——SPSS的应用毕业设计
多元线性回归SPSS实验报告
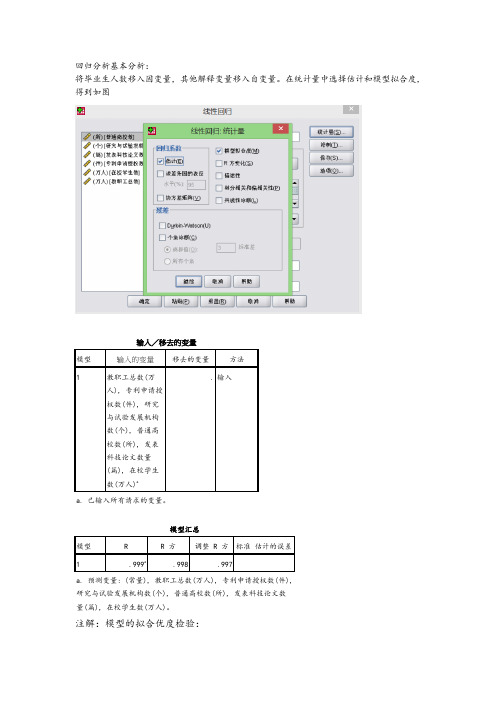
49%;可以认为:这些变量存在多重共线性。需要建立回归方程。
2.重建回归方程
模型
输入/移去的变量b
输入的变量
移去的变量
方法
1
教职工总数(万
人), 专利申请授
权数(件), 研究
b. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表 科技论文数量(篇)。 c. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 发表科技论文数量(篇)。 d. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 发表科技论文数量(篇)。 e. 预测变量: (常量), 教职工总数(万人), 发表科技论文数量(篇)。 f. 因变量: 毕业生数(万人)
. 输入
a. 已输入所有请求的变量。
模型汇总
模型
R
R 方 调整 R 方 标准 估计的误差
1
.999a
.998
.997
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构数(个), 普通高校数(所), 发表科技论文数 量(篇), 在校学生数(万人)。
注解:模型的拟合优度检验:
第五列:回归方程的估计标准误差=
Anovab
模型
平方和
df
均方
F
Sig.
1
回归
6
.000a
残差
7
总计
13
a. 预测变量: (常量), 教职工总数(万人), 专利申请授权数(件), 研究与试验发展机构 数(个), 普通高校数(所), 发表科技论文数量(篇), 在校学生数(万人)。 b. 因变量: 毕业生数(万人)
多元线性回归分析spss

多元线性回归分析spss
多元线性回归分析是一种常用的统计分析技术,用于对各因素之间的相互关系进行研究。
使用多元线性回归分析,可以检验一个或多个自变量对因变量具有统计学显著性的影响,从而推断出实际世界存在的不同因素可能带来的影响。
在spss中,我们使用下拉菜单选择“分析”>“回归”>“多元”来开始多元线性回归分析。
在多元线性回归窗口中,我们可以在右边的“可用变量”列中选择变量,拖拽到“因变量”和“自变量”栏中。
接下来,我们可以选择要使用的模型类型,其中包括多元线性回归,截距,变量中心以及相关的其他预测结果。
在进行模型拟合之前,我们可以在“多重共线性”复选框中对共线性进行调整,进行预测和显著性检验,并调整“参数估计”和“残差”复选框,自由地绘制结果。
在运行了多元线性回归分析之后,在spss中,我们可以在输出窗口中查看多元回归方程的系数和检验的结果,以及它们对回归系数的影响,残差分布情况,多重共线性分析和其他一些输出参数。
总而言之,spss中多元线性回归分析是一种有效的统计分析方法,可以用来检验多个自变量对回归方程的影响。
它具有许多内置功能,可以容易地针对回归系数和其他参数进行各种分析,提供了可信的结果,帮助人们深入了解各类因素对研究结果的影响。
运用SPSS做多元回归分析

结果二:方差分析表
• 表中显著度(Sig)<0.001,表明整个方程是显著的,也 就是说自变量与因变量之间具有显著的线性关系。 • 但这并不意味着每个自变量与因变量都具有显著的线性关 系,具体的结论还需要看后面对每个自变量的回归系数的 检验结果。
结果三:回归系数表
• 表中B栏的非标准化回归系数表明:
FOR EXAMPLE
一个变量的变化直接与另一组变量的变化有关:
人的体重与身高、胸围 血压值与年龄、性别、劳动强度、饮食习惯、吸烟 状况、家族史 糖尿病人的血糖与胰岛素、糖化血红蛋白、血清总 胆固醇、甘油三脂
多元回归分析数据格式
编号 1 2 ┇ i ┇ n
X1
X 11
X2
X 12
┅ ┅ ┅ ┇ ┅ ┇ ┅
多元回归模型必须满足的假定条件
1. 2.
因变量是连续随机变量; 自变量是固定数值型变量,且相互独立;
3.
4. 5. 6.
每一个自变量与因变量呈线性关系;
每一个自变量与随机误差相互独立; 观察个体的随机误差之间相互独立; 残差是随机变量,均值为零。
不良贷款(亿元)各项贷款余额(亿元)本年累计应收贷款(亿元)贷款项目个数(个) 本年固定资产投资额(亿元) 0.9 67.3 6.8 5 51.9 1.1 111.3 19.8 16 90.9 4.8 173 7.7 17 73.7 3.2 80.8 7.2 10 14.5 7.8 199.7 16.5 19 63.2 12.5 185.4 27.1 18 43.8 1 96.1 1.7 10 55.9 2.6 72.8 9.1 14 64.3 0.3 64.2 2.1 11 42.7 4 132.2 11.2 23 76.7 0.8 58.6 6 14 22.8 3.5 174.6 12.7 26 117.1 10.2 263.5 15.6 34 146.7 0.2 14.8 0.6 2 42.1 0.4 73.5 5.9 11 25.3 1 24.7 5 4 13.4 6.8 139.4 7.2 28 64.3 11.6 368.2 16.8 32 163.9 1.6 95.7 3.8 10 44.5 1.2 109.6 10.3 14 67.9 7.2 196.2 15.8 16 39.7
基于SPSS的多元回归分析模型选取的应用毕业论文

毕业论文题目基于SPSS的多元回归分析模型选取的应用基于SPSS的多元回归分析模型选取的应用摘要本文不仅对于复杂的统计计算通过常用的计算机应用软件SPSS来实现,同时通过对两组数据的实证分析,来研究统计学中多元回归分析中的变量选取,让大家对统计学中的多元回归分析中模型的选取以及变量的选取和操作方法有更深层次的了解. 一组数据是对于淘宝交易额的未来发展趋势的研究,一组数据时对于我国财政收入的研究. 本文通过两个实证即淘宝交易额研究和财政收入研究从不同程度上对非线性回归模型和变量选取的研究运用通俗的语言和浅显的描述将SPSS在多元回归分析中的统计分析方法呈现在大家面前,让大家对多元回归分析以及SPSS软件都可以有更深一步的了解. 通过SPSS软件对数据进行分析,对数据进行处理的方法进行总结,找出SPSS对于数据处理和分析的优缺点,最后得在对变量的选取和软件的操作提出建议.关键词:统计学,SPSS,变量选取,多元回归分析AbstractThis article not only for complex statistical calculations done by the commonly used computer application software of SPSS, through the empirical analysis of the two groups of data at the same time, to study the statistics of the variables in the multivariate regression analysis, let everybody in the multiple regression analysis of statistical model selection as well as the selection of variables and operation methods have a deeper understanding. Is a set of data for the future development trend of research taobao transactions, a set of data for the research of our country's fiscal revenue. In this paper, through two empirical taobao transactions and fiscal revenue research from different degree of the study of nonlinear regression model and variable selection using a common language and plain the SPSS statistical analysis method in multiple regression analysis of present in front of everyone, let everyone to multiple regression analysis and SPSS software can have a deeper understanding. Through SPSS software to analyze data, and summarizes method of data processing, find out the advantages and disadvantages of SPSS for data processing and analysis, finally had to put forward the proposal to the operation of the selection of variables and software.Keywords: Statistical, SPSS, The selection of variables, multiple regressionanalysis目录第一章引言 (3)第二章多元回归模型的选取 (4)2.1 多元回归分析概述 (4)2.2 相关系数概述 (5)2.3 非线性回归模型概述 (5)2.4 多元线性回归模型自变量的选取 (6)第三章非线性回归模型案例:淘宝交易额模型的研究 (7)3.1 回归模型变量的确定 (7)3.1.1 数据来源 (7)3.1.2 复相关系数 (8)3.1.3 散点图看线性关系 (9)3.1.4 回归分析看拟合度 (11)3.1.5 确定回归模型变量 (11)3.2 调整后的变量的相关分析 (12)3.2.1 散点图 (12)3.2.2 计算相关系数 (14)3.3 多元线性回归分析 (16)3.4 小结 (18)第四章线性回归分析变量选取案例:财政收入模型的研究 (18)4.1 数据来源及变量选取 (18)4.2 相关分析 (20)4.2.1 散点图 (20)4.2.2 计算相关系数 (21)4.3 线性回归分析 (24)4.4 逐步回归 (26)4.5 小结 (27)第五章总结 (28)参考文献 (30)第一章引言随着社会的发展,统计的运用围越来越广泛,统计学作为高等院校经济类专业和工商管理类专业的核心课程,不管是在经济管理领域,或是在军事、医学等领域的研究中对于数量分析与统计分析都需要更高的要求,需要用到的数学知识较多,应用方面的灵活性也较强,计算量大且复杂.然而科学研究的深入,研究的对象也日益变得复杂,复杂系统的研究问题更是成为当今研究的热点. 为了更好的描述一个复杂的现象,就需要大量的数据和信息,如何高效、准确地利用已知的信息便成为当今社会研究的一项重要课题.在科学技术飞速发展的今天,统计学通过不断吸收和融合相关学科的新理论,开发应用新技术和新方法,拓展新的领域的同时不断深化和丰富了统计学传统领域的理论与方法. 在我国,社会主义市场经济体制的逐步建立,实践发展的需要对统计学提出了新的更多、更高的要求. 随着我国社会主义市场经济的成长和不断完善,统计学的潜在功能将得到更充分更完满的开掘. 从20世纪60年代开始,关于回归自变量的选择成为统计学中研究的热点问题,统计学家提出了许多回归选元的准则,并提出了许多行之有效的选元方法. 在应用回归分析去处理实际问题时,回归自变量选择是首先要解决的重要问题. 通常在做回归分析时,人们根据所研究问题的目的,结合经济理论罗列出对因变量可能有影响的的一些因素作为自变量引进回归模型,把一些对因变量影响很小的,有些甚至是没有影响的自变量,不但使得计算量变大,估计和预测的精度也下降了. 此外,如果遗漏了某些重要变量,回归方程的效果肯定不好. SPSS软件作为当今国际上运用广泛的统计分析软件,其功能齐全带有各种特点,在各个领域都得到了迅速普及,并成为各个行业提高管理水平、形成科学决策的重要手段. 然而,我国对于该软件的运用和理解始终处于早期应用阶段,无论是在功能的研究开发还是实际生活当中的运用都与西方发达国家相差甚远. 尤其是在管理决策方面,都因为没有进行深度分析而造成了浪费,要么就是利用SPSS软件进行简单分析而未进行深度开发,导致所得的信息有限、各信息间的关系不明确,最终导致管理者的判断出现偏差.基于以上背景,本文通过总结和吸取其他国外学者对统计学研究的,并结合我国的实际情况,本文采用了案例一对于网络购物这块的的研究,通过对2005年到2012年的居民消费水平,以及我国网络普及度,我国人人均纯收入以及我国的居民消费水平对淘宝网的未来发展趋势进行非线性回归模型的研究以及案例二对于我国财政收入的进行变量选取研究,通过对1992年到2012年的人均国生产总值,城镇居民家庭人均可支配收入,全社会固定投资,进出口总额,居民消费价格水平对我国财政收入的影响进行定量数据的研究. 通过对数据的选取,回归模型的确定以及软件的操作方法来告知读者如何在SPSS的操作中变量选取的原则、要求和方法.第二章多元回归模型的选取2.1 多元回归分析概述回归分析是确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法(即寻找具有相关关系的变量减的数学表达式并进行统计推断的一种统计方法). 按照其所涉及的自变量,可分为一元回归分析和多元回归分析;线性回归分析和非线性回归分析是按照自变量和因变量之间的关系划分的.而本文运用了多元线性回归分析中的方法,多元线性回归分析就是指回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系. 多元回归分析的主要容有以下几点:(1)从一组数据出发,确定某些变量之间的定量关系式,即建立数学模型并估计其中的未知参数. 估计参数的常用方法是最小二乘法;(2)对这些关系式的可信程度进行检验;(3)在许多自变量共同影响着一个因变量的关系中,判断哪些自变量的影响是显著的,哪些自变量的影响是不显著的,将影响显著的自变量选入模型中,而剔除影响不显著的变量,通常用逐步回归等方法;(4)利用所求的关系式对某一生产过程进行预测或控制.回归分析研究的主要问题是确定Y与X间的定量关系表达式,这种表达式称为回归方程;对求得的回归方程的可信度进行检验;判断自变量X对因变量Y有无影响;利用所求得的回归方程进行预测和控制. 回归分析主要应用于研究两个变量之间到底是哪个变量受哪个变量的影响,影响程度如何,通过分析现象之间相关的具体形式,确定其因果关系,并用数学模型来表现其具体关系,并根据实测数据来求解模型的各个参数,然后评价回归模型是否能够很好的拟合实测数据;如果能够很好的拟合,则可以根据自变量作进一步预测.2.2 相关系数概述相关关系是一种非确定性的关系,相关系数是研究变量之间线性相关程度的量. 相关关系是现象间客观存在的,但数值又是不严格及不完全确定的相互依存关系.1)复相关系数在一元回归分析中我们用相关系数r 来说明两变量之间线性相关的程度,在多元回归分析中,仍用它来表示y 与其他自变量之间的线性密切程度,此为复相关系数. 复相关是指因变量与多个自变量之间的相关关系. 复相关系数只是反映变量间表面的非本质的联系,因为变量很有可能受到其他变量的影响.2)偏相关系数在多变量的情况下,变量之间的相关系数是相当复杂的. 任意两个变量之间都有可能存在着相关关系,因此,只知道被解释变量与解释变量的总的相关程度是不够的. 如果需要了解某两个变量间的相关程度,就应在消除其他变量影响的情况下来计算他们的相关系数,这就是偏相关系数. 偏相关系数与复相关系数不同,复相关系数的取值在0-1之间,而偏相关系数则是有正有负,所以复相关系数与偏相关系数之间也有可能相差很大. 变量之间本存在错综复杂的关系,甚至可能使得符号也相反,但是偏相关系数才是变现变量之间的本质联系的.偏相关的主要用途:偏相关主要是用来研究自变量与因变量之间的关系的,其通过得到的自变量与因变量数据来进行计算,通过偏相关系数可以看出哪些自变量对因变量的影响更大一些,同时对于偏相关系数较小的变量,可以剔除.2.3 非线性回归模型概述非线性回归模型是指在众多的现象中,分析变量之间的关系时不符合解释变量线性和参数线性的一种模型. 在实际的经济活动中,经济变量的关系是相当复杂的,直接表示为线性关系的情况也并不多见. 但大多数的非线性关系是可以通过一些简单的数学处理,使之转化为线性关系,从而通过线性回归来进行计算. 而非线性回归模型又分为可化为线性模型的非线性回归模型和不可化为线性模型的非线性回归模型.本文研究的是可转化为线性模型的非线性回归模型,而可转化为线性模型的非线性回归模型又有好几种方法可以对变量进行转换.其有以下几种模型:1)多项式函数模型对于形如:k k x x x y ββββ+⋅⋅⋅+++=22110 ,的模型为多项式模型.令21122,,,k k k z x z x z x === ,原模型可化为线性形式k k z z z y ββββ+⋅⋅⋅+++=22110 ,那么就可以用多元线性回归分析的方法进行处理了.2)指数函数模型对于形如:k x k x x e e e y ββββ+⋅⋅⋅+++=21210 ,的模型为指数函数模型. 令k x k x x e z e z e z =⋅⋅⋅==,,,2121 ,原模型可化为线性形式k k z z z y ββββ+⋅⋅⋅+++=22110 ,那么就可以用多元线性回归分析的方法进行处理了.3)双曲线模型;4)半对数模型和双对数模型等.本文将对指数函数型非线性模型进行案例说明,所以对于其他类型的非线性回归模型的道理是一致的,在这里就不进行一一解释.2.4 多元线性回归模型自变量的选择在多元线性回归模型中自变量的选择实质上就是模型的选择. 现设一切可供选择的变量是t 个 ,它们组成的回归模型称为全模型(记:1+=t m ),在获得n 组观测数据后,我们有模型:⎩⎨⎧+=),0(~2n n I N X Y σεεβ , 其中:Y 是1⨯n 的观测值,β是1⨯m 未知参数向量,X 是m n ⨯结构矩阵,并假定X 的秩为m .现从t x x x ,,,21 这t 个变量中选t '变量,不妨设t x x x ',,,21 ,那么对全模型中的参数β和结构矩阵X 可作如下的分块(记:1+'=t p ):()'=q p βββ, , ()q p X X X = .我们称下面的回归模型为选模型:⎩⎨⎧+=),0(~2n p p I N X Y σεεβ ,其中:Y 是1⨯n 的观测值,p β是1⨯p 未知参数向量, p X 是p n ⨯结构矩阵,并假定p X 的秩为p .自变量的选择可以看成是这样的两个问题,一是究竟是用全模型还是用选模型,二是若用选模型,则究竟应包含多少变量最适合. 然而自变量的选择与相关系数,回归分析都有密切的关系,自变量的选择需要通过一系列的验证,剔除之后才能得到最好的变量从而得到最好的回归模型. 下面我们用两个案例来对多元回归模型的选取来进行解释和探讨.第三章 非线性回归模型案例:淘宝交易额研究3.1 回归模型变量的确定3.1.1数据来源为研究淘宝网未来发展趋势,从新浪官方微博淘宝数据魔方中获得淘宝2009年聚划算中购物群众的年龄比例作为定性数据,进行研究年龄对淘宝购物的影响. 并在新浪财经网上获得淘宝网自2003年到2012年的淘宝交易额以及淘宝注册人数的数据. 在中商情报局里获得我国近网络普及度等数据并从国家统计年鉴中选取统计指标居民消费水平.淘宝注册人数(1x )在一定程度上反应了网络购物的群众的人数,反应了当今社会网络购物的普遍性. 同时淘宝的注册人数也展现了人们对网络购物的认可度,换言之也就是说接受了网络购物并会在网上进行消费,是对网络购物很大程度上的支持. 我国网络普及度(2x )是指我国近几年网络在我国普及的围,这一块更好的反映了网络对居民网络消费的影响,因为网络是网络消费的必要条件. 我国网络普及度反映的是在我国日趋发展的经济下,人们对网络的接受程以及信任程度也是直接影响到淘宝的网络购物.居民消费水平(3x )主要通过消费的物质产品和劳务的数量和质量来反映. 居民消费水平的提高也能很好的展现在网络消费上作出的贡献.第二产业增加值(4x )是指采矿业,制造业,电力、煤气及水的生产和供应业,建筑业. 而制造业的发展也相继影响着产品的销售,所以在这里采用第二产业对淘宝交易额的影响. 通过对以上这三个定量数据的研究来其与淘宝交易额的关系,从而研究淘宝未来的发展趋势以及优劣态. 原始数据如下:表3.1为消除数据之间因单位不同产生的量纲的影响,对数据进行标准化得如下数据得到表3.23.1.2 复相关系数对表3.2 的数据进行复相关系数的研究,看变量之间的复相关关系,得到如下表3.3的复相关系数表:表3.3表3.3中有带“**”号的结果表明有关的两变量在0.01的显著性水平下显著相关,由上图可知,y 与1x 的相关系数为0.987>0,表示变量之间存在线性关系,其相关系数检验对应的概率P 值为0.000,低于显著性水平0.05,说明淘宝交易额与淘宝注册人数之间相关性显著. y 与2x e 的相关系数为0.923>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明淘宝交易额与我国网络普及度之间相关性显著.y 与3x 的相关系数为0.963>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明淘宝交易额与居民消费水平之间相关性显著. y 与4x e 的相关系数为0.919>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明我国第二产业增加值与居民消费水平之间相关性显著.综上所述通过SPSS 得出的相关系数的矩阵得到为:=1yx r 0.987 ,=2yx r 0.923 ,=3yx r 0.963 ,=4yx r 0.919 .虽然变量都通过了检验,但是可以看到2yx r 和4yx r 较另外两个复相关系数较低,因此对变量进行散点图的分析来了解自变量与因变量的相关关系.3.1.3 散点图看线性关系对y 与各个变量作出散点图(1)淘宝注册人数1x 与淘宝网交易总额y 的相关性散点图:图3.1(2)网络普及度2x 与淘宝网交易总额y 的散点图:图3.2(3)我国居民消费水平3x 与淘宝交易额y 的散点图:图3.3(4)第二产业增加值4x 对淘宝交易额y 的散点图:图3.4图3.2和3.4分别是自变量2x 和4x 与因变量的相关系数图,可以看出自变量2x 和因变量y 之间呈明显的指数线性关系,而变量4x 也是同样与因变量y 之间呈明显的指数线性关系.他们之间是非线性回归模型的关系. 所拟合的效果不理想所以我们还需要对数据进行进一步的处理和分析,得到确切的答案.3.1.4 回归分析看拟合度对数据进行回归分析:表3.4表3.4是自变量与因变量得到的回归分析,可知,因变量y 与常数项和自变量1x ,2x ,3x ,4x 的回归的标准化回归系数分别为0.01,0.660,-0.229,1.439,-0.899.而通过P 检验可以看到由上表 2.4可以看出常数项以及各自变量的P 值分别为:0.906,0.000,0.018,0.000及0.000. 可以看出原始变量所得到的P 值并没有全部通过检验. 说明常数项对因变量影响不显著. 对数据进行t 值检验,在给定的05.0=α,自由度9211=-=n 的临界值时,查表得=9025.0t 2.262,其常数项的t 值为0.123小于2.262,说明常数项不显著. 综上所述,可以初步得到一个模型为:4321899.0439.1229.0660.001.0x x x x y -+-+= .3.1.5确定回归模型变量综上通过散点图、复相关系数以及回归分析可以知道由于自变量2x 和4x 与因变量y 之间是非线性关系,是呈指数线性关系为研究之间线性关系,所以得到的模型的拟合程度并不是很理想.因此对自变量2x 和4x 进行取e 的对数即2x e 和4x e 来对变量进行研究看拟合效果得到下表.表3.5下面对表3.5进行变量分析与研究,通过对非线性模型中的变量的研究来了解多元回归分析中变量的选取与使用,同时对自变量进一步进行分析.3.2 调整后变量的相关分析3.2.1 散点图对y与各个变量作出散点图x与淘宝网交易总额y的相关性散点图:(1)淘宝注册人数1图3.5(2)e的网络普及度次方2x e与淘宝网交易总额y的相关性检验:图3.6x与淘宝交易额y的相关性检验:(3)我国居民消费水平3图3.7(4)e的第二产业增加值的次方4x e对淘宝交易额y的影响:图3.8由以上四个散点图可知,其所有的点均落在了左上至右下的一条直线上,表明了数据之间存在显著相关关系. 所以我们还需要对数据进行进一步的分析,得到确切的答案.3.2.2 计算相关系数(1)复相关系数r 是用来衡量回归直线对于观察值配合的密切程度,即用来衡量因变量y 与自变量1x ,2x e ,3x ,4x e 之间相关的密切程度. 以下是用SPSS 对数据进行相关性分析,得到如下的相关系数图表3.6图中有带“**”号的结果表明有关的两变量在0.01的显著性水平下显著相关,由上图可知,y 与1x 的相关系数为0.987>0,表示变量之间存在线性关系,其相关系数检验对应的概率P 值为0.000,低于显著性水平0.05,说明淘宝交易额与淘宝注册人数之间相关性显著. y 与2x e 的相关系数为0.979>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明淘宝交易额与我国网络普及度之间相关性显著.y 与3x 的相关系数为0.963>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明淘宝交易额与居民消费水平之间相关性显著. y 与4x e 的相关系数为0.997>0,表示变量之间存在线性关系,其对应P 值为0.000,小于显著性水平0.05,说明我国第二产业增加值与居民消费水平之间相关性显著.综上所述通过SPSS 得出的相关系数的矩阵得到为:=1yx r 0.987 ,=2yx r 0.979 ,=3yx r 0.963 ,=4yx r 0.997 .由以上数据可以看出,各列之间存在正相关关系. 即淘宝网注册人数1x 、e 的我国网络普及度2x e 、我国居民消费水平3x 、e 的我国第二产业增加值次方4x e 与淘宝交易总额y 存在显著的相关关系.(2)计算偏相关系数:下面是用SPSS 作出的偏相关系数:① 消除我国网络普及度、第二产业增加值和居民消费水平的影响后,计算淘宝注册人数与淘宝交易额的偏相关系数为:表3.7由上可知,淘宝注册人数与淘宝交易额的偏相关系数为0.795.②消除淘宝交易额、第二产业增加值和居民消费水平的影响后,我国网络普及度和淘宝交易额的偏相关系数为:表3.8由上可知我国网络普及度与淘宝交易额的偏相关系数为0.733.③消除淘宝注册人数、第二产业增加值和我国网络普及度的影响后,我国居民消费水平和淘宝交易额的偏相关系数:表3.9由上可知,我国居民消费水平和淘宝交易额的偏相关系数为-0.932.④消除淘宝注册人数、我国网络普及度和居民消费水平的影响后,计算第二产业增加值与淘宝交易额的偏相关系数:表3.10由上可知,e的第二产业增加值次方与淘宝交易额的偏相关系数为0.946.⑤下表为各个变量之间的偏相关系数表,为方便,这里直接变各变量之间的偏相关系数:r y 1x 2x e3x 4x e y 0.795 0.773 -0.9320.946 1x 0.795 -0.611 0.758 -0.592x e0.773 -0.611 0.702 -0.521 3x-0.932 0.758 0.702 0.818 4x e 0.946 -0.59 -0.521 0.818表3.11这里我们对变量2x 和4x 采用的是其指数幂,是因为在对变量的相关性进行检验时,通过散点图可以看出2x 和4x 与因变量之间呈的是指数线性关系,是非线性关系所以对数据进行了处理,因为原始变量之间存在的非线性关系得出的结果不具有代表性. 可以通过散点图看到从以上的偏相关系数来看,如果2x e ,3x 和4x e 保持不变,y 与1x 之间存在相关关系,当1x ,3x 和4x e 的保持不变时,2x e 和y 之间存在相关关系,其他关系同上,在这里就不进行一一解释.我们也可以通过以上的偏相关系数表可以看出各个自变量之间也存在一定的偏相关关系,但是相对于自变量与因变量之间的偏相关关系较小,说明这些变量之间的选择比较显著.但是其关系强度较前者略低,所以经过以上系数得到的偏相关系数可以看出,其相关程度较原关系的强度低,应采用原数据的自变量和因变量. 即所采用的自变量和因变量保持不变.通过复相关系数的计算和偏相关系数的计算结果可以看出,复相关系数的取值在0-1之间,偏相关系数的取值在-1到1之间,由上数据便可看出偏相关系数与复相关系数之间的差距相差甚大,有的甚至改变了符号. 从上可以看出通过复相关系数不能很好的确定变量之间的相关关系,不能明确的解释变量,而偏回归系数可以看出变量是否符合要求. 从下面的回归分析中继续对变量进行研究.3.3 多元线性回归分析对数据进行回归分析,得到如下结果:表3.12复相关系数为1,判定系数为0.999,调整系数为0.999,估计值的标准误差为0.03296.表3.13由上面结果的看其显著性检验结果为,回归平方和为9.993,残差平方和0.007,总平方和10.000, F 统计量的值为2.299E3,对应的概率P 值为0.000,小于显著性水平0.05,即:淘宝交易总额y 与淘宝网注册人数1x 、e 的我国网络普及度次方2x e 、我国居民消费水平3x 和e 的我国第二产业增加值次方4x e 之间存在线性关系,所以可认为所建立的回归方程有效.表3.14由上表可知,因变量y 与常数项和自变量1x ,2x e ,3x ,4x e 的回归的标准化回归系数分别为-1.119,0.244,0.107,-0.321,0.615. 3个回归系数B 的显著性水平均小于0.05,这里可以认为自变量1x ,2x e ,3x ,4x e 对因变量y 有显著性影响. 于是得到回归方程为:42615.0321.0107.0244.0119.131x x e x e x y +-++-= , 由上图可知对数据进行t 值检验,在给定的05.0=α,自由度9211=-=n 的临界值时,查表得=9025.0t 2.262,因为1x ,2x e ,3x ,4x e 的参数对应的t 统计量的绝对值均大于2.262,这说明%5的显著性水平下,斜率系数均显著不为0,表明淘宝网注册人数1x ,e 的我国网络普及度次方2x e ,我国居民消费水平3x ,e 的我国第二产业增加值次方4x e 等变量联合起来对该商品的消费支出有显著的影响.P 检验:由上表可以看出各自变量以及常数项的P 值分别为:0.00,0.018,0.039,0.001及0.000,可以看出其P 值均小于0.05,均通过检验综上所述,四个自变量对因变量都有显著性影响,并都通过了检验可以得到最优方程式为:。
多元回归分析中的变量选取——SPSS的应用统计学

多元回归分析中的变量选取——SPSS的应用统计学在多元回归分析中,变量选取是一个非常重要的步骤,可以决定模型的准确性和可解释性。
本文将介绍如何使用SPSS进行变量选取,并给出一些常用的变量选取方法。
首先,打开SPSS软件并加载数据集。
然后,在菜单栏中选择“分析”→“回归”→“线性”。
将要分析的依赖变量(因变量)和独立变量(自变量)移动到右边的框中。
点击“方法”选项卡,打开“变量选择”对话框。
SPSS提供了多种变量选取方法,其中一种常用的方法是逐步回归分析。
逐步回归是一种逐渐添加或删除变量的方法,以找到与因变量最相关的自变量组合。
在“变量选择”对话框中,选择“逐步”方法,然后点击“设置”按钮配置选择变量的条件。
逐步回归有两种选择变量的模式:进入模式和删除模式。
进入模式是逐渐从模型中添加自变量,直到没有其他显著的自变量可以添加为止。
删除模式则是一开始将所有自变量添加到模型中,然后逐渐删除非显著的自变量,直到只剩下显著的变量。
在设置条件中,可以选择标准化方法、统计水平以及要使用的模式。
标准化方法有“逐步前向”和“逐步后向”两种选择。
逐步前向是添加变量到模型中,逐渐增加F值,逐步后向则是删除变量,逐渐减小F值。
在统计水平中,可以设置进入模型和离开模型的显著性水平。
通常设置为0.05或0.01点击“确定”后,SPSS将运行逐步回归分析,并显示结果。
结果中将显示模型的显著性、自变量的标准化系数、F值等信息。
在分析的同时,SPSS还会生成一份逐步回归的报告,其中包含了模型的统计指标、显著性检验等内容。
除了逐步回归,SPSS还提供了其他常用的变量选取方法,如逐步逆选择、全部进入、最佳子集等。
每种方法都有其适用的情况,根据具体的研究目的和数据特点选择合适的方法。
值得注意的是,变量选取只是多元回归分析中的一部分,它可以帮助我们找到与因变量最相关的自变量组合,但并不能保证得到最优模型。
因此,在进行变量选取之后,还需要对所选自变量进行进一步的检验和解释,以确保所建立的模型具有合理性和可解释性。
线性回归分析的SPSS操作(多元线性回归)

线性回归分析的SPSS操作本节内容主要介绍如何确定并建立线性回归方程。
包括只有一个自变量的一元线性回归和和含有多个自变量的多元线性回归。
为了确保所建立的回归方程符合线性标准,在进行回归分析之前,我们往往需要对因变量与自变量进行线性检验。
也就是类似于相关分析一章中讲过的借助于散点图对变量间的关系进行粗略的线性检验,这里不再重复。
另外,通过散点图还可以发现数据中的奇异值,对散点图中表示的可能的奇异值需要认真检查这一数据的合理性。
一、一元线性回归分析1.数据以本章第三节例3的数据为例,简单介绍利用SPSS如何进行一元线性回归分析。
数据编辑窗口显示数据输入格式如下图7-8(文件7-6-1.sav):图7-8:回归分析数据输入2.用SPSS进行回归分析,实例操作如下:2.1.回归方程的建立与检验(1)操作①单击主菜单Analyze / Regression / Linear…,进入设置对话框如图7-9所示。
从左边变量表列中把因变量y选入到因变量(Dependent)框中,把自变量x选入到自变量(Independent)框中。
在方法即Method一项上请注意保持系统默认的选项Enter,选择该项表示要求系统在建立回归方程时把所选中的全部自变量都保留在方程中。
所以该方法可命名为强制进入法(在多元回归分析中再具体介绍这一选项的应用)。
具体如下图所示:图7-9 线性回归分析主对话框②请单击Statistics…按钮,可以选择需要输出的一些统计量。
如Regression Coefficients(回归系数)中的Estimates,可以输出回归系数及相关统计量,包括回归系数B、标准误、标准化回归系数BETA、T值及显著性水平等。
Model fit项可输出相关系数R,测定系数R2,调整系数、估计标准误及方差分析表。
上述两项为默认选项,请注意保持选中。
设置如图7-10所示。
设置完成后点击Continue返回主对话框。
图7-10:线性回归分析的Statistics选项图7-11:线性回归分析的Options选项回归方程建立后,除了需要对方程的显著性进行检验外,还需要检验所建立的方程是否违反回归分析的假定,为此需进行多项残差分析。
SPSS多元线性回归解析总结报告实例操作步骤
合用标准文档SPSS 统计解析多元线性回归解析方法操作与解析实验目的:引入 1998~2021年上海市城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率和房屋空置率作为变量,来研究上海房价的变动因素。
实验变量:以年份、商品房平均售价〔元 / 平方米〕、上海市城市人口密度 ( 人/平方公里 ) 、城市居民人均可支配收入 ( 元) 、五年以上平均年贷款利率 (%) 和房屋空置率 (%)作为变量。
实验方法:多元线性回归解析法软件:操作过程:第一步:导入 Excel 数据文件1. open data document —— open data —— open;2. Opening excel data source——OK.第二步:1. 在最上面菜单里面选中 Analyze —— Regression —— Linear ,Dependent 〔因变量〕选择商品房平均售价, Independents 〔自变量〕选择城市人口密度、城市居民人均可支配收入、五年以上平均年贷款利率、房屋空置率; Method 选择 Stepwise.进入以下界面:2. 点击右侧 Statistics ,勾选 Regression Coefficients 〔回归系数〕选项组中的Estimates ;勾选 Residuals 〔残差〕选项组中的 Durbin-Watson 、Casewise diagnostics 默认;接着选择 Model fit 、Collinearitydiagnotics ;点击 Continue.3.点击右侧 Plots ,选择 *ZPRED〔标准化展望值〕作为纵轴变量,选择DEPENDNT〔因变量〕作为横轴变量;勾选选项组中的 Standardized Residual Plots 〔标准化残差图〕中的Histogram 、Normal probability plot;点击 Continue.4.点击右侧 Save,勾选 Predicted Vaniues 〔展望值〕和 Residuals 〔残差〕选项组中的 Unstandardized ;点击 Continue.5. 点击右侧 Options ,默认,点击 Continue.6.返回主对话框,单击 OK.输出结果解析:1.引入 / 剔除变量表Variables Entered/Removed aModel Variables Entered Variables Removed Method1城市人口密度 ( 人/ 平方公.Stepwise (Criteria:里 )Probability-of-F-to-enter<= .050,Probability-of-F-to-remove>= .100).2城市居民人均可支配收入( 元).Stepwise (Criteria:Probability-of-F-to-enter<= .050,Probability-of-F-to-remove>= .100).a. Dependent Variable:商品房平均售价〔元/ 平方米〕该表显示模型最先引入变量城市人口密度 ( 人/ 平方公里 ) ,第二个引入模型的是变量城市居民人均可支配收入 ( 元) ,没有变量被剔除。
多元回归分析SPSS案例

多元回归分析SPSS案例
一、案例背景
一所大学学术部门进行了一项有关学生毕业的调查,主要是为了探讨
学生毕业的影响因素,通过这个调查,大学试图及早发现潜在的学术发展
问题,从而改善学术教育和服务质量。
调查采用SPSS软件分析,将来自
一所大学学生的有关信息作为研究目标,本研究的研究对象为大学学生。
二、研究目的
1、探索影响大学生毕业的主要因素;
2、研究各变量对大学生毕业的影响程度;
3、提出适合大学学生的毕业提升策略。
三、研究变量
本研究采用多元线性回归分析方法,研究变量有:(1)身体健康程
度(即体检结果);(2)现金流(即家庭收入);(3)家庭教育水平;(4)学习成绩;(5)家庭状况,即与家庭成员的关系;(6)个人情感
状况;(7)考试作弊。
四、研究方法
1、获取研究数据:
通过与学校协商,确定调查对象,以及采集问卷的方法(如发放问卷、网络调查等),以获取有关学生毕业的数据;
2、数据处理:
清洗数据,将数据分类进行处理,去除无关信息;
3、多元回归分析:
计算自变量与因变量之间的线性关系,分析变量间关系,建立多元回归模型;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
毕业论文题目多元回归分析中的变量选取——SPSS的应用院(系)数学与统计学院专业年级 2010级统计学指导教师职称副教授多元回归分析中的变量选取——SPSS的应用殷婷摘要本文不仅对于复杂的统计计算通过常用的计算机应用软件SPSS来实现,同时通过对两组数据的实证分析,来研究统计学中多元回归分析中的变量选取,让大家对统计中的多元回归数据的选取和操作方法有更深层次的了解。
一组数据是对于淘宝交易额的未来发展趋势的研究,一组数据时对于我国财政收入的研究。
本文通过两个实证从不同程度上对数据选取的研究运用通俗的语言和浅显的描述将SPSS在多元回归分析中的统计分析方法呈现在大家面前,让大家对多元回归分析以及SPSS软件都可以有更深一步的了解。
通过SPSS软件对数据进行分析,对数据进行处理的方法进行总结,找出SPSS对于数据处理和分析的优缺点,最后得在对变量的选取和软件的操作提出建议。
关键词:统计学 SPSS 变量的选取多元回归分析AbstractIn this paper, not only for complex statistical calculations done by the commonly used computer application software of SPSS, through theempirical analysis of the two groups of data at the same time, to study the statistics of the variables in the multivariate regression analysis, leteverybody to select multiple regression in statistical data and operationmethods this paper, through two empirical to select data from differentextent research using a common language and plain the SPSS statisticalanalysis method in multiple regression analysis of present in front ofeveryone, let everyone to multiple regression analysis and SPSS softwarecan of the selection of variables and software.Keywords: Statistical SPSS The selection of variables multiple regression analysis目录摘要 (1)英文摘要 (1)引言 (3)第一章回归分析 (3)1.1自变量的选择 (4)1.2国内外研究现状 (5)第二章案例分析一:淘宝交易额的研究 (6)2.1数据的来源及变量的选取 (6)2.2相关分析 (7)2.2.1散点图 (7)2.2.2计算相关系数 (8)2.3回归分析 (11)2.4小结 (13)第三章案例分析二:财政收入的研究 (14)3.1数据的来源及变量的选取 (14)3.2相关分析 (15)3.2.1散点图 (15)3.2.2计算相关系数 (17)3.3回归分析 (19)3.4逐步回归 (21)3.5小结 (24)第四章总结及建议 (25)参考文献 (26)引言统计学是一门提供数据信息的收集、处理、归纳和分析的理论与方法的科学。
然而随着社会的发展,统计的运用范围越来越广泛,统计学作为高等院校经济类专业和工商管理类专业的核心课程,不管是在经济管理领域,或是在军事、医学等领域的研究中对于数量分析与统计分析都需要更高的要求,需要用到的数学知识较多,应用方面的灵活性也较强,计算量大且复杂。
随着我国社会主义市场经济的日趋完善,不管是在宏观经济的经济调控领域还是在微观的企业管理领域中,人们必须准确及时的获得经济运行中的各类信息才能得到高效的监控和科学的管理。
然而科学研究的深入,研究的对象也日益变得复杂,复杂系统的研究问题更是成为当今研究的热点。
为了更好的描述一个复杂的现象,就需要大量的数据和信息,如何高效、准确地利用已知的信息便成为当今社会研究的一项重要课题。
基于以上背景,本文通过总结和吸取其他国内外学者对统计学研究的,并结合我国的实际情况,本文采用了案例一对于网络购物这块的的研究,通过对2005年到2012年的居民消费水平,以及我国网络普及度,我国人人均纯收入以及我国的居民消费水平对淘宝网的未来发展趋势进行定量数据的研究以及案例二对于我国财政收入的研究,通过对2000年到2012年的人均国内生产总值,经济活动人口,全社会固定投资,进出口总额,居民消费价格水平对我国财政收入的影响进行定量数据的研究。
通过对数据的选取,以及软件的操作方法来告知读者如何在SPSS的操作中变量选取的原则、要求和方法。
第一章自变量的选择1.1自变量的选择在多元线性回归模型中,自变量的选择实质上就是模型的选择。
现设一切可供选择的变量是t个 ,它们组成的回归模型称为全模型(记:),在获得n组观测数据后,我们有模型其中:是的观测值,是未知参数向量,是结构矩阵,并假定X的秩为。
现从这t个变量中选变量,不妨设,那么对全模型中的参数和结构矩阵可作如下的分块(记:):,我们称下面的回归模型为选模型:其中:是的观测值,是未知参数向量,是结构矩阵,并假定的秩为。
自变量的选择可以看成是这样的两个问题,一是究竟是用全模型还是用选模型,二是若用选模型,则究竟应包含多少变量最适合。
如果全模型为真,而我们用了选模型,这就表示在方程中丢掉了部分有用变量,相反,如果选模型为真,而我们选用了全模型,这就表示在方程中引入了一些无用变量,下面从参数估计和预测两个角度来看一看由于模型选择不当带来的后果。
为了讨论方便起见,先引入几个记号:全模型中参数的估计:211ˆ[()]()Y I X X X X Y n R X σ-'''=--其中:为矩阵的秩。
在点点上的预测值为在选模型中参数的估计:121()1[()]()p p p pp p p p p p X X X Y Y I X X X X Y n R X βσ--''=''=--在()'''='''=+),(),()(11t p p qp x x x x x x x 上的预测值为 1.2国内外研究现状在科学技术飞速发展的今天,统计学广泛吸收和融合相关学科的新理论,不断开发应用新技术和新方法,深化和丰富了统计学传统领域的理论与方法,并拓展了新的领域。
今天的统计学已展现出强有力的生命力。
在我国,社会主义市场经济体制的逐步建立,实践发展的需要对统计学提出了新的更多、更高的要求。
随着我国社会主义市场经济的成长和不断完善,统计学的潜在功能将得到更充分更完满的开掘。
在应用回归分析去处理实际问题时,回归自变量选择是首先要解决的重要问题。
通常,在做回归分析时,人们根据所研究问题的目的,结合经济理论罗列出对因变量可能有影响的的一些因素作为自变量引进回归模型,其结果是把一些对因变量影响很小的,有些甚至没有影响的自变量也选入了回归模型中,这样一来,不但计算量变大,而且估计和预测的精度也会下降。
此外,如果遗漏了某些重要变量,回归方程的效果肯定不好。
在一些情况下,某些自变量的观测数据的获得代价昂贵,如果这些自变量本身对因变量的影响很小或根本没有影响,我们不加选择的引进回归模型,势必造成观测数据收集和模型应用的费用不必要的加大。
因此,在应用回归分析中,对进入模型的自变量作精心的选择是十分必要的。
SPSS软件作为当今国际上运用广泛的统计分析软件,因其具有自动统计绘图、数据的深入分析、易学易用、功能齐全等特点,在各个领域得到了迅速普及,并成为各行业管理组织提高管理水平、形成科学决策的重要手段。
然而,我国对该软件的理解和运用还处于早期应用阶段,对其功能的研究开发与实际生活当中的运用与西方发达国家相差甚远。
特别是在管理决策方面,管理者对客观现实的准确把握对于决策起着至关重要的作用,他们花费大量人力、物力、财力收集统计数据,但是由于没有进行深度分析而浪费,或者仅仅利用SPSS软件进行简单分析而未进行深度开发,致使所得信息有限、各信息间的关系不明确,最终导致管理者的判断出现偏差。
第二章案例分析一:淘宝交易额的研究2.1 数据的来源及变量的解释为研究淘宝网未来发展趋势,从新浪官方微博淘宝数据魔方中获得淘宝2009年聚划算中购物群众的年龄比例作为定性数据,进行研究年龄对淘宝购物的影响。
并在新浪财经网上获得淘宝网自2005年到2012年的淘宝交易额以及淘宝注册人数的数据。
在中商情报局里获得我国近网络普及度等数据并从国家统计年鉴中选取统计指标居民消费水平。
淘宝注册人数()在一定程度上反应了网络购物的群众的人数,反应了当今社会网络购物的普遍性。
同时淘宝的注册人数也展现了人们对网络购物的认可度,换言之也就是说接受了网络购物并会在网上进行消费,是对网络购物很大程度上的支持。
我国网络普及度()是指我国近几年网络在我国普及的范围,这一块更好的反映了网络对居民网络消费的影响,因为网络是网络消费的必要条件。
我国网络普及度反映的是在我国日趋发展的经济下,网络也得到了普遍的广泛,人们对网络的接受程度,信任程度也是直接影响到淘宝的网络购物。
居民消费水平()是指居民在物质产品和劳务的消费过程中,对满足人们生存、发展和享受需要方面所达到的程度。
通过消费的物质产品和劳务的数量和质量反映出来。
居民消费水平是指居民在物质产品和劳务的消费过程中,对满足人们生存、发展和享受需要方面所达到的程度。
它主要通过消费的物质产品和劳务的数量和质量来反映。
居民消费水平的提高也能很好的展现在网络消费上作出的贡献。
通过对以上这三个定量数据的研究来其与淘宝交易额的关系,从而研究淘宝未来的发展趋势以及优劣态。
原始数据如下:由于数据之间单位的不同,为了消除量纲的影响,把数据标准化进行处理,得到如下标准化的数据(所有取值保留了两位小数):2.2相关分析2.2.1散点图对y与各个变量作出散点图(1)淘宝注册人数与y的相关性散点图:(2)网络普及度与淘宝网交易总额的相关性检验:(3)我国居民消费水平与淘宝交易的相关性检验:由以上三个散点图可知,其所有的点均落在了左上至右下的一条直线上,表明了数据之间存在显著相关关系。
