电力系统分析课程设计-潮流计算
电力系统分析课程设计——电力系统潮流计算

信息工程学院课程设计报告书题目: 电力系统潮流计算专业:电气工程及其自动化班级:0310406学号:031040635学生姓名:陈代才指导教师:钟建伟2013年 4 月15 日信息工程学院课程设计任务书2013年4月15日目录1 任务提出与方案论证 (2)2 总体设计 (3)2.1潮流计算等值电路 (3)2.2建立电力系统模型 (3)2.3模型的调试与运行 (3)3 详细设计 (4)3.1 计算前提 (4)3.2手工计算 (7)4设计图及源程序 (11)4.1MA TLAB仿真 (11)4.2潮流计算源程序 (11)5 总结 (19)参考文献 (20)1 任务提出与方案论证潮流计算是在给定电力系统网络结构、参数和决定系统运行状态的边界条件的情况下确定系统稳态运行状态的一种基本方法,是电力系统规划和运营中不可缺少的一个重要组成部分。
可以说,它是电力系统分析中最基本、最重要的计算,是系统安全、经济分析和实时控制与调度的基础。
常规潮流计算的任务是根据给定的运行条件和网路结构确定整个系统的运行状态,如各母线上的电压(幅值及相角)、网络中的功率分布以及功率损耗等。
潮流计算的结果是电力系统稳定计算和故障分析的基础。
在电力系统运行方式和规划方案的研究中,都需要进行潮流计算以比较运行方式或规划供电方案的可行性、可靠性和经济性。
同时,为了实时监控电力系统的运行状态,也需要进行大量而快速的潮流计算。
因此,潮流计算是电力系统中应用最广泛、最基本和最重要的一种电气运算。
在系统规划设计和安排系统的运行方式时,采用离线潮流计算;在电力系统运行状态的实时监控中,则采用在线潮流计算。
是电力系统研究人员长期研究的一个课题。
它既是对电力系统规划设计和运行方式的合理性、可靠性及经济性进行定量分析的依据,又是电力系统静态和暂态稳定计算的基础。
潮流计算经历了一个由手工到应用数字电子计算机的发展过程,现在的潮流算法都以计算机的应用为前提用计算机进行潮流计算主要步骤在于编制计算机程序,这是一项非常复杂的工作。
电力系统课程设计-牛顿拉夫逊法潮流计算

课程设计说明书题目电力系统分析系 ( 部)专业( 班级 )姓名学号指导教师起止日期电力系统分析课程设计任务书系(部): 专业:指导教师:目录一、潮流计算基本原理1.1 潮流方程的基本模型1.2 潮流方程的讨论和节点类型的划分1.3、潮流计算的意义二、牛顿一拉夫逊法2.1 牛顿-拉夫逊法基本原理2.2节点功率方程2.3修正方程2.4 牛顿法潮流计算主要流程三、收敛性分析四、算例分析总结参考文献电力系统分析潮流计算一、潮流计算基本原理1.1潮流方程的基本模型电力系统是由发电机、变压器、输电线路及负荷等组成,其中发电机及负荷是非线性元件,但在进行潮流计算时,一般可以用接在相应节点上的一个电流注入量来代表。
因此潮流计算所用的电力网络系由变压器、输电线路、电容器、电抗器等静止线性元件所构成,并用集中参数表示的串联或并联等值支路来模拟。
结合电力系统的特点,对这样的线性网络进行分析,普通采用的是节点法,节点电压与节点电流之间的关系I=YV (1—1)其展开式为(i=1,2,3, …,n) (1—2)在工程实际中,已经的节点注入量往往不是节点电流而是节点功率,为此必须应用联系节点电流和节点功率的关系式 (i=1,2,3, …,n) (1—3)将 式 ( 1 - 3 ) 代 入 式 ( 1 - 2 ) 得 到 (i=1,2,3, …,n) (1-4)交流电力系统中的复数电压变量可以用两种极坐标来表示V =Vei8. (1-5)或 V=e+jf (1-6)而复数导纳为Y=G+jB (1-7)将式(1-6)、式(1- 7)代入以导纳矩阵为基础的式(1-4),并将实部与虚部分开,可以得到以下两种形式的潮流方程。
潮流方程的直角坐标形式为潮流方程的极坐标形式为(1—10)(1-11)以上各式中,j∈i表示乙号后的标号j的节点必须直接和节点i相联,并包括j=i的情况。
这两种形式的潮流方程通常称为节点功率方程,实牛顿一拉夫逊等潮流算法所采用的主要数学模型。
潮流计算的课程设计

潮流计算的课程设计一、教学目标本课程旨在让学生掌握潮流计算的基本理论、方法和应用,培养学生运用电力系统潮流计算解决实际问题的能力。
具体目标如下:1.知识目标:(1)掌握电力系统的基本概念、结构和参数。
(2)理解潮流计算的基本原理和方法。
(3)熟悉电力系统中常用的潮流计算算法及其特点。
(4)了解潮流计算在电力系统规划、设计和运行中的应用。
2.技能目标:(1)能够运用潮流计算软件进行电力系统潮流计算。
(2)具备分析电力系统潮流计算结果的能力。
(3)能够针对实际问题,运用所学知识进行潮流计算方法的选取和应用。
3.情感态度价值观目标:(1)培养学生对电力系统的兴趣,激发学生学习电力系统潮流计算的积极性。
(2)培养学生团队合作精神,提高学生解决实际问题的责任感。
二、教学内容本课程的教学内容主要包括以下几个部分:1.电力系统基本概念、结构和参数。
2.潮流计算基本原理和方法。
3.电力系统中常用的潮流计算算法及其特点。
4.潮流计算在电力系统规划、设计和运行中的应用。
5.潮流计算软件的使用和结果分析。
三、教学方法本课程采用多种教学方法,以激发学生的学习兴趣和主动性:1.讲授法:用于传授电力系统基本知识和潮流计算原理。
2.案例分析法:通过实际案例,让学生掌握潮流计算的方法和应用。
3.实验法:引导学生运用潮流计算软件进行实际操作,提高学生的动手能力。
4.讨论法:学生分组讨论,培养学生的团队合作精神和分析问题能力。
四、教学资源本课程所需教学资源包括:1.教材:《电力系统潮流计算》。
2.参考书:相关电力系统潮流计算的学术论文和专著。
3.多媒体资料:电力系统潮流计算的课件、视频等。
4.实验设备:潮流计算软件、计算机等。
教学资源应根据教学内容和教学方法的需求进行选择和准备,以支持教学的顺利进行,提高学生的学习效果。
五、教学评估本课程的教学评估采用多元化评价方式,全面客观地评价学生的学习成果。
评估方式包括:1.平时表现:通过课堂参与、提问、回答问题等方式,评价学生的学习态度和积极性。
简单电力系统分析潮流计算

简单电力系统分析潮流计算电力系统潮流计算是电力系统分析中的一项重要任务。
其目的是通过计算各个节点的电压、电流、有功功率、无功功率等参数,来确定系统中各个元件的运行状态和互相之间的相互影响。
本文将介绍电力系统潮流计算的基本原理、计算方法以及应用。
潮流计算的基本原理是基于电力系统的节点电压和支路功率之间的网络方程。
通过对节点电压进行迭代计算,直到满足所有支路功率平衡方程为止,得到系统的运行状态。
潮流计算的基本问题可以表示为以下方程组:P_i = V_i * (G_i * cos(θ_i - θ_j ) + B_i * sin(θ_i -θ_j )) - V_j * (G_i * cos(θ_i - θ_j ) - B_i * sin(θ_i -θ_j )) (1)Q_i = V_i * (G_i * sin(θ_i - θ_j ) - B_i * cos(θ_i -θ_j )) - V_j * (G_i * sin(θ_i - θ_j ) + B_i * cos(θ_i -θ_j )) (2)其中,P_i为节点i的有功功率注入;Q_i为节点i的无功功率注入;V_i和θ_i分别为节点i的电压幅值和相角;V_j和θ_j分别为节点j的电压幅值和相角;G_i和B_i分别为支路i的导纳的实部和虚部。
对于一个电力系统,如果知道了节点注入功率和线路的导纳,就可以通过潮流计算求解出各节点的电压和功率。
这是一种不断迭代的过程,直到系统达到平衡状态。
潮流计算的方法有多种,常见的有高斯-赛德尔迭代法、牛顿-拉夫逊迭代法等。
其中,高斯-赛德尔迭代法是最常用的一种方法。
高斯-赛德尔迭代法的思想是从已知节点开始,逐步更新其他节点的电压值,直到所有节点的电压值收敛为止。
具体步骤如下:1.初始化所有节点电压的初始值;2.根据已知节点的注入功率和节点电压,计算其他节点的电压值;3.判断节点电压是否收敛,如果收敛则结束计算,否则继续迭代;4.更新未收敛节点的电压值,返回步骤2高斯-赛德尔迭代法的优点是简单有效,但其收敛速度较慢。
电力系统潮流计算课程设计
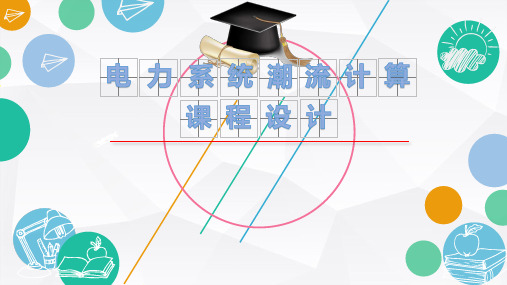
YG=YG+sparse(branch(i,1),branch(i,2),-yg(i,1),n,n)+sparse(branch(i,2),branch(i,1),-yg(i,1),n,n); %互电导
YG=YG+sparse(branch(i,1),branch(i,1),yg(i,1),n,n)+sparse(branch(i,2),branch(i,2),yg(i,1),n,n); %自电导
%% 计算功率不平衡量
%计算ΔPi有功的不平衡量
Pi=sparse(1,n);
Qi=sparse(1,n);
dP=sparse(P(1:n-1)-Pi(1:n-1)); %dP有n-1个
%计算ΔQi无功的不平衡量
for i=1:n
Qn=sparse(1,n);
for ii=1:size(xy,1)
if xy(ii,1)==i
break;
end
k=k+1; %若不满足继续迭代,迭代次数+1
%% 计算雅克比矩阵
H=sparse(n-1,n-1);
N=sparse(n-1,nPQ);
function Newton(cases)
%% 读取数据参数
bus=cases.bus; %读取母线参数
branch=cases.branch; %读取支路参数
gen=cases.gen; %读取发电机参数
n=size(bus,1); %获得结点数,即bus矩阵行数
baseMVA=cases.baseMVA; %功率基准值
P(i)=bus(i,3)/baseMVA;
Q(i)=bus(i,4)/baseMVA;
电力系统分析潮流计算最终完整版

电力系统分析潮流计算最终完整版电力系统潮流计算是电力系统运行的基础,它对电力系统的稳定运行和安全运行具有重要意义。
本文将介绍电力系统潮流计算的主要内容和步骤,并阐述其在电力系统运行中的应用。
电力系统潮流计算是指对电力系统中各节点的电压和功率进行计算和分析的过程。
它主要用于确定电力系统中各个节点的电压和相应的功率,以评估电力系统的稳定性和安全性。
潮流计算的结果可以用于电力系统的规划、调度和运行等各个环节。
潮流计算的主要步骤主要包括:建立电力系统潮流模型、制定潮流计算方程、选择潮流计算方法和求解潮流计算方程。
建立电力系统潮流模型是潮流计算的第一步,它主要包括确定电力系统的拓扑结构、电气参数和发电机和负荷模型等。
通过建立电力系统的拓扑结构和电气参数,可以确定电力系统中各个节点之间的连接关系和传输条件。
发电机和负荷模型则用于描述电力系统中的发电机和负荷之间的相互作用。
制定潮流计算方程是潮流计算的第二步,它主要是根据电力系统的拓扑结构和电气参数,建立潮流计算的数学模型。
潮流计算方程主要包括功率方程、节点电压方程和变压器方程等。
功率方程用于描述发电机和负荷之间的功率平衡关系,节点电压方程用于描述电力系统中各个节点的电压平衡关系,变压器方程用于描述变压器的运行状况。
选择潮流计算方法是潮流计算的第三步,它主要是选择合适的方法来求解潮流计算方程。
常见的方法包括直接迭代法、高斯-赛德尔迭代法、牛顿-拉夫逊迭代法和快速迭代法等。
不同的方法在精度和收敛速度上有所差异,根据实际情况选择合适的方法。
求解潮流计算方程是潮流计算的最后一步,它主要是通过迭代计算,求解潮流计算方程得到电力系统各个节点的电压和功率值。
在求解过程中,需要根据实际情况设置迭代的初始值和收敛条件,以保证计算结果的准确性和稳定性。
电力系统潮流计算在电力系统运行中具有广泛的应用。
它可以用于电力系统规划,通过计算电力系统中各个节点的电压和功率,评估电力系统的输电能力和供电质量,为电力系统的扩容和优化提供指导。
电力系统分析(潮流计算)

电力系统分析(一):电力系统的基本概念No.1电力系统的组成和接线方式1、电力系统的四大主要元件:发电机、变压器、电力线路、负荷。
2、动力系统包括动力部分(火电厂的锅炉和汽轮机、水电厂的水库和水轮机、核电厂的核反应堆和汽轮机)和电力系统。
3、电力网包括变压器和电力线路。
4、用户只能从一回线路获得电能的接线方式称为无备用接线方式。
No.2电力系统的运行特点1、电能的生产、传输、分配和消费具有:①重要性、②快速性、③同时性。
2、电力系统运行的基本要求:①安全可靠持续供电(首要要求)、②优质、③经济3、根据负荷的重要程度(供电可靠性)将负荷分为三级。
4、电压质量分为:①电压允许偏差、②三相电压允许不平衡度、③公网谐波、④电压允许波动与闪变5、衡量电能质量的指标:①电压、②频率、③波形(电压畸变率)6、10kV公用电网电压畸变率不超过4%。
7、抑制谐波的主要措施:①变压器星三角接线、②加装调谐波器、③并联电容/串联电抗、④增加整流器的脉冲次数8、衡量电力系统运行经济性的指标:①燃料损耗率、②厂用电率、③网损率9、线损包括:①管理线损、②理论线损、③不明线损10、线损计算方法:①最大负荷损耗时间法②最大负荷损失因数法③均方根电流法No.3电力系统的额定频率和额定电压1、电力线路的额定电压(也称电力网的额定电压)与用电设备的额定电压相同。
2、正常运行时电力线路首端的运行电压常为用电设备额定电压的105%,末端电压为额定电压。
3、发电机的额定电压比电力网的额定电压高5%。
4、变压器的一次绕组相当于用电设备,其额定电压与电力线路的额定电压相同;但变压器直接与发电机相连时,其额定电压与发电机额定电压相同,即为该电压级额定电压的105%。
5、变压器的二次绕组相当于电源,其输出电压应较额定电压高5%,但因变压器本身漏抗的电压损耗在额定负荷时约为5%,所以变压器二次侧的额定电压规定比额定电压高10%。
6、降压变压器二次侧连接10kV线路,当短路电压百分比小于7.5%(变压器本身漏抗的电压损耗较小)时,比线路额定电压高5%。
电力系统潮流计算课程设计报告

电力系统流量计算课程设计课程主题和要求1、题目的原始数据1、系统图:两座发电厂分别通过变压器和输电线路与四个变电站相连。
2.电厂信息:1、2为电厂高压母线。
第一电厂总装机容量为(300MW ),母线3为机压母线。
机压母线装机容量为(100MW ),最大和最小负荷分别为50MW 和20MW 。
;第二电厂总装机容量为(200MW )。
变电所1变电所母线电厂一 电厂二3、变电站信息:(一) 1、2、3、4变电站低压母线电压等级为:35KV 10KV 35KV 10KV (二)变电站负荷为:60MW 40MW 40MW 50MW (三) 各变电站功率因数cos φ=0.85;(四)1、3变电站分别配备两台容量为75MVA 的变压器,短路损耗为414KW ,短路电压(%)=16.7;变电站2、变电站4分别配备两台容量为63MVA 的变压器,短路损耗为245KW ,短路电压(%)=10.5;4、输电线路信息:电厂与变电站之间输电线路的电压等级和长度如图所示,Ω17.0单位长度电阻为 ,单位长度电抗Ω0.402为 ,单位长度电纳为S -610*2.78。
二、 课程设计的基本内容:1. 给定网络,并画出等效电路图。
2. 输入各支路数据,在变电站一定负荷条件下,通过给定程序计算各节点数据,并对计算结果进行分析。
3. 跟随变电站负荷按一定比例变化,进行潮流计算分析。
1) 4个变电站负荷同时增加2%; 2) 4个变电站负荷同时降低2%3) 1、4号变电站负荷同时下降2%,2、3号变电站负荷同时上升2%; 4. 在不同的负载条件下,分析潮流计算的结果,如果每条母线的电压不符合要求,则调整电压。
(变电站低压母线电压10KV 需要在9.5-10.5之间调整;35KV 电压需要在35-36之间调整)5. 断开支路双回线路之一,分析潮流分布。
(好几根树枝断了好几次)6. 使用DDRTS 软件,绘制系统图,分析上述各种情况的流程,并比较结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
摘要 (1)
1.任务及题目要求 (2)
2.计算原理 (3)
2.1牛顿—拉夫逊法简介 (3)
2.2牛顿—拉夫逊法的几何意义 (7)
3计算步骤 (7)
4.结果分析 (9)
小结 (11)
参考文献 (12)
附录:源程序 (13)
本科生课程设计成绩评定表....... 错误!未定义书签。
摘要
电力系统的出现,使高效,无污染,使用方便,易于调控的电能得到广泛应用,推动了社会生产各个领域的变化,开创了电力时代,发生率第二次技术革命。
电力系统的规模和技术水准已经成为一个国家经济发展水平的标志之一。
电力系统稳态分析包括潮流计算和静态安全分析。
电力系统潮流计算是电力系统最基本的计算,也是最重要的计算。
所谓潮流计算,就是已知电网的接线方式与参数及运行条件,计算电力系统稳态运行各母线电压、个支路电流与功率及网损。
对于正在运行的电力系统,通过潮流计算可以判断电网母线电压、支路电流和功率是否越限,如果有越限,就应采取措施,调整运行方式。
对于正在规划的电力系统,通过潮流计算,可以为选择电网供电方案和电气设备提供依据。
潮流计算还可以为继电保护和自动装置定整计算、电力系统故障计算和稳定计算等提供原始数据。
在电力系统运行方式和规划方案的研究中,都需要进行潮流计算以比较运行方式或规划供电方案的可行性、可靠性和经济性。
同时,为了实时监控电力系统的运行状态,也需要进行大量而快速的潮流计算。
因此,潮流计算是电力系统中应用最广泛、最基本和最重要的一种电气运算。
在系统规划设计和安排系统的运行方式时,采用离线潮流计算;在电力系统运行状态的实时监控中,则采用在线潮流计算。
关键词:电力系统潮流计算牛顿-拉夫逊法
1.任务及题目要求
对如下所诉系统编程进行潮流计算:
节点数:3 支路数:3 计算精度:0.00010
支路1:0.0300+j0.0900
1┠—————□—————┨2
支路2:0.0200+j0.0900
2┠—————□—————┨3
支路3:0.0300+j0.0900
3┠—————□—————┨1
节点1:PQ节点,S(1)=-0.5000-j0.2000
节点2:PQ节点,S(2)=-0.6000-j0.2500
节点3:平衡节点,U(3)=1.0000∠0.0000
经分析可知题目所给的系统为三节点组成的环形回路,且均为线路没有变压器。
有两个为PQ节点,这类节点的有功功率P和无功功率Q是给定的,节点电压是待求量。
节点3为平衡节点,在潮流分布算出来以前,网络中的功率损失是未知的,因此,至少要有一个节点的有功功率不能给定,这个节点承担了系统的有功功率平衡,故称之为平衡节点。
对系统进行潮流计算,要求各线路的功率分布及功率损耗,未知节点的电压等,并进行编程运行得到结果。
2.计算原理
潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如各母线上的电压(幅值及相角),网络中的功率分布及功率损耗等。
常用的计算潮流分析的方法有牛顿—拉夫逊法,P —Q 分解法等。
本次设计采用牛顿—拉夫逊法进行计算。
牛顿—拉夫逊法(简称牛顿法)在数学上是求解非线性代数方程式的有效方法,其要点是把非线性方程式的求解过程变成反复地对相应的线性方程式进行求解的过程,即通常所称的逐次线性化过程。
2.1牛顿—拉夫逊法简介
牛顿—拉夫逊法(Newton —Raphson 法)是求解非线性方程代数方程组的有效迭代计算方法。
在牛顿—拉夫逊法的每一次迭代过程中,对非线性方程通过线性化处理逐步近似。
下面以单变量加以说明。
设有单变量非线性方程
()0f x = (2-1)
求解此方程时。
先给出解的近似值(0)x 它与真解的误差为(0)x
∆,则(0)(0)x x x =+∆将满足方程,即 (0)(0)()0f x x +∆= (2-2)
将(2-2)式左边的函数在(0)x
附近展成泰勒级数,于是便得
2'''()(0)(0)(0)(0)(0)(0)(0)(0)(0)()()()()......()....
2!!()
()
n n f f n x x f f f x x x x x x x +∆=+∆++++∆∆ (2-3)
式中
'(0)()f x ,……()(0)()n f x 分别为函数()f x 在(0)x 处的一阶导数,….,n 阶导数。
如果差值(0)x ∆很小,2-3式右端(0)x ∆的二次及以上阶次的各项均可略去。
于是,2-3便简化为
'(0)(0)(0)(0)(0)()()()f f f x x x x x +∆=+
∆=0 (2-4) 这是对于变量的修正量
(0)x ∆的现行方程式,亦称修正方程式。
解此方程可得
修正量 (0)(0)'(0)()()f x x
f x ∆=- (2-5) 用所求的(0)x ∆去修正近似解,变得
(0)
(1)(0)(0)(0)'(0)()()f x x x x x f x =+∆=- (2-6)
由于2-6是略去高次项的简化式,因此所解出的修正量(0)x
∆也只是近似值。
修正后的近似解(1)x 同真解仍然有误差。
但是,这样的迭代计算可以反复进行下
去,迭代计算的通式是
()(1)()'()()()k k k k f x x
x f x +=- (2-7)
迭代过程的收敛判据为 ()1()k f x ε< (2-8)
或
()2k x ε∆< (2-9) 式中1ε,2ε为预先给定的小正数。
这种解法的几何意义可以从图1得到说明。
函数y =f(x)为图中的曲线。
f(x)=0的解相当于曲线与x 轴的交点。
如果第k 次迭代中得到()k x ,则过
()()(),()k k k f y x x ⎡⎤=⎢⎥⎣⎦
点作一切线,此切线同x 轴的交点便确定了下一个近似值(1)k x +。
由此可见,牛顿-拉夫逊法实质上就是切线法,是一种逐步线性化的方法。
应用牛顿法求解多变量非线性方程组2-1时,假定已给出各变量的初值1(0)
x ,2(0)x …. (0)n x ,令1(0)x ∆,2(0)x ∆,….. (0)n x ∆分别为各变量的修。
