静力学-刚体系统平衡习题课2
课题二:静力学公理教案

云南工业技师学院基础课教学备课教案课题二:静力学公理公理是人们在生活和生产实践中长期积累的经验总结,又经过实践反复检验,被确认是符合客观实际的最普遍、最一般的规律,是进行逻辑推理计算的基础与准则。
一、作用于反作用公理【问题引导】如图2-1所示,人拎物体时为何感觉物体向下坠的重感?引发学生讨论和思考。
图2-1 人拎物体总结解释:由牛顿第三定律可知:当人手拎着物体时,人的手臂给物体一个向上的力F,同时物体也给手臂一个向下的力F',F和F'大小相等、方向相反,作用在同一条直线上,若人松开手,物体就会向下掉,F和F'同时消失。
【理论讲解】由此得出作用与反作用公理一:两物体之间的作用力和反作用力总是同时存在,两力的大小相等、方向相反,沿着同一直线,分别作用在两个相互作用的物体上。
公理一的特点:二力同时存在,且大小相等,方向相反,作用在一条直线,两个物体上。
特别强调:这个公理概括了物体间相互作用的关系,而非平衡力表明作用力和反作用力总是成对出现的。
【公理一应用】游泳、划船、拔河、火箭发射等,如图2-2所示。
a) b)c) d)图2-2 公理一的应用a)游泳 b)划船 c)拔河 d)火箭发射【课程思政】如视频2-3所示火箭发射原理,引出中国航天三大精神,60多年来,中国航天事业从无到有、从小到大、从弱到强,走出了一条具有鲜明中国特色的发展道路。
伴随着航天事业的发展,在出成果、出人才的同时,航天科技工业培育形成了航天传统精神、“两弹一星”精神和载人航天精神。
图2-3 火箭发射原理2016年4月24日,在首个“中国航天日”到来之际,习近平总书记指出:探索浩瀚宇宙,发展航天事业,建设航天强国,是我们不懈追求的航天梦。
经过几代航天人的接续奋斗,我国航天事业创造了以“两弹一星”、载人航天、月球探测为代表的辉煌成就,走出了一条自力更生、自主创新的发展道路,积淀了深厚博大的航天精神。
二、二力平衡公理【问题引导】如图2-4所示,放在桌子上的书,杂技演员头顶上的大缸,它们显然是静止的,如何用力学角度解释这种现象?图2-4 二力平衡公理示例总结解释:书放在桌面上,书受到自身重力G和桌面对书的支持力F N的作用而处于平衡状态(静止)。
静力学1-2章习题课

1.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
1.压力体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
2.绘压力体图
p0 A B
pa
1、图算法 2、重力场中流体静压强
的分布规律 3、压力体的绘制
2.答案:
p0 A
B
pa
1、图算法 2、重力场中流体静压强
v 1.075m s
0.4cm
D=12cm L=14cm
牛顿内摩擦定律
第一、第二章 (流体静力学) 习题课
一、流体的主要物理性质 二、重力场中流体静压强的分布规律
z p c
p p0 gh
三、液体的相对平衡 四、液体作用在平面上的总压力 五、液体作用在曲面上的总压力
第一、第二章 (流体静力学) 习题课
8.压立体的绘制是求解曲面上液体总压力的关键。压力体的绘 制方法与方向的判断原则。
习题: 1.液体的粘滞性只有在流动时才表现出来。( ) 2.在相对静止的同种、连通、均质液体中,等压面就是水平面。 () 3.某点的真空度为65000Pa,当地大气压为0.1MPa,该点的 绝对压强为( )
(a)65000Pa (b)55000Pa (c) 35000Pa (d)165000Pa
5.
1、等压面 2、重力场中流体静压强的分布规律
5.
1、等压面 2、重力场中流体静压强的分布规律
3.计算举例
1.
静止流体中应力的特性
静止流体中应力的特性
2.如图:
已知h1=20mm,
h2=240mm,
h3
h3=220mm, 求水深H。
水银
《理论力学》静力学典型习题+答案00

1-3 试画出图示各结构中构件AB的受力图1-4 试画出两结构中构件ABCD的受力图1-5 试画出图a和b所示刚体系整体各个构件的受力图1-5a1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M 0)45sin(100=-+⋅⋅M a F A θ aM F A 354.0=其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4FF解:机构中AB杆为二力杆,点A,B出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C处的约束力方向也可确定,各杆的受力如图所示。
工程力学静力学所有课后习题答案

关于理论力学答案的网友求助帖理论力学第Ⅱ册(和兴锁) 课后答案科学出版社理论力学课后答案本书根据教育部高等工业学校理论力学教学的基本要求编写,分为两册。
第Ⅰ册内容包括静力学、运动学、质点动力学、质点的振动、动力学普遍定理和达朗贝尔原理等;第Ⅱ册内容包括碰撞、虚位移原理、拉格朗日方程、二自由度系统的振动和刚体动力学等。
全书例题丰富,并配有思考题、习题和答案。
7okey 8 小时前理论力学修订版(徐燕侯郭长铭) 课后答案中国科技大学出版社理论力学修订版无课后答案3okey 8 小时前理论力学(罗特军) 课后答案四川大学出版社理论力学课后答案《高等学校工科力学系列教材:理论力学》是四川省教改项目“工程力学精品课程建设”的研究成果,对传统的理论力学体系进行了较大的改进,以适应面向21世纪教学改革及大量培养高等科技人才的需要。
本书以理论力学的基本内容为主,适当提高了起点,力求做到逻辑清晰、易于教学。
本书可作为高等院校工科本科各专业的理论力学教材。
少学时理论力学课程可根据需要对内容进行取舍。
本书可供成人高校、高职高专的师生及有关工程技术人员参考。
4okey 8 小时前理论力学第2版(李卓球) 课后答案武汉理工大学出版社理论力学第2版无课后答案根据高等学校理论力学课程教学的基本要求,《理论力学(第2版)》结合工科相关专业应用基础的特点,在保留理论力学经典内容的前提下,适当更新和精炼了教材内容。
《理论力学(第2版)》主要内容为静力学、运动学、动力学三大部分。
《理论力学(第2版)》适用于高等学校工科力学和工程类各专业的理论力学教材,各专业可以根据需要选用全部或部分内容,也可供有关工程技术人员参考。
okey 8 小时前理论力学第2版课后答案(同济大学航空航天与力学学院基础力学教学研究部) 同济大学出版社理论力学第2版无课后答案《同济大学工程力学系列教材:理论力学(第2版)》共分三篇,分别为静力学、运动学和动力学。
本书保持了同济大学原理论力学教研室1990年版《理论力学》的体系和风格,但对该版教材的内容和习题作了部分调整。
2静力学第二章习题答案
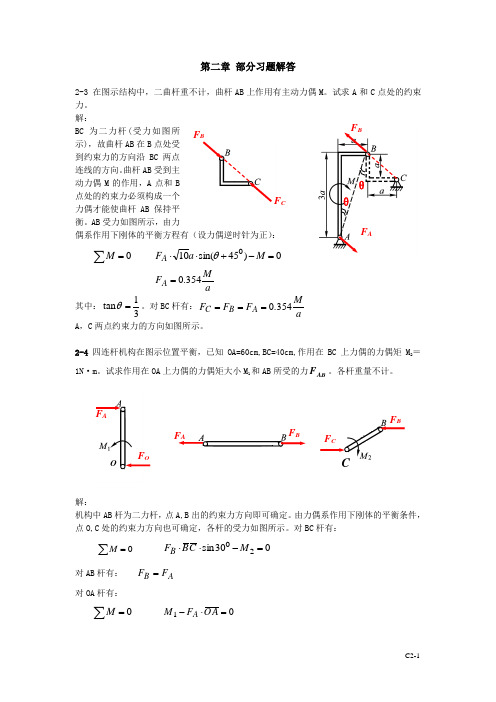
第二章 部分习题解答2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):0=∑M0)45sin(100=-+⋅⋅M a F A θ aMF A 354.0= 其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4四连杆机构在图示位置平衡,已知OA=60cm,BC=40cm,作用在BC 上力偶的力偶矩M 2=1N ·m 。
试求作用在OA 上力偶的力偶矩大小M 1和AB 所受的力AB F 。
各杆重量不计。
解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有: 0=∑M030sin 20=-⋅⋅M C B F B对AB 杆有: A B F F = 对OA 杆有:0=∑M01=⋅-A O F M AF B F A θ θ F BF C F AF OOF AF BF BF CC求解以上三式可得:m N M ⋅=31, N F F F C O AB 5===,方向如图所示。
2-6等边三角形板ABC,边长为a ,今沿其边作用大小均为F 的力321,,F F F ,方向如图a,b 所示。
试分别求其最简简化结果。
解:2-6a坐标如图所示,各力可表示为:j F i F F 23211+=, i F F =2, j F i F F 23213+-=先将力系向A 点简化得(红色的):j F i F F R3+=, k Fa M A 23=方向如左图所示。
运动力学刚体的平衡与静力学问题

运动力学刚体的平衡与静力学问题运动力学刚体的平衡和静力学问题是刚体力学中非常重要且常见的研究课题。
在这篇文章中,我们将讨论刚体平衡和静力学问题的一些基本概念和解决方法。
一、平衡的概念平衡是指物体处于静止状态或者匀速直线运动的状态。
对于刚体来说,平衡需要满足两个条件:力的合力为零,力的力矩为零。
力的合力为零意味着物体不受合外力的作用;力的力矩为零意味着物体不受合外力矩的作用。
二、平衡的条件为了实现平衡,刚体必须满足以下条件:1. 合力为零:合力(包括作用在刚体上的所有力矢量的矢量和)必须为零,否则刚体将出现加速度。
2. 力矩为零:刚体上作用的力产生的力矩(力乘以力臂,即力到刚体固定轴的垂直距离)的代数和必须为零。
三、静力学问题的解决方法静力学问题是讨论物体处于静止状态时的问题。
根据力和力矩的定义,我们可以通过以下步骤解决静力学问题:1. 绘制力的示意图:将作用在刚体上的所有力绘制成矢量图,这有助于我们清楚地理解问题。
2. 分解力:将力分解为沿坐标轴方向的分力和垂直于坐标轴方向的分力。
3. 求解合力:将沿坐标轴方向的分力相加,得到合力。
4. 求解力矩:对于充当杆的刚体,我们可以通过选择适当的支点计算力矩。
使用力乘以力臂的公式,计算每个力产生的力矩,并将它们相加。
5. 检查平衡条件:确保合力和力矩都为零。
如果不为零,则刚体不处于平衡状态。
四、平衡的应用举例平衡的概念和方法在日常生活和工程中都有广泛的应用。
以下是一些常见的例子:1. 摆钟:摆钟的平衡取决于重力和摆线的长度。
2. 桥梁:桥梁的平衡必须考虑到桥墩和主梁的力矩平衡。
3. 支架:支架的平衡用于支撑其他结构或物体。
4. 机械装置:机械装置中的各个部件必须在平衡状态下工作,以确保正常运转和安全性。
五、结论运动力学刚体的平衡与静力学问题是刚体力学中的重要内容。
理解平衡的概念和条件,并掌握解决静力学问题的方法,对于确保物体处于平衡状态具有重要意义。
通过应用平衡原理,我们可以解决日常生活和工程中的各种平衡问题,并为实际问题的解决提供有力支持。
静力学习题课

B. F2 F1
C. F1 F2
。
,
自由矢量 C. 定位矢量 D. 滑动矢量
。
,
5
题型二:选择题
3、重 W 80 kN 的物体自由地放在倾角为 30 的斜面上, 若物体与斜面间的静摩擦系数 f 3 4 ,动摩擦系数
f d 0.4 ,则作用在物体上的摩擦力的大小为: C
静力学习题课
1
题型一:判断题
1、力可以沿着作用线移动而不改变它对物体的运动效应。 (×)
2、作用于刚体的力可沿其作用线移动而不改变其对刚体的 运动效应。 (√ )
3、若作用在刚体上的三个力的作用线汇交于同一点,则 该刚体必处于平衡状态。 (×) 4、凡是受到两个力作用的刚体都是二力杆。 (×)
5、用解析法求平面汇交力系的平衡问题时,所建立的坐标 系x,y轴一定要相互垂直。 (× )
A. 27.7kN B. 40kN
。
C. 30kN D. 0
,
6
题型二:选择题
α 4、一重W 的物体置于倾角为 的斜面上,若摩擦因数为f, A 且 tgα < f , 则物体 ;
若增加物体重量,则物体 A ;
若减轻物体重量,则物体
A. 静止不动; B. 向下滑动;
A
。
,
C. 运动与否取决于平衡条件。
7
题型三:填空题
1、沿边长为 a=2m 的正方形各边分别作用有 F1, F 2 , F 3 , F 4 ,
主矢大小为 , 主矩大小为 16 kN· m 。
且 F 1 F 2 F 3 F 4 4kN , 该力系向B点简化的结果为:
0
m 向D点简化的结果是什么? FR=0; MD=16 kN·
习题课-静力学

习题课-静力学
3.图示力偶中等效的是(B)
NEFU- Junkai Lu
(A) a和c (B) a和b (C) b和c (D) b和d
36Fd顺
36Fd顺
36Fd逆
48Fd顺
4.关于力对点之矩的说法,下列哪个是错误的(B)
(A) 互相平衡的两个力,对同一点之矩的代数和等于零。
(B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。
4.关于力对点之矩的说法,下列哪个是错误的( ) (A) 互相平衡的两个力,对同一点之矩的代数和等于零。 (B) 力对点之矩与力的大小和方向有关,而与矩心位置无关。 (C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。 (D) 力对点之矩不会因为力矢沿其作用线移动而改变。
10
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
10. 力系的平衡
平面任意力系
Fx 0
Fy 0
M o 0
Fx 0
M A 0
M B 0
A、B两点 连线不得 与投影轴 x轴垂直
空间任意力系
Fix 0 Fiy 0 Fiz 0
(C) 力的数值为零、或力的作用线通过矩心时,力矩均为零。
(D) 力对点之矩不会因为力矢沿其作用线移动而改变。
力有关,力偶无关
11
School of Civil Engineering
习题课-静力学
NEFU- Junkai Lu
5.图示正方体顶角上作用着六个大小相等的力,此力系向任一点简化的结 果是( )
D
F3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p
FGy
G
3、再研究AG杆,求出 FGy
0 FGy
刚体系平衡求解
1、研究对象
2、受力分析
3、平衡条件 4、列方程、求解 尽量一个方程解一个未知量!
例:已知 F,求 AG 杆上的约束力。
A
a
C
F
2a E
a
B
a
a
a
D
a
解:1、研究AG杆, 画受力图. H
A
F
FDx FGx
G
O
FDy
D
M
D
(F ) 0
FGxa Fa 0
G
FGy
FGx F FDx 2F
G
M
(F ) 0
FDxa F 2a 0
A
a D
F
2a E
x
FDy
D
FGx F FGy 3F
FGy 3F
[AG]:
Fy 0
FDy 3F
FGy
G
A C a D a G
F
2a a
B E a H
研究图示构件,画受力图 B C
FDx D
a 2a
E a
H
O
a
O
FCG FDy
方法3 A
F
FDx FGx
求出
FDy
p
FH
FDy
D
M F
y
0 FDy
13 G G F A sin 45 8
D A
K C B Ⅰ
2. [DEC] 受力分析如图所示
列平衡方程
E
Ⅱ
M
其中
C
F 0,
D
F D B cos 45 2 l F K l F E y 2 l 0
G FK 2
FDB 3 2G 8
FDB
K
G
FK
F3= –500N, 再取[C节点]
3 32 42
3m 0
M F M
D
C
FBx
FBy
F
x
0, F1 F3
4 3 4
2 2
0
F1= –400N, [整体] MA=0, MA–4F – M–3F1=0 Fx=0, FAx–F 1=0 MA=3.4kN· m
F1
F3 F3
F2
[BD]
E
Ⅱ
D
G
x
0
F A c os 45 F E x 0
5G FEx 8 F A s in 45 F E y G 0
FEy 13 G G F A sin 45 8
FA
A
K
C
B Ⅰ
F
y
0
FEy
E
FEx
Ⅱ
G
5 2 FA G 8
FEx
FEy
5G 8
M
E
C
FAx
2 F 2
FB
M 2 F 2a 4
D
[整体]
MA
FAx
A
45 0
Fy 0
FB FAy FAy
2 F 0 2 M 2 F 2a 4
B
M
A
0
a
a
2 2 F 2a Fa M FB 2a M A 0 2 2
FAy
FB
M A 2 Fa
例题
A,B,C,D处均为光滑铰链,物块重为G,通过 绳子绕过滑轮水平地连接于杆AB的E点,各构件自重不 计,试求B处的约束力。
M F 0,
C
解: [整体]:受力分析如图
5r G 2r FAx 0
FAx 2.5G
G
FAy
FAx FCx
解得
FCy
[AB]:受力分析如图。
FCy
FCx C
FEy
E
FEx
例 :组合托架组成构件如图示,三根链杆自重不计,巳知: F=1kN, M=600N· m, 求:A 处约束反力。 解:取[整体]受力分析
Fy=0, FAy–F =0
FAx
A
2m
MA
FAy
2m
F
2m
2m
得:FAy= 1000N,
取[BD]受力分析
B
F1
1 2 3
M B 0, M F3 2
可得: FAx= –400N,
[C]
例 : 系统在图示位置平衡,已知F, M, a。求A, B处的约束力。
45
0
F
M
E
C
解:[整体]
D
Fx 0
FAx FAx
2a
2 F 0 2 2 F 2
[DE]
MA
FAxAΒιβλιοθήκη 450FDxB
45
0
F
M
E
D
FDy
FAy
a
a
2 F 0 2
FE
2 Fa M FDy 2a 0 2 M 2 FDy F 2a 4
F
x
0,
A
F Ax F Bx F E 0
FAy
M F 0 ,
2 r F B x 2 r F B y rF E 0
联立求解可得
FE
FAx
FBx 1 .5G , FBy 2G
FBx
FBy
例题
D
如图所示,已知重力 G , DC=CE=AC=CB=2l ;
B
a
[整体]
M
O
(F ) 0
F1 y 2a F 2a 0
H
C
F1 y F
a
a
F
F2
O
FCG FGy
F1x
F1 y
x
0
F1x
G
F1 y
F1x F
FGx
[销钉G]
F
x
0
A
F
FDx FGx
F1x cos 45 F1 y cos 45 FGx cos 45 FGy cos 45 0
B
A
K C
Ⅰ
定滑轮半径为 R ,动滑轮 半 径 为 r , 且 R=2r=l, θ=45°。试求: A , E 支 座的约束力及 BD 杆所受 的力。
E
Ⅱ
G
D
解: 1. [整体] 受力分析如图所示 列平衡方程
A
K
C
B Ⅰ
M E F 0
F
5 F A 2 2l G l 0 2 5 2 FA G 8
FB
FDx 2 F 2
ME 0
Fx 0
FDx
FDx '
D
FDx
FDy
C
FCx
FDy
2 F 2 M 2 F 2a 4
FCy
a a [DB]
B
FB
M
C
0
FB a FDy ' a FDx ' a 0
FB M 2 F 2a 4
45 0
F
