第7章习题详解
高鸿业主编《西方经济学》第五版课后习题答案 带图详解 完整版第七章 习题答案 (14)
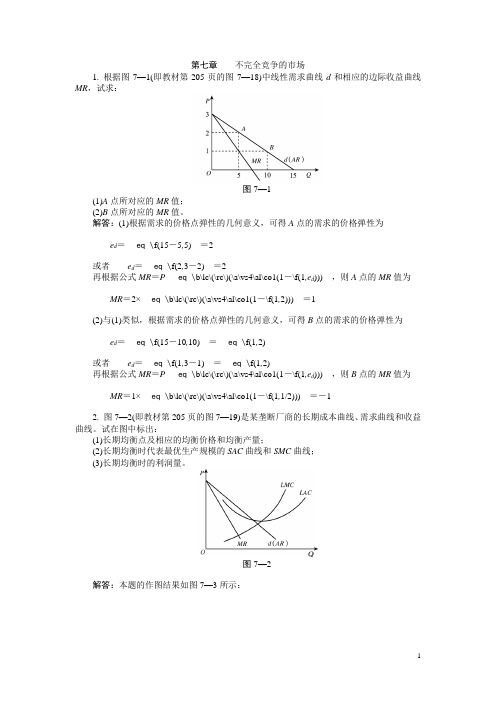
第七章不完全竞争的市场1. 根据图7—1(即教材第205页的图7—18)中线性需求曲线d和相应的边际收益曲线MR,试求:图7—1(1)A点所对应的MR值;(2)B点所对应的MR值。
解答:(1)根据需求的价格点弹性的几何意义,可得A点的需求的价格弹性为e d=eq \f(15-5,5)=2或者e d=eq \f(2,3-2)=2再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则A点的MR值为MR=2×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,2)))=1(2)与(1)类似,根据需求的价格点弹性的几何意义,可得B点的需求的价格弹性为e d=eq \f(15-10,10)=eq \f(1,2)或者e d=eq \f(1,3-1)=eq \f(1,2)再根据公式MR=P eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,e d))),则B点的MR值为MR=1×eq \b\lc\(\rc\)(\a\vs4\al\co1(1-\f(1,1/2)))=-12. 图7—2(即教材第205页的图7—19)是某垄断厂商的长期成本曲线、需求曲线和收益曲线。
试在图中标出:(1)长期均衡点及相应的均衡价格和均衡产量;(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线;(3)长期均衡时的利润量。
图7—2解答:本题的作图结果如图7—3所示:图7—3(1)长期均衡点为E点,因为在E点有MR=LMC。
由E点出发,均衡价格为P0,均衡数量为Q0。
(2)长期均衡时代表最优生产规模的SAC曲线和SMC曲线如图7—3所示。
在Q0的产量上,SAC曲线和LAC曲线相切;SMC曲线和LMC曲线相交,且同时与MR曲线相交。
(3)长期均衡时的利润量由图7—3中阴影部分的面积表示,即π=[AR(Q0)-SAC(Q0)]·Q 0。
曼昆《宏观经济学》(第6、7版)课后习题详解(第7章 经济增长Ⅰ:资本积累与人口增长)

曼昆《宏观经济学》(第6、7版)第3篇 增长理论:超长期中的经济第7章 经济增长Ⅰ:资本积累与人口增长课后习题详解跨考网独家整理最全经济学考研真题,经济学考研课后习题解析资料库,您可以在这里查阅历年经济学考研真题,经济学考研课后习题,经济学考研参考书等内容,更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验,从前辈中获得的经验对初学者来说是宝贵的财富,这或许能帮你少走弯路,躲开一些陷阱。
以下内容为跨考网独家整理,如您还需更多考研资料,可选择经济学一对一在线咨询进行咨询。
一、概念题1.索洛增长模型(Solow growth model )答:索洛增长模型是表明储蓄、人口增长和技术进步如何影响一个经济的产出水平及其随着时间推移而实现增长的一种经济增长模型。
它的基本假定有:(1)社会储蓄函数为S sY =,式中,s 是作为参数的储蓄率;(2)劳动力按照一个不变的比例增长;(3)生产的规模报酬不变。
其主要思想是:人均投资用于资本扩展化和资本深化,当人均投资大于资本扩展化时,人均产出就会增长;当人均投资等于资本扩展化时,经济达到稳定状态,人均产出不再增长,但总产出会继续增长,增长率等于人口增长率。
2.稳定状态(steady state )答:索洛模型的稳定状态是指长期中经济增长达到的一种均衡状态,在这种状态下,投资等于资本扩展化水平,人均资本存量维持不变,即()0k sf k k δ∆=-=。
这个维持不变的人均资本存量k *称之为稳定状态人均资本存量。
在稳定状态下,不论经济初始位于哪一点,随着时间的推移,经济总是会收敛于该人均资本水平k *。
在稳定状态,由于人均资本存量保持不变,所以人均产出也保持不变,即人均产出增长率为零。
3.资本的黄金律水平(golden rule level of capital )答:资本的黄金律水平是指在稳定状态人均消费最大化时所对应的人均资本水平,由经济学家费尔普斯于1961年提出。
现代通信原理指导书第七章信源编码习题详解

第七章 信源编码7-1已知某地天气预报状态分为六种:晴天、多云、阴天、小雨、中雨、大雨。
① 若六种状态等概出现,求每种消息的平均信息量及等长二进制编码的码长N 。
② 若六种状态出现的概率为:晴天—;多云—;阴天—;小雨—;中雨—;大雨—。
试计算消息的平均信息量,若按Huffman 码进行最佳编码,试求各状态编码及平均码长N 。
解: ①每种状态出现的概率为6,...,1,61==i P i因此消息的平均信息量为∑=-===6122/58.26log 1log i ii bit P P I 消息 等长二进制编码的码长N =[][]316log 1log 22=+=+L 。
②各种状态出现的概率如题所给,则消息的平均信息量为6212222221log 0.6log 0.60.22log 0.220.1log 0.10.06log 0.060.013log 0.0130.007log 0.0071.63/i i iI P P bit -== = ------ ≈ ∑消息Huffman 编码树如下图所示:由此可以得到各状态编码为:晴—0,多云—10,阴天—110,小雨—1110,中雨—11110, 大雨—11111。
平均码长为:6110.620.2230.140.0650.01350.0071.68i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯ =∑—7-2某一离散无记忆信源(DMS )由8个字母(1,2,,8)i X i =⋅⋅⋅组成,设每个字母出现的概率分别为:,,,,,,,。
试求:① Huffman 编码时产生的8个不等长码字; ② 平均二进制编码长度N ; ③ 信源的熵,并与N 比较。
解:①采用冒泡法画出Huffman 编码树如下图所示可以得到按概率从大到小8个不等长码字依次为:0100,0101,1110,1111,011,100,00,1087654321========X X X X X X X X②平均二进制编码长度为8120.2520.2030.1530.1240.140.0840.0540.052.83i ii N n P == =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯ =∑ ③信源的熵∑=≈-=81279.2log)(i i i P P x H 。
曼昆《宏观经济学》(第67版)习题精编详解(第7章经济增长资本积累与人口增长)

曼昆《宏观经济学》(第67版)习题精编详解(第7章经济增长资本积累与人口增长)Borntowin经济学考研交流群<<第3篇增长理论:超长期中的经济第7章经济增长Ⅰ:资本积累与人口增长一、判断题1.根据索洛增长模型,无论经济开始时处在什么位置,最终它都将调整至稳态。
()【答案】T【解析】假定经济的初始资本水平低于稳态,那么其投资水平大于折旧量,随着时间的推移,资本存量将一直上升到稳定状态为止。
当经济的初始资本水平高于稳态,那么投资小于折旧,资本的磨损快于更替,资本存量将一直减少到稳态水平为止。
2.资本存量黄金律是指人均资本或者每个效率工人的资本不增不减的稳态资本存量。
()【答案】F【解析】资本存量黄金律是指使得消费最大化的稳定状态的资本存量水平。
3.在不考虑人口和技术变动的索洛模型中,稳态即意味着yk。
()【答案】T【解析】稳态下,kikyk0,因此yk。
4.根据索洛增长模型,其他条件相同,储蓄率较高的国家的人均收入将高于储蓄率较低的国家的人均收入,虽然前者的增长率未必高于后者。
()【答案】T【解析】高储蓄率具有水平效应,即提高稳定状态的人均收入水平,因此储蓄率较高的国家的人均收入将高于储蓄率较低的国家的人均收入;因为储蓄率不具有增长效应,即不影响经济增长率,因此前者的增长率未必高于后者。
5.标准的新古典生产函数二阶导数是严格正的。
()【答案】F【解析】新古典增长模型假定边际报酬递减,则新古典生产函数的二阶导数必然小于零。
6.如果总量生产函数不再具有边际报酬递减的性质,那么索洛模型中稳定状态将会发生一定的变化,但是最终还是能达到新的稳定。
()【答案】F【解析】假定资本的边际报酬递增,则fk0,可能存在一种情况即实际投资始终985/211历年真题解析,答案,核心考点讲义,你想要的都在这→经济学历年考研真题及详解Borntowin经济学考研交流群<<大于持平投资,人均资本存量将不断增大,经济没有稳定状态。
高等数学习题详解-第7章多元函数微分学

1. 指出下列各点所在的坐标轴、坐标面或卦限:A (2,1,-6),B (0,2,0),C (-3,0,5),D (1,-1,-7).解:A 在V 卦限,B 在y 轴上,C 在xOz 平面上,D 在VIII 卦限。
2. 已知点M (-1,2,3),求点M 关于坐标原点、各坐标轴及各坐标面的对称点的坐标. 解:设所求对称点的坐标为(x ,y ,z ),则(1) 由x -1=0,y +2=0,z +3=0,得到点M 关于坐标原点的对称点的坐标为:(1,-2,-3). (2) 由x =-1,y +2=0,z +3=0,得到点M 关于x 轴的对称点的坐标为:(-1,-2,-3). 同理可得:点M 关于y 轴的对称点的坐标为:(1, 2,-3);关于z 轴的对称点的坐标为:(1,-2,3).(3)由x =-1,y =2,z +3=0,得到点M 关于xOy 面的对称点的坐标为:(-1, 2,-3).同理,M 关于yOz 面的对称点的坐标为:(1, 2,3);M 关于zOx 面的对称点的坐标为:(-1,-2,3).3. 在z 轴上求与两点A (-4,1,7)和B (3,5,-2)等距离的点. 解: 设所求的点为M (0,0,z ),依题意有|MA |2=|MB |2,即(-4-0)2+(1-0)2+(7-z)2=(3-0)2+(5-0)2+(-2-z)2.解之得z =11,故所求的点为M (0,0,149). 4. 证明以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 解:由两点距离公式可得21214M M =,2213236,6M M M M ==所以以M 1(4,3,1),M 2(7,1,2),M 3(5,2,3)三点为顶点的三角形是一个等腰三角形. 5. 设平面在坐标轴上的截距分别为a =2,b =-3,c =5,求这个平面的方程.解:所求平面方程为1235y x z++=-。
金太军《公共行政管理学新编》课后习题详解 第7章 行政执行

第7章行政执行1.行政执行的特点。
答:行政执行有着自身内在的特点,认识这些特点,对我们正确、有效地实施决策有着重要的意义。
一般来说,行政执行活动具有以下特点∶(1)目标性行政决策活动本质上是对未来公共行政管理活动作出的一种反映。
它指出了解决问题的目标和大致的方向,具有一定的理想成分。
如何把理想变成现实就是行政执行活动所要解决的问题,即如何通过实践使行政决策目标如期或提前变成现实。
可见行政执行是一种有目标导向的活动。
(2)综合性行政执行是一个复杂的动态活动过程。
在执行系统内部,要想使行政执行活动顺利而有效进行,就需要把人、财、物、时间、信息、管理技术、规章制度等因素加以系统与综合,使其处于一种协调、平衡的有序状态,以发挥出最大整体效应。
行政执行活动是一项非常复杂的管理活动,需要综合使用各种管理手段,如行政手段、法律手段、经济手段以及思想教育手段等才能完成行政执行的任务。
(3)强制性行政执行是依托行政权力,贯彻、落实国家方针政策和法令、法规的活动。
因此,在执行手段、执行方式等方面都有一定的强制性。
它要求执行对象服从执行者发出的执行指令,遵守执行的有关制度和规定。
否则,执行机关和执行人员就有权对其实行职权范围内的强制措施或处罚行动。
执行活动的强制性反映了执行活动的权威性和严肃性。
(4)具体性执行活动是对方针、政策、决定、命令的具体实施,它要求对决策的整体目标加以分解,使内容具体化,以便于实施部门的具体操作。
因此,行政执行活动是一项具体的、细致的和规范性的工作。
(5)时效性行政执行有很强的时限要求,行政执行必须做到果断、快速、高效、及时,保证行政执行的高效率。
(6)灵活性现实管理活动是错综复杂和不断变化的,在执行活动中新情况和新问题随时都会发生。
面对环境条件的变化和行政执行中所遇到的新问题,执行者要因地制宜、因时制宜、因势制宜,灵活变通地使决策目标得以实现。
灵活性是指根据实际情况合理地变通执行行政决策,从而保证上级的决策在各种情况下都能得到有效的执行。
第七章 战略性计划与计划实施 复习笔记与习题详解1

第七章战略性计划与计划实施复习笔记与习题详解(2010-10-24 17:52:52)转载标签:美国竞争对手目标管理核心能力进行杂谈分类:管理学第七章战略性计划与计划实施复习笔记1.战略愿景和使命陈述愿景和使命陈述包括两个主要部分:核心意识形态和远大的愿景。
核心意识形态由核心价值观和核心目标两部分构成,它给组织提供了长久存在的基础,是组织的精神。
远大的愿景由10~30年宏伟、冒险的目标和生动逼真的描述两部分构成。
核心意识形态包括:(1)核心价值观;(2)核心目标。
远大的远景包括:(1)10~30年宏伟的、大胆的、冒险的目标;(2)生动逼真的描述。
2.战略环境分析战略环境分析包括对外部一般环境,行业环境,竞争对手,企业自身和顾客的分析。
(1)外部一般环境外部一般环境,或称总体环境,是在一定时空内存在于社会中的各类组织均面对的环境,其大致可归纳为政治、社会、经济、技术、自然五个方面。
(2)行业环境公司环境最关键的部分是公司投人竞争的一个或几个行业的环境。
根据美国学者波特的研究,一个行业内部的竞争状态取决于五种基本竞争作用力,这些作用力汇集起来决定着该行业的最终利润潜力,并且最终利润潜力也会随着这种合力的变化而发生根本性的变化。
一个公司的竞争战略的目标在于使公司在行业内进行恰当定位,从而最有效地抗击五种竞争作用力并影响它们朝向自己有利的方向变化。
包括:①现有企业问的竞争研究。
②入侵者研究。
③替代品生产商研究。
④买方的讨价还价能力研究。
⑤供应商的讨价还价能力研究。
(3)竞争对手竞争对手可以从以下的群体中辨识出来:不在本行业但可以克服进入壁垒进入本行业的企业;进人本行业可以产生明显的协同效应的企业;由其战略实施而自然进人本行业的企业;那些通过后向或前向一体化进人本行业的买方或供方。
(4)企业自身根据价值链分析法,每个企业都是设计、生产、营销、交货以及对产品起辅助作用的各种价值活动的集合。
企业的各种价值活动分为两类,基本活动和辅助活动按价值活动的工艺顺序,(5)顾客(目标市场)企业顾客研究的主要内容是:总体市场分析、市场细分、目标市场确定和产品定位。
最新胡庆康《现代货币银行学教程》(第3版课后习题详解第7章货币理论(上精品资料

第7章 货币理论(上)本章思考题1.影响基础货币的因素有哪些?答:影响基础货币变化的根本因素有如下几个方面:影响基础货币变化的根本因素有如下几个方面:(1)政府的财政收支。
为改变政府的收支状况,有一系列的方法,其中有一部分为直接影响到基础货币的发放量,接影响到基础货币的发放量,增发通货,增发通货,扩大基础货币构成中的通货总量;扩大基础货币构成中的通货总量;向中央银行透支向中央银行透支弥补财政赤字也同样增加了基础货币的总投放量。
弥补财政赤字也同样增加了基础货币的总投放量。
(2)黄金存量变化和国际收支状况。
黄金是中央银行的资产项目,当中央银行向财政部购买黄金时,资产和负债同时增加,即放出了部分的本币通货,增加了基础货币量;同样,当中央银行在外汇市场上购入外汇时,也使中央银行的资产和负债同时增加,中央银行买进外币,放出本币,基础货币投放量增加。
外币,放出本币,基础货币投放量增加。
(3)技术和制度性因素。
典型的例子是在途票据,结算中的票据事实上是中央银行为结算而向存款机构提供的短期信贷。
若存款机构贷记该票据,而中央银行没有及时借记出票机构的准备金账户,总准备金则暂时增加。
机构的准备金账户,总准备金则暂时增加。
(4)中央银行的行为。
中央银行能通过公开市场业务的操作来达到影响基础货币投放量的目的。
中央银行在公开市场上买进政府债券,中央银行在公开市场上买进政府债券,放出本币,放出本币,中央银行的资产和负债同时等量增加,基础货币量也由于中央银行放出本币而增加。
这种操作的前提是要存在一个活跃的政府债券二级市场。
政府债券二级市场。
2.下列因素如何影响银行准备金的变化?(1)公众持有现金增加;(2)财政部在中央银行存款增加;(3)财政部购买黄金;(4)财政部发行通货;(5)财政部持有现金增加;(6)外国政府在中央银行存款增加;(7)中央银行买入政府债券; (8)中央银行向商业银行提供贷款;(9)中央银行提高法定准备金比率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题七1.设总体X 服从二项分布B (n ,p ),n 已知,X 1,X 2,…,X n 为来自X 的样本,求参数p 的矩法估计.【解】1(),(),E X np E X A X ===因此np =X所以p 的矩估计量 ˆXpn= 2.设总体X 的密度函数f (x ,θ)=22(),0,0,.x x θθθ⎧-<<⎪⎨⎪⎩其他X 1,X 2,…,X n 为其样本,试求参数θ的矩法估计. 【解】23022022()()d ,233x x E X x x x θθθθθθθ⎛⎫=-=-= ⎪⎝⎭⎰令E (X )=A 1=X ,因此3θ=X 所以θ的矩估计量为 ^3.X θ=3.设总体X 的密度函数为f (x ,θ),X 1,X 2,…,X n 为其样本,求θ的极大似然估计.(1) f (x ,θ)=,0,0,0.e x x x θθ-⎧≥⎨<⎩(2) f (x ,θ)=1,01,0,.x x θθ-⎧<<⎨⎩其他【解】(1) 似然函数111(,)ee eniii n nx x nn ii i L f x θθθθθθ=---==∑===∏∏1ln ln ni i g L n x θθ===-∑由1d d ln 0d d ni i g L n x θθθ===-=∑知 1ˆnii nxθ==∑所以θ的极大似然估计量为1ˆXθ=.(2) 似然函数11,01nni i i L x x θθ-==<<∏,i =1,2,…,n.1ln ln (1)ln ni i L n x θθ==+-∏由1d ln ln 0d ni i L nx θθ==+=∏知 11ˆln ln nniii i n nxx θ===-=-∑∏所以θ的极大似然估计量为 1ˆln nii nxθ==-∑求这批股民的收益率的平均收益率及标准差的矩估计值. 【解】 0.094x =- 0.101893s = 9n =0.094.EX x ==-由222221()()[()],()ni i x E X D X E X E X A n==+==∑知222ˆˆ[()]E X A σ+=,即有 ˆσ=于是 ˆ0.101890.0966σ=== 所以这批股民的平均收益率的矩估计值及标准差的矩估计值分别为-0.94和0.966. 5.随机变量X 服从[0,θ]上的均匀分布,今得X 的样本观测值:0.9,0.8,0.2,0.8,0.4,0.4,0.7,0.6,求θ的矩法估计和极大似然估计,它们是否为θ的无偏估计. 【解】(1) ()2E X θ=,令()E X X =,则ˆ2X θ=且ˆ()2()2()E E X E X θθ===, 所以θ的矩估计值为ˆ220.6 1.2x θ==⨯=且ˆ2X θ=是一个无偏估计.(2) 似然函数8811(,)i i L f x θθ=⎛⎫== ⎪⎝⎭∏,i =1,2, (8)显然L =L (θ)↓(θ>0),那么18max{}i i x θ≤≤=时,L =L (θ)最大,所以θ的极大似然估计值ˆθ=0.9. 因为E(ˆθ)=E (18max{}i i x ≤≤)≠θ,所以ˆθ=18max{}ii x ≤≤不是θ的无偏计. 6.设X 1,X 2,…,X n 是取自总体X 的样本,E (X )=μ,D (X )=σ2,2ˆσ=k 1211()n i i i X X -+=-∑,问k 为何值时2ˆσ为σ2的无偏估计. 【解】令 1,i i i Y X X +=-i =1,2,…,n -1,则 21()()()0,()2,i i i i E Y E X E X D Y μμσ+=-=-==于是 1222211ˆ[()](1)2(1),n ii E E k Yk n EY n k σσ-===-=-∑那么当22ˆ()E σσ=,即222(1)n k σσ-=时, 有 1.2(1)k n =-7.设X 1,X 2是从正态总体N (μ,σ2)中抽取的样本112212312211311ˆˆˆ;;;334422X X X X X X μμμ=+=+=+ 试证123ˆˆˆ,,μμμ都是μ的无偏估计量,并求出每一估计量的方差. 【证明】(1)11212212121ˆ()()(),333333E E X X E X E X μμμμ⎛⎫=+=+=+= ⎪⎝⎭21213ˆ()()()44E E X E X μμ=+=, 31211ˆ()()(),22E E X E X μμ=+= 所以123ˆˆˆ,,μμμ均是μ的无偏估计量. (2) 22221122145ˆ()()(),3399D D X D X X σμσ⎛⎫⎛⎫=+== ⎪ ⎪⎝⎭⎝⎭222212135ˆ()()(),448D D X D X σμ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭()223121ˆ()()(),22D D X D X σμ⎛⎫=+= ⎪⎝⎭8.某车间生产的螺钉,其直径X ~N (μ,σ2),由过去的经验知道σ2=0.06,今随机抽取6枚,测得其长度(单位mm )如下:14.7 15.0 14.8 14.9 15.1 15.2 试求μ的置信概率为0.95的置信区间. 【解】n =6,σ2=0.06,α=1-0.95=0.05,0.25214.95, 1.96,a x u u ===,μ的置信度为0.95的置信区间为/2(14.950.1 1.96)(14.754,15.146)x u α⎛±=±⨯= ⎝.9.总体X ~N (μ,σ2),σ2已知,问需抽取容量n 多大的样本,才能使μ的置信概率为1-α,且置信区间的长度不大于L ?【解】由σ2已知可知μ的置信度为1-α的置信区间为/2x u α⎛± ⎝,/2u α,/2u α≤L ,得n ≥22/224()u L ασ 10.设某种砖头的抗压强度X ~N (μ,σ2),今随机抽取20块砖头,测得抗压强度数据(单位:kg ·cm -2)如下(kg ·cm -2):64 69 49 92 55 97 41 84 88 99 84 66 100 98 72 74 87 84 48 81 (1) 求μ的置信概率为0.95的置信区间. (2) 求σ2的置信概率为0.95的置信区间. 【解】76.6,18.14,10.950.05,20,x s n α===-==/20.025222/20.0250.975(1)(19) 2.093,(1)(19)32.852,(19)8.907t n t n ααχχχ-==-===(1) μ的置信度为0.95的置信区间/2(1)76.6 2.093(68.11,85.089)a x n ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭(2)2σ的置信度为0.95的置信区间222222/21/2(1)(1)1919,18.14,18.14(190.33,702.01)(1)(1)32.8528.907n s n s n n ααχχ-⎛⎫--⎛⎫=⨯⨯= ⎪⎪--⎝⎭⎝⎭ 11.设总体X ~f (x )=(1),01;10,.x x θθθ⎧+<<>-⎨⎩其中其他X 1,X 2,…,X n 是X 的一个样本,求θ的矩估计量及极大似然估计量.【解】(1)1101()()d (1)d ,2E X xf x x x x θθθθ+∞+-∞+==+=+⎰⎰ 又1(),2X E X θθ+==+ 故21ˆ1X Xθ-=-所以θ的矩估计量 21ˆ.1X Xθ-=- (2) 似然函数11(1) 01(1,2,,)()()0n n ni i i i i x x i n L L f x θθθ==⎧+<<=⎪===⎨⎪⎩∏∏其他. 取对数11ln ln(1)ln (01;1),d ln ln 0,d 1nii i ni i L n x x i n L n x θθθθ===++<<≤≤=+=+∑∑所以θ的极大似然估计量为1ˆ1.ln nii nXθ==--∑12.设总体X ~f (x )= 36(),0;0,.xx x θθθ⎧-<<⎪⎨⎪⎩其他X 1,X 2,…,X n 为总体X 的一个样本 (1) 求θ的矩估计量∧θ;(2) 求ˆ()D θ.【解】(1) 236()()d ()d ,2x E X xf x x x x θθθθ+∞-∞=-=⎰⎰令 ,2EX X θ==所以θ的矩估计量 ˆ2.X θ= (2)4ˆ()(2)4(),D D X D X DX nθ===, 又322236()63()d ,2010x x E X x θθθθθ-===⎰于是222223()()(),10420D XE X EX θθθ=-=-=,所以2ˆ().5D nθθ=13.设某种电子元件的使用寿命X 的概率密度函数为f (x ,θ)= 2()2,;0,.x x x θθθ--⎧>⎨≤⎩e其中θ(θ>0)为未知参数,又设x 1,x 2,…,x n 是总体X 的一组样本观察值,求θ的极大似然估计值.【解】似然函数12()12e 0;1,2,,;()0ln ln 22(),;1,2,,,ni i x n i n i i i x i n L L L n x x i n θθθθ=--=⎧∑⎪⋅≥===⎨⎪⎩=--≥=∑其他.由d ln 20ln (),d Ln L θθ=>↑知 那么当01ˆˆmin{}ln ()max ln ()ii nx L L θθθθ>≤≤==时 所以θ的极大似然估计量1ˆmin{}ii nx θ≤≤=其中θ(0<θ<12)是未知参数,利用总体的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和极大似然估计值. 【解】813ˆ(1)()34,()4 28ii x E X E X x x x θθ=-=-====∑令得又 所以θ的矩估计值31ˆ.44x θ-== (2) 似然函数86241(,)4(1)(12).ii L P x θθθθ===--∏2ln ln 46ln 2ln(1)4ln(1),d ln 628628240,d 112(1)(12)L L θθθθθθθθθθθθ=++-+--+=--==---- 解2628240θθ-+=得1,272θ±=. 由于71,122> 所以θ的极大似然估计值为7ˆ2θ-=15.设总体X 的分布函数为F (x ,β)=1,,0,.x xx ββααα⎧->⎪⎨⎪≤⎩其中未知参数β>1,α>0,设X 1,X 2,…,X n 为来自总体X 的样本(1) 当α=1时,求β的矩估计量;(2) 当α=1时,求β的极大似然估计量; (3) 当β=2时,求α的极大似然估计量. 【解】当α=1时,11,1;(,)(,1,)0,1.x x f x F x x x ββββ+⎧≥⎪==⎨⎪<⎩当β=2时, 2132,;(,)(,,2)0,.x x f x F x x x ααααα⎧≥⎪==⎨⎪<⎩(1) 111()d 11E X x x x βββββββ+∞-+∞===--⎰令()E X X =,于是ˆ,1XX β=- 所以β的矩估计量ˆ.1XX β=- (2) 似然函数(1)1111,1,(1,2,,);()(,)0,.ln ln (1)ln ,d ln ln 0,d n n ni i i i i n i i ni i x x i n L L f x L n x L n x ββββββββ-+====⎧⎛⎫>=⎪ ⎪===⎨⎝⎭⎪⎩=-+=-=∏∏∑∑其他所以β的极大似然估计量1ˆ.ln nii nxβ==∑(3) 似然函数23112,,(1,2,,);(,)0,.n ni nn i i i i x i n L f x x ααα==⎧≥=⎪⎪⎛⎫==⎨ ⎪⎝⎭⎪⎪⎩∏∏其他显然(),L L α=↑那么当1ˆmin{}i i nx α≤≤=时,0ˆ()max ()a L L L αα>== , 所以α的极大似然估计量1ˆmin{}i i nx α≤≤=. 16.从正态总体X ~N (3.4,62)中抽取容量为n 的样本,如果其样本均值位于区间(1.4,5.4)内的概率不小于0.95,问n 至少应取多大?2/2()d zt z t ϕ-=⎰【解】26~ 3.4,X N n ⎛⎫⎪⎝⎭,则~(0,1),X Z N = {1.4 5.4}33210.95333Z P X P PZ ΦΦΦ<<<<=⎧=-<<⎨⎩⎭⎛⎫⎛⎛⎫=-=-≥- ⎪ ⎪⎝⎭⎝⎭⎝⎭于是0.975Φ≥ 1.96≥, ∴ n ≥35.17. 设总体X 的概率密度为f (x ,θ)=,01,1,12,0,.x x θθ<<⎧⎪-≤<⎨⎪⎩其他 其中θ是未知参数(0<θ<1),X 1,X 2,…,X n 为来自总体X 的简单随机样本,记N 为样本值x 1,x 2,…,x n 中小于1的个数.求: (1) θ的矩估计;(2) θ的最大似然估计. 解 (1) 由于121(;)d d (1)d EX xf x x x x x x θθθ+∞-∞==+⎰⎰⎰-133(1)222θθθ=+-=-. 令32X θ-=,解得32X θ=-, 所以参数θ的矩估计为32X θ=-.(2) 似然函数为1()(;)(1)nN n N i i L f x θθθθ-===-∏,取对数,得ln ()ln ()ln(1),L N n N θθθ=+--两边对θ求导,得d ln ().d 1L N n Nθθθθ-=-- 令 d ln ()0,d L θθ=得 Nn θ=,所以θ的最大似然估计为Nnθ=.。
