遗传算法及其改进措施
用于求解TSP问题的遗传算法改进
用于求解TSP问题的遗传算法改进一、TSP问题简介TSP问题，全称Traveling Salesman Problem，即旅行商问题。
所谓TSP问题是指，给定一些点和每一对点之间的距离，求出一条遍历每个点恰好一次的最短路径，该问题的解决方法对实际问题中的路径规划和优化有着很大的参考价值。
二、遗传算法的基本思想遗传算法，是模拟自然界中生物遗传进化过程的一种演化计算方法。
它通过模拟生物的繁殖、变异、适应性等生命过程来寻找问题的最优解。
其基本的过程如下：1. 初始化：随机生成一个初始群体，每个个体表示一种可能的解决方案。
2. 选择：根据适应度函数，选择一定数量的优秀个体作为繁殖的父亲。
3. 交叉：将所选父亲进行交叉操作，生成新的子代个体。
4. 变异：对于一部分子代个体，进行变异操作。
5. 替换：用新的子代个体替换掉一部分原有的个体，形成新一代群体。
6. 结束条件：当某种条件达到时结束算法，否则返回步骤二。
在TSP问题中，遗传算法的基本实现方法如下：1.初始化：随机生成一个初始群体，每个个体表示一个解决方案，其中每个基因表示一个城市的编号。
例如，假设有10个城市，则每个个体就是由这10个城市编号随机排列组成的，例如：1-2-5-8-4-3-7-9-6-10等。
2.适应度函数：对于每个个体，计算其总路程，将总路程作为适应度函数的值。
4.交叉：将所选父亲进行交叉操作，生成新的子代个体，交叉方式一般有：顺序交叉法、部分映射交叉法、环形交叉法、边交叉法等。
5.变异：对于一部分子代个体，进行变异操作，变异的方式一般是：交换变异、倒位变异、随机抽样变异等。
7.结束条件：当达到一定条件时结束算法，比如迭代次数达到上限或者群体的适应度达到一定的水平。
传统的遗传算法在求解TSP问题时，存在一些问题：1.收敛速度慢：由于集合了交叉、变异等算子，每一代都要进行大量的计算，所以收敛速度慢。
2.易受陷入局部最优解：由于遗传算法采用的是局部搜索策略，所以可能会陷入到局部最优解中。
遗传算法在数据库优化中的解决方案
遗传算法在数据库优化中的解决方案数据库优化是提高数据库性能和效率的关键步骤，而遗传算法作为一种优化算法，可以在数据库优化中发挥重要作用。
本文将探讨遗传算法在数据库优化中的解决方案。
一、遗传算法简介遗传算法是一种模拟自然选择和遗传机制的优化算法。
它通过模拟生物进化过程中的选择、交叉和变异等操作，来搜索问题的最优解。
遗传算法具有全局搜索能力和自适应性，适用于复杂问题的优化。
二、数据库优化问题在数据库中，性能问题常常涉及查询优化、索引设计、表结构调整等方面。
传统的优化方法往往需要人工经验和反复试错，效率低下且不一定能找到最优解。
而遗传算法可以通过不断迭代的方式，自动搜索最优解，提高数据库性能。
三、遗传算法在数据库查询优化中的应用数据库查询优化是提高查询效率的关键。
遗传算法可以通过优化查询语句的执行计划，从而提高查询性能。
具体而言，遗传算法可以通过选择合适的索引、调整表连接顺序、优化查询语句等方式，提高查询效率。
四、遗传算法在索引设计中的应用索引是提高数据库查询效率的重要手段。
传统的索引设计往往需要根据经验和统计数据进行调整，效果不一定理想。
而遗传算法可以通过自动搜索最优索引的方式，提高查询性能。
它可以通过选择合适的索引字段、调整索引顺序等方式，找到最优索引组合。
五、遗传算法在表结构调整中的应用数据库表结构的设计对性能有重要影响。
传统的表结构调整方法需要手动调整，效率低下。
而遗传算法可以通过自动搜索最优表结构的方式，提高数据库性能。
它可以通过调整表字段顺序、拆分大表等方式，优化表结构，提高查询效率。
六、遗传算法的优势和局限性遗传算法在数据库优化中具有以下优势：首先，它可以自动搜索最优解，减少了人工经验的依赖；其次，它具有全局搜索能力，可以找到全局最优解；此外，它具有自适应性，能够适应不同的问题。
然而，遗传算法也存在一些局限性，例如计算复杂度较高、算法参数的选择等问题。
七、结论遗传算法作为一种优化算法，在数据库优化中具有重要的应用价值。
遗传算法在组合优化中的解决方案
遗传算法在组合优化中的解决方案组合优化是一种重要的问题求解方法，它在现实生活中的应用非常广泛。
而遗传算法作为一种启发式搜索算法，被广泛应用于组合优化问题的求解中。
本文将探讨遗传算法在组合优化中的解决方案，并分析其优势和应用场景。
一、遗传算法的基本原理遗传算法是一种模拟自然进化过程的优化算法。
其基本原理是通过模拟遗传、变异和选择等过程，逐步优化问题的解。
具体而言，遗传算法主要包括以下几个步骤：1. 初始化种群：随机生成一定数量的个体，每个个体代表问题的一个可能解。
2. 评估适应度：根据问题的特定评价函数，计算每个个体的适应度值，用于衡量其解的优劣程度。
3. 选择操作：根据适应度值，选择一部分个体作为父代，用于产生下一代个体。
4. 交叉操作：通过交叉操作，将父代个体的某些特征进行组合，生成新的个体。
5. 变异操作：对新生成的个体进行变异操作，引入一定的随机性，增加问题的搜索空间。
6. 重复步骤2至5，直到满足终止条件。
二、遗传算法在组合优化中的应用遗传算法在组合优化中有广泛的应用，例如旅行商问题、背包问题、调度问题等。
下面以旅行商问题为例，说明遗传算法的应用。
旅行商问题是一个经典的组合优化问题，其目标是找到一条最短的路径，使得旅行商能够依次访问多个城市并最终回到起点。
遗传算法可以通过以下步骤解决该问题：1. 初始化种群：随机生成一定数量的路径，每个路径代表旅行商的一种可能行走顺序。
2. 评估适应度：根据路径的总长度，计算每个路径的适应度值。
3. 选择操作：根据适应度值，选择一部分路径作为父代。
4. 交叉操作：通过交叉操作，将父代路径的某些城市进行组合，生成新的路径。
5. 变异操作：对新生成的路径进行变异操作，引入一定的随机性。
6. 重复步骤2至5，直到满足终止条件。
通过以上步骤，遗传算法可以不断优化路径，最终找到一条最短的路径解决旅行商问题。
三、遗传算法的优势和应用场景遗传算法在组合优化中具有以下优势：1. 并行搜索能力：遗传算法可以同时搜索多个解，提高问题的求解效率。
最佳遗传算法参数调优方法
最佳遗传算法参数调优方法遗传算法是一种模拟自然界中生物进化过程的优化算法。
在解决复杂问题和优化函数方面具有广泛的应用。
然而，遗传算法的性能很大程度上取决于参数的选择。
本文将介绍一些最佳的遗传算法参数调优方法，以帮助提高算法的性能。
1. 交叉率的选择交叉是遗传算法中的一个重要操作，用于产生新的个体。
交叉率决定了父代个体中被交叉的比例。
如果交叉率过高，可能导致早熟收敛和搜索空间的过早收缩。
相反，如果交叉率过低，可能导致搜索的速度过慢。
因此，选择一个合适的交叉率至关重要。
一种常见的方法是采用自适应交叉率。
在算法开始时，可以使用较高的交叉率，以便更好地探索搜索空间。
随着算法的进行，可以逐渐降低交叉率，以便更多地利用已经找到的优秀解。
这样可以平衡探索和利用的关系，提高算法的性能。
2. 变异率的选择变异是遗传算法中的另一个重要操作，用于引入新的基因信息。
变异率决定了个体中基因发生变异的概率。
如果变异率过高，可能导致搜索过于随机，难以收敛到最优解。
相反，如果变异率过低，可能导致搜索的局部最优解。
一种常见的方法是采用自适应变异率。
在算法开始时，可以使用较高的变异率，以便更好地探索搜索空间。
随着算法的进行，可以逐渐降低变异率，以便更多地利用已经找到的优秀解。
这样可以平衡探索和利用的关系，提高算法的性能。
3. 种群大小的选择种群大小是指每一代中个体的数量。
种群大小的选择对算法的性能有很大影响。
如果种群大小过小，可能导致搜索的多样性不足，难以找到全局最优解。
相反，如果种群大小过大，可能导致计算资源的浪费。
一种常见的方法是采用自适应种群大小。
在算法开始时，可以使用较大的种群大小，以便更好地探索搜索空间。
随着算法的进行，可以逐渐减小种群大小，以便更多地利用已经找到的优秀解。
这样可以平衡探索和利用的关系，提高算法的性能。
4. 选择算子的选择选择算子用于选择较优个体作为下一代的父代。
选择算子的选择对算法的性能有很大影响。
常见的选择算子有轮盘赌选择、锦标赛选择等。
遗传算法基本原理及改进
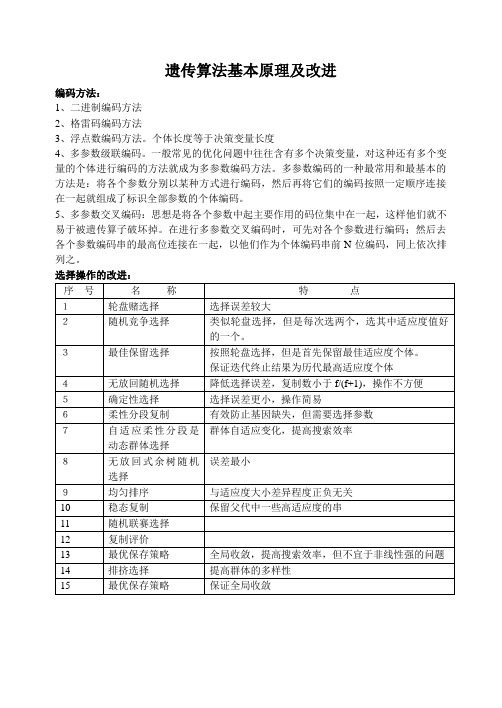
遗传算法基本原理及改进编码方法：1、二进制编码方法2、格雷码编码方法3、浮点数编码方法。
个体长度等于决策变量长度4、多参数级联编码。
一般常见的优化问题中往往含有多个决策变量，对这种还有多个变量的个体进行编码的方法就成为多参数编码方法。
多参数编码的一种最常用和最基本的方法是：将各个参数分别以某种方式进行编码，然后再将它们的编码按照一定顺序连接在一起就组成了标识全部参数的个体编码。
5、多参数交叉编码：思想是将各个参数中起主要作用的码位集中在一起，这样他们就不易于被遗传算子破坏掉。
在进行多参数交叉编码时，可先对各个参数进行编码；然后去各个参数编码串的最高位连接在一起，以他们作为个体编码串前N位编码，同上依次排列之。
改进遗传算法的方法：（1）改进遗传算法的组成成分或实用技术，如选用优化控制参数、适合问题的编码技术等。
（2）采用动态自适应技术，在进化过程中调整算法控制参数和编码精度。
（3）采用混合遗传算法（4）采用并行算法（5）采用非标准的遗传操作算子改进的遗传算法：（1）分层遗传算法（2）CHC算法（3）messy遗传算法；（4）自实用遗传算法（Adaptive Genetic Algorithm）（5）基于小生境技术的遗传算法（Niched Genetic Algorithm，简称NGA）。
（6）并行遗传算法（Parallel Genetic Algorithm）（7）混合遗传算法：遗传算法与最速下降法相结合的混合遗传算法；遗传算法与模拟退火算法相结合的混合遗传算法。
解决标准遗传算法早熟收敛和后期搜索迟钝的方案（1）变异和交叉算子的改进和协调采用将进化过程划分为渐进和突变两个不同阶段采用动态变异运用正交设计或均匀设计方法设计新的交叉和变异算子（2）采用局部搜索算法解决局部搜索能力差的问题（3）采用有条件的替代父代的方法，解决单一的群体更新方式难以兼顾多样性和收敛性的问题（4）收敛速度慢的解决方法；产生好的初始群体利用小生境技术使用移民技术采用自适应算子采用与局部搜索算法相结合的混合遗传算法对算法的参数编码采用动态模糊控制进行未成熟收敛判断。
论文遗传算法的研究和改进
遗传算法的研究和改进遗传算法是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法，其应用优势在于处理传统搜索方法难以解决的复杂和非线性问题，本论文研究内容包括：小生境遗传算法的改进、自适应遗传算子的设计、免疫的进化算法。
本文主要工作如下：（1）遗传算法的起源、其基本概念以及研究概况;（2）遗传算法的基本理论.主要介绍了模式定理、积木块假说、内在并行性、Walsh模式变换、欺骗问题等;（3）基本遗传算法.主要介绍了编码、适应度函数、遗传操作等.（4）遗传算法的改进.主要介绍了分层遗传算法、CHC算法、messy遗传算法、自适应遗传算法、基于小生境技术的遗传算法、混合遗传算法等几种遗传算法的改进.（5）遗传算法的应用.关键词：遗传算法;进化计算;进化规划;进化策略;遗传操作;适应度函数;Walsh函数ABSTRACTGenetic algorithm is a kind of random searching method using lives’ natural selection and genetic mechanism. Its application predominance lies in complicated and non-linear problems, which are difficult for traditional searching methods. Three improved algorithms are proposed in the dissertation: improved niche genetic algorithm, improved adaptive genetic algorithm, genetic algorithm based on immune mechanism. They are summarized as following:Firstly, the dissertation analyses characters of several traditional genetic algorithms for niche. Following this, a new method, combined parallelism evolution technique for niches based on local competition with parent mutation mechanism, is proposed which improved the genetic algorithms for niche. Compared with genetic algorithm with sharing, it has some improvements in both converging velocity and precision.Secondly, analyzing the inadequacies of the evaluation indices for premature convergence, a novel improved adaptive genetic algorithm (IAGA) is described. The calculation result of an example shows that IAGA is able to get the real-time information of population diversity during the process of evolution.Finally, applying the immune mechanism to genetic algorithm, the immune genetic algorithm expatiated on this paper comes over the phenomenon of premature in some extent. The result of experiment shows that the global convergence and searching velocity are both improved.Keyword: genetic algorithms, evolution strategy, Walsh function第一章 绪论§1.1 引言遗传算法（Genetic Algorithm ——GA ），是一类以达尔文的自然进化论与遗传变异理论为基础的求解复杂全局优化问题的仿生型算法[1]。
遗传算法及其改进措施
优化算法大作业一、题目本文利用遗传算法，依次完成下面三个目标函数的寻优：1Generalized Rosen brock’s valley Function048.2048.2)1()(100)(max 112221<<--+-⋅=∑-=+i n i i i i x x x x x f2 Generalized Rastrigin's Function12.512.5)10)2cos(10()(min 112<<-+⋅-=∑-=i n i i i x x x x f π3 Schaffer’s Function44))(001.01(5.0)(sin 5.0),(min 222212222121<<-+*+-+-=i x x x x x x x f二、本文思路遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法，本文利用遗传算法分别对上述三种函数进行全局寻优，具体思路如下：1. 编码与解码1) 编码：假设某一参数的取值范围是[u min , u max ]，我们用长度为l 的二进制编码符号串来表示该参数，则它总共能够产生 2l 种不同的编码，编码的长度越长，对应的精度越高。
● 第一题变量的取值范围是[-2.048,2.048]，本文采取十位数的编码，那么精度为：3min max 110004.412-⨯=--=lu u δ ● 第二题变量的取值范围是[-5.12,5.12]，本文采取的是十二位数的编码，那么精度为：3min max 210501.212-⨯=--=l u u δ● 第三题变量的取值范围是[-4,4]，本文采取的是十三位数的编码，那么精度为：3minmax 310442.212-⨯=--=lu u δ2) 解码：假设某一个个体的编码是1221b b b b b L i i i --=，那么对应的解码公式为：δ⋅⋅+=-=∑)2(11min i li i b u x2. 个体适应度评价1) 当优化目标是求函数最大值，并且目标函数总取正值时，可以直接设 定个体的适应度F(X)就等于相应的目标函数值f(X)，即：F (x )={f (x )−C min f (x )>C min0 f (x )≤C min其中min C 是函数最小值估计。
遗传算法调试及改进策略
遗传算法调试及改进策略遗传算法是一种基于生物进化理论的搜索算法，能够在解决各种优化问题上取得不错的效果。
但是在实际应用中，遗传算法的调试和改进策略也十分重要，本文就此展开讨论。
一、遗传算法的调试策略1、选择算子的调试选择算子是遗传算法中最重要的一步，其作用是筛选出适应度高的个体并进行后代产生。
调试选择算子时，需要注意以下几点：（1）选择算子应具有“竞争性”，即适应度高的个体应该有更大概率被选中，同时不适应度高的个体也有一定的被选中概率，以保证算法具有全局搜索能力。
（2）选择算子应具有一定的随机性，避免算法陷入局部最优解。
（3）选择算子应该能够处理不同类型的编码方式，如二进制编码、实数编码等。
2、交叉算子的调试交叉算子是遗传算法中产生后代的重要步骤，其作用是将两个个体的染色体进行交叉，从而产生新的后代个体。
调试交叉算子时，需要注意以下几点：（1）交叉算子应该具有“多样性”，即不同类型的交叉方式应该有一定的概率被选中，以保证算法的全局搜索能力。
（2）交叉算子应该能够处理不同类型的编码方式，如二进制编码、实数编码等。
（3）交叉算子的位置和长度应该有一定的随机性，以保证算法不会陷入局部最优解。
3、变异算子的调试变异算子是遗传算法中保持种群多样性的重要步骤，其作用是对个体的染色体进行随机变异，从而产生新的后代个体。
调试变异算子时，需要注意以下几点：（1）变异算子应该具有一定的“可控性”，即变异概率应该适当，过高或过低都会影响算法的性能。
（2）变异算子应该能够处理不同类型的编码方式，如二进制编码、实数编码等。
（3）变异算子的位置和长度应该有一定的随机性，以保证算法不会陷入局部最优解。
二、遗传算法的改进策略1、自适应参数调整在遗传算法中，参数的选择对算法的性能至关重要，如种群大小、交叉概率、变异概率等。
为了更好地平衡全局搜索和局部搜索之间的关系，可以采用自适应参数调整策略，根据算法的实际运行情况，动态地调整参数值。
改进遗传算法
5.停止准则
在基本的遗传算法中，一般采用最大迭代次数作为算法的 停止准则，此方法不太准确，因为可能在在最大的迭代次数 之前算法已经收敛，也可能在最大迭代次数时还没收敛，因 此采用另外一种停止准则，即根据种群的收敛程度，种群适 应值得一致性来判断是否算法停止。在算法的执行过程中保 留历史上最好的个体，观察指标
F Fmax
其中，F 为种群中所以个体适应值得平均值，Fmax 为所以个
体适应值得最大值，当上述指标趋近于1时，说明种群收 敛，此时算法停止。
谢谢
的是：循环交叉是用来解决指派这一类的问题的
2.变异修复策略
简单的二进制变异时候只需要把０变成１，１变成０， 而顺序编码的变异策略不能这样进行，一般由下面两种策略： ➢ 换位变异
➢ 换位变异是随机在染色体上选则两个基因，交换它们 的基因值
➢ 移位变异 ➢ 移位变异是任意选则一个基因，将其移到最前面。
的后期，希望选择压力较大，所以 k 取值较小，使不同个
体间的选择概率相差变大，种群将很快达到收敛，从而解决 了在最优解附近收敛较慢的问题。
➢ 幂律标定
幂律标定是采用如下的构造方式
F fα
其中，α是用来调节选择压力的，α >1时，选择压力加大， α<1时，选择压力减小，此标定比较费时，要针对不同问 题使用。
2.不合法编码的修复
对于普通的二进制编码，通常的交叉和变异不会改变 编码的合法性，但是对于顺序编码、实数编码，会造成编码 的不合法或者超出可行域，因此必须对不合法的编码进行处 理，通常的处理手段为拒绝或者修复。下面介绍修复的方法。
➢ 顺序编码的合法性修复 ➢ 实数编码的合法性修复
1. 顺序编码的修复
f1=1010,f2=1008,f3=1002,f4=1005,f5=1015
《改进遗传算法及其在TSP问题中的应用》范文
《改进遗传算法及其在TSP问题中的应用》篇一一、引言遗传算法是一种基于自然进化理论的搜索启发式算法，广泛应用于组合优化问题。
旅行商问题（Traveling Salesman Problem，简称TSP）作为典型的组合优化问题之一，吸引了众多研究者的关注。
本文旨在探讨改进遗传算法及其在TSP问题中的应用，通过分析现有遗传算法的优缺点，提出一种改进的遗传算法，并在TSP问题中验证其有效性和优越性。
二、遗传算法概述遗传算法模拟自然进化过程，通过种群个体的选择、交叉和变异等操作，实现全局搜索和优化。
其基本步骤包括初始化种群、计算个体适应度、选择操作、交叉操作和变异操作等。
三、现有遗传算法在TSP问题中的局限性在TSP问题中，遗传算法面临着多个挑战。
一方面，搜索空间随城市数量急剧增长；另一方面，由于问题的复杂性，传统遗传算法容易陷入局部最优解。
此外，传统遗传算法在处理城市间的距离计算和路径优化时，往往无法有效平衡全局搜索和局部搜索。
四、改进的遗传算法设计针对上述问题，本文提出一种改进的遗传算法。
该算法主要从以下几个方面进行优化：1. 初始化种群策略：采用更精细的编码方式，使个体更好地表示路径。
同时，引入随机性因素，扩大搜索空间。
2. 适应度函数设计：针对TSP问题，设计更为合理的适应度函数，将城市间的距离和路径长度综合考虑，提高搜索效率。
3. 选择操作：采用多种选择策略相结合的方式，如轮盘赌选择、锦标赛选择等，提高种群的多样性。
4. 交叉操作：引入多种交叉方式，如单点交叉、多点交叉和均匀交叉等，提高算法的搜索能力。
5. 变异操作：在变异过程中引入扰动机制，增加种群的活跃度，避免陷入局部最优解。
五、实验设计与结果分析为了验证改进的遗传算法在TSP问题中的有效性，本文设计了多组实验。
实验中，我们采用了不同规模的TSP问题实例（如城市数量从几十到几百不等），并与其他遗传算法进行比较。
实验结果表明，改进的遗传算法在TSP问题上具有更好的性能。
改善基于遗传算法的运筹学问题解决
改善基于遗传算法的运筹学问题解决
遗传算法(Genetic Algorithm, GA)可以用于解决各类运筹学问题，其优势在于可以解决大型复杂的问题，不受特定函数类型和维数的限制。
为了更好地解决运筹学问题，人们需要对GA 进行改进和优化，改善GA主要包括以下几方面：
一是自适应参数调整。
根据问题的不同特征，也就是不同的函数类型、变量维数，应当根据问题特性勤加调整GA的参数。
如遗传算子的选择、种群规模、选择机制、变异等等，以使得GA能够更好地找到最优解。
二是给不同的基因赋予赋予不同的权重。
在GA中，每个染色体有多个基因，假设现有多个目标函数，我们可以给不同的基因赋予不同的权重，从而使得GA能够更好地收敛到优化问题的最优解。
三是优化交叉算子。
在GA中，是否采用交叉算子或者某种特定的交叉算子，将会影响GA的收敛情况。
因此，需要根据问题特性优化交叉算子，以保证GA能够更好地收敛。
四是添加新的算子。
GA有时候无法找到最优解，这是因为种群历经多次变异及交叉之后，可能会处在局部最优解的区域，出现收敛停滞的情况。
为此，可以添加特定的搜索策略算子，如局部搜索算子等，以有效地突破局部最优解，发现更优解。
遗传算法及其改进设计
[2]朱灿.实数编码遗传算法机理分析及算法改进研究[D].中南大学，博士学位论文, 2009.
[3]许琦.基于遗传算法的高校排课问题的研究[D].华南理工大学，硕士学位论文, 2012.
系审核意见
负责人（签名）————————
备注：1、本任务书一式三份，系、指导教师、学生各执一份。
2、学生须将此任务书作为毕业论文（设计）说明书的附件，装订在说明书中。
（1）研究掌握遗传算法的原理；
（2）设计实现遗传算法的C语言程序；
（3）研究掌握通过matlab遗传算法工具箱进行问题优化的方法；
（4）分析普通遗传算法的缺点，并提出算法改进措施，并用matlab语言和遗传算法工具箱实现；
（5）对一些标准测试函数，用提出的改进算法进行优化，检验算法结果；
（6）选定某实际问题（可使用UCI机器学习数据库数据），用遗传算法进行优化；
工作阶段（包括时间划分和各阶段主要工作内容）
一、2012年12月查阅文献资料，确定设计方向；
二、1月至3月确定设计的研究方法并提交开题报告；
三、2013年1月至2013年3月完成毕业设计作品；
四、2013年4月完成毕业论文初稿。
五、2013年5月日，完成最终毕业论文。
其它要求（包括文献研究、实验实习等方面）
毕业论文（设计）任务书
学生姓名
学号
专业班级
指导教师
职称
题目
遗传算法及其改进设计
研究（设计）任务（包括目标和要求）
1、根据设计（论文）选题，查阅相关技术书籍、学校图书馆网站数据库文献资料，进一步明确选题的目的、意义和应用领域；
2、பைடு நூலகம்据选题进行理论验证，补充掌握进行设计需要补充的知识；
遗传算法论文：浅谈遗传算法的研究与改进
遗传算法论文：浅谈遗传算法的研究与改进【摘要】遗传算法是模拟自然界生物进化机制的概率性搜索算法，可以处理传统搜索方法难以解决的非线性问题。
但是经典遗传算法存在局部收敛、收敛速度慢等缺点，这使得经典遗传算法有时很难找到全局最优解。
本文针对经典遗传算法中所存在的缺点，采用阶段式的适应度函数、基于竞争机制的交叉方式和仿粒子群变异操作，使遗传算法的收敛速率、全局收敛概率都得到了较大的提高。
【关键词】遗传算法适应度交叉操作仿粒子群变异一遗传算法遗传算法（genetic algorithm，简称ga）是holland 在研究自然遗传现象与人工系统的自适应行为时，模拟生物进化现象，并采用自然进化机制来表现复杂现象的一种全局群体搜索算法。
遗传算法的基本思想起源于darwin进化论和mendel的遗传学说。
作为一类智能计算工具和学习算法，由于其实现简单、对目标函数要求不高等特性，遗传算法已广泛应用于如人工智能、组合优化等研究领域。
1．遗传算法的优越性遗传算法（genetic algorithm）利用某种编码技术作用在称为染色体的二进制串上，模拟由这些串组成的个体的进化过程。
通过有组织的、随机的信息交换来重新结合那些适应性好的串，在每一代中，利用上一代串结构中适应性好的位和段来形成一个新的串的群体，同时在串结构中尝试用新的位和段来代替原来的部分以形成新的个体，以增加种群的多样性。
遗传算法的最大优点是能够通过群体间的相互作用，保存已经搜索到的信息，这是基于单次搜索过程的优化方法所无法比拟的。
但是，遗传算法也存在着计算速度较慢，并且容易陷入局部最优解的问题中。
遗传算法的优越性归功于它与传统搜索方法不同的特定结构。
第一，遗传算法的操作对象是编码，对问题的限制极少，对函数的一些约束条件如连续性、可导性等不做要求，减少了要解决问题的复杂性。
第二，遗传算法同时搜索解空间内的许多点，因而可以有效地防止搜索过程中收敛到局部最优解，并获得全局最优解，与其他单点搜索的方法相比，在计算时间上也有较大的优势。
如何优化遗传算法的搜索空间与适应度函数
如何优化遗传算法的搜索空间与适应度函数优化遗传算法的搜索空间与适应度函数遗传算法是一种模拟自然选择和遗传机制的优化算法，它通过模拟生物进化的过程，逐步搜索最优解。
在实际应用中，如何优化遗传算法的搜索空间和适应度函数是非常重要的，本文将探讨这两个方面的优化方法。
一、优化搜索空间1. 确定合适的变量范围在遗传算法中，搜索空间的定义是非常重要的。
首先，需要确定变量的范围，即每个变量可以取值的范围。
合适的变量范围可以保证搜索空间不会过大或过小，从而提高算法的搜索效率。
2. 采用变量编码方式变量编码方式是指将变量转化为遗传算法中的染色体表示形式。
常用的编码方式有二进制编码、实数编码和排列编码等。
选择合适的编码方式可以更好地适应问题的特性，提高搜索效果。
3. 交叉与变异操作交叉和变异是遗传算法中的两个重要操作，可以增加搜索空间的多样性。
在进行交叉和变异操作时，需要根据具体问题的特点进行调整，以保证搜索空间的充分探索。
二、优化适应度函数1. 确定合适的目标函数适应度函数是遗传算法中评估个体适应度的函数，它决定了个体在进化过程中的生存能力。
确定合适的目标函数是优化适应度函数的关键。
目标函数应能准确地描述问题的目标，同时具备可计算性和可优化性。
2. 引入约束条件在实际问题中，往往存在一些约束条件，如等式约束、不等式约束等。
为了优化适应度函数，需要将这些约束条件引入到适应度函数中，从而保证搜索到的解满足问题的约束条件。
3. 适应度函数的动态调整在遗传算法的进化过程中，适应度函数的选择和调整也是非常重要的。
根据实际问题的需求，可以动态调整适应度函数的权重或参数，以提高算法的搜索效率。
三、优化遗传算法的综合策略1. 多样性保持策略在遗传算法的进化过程中，多样性是保证搜索空间充分探索的重要因素。
为了保持多样性，可以采用多样性保持策略，如精英保留策略、多样性保持操作等。
2. 改进选择策略选择策略是遗传算法中选择优秀个体的方法。
遗传算法的几种改进
遗传算法的⼏种改进《Matlab》【毕设】防⽌优良基因因为变异⽽遭到破坏【毕设】放弃赌轮选择：将种群中的个体按适应度⼤⼩排列排在前⾯的个体复制两份；中间的⼀份；后⾯的不复制；【毕设】早熟早熟的原因P36早熟表象：1，群体中所有的个体都陷于同⼀极值⽽停⽌进化。
2，接近最优解的个体总是被淘汰，进化过程不收敛。
解决：1，动态确定变异概率，防⽌优良基因因变异⽽遭破坏，⼜可在陷⼊局部最优解的时候引⼊新的基因。
2，改进选择⽅式，放弃赌轮选择，以避免早期的⾼适应度个体迅速占据种群和后期的种群中因个体的适应度相差不⼤⽽导致种群停⽌进化。
将种群中的个体按适应度⼤⼩排列排在前⾯的个体复制两份；中间的⼀份；后⾯的不复制；3，择优交叉4，由于种群的基因多样性可以减⼩陷⼊局优解的可能（多个原点，多条线去搜索，可以避免局部最优解。
？？？）。
⽽加快种群进化速度⼜可以提⾼算法的整体性能。
（⼀对⽭盾）（是不是可以⼀直保持6个适应度值，其他的不要？？？）【毕设】遗传算法改进⼀1，在初始种群中，对所有的个体按其适应度⼤⼩进⾏排序，然后计算个体的⽀持度和置信度。
2，按⼀定的⽐例复制（即将当前种群中适应度最⾼的两个个体结构完整地复制到待配种群中）3，安个体所处的位置确定其变异概率并变异；按优良个体复制4份，劣质个体不复制的原则复制个体4，从复制组中随机选择两个个体，对这两个个体进⾏多次交叉，从所得的结果中选择⼀个最优个体存⼊新种群；5，若满⾜结束条件，则停⽌，不然，跳转第（1）步，直⾄找到所有符合条件的规则。
该算法的优点是在各代的每⼀次演化过程中，⼦代总是保留了⽗代中最好的个体，以在“⾼适应度模式为祖先的家族⽅向”搜索出更好的样本，从⽽保证最终可以搜索到全局最优解。
【毕设】遗传算法改进⼆没读明⽩【毕设】遗传算法改进三早熟，后期搜索迟钝：解决⽅案：有条件的最佳保留机制；采⽤遗传-灾变算法；采⽤适应度⽐例机制和个体浓度选择机制的加权和；引⼊主群和属群的概念；适应度函数动态定标；多种群并⾏进化及⾃适应调整控制参数相结合的⾃适应并⾏遗传算法，对重要参数的选择采⽤⾃适应变化⽽⾮固定不变。
遗传算法求解路径规划问题优化参数调整技巧总结与改进
遗传算法求解路径规划问题优化参数调整技巧总结与改进遗传算法作为一种经典的优化算法，被广泛应用于路径规划问题的求解中。
然而，遗传算法的性能受到参数设置的影响较大。
本文将总结遗传算法求解路径规划问题时常用的参数调整技巧，并提出一些改进的思路。
1. 种群大小的选择种群大小决定了算法的搜索空间的广度和深度，直接影响算法的收敛速度和解的质量。
一般来说，种群大小应与问题的规模相关。
对于较小规模的问题，较小的种群大小可以在较短时间内找到较好的解；对于较大规模的问题，需要增大种群大小以增加搜索空间的广度。
然而，种群大小过大也会增加计算的复杂度，因此需要根据具体问题进行权衡。
2. 交叉概率和变异概率的设定交叉概率和变异概率是遗传算法中重要的参数，决定了遗传算子在每一代中的应用程度。
交叉概率较高可以增加种群的多样性，有利于全局搜索；变异概率较高可以增加种群的局部搜索能力，有利于找到更优的解。
通常情况下，交叉概率和变异概率应该相对较小，以避免搜索过早陷入局部最优解。
3. 选择算子的选择选择算子决定了下一代个体的选择方式。
常用的选择算子有轮盘赌选择、锦标赛选择等。
在路径规划问题中，记忆化选择算子是一种常用的选择算子，它可以保留一部分优秀个体，避免其丧失。
4. 编码方式的选择编码方式是指将问题的解进行编码，以适应遗传算法的运算。
常用的编码方式有二进制编码、浮点编码、整数编码等。
对于路径规划问题，常采用二进制编码或整数编码的方式，将路径的顺序作为个体的编码表示。
改进思路：1. 算法参数的自适应调整传统的遗传算法中，参数的设定通常是通过试错的方式来确定的。
然而，这种方式对问题的规模和复杂度敏感，并且需要大量的实验和人工干预。
因此，可以考虑使用自适应算法来动态调整算法的参数，使其更好地适应不同问题的求解。
2. 多目标遗传算法的引入路径规划问题通常具有多个目标，如最短路径和最小时间。
传统的遗传算法通常只考虑单一目标，不能很好地处理多目标问题。
遗传算法的一些改进及其应用共3篇
遗传算法的一些改进及其应用共3篇遗传算法的一些改进及其应用1遗传算法 (Genetic Algorithm) 是一种优化算法，它通过模拟生物进化过程来寻找最优解。
遗传算法最初由 J. Holland 在 1975 年提出，是模仿自然界生物的进化过程，利用选择、交叉和变异等基本遗传操作，搜索解空间中的最优解。
遗传算法优点在于能够处理复杂的非线性、多模优化问题，但在实际应用过程中存在一些问题，为了解决这些问题，对遗传算法进行了许多改进，下面介绍其中几种改进方法和应用。
改进一：精英选择策略在传统的遗传算法中，每次进行选择操作时都是随机选择个体进行交配，这导致一些较优秀的个体有可能被淘汰，因此提出了精英选择策略，即在每次进化过程中一定比例地选择适应度最好的个体，避免较好的个体被淘汰。
改进二：基因突变概率自适应策略在遗传算法中，变异操作可以增加个体的多样性，但是变异概率设置不当，可能会导致算法早熟收敛或者长时间停留在局部最优解。
为了避免这种情况，提出基因突变概率自适应策略，即根据当前代的适应度情况自适应计算变异概率，使变异概率既不过大，也不过小。
改进三：群体多样性保持策略为了保证遗传算法群体多样性，提出了数种策略：保持多样性的染色体种群操作，通过引进外来个体以增加多样性，以及通过避免重复染色体来保持多样性等方法。
应用一：函数优化函数优化是运用遗传算法的主要应用之一，它的目标是通过最小化目标函数，寻求函数的最小值或最大值。
应用遗传算法的一个优势在于它能够优化非凸性函数，而其他传统优化算法在优化过程中会陷入局部最优解。
应用二：机器学习机器学习需要寻找一个最佳的模型，而遗传算法可以用于选择合适的特征和参数，从而构建最佳的模型。
此外，遗传算法还可以用于优化神经网络的结构和权重，以提高神经网络的分类和预测性能。
应用三：工程优化遗传算法在工程中也有广泛的应用，如在电子电路设计中，可以通过遗传算法来寻找尽可能优秀的元器件匹配，从而达到最佳的电路性能。
遗传算法的研究与优化
遗传算法的研究与优化遗传算法是一种生物学启发式算法，它源自自然进化的基本原理，主要应用于寻找优化问题的解决方案。
在过去的几十年中，遗传算法已经得到广泛应用，并且展现出很高的效果。
本文将介绍遗传算法及其研究与优化。
1. 遗传算法的基本原理遗传算法主要源自自然进化的基本原理，包括选择、交叉和变异。
在遗传算法中，每个问题解决方案表示为一个基因组，其中的基因代表问题的特定部分。
这些基因在交叉和变异操作中被操作，从而创建新的解决方案。
在遗传算法的执行中，首先生成一个随机的种群，每个个体都是一个基因组。
接下来，基于适应度函数对每个个体进行评估。
适应度函数通常是一个应用于基因组的目标函数。
然后，依据评估结果，遗传算法选择最好的个体，也就是最能解决问题的个体。
最后，执行交叉和变异操作，生成新的解决方案。
遗传算法已经被广泛应用于许多领域，例如物理优化、生产设计、机器学习等等。
它们都可以视为一个优化问题，需要在复杂解空间中寻找最优解决方案。
以下是一些遗传算法的应用案例：- 动态调度问题动态调度是一种常见的优化问题，即如何更好地分配资源和工作。
在这种情况下，遗传算法被用于生成更好的调度程序，以最大化系统效率。
- 机器学习遗传算法被广泛用于机器学习问题，例如遗传算法训练神经网络和进行特征选择。
这些方法采用了遗传算法的选择、交叉和变异原理，利用人工选择不可行的解，通过交叉和变异创建新的解。
遗传算法可以用于生产机器人方案的优化。
生产机器人需要执行高度复杂的任务，在高维空间中找到最佳的解决方案，需要大量的计算和耗费时间等各种限制因素。
遗传算法虽然能够寻找出许多可行解，但它们不一定是最佳解。
可能存在多个局部最优解，例如遗传算法可能存在种群群体贪婪的选择倾向。
因此，遗传算法需要进行进一步调整和改进来提高其性能和效率。
- 交叉算子的改进简单的遗传算法交叉算法不能保障最优的结果，有时会压缩搜索空间。
因此，改进遗传算法的交叉算子是一种改进方法，特别是基于不同的交叉算子设计。
基本遗传算法及改进
第二章基本遗传算法及改进Holland创建的遗传算法是一种概率搜索算法，它利用某种编码技术作用于称为染色体的数串，其基本思想是模拟由这些串组成的个体进化过程。
该算法通过有组织地、然而是随机地进行信息交换，重新组合那些适应性好的串。
在每一代中，利用上一代串结构中适应好的位和段来生成一个新的串的群体；作为额外增添，偶尔也要在串结构中尝试用新的位和段来替代原来的部分。
遗传算法是一类随机优化算法，但是它不是简单的随机走动，它可以有效地利用已经有的信息处理来搜索那些有希望改善解质量的串。
类似于自然进化，遗传算法通过作用于染色体上的基因，寻找好的染色体来求解问题。
与自然界相似，遗传算法对待求解问题本身一无所知，它所需要的仅是对算法所产生的每个染色体进行评价，并基于适应度值来改变染色体，使适用性好的染色体比适应性差的染色体有更多的繁殖机会。
2.1 遗传算法的运行过程遗传算法模拟了自然选择和遗传中发生的复制、交叉和变异等现象，从任一初始种群(population)出发，通过随机选择、交叉和变异操作，产生一群更适应环境的个体，使群体进化到搜索空间中越来越好的区域，这样一代一代地不断繁衍进化，最后收敛到一群最适应环境的个体(Individual)，求得问题的最优解。
2.1.1 完整的遗传算法运算流程完整的遗传算法运算流程可以用图2.2来描述。
由图2.2可以看出，使用上述三种遗传算子(选择算子、交叉算子、变异算子) 的遗传算法的主要运算过程如下：(1) 编码：解空间中的解数据x，作为遗传算法的表现型形式。
从表现型到基因型的映射称为编码。
遗传算法在进行搜索之前先将解空间的解数据表示成遗传空间的基因型串结构数据，这些串结构数据的不同组合就构成了不同的点。
(2) 初始群体的生成：随机产生N个初始串结构数据，每个串结构数据称为一个个体，N 个个体构成了一个群体。
遗传算法以这N个串结构作为初始点开始迭代。
设置进化代数计数器t←0；设置最大进化代数T；随机生成M个个体作为初始群体P(0) 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七步：确定遗传算法的有关运行参数，即M,G,Pc,Pm等参数。
具体程序流程图见下图所示：
图1遗传算法流程图
四、优化过程
1.第一题
图2Rosen brock函数图像
图3遗传算法迭代寻优过程
程序运行结果如下：最优点函数取值
从上面的寻优结果可以看出，模拟退火算法解决了本例中遗传算法寻优陷入局部最优解的问题，最终找到了Schaffer Function函数的全局唯一最优解 。
问题二：寻优速度
基本的遗传算法中产生优良个体的主要手段是同过交叉重组，但这样并不能保证产生新个体的速度，即迭代寻优的速度很慢，考虑到为了保证较高的精度，本文的基因编码分别是十位、十二位与十三位，那么对于二元函数，染色体的长度就是二十、二十四与二十六，因此可以在交叉重组时，将较长的染色体分为若干段，并对每一小段进行两两配对交叉重组，这样相当于每个染色体在一次的迭代过程中参与了几次交叉重组，大大加快了新个体的产生速度。本文即将染色体分为了两段，进行交叉重组（程序见附录），加快了寻优速度。
第三题变量的取值范围是[-4,4]，本文采取的是十三位数的编码，那么精度为：
2)解码：假设某一个个体的编码是 ，那么对应的解码公式为：
2.个体适应度评价
1)当优化目标是求函数最大值，并且目标函数总取正值时，可以直接设定个体的适应度F(X)就等于相应的目标函数值f(X)，即：
其中 是函数最小值估计。
2)对于求目标函数最小值的优化问题，理论上只需简单地对其增加一个负号就可将其转化为求目标函数最大值的优化问题，即
其中 是函数的最大值估计。
3.复制、交叉、变异
1)比例算子：个体被选中并遗传到下一代的概率与个体的适应度成正比，本文采取的的赌轮盘选择法选，该方法较容易实现，易于编程。
2)交叉算子：交叉是遗传算法产生新个体的主要手段，通过交叉子代的基因值不同于父代，从而可以出现适应度更高的个体，本文采用的是单点交叉算子。
五、问题的发现与改进
1.问题一：局部最优解
从第三题的函数图像中可以看出，该函数有无限多个局部极大值点，只有一个全局最优点 ,此函数最导致峰周围有一圈脊，上面的取值均为0.990283。从上面的优化过程可以看出，当随机选定初始种群后，随着迭代次数的增加，种群最终都集中在了这一圈脊上，也就是寻优过程陷入了局部最优点，并没有找到函数的的最优点。对于遗传算法中的上述问题，我们采用的解决方案如下。
解决方法1：等值线法
初始种群的选取对函数能不能找到最优点有着重要的影响，本文通过分析函数的等值线缩小初始种群的随机产生范围，从而让种群朝着全局最优点进化。在Matlab下画出函数的等值线如下图：
图8目标函数的等值线图
从图中可以看出，以中心最优点为圆心，围绕着中心点分布着多条等值线，从中心的红色区域向外到蓝色区域，目标函数值先减小再增加最后又减小，所以本文以中间红色区域到蓝色区域中选取合适的等值线截面，并在该面上随机产生初始种群，这样可以有效防止迭代陷入局部最优解。改进后的寻优结果：
优化算法大作业
一、题目
本文利用遗传算法，依次完成下面三个目标函数的寻优：
1Generalized Rosen brock’s valley Function
2GeneralizedRastrigin'sFunction
3Schaffer’s Function
二、本文思路
遗传算法是模拟生物在自然环境下的遗传和进化过程而形成的一种自适应全局优化概率搜索方法，本文利用遗传算法分别对上述三种函数进行全局寻优，具体思路如下：
图10模拟推过算法实现过程
相关参数选择为：
初始温度Temperature=30
步长因子StepFactor=0.002
容差Tolerance=1e-7
马可夫链长度MarkovLength=1000
衰减参数DecayScale=0.95
程序运行结果为（程序见附录）：
最优点函数取值
寻优过程如下：
图11模拟退火算法的寻优过程
3)变异算子：变异也是产生新个体的一种方法，对于遗传算法中二进制编码符号串所表示的个体，若需要进行变异操作的某一基因座上的原有基因值为0，则变异操作将基因值变为1，反之，若原有的基因值为1，则变异操作将其变为0。
三、程序流程
对于一个需要进行优化的实际问题，一般可按下述步骤构造遗传算法：
第一步：确定决策变量及各种约束条件，即确定出个体的表现型X和问题的解空间；
图9改进后的遗传算法寻优过程
图6中的最终种群进化到了函数一圈“脊”上，但是这只是函数的局部最优点，而从图9可以清楚地看到，种群进化到最后都集中在了中心凸起点的附近，这也是函数的最大值点，可见改进后的遗传算法有效的解决了局部最优点的问题，顺利找到了函数的全局最优解。
解决方法2：模拟退火算法
模拟退火算法是模仿了自然界退火现象，利用了物理中固体物质的退火过程与一般问题的相似性，从某一初始温度开始，伴随着温度的不断下降，结合概率突跳特性在解空间中随机寻找全局最优解，它能有效的克服寻优陷入局部最小值的优化方法。其具体算法原理本文不详述，只给出采用模拟退火算法的实现过程如下图所示：
1.编码与解码
1)编码：假设某一参数的取值范围是[umin,umax]，我们用长度为l的二进制编码符号串来表示该参数，则它总共能够产生2l种不同的编码，编码的长度越长，对应的精度越高。
第一题变量的取值范围是[-2.048,2.048]，本文采取十位数的编码，那么精度为：
第二题变量的取值范围是[-5.12,5.12]，本文采取的是十二位数的编码，那么精度为：
第二步：建立优化模型，即确定出目标函数的类型及数学描述形式或量化方法；
第三步：确定表示可行解的染色体编码方法，即确定出个体的基因型x及遗传算法的搜索空间；
第四步：确定解码方法，即确定出由个体基因型x到个体表现型X的对应关系或转换方法；
第五步：确定个体适应度的ห้องสมุดไป่ตู้化评价方法，即确定出由目标函数值到个体适应度的转换规则；
2.第二题
图4：Rastrigin函数图像
图5：遗传算法迭代寻优过程
程序运行结果如下：最优点函数取值
3.第三题
图6Schaffer函数图像
图7遗传算法迭代寻优过程
程序运行结果如下：最优点函数取值
由仿真结果可知，随着进化过程的进行，群体中适应度较低的一些个体被逐渐淘汰掉，而适应度较高的一些个体会越来越多，并且它们都集中在所求问题的最优点附近，从而搜索到问题的最优解。