2-5-2在日常生活应用同步检测
第一单元 综合测试2024-2025学年七年级语文上册同步精品课堂(统编版2024)(解析版)

第一单元综合测试(时间:120分钟满分:120分)一、积累与运用(共20分)1.阅读下面一段文字,完成小题。
小山整把济南围了个圈儿,只有北边缺着点口儿。
这一圈小山在冬天特别可爱,好像是把济南放在一个小摇蓝里,它们全安静不动地低声地说:“你们放心吧,这儿准保暖和。
”真的,济南的人们在冬天是面上含笑的。
他们一看那些小山,心中便觉得有了着.落,有了依靠。
他们由天上看到山上,便不知不觉地想起:“明天也许就是春天了吧?这样的温暖,今天夜里山草也许就绿起来了吧?”就是这点huàn想不能一时实现,他们也并不着急,因为有这样cí善的冬天,干啥还希望别的呢!(1)给加点的字注音,或根据拼音写汉字。
(3分)huàn( ) 想着.( ) 落cí( )善(2)文中有错别字的一个词语是,它的正确写法是。
(2分)【答案】(1) 幻zhuó慈(2) 摇蓝摇篮【解析】(1)考查字音、字形。
幻想(huàn xiǎng):以个人或社会的理想和愿望为依据,对还没有实现的事物有所想象。
着落(zhuó luò):下落;来源。
慈善(cí shàn):指对人关怀而有同情心,仁慈而善良。
(2)考查字形。
摇蓝——摇篮。
“篮”是名词,篮子。
“蓝”是形容词,颜色。
2.(5分)根据提示默写填空。
(1)枯藤老树昏鸦,。
(马致远《天净沙·秋思》)(2),洪波涌起。
(曹操《观沧海》)(3)“ ”,刚起头儿,有的是工夫,有的是希望。
(朱自清《春》)(4)李白《闻王昌龄左迁龙标遥有此寄》中与张若虚的《春江花月夜》中的“此时相望不相闻,愿逐月华流照君”艺术境界相近的两句诗是:,。
【答案】小桥流水人家秋风萧瑟-年之计在于春我寄愁心与明月随君直到夜郎西【解析】考查默写句子的能力。
第(4)题是理解性默写,根据“愿逐月华流照君”可确定所填的诗句。
注意“萧瑟”“夜郎”的正确写法。
《第三单元 物质结构研究的意义》(同步训练)高中化学选择性必修2_苏教版_2024-2025学年

《第三单元物质结构研究的意义》同步训练(答案在后面)一、单项选择题(本大题有16小题,每小题3分,共48分)1、下列关于物质结构的研究意义叙述错误的是()A、有助于理解物质的物理性质B、揭示了物质之间相互作用的本质C、能够预测物质的化学性质D、推动了科技和工业的进步2、在物质结构研究中,以下哪个理论认为原子核是带正电的核心,电子在核外作椭圆轨迹运动?A. 氢原子模型B. 卢瑟福核式结构模型C. 波尔原子模型D. 电子云模型3、在物质结构的研究中,下列哪个实验装置可以用来验证电子的存在?A、光电效应实验装置B、α粒子散射实验装置C、原子光谱实验装置D、氢原子光谱实验装置4、下列关于原子轨道的说法正确的是:A. s轨道的形状为哑铃形B. p轨道的能量总是高于s轨道C. d轨道可以容纳最多6个电子D. f轨道开始出现在第四能级5、以下关于物质结构研究的意义,错误的是:A、有助于揭示物质的性质和变化规律B、为合成新材料提供理论基础C、有助于推动生物学、医学等领域的发展D、与日常生活中的烹饪无关6、下列关于物质结构研究的意义,说法正确的是()A、物质结构研究仅对科学家有意义,与普通学生无关。
B、物质结构研究是推动新材料、新药物研发的基础。
C、物质结构研究只是为了了解物质的存在形式,不涉及新技术或新应用。
D、物质结构研究对环境保护没有帮助。
7、以下哪个科学家提出了原子的.wrap model结构模型?A. 库仑B. 道尔顿C. 汤姆森D. 波尔8、在物质结构的研究中,下列哪个方法主要用于确定原子轨道的形状和方向?A. X射线衍射B. 磁共振波谱C. 质谱法D. 红外光谱9、下列关于分子间作用力的说法错误的是:A. 分子间作用力包括范德华力、氢键等B. 范德华力是一种较弱的作用力,主要影响物质的物理性质C. 氢键可以存在于分子内,也可以存在于不同分子之间D. 分子间作用力的强度总是大于化学键10、下列关于物质结构研究的意义的说法,错误的是()A. 物质结构的研究有助于揭示物质的性质和变化规律B. 物质结构的研究有助于开发新材料,推动科技进步C. 物质结构的研究有助于发展新的化学理论和实验方法D. 物质结构的研究与人类日常生活无关11、下列有关原子结构和元素周期律的说法中,正确的是()。
高中生物同步习题:2-5细胞中的无机物(必修1)
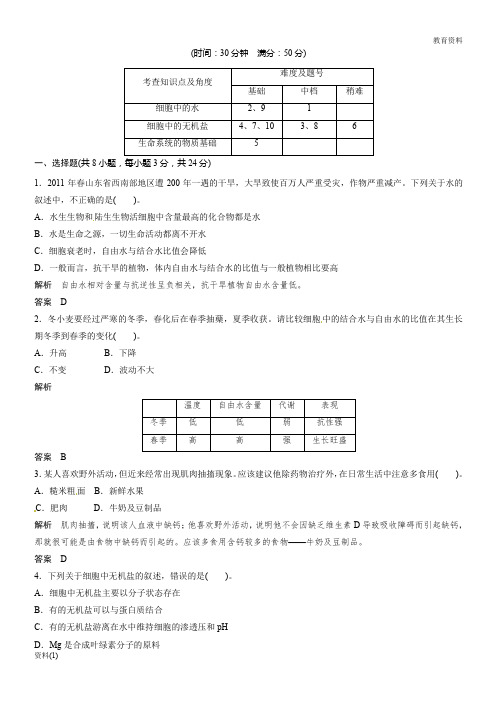
(时间:30分钟满分:50分)一、选择题(共8小题,每小题3分,共24分)1.2011年春山东省西南部地区遭200年一遇的干旱,大旱致使百万人严重受灾,作物严重减产。
下列关于水的叙述中,不正确的是()。
A.水生生物和陆生生物活细胞中含量最高的化合物都是水B.水是生命之源,一切生命活动都离不开水C.细胞衰老时,自由水与结合水比值会降低D.一般而言,抗干旱的植物,体内自由水与结合水的比值与一般植物相比要高解析自由水相对含量与抗逆性呈负相关,抗干旱植物自由水含量低。
答案 D2.冬小麦要经过严寒的冬季,春化后在春季抽蘖,夏季收获。
请比较细胞中的结合水与自由水的比值在其生长期冬季到春季的变化()。
A.升高B.下降C.不变D.波动不大解析答案 B3.某人喜欢野外活动,但近来经常出现肌肉抽搐现象。
应该建议他除药物治疗外,在日常生活中注意多食用()。
A.糙米粗面B.新鲜水果C.肥肉D.牛奶及豆制品解析肌肉抽搐,说明该人血液中缺钙;他喜欢野外活动,说明他不会因缺乏维生素D导致吸收障碍而引起缺钙,那就很可能是由食物中缺钙而引起的。
应该多食用含钙较多的食物——牛奶及豆制品。
答案 D4.下列关于细胞中无机盐的叙述,错误的是()。
A.细胞中无机盐主要以分子状态存在B.有的无机盐可以与蛋白质结合C.有的无机盐游离在水中维持细胞的渗透压和pHD.Mg是合成叶绿素分子的原料解析细胞中无机盐主要以离子状态存在。
答案 A5.下列说法错误的是(多选)()。
A.细胞是多种元素和化合物构成的生命系统B.细胞生命大厦的基本框架是各类有机化合物C.细胞中各类化合物的含量是稳定不变的,只有这样才能保障各项生理活动正常进行D.水和无机盐共同参与细胞生命活动的调节解析细胞中各种化合物的含量和比例处于不断变化中,但又保持相对稳定;水和无机盐可维持生命活动,但不可调节生命活动。
答案CD6.某植物培养液中含有甲、乙、丙3种离子,它们对植物的生长都有影响。
《5.4 信息时代离不开传感器》(同步训练)高中物理选择性必修第二册_沪教版

《5.4 信息时代离不开传感器》同步训练(答案在后面)一、单项选择题(本大题有7小题,每小题4分,共28分)1、传感器在信息时代的作用主要体现在以下哪个方面?A. 提高计算速度B. 采集和处理信息C. 增强设备自动化D. 提升能源利用效率2、以下哪项不属于常见的传感器类型?A. 光电传感器B. 温度传感器C. 声音传感器D. 磁场传感器3、传感器广泛应用于信息时代,下列选项中不属于传感器在智能交通系统中应用的是()A、使用红外传感器监测车辆速度B、利用摄像头识别车牌C、依靠超声波传感器检测前方障碍物D、采用温度传感器监控驾驶员体温4、在智能家居系统中,以下哪种传感器被用来检测环境中的湿度变化?A、温度传感器B、湿度传感器C、光照传感器D、压力传感器5、下列关于传感器的基本特性的描述,正确的是()。
A. 传感器的灵敏度越高越好。
B. 传感器的热稳定性越好,其性能越稳定。
C. 传感器的响应速度越快越好。
D. 传感器的测量范围越大越好。
6、以下哪一项不是电子传感器的基本组成部分()?A. 被测量部分B. 变换部分C. 输出信号处理部分D. 箱体连接部分7、下列哪项不是传感器应用的具体例子?()A、手机中的摄像头B、汽车的防撞雷达C、家用电器的定时器D、无人机的自动驾驶系统二、多项选择题(本大题有3小题,每小题6分,共18分)1、传感器的功能包括哪些?A、将物理量转换为易于测量的电信号B、对信号进行放大处理C、将电信号转换为其他形式的信号D、将电信号转换为数字信号2、以下哪些属于传感器的主要特点?A、灵敏度高B、响应速度快C、抗干扰能力强D、能长期稳定工作3、以下关于传感器的描述,正确的是()A、传感器是将非电学量转换为电学量的装置B、所有类型的传感器都能实现信号的放大C、温度传感器只能测量温度D、光传感器在光强变化时能产生相应的电信号三、非选择题(前4题每题10分,最后一题14分,总分54分)第一题题目假设某传感器系统广泛应用于智能交通系统中,该系统可以通过采集车流量信息来调整红绿灯的时长,以减少交通拥堵。
高中语文 5-2句子 手牵手 复句和关联词同步练习 新人教版选修(语言文字应用) 试题

5-2 句子“手牵手”——复句和关联词一、课内双基1.复句分为____(1)____和____(2)____两大类。
(1)又分为①并列关系,②____________,③____________,④____________,⑤____________;(2)又分为①因果关系,②____________,③____________,④____________,⑤____________,⑥____________。
【答案】(1)联合复句(2)主从复句(1)②选择关系③递进关系④连贯关系⑤解说关系(2)②目的关系③转折关系④条件关系⑤假设关系⑥让步关系2.下列说法不正确的一项是( )A.该用什么样的关联词,要依据上下文的意思来定,不能不顾上下文意强行添加。
句子即使添加上表示不同关系的关联词,也不能使句子的意思和关系改变。
B.有些复句不用加关联词,上下句之间的关系也是明确的。
C.“是……还是……”,“不是……就是……”,都是表示选择关系的关联词。
D.“为了”“以便”“以免”表示目的关系,“可是”“却”“不过”表示转折关系。
【答案】A.(句子添加上不同的关联词,句子的关系就改变了。
)3.将下面3个句子整合为一个单句。
(可调整语序、适当增删词语,不能改变原意)①王力先生认为,中国旧体诗以音步、平仄相间构成抑扬美。
②王力先生认为,中国旧体诗的音乐美分为抑扬美和回环美。
③王力先生认为,中国旧体诗以同韵字来来回回的重复构成了回环美。
______________________________________________________【答案】王力先生认为,中国旧体诗的音乐美分为以音步、平仄相间构成的抑扬美和以同韵字来来回回的重复构成的回环美。
(由三个短句可知①是谈“抑扬美”,③是谈“回环美”,②是谈“音乐美”。
把②确定为主干句,把①嵌入③中“抑扬美”前,把③嵌入①中“回环美”前,再增删个别词语,使句意顺畅即可。
第5-2 生活中的透镜(备好课)-2022-2023学年八年级物理上册同步精品课堂(人教版)

机自拍相比,利用“自拍神器”可以( )
A.减小物距
B.使像变大
C.增大取景范围 D.缩短景物到镜头的距离
【答案】 C 【详解】用手机拍照时,凸透镜成倒立、缩小的实像;凸透镜成实像时,物距越大,像距越小,像越小;与直接 拿手机自拍相比,利用自拍杆可以增大物距,减小像距,减小像的大小,则自拍杆的好处是增大取景范围,取得 更好的拍摄效果,故ABD不符合题意,C符合题意。
知识点 3 放大镜
生活中场用的放大镜也是一个凸透镜(短焦距),它是最常用 的化学仪器之一。 把放大镜放在物体跟眼睛之间,适当调整距离,当物距小于 放大镜焦距时,我们就能看清物体的细微之处。这时我们看 到的像是放大、正立的。
水滴形成半圆形,相当 鱼缸相当于一个凸透镜, 老花镜就是一个放大镜, 于放大镜,把物体放大。 看到的鱼比实际的大。 可以成正立、放大的虚像。
2.(2022·全国·八年级阶段练习)如图所示,小明同学用焦距较小的放大镜观察瓢虫,在保持眼睛和瓢虫的 距离不变的情况下,想让观察到的像更大一些,同时要保证观察到的像仍是清晰的,则他可以将放大镜适当 ______(选填“远离”或“靠近”)瓢虫。
【答案】远离 【详解】放大镜的成像原理:物距小于焦距时,成正立、放大的虚像;用焦距较小的放大镜观察瓢虫,在保持眼 睛和瓢虫的距离不变的情况下,要想让观察到的像更大一些,根据凸透镜成虚像的规律可知,应适当增大物距, 所以应将放大镜适当远离瓢虫。
新译林版三年级上册Unit 5 同步练习2(附答案)

新版-牛津译林版2021-2021学年小学英语三年级上册Unit 5 Look at me!同步练习B一、写出以下字母的左邻右舍。
1.在四线三格上写出以下字母的左邻右舍。
〔1〕________ K ________〔2〕________ Jj ________〔3〕________ Nn ________〔4〕________ Pp ________二、选择不同类的单词。
2.选择不同类的单词〔〕A. MikeB. TimC. Helen3.选择不同类的单词〔〕A. brotherB. motherC. Miss4.选择不同类的单词〔〕A.capB.redC.jacket5.选择不同类的单词〔〕A. heB. sheC. me6.选择不同类的单词〔〕A. greatB. lookC. nice三、上下文或所给情境,选择正确答案。
7.—Look at my shirt.—__________.A. It's greatB. Red8.想告诉波比,你的T恤衫是红色的,你可以说:A. My T-shirt is red.B. My T-shirt is great.9.当你晚上看见你的朋友,可以说:A. Good morning.B. Good evening.10.让刘涛猜猜你的T恤衫时什么颜色时,你说:A. Look at my T-shirt.B. What colour is my T-shirt?11.想让别人看你时,你会说:A. Look at me.B. This is me.12.字母P的小写有几笔?A. 1笔。
B. 2笔。
13.别人夸赞你的新衣服很漂亮时,你可以说:A. It's nice.B. Thank you.四、连词成句。
14.① at ② Lo ok ③ me (连词成句)15.① Look ② at ③ new ④ T-shirt ⑤ my (连词成句)16.① colour ② is ③ my ④ What ⑤ cap (连词成句)17.① red ② My ③ jacket ④ is (连词成句)18.① all ② They ③ great ④ look (连词成句)五、阅读理解19.阅读对话,选择最正确答案。
5.3.2 函数的极值与最大(小)值(第三课时 导数在函数有关问题及实际生活中的应用)同步检测

5.3.2 函数的极值与最大(小)值(第三课时)(同步检测)一、选择题1.设函数f (x)=13x -ln x ,则函数y =f (x)( ) A.在区间⎝ ⎛⎭⎪⎫1e ,1,(1,e)内均有零点 B.在区间⎝ ⎛⎭⎪⎫1e ,1,(1,e)内均无零点 C.在区间⎝ ⎛⎭⎪⎫1e ,1内有零点,在区间(1,e)内无零点 D.在区间⎝ ⎛⎭⎪⎫1e ,1内无零点,在区间(1,e)内有零点 2.根据以往经验,一超市中的某一商品每月的销售量y(单位:件)与销售价格x(单位:元/件)满足关系式y =60x -20+2(x -50)2,其中20<x <50.已知该商品的成本为20元/件,则该超市每月销售该商品所获得利润的最大值为( )A.8 600元B.8 060元C.6 870元D.4 060元3.若函数f(x)=e x (x 2-2x +1-a)-x 恒有2个零点,则a 的取值范围是( )A.⎝ ⎛⎭⎪⎫-1e ,+∞ B.(-∞,1) C.⎝ ⎛⎭⎪⎫0,1e D.⎝ ⎛⎭⎪⎫-∞,-1e 4.函数y =-x 4+x 2+2的图象大致为( )A B C D5.函数y =x 3e x (其中e 为自然对数的底数)的大致图象是( )A B C D6.函数f(x)=x 2ln x 2|x|的图象大致为( )A B C D7.方程x 3-6x 2+9x +m =0恰有三个不等的实数根,则实数m 的取值范围是( )A.(-∞,-4)B.(-4,0)C.(-∞,-4)∪(0,+∞)D.(0,+∞) 8.从长32 cm ,宽20 cm 的矩形薄铁板的四角剪去相等的正方形,做一个无盖的箱子,若使箱子的容积最大,则剪去的正方形边长为( )A.4 cmB.2 cmC.1 cmD.3 cm9.(多选)设x 3+ax +b =0(a ,b ∈R),下列条件中,使得该三次方程仅有一个实数根的是( )A.a =-3,b =2B.a =-3,b =-3C.a =-3,b >2D.a =1,b =2二、填空题10.海轮每小时使用的燃料费与它的航行速度的立方成正比,已知某海轮的最大航速为30 n mile/h ,当速度为10 n mile/h 时,它的燃料费是每小时25元,其余费用(无论速度如何)都是每小时400元.如果甲、乙两地相距800 n mile ,则要使该海轮从甲地航行到乙地的总费用最低,它的航速应为________n mile/h .11.某厂生产x 件某种产品的总成本为c(x)=⎝ ⎛⎭⎪⎫1 200+275x 3(万元),已知产品单价的平方与产品件数x 成反比,生产100件这样的产品单价为50万元,则产量定为________件时,总利润最大.12.某产品的销售收入y 1(万元)关于产量x(千台)的函数关系式为y 1=17x 2,生产成本y 2(万元)关于产量x(千台)的函数关系式为y 2=2x 3-x 2,已知x >0,为使利润最大,应生产该产品______千台.13.已知函数f(x)=xe 2x -1,则函数f(x)的极小值为________,零点有________个.三、解答题14.若方程a x =x(a >0,a ≠1)有两个不等实数根,求实数a 的取值范围.15.某单位在甲地成立了一家医疗器械公司吸纳附近村民就工,已知该公司生产某种型号医疗器械的月固定成本为20万元,每生产1千件需另投入5.4万元,设该公司一月内生产该型号医疗器械x 千件且能全部销售完,每千件的销售收入为g(x)万元,已知g(x)=⎩⎪⎨⎪⎧ 11.8-130x 2(0<x ≤10),154x -2 0003x 2(x >10).(1)请写出月利润y(万元)关于月产量x(千件)的函数解析式.(2)月产量为多少千件时,该公司在这一型号医疗器械的生产中所获月利润最大?并求出最大月利润(精确到0.1万元).16.已知A,B两地相距200千米,一只船从A地逆水航行到B地,水速为8千米/时,船在静水中的航行速度为v千米/时(8<v≤v0).若船每小时航行所需的燃料费与其在静水中的航行速度的平方成正比,当v=12千米/时时,船每小时航行所需的燃料费为720元.为了使全程燃料费最省,船在静水中的航行速度v应为多少?参考答案及解析:一、选择题1.D 解析:当x ∈⎝ ⎛⎭⎪⎫1e ,e 时,函数图象连续不断,且f ′(x)=13-1x =x -33x <0,所以函数f(x)在⎝ ⎛⎭⎪⎫1e ,e 上单调递减.又因为f ⎝ ⎛⎭⎪⎫1e =13e +1>0,f(1)=13>0,f(e)=13e -1<0,所以函数f (x)有唯一的零点在区间(1,e)内.2.B 解析:设超市每月销售该商品所获得的利润为f(x)元,则f(x)=(x -20)⎣⎢⎡⎦⎥⎤60x -20+2(x -50)2=60+2(x -20)·(x -50)2,20<x <50,f ′(x)=2[(x -50)2+2(x -50)(x -20)]=6(x -30)(x -50), 令f ′(x)>0, 得20<x <30,则f(x)在(20,30)上单调递增;令f ′(x)<0,得30<x <50,则f(x)在(30,50)上单调递减.所以f(x)的最大值为f(30)=8 060.故选B .3.A4.D 解析:当x =0时,y =2,排除A ,B ;y′=-4x 3+2x =-2x(2x 2-1),由f ′(x)>0得2x(2x 2-1)<0,得x <-22或0<x <22,此时函数单调递增,排除C .故选D . 5.B 解析:由函数y =x 3ex 可知,当x =0时,y =0,排除C ;当x <0时,y <0,排除A ;当x →+∞时,y →0.故选B .6.B7.B8.A 解析:设剪去的正方形的边长为x cm ,则做成的无盖的箱子的底是长为(32-2x)cm ,宽为(20-2x)cm 的矩形,箱子的高为x cm ,所以箱子的容积,V =(32-2x)(20-2x)·x =4(x 3-26x 2+160x),V′=12(x -4)⎝ ⎛⎭⎪⎫x -403, 当0<x<10时,V′=0只有一个解x =4,在x =4附近,V′是左正右负,V 在x =4处取得极大值即为最大值,所以若使箱子的容积最大,则剪去的正方形边长为4 cm.9.BCD二、填空题10.答案:20 解析:由题意设燃料费y 1与航速v 间满足y 1=a v 3(0≤v ≤30),又∵25=a·103,∴a =140.设从甲地到乙地海轮的航速为v n mile/h ,总费用为y 元, 则y =a v 3×800v +800v ×400=20v 2+320 000v .由y′=40v -320 000v 2=0,得v =20<30. 当0<v <20时,y′<0;当20<v <30时,y′>0,∴当v =20时,y 最小.11.答案:2512.答案:6 解析:由题意,利润y =y 1-y 2=17x 2-(2x 3-x 2)=18x 2-2x 3(x >0). y′=36x -6x 2,由y′=36x -6x 2=6x(6-x)=0,得x =6(x =0舍去),当x ∈(0,6)时,y′>0,当x ∈(6,+∞)时,y′<0,∴函数在(0,6)上单调递增,在(6,+∞)上单调递减.则当x =6时,y 有最大值.13.答案:-12e-1,1 三、解答题14.解:由a x =x 知x >0,故x·ln a -ln x =0⇒ln a =ln x x, 令f(x)=ln x x (x >0),则f ′(x)=1-ln x x 2. 当x ∈(0,e)时,f ′(x)>0,f(x)单调递增;当x ∈(e ,+∞)时,f ′(x)<0,f(x)单调递减,故当x =e 时,f(x)取得最大值f(e)=1e ,即ln a <1e,即a <1e e .画出函数y =a x (a >0,a ≠1)与y =x 的图象(图略),结合图象可知,若方程a x =x(a >0,a ≠1)有两个不等实数根,则a >1.综上可知,实数a 的取值范围为11e (,e )15.解:(1)当0<x ≤10时,y =x ⎝ ⎛⎭⎪⎫11.8-130x 2-20-5.4x =6.4x -130x 3-20, 当x >10时,y =⎝ ⎛⎭⎪⎫154x -2 0003x 2x -20-5.4x =134-2⎝ ⎛⎭⎪⎫1 0003x +2.7x , ∴y =⎩⎪⎨⎪⎧ 6.4x -130x 3-20,0<x ≤10,134-2⎝ ⎛⎭⎪⎫1 0003x +2.7x ,x >10. (2)①当0<x ≤10时,y′=6.4-110x 2, 令y′=0可得x =8,x ∈(0,8)时,y′>0,x ∈(8,10]时,y′<0,∴x =8时,y max =21215≈14.1(万元). ②当x >10时,y =134-2⎝ ⎛⎭⎪⎫1 0003x +2.7x ≤134-120=14(万元)(当且仅当x =1009时取等号), 综合①②知:当x =8时,y 取最大值14.1,故当月产量为8千件时,该公司在这一型号医疗器械的生产中所获月利润最大,最大月利润为14.1万元.16.解:设船每小时航行所需的燃料费为y 1元,比例系数为k(k >0),则y 1=k v 2.∵当v =12时,y 1=720,∴720=k·122,得k =5,则y 1=5v 2.设全程燃料费为y 元,由题意,得y =y 1·200v -8=1 000v 2v -8,∴y′=2 000v(v-8)-1 000v2(v-8)2=1 000v2-16 000v(v-8)2.令y′=0,解得v=0(舍去)或v=16.若v0≥16,当v∈(8,16)时,y′<0,y单调递减;当v∈(16,v0]时,y′>0,y单调递增.故当v=16千米/时时,y取得极小值,也是最小值,此时全程燃料费最省.若v0<16,则v∈(8,v0],且y′<0,y在(8,v0]上单调递减.故当v=v0时,y取得最小值,此时全程燃料费最省.综上可得,若v0≥16,则当v=16千米/时时,全程燃料费最省,为32 000元;若v0<16,则当v=v0时,全程燃料费最省,为1 000v20v0-8元.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-5-2在日常生活应用同步检测基础巩固强化一、选择题1.若三角形的三内角成等差数列,对应的三边成等比数列,则三内角的公差为( )A .0°B .15°C .30°D .45°2.一个直角三角形三边的长成等比数列,则( ) A .三边边长之比为3:4:5 B .三边边长之比为1: 3 :3 C .较小锐角的正弦为5-12 D .较大锐角的正弦为5-123.公差不为零的等差数列的第二、第三、第六项构成等比数列,则公比为( )A .1B .2C .3D .44.互不相等的正数a ,b ,c ,d 成等比数列,那么bc 与a +d2的大小关系是( )A.bc >a +d2 B.bc =a +d2 C.bc <a +d2D.bc 与a +d2的大小关系不能确定5.△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边,如果a 、b 、c 成等差数列,∠B =30°,△ABC 的面积为0.5,那么b 为( )A .1+ 3B .3+ 3C.3+33 D .2+ 36.等比数列{a n }的前n 项和为S n ,且4a 1,2a 2,a 3成等差数列.若a 1=1,则S 4=( )A .7B .8C .15D .16二、填空题7.已知a ,b ,c 成等比数列,a ,x ,b 成等差数列,b ,y ,c 也成等差数列,则a x +cy 的值为__________.8.a n =sin n π6,则a 1+a 2+a 3+…+a 2010=________.9.(2010~2011·内蒙古赤峰市田家炳中学高二期中)已知数列{a n }的通项公式a n =log 2n +1n +2(n ∈N *),其前n 项之和为S n ,则使S n <-5成立的正整数n 的最小值是________.三、解答题10.数列{a n }共有k 项(k 为定值),它的前n 项和S n =2n 2+n (n ≤k ,n ∈N *),现从k 项中抽取某一项(不抽首末两项),余下的k -1项的平均数为79.(1)求数列{a n }的通项;(2)求数列的项数,并求抽取的是第几项.能力拓展提升一、选择题11.一个项数是偶数的等比数列,它的偶数项和是奇数项和的2倍,又它的首项为1,且中间两项的和为24,则此等比数列的项数为()A.6 B.8C.10 D.1212.(2011·宁夏银川一中高二期中)△ABC的内角A、B、C的对边分别为a、b、c.若a、b、c成等比数列,且c=2a,则cos B=()A.14 B.34C.24 D.2313.在数列{a n}中,a1,a2,a3成等差数列,a2,a3,a4成等比数列,a3,a4,a5的倒数成等差数列,则a1,a3,a5()A.成等差数列B.成等比数列C.倒数成等差数列D.不确定14.在如下表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,则a+b+c的值为()A.1C.3 D.9 8二、填空题15.(2009·江苏)设{a n}是公比为q的等比数列,|q|>1,令b n=a n+1(n=1,2,…),若数列{b n}中有连续四项在集合{-53,-23,19,37,82}中,则q=________.16.(2011·浙江宁波八校联考)在如图的表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列成等比数列,且从上到下所有公比相等,则a +b +c 的值为________.三、解答题17.(2009·陕西)已知数列{a n }满足,a 1=1,a 2=2,a n +1=a n +a n -12,n ∈N *. (1)令b n =a n +1-a n ,证明:{b n }是等比数列; (2)求{a n }的通项公式.18.(2012·福建文,17)在等差数列{a n }和等比数列{b n }中,a 1=b 1=1,b 4=8,{a n }的前10项和S 10=55.(1)求a n 和b n ;(2)现分别从{a n }和{b n }的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.2-5-2在日常生活应用同步检测详解答案 1[答案] A[解析] 取特例正三角形两条件都满足排除B 、C 、D ,∴选A. 2[答案] C[解析] 设三边为a ,b ,c (0<a <b <c ),则⎩⎨⎧b 2=ac a 2+b 2=c2 , ∴a 2+ac -c 2=0,∴ac =5-12.3[答案] C[解析] 由题设a 23=a 2·a 6 ∴(a 1+2d )2=(a 1+d )(a 1+5d ) ∴d =-2a 1,∴a n =(3-2n )a 1. 公比q =a 3a 2=-3a 1-a 1=3.4[答案] C[解析] ∵bc =ad ,∴bc =ad , ∵a +d 2-bc =a +d 2-ad =(a -d )22>0.[点评] 请学过下一章后,尝试用基本不等式解决. 5[答案] C[解析] 12ac sin B =12,∴ac =2, 又2b =a +c ,∴a 2+c 2=4b 2-4, 由余弦定理b 2=a 2+c 2-2ac cos B 得,b =3+33.6[答案] C[解析] 设等比数列{a n }的首项为a 1,公比为q ; 由4a 1,2a 2,a 3成等差数列得,4a 2=4a 1+a 3, ∴4a 1q =4a 1+a 1q 2,∵a 1=1,∴q 2-4q +4=0,∴q =2, ∴S 4=a 1(1-q 4)1-q =1×(1-24)1-2=15.7[答案] 2[解析] b 2=ac,2x =a +b,2y =b +c , ∴a x +c y =2a a +b +2cb +c=2ab +4b 2+2bc (a +b )(b +c )=2b (a +2b +c )b (a +2b +c )=2.8[答案] 2+ 3[解析] a n =sin n π6的周期为12, 且a 1+a 2+…+a 12=0.∴a 1+a 2+…+a 2010=a 1+a 2+a 3+a 4+a 5+a 6 =2+ 3. 9[答案] 63[解析] S n =a 1+a 2+…+a n =log 223+log 234+…+log 2n +1n +2=log 2(23×34×…+n +1n +2)=log 22n +2<-5,∴2n +2<132,∴n >62, ∵n ∈Z ,∴n 的最小值为63.10[解析] (1)当n =1时,a 1=S 1=3; 当n ≥2时,a n =S n -S n -1=4n -1. ∵当n =1时也适合, ∴a n =4n -1(n ∈N *).(2)设抽取的为第t 项,则1<t <k . 由题意知S k =79×(k -1)+a t , 即2k 2+k =79k -79+4t -1∴2t =k 2-39k +40,∴2<k 2-39k +40<2k .则38<k <40,∵k ∈N *.∴k =39,t =20. 故抽取的为第20项,共有39项. 11[答案] B[解析] 设项数为2n ,则由已知得a 2+a 4+a 6+…+a 2na 1+a 3+a 5+…+a 2n -1=q =2,又a 1=1,得a n =2n -1,其中间两项和为a n+a n +1=2n -1+2n =24,可解得n =4,故得项数2n =8,应选B.12[答案] B[解析] ∵a 、b 、c 成等比数列,∴b 2=ac ,又∵c =2a ,∴b 2=2a 2,∴cos B =a 2+c 2-b 22ac =a 2+4a 2-2a 22a ×2a=34.[点评] 在知识的交汇处命题是高考命题的一种基本形式.本题融数列与三角函数于一体,集中考查正弦定理、余弦定理、等比数列等基础知识.体现了数列、三角函数等内容是高考中的热点问题.13[答案] B [解析] a 23=a 2·a 4, (1) 2a 4=1a 3+1a 5.(2)∵2a 2=a 1+a 3,∴a 2=a 1+a 32, 代入(1)得,a 4=2a 23a 1+a 3,代入(2)得,a 1+a 3a 23=1a 3+1a 5,∴a 23=a 1a 5. 14[答案] D[解析] 按题意要求,每一横行成等差数列,每一纵列成等比数列填表如图,故a =12,b =38,c =14,则a +b +c =98.∴选D.15[答案] -32[解析] 设等比数列{a n }的首项为a 1, 由题意知,a n =a 1q n -1,|q |>1, 由b n =a n +1,∴b n -1=a 1q n -1.∴{b n -1}是等比数列,{b n -1}有连续四项在集合{-54,-24,18,36,81}中,经分析可知是-24,36,-54,81,∴公比q =-32. 16[答案] 22[解析] 由横行成等差数列知,6下边为3,从纵列成等比数列及所有公比相等知,公比q =2,∴b =2×2=4由横行等差知c 下边为4+62=5,故c =5×2=10,由纵列公比为2知a =1×23=8,∴a +b +c =22.17[解析] 解:(1)b 1=a 2-a 1=1, 当n ≥2时,b n =a n +1-a n =a n -1+a n2-a n =-12(a n -a n -1)=-12b n -1.∴{b n }是以1为首项,-12为公比的等比数列; (2)由(1)知b n =a n +1-a n =⎝ ⎛⎭⎪⎫-12n -1,当n ≥2时,a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=1+1+⎝ ⎛⎭⎪⎫-12+…+⎝ ⎛⎭⎪⎫-12n -2 =1+1-⎝ ⎛⎭⎪⎫-12n -11-⎝ ⎛⎭⎪⎫-12=1+23⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫-12n -1=53-23⎝ ⎛⎭⎪⎫-12n -1,当n =1时,53-23⎝ ⎛⎭⎪⎫-121-1=1=a 1,∴a n =53-23⎝ ⎛⎭⎪⎫-12n -1(n ∈N *).18[解析] (1)设{a n }的公差为d ,{b n }的公比为q .依题意得 S 10=10+10×92d =55,b 4=q 3=8, 解得d =1,q =2, 所以a n =n ,b n =2n -1.(2)分别从{a n }和{b n }的前3项中各随机抽取一项,得到的基本事件有9个: (1,1),(1,2),(1,4),(2,1),(2,2),(2,4),(3,1),(3,2),(3,4). 符合题意的基本事件有2个:(1,1),(2,2). 故所求的概率P =29.[点评] 在等差数列和等比数列中,已知具体项或某几项的和等条件时,常选用“基本量法”来求解,即把已知条件均用数列的首项、公差或首项、公比来表示;概率中的古典概型关键是能正确列举出所有的基本事件和满足条件的基本事件.。
