电力系统分析基础(第四章)n
《电力系统分析》第四章

一、节点导纳矩阵的节点电压方程
在电路理论中,已经讲过了节点导纳矩阵的节点电压 方程 对于n个节点的网络其展开为
上式中, U B是节点电压的 I B 是节点注入电流的列向量。 列向量。YB是一个n×n阶节点导纳矩阵。
以网络节点导纳矩阵表示的节点电压方程在进行潮流计 算时,可以减少计算机的内存,提高运算速度,因此是最为 常用的.
二、节点阻抗矩阵的节点电压方程 1 1 由 I B YBU B 的两边都左乘YB ,可得 YB I B U B , 而 YB1 Z B,则节点电压方程为
ZB IB UB
第二节
等值变压器模型及其应用
一、变压器为非标准变比时的修正
无论采用有名制或标么制,凡涉及多电压级网络的计 算,在精确计算时都必须将网络中所有参数和变量按市价 变比归算到同一电压等级。实际上,在电力系统计算中总 是有些变压器的实际变比不等于变压器两侧所选电压基准 值之比,也就是不等于标准变比,而且变压器的变比在运 行中是可以改变的。这将使每改变一次变比都要从新计算 元件参数,很不方便。下面将介绍另一种可等值地体现变 压器电压变换功能的模型。
i
Zij
j
N
i
i
i
N j
Zij
N
j
Zij
N
j
Zij
Z ij
(a)
(b)
(c)
(d)
图三 电力网络接线变更示意图
(1)从原有网络中引出一条新的支路,图三(a)。同 时增加一个新的节点。 新增加节点的对角元素为:
新增加非对角元素为:
原有节点的自导纳增量为:
(2)在原有节点 i 和 j 间增加一条支路,图三(b)。此 情况下节点导纳矩阵的阶数不变。有关元素修改如下:
电力系统基础第四章习题

()第四章 电力系统的正常运行与控制填空题无功负荷指的是 _____________ 。
无功损耗是指电网中 _________ 和 ____________ 产生无功损耗 。
电力系统稳态运行中,用电设备所取用的功率随电压变化的关系称为 ________________________ 。
电力系统中无功电源有 _________ 、 ____________ 和 __________ 。
电 力 系 统 的调压措施 电力线路等值电路并联支路的电纳无功功率又称为________ 是唯一即可以提供有功功率,又可以提供无功功率的设备 我国电力系统采用的标准频率是_________ ,允许偏差为 ______________ 0 电力系统中有功功率的最优分配包括____________ 和 ____________________ 发电设备单位时间内消耗的能源与发出的有功功率的关系称为 _______________ 电力系统的频率调整分 ___________ 、 ____________ 、 ____________ 0 系统频率的一次调整是由 __________________ 完成。
系统频率的二次调整是由 __________________ 完成。
电力系统中的有功功率电源是 _______________________________________ , 无功功率电源 判断题电力系统稳态运行中,随着电压的升高,用电设备所取的无功功率比有功功率快速增加。
( ) 利用发电机即可满足电力系统的电压调整要求。
减小系统的负荷无功功率有利于电压的调整。
无功功率不做功,故不用考虑。
架空线路短线路只消耗有功功率。
电力网中发电机只提供有功功率,变压器提供无功功率。
无功平衡和电压调整可以按电压等级分片就地解决。
电力系统把频率的调整转化为功率的调整。
频率的一次调整是由调频器完成的。
丰水季节通常把大型水电厂作为电网功率调节的主要对象 丰水季节通常把火电厂作为电网功率调节的主要对象。
《电力系统分析》第四章 第三节

Z kk 可当作把节点k作为一端,参考节
点(地)为另一端,从这两端点看进去 的无源网络的等值阻抗。
k
Z kk
0
Z
Z11 Z = 21 Z n1
Z12 Z 22 Z n2
Z1n Z 2n Z nn
电力网络一般是连贯的,网络的各部分之间存在着电或磁的联系。 单独在节点k注入电流,总会在任一节点上出现电压。 因此,阻抗矩阵没有零元素,是一个满矩阵。 如何求取阻抗矩阵? 方法一:支路追加法 方法二:从节点导纳矩阵求取逆阵
2、追加连支
k
z km
网络的节点阻抗矩阵阶次不变。 连支的接入将改变网络中的电
m
压分布。因此,对原有矩阵各元素 都要作相应的修改。
Z11 Z k1 Z m1 Z p1
Z1k Z kk Z mk Z pk
Z1m Z km Z mm Z pm
Z1′p ′ Z kp ′ Z mp Z′ pp
Z ij
? Z′
′ = Z ij − Z ij Z kk + Z mm − 2 Z km + z km
( Z ik − Z im )( Z kj − Z mj )
k
z km
m
k
′ = Z ij − Z ij Z kk + Z mm − 2 Z km + z km
Z1′p ′ Z kp ′ Z mp Z′ pp
Z ij
?
′ Z ij
Z11 Z k1 Z m1 Z p1
Z1k Z kk Z mk Z pk
电力系统分析第四章(黑板)

基本要求: 本章着重介绍运用电子计算机计算电力系统潮流分 布的方法。它是复杂电力系统稳态和暂态运行的基础。 运用计算机计算的步骤,一般包括:建立数学模型;确定解
算方法;制定框图和编制程序;上机调试,运行计算程序;分析计算
结果。本章着重前两步。
1
本章知识点:
电力网络的数学模型 节点导纳矩阵 节点导纳矩阵各元素的物理意义,如何由 节点导纳矩阵形成节点阻抗矩阵,节点阻抗矩阵各元素 的物理意义,导纳矩阵与阻抗矩阵的对称性和稀疏性; 功率方程和变量及节点分类 高斯-赛德尔法潮流原理 非线性节点电压方程的高斯-赛 德尔迭代形式,PV节点向PQ节点转化的原因和方法; 牛顿-拉夫逊迭代法原理 牛顿-拉夫逊迭代法直角坐标 形式的功率误差方程和电压误差方程,牛顿-拉夫逊迭代法极
Y U Y11U I 1 12 2 1 Y U Y U Y U 0 Y21U 1 22 2 23 3 24 4 Y U Y U 0 Y32U 2 33 3 34 4 Y U Y U I Y U
42 2 43 3 44 4
I ( i 1,2, , n) YikU k i I i Yik U
k U j 0, j k
12
节点电压方程
1、节点导纳方程
Y 矩阵元素的物理意义
自导纳
if i k I k Ykk U 0, j k ) k (U j Ykk yk 0 y kj
9
节点电压方程 1、节点导纳方程
n 个独立节点的网络,n 个节点方程
Y11 Y12 Y Y 21 22 Yn1 Yn 2
I Y1n U 1 1 Y2 n U 2 I 2 Ynn U n In
电力系统分析第4-6章课后习题参考答案

4-1.选择填空1.电力系统稳态分析中所用阻抗指的是( A )A.一相等值阻抗B.两相阻抗C.三相阻抗D.四相阻抗2.节点导纳矩阵为方阵,其阶数等于( B )A.网络中所有节点数B.网络中除参考节点以外的所有节点数C.网络中所有节点数加1 D.网络中所有节点数减23.牛顿-拉夫逊潮流计算的功率方程是由下列什么方程推导得到的(C)A.回路电流方程 B.支路电流方程C.节点电压方程D.以上都不是4.对PQ节点来说,其待求量是( A )A.电压的大小U和电压的相位角δ B. 有功功率P和无功功率QC. 有功功率P和电压的大小UD. 无功率Q和节点电压的相位角δ5.对PV节点来说,其待求量是(D)A.电压的大小U和电压的相位角δ B. 有功功率P和无功功率QC. 有功功率P和电压的大小UD. 无功率Q和节点电压的相位角δ6)PQ节点是指( B )已知的节点。
A.电压的大小U和电压的相位角δ B. 有功功率P和无功功率QC. 有功功率P和电压的大小UD. 无功率Q和节点电压的相位角δ7.以下说法不正确的是(B)A.功率方程是非线性的。
B.雅可比矩阵是对称的。
C.导纳矩阵是对称的。
D.功率方程是从节点电压方程中推导得到的。
8.潮流计算的P—Q分解法是在哪一类方法的基础上派生而来的(C)A.阻抗法B.直角坐标形式的牛顿—拉夫逊法C.极坐标形式的牛顿—拉夫逊法D.以上都不是9.如果已知某一电力网有6个独立节点,其中1个平衡节点,3个PQ节点,2个PV节点,则以下说法不正确的是( D )。
A.其导纳矩阵为6阶。
B.其B'矩阵为5阶。
C.其B''矩阵为3阶。
D.其雅可比矩阵为6阶。
10.P—Q分解法和牛顿—拉夫逊法进行潮流计算时,当收敛到同样的精度时,二者的迭代次数是(A)A.P—Q分解法多于牛顿—拉夫逊法B.牛顿—拉夫逊法多于P—Q分解法C.无法比较D.两种方法一样4-2.填空1.用牛顿-拉夫逊法进行潮流计算是指(用牛顿-拉夫逊迭代法求解电力网的非线性功率方程组)。
电力系统分析-第四章教程
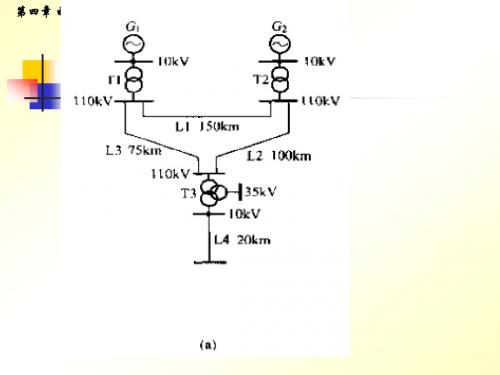
第四章 电力系统潮流的计算机算法
PV节点向PQ节点的转化※
背景:
对节点注入功率约束不满足:威胁机组安全 对节点电压大小约束不满足:影响电能质量 对电压相位角约束不满足:危机系统稳定性
第四章 电力系统潮流的计算机算法
PV节点向PQ节点的转化
指迭代过程中,经过校验发现,为保持给定的电 压大小,某一个或几个PV节点所注入的无功功率 已经越出了给定的限额,为了保持机组的安全运 行,不得已取Qi=Qimax;Qi=Qimin。显然,这样 做不能维持给定的电压大小,只能任凭相应节点 电压大小偏移给定值,这样处理实际上就在迭代 过程中允许某些PV节点转化为PQ节点。
第四章 电力系统潮流的计算机算法
二、用节点阻抗矩阵表示的网络方程式
当节点导纳矩阵可逆时
由 I B YBU B 的两边都左乘 YB1 ,可 得 ,而 YB1 I B U B
YB1 Z B 则节点电压方程为
,
ZB IB UB
阻抗矩阵
第四章 电力系统潮流的计算机算法
第二节 潮流计算的节点功率方程和节点分类
第四章 电力系统潮流的计算机算法
二、功率方程
等值电源功率 G 1
~ ~ SG1 PG1 jQG1 SG 2 PG 2 jQG 2
U 1 U 2
G 2
~ SL1 PL1 jQL1
~ SL2 PL2 jQL2
等值负荷功率 (a)简单系统
第四章 电力系统潮流的计算机算法
因此,潮流计算可以归结为求解一组非线性方程组,并 使其解答满足一定的约束条件。
第四章 电力系统潮流的计算机算法
第四章 电力系统潮流的计算机算法
国网考试之电力系统分析:第四章复习题---3页

第四章复习题一、选择题1、n节点电力系统中,PQ节点的数目为m,平衡节点的数目应为()。
A.n-m-1 B.n-m-2 C.1 D.可以为02、在电力系统潮流计算中,PV节点的待求量是()A.Q、δB.P、Q C.V、δD.P、V3、计算机解潮流方程时,经常采用的方法是()A.递推法B.迭代法C.回归法D.替代法4、潮流计算中的P-Q分解法是在哪一类方法的基础上简化来的()A.阻抗法B.直角坐标形式的牛顿——拉夫逊法C.高斯——赛德尔法D.极坐标形式的牛顿——拉夫逊法5、电力系统潮流计算时某物理量的单位为Mvar,则该量是( )A.有功功率B.无功功率C.视在功率D.有功电量6、在电力系统中平衡节点的数量( )A.必有一个B.是大量的C.少量或没有D.数量最多7、一般潮流分析中将节点分为几类( )A.四类B.三类C.二类D.一类8、潮流计算时,下列节点中,哪一类节点一般只有一个,且必需有一个( )A.PQ节点B.PU节点C.平衡节点D.QU节点9、用牛顿—拉夫逊法进行潮流计算时,线性修正方程求解的是()A.线路的功率B.节点的注入功率C.节点的电压值D.节点电压的修正量10、节点导纳矩阵为方阵,其阶数等于()A.网络中所有节点数B.网络中除参考节点以外的节点数C.网络中所有节点数加1 D.网络中所有节点数加211、潮流方程是( )A.代数方程B.微分方程C.代数方程组D.微分方程组12、计算潮流时牛顿—拉夫逊法与高斯—塞德尔法相比的主要优点是()A.对初值要求低B.占用内存少C.收敛性好,计算速度快D.复杂13、解潮流方程的方法是( )A.解析法B.数值方法C.手算法D.对数法二、判断题1、用牛顿—拉夫逊法进行潮流计算时,线性修正方程求解的是节点的电压值。
()2、同样的迭代次数,牛顿-拉夫逊法比PQ分解法精度高。
()三、填空题1、在计算机算法中,若PV节点的无功功率越限,则该节点应________________________。
电力系统暂态分析(第四章习题答案)

za + zb + zc Z2 Z1
Z1 za + zb + zc
Z2
Z2 Z1 za + zb + zc
其中: Z1 = za + a2zb + azc; Z2 = za + azb + a2zc
1) 当 za = zb = zc 时 , 非 对 角 元 素 Z1 = za 1 + a2 +
a = Z2 = 0,则三序分量可以解藕。
33 13 (6 + 6 ) − j(6 + 6 )
=
33
13
6 − 6 + j(− 6 + 6 )
1 j3
②各序分量解藕单独作用分别求解序电流
正序电流:
I1
=
E1 j2
=
(−
1 12
−
3 12)
−
3 j(12
+
3 12)
负序电流:
I2
=
E2 j2
=
(−
1 12
+
3 12)
−
3 j(12
−
3 12)
零序电压标幺值:
10
U(0) = 220/
= 0.0797 3
按等值电路可求得各側电流:
0.0787 I1 = −0.12+(−0.014)//0.244) = 0.748
0.244 I2 = I1 × ( − 0.014 + 0.244) = 0.794
I3 = I1 − I2 = −0.0455 电流有名值:
障时的正序、负序、零序等效电路; 解:正序: 负序:
零序:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Y12 = Y 21 = y 1 2 Y 23 = Y 32 = y 2 3 Y12 = Y 31 = y 1 3
y30
注:Y距阵的维数(n-1)
第一节 电力网的数学模型
2、导纳矩阵的形成
I. 1 Y11 . I 2 = Y 21 . In Yn 1 Y12 Y 22 Yn 2
•导纳矩阵的阶数不变
• Yii = Yjj = yij • Yij = Yji = - yij
i j
yij
第一节 电力网的数学模型
3) 切除一条支路
•相当于增加一导纳为( -yij )的支路
•导纳矩阵的阶数不变 • Yii = Yjj = - yij • Yij = Yji = yij 4) 修改一条支路的导纳值( yij 改变为yij ')
. Y1n U1 . Y 2n U 2 . Ynn Un
I= YU
节点导纳距阵的特点: 节点i: 加单位电压 U = 1
i
.
.
自 导 纳
. I 互 Y = . Yij = 导 纳 U ( U = 0, j i )
i j
- yij
•导纳矩阵的阶数不变
• Yii = Yjj = yij ' - yij • Yij = Yji = yij - yij '
i j
-yij
yij '
第一节 电力网的数学模型
5) 修改一条支路的变压器变比值( k*改变为k* ')
yT / k*
i j
yT(k*-1) / k*
①
y12 y13 y23 ②
U2
.
① ③
②
.
.
.
E1
U1 U3
U2
E2
.
I1
y10
U3 ③
y30
y20
.
I2
参考节点的选取—接地点
Z12 ① Z1
.
② ③ Z3
I 1 = U 1 y 1 0 ( U 1 U 2 )y 1 2 ( U 1 U 3 )y 1 3
Z2
.
.
.
.
.
I 1 = ( y 10 y 20 y 30) U 1 y 12 U 2 y 13 U 3 = Y11 U 1 Y12 U 2 Y13 U 3 I 2 = y 21 U 1 ( y 20 y 21 y 23) U 2 y 23 U 3 = Y 21 U 1 Y 22 U 2 Y 23 U 3 0 = y 31 U 1 y 32 U 2 ( y 30 y 31 y 32) U 3 = Y 31 U 1 Y 32 U 2 Y 33 U 3
4. 牛顿—拉夫逊法计算潮流
原理:局部线性化 直角座标法、极座标法、PQ分解法 用于潮流计算———速度快、但注意初值选择
第一节 电力网的数学模型
一、节点电压方程
. .
IB = Y B U
二、导纳矩阵的形成
B
YB—节点导纳矩阵
三、导纳矩阵的修改
第一节 电力网的数学模型
1、节点电压方程(示例)
.
U1
第三节 高斯—塞德尔迭代法潮流计算 二、高斯-塞德尔迭代法原理及求解步骤
• 迭代公式:
(1) (1) (0) (0) (0) x2 = g 2 ( x1 , x2 , x3 xn ) (1) (1) (1) (1) (1) (0) (0) xi = gi ( x1 , x2 , x3 xi1, xi , xn ) (1) (1) (1) (1) (1) (0) xn = g n ( x1 , x2 , x3 xn1 , xn ) x = g1 ( x , x , x x )
n n
Ui
(4 36a)
Pi = U i U j (Gij cos ij Bij sin ij ) 极坐标形式: j =1 (4 36b ) n Qi = U i U j (Gij sin ij Bij cos ij ) j =1 非线性方程组,不能用常规代数求解方程方法求解 。
第二节 功率方程、节点分类及约束条件 三、约束条件
• 实际电力系统运行要求:
–电能质量约束条件:Uimin Ui Uimax
–电压相角约束条件 |ij|=| i - j | ijmax, 稳定运行的一个重要条件。 –有功、无功约束条件 Pimin Pi Pimax
Qimin Qi Qimax
如电压中枢点。
第二节 功率方程、节点分类及约束条件 二、节点分类
3、平衡节点 (Slack Bus or Voltage Reference bus)
–已知Ui
,
i,,求, Pi, Qi, ,只设一个。
–设置平衡节点的目的
在结果未出来之前,网损是未知的,至少需 要一个节点的功率不能给定,用来平衡全网 功率。 电压计算需要参考节点。
n
第三节 高斯—塞德尔迭代法潮流计算
两种常见的求解非线性方程的方法:
• 高斯-塞德尔迭代法 • 牛顿-拉夫逊迭代法
第三节 高斯—塞德尔迭代法潮流计算 二、高斯-塞德尔迭代法原理及求解步骤
[例6-1]1 已知方程组 3x 2 x x 1 = 0 x1(1) = 0 3 = 0.3333 1 1 2
第三节 高斯—塞德尔迭代法潮流计算 一、功率方程的非线性
~ * S I = YU and I = U
( Pi jQi )*
*
= Yij U j
j =1
n
.
(i = 1,2,n)
(4 35)
Pi = ei (Gij e j Bij f j ) fi (G ij f j Bij e j ) j =1 j =1 直角坐 n n 标形式: Q = f (G e B f ) e (G f B e ) i i ij j ij j i ij j ij j j =1 j =1
= Yij U j
n
(i = 1,2,n)
~ * S I = U (4 35)
(4 36a)
(4 36b)
第二节 功率方程、节点分类及约束条件
二、节点分类
• 一个电力系统有n个节点,每个节点可能有4个变量Pi,Qi ,ei, fi或Pi,Qi ,Ui, i,,则共有4n个变量,而上述功率方程只有 2n个,所以需要事先给定2n个变量的值。根据各个节点的已 知量的不同,将节点分成三类:PQ节点、PV 节点、平衡节 点。 • 1、PQ节点(Load Buses) –已知Pi,Qi ,求,ei, fi( Ui, i, ),负荷节点(或发固 定功率的发电机节点),数量最多。 • 2、PU节点(Voltage Control Buses) –已知Pi, Ui ,求, Qi, i, ,对电压有严格要求的节点,
j ij i j
. n 其余节点j: 1、阶数 全部接地 I Yii = yi 0 yij 节点 i 注入网络电流 Y = . j= 1 2、对称性 j i U ( U = 0, j i ) Yii≠0
i ii i j
Uj = 0
3、稀疏性 节点i: 加单位电压
• Yii = 0
yT(1- k*) / k*2
•Yjj =(1/ k*'2 - 1/ k*2 ) yT • Yij = Yji =-(1/ k*' - 1/ k*) yT
第二节 功率方程、节点分类及约束条件 一、功率方程
( Pi jQi )*
*
I= YU
.
.
.
j =1 Ui n n Pi = ei (Gij e j Bij f j ) f i (G ij f j Bij e j ) j =1 j =1 n n Qi = f i (Gij e j Bij f j ) ei (G ij f j Bij e j ) j =1 j =1 n Pi = U i U j (Gij cos ij Bij sin ij ) j =1 n Qi = U i U j (Gij sin ij Bij cos ij ) j =1
( x21) = 0 2 = 0.6667 3
( 2)
3x2 x1 x2 2 = 0
x1 = 0.4815 用高斯-塞德尔求解(ε<0.01)。
2 (k ) (k ) 1 ( k 1) = x1 x2 x1 x1 = 0.5817 3 3 改写成迭代公式: ( x23) = 0.8167 x ( k 1) = 1 x ( k ) x ( k ) 2 1 2 2 直到|x(k+1)-x(k)|< ε 3 3
.
.
Z13
Z23
I 2 = U 2 y 2 0 ( U 2 U 1 )y 2 1 ( U 2 U 3 )y 2 3 0 = U 3 y 3 0 ( U 3 U 1 )y 3 1 ( U 3 U 2 )y 3 2
. . . . ..来自...
.
.
E1
E2
第一节 电力网的数学模型
自 导 纳
. . . . . . . . . . . . . . . . . . . .
Y 11 = y10 y12 y13 Y 22 = y 20 y 21 y 23 Y 33 = y 30 y 31 y 32
互 导 纳
.
y12 ① y13 ③ y23 ②
