2020年中考数学必考34个考点专题10:一元一次不等式(组)及其应用
2020年中考数学人教版专题复习教案设计:一元一次不等式组及其应用
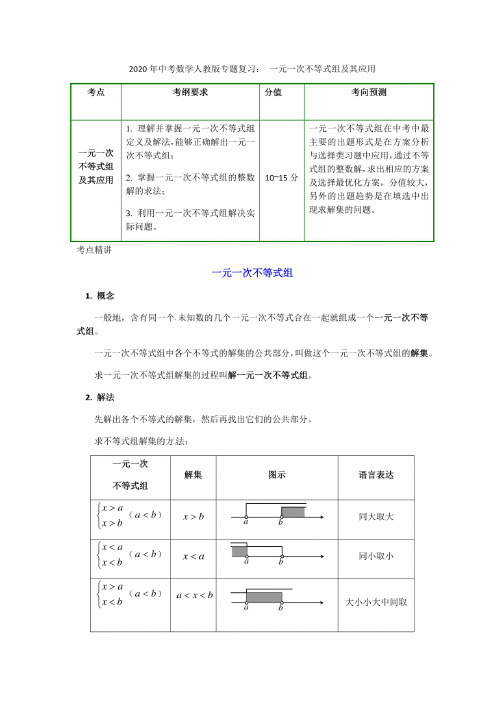
2020年中考数学人教版专题复习:一元一次不等式组及其应用考点考纲要求分值考向预测一元一次不等式组及其应用1.理解并掌握一元一次不等式组定义及解法,能够正确解出一元一次不等式组;2.掌握一元一次不等式组的整数解的求法;3.利用一元一次不等式组解决实际问题。
10~15分一元一次不等式组在中考中最主要的出题形式是在方案分析与选择类习题中应用,通过不等式组的整数解,求出相应的方案及选择最优化方案,分值较大,另外的出题趋势是在填选中出现求解集的问题。
考点精讲一元一次不等式组1.概念一般地,含有同一个.未知数的几个一元一次不等式合在一起就组成一个一元一次不等式组。
一元一次不等式组中各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集。
求一元一次不等式组解集的过程叫解一元一次不等式组。
2.解法先解出各个不等式的解集,然后再找出它们的公共部分。
求不等式组解集的方.法:一元一次不等式组解集图示语言表达V x>a,(Q<Z?) x>b x>b-J___I________>a b同大取大x<a,(a<b) x<b x<a一1____,同小取小□___i____>a bV x>a i(a<b) x<b a<x<b-J___1____>a b大小小大中间取【重要提示】V x < a,(a < b)x> b 无解i >a b 大大小小无解答求不等式组解集的关键是找不等式解集的“公共部分”。
若有“公共部分”,“公共部分” 即为解集;若无“公共部分”,则不等式组无解。
【随堂练习】2x-l>5①(黄冈)解不等式组: ,并在数轴上表示出不等式组的解集。
竺二-1小②I 2答案:解:由①得:x>3,由②得:x>l,则不等式组的解集是:x>3…思路分析:先求出不等式组中每一个不等式的解集,再把不等式的解集表示在数轴上, 然后求出它们的“公共部分”即可。
2020年中考数学必考考点专题10 一元一次不等式(组)及其应用(原卷版)

专题10 一元一次不等式(组)及其应用1.用不等号“<”“>”“≤ ”“≥”表示不相等关系的式子叫做不等式。
2.不等式的解:使不等式成立的未知数的值,叫做不等式的解。
3.不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
4.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
5.一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
6.不等式的性质:性质1:不等式的两边都加上(或减去)同一个数,不等号的方向不变。
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
7.一元一次不等式的解法的一般步骤:(1)去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化为1.8.不等式解集在数轴上的表示方法:含≥或≤,用空心圆圈,含>或<用实心圆点。
9.一元一次不等式组的解法(1)分别求出不等式组中各个不等式的解集(2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
10.求不等式组解集的规律:不等式组的解集有四种情况:若a>b,(1)当x ax b>⎧⎨>⎩时, 则不等式的公共解集为x>a;(2)x ax b<⎧⎨>⎩时,不等式的公共解集为b<x<a;专题知识回顾(3)x ax b<⎧⎨<⎩时,不等式的公共解集为x<b;(4)当x ax b>⎧⎨<⎩时,不等式组无解.【例题1】(2019江苏镇江)解不等式:14(1)2x x--<【例题2】(2019四川省雅安市)不等式组2442xx->⎧⎪⎨≤⎪⎩的解集为()A.6≤x<8 B.6<x≤8 C.2≤x<4 D.2<x≤8【例题3】(2019•山东省德州市)不等式组的所有非负整数解的和是()A.10B.7C.6D.0【例题4】(2019广西北部湾)解不等式组351342163x xx x-+⎧⎪--⎨⎪⎩<≤,并利用数轴确定不等式组的解集.【例题5】(2019•江苏无锡)某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a个零件(a为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a的值至少为()A.10B.9C.8D.7一、选择题1.(2019甘肃省陇南市) 不等式2x+9≥3(x+2)的解集是()A.x≤3 B.x≤﹣3 C.x≥3D.x≥﹣32.(2019•河北)语句“x的与x的和不超过5”可以表示为()专题典型题考法及解析专题典型训练题A .+x ≤5B .+x ≥5C .≤5D .+x =53.(2019•浙江宁波)不等式>x 的解为( ) A .x <1 B .x <﹣1C .x >1D .x >﹣1 4.(2019广西河池)不等式组23121x x x -⎧⎨>+⎩„的解集是( ) A .2x … B .1x < C .12x <„ D .12x <„5.(2019黑龙江绥化)不等式组10842x x x -≥⎧⎨+>+⎩的解集在数轴上表示正确的是( )6.(2019湖北仙桃)不等式组{x −1>0,5−2x ≥1的解集在数轴上表示正确的是( )7.(2019吉林长春)不等式-x +2≥0的解集为( )A.x ≥-2B.x ≤-2C.x ≥2D.x ≤2.(2019辽宁本溪) 不等式组3280x x -⎧⎨-⎩>0≤的解集是( ) A .x >3 B.x ≤4 C. x <3 D.3<x ≤49.(2019江苏镇江)下列各数轴上表示的x 的取值范围可以是不等式组2(21)60x a a x +>⎧⎨--<⎩的解集的是( ) A . B .C .D .10.(2019•绵阳)红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )A .3种B .4种C .5种D .6种11.(2019•常德)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x (元)所在的范围为( )A .10<x <12B .12<x <15C .10<x <15D .11<x <1412.(2019•湖南怀化)为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共( )只.A .55B .72C .83D .89二、填空题 13.(2019黑龙江哈尔滨)不等式组⎪⎩⎪⎨⎧≥+≤-123023x x 的解集是 .14.(2019山东东营)不等式组()32421152x x x x -->,-+≤ìïïïíïïïïî的解集为____________. 15.(2019•河南)不等式组的解集是 .16.(2019内蒙古包头市)已知不等式组{2x +9>−6x +1x −k >1的解集为x >-1,则k 的取值范围是 . 17.(2019黑龙江大庆)已知x =4是不等式ax -3a -1<0的解,x =2不是不等式ax -3a -1<0的解,则实数a 的取值范围是______.18.(2019•铜仁)如果不等式组的解集是x <a ﹣4,则a 的取值范围是 .19.(2019湖南邵阳)不等式组43113x x +<⎧⎪-⎨⎪⎩„的解集是 . 20.(2019•大渡口区)商店购进一批文具盒,进价每个4元,零售价每个6元,为促销决定打折销售,但利润率仍然不低于20%,那么该文具盒实际价格最多可打 折销售.三、解答题21.(2019广西省贵港市)解不等式组:622(4)23323x x x x ->-⎧⎪-⎨--⎪⎩…,并在数轴上表示该不等式组的解集.22.(2019北京市)解不等式组:4(1)2,7.3x x x x -<+⎧⎪+⎨>⎪⎩23.(2019•江苏扬州)解不等式组,并写出它的所有负整数解.24.(2019贵州省安顺市)先化简(1+32-x )÷96122+--x x x ,再从不等式组⎩⎨⎧+<<-42342x x x 的整数解中选一个合适的x 的值代入求值.25.(2019•新疆)解不等式组:并把解集在数轴上表示出来.26.(2019▪黑龙江哈尔滨)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?27.(2019四川巴中)在“扶贫攻坚”活动中,某单位计划选购甲、乙两种物品慰问贫困户.已知甲物品的单价比乙物品的单价高10元,若用500元单独购买甲物品与450元单独购买乙物品的数量相同.①请问甲、乙两种物品的单价各为多少?②如果该单位计划购买甲、乙两种物品共55件,总费用不少于5000元且不超过5050元,通过计算得出共有几种选购方案?28.(2019▪湖北黄石)若点P的坐标为(,2x﹣9),其中x满足不等式组,求点P 所在的象限.29.(2019•山东省滨州市)有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.30.(2019•遵义)某校计划组织240名师生到红色教育基地开展革命传统教育活动.旅游公司有A,B两种客车可供租用,A型客车每辆载客量45人,B型客车每辆载客量30人.若租用4辆A型客车和3辆B型客车共需费用10700元;若租用3辆A型客车和4辆B型客车共需费用10300元.(1)求租用A,B两型客车,每辆费用分别是多少元;(2)为使240名师生有车坐,且租车总费用不超过1万元,你有哪几种租车方案?哪种方案最省钱?。
中考重点一元一次不等式的应用

中考重点一元一次不等式的应用一元一次不等式是中考数学中非常重要的内容之一。
它不仅有着广泛的应用,在解题中也常常起到关键的作用。
本文将重点探讨一元一次不等式的应用,并通过实例来说明其解题方法。
一、线性不等式的符号表示法在讨论一元一次不等式之前,我们首先需要了解其符号表示法。
与一元一次方程相似,一元一次不等式也采用带有不等号的形式,常见的不等号包括大于号(>)、小于号(<)、大于等于号(≥)、小于等于号(≤)等。
例如,“x > 3”表示x大于3,“x ≤ -2”表示x小于等于-2。
二、一元一次不等式的解集表示法解一元一次不等式时,我们需要找出使不等式成立的所有实数的取值范围,并将其表示为解集。
解集的表示方法可以通过数轴上的区间表示法,也可以通过集合的形式表示。
例如,对于不等式“x > 3”,解集可以表示为开区间(3, +∞),即大于3的所有实数;对于不等式“x ≤ -2”,解集可以表示为闭区间[-∞, -2],即小于等于-2的所有实数。
三、一元一次不等式的应用举例1. 企业成本问题假设某企业的固定成本为10000元,每生产一件产品的变动成本为10元。
现在企业希望通过生产来获得一定的利润。
问该企业生产的产品数量x至少需要多少件?解:设生产产品x件后的利润为P。
根据题意,可列出等式:P =10x - 10000。
由于企业希望获得利润,因此P必须大于0。
即有不等式:10x - 10000 > 0。
将这个不等式进行变形可以得到10x >10000,进一步计算可得x > 1000。
因此,该企业生产的产品数量至少需要1001件。
2. 温度变化问题某城市一天的气温范围为-10°C至20°C。
请问这一天的气温平均值至少是多少?解:设这一天的气温平均值为T。
根据题意,可列出不等式:-10 ≤T ≤ 20。
为了得到平均值,T必须大于等于-10且小于等于20。
一元一次不等式组及其应用

制造商在有限的生产资源下,通过一元一次不等式组可以制定最优 生产计划,以满足市场需求并最小化成本。
时间规划问题
项目进度安排
在项目管理中,一元一次不等式组可以帮助制定项目的时间表,确 保各项任务在规定时间内完成。
时间分配
对于个人或团队来说,可以利用一元一次不等式组来合理规划时间 ,确保各项工作或活动得到合理安排,提高时间利用效率。
没有交集,则不等式组无解。
01
一元一次不等式组的解法
图形解法
优点
图形解法能够直观地展示不等式 组的解集,特别适用于较为简单
的一元一次不等式组。
作图步骤
首先,分别画出各个一元一次不 等式的解集图形;然后,找出各 个解集的交集部分,即为不等式
组的解集。
适用范围
图形解法主要适用于一元一次不 等式组的解集在数轴上能够直观
目标设定
通过一元一次不等式组,企业可以设定不同的营销目标( 如销售额、市场份额、品牌知名度等),并在预算约束下 求出最优解。
营销策略
根据不等式组的解,企业可以调整营销策略,实现预算内 最优的营销效果。
个人理财中的投资规划问题
投资选择
个人理财过程中,投资者需要在多种投资品种(如股票、债券、基金、房产等)中选择合 适的投资组合。
风险控制
通过一元一次不等式组,投资者可以设定不同的风险控制目标(如最大亏损限额、预期收 益水平等),从而在各种投资品种中寻求最优配置。
投资决策
基于不等式组的解,投资者可以制定个性化的投资规划,实现风险可控前提下的投资收益 最大化。
01
总结与展望
一元一次不等式组的重要性总结
基础数学知识
01
一元一次不等式组是初中数学的基础知识之一,对于后续学习
2020中考数学试题分类汇编 知识点10 一元一次不等式(组)

....知识点10 一元一次不等式(组)一、选择题1. (2018四川绵阳,6,3分) 等式1313+-=+-x x x x 成立的x 的取值范围在数轴上可表示为A B C D 【答案】 B【解析】解:由等式1313+-=+-x x x x 成立,可得⎩⎨⎧+≥-0103>x x ,解得x ≥3.故选B.【知识点】解一元一次不等式组,在数轴上表示不等式组的解集2. (2018山东滨州,5,3分)把不等式组1326x x +⎧⎨--⎩≥>-4中每个不等式的解集在同一条数轴上表示出来,正确的为( )A B C D 【答案】B【解析】不等式组中两个不等式的解集分别为:x ≥2,x <-1,大于等于用实点,小于用圆圈,故每个不等式的解集在同一条数轴上表示出来为选项B 【知识点】数形结合、解不等式(组)3.(2018浙江衢州,第7题,3分)不等式3x +2≥5的解集是( )....A .x ≥1B .73x ≥C .x ≤1D .x ≤-1 【答案】A【解析】本题考查了解一元一次不等式,根据不等式的基本性质两边移项化系数为1即可.故选A. 【知识点】解一元一次不等式4. (2018山东聊城,6,3分)已知不等式2241232x x x ---≤<,其解集在数轴上表示正确的是( ) A.B.C .D.【答案】 【解析】不等式2241232x x x ---≤<可化为 2242324132x x x x --⎧⎪⎪⎨--⎪⎪⎩≤①<②, 解①得x ≥2, 解①得x <5,....在数轴上表示解集为【知识点】不等式组的解法、在数轴上表示不等式组的解集5. (2018四川省南充市,第6题,3分)不等式121x x +≥-的解集在数轴上表示为( )A .B .C .D . 【答案】B【解析】解:x +1≥2x -1,x -2x ≥-1-1,-x ≥-2,x ≤2,故选B. 【知识点】解一元一次不等式6.(2018湖南衡阳,10,3分)不等式组10260x x +>⎧⎨-≤⎩的解集在数轴上表示正确的是( )【答案】C.【解析】解:10260x x +>⎧⎨-≤⎩由①得,x >-1,由②得,x ≤3,故原不等式组的解集为:-1<x ≤3, 在数轴上表示为:故选C.【知识点】解一元一次不等式组、在数轴上表示一元一次不等式组的解集7. (2018湖南长沙,6题,3分)不等式组的解集在数轴上表示正确的是( )【答案】C【解析】解不等式组可得-2<x≤2,故选C 【知识点】解不等式组,数轴表示解集8. (2018山东临沂,5,3分)不等式组123122x x -<⎧⎪⎨+≤⎪⎩的正整数解的个数是( )A .5B .4C .3D .2【答案】C【解析】解不等式1-2x <3得x >-1,解不等式221≤+x 得x ≤3,所以原不等式组的解集是-1<x ≤3,其正整数解是1,2,3,有3个,故选C. 【知识点】不等式组的解法 整数解9.(2018四川省德阳市,题号11,分值:3)如果关于x的不等式组的整数解仅有x=2,x=3,那么适合这个不等式组的整数a,b组成的有序数对(a,b)共有()A.3个B.4个C.5个D.6个【答案】D.【解析】解得,又∵整数解有x=2,x=3,∴解得又∵a,b为整数,∴a=3或4,b=9或10或11,∴(a,b)共有(3,9),(3,10),(3,11),(4,9),(4,10),(4,11),有6种.【知识点】不等式组的整数解10. (2018湖南岳阳,5,3分)已知不等式组2010xx-<⎧⎨+≥⎩,其解集在数轴上表示正确的是()A. B. C. D.【答案】D.【解析】解:⎩⎨⎧≥+-②01①02x x <,解不等式①,得x <2, 解不等式②,得x ≥-1, 不等式组的解集为-1≤x <2, 不等式组的解集在数轴上表示为:故选D .【知识点】解一元一次不等式组1 1.(2018安徽省,11,5分)不等式128>-x 的解集是 【答案】x >10【解析】根据解一元一次不等式得基本步骤依次计算可得. 解:去分母,得:x-8>2, 移项,得:x >2+8, 合并同类项,得:x >10, 故答案为:x >10.【知识点】解一元一次不等式.22. (2018山东聊城,17,3分)若x 为实数,则[x]表示不大于x 的最大整数,例如[1.6]=1,[π]=3,[-2.82]=-3等.[x]+1的大于x 的最小整数,对任意的实数x 都满足不等式[x]<x <[x]+1.①利用这个不等式①,求出满足[x]=2x-1的所有解,其所有解为 . 【答案】12【解析】∵[x]<x <[x]+1,[x]=2x-1,∴21211x xx x-⎧⎨-+⎩<<,即1xx⎧⎨⎩<>,∴0<x<1,∴[x]=2x-1=0,∴x=12.【知识点】新定义运算、一元一次不等式组的解法、一元一次方程的解法1. (2018湖南益阳,3,4分)不等式组213,312xx+<⎧⎨+≥-⎩的解集在数轴上表示正确的是()【答案】A【解析】解不等式2x+1<3,得x<1;解不等式3x+1≥-2,得x≥-1.所以不等式组的解集为-1≤x<1,表示-1的为实心,表示1的为空心,故选择A.【知识点】解一元一次不等式组2.(2018·重庆A卷,12,4)若数a使关于x的不等式组112352x xx x a-+⎧<⎪⎨⎪-≥+⎩有且只有四个整数解,且使关于y的分式方程2211y a ay y++=--的解为非负数,则符合条件的所有整数a的和为()A.-3 B.-2 C.1 D.2 【答案】C.【解析】解不等式组得24a+≤x<5.∵该不等式组有且只有四个整数解:4,3,2,1, ∴0<24a +≤1,从而-2<a ≤2. 解方程,得y =2-a ,且2-a ≠1,即y =2-a (a ≠1). ∵方程的解为非负数, ∴2-a ≥0,解得a ≤2.又∵-2<a ≤2,且a ≠1,a 为整数,∴符合条件的整数a 的值为-1、0、2,其和为1. 故选C .【知识点】一元一次不等式组的解法 分式方程的解法3. (2018四川雅安,8题,3分)不等式组2151132513(1)x x x x -+⎧-≤⎪⎨⎪-<+⎩的整数解的个数是 A.0个 B.2个 C.3个 D.4个 【答案】C【解析】解①得,x ≥-1;解②得,x<2;原不等式的解集为:-1≤x<2,故整数解有3个,选C 【知识点】不等式的特殊解4. (2018湖北荆门,7,3分) 已知关于x 的不等式310x m -+>的最小整数解为2,则实数m 的取值范围是( )A .47m ≤<B .47m << C. 47m ≤≤ D .47m <≤ 【答案】A.【解析】解:解不等式310x m -+>,得31>-m x ,∵不等式有最小整数解2, ∴2<311-≤m , 解得4≤m <7. 故选A.【知识点】一元一次不等式的整数解,解一元一次不等式5. (2018湖南省永州市,10,4)甲从商贩A 处购买了若干斤西瓜,又从商贩B 处购买了若干斤西瓜,A 、B 两处所购买的西瓜重量之比为3:2,然后将买回的西瓜以从A 、B 两处购买单价的平均数为单价全部卖给了乙,结果发现他赔钱了,这是因为( )A .商贩A 的单价大于商贩B 的单价B .商贩A 的单价等于商贩B 的单价C. 商贩A 的单价小于商贩B 的单价 D .赔钱与商贩A 、商贩B 的单价无关 【答案】A【解析】利润=总售价-总成本=a+b2×5-(3a+2b )=0.5b-0.5a ,赔钱了说明利润<0,∴0.5b-0.5a <0,∴a >b. 因此,本题选A .【知识点】不等式 平均数2.6.(2018湖北省襄阳市,5,3分) 不等式组⎩⎨⎧-+-142x,12x x x <>的解集为(▲)A.31>xB.x >1C.131<<xD.空集【答案】B【解析】解:解不等式①得,31>x ;解不等式②得,x >1. ∴不等式组的解集为x >1.【知识点】解一元一次不等式组7. (2018湖北省孝感市,3,3分)下列某不等式组的解集在数轴上表示如图所示,则该不等式组是()A .1313x x -<⎧⎨+<⎩ B .1313x x -<⎧⎨+>⎩ C .1313x x ->⎧⎨+>⎩ D .1313x x ->⎧⎨+<⎩【答案】B【解析】根据题图可知:该不等式组的解集是2<x <4. 通过计算可知:A. 解集为x <-1;B. 解集为2<x <4;C. 解集为x >4;D. 无解. 故选B.【知识点】解一元一次不等式组;在数轴上表示不等式的解集.8. (2018江苏省宿迁市,5,3)若a <b ,则下列结论不一定...成立的是( ) A .a -1<b -1 B .2a <2b C .-3a >-3bD .a 2<b 2【答案】D【解析】A 选项,不等式两边同时减去1,不等号方向不变,故A 成立.B 选项,不等式两边同时乘以2,不等号方向不变,故B 成立. C 选项,不等式两边同时乘以-31,不等号方向改变,故C 成立.选项D ,举例,-5<-2,但(-5)2>(-2)2.故D 不成立.故选D . 【知识点】不等式的性质9.(2018山东省泰安市,8,3)不等式组111324(1)2()x x x x a -⎧-<-⎪⎨⎪-≤-⎩有3个整数解,则a 的取值范围是( ) A .65a -≤<- B .65a -<≤- C .65a -<<- D .65a -≤≤- 【答案】B【解析】首先解不等式组求得不等式组的解集,然后根据不等式组的整数解的个数从而确定a 的范围.解:解①得:4x >, 解②得:2x a ≤-. 则不等式组的解集是42x a <≤-.∵不等式组有3个整数解, ∴ 728a ≤-<,解得:65a -<≤-,故选B . 【知识点】一元一次不等式(组)的应用---与整数解有关的问题 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28.29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. 二、填空题1. (2018四川省宜宾市,10,3分)不等式组1<12x-2≤2的所有整数解的和为 .【答案】15【知识点】解不等式组2. (2018浙江温州,14,5)不等式组20262->⎧⎨->⎩x x 的解是 .【答案】x>4【解析】本题考查了一元一次不等式组的解法。
2020年中考数学复习专题06 一元一次不等式(组)及其应用 全面复习系列讲座

考点
考点1 考点2 考点3 考点4
一元一次不等式组及其解法
3.解集的表示(假设a<b)
不等式组
在数轴上的表示
不等式组的解集
口诀
x>⑦ b 同大取大
x<⑧ a
同小取小
⑨ a<x<b 大小小大中间找
⑩ 无解 大大小小无解了
考点
一元一次不等式的应用
考点1 考点2 考点3 考点4
1.列不等式解应用题的一般步骤
错用不等式性质,导致解集错误 解不等式3x-7<1+7x. 解:移项,得3x-7x<1+7, 合并同类项,得-4x<8, 系数化为1,得x>-2. 注:本题中,系数化为1时,不等式两边同除以负数, 不等号的方向易忘记变号.
考点
一元一次不等式组及其解法
考点1 考点2 考点3 考点4
1.定义 由几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不 等式组. 这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集. 求一元一次不等式组解集的过程叫做解不等式组. 2.解法步骤 (1)分别求出每个不等式的解集; (2)在同一数轴上表示出各个解集,找出所有解集的公共部分; (3)写出不等式组的解集.
方法
命题角度 2 解一元一次不等式组
3.(数学运算)[2019湖北襄阳]不等式组 是
的解集在数轴上用阴影表示正确的 ( C)
解析:C 解不等式2x<x+4,得x<4;解不等式3+x≥3x+9,得x≤-3,故该不等式组的解集为 x≤-3.在数轴上表示该不等式组的解集如选项C所示,故选C.
方法
命题角度 2 解一元一次不等式组
2020年中考数学必考34个考点专题10:一元一次不等式(组)及其应用

专题10 一元一次不等式(组)及其应用1.用不等号“<”“>”“≤”“≥”表示不相等关系的式子叫做不等式。
2.不等式的解:使不等式成立的未知数的值,叫做不等式的解。
3.不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
4.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
5.一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
6.不等式的性质:性质1:不等式的两边都加上(或减去)同一个数,不等号的方向不变。
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
7.一元一次不等式的解法的一般步骤:(1)去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化为1.8.不等式解集在数轴上的表示方法:含≥或≤,用空心圆圈,含>或<用实心圆点。
9.一元一次不等式组的解法(1)分别求出不等式组中各个不等式的解集(2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
10.求不等式组解集的规律:不等式组的解集有四种情况:若a>b,(1)当x ax b>⎧⎨>⎩时,•则不等式的公共解集为x>a;(2)x ax b<⎧⎨>⎩时,不等式的公共解集为b<x<a;专题知识回顾(3)x a x b<⎧⎨<⎩时,不等式的公共解集为x<b;(4)当x a x b >⎧⎨<⎩时,不等式组无解.【例题1】(2019江苏镇江)解不等式:14(1)2x x --< 【答案】不等式的解集为32x <. 【解析】解一元一次不等式。
按照去括号,移项,合并同类项,系数化为1来解即可.化简14(1)2x x --<得 1442x x --< 932x ∴<32x ∴< ∴原不等式的解集为32x <. 【例题2】(2019四川省雅安市)不等式组2442x x ->⎧⎪⎨≤⎪⎩的解集为( ) A .6≤x <8 B .6<x ≤8 C .2≤x <4 D .2<x ≤8【答案】B【解析】分别求出不等式组中的两个不等式的解集 ,再找它们的公共部分,由第1个不等式得x>6,由第2 个不等式得x ≤8,它们的公共部分是6<x ≤8 ,故选B .【例题3】(2019•山东省德州市)不等式组的所有非负整数解的和是( ) A .10B .7C .6D .0【答案】A 专题典型题考法及解析【解析】不等式组的非负整数解。
专题10 一元一次不等式(组)(课件)2023年中考数学一轮复习(全国通用)

1. 一元一次不等式的定义:不等式中只含有一个未知数,未知数的次数是1,且不 等式的两边都是整式,这样的不等式叫做一元一次不等式.
2. 一元一次不等式的解法: 一般步骤:(1)去分母(2)去括号(3)移项(4)合并同类项(5)将未知项的 系数化为1.
知识点2:一元一次不等式及其解法
典型例题
知识点3:一元一次不等式组及其解法
知识点梳理
3. 解不等式组:求不等式组的解集的过程,叫做解不等式组.
4. 一元一次不等式组的解法: (1)分别求出不等式组中各个不等式的解集; (2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集.
知识点3:一元一次不等式组及其解法
知识点梳理
5. 解集在数轴上的表示(令a>b):
典型例题
【例8】(2022•聊城)关于x,y的方程组
2x y x 2 y
2k k
3
的解中x与y的和不小于5,
则k的取值范围为( )
A.k≥8 B.k>8 C.k≤8 D.k<8
【解答】解:把两个方程相减,可得x+y=k-3, 根据题意得:k-3≥5, 解得:k≥8. 所以k的取值范围是k≥8. 故选:A.
知识点4:一元一次不等式(组)的实际应用
典型例题
【解答】解:(1)设生产A产品x件,B产品y件,
根据题意,得
100x 75y 8250 (120 100)x (100 75) y 2350
.
解这个方程组,得
x 30
y
70
,
所以,生产A产品30件,B产品70件.
知识点4:一元一次不等式(组)的实际应用
知识点梳理
知识点1:不等式及其性质
5. 不等式基本性质:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题10 一元一次不等式(组)及其应用1.用不等号“<”“>”“≤”“≥”表示不相等关系的式子叫做不等式。
2.不等式的解:使不等式成立的未知数的值,叫做不等式的解。
3.不等式的解集:一个含有未知数的不等式的所有解,组成这个不等式的解集。
4.一元一次不等式:不等式的左、右两边都是整式,只有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
5.一元一次不等式组:一般地,关于同一未知数的几个一元一次不等式合在一起,就组成了一个一元一次不等式组。
6.不等式的性质:性质1:不等式的两边都加上(或减去)同一个数,不等号的方向不变。
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。
性质3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
7.一元一次不等式的解法的一般步骤:(1)去分母; (2)去括号; (3)移项; (4)合并同类项; (5)系数化为1.8.不等式解集在数轴上的表示方法:含≥或≤,用空心圆圈,含>或<用实心圆点。
9.一元一次不等式组的解法(1)分别求出不等式组中各个不等式的解集(2)利用数轴求出这些不等式的解集的公共部分,即这个不等式组的解集。
10.求不等式组解集的规律:不等式组的解集有四种情况:若a>b,(1)当x ax b>⎧⎨>⎩时,•则不等式的公共解集为x>a;(2)x ax b<⎧⎨>⎩时,不等式的公共解集为b<x<a;专题知识回顾(3)x ax b<⎧⎨<⎩时,不等式的公共解集为x<b;(4)当x ax b>⎧⎨<⎩时,不等式组无解.【例题1】(2019江苏镇江)解不等式:14(1)2x x --< 【答案】不等式的解集为32x <. 【解析】解一元一次不等式。
按照去括号,移项,合并同类项,系数化为1来解即可. 化简14(1)2x x --<得 1442x x --< 932x ∴<32x ∴<∴原不等式的解集为32x <. 【例题2】(2019四川省雅安市)不等式组2442x x ->⎧⎪⎨≤⎪⎩的解集为( )A .6≤x <8B .6<x ≤8C .2≤x <4D .2<x ≤8 【答案】B【解析】分别求出不等式组中的两个不等式的解集 ,再找它们的公共部分,由第1个不等式得x>6,由第2 个不等式得x ≤8,它们的公共部分是6<x ≤8 ,故选B . 【例题3】(2019•山东省德州市)不等式组的所有非负整数解的和是( )A .10B .7C .6D .0【答案】A专题典型题考法及解析【解析】不等式组的非负整数解。
分别求出每一个不等式的解集,即可确定不等式组的解集,继而可得知不等式组的非负整数解.,解不等式①得:x >﹣2.5, 解不等式②得:x ≤4,∴不等式组的解集为:﹣2.5<x ≤4,∴不等式组的所有非负整数解是:0,1,2,3,4, ∴不等式组的所有非负整数解的和是0+1+2+3+4=10【例题4】(2019广西北部湾)解不等式组351342163x x x x -+⎧⎪--⎨⎪⎩<≤,并利用数轴确定不等式组的解集.【答案】见解析。
【解析】本题主要考查了解一元一次不等式组,分别解两个不等式得到x <3和x ≥-2,再根据大小小大中间找确定不等式组的解集.然后利用数轴表示其解集.【解题过程】解:351342163x x x x -+⎧⎪⎨--⎪⎩<①≤②解①得x <3, 解②得x ≥-2,所以不等式组的解集为-2≤x <3. 用数轴表示为:【例题5】(2019•江苏无锡)某工厂为了要在规定期限内完成2160个零件的任务,于是安排15名工人每人每天加工a 个零件(a 为整数),开工若干天后,其中3人外出培训,若剩下的工人每人每天多加工2个零件,则不能按期完成这次任务,由此可知a 的值至少为( ) A .10B .9C .8D .7【答案】B【解析】根据15名工人的前期工作量+12名工人的后期工作量<2160列出不等式并解答.设原计划n天完成,开工x天后3人外出培训,则15an=2160,得到an=144.所以15ax+12(a+2)(n﹣x)<2160.整理,得4x+4an+8n﹣8x<720.∵an=144.∴将其代入化简,得ax+8n﹣8x<144,即ax+8n﹣8x<an,整理,得8(n﹣x)<a(n﹣x).∵n>x,∴n﹣x>0,∴a>8.∴a至少为9.专题典型训练题一、选择题1.(2019甘肃省陇南市) 不等式2x+9≥3(x+2)的解集是()A.x≤3 B.x≤﹣3 C.x≥3 D.x≥﹣3【答案】A【解析】先去括号,然后移项、合并同类项,再系数化为1即可.去括号,得2x+9≥3x+6,移项,合并得﹣x≥﹣3系数化为1,得x≤3。
2.(2019•河北)语句“x的与x的和不超过5”可以表示为()A.+x≤5 B.+x≥5 C.≤5 D.+x=5【答案】A【解析】“x的与x的和不超过5”用不等式表示为x+x≤5.3.(2019•浙江宁波)不等式>x 的解为( )A .x <1B .x <﹣1C .x >1D .x >﹣1【答案】A【解析】去分母、移项,合并同类项,系数化成1即可.>x , 3﹣x >2x , 3>3x ,x <14.(2019广西河池)不等式组23121x x x -⎧⎨>+⎩…的解集是( )A .2x …B .1x <C .12x <…D .12x <…【答案】D .【解析】23121x x x -⎧⎨>+⎩①②…,解①得:2x …, 解②得:1x >.则不等式组的解集是:12x <…. 故选:D .5.(2019黑龙江绥化)不等式组10842x x x -≥⎧⎨+>+⎩的解集在数轴上表示正确的是( )【答案】B【解析】解不等式组,用数轴表示不等式组的解集 解①得,x ≥1, 解②得,x<2,∴原不等式组的解集为1≤x<2,故选B.6.(2019湖北仙桃)不等式组 > ,的解集在数轴上表示正确的是( )【答案】C【解析】解一元一次不等式组;在数轴上表示不等式的解集。
解不等式x﹣1>0得x>1,解不等式5﹣2x≥1得x≤2,则不等式组的解集为1<x≤27.(2019吉林长春)不等式-x+2≥0的解集为()A.x≥-2B.x≤-2C.x≥2D.x≤2 【答案】D【解析】解一元一次不等式.-x+2≥0,移项得:-x≥-2,系数化为1,得x≤2∴不等式的解集为:x≤28.(2019辽宁本溪)不等式组3280xx-⎧⎨-⎩>0≤的解集是A.x>3B.x≤4C. x<3D.3<x≤4 【答案】 D.【解析】3280xx-⎧⎨-⎩>0①≤②,由①得:x>3,由②得:x≤4,则不等式组的解集为3<x≤49.(2019江苏镇江)下列各数轴上表示的x的取值范围可以是不等式组2(21)60x aa x+>⎧⎨--<⎩的解集的是()A. B.C. D.【答案】B【解析】由2x a+>得2x a>-,A.由数轴知3x>-,则1a=-,360x∴--<,解得2x>-,与数轴不符;B.由数轴知0x>,则2a=,360x∴-<,解得2x<,与数轴相符合;C.由数轴知2x>,则4a=,760x∴-<,解得67x<,与数轴不符;D.由数轴知2x>-,则0a=,60x∴--<,解得6x>-,与数轴不符。
10.(2019•绵阳)红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有()A.3种B.4种C.5种D.6种【答案】C【解析】设该店购进甲种商品x件,则购进乙种商品(50﹣x)件,根据“购进甲乙商品不超过4200元的资金、两种商品均售完所获利润大于750元”列出关于x的不等式组,解之求得整数x的值即可得出答案.设该店购进甲种商品x件,则购进乙种商品(50﹣x)件,根据题意,得:,解得:20≤x<25,∵x为整数,∴x=20、21、22、23、24,∴该店进货方案有5种。
11.(2019•常德)小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为()A.10<x<12 B.12<x<15 C.10<x<15 D.11<x<14【答案】B【解析】根据题意得出不等式组解答即可.根据题意可得:,可得:12<x <15, ∴12<x <1512.(2019•湖南怀化)为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只;若每户发放母羊5只,则多出17只母羊,若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共( )只. A .55 B .72C .83D .89【答案】C【解析】设该村共有x 户,则母羊共有(5x +17)只,根据“每户发放母羊7只时有一户可分得母羊但不足3只”列出关于x 的不等式组,解之求得整数x 的值,再进一步计算可得. 设该村共有x 户,则母羊共有(5x +17)只, 由题意知,解得:<x <12,∵x 为整数, ∴x =11,则这批种羊共有11+5×11+17=83(只) 二、填空题13.(2019黑龙江哈尔滨)不等式组⎪⎩⎪⎨⎧≥+≤-123023x x的解集是 .【答案】:x ≥3.【解析】解不等式32x-≤0,得x ≥3, 解不等式3x +2≥1,得x ≥﹣13,∴不等式组的解集为x ≥3, 故答案为:x ≥3.14.(2019山东东营)不等式组()32421152x x x x -->,-+≤ìïïïíïïïïî的解集为____________. 【答案】-7≤x <1【解析】一元一次不等式组的解法。
()32421152x x x x -->,①-+②≤ìïïïíïïïïî解不等式①,得x <1;解不等式②,得x ≥-7, ∴不等式组的解集是-7≤x <1. 15.(2019•河南)不等式组的解集是 .【答案】x ≤﹣2.【解析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集. 解不等式≤﹣1,得:x ≤﹣2, 解不等式﹣x +7>4,得:x <3, 则不等式组的解集为x ≤﹣216.(2019内蒙古包头市)已知不等式组 > > 的解集为x >-1,则k 的取值范围是 .【答案】k ≤-2. 【解析】 不等式组> ① > ②解不等式①得,x >-1; 解不等式②得,x >k +1; ∵原不等式组的解集为x >-1, ∴k +1≤-1 解得,k ≤-2.17.(2019黑龙江大庆)已知x =4是不等式ax -3a -1<0的解,x =2不是不等式ax -3a -1<0的解,则实数a的取值范围是______. 【答案】a ≤-1【解析】∵x =4是不等式ax -3a -1<0的解,所以4a -3a -1<0,a<1, 因为x =2不是不等式ax -3a -1<0的解, 所以2a -3a -1≥0,所以a ≤-1,所以a ≤-1. 18.(2019•铜仁)如果不等式组的解集是x <a ﹣4,则a 的取值范围是 .【答案】a ≥﹣3.【解析】解这个不等式组为x <a ﹣4, 则3a +2≥a ﹣4, 解这个不等式得a ≥﹣3 故答案a ≥﹣3.19.(2019湖南邵阳)不等式组43113x x +<⎧⎪-⎨⎪⎩…的解集是 .【答案】21x -<-…【解析】解不等式43x +<,得:1x <-, 解不等式113x-…,得:2x -…, 则不等式组的解集为21x -<-…, 故答案为:21x -<-….20.(2019•大渡口区)商店购进一批文具盒,进价每个4元,零售价每个6元,为促销决定打折销售,但利润率仍然不低于20%,那么该文具盒实际价格最多可打 折销售. 【答案】8【解析】由题意可知:利润率为20%时,获得的利润为4×20%=0.8元;若打x 折该商品获得的利润=该商品的标价×﹣进价,列出不等式,解得x 的值即可.设可以打x 折出售此商品,由题意得:,解得:x ≥8,答:该文具盒实际价格最多可打8折。
