组合-2

合集下载

魔能2各元素魔法技能组合列表

魔能2-各元素魔法技能组合列表魔能2全魔法技能组合魔能2有哪些魔法技能魔能2中有8⼤元素，各种元素之间还可以有不同的搭配，这样组合起来的技能多不胜数，铸就这样缤纷多彩的幻想世界A P R G游戏。

这⾥N i c h o 为⼴⼤玩家奉上魔能2技能⼤全，⽤图⽂详细介绍下所有魔能2所有魔法技能组合，好在有⼏种元素是相冲突的，有的先后顺序不⽤在意(特殊技能除外)，不然那可真是成百上千种技能了。

在展⽰组合列表之前，我们得先做⼀些基础说明; ⼋种元素：⽔、⽣命、护盾、冰、闪电、死亡、⼟、⽕;对应按键图标所⽰。

释放⽅式有⿏标中间(对⾃⼰释放)、⿏标右键(投掷喷射)、S H I F T+⿏标右键(给武器增加元素效果)、S H I F T+⿏标中键(以⾃⼰为中⼼的范围伤害技能)。

个别拥有冷却C D的特殊技能可以直接使⽤数字键1234，也可以按其指定顺序组合后，使⽤空格键释放，这样就没有C D了。

此外，某些元素还是相互抵抗的，⽐⽅说按Q⽔元素，再按A电元素，那么⽔元素的魔法球就会消除⼀个。

⽣命元素和死亡元素冲突，冰元素和⽕元素、电元素和⼟元素冲突等。

魔能2所有魔法技能组合列表：(以键⿏为例) 单元素技能：按1-5次皆可，威⼒不同⽽已。

1.⽔元素Q Q、⿏标右键：喷⽔ Q、⿏标中键：⾝体潮湿 Q、S H I F T+右：武器附上⽔元素 Q、S H I F T+⿏标中键：释放⽔爆 2.⽣命元素W W、⿏标中键：对⾃⼰医疗，可以按着不放持续施法 W、S H I F T+右：医疗剑，击打回⾎ W、S H I F T+⿏标中键：医疗罩，范围内回⾎ 3.护盾E E、⿏标右键：设置⼀个防护墙 E、⿏标中键：变⾝⼩⾦⼈，抵抗⼀些伤害 E、S H I F T+右：剑缠绕着黄光，挥动会产⽣盾墙 E、S H I F T+⿏标中键：产⽣防护罩 4.冰元素R R、⿏标右键：喷射冰霜，冷冻敌⼈ R、⿏标中键：冷冻⾃⼰ R、S H I F T+右：冰剑，挥砍有冰冻效果 R、S H I F T+⿏标中键：范围冰冻效果 5.闪电元素A A、⿏标右键：释放线状闪电 A、⿏标中键：电击⾃⼰，伤⾎ A、S H I F T+右：电⼑，攻击敌⼈有电击特效 A、S H I F T+⿏标中键：⼤范围闪电，⾃动攻击周围敌⼈ 6.死亡元素S S、⿏标中键：对⾃⼰释放，减⾎ S、S H I F T+右：死亡剑，⼤幅增加攻击 S、S H I F T+⿏标中键：造成巨⼤A E O伤害 7、⼟元素D D、⿏标右键：投掷⼀个⽯头，按着右键不放可以蓄⼒ D、⿏标中键：⽯头从天⽽降，如果不躲开会砸伤⾃⼰ D、S H I F T+右：⽯剑，对地下挥可发动冲击波 D、S H I F T+⿏标中键：⼤地践踏，地震会将周围⼈振倒，但是不会受到伤害 8.⽕元素F F、⿏标右键：喷射⽕焰 F、⿏标中键：⾃⼰着⽕，会持续减⾎ F、S H I F T+右：⽕焰剑，附加攻击 F、S H I F T+⿏标中键：烈焰轰炸，⼤范围⽕焰伤害双元素技能：两种元素配合，顺序⽆需太注重，⽐如说Q W Q W Q和Q Q Q W W效果都是⼀样。

高中数学第一章计数原理1.2.2组合与组合数公式2课件新人教A版选修2_3

解析答案
(2)四面体的顶点和各棱中点共10个点，在其中取4个不共面的点，有多少
种不同的取法.
解 (间接法)如图，从 10 个点中取 4 个点的取法有 C410种，
除去4点共面的取法种数可以得到结果.
从四面体同一个面上的6个点取出的4点必定共面.
有 4C46 ＝60(种)，四面体的每一棱上3点与相对棱中点共面，共有6种共面情况，
第一章 §1.2 排列与组合
1.2.2 组合(二)
学习目标
1.能应用组合知识解决有关组合的简单实际问题. 2.能解决有限制条件的组合问题.
题型探究
达标检测
题型探究
重点难点个个击破
类型一简单的组合应用题例1 男运动员6名，女运动员4名，其中男女队长各1名，选派5人外出比赛，在下列情形中各有多少种选派方法？ (1)男运动员3名，女运动员2名；解第一步：选 3 名男运动员，有 C36种选法；第二步：选 2 名女运动员，有 C24种选法，故共有 C36·C24＝120(种)选法.
解析答案
类型二与几何有关的组合应用题例2 平面内有12个点，其中有4个点共线，此外再无任何3点共线.以这些点为顶点，可构成多少个不同的三角形？
反思与感悟解析答案
跟踪训练2 (1)四面体的一个顶点为A，从其他顶点和各棱中点中取3个点，使它们和点A在同一平面上，有多少种不同的取法？解 (直接法)如图，含顶点A的四面体的3个面上，除点A外都有5个点，从中取出 3 点必与点 A 共面共有 3C35种取法；含顶点A的三条棱上各有三个点，它们与所对的棱的中点共面，共有3种取法. 根据分类加法计数原理，与顶点A共面的三点的取法有 3C35 ＋3＝33(种).
解析答案

课件7：1.2.2 第二课时　组合的综合应用

法二：(间接法)C46－C24＝9 种．
【答案】A
考点二与几何有关的组合问题例2.平面内有12个点，其中有4个点共线，此外再无任何3点共线．以这些点为顶点，可构成多少个不同的三角形？ [思路点拨] 解答本题可以从共线的4个点中选取2个、1个、0个作为分类标准，也可以从反面考虑，任意三点的取法种数减去共线三点的取法种数．
1.2 排列与组合 1.2.2 组合
第二课时组合的综合应用
考点一有限制条件的组合问题例1.现有10件产品，其中有2件次品，任意抽出3件检查． (1)恰有一件是次品的抽法有多少种？ (2)至少有一件是次品的抽法有多少种？ [思路点拨] 分清“恰有”“至少”的含义，正确地分类或分步．
解:(1)从 2 件次品中任取 1 件，有 C12种抽法．从 8 件正品中取 2 件，有 C28种抽法．由分步乘法计数原理可知，不同的抽法共有 C12×C28＝56 种． (2)法一：含 1 件次品的抽法有 C12×C28种，含 2 件次品的抽法有 C22×C18种．由分类加法计数原理知，不同的抽法共有 C12×C28＋C22×C18＝56＋8＝64 种．

解：分两类：第一类，甲被选中，共有 C25C24C14A44种分派方案；第二类，甲不被选中，共有 C35C24A55种分派方案．根据分类加法计数原理，共有 C25C24C14A44＋C35C24A55＝5 760＋7 200＝12 960 种分派方案．
[一点通] 本题是一道“既选又排”的排列、组合综合题，解决这类问题的方法是“先选后排”，同时要注意特殊元素、特殊位置优先安排的原则．
法二(间接法)：从 12 个点中任意取 3 个点，有 C312＝220 种取法，而在共线的 4 个点中任意取 3 个均不能构成三角形，即不能构成三角形的情况有 C34＝4 种．

魔能2各元素魔法技能组合列表

在展⽰组合列表之前，我们得先做⼀些基础说明; ⼋种元素：⽔、⽣命、护盾、冰、闪电、死亡、⼟、⽕;对应按键图标所⽰。

释放⽅式有⿏标中间(对⾃⼰释放)、⿏标右键(投掷喷射)、S H I F T+⿏标右键(给武器增加元素效果)、S H I F T+⿏标中键(以⾃⼰为中⼼的范围伤害技能)。

个别拥有冷却C D的特殊技能可以直接使⽤数字键1234，也可以按其指定顺序组合后，使⽤空格键释放，这样就没有C D了。

此外，某些元素还是相互抵抗的，⽐⽅说按Q⽔元素，再按A电元素，那么⽔元素的魔法球就会消除⼀个。

⽣命元素和死亡元素冲突，冰元素和⽕元素、电元素和⼟元素冲突等。

魔能2所有魔法技能组合列表：(以键⿏为例) 单元素技能：按1-5次皆可，威⼒不同⽽已。

组合综合--2

组合综合问题(2)1.记数集},...,,{21n a a a A =中所有元素的算术平均值为)(A P .若B 是A 的非空子集,且)()(A P B P =,则称B 是A 的一个“均衡子集”．试求数集}9,8,7,6,5,4,3,2,1{=M 的所有“均衡子集”的个数．解:由于()5P M =,令{}{}54,3,2,1,0,1,2,3,4M x x M '=-∈=----,则()0P M '=,依照此平移关系,M 和M '的均衡子集可一一对应.用()f k 表示M '的k 元均衡子集的个数,显然,可得(9)(1)1f f ==(M '的9元均衡子集只有M ',一元均衡子集只有{}0)．M '的二元均衡子集共四个,为{,},1,2,3,4i B i i i =-=, 因此(2)4f =． M '的三元均衡子集有两种情况:(1)含有元素0的为{0}{,0,},1,2,3,4i B i i i =-= ,共四个；(2)不含元素0的,由于等式312,413=+=+可表示为3120,3120-++=--=以及4130,413-++=--=,得到4个均衡子集{3,1,2},{3,1,2},{4,1,3},{4,1,3}------,故8)3(=f ．M '的四元均衡子集有三种情况:(1)每两个二元均衡子集之并:,14i j B B i j ≤<≤ , 共6个集； (2)不含元素0的三元均衡子集与{}0的并集,共4个集；(3)以上两种情况之外者,由于等式1423+=+可表为14230--++=以及14230+--=得2个均衡子集{1,4,2,3}--与{1,4,2,3}--,因此()464212f =++=．又注意到,除M '本身外,若B '是M '的均衡子集,当且仅当其补集''M C B 也是M '的均衡子集,二者一一对应.因此(9)(),1,2,3,4f k f k k -==．故M '的均衡子集为9411()(9)2()12(14812)51k k f k f f k ===+=++++=∑∑个,即M 的均衡子集有51个.2.若集合{}1,2,,200M = 的子集A 中的每个元素都可表为两个自然数(允许相同)的平方和,求这种集A 中元素个数的最大值.解:首先,不超过200的平方数有22220,1,2,,14 .显然,在2221,2,,14 中的每一个数2k 都可以表为220k +形式,这种数共有14个；而2221,2,,10 中的每一对数(允许相同)的和在M 中,这种数有2101055C +=个,(其中,22x x +形式的数10个,()22 x y x y +≠形式的数210C 个).其次,()2211 1,2,,8x x += 形式的数8个；()2212 1,2,,7x x += 形式的数7个； ()2213 1,2,,5x x += 形式的数5个；()2214 1,2x x +=形式的数2个；共得22个.再考虑重复情况,利用如下事实:若()2222, ,, ,x a b y c d a b c d =+=+≠≠则()()()()2222xy ac bd ad bc ac bd ad bc =++-=-++. 不超过40且能表为两个不同正整数的平方和的数有5,10,13,17,20,25,26,29,34,37,40,该组中的每个数与5的积,以及213都在集M 中,且都可用两种方式表为平方和,故各被计算了两次,累计有12次重复(10,13,17,20与10的积已包含在以上乘积组中).因此,集A 中元素个数的最大值为1455221279++-=.3.将前九个正整数1,2,,9 分成三组,每组三个数,使得每组中的三数之和皆为质数,求不同分法的种数．证:(1)由于在1,2,,9 中,三个不同的数之和介于6和24之间,其中的质数有7,11,13,17,19,23这六个,今将这六数按被3除的余数分为两类:{}7,13,19A =,其中每个数被3除余1；{}11,17,23B =,其中每个数被3除余2；假若分成的,,A B C 三组数对应的和,,a b c p p p 为互异质数,则因12945a b c p p p ++=+++= 被3整除,故三个和数,,a b c p p p 必为同一类数,因为A 类三数和713193945++=<,B 类三数和1117235145++=>,矛盾！故三个和数中必有两个相等．(2)据(1)知,将45表成7,11,13,17,19,23中的三数和(其中有两数相等),只有四种情况:①19197++；②171711++；③131319++；④111123++．由于在1,2,,9 中有5个奇数,故分成的三组中必有一组,三数全为奇数,另两组各有一个奇数．对于情形①,和为7的组只有{}1,2,4,剩下六数3,5,6,7,8,9,分为和为19的两组,且其中一组全为奇数,只有唯一的分法:{}3,7,9与{}5,6,8；对于情形②,若三奇数的组为{}1,7,9,则另两组为 {}{}4,5,8,2,3,6；或{}{}3,6,8,2,4,5；若三奇数的组为{}3,5,9,则另两组为 {}{}2,8,7,1,4,6,或{}{}4,6,7,1,2,8；若三奇数的组为{}1,3,7,则另两组为{}{}2,6,9,4,5,8；共得分法5种；对于情形③,若三奇数的组为{}3,7,9,则另两组为 {}{}1,4,8,2,5,6；若三奇数的组为{}1,3,9,则另两组为 {}{}2,4,7,5,6,8或{}{}2,5,6,4,7,8；若三奇数的组为{}1,5,7,则另两组为 {}{}3,4,6,2,8,9或{}{}2,3,8,4,6,9；共得分法5种；对于情形④,和为23的组只有{}6,8,9,则另两组为 {}{}1,3,7,2,4,5；据以上,共计得到155112+++=种分法．4.设{}1,2,,17M = ,若有四个互异数,,,a b c d M ∈,使得()mod17a b c d +≡+,就称{},a b 与{},c d 是集M 的一个“平衡对”,求集M 中“平衡对”的个数．解:将圆周17等分,其分点按顺时针方向顺次记为1217,,,A A A ,则()mod17m n k l +≡+当且仅当弦m n A A ∥k l A A ．注意如下事实:圆周17等分点的任一对分点连线都不是直径,因此全部弦共有17个方向(分别与过i A 的切线平行,1,2,,17i = )．与过i A 的切线平行的弦有8条,共形成2828C =个“平行弦对”,若考虑所有17个方向,共得2817476⨯=个“平行弦对”．即M 中有476个平衡对．5.某校有2009名新生,每人至少认识其中n 人,试求n 的最小值,使得其中必存在彼此认识的8个人.解:记该校2009名新生的集合为{}122009,,,M v v v = ,i v 所认识的人的集合为, 1,2,2009i A i = ,则i A n ≥,且 1,2,2009i i v A i ∉= ,若12,v v 是M 中相识的两人,则有121222009A A A A A B n =+-≥- , 当220091n -≥,则有312v A A ∈ ,且123,,v v v 两两相识,而()123123123322009A A A A A A A A A n =+-≥-⋅ . 当3220091n -⋅≥,则有4123v A A A ∈ ,且1234,,,v v v v 两两相识,而()123412341234432009A A A A A A A A A A A A n =+-≥-⋅ ,1234567891011121314151617如此继续,得127,,,v v v 两两相识,而76677111762009i i i i i i A A A A A n ===⎛⎫=+-≥-⋅ ⎪⎝⎭.当7620091n -⋅≥,则有781, i i v A =∈ 且128,,,v v v 两两相识,而由7620091n -⋅≥得6200917n ⋅+≥,n 为整数,则1723n ≥.再说明1723n =是最小的.若1722n =,我们可构造一种情形,使得M 中不存在相互认识的8个人．为此,将2009个人均分为127,,,B B B 等7组,每组287个人,令同组的人互不相识,而异组的任两人皆相识,则M 中任一人v 所认识的人的个数皆为()62871722d v =⨯=,从M 中任取8个人,必有两个人属于这7组中的同一个组,于是这两人互不相识,因此M 中不存在相互认识的8个人.从而n 的最小值为1723.6.12个赌徒每日聚赌一次,每次4人一桌,共设三桌.若任两人都至少同桌一次,问赌博至少需多少天？解:至少持续了五天.先说明,5天已够.记12个人为1,2,,12 ,将其两两搭配,记()1,2a =,()()()()()3,4, 5,6, 7,8, 9,10, 11,12b c d e f =====.先作模式搭配,安排如下:(一) ab cd ef ； (二) ac be df ； (三) ad bf ce ； (四) ae bd cf ； (五) af bc de .即: (一) ()()()1,2,3,4 5,6,7,8 9,10,11,12；(二) ()()()1,2,5,6 3,4,9,10 7,8,11,12； (三) ()()()1,2,7,8 3,4,11,12 5,6,9,10；(四) ()()()1,2,9,10 3,4,7,8 5,6,11,12； (五) ()()()1,2,11,12 3,4,5,6 7,8,9,10.其次说明至少需要五天,改记这12人为 1212,,,A A A ,任取一人1A ,他要与其他11人中的每个人分别同桌,每次同桌都有另外三人作陪,这样至少需要4天,但是11人不能等分成四个“三人组”,于是必有一人,例如2A ,至少两次与1A 同桌,设这两次为:12341256 , A A A A A A A A . 若只安排四天,在后续的两天中,其余6人 7812,,,A A A ,分别要与12,A A 同桌；为使1A 在这两天中能与这6人都同桌,需将6人等分成两组,每组3人,设这两天1A 所在的桌为:1789A A A A 与1101112A A A A ,为使2A 在这两天中也能与这6人都同桌,则这两天2A 所在的桌为:2101112A A A A 与2789A A A A ；由于12个赌徒每天都必需出场一次,于是在这两天中,第三桌的人都是3456A A A A ；但是7812,,,A A A 中至多有三人在第二天与3A 同桌,因此在这四天中,7812,,,A A A 中至少有三人与3A仍不能同桌,矛盾！因此至少需要五天.7.若四元集{,,,}E a b c d =中的四个数,,,a b c d 能够分成和相等的两组,则称E 为“平衡集”.试求集{1,2,,100}M = 的平衡子集的个数.引理:对于给定的正整数k 与集合{1,2,,}N n = ,用(,)f n k 表示不定方程x y k +=(其中; ,x y x y N <∈) ……… ①的解 (,)x y 的个数,则有()1 1 21(,)1 22 1 20 2 1k k n k f n k k n n k n k n ⎧-⎡⎤≤+⎪⎢⎥⎣⎦⎪⎪-⎡⎤=---+≤≤-⎨⎢⎥⎣⎦⎪⎪⎪>-⎩当当当 ……② 证:当1k n ≤+时,由x y k <<2x x y k ⇒<+=12k x -⇒≤12k x -⎡⎤⇒≤⎢⎥⎣⎦,而当x 取定后,y 的值便唯一确定,故此时()1,2k f n k -⎡⎤=⎢⎥⎣⎦. 当221n k n +≤≤-时,如在集N 中添加元素1,2,,1n n k ++- ,则可得12k -⎡⎤⎢⎥⎣⎦个解, 但是下列1k n --个解()()()(),1,1,2,2,,1,(1)x y k k k n k k n =------- 中皆含有添加元,不合条件.于是此时①的解数为()()1,12k f n k k n -⎡⎤=---⎢⎥⎣⎦. 又因集N 中的任两数之和21n ≤-,故当2 1 k n >-时, (),0f n k =.引理证完.回到本题,对于集M 中的平衡子集{,,,}E a b c d =, 如果,,,a b c d 中某两数之和等于另两数之和, 则称E 为A -型集；如果,,,a b c d 中某一数等于另三数之和,则称E 为B -型集. 一、先求A -型集的个数(记为()A ϕ). (1)当101k ≤,其个数为()1011011012111100,115111()1()()222f k k k k k k k k A CA A ϕϕϕ===-⎛-⎫⎡⎤⎡⎤'''==-==++ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭∑∑∑∑∑ 为奇数为偶数. 当k 为奇数时,记21k m =+,则当k 通过集{}5,6,,101 中的奇数时, m 通过集{}2,3,,50 , 所以()()501212m m m A ϕ=-'=∑.当k 为偶数时,记22k m =+,则当k 通过集{}5,6,,101 中的偶数时,m 通过集{}2,3,,49 ,所以()()491212m m m A ϕ=-''=∑.故()()()()491112504912m A A A m m ϕϕϕ=⨯'''=+=-+∑()48112549j j j ==++⨯∑40425=. (2)当102199,k ≤≤其个数为 ()()()()19919922100,102102111101100222f k k k k k A Ck k ϕ==⎛-⎫⎛-⎫⎡⎤⎡⎤==---- ⎪⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭∑∑, 令101,k k '=- 则 1100.k k '-=+ k '通过 {}1,2,,98. 于是()982115049222k k k A k k ϕ'=''⎛⎫⎛⎫⎡⎤⎡⎤''=-+-+ ⎪⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭⎝⎭∑k k ''=+∑∑ 为奇数为偶数()()22A A .ϕϕ'''+当k '为奇数时,令21k m '=+.当k '跑遍{1,2,,98} 中奇数时,m 跑遍{}0,1,,48 ,所以48484820011(1)(1)()(49)(48)222m j j j j j j A m m ϕ===++'=--==∑∑∑. 当k '为偶数时,令2k m '=. 当k '跑遍{1,2,,98} 中偶数时,m 跑遍{}1,2,,48 ,所以48482111(1)()(50)(49)22m j j j A m m ϕ==+''=--=∑∑.所以,()482221()()()139200j A A A j j ϕϕϕ='''=+=+=∑.因此,A 型集的个数为12()()()404253920079625A A A ϕϕϕ=+=+=. 二、再求B -型集的个数(记为()B ψ).对100k ≤,不定方程x y z k ++=(其中x y z <<,,,x y z M ∈)… ③的解数记为()g k . 显然,当5k ≤时,()0,g k =且由6123, 7124, 8125134=++=++=++=++知(6)1, (7)1, (8)2g g g ===.一般有, 当6k ≥,()(3)22k g k g k ⎡⎤--=-⎢⎥⎣⎦……… ④证明如下:对于k 的全体3元分拆 , k x y z x y z =++<< 将其分作两类:(1)含1的分拆x y z k ++=,其中1x =,将左边诸元,,x y z 各减1,化为(1)(1)3y z k -+-=-,即3y z k ''+=-形式,归入引理,即②式中的第一情形,其解数为(3)1222k k --⎡⎤⎡⎤=-⎢⎥⎢⎥⎣⎦⎣⎦. (2)不含1的分拆 x y z k ++=,其中1x >,将左边诸元各减1,化为(1)(1)(1)3,x y z k -+-+-=-即3x y z k '''++=-形式,其中1x y z '''≤<<,其解数为(3)g k -.因此()(3)22k g k g k ⎡⎤=-+-⎢⎥⎣⎦,即④成立.进而有6(6)(3)2122k k g k g k +⎡⎤⎡⎤+-+=-=+⎢⎥⎢⎥⎣⎦⎣⎦⑤ 31(3)()2122k k g k g k ++⎡⎤⎡⎤+-=-=-⎢⎥⎢⎥⎣⎦⎣⎦⑥ ⑤+⑥并注意,对任何k N ∈,有1,22k k k +⎡⎤⎡⎤+=⎢⎥⎢⎥⎣⎦⎣⎦ 所以(6)()g k g k k +=+ ⑦ 利用⑦递推得:,(6)()3(1)n N g k n g k kn n n ∀∈+=++- ⑧于是 2(99)(3616)(3)316316(161)316768g g g =+⨯=+⨯+⨯⨯-=⨯=,(100)(4616)(4)416316(161)784g g g =+⨯=+⨯+⨯⨯-=. 从而()()()()()()1001001581303991006m m n k B g m g m g g g k n ψ=======+++∑∑∑∑()()15880331552181n k k g k n k n n ===⎡⎤=+++-⎢⎥⎣⎦∑∑∑()1501552433181n n n n ==+++-⎡⎤⎣⎦∑()1521552641815n nn ==+++=∑15163115161616181525736.62⨯⨯⨯+⨯+⨯= 故M 中的平衡子集个数为()()7962525736105361A B ϕψ+=+=.8.设集合(){,M m n =│,m n 互质,}2009,02009m n m n +><<≤,求和(),1m n Mmns ∈=∑. 解:由于所给的数值2009较大,于是一般化,将2009换成任一不小于2的整数,k 为此取(){,,k M m n m n =互质,},0m n k m n k +><<≤,并记(),1kk m n M s mn∈=∑,分析k s 的变化趋势,易知, 2311111,,12213232s s ===+=⋅⋅⋅41111,1423342s =++=⋅⋅⋅ , 进而猜想,对于每个2,k ≥都有12k s =.转而考虑证明,对每个2,k ≥都有10k k s s +-=.其中(),1kk m n M s mn ∈=∑,()11,1k k m n M s mn++∈=∑. 先分解求和区间(和式展布集):(){,,k M m n m n =互质,},0m n k m n k +><<≤ {}1,0m n k m n k =+=+<<≤ {}1,0*m n k m n k M M '+>+<<≤= , (){1,,k M m n m n +=互质,}1,01m n k m n k +>+<<≤+{}{}1,011,0*m n k m n k m n k m n k M M ''=+>+<<=++>+<<≤= . 于是()()121111111k k k M M m k m s s mn mn m k m k m ++'''≤<-=-=-++-∑∑∑∑ ○1 (右端最后一个和式的求和范围是由于 1,m n k m <=+- 则 12k m +<).由于 ()11221111111k k m m m k m k m k m ++<<⎛⎫=-= ⎪+-++-⎝⎭∑∑112211111k k m m k m k m ++<<⎛⎫⎪+ ⎪++- ⎪⎝⎭∑∑ ○2 当 112k m +≤<时,112k k m k +<+-≤,则1112221111k k k m t k m kk m t m +++<<≤<≤==+-∑∑∑. 且由1m n k +=+ 以及 (),1m n =知,12k + 不会被,m n 取到. 从而○2式右端可合并为 111m k k m ≤+∑.据○1,即有 ()()111011k km k m k s s m k m k +≤≤-=-=++∑∑.于是可得1212k k s s s -====,因此200912s s ==.。

内力组合 (2)

5.7 内力组合： 5.7.1 确定抗震等级：结构抗震等级应根据烈度、结构类型和房屋高度确定。

对于框架—剪力墙结构，还应判别总框架承受的地震倾覆力矩是否大于总地震倾覆力矩（0M ）的50%，为此，应计算总框架承受的地震倾覆力矩（0v M ）。

由前表得：1001111417.037v fii i M Vh KN m ==⋅=∑0235322.937311.55240.5247940.793M KN m =+⨯=则有：0011417.0130.0.4490.50247940.793v M M ==< 因此，本工程应按框架—剪力墙结构中的框架确定抗震等级，查规范得本工程的框架抗震等级为三级，剪力墙抗震等级为二级。

5.7.2 组合表见附录 5.8 截面设计： 5.8.1 内力调整：对第1、7、9层构件内力进行调整，且为实现大震不倒的目标仅对有地震力参与的内力进行调整.5.8.1.1 强柱弱梁的调整——放大柱端弯矩顶层柱柱端弯矩不必放大，一层柱下端直接乘以放大系数1.15，其余层柱对轴压比0.15≥的进行柱端弯矩放大，放大系数 1.1c η=。

下面以第7层A 柱上端截面为例说明计算方法，其余计算过程从略，计算结果见表1-47。

柱轴压比31803.71100.310.1519.1550550c Nf A μ⨯===>⨯⨯，可见需调整内力' 1.1421.30463.43224.79''463.43260.61224.79174.94174.94''463.43202.82224.79174.94ccbcb cb c cb ct ct ct c cb ct MMKN mM M M KN m M M M M M KN mM M η==⨯===⨯=++==⨯=++∑∑∑∑表1-47 强柱弱梁内力调整计算表)m调整后-189.80 表中：弯矩正、负号同内力组合值。

组合1-2

注为了使上面的公式在m＝n时也能成立，
我们规定 Cn0 =1.
随堂练习
1.若C
2x 25 x2 15
，可分为以下2步：
一般地，求从n个不同元素中取出m个元
m 素的排列数 An ，可分为以下2步：
第1步，先求出从这n个不同元素中取出
m C m个元素的组合数 n ；
第2步，求每一个组合中m个元素的全排列数
m ． Am
根据分步计数原理，得到
A C A
m n m n
m m
•
m A n(n 1)(n 2) (n m 1) m n 因此. Cn m Am m!
C C
7 10
3 10
性质 1：C C
m n
nm n
• 证明：根据组合数的公式有
C
nm n
n! n! m Cn (n m)![n (n m)]! (n m)!m!

C C
m n
n m n
n 为简化计算，当 m> 时，通常将计 2
nm 算 Cnm 改为计算 C
2 A 43 2 4 6. 例如， C4 2 A2 2!
因为
n! A ，所以，上面的组合 (n m)!
m n
数公式还可以写成
n! C m !(n m)!
m n
例1．计算： 4 （1） C7 （1）解： C 4 7 6 5 4 35 7 4! （2）
答：以10个点中每2个点为端点的有向线段共
例4、甲，乙，丙，丁4个足球队举行单循环赛：（1）共需比赛多少场？列出各场比赛的双方；（2）冠亚军共有多少种可能？列出所有冠亚军情况。
43 6 场比赛.分别为解：（1）共需 C 2 1

飞星九星断事法

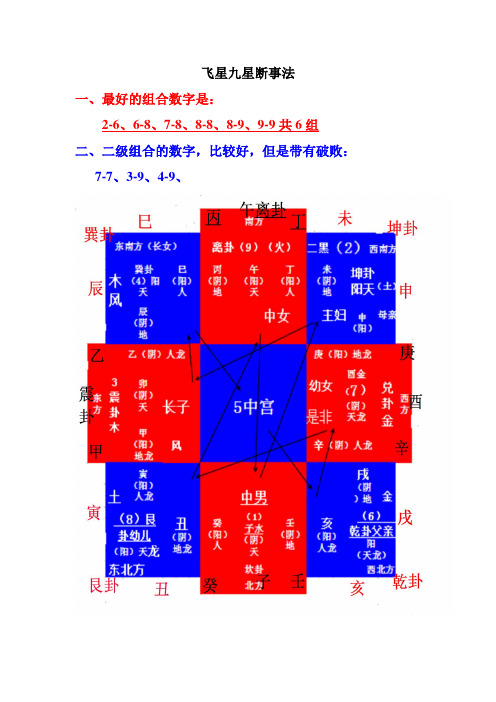
飞星九星断事法一、最好的组合数字是：2-6、6-8、7-8、8-8、8-9、9-9共6组二、二级组合的数字，比较好，但是带有破败：7-7、3-9、4-9、飞星组合容易发生哪些问题？1-1组合：为坎-水-子-正北方；代表中男、肾脏、性功能。

失令时，凡1的组合，都有点带凶、淫荡、不吉祥。

（1-1组合招小偷横祸，贪官污吏）1-2组合：1为水，2为土，代表母亲，土克水，有母亲赶走中男、或被年长、邻居的女人欺负的意思，不论一二同宫或是二一同宫，结果都一样。

（1-2组合，中男受气，离家出走不还乡）1-3组合：长男3震（东方木）与中男1坎（北方水）在一起，代表结伙招惹是非。

（1-3组合男人拉帮结派惹是非、关系不和）1-4组合：4为东南方（巽-木-长女）与1中男水在一起，有2种情况产生：（1）、当令时，(兴旺发达，风驰身贵，声名显赫)。

（2）、失令时，产生淫荡。

（1-4组合淫荡坏）1-5组合：5为五黄，土，克水，代表包二奶，患精神病、肾病、性病、肠病；中男在少年时有灾难。

（有病、中男少年时有灾难）。

（1-5组合中男大病有灾难）1-6组合：6为金，生水，水太旺。

精力好、家中混乱，年长男人和年轻男人都是色情。

（1-6组合全家男人嫖、败家）1-7组合：7为兑金，代表西方、白虎，生水，孕妇易堕胎、六畜伤亡、因水灾搬家。

（1-7组合孕妇有大难、全家水灾、财产损失；天灾人祸）1-8组合：8为东北方，幼男艮卦，属土，克水。

结果与1和2的组合是一样的。

（幼男受气，离家出走不还乡；小儿子有灾难）。

1-9组合：9为南方火，离卦，中女。

水克火。

如果水与火的关系处理得好，可以当皇帝、生男孩；处理不好，那就水火相冲，刀兵相见。

（19组合有好中介搭桥当皇帝，否则水火相冲，刀兵相见；家庭不团结）2-1组合与1-2组合相同。

（2-1伤仲子；中男有灾难）2-2组合：2为西南方，坤母，土。

得令时，子孙可以得到很多财产；失令时为大凶，2为病符，丈夫病死当寡妇。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例题3
课堂练习
例题4
abc
abd
acd
bcd
C 4
3 4
d
c
b
a
C 4
1 4
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
abc
abd
acd
bcd
2 3
C 4
3 4
含元素a 的组合数: 不含元素a 的组合数:
C 3
C 1
3 3

C C C

C C
.
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
写出从 a , b , c , d 四个元素中任取三个元素的所有组合。 c b d a c d b c d
abc ， abd ， acd ， bcd .
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
复习
一、组合的定义二、组合数公式
n(n 1)( n 2) (n m 1) P C m m! Pm
m n m n
n! C m !( n m ) !
m n
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
(1) C
m n 1 m 1 n m n 1 m 1 n 1
C
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
例3 平面内有12个点，任何3点不在同一直线上,以每3点为顶点画一个三角形,一共可画多少个三角形?
C
3 12
12 11 10 3 2 1
220
答:一共可画220个三角形.
(C 7 C C 21 15 6 42)
2 2 6 2 4
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
;
风水
hnq913dgk
160 条
很多，不厌其烦地说道，“这几年啤酒厂效益还算不错，企业人数不断扩大，进了不少人，目前共有七百多人。部门有单位办公室、财务科、生产科、质量科、供应科、物管科、总务科、销售科、人保科、宣教科、党委、工会、能计科、技改办、医务室、杂工组，还有幼儿园和计划生育办公室，反正该设的部门都设了，也许是为了和管理相关部门对接的方便。”“呵！人还真不少，为什么还要到外面去招人？”马启明不解地问道。张钢铁不是一般的健谈，而是相当健谈，对马启明的提问都能做出圆满地回答。马启明也尽量想从张钢铁那里了解啤酒厂的过去、现在。不是有一句话，忘记历史就等于背叛，为了更好地开创未来嘛。“你们是大学生，是技术人员，厂里很需要你们这些人，目前厂内有文凭的人还真不多。你们来的那天，厂长、总工都请你们吃饭，这说明啥？说明厂子对你们重视，好好干吧。你们将来大有用武之地。”“张主任，这个厂年产啤酒是多少？”马启明紧接着又问道，面对马启明接二连三的提问，张钢铁谈性更浓了，可以说是汹涌澎拜了。他立刻答道：“当初每年只有3000吨啤酒，现在每年啤酒产量大概是3万多吨。八十年代，花开啤酒在轻工部举办的全国啤酒竞赛中还获得了金奖，这在当时，真的是天大的荣誉。”张钢铁沉浸在美好的记忆当中，喜悦和自豪之情溢于言表。马启明激情被点燃了，脑海中突然灵光一动，迸出一个想法并脱口而出：“花开啤酒,雄鹰！”当初牛顿被苹果砸到头的时候，也是这样的吗！“花开啤酒，雄鹰，你说的是什么杲梓？”张钢铁有点丈二高的和尚——摸不着头脑。看着张钢铁不解的表情，马启明突然笑了：“我也不知怎地‘呼’地一下子感到花开啤酒就像一只展翅翱翔的雄鹰。”张钢铁仔细地想了一下，笑着说道：“对对对，花开啤酒就像一只雄鹰，在天空中翱翔的雄鹰，这个比喻比得好，花开啤酒就像雄鹰一样。”说着，他用欣喜的目光看着马启明，心想看来马启明没有把书念到狗肚里，这比喻打得贴切生动。马启明也迷茫地望着他，显而易见，刚才“杲梓”两字在他的脑子里还是一片空白。“杲梓是什么意思？”马启明问道。“杲梓是我们这个地方方言，就是东西的意思。言归正传，说到花开啤酒在全国啤酒竞赛中获得金奖的事，就不能不提到一个人，就是我们厂的总工程师、高级工程师、我国第一代啤酒专家、啤酒界的技术权威冯力雄。有一次我陪他出去参加全国性的啤酒技术研讨会，他在大会上做的专题报告，题目到现在我还记得，叫做《啤酒生产新技术与装备发展与展望》。演讲时整个会场鸦雀无声，会后向他请教的人挤得密密匝匝，那场面至今还历历在目，全国啤酒研讨会呀！”张钢铁看了一眼马启明、自豪地说。马启明也注意到，他在
10)
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2例题3课堂源自习例题4例4 有13个队参加篮球赛,比赛时先分成两组,第一组7个队,第二组6个队. 各组都进行单循环赛(即每队都要与本组其它各队比赛一场),然后由各组的前两名共4个队进行单循环赛决出冠军、亚军,共需要比赛多少场?
3 4 2 3
3 3
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
定理 2 :
C
m n
m n 1
C C .
m n m 1 n
证明 :
C C
m 1 n
n! n! m!( n m)! ( m 1)![ n ( m 1)]! n!( n m 1) n! m ( n m 1 m) n! m!( n m 1)! m!( n 1 m)! ( n 1)! m C n1 . m![( n 1) m]!
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
课堂练习
1. 从9名学生中选出3人做值日,有多少种不同的选法?
(C 9
3
987 3 2 1
84)
2. 有5 本不同的书,某人要从中借2本, 有多少种不同的借法?
(C 5
2
5 4 2 1
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
例１计算：
(1) C
198 200
;
(C 2 0 0
2
200 199 2 1
19900 )
(2) C C ;
3 99 2 99
C
3 100
100 99 98 3 2 1
3 9 2 8
161700
( 3 ) 2C C C .
3 8
单击课程内任何部分就转到下一步，或单击课程顶部对应内容
2 C (C C ) C C 56
3 8 3 8 2 8 2 8 3 8
复习
性质1
性质2
例题1
例题2
例题3
课堂练习
例题4
例2 求证:
C C ; m 1 m 1 m m 1 ( 2 ) C n C n 2C n C n 2 . m 1 m m 1 C n C n1 C n1 证明: ( 1 ) m 1 m 1 m m 1 C n m 2C n (2) C n Cn Cn m 1 m m m 1 (C ) ( ) C C C nm n n n C n1 . m 1 m C n1 C n1 m 1 C n 2 . 单击课程内任何部分就转到下一步，或单击课程顶部对应内容
性质2
例题1
例题2
例题3
课堂练习
例题4
组合数的两个性质
定理 1 :
C C
m n
m n
nm n
.
n！证明 : C , m（ ! n m） !
C
nm n
n！ n！ ( n m) ![ n （ n m） ] ! m !( n m ) !
m nm n n 单击课程内任何部分就转到下一步，或单击课程顶部对应内容

组合-2

魔能2各元素魔法技能组合列表

高中数学第一章计数原理1.2.2组合与组合数公式2课件新人教A版选修2_3

课件7：1.2.2 第二课时 组合的综合应用

魔能2各元素魔法技能组合列表

组合综合--2

内力组合 (2)

组合1-2

飞星九星断事法

课件7：1.2.2 第二课时　组合的综合应用