2019中考数学复习隐形圆问题大全(后有专题练习无答案)
2019中考-“隐形圆”问题(共22张PPT)全面.ppt

..
24
会出现。
..
3
..
4
..
5
..
6
对应练
1、如图,四边形ABCD中,AB=AC=AD,若 ∠CAD=76∘,则∠CBD=______度。
..
7
真题演练
1. 如图 1,四边形 ABCD 中,AB=AC=AD,若 ∠ CAD=76°,则∠ CBD= 度。
简答:如图 2,因为 AB=AC=AD,故 B、C、D 三点
..
23
班主任的专业发展一如治学之道,它 不是遥不可及的事情,而是我们正在
谢 谢! 实践的工作;但也不是一蹴而就的,
而是一个不断发展,持续提高的过程 。只要我们留守心中那盏信念的灯, 拥有一颗热爱教育,热爱学生的心, 再加上善于观察和反思教育生活的习 惯,必然会收获内心的幸福,获得丰
满的教育人生。
..
17
真题演练
1.如图 ,长 2 米的梯子 AB 竖直放在墙角,在沿着墙角缓慢下滑
直至水平地面过程中,梯子 AB 的中点 P 的移动轨迹长度为 ()
简答:由斜边上的中点等于斜边的一半可知,OP=1,动点P
到定点O的距离始终等于1, 满足圆的定义(到定点的距离
等于定长的点的集合叫做圆),故P的运动轨迹是圆弧,圆
简答:如图 2,因为 AP⊥BP,
∠P=90°(定角),AB=6(定弦),
故 P 在以 AB 为直径的⊙H 上 , 当
H 、 P 、 C 三 点 共 线 时 CP 最
短 ,HB=3,BC=4 则 HC=5, 故
CP=5-3=2 。
..
22
小结
以上例题说明,在求一类线段最值问题中,如果遇到
动点的运动路径是圆时,只需利用上面提到的方案1或方
中考数学“隐形圆模型”,“圆”来如此简单
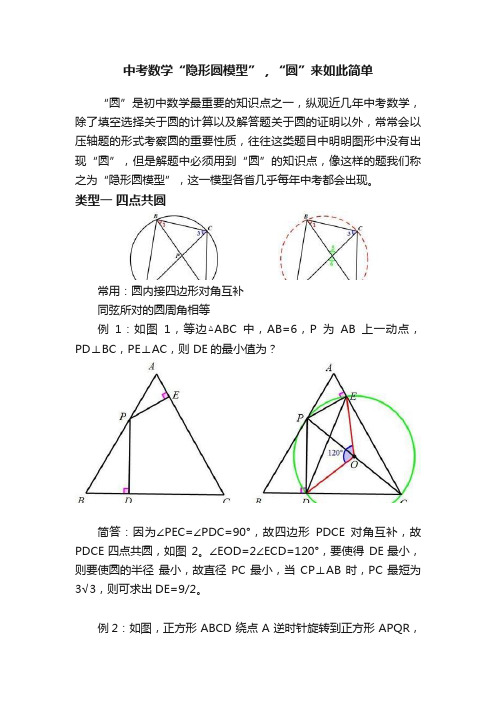
中考数学“隐形圆模型”,“圆”来如此简单“圆”是初中数学最重要的知识点之一,纵观近几年中考数学,除了填空选择关于圆的计算以及解答题关于圆的证明以外,常常会以压轴题的形式考察圆的重要性质,往往这类题目中明明图形中没有出现“圆”,但是解题中必须用到“圆”的知识点,像这样的题我们称之为“隐形圆模型”,这一模型各省几乎每年中考都会出现。
类型一四点共圆常用:圆内接四边形对角互补同弦所对的圆周角相等例1:如图1,等边△ABC中,AB=6,P为AB上一动点,PD⊥BC,PE⊥AC,则 DE的最小值为?简答:因为∠PEC=∠PDC=90°,故四边形PDCE对角互补,故PDCE四点共圆,如图2。
∠EOD=2∠ECD=120°,要使得DE最小,则要使圆的半径最小,故直径PC最小,当CP⊥AB时,PC最短为3√3,则可求出DE=9/2。
例2:如图,正方形 ABCD 绕点 A 逆时针旋转到正方形 APQR,连接 CQ,延长 BP 交于 CQ 于点 E,求证:E 是线段 CQ 的中点简答:因为 AC=AQ,AB=AP 且∠BAP=∠CAQ(旋转角相等)故△APB∽△AQC,故∠ABP=∠ACQ ,又因为∠1=∠2,故A、B、C、E 四点共圆(如图 2),因为∠ABC=90°,故 AC 是直径,故∠AEC=90°,又因为 AQ=AC,所以 AE 垂直且平分 QC(三线合一)类型二定义—动点到定点等于定长同一个端点处有多条相等线段时,要想到构造圆。
例:1:如图 1,四边形 ABCD 中,AB=AC=AD,若∠CAD=76°,则∠CBD= 度。
简答:如图 2,因为 AB=AC=AD,故 B、C、D 三点在以 A 为圆心的圆上,故∠CBD= 1/2∠CAD=38°例2:如图 1,长 2 米的梯子 AB 竖直放在墙角,在沿着墙角缓慢下滑直至水平地面过程中,梯子 AB 的中点 P 的移动轨迹长度为?.简答:由斜边上的中点等于斜边的一半可知,OP=1,动点P到定点O的距离始终等于1,满足圆的定义(到定点的距离等于定长的点的集合叫做圆),故P的运动轨迹是圆弧,圆心角为90°,轨迹长度为四分之一圆的长度。
中考数学专题:隐形圆解析

D
O
E
C
B
【分析】连接 CE ,由于 CD 为直径,故∠CED=90°,考虑到 CD 是动线段,故可以将此 题看成定线段 CB 对直角∠CEB .
A
D
E O
C
B
取 CB 中点 M,所以 E 点轨迹是以 M 为圆心、CB 为直径的圆弧.
A
D
E O
CM
B
连接 AM,与圆弧交点即为所求 E 点,此时 AE 值最小, AE AM EM 102 22 2 2 26 2 .
【2017 四川德阳】 如图,已知圆 C 的半径为 3,圆外一定点 O 满足 OC=5,点 P 为圆 C 上一动点,经过点 O 的直线 l 上有两点 A、B,且 OA=OB,∠APB=90°,l 不经过点 C,则 AB 的最小值为________.
C P
l AO B
【分析】连接 OP,根据△APB 为直角三角形且 O 是斜边 AB 中点,可得 OP 是 AB 的一半, 若 AB 最小,则 OP 最小即可.
【2019 扬州中考】 如图,已知等边△ABC 的边长为 8,点 P 是 AB 边上的一个动点(与点 A 、B 不重合).直 线 l 是经过点 P 的一条直线,把△ABC 沿直线 l 折叠,点 B 的对应点是点 B’.当 PB=6 时, 在直线 l 变化过程中,求△ACB ’面积的最大值.
A P
B
A
P F
C
E
B
【分析】考虑到将△FCE 沿 EF 翻折得到△FPE,可得 P 点轨迹是以 F 点为圆心,FC 为半径的圆弧. A
P F
C
E
B
过 F 点作 FH ⊥AB,与圆的交点即为所求 P 点,此时点 P 到 AB 的距离最小.由相似先求 FH ,再减去 FP, 即可得到 PH .
第24章 圆之专题练习:隐形的圆——“道是无圆却有圆”

专题:隐形的圆——“道是无圆却有圆”方法技巧常见的隐圆有两类:(1)到定点的距离等于定长的点在同一个圆上(圆的定义);(2)若定长线段的张角是定角(定弦定角),则定角的顶点在定弦所对的一条弧上运动.利用“辅助圆”的丰富性质转换角,求线段的长或最值是隐圆类问题的基本模式.题型一利用“定点定长”构隐圆【例1】如图,在 ABCD中,AB=4,BC=3,∠ABC=60°,点E为平面内的一动点,点P为CE的中点,若AE=1,求BP的最大值.【例2】如图,O是长度为4的线段AB上的一点,且OA=1,以OA为半径作⊙O,点M是⊙O上的一动点,连接MB,以MB为腰作等腰Rt△MBC,使∠MBC=90°(M,B,C三点为逆时针顺序),连接AC.求AC长度的取值范围.题型二 利用“定弦定角”构隐圆【例3】如图,在正方形ABCD 中,AC ,BD 是对角线,点P 为对角线BD 上的一点,作PE ⊥AP 交BC 于点E .若∠CAE =15°,求PBPE的值.【例4】如图,⊙O 的半径为1,AB 为⊙O 的弦,将弦AB 绕点A 逆时针旋转120°,得到AC ,连接OC ,求OC 长度的最大值.针对练习61.如图,已知AB 是⊙O 的直径,CD 是⊙O 的弦(CD 与AB 不平行),点M 是CD 的中点,CE ⊥AB 于点E ,DF ⊥AB 于点F .①当∠EMF =60°时,求CDAB的值;②当∠EMF =90°时,CD AB 的值为 ;当∠EMF =120°时,CDAB的值为 .AC上的一动点,PEAB上的一点,且∠AOC=120°,点P是⌒2.如图,AB是半圆⊙O的直径,点C是⌒⊥OA于点E,PF⊥OC于点F,CD⊥OB于点D,求证:EF=CD.3.如图,在四边形ABCD中,∠DAB=∠ABC=90°,AD=AB=1,BC=2,点P为射线DA上的一动点,过B,D,P三点的圆交PC于点Q.求DQ的最小值.4.如图,△ABC的两个顶点A,B在半径为6的⊙O上,∠A=30°,∠B=90°,点C在⊙O内.当点A在圆上运动,且OC的长最小时,求弦AB的长.。
2019中考复习 “隐形圆”问题(共22张PPT).ppt

∠P=90°(定角),AB=6(定弦),
故 P 在以 AB 为直径的⊙H 上 , 当
H 、 P 、 C 三 点 共 线 时 CP 最
短 ,HB=3,BC=4 则 HC=5, 故
CP=5-3=2 。
小结
以上例题说明,在求一类线段最值问题中,如果遇到
动点的运动路径是圆时,只需利用上面提到的方案1或方
1
在以 A 为圆心的圆上,故∠CBD= 2∠CAD=38°
对应练
1、如图①,在Rt△ABC中,AB=4,BC=3,将△ABC绕点B顺 时针旋转α(0<α<120∘)得△DBE,连接AD,EC,直线 AD、EC交于点M.在旋转的过程中,四边形ABCM的面 积是否存在最大值?若存在,求出四边形ABCM面积的 最大值;若不存在,请说明理由;
真题演练
1.如图 ,长 2 米的梯子 AB 竖直放在墙角,在沿着墙角缓慢下滑
直至水平地面过程中,梯子 AB 的中点 P 的移动轨迹长度为 ()
简答:由斜边上的中点等于斜边的一半可知,OP=1,动点P 到定点O的距离始终等于1, 满足圆的定义(到定点的距离 等于定长的点的集合叫做圆),故P的运动轨迹是圆弧,圆 心角为 90°,轨迹长度为四分之一圆的长度。
AC=6,BC=8,点 F 在边 AC 上,并且
CF=2,点 E为边 BC 上的动点,将△CEF
沿直线 EF 翻折,点 C 落在点 P 处,则
点 P 到边 AB 距离的最小值是( )。
简答:E 是动点,导致 EF、EC、EP 都在变化,但是 FP=FC=2 不变,故 P 点到 F 点的距离永远等于 2,故 P 在 ⊙F 上运动,如图 。由垂线段最短可 知,FH⊥AB 时,FH 最短, 当 F、P、 H 三点共线时,PH 最短,又因为 △AFH∽△ABC,所以 AF:FH:AH=5:4:3,又因为 AF=4,故 FH=3.2,又因为 FP=2,故 PH 最短为 1.2
2019年中考初三数学专题隐形圆

2019年中考初三数学专题系列辅助圆模型一:“隐形圆”解点的存在性模型分析“定边、定角”圆上找.具体来说:当边长一定,其所对角度也一定时,该角顶点在两段弧上.1. 如图,已知线段AB.(1)请你在图①中画出使∠APB=90°的所有满足条件的点P;(2)请你在图②中画出使∠APB=60°的所有满足条件的点P;(3)请你在图③中画出使∠APB=45°的所有满足条件的点P.2. (1)如图①,在矩形ABCD中,AB=2,BC=5.请你在图①中矩形ABCD的边上画出使∠BPC=90°的点P;(2)如图②,在矩形ABCD中,AB=2,BC=.请你在图②中矩形ABCD的边上画出使∠BPC=60°的点P;(3)如图③,在正方形ABCD中,AB=2,BC=.请你在图③正方形ABCD的边上画出使∠BPC=45°的点P.3. 如图,线段AB和动点C构成△ABC,AB=2,∠ACB=120°,则△ABC周长的最大值为___________..模型二:“隐形圆”解角的最值模型分析同弧所对的圆周角相等,其所对的“圆外角”小于圆周角,“圆内角”大于圆周角. 如图①,∠B=∠D =∠E;如图②,∠F>∠B>∠G.4. 如图,线段AB是球门的宽,球员(前锋)在距球门前一定距离的直线b上,在直线b上是否存在一点P,使得球员在P点射门更易进球?若存在这样的点,请找出;若不存在,请说明理由.5. 如图,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点.(1)使∠APB=30°的点P有________个;(2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标;(3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,请说明理由.模型三:“隐形圆”解线段的最值模型分析平面内一定点D和⊙O上动点E的连线中,当连线过圆心O时,线段DE有最大值和最小值. 具体分以下三种情况讨论(规定OD=d,⊙O半径为r):第一种:当点D在⊙O外时,d>r,如图①、②:当D,E,O三点共线时,线段DE出现最值,DE的最大值为(d+r),DE的最小值为(d-r);第二种:当点D在圆上时,d=r,如图③:当D,E,O三点共线时,线段DE出现最值,DE的最大值为d+r=2r (即为⊙O的直径),DE的最小值为d-r=0(点D,E重合);第三种:当点D在⊙O内时,d<r,如图④、⑤:当D、E、O三点共线时,线段DE出现最值,DE的最大值为d+r,DE的最小值为r-d.6. 如图,已知⊙O及其圆外一点C,请在⊙O上找一点P,使其到点C的距离最近.7. 如图,已知正方形ABCD的边长为4.点M和N分别从B,C同时出发,以相同的速度沿BC,CD方向向终点C和D 运动.连接AM和BN,交于点P,则PC长的最小值为_________(请在图中画出点P的运动路径)8. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB上一个动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C的最小值为___________.(请在图中画出点A′的运动路径)9. 如图,∠AOB=45°,边OA,OB上分别有两个动点C,D,连接CD,以CD为直角边作等腰直角△CDE,当CD长保持不变且等于2 cm时,则OE的最大值为___________..模型四:“隐形圆”解面积的最值模型分析三角形中,若一边长为定值,这一边所对的角度也为定值,则满足条件的点在两段弧上运动,当这个角的顶点在其对边的中垂线与弧的交点处时该三角形的面积达到最大,此时该三角形为等腰三角形.例:如图,AB=2,∠APB=90°,要求S△APB的最大值,当且仅当PO⊥AB时,△APB的面积最大.10. 如图,在四边形ABCD中,AD∥BC,BD⊥DC,若AD=2,BC=4,则四边形ABCD面积的最大值是___________..11. 如图,已知在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=30°,AC=4,则四边形ABCD面积的最小值是___________.12. 如图,在△ABC中,AB=2,∠ACB=45°,分别以AC,BC为边向外作正方形ACED,正方形CBMN,连接EN,则△ECN面积的最大值为___________.___..13.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为()A. B. C. D.13.如图,在Rt△ABC中,∠B=60∘,BC=3,D为BC边上的三等分点,BD=2CD,E为AB边上一动点,将△DBE沿DE折叠到△DB′E的位置,连接AB′,则线段AB′的最小值为:___________.14.如图,O 的直径为4,C 为O 上一个定点,∠ABC =30∘,动点P 从A 点出发沿半圆弧AB ˆ向B 点运动(点P 与点C 在直径AB 的异侧),当P 点到达B 点时运动停止,在运动过程中,过点C 作CP 的垂线CD 交PB 的延长线于D 点。
隐形圆最值问题初中题型

隐形圆最值问题初中题型隐形圆最值问题是初中数学中的一个常见题型,它涉及到圆的最值问题,需要通过分析,计算得出圆的最大或最小值。
这个问题一般涉及到最大面积、最小周长或最小直径等方面,下面我将以最大面积为例来详细介绍。
我们来解释什么是隐形圆。
隐形圆是指在平面上已知一个角度和一个弦长,需要求得这个角度上的圆的最大面积。
我们可以先确定圆心在这个角的端点上,然后通过圆心和角的端点来画圆。
这个圆称为隐形圆,因为它不是直接给出的,而是需要我们通过问题的条件来确定。
解决隐形圆最值问题的关键是画出合适的图形并找到相关的性质和定理。
在求解最大面积问题时,我们可以使用面积公式S=πr²来表示圆的面积,其中r是半径。
由于隐形圆的圆心位于角的端点上,因此圆心和角的两个端点构成一个等腰三角形,这是求解问题的关键。
为了方便分析,我们可以将该等腰三角形的一个顶点放在坐标系的原点,另一个顶点放在x轴上,并设该顶点的坐标为(1, 0)。
由于是等腰三角形,所以圆心的坐标也可以设为(a, b),其中a和b是待定的参数。
假设圆的半径为r,则圆的方程为(x - a)² + (y - b)² = r²根据等腰三角形的性质,我们可以得到圆心的另一个坐标(a, b)满足a² + b² = 1。
这个条件可以用来确定圆心的位置。
接下来,我们要利用已知的角度和弦长的信息来确定圆心和半径。
设角的顶点坐标为(cosθ, sinθ),其中θ是已知的角度。
根据弦长的性质,我们可以得到圆心到角的顶点的距离为r,即(a - cosθ)² + (b - sinθ)² = r²将圆心的坐标代入上式,得到(cosθ - a)² + (sinθ - b)² = r²综合以上两个方程,我们可以得到关于a和b的方程组。
通过求解这个方程组,我们可以得到圆的半径r。
微专题09.02 “隐形圆”问题

微专题08.02 “隐形圆”问题一、问题概述江苏高考考试说明中圆的方程是C 级知识点,每年都考,但有些时候,在条件中没有直接给出圆的相关信息,而是将圆隐藏于题目中的,隐晦地考查点和圆、直线和圆、圆和圆的位置关系。
要通过分析和转化,发现圆(或是圆的方程),从而最终可以利用圆的知识来求解,我们称此类问题为“隐形圆”问题.如何发现“隐形圆”(或圆的方程)是本讲内容的关键,常见的有以下策略: 二、释疑拓展策略一 利用圆的定义(到定点距离等于定长的点的轨迹)确定隐形圆1.如果圆()()43222=--+-a y a x 上总存在两个点到原点的距离为1,则实数a 的取值范围是_________.2.【2016南京二模】已知圆O :122=+y x ,圆M :()()1422=+-+-a y a x ,若圆M 上存在点P ,过点P 作圆O 的两条切线,切点为A ,B ,使得ο60=∠APB ,则a 的取值范围为_________.3.【2017苏北四市一模.13题】已知B A 、是圆1:221=+y x C 上的动点,3=AB ,P是圆()()143:222=-+-y x C 的取值范围是_________.策略二 动点对两定点A 、B 的张角是ο90()01=•-=•K K PB PA 或确定隐形圆1.【2014.北京高考】已知圆()()14322=-+-y x C :和两点()()0,,0,m B m A -若圆上存在点P ,使得∠APB =90°则m 的取值范围是_________.2.(2017南京二模)在平面直角坐标系xoy 中,直线021=+-y kx l :与直线02:2=-+ky x l 相交于点P ,则当实数k 变化时,点P 到直线04=--y x 的最大值为_________.3.【南通市通州区2017届高三下学期开初检测】设R m ∈,直线0:1=+my x l 与直线042:2=---m y mx l 交于),(00y x P ,则020202x y x ++的取值范围_________.策略三 两定点A 、B ,动点P 满足λ=•确定隐形圆1.(2017南通密卷3)已知点A (2,3),点B (6,-3),点P 在直线0343=+-y x 上,若满足不等式02.=+λ的点P 有两个,则实数λ的取值范围是_________.2.【盐城市2016届高三三模.11题】已知线段AB 的长为2,动点C 满足CA CB λ⋅=u u u r u u u r(λ为常数),且点C 总不在以点B 为圆心,12为半径的圆内,则负数λ的最大值是_________.策略四 两定点A 、B ,动点P 满足22PB PA +是定值确定隐形圆1.在平面直角坐标系xoy 中,已知圆()()1222=+-+-a y a x C :,点A(0,2),若圆C 上存在点M ,满足1022=+MO MA ,则实数a 的取值范围是_________.2.(徐州市2017届高三考前模拟卷)已知,,,A B C D 四点共面,2BC =,2220AB AC +=,3CD CA=u u u r u u u r,则||BD uuu r 的最大值为 .延伸:到两个动点A 、B (A 、B 间距离定),动点P 满足22PB PA +是定值确定隐形圆 3.已知A 、B 为直线x y l -=:上两动点,且AB=4圆026622=+--+y x y x C :满足1022=+PB PA 则线段AB 中点M 的横坐标取值范围为_________.策略五 已知两定点A 、B ,动点P 满足()10≠>=λλλ且PBPA确定隐形圆(阿波罗尼斯圆)1.(2008江苏高考)满足条件AB = 2,AC = 2BC 的∆ABC 的面积的最大值是______. 2.【南通市2016届高三下学期第一次调研测试11题】在平面直角坐标系xOy 中,点)0,4(),0,1(B A .若直线0=+-m y x 上存在点P ,使得PB PA 21=,则实数m 的取值范围是 .3.【常州市2016届高三第一学期期末考试】在平面直角坐标系xOy 中,已知圆O :x 2+y 2=1,O 1:(x -4)2+y 2=4,动点P 在直线x +3y -b =0上,过P 分别作圆O ,O 1的切线,切点分别为A ,B ,若满足PB =2PA 的点P 有且只有两个,则实数b 的取值范围是________.策略六 相关点法确定隐形圆1.在平面直角坐标系xOy 中,若直线(y k x =-上存在一点P ,圆22(1)1x y +-=上存在一点Q ,满足3OP OQ =u u u r u u u r,则实数k 的最小值为_________.2.【苏北四市2018届高三第一次调研检测12题】在平面直角坐标系xOy 中,若圆1C :222(1)(0)x y r r +-=>上存在点P ,且点P 关于直线0x y -=的对称点Q 在圆2C :22(2)(1)1x y -+-=上,则r 的取值范围是 .策略七 利用圆周角的性质确定隐形圆1.已知,a ,b ,c 是△ABC 的三角内角A,B,C 的对边,2=a ,C b c B A b a sin )()sin )(sin (-=-+,则△ABC 面积的最大值是 .2.【2017年常州一模】在△ABC 中,∠C=45。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.应用:
(1)如图,四边形ABCD
二定线+定角
1.依据:与一条定线的两端夹角一定的动点路径是以定线为弦,定角为圆周角的弧。
2.应用:
(1)矩形ABCD中,AB=10,AD=4,点P是CD上的动点,当∠APB=90°时求DP的长.
简析:AB为定线,∠APB为定角(90°),P点路径为以AB为弦(直径)的弧,如下图,易得DP为2或8。
(2)如图,∠XOY = 45°,等边三角形ABC的两个顶点A、B分别在OX、OY上移动,AB = 2,那么OC的最大值为.
简析:作ΔABC的处接圆
(4)如图,在平面直角坐标系中
三三点定圆
1.依据:不在同一直线上的三点确定一个圆。
2.应用:
ΔABC中,∠A=45°,AD⊥BC于D,BD=4,CD=6,求AD的长。
简析:作ΔABC的外接圆,如下图,易得AD=7+5=12。
四四点共圆
1.依据:对角互补的四边形四个顶点共圆(或一边所对两个角相等)。
2.应用:
如图,在矩形ABCD中, AB=6,AD=8,P、E分别是线段AC、BC上的点,四边形PEFD为矩形,若AP=2,求CF的长。
简析:因∠PEF=∠PDF=∠DCE=90°,知D、F、C、E、P共圆,如下图,由∠1=∠2、∠4=∠5,易得ΔAPD∼ΔDCF,CF:AP=CD:AD,得CF=1.5。
五旋转生圆
1.如图,圆O的半径为5,A、B是圆上任意两点,且AB=6,以为AB边作正方形ABCD(点D、P在直线两侧),若AB边绕点P旋转一周,则CD边扫过的面积为_____ 。
简析:CD旋转一周扫过的图形可以用两点确定,一是最远点距离为PC,二是最近点距离为P到直线CD的垂线段,从而确定两个圆,CD即为两圆之间的圆环,如下图。
2.如图,在ΔABC中,∠BAC=90°,AB=5cm,AC=2cm,将ΔABC绕顶点C按顺时针方向旋转至ΔA'B'C的位置,则线段AB扫过区域的面积为_____。
简析:扫过的阴影部分旋转拼合成如下圆心角为45度的扇环。
六动圆综合
1.动圆+定弦:依据直径是圆中最长的弦,知此弦为直径时,圆最小。
如图, △ABC中, ∠ABC=90°, AB=6, BC=8, O为AC的中点, 过O作OE⊥OF, OE、OF分别交射线AB、BC于E、F, 则EF的最小值为.
简析:图中显然O、E、F、B共圆,圆是动的,但弦BO=5,当BO为直径时最小,所以EF最小为5.
2.动圆+定线:相切时为临界值。
如图, Rt△ABC中, ∠C=90°, ∠ABC=30°, AB=6, 点D在AB边上, 点E是BC边上一点 (不与点B、C重合), 且DA=DE, 则AD的取值范围是。
简析:因DA=DE,可以D点为圆心以DA为半径作圆,则圆D与BC相切时,半径DE最小。
E向B点移动半径增大直至D到B处(不含B点),得2≤AD<3。
3.动弦+定角:圆中动弦所对的角一定,则当圆的直径最小时此弦长最小。
已知:△ABC中,∠B=45°,∠C=60°,D、E分别为AB、AC边上的一个动点,过D分别作DF⊥AC于F,DG⊥BC于G,过E作EH⊥AB于H,EI⊥BC 于I,连FG、HI,
求证:FG与HI的最小值相等。
简析:可以看HI何时最小,因B、H、E、I共圆,且弦HI所对圆周角一定,所以当此圆直径最小时弦HI最小,即当BE最小时,此时BE⊥AC,解△OHI 可得HI的最小长度。
同样可求FG的最小长度。
此题可归纳一般结论:当∠ABC=α,∠ACB=β,BC=m时,FG和HI的最小值均为m*sinα*sinβ。
达标测试:
1.BC=AC=6,∠BCA=90°,∠BDC=45°,AD=2,求BD.
2.如图,将线段AB绕点A逆时针旋转60°得到线段AC,继续旋转α(0°<α<120°)得到线段AD,连接CD,BD,则∠BDC的度数为.
3.如图,在边长为2√3的等边△ABC中,动点D、E分别在BC、AC边上,且保持AE=CD,连接BE、AD,相交于点P,则CP的最小值为____.
4.如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC 的外角平分线于点F,求证:FE=DE.
5.当你站在博物馆的展厅中时,你知道站在何观赏最理想吗?如图,设墙壁上的展品最高点P距离地面2.5米,最低点Q距地面2米,观察者的眼睛E距地面1.6米,当视角∠PEQ最大时,站在此处观赏最理想,则此时E 到墙壁的距离为米.
6.如图直线y=x+2分别与x轴,y轴交于点M、N,边长为1的正方形OABC 的一个顶点O在坐标系原点,直线AN与MC交于点P,若正方形OABC绕点O旋转一周,则点P到点(0, 1)长度的最小值是____.。
