2020届中考数学复习第四章几何初步与三角形第三节等腰三角形与直角三角形随堂演练_
2020年初三数学中考复习 :等腰三角形和直角三角形 知识点梳理和练习 无答案
等腰三角形和直角三角形知识框架知识点梳理:一、等腰三角形1.等腰三角形定义:有相等的三角形叫做等腰三角形。
2.等腰三角形的性质:等腰三角形的两个底角,简称:等边对等角。
(2)等腰三角形的、、互相重合,简称:三线合一。
等腰三角形是轴对称图形,它的对称轴是。
3.等腰三角形的判定:有相等的三角形是等腰三角形;(2)有相等的三角形是等腰三角形。
4.等边三角形:的三角形叫做等边三角形;等边三角形的每个角都是,各边;等边三角形的外心、、互相重合成一点;等边三角形是轴对称图形,有条对称轴;若等边三角形边长为a,则其外接圆半径R=,内切圆半径r=,一边上的高h=,其面积S=.5.等边三角形的判定:(1)的三角形是等边三角形;(2)三个角的三角形是等边三角形;(3)有一个是60°的是等边三角形。
二、直角三角形1.直角三角形定义(1)有一个角是的三角形叫做直角三角形。
2.直角三角形的性质(1)直角三角形中,两个锐角;(2)直角三角形中,斜边上的中线等于;(3)在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于。
3.直角三角形的判定(1)两个内角的三角形是直角三角形(2)有一边上的等于这边的一半的三角形是直角三角形。
4.勾股定理及其逆定理(1)勾股定理:直角三角形的两直角边a、b 的,等于斜边c的,即:。
(2)勾股定理的逆定理:如果三角形的三边长a、b、 c有关系:,那么这个三角形是直角三角形。
故勾股定理的逆定理可以判断某三角形是否为直角三角形、证明两条线段是否垂直。
DF EA BC复习练习1已知等腰三角形的两边长为2和5,则它的周长为( ) A .12或9 B .12 C .9 D .72某地地震过后,河沿村中学的同学用下面的方法检测教室的房梁是否水平:在等腰直角三角尺斜边中点拴一条线绳,线绳的另一端拴一个铅锤,把这块三角尺的斜边贴在房梁上,结果线绳经过三角尺的直角顶点,同学们由此确信房梁是水平的,它们判定的依据是( )A .等边对等角B .等角对等边C .等腰三角形底边上的中线和底边上的高重合D .等腰三角形平分线与底边上的中线重合3如图,在△ABC 中,BE 、CE 分别是∠ABC 和∠ACB 的平分线,过点E 作DF ∥ BC 交AB 于D ,交AC 于F ,若AB =4, AC=3,则△ADF 周长为( )A .6B .7C .8D .104. 如图,在△ABC 中,∠C=90°,AB 的垂直平分线MN 分别交AC ,AB 于点D ,E . 若∠CBD : ∠DBA =3:1,则∠A 为( ).A .18°B .20°C .22.5°D .30°ED C BANM5.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为().A.1 B.1.5 C.2 D.2.56. 如图所示,长方形ABCD中,AB=4,BC=43,点E是折线段A—D—C上的一个动点(点E与点A不重合),点P是点A关于BE的对称点.在点E运动的过程中,能使△PCB为等腰三角形.....的点E的位置有().A.2个 B.3个 C.4个 D.5个7. 如下图,矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为()A.14 B.16 C.20 D.288. 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8 m,则乘电梯从点B到点C 上升的高度h是()A.43m B.8 m C.833m D.4 m AB CDEPAC D15h9.《九章算术》是我国古代的数学名著,书中的“折竹抵地”问题: 今有竹高一丈,末折抵地,去本三尺.问折者高几何?意思是:一根竹子,原高一丈(一丈=10尺),一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部3尺远, 问折断处离地面的高度是多少?设折断后离地面的高度为x 尺,则可列方程为( )A .223(10)x x -=-B .2223(10)x x -=-C .223(10)x x +=-D .2223(10)x x +=-10.如图,钝角三角形纸片ABC 中,∠BAC=110°,D 为AC 边的中点.现将纸片沿过点D 的直线折叠,折痕与BC 交于点E ,点C 的落点记为F .若点F 恰好在BA 的延长线上,则∠ADF = .11. 如图,△ABC 是等边三角形,D 是BC 边的中点,点 E 在AC 的延长线上,且∠CDE =30°.若DE=_________.12.如图,在∆ABC 中,AD 平分∠BAC ,⊥BD AD ,点E 是BC 的中点,连结DE ,且6=AB ,10=AC ,则=DE .12.下图是由三个直角三角形组成的梯形,根据图形,写出一个正确的等ECD ABDAEBC式 .13.2002年8月,在北京召开国际数学家大会,大会的会标取材于我国古代数学家赵爽的《勾股圆方图》.其中的“弦图”是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,如图所示.如果直角三角形的直角边分别为a,b(a>b),斜边为c,那么小正方形的面积可以表示为___________.14.如图是矗立在高速公路边水平地面上的交通警示牌,经过测量得到如下数据:AM=4米,AB=8米,∠MAD=45°,∠MBC=30°,则CD的长为米.(结果保留根号)15.如图,一张三角形纸片ABC,其中∠C=90,AC=6,BC=8.小静同学将纸片做两次折叠:第一次使点A落在C处,折痕记为m;然后将纸片展平做第二次折叠,使点A落在B处,折痕记为n.则m,n的大小关系是.AB Cbaa b16.下面是小明同学设计的“已知底边及底边上的高作等腰三角形”的尺规作图的过程.已知:如图1,线段a 和线段b .求作:△ABC ,使得AB = AC ,BC = a ,BC 边上的高为b . 作法:如图2,① 作射线BM ,并在射线BM 上截取BC = a ; ②作线段BC 的垂直平分线PQ ,PQ 交BC 于D ; ③ 以D 为圆心,b 为半径作圆,交PQ 于A ; ④连接AB 和AC .则△ABC 就是所求作的图形.根据上述作图过程,回答问题:(1)用直尺和圆规,补全图2中的图形; (2)完成下面的证明:证明:由作图可知BC = a ,AD = b .∵ PQ 为线段BC 的垂直平分线,点A 在PQ 上, ∴ AB = AC ( )(填依据). 又∵ AD 在线段BC 的垂直平分线PQ 上, ∴ AD ⊥BC .∴ AD 为BC 边上的高,且AD = b .17.下面是小东设计的“已知两线段,求作直角三角形”的尺规作图过程. 已知:线段a 及线段b (a b ).图1图2MD B求作:Rt△ABC,使得a ,b 分别为它的直角边和斜边. 作法:如图,①作射线CM ,在CM 上顺次截取CB BD a ==;②分别以点C ,D 为圆心,以b 的长为半径画弧,两弧交于点A ; ③连接AB ,AC .则△ABC 就是所求作的直角三角形. 根据小东设计的尺规作图过程, (1)补全图形,保留作图痕迹; (2)完成下面的证明. 证明:连接AD∵ =AD ,CB= ,∴90ABC ∠=︒( )(填推理的依据).18.如图,河的两岸l 1与l 2互相平行,A 、B 是l 1上的两点,C 、D 是l 2上的两点.某同学在A 处测得∠CAB=90°,∠DAB=30°,再沿AB 方向走20米到达点E (即AE=20),测得∠DEB=60°.求:C ,D 两点间的距离.119.如图,在Rt△ABC中,∠ABC=90 °,CD平分∠ACB交AB于点D,DE⊥AC 于点E,BF∥DE交CD于点F.求证: DE=BF.20.如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12.(1)求AD的长;(2)若∠CAB=30°,求四边形ABCD的周长.AC DE21.已知:如图,Rt△ABC,BM是边AC上的中线,AC=AD,N是CD边中点,连接MN.求证:△BMN是等腰三角形22.如图△ABC中,∠C=90°,M是CB的中点,MD⊥AB于D,请说明三条线段AD、BD、AC总能构成一个直角三角形.AD23.△ABC是等边三角形,以点C为旋转中心,将线段CA顺时针方向旋转60°得到线段CD,连接BD交AC于点O.(1)如图1,①求证:AC垂直平分BD;②点M在BC的延长线上,点N在线段CO上,且ND=NM,连接BN,判断△MND 的形状,并加以证明;(2)如图2,点M在BC的延长线上,点N在线段AO上,且ND=NM,补全图2.求证: NA = MC.24.如图,△ABC和△ADE中,AB=AD=6,BC=DE,∠B=∠D=30°,边AD 与边BC交于点P(不与点B,C重合),点B,E在AD异侧,I为△APC的内心.(1)求证:∠BAD=∠CAE;(2)设AP=x,请用含x的式子表示PD,并求PD的最大值;(3)当AB⊥AC时,∠AIC的取值范围为m°<∠AIC<n°,分别直接写出m,n的值.。
人教版初中数学中考考点系统复习 第19讲 等腰三角形与直角三角形

60°
的三角形是等边三角形;
(2)三个内角都⑰
的三角形是等边三角形;
定
(3)有一个角是⑱
的等腰三角形是等边三角形
面
【拓展补充】如图,顶角为36°(或底角为72°)的等腰三角形叫做黄金三角形. 性质:
(2)底角的平分线BF将其分成底角为36°(△ABF)和顶角为36°(△BCF)的 等腰三角形; (3)过点F作FE⊥AB于点E,则EF为腰AB的垂直平分线.
A.60°
B.70°
C.80°
D.90°
第2题图
3.(甘肃中考)如图,等边三角形OAB的边长为2,则点B的坐标为( B )
A.(1,1)
第3题图
4.在平面直角坐标系中,已知A(2,2),B(4,0).若在坐标轴上取点C,使 △ABC为等腰三角形,则满足条件的点C的个数是( A )
A.5
B.6
C.7
三角形的性质或三角函数进行求解.
对点训练 8.(2022·荆门)如图,一座金字塔被发现时,顶部已经荡然无存,但底部未曾受
损.已知该金字塔的下底面是一个边长为120 m的正方形,且每一个侧面与地面 的夹角为60°,则金字塔原来的高度为( B ) A.120 m
9.(陕西中考)如图,在3×3的正方形网格中,每个小正方形的边长均为1,点 A,B,C都在格点上,若BD是△ABC的高,则BD的长为( D )
质 (4)等腰三角形是轴对称图形,有1条对称轴,对称轴为顶角⑤ 平分
线 所在的直线(如图中AD所在的直线)
(1)有两条边相等的三角形是等腰三角形; 判
(2)如果一个三角形有两个角⑥ 相等 ,那么这两个角所对的边也
(部编版)2020届中考数学一轮复习第四章几何初步第3节全等三角形试题7

第三节全等三角形课标呈现指引方向1.理解全等三角形的概念,能识别全等三角形中的对应边、对应角.2.掌握基本事实:两边及其夹角分别相等的两个三角形全等.3.掌握基本事实:两角及其夹边分别相等的两个三角形全等.4.掌握基本事实:三边分别相等的两个三角形全等.5.证明定理:两角分别相等且其中一组等角的对边相等的两个三角形全等,考点梳理夯实基础1.全等图形:能够完全重合的两个图形叫做__全等图形__.注:能够完全重合即形状、大小完全相同.2.全等三角形:能够完全重合的两个三角形叫做__全等__三角形.3.全等三角形的性质:(1)全等三角形的对应边__相等__;全等三角形的对应角__相等__.(2)全等三角形的对应线段(角平分线、中线、高线)__相等__,周长__相等__,面积__相等__.4.一般三角形全等的判定:(1)若两个三角形的三条边分别__对应相等__,那么这两个三角形全等,简记为“SSS”;(2)若两个三角形的两边及其__夹角__分别相等,那么这两个三角形全等,简记为“SAS”:(3)若两个三角形的两角及其__夹边__分别相等,那么这两个三角形全等,简记为“ASA”:(4)若丙个三角形的两角及其中一角的对边分别对应相等,那么这两个三角形全等,简记为__“AAS"__.5.直角三角形全等的判定:(1)两直角边对应相等的两个直角三角形全等;(2)一边一锐角对应相等的两个直角三角形全等;(3)若两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等,简记为__“HL”__.6.寻找对应边、对应角的方法:(1)有公共边的,公共边一定是对应边;(2)有公共角的,公共角一定是对应角;(3)有对顶角的,对顶角一定是对应角;(4)两个全等三角形中一对最长的边(或最大的角)是对应边(角),一对最短的边(或最小的角)是对应边(或角).7.证明三角形全等的思路:(1)已知两边:①找夹角(SAS);②找直角(HL);③找第三边( SSS).(2)已知一边和一角:①边为角的对边,找任意一角(AAS);②边为角的邻边,找夹角的另一边(SAS);③找夹边的另一角(ASA);④找边的对角(AAS).(3)已知两角:①找夹边(ASA);②找角的对边(AAS).考点精析专项突破考点一三角形全等判定方法的选择【例l】(2016云南)如图,已知∠ABC= ∠BAD,添加下列条件还不能判定△ABC≌△BAD的是 ( A )A.AC = BDB.∠CAB=∠DBAC.∠C=∠DD.BC=ADAAA 、SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角. 【例2】(2015泰州)如图,△ABC 中,AB =AC ,D 是BC 的中点,AC 的垂直平分线分别交AC 、AD 、AB 于点E 、O 、F ,则图中全等三角形的对数是 ( D ) A .1对B .2对 C .3对D .4对解题点拨:根据已知条件“AB =AC .D 为BC 中点”,得出△ABD ≌△ACD ,然后再由AC 的垂直平分线分别交AC 、AD 、AB 于点E 、O 、F ,推出△AOE ≌△EOC ,从而根据“SSS ”或“SAS ”找到更多的全等三角形,要由易到难,不重不漏.考点二 全等三角形的性质与判定综合【例3】如图,在平行四边形ABCD 中,∠B = ∠AFE ,EA 是∠BEF 的角平分线.求证: (1)△ABE ≌△AFE ; (2)∠FAD = ∠CDE .解题点拨:此题主要考查了平行四边形的性质,以及全等三角 形的判定与性质,(2)问关键是正确证明△AFD ≌△DCE . 证明:(1)∵EA 是∠BEF 的角平分线, ∴∠1=∠2.在△ABE 和△AFE 中,,12,,B AFE AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△AFE (AAS ). (2)∵△ABE ≌△AFE , ∴AB =AF ,∵四边形ABCD 是平行四边形. ∴AB =CD ,AD ∥CB ,AB ∥CD ,∴AF =CD ,∠ADF = ∠DEC ,∠B +∠C =180°, ∴∠B = ∠AFE ,∠AFE +∠AFD =180°, ∴AFD = ∠C ,在△AFD 和△DCE 中,,,,ADF FEC C AFD AF DC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AFD ≌△DCE (AAS ) , ∴∠FAD = ∠CDE .1.如图,已知AB =AD ,那么添加下列一个条件后,仍无法判定△ABC ≌△ADC 的是 ( C ) A .CB = CDB .∠BAC = ∠DAC C .∠BCA =∠DCAD .∠B =∠D = 90°2.如图,平行四边形ABCD 中,E ,F 是对角线BD 上的两点,如果添加一个条件使△4BE 竺△CDF .则添加的条件不能是 ( A )A .AE =CFB .BE = FDC .BF = DED .∠1= ∠2 3.(2016成都)如图,△ABC ≌△A 'B 'C ',其中∠A = 36°, ∠C '=24°,则∠B = __120°__.4.已知,如图.AB =AC ,BD =CD ,DE ⊥AB 于点E ,DF ⊥AC 于点F ,求证:DE =DF .证明:连接AD ,在△ACD 和△ABD 中,,,,AC AB CD BD AD AD =⎧⎪=⎨⎪=⎩△ACD ≌△ABD (SSS ),∴∠EAD =∠FAD ,即AD 平分∠EAF , ∵DE ⊥AE .DF ⊥AF . ∴DE =DF .中考达标 模拟自测A 组 基础训练1.如图,△ABC和△DEF中,AB= DE,/B= LDEF,添加下列哪一个条件无法证明△ABC≌△DEF ( C )A.AC∥DFB.∠A =∠D C.AC=DFD.∠ACB= ∠F2.(2016陕西)如图,在正方形ABCD中,连接BD,点O是BD的中点,若M、N是边AD上的两点,连接MO、NO,并分别延长交边BC于两点M'、N',则图中的全等三角形共有 ( C )A.2对B.3对C.4对D.5对3.如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F.若AC= BD,AB= ED,BC= BE,则∠ACB等于 ( C )A.∠EDBB.∠BEDC.12∠AFBD.2∠ABF4.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°,把△DCE绕点C 顺时针旋转15°得到△D1CE1,如图②,连接D1B则∠E1D1B的度数为 ( D )A.10°B.20°C.7.5°D.15°二、填空题5.如图,AC、BD相交于点O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件__AB=CD__(填出6.如图,△ABD ≌△CBD ,若∠A =80°,∠ABC = 70°,则∠ADC 的度数为__130°__.7.在Rt △ABC 中,∠ACB =90°,BC =2cm ,CD ⊥AB ,在AC 上取一点E ,使EC =BC ,过点E 作EF ⊥AC 交CD 的延长线于点F .若EF = 5cm .则AB =cm .三、解答题 8.(2016重庆)如图,点A ,B ,C ,D 在同一条直线上,CE ∥DF ,EC =BD ,AC =FD .求证:AE =FB .证明:CE ∥DF , ∴∠ACE = ∠D ,在△ACE 和△FDB 中,,,,AC FD ACE D EC BD =⎧⎪∠=∠⎨⎪=⎩△ACE ≌△FDB , ∴AE =FB .9.如图,∠ABC = 90°,D 、E 分别在BC 、AC 上,AD ⊥DE ,且AD = DE .点F 是AE 的中点.FD 与AB 相交于点M . (1)求证:∠FMC = ∠FCM ;解:(1)证明:∵△ADE 是等腰直角三角形,F 是AE 中点, ∴DF ⊥AE ,DF =AF = EF ,又∵∠ABC =90, ∠DCF ,∠AMF 都与∠MAC 互余, ∴∠DCF =∠AMF . 在△DFC 和△AFM 中.,,,DCF AMF MFA CFD DF AF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DCF ≌△AMF (AAS ),∴CF =MF ,∴∠FMC =∠FCM ; (2)AD ⊥MC ,理由:由 (1)知,∠MFC = 90°,FD = EF ,FM = FC ,∴∠FDE =∠FMC =45°, ∴DE //CM ,∴AD ⊥MC .B 组提高练习10.(2016丹东)如图,在△ABC 中,AD 和BE 是高,∠ABE = 45°,点F 是AB 的中点,AD 与FE 、BE 分别交于点G 、H ,∠CBE = ∠BAD .有下列结论:①FD =FE ;②AH =2CD ;③BC ·ADAE 2;④4ABC ADF S S ∆∆=其中正确的有 ( D)A .1个B .2个C .3个D .4个(提示:∵在△ABC 中,AD 和BE 是高,∴∠ADB =∠AEB =∠CEB =90°,∵点F 是AB 的中点,∴FD =12AB ,∵∠ABE =45°,∴△ABE 是等腰直角三角形,∴AE =BE ,∵点F 是AB 的中点,∴FE =12AB ,∴FD =FE ,①正确;∵∠CBE =∠BAD ,∠CBE + ∠C = 90°,∠BAD +∠ABC =90°,∴∠ABC = ∠C ,∴AB =AC ,∴AD ⊥BC ,∴BC = 2CD ,∠BAD =∠CAD = ∠CBE ,在△AEH 和△BEC 中, ,,,AEH CEB AE BE EAH CBE ∠=∠⎧⎪=⎨⎪∠=∠⎩∠ADB =∠CEB ,..,△ABD ∽△BCE ,BC BE AB AD=,即BC ·AD =AB ·BEAE 2=AB ·AE =AB ·BE ,∴BC ·ADAE 2;③正确;∵F 是AB 的中点,BD = CD ,∴24ABC ABD ADF S S S ∆∆∆==.④正确;故选:D .)11.(2016丹东)如图,在平面直角坐标系中,A 、B 两点分别在x 轴、y 轴上,OA =3,OB =4,连接AB .点P 在平面内,若以点P \A 、B 为顶点的三角形与△AOB 全等(点P 与点O 不重合),则点P 的坐标为__(3,4),(9625,7225),(2125-,2825)__.(提示:如图所示:①∵OA =3,OB =4,∴P 1(3,4); ②连结OP 2,设AB 的解析式为y =kx +b ,则30,4,k b b +=⎧⎨=⎩解得4,34.k b ⎧=-⎪⎨⎪=⎩故AB 解析式为y =43-x +4,则OP 2的解析式为y =43x ,联立方程组得44,33,4y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得48,253625x y ⎧=⎪⎪⎨⎪=⎪⎩,则P 2(9625,7225);③连结P 2P 3,则四边形AP 2BP 3为平行四边形,则E 为线段AB 和P 2P 3的中点,设P 3(x ,y ),则96032522x ++=,72042522x ++=, ∴x =2125-,y =2825,∴P 3(2125-,2825),故点P 的坐标为(3,4)或(9625,7225)或(2125-,2825).12.如图,△ABC 中,∠ABC =45°,过点C 作CD ⊥AB 于点D ,过点B 作BM ⊥AC 于点M ,BM 交CD 于点E ,且点E 为CD 的中点,连接MD ,过点D 作ND ⊥MD 于点D ,DN 交BM 于点N . (1)若BC =22,求△BDE 的周长; (2)求证:NE -ME =CM .在△DEF 和△CEM 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CE DE CEM DEF CME DFE , ∴△DEF ≌△CEM (AAS ), ∴DF =CM ,EF =ME ,∴NE -ME =NE -EF =NF =DF =CM , 即NE -ME =CM .。
2024年中考数学一轮复习考点课件:等腰三角形与直角三角形

9,12,15 ).
(2) 研究直角三角形的勾股数时,古希腊的哲学家柏拉图曾指出:如
果n表示大于1的整数,x=2n,y=n2-1,z=n2+1,那么以x,y,z为三
边的三角形为直角三角形[即(x,y,z)为勾股数],请你加以证明.
解:∵ x2+y2=(2n)2+(n2-1)2=4n2+n4-2n2+1=n4+2n2+1=
B. 15°
C. 20°
D. 25°
考点二
等腰三角形的判定
典例4 如图,下列说法中,正确的是( B )
A. ①是等腰三角形
B. ②是等腰三角形
C. ①和②均是等腰三角形
D. ①和②都不是等腰三角形
典例4图
典例5 (2023·蚌埠模拟)在如图所示的网格中找到格点C,使△ABC为
等腰三角形,则这样的点有( C )
开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形
模型(示意图如图所示),它的顶角为120°,腰长为12m,则底边上的
高是( B )
第4题
A. 4m
B. 6m
1
2
3
C. 10m
4
5
6
7
8
D. 12m
9
10
11
12
13
14
15
5. 如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使
三边相等,即==(如图1)
三个内角相等,每一个角都等于60°,
性质 即∠=∠=∠ = 60° 如图1
等边三角形
等边三角形是轴对称图形,有⑤
三 条对称轴
三条边相等的三角形是等边三角形(定义)
判定 三个角都相等的三角形是等边三角形
中考数学 第一编 教材知识梳理篇 第四章 图形的初步认识与三角形、四边形 第三节 等腰三角形与直角三角形试
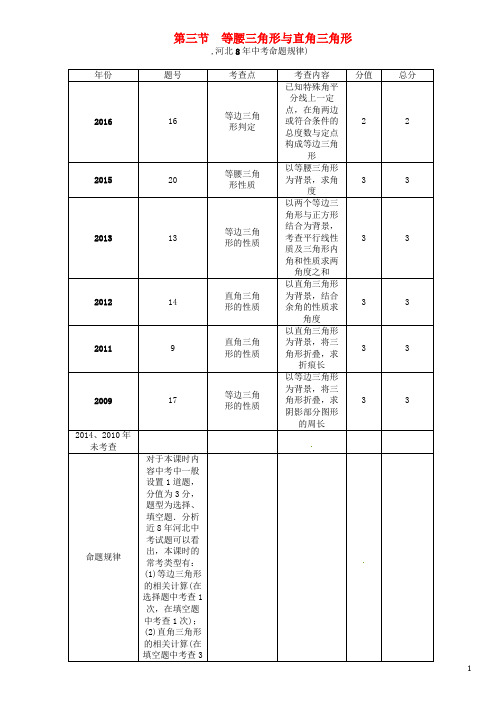
第三节等腰三角形与直角三角形,河北8年中考命题规律),河北8年中考真题及模拟)等边三角形判定和的相关计算1.(2016河北16题2分)如图,∠AOB =120°,OP 平分∠AOB,且OP =2.若点M ,N分别在OA ,OB 上,且△PMN 为等边三角形,则满足上述条件的△PMN 有( D )A .1个B .2个C .3个D .3个以上2.(2013河北13题3分)一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( B )A .90°B .100°C .130°D .180°(第2题图)(第3题图)3.(2009河北17题3分)如图,等边△ABC 的边长为1 cm ,D ,E 分别是AB ,AC 上的点,将△ABC 沿直线DE 折叠,点A 落在点A′处,且点A′在△ABC 外部,则阴影部分图形的周长为__3__cm .4.(2015河北20题3分)如图,∠BOC =9°,点A 在OB 上,且OA =1,按下列要求画图: 以A 为圆心,1为半径向右画弧交OC 于点A 1,得第1条线段AA 1; 再以A 1为圆心,1为半径向右画弧交OB 于点A 2,得第2条线段A 1A 2; 再以A 2为圆心,1为半径向右画弧交OC 于点A 3,得第3条线段A 2A 3; ……这样画下去,直到得第n 条线段,之后就不能再画出符合要求的线段了,则n =__9__.直角三角形的相关计算5.(2011河北9题3分)如图,在△ABC 中,∠C =90°,BC =6,D ,E 分别在AB ,AC 上,将△ABC 沿DE 折叠,使点A 落在点A′处,若A′为CE 的中点,则折痕DE 的长为( B )A .12B .2C .3D .4(第5题图)(第6题图)6.(2016邢台金华中学一模)如图,在△ABC 中,∠C =90°,∠B =30°,AD 是△ABC 的角平分线,DE ⊥AB ,垂足为点E ,DE =1,则BC 的长是( C )A . 3B .2C .3D .3+27.(2016廊坊二模)下列四组线段中,可以构成直角三角形的是( B ) A .4,5,6 B .1.5,2,2.5 C .2,3,4 D .1,2,38.(2016秦皇岛二模)如图,在△ABC 中,AB =AC ,∠A =120°,BC =6 cm ,AB 的垂直平分线交BC 于点M ,交AB 于点E ,AC 的垂直平分线交BC 于点N ,交AC 于点F ,则MN 的长为( C )A .4 cmB .3 cmC .2 cmD .1 cm(第8题图)(第12题图)9.(2016河北唐山五十四中一模)若等腰三角形的顶角为80°,则它的底角度数为( B ) A .80° B .50° C .40° D .20°10.(2016河北唐山友谊中学一模)已知等腰三角形ABC 的两边长分别为2和3,则等腰三角形ABC 的周长为( D )A .7B .8C .6或8D .7或811.(2016保定育德中学二模)一直角三角形的两边长分别为3和4,则第三边的长为( D)A.5 B.7C. 5 D.5或712.(2012河北14题3分)如图,AB,CD相交于点O,AC⊥CD于点C,若∠BOD=38°,∠A等于__52°__.13.(2016唐山路北区二模)如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.(1)求∠F的度数;(2)若CD=2,求DF的长.解:(1)∵△ABC是等边三角形,∴∠B=60°,∵DE∥AB,∴∠EDC=∠B=60°.∵EF⊥DE,∴∠DEF=90°,∴∠F=90°-∠EDC=30°;(2)∵∠ACB=60°,∠EDC=60°,∴△EDC是等边三角形,∴ED=DC=2.∵∠DEF=90°,∠F=30°,∴DF=2DE=4.,中考考点清单)等腰三角形的性质与判定1等腰三角形顶角的平分线、底边上的高和底边的中线互相重合;面积: S △ABC =如果一个三角形有两个角相等,那么这个三角形是等腰三角形,其中,两个相等的(简称“__等角对等边__”)等边三角形三边相等的三角形是等边三角形等边三角形三边相等(即等边三角形三角相等,且每一个角都等于__60__);等边三角形内、外心重合;等边三角形是轴对称图形,有三条对称轴;面积:S △ABC =12BC 三边都相等的三角形是等边三角形;三个角相等的三角形是等边三角形;°的等腰三角形是等边三角形直角三角形的性质与判定(高频考点)直角三角形的性质与判定近8年考查3次,题型均为填空题,设问方式为:1.求角度;2.求线段长度;3.求周长.结合的背景有:1.与三角形折叠结合;2.以赵爽弦图为背景;3.利用三角形余角的性质求角度.390°的三角形叫做直角三角形直角三角形的两个锐角之和等于__中线__等于斜边的一半角所对应的直角边等于斜边的一半勾股定理:如果直角三角形两直角边分别为a ,在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°有一个角为90°的三角形是直角三角形;一条边的中线等于这条边的一半的三角形是直角三角形;有两个角互余的三角形是直角三角形4.定义顶角为90°的等腰三角形是等腰直角三角形性质等腰直角三角形的顶角是直角,两底角为45°判定(1)用定义判定;(2)有两个角为45°的三角形,中考重难点突破)等腰三角形的相关计算【例1】在△ABC中,AB=AC,AB的垂直平分线与AC所在直线相交所得的锐角为50°,则底角∠B=________.【学生解答】70°或20°【点拨】在等腰三角形中,只要知道其中一个内角的度数,就能算出其他两个内角的度数,如果题中没有确定这个内角是顶角还是底角,必须分成两种情况来讨论.此题的两种情况如图所示:1.(2016湘西中考)一个等腰三角形一边长为4 cm,另一边长为5 cm,那么这个等腰三角形的周长是( C)A.13 cmB.14 cmC.13 cm或14 cmD.以上都不对2.如图,在等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,且∠DBC=15°,则∠A=__50°__.等腰三角形、等边三角形的判定与性质【例2】如图,在△ABC 中,AB =AC ,D ,E 是△ABC 内的两点,AD 平分∠BAC,∠EBC =∠E=60°,若BE =6 cm ,DE =2 cm ,则BC =________cm .【解析】如图,延长AD 交BC 于点M ,由AB =AC ,AD 是∠BAC 的平分线可得AM⊥BC,BM =MC =12BC ,延长ED交BC 于点N ,则△BEN 是等边三角形,从而求出DN 的长,利用在直角三角形中,30°的角所对的直角边等于斜边的一半,求出MN 的长,进而求BM ,BC 的值.【学生解答】83.(2016沧州八中二模)如图,在△ABC 中,∠A =36°,AB =AC ,BD 是△ABC 的角平分线,若在边AB 上截取BE =BC ,连接DE ,则图中等腰三角形共有( D )A .2个B .3个C .4个D .5个(第3题图)(第4题图)4.(2016漳州中考)如图,在△ABC 中,AB =AC =5,BC =8,D 是线段BC 上的动点(不含端点B ,C),若线段AD 长为正整数,则点D 的个数共有( C )A .5个B .4个C .3个D .2个直角三角形的性质判定和勾股定理【例3】如图,在Rt △ABC 中,AB =AC ,∠A =90°,D 为BC 上任意一点,DF ⊥AB 于点F ,DE ⊥AC 于点E ,M 为BC 的中点,连接EM ,FM ,给出以下五个结论:①AF=CE ;②AE=BF ;③△EFM 是等腰直角三角形;④S 四边形AEMF=12S △ABC ;⑤EF=BM =MC.当点D 在BC 上运动时(点D 不与B ,C 重合),上述结论中始终正确的有( ) A .2个 B .3个 C .4个 D .5个【解析】连接AM ,易证AE =DF =BF ,AF =DE =CE ,△AME ≌△BMF ,∴ME =MF ,∠AME =∠BMF,∴△EMF 是等腰直角三角形.S 四边形A EMF =S △A FM +S △AEM =S △AFM +S △BFM =S △ABM =12S △ABC ,但是EF 与BM 不一定相等,只有四边形AFME为矩形时,EF =BM.【学生解答】C5.(2016株洲中考)如图,以直角三角形a 、b 、c 为边,向外作等边三角形,半圆,等腰直角三角形和正方形,上述四各情况的面积关系满足S 1+S 2=S 3图形个数有( D )A .1个B .2个C .3个D .4个6.(2016苏州中考)如图,长4 m 的楼梯AB 的倾斜角∠ABD 为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD 为45°,则调整后的楼梯AC 的长为( B )A .2 3 mB .2 6 mC .(23-2)mD .(26-2)m7.如图,在四边形ABCD 中,AB ⊥BC ,AB =5,BC =12,AD =9,CD =510,求四边形ABCD 的面积.解:连接AC ,∵AB ⊥BC ,∴∠B =90°,∴AC =AB 2+BC 2=52+122=13,∵在△ACD 中,AC 2+AD 2=132+92=169+81=250,CD 2=(510)2=250,∴AC 2+AD 2=CD 2,∴∠DAC =90°, ∴S 四边形ABCD =S △ABC +S △ACD =12BC ·AB +12AD ·AC =12×12×5+12×9×13 =1772.中考备考方略)1.(2016秦皇岛二模)若实数x ,y 满足|x -4|+y -8=0,则以x ,y 的值为两边长的等腰三角形的周长是( D )A .12B .16C .16或20D .202.(2016益阳中考)小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA 的高度与拉绳PB 的长度相等.小明将PB 拉到PB′的位置,测得∠PB′C=α(B′C 为水平线),测角仪B′D 的高度为1 m ,则旗杆PA 的高度为( A )A .11-sin α mB .11+sin αmC.11-cosαm D.11+cosαm3.(2016泰安中考)如图,在△PAB中,PA=PB,M,N,K分别是边PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( D)A.44°B.66°C.88°D.92°(第3题图)(第4题图)4.(2016沧州八中模拟)如图,在锐角三角形ABC中,AD,CE分别是边BC,AB上的高,垂足分别是D,E,AD,CE相交于点O,若∠B=60°,则∠AOE的度数是( A)A.60°B.50°C.70°D.80°5.(2016保定十七中模拟)在△ABC中,若AC=15,BC=13,AB边上的高CD=12,则△ABC的周长为( D) A.32 B.42C.40或42 D.32或426.(2016宜昌中考)任意一条线段EF,其垂直平分线的尺规作图痕迹如图所示,若连接EH,HF,FG,GE,则下列结论中,不一定正确的是( B)A.△EGH为等腰三角形B.△EGF为等边三角形C.四边形EGFH为菱形D.△EHF为等腰三角形7.具备下列条件的△ABC中,不是直角三角形的是( D)A.∠A+∠B=∠CB.∠A-∠B=∠CC.∠A∶∠B∶∠C=1∶2∶3D.∠A=∠B=3∠C8.(2016深圳中考)如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( D)A.∠2=60°B.∠3=60°C.∠4=120°D.∠5=40°9.(2016杭州中考)已知直角三角形纸片的两条直角边分别为m和n(m<n),过锐角三角形顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( C)A.m2+2mn+n2=0 B.m2-2mn+n2=0C.m2+2mn-n2=0 D.m2-2mn-n2=010.(2016东营中考)在△ABC中,AB=10,AC=210,BC边上的高AD=6,则另一边BC等于( C)A .10B .8C .6或10D .8或1011.(2016齐齐哈尔中考)有一面积为53的等腰三角形,它的一个内角是30°,则以它的腰长为边的正方形的面积为.12E 是AB 上的动点,点E 与点A ,B 不重合,点D 在CB 的延长线上,且EC =ED.(1)当BE =AE 时,求证:BD =AE ; (2)当BE≠AE 时,“BD =AE”还成立吗?若你认为不成立,请直接写出BD 与AE 数量关系式,若你认为成立,请给予证明.证明:(1)如图(1),在等边△ABC 中, ∠ABC =∠ACB=60°.∵BE =AE ,∴∠ACE =∠ECB=30°. 又∵CE=DE ,∴∠D =∠ECD=30°. ∴∠DEB =30°,∴BE =BD ,∴BD =AE ; (2)BD =AE 还成立.理由如下:如图(2),过点E 作EF∥AC 交BC 于点F.易证△EFB 为等边三角形. ∴EF =FB =BE.∴∠EFB=∠EBF. ∴∠CFE =∠EBD.∵CE =DE ,∴∠ECD =∠D.∴△EBD≌△EFC(AAS ),∴CF =BD.∵AB=BC ,∴AB -BE =BF -CF ,即AE =CF ,∴BD =AE.13.(2016威海中考)如图,已知AB =AC =AD ,∠CBD =2∠BDC,∠BAC =44°,则∠CAD 的度数为( B ) A .68° B .88° C .90° D .112°,(第13题图)) ,(第15题图))14.(2016内江中考)已知等边三角形的边长为3,点P 为等边三角形内任意一点,则点P 到三边的距离之和为( B )A .32B .332C .32D .不能确定 15.(2016连云港中考)如图①,分别以直角三角形三边为边向外作等边三角形,面积分别为S 1、S 2、S 3;如图②,分别以直角三角形三个顶点为圆心,三边长为半径向外作圆心角相等的扇形,面积分别为S 4、S 5、S 6.其中S 1=16,S 2=45,S 5=11,S 6=14,则S 3+S 4=( C )A .86B .64C .54D .4816.(2016随州中考)如图,在△ABC 中,∠ACB =90°,M ,N 分别是AB ,AC 的中点,延长BC 至点D ,使CD =13BD ,连接DM ,DN ,MN.若AB =6,则DN =__3__.(第16题图)(第18题图)17.(2016潍坊中考)已知∠AOB=60°,点P 是∠AOB 的平分线OC 上的动点,点M 在边OA 上,且OM =4,则点P 到点M 与到边OA 的距离之和的最小值是__23__.18.(2016武汉中考)如图,在四边形ABCD 中,∠ABC =90°,AB =3,BC =4,CD =10,DA =55,则BD 的长为__241__.19.(2016邯郸十一中一模)如图,∠ABC =90°,D ,E 分别在BC ,AC 上,AD ⊥DE ,且AD =DE ,点F 是AE 的中点,FD 与AB 相交于点M.(1)求证:∠FMC=∠FCM;(2)AD 与MC 垂直吗?并说明理由.证明:(1)∵△ADE 是等腰直角三角形,F 是AE 中点,∴DF ⊥AE ,DF =AF =EF.又∵∠ABC=90°,∴∠DCF ,∠AMF 都与∠MAC 互余,∴∠DCF =∠AMF,又∵∠DFC=∠AFM=90°,∴△DFC ≌△AFM ,∴CF =MF.∴∠FMC =∠FCM;(2)AD⊥MC.理由:由(1)知∠MFC=90°,FD =FE ,FM =FC.∴∠FDE =∠FMC=45°.∴DE ∥CM ,由题意得AD⊥DE,∴AD ⊥MC.20.(2016北京中考)如图,在四边形ABCD 中,∠ABC =90°,AC =AD ,M ,N 分别为AC ,CD 的中点,连接BM ,MN ,BN.(1)求证:BM =MN ;(2)若∠BAD=60°,AC 平分∠BAD,AC =2,求BN 的长.解:(1)在△ACD 中,∵M ,N 分别是AC ,CD 的中点,∴MN ∥AD 且MN =12AD. 在Rt △ABC 中,∵M 是AC 的中点.∴BM =12AC.又∵AC=AD ,∴MN =BM ; (2)∵∠BAD=60°且AC 平分∠BAD.∴∠BAC =∠DAC=30°.由(1)知,BM =12AC =AM =MC. ∴∠BMC =∠BAM+∠ABM=2∠BAM=60°.∵MN ∥AD ,∴∠NMC =∠DAC=30°.∴∠BMN =∠BMC+∠NMC=90°.∴BN 2=BM 2+M N 2.而由(1)知,MN =BM =12AC =12×2=1,BN = 2.。
2020年中考数学(华师大版)总复习知识点梳理:第四单元 图形的初步认识与三角形
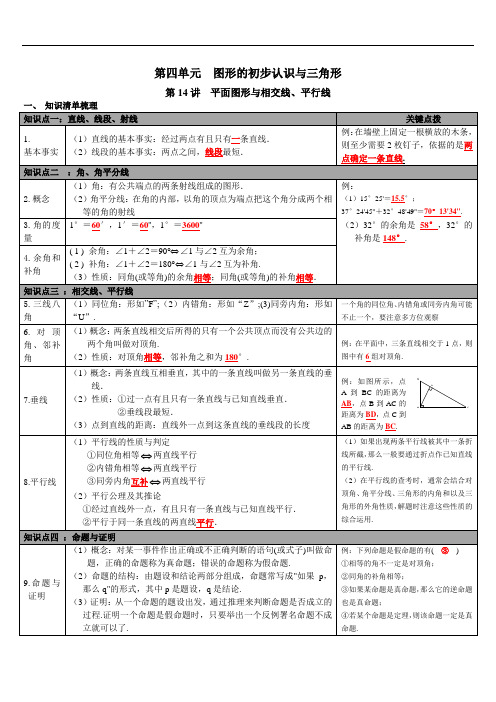
角形的性 (3)全等三角形的周长等、面积两边和它 ASA(两角和它 AAS(两角和其
三 角 应相等)
们的夹角对应 们的夹角对应相 中一个角的对边
形全
相等)
等)
对应相等)
7. 三 角 形 等
失分点警示:运用全等三角 形的性质时,要注意找准对 应边与对应角.
(1)内角和定理:
①三角形的内角和等 180°;
②推论:直角三角形的两锐角互余.
(2)外角的性质:
①三角形的一个外角等于与它不相邻的两个内角和.
②三角形的任意一个外角大于任何和它不相邻的内角.
四线
性质
角平分线
(1) 角平线上的点到角两边的距离相等 (2) 三角形的三条角平分线的相交于一点(内心)
中线
5. 三 角 形
中内、外 角与角 平分线 的规律 总结
如图①,AD 平分∠BAC,AE⊥BC,则∠α= 1 ∠BAC-∠CAE= 1 (180°-∠B-
2
2
∠C)-(90°-∠C)= 1 (∠C-∠B); 2
如图②,BO、CO 分别是∠ABC、∠ACB 的平分线,则有∠O= 1 ∠A+90°; 2
如图③,BO、CO 分别为∠ABC、∠ACD、∠OCD 的平分线,则∠O= 1 ∠A,∠O’= 1
(2)平行公理及其推论 ①经过直线外一点,有且只有一条直线与已知直线平行. ②平行于同一条直线的两直线平行.
(1)如果出现两条平行线被其中一条折 线所截,那么一般要通过折点作已知直线 的平行线. (2)在平行线的查考时,通常会结合对 顶角、角平分线、三角形的内角和以及三 角形的外角性质,解题时注意这些性质的 综合运用.
②垂线段最短.
例:如图所示,点 A D
中考数学一轮复习 第四章 几何初步与三角形 第三节 等腰三角形与直角三角形课件

2021/12/8
第二十三页,共四十四页。
考点二 勾股定理及其逆定理 (5年4考)
例3 (2013·济南)如图,小亮将升旗的绳子拉到旗杆底端,
绳子末端刚好接触(jiēchù)到地面,然后将绳子末端拉到距离旗杆8 m
处,发现此时绳子末端距离地面2 m,则旗杆的高度为(滑轮
上方的部分忽略不计)为(
)
A.12m B.13m C.16m D.17m
∠ACD=2∠B,则BD的长是( C) A.12 B.14 C.16 D.18
2021/12/8
第二十七页,共四十四页。
7.如图,四边形ABCD中,AB⊥AD于A,AB=8 ,A6 D=8 , 3 BC=7,CD=25,则四边形ABCD的面积(miàn jī)为84_+_9_6__2____.
2021/12/8
第二十八页,共四十四页。
考点(kǎo diǎn)三 直角三角形的性质 (5年1考) 例4 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M,N在边 OB上,PM=PN.若MN=2,则OM=( ) A.3 B.4 C.5 D.6
2021/12/8
第二十九页,共四十四页。
【分析】 过点P作PH⊥MN于H,根据(gēnjù)等腰三角形的性质求
直角边等于斜边的一半.
2021/12/8
第三十一页,共四十四页。
8.如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠(zhédié)
,
C
使点A落在边CB上A′处,折痕为CD,则∠A′DB=(
)
A.40° B.30°
C.20° D.10°
2021/12/8
第三十二页,共四十四页。
9.如图,正方形网格(wǎnɡ ɡé)的边长为1,点A,B,C在网格的格点 上,点P为BC的中点,则AP=_____5_.2
云南中考数学第一部分教材知识梳理第四章第三节等腰三角形与直角三角形课件

故选A.
拓展题1图
类型二 直角三角形的相关计算 例2(’14 宿迁)如图,在Rt△ABC中,∠ACB= 90°,AD平分∠BAC与BC相交于点D,若BD=4, CD=2,则AB的长是_________.
例2题图
【解析】如解图,过点D作DE⊥AB,∵∠ACB
= 90° , AD 平 分 ∠ BAC , ∴ DE = CD = 2 , 在
类型一 等腰三角形的相关计算 例1 如图,在△ABC中,AB=AC,AD⊥BC于点D, 若AB=6,CD=4,则△ABC的周长是______.
例1题图
【解析】在△ABC中,∵AB=AC, AD⊥BC,∴BD=CD= 1 BC,
2
∴ BC = 2CD = 8 , AC = AB = 6 ,
∴△ABC的周长是6+6+8= 20 .
是50°.故选A.
解法二:由题意知三角形的一个内角为50°,则底角 = 1(180°-50°)=65°.故选B.
2
上述解法出现错误的原因是
_未__对__等__腰__三__角__形__的__底__角__和___顶__角__分__类__讨__论__,应改为 _当__5_0_°__角__为__顶__角__时__,__它__的__底__角__为___1_(_1_8_0_°__-__5_0_°__)_=___
判定
(1)三边都相等的三角形是等边三角形 (2)三个角都相等的三角形是等边三角 形 (3)有一个角是④___6_0_°___的等腰三角 形是等边三角形
面积 S= 1 ah 3 a(2 h= 3 a)
2
4
2
考点二 直角三角形的性质及判定
性质
(1)两锐角之和等于⑤__9_0_°_ (2)斜边上的中线等于斜边的⑥_一__半____ (3)30°角所对的直角边等于斜边的⑦ __一__半___ (4)勾股定理:若直角三角形的两直角边分 别为a,b,斜边为c,则有a2+b2=c2 (5)在直角三角形中,如果一条直角边等于 斜边的一半,那么这条直角边所对的锐角等 于⑧3_0_°___
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰三角形与直角三角形
随堂演练
1.(2017·滨州)如图,在△ABC 中,AB =AC ,D 为BC 上一点,且DA =DC ,BD =BA ,则∠B 的大小为( )
A .40°
B .36°
C .30°
D .25°
2.如图,在△ABC 中,∠C=90°,∠B=30°,AD 是△ABC 的角平分线,DE⊥AB,垂足为E ,DE =1,则BC =( )
A. 3 B .2 C .3 D.3+2
3.(2016·德州)如图,在△ABC 中,∠B=55°,∠C=30°,分别以点A 和点C 为圆心,大于12
AC 的长为半径画弧,两弧相交于点M ,N ,作直线MN ,交BC 于点D ,连接AD ,则∠BAD 的度数为( )
A .65°
B .60°
C .55°
D .45°
4.(2017·聊城)如图是由8个全等的矩形组成的大正方形,线段AB 的端点都在小矩形的顶点上.如果点P 是某个小矩形的顶点,连接PA ,P B ,那么使△ABP 为等腰直角三角形的点P 的个数是( )
A .2
B .3
C .4
D .5
5.(2016·东营)在△ABC 中,AB =10,AC =210,BC 边上的高AD =6,则另一边BC 等于( )
A .10
B .8
C .6或10
D .8或10
6.如图,△ABC 中,CD⊥AB 于点D ,E 是AC 的中点.若AD =6,DE =5,则CD 的长等于______.
7.(2017·淄博)在边长为4的等边三角形ABC 中,D 为BC 边上的任意一点,过点D 分别作DE⊥AB,DF⊥AC,垂足分别为E ,F ,则D E +DF =_____.
8.将n +1个腰长为1的等腰直角三角形按如图所示放在同一直线上,设△B 2D 1C 1的面积为S 1,△B 3D 2C 2的面积为S 2,…,△B n +1D n C n 的面积为S n ,则S n =_____.
参考答案1.B 2.C 3.A 4.B 5.C
6.8 7.2 3 8.
n
2n+2。
