人教版数学九年级上同步练习 24.1.3 弧、弦、圆心角
人教版九年级上《24.1.3弧、弦、圆心角》同步练习(含答案解析)
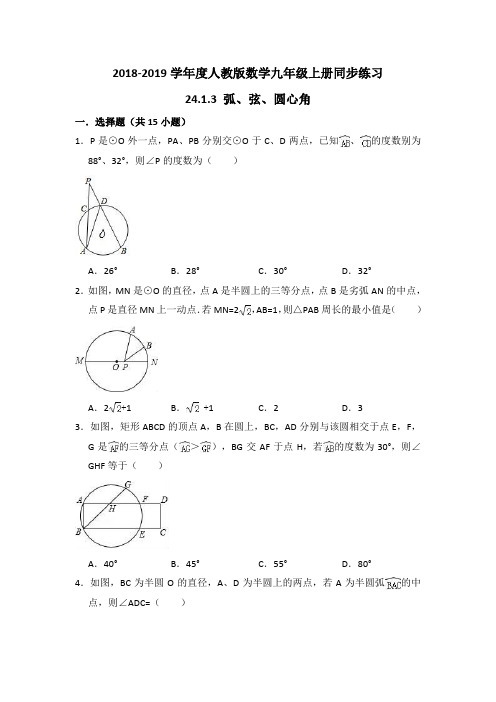
2018-2019学年度人教版数学九年级上册同步练习24.1.3 弧、弦、圆心角一.选择题(共15小题)1.P是⊙O外一点,PA、PB分别交⊙O于C、D两点,已知、的度数别为88°、32°,则∠P的度数为()A.26°B.28°C.30°D.32°2.如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2,AB=1,则△PAB周长的最小值是()A.2+1B. +1C.2D.33.如图,矩形ABCD的顶点A,B在圆上,BC,AD分别与该圆相交于点E,F,G是的三等分点(>),BG交AF于点H,若的度数为30°,则∠GHF等于()A.40°B.45°C.55°D.80°4.如图,BC为半圆O的直径,A、D为半圆上的两点,若A为半圆弧的中点,则∠ADC=()A.105°B.120°C.135°D.150°5.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对6.下列语句,错误的是()A.直径是弦B.相等的圆心角所对的弧相等C.弦的垂直平分线一定经过圆心D.平分弧的半径垂直于弧所对的弦7.点A、C为半径是4的圆周上两点,点B为的中点,以线段BA、BC为邻边作菱形ABCD,顶点D恰在该圆半径的中点上,则该菱形的边长为()A.或2B.或2C.2或2D.2或28.将一个圆分割成三个扇形,它们的圆心角的度数比为1:2:3,则这个扇形中圆心角度数最大的是()A.30°B.60°C.120°D.180°9.如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=()A.220°B.230°C.240°D.250°°10.如图,AB是⊙O的直径,==,∠COD=38°,则∠AEO的度数是()A.52°B.57°C.66°D.78°11.如图,已知A,B,C,D是圆上的点,弧AD=弧BC,AC,BD交于点E,则下列结论正确的是()A.AB=AD B.BE=CD C.AC=BD D.BE=AD12.如图,圆心角∠AOB=25°,将AB旋转n°得到CD,则∠COD等于()A.25°B.25°+n°C.50°D.50°+n°13.如图,⊙O的半径为1,动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示的位置,第2秒中P点位于点C 的位置,……,则第2018秒点P所在位置的坐标为()A.(,)B.(0,1)C.(0,﹣1)D.(,﹣)14.下列语句中不正确的有()①相等的圆心角所对的弧相等;②平分弦的直径垂直于弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④长度相等的两条弧是等弧.A.3个B.2个C.1个D.4个15.如图所示,在⊙O中,A,C,D,B是⊙O上四点,OC,OD交AB于点E,F,且AE=FB,下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④=,其中正确的有()A.4个B.3个C.2个D.1个二.填空题(共10小题)16.如图,AB,CD是⊙O的直径,弦CE∥AB,弧CE的度数为40°,∠AOC的度数.17.⊙O的半径为5,弦AB与弦CD相等,且AB⊥CD于H,若OH=3,则线段BH长为.18.如图,C为弧AB的中点,CN⊥OB于N,CD⊥OA于M,CD=4cm,则CN= cm.19.将一个圆分割成三个扇形,它们圆心角度数之间的关系为2:3:4,则这三个扇形中圆心角最小的度数是度.20.如图,⊙O中,已知弧AB=弧BC,且弧AB:弧AmC=3:4,则∠AOC=度.21.如图,在⊙O中,=,∠1=30°,则∠2=.22.如图,在四边形ABCD中,∠BAD=∠CDA=90°,AB=1,CD=2,过A,B,D三点的⊙O分别交BC,CD于点E,M,下列结论:①DM=CM;②;③⊙O的直径为2;④AE=AD.其中正确的结论有(填序号).23.如图,在⊙O中,AB=DC,∠AOB=50°,则∠COD=.24.如图,已知AB、CD是⊙O中的两条直径,且∠AOC=50°,过点A作AE∥CD交⊙O于点E,则的度数为.25.如图,已知⊙O中,直径AB平分弦CD,且交CD于点E,如果OE=BE,那么弦CD所对的圆心角是度.三.解答题(共6小题)26.如图,在⊙O中,弦AB与DC相交于E,且BE=DE,求证:=.27.如图,OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.探索∠ACB与∠BAC 之间的数量关系,并说明理由.28.如图,在⊙O中,AB=CD.求证:AD=BC.29.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.(1)求证:AB=CD;(2)如果⊙O的半径为5,DE=1,求AE的长.30.将一个圆分割成甲、乙、丙、丁四个扇形,使它们的圆心角的度数比为1:2:3:4,分别求出这四个扇形的圆心角的度数.31.如图,已知⊙O的弦AB,E,F是弧AB上两点,=,OE、OF分别交于AB于C、D两点,求证:AC=BD.参考答案与试题解析一.选择题(共15小题)1.【解答】解:∵和所对的圆心角分别为88°和32°,∴∠A=×32°=16°,∠ADB=×88°=44°,∵∠P+∠A=∠ADB,∴∠P=∠ADB﹣∠A=44°﹣16°=28°.故选:B.2.【解答】解:作点A关于MN的对称点A′,连接A′B,交MN于点P,连接OA′,OA,OB,PA,AA′,∵点A与A′关于MN对称,点A是半圆上的一个三等分点,∴∠A′ON=∠AON=60°,PA=PA′,∵点B是弧AN的中点,∴∠BON=30°,∴∠A′OB=∠A′ON+∠BON=90°,又∵OA=OA′=,∴A′B=2.∴PA+PB=PA′+PB=A′B=2,∴△PAB周长的最小值是2+1=3,故选:D.3.【解答】解:连接BF,∵的度数为30°,∴的度数为150°,∠AFB=15°,∵G是的三等分点,∴的度数为50°,∴∠GBF=25°,∴∠GHF=∠GBF+∠AFB=40°,故选:A.4.【解答】解:连接AC,∵BC为半圆的直径,∴∠BAC=90°,又A为半圆弧的中点,∴AB=AC,∴∠B=∠ACB=45°,∵A、B、C、D四点共圆,∴∠ADC+∠B=180°,∴∠ADC=180°﹣45°=135°.故选:C.5.【解答】解:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距相等.故选:D.6.【解答】解:直径是弦,A正确,不符合题意;在同圆或等圆中,相等的圆心角所对的弧相等,B错误,符合题意;弦的垂直平分线一定经过圆心,C正确,不符合题意;平分弧的半径垂直于弧所对的弦,D正确,不符合题意;故选:B.7.【解答】解:过B作直径,连接AC交AO于E,∵点B为的中点,∴BD⊥AC,如图①,∵点D恰在该圆直径上,D为OB的中点,∴BD=×4=2,∴OD=OB﹣BD=2,∵四边形ABCD是菱形,∴DE=BD=1,∴OE=1+2=3,连接OC,∵CE===,在Rt△DEC中,由勾股定理得:DC===2;如图②,OD=2,BD=4+2=6,DE=BD=3,OE=3﹣2=1,由勾股定理得:CE===,DC===2,故选:C.8.【解答】解:由题意可得,三个圆心角的和为360°,∵三个圆心角的度数比为1:2:3,∴最大的圆心角度数为:360°×=180°.故选:D.9.【解答】解:连接OA、OB、OC,如图所示:∵∠BAC=50°,∴∠BOC=2∠BAC=100°,∴∠AOB+∠AOC=360°﹣100°=260°,∵∠D=(∠BOC+∠AOC),∠E=(∠BOC+∠AOB),∴∠D+∠E=(∠BOC+∠AOC+∠BOC+∠AOB)=(260°+100°+100°)=230°.故选:B.10.【解答】解:∵==,∠COD=38°,∴∠BOC=∠EOD=∠COD=38°,∴∠AOE=180°﹣∠EOD﹣∠COD﹣∠BOC=66°.又∵OA=OE,∴∠AEO=∠OAE,∴∠AEO=×(180°﹣66°)=57°.故选:B.11.【解答】解:连接BC,∵,∴,∴,∴AC=BD,故选:C.12.【解答】解:∵将AB旋转n°得到CD,∴=,∴∠COD=∠AOB=25°,故选:A.13.【解答】解:作PE⊥OA于E,∵OP=1,∠POE=45°,∴OE=PE=,即点P的坐标为(,),则第2秒P点为(0,1),根据题意可知,第3秒P点为(﹣,),第4秒P点为(﹣1,0),第5秒P点为(﹣,﹣),第6秒P点为(0,﹣1),第7秒P点为(,﹣),第8秒P点为(1,0),2018÷8=252……2,∴第2018秒点P所在位置的坐标为(0,1),故选:B.14.【解答】解:①和④、错误,应强调在同圆或等圆中;②、错误,应强调不是直径的弦;③、错误,应强调过圆心的直线才是它的对称轴.故选D.15.【解答】解:连接OA,OB,∵OA=OB,∴∠OAB=∠OBA.在△OAE与△OBF中,,∴△OAE≌△OBF(SAS),∴OE=OF,故①正确;∠AOE=∠BOF,即∠AOC=∠BOD,∴,故④正确;连结AD.∵,∴∠BAD=∠ADC,∴CD∥AB,故③正确;∵∠BOD=∠AOC不一定等于∠COD,∴弧AC=弧BD不一定等于弧CD,∴AC=BD不一定等于CD,故②不正确.正确的有3个,故选B.二.填空题(共10小题)16.【解答】解:连接OE,如图,∵弧CE的度数为40°,∴∠COE=40°,∵OC=OE,∴∠OCE=∠OEC,∴∠OCE=(180°﹣40°)÷2=70°,∵弦CE∥AB,∴∠AOC=∠OCE=70°.17.【解答】解:①过点O作OE⊥AB,OF⊥CD,∴AE=BE,∵AB=CD,∴OE=OF,∵OH=3,OA=5,∴OE=3,∴AE=BE=4,∴BH=BE﹣HE=4﹣3=1;②根据①得出BE=4,HE=3,∴BH=HE+BE=3+4=7.18.【解答】解:∵CM⊥OA,即OM⊥CD,由垂径定理得:CD=2CM=4cm,连接OC,∵C为弧AB的中点,∴弧AC=弧BC,∴∠AOC=∠BOC,∵CN⊥OB,CD⊥OA∴∠CMO=∠CNO∴∴△CMO≌△CNO∴CN=CM=2cm,故答案为:2.19.【解答】解:∵周角的度数是360°,∴这三个扇形中圆心角最小的度数是,故答案为:80.20.【解答】解:∵弧AB=弧BC,且弧AB:弧AmC=3:4,∴弧ABC:弧AmC=6:4,∴∠AOC的度数为(360°÷10)×4=144°.21.【解答】解:∵在⊙O中,=,∴=,∴∠1=∠2=30°.故答案是:30°.22.【解答】解:如下图,连接AM,连接MB,过点O作OG⊥AM,OH⊥AM,∵∠BAD=∠CDA=90°,∴AM过圆心O,而A、D、M、B四点公圆,∴四边形ADMB为矩形,而AB=1,CD=2,∴CM=2﹣1=1=AB=DM,即:①DM=CM,正确;又AB∥CD,∴四边形ABMC为平行四边形,∴∠AEB=∠MAE,=,故②正确;∵四边形ADMB为矩形,∴AB=DM,∴=,∴∠DAM=∠EAM,过点O作OG⊥AM,OH⊥AM,∴OG=OH,∴AD=AE,∴④正确;由题设条件求不出直径的大小,故③⊙O的直径为2,错误;故答案为①②④.23.【解答】解:∵AB=CD,∴∠COD=∠AOB,∵∠AOB=50°,∴∠COD=50°,故答案是:50°.24.【解答】解:∵AEE∥CD,∠AOC=50°,∴∠EAO=∠C=50°,∵OA=OE,∴∠AEO=∠EAO=50°,∴∠AOE=180°﹣∠EAO﹣∠AEO=80°,即的度数为80°,故答案为:80°.25.【解答】解:连接OC,BC,OD,∵直径AB平分弦CD,OE=BE,∴OC=BC=OB,∴△OCB是等边三角形,∴∠COB=60°,∴∠COD=120°,即弦CD所对的圆心角是120°,故答案为:120三.解答题(共6小题)26.【解答】证明:在△AED和△CEB中,,∴△AED≌△CEB(AAS).∴AD=BC,∴=.27.【解答】解:∠ACB=2∠BAC.证明:∵∠ACB=∠AOB,∠BAC=∠BOC;又∵∠AOB=2∠BOC,∴∠ACB=2∠BAC.28.【解答】证明:∵AB=CD,∴=,∴﹣=﹣,即=,∴AD=BC.29.【解答】(1)证明:如图,∵AD=BC,∴=,∴﹣=﹣,即=,∴AB=CD;(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.则AF=FD,BG=CG.∵AD=BC,∴AF=CG.在Rt△AOF与Rt△COG中,,∴Rt△AOF≌Rt△COG(HL),∴OF=OG,∴四边形OFEG是正方形,∴OF=EF.设OF=EF=x,则AF=FD=x+1,在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,解得x=3.则AF=3+1=4,即AE=AF+3=7.30.【解答】解:∵甲、乙、丙、丁四个扇形的面积之比为1:2:3:4,∴各个扇形的面积分别占整个圆面积的,,,,∴各个扇形的圆心角的度数分别360°×=36°,360°×=72°,360°×=108°,360°×=144°,答:甲、乙、丙、丁四个扇形的圆心角的度数分别是36°,72°,108°,144°.31.【解答】证明:连接OA、OB,∵OA=OB,∴∠A=∠B,∵=,∴∠AOC=∠BOD,在△AOC和△BOD中,,∴△AOC≌△BOD,∴AC=BD.。
人教版九年级数学上册 24.1.3 弧、弦、圆心角 同步练习卷
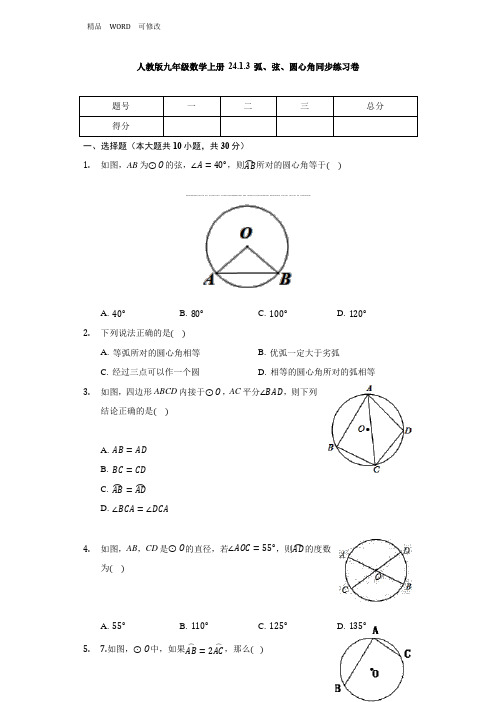
人教版九年级数学上册24.1.3 弧、弦、圆心角同步练习卷题号一二三总分得分一、选择题(本大题共10小题,共30分)1.如图,AB为⊙O的弦,∠A=40°,则AB⏜所对的圆心角等于()A. 40°B. 80°C. 100°D. 120°2.下列说法正确的是()A. 等弧所对的圆心角相等B. 优弧一定大于劣弧C. 经过三点可以作一个圆D. 相等的圆心角所对的弧相等3.如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A. AB=ADB. BC=CDC. AB⏜=AD⏜D. ∠BCA=∠DCA4.如图,AB,CD是⊙O的直径,若∠AOC=55°,则AD⏜的度数为()A. 55°B. 110°C. 125°D. 135°5.7.如图,⊙O中,如果AB⌢=2AC⌢,那么()A. AB=ACB. AB=2ACC. AB<2ACD. AB>2AC6.如图,在⊙O中AC⏜=BD⏜,∠AOB=40°,则∠COD的度数()A. 20°B. 40°C. 50°D. 60°7.如图,AB,CD是⊙O的直径,AE⏜=BD⏜.若∠AOE=32°,则∠COE的度数是()A. 32°B. 60°C. 68°D. 64°8.如图,在⊙O中,已知弦AB长为16cm,C为弧AB的中点,OC交AB于点M,且OM∶MC=3∶2,则CM长为()A. 2cmB. 4cmC. 6cmD. 8cm9.如图,AB是⊙O的直径,C,D分别是⊙O上的两点,OC⊥OD,AC=2cm,BD=√2cm,则⊙O的半径是()A. √3cmB. 2cmC. √5cmD. 3cm10.如图,AB是⊙O的直径,C是AB⏜的中点,连接OC,点E,F分别是OA,OC上的点,若EF//AC,则∠EFC的度数为()A. 45°B. 60°C. 135°D. 160°二、填空题(本大题共5小题,共15分)11.已知圆O的半径长为6,若弦AB=6√3,则弦AB所对的圆心角等于______ .12.如图,在⊙O中,点C为弧AB的中点,OC交弦AB于D,如果AB=8,OC=5,那么OD的长为______.13.如图,在⊙O中,AB⏜=CD⏜,∠AOB与∠COD的关系是______.14.如图,AB是⊙O的直径,弦CD⊥AB于点E,如果AC⏜=CD⏜,则∠ACD的度数是______.15.如图所示,PO是⊙O直径所在的直线,且PO平分∠BPD,OE⊥AB,OF⊥CD,则:①AB=CD;②AB⌢=CD⌢;③PO=PE;④BG⌢=DG⌢;⑤PB=PD.其中结论正确的是_________.(填序号)三、解答题(本大题共5小题,共55分)16.如图,已知AB为圆O的直径,M,N分别为OA,OB的中点,CM⊥AB,DN⊥AB,垂足分别为M,N,连结OC,OD,求证:AC⏜=BD⏜.17.如图,已知⊙O的弦AB,E,F是弧AB上两点,AE⏜=BF⏜,OE、OF分别交于AB于C、D两点,求证:AC=BD.18.如图,在⊙O中,AB⏜=BC⏜,∠BOC=32°,求∠D的度数.19.如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断EF⌒和FG⌒是否相等,并说明理由.20.已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧AD⏜上到一点E使∠EBC=∠DEC,延长BE依次交AC于G,交⊙O于H.(1)求证:AC⊥BH;(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求①CGCD的值;②EH的长.1、最困难的事就是认识自己。
(人教版数学)初中9年级上册-同步练习-24.1.3 弧、弦、圆心角-九年级数学人教版(上)(解析版

第二十四章圆24.1.3弧、弦、圆心角一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.如图,已知AB是O的直径,D,C是劣弧EB的三等分点,∠BOC=40°,那么∠AOE=A.40°B.60°C.80°D.120°【答案】B2.将一个圆分割成四个大小相同的扇形,则每个扇形的圆心角是()度.A.45 B.60C.90 D.120【答案】C【解析】∵圆心处构成一个周角,∴圆心角为360°,∵将圆分割成四个大小相同的扇形,∴每个扇形的圆心角是90°,故选C.【名师点睛】本题考查了扇形和圆心角的定义,解题的关键是掌握一个圆的圆心角为360°.3.已知AB与A′B′分别是O与O′的两条弦,AB=A′B′,那么∠AOB与∠A′O′B′的大小关系是A.∠AOB=∠A′O′B′ B.∠AOB>∠A′O′B′C.∠AOB<∠A′O′B′ D.不能确定【答案】D【解析】由弦相等推弦所对的圆心角相等,必须保证在同圆或等圆中.此题没有限制,所以不能确定∠AOB 和∠A′O′B′的大小关系.4.下列图形中表示的角是圆心角的是A .AB .BC .CD .D【答案】A【解析】根据圆心角的定义:顶点在圆心的角是圆心角可知,B,C,D 项图形中的顶点都不在圆心上,所以它们都不是圆心角.故选A. 5.如果两个圆心角相等,那么 A .这两个圆心角所对的弦相等B .这两个圆心角所对的弧相等C .这两个圆心角所对的弦的弦心距相等D .以上说法都不对 【答案】D6.在同圆中,下列四个命题:(1)圆心角是顶点在圆心的角;(2)两个圆心角相等, 它们所对的弦也相等;(3)两条弦相等,它们所对的弧也相等;(4)等弧所对的圆心角相等.其中真命题有A .4个B .3个C .2个D .1个【答案】B【解析】圆心角是顶点在圆心的角,所以①正确,为真命题;在同圆中,两个圆心角相等,它们所对的弦也相等,所以②正确,为真命题;在同圆中,两条弦相等,所对的劣弧也相等,所以③错误,为假命题;等弧所对的圆心角相等,所以④正确,为真命题. 故选B .7.如图,已知A 、B 、C 、D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有 ①AB CD =;②BD AC =;③AC =BD ;④∠BOD =∠AO C .A.1个B.2个C.3个D.4个【答案】D二、填空题:请将答案填在题中横线上.8.如图,AB是⊙O的直径,点C在⊙O上,∠AOC=40°,D是弧BC的中点,则∠ACD= ________.【答案】125°【解析】连接OD,∵AB是⊙O的直径,∠AOC=40°,∴∠BOC=140°,∠ACO=(180°-40°)÷2=70°,∵D是弧BC的中点,∴∠COD=70°,∴∠OCD=(180°-70°)÷2=55°,∴∠ACD=∠ACO+∠OCD=70°+55°=125°,故答案为125°.9.在半径为R的⊙O中,有一条弦等于半径,则弦所对的圆心角为 ________.【答案】60°【解析】如图,AB=OA=OB,所以△ABC为等边三角形,所以∠AOB=60°.故答案为60°.10.弦AB将⊙O分成度数之比为1:5的两段弧,则∠AOB= _________°.【答案】60三、解答题:解答应写出文字说明、证明过程或演算步骤.11.如图,AB,CD,EF都是O的直径,且∠1=∠2=∠3,求证:AC=EB=DF.【解析】在O中,∵∠1=∠2=∠3,又∵AB,CD,EF都是O的直径,∴∠FOD=∠AOC=∠BOE.∴DF=AC=EB,∴AC=EB=DF.。
2020年人教版九年级数学上册24.1.3《弧、弦、圆心角》同步练习 学生版

别交 BC,CD 于点 E,M,下列结论:①DM=CM;② AE=AD.其中正确的结论有 (填序号).
;③⊙O 的直径为 2;④
23.如图,在⊙O 中,AB=DC,∠AOB=50°,则∠COD= .
24.如图,已知 AB、CD 是⊙O 中的两条直径,且∠AOC=50°,过点 A 作 AE∥CD 交⊙O 于点 E,则 的度数为 .
B.BE=CD
C.AC=BD
D.BE=AD
12.如图,圆心角∠AOB=25°,将 AB 旋转 n°得到 CD,则∠COD 等于( )
A.25°
B.25°+n°
C.50°
D.50°+n°
13.如图,⊙O 的半径为 1,动点 P 从点 A 处沿圆周以每秒 45°圆心角的速度逆时针匀速 运动,即第 1 秒点 P 位于如图所示的位置,第 2 秒中 P 点位于点 C 的位置,……,则第 2018 秒点 P 所在位置的坐标为( )
下列结论:①OE=OF;②AC=CD=DB;③CD∥AB;④ = ,其中正确的有( )
A.4 个
B.3 个
C.2 个
D.1 个
二.填空题
16.如图,AB,CD 是⊙O 的直径,弦 CE∥AB,弧 CE 的度数为 40°,∠AOC 的度
数 .
17.⊙O 的半径为 5,弦 AB 与弦 CD 相等,且 AB⊥CD 于 H,若 OH=3 ,则线段 BH 长 为 . 18.如图,C 为弧 AB 的中点,CN⊥OB 于 N,CD⊥OA 于 M,CD=4cm,则 CN= cm.
A.40°
B.45°
C.55°
D.80°
4.如图,BC 为半圆 O 的直径,A、D 为半圆上的两点,若 A 为半圆弧 ADC=( )
人教版九年级上数学《24.1.3弧、弦、圆心角》练习题(含答案)

24.1.3 弧、弦、圆心角01 基础题知识点1 圆心角的概念及其计算1.下面图形中的角是圆心角的是(D)A B C D2.已知⊙O 的半径为5 cm ,弦AB 的长为5 cm ,则弦AB 所对的圆心角∠AOB =60°.知识点2 弧、弦、圆心角之间的关系3.下列说法正确的是(B)A .相等的圆心角所对的弧相等B .在同圆中,等弧所对的圆心角相等C .弦相等,圆心到弦的距离相等D .圆心到弦的距离相等,则弦相等4.(兰州中考)如图,在⊙O 中,点C 是的中点,∠A =50°,则∠BOC =(A)AB ︵ A .40° B .45° C .50° D .60°5.(教材P85练习T2变式)(贵港中考)如图,AB 是⊙O 的直径,==,∠COD =34°,则∠AEO 的BC ︵ CD ︵ DE ︵ 度数是(A)A .51°B .56°C .68°D .78°6.如图,已知A ,B ,C ,D 是⊙O 上的点,∠1=∠2,则下列结论中正确的有(D)①=;②=;③AC =BD ;④∠BOD =∠AOC.AB ︵ CD ︵ BD ︵ AC ︵ A .1个 B .2个 C .3个 D .4个7.如图,AB 是⊙O 的直径,BC ,CD ,DA 是⊙O 的弦,且BC =CD =DA ,则∠BCD 的度数为(C)A .100°B .110°C .120°D .135°8.如图,AB ,DE 是⊙O 的直径,C 是⊙O 上的一点,且=.BE 与CE 的大小有什么关系?为什么?AD ︵ CE ︵解:BE =CE.理由如下:∵AB ,DE 是⊙O 的直径,∴∠AOD =∠BOE.∴=.AD ︵ BE ︵ ∵=,∴=.AD ︵ CE ︵ BE ︵ CE ︵ ∴BE =CE.9.如图,M 为⊙O 上一点,OD ⊥AM 于点D ,OE ⊥BM 于点E.若OD =OE ,求证:=.AM ︵ BM ︵证明:连接OM.∵OD ⊥AM ,OE ⊥BM ,∴AD =MD ,ME =BE ,∠ODM =∠OEM =90°.在Rt △DMO 和Rt △EMO 中,{OD =OE ,OM =OM ,)∴Rt △DMO ≌Rt △EMO(HL).∴DM =EM.∴AM =BM.∴=.AM ︵ BM ︵ 易错点 对圆中的有关线段的关系运用不当而致错10.如图,A ,B ,C ,D 是⊙O 上的四点,且AD =BC ,则AB 与CD 的大小关系为(B)A .AB>CDB .AB =CDC .AB<CDD .不能确定02 中档题11.如图,已知A ,B ,C 在圆O 上,D ,E ,F 是三边的中点.若=,则四边形AEDF 的形状是(B)AB ︵ AC ︵ A .平行四边形B .菱形C .正方形D .矩形12.已知⊙O 中,M 为的中点,则下列结论正确的是(C)AB ︵ A .AB >2AMB .AB =2AMC .AB <2AMD .AB 与2AM 的大小不能确定13.如图,AB 是半圆O 的直径,E 是OA 的中点,F 是OB 的中点,ME ⊥AB 于点E ,NF ⊥AB 于点F.在下列结论中:①==;②ME =NF ;③AE =BF ;④ME =2AE.AM ︵ MN ︵ BN ︵ 正确的有①②③.14.如图,AB 是⊙O 的直径,=,∠COD =60°.AC ︵ CD ︵ (1)△AOC 是等边三角形吗?请说明理由;(2)求证:OC ∥BD.解:(1)△AOC 是等边三角形.理由:∵=,AC ︵ CD ︵ ∴∠AOC =∠COD =60°.又∵OA =OC ,∴△AOC 是等边三角形.(2)证明:∵∠AOC =∠COD =60°,∴∠BOD =180°-(∠AOC +∠COD)=60°.∵OD =OB ,∴△ODB 为等边三角形.∴∠ODB =60°.∴∠ODB =∠COD =60°.∴OC ∥BD.15.(教材P84例3变式)如图,A ,B ,C 为圆O 上的三等分点.(1)求∠BOC 的度数;(2)若AB =3,求圆O 的半径长及S △ABC .解:(1)∵A ,B ,C 为圆O 上的三等分点,∴==.AB ︵ BC ︵ AC ︵ ∴∠BOC =×360°=120°.13(2)过点O 作OD ⊥AB 于点D ,∵A ,B ,C 为圆O 上的三等分点,∴AB =AC =BC =3,即△ABC 是等边三角形.∴∠BAO =∠OBA =30°.则AD =,故DO =,OA =,即圆O 半径长为.323233∴S △ABC =3××DO·AB =.1293403 综合题16.如图,∠AOB =90°,C ,D 是的三等分点,连接AB 分别交OC ,OD 于点E ,F ,求证:AB ︵ AE =BF =CD.证明:连接AC ,BD.∵C ,D 是的三等分点,AB ︵ ∴==.AC ︵ CD ︵ DB ︵ ∴AC =CD =DB.又∠AOB =90°,∴∠AOC =∠COD =∠BOD =∠AOB =×90°=30°.1313∵OA =OB ,∴∠OAB =∠OBA =45°.∴∠AEC =∠AOC +∠OAB =75°.在△AOC 中,OA =OC ,∴∠ACO ===75°.180°-∠AOC 2180°-30°2∴∠AEC =∠ACO.∴AE =AC.同理BF =BD.∴AE =BF =CD.。
人教版数学九年级上册:24.1.3 弧、弦、圆心角 同步练习(附答案)

24.1.3 弧、弦、圆心角1.如图,图中的圆心角(小于平角的)有( )A .1个B .2个C .3个D .4个2.已知⊙O 的半径为5 cm ,弦AB 的长为5 cm ,则弦AB 所对的圆心角∠AOB = . 3.如图,A ,B ,C ,D 是⊙O 上的四点,且AD =BC ,则AB 与CD 的大小关系为( )A .AB>CDB .AB =CDC .AB<CD D .不能确定4.如图,在⊙O 中,点C 是AB ︵的中点,∠A =50°,则∠BOC =( )A .40°B .45°C .50°D .60°5.如图,AB 是⊙O 的直径,BC ︵=CD ︵=DE ︵,∠COD =34°,则∠AEO 的度数是( )A .51°B .56°C .68°D .78°6.如图,在⊙O 中,AB ︵=AC ︵,∠A =30°,则∠B =( )A .150°B .75°C .60°D .15°7.如图,AB 是⊙O 的直径,C ,D 为半圆的三等分点,CE ⊥AB 于点E ,则∠ACE 的度数为 .8.如图,AB ,DE 是⊙O 的直径,点C 是⊙O 上的一点,且AD ︵=CE ︵,求证:BE =CE.9.如图,在⊙O 中,AB ︵=2CD ︵,试判断AB 与2CD 的大小关系,并说明理由.10.如图,在⊙O 中,已知弦AB =DE ,OC ⊥AB ,OF ⊥DE ,垂足分别为C ,F ,则下列说法中正确的个数为( )①∠DOE =∠AOB ;②AB ︵=DE ︵;③OF =OC ;④AC =EF. A .1个 B .2个 C .3个 D .4个11.如图,点A ,B ,C 是⊙O 上的三点,且四边形ABCO 是平行四边形,OF ⊥AB 交⊙O 于点F ,则∠BAF 等于( )A .12.5°B .15°C .20°D .22.5°12.如图,AB 是半圆O 的直径,E 是OA 的中点,F 是OB 的中点,ME ⊥AB 于点E ,NF ⊥AB 于点F.下列结论:①AM ︵=MN ︵=BN ︵;②ME =NF ;③AE =BF ;④ME =2AE.其中正确结论的序号是 .13.如图,以▱ABCD 的顶点A 为圆心,AB 为半径作圆,交AD ,BC 于E ,F ,延长BA 交⊙A 于点G ,求证:GE ︵=EF ︵.14.如图,AB 是⊙O 的直径,AC ︵=CD ︵,∠COD =60°. (1)△AOC 是等边三角形吗?请说明理由; (2)求证:OC ∥BD.15.如图,∠AOB =90°,C ,D 是AB ︵的三等分点,连接AB 分别交OC ,OD 于点E ,F ,求证:AE =BF =CD.参考答案:1.B 2. 60°. 3.B 4.A 5.A 6.B 7. 30°.8.证明:∵∠BOE =∠AOD , ∴BE ︵=AD ︵. 又∵AD ︵=CE ︵, ∴BE ︵=CE ︵. ∴BE =CE.9.解:∵在同圆或等圆中,同弧或等弧所对的弦相等,∴当AB ︵=2CD ︵时,AB =2CD. 以上解答是否正确?若不正确,请改正. 解:不正确.AB <2CD.理由:取AB ︵的中点E ,连接AE ,BE , ∵AB ︵=2CD ︵,∴AE ︵=BE ︵=CD ︵,∴AE =BE =CD. ∵AE +BE >AB ,∴AB <2CD. 10.D 11.B 12.①②③.13.证明:连接AF.∵四边形ABCD 为平行四边形, ∴AD ∥BC. ∴∠GAE =∠B , ∠EAF =∠AFB.又∵AB ,AF 为⊙A 的半径,AB =AF , ∴∠B =∠AFB. ∴∠GAE =∠EAF. ∴GE ︵=EF ︵.14.解:(1)△AOC 是等边三角形. ∵AC ︵=CD ︵,∴∠AOC =∠COD =60°. 又∵OA =OC ,∴△AOC 是等边三角形. (2)证明:∵AC ︵=CD ︵,∴OC ⊥AD. ∵∠AOC =∠COD =60°,∴∠BOD =180°-(∠AOC +∠COD )=60°. ∵OD =OB ,∴△ODB 为等边三角形. ∴∠ODB =60°. ∴∠ODB =∠COD =60°. ∴OC ∥BD.15.证明:连接AC ,BD. ∵AC ︵=CD ︵=DB ︵,∠AOB =90°,∴∠AOC =∠COD =∠DOB =13∠AOB =13×90°=30°,AC =CD =BD.∵OA =OB ,∴∠OAB =∠ABO =45°. ∴∠AEC =∠AOC +∠OAB =75°. ∵在△AOC 中,OA =OC ,∴∠ACO =180°-∠AOC 2=180°-30°2=75°.∴∠AEC =∠ACO. ∴AE =AC. 同理BF =BD. ∴AE =BF =CD.。
初三数学九年级上册同步练习24.1.3 弧、弦、圆心角

24.1.3 弧、弦、圆心角一、课内练习:1.下列命题中,正确的有()A.圆只有一条对称轴B.圆的对称轴不止一条,但只有有限条C.圆有无数条对称轴,每条直径都是它的对称轴D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴2.下列说法中,正确的是()A.等弦所对的弧相等B.等弧所对的弦相等C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等3.下列命题中,不正确的是()A.圆是轴对称图形B.圆是中心对称图形C.圆既是轴对称图形,又是中心对称图形D.以上都不对4.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等; D.以上说法都不对5.如图1,半圆的直径AB=4,O为圆心,半径OE⊥AB,F为OE的中点,CD∥AB,则弦CD的长为()A.23B.3C.5D.256.已知:如图2,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O 的半径为()A.4cm B.5cm C.42cm D.23cm7.如图3,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为()A.3:2 B.5:2 C.5:2D.5:48.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为()A.42B.82C.24 D.169.如果两条弦相等,那么()A.这两条弦所对的弧相等B.这两条弦所对的圆心角相等C.这两条弦的弦心距相等D.以上答案都不对10.半径为5的⊙O内有一点P,且OP=4,则过点P的最短的弦长是,最长的弦长是.11.弓形的弦长6cm,高为1cm,则弓形所在圆的半径为 cm.12.一条弦把圆分成1:3两部分,则弦所对的圆心角为.13.弦心距是弦的一半时,弦与直径的比是,弦所对的圆心角是.14.如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.O。
人教版九年级上册上册数学 24.1.3弧、弦、圆心角 同步测试(含解析)

24.1.3弧、弦、圆心角同步测试一.选择题(共10小题)1.如图所示,AB是⊙O直径,CM是AO的垂直平分线,DN是OB的垂直平分线,则下列结论正确的是()A.==B.=<C.=>D.<<2.已知,如图,∠AOB=∠COD,下列结论不一定成立的是()A.AB=CDB.=C.△AOB≌△CODD.△AOB、△COD都是等边三角形3.如果两个圆心角相等,那么()A.这两个圆心角所对的弦相等B.这两个圆心角所对的弧相等C.这两个圆心角所对的弦的弦心距相等D.以上说法都不对4.⊙O中,M为的中点,则下列结论正确的是()A.AB>2AMB.AB=2AMC.AB<2AMD.AB与2AM的大小不能确定5.下列说法中正确的有()①直径相等的圆一定是等圆;②两个半圆一定是等弧;③平分弦的直径垂直于弦;④等弧所对的弦相等;⑤相等的圆心角所对的弦相等.A.①②③B.①③④C.①④⑤D.①④6.如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是()A.=B.>C.<D.无法确定7.如图⊙O的半径为1cm,弦AB、CD的长度分别为,则弦AC、BD所夹的锐角α为()A.75°B.45°C.60°D.30°8.已知AB是⊙O的直径,弧AC的度数是30°.如果⊙O的直径为4,那么AC2等于()A.B.C.D.29.如图,AB是半圆的直径,∠BAC=20°,D是的中点,则∠DAC的度数是()A.30°B.35°C.45°D.70°10.下列说法中正确的是()①圆心角是顶点在圆心的角;②两个圆心角相等,它们所对的弦相等;③两条弦相等,圆心到这两弦的距离相等;④在等圆中,圆心角不变,所对的弦也不变.A.①③B.②④C.①④D.②③二.填空题(共5小题)11.已知圆O的半径为5,弦AB的长为5,则弦AB所对的圆心角∠AOB=.12.如图,在⊙O中,直径AB∥弦CD,若∠COD=120°,则∠BOD=°.13.如图,AB是直径,==,∠BOC=50°,∠AOE的度数是.14.如图,AB是⊙O的直径,如果∠COA=∠DOB=60°,那么与线段OA相等的线段是;与相等的弧是.15.如图,AD为直径,∠AOB=∠BOC=∠COD,O为圆心,那么(1)弧AB所对的圆心角是;(2)弧BD所对的圆心角是.三.解答题(共3小题)16.如图,已知⊙O中,点A,B,C,D在圆上,且AB=CD,求证:AC=BD.17.已知,如图,⊙O的两条弦AB,CD相交于点E,且AB=CD,连结BC,AD,求证:AE=CE.18.如图,在⊙O中,弦AB∥弦CD,∠A=28°,∠B=45°,=3,求的度数.参考答案1.解:连接AC,OC,OD,BD,∵CM是AO的垂直平分线,DN是OB的垂直平分线,∴AC=OC,BD=OD,∵OC=OD=OA=OB,∴△AOC,△BOD是等边三角形,∴∠AOC=∠BOD=60°,∵AB是⊙O直径,∴∠COD=60°,∴==,故选:A.2.解:∵∠AOB=∠COD,∴AB=CD,=,∵OA=OB=OC=OD,∴△AOB≌△COD,∴ABC成立,则D不成立,故选:D.3.解:在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距相等.故选:D.4.解:连接BM.∵M为的中点,∴AM=BM,∵AM+BM>AB,∴AB<2AM.故选:C.5.解:①直径相等的圆一定是等圆,本小题说法正确;②两个半径相等的半圆一定是等弧,本小题说法错误;③平分弦(不是直径)的直径垂直于弦,本小题说法错误;④等弧所对的弦相等,本小题说法正确;⑤在同圆或等圆中,相等的圆心角所对的弦相等,本小题说法错误;故选:D.6.证明:连接AC,∵AD∥BC,∴∠DAC=∠ACB,∴=.故选:A.7.解:连接OA、OB、OC、OD,∵OA=OB=OC=OD=1,AB=,CD=1,∴OA2+OB2=AB2,∴△AOB是等腰直角三角形,△COD是等边三角形,∴∠OAB=∠OBA=45°,∠ODC=∠OCD=60°,∵∠CDB=∠CAB,∠ODB=∠OBD,∴α=180°﹣∠CAB﹣∠OBA﹣∠OBD=180°﹣∠OBA﹣(∠CDB+∠ODB)=180°﹣45°﹣60°=75°.8.解:如图,连接OC.过点C作CD⊥OA于点D.∵⊙O的直径为4,∴AB=4,∴OA=OC=2.∵弧AC的度数是30°,∴∠COD=30°,∴CD=1,∴OD==,则AD=2﹣,∵AB是直径,∴∠ACB=90°.∴AC2=AD•AB=(2﹣)×4=8﹣4.故选:C.9.解:连接BC,∵AB是半圆的直径,∴∠C=90°,∵∠BAC=20°,∴∠CBA=90°﹣∠BAC=70°,∵D是的中点,∴∠DAC=∠ABC=35°.10.解:圆心角是顶点在圆心的角,所以①正确;在同圆和等圆中,两个圆心角相等,它们所对的弦相等,所以②错误;③在同圆和等圆中,两条弦相等,圆心到这两弦的距离相等,所以③错误;在等圆中,圆心角不变,所对的弦也不变,所以④正确.故选:C.11.解:如图,∵OA=OB=5,AB=5,∴OA=OB=AB,∴△OAB为等边三角形,∴∠AOB=60°.故答案为60°.12.解:∵OC=OD,∴∠C=∠D,∵∠COD=120°,∴∠C=∠D=30°,∵AB∥CD,∴∠BOD=∠D=30°,故答案为30.13.解:∵==,∴∠BOC=∠COD=∠DOE=50°,∴∠AOE=180°﹣3×50°=30°.故答案为30°.14.解:∵AB是⊙O的直径,∠COA=∠DOB=60°,∴∠AOC=∠COD=∠BOD=60°;又∵OA=OC=OD=OB,∴△OAC、△OCD、△BOD是全等的等边三角形;∴OA=AC=OC=CD=OD=BD=OB;∴,故答案为:AC,OC,CD,OD,BD,OB;、.15.解:(1)弧AB所对的圆心角是∠AOB=60°;(2)弧BD所对的圆心角是∠BOD=120°.故答案为60°,120°.16.解:∵AB=CD,∴=,∴+=+,即=,∴AC=BD.17.证明:∵AB=CD,∴=,∴﹣=﹣,即=,∴AD=BC,在△AED和△CEB中,,∴△AED≌△CEB,∴AE=CE.18.解:连接AE,DE,∵∠A=28°,=3,∴∠AED=3∠A=84°,∠ADE=∠B=45°,∴∠EAD=180°﹣∠ADE﹣∠AED=51°,∴的度数是102°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教版数学九年级上同步练习 24.1.3 弧、弦、圆心角
一、课内练习:
1.下列命题中,正确的有()
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
2.下列说法中,正确的是()
A.等弦所对的弧相等B.等弧所对的弦相等
C.圆心角相等,所对的弦相等D.弦相等所对的圆心角相等
3.下列命题中,不正确的是()
A.圆是轴对称图形B.圆是中心对称图形
C.圆既是轴对称图形,又是中心对称图形D.以上都不对
4.如果两个圆心角相等,那么()
A.这两个圆心角所对的弦相等; B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等; D.以上说法都不对
5.如图1,半圆的直径AB=4,O为圆心,半径OE⊥AB,F为OE的中点,CD∥AB,则弦CD的长为()
A.23B.3C.5D.25
6.已知:如图2,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O 的半径为()
A.4cm B.5cm C.42cm D.23cm
7.如图3,同心圆中,大圆的弦AB交小圆于C、D,已知AB=4,CD=2,AB的弦心距等于1,那么两个同心圆的半径之比为()
A.3:2 B.5:2 C.5:2D.5:4
8.在⊙O中,圆心角∠AOB=90°,点O到弦AB的距离为4,则⊙O的直径的长为()
A.42B.82C.24 D.16
9.如果两条弦相等,那么()
A.这两条弦所对的弧相等B.这两条弦所对的圆心角相等
C.这两条弦的弦心距相等D.以上答案都不对
10.半径为5的⊙O内有一点P,且OP=4,则过点P的最短的弦长是,最长的
弦长是.
11.弓形的弦长6cm,高为1cm,则弓形所在圆的半径为 cm.
12.一条弦把圆分成1:3两部分,则弦所对的圆心角为.
13.弦心距是弦的一半时,弦与直径的比是,弦所对的圆心角是.14.如图,∠AOB=90°,C、D是弧AB的三等分点,AB分别交OC、OD于点E、F,求证:AE=BF=CD.
O。
