2018年天津市北辰区二模数学试题及答案
北辰区第二中学2018-2019学年上学期高二数学12月月考试题含解析

北辰区第二中学2018-2019学年上学期高二数学12月月考试题含解析班级__________ 姓名__________ 分数__________一、选择题1.已知命题“p:∃x>0,lnx<x”,则¬p为()A.∃x≤0,lnx≥x B.∀x>0,lnx≥x C.∃x≤0,lnx<x D.∀x>0,lnx<x2.命题“若a>b,则a﹣8>b﹣8”的逆否命题是()A.若a<b,则a﹣8<b﹣8 B.若a﹣8>b﹣8,则a>bC.若a≤b,则a﹣8≤b﹣8 D.若a﹣8≤b﹣8,则a≤b3.如图,四面体D﹣ABC的体积为,且满足∠ACB=60°,BC=1,AD+=2,则四面体D﹣ABC中最长棱的长度为()A.B.2 C.D.34.已知在R上可导的函数f(x)的图象如图所示,则不等式f(x)•f′(x)<0的解集为()A.(﹣2,0)B.(﹣∞,﹣2)∪(﹣1,0)C.(﹣∞,﹣2)∪(0,+∞)D.(﹣2,﹣1)∪(0,+∞)5.sin570°的值是()A.B.﹣C.D.﹣6.下列函数中哪个与函数y=x相等()A .y=()2B .y=C .y=D .y=7. △ABC 的内角A ,B ,C 所对的边分别为,,,已知a =b =6A π∠=,则B ∠=( )111]A .4πB .4π或34πC .3π或23πD .3π8. 已知m ,n 为不同的直线,α,β为不同的平面,则下列说法正确的是( ) A .m ⊂α,n ∥m ⇒n ∥αB .m ⊂α,n ⊥m ⇒n ⊥αC .m ⊂α,n ⊂β,m ∥n ⇒α∥βD .n ⊂β,n ⊥α⇒α⊥β9. 两座灯塔A 和B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东20°,灯塔B 在观察站C 的南偏东40°,则灯塔A 与灯塔B 的距离为( )A .akmB .akmC .2akmD .akm 10.如图所示,函数y=|2x ﹣2|的图象是( )A .B .C .D .11.S n 是等差数列{a n }的前n 项和,若3a 8-2a 7=4,则下列结论正确的是( ) A .S 18=72 B .S 19=76 C .S 20=80 D .S 21=84 12.函数f (x )=2x ﹣的零点个数为( ) A .0B .1C .2D .3二、填空题13.将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记,则S 的最小值是 .14.某高中共有学生1000名,其中高一年级共有学生380人,高二年级男生有180人.如果在全 校学生中抽取1名学生,抽到高二年级女生的概率为19.0,先采用分层抽样(按年级分层)在全校抽取 100人,则应在高三年级中抽取的人数等于 . 15.给出下列命题:(1)命题p:;菱形的对角线互相垂直平分,命题q:菱形的对角线相等;则p∨q是假命题(2)命题“若x2﹣4x+3=0,则x=3”的逆否命题为真命题(3)“1<x<3”是“x2﹣4x+3<0”的必要不充分条件(4)若命题p:∀x∈R,x2+4x+5≠0,则¬p:.其中叙述正确的是.(填上所有正确命题的序号)16.已知=1﹣bi,其中a,b是实数,i是虚数单位,则|a﹣bi|=.17.由曲线y=2x2,直线y=﹣4x﹣2,直线x=1围成的封闭图形的面积为.18.如图,在平行四边形ABCD中,点E在边CD上,若在平行四边形ABCD内部随机取一个点Q,则点Q 取自△ABE内部的概率是.三、解答题19.已知集合A={x|x2+2x<0},B={x|y=}(1)求(∁R A)∩B;(2)若集合C={x|a<x<2a+1}且C⊆A,求a的取值范围.20.已知命题p:不等式|x﹣1|>m﹣1的解集为R,命题q:f(x)=﹣(5﹣2m)x是减函数,若p或q为真命题,p且q为假命题,求实数m的取值范围.21.设函数f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=﹣f(x),当x∈[0,2]时,f(x)=2x﹣x2.(1)求证:f(x)是周期函数;(2)当x∈[2,4]时,求f(x)的解析式;(3)求f(0)+f(1)+f(2)+…+f(2015)的值.22.(本小题满分12分)如图长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=4,D1F=8,过点E,F,C的平面α与长方体的面相交,交线围成一个四边形.(1)在图中画出这个四边形(不必说明画法和理由);(2)求平面α将长方体分成的两部分体积之比.23.已知等差数列{a n}中,其前n项和S n=n2+c(其中c为常数),(1)求{a n}的通项公式;(2)设b1=1,{a n+b n}是公比为a2等比数列,求数列{b n}的前n项和T n.24.已知椭圆C:+=1(a>b>0)的短轴长为2,且离心率e=,设F1,F2是椭圆的左、右焦点,过F2的直线与椭圆右侧(如图)相交于M,N两点,直线F1M,F1N分别与直线x=4相交于P,Q两点.(Ⅰ)求椭圆C的方程;(Ⅱ)求△F2PQ面积的最小值.北辰区第二中学2018-2019学年上学期高二数学12月月考试题含解析(参考答案)一、选择题1.【答案】B【解析】解:因为特称命题的否定是全称命题,所以,命题“p:∃x>0,lnx<x”,则¬p为∀x>0,lnx≥x.故选:B.【点评】本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.2.【答案】D【解析】解:根据逆否命题和原命题之间的关系可得命题“若a>b,则a﹣8>b﹣8”的逆否命题是:若a﹣8≤b ﹣8,则a≤b.故选D.【点评】本题主要考查逆否命题和原命题之间的关系,要求熟练掌握四种命题之间的关系.比较基础.3.【答案】B【解析】解:因为AD•(BC•AC•sin60°)≥V D﹣ABC=,BC=1,即AD•≥1,因为2=AD+≥2=2,当且仅当AD==1时,等号成立,这时AC=,AD=1,且AD⊥面ABC,所以CD=2,AB=,得BD=,故最长棱的长为2.故选B.【点评】本题考查四面体中最长的棱长,考查棱锥的体积公式的运用,同时考查基本不等式的运用,注意等号成立的条件,属于中档题.4.【答案】B【解析】解:由f(x)图象单调性可得f′(x)在(﹣∞,﹣1)∪(0,+∞)大于0,在(﹣1,0)上小于0,∴f(x)f′(x)<0的解集为(﹣∞,﹣2)∪(﹣1,0).故选B.5.【答案】B【解析】解:原式=sin(720°﹣150°)=﹣sin150°=﹣.故选B【点评】此题考查了运用诱导公式化简求值,熟练掌握诱导公式是解本题的关键.6.【答案】B【解析】解:A.函数的定义域为{x|x≥0},两个函数的定义域不同.B.函数的定义域为R,两个函数的定义域和对应关系相同,是同一函数.C.函数的定义域为R,y=|x|,对应关系不一致.D.函数的定义域为{x|x≠0},两个函数的定义域不同.故选B.【点评】本题主要考查判断两个函数是否为同一函数,判断的标准是判断函数的定义域和对应关系是否一致,否则不是同一函数.7.【答案】B【解析】试题分析:由正弦定理可得:(),sin0,,sin24sin6B B BBπππ=∴=∈∴=或34π,故选B.考点:1、正弦定理的应用;2、特殊角的三角函数.8.【答案】D【解析】解:在A选项中,可能有n⊂α,故A错误;在B选项中,可能有n⊂α,故B错误;在C选项中,两平面有可能相交,故C错误;在D选项中,由平面与平面垂直的判定定理得D正确.故选:D.【点评】本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.9.【答案】D【解析】解:根据题意,△ABC中,∠ACB=180°﹣20°﹣40°=120°,∵AC=BC=akm,∴由余弦定理,得cos120°=,解之得AB=akm ,即灯塔A 与灯塔B 的距离为akm ,故选:D .【点评】本题给出实际应用问题,求海洋上灯塔A 与灯塔B 的距离.着重考查了三角形内角和定理和运用余弦定理解三角形等知识,属于基础题.10.【答案】B【解析】解:∵y=|2x﹣2|=,∴x=1时,y=0, x ≠1时,y >0. 故选B .【点评】本题考查指数函数的图象和性质,解题时要结合图象进行求解.11.【答案】【解析】选B.∵3a 8-2a 7=4, ∴3(a 1+7d )-2(a 1+6d )=4,即a 1+9d =4,S 18=18a 1+18×17d 2=18(a 1+172d )不恒为常数.S 19=19a 1+19×18d2=19(a 1+9d )=76,同理S 20,S 21均不恒为常数,故选B. 12.【答案】C【解析】解:易知函数的定义域为{x|x ≠1}, ∵>0,∴函数在(﹣∞,1)和(1,+∞)上都是增函数,又<0,f(0)=1﹣(﹣2)=3>0,故函数在区间(﹣4,0)上有一零点;又f(2)=4﹣4=0,∴函数在(1,+∞)上有一零点0,综上可得函数有两个零点.故选:C.【点评】本题考查函数零点的判断.解题关键是掌握函数零点的判断方法.利用函数单调性确定在相应区间的零点的唯一性.属于中档题.二、填空题13.【答案】.【解析】解:设剪成的小正三角形的边长为x,则:S==,(0<x<1)令3﹣x=t,t∈(2,3),∴S===,当且仅当t=即t=2时等号成立;故答案为:.14.【答案】25【解析】考点:分层抽样方法.15.【答案】(4)【解析】解:(1)命题p:菱形的对角线互相垂直平分,为真命题.命题q:菱形的对角线相等为假命题;则p∨q是真命题,故(1)错误,(2)命题“若x2﹣4x+3=0,则x=3或x=1”,即原命题为假命题,则命题的逆否命题为假命题,故(2)错误,(3)由x2﹣4x+3<0得1<x<3,则“1<x<3”是“x2﹣4x+3<0”的充要条件,故(3)错误,(4)若命题p:∀x∈R,x2+4x+5≠0,则¬p:.正确,故答案为:(4)【点评】本题主要考查命题的真假判断,涉及复合命题的真假关系,四种命题,充分条件和必要条件以及含有量词的命题的否定,知识点较多,属于中档题.16.【答案】.【解析】解:∵=1﹣bi,∴a=(1+i)(1﹣bi)=1+b+(1﹣b)i,∴,解得b=1,a=2.∴|a﹣bi|=|2﹣i|=.故答案为:.【点评】本题考查了复数的运算法则、模的计算公式,考查了计算能力,属于基础题.17.【答案】.【解析】解:由方程组解得,x=﹣1,y=2故A(﹣1,2).如图,故所求图形的面积为S=∫﹣11(2x2)dx﹣∫﹣11(﹣4x﹣2)dx=﹣(﹣4)=故答案为:【点评】本题主要考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.18.【答案】.【解析】解:由题意△ABE的面积是平行四边形ABCD的一半,由几何概型的计算方法,可以得出所求事件的概率为P=,故答案为:.【点评】本题主要考查了几何概型,解决此类问题的关键是弄清几何测度,属于基础题.三、解答题19.【答案】【解析】解:(1)A={x|x2+2x<0}={x|﹣2<x<0},B={x|y=}={x|x+1≥0}={x|x≥﹣1},∴∁R A={x|x≤﹣2或x≥0},∴(∁R A)∩B={x|x≥0};…(2)当a≥2a+1时,C=∅,此时a≤﹣1满足题意;当a<2a+1时,C≠∅,应满足,解得﹣1<a≤﹣;综上,a的取值范围是.…20.【答案】【解析】解:不等式|x﹣1|>m﹣1的解集为R,须m﹣1<0,即p是真命题,m<1f(x)=﹣(5﹣2m)x是减函数,须5﹣2m>1即q是真命题,m<2,由于p或q为真命题,p且q为假命题,故p、q中一个真,另一个为假命题因此,1≤m<2.【点评】本题考查在数轴上理解绝对值的几何意义,指数函数的单调性与特殊点,分类讨论思想,化简这两个命题是解题的关键.属中档题.21.【答案】【解析】(1)证明:∵f(x+2)=﹣f(x),∴f(x+4)=f[(x+2)+2]=﹣f(x+2)=f(x),∴y=f(x)是周期函数,且T=4是其一个周期.(2)令x∈[﹣2,0],则﹣x∈[0,2],∴f(﹣x)=﹣2x﹣x2,又f(﹣x)=﹣f(x),∴在x∈[﹣2,0],f(x)=2x+x2,∴x∈[2,4],那么x﹣4∈[﹣2,0],那么f(x﹣4)=2(x﹣4)+(x﹣4)2=x2﹣6x+8,由于f(x)的周期是4,所以f(x)=f(x﹣4)=x2﹣6x+8,∴当x∈[2,4]时,f(x)=x2﹣6x+8.(3)当x∈[0,2]时,f(x)=2x﹣x2.∴f(0)=0,f(1)=1,当x∈[2,4]时,f(x)=x2﹣6x+8,∴f(2)=0,f(3)=﹣1,f(4)=0∴f(1)+f(2)+f(3)+f(4)=1+0﹣1+0=0,∵y=f(x)是周期函数,且T=4是其一个周期.∴2016=4×504∴f(0)+f(1)+f(2)+…+f(2015)=504×[f(0)+f(1)+f(2)+f(3)]=504×0=0,即求f (0)+f (1)+f (2)+…+f (2015)=0.【点评】本题主要考查函数周期性的判断,函数奇偶性的应用,综合考查函数性质的应用.22.【答案】 【解析】解:(1)交线围成的四边形EFCG (如图所示). (2)∵平面A 1B 1C 1D 1∥平面ABCD , 平面A 1B 1C 1D 1∩α=EF , 平面ABCD ∩α=GC , ∴EF ∥GC ,同理EG ∥FC . ∴四边形EFCG 为平行四边形, 过E 作EM ⊥D 1F ,垂足为M , ∴EM =BC =10,∵A 1E =4,D 1F =8,∴MF =4. ∴GC =EF =EM 2+MF 2=102+42=116,∴GB =GC 2-BC 2=116-100=4(事实上Rt △EFM ≌Rt △CGB ).过C 1作C 1H ∥FE 交EB 1于H ,连接GH ,则四边形EHC 1F 为平行四边形,由题意知,B 1H =EB 1-EH =12-8=4=GB .∴平面α将长方体分成的右边部分由三棱柱EHG -FC 1C 与三棱柱HB 1C 1GBC 两部分组成. 其体积为V 2=V 三棱柱EHG -FC 1C +V 三棱柱HB 1C 1GBC =S △FC 1C ·B 1C 1+S △GBC ·BB 1 =12×8×8×10+12×4×10×8=480, ∴平面α将长方体分成的左边部分的体积V 1=V 长方体-V 2=16×10×8-480=800. ∴V 1V 2=800480=53, ∴其体积比为53(35也可以).23.【答案】【解析】解:(1)a 1=S 1=1+c ,a 2=S 2﹣S 1=3,a 3=S 3﹣S 2=5﹣﹣﹣﹣﹣(2分)因为等差数列{a n},所以2a2=a1+a3得c=0﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)∴a1=1,d=2,a n=2n﹣1﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(2)a2=3,a1+b1=2∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)【点评】本题主要考查等差数列的定义及数列求和的方法,考查学生的运算求解能力,属中档题.24.【答案】【解析】解:(Ⅰ)∵椭圆C:+=1(a>b>0)的短轴长为2,且离心率e=,∴,解得a2=4,b2=3,∴椭圆C的方程为=1.(Ⅱ)设直线MN的方程为x=ty+1,(﹣),代入椭圆,化简,得(3t2+4)y2+6ty﹣9=0,∴,,设M(x1,y1),N(x2,y2),又F1(﹣1,0),F2(1,0),则直线F1M:,令x=4,得P(4,),同理,Q(4,),∴=||=15×||=180×||,令μ=∈[1,),则=180×,∵y==在[1,)上是增函数,∴当μ=1时,即t=0时,()min=.【点评】本题考查椭圆方程的求法,考查三角形面积的最小值的求法,是中档题,解题时要认真审题,注意韦达定理、直线方程、弦长公式、函数单调性、椭圆性质的合理运用.。
2018年天津市部分区高考数学二模试卷(文科)(解析版)

2018年天津市部分区高考数学二模试卷(文科)一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知全集U={1,2,3,4,5,6,7},集合M={2,3,4,5},集合N={4,5,6},则集合∁U(M∩N)=()A.{1,2,3,5}B.{2,3,6,7}C.{1,2,3,5,6,7}D.{1,2,3,6,7}2.(5分)设变量x、y满足约束条件,则目标函数z=2x+y的最小值为()A.6B.4C.3D.23.(5分)阅读如图的程序框图,运行相应的程序,则输出S的值为()A.15B.37C.83D.1774.(5分)已知双曲线(a>0,b>0)的一条渐近线方程是y=,且它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程是()A.B.C.D.5.(5分)设x∈R,则“x>﹣1”是“|x﹣5|<4”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件6.(5分)已知向量与的夹角为120°,||=5,||=2,若=,且=﹣6,则实数λ的值为()A.﹣B.C.D.7.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位长度后得到函数g(x)的图象,若g(x)在区间[0,]上单调递增,则实数φ的取值范围是()A.[﹣]B.[)C.(]D.(0,] 8.(5分)设函数f(x)是定义在R上的奇函数,且当x>0时f(x)=lnx,记a=f(()),b=﹣f(),c=f(3),则a,b,c的大小关系为()A.c>b>a B.b>c>a C.b>a>c D.a>b>c二、填空题:本大题共有6小题,每小题5分,共30分.9.(5分)已知i为虚数单位,复数z满足z(1+i)=2﹣3i,则z的虚部为.10.(5分)已知函数f(x)=,f′(x)为f(x)的导函数,则f′(1)=.11.(5分)已知直线k(x+1)+y+2=0恒过定点C,且以C为圆心,5为半径的圆与直线3x+4y+1=0相交于A、B两点,则弦AB的长为.12.(5分)已知一个几何体的三视图如图所示(单位:cm),则该几何体的体积为cm3.13.(5分)已知函数y=a log2x﹣b(a>0,b>0)的图象过点(),则的最小值为.14.(5分)已知函数f(x)=,若函数g(x)=﹣f(x)+b在区间[﹣2,6]内有3个零点,则实数b的取值范围是.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)已知△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cos B=.(Ⅰ)求c和sin A的值;(Ⅱ)求sin(2A﹣B)的值.16.(13分)某区的区大代表中有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为A1,A2,乙校教师记为B1,B2,丙校教师记为C,丁校教师记为D.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.(Ⅰ)请列出十九大报告宣讲团组成人员的全部可能结果;(Ⅱ)求教师A1被选中的概率;(Ⅲ)求宣讲团中没有乙校教师代表的概率.17.(13分)在等腰梯形ABCD中,AB∥CD,直线FC⊥平面ABCD,ED∥FC,点G为AB的中点,且FC=AB=2ED=2CD=2,∠ABC=60°.(Ⅰ)求证:AE∥平面GCF;(Ⅱ)求证:平面ACF⊥平面BCF;(Ⅲ)求直线FB与平面ADE所成角的正弦值.18.(13分)已知数列{a n}为等比数列,数列{b n}为等差数列,且b1=a1=1,b2=a1+a2,a3=2b3﹣6.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)设c n=,数列{c n}的前n项和为T n,证明:.19.(14分)已知椭圆C:(a>b>0)的离心率为,椭圆的一个顶点与两个焦点构成的三角形的面积为2.(Ⅰ)求椭圆C的方程;(Ⅱ)已知直线y=k(x﹣1)(k>0)与椭圆C相交于A、B两点,且与x轴,y 轴交于M、N两点.(i)若=,求k的值;(ii)若点Q的坐标为(),求证:为定值.20.(14分)设函数f(x)=2lnx+,g(x)=2x﹣alnx(a∈R).(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数g(x)在(0,e2]上恰有2个零点,求a的取值范围;(Ⅲ)当a=1时,若h(x)=f(x)+2g(x)时,若对任意的正整数n在区间[]上始终存在m+5个数使得h(a1)+h(a2)+h(a3)+…+h(a m)<h(a m+1)+h(a m+2)+h(a m+3)+h(a m+4)+h(a m+5)成立,试问:正整数m是否存在最大值?若存在,求出这个最大值,;若不存在,说明理由.2018年天津市部分区高考数学二模试卷(文科)参考答案与试题解析一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. 1.(5分)已知全集U={1,2,3,4,5,6,7},集合M={2,3,4,5},集合N={4,5,6},则集合∁U(M∩N)=()A.{1,2,3,5}B.{2,3,6,7}C.{1,2,3,5,6,7}D.{1,2,3,6,7}【解答】解:全集U={1,2,3,4,5,6,7},集合M={2,3,4,5},集合N={4,5,6},∴M∩N={4,5},集合∁U(M∩N)={1,2,3,6,7}.故选:D.2.(5分)设变量x、y满足约束条件,则目标函数z=2x+y的最小值为()A.6B.4C.3D.2【解答】解:由变量x、y满足约束条件作出可行域如图,化目标函数z=2x+y为y=﹣2x+z,由图可知,当直线y=﹣2x+z过A(1,1)时直线在y轴上的截距最小,z最小,为2×1+1=3.故选:C.3.(5分)阅读如图的程序框图,运行相应的程序,则输出S的值为()A.15B.37C.83D.177【解答】解:当i=1时,不满足退出循环的条件:S=1,i=3;当i=3时,不满足退出循环的条件:S=5,i=5;当i=5时,不满足退出循环的条件:S=15,i=7;当i=7时,不满足退出循环的条件:S=37,i=9;当i=9时,满足退出循环的条件,故输出的S值为37,故选:B.4.(5分)已知双曲线(a>0,b>0)的一条渐近线方程是y=,且它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程是()A.B.C.D.【解答】解:∵双曲线=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线l:x=﹣6上,∴,解得a=3,b=3,∴双曲线方程为.故选:C.5.(5分)设x∈R,则“x>﹣1”是“|x﹣5|<4”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:“|x﹣5|<4”⇔﹣4<x﹣5<4⇔1<x<9,∴“x>﹣1”是“|x﹣5|<4”的必要不充分条件.故选:B.6.(5分)已知向量与的夹角为120°,||=5,||=2,若=,且=﹣6,则实数λ的值为()A.﹣B.C.D.【解答】解:,,;∴==﹣25λ﹣5(λ﹣1)+4=﹣6;解得.故选:B.7.(5分)将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位长度后得到函数g(x)的图象,若g(x)在区间[0,]上单调递增,则实数φ的取值范围是()A.[﹣]B.[)C.(]D.(0,]【解答】解:将函数f(x)=sin2x的图象向右平移φ(0<φ<)个单位长度后得到函数g(x)的图象,则g(x)=sin2(x﹣φ)=sin(2x﹣2φ),若g(x)在区间[0,]上单调递增,则2kπ﹣≤2x﹣2φ≤2kπ+,k∈Z,得2kπ﹣+2φ≤2x≤2kπ++2φ,k∈Z,即kπ﹣+φ≤x≤kπ++φ,k∈Z,即函数的单调递增区间为[kπ﹣+φ,kπ++φ],k∈Z,∵若g(x)在区间[0,]上单调递增,∴满足,即,则﹣kπ﹣≤φ≤﹣kπ+,k∈Z,当k=0时,﹣≤φ≤,又因为:0<φ<所以φ的取值范围是(0,],故选:D.8.(5分)设函数f(x)是定义在R上的奇函数,且当x>0时f(x)=lnx,记a=f(()),b=﹣f(),c=f(3),则a,b,c的大小关系为()A.c>b>a B.b>c>a C.b>a>c D.a>b>c【解答】解:x>0时,f(x)=lnx;∴f(x)在(0,+∞)上单调递增;∵f(x)是定义在R上的奇函数;=;,;∴;∴;∴a<b<c;即c>b>a.故选:A.二、填空题:本大题共有6小题,每小题5分,共30分.9.(5分)已知i为虚数单位,复数z满足z(1+i)=2﹣3i,则z的虚部为.【解答】解:由z(1+i)=2﹣3i,得,则z的虚部为.故答案为:.10.(5分)已知函数f(x)=,f′(x)为f(x)的导函数,则f′(1)=.【解答】解:;∴.故答案为:.11.(5分)已知直线k(x+1)+y+2=0恒过定点C,且以C为圆心,5为半径的圆与直线3x+4y+1=0相交于A、B两点,则弦AB的长为2.【解答】解:由得,即直线恒过定点C(﹣1,﹣2),以C为圆心,5为半径的圆的标准方程为(x+1)2+(y+2)2=25,圆心到直线的距离d==,则AB的长度为|AB|=2=2=2,故答案为:212.(5分)已知一个几何体的三视图如图所示(单位:cm),则该几何体的体积为cm3.【解答】解:根据几何体的三视图,得;该几何体是上部为四棱锥,下部为半个圆柱的组合体,四棱锥的高为2,底面矩形的宽为2,长为4,圆柱的高为4,底面半径为1,∴该组合体的体积为V=×2×4×2+×π×12×4=+2π.故答案为:+2π.13.(5分)已知函数y=a log2x﹣b(a>0,b>0)的图象过点(),则的最小值为9.【解答】解:∵函数y=a log2x﹣b(a>0,b>0)的图象过点(),∴a log2﹣b=﹣1⇒2a+b=1,∴=(2a+b)()=4++1+,(当且仅当,即a=b时取等号).故答案为:9.14.(5分)已知函数f(x)=,若函数g(x)=﹣f (x)+b在区间[﹣2,6]内有3个零点,则实数b的取值范围是(].【解答】解:若0≤x≤2,则﹣2≤x﹣2≤0,∴f(x)=f(x﹣2)=1﹣|x﹣2+1|=1﹣|x﹣1|,0≤x≤2.若2≤x≤4,则0≤x﹣2≤2,∴f(x)=f(x﹣2)=1﹣|x﹣2﹣1|=1﹣|x﹣3|,2≤x≤4.若4≤x≤6,则2≤x﹣2≤4,∴f(x)=f(x﹣2)=1﹣|x﹣2﹣3|=1﹣|x﹣5|,4≤x≤6.∴f(1)=1,f(2)=0,f(3)=1,f(5)=1,设y=f(x)和y=x+b,则方程f(x)=x+b在区间[﹣2,6]内有3个不等实根,等价为函数y=f(x)和y=x+b在区间[﹣2,6]内有3个不同的零点.作出函数f(x)和y=x+b的图象,如图:当直线经过点F(4,0)时,两个图象有2个交点,此时直线y=x+b为y=x﹣,当直线经过点D(5,1),E(2,0)时,两个图象有3个交点;当直线经过点O(0,0)和C(3,1)时,两个图象有3个交点,此时直线y=x+b为y=x,当直线经过点B(1,1)和A(﹣2,0)时,两个图象有3个交点,此时直线y=x+b为y=x+,∴要使方程f(x)=x+b,两个图象有3个交点,在区间[﹣2,6]内有3个不等实根,则b∈(],故答案为:(].三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.15.(13分)已知△ABC的内角A,B,C所对的边分别为a,b,c,且a+c=6,b=2,cos B=.(Ⅰ)求c和sin A的值;(Ⅱ)求sin(2A﹣B)的值.【解答】解:(Ⅰ)△ABC中,由余弦定理b2=a2+c2﹣2ac cos B,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)得b2=(a+c)2﹣2ac(1+cos B),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)又a+c=6,b=2,cos B=,所以ac=9,解得a=3,c=3;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)在△ABC中,sin B==,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)由正弦定理得sin A==,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)∴c=3,sin A=;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(II)因a=c,则A为锐角,所以cos A==,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)∴sin2A=2sin A cos A=2××=,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)cos2A=1﹣2sin2A=1﹣2×=﹣;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)∴sin(2A﹣B)=sin2A cos B﹣cos2A sin B=×﹣(﹣)×=…(13分)16.(13分)某区的区大代表中有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为A1,A2,乙校教师记为B1,B2,丙校教师记为C,丁校教师记为D.现从这6名教师代表中选出3名教师组成十九大报告宣讲团,要求甲、乙、丙、丁四个学校中,每校至多选出1名.(Ⅰ)请列出十九大报告宣讲团组成人员的全部可能结果;(Ⅱ)求教师A1被选中的概率;(Ⅲ)求宣讲团中没有乙校教师代表的概率.【解答】(本小题满分13分)解:(Ⅰ)某区的区大代表中有教师6人,分别来自甲、乙、丙、丁四个学校,其中甲校教师记为A1,A2,乙校教师记为B1,B2,丙校教师记为C,丁校教师记为D.从这6名教师代表中选出3名教师组成十九大政策宣讲团,组成人员的全部可能结果有12种,分别为:{A1,B1,C},{A1,B1,D},{A1,B2,C},{A1,B2,D},{A1,C,D},{A2,B1,C},{A2,B1,D},{A2,B2,C},{A2,B2,D},{A2,C,D},{B1,C,D},{B2,C,D}.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)(II)组成人员的全部可能结果中,A1被选中的结果有{A1,B1,C},{A1,B1,D},{A1,B2,C},{A1,B2,D},{A1,C,D},共有5种,所以教师A1被选中的概率为p=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)(III)宣讲团中没有乙校代表的结果有{A1,C,D},{A2,C,D},共2种结果,所以宣讲团中没有乙校教师代表的概率为p=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)17.(13分)在等腰梯形ABCD中,AB∥CD,直线FC⊥平面ABCD,ED∥FC,点G为AB的中点,且FC=AB=2ED=2CD=2,∠ABC=60°.(Ⅰ)求证:AE∥平面GCF;(Ⅱ)求证:平面ACF⊥平面BCF;(Ⅲ)求直线FB与平面ADE所成角的正弦值.【解答】(本小题满分13分)证明:(I)取FC中点N,连接EN,因为ED∥FC,FC=2ED,所以ED NC,所以四边形EDCN是平行四边形,所以EN DC,连接NG,EN DC,又DC AG,所以EN AG,所以四边形EAGN是平行四边形,所以EA∥NG,…………(2分)又EA⊄平面GCF,NC⊂平面GCF,所以AE∥平面GCF.………………(4分)解:(II)∵DC AG,∴四边形AGCD为平行四边形,∴AD=GC,∵AD=BC,∴BC=GC,∵∠ABC=60°,∴△BCG为等边三角形,∵AB=2,∴BC=BG==1,由余弦定理得AC2=AB2+BC2﹣2AB•BC•cos∠ABC=3,所以AC2+BC2=AB2,∴∠ACB=90°,………………………………(6分)所以AC⊥BC,又AC⊥CF,BC∩FC=C,所以AC⊥平面BCF,又AC⊂平面ACF,所以平面ACF⊥平面BCF.…………………………(8分)(III)因为ED∥FC,ED⊄平面GCF,FC⊂平面GCF,所以ED∥平面GCF,由(I)知AE∥平面GCF,且AD∩ED=D,所以平面ADE∥平面GCF,所以直线FB与平面ADE所成角也为直线FB与平面GCF所成角.由(II)知CG=BG=BC=1,设Q为CG中点,连接BQ、FQ,所以BQ⊥GC.因为FC⊥平面ABCD,所以FC⊥BQ,因为FC∩GC=C,所以BQ⊥平面GCF,所以∠BFQ为直线FB与平面GCF所成角,……………(11分)因为BQ=CG=,在直角△BCF中,FB==,sin∠BFQ===,所以直线FB与平面ADF所成角正弦值为.……………(13分)18.(13分)已知数列{a n}为等比数列,数列{b n}为等差数列,且b1=a1=1,b2=a1+a2,a3=2b3﹣6.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)设c n=,数列{c n}的前n项和为T n,证明:.【解答】解:(I)设数列{a n}的公比为q,数列{b n}的公差为d.…………………………(1分)由题意得:1+d=1+q,q2=2(1+2d)﹣6,…………(2分)解得:d=q=2,…………………(3分)所以:a n=n﹣1,b n=2n﹣1.……………………………(5分)(II)证明:因为c n===,……(7分)所以T n=[(1﹣)+(﹣)+…+﹣+﹣]=(1+﹣﹣)=……………(10分),n→+∞时,→因为T n在[1,+∞)单调递增,所以当n=1时,T n取最小值T1=,…(12分)所以..…………………………………………(13分)19.(14分)已知椭圆C:(a>b>0)的离心率为,椭圆的一个顶点与两个焦点构成的三角形的面积为2.(Ⅰ)求椭圆C的方程;(Ⅱ)已知直线y=k(x﹣1)(k>0)与椭圆C相交于A、B两点,且与x轴,y 轴交于M、N两点.(i)若=,求k的值;(ii)若点Q的坐标为(),求证:为定值.【解答】解:(Ⅰ)∵e==,∴a2=2c2,代入a2=b2+c2得b=c.又椭圆的一个顶点与两个焦点构成的三角形的面积为2,即b×2c=2,即bc=2,以上各式联立解得a2=4,b2=2,则椭圆方程为+=1.(Ⅱ)(ⅰ)直线y=k(x﹣1)与x轴交点为M(1,0),与y轴交点为N(0,﹣k),联立消去y得:(1+2k2)x﹣4k2x+2k2﹣4=0,△=16k4﹣4(1+2k2)(2k2﹣4)=24k2+16>0,设A(x1,y1),B(x2,y2),则x1+x2=,又=(x2﹣1,y2),=(﹣x1,﹣k﹣y1),由=得:x1+x2==1,解得:k=±.由k>0得k=;证明(ⅱ)由(ⅰ)知x1+x2=,x1x2=,∴=(x1﹣,y1)•(x2﹣,y2)=(x1﹣)•(x2﹣)+y1•y2,=(x1﹣)•(x2﹣)+k2(x1﹣1)(x2﹣1),=(1+k2)x1x2+(﹣﹣﹣k2)(x1+x2)+k2+,=(1+k2)+(﹣﹣﹣k2)+k2+,=+=﹣4+=﹣为定值.∴为定值.20.(14分)设函数f(x)=2lnx+,g(x)=2x﹣alnx(a∈R).(Ⅰ)求曲线y=f(x)在点(1,f(1))处的切线方程;(Ⅱ)若函数g(x)在(0,e2]上恰有2个零点,求a的取值范围;(Ⅲ)当a=1时,若h(x)=f(x)+2g(x)时,若对任意的正整数n在区间[]上始终存在m+5个数使得h(a1)+h(a2)+h(a3)+…+h(a m)<h(a m+1)+h(a m+2)+h(a m+3)+h(a m+4)+h(a m+5)成立,试问:正整数m是否存在最大值?若存在,求出这个最大值,;若不存在,说明理由.【解答】解:(I)函数f(x)的定义域为(0,+∞),所以f′(x)=﹣=……………(2分)所以f′(1)=1且f(1)=1,由导数几何意义知f(x)在点(1,f(1))处切线方程为:y﹣1=x﹣1,即x﹣y=0.………………………………(4分)(II)由g(x)=2x﹣alnx=0,∴=………………………(5分)令p(x)=,所以p′(x)=,所以p(x)在(0,e)上单调递增,在(e,e2]上单调递减,所以当x=e时,p(x)取得极大值,也是最大值.…………………(7分)因为p(e)=,p(e2)=且x→0时,p(x)→﹣∞,故≤<,所以2e<a≤e2………(9分)(III)由题意h(x)=+4x,h′(x)=.……………………(10分)因为x∈[,6+n+],所以h′(x)≥0,所以h(x)在[,6+n+]单调递增,∴h(x)min=h()=4,h(x)max=h(6+n+).由题意,mh()<5h(6+n+)恒成立.……………………………(12分)令k=6+n+≥8,且h(k)在[6+n+,+∞)上单调递增,h min(k)=,因此4m<5×,而m是正整数,故m≤40,所以m=40时,存在a1=a2=…=a40=,a m+1=a m+2=a m+3=a m+4=a m+5=8时,对所有n满足题意,∴m max=40.…(14分)。
北辰区第二中学2018-2019学年高二上学期数学期末模拟试卷含解析

24.在正方体 ABCD A1 B1C1 D1 中 E , G , H 分别为 BC , C1 D1 , AA1 的中点. (1)求证: EG A平面 BDD1 B1 ; (2)求异面直线 B1 H 与 EG 所成的角]
第 7 页,共 18 页
北辰区第二中学 2018-2019 学年高二上学期数学期末模拟试卷含解析(参考答案) 一、选择题
21.某志愿者到某山区小学支教,为了解留守儿童的幸福感,该志愿者对某班 40 名学生进行了一 次幸福指数的调查问卷,并用茎叶图表示如图(注:图中幸福指数低于 70,说明孩子幸福感弱;幸福指 数不低于 70,说明孩子幸福感强).
(1)根据茎叶图中的数据完成 2 2 列联表,并判断能否有 95% 的把握认为孩子的幸福感强与是否是留 守儿童有关? 幸福感强 留守儿童 非留守儿童 总计 求这 2 个学生中恰有一人幸福感强的概率. 参考公式: K
北辰区第二中学 2018-2019 学年高二上学期数学期末模拟试卷含解析 班级__________ 一、选择题
1. 如图,在平面直角坐标系中,锐角 α、β 及角 α+β 的终边分别与单位圆 O 交于 A,B,C 三点.分别作 AA' 、BB'、CC'垂直于 x 轴,若以|AA'|、|BB'|、|CC'|为三边长构造三角形,则此三角形的外接圆面积为( )
9. 将函数 f ( x) 2 sin( 则 g ( x) 的解析式为( A. g ( x) 2 sin(
x ) 的图象向左平移 个单位,再向上平移 3 个单位,得到函数 g ( x) 的图象, 3 6 4
) B. g ( x) 2 sin(
x )3 3 4 x C. g ( x) 2 sin( ) 3 3 12
北辰区第二中学2018-2019学年高二上学期第二次月考试卷数学

北辰区第二中学2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 如图,设全集U=R ,M={x|x >2},N={0,1,2,3},则图中阴影部分所表示的集合是( )A .{3}B .{0,1}C .{0,1,2}D .{0,1,2,3}2. 一个多面体的直观图和三视图如图所示,点M 是边AB 上的动点,记四面体FMC E -的体积为1V ,多面体BCE ADF -的体积为2V ,则=21V V ( )1111] A .41 B .31 C .21D .不是定值,随点M 的变化而变化3. 如图Rt △O ′A ′B ′是一平面图形的直观图,斜边O ′B ′=2,则这个平面图形的面积是( )A .B .1C .D .4. 若⎩⎨⎧≥<+=-)2(,2)2(),2()(x x x f x f x则)1(f 的值为( ) A .8 B .81 C .2 D .215. 函数f (x )=()x2﹣9的单调递减区间为( ) A .(﹣∞,0) B .(0,+∞) C .(﹣9,+∞) D .(﹣∞,﹣9)6. 等比数列{a n }中,a 4=2,a 5=5,则数列{lga n }的前8项和等于( )A .6B .5C .3D .47. 已知函数()cos()3f x x π=+,则要得到其导函数'()y f x =的图象,只需将函数()y f x =的图象( )A .向右平移2π个单位 B .向左平移2π个单位 C. 向右平移23π个单位 D .左平移23π个单位8. 抛物线x 2=4y 的焦点坐标是( )A .(1,0)B .(0,1)C .()D .()9. 已知命题p :2≤2,命题q :∃x 0∈R ,使得x 02+2x 0+2=0,则下列命题是真命题的是( ) A .¬p B .¬p ∨qC .p ∧qD .p ∨q10.sin (﹣510°)=( )A .B .C .﹣D .﹣11.已知向量=(1,1,0),=(﹣1,0,2)且k +与2﹣互相垂直,则k 的值是( )A .1B .C .D .12.三个数a=0.52,b=log 20.5,c=20.5之间的大小关系是( ) A .b <a <c B .a <c <b C .a <b <c D .b <c <a二、填空题13.在数列中,则实数a= ,b= .14.设函数f (x )=的最大值为M ,最小值为m ,则M+m= .15.直线l 过原点且平分平行四边形ABCD 的面积,若平行四边形的两个顶点为B (1,4),D (5,0),则直线l 的方程为 .16.已知点A 的坐标为(﹣1,0),点B 是圆心为C 的圆(x ﹣1)2+y 2=16上一动点,线段AB 的垂直平分线交BC 与点M ,则动点M 的轨迹方程为 .17.若与共线,则y= .18.在三角形ABC 中,已知AB=4,AC=3,BC=6,P 为BC 中点,则三角形ABP 的周长为 .三、解答题19.已知函数f (x )=x 3﹣x 2+cx+d 有极值.(Ⅰ)求c 的取值范围;(Ⅱ)若f (x )在x=2处取得极值,且当x <0时,f (x )<d 2+2d 恒成立,求d 的取值范围.20.已知椭圆()2222:10x y C a b a b +=>>的左右焦点分别为12,F F ,椭圆C 过点1,2P ⎛⎫⎪ ⎪⎝⎭,直线1PF 交y 轴于Q ,且22,PF QO O =为坐标原点.(1)求椭圆C 的方程;(2)设M 是椭圆C 上的顶点,过点M 分别作出直线,MA MB 交椭圆于,A B 两点,设这两条直线的斜率 分别为12,k k ,且122k k +=,证明:直线AB 过定点.21.(本小题满分12分)如图,在四棱锥ABCD S -中,底面ABCD 为菱形,Q P E 、、分别是棱AB SC AD 、、的中点,且⊥SE 平面ABCD .(1)求证://PQ 平面SAD ; (2)求证:平面⊥SAC 平面SEQ .22.如图,点A是单位圆与x轴正半轴的交点,B(﹣,).(I)若∠AOB=α,求cosα+sinα的值;(II)设点P为单位圆上的一个动点,点Q满足=+.若∠AOP=2θ,表示||,并求||的最大值.23.根据下列条件,求圆的方程:(1)过点A(1,1),B(﹣1,3)且面积最小;(2)圆心在直线2x﹣y﹣7=0上且与y轴交于点A(0,﹣4),B(0,﹣2).24.(本小题满分12分)已知12,F F 分别是椭圆C :22221(0)x y a b a b +=>>的两个焦点,(1,2P 是椭圆上1122|,||PF F F PF 成等差数列.(1)求椭圆C 的标准方程;、(2)已知动直线l 过点F ,且与椭圆C 交于A B 、两点,试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.北辰区第二中学2018-2019学年高二上学期第二次月考试卷数学(参考答案)一、选择题1. 【答案】C【解析】解:由图可知图中阴影部分所表示的集合∁M ∩N , ∵全集U=R ,M={x|x >2},N={0,1,2,3}, ∴∁M ={x|x ≤2}, ∴∁M ∩N={0,1,2}, 故选:C【点评】本题主要考查集合的基本运算,根据条件确定集合的基本关系是解决本题的关键.2. 【答案】B 【解析】考点:棱柱、棱锥、棱台的体积. 3. 【答案】D【解析】解:∵Rt △O'A'B'是一平面图形的直观图,斜边O'B'=2,∴直角三角形的直角边长是,∴直角三角形的面积是,∴原平面图形的面积是1×2=2故选D .4. 【答案】B 【解析】试题分析:()()311328f f -===,故选B 。
北辰区二中2018-2019学年高二上学期二次月考试数学

北辰区二中2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 在△ABC 中,,则这个三角形一定是( )A .等腰三角形B .直角三角形C .等腰直角三角D .等腰或直角三角形2. 方程1x -=表示的曲线是( )A .一个圆B . 两个半圆C .两个圆D .半圆 3. 若函数()()()()()1cos sin cos sin 3sin cos 412f x x x x x a x x a x =-++-+-在02π⎡⎤-⎢⎥⎣⎦,上单调递增,则实数的取值范围为( )A .117⎡⎤⎢⎥⎣⎦,B .117⎡⎤-⎢⎥⎣⎦,C.1(][1)7-∞-+∞,,D .[1)+∞, 4. 若a <b <0,则下列不等式不成立是( )A .>B .>C .|a|>|b|D .a 2>b 25. (理)已知tan α=2,则=( )A .B .C .D .6. 如图,△ABC 所在平面上的点P n (n ∈N *)均满足△P n AB 与△P n AC 的面积比为3;1, =﹣(2x n +1)(其中,{x n }是首项为1的正项数列),则x 5等于( )A .65B .63C .33D .317. 某工厂生产某种产品的产量x (吨)与相应的生产能耗y (吨标准煤)有如表几组样本数据:0.7,则这组样本数据的回归直线方程是( )A . =0.7x+0.35B . =0.7x+1C . =0.7x+2.05D . =0.7x+0.458. 某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,俯视图是半径为 1的半圆,则其侧视图的面积是( )A .B .C .1D .9. 已知表示数列的前项和,若对任意的满足,且,则( )A .B .C .D .10.已知等差数列{a n }满足2a 3﹣a+2a 13=0,且数列{b n } 是等比数列,若b 8=a 8,则b 4b 12=( )A .2B .4C .8D .1611.若直线:1l y kx =-与曲线C :1()1e xf x x =-+没有公共点,则实数k 的最大值为( )A .-1B .12C .1D 【命题意图】考查直线与函数图象的位置关系、函数存在定理,意在考查逻辑思维能力、等价转化能力、运算求解能力.12.如图,圆O 与x 轴的正半轴的交点为A ,点C 、B 在圆O 上,且点C 位于第一象限,点B 的坐标为(,﹣),∠AOC=α,若|BC|=1,则cos 2﹣sincos﹣的值为( )A .B .C .﹣D .﹣二、填空题13.函数()y f x =图象上不同两点()()1122,,,A x y B x y 处的切线的斜率分别是A B k k ,,规定(),A Bk k A B ABϕ-=(AB 为线段AB 的长度)叫做曲线()y f x =在点A 与点B 之间的“弯曲度”,给 出以下命题:①函数321y x x =-+图象上两点A 与B 的横坐标分别为1和2,则(),A B ϕ ②存在这样的函数,图象上任意两点之间的“弯曲度”为常数; ③设点A,B 是抛物线21y x =+上不同的两点,则(),2A B ϕ≤;④设曲线xy e =(e 是自然对数的底数)上不同两点()()112212,,,,1A x y B x y x x -=且,若(),1t A B ϕ⋅<恒成立,则实数t 的取值范围是(),1-∞.其中真命题的序号为________.(将所有真命题的序号都填上)14.某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为 小时.15.已知数列1,a 1,a 2,9是等差数列,数列1,b 1,b 2,b 3,9是等比数列,则的值为 .16.设A={x|x ≤1或x ≥3},B={x|a ≤x ≤a+1},A ∩B=B ,则a 的取值范围是 .17.x 为实数,[x]表示不超过x 的最大整数,则函数f (x )=x ﹣[x]的最小正周期是 .18.二面角α﹣l﹣β内一点P到平面α,β和棱l的距离之比为1::2,则这个二面角的平面角是度.三、解答题19.在平面直角坐标系xOy中,点P(x,y)满足=3,其中=(2x+3,y),=(2x﹣﹣3,3y).(1)求点P的轨迹方程;(2)过点F(0,1)的直线l交点P的轨迹于A,B两点,若|AB|=,求直线l的方程.20.甲、乙两位同学参加数学竞赛培训,在培训期间他们参加5次预赛,成绩如下:甲:78 76 74 90 82乙:90 70 75 85 80(Ⅰ)用茎叶图表示这两组数据;(Ⅱ)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适?说明理由.21.在平面直角坐标系xOy中,圆C:x2+y2=4,A(,0),A1(﹣,0),点P为平面内一动点,以PA为直径的圆与圆C相切.(Ⅰ)求证:|PA1|+|PA|为定值,并求出点P的轨迹方程C1;(Ⅱ)若直线PA与曲线C1的另一交点为Q,求△POQ面积的最大值.22.已知等差数列满足:=2,且,成等比数列。
北辰区四中2018-2019学年高二上学期第二次月考试卷数学
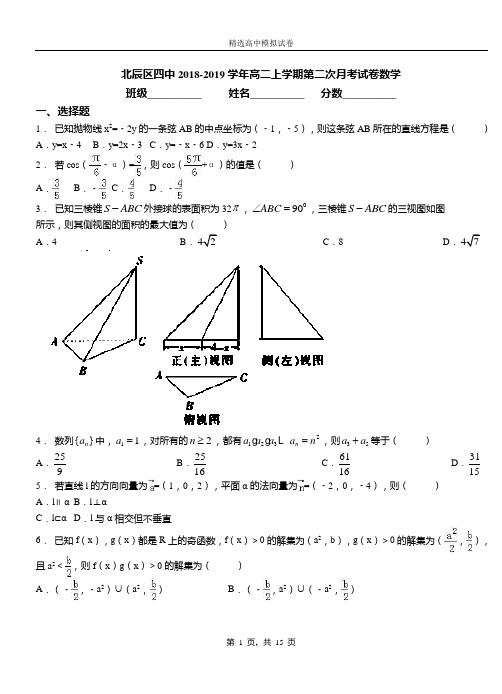
北辰区四中2018-2019学年高二上学期第二次月考试卷数学 班级__________ 姓名__________ 分数__________一、选择题1. 已知抛物线x 2=﹣2y 的一条弦AB 的中点坐标为(﹣1,﹣5),则这条弦AB 所在的直线方程是( ) A .y=x ﹣4 B .y=2x ﹣3 C .y=﹣x ﹣6 D .y=3x ﹣22. 若cos (﹣α)=,则cos (+α)的值是( )A .B .﹣C .D .﹣3. 已知三棱锥S ABC -外接球的表面积为32π,090ABC ∠=,三棱锥S ABC -的三视图如图 所示,则其侧视图的面积的最大值为( )A .4B .C .8D .4. 数列{}n a 中,11a =,对所有的2n ≥,都有2123n a a a a n =,则35a a +等于( )A .259B .2516C .6116D .31155. 若直线l 的方向向量为=(1,0,2),平面α的法向量为=(﹣2,0,﹣4),则( ) A .l ∥α B .l ⊥αC .l ⊂αD .l 与α相交但不垂直6. 已知f (x ),g (x )都是R 上的奇函数,f (x )>0的解集为(a 2,b ),g (x )>0的解集为(,),且a 2<,则f (x )g (x )>0的解集为( )A .(﹣,﹣a 2)∪(a 2,)B .(﹣,a 2)∪(﹣a 2,)C .(﹣,﹣a 2)∪(a 2,b )D .(﹣b ,﹣a 2)∪(a 2,)7. 已知a >b >0,那么下列不等式成立的是( )A .﹣a >﹣bB .a+c <b+cC .(﹣a )2>(﹣b )2D .8. 若定义在R 上的函数f (x )满足:对任意x 1,x 2∈R 有f (x 1+x 2)=f (x 1)+f (x 2)+1,则下列说法一定正确的是( )A .f (x )为奇函数B .f (x )为偶函数C .f (x )+1为奇函数D .f (x )+1为偶函数9. 阅读如图所示的程序框图,运行相应的程序.若该程序运行后输出的结果不大于20,则输入的整数i 的最大值为( )A .3B .4C .5D .610.函数2-21y x x =-,[0,3]x ∈的值域为( ) A. B. C. D. 11.下列说法正确的是( )A.圆锥的侧面展开图是一个等腰三角形;B.棱柱即是两个底面全等且其余各面都是矩形的多面体;C.任何一个棱台都可以补一个棱锥使他们组成一个新的棱锥;D.通过圆台侧面上的一点,有无数条母线.12.若⎩⎨⎧≥<+=-)2(,2)2(),2()(x x x f x f x则)1(f 的值为( )A .8B .81 C .2 D .21 二、填空题13.已知正整数m 的3次幂有如下分解规律:113=;5323+=;119733++=;1917151343+++=;…若)(3+∈N m m 的分解中最小的数为91,则m 的值为 .【命题意图】本题考查了归纳、数列等知识,问题的给出比较新颖,对逻辑推理及化归能力有较高要求,难度中等.14.已知一个算法,其流程图如图,则输出结果是 .15.【徐州市2018届高三上学期期中】已知函数(为自然对数的底数),若,则实数 的取值范围为______.16.【盐城中学2018届高三上第一次阶段性考试】已知函数()()ln f x x x ax =-有两个极值点,则实数a 的取值范围是.17.如图,在矩形ABCD 中,AB = 3BC =, E 在AC 上,若BE AC ⊥, 则ED 的长=____________18.设函数f (x )=若f[f (a )],则a 的取值范围是 .三、解答题19.已知函数f (x )=4sinxcosx ﹣5sin 2x ﹣cos 2x+3.(Ⅰ)当x ∈[0,]时,求函数f (x )的值域;(Ⅱ)若△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且满足=,=2+2cos (A+C ),求f (B )的值.20.(本小题满分13分)椭圆C :22221(0)x y a b a b+=>>的左、右焦点分别为1F 、2F ,直线:1l x my =-经过点1F 与椭圆C 交于点M ,点M 在x 轴的上方.当0m =时,1||2MF =.(Ⅰ)求椭圆C 的方程;(Ⅱ)若点N 是椭圆C 上位于x 轴上方的一点, 12//MF NF ,且12123MF F NF F S S ∆∆=,求直线l 的方程.21.函数f (x )=Asin (ωx+φ)(A >0,ω>0,|φ|<)的一段图象如图所示.(1)求f (x )的解析式;(2)求f (x )的单调减区间,并指出f (x )的最大值及取到最大值时x 的集合;(3)把f (x )的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数.22.已知等差数列{a n},等比数列{b n}满足:a1=b1=1,a2=b2,2a3﹣b3=1.(Ⅰ)求数列{a n},{b n}的通项公式;(Ⅱ)记c n=a n b n,求数列{c n}的前n项和S n.23.在直角坐标系xOy中,过点P(2,﹣1)的直线l的倾斜角为45°.以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,曲线C的极坐标方程为ρsin2θ=4cosθ,直线l和曲线C的交点为A,B.(1)求曲线C的直角坐标方程;(2)求|PA|•|PB|.24.如图,已知AB是圆O的直径,C、D是圆O上的两个点,CE⊥AB于E,BD交AC于G,交CE于F,CF=FG.(Ⅰ)求证:C是劣弧的中点;(Ⅱ)求证:BF=FG.北辰区四中2018-2019学年高二上学期第二次月考试卷数学(参考答案)一、选择题1. 【答案】A【解析】解:设A 、B 两点的坐标分别为(x 1,y 1),(x 2,y 2),则x 1+x 2=﹣2,x 12=﹣2y 1,x 22=﹣2y 2.两式相减可得,(x 1+x 2)(x 1﹣x 2)=﹣2(y 1﹣y 2) ∴直线AB 的斜率k=1,∴弦AB 所在的直线方程是y+5=x+1,即y=x ﹣4. 故选A ,2. 【答案】B【解析】解:∵cos (﹣α)=,∴cos (+α)=﹣cos=﹣cos (﹣α)=﹣.故选:B .3. 【答案】A 【解析】考点:三视图.【方法点睛】本题主要考查几何体的三视图,空间想象能力.空间几何体的三视图是分别从空间几何体的正面,左面,上面用平行投影的方法得到的三个平面投影图.因此在分析空间几何体的三视图时,先根据俯视图确定几何体的底面,然后根据正视图或侧视图确定几何体的侧棱与侧面的特征,调整实线和虚线所对应的棱,面的位置,再确定几何体的形状,即可得到结果. 要能够牢记常见几何体的三视图. 4. 【答案】C 【解析】试题分析:由2123n a a a a n =,则21231(1)n a a a a n -=-,两式作商,可得22(1)n n a n =-,所以22352235612416a a +=+=,故选C .考点:数列的通项公式. 5. 【答案】B【解析】解:∵ =(1,0,2),=(﹣2,0,4),∴=﹣2,∴∥, 因此l ⊥α. 故选:B .6. 【答案】A【解析】解:∵f (x ),g (x )都是R 上的奇函数,f (x )>0的解集为(a 2,b ),g (x )>0的解集为(,),且a 2<,∴f (x )<0的解集为(﹣b ,﹣a 2),g (x )<0的解集为(﹣,﹣),则不等式f (x )g (x )>0等价为或,即a 2<x <或﹣<x <﹣a 2,故不等式的解集为(﹣,﹣a 2)∪(a 2,),故选:A . 【点评】本题主要考查不等式的求解,根据函数奇偶性的对称性的性质求出f (x )<0和g (x )<0的解集是解决本题的关键.7. 【答案】C 【解析】解:∵a >b >0,∴﹣a <﹣b <0,∴(﹣a )2>(﹣b )2,故选C .【点评】本题主要考查不等式的基本性质的应用,属于基础题.8. 【答案】C【解析】解:∵对任意x 1,x 2∈R 有 f (x 1+x 2)=f (x 1)+f (x 2)+1, ∴令x 1=x 2=0,得f (0)=﹣1∴令x 1=x ,x 2=﹣x ,得f (0)=f (x )+f (﹣x )+1,∴f (x )+1=﹣f (﹣x )﹣1=﹣[f (﹣x )+1], ∴f (x )+1为奇函数. 故选C【点评】本题考查函数的性质和应用,解题时要认真审题,仔细解答.9. 【答案】B【解析】解:模拟执行程序框图,可得 s=0,n=0满足条件n <i ,s=2,n=1 满足条件n <i ,s=5,n=2 满足条件n <i ,s=10,n=3 满足条件n <i ,s=19,n=4 满足条件n <i ,s=36,n=5所以,若该程序运行后输出的结果不大于20,则输入的整数i 的最大值为4, 有n=4时,不满足条件n <i ,退出循环,输出s 的值为19. 故选:B .【点评】本题主要考查了循环结构的程序框图,属于基础题.10.【答案】A 【解析】试题分析:函数()222112y x x x =--=--在区间[]0,1上递减,在区间[]1,3上递增,所以当x=1时,()()min 12f x f ==-,当x=3时,()()max 32f x f ==,所以值域为[]2,2-。
北辰区二中2018-2019学年上学期高二数学12月月考试题含解析

北辰区二中2018-2019学年上学期高二数学12月月考试题含解析班级__________ 姓名__________ 分数__________一、选择题1. 设函数f (x )的定义域为A ,若存在非零实数l 使得对于任意x ∈I (I ⊆A ),有x+l ∈A ,且f (x+l )≥f (x ),则称f (x )为I 上的l 高调函数,如果定义域为R 的函数f (x )是奇函数,当x ≥0时,f (x )=|x ﹣a 2|﹣a 2,且函数f (x )为R 上的1高调函数,那么实数a 的取值范围为( )A .0<a <1B .﹣≤a ≤C .﹣1≤a ≤1D .﹣2≤a ≤22. 已知三棱柱111ABC A B C - 的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点, 则异面直线AB 与1CC 所成的角的余弦值为( )A .4 B .4 C.4D .343. 双曲线E 与椭圆C :x 29+y 23=1有相同焦点,且以E 的一个焦点为圆心与双曲线的渐近线相切的圆的面积为π,则E 的方程为( ) A.x 23-y 23=1 B.x 24-y 22=1 C.x 25-y 2=1 D.x 22-y 24=14. 已知定义在R 上的可导函数y=f (x )是偶函数,且满足xf ′(x )<0, =0,则满足的x 的范围为( )A .(﹣∞,)∪(2,+∞)B .(,1)∪(1,2)C .(,1)∪(2,+∞)D .(0,)∪(2,+∞)5. 已知平面向量(12)=,a ,(32)=-,b ,若k +a b 与a 垂直,则实数k 值为( ) A .15- B .119 C .11 D .19【命题意图】本题考查平面向量数量积的坐标表示等基础知识,意在考查基本运算能力.6. “x >0”是“>0”成立的( )A .充分非必要条件B .必要非充分条件C .非充分非必要条件D .充要条件7. 下列函数在(0,+∞)上是增函数的是( )A .B .y=﹣2x+5C .y=lnxD .y=8. 已知命题p :存在x 0>0,使2<1,则¬p 是( )A .对任意x >0,都有2x ≥1B .对任意x ≤0,都有2x <1C .存在x 0>0,使2≥1 D .存在x 0≤0,使2<19. 函数y=2x 2﹣e |x|在[﹣2,2]的图象大致为( )A .B .C .D .10.以下四个命题中,真命题的是( ) A .(0,)x π∃∈,sin tan x x =B .“对任意的x R ∈,210x x ++>”的否定是“存在0x R ∈,20010x x ++<C .R θ∀∈,函数()sin(2)f x x θ=+都不是偶函数D .ABC ∆中,“sin sin cos cos A B A B +=+”是“2C π=”的充要条件【命题意图】本题考查量词、充要条件等基础知识,意在考查逻辑推理能力. 11.已知函数f (x )=2x ,则f ′(x )=( )A .2xB .2x ln2C .2x +ln2D .12.从1、2、3、4、5中任取3个不同的数、则这3个数能构成一个三角形三边长的概率为( ) A.110 B.15 C.310 D.25二、填空题13.【2017-2018学年度第一学期如皋市高三年级第一次联考】已知函数()211{52128lnx x xf x m x mx x +>=-++≤,,,,若()()g x f x m =-有三个零点,则实数m 的取值范围是________.14.下列命题:①函数y=sinx 和y=tanx 在第一象限都是增函数;②若函数f (x )在[a ,b]上满足f (a )f (b )<0,函数f (x )在(a ,b )上至少有一个零点; ③数列{a n }为等差数列,设数列{a n }的前n 项和为S n ,S 10>0,S 11<0,S n 最大值为S 5; ④在△ABC 中,A >B 的充要条件是cos2A <cos2B ;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强.其中正确命题的序号是 (把所有正确命题的序号都写上).15.考察正三角形三边中点及3个顶点,从中任意选4个点,则这4个点顺次连成平行四边形的概率等于 . 16.函数f (x )=a x +4的图象恒过定点P ,则P 点坐标是 .17.满足关系式{2,3}⊆A ⊆{1,2,3,4}的集合A 的个数是 . 18.下列四个命题:①两个相交平面有不在同一直线上的三个公交点 ②经过空间任意三点有且只有一个平面 ③过两平行直线有且只有一个平面 ④在空间两两相交的三条直线必共面 其中正确命题的序号是 .三、解答题19.为了培养学生的安全意识,某中学举行了一次安全自救的知识竞赛活动,共有800 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100 分)进行统计,得到如下的频率分布表,请你根据频率分布表解答下列问题: (1)求出频率分布表中①、②、③、④、⑤的值;(2)为鼓励更多的学生了解“安全自救”知识,成绩不低于85分的学生能获奖,请估计在参加的800名学生中大约有多少名学生获奖?(3)在上述统计数据的分析中,有一项指标计算的程序框图如图所示,则该程序的功能是什么?求输出的S 的值.合计20.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sinA﹣sinC(cosB+sinB)=0.(1)求角C的大小;(2)若c=2,且△ABC的面积为,求a,b的值.21.(1)求与椭圆有相同的焦点,且经过点(4,3)的椭圆的标准方程.(2)求与双曲线有相同的渐近线,且焦距为的双曲线的标准方程.22.已知函数f(x)=x2﹣ax+(a﹣1)lnx(a>1).(Ⅰ)讨论函数f(x)的单调性;(Ⅱ)若a=2,数列{a n}满足a n+1=f(a n).(1)若首项a1=10,证明数列{a n}为递增数列;(2)若首项为正整数,且数列{a n}为递增数列,求首项a1的最小值.23.某同学在研究性学习中,了解到淘宝网站一批发店铺在今年的前五个月的销售量(单位:百件)的数据如(Ⅰ)该同学为了求出y关于x的回归方程=x+,根据表中数据已经正确算出=0.6,试求出的值,并估计该店铺6月份的产品销售量;(单位:百件)(Ⅱ)一零售商现存有从该淘宝批发店铺2月份进货的4件和3月份进货的5件产品,顾客甲现从该零售商处随机购买了3件,后经了解,该淘宝批发店铺今年2月份的产品都有质量问题,而3月份的产品都没有质量问题.记顾客甲所购买的3件产品中存在质量问题的件数为X,求X的分布列和数学期望.24.某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:x 2 4 5 6 8y 30 40 60 50 70(1)画出散点图;(2)求线性回归方程;(3)预测当广告费支出7(百万元)时的销售额.北辰区二中2018-2019学年上学期高二数学12月月考试题含解析(参考答案)一、选择题1.【答案】B【解析】解:定义域为R的函数f(x)是奇函数,当x≥0时,f(x)=|x﹣a2|﹣a2=图象如图,∵f(x)为R上的1高调函数,当x<0时,函数的最大值为a2,要满足f(x+l)≥f(x),1大于等于区间长度3a2﹣(﹣a2),∴1≥3a2﹣(﹣a2),∴﹣≤a≤故选B【点评】考查学生的阅读能力,应用知识分析解决问题的能力,考查数形结合的能力,用图解决问题的能力,属中档题.2.【答案】D【解析】考点:异面直线所成的角. 3. 【答案】【解析】选C.可设双曲线E 的方程为x 2a 2-y 2b2=1,渐近线方程为y =±bax ,即bx ±ay =0,由题意得E 的一个焦点坐标为(6,0),圆的半径为1, ∴焦点到渐近线的距离为1.即|6b |b 2+a2=1,又a 2+b 2=6,∴b =1,a =5,∴E 的方程为x 25-y 2=1,故选C.4. 【答案】D【解析】解:当x >0时,由xf ′(x )<0,得f ′(x )<0,即此时函数单调递减, ∵函数f (x )是偶函数,∴不等式等价为f (||)<,即||>,即>或<﹣,解得0<x <或x >2,故x 的取值范围是(0,)∪(2,+∞) 故选:D【点评】本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.5. 【答案】A6. 【答案】A【解析】解:当x>0时,x2>0,则>0∴“x>0”是“>0”成立的充分条件;但>0,x2>0,时x>0不一定成立∴“x>0”不是“>0”成立的必要条件;故“x>0”是“>0”成立的充分不必要条件;故选A【点评】判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p 为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.7.【答案】C【解析】解:对于A,函数y=在(﹣∞,+∞)上是减函数,∴不满足题意;对于B,函数y=﹣2x+5在(﹣∞,+∞)上是减函数,∴不满足题意;对于C,函数y=lnx在(0,+∞)上是增函数,∴满足题意;对于D,函数y=在(0,+∞)上是减函数,∴不满足题意.故选:C.【点评】本题考查了基本初等函数的单调性的判断问题,是基础题目.8.【答案】A【解析】解:∵命题p:存在x0>0,使2<1为特称命题,∴¬p为全称命题,即对任意x>0,都有2x≥1.故选:A9.【答案】D【解析】解:∵f(x)=y=2x2﹣e|x|,∴f(﹣x)=2(﹣x)2﹣e|﹣x|=2x2﹣e|x|,故函数为偶函数,当x=±2时,y=8﹣e2∈(0,1),故排除A,B;当x∈[0,2]时,f(x)=y=2x2﹣e x,∴f′(x)=4x﹣e x=0有解,故函数y=2x2﹣e|x|在[0,2]不是单调的,故排除C,故选:D10.【答案】D11.【答案】B【解析】解:f(x)=2x,则f'(x)=2x ln2,故选:B.【点评】本题考查了导数运算法则,属于基础题.12.【答案】【解析】解析:选C.从1、2、3、4、5中任取3个不同的数有下面10个不同结果:(1,2,3),(1,2,4),(1,2,5),(1,3,4),(1,3,5),(1,4,5),(2,3,4),(2,3,5),(2,4,5),(3,4,5),能构成一个三角形三边的数为(2,3,4),(2,4,5),(3,4,5),故概率P=310.二、填空题13.【答案】7 14⎛⎤ ⎥⎝⎦,【解析】14.【答案】②③④⑤【解析】解:①函数y=sinx和y=tanx在第一象限都是增函数,不正确,取x=,,但是,,因此不是单调递增函数;②若函数f(x)在[a,b]上满足f(a)f(b)<0,函数f(x)在(a,b)上至少有一个零点,正确;③数列{a n}为等差数列,设数列{a n}的前n项和为S n,S10>0,S11<0,∴=5(a6+a5)>0,=11a6<0,∴a5+a6>0,a6<0,∴a5>0.因此S n最大值为S5,正确;④在△ABC中,cos2A﹣cos2B=﹣2sin(A+B)sin(A﹣B)=2sin(A+B)sin(B﹣A)<0⇔A>B,因此正确;⑤在线性回归分析中,线性相关系数越大,说明两个量线性相关性就越强,正确.其中正确命题的序号是②③④⑤.【点评】本题综合考查了三角函数的单调性、函数零点存在判定定理、等差数列的性质、两角和差化积公式、线性回归分析,考查了推理能力与计算能力,属于难题.15.【答案】.【解析】解:从等边三角形的三个顶点及三边中点中随机的选择4个,共有=15种选法,其中4个点构成平行四边形的选法有3个,∴4个点构成平行四边形的概率P==.故答案为:.【点评】本题考查古典概型及其概率计算公式的应用,是基础题.确定基本事件的个数是关键.16.【答案】(0,5).【解析】解:∵y=a x的图象恒过定点(0,1),而f(x)=a x+4的图象是把y=a x的图象向上平移4个单位得到的,∴函数f(x)=a x+4的图象恒过定点P(0,5),故答案为:(0,5).【点评】本题考查指数函数的性质,考查了函数图象的平移变换,是基础题.17.【答案】4.【解析】解:由题意知,满足关系式{2,3}⊆A⊆{1,2,3,4}的集合A有:{2,3},{2,3,1},{2,3,4},{2,3,1,4},故共有4个,故答案为:4.18.【答案】③.【解析】解:①两个相交平面的公交点一定在平面的交线上,故错误;②经过空间不共线三点有且只有一个平面,故错误;③过两平行直线有且只有一个平面,正确;④在空间两两相交交点不重合的三条直线必共面,三线共点时,三线可能不共面,故错误,故正确命题的序号是③,故答案为:③三、解答题19.【答案】【解析】解:(1)由分布表可得频数为50,故①的数值为50×0.1=5,②中的值为=0.40,③中的值为50×0.2=10,④中的值为50﹣(5+20+10)=15,⑤中的值为=0.30;(2)不低于85的概率P=×0.20+0.30=0.40,∴获奖的人数大约为800×0.40=320;(3)该程序的功能是求平均数,S=65×0.10+75×0.40+85×0.20+95×0.30=82,∴800名学生的平均分为82分20.【答案】【解析】(本题满分为12分)解:(1)∵由题意得,sinA=sin(B+C),∴sinBcosC+sinCcosB﹣sinCcosB﹣sinBsinC=0,…(2分)即sinB(cosC﹣sinC)=0,∵sinB≠0,∴tanC=,故C=.…(6分)(2)∵ab×=,∴ab=4,①又c=2,…(8分)∴a2+b2﹣2ab×=4,∴a2+b2=8.②∴由①②,解得a=2,b=2.…(12分)【点评】本题主要考查了三角形内角和定理,三角函数恒等变换的应用,三角形面积公式,余弦定理在解三角形中的综合应用,考查了转化思想,属于基础题.21.【答案】【解析】解:(1)由所求椭圆与椭圆有相同的焦点,设椭圆方程,由(4,3)在椭圆上得,则椭圆方程为;(2)由双曲线有相同的渐近线,设所求双曲线的方程为﹣=1(λ≠0),由题意可得c2=4|λ|+9|λ|=13,解得λ=±1.即有双曲线的方程为﹣=1或﹣=1.22.【答案】【解析】解:(Ⅰ)∵,∴(x>0),当a=2时,则在(0,+∞)上恒成立,当1<a<2时,若x∈(a﹣1,1),则f′(x)<0,若x∈(0,a﹣1)或x∈(1,+∞),则f′(x)>0,当a>2时,若x∈(1,a﹣1),则f′(x)<0,若x∈(0,1)或x∈(a﹣1,+∞),则f′(x)>0,综上所述:当1<a<2时,函数f(x)在区间(a﹣1,1)上单调递减,在区间(0,a﹣1)和(1,+∞)上单调递增;当a=2时,函数(0,+∞)在(0,+∞)上单调递增;当a>2时,函数f(x)在区间(0,1)上单调递减,在区间(0,1)和(a﹣1,+∞)上单调递增.(Ⅱ)若a=2,则,由(Ⅰ)知函数f(x)在区间(0,+∞)上单调递增,(1)因为a1=10,所以a2=f(a1)=f(10)=30+ln10,可知a2>a1>0,假设0<a k<a k+1(k≥1),因为函数f(x)在区间(0,+∞)上单调递增,∴f(a k+1)>f(a k),即得a k+2>a k+1>0,由数学归纳法原理知,a n+1>a n对于一切正整数n都成立,∴数列{a n}为递增数列.(2)由(1)知:当且仅当0<a1<a2,数列{a n}为递增数列,∴f(a1)>a1,即(a1为正整数),设(x≥1),则,∴函数g(x)在区间上递增,由于,g(6)=ln6>0,又a1为正整数,∴首项a1的最小值为6.【点评】本题考查导数的运用:求单调区间,同时考查函数的零点存在定理和数学归纳法的运用,考查运算能力,属于中档题.选做题:本题设有(1)(2)(3)三个选考题,每题7分,请考生任选2题作答,满分7分.如果多做,则按所做的前两题计分.【选修4-2:矩阵与变换】 23.【答案】【解析】解:(1), =5…且,代入回归直线方程可得∴=0.6x+3.2,x=6时, =6.8,…(2)X 的取值有0,1,2,3,则,,,…0 1 2 3【点评】本题考查线性回归方程、离散型随机变量的分布列及其数学期望,考查学生分析解决问题的能力.24.【答案】【解析】解:(1)(2)设回归方程为=bx+a则b=﹣5/﹣5=1380﹣5×5×50/145﹣5×52=6.5故回归方程为=6.5x+17.5(3)当x=7时,=6.5×7+17.5=63,所以当广告费支出7(百万元)时,销售额约为63(百万元).【点评】本题考查线性回归方程的求法和应用,本题解题的关键是利用最小二乘法求出线性回归方程的系数,这是解答正确的主要环节.。
北辰区第二中学2018-2019学年上学期高三数学10月月考试题

北辰区第二中学2018-2019学年上学期高三数学10月月考试题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题1. 已知数列{}n a 是各项为正数的等比数列,点22(2,log )M a 、25(5,log )N a 都在直线1y x =-上,则数列{}n a 的前n 项和为( )A .22n- B .122n +- C .21n - D .121n +-2. 设定义域为(0,+∞)的单调函数f (x ),对任意的x ∈(0,+∞),都有f[f (x )﹣lnx]=e+1,若x 0是方程f (x )﹣f ′(x )=e 的一个解,则x 0可能存在的区间是( ) A .(0,1) B .(e ﹣1,1) C .(0,e ﹣1)D .(1,e )3. 已知双曲线2222:1(0,0)x y C a b a b-=>>,12,F F 分别在其左、右焦点,点P 为双曲线的右支上的一点,圆M 为三角形12PF F 的内切圆,PM 所在直线与轴的交点坐标为(1,0),与双曲线的一条渐近线平行且距离为2,则双曲线C 的离心率是( )A B .2 C D .24. 设βα,是两个不同的平面,是一条直线,以下命题正确的是( ) A .若α⊥l ,βα⊥,则β⊂l B .若α//l , βα//,则β⊂l C .若α⊥l ,βα//,则β⊥l D .若α//l ,βα⊥,则β⊥l5. 若实数x ,y 满足,则(x ﹣3)2+y 2的最小值是( )A .B .8C .20D .26. 阅读右图所示的程序框图,若8,10m n ==,则输出的S 的值等于( ) A .28 B .36 C .45 D .120 7. 下列函数在其定义域内既是奇函数又是增函数的是( ) A .B .C .D .8. 若圆心坐标为()2,1-的圆在直线10x y --=上截得的弦长为 ) A .()()22210x y -++= B .()()22214x y -++= C .()()22218x y -++= D .()()222116x y -++=9. 2016年3月“两会”期间,有代表提出适当下调“五险一金”的缴存比例,现拟从某工厂职工中抽取20名代表调查对这一提案的态度,已知该厂青年,中年,老年职工人数分别为350,500,150,按分层抽样的方法,应从青年职工中抽取的人数为( ) A. 5 B.6 C.7D.10【命题意图】本题主要考查分层抽样的方法的运用,属容易题.10.我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大的创举,这个伟大创举与我国古老的算法——“辗转相除法”实质一样,如图的程序框图源于“辗转相除法”.当输入a =6 102,b =2 016时,输出的a 为( )A .6B .9C .12D .1811.已知直线l 1:(3+m )x+4y=5﹣3m ,l 2:2x+(5+m )y=8平行,则实数m 的值为( )A .﹣7B .﹣1C .﹣1或﹣7D .12.已知△ABC 中,a=1,b=,B=45°,则角A 等于( )A .150°B .90°C .60°D .30°二、填空题13.【泰州中学2018届高三10月月考】设二次函数()2f x ax bx c =++(,,a b c 为常数)的导函数为()f x ',对任意x R ∈,不等式()()f x f x ≥'恒成立,则222b ac +的最大值为__________. 14.如果实数,x y 满足等式()2223x y -+=,那么y x的最大值是 .15.某种产品的加工需要 A ,B ,C ,D ,E 五道工艺,其中 A 必须在D 的前面完成(不一定相邻),其它工艺的顺序可以改变,但不能同时进行,为了节省加工时间,B 与C 必须相邻,那么完成加工该产品的不同工艺的排列顺序有 种.(用数字作答)16.正六棱台的两底面边长分别为1cm ,2cm ,高是1cm ,它的侧面积为 .三、解答题17.(本小题满分12分)设椭圆2222:1(0)x y C a b a b+=>>的离心率12e =,圆22127x y +=与直线1x y a b +=相切,O 为坐标原点.(1)求椭圆C 的方程;(2)过点(4,0)Q -任作一直线交椭圆C 于,M N 两点,记MQ QN λ=,若在线段MN 上取一点R ,使 得MR RN λ=-,试判断当直线运动时,点R 是否在某一定直一上运动?若是,请求出该定直线的方 程;若不是,请说明理由.18.(本小题满分12分)已知点()()(),0,0,4,4A a B b a b >>,直线AB 与圆22:4430M x y x y +--+=相交于,C D 两点, 且2CD =,求.(1)()()44a b --的值; (2)线段AB 中点P 的轨迹方程; (3)ADP ∆的面积的最小值.19.某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),[90,100)后得到如图的频率分布直方图.(Ⅰ)求图中实数a的值;(Ⅱ)根据频率分布直方图,试估计该校高一年级学生其中考试数学成绩的平均数;(Ⅲ)若从样本中数学成绩在[40,50)与[90,100]两个分数段内的学生中随机选取2名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.20.已知椭圆:的长轴长为,为坐标原点.(Ⅰ)求椭圆C的方程和离心率;(Ⅱ)设动直线与y轴相交于点,点关于直线的对称点在椭圆上,求的最小值.21.已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且有最小值是.(1)求f(x)的解析式;(2)求函数h(x)=f(x)﹣(2t﹣3)x在区间[0,1]上的最小值,其中t∈R;(3)在区间[﹣1,3]上,y=f(x)的图象恒在函数y=2x+m的图象上方,试确定实数m的范围.22.解关于x的不等式12x2﹣ax>a2(a∈R).北辰区第二中学2018-2019学年上学期高三数学10月月考试题(参考答案)一、选择题1. 【答案】C【解析】解析:本题考查等比数列的通项公式与前n 项和公式.22log 1a =,25log 4a =,∴22a =,516a =,∴11a =,2q =,数列{}n a 的前n 项和为21n-,选C .2. 【答案】 D【解析】解:由题意知:f (x )﹣lnx 为常数,令f (x )﹣lnx=k (常数),则f (x )=lnx+k . 由f[f (x )﹣lnx]=e+1,得f (k )=e+1,又f (k )=lnk+k=e+1, 所以f (x )=lnx+e ,f ′(x )=,x >0.∴f (x )﹣f ′(x )=lnx ﹣+e ,令g (x )=lnx ﹣+﹣e=lnx ﹣,x ∈(0,+∞)可判断:g (x )=lnx ﹣,x ∈(0,+∞)上单调递增,g (1)=﹣1,g (e )=1﹣>0, ∴x 0∈(1,e ),g (x 0)=0,∴x 0是方程f (x )﹣f ′(x )=e 的一个解,则x 0可能存在的区间是(1,e ) 故选:D .【点评】本题考查了函数的单调性,零点的判断,构造思想,属于中档题.3. 【答案】C 【解析】试题分析:由题意知()1,0到直线0bx ay -==,得a b =,则为等轴双曲故本题答案选C. 1 考点:双曲线的标准方程与几何性质.【方法点睛】本题主要考查双曲线的标准方程与几何性质.求解双曲线的离心率问题的关键是利用图形中的几何条件构造,,a b c 的关系,处理方法与椭圆相同,但需要注意双曲线中,,a b c 与椭圆中,,a b c 的关系不同.求双曲线离心率的值或离心率取值范围的两种方法:(1)直接求出,a c 的值,可得;(2)建立,,a b c 的齐次关系式,将用,a c 表示,令两边同除以或2a 化为的关系式,解方程或者不等式求值或取值范围.4. 【答案】C 111] 【解析】考点:线线,线面,面面的位置关系 5. 【答案】A【解析】解:画出满足条件的平面区域,如图示:,由图象得P (3,0)到平面区域的最短距离d min =,∴(x ﹣3)2+y 2的最小值是:.故选:A .【点评】本题考查了简单的线性规划问题,考查数形结合思想,是一道基础题.6. 【答案】C【解析】解析:本题考查程序框图中的循环结构.121123mn n n n n m S C m---+=⋅⋅⋅⋅=,当8,10m n ==时,82101045m n C C C ===,选C .7. 【答案】B【解析】【知识点】函数的单调性与最值函数的奇偶性 【试题解析】若函数是奇函数,则故排除A 、D ;对C :在(-和(上单调递增,但在定义域上不单调,故C 错; 故答案为:B 8. 【答案】B【解析】考点:圆的方程.1111]9.【答案】C10.【答案】【解析】选D.法一:6 102=2 016×3+54,2 016=54×37+18,54=18×3,18是54和18的最大公约数,∴输出的a=18,选D.法二:a=6 102,b=2 016,r=54,a=2 016,b=54,r=18,a=54,b=18,r=0.∴输出a=18,故选D.11.【答案】A【解析】解:因为两条直线l1:(3+m)x+4y=5﹣3m,l2:2x+(5+m)y=8,l1与l2平行.所以,解得m=﹣7.故选:A.【点评】本题考查直线方程的应用,直线的平行条件的应用,考查计算能力.12.【答案】D【解析】解:∵,B=45°根据正弦定理可知∴sinA==∴A=30°故选D.【点评】本题主要考查正弦定理的应用.属基础题.二、填空题13.【答案】2【解析】试题分析:根据题意易得:()'2f x ax b =+,由()()'f x f x ≥得:()220ax b a x c b +-+-≥在R上恒成立,等价于:0{ 0a >≤,可解得:()22444b ac a a c a ≤-=-,则:222222241441c b ac a aa c a c c a ⎛⎫- ⎪-⎝⎭≤=++⎛⎫+ ⎪⎝⎭,令1,(0)c t t a =->,24422222t y t t t t==≤=++++,故222b ac +的最大值为2. 考点:1.函数与导数的运用;2.恒成立问题;3.基本不等式的运用 14.【解析】考点:直线与圆的位置关系的应用. 1【方法点晴】本题主要考查了直线与圆的位置关系的应用,其中解答中涉及到点到直线的距离公式、直线与圆相切的判定与应用,着重考查了学生分析问题和解答问题的能力,以及推理与运算能力和转化与化归的思想方法,本题的解答中把yx的最值转化为直线与圆相切是解答的关键,属于中档试题. 15.【答案】 24【解析】解:由题意,B 与C必须相邻,利用捆绑法,可得=48种方法,因为A 必须在D 的前面完成,所以完成加工该产品的不同工艺的排列顺序有48÷2=24种,故答案为:24.【点评】本题考查计数原理的应用,考查学生的计算能力,比较基础.16.【答案】cm2.【解析】解:如图所示,是正六棱台的一部分,侧面ABB1A1为等腰梯形,OO1为高且OO1=1cm,AB=1cm,A1B1=2cm.取AB和A1B1的中点C,C1,连接OC,CC1,O1C1,则C1C为正六棱台的斜高,且四边形OO1C1C为直角梯形.根据正六棱台的性质得OC=,OC1==,1∴CC1==.又知上、下底面周长分别为c=6AB=6cm,c′=6A1B1=12cm.∴正六棱台的侧面积:S=.==(cm2).故答案为:cm2.【点评】本题考查正六棱台的侧面积的求法,是中档,解题时要认真审题,注意空间思维能力的培养.三、解答题17.【答案】(1)22143x y +=;(2)点R 在定直线1x =-上. 【解析】试题解析:(1)由12e =,∴2214e a =,∴2234a b =,又22221ab a b =+, 解得2,3a b ==,所以椭圆C 的方程为22143x y +=.设点R 的坐标为00(,)x y ,则由MR RN λ=-⋅,得0120()x x x x λ-=--,解得1121221212011224424()41()814x x x x x x x x x x x x x x x λλ++⋅-+++===+-++++又2212122226412322424()24343434k k x x x x k k k---++=⨯+⨯=+++, 212223224()883434k x x k k -++=+=++,从而121201224()1()8x x x x x x x ++==-++, 故点R 在定直线1x =-上.考点:1.椭圆的标准方程与几何性质;2.直线与椭圆的位置关系.18.【答案】(1)()()448a b --=;(2)()()()2222,2x y x y --=>>;(3)6. 【解析】试题分析:(1)利用2CD =,得圆心到直线的距离2d =2=,再进行化简,即可求解()()44a b --的值;(2)设点P 的坐标为(),x y ,则22a xb y ⎧=⎪⎪⎨⎪=⎪⎩代入①,化简即可求得线段AB 中点P 的轨迹方程;(3)将面积表示为()()()114482446224ADP b S a a b a b ab ∆==+-=+-=-+-+,再利用基本不等式,即可求得ADP ∆的面积的最小值.(3)()()()11448244666224ADP b S a a b a b a b ∆==+-=+-=-+-+≥=,∴当4a b ==+, 面积最小, 最小值为6.考点:直线与圆的综合问题.【方法点晴】本题主要考查了直线与圆的综合问题,其中解答中涉及到点到直线的距离公式、轨迹方程的求解,以及基本不等式的应用求最值等知识点的综合考查,着重考查了转化与化归思想和学生分析问题和解答问题的能力,本题的解答中将面积表示为()()446ADP S a b ∆=-+-+,再利用基本不等式是解答的一个难点,属于中档试题. 19.【答案】【解析】解:(Ⅰ)由频率分布直方图,得: 10×(0.005+0.01+0.025+a+0.01)=1, 解得a=0.03.(Ⅱ)由频率分布直方图得到平均分:=0.05×45+0.1×55+0.2×65+0.3×75+0.25×85+0.1×95=74(分).(Ⅲ)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A ,B , 数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C ,D ,E ,F , 若从数学成绩在[40,50)与[90,100)两个分数段内的学生中随机选取2名学生, 则所有的基本事件有:(A ,B ),(A ,C ),(A ,D ),(A ,E ),(A ,F ),(B ,C ),(B ,D ),(B ,E ), (B ,F ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ),共15个, 如果这两名学生的数学成绩都在[40,50)或都在[90,100)内, 则这两名学生的数学成绩之差的绝对值不大于10,记“这两名学生的数学成绩之差的绝对值不大于10”为事件M ,则事件M 包含的基本事件有:(A ,B ),(C ,D ),(C ,E ),(C ,F ),(D ,E ),(D ,F ),(E ,F ),共7个,所以这两名学生的数学成绩之差的绝对值不大于10的概率P=.【点评】本题考查频率和概率的求法,二查平均分的求法,是中档题,解题时要认真审题,注意频率分布直方图和列举法的合理运用.20.【答案】【解析】【知识点】圆锥曲线综合椭圆 【试题解析】(Ⅰ)因为椭圆C :,所以,,故,解得,所以椭圆的方程为.因为,所以离心率.(Ⅱ)由题意,直线的斜率存在,设点,则线段的中点的坐标为,且直线的斜率,由点关于直线的对称点为,得直线,故直线的斜率为,且过点,所以直线的方程为:,令,得,则,由,得,化简,得.所以.当且仅当,即时等号成立.所以的最小值为.21.【答案】【解析】解:(1)二次函数f(x)图象经过点(0,4),任意x满足f(3﹣x)=f(x)则对称轴x=,f(x)存在最小值,则二次项系数a>0设f(x)=a(x﹣)2+.将点(0,4)代入得:f(0)=,解得:a=1∴f(x)=(x﹣)2+=x2﹣3x+4.(2)h(x)=f(x)﹣(2t﹣3)x=x2﹣2tx+4=(x﹣t)2+4﹣t2,x∈[0,1].当对称轴x=t≤0时,h(x)在x=0处取得最小值h(0)=4;当对称轴0<x=t<1时,h(x)在x=t处取得最小值h(t)=4﹣t2;当对称轴x=t≥1时,h(x)在x=1处取得最小值h(1)=1﹣2t+4=﹣2t+5.综上所述:当t≤0时,最小值4;当0<t<1时,最小值4﹣t2;当t≥1时,最小值﹣2t+5.∴.(3)由已知:f(x)>2x+m对于x∈[﹣1,3]恒成立,∴m<x2﹣5x+4对x∈[﹣1,3]恒成立,∵g(x)=x2﹣5x+4在x∈[﹣1,3]上的最小值为,∴m<.22.【答案】【解析】解:由12x2﹣ax﹣a2>0⇔(4x+a)(3x﹣a)>0⇔(x+)(x﹣)>0,①a>0时,﹣<,解集为{x|x<﹣或x>};②a=0时,x2>0,解集为{x|x∈R且x≠0};③a<0时,﹣>,解集为{x|x<或x>﹣}.综上,当a>0时,﹣<,解集为{x|x<﹣或x>};当a=0时,x2>0,解集为{x|x∈R且x≠0};当a<0时,﹣>,解集为{x|x<或x>﹣}.。
