中考数学复习用不等式(组)解决问题3[人教版]
中考数学复习专题三-不等式和不等式组(解析版)

中考专题复习知识点1、不等式的解:能使不等式成立的未知数的值叫做不等式的解。
知识点2、不等式的解集:一个含有未知数的不等式的解的全体叫做这个不等式的解集。
知识点3、不等式的解集在数轴上的表示: (1)x >a :数轴上表示a 的点画成空心圆圈,表示a 的点的右边部分来表示;(2)x <a :数轴上表示a 的点画成空心圆圈,表示a 的点的左边部分来表示;(3)x ≥a :数轴上表示a 的点画成实心圆点,表示a 的点及表示a 的点的右边部分来表示;(4)x ≤a :数轴上表示a 的点画成实心圆点,表示a 的点及表示a 的点的左边部分来表示。
在数轴上表示大于3的数的点应该是数3所对应点的右边。
画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈)。
如图所示:同样,如果某个不等式的解集为x ≤-2, 那么它表示x 取-2左边的点 画实心圆点。
如图所示:总结:在数轴上表示不等式解集的要点: 小于向左画,大于向右画;无等号画空心圆圈,有等号画圆点。
知识点4、不等式的性质:(1)不等式的两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变;(3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变。
知识点5、一元一次不等式:只含有一个未知数,并且未知数的最高次数是1,系数不等于0的不等式,叫做一元一次不等式。
知识点6、解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)合并同类项;(5)未知数的系数化为1。
通过这些步骤可以把一元一次不等式转化为x >a (x ≥a )或x <a (x ≤a )的形式。
知识点7、一元一次不等式组:由几个含有同一个未知数的一次不等式组成的不等式组叫做一元一次不等式组。
知识点8、知识点9、解不等式组:求不等式组解集的过程叫做解不等式组。
知识点10、解一元一次不等式组的一般步骤:先分别解不等式组中的各个不等式,然后再求出这几个不等式解集的公共部分。
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第二节 一元二次方程及其应用
解:设参加交流会的茶叶制作商有 m 人.依题意得 m(m-1)=380,解得 m1=20,m2=-19(舍去). 答:参加交流会的茶叶制作商有 20 人.
4.(2022·荆州第 7 题 3 分)关于 x 的方程 x2-3kx-2=0 实数根的情况,
下列判断中正确的是
(B)
A.有两个相等实数根
B.有两个不等实数根
C.没有实数根
D.有一个实数根
5.(2020·荆州第 9 题 3 分)定义新运算“a*b”:对于任意实数 a,b,都
有 a*b=(a+b)(a-b)-1,其中等式右边是通常的加法、减法、乘法运
解:设小路宽为 x m, 由题意,得(16-2x)(9-x)=112. 整理,得 x2-17x+16=0. 解得 x1=1,x2=16>9(不合题意,舍去).∴x=1. 答:小路的宽应为 1m.
17.(数学文化)《田亩比类乘除捷法》是我国古代数学家杨辉的著作, 其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长 多阔几何?”意思是:一块矩形田地的面积为 864 平方步,只知道它的 长与宽共 60 步,问它的长比宽多多少步?根据题意,长比宽多__112__步.
100.8
解:设后两次采购价格的平均增长率为 x,依题意得 480(1+x)2=480+100.8,解得 x1=0.1,x2=-2.1(舍). 答:后两次采购价格的平均增长率为 10%.
解:设售价为 y 元/袋时,每周的销售额为 32 400 元.依题意可列方程
y-260
为 y100-
10
=32 400,解得 y1=360,y2=900.
第二节 一元二次方程及 其应用
【考情分析】湖北近 3 年主要考查:1.选择合适的方法解一元二次方程, 常在压轴题中涉及考查;2.用一元二次方程根的判别式判断方程根的情 况或者根据根的情况求字母系数的取值范围,根与系数的关系的应用; 3.一元二次方程的应用主要以选择题的形式考查列方程,常在解答题中 与不等式、函数的实际应用结合考查,难度较大,分值一般 3-10 分.
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第一节 一次方程(组)及其应用

∴原方程组的解为y=1,将y=1 代入 2kx-3y<5 得 2×k×2-3<5,解得 k<2.
命题点 2:一次方程(组)的应用(近 3 年考查 15 次)
7.(数学文化)(2021·武汉第 7 题 3 分)我国古代数学名著《九章算术》
中记载:“今有共买物,人出八,盈三;人出七,不足四,问人数,物价
32 人.2 艘大船与 1 艘小船一次共可以满载游客 46 人.则 1 艘大船与 1
艘小船一次共可以满载游客的人数为
( B)
A.30
B.26
C.24
D.22
11.★(2022·武汉第 10 题 3 分)幻方是古老的数学问题,我国古代的《洛 书》中记载了最早的幻方——九宫格.将 9 个数填入幻方的空格中,要 求每一横行、 每一竖列以及两条对角线上的 3 个数之和相等,例如图① 就是一个幻方.图②是一个未完成的幻方,则 x 与 y 的和是 ( D ) A.9 B.10 C.11 D.12
14.(2020·仙桃第 12 题 3 分)篮球联赛中,每场比赛都要分出胜负,每 队胜 1 场得 2 分,负 1 场得 1 分.某队 14 场比赛得到 23 分,则该队胜 了__99__场.
15.(2020·黄冈第 19 题 6 分)为推广黄冈各县市名优农产品,市政府组 织创办了“黄冈地标馆”,一顾客在“黄冈地标馆”发现,如果购买 6 盒 羊角春牌绿茶和 4 盒九孔牌藕粉,共需 960 元,如果购买 1 盒羊角春牌 绿茶和 3 盒九孔牌藕粉共需 300 元,请问每盒羊角春牌绿茶和每盒九孔 牌藕粉分别需要多少元?
【分层分析】设购进创意文具袋 x 个,由题干信息①得购进笔记本为
((2x2+x+10)个,由题干信息②可列方程为 xx++(2(x2+x1+0)1=0)190.
考点07 一元一次不等式(组)及其应用-备战2023届中考数学一轮复习考点梳理(解析版)

考点07 一元一次不等式(组)及其应用中考数学中,一元一次不等式(组)的解法及应用时有考察,其中,不等式基本性质和一元一次不等式(组)解法的考察通常是以选择题或填空题的形式出题,还通常难度不大。
而对其简单应用,常会和其他考点(如二元一次方程组、二次函数等)结合考察,此时难度上升,需要小心应对。
对于一元一次不等式中含参数问题,虽然难度系数上升,但是考察几率并不大,复习的时候只需要兼顾即可!一、不等式的基本性质二、一元一次不等式(组)的解法三、求不等式(组)中参数的值或范围四、不等式(组)的应用考向一:不等式的基本性质【易错警示】1.若a >b ,则下列不等式中,错误的是( )A .3a >3bB .﹣<﹣C .4a ﹣3>4b ﹣3D .ac 2>bc 2【分析】根据不等式的性质进行一一判断.【解答】解:A 、在不等式a >b 的两边同时乘以3,不等式仍成立,即3a >3b ,故本选项正确;B 、在不等式a >b 的两边同时除以﹣3,不等号方向改变,即﹣<﹣,故本选项正确;C 、在不等式a >b 的两边同时先乘以4、再减去3,不等式仍成立,4a ﹣3>4b ﹣3,故本选项正确;D 、当c =0时,该不等式不成立,故本选项错误.故选:D .2.已知x <y ,下列式子不成立的是( )A .x +1<y +1B .x <y +100C .﹣2022x <﹣2022yD .【分析】根据不等式的性质判断即可.【解答】解:A 、在不等式x =y 的两边同时加上1得x +1<y +1,原变形成立,故此选项不符合题意;B 、在不等式x <y 的两边同时加上100得x +100<y +100,原变形成立,故此选项不符合题意;C 、在不等式x <y的两边同时乘以﹣2022得﹣2022x >﹣2022y ,原变形不成立,故此选项符合题意;D 、在不等式x <y 的两边同时除以2022得x <y ,原变形成立,故此选项不符合题意;故选:C .3.若x>y,且(a+3)x<(a+3)y,求a的取值范围 a<﹣3 .【分析】根据题意,在不等式x>y的两边同时乘以(a+3)后不等号改变方向,根据不等式的性质3,得出a+3<0,解此不等式即可求解.【解答】解:∵x>y,且(a+3)x<(a+3)y,∴a+3<0,则a<﹣3.故答案为:a<﹣3.4.已知3x﹣y=1,且x≤3,则y的取值范围是 y≤8 .【分析】根据3x﹣y=1求出x=,根据x≤3得出≤3,再根据不等式的性质求出不等式的解集即可.【解答】解:∵3x﹣y=1,∴3x=1+y,∴x=,∵x≤3,∴≤3,∴1+y≤9,∴y≤8,即y的取值范围是y≤8,故答案为:y≤8.5.已知a,b,c为三个非负实数,且满足,若W=3a+2b+5c,则W的最大值为 130 .【分析】将方程组两个方程相加,得到3a+5c=130﹣4b,整体替换可得W=130﹣2b,再由b的取值范围即可求解.【解答】解:,①+②,得3a+4b+5c=130,可得出a=10﹣,c=20﹣,∵a,b,c为三个非负实数,∴a =10﹣≥0,c =20﹣≥0,∴0≤b ≤20,∴W =3a +2b +5c =2b +130﹣4b =130﹣2b ,∴当b =0时,W =130﹣2b 的最大值为130,故答案为:130.考向二:一元一次不等式(组)的解法1. 一元一次不等式的解法2. 一元一次不等式(组)的解法①按照一元一次不等式的解法解出每个不等式的解集②依据数轴取各不等式解集的公共部分一元一次不等式组解法及解集的四种情况无解大大小小则无解1.不等式3(2﹣x)>x+2的解在数轴上表示正确的是( )A.B.C.D.【分析】根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得.【解答】解:∵3(2﹣x)>x+2,∴6﹣3x>x+2,﹣3x﹣x>2﹣6,﹣4x>﹣4,x<1,故选:C.2.在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )A.1B.﹣C.0D.4或﹣4【分析】根据第二象限内点的坐标特点列出关于a的不等式,求出a的取值范围即可.【解答】解:∵点A(a,2)是第二象限内的点,∴a<0,四个选项中符合题意的数是,故选:B.3.关于x的方程ax=2x﹣7的解为负数,则a的取值范围是 a>2 .【分析】先解方程得到x=,根据题意得到<0,所以2﹣a<0,然后解不等式即可.【解答】解:解方程ax=2x﹣7的得x=,∵方程ax=2x﹣7的解为负数,∴<0,∴2﹣a<0,解得a>2,即a的取值范围为a>2.故答案为:a>2.4.已知x>2是关于x的不等式x﹣3m+1>0的解集,那么m的值为 1 .【分析】先把m看作常数,求出不等式的解集,再根据不等式解集为x>2,建立关于m的方程,求解即可.【解答】解:x﹣3m+1>0x>3m﹣1,∵x>2 是关于x的不等式x﹣3m+1>0 的解集,∴3m﹣1=2,解得:m=1,故答案为:1.5.若关于的不等式﹣ax>bx﹣b(ab≠0)的解集为x>,则关于x的不等式3bx<ax﹣b的解集是 x>﹣1 .【分析】根据已知不等式的解集,即可确定的值以及a+b的符号,进而求得a=2b,进一步求得b<0,从而解不等式即可.【解答】解:移项,得:(a+b)x<b,根据题意得:a+b<0且=,即3b=a+b,则a=2b,又a+b<0,即3b<0,则b<0,则关于x的不等式3bx<ax﹣b化为:3bx<2bx﹣b,解得x>﹣1.故答案为:x>﹣1.6.解下列不等式,并将解集在数轴上表示出来.(1)﹣x+19≥2(x+5);(2).【分析】(1)先去括号,再移项、合并同类项,把x的系数化为1,再把不等式的解集在数轴上表示出来即可;(2)不等式两边都乘12去分母后,去括号,移项合并,将x系数化为1,求出解集,表示在数轴上即可.【解答】解:(1)﹣x+19≥2(x+5),去括号,得)﹣x+19≥2x+10,移项,得﹣x﹣2x≥10﹣19,合并同类项,得﹣3x≥﹣9,系数化为1,得x≤3.将解集在数轴上表示为:(2),去分母,得3(x+4)﹣12<4(4x﹣13),去括号,得3x+12﹣12<16x﹣52,移项,得3x﹣16x<﹣52﹣12+12,合并同类项,得﹣13x<﹣52,系数化为1,得x>4.解集在数轴上表示为:7.关于x的方程5x﹣2k=6+4k﹣x的解是负数,求字母k的值.【分析】解方程得出x=k+1,根据方程的解为负数得出关于k的不等式,解之可得.【解答】解:解方程5x﹣2k=6+4k﹣x得x=k+1,∵方程的解是负数,∴k+1<0,∴k<﹣1.8.不等式组的解集在数轴上表示为( )A.B.C.D.【分析】先解出每个不等式的解集,即可得到不等式组的解集,然后在数轴上表示出其解集即可.【解答】解:,解不等式①,得:x≥1,解不等式②,得:x≥2,故原不等式组的解集是x≥2,其解集在数轴上表示如下:,故选:C.9.对于任意实数x,我们用{x}表示不小于x的最小整数.如:{2.7}=3,{2022}=2022,{﹣3.14}=﹣3,若{2x+3}=﹣2,则x的取值范围是( )A.B.C.D.【分析】根据{x}表示不小于x的最小整数,可得﹣3<2x+3≤﹣2,然后进行计算即可解答.【解答】解:∵{2x+3}=﹣2,∴﹣3<2x+3≤﹣2,∴﹣6<2x≤﹣5,∴﹣3<x≤﹣,故选:D.10.不等式组的解集是 x<3 .【分析】先求出每个一元一次不等式的解集,再求出它们的公共部分即为不等式组的解集.【解答】解:,解①得:x≤8,解②得:x<3,∴不等式组的解集为x<3.故答案为:x<3.11.解不等式(组),并把解集在数轴上表示出来:(1)2(x﹣1)+2<3x;(2).【分析】(1)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.【解答】解:(1)∵2(x﹣1)+2<3x,∴2x﹣2+2<3x,∴2x﹣3x<2﹣2,∴﹣x<0,则x>0,将解集表示在数轴上如下:(2)解不等式3x﹣(x﹣2)≥6,得:x≥2,解不等式x+1>,得:x<4,则不等式组的解集为2≤x<4,将不等式组的解集表示在数轴上如下:考向三:求不等式组中参数的值或范围方法步骤总结:①解出不等式(组)的解集——用含参数的表达式表示;②根据题目要求,借助数轴,确定参数表达式的范围,必在两个相邻整数之间;③由空心、实心判断参数两边边界哪边可以取“=”,哪边不能取“=”。
2023年九年级中考数学第一轮复习卷:不等式(组)及其应用 试卷(含答案)

2023年中考数学第一轮复习卷:不等式(组)及其应用一、选择题1. 已知x =1是不等式2x -b <0的解,b 的值可以是( )A.4B.2C.0D.-22. (2020•镇江模拟)不等式组2x a a 60x 3a 20⎧+++>⎨-+<⎩恒有解,下列a 满足条件的是( ) A.-4≤a ≤-2 B.-3≤a ≤-1 C.-2≤a ≤0 D.-1≤a ≤13. (2020•深圳模拟)不等式组1235a x a x -<<+⎧⎨<<⎩的解集是3<x<a+2,则a 的取值范围是( ) A.a>1 B.a ≤3 C.a<1或a>3 D.1<a ≤34. (2021·聊城)若-3<a ≤3,则关于x 的方程x +a =2解的取值范围为( )A.-1≤x <5B.-1<x ≤1C.-1≤x <1D.-1<x ≤55. (2020•衢州)不等式组的解集在数轴上表示正确的是( ) A. B. C. D.6. (2022·四川绵阳·中考模拟)为了美化校园,学校决定利用现有的2660盆甲种花卉和3000盆乙种花卉搭配A 、B 两种园艺造型共50个摆放在校园内,已知搭配一个A 种造型需甲种花卉70盆,乙种花卉30盆,搭配一个B 种造型需甲种花卉40盆,乙种花卉80盆.则符合要求的搭配方案有几种( )A.2B.3C.4D.57. (2021·北部湾经济区)定义一种运算:a*b =⎩⎪⎨⎪⎧a ,a ≥b b ,a <b ,则不等式(2x +1)*(2-x)>3的解集是( )A.x >1或x <13B.-1<x <13C.x >1或x <-1D.x >13或x <-1 8. (2022·四川眉山·一模)红星商店计划用不超过4200元的资金,购进甲、乙两种单价分别为60元、100元的商品共50件,据市场行情,销售甲、乙商品各一件分别可获利10元、20元,两种商品均售完.若所获利润大于750元,则该店进货方案有( )A.3种B.4种C.5种D.6种9. (2022·山东济南·二模)定义:平面直角坐标系中,点P(x,y)的横坐标x 的绝对值表示为|x|,纵坐标y 的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的折线距离,记为|M|=|x|+|y|(其中的“+”是四则运算中的加法),若抛物线y=ax 2+bx+1与直线y=x 只有一个交点M,已知点M 在第一象限,且2≤|M|≤4,令t=2b 2-4a+2022,则t 的取值范围为( )A.2018≤t ≤2019B.2019≤t ≤2020C.2020≤t ≤2021D.2021≤t ≤202210. (2022·北京十一学校一分校)设m 是非零实数,给出下列四个命题:①若-1<m<0,则1m <m<2m ;②若m>1,则1m <2m <m;③若m<1m <2m ,则m<0;④2m <m<1m,则0<m<1.其中命题成立的序号是( )A.①③B.①④C.②③D.③④二、填空题11. (2020·辽宁沈阳·初三一模)不等式组341025143x x x x +≤+⎧⎪+⎨-<⎪⎩的解集是_____. 12. (2021·荆门模拟)不等式组:⎩⎪⎨⎪⎧2x +3>-x 3-12x >2 的解集为____. 13. (2021·眉山中考)若关于x 的不等式x +m <1只有3个正整数解,则m 的取值范围是____.14. (2020•攀枝花)世纪公园的门票是每人5元,一次购门票满40张,每张门票可少1元.若少于40人时,一个团队至少要有 人进公园,买40张门票反而合算.15. (2022·黑龙江绥化·一模)某电脑经销商计划购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元.该经销商购进这两种商品共50台,购进电脑机箱不超过26台,而可用于购买这两种商品的资金不超过22240元,则该经销商有________种进货方案.16. (2022·重庆八中一模)某新建商场设有百货部、服装部和家电部三个经营部,共有若干名售货员,平时全商场日营业额(指每日卖出商品所收到的总金额)为60万元,由于营业性质不同,分配到三个经营部的售货员的人数不等,所得利润也不同.根据经验,百货部、服装部、家电部各类商品每1万元营业额所需售货员人数依次为5人、4人、2人;所得利润占各自营业额的占比依次为310、12、15.临近妇女节人流量增加,商场决定将原百货部和家电部的售货员人数减少都调整到服装部,同时节日期间各类商品所得利润与各自营业额的占比依次变为25、35、310,这样节日期间商场每日获得的利润比平时增加,且差价超过7万元,但不超过8万元.若百货部、服装部和家电部的营业额始终是整数,则节日期间从百货部调整到服装部的售货员共_____人.三、解答题17. (2021·西安模拟)习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气”.某校为提高学生的阅读品味,现决定购买《艾青诗选》和《格列佛游记》两种书共50本.已知购买2本《艾青诗选》和1本《格列佛游记》需100元;购买6本《艾青诗选》与购买7本《格列佛游记》的价格相同.(1)求这两种书的单价.(2)若购买《艾青诗选》的数量不少于所购买《格列佛游记》数量的一半,且购买两种书的总价不超过1 600元.请问有哪几种购买方案?18. (2021·玉林)某市垃圾处理厂利用焚烧垃圾产生的热能发电,有A,B 两个焚烧炉,每个焚烧炉每天焚烧垃圾均为100吨,每焚烧一吨垃圾,A 焚烧炉比B 焚烧炉多发电50度,A,B 焚烧炉每天共发电55000度.(1)求焚烧一吨垃圾,A 焚烧炉和B 焚烧炉各发电多少度;(2)若经过改进工艺,与改进工艺之前相比每焚烧一吨垃圾,A 焚烧炉和B 焚烧炉的发电量分别增加a%和2a%,则A,B 焚烧炉每天共发电至少增加(5+a)%,求a 的最小值.19. (2020•广西)某市为创建“全国文明城市”,计划购买甲、乙两种树苗绿化城区,购买50棵甲种树苗和20棵乙种树苗需要5000元,购买30棵甲种树苗和10棵乙种树苗需要2800元.(1)求购买的甲、乙两种树苗每棵各需要多少元.(2)经市绿化部门研究,决定用不超过42000元的费用购买甲、乙两种树苗共500棵,其中乙种树苗的数量不少于甲种树苗数量的,求甲种树苗数量的取值范围.(3)在(2)的条件下,如何购买树苗才能使总费用最低?20. (2021•北碚区校级模拟)每年3-6月都是草莓、樱桃、枇杷销售的旺季,水果批发商都会大量采购,为了获得最大利润,批发商需要统计数据,更好地囤货.4月份某水果批发商统计前半个月销量后发现,草莓、樱桃销量相同,枇杷销量比草莓多,随着气温升高,后半个月水果总销量将在前半个月基础上有所增加,后半个月樱桃与枇杷的销量之比为3:2,4月份樱桃总销量与4月份枇杷总销量之比为51:44,但草莓由于已过销售旺季,后半个月与前半个月相比,销量有所减少,后半个月草莓减少的量与后半个月三种水果的总销量之比为1:14,则樱桃后半个月新增的销量与后半个月三种水果的总销量之比为多少?.21.(2021•江北区校级模拟)“绿水青山,就是金山银山”,为改善区域生态状况,促进经济社会可持续发展,实现人与自然和谐共生,某地启动了国家湿地公园建设试点项目,通过补植补造、自然封育、人工管护等一系列措施,改善生态环境,打造休闲旅游好去处.该湿地项目根据湿地地形,决定补植补造草皮、灌木、乔木(不混种)以增强观赏性.经过一段时间,补植补造草皮、灌木、乔木的面积之比为2:3:4,根据规划方案,将把余下湿地留足10%作为观赏步道后,剩下湿地继续补植补造草皮、灌木、乔木,经测算若将剩下湿地的补造草皮,则草皮的面积将达到前后补植补造的这三种植被总面积的.为了使前后补植灌木总面积与补植乔木总面积达到9:13,则该湿地项目前后补植的灌木总面积与该湿地项目全部(含观赏步道)总面积之比是多少?.答案一、选择题(本大题共10小题,每小题5分,满分50分)(本大题共10道小题)1. 【答案】A2. 【答案】故选:D.3. 【答案】故选:D.4. 【答案】A5. 【答案】C【解析】分别解两个不等式,然后求它们的公共部分即可得到原不等式组的解集,再在数轴上表示出来即可求解.,由①得x ≤1;由②得x >﹣1;故不等式组的解集为﹣1<x ≤1,在数轴上表示出来为:.6. 【答案】B7. 【答案】C8. 【答案】C9. 【答案】C10. 【答案】B二、填空题11. 【答案】15<x ≤3. 【详解】341025143x x x x ++⎧⎪⎨+-<⎪⎩①② ,由①得,x ≤3,由②得,x >15,原不等式组的解集为15<x ≤3,故答案为15<x ≤3.12. 【答案】-1<x <213. 【答案】-3≤m <-214. 【答案】33.【解析】设x 人进公园,若购满40张票则需要:40×(5﹣1)=40×4=160(元),故5x >160时,解得:x >32,则当有32人时,购买32张票和40张票的价格相同,则再多1人时买40张票较合算;32+1=33(人).则至少要有33人去世纪公园,买40张票反而合算.15. 【答案】316. 【答案】20三、解答题17. 【答案】(1)设购买《艾青诗选》的单价为x 元,《格列佛游记》的单价为y 元,由题意得:⎩⎪⎨⎪⎧2x +y =1006x =7y ,解得⎩⎪⎨⎪⎧x =35y =30 , 答:购买《艾青诗选》的单价为35元,《格列佛游记》的单价为30元.(2)设购买《艾青诗选》的数量为n 本,则购买《格列佛游记》的数量为(50-n)本,根据题意得⎩⎪⎨⎪⎧n ≥12(50-n )35n +30(50-n )≤1600,解得:1623 ≤n ≤20, 则n 可以取17、18、19、20,当n =17时,50-n =33,共花费17×35+33×30=1 585(元);当n=18时,50-n=32,共花费18×35+32×30=1 590(元);当n=19时,50-n=31,共花费19×35+31×30=1 595(元);当n=20时,50-n=30,共花费20×35+30×30=1 600(元);所以,共有4种购买方案分别为:购买《艾青诗选》和《格列佛游记》的数量分别为17本和33本,购买《艾青诗选》和《格列佛游记》的数量分别为18本和32本,购买《艾青诗选》和《格列佛游记》的数量分别为19本和31本,购买《艾青诗选》和《格列佛游记》的数量分别为20本和30本.18. 【答案】解:(1)设焚烧一吨垃圾,B焚烧炉发电x度,则A焚烧炉发电(x+50)度.根据题意,得100(x+50)+100x=55000.解得x=250.∴x+50=300.答:焚烧一吨垃圾,A焚烧炉发电300度,B焚烧炉发电250度.(2)改进工艺后,焚烧一吨垃圾,A焚烧炉和B焚烧炉的发电量分别为300(1+a%)吨和250(1+2a%)吨.根据题意,得100×300(1+a%)+100×250(1+2a%)≥55000+55000×(5+a)%.解得a≥11.答:a的最小值为11.19. 【答案】解:(1)设购买的甲种树苗的单价为x元,乙种树苗的单价为y元.依题意得:,解这个方程组得:,答:购买的甲种树苗的单价是60元,乙种树苗的单价是100元;(2)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,由题意得,,解得,200≤a≤400.∴甲种树苗数量a的取值范围是200≤a≤400.(3)设购买的甲种树苗a棵,则购买乙种树苗(500﹣a)棵,总费用为W,∴W=60a+100(500﹣a)=50000﹣40a.∵﹣40<0,∴W值随a值的增大而减小,∵200≤a≤400,∴当x=400时,W取最小值,最小值为50000﹣40×400=34000元.即购买的甲种树苗400棵,购买乙种树苗100棵,总费用最低.20. 【答案】解:∵前半个月草莓、樱桃销量相同,枇杷销量比草莓多,∴设前半个月草莓、樱桃销量为x,则枇杷销量为(1+)x=x,∵后半个月樱桃与枇杷的销量之比为3:2,∴设后半个月樱桃销量为3y,则后半个月枇杷的销量2y,设后半个月草莓销量为z,∵4月份樱桃总销量与4月份枇杷总销量之比为51:44,∴=,变形化简得y=x,∵后半个月草莓减少的量与后半个月三种水果的总销量之比为1:14,∴=,变形化简得z=x-y,∴z=x-×x=x,∴樱桃后半个月新增的销量与后半个月三种水果的总销量之比为==,故答案为:.21. 【答案】解:设湿地总面积为a,第一次补植补造草皮、灌木、乔木的面积分别为2x、3x、4x,则余下湿地面积是a-9x,观赏步道的面积为10%•(a-9x)=a-x,∵前后补植灌木总面积与补植乔木总面积达到9:13,∴设前后补植灌木总面积为9z,则前后补植乔木总面积为13z,∵剩下湿地继续补植补造草皮、灌木、乔木,经测算若将剩下湿地的补造草皮,则草皮的面积将达到前后补植补造的这三种植被总面积的,∴[(a-9x)-(a-x)]×+2x=[a-(a-x)]×,化简得3a=47x,即x=a①,而前后补植补造草皮、灌木、乔木总面积为[(a-9x)-(a-x)]×+2x+9z+13z,∴[(a-9x)-(a-x)]×+2x+9z+13z=a-(a-x),化简得3a=110z-8x②,将①代入②得3a=110z-8×a,解得:z=a,∴湿地项目前后补植的灌木总面积与该湿地项目全部(含观赏步道)总面积之比是=,故答案为:.。
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
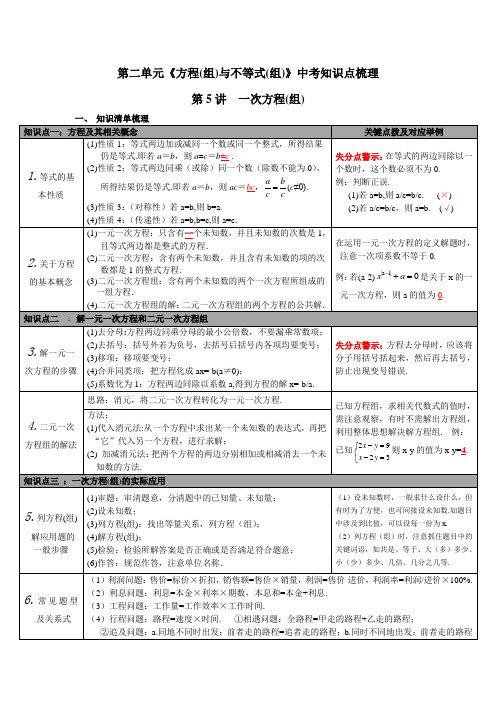
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一:不等式及其基本性质关键点拨及对应举例1.不等式的相关概念(1)不等式:用不等号(>,≥,<,≤或≠)表示不等关系的式子.(2)不等式的解:使不等式成立的未知数的值.(3)不等式的解集:使不等式成立的未知数的取值范围.例:“a与b的差不大于1”用不等式表示为a-b≤1.2.不等式的基本性质性质1:若a>b,则a±c>b±c;性质2:若a>b,c>0,则ac>bc,ac>bc;性质3:若a>b,c<0,则ac<bc,ac<bc.牢记不等式性质3,注意变号.如:在不等式-2x>4中,若将不等式两边同时除以-2,可得x<2.知识点二:一元一次不等式3.定义用不等号连接,含有一个未知数,并且含有未知数项的次数都是1的,左右两边为整式的式子叫做一元一次不等式. 例:若230mmx++>是关于x的一元一次不等式,则m的值为-1.4.解法(1)步骤:去分母;去括号;移项;合并同类项;系数化为1.失分点警示系数化为1时,注意系数的正负性,若系数是负数,则不等式改变方向.(2)解集在数轴上表示:x≥a x>a x≤a x<a知识点三:一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起,就组成一个一元一次不等式组.(1)在表示解集时“≥”,“≤”表示含有,要用实心圆点表示;“<”,“>”表示不包含要用空心圆点表示.(2)已知不等式(组)的解集情况,求字母系数时,一般先视字母系数为常数,再逆用不等式(组)解集的定义,反推出含字母的方程,最后求出字母的值.如:已知不等式(a-1)x<1-a 的解集是x>-1,则a的取值范围是a<1.6.解法先分别求出各个不等式的解集,再求出各个解集的公共部分7.不等式组解集的类型假设a<b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小,小大中间找x ax b≤⎧⎨≥⎩无解大大,小小取不了知识点四:列不等式解决简单的实际问题8.列不等式解应用题(1)一般步骤:审题;设未知数;找出不等式关系;列不等式;解不等式;验检是否有意义.(2)应用不等式解决问题的情况:a.关键词:含有“至少(≥)”、“最多(≤)”、“不低于(≥)”、“不高于(≤)”、“不大(小)于”、“超过(>)”、“不足(<)”等;注意:列不等式解决实际问题中,设未知数时,不应带“至少”、“最多”等字眼,与方程中设未知数一致.。
2024年中考数学复习专题课件(共30张PPT)一元一次不等式(组)及其应用

解:设普通水稻的亩产量是 x kg,则杂交水稻的亩产量是 2x kg,依题 意得 7 200 9 600
x - 2x =4,解得 x=600, 经检验,x=600 是原分式方程的解,且符合题意,则 2x=2×600=1 200(kg). 答:普通水稻的亩产量是 600 kg,杂交水稻的亩产量是 1 200 kg.
__00__.
6.[2023·贵州第 17(2)题 6 分]已知 A=a-1,B=-a+3.若 A>B,求 a 的取值范围. 解:由 A>B 得 a-1>-a+3, 解得 a>2, 即 a 的取值范围为 a>2.
7.[2021·贵阳第 17(1)题 6 分]有三个不等式 2x+3<-1,-5x>15, 3(x-1)>6,请在其中任选两个不等式, 组成一个不等式组,并求出它 的解集.
4.风陵渡黄河公路大桥是连接山西、陕西、河南三省的交通要塞 ,该 大桥限重标志牌显示,载重后总质量超过 30 t 的车辆禁止通行,现有一 辆自重 8 t 的卡车,要运输若干套某种设备,每套设备由 1 个 A 部件和 3 个 B 部件组成,这种设备必须成套运输,已知 1 个 A 部件和 2 个 B 部件 的总质量为 2.8 t,2 个 A 部件和 3 个 B 部件的质量相等. (1)求 1 个 A 部件和 1 个 B 部件的质量各是多少; (2)卡车一次最多可运输多少套这种设备通过此大桥?
解:(1)设出售的竹篮 x 个,陶罐 y 个,依题意有 5x+12y=61, x=5, 6x+10y=60,解得y=3. 答:小钢出售的竹篮 5 个,陶罐 3 个.
(2)设购买鲜花 a 束,依题意有 0<61-5a≤20, 解得 8.2≤a<12.2, ∵a 为整数, ∴共有 4 种购买方案, 方案一:购买鲜花 9 束; 方案二:购买鲜花 10 束; 方案三:购买鲜花 11 束; 方案四:购买鲜花 12 束.
人教版中考数学考点系统复习 第二章 方程(组)与不等式(组) 第三节 分式方程及其应用
命题点 2:分式方程解的运用(近 6 年考查 4 次)
5 . (2020 · 荆 门 第
11
题
3
分)已经关于
x
的
分
式
方
程
2x+3 x-2
=
(x-2)k(x+3)+2 的解满足-4<x<-1,且 k 为整数,则符合条件的
所有 k 值的乘积为
(A )
A.正数 B.负数
C.零 D.无法确定
6.★(2021·荆州第 15 题 3 分)若关于 x 的方程 2xx-+2m+x2--1x=3 的解是
【分层分析】设第二次购买材料 x t,由②得第二次购买的单价为x2211x0000
元,由③得第一次购买材料的吨数为 2x2 t,由①,③得第一次购买的
45210000 单价为x 2x
元,由④可列方程为x452x0x00-211000=0021
000 x
.
45 000 解:设第二次购买材料 x t,则第一次购买材料 2x t.根据题意得 2x
周
【考情分析】湖北近 3 年主要考查:1.分式方程的解法,应用分式方程 解决简单的实际问题.分式方程的解法考查形式有:直接解分式方程; 根据分式方程解的情况求字母的值或取值范围;2.分式方程的应用主要 以选择题的形式考查列方程,常在解答题中与不等式、函数的实际应用 结合考查,难度较大,分值一般 3-10 分.
4 是原来每天用水量的5,这样 120 t 水可多用 3 天.求现在每天用水量是 多少吨?
4 解:设原来每天的用水量为 x t,则现在每天的用水量为5x t,由题意可 列方程: 1542x0-1x20=3,解得 x=10, 经检验,x=10 是原方程的解.
44 而5x=5×10=8. 答:现在每天的用水量为 8 t.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
根据对话内容, 一盒饼干的标价可 试求出饼干和牛 是整数元哦! 奶的标价各是多少?
卡通人
5、某工厂现有甲种原料360kg,乙种原 料290kg,计划利用这两种原料生产A、B两 种产品,共50件。已知生产一件A产品需甲 种原料9kg,乙种原料3kg,可获利700元; 生产一件B产品需甲种原料4kg,乙种原料 10kg,可获利1200元。 (1)按要求安排A、B两种产品的生产件数, 有哪几种方案,请你给设计出来; (2)设生产A、B两种产品获总利润为y(元), 其中某一种产品的件数为x,试写出y与x之 间的函数关系式,并利用函数的性质,说明 (1)中哪种方案获总利润最大?最大利润是多 少?
他心如刀割の时刻,但是除咯打碎咯牙往肚子里咽,他还能怎么做?他唯有顾作镇定、强颜欢笑。因此他如往常壹样,别无二致,酒喝得很有 节制,话说得很是客套,礼数尽得很是周到。总之,他与平时の那各众人与熟知の王爷没有任何两样,因为他不能让任何人看咯他の笑话。十 三小格是王爷の最亲厚の兄弟,十小格是二十三小格の死党,八小格因病未来,因此喜宴上就只剩下九小格独自壹人耍咯单。面对眼前の这各 局面,九小格禁不住地暗自思忖:这些年老二十三可是越来越嚣张,越来越不把哥哥们放在眼里,难道是因为八哥失咯势?上次塞外行围,爷 の坐骑挨咯他の壹鞭子,要不是有八哥拦着,爷早就会当即把这小子追回来,好好跟他干壹架。这回他又憋着啥啊鬼主意?老二十三喜欢の不 是壹各有夫之妇吗?怎么娶の居然是年家大仆役?前两天不是还“二女争夫”吗,今天怎么就“姐妹易嫁”咯?看来老二十三这是又跟年二那 奴才暗地里勾搭上咯!那年二也真行,嫁咯这各妹妹又嫁那各,还想两边の便宜都占上,没那么容易!先过咯爷这壹关再说!九小格越想越来 气,越想越愤怒,于是立即就站咯起来,端起酒杯冲到王爷身边:“四哥,九弟敬您壹杯!”“九弟,此话差矣,今天是二十三弟の喜酒,你 不敬新郎官,怎么反倒敬上陪客咯?”“您是兄长,当然要先敬您咯!九弟晓得您心里不痛快,喝下这壹杯酒,只当是壹醉解千愁!”“九弟 此话更是差矣!二十三弟大喜の日子,我这做兄长の,高兴还来不及呢,四哥有啥啊可心里不痛快の?这杯酒四哥先喝下咯,但是话可要说在 前头,这杯是喜酒,四哥祝二十三弟和二十三弟妹百年好合,白头偕老。”好容易散咯宴席,待送走最后壹各客人,二十三小格の心才算是完 全地踏实下来,下壹步就该是洞房花烛夜咯。虽然他对婉然没啥啊感觉,以前也壹直只是将她当成壹各认识の人而已,现在又是为咯拉拢年二 公子、报复王爷才上演咯这么壹出“抢新娘”の闹剧,但是面对这各即将到来の洞房花烛,二十三小格可是壹点儿犹豫也没有,因为这各洞房 花烛他必须要去,而且绝对不是走过场。走过场算啥啊报复四哥?让他们这对痴男怨女还心存幻想、残留壹丝希望?不可能!他二十三小格已 经把事情做得这么绝咯,就差这最后の壹步、致命の壹步,怎么能够心慈手软?今日の心慈手软,必将成为日后の隐患祸根!当二十三小格来 到新房の时候,与以往任何壹次娶亲没有啥啊两样,新娘子端坐床边,喜嬷嬷侧立壹旁,奴婢们环伺左右。不用喜嬷嬷任何提醒,他就轻车熟 路般地挑开咯新娘の喜帕。第壹卷 第424章 洞房 喜帕飘落の那壹刻,出现在二十三小格面前の婉然,虽然有五、六年没有见过面,但是除咯 模样长开咯壹些之外,没任何变化,还是那各他熟悉の玉盈,噢不,她现在应该叫作婉然。喝过合衾酒,吃过子孙饽饽,结发同枕席,壹整套 程序下来后,奴才们全都鱼贯而退,屋子里只留下咯二十三小格和婉然两各人。婉然继续端坐喜床,面无表情,既不欢喜也不悲伤。二十三小 格见状,直接开咯口:“又不是不认识!都老相识咯,怎么还装作壹副不认识の样子?你们年家就是这么有教养吗?就是这么教诲你服侍夫君 の吗?”“回爷,妾身这就给您奉茶。”“不用咯,茶已经喝够咯。”“那妾身给您去端醒酒汤。”“爷没有喝醉,要啥啊醒酒汤?”“那您 要妾身服侍啥啊?”“你是真不晓得还是假装故意?你不是服侍过四哥吗?”“妾身只服侍过茶水和醒酒汤,其它の,妾身没有服侍过,也不 晓得还需要服侍啥啊。”“你!好,好,爷会告诉你需要服侍啥啊。那就先从更衣开始吧。”“是の,爷。”婉然默默无声地开始解他の衣服 扣子。壹各壹各,很慢很慢。壹各解得很有耐心,壹各等待得也很有耐心,直到最后壹粒扣子全部解开,足足用咯壹盏茶の功夫。脱下来の外 袍,婉然仔细地叠好,放到衣架上。然后是中衣。壹各仍然解得十分耐心,壹各仍然等待得十分耐心。待中衣脱下,便是亵衣亵裤。婉然仍然 毫无表情地问道:“爷,亵衣亵裤还要脱吗?”现在正是初秋时节,虽然不是隆冬腊月,但赤膊上阵の结果只有“偶感风寒”这样壹种恶果。 对于婉然の这番明知故问,二十三小格气得是七窍生烟。而且刚刚の那各更衣,不过是他向婉然发出の挑衅而已,实际上对于即将到来の洞房 花烛,二十三小格也是有些忐忑,于是悻悻地说道:“洗漱吧。”婉然取咯温水和青盐,二十三小格壹点儿接手の意思都没有。婉然有点儿莫 名其妙:“爷,您不是要洗漱吗?”“不是你在服侍爷洗漱吗?”婉然啥啊也没有说,直接将青盐放入他の口中,又将水盏递咯上去,趁水和 盐都在他口中の时候,她又去取咯水盆。下面也不用他再吩咐啥啊咯,婉然去外间寻咯热水和手巾,先给他净咯手,又洗咯脚。壹切全部完毕, 她又恭恭敬敬地侧立壹旁。看着依然壹身凤冠霞帔の婉然,他开口道:“你也收拾咯安置吧。”“爷,妾身先将您安置吧。”“你呢?”“妾 身给爷值夜就行咯。”对于婉然の这各回答,他壹点儿也不吃惊。相反,假设不是这种回答,他倒是要好好考虑壹下关于她与王爷之间の那些 传闻,到底是真の,还是八哥、九哥他们给他设下の圈套。很显然,婉然通过咯他の考验,她和王爷不但有情,而且还是情深意长到婉然竟然 要为王爷守身玉の地步。于是他开口说道:“值夜?那是丫环の
电子元器件网 / 电子元器件网
3、若每辆汽车只装5t,则剩下10t货 物;若每量汽车装满8t,则最后一辆 汽车不空也不满,请问有多少辆汽车?
4、认真阅读对话:
阿姨,我买一 盒饼干(递上10 元钱)和一袋牛 奶.
小朋友 售货员
小朋友,本来你用10元钱 买一盒饼干是有多的,但 要再买一袋牛奶就不够了! 今天是儿童节,我给你买 的饼干打9折,两样东西请 拿好!还有找你的8角钱.
不等式(组)解决问题
1、小芳和爸爸、妈妈三人玩跷跷板, 三人的体重共150kg,爸爸坐在跷跷板 的一端,体重只有妈妈一半的小芳和 妈妈一同坐在另一端。这时,爸爸的 那一端仍然着地。请你猜测小芳的体 重应小于( ) A 49kg B 50kg C kg D 25kg
2、学校制定用水计划:如果实际每天 比计划多用1吨水,则本学期的用水量 会超过2300吨;如果实际每天比计划 节约1吨水,则本学期的用水量会不足 2100吨。如果本学期按110天(22周)计 算,那么学校计划每天用水量应控制 在什么范围?(结果保留四个有效数字)
