典例练习

合集下载

中考典例解方程练习题大全

中考典例解方程练习题大全方程是数学中的重要内容，也是中考数学的重点之一。

掌握解方程的方法和技巧对于中考数学的顺利通过至关重要。

为了帮助同学们更好地复习和掌握解方程的知识，本文将为大家提供一份中考典例解方程练习题大全。

通过解答这些典例题，我们将掌握解方程的基本方法和技巧，并为中考打下坚实的数学基础。

一、一元一次方程1. 求下列方程的解：（1）2x + 5 = 17（2）3(x - 4) = 15（3）5 - 2x = -3解答：（1）2x + 5 = 17首先将方程两边的常数项移到一边：2x = 17 - 52x = 12然后将方程两边的系数化简：x = 12 ÷ 2x = 6（2）3(x - 4) = 15首先化简方程内的括号：3x - 12 = 15然后将方程两边的常数项移到一边：3x = 15 + 123x = 27最后化简方程两边的系数：x = 27 ÷ 3x = 9（3）5 - 2x = -3首先将方程两边的常数项移到一边：-2x = -8然后将方程两边的系数化简：x = -8 ÷ -2x = 4通过解答以上一元一次方程的例题，我们可以得出结论：一元一次方程的解是唯一的，并且可以通过逆向运算得到解。

二、一元一次方程组1. 求下列一元一次方程组的解：（1）{x + y = 7{2x - y = 1解答：通过消元法解方程组，将第二个方程的系数化简为与第一个方程系数相等的形式：2(x + y) = 2 * 7化简得：2x + 2y = 14将第一个方程和化简后的方程相加，消去变量y：(x + y) + (2x + 2y) = 7 + 14化简得：3x + 3y = 21化简方程，得：x + y = 7由此可知，原方程组的两个方程是等价的，因此它们表示同一直线上的点。

解为x + y = 7。

2. 求下列一元一次方程组的解：（2）{3x - 2y = 5{6x - 4y = 10解答：同样利用消元法解方程组，将第二个方程的系数化简为与第一个方程系数相等的形式：2(3x - 2y) = 2 * 5化简得：6x - 4y = 10将第一个方程和化简后的方程相减，消去变量x：(3x - 2y) - (6x - 4y) = 5 - 10化简得：-3x + 2y = -5由此可知，原方程组的两个方程是等价的，因此它们表示同一直线上的点。

小学数学鸡兔同笼问题典型例题

小学数学鸡兔同笼问题典型例题例1 （古典题）鸡兔同笼，头共46，足共128，鸡兔各几只？分析如果46只都是兔，一共应有4×46=184只脚，这和已知的128只脚相比多了184-128=56只脚.如果用一只鸡来置换一只兔，就要减少4-2=2（只）脚.那么，46只兔里应该换进几只鸡才能使56只脚的差数就没有了呢？显然，56÷2=28，只要用28只鸡去置换28只兔就行了.所以，鸡的只数就是28，兔的只数是46-28=18。

解：①鸡有多少只？（4×6-128）÷（4-2）=（184-128）÷2=56÷2=28（只）②免有多少只？46-28=18（只）答：鸡有28只，免有18只。

我们来总结一下这道题的解题思路：先假设它们全是兔.于是根据鸡兔的总只数就可以算出在假设下共有几只脚，把这样得到的脚数与题中给出的脚数相比较，看相差多少.每差2只脚就说明有一只鸡；将所差的脚数除以2，就可以算出共有多少只鸡.我们称这种解题方法为假设法.概括起来，解鸡兔同笼问题的基本关系式是：鸡数=（每只兔脚数×兔总数-实际脚数）÷（每只兔子脚数-每只鸡的脚数）兔数=鸡兔总数-鸡数当然，也可以先假设全是鸡。

例2 鸡与兔共有100只，鸡的脚比兔的脚多80只，问鸡与兔各多少只？分析这个例题与前面例题是有区别的，没有给出它们脚数的总和，而是给出了它们脚数的差.这又如何解答呢？假设100只全是鸡，那么脚的总数是2×100=200（只）这时兔的脚数为0，鸡脚比兔脚多200只，而实际上鸡脚比兔脚多80只.因此，鸡脚与兔脚的差数比已知多了（200-80）=120（只），这是因为把其中的兔换成了鸡.每把一只兔换成鸡，鸡的脚数将增加2只，兔的脚数减少4只.那么，鸡脚与兔脚的差数增加（2+4）=6（只），所以换成鸡的兔子有120÷6=20（只）.有鸡（100-20）=80（只）。

人教版一年级数学易错题典例讲练

人教版一年级数学易错题典例讲练（1）易错题案例：50比（）大1，比（）小1。

错误原因分析：小朋友们容易被题中的“大”、“小”所“骗过”，看见“大”就填大些的数，看见“小”就填小些的数，错误地填成50比（51）大1，比（49）小1。

解题思路点拨：解这种题时，可以将“大”、“小”后面的部分遮去，如“50比（）大1，”把“大”后面的“1”遮去，看成“50比（）大”，搞清楚是谁和谁在比，比得结果怎样，填完后，要仔细将这句话连起来再读一读。

还可以像这样先写下来：49，50，51。

50比它前面的数大1，比它后面的数小1。

解题过程：50比（49）大1，比（51）小1。

变式矫正：30比（）大1，比（）小1。

（）比80大1，（）比80小1。

易错题1：□－□=□－□=□－□=1错例：9-8=1-8=7-6=1。

方法指导：先让学生认识“=”的含义，即把□－□看成是一个整体，可以在其下面画出一条横线起到强调作用，所有这样的整体都等于1。

再让学生思考□－□=1，最后完成后可以这样来读一读深化学生对整体的认识——5-4=1，3-2=1等。

易错题2：□●○★☆■△▲（1）从左起，□是第（）个，（）是第5个。

（2）▲是第一个，○是第（）个，第6个是（）。

错例：（1）从左起，□是第（8 ）个，（★）是第5个。

（2）▲是第一个，○是第（3）个，第6个是（■）。

方法指导：（1）提醒学生根据第一句话可以确定从左向右数，先找到左面，再按照从左到右的顺序数一数，确定图形的位置和画出相应位置的图形。

（2）提醒学生根据第一句话确定从右向左数，先找到右面，再按照从左到右的顺序数一数，确定图形的位置和画出相应位置的图形。

易错题3：排队时，小华前面有4人，后面有3人，一共有（）人。

错例：排队时，小华前面有4人，后面有3人，一共有（7 ）人。

方法指导：这是非常熟悉的生活场景，可以请一位学生来做小华，4人排在前面，3人排在后面，试问“这条队伍可以分成几部分，是哪几个部分？”学生容易把小华遗忘，在学生确认可以分为小华前面的、小华后面的和小华后，不难列出4+3+1的连加算式从而得出共有9人。

《毛细现象》典例分析与同步练习1

典例分析与同步练习例1液体和固体接触时，附着层表面具有缩小的趋势是因为：A．附着层里液体分子比液体内部分子稀疏；B．附着层里液体分子相互作用表现为引力；C．附着层里液体分子相互作用表现为斥力；D．固体分子对附着层里液体分子的引力比液体分子之间的引力强．选题角度：考查微观解释浸润和不浸润现象．解析：首先从题设中看出液体对固体来说是不浸润的，而后再对附着层液体分子的作用进行研究．在出现不浸润现象时，在附着层里出现了眼表面张力相似的收缩力，即引力．并且附着层里分子的分布，虽比起表面层要密一些，但比起液内还是要稀疏，所以附着层分子受引力比液内分子受引力要大些．因此，本题答案为Ｂ、Ｄ．例2液体在毛细管中，液面上升是由于液体层分子的力和层分子间的相互作用的结果。

当与上升液柱相等时，液柱就不再上升。

答案：附着层、相斥、表面层、表面张力、重力。

例3：关于浸润与不浸润现象，下面的几种说法中正确的是（）A．水是浸润液体B．水银是不浸润液体C．同一种液体对不同的固体，可能是浸润的，也可能是不浸润的D．只有浸润液体在细管中才会产生毛细现象选题角度：考查对浸润与不浸润的理解．解析：浸润或不浸润，是指一种液体对另一种固体来说的．同一种液体对不同的固体，可能浸润，也可能不浸润，例如水对玻璃浸润，而对荷叶就不浸润．浸润液体在细管中上升，不浸润液体在细管中下降，都属于毛细现象．只有选项C 正确．例4：为什么把地面的土壤锄松，可以保存地下水分？选题角度：考查对毛细现象的理解和应用．解析：土壤里有许多毛细管，地下水分可以沿着它们上升到地面蒸发，将地面的土壤锄松，破坏了这些土壤的毛细管，这样就可以保存地下水分．习题精选一、选择题1．关于浸润与不浸润，下列说法正确的是（）A．水是浸润液体，水银不是浸润液体B．液体是否浸润固体，是由液体和相接触的固体共同决定的C．水能浸润玻璃，但不能浸润石蜡D．水银能浸润锌，但不能浸润玻璃2．在下图所示情况中，哪些是浸润现象（）3．用内径很小的玻璃管做成的水银气压计，其读数比实际气压（）A．偏大 B．偏小C．相同 D．无法判断4．下列说法正确的是（）A．水是浸润液体，水银不是浸润液体B．水是不浸润液体，水银是浸润液体C．浸润现象中，附着层里的分子比液体内部稀疏D．不浸润现象中，附着层里的分子比液体内部稀疏5．不浸润现象中，附着层里的液体分子稀疏的原因是（）A．附着层里液体分子间的斥力，比液体内部分子的斥力强B．附着层里液体分子间的引力，比液体内部分子的引力强C．固体分子对附着层中液体分子的吸引，比液体内部分子的吸引弱D．固体分子对附着层中液体分子的吸引，比液体内部分子的吸弓；强6．下列现象中属于不浸润现象的是哪些？（）A．使用钢笔难以在油纸上写出字迹B．洒在玻璃板上的水滴会迅速向四周扩展C．少量的水洒在蜡纸上，成球形水珠D．从房檐滴落的水成下大上小的水滴7．在下列的哪种情况中液体的附着层具有收缩趋势（）A．浸润固体的液体B．不浸润固体的液体C．表面张力较大的液体D．表面张力较小的液体8．下列说法中正确的是（）A．附着层分子密度和表面层分子密度一样，小于液体内部的分子密度B．若固体分子和液体分子间相互引力较弱，则附着层中分子密度小于液体内部分子密度，但大于表面层分子密度C．由于固体分子对液体分子的引力，肯定大于液体内部的分子引力，所以附着层分子密度肯定大于液体内部分子密度D．若固体分子和液体分子间引力比较大，则附着层分子密度就大于液体内部分子密度9．下列现象中与毛细现象有关的是哪些（）A．砖块吸水B．毛巾的一只角浸入水中，水会沿毛巾上升，使毛巾湿润C．洗净的衣服在太阳下被晒干D．自来水笔从墨水瓶里把墨水吸进笔中10．洗涤剂能除去衣服上的污垢，其原因是（）A．降低了水的表面张力，使水和洗涤剂容易进入被洗物质的纤维和附着的污垢粒子之间B．增加了水的表面张力，使水和洗涤剂容易进入被洗物质的纤维和附着的污垢粒子之间C．洗涤剂分子的吸引力将污垢粒子吸入水中D．洗涤剂的分子斥力将污垢粒子推离织物表面二、解答题1．砖铺的地面为什么容易返潮？2．要想把凝在衣料上面的蜡或油脂去掉，只要把两层吸墨纸分别放在这部分衣料的上面和下面，然后用熨斗来熨就可以了．为什么这样做可以去掉衣料上的蜡或油脂？参考答案：一、1．BCD 2．BC 3 ．B 4．D 5．C 6．AC 7．B 8．BD 9．AB 10．A二、１．因为土壤和砖块里都有许多细小孔道，这些细小孔道起着毛细管的作用，土壤中的水可以通过这些毛细管上升到地面上来，所以容易返潮．2．放在衣料上、下的吸墨纸内有许多细小的孔道起着毛细管的作用．当蜡或油脂受热熔化成液体后，由于毛细现象，它们就会被吸墨纸吸掉．。

高中语文2024高考复习修改病句专项练习(真题+典例)(附参考答案和相关知识讲解)

高考语文修改病句专项练习班级考号姓名总分一、真题练习1、（2023新课标全国Ⅰ卷）……有一位记者，①拥有人们只能望其项背的超强记忆力。

②他虽然能轻松地记住一长串数字，③却发现不了其中的规律；④他脑海里充满各种孤立的事实，⑤却不能归纳出一些模式将它们组织起来。

⑥这促使他不能理解隐喻等修辞手法，⑦甚至复杂一点的句子。

⑧记忆大师奥布莱恩曾多次获得世界记忆锦标赛冠军，⑨虽然他的阅读理解能力比常人低很多，⑩听课的时候也很难集中注意力。

也许正是牺牲了一部分记忆，我们才有了独一无二的归纳和抽象思维能力。

……文中第二段有三处表述不当，请指出其序号并做修改，使语言表达准确流畅，逻辑严密。

不得改变原意。

2、（2023新高考全国Ⅱ卷）文中画横线的部分有语病，请进行修改，使语言表达准确流畅。

可增删少量词语，但不得改变原意。

……对耳朵来说，过大的声音就是噪音，噪音会对耳道产生压力，压力又会撞击鼓膜听骨链传到内耳，震荡前庭淋巴液，这一系列连锁反应下来，会出现晕车一样的头晕症状。

声音过大还会损坏耳蜗中的听觉毛细胞，导致耳鸣。

如果长时间暴露在过大的声音中，会使听觉毛细胞失去敏感性，无法接收声音的信号，形成暂时或永久性听力下降。

3、（2023全国甲卷）文中画横线的语句中有一处表述不当，请标出原句序号后再做修改，并使修改后的语句与上下文的衔接流畅自然。

事有凑巧，在不同的时间和不同的地方，我听见过三位老师讲“破釜沉舟”这个成语。

第一位教师是这样讲的：“‘破釜沉舟’表示坚决的意思。

做事一定要坚决。

无论做什么，只要是正当的、应该做的事，就必须抱定只许前进而不许后退、只许胜利而不许失败的决心，只有这样才能得到成功。

如果（），工作还没开始就准备下失败的退路，那样一定不会成功。

①当然，②前进的目的必须正确。

③在这一点上，④我们不能跟古人相提并论。

……4.(2022全国乙卷)阅读下面的文字，完成下题。

视网膜动脉阻塞时，视网膜缺血时间越长，对视功能危害越大。

同时做几件事情的典例

同时做几件事情的典例
进门第一件事情就是打开了收音机，因为这个时间段交通文艺台正在联播我的长篇小说，每天半个小时的评书时间；第二件事是打开电脑去写小说；第三件事是打开电视看电视节目。

这三件事差不多同时进行，你有过和我一样的经历吗？那边是收音机的声音，这边是电视机的声音，面前是电脑？好在妻子不在家，要不，她一定会批评我浪费国家电力资源了。

昨天又接到了一个邀请，去参加他们下月第一个周六晚上的直播访谈节目，主要谈玄幻及恐怖小说的创作，我欣然同意，并说只要没有特殊事情，一定去参加。

下午两次接到铁刚的电话，都是说他长篇科幻小说创作的事情，告诉我，还有三天就要完稿了。

这个笨蛋老兄居然先写在稿纸上，然后花钱请人打字，我说我的六部长篇小说加起来有上百万字，都是一个字一个字敲打到电脑上去的，你怎么就不练习打字呢？有个朋友找我要手稿，我说自己基本上都是在电脑上写字，他很遗憾的说，假如你哪天出名了，有了你的手稿，还可以卖俩儿钱花花。

这混球居然这都想到了，看来他很有经济头脑。

又是一天。

有的时候，我总是在想，每个人都在经历着自己的每一天，办着自己的事情。

虽然目标和目的地各不相同，但是，时间都是一样的，时间是世界上最公平的尺子，绝对不会给任何人缺厘少毫的，就看你怎样去利用和分配。

追及问题的经典例题

追及问题课时一初步理解追及问题一、导入今天我们来学习行程问题当中的追及问题，它属于同向运动中的一种，下面我们就通过一个例子来给大家讲叙怎样解决追及问题。

例：兔子在狗前面150米，一步跳2米，狗更快，一步跳3米，狗追上兔子需要跳多少步？我们知道，狗跳一步要比兔子跳一步远3—2=1（米），也就是狗跳一步可以追上兔子1米，现在狗与兔子相距150米，因此，只要算出150米中有几个1米，那么就知道狗跳了多少步追上兔子的。

不难看出150÷1=150（步），这是狗跳的步数。

这里兔子在前面跳，狗在后面追，它们一开始相差150米，这150米叫做“追及距离”；兔子每步跳2米，狗每步跳3米，它们每步相差1米，这个叫“速度差”；狗追上兔子所需的步数叫做“追及步数”有时是以秒、分钟、小时计算，则叫“追及时间”，像这种包含追及距离、速度差和追及时间（追及步数）三个量的应用题，叫做追及问题。

二、新课讲授1、速度差：快车比慢车单位时间内多行的路程。

即快车每小时比慢车多行的或每分钟多行的路程。

追及时间：快车追上慢车所用的时间。

路程差：快车开始和慢车相差的路程。

2．熟悉追及问题的三个基本公式：路程差=速度差×追及时间；速度差=路程差÷追及时间；追及时间=路程差÷速度差3．解题技巧：在理解行驶时间、地点、方向等关系的基础上画出线段图，分析题意思，寻找路程差及另外两个量之间的关系，最终找到解答方法。

三、例题分析例1 甲、乙两人相距150米，甲在前，乙在后，甲每分钟走60米，乙每分钟走75米，两人同时向南出发，几分钟后乙追上甲？思路分析：这道问题是典型的追及问题，求追及时间，根据追及问题的公式：追及时间=路程差÷速度差150÷（75-60）=10（分钟）答：10分钟后乙追上甲。

例2 骑车人与行人同一条街同方向前进，行人在骑自行车人前面450米处，行人每分钟步行60米，两人同时出发，3分钟后骑自行车的人追上行人，骑自行车的人每分钟行多少米？思路分析这道题目，是同时出发的同向而行的追及问题，要求其中某个速度，就必须先求出速度差，根据公式：速度差=路程差÷追及时间：速度差：450÷3=150（米）自行车的速度：150+60=210（米）答：骑自行车的人每分钟行210米。

等腰三角形典型例题

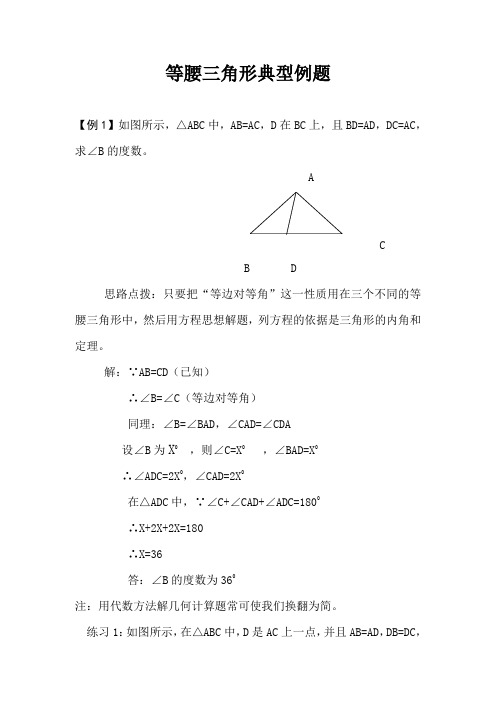
等腰三角形典型例题【例1】如图所示，△ABC中，AB=AC，D在BC上，且BD=AD，DC=AC，求∠B的度数。

ACB D思路点拨：只要把“等边对等角”这一性质用在三个不同的等腰三角形中，然后用方程思想解题，列方程的依据是三角形的内角和定理。

解：∵AB=CD（已知）∴∠B=∠C（等边对等角）同理：∠B=∠BAD，∠CAD=∠CDA设∠B为X0，则∠C=X0，∠BAD=X0∴∠ADC=2X0，∠CAD=2X0在△ADC中，∵∠C+∠CAD+∠ADC=1800∴X+2X+2X=180∴X=36答：∠B的度数为360注：用代数方法解几何计算题常可使我们换翻为简。

练习1：如图所示，在△ABC中，D是AC上一点，并且AB=AD，DB=DC，若∠C=290，则∠A=__＿练习2：如图在△ABC 中，AB=AC,点D 在AC 上，且BD=BC=AD,求△ABC 各角的度数？【例2】如图所示，在△ABC 中，AB=AC ，O 是△ABC 内一点，且OB=OC 。

求证：AO ⊥BC思路点拨：要证AO ⊥BC ，即证AO是等腰三角形底边上的高，根据三线合一定理，只要先证AO 是顶角的平分线即可。

B证明：延长AO 交BC 于DAB=AC （已知）在△ABO 和△ACO 中 OB=OC （已知） AO=AO（公共边） ∴△ABO ≌△ACO （SSS ） ∴∠BAO=∠CAO即∠BAD=∠CAD （全等三角形的对应角相等）∴AD ⊥BC ，即AO ⊥BC （等腰三角形顶角的平分线与底边上的高互相重合）评注：本题用两次全等也可达到目的.。

练习：如图所示，点D 、E 在△ABC 的边BC 上，AB=AC ，AD=AE 求证：BD=CE【例3】求证等腰三角形底边上任一点到两腰的距离之和等于一腰上C的高。

思路点拨：本题为文字题，文字题必须按下列步骤进行：（1）根据题意画出图形；（2）根据图形写出“已知”、“求证”；（3）写出证明过程。

六年级期中复习典例(+)举一反三

小学六年级期中复习典例（＋）举一反三典例1：1.一个压路机的滚筒的横截面直径是1米，它的长是1.8米。

如果滚筒每分钟转动8周，5分钟能压路多少平方米？举一反三：1.一个压路机的滚筒横截面的直径是1米，长是1.8米，滚筒转一周能压路多少平方米？如果每分钟转8周，半小时能压路多少平方米？典例2：1.一个圆柱形，侧面展开是一个边长为62.8厘米的正方形，这个圆柱形的表面积是多少平方厘米？举一反三：如果一个圆柱的侧面展开是一个边长为3.14分米的正方形，则该圆柱的高是（）分米，底面积是（）平方分米，体积是（）立方分米。

判断：一个圆柱的底面直径是3厘米，高是9.42厘米，它的侧面展开是一个正方形。

（）典例3：1.一个圆柱，它的高增加1厘米，它的侧面积就增加50.24平方厘米，这个圆柱的底面半径是多少厘米？典例4：一根长2米，底面积半径是4厘米的圆柱形木段，把它据成同样长的4根圆柱形的木段。

表面积比原来增加了多少平方厘米？举一反三：1. 把一个底面半径6分米，高1米的圆柱切成3个小圆柱，表面积增加了多少？2. 工人叔叔把一根高1米的圆柱形木料，沿与底面平行的方向锯成两段，这时表面积比原来增加了25.12平方分米，求这根料的底面半径是多少？3. 一圆柱底面直径是4米，高是6米，沿着底面直径把圆柱切成两半，求这个圆柱的表面积增加多少？典例5：1、一个圆锥的体积是90dm3，与它等底等高的圆柱体体积是（）。

A、30dm3B、90dm3C、270dm3举一反三：一个圆柱体和一个圆锥体等底等高，他们的体积相差50.24立方厘米，如果圆锥的底面半径是2厘米，求这个圆锥体的高是多少？典例6：一个圆锥，底面半径扩大到原来的2倍，高缩小到原来的一半，它的体积（）。

A、不变B、扩大到原来的2倍C、缩小到原来的一半举一反三：把一个圆柱形的橡皮泥揉成一个与它等底的圆锥体，圆锥的高将（）A扩大3倍B缩小3倍C扩大6倍D缩小6倍圆柱的底面积缩小3倍，高扩大2倍，它的体积就（）A扩大6倍B缩小6倍C缩小1.5倍典例7:10、把一个圆柱体削成一个最大的圆锥体，削去的体积是120cm3，则圆锥的体积是（）cm3。

典型例题

练习1、一列客车长200米，一列货车长280米，在平行的轨道上相向行驶，从相遇到车尾离开经过18秒，客车与货车的速度比是5:3，问两车的速度是多少？设客车与货车的速度分别为5x米/ 秒,3x米/秒。由题意得方程 18（5x+3x）=200+280
等量关系：顺风速度=无风飞行速度＋风速逆风速度=无风飞行速度-风速
顺风速度—逆风速度=2风速
超车、错车问题例1、在一段双轨道上，两列火车同向行驶，A列车车速为20米/秒，B列车车速为 24米/秒.若A列车全长180米，B列车全长 160米（1）B列车由追上A列车至完全超过A列车（即超车）所用时间是多少？（2）若两列车相向，则B列车由车头与A列车车头相遇至两列车车尾刚好离开（即错车）所用时间是多少？
由题意可得24x 20x 180 160
练习：甲，乙两列火车，长为144米和180 米，甲车比乙车每秒钟多行4米，两列火车相向而行，从相遇到错开需要9秒钟，问两车的速度各是多少？
解：设乙车的速度为 x米 / 秒，则甲车的速度为 ( x 4)米 / 秒, 由题意可得： 9x 9(x 4) 144 180
等量关系：超车问题两车路程差=两车车长的和（追及问题）错车问题两车路程和=两车车长的和（相遇问题）
分析：乙
甲
分析： 180 乙
甲
160
分析： 180 乙
甲
160
分析： 180
乙
甲
160
分析： 180
乙
甲
160
分析： 180
乙
甲
160
分析： 180
乙
甲
160
分析： 180
议一议：育红学校七年级学生步行到郊外旅行。（1）班的学生组成前队，步行速度为4千米/时，（2）班的学生组成后队，速度为6千米/时。前队出发1小时后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12千米/时。根据上面的事实提出问题并尝试去解答. 问题1：后队追上前队用了多长时间？问题2：后队追上前队时联络员行了多少路程？问题3：联络员第一次追上前队时用了多长时间？问题4：当后队追上前队时，前、后队行走了多少路程？

有理数典型例题

一只乌龟沿南北方向的河岸来回爬行，假定向北爬行的路程记为正数，向南爬行的路程记为负数，它爬行的过程记录如下（单位m）：－8，7，－3，9，－6，-4，10.
〔解答〕（1）－8+7－3+9－6-4+10=5,所以在出发点的北边；（2）|－8|+7+|－3|+|9|+|－6|+|-4|+10=47；所以乌龟在整个过程中一共爬行了47米．
练一练:
有一个农民家库存了10袋小麦，以每袋 100千克数记作负数，称重如下：+4，-3， +5，+1，+3，0，+3，+2，+1，-7，问这 10袋小麦的总重量是多少？
例2、一只乌龟沿南北方向的河岸来回爬行，假定向北爬行的路程记为正数，向南爬行的路程记为负数，它爬行的过程记录如下（单位m）：－8，7，－3，9，－6，-4，10. （1）乌龟最后距离出发点多远，在出发点的南边还是北边；（2）求乌龟在整个过程中一共爬行了多远的距离．
有理数典型例题
例1、 +7，+5，－4，+6，+4 +3，－3，－2，+8，+1 10袋小麦称重记录如上，以每袋90千克为准，超过的千克数记作正数，不足的千克数记作负数。总计是超过多少千克或不足多少千克？ 10袋小麦的总重量是多少？
解：7+5+(－4)+6+4+3+(－3)+(－2)+8+1
=〔(-4)+4〕+〔5+(-3) +(-2) 〕 +(7+6+3+8+1) =0+0+25 =25 90×10+25=925 答：总计超过25千克，总重量是925千克。

典型例题汇总

典型例题分析例、请你分别计算出下面每个长方体或正方体向上、向左的面的面积。

5厘米厘米7厘米5厘米①②分析与解：首先要弄清楚每个长方体（含正方体）向上、向左的面是哪个面，如果是长方形，长和宽分别是多少厘米；如果是正方形，边长又是多少厘米，这样即可求出所求面的面积。

图①向上的面积是7×2 = 14（平方厘米），向左的面积是2×5 = 10（平方厘米）。

图②向上、向左的面积都是5×5 = 25（平方厘米）。

例、江宁体育馆有一个长方体形状的游泳池，长50米，宽30米，深3米，现在要在游泳池的各个面上抹上一层水泥，抹水泥的面积有多少平方米？如果每平方米用水泥12千克，22吨够吗？分析与解：求水泥的面积有多少平方米，实际就是求这个长方体游泳池的表面积。

要计算前、后、左、右、下这5个面的面积之和。

再根据每平方米用水泥的千克数，算出这个游泳池共用水泥多少千克，即可知道22吨水泥够不够用。

50×30 + 50×3×2 + 30×3×2= 1500 + 300 + 180= 1980（平方米）12×1980=23760（千克）=23.76（吨）23.76 > 22 所以，22吨水泥不够用。

答：抹水泥的面积有1980平方米。

22吨水泥够不够用。

例4、厂商生产的一幅扑克牌长9厘米、宽6.5厘米、高2厘米，现在要把相同的两幅扑克牌放在一起包装（如右图），请问这个包装盒的表面积至少是多少平方厘米？分析与解：由上图可知，这个长方体包装盒的长是13厘米（6.5×2=13厘米），宽应是9厘米，高为2厘米，根据分析结果，能准确算出这个包装盒的表面积。

（13×9 + 13×2 + 9×2）×2=（117 + 26 + 18）×2= 161×2= 322（平方厘米）答：这个包装盒的表面积是322平方厘米。

典型例题(整理)

向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

实际比计划多生产百分之几？向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

计划比实际少生产百分之几？一筐苹果比一筐梨重 20％，那么一筐梨就比一筐苹果轻 20％一种电子产品，原价每台 5000 元，现在降低到 3000 元。

降价百分之几？一项工程，原计划 10 天完成，实际 8 天就完成了任务，实际每天比原计划多修百分之几？益民五金公司去年的营业总额为 400 万元。

如果按营业额的 3％缴纳营业税，去年应缴纳营业税多少万元？王叔叔买了一辆价值 16000 元的摩托车。

按规定，买摩托车要缴纳 10％的车辆购置税。

王叔叔买这辆摩托车一共要花多少钱？李明把 500 元钱按三年期整存整取存入银行，到期后应得利息多少元？根据国家税法规定，个人在银行存款所得的利息要按 5％的税率缴纳利息税。

例 1 中纳税后李明实得利息多少元？方明将 1500 元存入银行，定期二年，年利率是 4.50％。

两年后方明取款时要按 5％缴纳利息税，到期后方明实得利息多少元？一本书现价 6.4 元，比原价便宜 1.6 元。

这本书是打几折出售的？“国庆”商场促销，一套西服打八五折出售是 1020 元，这套西服原价多少元？一台液晶电视 6000 元，若打七五折出售，可降价 2000 元？一批电冰箱，原来每台售价 2000 元，现促销打九折出售，有一顾客购买时，要求再打九折，如果能够成交，售价是多少元？商店以 40 元的价钱卖出一件商品，亏了 20％。

这件商品原价多少元，亏了多少元？某商店同时卖出两件商品，每件各得 30 元，其中一件盈利 20％，另一件亏本 20％。

这个商店卖出这两件商品总体上是盈利还是亏本？具体是多少？一根绳子长 48 米，截成甲、乙两段，其中乙绳长度是甲绳的 60％。

甲、乙两绳各长多少米？体育馆内排球的个数是篮球的 75％，篮球比排球多 6 个。

初中化学经典例题及讲解(50道题)

[例 2]1 为了探究水电解的微观过程，某同学做了一些如下图所示的分子、原子的模型，若用“”表示氢原子，用“”表示氧原子，其中能保持氢气化学性质的粒子模型是（）
解析：准确理解分子的含义。答案：A 1 [例 3] 1 下列说法中，错误的是（） A. 质子数相同的粒子，可能分别是同一种元素的原子和离子，也可能分别是同一种元素的两种离子 B. 只含有一种元素的物质一定不是化合物，可能是混合物 C. 由不同元素组成的物质一定是化合物 D. 任何离子中所带的质子总数与电子总数一定不相等解析：对元素中各种粒子的相互关系应准确掌握。
应是交叉关系，但有很多化合反应不属于氧化反应；在 D 中，有许多还原反应不是
置换反应。答案：B
[例 3] 表中 1～5 组的物质分类正确的是（）
1
2
3
4
5
酸硝酸硫酸盐酸酸式硫氢硫酸
第 2 页共 42 页
酸钠
碱烧碱
碱式碳
纯碱苛性钠
消石灰
酸铜
盐大理石胆矾纯碱蓝矾石灰石
A. ①③④ B. ②③⑤ C. ④⑤ D. ①③⑤
③ 与碱作用
CO2 Ca(OH )2 CaCO3 H2O
： ②
还原性：
④氧化性： C CO2 高温 2CO
3CO Fe2O3 高温
是酸性氧化物。
2Fe 3CO2 CO CuO Cu CO2
是不成盐氧化物。
制 ① 工业制法：煅烧石灰石 ① 工业制法：碳不充
法
CaCO3 高温 CaO CO2
别和联系。对纯净物和混合物、化合反应和分解反应等，则可采取辩证的方法。有
第 3 页共 42 页
些易混淆的概念，可以运用综合练习的习题复习法。

十字相乘法典型例题

十字相乘法典型例题例1 把下列各式分解因式：(1)1522--x x ； (2)2265y xy x +-．例2 把下列各式分解因式：(1)3522--x x ； (2)3832-+x x ．例3 把下列各式分解因式：(1)91024+-x x ；(2))(2)(5)(723y x y x y x +-+-+；(3)120)8(22)8(222++++a a a a ．例4 分解因式：90)242)(32(22+-+-+x x x x ．例5 分解因式653856234++-+x x x x ．例6 分解因式655222-+-+-y x y xy x ．例7 分解因式：ca (c －a )＋bc (b －c )＋ab (a －b )．例8、已知12624+++x x x 有一个因式是42++ax x ，求a 值和这个多项式的其他因式．(1)22157x x ++ (2) 2384a a -+ (3) 2576x x +- (4) 261110y y --(5) 2252310a b ab +- (6) 222231710a b abxy x y -+(7) 22712x xy y -+(8) 42718x x +- (9) 22483m mn n ++(10) 53251520x x y xy --一、选择题1．如果))((2b x a x q px x ++=+-，那么p 等于 () A ．ab B ．a ＋b C ．－ab D ．－(a ＋b )2．如果305)(22--=+++⋅x x b x b a x ，则b 为 ()A ．5B ．－6C ．－5D ．63．多项式a x x +-32可分解为(x －5)(x －b )，则a ，b 的值分别为 ( )A ．10和－2B ．－10和2C ．10和2D ．－10和－24．不能用十字相乘法分解的是 ( ) A ．22-+x x B ．x x x 310322+- C ．242++x x D ．22865y xy x -- 5．分解结果等于(x ＋y －4)(2x ＋2y －5)的多项式是 ( ) A ．20)(13)(22++-+y x y x B ．20)(13)22(2++-+y x y xC ．20)(13)(22++++y x y xD ．20)(9)(22++-+y x y x6．将下述多项式分解后，有相同因式x －1的多项式有 ( )①672+-x x ； ②1232-+x x ； ③652-+x x ；④9542--x x ； ⑤823152+-x x ； ⑥121124-+x xA ．2个B ．3个C ．4个D ．5个二、填空题7．=-+1032x x __________．8．=--652m m (m ＋a )(m ＋b )． a ＝__________，b ＝__________．9．=--3522x x (x －3)(__________)．10．+2x ____=-22y (x －y )(__________)．11．22____)(____(_____)+=++a m na ．12．当k ＝______时，多项式k x x -+732有一个因式为(__________)．13．若x －y ＝6，3617=xy ，则代数式32232xy y x y x +-的值为__________．三、解答题14．把下列各式分解因式：(1)6724+-x x ； (2)36524--x x ；(3)422416654y y x x +-；(4)633687b b a a --； (5)234456a a a --； (6)422469374b a b a a +-．15．把下列各式分解因式：(1)2224)3(x x --； (2)9)2(22--x x ； (3)2222)332()123(++-++x x x x ；(4)60)(17)(222++-+x x x x ；(5)8)2(7)2(222-+-+x x x x ；(6)48)2(14)2(2++-+b a b a ．16．已知x ＋y ＝2，xy ＝a ＋4，2633=+y x ，求a 的值．（注：文档可能无法思考全面，请浏览后下载，供参考。

铁及其化合物典型例题(有答案)

;第三节铁及其重要化合物考纲导引考点梳理了解铁及其重要化合物的主要性质及应用 1.铁的化学性质。

2.铁的氧化物与氢氧化物。

一、铁的三角转化关系^1.关系：【典例1】将 1.12 g 铁粉加入 25 mL 2 mol/L 的氯化铁溶液中，充分反应后，其结果是() A．铁有剩余，溶液呈浅绿色，Cl－浓度基本不变B．往溶液中滴入无色 KSCN 溶液，显红色C．Fe2＋和Fe3＋的物质的量之比为5∶1 D．氧化产物与还原产物的物质的量之比为2∶5二、Fe2+和Fe3+的检验【典例2】要证明某溶液中不含Fe 3＋而可能含有Fe2＋进行如下实验操作时，最佳顺序为( )①加入足量氯水②加入足量KMnO4③加入少量KSCN溶液/A．①③ B．③② C．③① D．①②③一、选择题1．把生铁冶炼成碳素钢要解决的主要问题是（）。

A．除去生铁中的各种杂质，把生铁提纯B．适当降低生铁里的含碳量，除去大部分硫、磷等有害杂质C．用还原剂把铁的氧化物还原成铁D．加入合金元素改善生铁性能2．制印刷电路时常用氯化铁溶液作为“腐蚀液”：发生的反应为2FeCl3+Cu＝2FeCl2+CuCl2向盛有氯化铁溶液的烧杯中同时加入铁粉和铜粉，反应结束后，下列结果不可能出现的是（）。

@A.烧杯中有铜无铁B.烧杯中有铁无铜C.烧杯中铁、铜都有D.烧杯中铁、铜都无3．下列实验操作中，仪器需插入液面下的是（）。

A．分液时，分液漏斗的长颈插入下层液体里 B．用水吸收氨气的导气管C．制备Fe(OH)2，用胶头滴管将NaOH溶液滴入FeSO4溶液中D．往NaOH溶液中滴加酚酞4．根据Fe＋Cu2＋＝Fe2＋＋Cu、2FeCl3＋Cu＝2FeCl2＋CuCl2两个反应，判断Fe3＋、Fe2＋、Cu2＋的氧化性顺序为（）。

A．Cu2＋＞Fe2＋＞Fe3＋ B．Fe3＋＞Fe2＋＞Cu2＋C．Fe3＋＞Cu2＋＞Fe2＋ D．Fe2＋＞Fe3＋＞Cu2＋|5．将8.4 g铁粉和3.2 g硫粉均匀混合密闭加热至红热，冷却后加入足量的盐酸，在标准状况下收集到的气体体积是（）。

电功率-典型例题

电功率练习题例1：指出电流通过下列用电器时，分别将电能转化为何种形式的能。

电扇______；普通电灯______；电烙铁______；洗衣机______。

例2：关于电功和电功率的说法，正确的是A.电流做功越多，功率越大B.电流做同样多的功，用的时间越长，功率越大C.电流做功时间越短，功率越大D.相同时间内，做功越多，功率越大例3：判断灯亮度的主要依据是A.加在电灯两端的电压B.通过电灯的电流C.电灯的额定功率D.电灯的实际功率例4：有两个电阻R1和R2，R1=9 Ω，R2=3 Ω，采用下列四种连接方式分别接到电压为12 V的电源上，通电10 min，电流做功最少的连接方式是A.R1和R2并联B.R1和R2串联C.只接入R1D.只接入R2例5：某人家装有“220 V 40 W”的电灯3盏，100 W的彩电一台，每天用电4 h，每天消耗的电能为_____kW·h，合_____J ；若他家月初电能表的示数为，那么下月初（30天）电能表的示数为。

例6：如图20—18所示的电路中，电源电压恒定为12 V，R2=40 Ω，开关S闭合后，电流表示数为0.8 A，求：1 min内电阻R1消耗的电能是多少？R1的电功率是多少?例7：如图20—17是一只家用电能表的表盘，则（1）该电能表所在电路中同时使用的用电器总功率不得超过多少W？（2）若该电路中只有同一种规格的两个灯泡在工作，5 min内，电能表的转盘转动25 r，则所用灯泡的电功率是多大？例8：一个额定电压为2.5 V的小灯泡，正常发光时通过灯丝的电流为0.2 A，求:（1）小灯泡的额定功率；（2）小灯泡发光时的灯丝电阻；（3）通电1 min小灯泡消耗多少电能？例9：某学校电能表允许通过的最大电流是25 A，学校里已经装了40 W的电灯50盏，60 W的电灯20盏，想要再装些电灯，至少可以再装多少盏40 W的电灯？例10：一个同学家电能表的示数是，现在他家里有40 W的电灯4盏，平均每天用电2.5 h，用了30天，共用了几度电？此时电表的示数为多少？例11：每个家庭都需要照明灯泡，目前市场上既有白炽灯，又有电子节能灯，究竟选择哪一种好呢？某中学“STS”课外活动小组的同学就这个问题进行了调查，了解到在正常工作时，25 W的白炽灯与5 W的电子节能灯、45 W的白炽灯与9 W的电子节能灯、60 W的白炽灯与11 W的电子节能灯的发光效果相当.他们选择其中的一组进行研究，收集了有关数据如下表：名称额定电压（V）额定功率（W）寿命（h）每只售价（元）每度电费(元)白炽灯220 60 1000 1.5 0.4电子节能灯220 11 5000 30 0.4 根据以上数据，通过计算，说明你买照明灯时将做怎样的选择（写出依据的物理原理并有必要的文字说明）。

《同位角、内错角、同旁内角》重难点专项练习【四大题型】(解析版)

5.1.3《同位角、内错角、同旁内角》重难点题型专项练习考查题型一同位角典例1．（2022·广西贺州·统考三模）如图，直线a 、b 被直线c 所截，∠1的同位角是（）A ．∠2B ．∠3C ．∠4D ．∠5【答案】A【分析】根据同位角的定义逐个判断即可．【详解】解：A 、∠2与∠1是同位角，故本选项符合题意；B 、∠3与∠1不是同位角，故本选项不符合题意；C 、∠4与∠1不是同位角，故本选项不符合题意；D 、∠5与∠1不是同位角，故本选项不符合题意；故选：A ．【点睛】本题考查了同位角，内错角，同旁内角等知识点，能熟记同位角的定义是解此题的关键．变式1-1．（2022·广西柳州·统考一模）如图，与1∠是同位角的是（）A ．2∠B ．3∠C ．4∠D ．5∠【答案】C【分析】根据同位角的定义：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角即可求解．【详解】解：观察图形可知，与∠1是同位角的是∠4．故选：C ．【点睛】本题考查了同位角、内错角、同旁内角，三线八角中的某两个角是不是同位角、内错角或同旁内角，完全由那两个角在图形中的相对位置决定．在复杂的图形中判别三类角时，应从角的两边入手，具有上述关系的角必有两边在同一直线上，此直线即为截线，而另外不在同一直线上的两边，它们所在的直线即为被截的线．同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．变式1-2．（2022·广西贺州·统考中考真题）如图，直线a ，b 被直线c 所截，下列各组角是同位角的是（）A ．1∠与2∠B ．1∠与3∠C ．2∠与3∠D ．3∠与4∠【答案】B【分析】两条线a 、b 被第三条直线c 所截，在截线的同旁，被截两直线的同一方，把这种位置关系的角称为同位角，据此作答即可．【详解】解：∠1与∠2是对顶角，选项A 不符合题意；∠1与∠3是同位角，选项B 符合题意；∠2与∠3是内错角，选项C 不符合题意；∠3与∠4是邻补角，选项D 不符合题意；故选：B ．【点睛】此题考查了同位角、内错角、同旁内角，熟记同位角、内错角、同旁内角的定义是解题的关键．变式1-3．（2022秋·浙江杭州·七年级校考期中）如图，∠1和∠2是同位角的是（）．A ．B ．C ．D ．【答案】C 【分析】根据同位角的定义，逐一判断选项，即可．【详解】解：A 、∠1和∠2不是同位角，故选项A 不合题意；B 、 ∠1和∠2 不是同位角，故选项B 不合题意；C 、 ∠1和∠2 是同位角，故选项C 符合题意；D 、∠1和∠2 不是同位角，故选项D 不合题意．故答案为：C ．【点睛】本题主要考查同位角的定义，掌握“两条直角被第三条直线所截，在两条直线的同侧，在第三条直线的同旁的两个角，叫做同位角”，是解题的关键．考查题型二内错角典例2．（2022秋·江苏淮安·七年级校考阶段练习）下列四个图形中，1∠和2∠是内错角的是（） A ． B ．C ．D ．【答案】B【分析】根据内错角的概念：处于两条被截直线之间，截线的两侧，再逐一判断即可．【详解】解：A 、∠1与∠2不是内错角，选项不符合题意；B 、∠1与∠2是内错角，选项符合题意；C 、∠1与∠2不是内错角，选项不符合题意；D 、∠1和∠2不是内错角，选项不符合题意；故选：B ．【点睛】本题考查了内错角，关键是根据内错角的概念解答．注意：内错角的边构成“Z”形．变式2-1．（2022秋·湖北武汉·七年级校考阶段练习）如图，下列各组角中，互为内错角的是（）A ．1∠与3∠B ．2∠与5∠C ．3∠与5∠D ．4∠与5∠【答案】C【分析】根据内错角的定义结合具体的图形进行判断即可．【详解】解：A. 1∠与3∠是直线a ，直线b 被直线c 所截的同位角；B. 2∠与5∠不具备特殊位置关系；C.3∠和5∠是直线a ，直线b 被直线c 所截的内错角；∠是直线a，直线b被直线c所截的同旁内角；D. 4∠和5故选：C．【点睛】本题考查内错角，理解内错角的定义是正确判断的前提．两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．变式2-2．（2022秋·新疆乌鲁木齐·七年级乌鲁木齐市第四十一中学校考期末）如图中1∠是内错角是∠与2（）A．①②B．②③C．③④D．②④【答案】D【分析】根据内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角进行分析即可．【详解】解：由内错角的定义可知，图②和图④中，1∠是内错角，∠和2故选：D．【点睛】本题考查了内错角、同位角、同旁内角的概念，同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．变式2-3．（2022秋·安徽安庆·七年级校考阶段练习）如图，直线a，b被直线c所截，则∠1与∠2是（）A．内错角B．同位角C．对顶角D．邻补角【答案】A【分析】根据同位角、内错角、同旁内角的定义逐个判断即可．【详解】解：直线a，b被直线c所截，则∠1与∠2是内错角．故选：A ．【点睛】本题考查了同位角、内错角、同旁内角的定义，能理解同位角、内错角、同旁内角的定义是解此题的关键，注意：数形结合思想的运用．考查题型三同旁内角典例3．（2022秋·浙江宁波·七年级校考期中）如图，直线AB 、CD 被直线EF 所截，则∠1的同旁内角是（）A ．∠2B ．∠3C ．4∠D ．5∠【答案】B【分析】根据同旁内角的定义，结合已给图形分析，即可得到答案．【详解】解：由同旁内角的定义知，∠1和∠3在直线AB 和CD 之间，且在直线EF 的同一侧，所以，∠1的同旁内角是∠3．故选：B【点睛】本题考查同旁内角的定义，解题的关键是结合图形，牢记定义内容去分析判断．变式3-1．（2022秋·湖北鄂州·七年级统考期中）如图，与2∠互为同旁内角的角是（）A ．1∠与5∠B ．8∠与9∠C ．3∠与12∠D ．7∠与10∠【答案】B【分析】根据两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角进行解答即可．【详解】解：根据题意得： 9∠与2∠互为同旁内角，8∠与2∠互为同旁内角．故选：B【点睛】本题考查了同旁内角的定义．注意在截线的同旁找同旁内角．要结合图形，熟记同旁内角的位置特点．变式3-2．（2022秋·浙江温州·七年级统考期中）如图，1∠和2∠是（）A ．同位角B ．内错角C ．对顶角D ．同旁内角【答案】D【分析】利用同旁内角的定义解答．两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角．【详解】解：∠1和∠2是同旁内角．故选：D ．【点睛】本题主要考查了同旁内角，解题时要注意：同位角的边构成“F”形，内错角的边构成“Z”形，同旁内角的边构成“U”形．变式3-3．（2022秋·湖北孝感·七年级校联考阶段练习）如图，与∠3是同旁内角的是（）A ．∠2B ．∠3C ．∠4D ．∠5【答案】C【分析】根据同位角、内错角、同旁内角的定义逐个判断即可．【详解】解：A ．∠2与∠3是内错角，不是同旁内角，故本选项不符合题意；B ．∠3与∠3是同一个角，不是同旁内角，故本选项不符合题意；C ．∠4与∠3是同旁内角，故本选项符合题意；D ．∠5与∠3是同位角，不是同旁内角，故本选项不符合题意；故选：C ．【点睛】本题考查了同位角、内错角、同旁内角的定义等知识点，能正确识图是解此题的关键．考查题型四同位角、内错角、同旁内角的综合判断典例4．（2022秋·辽宁沈阳·七年级沈阳市南昌初级中学（沈阳市第二十三中学）阶段练习）如图，下列说法中错误的是（）A ．3∠和5∠是同位角B ．4∠和5∠是同旁内角C ．2∠和4∠是对顶角D ．2∠和5∠是内错角【答案】D【分析】根据同位角，同旁内角，对顶角以及内错角的定义进行判断．【详解】解：A ．3∠和5∠是同位角，正确，不符合题意；B ．4∠和5∠是同旁内角，正确，不符合题意；C ．2∠和4∠是对顶角，正确，不符合题意；D ．2∠和5∠不是内错角，错误，符合题意．故选D ．【点睛】考查了同位角、内错角、同旁内角以及对顶角．解答此类题确定三线八角是关键，可直接从截线入手．变式4-1．（2022春·河北邯郸·八年级校考开学考试）如图，下列判断正确的是（）A ．3∠与6∠是同旁内角B ．2∠与4∠是同位角C ．1∠与6∠是对顶角D ．5∠与3∠是内错角【答案】A【分析】根据同位角、同旁内角、内错角和对顶角的概念解答即可．【详解】解：A 、3∠与6∠是同旁内角，故本选项符合题意；B 、2∠与4∠不是同位角，故本选项不合题意；C 、1∠与6∠不是对顶角，故本选项不合题意；D 、5∠与3∠不是内错角，故本选项不合题意；故选：A ．【点睛】本题考查了同位角、内错角、同旁内角的定义，两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线(截线)的同旁，则这样一对角叫做同位角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线(截线)的同旁，则这样一对角叫做同旁内角；两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线(截线)的两旁，则这样一对角叫做内错角．变式4-2．（2022秋·浙江杭州·七年级校考期中）如图所示，下列说法中，错误的是（）A ．∠3与∠B 是同旁内角 B ．∠A 与∠1是同位角C ．∠2与∠3是内错角D ．∠1与∠B 是同位角【答案】D【分析】根据两线被第三线所截，同旁内角，内错角和同位角的定义进行判断即可．【详解】解：A 、∠3与∠B 是同旁内角，选项正确，不符合题意；B 、∠A 与∠1是同位角，选项正确，不符合题意；C 、∠2与∠3是内错角，选项正确，不符合题意；D 、∠1与∠B 不是同位角，选项错误，符合题意；故选D ．【点睛】本题考查三线八角，在找角的时候，首先要确定截线，然后根据它们之间的位置关系进行确定．变式4-3．（2022秋·陕西渭南·七年级统考阶段练习）如图，下列说法错误的是（）A．∠1与∠2是同旁内角B．∠3与∠5是同位角C．∠1与∠4是内错角D．∠5与∠6是内错角【答案】C【分析】根据同位角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的同侧，并且在第三条直线（截线）的同旁，则这样一对角叫做同位角．内错角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的两旁，则这样一对角叫做内错角．同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角分别进行分析可得答案．【详解】解：A、∠1与∠2是同旁内角，原题说法正确，不符合题意；B、∠3与∠5是同位角，原题说法正确，不符合题意；C、∠1与∠4不是内错角，原题说法错误，符合题意；D、∠5与∠6是内错角，原题说法正确，不符合题意；故选：C．【点睛】此题主要考查了三线八角，关键是掌握同位角的边构成“F“形，内错角的边构成“Z“形，同旁内角的边构成“U”形．。