高中数学 2.3排序问题教学设计 北师大版必修3
高中数学新北师大版精品教案《北师大版高中数学选修2-3 排列》5

《生活中的排列问题》教学设计南昌二十三中郭佩一、教材分析1、教材的地位和作用:本节课是高中数学北师大版《选修2-3》第一章第二节《排列》的第二课时,是高二下学期的教学内容。
本节是在学习了排列及排列数的基础上进行的,处于一个承上启下的地位,为后面学习概率奠定基础。
本部分内容日常生活密切相关,易激发学生的学习趣及求知欲,同时这部分内容是高考必考的内容2、教学目标:基础知识目标:理解排列和排列数的意义,利用排列思想解决实际问题。
能力训练目标:(1)掌握排列问题中的捆绑法,插空法,特殊优先法,定序法。
(2)通过启发、引导学生自主探究,培养学生的分类讨论能力、抽象能力和逻辑思维能力。
情感目标:设置问题情境让学生认识到课堂知识与实际生活的联系,感受数学教学重点和难点:教学重点:解决排列问题的策略和方法。
教学难点:利用分类讨论思想解决排列问题。
4、学情分析:对于高二的学生,知识经验已较为丰富,他们已具备了一定的抽象思维能力和演绎推理能力,根据这类学生的心理发展特点,我在授课时注重引导、启发、研究和探讨,从而促进思维能力的进一步发展。
二、教学方法1、说教法:本节课我采用启发式、讨论式以及讲练结合的教学方法2、说学法:引导学生主动参与、亲身实践、独立思考、合作探究。
三、教学流程教学环节一:复习引入1、两个计数原理2、排列的定义?排列数的定义?排列数的两个公式是什么?设计意图:复习排列与排列数的概念,及排列数的运算公式,为后面解决问题打好基础。
教学环节二:问题探究问题一、排队问题播放学生红色经典诵读排练视频引入问题一:例1、我班五名男生,三名女生参加朗诵表演例1、我班五名男生,三名女生参加五四青年节的红色经典诵读表演(1)若八名同学站一排,有多少种不同的排法?(2)女生全排一起,有多少种不同的排法?(3)女生互不相邻,有多少种不同的排法?(4)女生不站两端,有多少种不同的排法?(5)甲不能站排头,乙不能站排尾(6)甲、乙、丙按从左到右的顺序排列(不一定相邻),有多少种不同的排法?练一练:(1)需两名同学站在前一排领诵,其它同学站后一排有多少种不同的排法?(2)甲乙两名同学需站在前一排领诵,其它同学站后一排,有多少种不同的排法?(3)将8名同学排成两排,每排4人,有多少种不同排法?(4)甲、乙两人相邻,但都不与丙相邻,有多少种不同的排法(5)演出结束,从8名同学中选出5名同学上台领奖,其中甲乙不能站在正中间,有多少种不同的排法?设计意图:从学生身边有趣的实例出发,激发学生的学习兴趣,让学生感受到生活中的数学。
高中数学(北师大版)选修2-3教案:第1章 拓展资料:排列问题既要会“排”又要会“列”

排列问题既要会“排”又要会“列”排列应用问题的应用情景多样,思维灵活,是高中数学的一个难点,也是高考的必考内容。
对于排列问题,我们既要会“排”又要会“列”,下面举例说明。
一、排列问题要会“排”1、要会排课例1、某班上午要上语文、数学、体育和外语4门课,又体育老师因故不能排第一节和第四节,则不同的排课方案种数为多少?分析:以特殊元素“体育老师”为解题突破口。
解:由题可知体育老师共有2种不同的排法,其它老师不受影响,故共有12233 A 种不同的排课方案种数。
点评:排课是最接近同学们实际情况的排列应用题。
2、要会排队例2、4个男同学,3个女同学站成一排,其中甲、乙两同学之间必须恰有3人,有多少种不同的排法?分析:根据题意,可采用“捆邦法”求解。
解:甲、乙2人先排好,有22A 种排法,再从余下的5人中选3人排在甲、乙2人中间,有35A 种排法,这时把已排好的5人视为一个整体,与最后剩下的2人再排,又有33A 种,故共有22A 35A 33A =720种不同排法。
点评:捆绑法”主要解决“相邻”排列问题。
其操作过程是将相邻的若干元素“捆绑”为一个“大元素”,与其它元素全排列,此时切莫遗忘“大元素”内部进行排列。
3、要会排数例3、从0到9十个数字中,可以组成多少个没有重复数字的四位数?分析:根据数的实际情况,优先考虑特殊位置“千位”。
解:千位不能放“0”,故千位放数字共有9种,其它3个位置放39A 种。
故共有939A =4536个。
点评:优先法适用于存在限制条件的元素或位置问题。
即先排特殊元素或特殊位置,再排其它非受限元素或位置。
4、要会排节目例4、某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目。
如果将这两个节目插入原节目单中,且两个新节目不相邻,那么不同插法的种数为( )A 、6B 、12C 、15D 、30分析:根据题意,可采用“插空法”求解。
解:原来的5个节目中间和两端共产生6个空位。
排列-北师大版选修2-3教案

排列-北师大版选修2-3教案一、知识点概述排列是离散数学中非常重要的知识点,也是高中数学中必修的内容。
在学习排列之前,需要了解全排列与部分排列的概念。
全排列是将一组不同的事物进行排列,能够得到的所有不同的排列方式,称为全排列。
全排列的个数可以用数学公式n!来表示,其中n为选取的事物总数。
而部分排列是由一组不同的事物中选取部分事物进行排列,得到的所有不同的排列方式,称为部分排列。
如果在一组不同的事物中,选取m个进行排列,可以得到的所有不同的排列方式,称为n个不同事物的m元排列,计数公式为A_n^m=n!/(n-m)!。
在学习排列之后,还需要掌握排列的一些基本性质,如可重复排列、循环排列等。
二、教学目标本节课的教学目标有:•掌握全排列、部分排列的概念和计数公式;•理解排列的基本性质;•掌握通过公式计算排列的方法;•能够应用排列解决实际问题。
三、教学重点本节课的教学重点有:•全排列、部分排列的概念和计数公式;•可重复排列、循环排列等排列的基本性质;•通过公式计算排列的方法。
本节课的教学难点有:•如何应用排列解决实际问题;•如何确定计数公式的适用范围;•如何理解排列的基本性质。
五、教学过程1. 导入通过一个实例引入排列的概念:有三个不同的球,分别标有1、2、3号。
现在从中任选两个球进行排列,问共有多少种不同的排列方式?2. 呈现将球的选择情况用表格呈现出来,通过图示的方式解释全排列和部分排列的概念,并引出它们的计数公式。
3. 讨论引导学生探讨全排列与部分排列中的重复问题,并提出可重复排列、循环排列等基本性质。
4. 讲解讲解排列的计算公式,并通过例题讲解如何应用公式计算排列数。
5. 课堂练习通过课堂练习,巩固学生对排列知识的掌握程度。
6. 实践应用结合生活实际,引导学生运用排列解决实际问题,并进行思考和讨论。
本节课的教学评价方式主要包括:•课堂练习,检测学生对排列知识掌握情况;•实践应用,考查学生的思考能力和解决实际问题的能力;•反馈评价,在课后进行答疑和评估,及时纠正学生的错误认识和不足之处。
高中数学必修3北师大版2.1.2排序问题与算法的多样性教案
法
自主学习
复习回顾:
1算法的概念:
2算法的特征:
新知探究:
1什么叫排序?
2什么叫有序列?
3写出有序列直接插入排序的算法:
4写出折半插入排序的算法:
5如何对无序的数据列排序?
精讲互动
例1对有序列{13,27,51,57,82},现在要将数据52插入到数据列中.请设计算法确定数据52在序列中的位置,并用自然语言表述算法.
13
27
51
57
82
基本思路:
算法流程图:
例2对无序的数列{49,38,65,97,76,13,27,49}排序.
例3用折半插入排序法将60插入有序列{20,25,56,67,90},构成一个新的有序列.
达标训练
课本练习
作业
布置
习题2-1 A组8、9
学习小结/教学
反思
2.1.2排序问题与算法的多样性
授课
时间
第周星期第节
课型
新授课
主备课人
学习
目标
1.通过对具体实例的解决过程与步骤的分析,了解排序问题;
2.通过经历算法设计的全过程,体会构造性解决问题的方法.
重点难点
重点:有序列的直接插入排序;算法设计和算法流程图.
难点:通过分析具体问题,抽象出算法设计的过程.学习 Nhomakorabea过程
顺序结构与选择结构 北师大版高中数学必修3教案

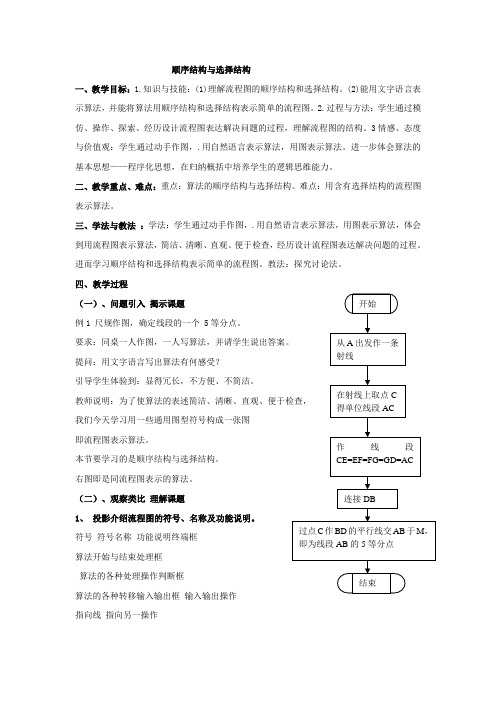
所以一个完整的流程图的首末两端必须是起止框。
(2表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置。
图1-1中有三个输入、输出框。
第一个出现在开始后的第一步,它的作用是输入未知数的系数a11,a12,a21,a22和常数项b1,b2,通过这一步,就可以把给定的数值写在输入框内,它实际上是把未知数的系数和常数项的值通知给了计算机,另外两个是输出框,它们分别位于由判断分出的两个分支中,它们表示最后给出的运算结果,左边分支中的输出分框负责输出D≠0时未知数x1,x2的值,右边分支中的输出框负责输出D=0时的结果,即输出无法求解信息。
(3它是采用来赋值、执行计算语句、传送运算结果的图形符号。
图1-1中出现了两个处理框。
第一个处理框的作用是计算D=a11a22-a21a12的值,第二个处理框的作用是计算x1=(b1a22-b2a12)/D,x2=(b2a11-b1a21)/D的值。
(4)判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y”与“N”)两个分支,在图1-1中,通过判断框对D的值进行判断,若判断框中的式子是D=0,则说明D=0时由标有“是”的分支处理数据;若D≠0,则由标有“否”的分支处理数据。
例如,我们要打印x的绝对值,可以设计如下框图。
打印x -打印x从图中可以看到由判断框分出两个分支,构成一个选择性结构,其中选择的标准是“x ≥0”,若符合这个条件,则按照“是”分支继续往下执行;若不符合这个条件,则按照“否”分支继续往下执行,这样的话,打印出的结果总是x 的绝对值。
在学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:(1)使用标准的图形符号。
(2)框图一般按从上到下、从左到右的方向画。
(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点。
高中数学必修3北师大版 顺序结构与选择结构 教案
所以一个完整的流程图的首末两端必须是起止框。
(2表示数据的输入或结果的输出,它可用在算法中的任何需要输入、输出的位置。
图1-1中有三个输入、输出框。
第一个出现在开始后的第一步,它的作用是输入未知数的系数a11,a12,a21,a22和常数项b1,b2,通过这一步,就可以把给定的数值写在输入框内,它实际上是把未知数的系数和常数项的值通知给了计算机,另外两个是输出框,它们分别位于由判断分出的两个分支中,它们表示最后给出的运算结果,左边分支中的输出分框负责输出D ≠0时未知数x1,x2的值,右边分支中的输出框负责输出D=0时的结果,即输出无法求解信息。
(3它是采用来赋值、执行计算语句、传送运算结果的图形符号。
图1-1中出现了两个处理框。
第一个处理框的作用是计算D=a11a22-a21a12的值,第二个处理框的作用是计算x1=(b1a22-b2a12)/D,x2=(b2a11-b1a21)/D 的值。
(4)判断框一般有一个入口和两个出口,有时也有多个出口,它是惟一的具有两个或两个以上出口的符号,在只有两个出口的情形中,通常都分成“是”与“否”(也可用“Y ”与“N ”)两个分支,在图1-1中,通过判断框对D 的值进行判断,若判断框中的式子是D=0,则说明D=0时由标有“是”的分支处理数据;若D≠0,则由标有“否”的分支处理数据。
例如,我们要打印x的绝对值,可以设计如下框图。
从图中可以看到由判断框分出两个分支,构成一个选择性结构,其中选择的标准是“x ≥0”,若符合这个条件,则按照“是”分支继续往下执行;若不符合这个条件,则按照“否”分支继续往下执行,这样的话,打印出的结果总是x 的绝对值。
在学习这部分知识的时候,要掌握各个图形的形状、作用及使用规则,画程序框图的规则如下:(1)使用标准的图形符号。
(2)框图一般按从上到下、从左到右的方向画。
(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点。
判断框具有超过一个退出点的惟一符号。
北师大版高中数学必修三课件:2.3 排序问题(共19张PPT)

4
4 2
4 2 1
4 2 3 4 3 1 4 3 2
3 4
4 3
一. 元素: 我们把被取的对象叫做元素。 二. 排列:一般的,从n个不同的元素中,任 取m(m n)个元素,按照一定的顺序排成一 列,叫做从n个不同元素中取出m个元素的一 个排列。
想一想?
如果有两个排列相同,满足什么样的条件?
从排列定义可知:如果两个排列相同,不仅 这两个排列的元素必须完全相同,而且排列 的顺序也必须完全相同。
如果所取的元素不完全相同,他们就是两个 不同的排列;即使所取得元素完全相同,但 排列的顺序不同,也不是相同的排列。
例1:已知 a,b,c,d四个元素,写出每次取出3个元素的 所有排列。
a b c d b c a b d a b d a d b b a c a c d b d c c a d a d b c a c b b c d a d c
用树图表示如下: 起点站 北京 终点站
上海
广州
飞机票
北---上 北---广 上---北
上海
北京
广州
上---广
广---北
广州
北京
上海
广---上
由1、2、3、4这4个数字,可以组成多少 个没有重复数字的3位数?
分析: 要确定一个3位数,分三步完成,第一步确 定百位,有4种方法,第二步确定十位,有3种方法 ,同理,第三步确定个位,有2种方法,根据乘法原 理,共有4 × 3 × 2 = 24种不同的方法。
什么是加法原理?
做一件事情,完成它可以有 n 类办法,在第 一类办法中有 m1种不同的方法,在第二类办 法中有m2种不同的方法,……,在第n类办法 中有 mn种不同的方法。那么完成这件事共有 N= m1 m2 m3 mn 种不同的方法。
高中数学 2.3排序问题教学设计 北师大版必修3

第四课时 2.3 排序问题教学重点:有序列插入排序方法和折半插入排序方法的原理与过程。
教学难点:用算法语句描述排序方法。
教学目标:1. 理解有序列插入排序方法和折半插入排序,并会设计算法2.通过实例,发展用有序列插入排序方法和折半插入排序解决问题的能力。
教学过程:为了便于查询,常常需要根据要求将被查寻的对象按照一定的顺序排列,通常称为排序。
例如:新来的同学小黄身高175c m,在班上是中等身高,因为做操的需要,体育老师要将他插到队中,你认为老师应该怎样做?象这样在已经按一定顺序排好的系列(有序列)中插入一个数据,我们就叫它有序列插入排序。
有序列直接插入排序法有序列直接插入排序:用有序列直接插入排序算法完成无序列排序问题,其基本思想非常简单,即反复使用有序列直接插入排序算法,使有序列的长度不断增加,一直到完成整个无序列的有序排列为止.一般地,对于一个有序列:a1≤a2≤a3≤…≤an,欲将新数据A插入到有序列中,形成新的有序列,其做法是:将数据A与原有序列中的数据从右到左依次进行比较,直到发现某一数据ai,使得ai≤A,把A插入到ai的右边;如果数据A小于原有序列中的所有数据,则将A插入到原序列的最左边.上面的排序算法通常称为有序列直接插入排序的算法.我们在一个已经排好顺序的一系列数中插入一个数据,成为一个新的系列,且仍按原来的规则排序。
例如:要将8插入到{1,3,5,7,9,11,13}中,我们怎样考虑?首先确定8在原系列中的位置,使8小于或等于原系列中右边的数据,大于或等于左边的数据,将这个位置空出来,将数据8插进去1 3 5 7 8 9 11 13例题分析:例1已知有一组系列{13,27,38,39,43,47,48,51,57,66,74},现要将数据52插入到数据中。
数据序列号 1 2 3 4 5 6 7 8 9 10 11 原序列13 27 38 39 43 47 48 51 57 66 74(1)请设计算法,确定52在新数据中的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四课时 2.3 排序问题
教学重点:
有序列插入排序方法和折半插入排序方法的原理与过程。
教学难点:
用算法语句描述排序方法。
教学目标:
1. 理解有序列插入排序方法和折半插入排序,并会设计算法
2.通过实例,发展用有序列插入排序方法和折半插入排序解决问题的能力。
教学过程:
为了便于查询,常常需要根据要求将被查寻的对象按照一定的顺序排列,通常称为排序。
例如:新来的同学小黄身高175c m,在班上是中等身高,因为做操的需要,体育老师要将他插到队中,你认为老师应该怎样做?象这样在已经按一定顺序排好的系列(有序列)中插入一个数据,我们就叫它有序列插入排序。
有序列直接插入排序法
有序列直接插入排序:用有序列直接插入排序算法完成无序列排序问题,其基本思想非常简单,即反复使用有序列直接插入排序算法,使有序列的长度不断增加,一直到完成整个无序列的有序排列为止.
一般地,对于一个有序列:a1≤a2≤a3≤…≤an,欲将新数据A插入到有序列中,形成新的有序列,其做法是:将数据A与原有序列中的数据从右到左依次进行比较,直到发现某一数据ai,使得ai≤A,把A插入到ai的右边;如果数据A小于原有序列中的所有数据,则将A插入到原序列的最左边.上面的排序算法通常称为有序列直接插入排序的算法.我们在一个已经排好顺序的一系列数中插入一个数据,成为一个新的系列,且仍按原来的规则排序。
例如:要将8插入到{1,3,5,7,9,11,13}中,我们怎样考虑?
首先确定8在原系列中的位置,使8小于或等于原系列中右边的数据,大于或等于左边的数据,将这个位置空出来,将数据8插进去
例题分析:
例1已知有一组系列{13,27,38,39,43,47,48,51,57,66,74},现要将数据52插入到数据中。
9
(1)请设计算法,确定52在新数据中的位置。
(2)在确定52的序列号后,请将52插入系列中
(3)请用流程图描述这个插入过程的算法
方法1.手工插入:
①确定52的序号:9;
②把原序列中9~11号的数据依次向右挪一位,空出9号位置来,并插入52,得到一个新序列。
方法2.
即从右边最后一位开始,与52比较,若比52大就右挪,否则插入52.
有序列插入排序算法的另一种方法
折半插入排序法
问题思考:对于一组无序的数据列{49,38,65,97,76,13,27,49}如何完成排序工作呢?
折半插入排序
如果R[1..i-1] 是一个按关键字有序的有序序列,则可以利用折半查找实现“在
R[1..i-1]中查找R[i]的插入位置”,如此实现的插入排序为折半插入排序。
折半插入排序性能分析
1)折半插入排序所需附加存储空间和直接插入排序相同,从时间上来看,折半插入排序减少了关键字的比较次数,但是移动次数不变。
2)折半插入排序的时间复杂度为o(n2)。
3)折半插入排序是一个稳定的排序方法。
例2 中国乒乓球女队原有11名队员,她们的身高由小到大分别为158,159,160,162, 163,165,166,170, 171,172,175(单位:cm).现为备战某项比赛,加入一名优秀队员,这名队员身高167 cm.请设计用折半插入排序法找出该队员在序列中的位置,并用自然语言描述算法。
解析:由题目可获取以下主要信息:
①11名队员的身高;
②加入一名身高167 cm的队员;
③用折半插入排序法找出新加入队员在序列中的位置.
解答本题可先确定数据个数11.找到“中间位置”的数据a6=165,与167进行比较,然后把剩下数据“中间位置”的数据依次与167比较,直到得到167的位置。
解:要将167插入有序列:{158,159,160,162,163,165,166,170,171,172,175},共有11个数据。
列表为:
首先选择有序列的“中间位置”的数据a6=165,将167与a6比较,显然167>165,所以167应排在a6的右边。
再取余下数据列{a7,a8,a9,a10,a11}的“中间位置”的数据a9=171,显然167<171,所以167在a9的左边,再取余下数据列{a7,a8}的“中间位置”的数据a7=166,显然167>166,所以167应在a7、的右边.又167<a8,所以167应插在a7与a8之间。
评析:用折半插入排序法向有序列中插入新数据时,首先确定原有序列中数据的个数
是偶数2n还是奇数2n+1.若为偶数,则“中间位置”的数据是第n个数据;若为奇数,则“中间位置”的数据为第n+1个数据,然后将新数据与“中间位置”的数据比较,若新数据大于“中间位置”的数据,则在右半边进行下一步骤;若新数据小于“中间位置”的数据,则在左半边进行下一步骤;依次类推,就可以确定新数据在序列中的位置。
变式练习
将52插入有序列{13,27,38,39,43,47,48,51,57,66,74,82}中,构成一个新的有序列。
[解] 首先选择有序列中具有中间位置序号的数据47,将52与47进行比较,显然52>47,故52不能插入到47的左边的任何位置。
所以,应该排在47的右边,再将余下数据的中间位置的数据57与52比较,显然52<57,因此应插到57的左边,又51<52,则52插入到51的右边,57的左边,即可得到52的位置。
小结和作业
本次课主要介绍了:
(1)有关排序的基础知识
1.定义
2.稳定性和存储方式
3.排序算法的评价
(2)直接插入排序
1.基本思想
2.实例模拟
3.算法描述
4.算法的复杂度
(3)折半插入排序
1.基本思想
2.实例模拟
3.算法描述
4.算法的复杂度
课堂练习
1.将27插入到有序列{10,12,14,16,18,20,22,23,24,37,38,39,42,51,62}中,如果用折半插入排序可以进行几次比较就能完成,并设计算法。
解:首先中间的数(即第8个数)23比较,由于27>23,故27在23的右边;在于23右边的7个数中的中间的数39比较,由于27<39,故27在39的左边;再与23右边39左边的3个数中间数37比较,由于27<37,故27在37的左边;最后27与24比较,由于27>24,故27在2,4的右边,所以27应排在24与37之间,因此共进行4次比较即可完成。
2.将数据组 {49,38,65,97,76,13,27,49} 按照从小到大的顺序排列。
解:
38,49,65,97,76,13,27,49
38,49,65,97,76,13,27,49
38,49,65,97,76,13,27,49
38,49,65,76,97,13,27,49
38,49,65,76,13,97,27,49
38,49,65,76,13,27,97,49
38,49,65,76,13,27,49,97
3.无序列{15,3,10,12,8}用直接插入排序法按从小到大排列,第三次插入后的有序列为( B )
A {3,8,10,12,8}
B {3,10,12,15}
C {3,8,10}
D {3,10,5}
4.将无序列{7,5,4,9,1}按从大到小的顺序排列,将{7}看成有序列,将5插入此有序列,
得到新的有序列是 : {7,5}
5.对无序列{12,15,,4 ,11,9,22,2,35}用直接插入排序法排序时,在排序过程中,11插入在( B )
A 2与12之间
B 4与12之间
C 9与12之间
D 4与15之间。
