(完整word版)特殊四边形的性质与判定练习题
特殊四边形的性质与判定练习题

PMNABCDR特殊四边形的性质与判定练习题1. 若矩形的一条角平分线分一边为3cm 和5cm 两部分,则矩形的周长为 ( ) A .22 B .26C .22或26D .282.已知一矩形的周长是24cm ,相邻两边之比是1:2,那么这个矩形的面积是 ( ) A .24cm 2B .32cm 2C .48cm 2D .128cm 23.由矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对角线的夹角为( )A 、22.5°B 、45°C 、30°D 、60°4.如图,在矩形ABCD 中,DE ⊥AC,∠ADE= ∠CDE,那么∠BDC 等于( )A .60°B .45°C .30°D .22.5°5.如图,过矩形ABCD 的对角线BD 上一点R 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMRP的面积S 1,与矩形QCNR 的面积S 2的大小关系是 ( ) A. S 1> S 2 B. S 1= S 2 C. S 1< S 2 D. 不能确定6.平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是() A.4cm 和6cm B.6cm 和8cm C.8cm 和10cm D.10cm 和12cm7.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( ) A.AC =BD ,AB =CD ,AB ∥CD B.AD //BC ,∠A =∠CC.AO =BO =CO =DO ,AC ⊥BDD.AO =CO ,BO =DO ,AB =BC8.下列命题中,真命题是( )A 、有两边相等的平行四边形是菱形B 、对角线垂直的四边形是菱形C 、四个角相等的菱形是正方形D 、两条对角线相等的四边形是矩形 9.平行四边形各角平分线若围成一个四边形,则这个四边形一定是( ) A 、矩形 B 、平行四边形 C 、菱形 D 、正方形10.任意四边形四边中点所得的四边形一定是()A、平行四边形B、矩形C、菱形D、正方形11.已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.12.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )A.AC=BD,AB=CD,AB∥CDB.AD//BC,∠A=∠CC.AO=BO=CO=DO,AC⊥BDD.AO=CO,BO=DO,AB=BC13、矩形ABCD的两条对角线相交于O,∠AOB=60o,AB=8,则矩形对角线的长___14、矩形的两条对角线的夹角为60°,若一条对角线与短边的和为15,则短边的长是,对角线的长是。
八下数学专题卷三特殊四边形的判定与性质的综合习题新人教版

(2)若∠AFB=90°,AB=4,求四边形 BEFD的周长. (2)解:∵∠AFB=90°,D是AB的中点,AB=4,
∴DF=DB=DA= 1 AB=2.
2
∵四边形BEFD是平行四边形,
∴四边形BEFD是菱形.
∵DB=2,∴四边形BEFD的周长为4×2=8.
类型二 菱形的判定与性质
3.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线 AC,BD交于点O,AC平分∠BAD.
6.如图,在▱ABCD中,AB>AD,DE平分 ∠ADC,AF⊥BC于点F,交DE于点G, 延–长(1)求BC证:至四点边形HA,FH使D是C矩H形=; BF,连接DH.
(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.
∵CH=BF,∴BF+CF=CH+CF,即BC=FH,
∴AD=FH,∴四边形AFHD是平行四边形.
– (1)求证:四边形ABCD是菱形;
(1)证明:∵AB∥CD,∴∠BAC=∠DCA. ∵AC为∠DAB的平分线,∴∠BAC=∠DAC, ∴∠DCA=∠DAC,∴CD=AD=AB. ∵AB∥CD,∴四边形ABCD是平行四边形. ∵AD=AB,∴▱ABCD是菱形.
(2)过点C作CE⊥AB,交AB的延长线5 于点 E,连接OE.若AB=2 ,BD=4,求OE
(3)如图2,把正方形ABCD改为菱形ABCD ,其他条件不变,∠ABC=120°,连接 (A3)解E:,AE试=PC探.证究明如线下:段∵四A边E形与ABC线D是段菱形P,C的数量关系 ,并给予证明. ∴AD=CD,∠ADC=∠ABC=120°,∠ADP=∠CDP.
又∵DP=DP,∴△ADP≌△CDP(SAS),∴PA=PC,∠PAD=∠PCD.
2024年中考数学复习(全国版)第二讲 特殊四边形的性质与判定(原卷版)
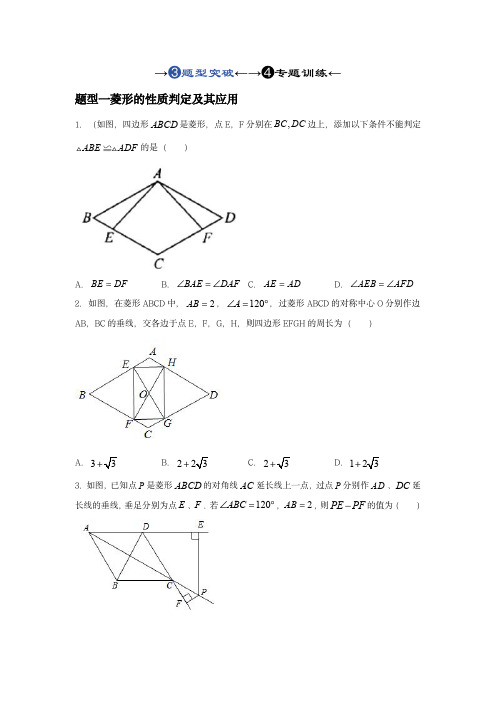
→➌题型突破←→➍专题训练←题型一菱形的性质判定及其应用1.(如图,四边形ABCD 是菱形,点E,F 分别在,BC DC 边上,添加以下条件不能判定ABE ADF ≌的是()A.BE DF B.BAE DAF C.AE AD D.AEB AFD2.如图,在菱形ABCD 中,2AB ,120A ,过菱形ABCD 的对称中心O 分别作边AB,BC 的垂线,交各边于点E,F,G,H,则四边形EFGH 的周长为()A.3 B.2 C.2 D.1 3.如图,已知点P 是菱形ABCD 的对角线AC 延长线上一点,过点P 分别作AD 、DC 延长线的垂线,垂足分别为点E 、F .若120ABC ,2AB ,则PE PF 的值为()A.32B.C.2D.524.如图,在菱形ABCD 中,60ABC ,连接AC 、BD ,则AC BD的值为()A.12B.22C.32D.335.如图,菱形ABCD 的对角线AC 与BD 相交于点O ,点E 在BD 上,连接AE ,CE ,60ABC ,15BCE ,2ED ,则AD ()A.4B.3C.D.27.如图,在菱形ABCD 中,对角线AC,BD 相交于点O,点E 是CD 中点,连接OE,则下列结论中不一定正确的是()A.AB=AD B.OE 12 AB C.∠DOE=∠DEO D.∠EOD=∠EDO8.如图,在菱形ABCD 中,点E,F 分别在AB,CD 上,且BE=2AE,DF=2CF,点G,H分别是AC 的三等分点,则S 四边形EHFG ÷S 菱形ABCD 的值为()A.19B.16C.13D.299.如图,菱形ABCD 的对角线AC 、BD 相交于点O,OE AD ,垂足为E,8AC ,6BD ,则OE 的长为______.10.菱形ABCD 中,对角线10, 24AC BD ,则菱形的高等于___________.11.如图,在菱形ABCD 中,对角线12AC ,16BD ,分别以点A,B,C,D 为圆心,12AB 的长为半径画弧,与该菱形的边相交,则图中阴影部分的面积为__________.(结果保留 )12.如图1,菱形ABCD 的对角线AC 与BD 相交于点O,P、Q 两点同时从O 点出发,以1厘米/秒的速度在菱形的对角线及边上运动.点P 的运动路线为O A D O ,点Q 的运动路线为O C B O .设运动的时间为x 秒,P、Q 间的距离为y 厘米,y 与x 的函数关系的图象大致如图2所示,当点P 在A D 段上运动且P、Q 两点间的距离最短时,P、Q 两点的运动路程之和为__________厘米.13.如图,在菱形ABCD 中,60A ,G 为AD 中点,点E 在BC 延长线上,F 、H 分别为CE 、GE 中点,EHF DGE ,CF AB _____.14.如图,四边形ABCD 是菱形,点E 、F 分别在边AB 、AD 的延长线上,且BE DF .连接CE 、CF .求证:CE CF .15.如图,在ABC 中,BAC 的角平分线交BC 于点D,//,//DE AB DF AC .(1)试判断四边形AFDE 的形状,并说明理由;(2)若90BAC ,且AD ,求四边形AFDE 的面积.16.如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O,过点O 的直线EF 与BA、DC 的延长线分别交于点E、F.(1)求证:AE=CF;(2)请再添加一个条件,使四边形BFDE 是菱形,并说明理由.题型二矩形的性质判定及其应用17.如图,矩形ABCD 的对角线AC ,BD 交于点O ,6AB ,8BC ,过点O 作OE AC ,交AD 于点E ,过点E 作EF BD ,垂足为F ,则OE EF 的值为()A.485B.325C.245D.12518.如图,在矩形ABCD 中,AB=5,AD=3,点E 为BC 上一点,把△CDE 沿DE 翻折,点C 恰好落在AB 边上的F 处,则CE 的长是()A.1B.43C.32D.5319.如图,在矩形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别是AO ,AD 的中点,连接EF ,若6AB cm ,8BC cm ,则EF 的长是()A.2.2cm B.2.3cm C.2.4cm D.2.5cm20.如图1,动点P 从矩形ABCD 的顶点A 出发,在边AB,BC 上沿A→B→C 的方向,以1cm/s 的速度匀速运动到点C,APC △的面积S(cm 2)随运动时间t(s)变化的函数图象如图2所示,则AB 的长是()A.3cm 2B.3cm C.4cm D.6cm21.如图,将矩形纸片ABCD 的两个直角进行折叠,使CB,AD 恰好落在对角线AC 上,B′,D′分别是B,D 的对应点,折痕分别为CF,AE.若AB=4,BC=3,则线段B D 的长是()A.52B.2C.32D.122.如图,在矩形纸片ABCD 中,7AB ,9BC ,M 是BC 上的点,且2CM .将矩形纸片ABCD 沿过点M 的直线折叠,使点D 落在AB 上的点P 处,点C 落在点C 处,折痕为MN,则线段PA 的长是()A.4B.5C.6D.523.如图,在矩形ABCD 中,4,8AB AD ,点E,F 分别在边,AD BC 上,且3AE ,按以下步骤操作:第一步,沿直线EF 翻折,点A 的对应点'A 恰好落在对角线AC 上,点B 的对应点为'B ,则线段BF 的长为_______;第二步,分别在,'EF A B ¢上取点M,N,沿直线MN 继续翻折,使点F 与点E 重合,则线段MN 的长为_______.24.如图,矩形ABCD 中,6AB ,8BC ,对角线BD 的垂直平分线EF 交AD 于点E 、交BC 于点F ,则线段EF 的长为__.25.如图,在矩形ABCD 中,E 为AD 的中点,连接CE ,过点E 作CE 的垂线交AB 于点F,交CD 的延长线于点G,连接CF.已知12AF ,5CF ,则EF _________.26.如图,将矩形纸片ABCD 折叠(AD AB ),使AB 落在AD 上,AE 为折痕,然后将矩形纸片展开铺在一个平面上,E 点不动,将BE 边折起,使点B 落在AE 上的点G 处,连接DE ,若DE EF ,2CE ,则AD 的长为________.27.如图,点E 是矩形ABCD 边AD 上一点,点F,G,H 分别是BE,BC,CE 的中点,3AF ,则GH 的长为________.28.如图,在矩形ABCD 中,8cm AB ,12cm AD ,点P 从点B 出发,以2cm/s 的速度沿BC 边向点C 运动,到达点C 停止,同时,点Q 从点C 出发,以cm/s v 的速度沿CD 边向点D 运动,到达点D 停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v 为_____时,ABP △与PCQ △全等.29.已知:如图,矩形ABCD 的对角线,AC BD 相交于点O,120,2BOC AB .(1)求矩形对角线的长.(2)过O 作OE AD 于点E,连结BE.记ABE ,求tan 的值.30.如图,点C 是BE 的中点,四边形ABCD 是平行四边形.(1)求证:四边形ACED 是平行四边形;(2)如果AB AE ,求证:四边形ACED 是矩形.31.如图,在▱ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F,连接BF,AC,若AD=AF,求证:四边形ABFC 是矩形.32.如图,在△ABC 中,AB=AC,点D、E 分别是线段BC、AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F,连接CF.(1)求证:△BDE≌△FAE;(2)求证:四边形ADCF 为矩形.33.如图,菱形ABCD 的对角线AC,BD 相交于点O,E 是AD 的中点,点F,G 在AB 上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG 是矩形;(2)若AD=10,EF=4,求OE 和BG 的长.题型三正方形的性质判定及其应用34.如图,正方形ABCD 的对角线AC,BD 交于点O,M 是边AD 上一点,连接OM,过点O 做ON⊥OM,交CD 于点N.若四边形MOND 的面积是1,则AB 的长为()A.12C.2D.2235.如图,在边长为3的正方形ABCD 中,30 CDE ,DE CF ,则BF 的长是()A.1D.236.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示.过点D 作DF 的垂线交小正方形对角线EF 的延长线于点G ,连结CG ,延长BE 交CG 于点H .若2AE BE ,则CG BH 的值为()A.32C.3107D.35537.如图,在边长为4的正方形ABCD 中,点E,F 分别在CD,AC 上,BF EF ,1CE ,则AF 的长是()A.D.5438.如图,把含30°的直角三角板PMN 放置在正方形ABCD 中,30PMN ,直角顶点P 在正方形ABCD 的对角线BD 上,点M,N 分别在AB 和CD 边上,MN 与BD 交于点O,且点O 为MN 的中点,则AMP 的度数为()A.60°B.65°C.75°D.80°39.如图,矩形AOBC 的顶点A、B 在坐标轴上,点C 的坐标是(﹣10,8),点D 在AC 上,将 BCD 沿BD 翻折,点C 恰好落在OA 边上点E 处,则tan∠DBE 等于()A.34B.35D.1240.如图,在正方形ABCD 中,6AB ,M 是AD 边上的一点,:1:2AM MD .将BMA △沿BM 对折至BMN △,连接DN,则DN 的长是()A.52B.8C.3D.541.如图,正方形ABCD 的边长为3,E 为BC 边上一点,BE=1.将正方形沿GF 折叠,使点A 恰好与点E 重合,连接AF,EF,GE,则四边形AGEF 的面积为()C.6D.542.如图,在边长为2的正方形ABCD 中,若将AB 绕点A 逆时针旋转60 ,使点B 落在点B 的位置,连接B B ,过点D 作DE⊥BB ,交'BB 的延长线于点E,则B E 的长为()31B.232 23343343.如图,正方形OABC 的边长为2,将正方形OABC 绕点O 逆时针旋转角α(0°<α<180°)得到正方形OA′B′C′,连接BC′,当点A′恰好落在线段BC′上时,线段BC′的长度是___.44.已知ABC 的三个顶点都是同一个正方形的顶点,ABC 的平分线与线段AC 交于点D.若ABC 的一条边长为6,则点D 到直线AB 的距离为__________.45.如图,四边形ABCD 是正方形,△ECF 为等腰直角三角形,∠ECF=90°,点E 在BC 上,点F 在CD 上,N 为EF 的中点,连结NA,以NA,NF 为邻边作□ANFG.连结DG,DN,将Rt△ECF 绕点C 顺时针方向旋转,旋转角为 (0°≤ ≤360°).(1)如图1,当 =0°时,DG 与DN 的关系为____________________;(2)如图2,当045 时,(1)中的结论是否成立?若成立,请写出证明过程;若不成立,请说明理由;(3)在Rt△ECF 旋转的过程中,当□ANFG 的顶点G 落在正方形ABCD 的边上,且AB=12,EC=GN,请直接写出GN 的长.46.已知正方形ABCD ,E ,F 为平面内两点.(探究建模)(1)如图1,当点E 在边AB 上时,DE DF ,且B ,C ,F 三点共线.求证:AE CF ;(类比应用)(2)如图2,当点E 在正方形ABCD 外部时,DE DF ,AE EF ,且E ,C ,F 三点共线.猜想并证明线段AE ,CE ,DE 之间的数量关系;(拓展迁移)(3)如图3,当点E 在正方形ABCD 外部时,AE EC ,AE AF ,DE BE ,且D ,F ,E 三点共线,DE 与AB 交于G 点.若3DF ,AECE 的长.。
2024年中考特殊四边形的性质与判定专题训练

2024年中考特殊四边形的性质与判定专题训练1.如图,菱形ABCD的对角线交于点O,点E是菱形外一点,DE∥AC,CE∥BD.(1)求证:四边形DECO是矩形;(2)连接AE交BD于点F,当∠ADB=30°,DE=4时,求AF的长度.2.在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)求证:四边形ACDE是平行四边形。
(2)(2)若AC=8,BD=6,求△ADE的周长3.如图,在▱ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,连接AE交CD于点F.(1)求证:四边形ADEC是矩形;(2)在▱ABCD中,取AB的中点M,连接CM,若CM=5,且AC=8,求四边形ADEC的面积.4.如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度5.在▱ABCD中,E、F分别是AB、CD的中点,连接AF、CE.(1)求证:△BEC≌△DFA;(2)连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论.6.已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.(1)求证:AB=AF;(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.7.如图,在平行四边形ABCD 中,过点A 作AE ⊥DC 交DC 的延长线于点E ,过点D 作DF ⊥BA 交BA 的延长线于点F.(1)求证:四边形AEDF 是矩形;(2)连接BD ,若AB =AE =2,tan ∠FAD =52,求BD 的长.8.如图,已知点A (-4,2)、B (-1,-2),□ABCD 的对角线交于坐标原点O(1) 请直接写出点C 、D 的坐标(2) 写出从线段AB 到线段CD 的变换过程(3) 直接写出□ABCD 的面积9.如图,AC 是四边形ABCD 的对角线,∠1=∠B ,点E 、F 分别在AB 、BC 上,BE =CD ,BF =CA ,连接EF .(1)求证:∠D =∠2;(2)若EF ∥AC ,∠D =78°,求∠BAC 的度数.10.如图,在平行四边形ABCD中,AC⊥AD,延长DA于点E,使得DA=AE,连接BE.(1)求证:四边形AEBC是矩形;(2)过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若AB=6,∠CAB=30°,求△OGC的面积.11.如图,在▱ABCD中,对角线AC与BD相交于点O,∠CAB=∠ACB,过点B作BE⊥AB交AC 于点E.(1)求证:AC⊥BD;(2)若AB=14,cos∠CAB=,求线段OE的长.12.如图,在平行四边形ABCD中,DB DA=,点F是AB的中点,连接DF并延长,交CB的延长线于点E,连接AE.(1)求证:四边形AEBD是菱形;(2)若10DC=,tan3DCB∠=,求菱形AEBD的面积OABCDx y13.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=OC,BO=OD,且∠AOB =2∠OAD.(1)求证:四边形ABCD是矩形;(2)若∠AOB:∠ODC=4:3,求∠ADO的度数.14.如图,下列网格中,每个小方格的边长都是1.(1)分别作出四边形ABCD关于x轴、y轴、原点的对称图形;(2)求出四边形ABCD的面积.15.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BD平分∠ABC,且与AE交于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若AC=6,BD=8,AM⊥BC于M,求AM的长.16.在△ABC 中,AB=AC ,AD 是BC 上的中线,分别过点A ,D 作BC ,AC 的平行线交于点E ,且DE 交AB 于点O ,连接BE .(1)求证:四边形ADBE 是矩形;(2)若AD:BD=2:3,求sin ∠AOD 的值.17.如图,点P 是正方形ABCD 的对角线AC 上一动点(不与点A 重合),连接DP ,过点P 作DP 的垂线,与边BC 相交于点E ,连接DE .(1)求证:△PDE 是等腰直角三角形.(2)若正方形ABCD 的边长为2,时当CDE ADP ∠=∠,求AP 的值.。
沪科版数学八年级下册专项练习特殊平行四边形的性质与判断(含图片答案)

数学八年级下册专项练习特殊平行四边形的性质与判断类型一 菱形的性质与判定1.下列说法中,错误的是( ).A.平行四边形的对角线互相平分B.对角线互相平分的四边形是平行四边形C.菱形的对角线互相垂直D.对角线互相垂直的四边形是菱形2.如图1,在∠MON 的两边上分别截取OA ,OB ,使OA=OB,分别以点A ,B 为圆心,OA 长为半径作弧,两弧交于点C ,连接AC ,BC ,AB ,OC .若AB =2cm ,四边形OACB 的面积为4cm 2,则OC 的长为()cm .A.2B.3C.4D.53.如图2,在四边形ABCD 中,AD ∥BC,AB=AD,AC 平分∠BAD.(1)求证:四边形ABCD 是菱形.(2)过点A 作AE ⊥AC ,交CB 的延长线于点E ,若 BC=10,AC=16,求AE 的长.4.如图3,四边形ABCD是平行四边形,对角线AC,BD交于点O,AC=2AB,BE∥AC,OE∥AB.(1)求证:四边形ABEO是菱形.(2)若 AC=54,BD=8,求四边形ABEO的面积.类型二矩形的性质与判定5.下列说法正确的是().A.对角线相等的四边形是矩形B.矩形的对角线相等且互相平分C.对角线互相垂直的四边形是菱形D.一组对边相等,另一组对边平行的四边形是平行四边形6.如图4,在Rt △ABC 中,∠BAC =90°,AB=3,AC=4,P 为边BC 上一动点,过点P 作PE ⊥AB 于点E ,PF ⊥AC 于点F ,连接EF ,则EF 的最小值是( ).C.2D.2.4A.1.2B.1.5 7.如图5,▱ABCD 的对角线AC ,BD 相交于点O ,△AOB 是等边三角形.(1)求证:▱ABCD 为矩形.(2)若AB =4,求▱ABCD的面积.8.如图6,四边形ABCD 是平行四边形,过点D 作DE ⊥AB 于点E ,点F 在边CD 上,CF =AE ,连接AF ,BF.(1)求证:四边形BFDE 是矩形.(2)若AF 是∠DAB 的平分线.若 CF=6,BF=8,求DC 的长.9.如图7,在四边形ABCD 中,AD ∥BC ,CD ⊥BC ,BC =2AD , 是BC 的中点.(1)如图7①,求证:四边形AFCD 是矩形.(2)如图7②,过点C 作CE ⊥AB 于点E ,连接DE ,EF .求证:DE=DC.类型三正方形的性质与判定10.如图8,正方形ABCD中,AB=32,点E是对角线AC上的一点,连接DE.过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连接AG.(1)求证:矩形DEFG是正方形.(2)求AG+AE的值.(3)若F恰为AB的中点,求正方形DEFG的面积.11.如图9①,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.(1)求证:BE=DE.(2)如图9②,过点E作EF⊥DE,交边BC于点F,以DE,EF 为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形.②若正方形ABCD的边长为9,,CG=32,求正方形DEFG的边长.12.如图10①,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.(1)证明:PC=PE.(2)求∠CPE的度数.(3)如图10②,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=116°°时,求∠CPE的度数.特殊平行四边形的性质与判断。
特殊四边形练习题

特殊四边形练习题一、选择题1. 下列四边形中,哪一个是平行四边形?A. 两组对边分别平行的四边形B. 两组对边分别相等的四边形C. 对角线互相平分的四边形D. 一组对边相等且平行的四边形2. 菱形的对角线具有以下哪个性质?A. 垂直平分B. 互相垂直C. 互相平行D. 相等3. 矩形的四个角都是:A. 锐角B. 直角C. 钝角D. 平角4. 梯形中,上底和下底平行,且两腰相等的梯形是:A. 等腰梯形B. 直角梯形C. 等腰直角梯形D. 普通梯形5. 正方形的对角线具有以下哪个性质?A. 垂直平分B. 互相垂直C. 互相平行D. 相等且垂直二、填空题6. 平行四边形的对角线______,矩形的对角线______。
7. 菱形的四条边都______,且对角线______。
8. 等腰梯形的两腰相等,且上底和下底______。
9. 正方形的四条边都______,且四个角都是______。
10. 如果一个四边形的两组对边分别相等,那么这个四边形可能是______或______。
三、判断题11. 所有平行四边形都是矩形。
()12. 所有菱形都是平行四边形。
()13. 所有矩形都是正方形。
()14. 所有正方形都是菱形。
()15. 所有等腰梯形都是平行四边形。
()四、简答题16. 请简述平行四边形、矩形、菱形、正方形和梯形的定义。
17. 请说明为什么矩形的对角线相等,而菱形的对角线垂直。
18. 请解释等腰梯形的判定方法。
五、计算题19. 若一个平行四边形的两组对边分别是10cm和8cm,求其对角线的长度范围。
20. 已知一个矩形的长为15cm,宽为10cm,求其对角线的长度。
21. 如果一个菱形的边长为6cm,求其对角线的长度。
22. 已知一个正方形的边长为8cm,求其对角线的长度。
23. 若一个等腰梯形的上底为4cm,下底为10cm,高为3cm,求其两腰的长度。
六、证明题24. 证明:平行四边形的对角线互相平分。
人教版八年级数学下册18.2 专题训练 特殊平行四边形的性质与判定(含答案)

18.2 专题训练特殊平行四边形的性质与判定1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE 是平行四边形,求证:四边形ADBE是矩形.2.在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB 的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.4.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF =AE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.5.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD 的中点.(1)当四边形ABCD是矩形时,四边形EFGH是菱形,请说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.6.如图,等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.7.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.8.如图,在矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断.9.如图,在▱ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.10.如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD 上一动点(不与点D重合),PO的延长线交BC于Q点.(1)求证:四边形PBQD为平行四边形;(2)若AB=3 cm,AD=4 cm,点P从点A出发,以1 cm/s的速度向点D匀速运动.设点P运动时间为t s,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.11.如图1,在▱ABCD中,AF平分∠BAD交BC于点F,CE平分∠BCD交AD于点E.图1 图2(1)求证:四边形AFCE是平行四边形;(2)如图2,若BE⊥EC,求证:四边形ABFE是菱形.12.如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.(1)求证:四边形BEDF是平行四边形;(2)当四边形BEDF是菱形时,求EF的长.13.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.14.如图,菱形ABCD 的对角线AC,BD 相交于点O,分别延长OA,OC 到点E,F,使AE =CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC =50°,则当∠EBA=20° 时,四边形BFDE是正方形.15.已知:如图,在菱形ABCD 中,点E,O,F 分别是边AB,AC,AD 的中点,连接CE,CF,OF.(1)求证:△BCE≌△DCF;(2)当AB与BC满足什么条件时,四边形AEOF是正方形?请说明理由.16.如图,在四边形ABCD中,AB∥CD,AB≠CD,BD=AC.(1)求证:AD=BC;(2)若E,F,G,H分别是AB,CD,AC,BD的中点,求证:线段EF与线段GH互相垂直平分.17.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.18.如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE. 求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.19.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.20.已知:如图,在▱ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.参考答案18.2 专题训练特殊平行四边形的性质与判定1.如图,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE 是平行四边形,求证:四边形ADBE是矩形.解:∵AB=AC,AD是BC边上的中线,∴AD⊥BC.∴∠ADB=90°.又∵四边形ADBE是平行四边形,∴四边形ADBE是矩形.2.在△ABC中,M是AC边上的一点,连接BM.将△ABC沿AC翻折,使点B落在点D处,当DM∥AB时,求证:四边形ABMD是菱形.证明:∵AB∥DM,∴∠BAM=∠AMD.由折叠性质得:∠CAB=∠CAD,AB=AD,BM=DM.∴∠DAM=∠AMD.∴DA=DM=AB=BM.∴四边形ABMD是菱形.3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB 的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形;(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.解:(1)证明:∵点O为AB的中点,∴OA=OB.又∵OE=OD,∴四边形AEBD是平行四边形.∵AB=AC,AD是△ABC的角平分线,∴AD⊥BC,即∠ADB=90°.∴四边形AEBD是矩形.(2)当∠BAC=90°时,矩形AEBD是正方形.理由:∵AB=AC,AD是△ABC的角平分线,∴BD=CD.又∵∠BAC=90°,∴AD=BD.∴矩形AEBD是正方形.4.如图,在▱ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF =AE,连接AF,BF.(1)求证:四边形BFDE是矩形;(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.又∵CF=AE,∴BE=DF.又∵BE∥DF,∴四边形BFDE为平行四边形.∵DE⊥AB,∴∠DEB=90°.∴四边形BFDE是矩形.(2)∵四边形BFDE是矩形,∴∠BFD=90°.∴∠BFC=90°.在Rt△BFC中,由勾股定理,得BC=CF2+BF2=62+82=10.∴AD=BC=10.又∵DF=10,∴AD=DF.∴∠DAF=∠DFA.∵AB∥CD,∴∠DFA=∠FAB.∴∠DAF=∠FAB.∴AF是∠DAB的平分线.5.如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD 的中点.(1)当四边形ABCD是矩形时,四边形EFGH是菱形,请说明理由;(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.解:(1)理由:∵四边形ABCD是矩形,∴AC=BD.由题意,得EF=12AC,EH=12BD,GH=12AC,GF=12BD,∴EF=EH=GH=GF.∴四边形EFGH是菱形.(2)当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH为正方形.理由:∵E,F分别是四边形ABCD的边AB,BC的中点,∴EF∥AC,EF=12AC.同理:EH∥BD,EH=12BD,GF=12BD,GH=12AC.又∵AC=BD,∴EF=EH=GH=GF.∴四边形EFGH是菱形.∵AC⊥BD,∴EF⊥EH.∴四边形EFGH是正方形.6.如图,等腰△ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.证明:(1)∵AB=AC,AH⊥BC,∴BH=HC.又∵FH=EH,∴四边形EBFC是平行四边形.又∵AH⊥BC,∴四边形EBFC是菱形.(2)∵四边形EBFC是菱形,∴∠ECH=∠FCH=12∠ECF.∵AB=AC,AH⊥BC,∴∠CAH=12∠BAC.∵∠BAC=∠ECF,∴∠CAH=∠FCH.∵AH⊥BC,∴∠CAH+∠ACH=90°.∴∠FCH+∠ACH=∠ACF=90°.∴AC⊥CF.7.如图,四边形ABCD是菱形,点M,N分别在AB,AD上,且BM=DN,MG∥AD,NF∥AB,点F,G分别在BC,CD上,MG与NF相交于点E.求证:四边形AMEN是菱形.证明:∵MG∥AD,NF∥AB,∴四边形AMEN是平行四边形.∵四边形ABCD是菱形,∴AB=AD.∵BM=DN,∴AB-BM=AD-DN,即AM=AN.∴四边形AMEN是菱形.8.如图,在矩形ABCD中,AB=2,BC=5,E,P分别在AD,BC上,且DE=BP=1.(1)判断△BEC的形状,并说明理由;(2)判断四边形EFPH是什么特殊四边形?并证明你的判断.解:(1)△BEC是直角三角形.理由:∵四边形ABCD为矩形,∴∠ADC=∠BAD=90°,AD=BC=5,AB=CD=2.由勾股定理,得CE=CD2+DE2=22+12=5,BE=AB2+AE2=22+(5-1)2=2 5.∴CE2+BE2=5+20=25.∵BC2=52=25,∴BE2+CE2=BC2.∴∠BEC=90°.∴△BEC是直角三角形.(2)四边形EFPH为矩形.证明:∵四边形ABCD为矩形,∴AD=BC,AD∥BC.又∵DE=BP,∴四边形DEBP是平行四边形.∴BE∥DP.∵AD=BC,DE=BP,∴AE=CP.∴四边形AECP是平行四边形.∴AP∥CE.又∵BE∥DP,∴四边形EFPH是平行四边形.又∵∠BEC=90°,∴四边形EFPH是矩形.9.如图,在▱ABCD中,AB=DB,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F.求证:四边形DFBE是矩形.证明:∵四边形ABCD是平行四边形,∴AD∥BC,CD∥AB.∴∠CDB=∠ABD.∵BE平分∠ABD,DF平分∠CDB,∴∠FDB=12∠CDB,∠EBD=12∠ABD.∴∠FDB=∠EBD.∴DF∥EB.又∵AD∥BC,∴四边形DFBE是平行四边形.∵AB=DB,BE平分∠ABD,∴BE⊥AD.∴∠DEB=90°.∴四边形DFBE是矩形.10.如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD 上一动点(不与点D重合),PO的延长线交BC于Q点.(1)求证:四边形PBQD 为平行四边形;(2)若AB =3 cm ,AD =4 cm ,点P 从点A 出发,以1 cm/s 的速度向点D 匀速运动.设点P 运动时间为t s ,问四边形PBQD 能够成为菱形吗?如果能,求出相应的t 值;如果不能,说明理由.解:(1)证明:∵四边形ABCD 是矩形,∴AD ∥BC ,OD =OB .∴∠PDO =∠QBO .在△POD 和△QOB 中,⎩⎨⎧∠PDO =∠QBO ,OD =OB ,∠POD =∠QOB ,∴△POD ≌△QOB (ASA).∴OP =OQ .又∵OB =OD ,∴四边形PBQD 为平行四边形.(2)点P 从点A 出发运动t s 时,AP =t cm ,PD =(4-t )cm.当四边形PBQD 是菱形时,PB =PD =(4-t )cm.∵四边形ABCD 是矩形,∴∠BAP =90°.在Rt △ABP 中,AB =3 cm ,AP 2+AB 2=PB 2,即t 2+32=(4-t )2,解得t =78.∴点P 运动时间为78 s 时,四边形PBQD 为菱形.11.如图1,在▱ABCD 中,AF 平分∠BAD 交BC 于点F ,CE 平分∠BCD交AD 于点E.图1 图2(1)求证:四边形AFCE 是平行四边形;(2)如图2,若BE ⊥EC ,求证:四边形ABFE 是菱形.证明:(1)∵AF 平分∠BAD ,CE 平分∠BCD ,∴∠FAE =12∠BAE ,∠FCE =12∠FCD.∵四边形ABCD 是平行四边形,∴∠BAE =∠FCD ,AD ∥BC.∴∠FAE =∠FCE ,∠FCE =∠CED.∴∠FAE =∠CED.∴AF ∥EC.又∵AE ∥CF ,∴四边形AFCE 为平行四边形.(2)∵AF ∥EC ,BE ⊥EC ,∴∠AOE =∠BEC =90°.∴∠AOE =∠AOB =90°.在△ABO 和△AEO 中,⎩⎨⎧∠BAO =∠EAO ,AO =AO ,∠AOB =∠AOE ,∴△ABO ≌△AEO(ASA ).∴BO =EO.同理可得△ABO ≌△FBO ,∴AO =FO.∴四边形ABFE 是平行四边形.又∵AF ⊥BE ,∴平行四边形ABFE 是菱形.12.如图,矩形ABCD 中,AB =6,BC =4,过对角线BD 中点O 的直线分别交AB ,CD 边于点E ,F.(1)求证:四边形BEDF 是平行四边形;(2)当四边形BEDF 是菱形时,求EF 的长.解:(1)证明:∵四边形ABCD 是矩形,O 是BD 的中点,∴∠A =90°,AD =BC =4,AB ∥DC ,OB =OD .∴∠OBE =∠ODF .在△BOE 和△DOF 中,⎩⎨⎧∠OBE =∠ODF ,OB =OD ,∠BOE =∠DOF ,∴△BOE ≌△DOF (ASA).∴EO =FO .又∵OB =OD .∴四边形BEDF 是平行四边形.(2)∵四边形BEDF是菱形,∴BD⊥EF.设BE=x,则DE=x,AE=6-x.在Rt△ADE中,DE2=AD2+AE2,∴x2=42+(6-x)2.解得x=13 3.∵BD=AD2+AB2=213,∴OB=12BD=13.∵BD⊥EF,∴EO=BE2-OB2=213 3.∴EF=2EO=413 3.13.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.解:(1)证明:∵DE⊥BC,∴∠DFB=90°.又∵∠ACB=90°,∴∠ACB=∠DFB.∴AC∥DE.又∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形.∴CE=AD.(2)四边形BECD是菱形.理由:∵D为AB中点,∴AD=BD.又由(1)得CE=AD,∴BD=CE.又∵BD∥CE,∴四边形BECD是平行四边形.又∵DE⊥BC,∴四边形BECD是菱形.(3)当∠A=45°时,四边形BECD是正方形.理由:∵∠ACB=90°,∠A=45°,∴∠ABC=∠A=45°.∴AC=BC.又∵D为AB中点,∴CD⊥AB,即∠CDB=90°.又∵四边形BECD是菱形,∴四边形BECD是正方形.∴当∠A=45°时,四边形BECD是正方形.14.如图,菱形ABCD 的对角线AC ,BD 相交于点O ,分别延长OA ,OC 到点E ,F ,使AE =CF ,依次连接B ,F ,D ,E 各点.(1)求证:△BAE ≌△BCF ;(2)若∠ABC =50°,则当∠EBA =20° 时,四边形BFDE 是正方形. 证明:∵在菱形ABCD 中,BA =BC ,∴∠BAC =∠BCA .∴∠BAE =∠BCF .在△BAE 和△BCF 中,⎩⎨⎧BA =BC ,∠BAE =∠BCF ,AE =CF ,∴△BAE ≌△BCF (SAS).15.已知:如图,在菱形ABCD 中,点E ,O ,F 分别是边AB ,AC ,AD 的中点,连接CE ,CF ,OF.(1)求证:△BCE ≌△DCF ;(2)当AB 与BC 满足什么条件时,四边形AEOF 是正方形?请说明理由.解:(1)证明:∵四边形ABCD 为菱形,∴AB =BC =CD =DA ,∠B =∠D.又∵E ,F 分别是AB ,AD 的中点,∴BE =DF.在△BCE 和△DCF 中,⎩⎨⎧BC =DC ,∠B =∠D ,BE =DF ,∴△BCE ≌△DCF(SAS ).(2)当AB 与BC 满足AB ⊥BC 时,四边形AEOF 为正方形.理由如下: ∵E ,O 分别是AB ,AC 的中点,∴EO ∥BC.又∵BC ∥AD ,∴OE ∥AD ,即OE ∥AF.同理可证OF ∥AE ,∴四边形AEOF 为平行四边形.∵在菱形ABCD 中,点E ,F 分别是边AB, AD 的中点,∴AE =AF.∴四边形AEOF 为菱形.∵AB ⊥BC ,∴∠BAD =∠B =90°.∴四边形AEOF 为正方形.16.如图,在四边形ABCD 中,AB ∥CD ,AB≠CD ,BD =AC.(1)求证:AD =BC ;(2)若E ,F ,G ,H 分别是AB ,CD ,AC ,BD 的中点,求证:线段EF 与线段GH 互相垂直平分.证明:(1)延长DC 至K ,使CK =AB.连接BK.∵AB CK ,∴四边形ABKC 是平行四边形.∴AC BK.∴∠ACD =∠K.∵BD =AC ,AC =BK ,∴BD =BK.∴∠BDC =∠K.∴∠ACD =∠BDC.在△ACD 和△BDC 中,⎩⎨⎧AC =BD ,∠ACD =∠BDC ,CD =DC ,∴△ACD ≌△BDC(SAS ).∴AD =BC.(2)分别连接EH ,HF ,FG 和GE.∵E ,H 分别是AB ,BD 的中点,∴EH 为△ABD 的中位线.∴EH =12AD.同理:GF =12AD ,EG =12BC ,HF =12BC.又由(1)知AD =BC ,∴EH =HF =FG =GE.∴四边形EHFG 是菱形.∴线段EF 与线段GH 互相垂直平分.17.如图,在Rt △ABC 中,∠B =90°,点E 是AC 的中点,AC =2AB ,∠∥∥BAC 的平分线AD 交BC 于点D ,作AF ∥BC ,连接DE 并延长交AF 于点F ,连接FC.求证:四边形ADCF 是菱形.证明:∵AF ∥CD ,∴∠AFE =∠CDE.在△AFE 和△CDE 中,⎩⎨⎧∠AFE =∠CDE ,∠AEF =∠CED ,AE =CE ,∴△AFE ≌△CDE(AAS ).∴AF =CD.∵AF ∥CD ,∴四边形ADCF 是平行四边形.∵点E 是AC 的中点,AC =2AB ,∴AE =AB.∵AD 平分∠BAC ,∴∠EAD =∠BAD.又∵AD =AD ,∴△AED ≌△ABD(SAS ).∴∠AED =∠B =90°,即DF ⊥AC.∴四边形ADCF 是菱形.18.如图,△ABC ≌△ABD ,点E 在边AB 上,CE ∥BD ,连接DE. 求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.证明:(1)∵△ABC≌△ABD,∴∠ABC=∠ABD.∵CE∥BD,∴∠CEB=∠ABD.∴∠CEB=∠CBE.(2)∵△ABC≌△ABD,∴BC=BD.由(1)得∠CEB=∠CBE,∴CE=CB.∴CE=BD.又∵CE∥BD,∴四边形BCED是平行四边形.又∵BC=BD,∴四边形BCED是菱形.19.如图所示,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.(1)求证:D是BC的中点;(2)若AB=AC,试判断四边形AFBD的形状,并证明你的结论.解:(1)证明:∵AF∥BC,∴∠AFC=∠FCB.又∵∠AEF=∠DEC,AE=DE,∴△AEF≌△DEC(AAS).∴AF=DC.又∵AF=BD,∴BD=DC,即D是BC的中点.(2)四边形AFBD是矩形.证明:∵AF∥BC,AF=BD,∴四边形AFBD是平行四边形.∵AB=AC,D是BC的中点,∴AD⊥BC,即∠ADB=90°.∴四边形AFBD是矩形.20.已知:如图,在▱ABCD中,AF,BH,CH,DF分别是∠BAD,∠ABC,∠BCD,∠ADC的平分线.求证:四边形EFGH为矩形.证明:∵四边形ABCD是平行四边形,∴∠DAB+∠ADC=180°.∵AF,DF分别平分∠DAB,∠ADC,∴∠FAD=∠BAF=12∠DAB,∠ADF=∠CDF=12∠ADC.∴∠FAD+∠ADF=90°.∴∠AFD=90°.同理可得:∠BHC=∠HEF=90°.∴四边形EFGH是矩形.。
专 四边形的判定与性质综合大题专项训练(30道)(解析版)

专题9.10 四边形的判定与性质综合大题专项训练(30道)【苏科版】1.(2021秋•九江期末)如图,在四边形ABCD中,∠B=∠C.点E、F、G分别在边AB、BC、CD上,AE=GF=GC.(1)求证:四边形AEFG是平行四边形;(2)当∠FGC与∠EFB满足怎样的关系时,四边形AEFG是矩形.请说明理由.【分析】(1)要证明该四边形是平行四边形,只需证明AE∥FG.根据对边对等角∠GFC =∠C,和等腰梯形的性质得到∠B=∠C,则∠B=∠GFC,得到AE∥FG.(2)在平行四边形的基础上要证明是矩形,只需证明有一个角是直角.根据三角形FGC 的内角和是180°,结合∠FGC=2∠EFB和∠GFC=∠C,得到∠BFE+GFC=90°.则∠EFG=90°,于是得到结论.【解答】(1)证明:在四边形ABCD中,∠B=∠C,∵GF=GC,∴∠C=∠GFC,∠B=∠GFC,∴AB∥GF,即AE∥GF,∵AE=GF,∴四边形AEFG是平行四边形.(2)解:当∠FGC=2∠EFB时,四边形AEFG是矩形,理由:∵∠FGC+∠GFC+∠C=180o,∠GFC=∠C,∠FGC=2∠EFB,∴2∠GFC+2∠EFB=180°,∴∠BFE+∠GFC=90°.∴∠EFG=90°.∵四边形AEFG是平行四边形,∴四边形AEFG是矩形.2.(2021秋•崂山区期末)如图,在▱ABCD中,AC⊥CD.(1)延长DC到E,使CE=CD,连接BE,求证:四边形ABEC是矩形;(2)若点F,G分别是BC,AD的中点,连接AFCG,试判断四边形AFCG是什么特殊的四边形?并证明你的结论.【分析】(1)先证四边形ABEC是平行四边形,再证∠ACE=90°,即可得出结论;(2)先证四边形AFCG是平行四边形,再由矩形的性质得∠BAC=90°,然后由直角三角形斜边上的中线性质得AF=12BC=CF,即可得出结论.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∵CE=CD,∴AB=CE,∴四边形ABEC是平行四边形,又∵AC⊥CD,∴∠ACE=90°,∴平行四边形ABEC是矩形;(2)解:四边形AFCG是菱形,理由如下:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵点F,G分别是BC,AD的中点,∴CF=12BC,AG=12AD,∴CF=AG,∴四边形AFCG是平行四边形,由(1)可知,四边形ABEC是矩形,∴∠BAC=90°,∵F是BC的中点,∴AF=12BC=CF,∴平行四边形AFCG是菱形.3.(2021秋•渝中区校级期末)如图,平行四边形ABCD的对角线AC,BD相交于O点,DE ⊥AC 于E 点,BF ⊥AC 于F .(1)求证:四边形DEBF 为平行四边形;(2)若AB =20,AD =13,AC =21,求△DOE 的面积.【分析】(1)根据平行四边形的性质和全等三角形的判定和性质解答即可;(2)根据勾股定理和三角形面积公式解答即可.【解答】证明:(1)∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∴∠DAE =∠BCF ,∵DE ⊥AC 于E 点,BF ⊥AC 于F ,∴∠DEA =∠BFC =90°,在△DEA 与△BFC 中,{∠DEA =∠BFC ∠DAE =∠BCF AD =CB,∴△DEA ≌△BFC (AAS ),∴DE =BF ,∵∠DEA =∠BFC =90°,∴∠DEO =∠BFO =90°,∴DE ∥BF ,∴四边形DEBF 是平行四边形;(2)∵四边形ABCD 是平行四边形,∴AB =DC =20,AO =OC =10.5,∵DE ⊥AC ,在Rt △ADE 中,AD 2﹣AE 2=DE 2,在Rt △DEC 中,DC 2﹣EC 2=DE 2,即132﹣AE 2=202﹣(21﹣AE )2,解得:AE =5,∴OE =OA ﹣AE =10.5﹣5=5.5,DE =12,∴△DOE 的面积=12OE ⋅DE =12×12×5.5=33.4.(2021秋•沙坪坝区校级期末)如图,在▱ABCD 中,E 、F 分别为AB 、CD 边上两点,FB 平分∠EFC .(1)如图1,若AE =2,EF =5,求CD 的长;(2)如图2,∠BCD =45°,BC ⊥BD ,若G 为EF 上一点,且∠GBF =∠EFD ,求证:FG +2FD =AB .【分析】(1)由平行四边形的性质可得∠ABF =∠BFC ,AB =CD ,结合角平分线的定义可求得∠ABF =∠EFB ,即可求BE =EF =5,进而可求解;(2)在FC 上截取FH =FG ,连接BH ,利用SAS 证明△BGF ≌△BHF 可得∠BGF =∠BHF ,结合三角形的内角和定理可得∠BFD =∠BHC ,结合等腰直角三角形的性质利用AAS 证明△BDF ≌△BCH 可得DF =CH ,进而可证明结论.【解答】(1)解:在▱ABCD 中,AB ∥CD ,AB =CD ,∴∠ABF =∠BFC ,∵FB 平分∠EFC ,∴∠EFB =∠BFC ,∴∠ABF =∠EFB ,∵AE =2,EF =5,∴BE =EF =5,∴CD =AB =AE +EF =2+5=7;(2)证明:在FC 上截取FH =FG ,连接BH ,在△BGF 和△BHF 中,{FG =FH ∠BFE =∠BFC FB =FB,∴△BGF ≌△BHF (SAS ),∴∠BGF =∠BHF ,∵∠GBF =∠EFD ,∵∠EFD +∠EFB +∠BFH =180°,∠EFB +∠BGF +∠GBF =180°,∴∠BFH =∠BGF ,∴∠BFH =∠BHF ,∴∠BFD =∠BHC ,∵∠BCD =45°,BC ⊥BD ,∴∠BDF =45°=∠BCH ,∴BD =BC ,在△BDF 和△BCH 中,{∠BFD =∠BHC ∠BDF =∠BCH BD =BC,∴△BDF ≌△BCH (AAS )∴DF =CH ,∴AB =CD =DF +FH +CH =FG +2FD ,即FG +2FD =AB .5.(2021秋•莱芜区期末)点E 是▱ABCD 的边CD 上的一点,连接EA 并延长,使EA =AM ,连接EB 并延长,使EB =BN ,连接MN ,F 为MN 的中点,连接CF ,DM .(1)求证:四边形DMFC 是平行四边形;(2)连接EF ,交AB 于点O ,若OF =2,求EF 的长.【分析】(1)利用三角形的中位线可得AB ∥MF ,AB =MF ,结合平行四边形的性质可得MF ∥CD ,MF =CD ,进而可证明结论;(2)连接AF ,BF ,则AF 是△MNE 的中位线,证明四边形AFBE 是平行四边形,再利用平行四边形的性质可求解.【解答】(1)证明:∵AE =AM ,EB =BN ,∴AB 为△EMN 的中位线,∴AB∥MN,AB=12MN,∵MF=12MN,∴AB∥MF,AB=MF,∵四边形ABCD为平行四边形,∴AB∥CD,AB=CD,∴MF∥CD,MF=CD,∴四边形MFCD为平行四边形;(2)解:连接AF,BF,则AF是△MNE的中位线,∴AF∥EB,AF=EB,∴四边形AFBE是平行四边形,∴OF=OE=2,∴EF=4.6.(2021秋•市南区期末)已知:在平行四边形ABCD中,分别延长BA,DC到点E,H,使得BE=2AB,DH=2CD.连接EH,分别交AD,BC于点F,G.(1)求证:AF=CG;(2)连接BD交EH于点O,若EH⊥BD,则当线段AB与线段AD满足什么数量关系时,四边形BEDH是正方形?【分析】(1)要证明AF=CG,只要证明△EAF≌△HCG即可;(2)利用已知可得四边形BEDH是菱形,所以当AE2+DE2=AD2时,∠BED=90°,四边形BEDH是正方形.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∠BAD=∠BCD,∴∠AEF=∠CHG,∵BE=2AB,DH=2CD,∴BE=DH,∴BE﹣AB=DH﹣DC,∴AE=CH,∵∠BAD+∠EAF=180°,∠BCD+∠GCH=180°,∴∠EAF=∠GCH,∴△EAF≌△HCG(ASA),∴AF=CG;(2)当AD=√5AB时,四边形BEDH是正方形,理由:∵BE∥DH,BE=DH,∴四边形EBHD是平行四边形,∵EH⊥BD,∴四边形EBHD是菱形,∴ED=EB=2AB,当AE2+DE2=AD2时,则∠BED=90°,∴四边形BEDH是正方形,即AB2+(2AB)2=AD2,∴AD=√5AB,∴当AD=√5AB,四边形BEDH是正方形.7.(2021秋•砚山县期末)如图,四边形ABCD是菱形,点H为对角线AC的中点,点E 在AB的延长线上,CE⊥AB,垂足为E,点F在AD的延长线上,CF⊥AD,垂足为F,∠ECA=60°.(1)求证:四边形CEHF是菱形;(2)已知四边形CEHF的周长为16cm,求菱形ABCD的面积.【分析】(1)证CE=CF=EH=FH,即可得出结论;(2)连接BD,求出AC、BD的长,即可解决问题.【解答】(1)证明:∵CE⊥AB,CF⊥AD,∴∠AEC=∠AFC=90°,∵∠ECA=60°,∴∠CAE=30°,∴CE=12AC,∵点H为对角线AC的中点,∴EH=FH=12AC,∴CE=EH=FH,∵四边形ABCD是菱形,∴∠BAC=∠DAC,又∵CE⊥AB,CF⊥AD,∴CE=CF,∴CE=CF=EH=FH,∴四边形CEHF是菱形;(2)解:连接BD,∵四边形CEHF是菱形,周长为16cm,∴CE=4cm,∴AC=2CE=8(cm),∵四边形ABCD是菱形,点H为对角线AC的中点,∴AH=12AC=4(cm),BH=DH,AC⊥BD,∴∠AHB=90°,∵∠CAE=30°,BH=√33AH=4√33(cm),∴BD=2BH=8√33(cm),∴菱形ABCD的面积=12AC×BD=12×8×8√33=32√33(cm2).8.(2021秋•寿光市期末)如图,点E是平行四边形ABCD对角线AC上一点,点F在BE 延长线上,且EF=BE,EF与CD交于点G.(I)求证:DF∥AC;(2)连接DE、CF,若2AB=BF,G恰好是CD的中点,求证:四边形CFDE是矩形.【分析】(1)连接BD,交AC于点O,证出OE是△BDF的中位线,得OE∥DF即可;(2)先证△DFG≌△CEG(AAS),得FG=EG,则四边形CFDE是平行四边形,再证CD=EF,即可得出结论.【解答】(1)证明:连接BD,交AC于点O,如图所示:∵四边形ABCD是平行四边形,∴BO=DO,∵BE=EF,∴OE是△BDF的中位线,∴OE∥DF,即DF∥AC;(2)证明:如图所示:由(1)得:DF∥AC,∴∠DFG =∠CEG ,∠GDF =∠GCE ,∵G 是CD 的中点,∴DG =CG ,在△DFG 和△CEG 中,{∠DFG =∠CEG ∠GDF =∠GCE DG =CG,∴△DFG ≌△CEG (AAS ),∴FG =EG ,∴四边形CFDE 是平行四边形,∵四边形ABCD 是平行四边形,∴AB =CD ,∵2AB =BF ,∴2CD =BF ,又∵EF =BE ,∴CD =EF ,∴平行四边形CFDE 是矩形.9.(2021秋•成都期末)如图,在四边形ABCD 中AD ∥CB ,O 为对角线AC 的中点,过点O 作直线分别与四边形ABCD 的边AD ,BC 交于M ,N 两点,连接CM ,AN .(1)求证;四边形ANCM 为平行四边形;(2)当MN 平分∠AMC 时,①求证;四边形ANCM 为菱形;②当四边形ABCD 是矩形时,若AD =8,AC =4√5,求DM 的长.【分析】(1)根据全等三角形的性质得到AM =CN ,根据平行四边形的判定定理即可得到结论;(2)①根据角平分线的定义得到∠AMN =∠CMN ,根据平行线的性质得到∠AMN =∠CNM ,得到CM =CN ,根据菱形的判定定理得到平行四边形ANCM 为菱形;②根据菱形的性质得到∠ABN =90°,BC =AD =8,根据勾股定理得到即可得到结论.【解答】(1)证明:∵AD ∥BC ,O 为对角线AC 的中点,∴AO =CO ,∠OAM =∠OCN ,在△AOM 和△CON 中,{∠OAM =∠OCN ∠AMO =∠CNO AO =CO,∴△AOM ≌△CON (AAS ),∴AM =CN ,∵AM ∥CN ,∴四边形ANCM 为平行四边形;(2)解:①∵MN 平分∠AMC ,∴∠AMN =∠CMN ,∵AD ∥BC ,∴∠AMN =∠CNM ,∴∠CMN =∠CNM ,∴CM =CN ,∴平行四边形ANCM 为菱形;②∵四边形ABCD 是矩形,∴∠ABN =90°,BC =AD =8,∴AB =√AC 2−BC 2=√(4√5)2−82=4,AM =AN =NC =AD ﹣DM ,在Rt △ABN 中,根据勾股定理,得AN 2=AB 2+BN 2,∴(8﹣DM )2=42+DM 2,解得DM =3.故DM 的长为3.10.(2021秋•南岗区期末)已知:在▱ABCD 中,对角线AC 与BD 交于点O ,过点O 作EF ⊥BD ,分别交AB ,DC 于点E ,F ,连接BF ,DE .(1)如图1,求证:四边形DEBF 是菱形;(2)如图2,AD ∥EF ,且AD =AE ,在不添加任何辅助线的条件下,请直接写出图2中四个度数为30°的角.【分析】(1)证△DOF ≌△BOE (ASA ),得到DF ∥BE ,DF =BE ,则四边形DEBF 为平行四边形,再根据对角线互相垂直的平行四边形是菱形从而证得结论;(2)证四边形ADFE 是平行四边形,得AE =DF ,再证△ADE 是等边三角形,得∠AED =60°,然后由等腰三角形的性质和三角形的外角性质得∠EDB =∠EBD =12∠AED =30°,同理∠FDB =∠FBD =30°.【解答】(1)证明:∵四边形ABCD 为平行四边形,∴AB ∥CD ,∴∠OBE =∠ODF ,在△BOE 和△DOF 中,{∠OBE =∠ODF OB =OD ∠BOE =∠DOF,∴△BOE ≌△DOF (ASA ),∴BE =DF ,∵BE ∥DF ,∴四边形DEBF 是平行四边形,∵EF ⊥BD ,∴四边形DEBF 是菱形;(2)解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,∵AD ∥EF ,∴四边形ADFE 是平行四边形,∴AE =DF ,由(1)得:四边形DEBF 是菱形,∴DE =DF =BE ,∴AD =DE ,∵AD =AE ,∴AD =AE =DE ,∴△ADE 是等边三角形,∴∠AED =60°,∵DE =BE ,∴∠EDB =∠EBD =12∠AED =30°,同理:∠FDB =∠FBD =30°,即图2中四个度数为30°的角为∠EDB 、∠EBD 、∠FDB 、∠FBD .11.(2021秋•和平县期末)如图,在平行四边形ABCD 中,对角线AC 与BD 相交于点O ,点E ,F 分别在BD 和DB 的延长线上,且DE =BF ,连接AE ,CF .(1)求证:CF =AE ;(2)当BD 平分∠ABC 时,四边形AFCE 是什么特殊四边形?请说明理由.【分析】(1)根据四边形ABCD 是平行四边形,得AD =BC ,AD ∥BC ,可证∠ADE =∠CBF ,然后通过SAS 证△ADE ≌△CBF 即可证得结论;(2)由BD 平分∠ABC ,得∠ABD =∠CBD ,又因为∠ADB =∠CBD ,则∠ABD =∠ADB ,有AB =AD ,可证出AC ⊥BD ,然后证出四边形AFCE 为平行四边形即可解决问题.【解答】(1)证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∴∠ADB =∠CBD ,∴∠ADE =∠CBF ,在△ADE 和△CBF 中,{AD =CB ∠ADE =∠CBF DE =BF,∴△ADE ≌△CBF (SAS ),∴CF =AE ;(2)解:四边形AFCE 是菱形,理由如下:∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD ,∵DE =BF ,∴OD +DE =OB +BF ,即OE =OF ,∴四边形AFCE 是平行四边形,∵BD 平分∠ABC ,∴∠ABD=∠CBD,∵AD∥BC,∴∠ADB=∠CBD,∴∠ABD=∠ADB,∴AB=AD,∴平行四边形ABCD是菱形,∴AC⊥EF,∴四边形AFCE是菱形.12.(2021秋•太平区期末)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.(1)求证:CE=AD;(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)【分析】(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;(3)当∠A=45°,四边形BECD是正方形.【解答】(1)证明:∵DE⊥BC,∴∠DFB=90°,∵∠ACB=90°,∴∠ACB=∠DFB,∴AC∥DE,∵MN∥AB,即CE∥AD,∴四边形ADEC是平行四边形,∴CE=AD;(2)解:四边形BECD是菱形,理由是:∵D为AB中点,∴AD=BD,∵CE=AD,∴BD=CE,∵BD∥CE,∴四边形BECD是平行四边形,∵∠ACB=90°,D为AB中点,∴CD=BD,∴四边形BECD是菱形;(3)解:当∠A=45°时,四边形BECD是正方形,理由:∵∠ACB=90°,∴∠ABC=45°,由(2)可知,四边形BECD是菱形,∴∠ABC=∠CBE=45°,∴∠DBE=90°,∴四边形BECD是正方形.13.(2021秋•法库县期末)如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.(1)如图1,求证:四边形ABCD为矩形;(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.【分析】(1)先证四边形ABCD是平行四边形,得出OA=OC=12AC,OB=OD=12BD,再证出AC=BD,即可得出结论;(2)由勾股定理可求AC=BD=13,由面积法可求解.【解答】证明:(1)∵AD∥BC,∴∠ABC +∠BAD =180°,∠ADC +∠BCD =180°,∵∠ABC =∠ADC ,∴∠BAD =∠BCD , ∴四边形ABCD 是平行四边形,∴OA =OC =12AC ,OB =OD =12BD ,∵OA =OB ,∴AC =BD ,∴四边形ABCD 是矩形;(2)如图,连接OP ,∵AD =12,AB =5,∴BD =√AB 2+AD 2=√144+25=13, ∴BO =OD =AO =CO =132,∵S △AOD =14S 矩形ABCD =14×12×5=15,∴S △AOP +S △POD =15,∴12×132×FP +12×132×EP =15,∴PE +PF =6013.14.(2021秋•兰州期末)如图,在正方形ABCD 中,点E 、F 分别为边BC 、CD 上两点,∠EAF =45°,过点A 作∠GAB =∠F AD ,且点G 为边CB 延长线上一点.①△GAB ≌△F AD 吗?说明理由.②若线段DF =4,BE =8,求线段EF 的长度.③若DF =4,CF =8.求线段EF 的长度.【分析】①由正方形的性质可知AB =AD ,∠ABG =∠D ,然后依据ASA 证明两个三角形全等即可;②依据SAS证明△AGE≌△AFE,从而可得到EF=GE,然后再由GB=DF可得到EF=BE+DF;③设EF=x,则EC=16﹣x,然后在Rt△EFC中,依据勾股定理列方程求解即可.【解答】解:①全等.证明:∵四边形ABCD为正方形∴AB=AD,∠ABG=∠D,在△ABG和△ADF中,∠GAB=∠F AD,AB=AD,∠ABG=∠D∴△GAB≌△F AD.②解:∵∠BAD=90°,∠EAF=45°∴∠DAF+∠BAE=45°∵△GAB≌△F AD∴∠GAB=∠F AD,AG=AF∴∠GAB+∠BAE=45°∴∠GAE=45°∴∠GAE=∠EAF在△GAE和△F AE中∵AG=AF,∠GAE=∠EAF,AE=AE∴△GAE≌△F AE(SAS)∴EF=GE.∵△GAB≌△F AD∴GB=DF∴EF=GE=GB+BE=FD+BE=8+4=12.③设EF=x,则BE=GE﹣BG=x﹣4.∵EC=BC﹣BE,∴EC=12﹣(x﹣4)=16﹣x.在Rt△EFC中,依据勾股定理可知:EF2=FC2+EC2,即(16﹣x)2+82=x2,解得:x=10.∴EF=10.15.(2020秋•安丘市期末)如图,在平行四边形ABCD中,对角线AC与BD交于点O,点M,N分别为OA、OC的中点,延长BM至点E,使EM=BM,连接DE.(1)求证:△AMB≌△CND;(2)若BD=2AB,且AM=3,DN=4,求四边形DEMN的面积.【分析】(1)依据平行四边形的性质,即可得到△AMB ≌△CND ;(2)依据全等三角形的性质,即可得出四边形DEMN 是平行四边形,再根据等腰三角形的性质,即可得到∠EMN 是直角,进而得到四边形DEMN 是矩形,即可得出四边形DEMN 的面积.【解答】(本题满分12分)(1)证明:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD ,OA =OC ,∴∠BAC =∠DCA ,又点M ,N 分别为OA 、OC 的中点,∴AM =12AO =12CO =CN ,在△AMB 和△CND 中,{AB =CD ∠BAC =∠DCA AM =CN,∴△AMB ≌△CND (SAS ).(2)解:BD =2BO ,又已知BD =2AB ,∴BO =AB ,∴△ABO 为等腰三角形;又M 为AO 的中点,∴由等腰三角形的“三线合一”性质可知:BM ⊥AO ,∴∠BMO =∠EMO =90°,同理可证DN ⊥CO ,∠DNO =90°,∵∠EMO +∠DNO =90°+90°=180°,∴EM ∥DN ,∵△AMB ≌△CND (SAS )∴BM =DN ,∵EM =BM ,∴EM ∥DN ,∵△AMB ≌△CND (SAS )∴BM =DN ,∵EM=BM,∴EM=DN,∴四边形EMND为平行四边形,∵四边形ABCD是平行四边形,又点M,N分别为OA、OC的中点,∴AM=MO﹣ON=NC=3,∴MN=MO+ON=2AM=6,∴矩形DEMN的面积为:MN×DN=6×4=24.16.(2020秋•市南区期末)已知:如图,在平行四边形ABCD中,E、F分别为AB、CD 的中点,G、H分别为DE、BF的中点.(1)试判断四边形EHFG的形状,并证明;(2)若∠ABC=90°,试判断四边形EHFG的形状并加以证明.【分析】(1)由平行四边形的性质可得AB=CD,AB∥CD,由中点的性质BE=DF,可证四边形BEDF是平行四边形,可得DE∥BF,DE=BF,由中点的性质可得EG=HF,可证四边形EHFG是平行四边形;(2)由直角三角形的性质可证EH=HF,可得结论.【解答】解:(1)四边形EHFG是平行四边形,理由如下:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∵点E、F分别为AB、CD的中点,∴BE=12AB,DF=12CD,∴BE=DF,又∵BE∥DF,∴四边形BEDF是平行四边形,∴DE∥BF,DE=BF,∵G、H分别为DE、BF的中点,∴EG=12DE=12BF=HF,∴四边形EHFG是平行四边形;(2)四边形EHFG是菱形,理由如下:如图,连接EF,∵AE=BE=DF=CF,AB∥DF,∴四边形AEFD是平行四边形,∴AD∥EF,∵∠ABC=90°,∴∠BEF=90°,∵BH=HF,∴EH=HF,∴平行四边形EHFG是菱形.17.(2020秋•沈北新区校级期末)如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=12AC,连接AE、CE.(1)求证:四边形OCED为矩形;(2)若菱形ABCD的边长为8,∠BCD=60°,则AE=4√13.【分析】(1)先证四边形OCED是平行四边形,再由∠DOC=90°,即可得出结论;(2)先证△BCD是等边三角形,得BD=BC=8,再由勾股定理得OC=4√3,则AC=2OC=8√3,然后由矩形的性质得CE=OD=4,∠OCE=90°,最后由勾股定理即可得出答案.【解答】(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,AO=OC=12AC,∴∠DOC=90°,∵DE∥AC,DE=12AC,∴DE=OC,DE∥OC,∴四边形OCED是平行四边形,又∵∠DOC=90°,∴平行四边形OCED是矩形;(2)解:∵四边形ABCD是菱形,∴AC⊥BD,BC=CD=8,OB=OD,AO=OC=12AC,∵∠BCD=60°,∴△BCD是等边三角形,∴BD=BC=8,∴OD=OB=4,∴OC=√BC2−OB2=√82−42=4√3,∴AC=2OC=8√3,由(1)得:四边形OCED为矩形,∴CE=OD=4,∠OCE=90°,在Rt△ACE中,由勾股定理得:AE=√CE2+AC2=√42+(8√3)2=4√13,故答案为:4√13.18.(2021春•冠县期末)如图,在△ABC中,O是AC边上一点,过点O作BC的平行线,交∠BCA的平分线于点E,交外角∠ACD的平分线于点F.(1)求证:EO=OF;(2)连接AE,AF,当点O沿AC移动时,四边形AECF是否能成为一个矩形?此时,点O在什么位置?说明理由【分析】(1)由平行线的性质和角平分线的定义得出∠OCE=∠OEC,∠OCF=∠OFC,则EO=CO,FO=CO,即可得出结论;(2)先证明四边形AECF是平行四边形,再由对角线相等,即可得出结论.【解答】(1)证明:∵EF∥BC,∴∠OEC=∠BCE,∠OFC=∠DCF,又∵CE平分∠BCO,CF平分∠DCO,∴∠OCE=∠BCE,∠OCF=∠DCF,∴∠OCE=∠OEC,∠OCF=∠OFC,∴EO=CO,FO=CO,∴EO=FO;(2)解:当点O运动到AC的中点时,四边形AECF是矩形;理由如下:∵当点O运动到AC的中点时,AO=CO,又∵EO=FO,∴四边形AECF是平行四边形,∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴平行四边形AECF是矩形,即当点O沿AC移动时,四边形AECF能成为一个矩形,此时,点O在AC的中点.19.(2021•长兴县模拟)如图,在▱ABCD中,对角线AC,BD相交于点O,BD=2AD,点E在线段OC上,且OE=CE.(1)求证:∠OBE=12∠ADO;(2)若F,G分别是OD,AB的中点,且BC=10,①求证:△EFG是等腰三角形;②当EF⊥EG时,求▱ABCD的面积.【分析】(1)根据平行四边形的性质可得∠ADB=∠DBC,再证明△BOC是等腰三角形,根据等腰三角形的性质可得∠OBE=12∠OBC,进而可证明结论;(2)①首先证明EG=12AB,再根据三角形中位线的性质可得EF=12CD,进而得到EG=EF,可证明结论;②由①得EF∥AB,由EF⊥EG,G是AB的中点,可证得AE=BE,设CE=x,则AO=CO=2CE=2x,利用勾股定理可求解x值,进而可求解AC,BE,再利用平行四边形的面积公式可求解.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,DO=BO=12BD,∴∠ADB=∠DBC,∵BD=2AD,∴AD=DO,∴BC=BO,∵E是CO中点,∴∠OBE=12∠OBC,∴∠OBE=12∠ADO;(2)①证明:∵BC=BO,∴△BOC是等腰三角形,∵E是CO中点,∴EB⊥CO,∴∠BEA=90°,∵G为AB中点,∴EG=12AB,∵四边形ABCD是平行四边形,∴AB=CD,∵E、F分别是OC、OD的中点,∴EF=12CD∴EG=EF,∴△EFG是等腰三角形;②解:由①得EF∥AB,∵EF⊥EG,∴EG⊥AB,∵G是AB的中点,∴AE=BE,设CE=x,则AO=CO=2CE=2x,∴BE=AE=3x,在Rt△BEC中,BC=10,∴EC2+BE2=BC2,即x2+(3x)2=102,解得x=√10,∴AC=4√10,BE=3√10,∴S▱ABCD=2S△ABC=2×12×4√10×3√10=120.20.(2021春•富平县期末)在▱ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F,连接BF、DE如图1.(1)求证:四边形BEDF是平行四边形;(2)若DE=DC,∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H 、P 如图2.①当CD =6.CE =4时,求BE 的长;②求证:CD =CH .【分析】(1)通过ASA 证明△BOE ≌△DOF ,得DF =BE ,又DF ∥BE ,即可证明四边形BEDF 是平行四边形;(2)①过点D 作DN ⊥EC 于点N ,先根据勾股定理求出DN =4√2,由∠DBC =45°得BN =DN ,即可求出答案;②根据DN ⊥EC ,CG ⊥DE ,得∠CEG +∠ECG =90°,∠DEN +∠EDN =90°,则有∠EDN =∠ECG ,再证∠CDH =∠CHD ,得出CD =CH .【解答】(1)证明:∵在平行四边形ABCD 中,点O 是对角线BD 的中点,∴AD ∥BC ,BO =DO ,∴∠ADB =∠CBD ,在△BOE 与△DOF 中,{∠CBD =∠ADB BO =DO ∠BOE =∠DOF,∴△BOE ≌△DOF (ASA ),∴DF =BE 且DF ∥BE ,∴四边形BEDF 是平行四边形;(2)①解:如图,过点D 作DN ⊥EC 于点N ,∵DE =DC =6,DN ⊥EC ,CE =4,∴EN =CN =2,∴DN =√DC 2−CN 2=√36−4=4√2, ∵∠DBC =45°,DN ⊥BC ,∴∠DBC=∠BDN=45°,∴DN=BN=4√2,∴BE=BN﹣EN=4√2−2,②证明:∵DN⊥EC,CG⊥DE,∴∠CEG+∠ECG=90°,∠DEN+∠EDN=90°,∴∠EDN=∠ECG,∵DE=DC,DN⊥EC,∴∠EDN=∠CDN,∴∠ECG=∠CDN,∵∠DHC=∠DBC+∠BCH=45°+∠BCH,∠CDB=∠BDN+∠CDN=45°+∠CDN,∴∠CDB=∠DHC,∴CD=CH.21.(2021春•临沧期末)如图,菱形ABCD的对角线AC、BD相交于点O,过点B作BE∥AC,且BE=12AC,连接EC.(1)求证:四边形BECO是矩形;(2)连接ED交AC于点F,连接BF,若AC=6,AB=5,求BF的长.【分析】(1)由菱形的性质得∠BOC=90°,OC=12AC,推出BE=OC,则四边形BECO是平行四边形,再由∠BOC=90°,即可得出结论;(2)由勾股定理求出OB=4,则BD=2OB=8,再证△ODF≌△CEF(ASA),得DF =EF,然后由直角三角形斜边上的中线性质即可求解.【解答】(1)证明:∵四边形ABCD是菱形,∴∠BOC=90°,OC=OA=12AC,∵BE=12AC,∴BE=OC,∵BE∥AC,∴四边形BECO是平行四边形,∵∠BOC=90°,∴平行四边形BECO是矩形;(2)解:∵四边形ABCD是菱形,∴BC=AB=5,OC=12AC=3,OB=OD,AC⊥BD,在Rt△OBC中,由勾股定理得:OB=√BC2−OC2=√52−32=4,∴BD=2OB=8,由(1)得:四边形BECO是矩形,∴BE=OC=3,∠OBE=∠ECO=90°,OB=CE,OB∥CE,∴DE=√BD2+BE2=√82+32=√73,∠ODF=∠CEF,OD=CE,∵∠DOF=∠ECF=90°,∴△ODF≌△CEF(ASA),∴DF=EF,∵∠DBE=90°,∴BF=12DE=√732.22.(2021春•淮阳区校级期末)如图,在平行四边形ABCD中,M,N是对角线BD上的点,且BM=DN,DE平分∠ADB交AB于点E,BF平分∠DBC交CD于点F.(1)求证:四边形EMFN是平行四边形;(2)当四边形EMFN是菱形时,求证:四边形BEDF是菱形.【分析】(1)连接EF交MN于O,证△ADE≌△CBF(ASA),得DE=BF,再证DE ∥BF,则四边形BEDF是平行四边形,得OE=OF,OB=OD,然后证OM=ON,即可得出结论;(2)由菱形的性质得EF⊥MN,由(1)得四边形BEDF是平行四边形,即可得出结论.【解答】证明:(1)连接EF交MN于O,∵四边形ABCD是平行四边形,∴∠A=∠C,AD=BC,AD∥BC,∴∠ADB=∠DBC,∵DE平分∠ADB,BF平分∠DBC,∴∠ADE =∠EDB =∠CBF =∠FBD ,在△ADE 和△CBF 中,{∠A =∠C AD =BC ∠ADE =∠CBF,∴△ADE ≌△CBF (ASA ),∴DE =BF ,∵∠EDB =∠FBD ,∴DE ∥BF ,∴四边形BEDF 是平行四边形,∴OE =OF ,OB =OD ,∵BM =DN ,∴OB ﹣BM =OD ﹣DN ,即OM =ON ,∴四边形EMFN 是平行四边形;(2)∵四边形EMFN 是菱形,∴EF ⊥MN ,由(1)得:四边形BEDF 是平行四边形,∴平行四边形BEDF 是菱形.23.(2021春•肥东县期末)如图1,在平行四边形ABCD 中,AB =8,AD =14,∠BAD 的平分线交BC 于点E 交DC 的延长线于F ,以EC ,CF 为邻边作▱ECFG .(1)求EC 的长;(2)求证:▱ECFG 是菱形;(3)如图2,若∠ABC =90°,M 是EF 的中点,求DM 的长.【分析】(1)证∠BAE=∠BEA,则BE=AB=8,即可求解;(2)证∠CEF=∠CFE,则CE=CF,即可得出结论;(3)过M作MH⊥DF于H,证四边形ECFG为正方形,则∠CEF=45°,∠ECF=90°,得BE=AB=8,则CE=CF=6,再证MH是△CEF的中位线,得CH=FH=12CF=3,MH=12CE=3,则DH=CD+CH=11,然后由勾股定理求解即可.【解答】(1)解:∵四边形ABCD是平行四边形,∴BC=AD=14,AD∥BC,∴∠DAE=∠BEA,∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠BEA,∴BE=AB=8,∴EC=BC﹣BE=14﹣8=6;(2)证明:∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴▱ECFG是菱形;(3)解:过M作MH⊥DF于H,如图2所示:∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,∴∠BCD=∠ECF=90°,由(2)可知:四边形ECFG为菱形,∴四边形ECFG为正方形,∴∠CEF=45°,∠ECF=90°,∴∠AEB=∠CEF=45°,CE⊥CF,∴BE=AB=8,∴CE=CF=14﹣8=6,∵M是EF的中点,∴EM=FM,∵MH⊥CF,∴MH∥CE,∴MH是△CEF的中位线,∴CH=FH=12CF=3,MH=12CE=3,∴DH=CD+CH=8+3=11,∴DM=√DH2+MH2=√112+32=√130.24.(2021春•大连期末)如图,四边形ABCD和CEFG都是正方形,点E在BC的延长线上,且CE<BC,连接BG并延长交DE于H.(1)写出BH与DE的位置关系,并证明;(2)求证:∠BHC=45°.【分析】(1)根据正方形的性质利用SAS判定△BCG≌△DCE,全等三角形的对应边相等,得到∠CBG=∠CDE,再根据角之间的关系可得到∠EHB=90°,即BH⊥DE.(2)过点C作CM⊥BH于M,过C作CN⊥DE于N,通过正方形的性质利用AAS证明△BCM≌△DCN,得到CM=CN,进而得到CH平分∠BHE,进而可证∠BHC=45°.【解答】解:(1)BH⊥DE,理由如下:∵四边形ABCD和CEFG都是正方形,∴BC =DC ,∠BCG =∠DCE =90°,CG =CE ,∴∠CDE +∠DEC =90°,在△BCG 和△DCE 中,{BC =DC ∠BCG =∠DCE CG =CE,∴△BCG ≌△DCE (SAS ),∴∠CBG =∠CDE ,∴∠CBG +∠DEC =90°,∴∠EHB =90°,∴BH ⊥DE .(2)过点C 作CM ⊥BH 于M ,过C 作CN ⊥DE 于N ,∴∠CMB =∠CND =90°,在△BCM 和△DCN 中,{∠CMB =∠CND =90°∠CBM =∠CDN BC =CD,∴△BCM ≌△DCN (AAS ),∴CM =CN ,∵CM ⊥BH ,CN ⊥DE∴CH 平分∠BHE ,∴∠BHC =45°.25.(2021春•法库县期末)如图,平行四边形ABCD 中,CG ⊥AB 于点G ,∠ABF =45°,点F 在CD 上,BF 交CG 于点E ,连接AE ,AE ⊥AD . (1)若BG =1,BC =√5,求EF 的长度;(2)求证:△BCG ≌△EAG ;(3)直接写出三条线段CD ,CE ,BE 之间的数量关系.【分析】(1)根据勾股定理得出CG,进而利用平行四边形的性质解答即可;(2)延长AE交BC于H,根据平行四边形的性质得到BC∥AD,根据平行线的性质得到∠AHB=∠HAD,推出∠GAE=∠GCB,则可证明△BCG≌△EAG;(3)根据全等三角形的性质得到AG=CG,于是得到结论.【解答】解:(1)∵CG⊥AB,∴∠AGC=∠BGC=90°,∵BG=1,BC=√5,∴CG=√BC2−BG2=2,∵∠ABF=45°,∴BG=EG=1,∴EC=1,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠GCD=∠BGC=90°,∠EFC=∠GBE=45°,∴CF=CE=1,∴EF=√EC2+CF2=√2;(2)如图,延长AE交BC于H,∵四边形ABCD是平行四边形,∴BC∥AD,AB=CD,∵AE⊥AD,∴∠AHB=∠HAD=90°,∴∠BAH+∠ABH=∠BCG+∠CBG=90°,∴∠GAE =∠GCB ,在△BCG 与△EAG 中,{∠AGE =∠CGB =90°∠GAE =∠GCB GE =BG,∴△BCG ≌△EAG (AAS ),(3)CD ﹣CE =√2BE ,∵△BCG ≌△EAG ,∴BG =GE ,CG =AG , ∵∠BGC =90°,∴BE =√2BG =√2GE ,(2)CE +BE =√2CD ,∵△BCG ≌△EAG (AAS ),∴AG =CG ,∴AB =BG +AG =CE +EG +BG ,∵BG =EG =√22BE ,∴CE +√2BE =AB =CD .26.(2021春•迁安市期末)已知:如图,在▱ABCD 中,对角线AC 、BD 相交于点O ,点G 、H 分别是AD 、BC 的中点,点E 、O 、F 分别是对角线BD 上的四等分点,顺次连接G 、E 、H 、F .(1)求证:四边形GEHF 是平行四边形;(2)若四边形GEHF 是菱形.①线段AB 和BD 有何位置关系?请说明理由.②若AB =2,BD =2AB 时,求四边形GEHF 的面积.【分析】(1)由三角形中位线定理可得GF ∥OA ,GF =12OA ,EH ∥OC ,EH =12OC ,可得EH ∥GF ,EH =GF ,可得结论;(2)①先证四边形ABHG 是平行四边形,可得AB ∥GH ,由菱形的性质可得GH ⊥BD ,即可得结论;②分别求出GH ,EF 的长,由菱形的面积公式可求解.【解答】证明:(1)∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD.∵E,O,F分别是对角线BD上的四等分点,∴E,F分别为OB,OD的中点,∵G是AD的中点,∴GF为△AOD的中位线,∴GF∥OA,GF=12OA,同理EH∥OC,EH=12OC,∴EH∥GF,EH=GF,∴四边形GEHF是平行四边形;(2)①AB⊥BD,理由如下:如图,连接GH,∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵点G、H分别是AD、BC的中点,∴AG=12AD,BH=12BC,∴AG=BH,∴四边形AGHB是平行四边形,∴AB∥HG,∵四边形GEHF是菱形,∴GH⊥EF,∴AB⊥EF,即AB⊥BD;②∵AB=2,BD=2AB,∴BD=4,∵点E、O、F分别是对角线BD上的四等分点,∴EO=OF=1,∴EF=2,∵四边形AGHB是平行四边形,∴GH=AB=2,∵四边形GEHF是菱形,∴四边形GEHF的面积=12×EF×GH=12×2×2=2.27.(2021春•上城区校级期末)如图,在△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交△ABC的外角∠ACD的平分线于点F.(1)探究线段OE与OF的数量关系并说明理由.(2)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?请说明理由.(3)当点O在边AC上运动时,四边形BCFE不可能是菱形(填“可能”或“不可能”).请说明理由.【分析】(1)由直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;(2)正方形的判定问题,AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;(3)菱形的判定问题,若使菱形,则必有四条边相等,对角线互相垂直.【解答】解:(1)OE=OF.理由如下:∵CE是∠ACB的角平分线,∴∠ACE=∠BCE,又∵MN∥BC,∴∠NEC=∠ECB,∴∠NEC=∠ACE,∴OE=OC,∵CF是∠BCA的外角平分线,∴∠OCF=∠FCD,又∵MN∥BC,∴∠OFC=∠FCD,∴∠OFC=∠OCF,∴OF=OC,∴OE=OF;(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:∵当点O运动到AC的中点时,AO=CO,又∵EO=FO,∴四边形AECF是平行四边形,∵FO=CO,∴AO=CO=EO=FO,∴AO+CO=EO+FO,即AC=EF,∴四边形AECF是矩形.已知MN∥BC,当∠ACB=90°,则∠AOF=∠COE=∠COF=∠AOE=90°,∴AC⊥EF,∴四边形AECF是正方形;(3)不可能.理由如下:如图,∵CE平分∠ACB,CF平分∠ACD,∴∠ECF=12∠ACB+12∠ACD=12(∠ACB+∠ACD)=90°,若四边形BCFE是菱形,则BF⊥EC,但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.故答案为不可能.28.(2021春•酒泉期末)(1)如图1,正方形ABCD中,E、F分别是BC、CD边上的点,且满足BE=CF,连接AE、BF交于点H.请直接写出线段AE与BF的数量关系和位置关系.(2)如图2,在正方形ABCD中,E、F分别是BC、CD边上的点,连接BF,过点E作EG⊥BF于点H,交AD于点G,试判断线段BF与GE的数量关系,并证明你的结论.【分析】(1)根据全等三角形的判定得到△ABE ≌△BCF ,由全等三角形的性质得到AE =BF ,∠BAE =∠CBF ,求出∠CBF +∠AEB =90°,求出∠BHE =90°即可;(2)过点A 作AM ∥GE 交BC 于M ,根据全等三角形的判定定理得到△ABM ≌△BCF ,由全等三角形的性质得到AM =BF ,根据AM ∥GE 且AD ∥BC 推出AM =GE 即可.【解答】解:(1)AE =BF 且AE ⊥BF ,理由是:∵四边形ABCD 是正方形,∴∠ABE =∠C =90°,AB =BC ,在△ABE 和△BCF 中{AB =BC ∠ABC =∠C BE =CF,∴△ABE ≌△BCF (SAS ),∴AE =BF ,∠BAE =∠CBF ,∵∠ABE =90°,∴∠BAE +∠AEB =90°,∴∠CBF +∠AEB =90°,∴∠BHE =180°﹣90°=90°,∴AE ⊥BF .(2)BF =GE ,证明:过点A 作AM ∥GE 交BC 于M ,∵EG ⊥BF ,∴AM ⊥BF ,∴∠BAM +∠ABF =90°,∵四边形ABCD 是正方形,∴AB =BC ,AD ∥BC ,∠ABC =∠BCD =90°,∴∠CBF +∠ABF =90°,∴∠BAM =∠CBF ,在△ABM 和△BCF 中{∠BAM =∠CBF AB =BC ∠ABM =∠C,∴△ABM ≌△BCF (ASA ),∴AM =BF ,∵AM ∥GE 且AD ∥BC ,∴AM =GE ,∴BF=GE.29.(2021春•鞍山期末)如图,在正方形ABCD中,边长为3.点M,N是边AB,BC上两点,且BM=CN=1,连接CM,DN;(1)则DN与CM的数量关系是CM=DN,位置关系是DN⊥CM.(2)若点E,F分别是DN与CM的中点,计算EF的长;(3)延长CM至P,连接BP,若∠BPC=45°,试求PM的长.【分析】(1)证△BCM≌△CDN,得出CM=DN,∠BCM=∠CDN,再证∠CDN+∠DCM=90°即可;(2)连CE并延长交AD于G,求出GM长,再根据中位线的性质求出EF即可;(3)过点B作BH⊥CM于点H,根据勾股定理求出BH=PH=3√1010,CM=√10,PC=6√105即可.【解答】解:(1)如图1,设CM与DN相交于点O,∵四边形ABCD是正方形,∴BC=CD,∠B=∠NCD=90°,∵BM=CN,∴△BCM≌△CDN(SAS),。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P
M
N
A
B
C
D
R
特殊四边形的性质与判定练习题
1. 若矩形的一条角平分线分一边为3cm 和5cm 两部分,则矩形的周长为 ( ) A .22 B .26
C .22或26
D .28
2.已知一矩形的周长是24cm ,相邻两边之比是1:2,那么这个矩形的面积是 ( ) A .24cm 2
B .32cm 2
C .48cm 2
D .128cm 2
3.由矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对
角线的夹角为( )
A 、22.5°
B 、45°
C 、30°
D 、60°
4.如图,在矩形ABCD 中,DE ⊥AC,∠ADE= ∠CDE,那么∠BDC 等于( )
A .60°
B .45°
C .30°
D .22.5°
5.如图,过矩形ABCD 的对角线BD 上一点R 分别作矩形两边的平行线MN 与PQ ,那么图中矩形AMRP
的面积S 1,与矩形QCNR 的面积S 2的大小关系是 ( ) A. S 1> S 2 B. S 1= S 2 C. S 1< S 2 D. 不能确定
6.平行四边形的一边长是10cm ,那么这个平行四边形的两条对角线的长可以是() A.4cm 和6cm B.6cm 和8cm C.8cm 和10cm D.10cm 和12cm
7.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是( ) A.AC =BD ,AB =CD ,AB ∥CD B.AD //BC ,∠A =∠C
C.AO =BO =CO =DO ,AC ⊥BD
D.AO =CO ,BO =DO ,AB =BC
8.下列命题中,真命题是( )
A 、有两边相等的平行四边形是菱形
B 、对角线垂直的四边形是菱形
C 、四个角相等的菱形是正方形
D 、两条对角线相等的四边形是矩形 9.平行四边形各内角平分线若围成一个四边形,则这个四边形一定是( ) A 、矩形 B 、平行四边形 C 、菱形 D 、正方形
10.任意四边形四边中点所得的四边形一定是()
A、平行四边形
B、矩形
C、菱形
D、正方形
11.已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.
12.在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的条件是( )
A.AC=BD,AB=CD,AB∥CD
B.AD//BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
13、矩形ABCD的两条对角线相交于O,∠AOB=60o,AB=8,则矩形对角线的长___
14、矩形的两条对角线的夹角为60°,若一条对角线与短边的和为15,则短边的长是,对角线的长是。
15.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,
设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
①EO与FO有何等量关系
②当O点运动到何处时,四边形AECF是什么四边形
16.下面性质中菱形有而矩形没有的是()
(A)邻角互补(B)内角和为360°(C)对角线相等(D)对角线互相垂直
17.菱形ABCD中,∠BAD=60°,BD=4,则菱形ABCD的周长是_______.
18.知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是______cm.
19.知四边形ABCD是平行四边形,下列结论不正确的是()
A. 当AB=BC时,它是菱形;
B. 当AC⊥BD时,它是菱形;
C. 当∠ABC=90°时,它是矩形;
D. 当AC=BD时,它是菱形
20.圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是()
A、一组临边相等的四边形是菱形
B、每条对角线平分一组对角的平行四边形是菱形
C、对角线互相垂直的平行四边形是菱形
D、四边相等的四边形是菱形
21.顺次连结一个四边形的四边中点所组成的四边形是矩形,则原四边形一定是()A.一般平行四边形 B.对角线互相垂直的四边形 C.对角线相等的四边形 D.矩形
22、如图,矩形ABCD 的对角线相交于点O ,DE ∥CA ,AE ∥BD . (1)则四边形AODE 是什么四边形?__________________
(2)若将题设中“矩形ABCD ”这一条件改为“菱形ABCD ”,其余条件不变, 则四边形AODE 又是什么四边形?__________________ 23.列条件中,能判断一个四边形是矩形的有( )个
A. 一组对边平行且相等,有一个内角是直角 B 对角线互相平分且相等 C. 对角线互相垂直且相等 D对边平行,另一组对边相等.且两条对角线相等 24.下列条件中,不能判定四边形ABCD 为矩形的是( ). A .AB ∥CD ,AB=CD ,AC=BD B .∠A=∠B=∠D=90° C .AB=BC ,AD=CD ,且∠C=90° D .AB=CD ,AD=BC ,∠A=90° 25.如图,四边形ABCD 是由两个全等的正三角形ABD 和BCD 组成的, M 、N•分别为BC 、AD 的中点.则边形BMDN 是什么四边形 26.如图,在梯形ABCD 中,AD BC AB DE AF DC E F ∥,∥,∥,、 两点在边BC 上,且四边形AEFD 是平行四边形.则 (1)AD 与BC 有何等量关系
(2)当AB DC 时,□AEFD 是什么四边形 27.在矩形ABCD 中,E 是BC 的中点,且EA ⊥ED .•若矩形ABCD•的 周长为48cm ,•则矩形ABCD 的面积为_______cm 2
.
28、矩形一个角的平分线分矩形一边成2cm 和3cm ,则这个矩形的面积为 。
29.在矩形ABCD 中,AE 平分∠BAD ,∠1=15°. (1)求∠2的度数.(2)求证:BO =BE
A D
C
E B
N
M D C
B
A
30.已知:AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC.求证:四边形EBCF是矩形.
31.在平行四边形ABCD中,AE平分∠BAD,与BC相交于点E,EF//AB,与AD相交于点F.
求证:四边形ABEF是菱形.
32.平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是CD的中点,过点A作AG∥BD,交CB的延长线于点G.
(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明.
F
E
B
A
33、在△ABC 中,∠ACB=90°,BC 的垂直平分线DE 交BC 于D ,交AB 于E ,F 在DE 上,且AF=CE=AE . (1)说明四边形ACEF 是平行四边形;
(2)当∠B 满足什么条件时,四边形ACEF 是菱形,并说明理由.
34.已知:在▱ABCD 中,O 为对角线BD 的中点,过点O 的直线EF 分别交AD ,BC 于E ,F 两点,连结BE ,DF . (1)求证:△DOE ≌△BOF .
(2)当∠DOE 等于多少度时,四边形BFED 为菱形?请说明理由.
35.在△ABC 和△DCB 中,AB = DC ,AC = DB ,AC 与DB 交于点M . (1)求证:△ABC ≌△DCB ;
(2)过点C 作CN ∥BD ,过点B 作BN ∥AC ,CN 与BN 交于点N ,试判断线段
BN 与CN 的数量关系,并证明你的结论.
B C
A D
M
N。
