现代密码学——流密码系统(实验报告)
密码学案例实验报告书

一、实验背景随着信息技术的飞速发展,信息安全问题日益突出。
密码学作为保障信息安全的核心技术,在数据加密、身份认证、数字签名等领域发挥着重要作用。
为了加深对密码学原理的理解,提高实际应用能力,我们开展了本次密码学案例实验。
二、实验目的1. 掌握DES加密算法的基本原理和操作步骤。
2. 熟悉RSA加密算法的原理和应用。
3. 学习数字签名技术的应用。
4. 培养动手实践能力,提高解决实际问题的能力。
三、实验内容1. DES加密算法(1)实验目的:了解DES加密算法的基本原理,掌握DES加密和解密过程。
(2)实验内容:① 设计一个简单的DES加密程序,实现明文到密文的转换。
② 设计一个简单的DES解密程序,实现密文到明文的转换。
(3)实验步骤:① 编写DES加密程序,输入明文和密钥,输出密文。
② 编写DES解密程序,输入密文和密钥,输出明文。
2. RSA加密算法(1)实验目的:了解RSA加密算法的基本原理,掌握RSA加密和解密过程。
(2)实验内容:① 设计一个简单的RSA加密程序,实现明文到密文的转换。
② 设计一个简单的RSA解密程序,实现密文到明文的转换。
(3)实验步骤:① 编写RSA加密程序,输入明文和密钥对,输出密文。
② 编写RSA解密程序,输入密文和私钥,输出明文。
3. 数字签名技术(1)实验目的:了解数字签名技术的基本原理,掌握数字签名的生成和验证过程。
(2)实验内容:① 设计一个简单的数字签名程序,实现签名生成和验证。
(3)实验步骤:① 编写数字签名程序,输入明文、私钥和签名算法,输出签名。
② 编写数字签名验证程序,输入明文、公钥和签名,验证签名是否正确。
四、实验结果与分析1. DES加密算法实验结果通过编写DES加密和解密程序,成功实现了明文到密文和密文到明文的转换。
实验结果表明,DES加密算法在保证数据安全的同时,具有较高的效率。
2. RSA加密算法实验结果通过编写RSA加密和解密程序,成功实现了明文到密文和密文到明文的转换。
现代密码学第五讲(一):流密码

现代密码学第五讲(一):流密码《现代密码学》第五讲流密码(一)上讲内容回顾分组密码定义(分组填充)分组密码的发展历史(Shannon DES AES。
)保密系统的安全性分析及分组密码的攻击(主动/被动唯密文/已知明(密)文/选择明(密)文/自适应选择明(密)文)数据加密标准(DES)算法介绍高级加密标准(AES)算法介绍中国无限局域网标准(SMS4)算法介绍?分组密码算法的运行模式本章主要内容流密码(序列密码)的思想起源?流密码技术的发展及分类基于移位寄存器的流密码算法?其它流密码算法Estream推荐流密码算法软件算法硬件算法密钥流生成器种子密钥明文m1k1c1m2k2c2加密过程密钥流生成器种子密钥密文c1k1m1c2k2m2解密过程设明文为m=m1m2… m i∈GF(2), i>0?设密钥为k=k1k2… ki∈GF(2), i>0?设密文为c=c1c2… c i∈GF(2), i>0?则加密变换为c i=m i+ k i(mod 2) i>0?则解密变换为m i=c i+ k i(mod 2) i>0思想起源:20世纪20年代的Vernam 体制,即“一次一密”密码体制。
香农利用信息论证明“一次一密”密码体制在理论上不可破译?由有限的种子密钥生成无限长的随机密钥序列?流密码研究内容——设计安全高效的伪随机序列发生器密钥流生成、存储和分发困难随机序列计算机无法实现评测标准:线性复杂度高;周期大Golomb伪随机性测试周期为r的0-1序列的随机性公设如下:r是奇数,则0-1序列{si}的一个周期内0的个数比1的个数多一个或少一个;若r是偶数,则0的个数与1的个数相等.在长度为r的周期内,长为1的游程的个数为游程总数的1/2,长为2的游程的个数占游程总数的1/22,…, 长为c的游程的个数占总游程的1/2c.而且对于任意长度,0的游程个数和1的游程个数相等.例:0110111101中,4个游程长度为1,1个游程长度为2,1个游程长度为4异相自相关函数是一个常数.设一个周期为r的序列a1, a2,…, a r, a r+1, a r+2,…,将序列平移T位得到另外一个序列a T, a T+1,… a r+T, a r+T+1,…,若a i= a i+T, 则称对应第i位相等。
现代密码学-流密码

7
2.1 流密码一般模型
流密码的分类 同步流密码(SSC: synchronous stream cipher)
产生密钥序列的算法与明文、密文无关.
i F ( i 1 , k ), zi f ( i , k ),
ci E ( zi , mi ).
k
密钥流生成器
i : 密钥流生成器的内部状态 0 : 密钥流生成器的初始状态
满足上述三个条件的序列称 sequence), 简记为: PN序列. PN序列在CDMA,通信同步, 导航, 雷达测距等领域 有重要应用.
18
Solomon W. Golomb: Shimonoseki, Japan, October 10-14, 2005
(G1):在一个周期内,0与1出现的个数至多相差1。也即, 如果N为偶数,则在一个周期内0与1的数目各占N/2; 如果N为奇数,则在一个周期内0的数目为(N+1)/2或者 (N-1)/2,相应地1的数目为(N-1)/2或者(N+1)/2。 (G2):在一个周期内,长度为i 的游程个数占游程总数的 1/2i,i=1,2, …。且在长度为i的游程中,0的游程与1的 游程数目相等或至多相差一个。 (G3):序列的异相自相关函数是一个常数。
20
伪随机序列
反馈移位寄存器(FSR: Feedback Shift Register)
n个寄存器: 从右至左依次称为第1,2,…,n 级 反馈函数 f(x0, x1,…,xn-1): GF(2)nGF(2). 工作原理: 当一个时钟脉冲来到时, 第i 级寄存器的内容传送给第 i-1级寄存器(i=2,3,…,n),第1 级寄存器的内容为反馈移位寄存器 的输出. 反馈函数 f(x0, x1,…,xn-1)的值传送给第n级寄存器. FSR的输出序列: a0, a1,a2,…,an,… 称为反馈移位寄存器序列(FSR 序列).
密码学报告

实验一古典密码(认识密码学)一、实验目的通过实现简单的古典密码算法,理解密码学的相关概念如明文(plaintext )、密文(ciphertext )、加密密钥(encryption key)、解密密钥(decryption key )、加密算法(encryption algorithm)、解密算法(decryption algorithm)等。
二、实验内容1.用C\C++语言实现仿射变换(Affine )加/解密算法;2.用C\C++语言实现统计26个英文字母出现的频率的程序;3.利用仿射变换加/解密程序对一段较长的英文文章进行加密,再利用统计软件对明文和密文中字母出现的频率进行统计并作对比,观察有什么规律。
放射变换:加密:()26mod ,b am m E c b a +== 解密:()()26mod 1,b c ac D m b a -==-其中a, b 为密钥,25,0≤≤b a ,且gcd(a, 26)=1三、实验要求加/解密程序对任意满足条件的a 、b 都能够处理。
四、实验步骤(1)统计26个英文字母出现的频率(源程序见附录)运行结果:(1)仿射变换加/解密程序对一段较长的英文文章进行加密运行结果:明文:密文:解密:实验二流密码(认识LFSR及流密码)一、实验目的通过实现简单的线性反馈移位寄存器(LFSR),理解LFSR的工作原理、本原多项式重要意义。
二、实验内容(1)利用C\C++语言实现LFSR(其中LFSR已给定);(2)通过不同初始状态生成相应的序列,并观察他们的周期有什么特点;(3)利用生成的序列对文本进行加/解密(按对应位作模2加运算)。
其中的LFSR为:三、实验结果及分析运行结果:明文:密文:解密:流密码(生成非线性序列)一、实验目的以LFSR序列为基础,生成非线性序列,并利用该序列对文件进行加密、解密。
二、实验内容1)利用C\C++实现Geffe序列生成器及J-K触发器;2)利用生成的非线性序列对文件进行加密、解密(按对应位作模2加运算)。
现代密码学——古典密码算法(实验报告)
安全SnoWolF/百度B英俊制作课程名称现代密码学实验实验项目名称古典密码算法练习一 Caesar密码加密时每一个字母向前推移k位,例如当k=5时,置换表如表2所示。
表2 Caesar置换表于是对于明文:datasecurityhasevolvedrapidly经过加密后就可以得到密文:IFYFXJHZWNYDMFXJATQAJIWFUNIQD若令26个字母分别对应整数0~25,如表3所示。
表3 Caesar置换表则Caesar加密变换实际上是:c=(m+k)mod26其中m是明文对应的数据,c是与明文对应的密文数据,k是加密用的参数,也称为密钥。
很容易得到相应的Caesar解密变换是:m=D(c)=(c–k)mod26例如明文:datasecurity对应的数据序列:301901842201781924当k=5时经过加密变换得到密文序列:852452397252213243对应的密文为:IFYFXJHZWNYD【实验步骤】本练习主机A、B为一组,C、D为一组,E、F为一组。
首先使用“快照X”恢复Windows系统环境。
一.手动完成Caesar密码(1) 在实验原理部分我们已经了解了Caesar密码的基本原理,那么请同学们写出当密钥k=3时,对应明文:data security has evolved rapidly的密文: GDWD VHFXULWB KDV HYROYHG UDSLGOB 。
(2) 进入实验平台,单击工具栏中的“密码工具”按钮,启动密码工具,在向导区点击“Caesar密码”。
在明文输入区输入明文:data security has evolved rapidly。
将密钥k调节到3,查看相应的密文,并与你手动加密的密文进行比较。
请根据密钥验证密文与明文对应关系是否正确。
二.Caesar加密(1) 进入“加密解密”|“Caesar密码”视图,在明文输入区输入明文(明文应为英文),单击“加密”按钮进行加密。
第2章 流密码 现代密码学教案
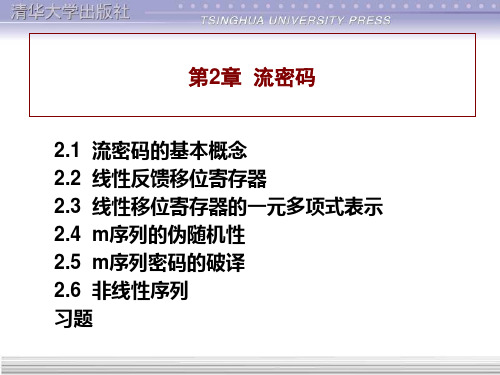
图2.1 分组密码和流密码的比较
2.1.1 同步流密码
根据加密器中记忆元件的存储状态σi是否依赖于输入 的明文字符,流密码可进一步分成同步和自同步两 种。σi独立于明文字符的叫做同步流密码,否则叫做 自同步流密码。由于自同步流密码的密钥流的产生 与明文有关,因而较难从理论上进行分析。目前大 多数研究成果都是关于同步流密码的。在同步流密 码中,由于zi=f(k,σi)与明文字符无关,因而此时密文 字符yi=Ezi(xi)也不依赖于此前的明文字符。因此,可 将同步流密码的加密器分成密钥流产生器和加密变 换器两个部分。如果与上述加密变换对应的解密变 换为xi=Dzi(yi),则可给出同步流密码体制的模型如图 2.2所示。
一次一密密码是加法流密码的原型。事实上,如果 (即密钥用作滚动密钥流),则加法流密码就退化 成一次一密密码。实际使用中,密码设计者的最大 愿望是设计出一个滚动密钥生成器,使得密钥经其 扩展成的密钥流序列具有如下性质:极大的周期、 良好的统计特性、抗线性分析、抗统计分析。
2.1.2 有限状态自动机
q(x)=p(x)r(x),所以p(x)|q(x)。
(证毕)
上述定理说明可用n级LFSR产生的序列,也可用级 数更多的LFSR来产生。
定义2.2 设p(x)是GF(2)上的多项式,使p(x)|(xp-1)的 最小p称为p(x)的周期或阶。
定理2.3 若序列{ai}的特征多项式p(x)定义在GF(2)上, p是p(x)的周期,则{ai}的周期r|p。
有限状态自动机是具有离散输入和输出(输入集和 输出集均有限)的一种数学模型,由以下3部分组成: ① 有限状态集S={si|i=1,2,…,l}。 ② 有限输入字符集A1={A(1)j|j=1,2,…,m}和有限输出 字符集A2={A(2)k|k=1,2,…,n}。 ③ 转移函数A(2)k=f1(si,A(1)j),sh=f2(si,A(1)j)即在状态为 si,输入为A(1)j时,输出为A(2)k,而状态转移为sh。
现代密码学:第16讲 A5流密码算法

现代密码学第十六讲A5流密码算法信息与软件工程学院第十六讲A5流密码算法A5流密码算法的基本用法A5流密码算法的基本原理通信模式用户A 用户B基站1 基站2基站n A5/1流密码算法的基本用法•用于蜂窝式移动电话系统语音和数字加密。
•A5/1算法用于用户的手机到基站之间的通信加密,通信内容到基站后先解密变成明文,然后再进行基站到基站之间、以及基站到用户手机之间的信息加密,完成通信内容在通信过程的加密保护•应用环节•只需考察用户A到基站1之间通信内容的加解密,中间消息的传送由基站到基站之间的加密完成,而接收方用户B对消息的加解密与用户A到基站1之间的通信完全类似,只不过是用户B先解密消息。
•基本密钥K A1•基本密钥K A1:预置在SIM卡中,与基站1共享。
•生存期:一旦植入SIM卡将不再改变。
•用途:用来分配用户和基站之间的会话密钥。
•会话密钥k•产生方式:在每次会话时,基站产生一个64比特的随机数k 。
•分配方式:利用基本密钥K A1,使用其它密码算法将k 加密传给用户手机。
•生存期:仅用于一次通话时间。
•明文处理•按每帧228比特分为若干帧后逐帧加密,每帧处理方式相同。
||||||||21i M M M M =228||=i M 发送114比特接收114比特加密后发送接收后解密•加密方式•加密:•一次通话使用一个会话密钥,对每帧使用不同的帧密钥•帧会话密钥:帧序号,长度为22比特•帧会话密钥共产生228比特密钥流,实现对本帧228比特通信数据的加解密•明密结合方式:逐位异或•一次通话量:至多222帧数据,约0.89×230比特)()()()(332211M E M E M E M E k k k k1)(141718191⊕⊕⊕⊕=x x x x x f LFSR-11)(131721222⊕⊕⊕⊕=x x x x x f LFSR-21)(181922233⊕⊕⊕⊕=x x x x x f LFSR-3注:A5/1算法中,LFSR 的移位方式是左移方式。
密码学相关实验报告

一、实验目的1. 理解并掌握常见的加密算法和密码体制的基本原理。
2. 学会使用密码学工具进行加密和解密操作。
3. 增强网络安全意识,提高对密码学在实际应用中的认识。
二、实验内容1. 仿射密码2. 单表代替密码3. 维吉尼亚密码4. AES加密算法三、实验原理1. 仿射密码:加密原理为将明文进行0~25字母编码,按照加密公式计算出密文对应位置的字母编码,最后从密文的字母编码还原出密文对应位置的字母。
解密原理与加密原理相反。
2. 单表代替密码:加密原理为利用代替表,将明文中的每个字符映射到密文。
解密原理为对代替表进行反向查找,由密文映射回明文。
3. 维吉尼亚密码:加密原理为通过加密方程Ci (pi k(i mod m)) mod 26,由明文得到密文。
解密原理为解密过程是加密过程的逆过程,通过解密方程pi (Cik(i mod m)) mod 26。
4. AES加密算法:是一种分组加密算法,将128位明文分为128位的数据块,使用密钥进行加密,得到128位的密文。
解密过程与加密过程相反。
四、实验步骤1. 仿射密码(1)选择明文:选择一段英文或数字,例如:"Hello World!"(2)选择密钥:选择一个密钥a和模数m,例如:a=5,m=26。
(3)加密:将明文进行0~25字母编码,按照加密公式计算出密文对应位置的字母编码,最后从密文的字母编码还原出密文对应位置的字母。
(4)解密:将密文进行0~25字母编码,按照解密公式计算出明文对应位置的字母编码,最后从明文的字母编码还原出明文对应位置的字母。
2. 单表代替密码(1)构造代替表:选择一个代替表,将明文中的每个字符映射到密文。
(2)加密:将明文中的每个字符按照代替表进行映射,得到密文。
(3)解密:将密文中的每个字符按照代替表的逆映射,得到明文。
3. 维吉尼亚密码(1)选择密钥:选择一个密钥,例如:"KEY"(2)加密:将明文和密钥进行异或操作,得到密文。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安全SnoWolF/百度B英俊制作 课程名称 现代密码学实验 实验项目名称 流密码系统
练习一 流密码系统 【实验目的】 理解流密码加密解密过程,通过程序的实现掌握Geffe、JK触发器和LFSR的工作过程。 【实验人数】 1人 【系统环境】 Windows 【网络环境】 交换网络结构 【实验工具】 Visual Studio 2019 【实验类型】 综合型 【实验原理】 1. 流密码体制模型
2. 分类 根据加密器中记忆元件的存储状态是否依赖于输入的明文字符可分为两类: 1.同步流密码 #独立于明文字符 安全SnoWolF/百度B英俊制作 2.自同步流密码 #依赖于输入的明文字符 目前最常用的流密码体制是二元加法流密码,是一种同步流密码,其加密变换可表示为异或函数。
3. 线性反馈移位寄存器 移位寄存器是流密码长产生密钥流的一个主要组成部分。 线性反馈移位寄存器( LFSR)是指,给定前一状态的输出,将该输出的线性函数再用作输入的移位寄存器。异或运算是最常见的单比特线性函数:对寄存器的某些位进行异或操作后作为输入,再对寄存器中的各比特进行整体移位。 线性反馈移位寄存器输出序列的性质完全由其反馈函数决定。 1、n级线性反馈移位寄存器最多有2n个不同的状态 2、n级n级线性反馈移位寄存器的状态周期小于等于2n-1 3、周期达到最大值的序列称为m序列 仅能被非0常数或自身的常数倍除尽,但不能被其他多项式除尽的多项式称为即约多项式或不可约多项式。 n级LFSR产生的序列有最大周期2n-1的必要条件是其特征多项式为不可约的。 若n次不可约多项式p(x)的阶为2n-1,则称p(x)是n次本原多项式。{ai}为m序列的充要条件为p(x)是本原多项式。
4. 伪随机序列 Golomb对伪随机周期序列提出了应满足的如下3个随机公设: (1)在序列的一个周期内,0与1的个数相差至多为1。 (2)在序列的一个周期内,长为1的游程占游程总数的1/2,长为2的游程占游程总数的1/4,长多为 i 的游程占游程总数的 1/2i ,且在等长的游程中0的游程个数和1的游程个数相等。 (3)异自相关函数是一个常数。 n长m序列满足Golomb的3个随机性公设,具有如下性质: (1)在一个周期内,0和1出现的次数分别为2n-1-1和2n-1。 (2)在一个周期内,总游程数为2n-1;对 1≤ i ≤ n-2,长为 i 的游程有2n-i-1个,且0和1游程各半;长为n-1的0游程一个,长为n的1游程一个。
【实验内容】
自行查找相关资料,结合上次实验的主函数框架,实现流密码系统。具体内容:线性反馈寄存器(LFSR) + 一个非线性组合子系统(Geffe序列生成器或J-K触发器)
1) 可参考网上资料。 2) 结合参考教材上 pp17的图 2-10,pp27的图2-12,图 2-14。 3) 不要求输出密钥流是m序列,但需给出周期大小。 4) 实验报告需明确给出LFSR的线性反馈函数的递推形式,初始状态。流秘钥生成器的输出。加密解密的输入输出过程。
【实验过程与结果】 安全SnoWolF/百度B英俊制作 1. 实验源码 #include #include #include #include //定义二进制bitset所需的头文件 #include //文件读写操作所需的头文件 using namespace std;
#define CHAR_SIZE 26 #define DECRYPT_FILE "Caesar密文.txt" #define ENCRYPT_FILE "Caesar明文.txt" #define N 8 //常量N指定二进制位大小,也是LFSR最大级数限定
typedef struct { bitsetlfsrInit; //LFSR初始态 int scale = 8; //级数,默认为8 string key; //周期密钥流 int lfsrCycle = 0; //周期 }LFSR; typedef struct { LFSR register1; //LFSR1 LFSR register2; //LFSR2 LFSR register3; //LFSR3 string keyStream; //扩展后真正被使用到的密钥流 }GEFFE; //返回命令提示信息 void Usage(const char* appname) { printf("\n\tusage: stream -e 明文文件 密钥k\n"); printf("\tusage: stream -d 密文文件 密钥k\n"); } //校验应用程序入口参数,若参数合法返回true,否则返回false bool CheckParse(int argc, char** argv) { if (argc != 5 || (argv[2][1] != 'e' && argv[2][1] != 'd')) { Usage(argv[1]); return false; } return true; } 安全SnoWolF/百度B英俊制作 //加/解密结果输出到当前目录磁盘文件中,strOut指向输出字符缓冲区,strFile为输出文件 bool FileOut(const string strOut, string strFile) { if (strOut.empty()) //判断字符缓冲区是否为空 return false; ofstream fileOut(strFile); //打开文件 fileOut << strOut; //写入文件 fileOut.close(); //关闭文件 return true; } //加/解密内容输入到字符缓冲区中, strIn指向输出字符缓冲区, strFile为输入文件 bool FileIn(char* strIn, const char* strFile) { ifstream fileIn(strFile); //打开文件 if (!fileIn.is_open()) //判断文件是否成功打开 { std::cout << "Error opening file"; return false; } while (!fileIn.eof()) //直到读取到文件末尾 { fileIn.getline(strIn, 100); //读取文件,每次读100byte } return true; } //线性反馈寄存器LFSR void Lfsr(LFSR& lfsr, int k) { bitsetbint(lfsr.lfsrInit); //将初始态存为二进制数 bitsetstr(bint); string s1;//保存输出结果 cout << "初始状态为:"; /*for (int i = lfsr.scale - 1; i >= 0; i--) //遍历bint中的数字 cout << bint[i]; cout << endl;*/ do //生成LFSR的状态变化 { int j = bint[lfsr.scale - 1] ^ bint[0];//所有LFSR递归式设置为f(a1,...an)=an^a1 bint.operator>>=(1);//向右移1位 bint[lfsr.scale - 1] = j;//第1个数据和第n个数据异或然后赋值给第n个 for (int i = lfsr.scale - 1; i >= 0; i--) cout << bint[i]; cout << endl; bitset<1>binTemp(bint[k % lfsr.scale]);//根据密钥k,每次取移位后二进制数据的第安全SnoWolF/百度B英俊制作 k位 s1 = binTemp.to_string();//把binTemp转换成string放入s1 lfsr.key.push_back(s1[0]);//转成char,放入LFSR密钥流 ++lfsr.lfsrCycle; //周期递增 } while (str.to_string() != bint.to_string());//直到移位后数据与初始态相同 cout << "输出周期密钥流序列为:" << endl << lfsr.key << endl; cout << "周期为:" << lfsr.lfsrCycle << endl << endl; } //Geffe序列生成器,连同加密解密的操作,k为密钥 bool Geffe(GEFFE& geffe, const string strIn, string::size_type strLen, string& strOut, string::size_type k) {//k对序列生成器的影响:从拓展后密钥流的第k位开始,对明/密文进行加/解密操作 if (strIn.empty()) //判断输入字符缓冲区是否为空 return false; int iCount = 0; for (string::size_type i = k; i < strLen + k && iCount < strLen; ++i, ++iCount) {// bitset<1>bitvec1(geffe.register1.key, i % geffe.register1.key.size(), 1);//从LFSR1中周期序列取1位 bitset<1>bitvec2(geffe.register2.key, i % geffe.register2.key.size(), 1);//从LFSR2中周期序列取1位 bitset<1>bitvec3(geffe.register3.key, i % geffe.register3.key.size(), 1);//从LFSR3中周期序列取1位 bitset<1>bitvecKey((bitvec1 & bitvec2) ^ (bitvec3 & (~bitvec2)));//运算得1位密钥 bitset<1>bitvecIn(strIn, iCount, 1);//从明/密文中取1位 bitset<1>bitvecOut(bitvecKey ^ bitvecIn);//加/解密操作 strOut += bitvecOut.to_string(); //将1位结果写入输出缓冲区 geffe.keyStream += bitvecKey.to_string(); //保存使用的密钥 } return true; } //初始化geffe和LFSR void Init(GEFFE& geffe, char** argv) { geffe.register1.scale = 7; //设置LFSR级数 geffe.register2.scale = 5; geffe.register3.scale = 3; geffe.register1.lfsrInit = 64; //设置初始态 geffe.register2.lfsrInit = 16; geffe.register3.lfsrInit = 4; cout << "LFSR1:" << endl; Lfsr(geffe.register1, atoi(argv[4]));//传入LFSR1和密钥k cout << "LFSR2:" << endl;
