第1章-质点运动学1
大学物理质点力学第一章 质点运动学 PPT

方向:
cosa
=
x r
cosβ=
y r
cosγ=
z r
路程:质点所经路径得总长度。
三、速度
描述位置矢量随时间变化快慢得物理量
1、平均速度
在移质为点r由)A,到单B的位过时程间中内(的所平用均时位间移为称为t该,质所点发在生该的过位
程中的平均速度。
v
=
Δ Δ
r t
=
Δx Δt
i
+ΔΔ
y t
j
+
Δ Δ
0
Δx
Δ t —割线斜率(平均速度)
dx —切线斜率(瞬时速度) dt
x~t图
t tt
1
2
2、 v ~ t 图
v ~ t图
割线斜率:
Δv Δt = a
v v2
切线斜率:
dv dt
=a
v1
v ~ t 图线下得面积(位移):
0 t1
t2
x2
dt dx x2 x1 x
t1
x1
t2 t
3、 a ~ t 图
=
dθ
dt
B
Δθ A
θ
0
x
(3)、角加速度
β =ΔΔωt
β
=
lim
Δt
Δω
0Δ t
=ddωt
=ddθt2 2
(4)、匀变速率圆周运动
0
t
1 2
t2
0 t
2
2 0
2
(5)、线量与角量得关系
Δ s = rΔθ
lim Δ s
Δt 0Δ t
=
lim
Δt 0
r
Δθ
第1章-质点运动学
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
大学物理第1章质点运动学

大学物理第1章质点运动学质点运动学是物理学中研究物体运动的学科,它是物理学的一个重要分支,是学习物理的基础之一。
一、质点运动学的概念质点运动学是研究质点运动的学科,它把物体看作质点,即把物体看成一个点,而不考虑其体积大小。
质点运动学的主要研究内容包括:位置、速度、加速度等运动量的描述,以及运动的曲线形状、动量、能量等方面的分析。
二、质点的运动质点的运动可以分为匀速运动和非匀速运动两种情况。
1.匀速运动匀速运动是指质点在单位时间内沿着同一直线等距离地移动的运动。
匀速运动的速度大小是恒定的,可以用速度公式v=d/t来计算。
2.非匀速运动非匀速运动是指质点在单位时间内沿任意曲线路径移动的运动。
非匀速运动中质点的速度大小是变化的,需要用微积分的方法进行分析和计算。
三、质点运动中的基本物理量在质点运动中,需要描述质点的运动状态和变化情况。
主要的量包括:1.位置位置是指质点在空间中所处的位置,通常使用坐标表示。
我们可以通过坐标系建立一个参照系,来描述质点的位置。
2.位移位移是指质点从一个位置到另一个位置的距离和方向,通常用符号Δr表示。
位移的大小可以用位移公式Δr=r2-r1来计算。
3.速度速度是指质点在单位时间内所改变的位置,通常用符号v 表示。
速度的大小可以用速度公式v=Δr/Δt来计算。
4.加速度加速度是指质点在单位时间内速度所改变的量,通常用符号a表示。
加速度的大小可以用加速度公式a=Δv/Δt来计算。
四、质点的曲线运动在质点运动中,一些运动路径可能是曲线运动。
曲线运动的路径通常可以用弧长s、曲率半径r、圆心角等来表征。
1.弧长弧长是指质点在曲线路径上所走过的曲线长度,通常用符号s表示。
弧长的大小可以用弧长公式s=rθ来计算。
2.曲率半径曲率半径是指曲线在任一点上的曲率半径,通常用符号r 表示。
曲率半径可以根据曲线的形状计算得出。
3.圆心角圆心角是指质点所在的路径所对应的圆所对应的圆心角度数,通常用符号θ表示。
上海理工大学 大学物理 第一章 质点运动学(1)

y
v0
y
v0
v0 x v0 cos v0 y v0 sin
质点在运动过程中 加速度始终为: 质点在任一时刻的 运动速度为:
O
v0x
y x
m
x
m
a gj
v (v0 cos )i (v0 sin gt) j
因为
dr v dt
1 2 t r v dt (v0t cos )i (v0t sin gt ) j 0 2
质点运动的轨迹可以看成v0方向的匀速直线运动和自由落体运 动的叠加;
x v0t cos 1 2 y v0t sin gt 2
1 x2 y xtg g 2 2 2 v0 cos
从上述方程式看,x,y构成一条抛物线,所以抛体运动又称为 “抛物线运动”。
1 x y xtg g 2 2 2 v0 cos
上述抛物线与x轴相交两点,其中x=0处为起点,另一交点的x 坐标为: 2 v0 sin 2 xm
2
g
可以令sin2=1,即=450时射程最远。
xm是上述抛物运动的射程。当初速度v0一定时,欲使射程最大,
同样,我们也可以根据运动速度求出ym,即上述抛物运动最高 点,此时Vy=0
v y v0 sin gt t (v0 sin ) / g
x
z
v v x v y vz
v v
称速率。
v x i v y j vz k
例1 设质点的运动方程为 r(t ) x(t )i y(t ) j ,其中
(1) 求t =3s 时的速度。(2)作出质点的运动轨迹图。
解:(1) 速度分量为:v x
第1章 质点运动学
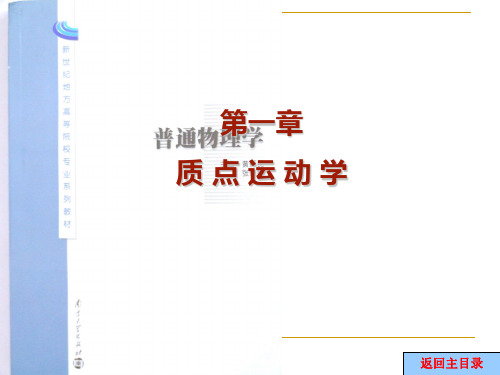
100t
4
t3
0
3
x x0
t
t0 vx (t)dt 0
t
(100t
4
t3 )dt
50t 2
1
t4
0
3
3
第一章 质点运动学
1-5 曲线运动
一、匀速圆周运动
1、匀速圆周运动的加速度
A v B
vA B vB
设质△|量=圆点 t|时vvv周处|存'刻。的在在,质半圆。v质点径周根点从为上据在PR点的加Q,运P处速处圆动,度,心到速的速为Q度定度O点为义,为有vv可v在,速;' 得t其度时在瞬中增刻t+时|,v
解:由
a
ann a
v2 R
n
dv dt
v
ds dt
20
0.6t 2 (m
/
s)
当t=1s时
an
v2 r
(20 0.6)2 200
m / s2
1.88m / s2
a
dv dt
1.2t
1.2m / s2
a a2 an2 2.23m / s2
dt
v0 v
0
v
v e(1.0s1 )t 0
由速度的定义: v
dy dt
v e(1.0s1 )t 0
y
t
dy v0 e dt (1.0s1 )t
y 10 1 e( 1.0s1 )t
0
0
由以上结果, t 时, v 0,此时y 10m。
但实际情况是:t 9.2s时, v 0,此时y 10m。
加速度分量
加速度大小 加速度余弦方向
a | a| a2x a2y a2z
第1章-质点运动学

位移
rrrBArxBxBAii
rA
yA
yB
j j
y
yB A r
r y A A
rB
B
yB yA
(xB xA)i ( yB yA) j
xi yj
o
xA
xB x
xB xA
若质点r 在 (三x维B 空x间A中)i运动( yB
yA)
j
(zB
z A )k
位移的大小为 r x2 y2 z2
23
1-2 求解运动学问题举例
例3 有 一个球体在某液体中竖直下落, 其初速度
为 v0 10 j , 它的加速度为 a 1.0v j. 问:(1)经
过多少时间后可以认为小球已停止运动, (2)此球体
在停止运动前经历的路程有多长?
解:由加速度定义
v dv 1.0
t
dt
,
v v0
0
a dv 1.0v dt
v v2
位矢量
t
0,
t 0
0,
tv
rv
a
dv dt
v2 r
en
2ren
法向单 位矢量
vB
r
o
en
v
vB
vA et r
vA
31
1-3 圆周运动
三alitlami tm 变00速litdmdv圆vvvt0tt周nt运vtavt动dvdttrev2ttleeit切mntv向a0nn加aaevn速tntneen度t 和法向v加2v速tove度2vnrevtv1vn1
一 圆周运动的角速度和角加速度
角坐标 (t)
角速度 (t) d (t)
dt
速率
大学物理——第1章-质点运动学

21
★ 角速度 ω 大小: ω = lim 单位:rad/s ★ 角加速度 β
v
θ dθ = t →0 t dt
v
ω dω d2θ 大小: β = lim = = 2 t →0 t dt dt
单位:rad/s2
22
★ 线量与角量的关系
dS = R dθ
16
取CF的长度等于CD
v v v v vτ vn v v v = lim + lim 加速度: a = lim = aτ + an t →0 t →0 t →0 t t t
v v 当 t →0 时,B点无限接近A点,vA与 vB v v 的夹角 θ 趋近于零,vτ 的极限方向与 vA v 相同,是A点处圆周的切线方向;vn的极 v 限方向垂直于 vA ,沿圆轨道的半径,指向
y
v v v r = r′ + R
v v v dr dr ′ dR 求导: = + dt dt dt
o
y′ M v u v v r′ r v o′ R
x′
z′
x
z v称为质点M的绝对速度, v称为质点M的相对速度, υ υ′
v 称为牵连速度. u
27
v v υ =υ′ +u
v
in 例1-6 一人向东前进,其速率为 υ1 = 50m/ m ,觉得风从 正南方吹来;假若他把速率增大为υ2 = 75m/ m , in
t
9
初始条件:t = 0 , x = 5m 【不定积分方法】
速度表达式是: v = 4+ 2t
x = ∫ vdt = ∫ (4 + 2t)dt = 4t + t 2 + C
第一章 质点运动学

物理学
已知:x(t ) 1.0t 2.0,y(t ) 0.25t 2 2.0, 解 (1) 由题意可得
dx dy vx 1.0, vy 0.5t dt dt t 3s 时速度为 v 1.0i 1.5 j
速度 v 与
x 轴之间的夹角
第一章 质点运动学
第一章 质点运动学
14
物理学
讨论 一运动质点在某瞬 y 时位于矢径 r ( x, y ) 的 y 端点处,其速度大小为
dr ( A) dt dr ( C) dt
注意
dr (B) dt
r (t )
x
o
x
dx 2 dy 2 ( D) ( ) ( ) dt dt
dr dr dt dt
1.5 0 arctan 56.3 1.0
17
物理学
x(t ) 1.0t 2.0, (2)运动方程 2 y(t ) 0.25t 2.0,
消去参数 t 可得轨迹方程为
y 0.25x x 3.0
2
轨迹图 t 4s
y/m
6 2
t 4s
t 2s 4
-6 -4 -2 0
dx B v A v x i i vi dt l dy vB v y j j o dt 2 2 2 x y l dx dy 两边求导得 2 x 2y 0 dt dt
第一章 质点运动学
解
y
A
v
x
20
物理学
dy x dx y 即 dt y dt B x dx vB j y dt dx o v dt vB vtan j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可表为 则
a b Se n
S a b sin
叉乘之值是以两矢量为邻边构成的平行四边形 的面积.
14
叉乘的运算规则
1)叉乘的反交换律
矢量a,b均不为0
a b (b a)
2)叉乘与数乘的结合律 (a b) (a) b a (b)
行星
可以把行星绕太阳的运动看做是质点的运动。 太阳
20
1-1-2
参考系和坐标系
• 物质的运动具有绝对性 • 描述物质运动具有相对性
参考系:
为描述物体的运动而选取的参考物体。
坐标系:
用以标定物体的空间位置而设置的坐标系统。
21
§1-2 描述质点运动的物理量
1-2-1 位置矢量与运动方程
上海
热带风暴
z
• 平均速度
A
rA
O x
r
B
设质点做一般曲线运动 tA时刻位于A点 tB时刻位于B点
rB
y
在 t 时间内发生位移:
r rB rA
27
r 平均速度: v t
单位: m s 1
平均速度的方向与 t 时间内位移的方向一致
• 瞬时速度
质点在某一时刻所具有的速度
( x ) n x
n
n 1
1 (ln x) x
(sin x) cos x
(cos x) sin x
大学物理常用积分
cos xdx
sin x C
sin xdx cos x C 1 dx ln x C x
5
一.
二 矢量运算
A
A
• 大小为矢量的模, 记为 A
(u v) u v (uv) uv uv
u uv uv ( ) (v 0) 2 v v
特别 推广
你记住了 吗?
(Cu ) Cu
1 v ( ) 2 (v 0) v v
3
(uvw) uvw uvw uvw
1. 常数和基本初等函数的导数
注意:矢量的微商仍是矢量 质点位置函数的时变率即质点的速度,速度为矢量。 速度的方向:位置函数空间曲线的任意点切线方向。
10
r lim 如果极限t 0 存在,此极限就是矢量函数 r (t ) t 在自变量为 t 时的微商,记为 r (t )
四.矢量的点乘(标量积)
a b a b cos 1)点乘的交换律 a b b a
O x
rA r B
y
r
s
B
2 2 2 r x y z
路程:质点在轨道上所经过的曲线长度Δs
s r
lim s lim r
t 0 t 0
ds dr
26
1-2-3 速度
速度是反映质点运动快慢和方向的物理量
速度:单位时间内质点所发生的位移。
z
r1
r2
v1 v2
y
o
x
v v2 v1
v1 v2
v 平均加速度: a 单位:m s 2 t
v
结论:平均加速度的方向与速度增量的方向一致。
31
当t0时,平均加速度的极限即为瞬时加速度。
v dv d 2 r a lim 2 单位:m s 2 瞬时加速度: dt dt t 0 t
矢量的概念起源于对运动和 力的研究。力和速度等物理 量需要用其大小和方向来表示
• 长度为零的矢量 叫零矢量
• 长度为1的矢量叫 单位矢量,记 e 单位矢量用来表示 空间的方向
依据事物自身的规律,按矢 量运算规则运算的量叫矢量 • 大小相等、方向相反的矢量 互为负矢量,如 a 与
a (a) 0
a
7Байду номын сангаас
i j k 为三坐标轴的单位矢量 a xa i ya j za k
矢量与三个轴的夹角为 , ,
三.直角坐标中的矢量,位矢和速度
z (k )
a
o
y ( j)
x (i )
xa ya za cos , cos , cos a a a
22
位置矢量 (位矢)
从坐标原点O出发,指向质点 所在位置P的一有向线段
位矢用坐标值表示为:
Z
P
r xi yj zk
2 2 2
k O i
ββ
j
r
z x
Y
X
位矢的方向:
x cos r
y
轨 道
z cos r
23
位矢的大小为:
r x y z
x
y
( Ay Bz Az By )i ( Az Bx Ax Bz ) j ( Ax By Ay Bx )k
两矢量的叉积又可表示为:
A B Ax Bx
ˆ ax
ˆ ay Ay By
ˆ az Az Bz
16
第一章
质点运动学
17
机械运动
一个物体相对于另一个物体的空间位置 随时间发生变化; 或一个物体的某一部分相 对于其另一部分的位置随时间而发生变化的 运动。
(C ) 0 (sin x) cos x (tan x) sec 2 x
(a ) a ln a
x
( x n ) n x n 1
(cos x) sin x (cot x) csc 2 x
( e )
x
x
e
x
1 (ln x) x
4
大学物理常用导数
点乘运算规则
a
b
2)点乘与数乘的结合律 (a b) (a) b a (b) 3)点乘的分配律 (a b) c a c b c
点乘的常用性质还有
2 1)a a a ; 2)a b, a b 0 i i j j k k 3)直角坐标中 i j j k k i i j j k k i 0 i i j j k k 1
y cos r
运动方程:
r r (t )
r x(t )i y(t ) j z (t )k
z
矢量形式:
参数形式: x x(t )
y y (t ) z z (t )
轨道方程:
O x
r
y
24
F ( x, y, z ) 0
1-2-2 位移与路程
i j j k k i i j k, j k i , k i j
15
在直角坐标系中,两矢量的叉积运算如下:
z
A B
( Axi Ay j Az k ) ( Bxi By j Bz k )
位移
r r (t t ) r (t )
9
矢量的微商、速度 位移
r r (t t ) r (t )
r dr dx(t ) dy (t ) dz (t ) r(t ) lim i j k t 0 t dt dt dt dt x(t ) i y(t ) j z(t )k
力学
研究物体机械运动及其规律的学科。
18
运动学:
研究物体在空间的位置随时间的变化规 律以及运动的轨道问题,而并不涉及物体发 生机械运动的变化原因。
动力学:
以牛顿运动定律为基础,研究物体运动 状态发生变化时所遵循规律的学科。
19
§1-1 质点 参考系 坐标系
1-1-1 质点
质点:具有一定质量的,大小 和形状可以忽略的理想物体。
3)叉乘的分配律 a (b c) a b a c
4)叉乘可得 a, b同向和反向(平行)的充分必要条件
ab 0
直角坐标系中的叉乘运算
i i j j k k i i j j k k 0
11
有两矢量点积:
A B ( Axi Ay j Az k ) (Bxi By j Bz k )
Ax Bx Ay By Az Bz
• 结论:两矢量点积等于对应分 量的乘积之和。
12
五.矢量的叉乘(矢量积) (一)叉乘的运算规则 在物理中常有两个相互垂直的矢量相互作用, 呈现出某些特殊效应,例如动量矩、力矩及运 动电荷伴存的磁场等.叉乘是描述这类效应的 矢量运算.叉乘用 表示,其积为矢量,所以叫 矢量积. 若 a, b 是交角为 的两个矢量,则叉乘定义为
矢量的方向余弦是该矢量同方向的单位矢量的坐标
cos cos cos 1
2 2 2
8
质点的位矢和位移
y
r (t )
o
r
r (t t ) x
P( x, y, z ) 点的位矢
r (t ) x(t ) i y(t ) j z (t )k
t t t
加速度的矢量式:
设质点做曲线运动 z
A
t时刻位于A点,位矢 rA
t+t时刻位于B点,位矢 rB
x
O
rA r B
y
r
B
位移矢量:
在t 时间内,位矢的变化量(即A到B的有向 线段),简称位移。
25
在直角坐标系中
