江苏省南京市2018届高三9月学情调研考试数学试题

合集下载

江苏省南京市届三9月学情调研数学试题x

江苏省南京市届三9月学情调研数学试题x南京市 20xx 届高三年级学情调研卷数学20xx.09．．．．．．．一、填空题：本大题共14 小题，每小题5 分，共70 分．请把答案填写在答题卡相应位置上．22▲．1．函数 f(x)＝ cos x－ sin x 的最小正周期为1，其中 i 是虚数单位，则 |z|＝▲．2．已知复数 z＝ 1＋i3．某学校高一、高二、高三年级的学生人数之比为4：3： 3，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为80 的样本，则应从高一年级抽取▲名学生．4．从甲、乙、丙、丁 4 位同学中随机选出 2 名代表参加学校会议，则甲被选中的概率是▲．5．已知向量a＝ (2， 1)， b＝ (0，－ 1)．若 (a＋λb) ⊥ a，则实数λ＝▲．6．右图是一个算法流程图，则输出S 的值是▲．开始S←0k← 1k←k＋2 S←S＋ k2 Nk＞5Y输出 S7．已知双曲线x2y2结束2－ 2＝ 1(a＞ 0， b＞0)的渐近线方程ab（第 6为 y＝±3x，则该双曲线的离心率为▲．题图）8．已知圆锥的侧面展开图是一个半径为2 的半圆，则这个圆锥的高是▲．9．设 f(x)＝ x2－ 3x＋ a．若函数 f(x)在区间 (1，3) 内有零点，则实数 a 的取值范围为▲．10．在△ ABC 中，角 A，B， C 所对边的长分别为a， b，c．已知 a＋2c＝ 2b， sinB＝ 2sinC，则 cosA＝▲．a，x 1，11．若 f(x)＝ xa 的取值范围为是 R 上的单调函数，则实数▲．x＋ 3a， x＜112．记数列 { an} 的前 n 项和为 Sn．若 a1＝ 1，Sn ＝2(a1 ＋an )(n≥2，n∈ N*) ，则 Sn ＝▲．13．在平面直角坐标系 xOy 中，已知圆 C：x2＋ y2－ 6x＋ 5＝ 0，点 A，B 在圆 C 上，且 AB＝ 23，则→→| OA ＋ OB |的最大值是▲．14．已知函数f(x)＝ x－ 1－ (e－ 1)ln x，其中e 为自然对数的底，则满足f(ex)＜ 0的x 的取值范围为▲．二、解答题：本大题共 6 小题，共计．．．．．．．． 90 分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14 分）π已知函数f(x)＝ 2sin(2x＋φ)(0 ＜φ＜2π)的图象过点 (2 ，－2)．（ 1）求φ的值；α 6，－πα－π（ 2）若 f()＝＜α＜ 0，求 sin(2) 的值．252616．（本小题满分14 分）如图，三棱柱 ABC－A1B1C1 中， M， N 分别为 AB， B1C1 的中点．1）求证：MN ∥平面 AA1C1C；2）若 CC1＝ CB1， CA＝CB ，平面CC1B1B⊥平面 ABC，求证： AB 平面 CMN ．C1NB1 A1CB M A（第 16 题图）17．（本小题满分14 分）已知 { an} 是等差数列，其前n 项的和为Sn， { bn} 是等比数列，且a1＝ b1＝ 2， a4＋ b4＝ 21，S4＋ b4＝ 30．1）求数列 { an} 和 { bn} 的通项公式；2）记 cn＝ an bn，n∈ N* ，求数列 { cn} 的前 n 项和．18．（本小题满分16 分）x2y22222给定椭圆 C：a2＋b2＝ 1(a＞ b＞ 0)，称圆 C1： x＋ y＝a ＋ b为椭圆 C 的“伴随圆”．已知椭圆3C 的离心率为 2 ，且经过点 (0， 1)．（ 1）求实数 a， b 的值；（ 2）若过点 P(0， m)(m＞ 0)的直线 l 与椭圆 C 有且只有一个公共点，且 l 被椭圆 C 的伴随圆 C1所截得的弦长为 2 2，求实数m 的值．19．（本小题满分16 分）如图（示意），公路AM、 AN 围成的是一块顶角为α的角形耕地，其中tanα＝－ 2．在该块土地中 P 处有一小型建筑，经测量，它到公路AM ，AN 的距离分别为3km，5km ．现要过点P 修建一条直线公路 BC，将三条公路围成的区域ABC 建成一个工业园．为尽量减少耕地占用，问如何确定 B 点的位置，使得该工业园区的面积最小？并求最小面积．NC·PαMA B（第 19 题图）20．（本小题满分16 分）已知函数f(x)＝ ax3＋ |x－ a|，a∈ R ．1）若 a＝－ 1，求函数 y＝f(x) (x∈ [0，＋∞ ))的图象在 x＝ 1 处的切线方程；2）若 g(x)＝ x4，试讨论方程 f(x)＝ g(x)的实数解的个数；（ 3）当 a＞ 0 时，若对于任意的x1∈ [a，a＋ 2]，都存在x2∈[a ＋2，＋∞ )，使得 f(x1)f(x2)＝ 1024，求满足条件的正整数 a 的取值的集合．南京市 20xx 届高三年级学情调研卷数学附加题20xx.09．．．．21．【选做题】在 A、 B、C、 D 四小题中只能选做 2 题，每小题10 分，共计 20 分．请在答卷卡指．．．．定区域内作答．解答应写出文字说明、证明过程或演算步骤．A．选修 4— 1：几何证明选讲如图， PA 是圆 O 的切线， A 为切点， PO 与圆 O 交于点 B、C，AQ OP，垂足为 Q．若 PA＝ 4，PC＝ 2，求 AQ 的长．AP C Q O BB．选修 4— 2：矩阵与变换（第 21 题 A 图）已知矩阵 A＝2b113属于特征值的一个特征向量为α＝－ 1．（ 1）求实数 b，的值；（ 2）若曲线 C 在矩阵 A 对应的变换作用下，得到的曲线为 C ： x2＋2y2＝ 2，求曲线 C 的方程．C．选修 4— 4：坐标系与参数方程3在平面直角坐标系xOy 中，已知直线x＝3＋2 t，)，圆 C 的参数l 的参数方程为1(t 为参数y＝ 2＋2t方程为 x＝ 3＋cosθ，(θ为参数 ) ．若点 P 是圆 C 上的动点，求点P 到直线 l 的距离的最小值．y＝sinθD．选修 4— 5：不等式选讲已知 a， b 是正数，且a＋ b＝ 1，求证： (ax＋ by)( bx＋ay)≥xy．．．．．．．．．【必做题】第 22 题、第 23 题，每题10 分，共计20 分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．22．如图，已知长方体ABCD － A1B1C1D1 中， AB＝ 3，BC ＝2，CC1＝ 5，E 是棱 CC1 上不同于端→→点的点，且CE ＝λCC1．（ 1）当∠ BEA1 为钝角时，求实数λ的取值范围；2（ 2）若λ＝ 5，记二面角 B1－ A1B－ E 的的大小为θ，求|cosθ|．D 1 C1B1A1EDCA B（第 22 题图）23．某商店为了吸引顾客，设计了一个摸球小游戏，顾客从装有 1 个红球， 1 个白球， 3 个黑球的袋中一次随机的摸2 个球，设计奖励方式如下表：结果奖励1 红 1 白10 元1 红 1 黑5 元2 黑2 元1 白 1 黑不获奖1）某顾客在一次摸球中获得奖励X 元，求 X 的概率分布表与数学期望； 2）某顾客参与两次摸球，求他能中奖的概率．20xx 届高三年级学情调研卷数学参考答案及评分标准20xx.09一、填空题：本大题共14小题，每小题5 分，共 70分．1．π2．24． 15． 522926． 357． 28． 39． (0， 4]10． 411． [1，＋∞ )12． 2－ 2n－ 113． 814．(0， 1)2二、解答题：本大题共6 小题，共计90 分．15．（本小题满分14 分）π解：（ 1）因为函数 f(x)＝2sin(2 x＋φ)(0 ＜φ＜2π)的图象过点( ，－ 2)，2π所以 f(2)＝2sin(π＋φ)＝－ 2，即sinφ＝ 1．,,,,,,,,,,,,,,,,,π因为 0＜φ＜2π，所以φ＝2．,,,,,,,,,,,,,,,,,6 分（ 2）由（ 1）得， f( x)＝ 2cos2x．,,,,,,,,,,,,,,,,8 分α63因为 f()＝5，所以cosα＝．25又因为－π4．,,,,,,,,,,,,,,10 分＜α＜ 0，所以sinα＝－252427所以sin2α＝2sinαcosα＝－ 25，cos2α＝2cos α－ 1＝－25．,,,,,,,,12 分从而sin(2α－πππ7－ 24 3,,,,,,,,14 分6)＝sin2αcos －cos2αsin ＝．665016．（本小题满分 14 分）证明：（ 1）取 A1C1 的中点 P，连接 AP， NP．C1NP1因为 C1 N＝ NB1， C1P＝ PA1 ，所以NP∥ A1B1， NP＝B12 分A1B1 ． ,,,,,,,,A12在三棱柱 ABC－ A1B1C1 中，A1B1∥ AB， A1B1＝ AB． C故NP∥ AB，且1NP＝AB ．2BMA（第 16 题图）因为 M 为 AB 的中点，所以1AM ＝ AB．2所以 NP＝ AM，且NP∥ AM．所以四边形 AMNP 为平行四边形．所以MN ∥ AP．,,,,,,,,,,,,,,,4 分因为 AP平面 AA1C1C，MN平面 AA1C1C，所以MN ∥平面 AA1C1C．,,,,,,,,,,,,,,,,,,6 分（ 2）因为 CA＝ CB， M 为 AB 的中点，所以CM ⊥ AB． ,,,,,,,,,,,8 分因为 CC1＝ CB1， N 为 B1C1 的中点，所以CN⊥B1C1．在三棱柱 ABC－ A1B1C1 中，BC∥B1C1，所以 CN BC．因为平面CC 1B1B⊥平面 ABC ，平面CC1B1B∩平面 ABC＝ BC． CN平面 CC1B1B，所以CN⊥平面 ABC．,,,,,,,,,,,,,,10 分因为 AB平面 ABC ，所以CN⊥ AB．,,,,,,,,,,,,,,12 分因为 CM平面 CMN ， CN 平面 CMN ，CM ∩ CN＝ C，所以AB⊥平面 CMN ．,,,,,,,,,,,,,,14 分17．（本小题满分 14 分）解：（1）设等差数列 { an } 的公差为 d，等比数列 { bn} 的公比为q．由 a1＝ b1＝ 2，得 a4＝ 2＋ 3d， b4＝ 2q3， S4＝ 8＋ 6d．,,,,,,,,,,,, 3 分由条件 a4＋ b4＝21， S4＋ b4＝ 30，得方程组2＋ 3d＋ 2q3＝ 21，解得d＝ 1，3q＝ 2．8＋ 6d＋ 2q ＝ 30，所以 an＝ n＋1， bn＝ 2n，n∈ N* ．,,,,,,,,,,,,7 分（ 2）由题意知， cn＝ (n＋1)× 2n．Tn＝ c1＋ c2＋ c3＋, ＋ cn．Tn＝ c1＋ c2＋ c3＋, ＋ cn＝2× 2＋3× 22＋4× 23＋, ＋n× 2n－ 1＋(n＋1)× 2n，2 Tn＝2× 22＋3× 23 ＋, ＋ (n－1)× 2n－ 1＋n× 2n＋(n＋ 1)2n＋ 1，232n)－ (n＋n＋1， ,,,,,,,,,,,11 分所以－ Tn ＝2× 2＋ (2 ＋ 2 ＋, ＋1)× 2即 Tn＝n· 2n＋ 1，n∈ N* ．,,,,,,,,,,,,14 分18．（本小题满分16 分）解：（1）记椭圆C 的半焦距为 c．由题意，得b＝ 1， ac＝ 23， c2＝ a2＋ b2，解得 a＝ 2， b＝ 1．,,,,,,,,,,,,,,,,,, 4 分22）由（ 1）知，椭圆 C 的方程为 x ＋ y2＝ 1，圆 C1 的方程为 x2＋ y2＝ 5． 4显然直线l 的斜率存在．设直线 l的方程为 y＝ kx＋m，即 kx－ y＋ m＝ 0． ,,,,,,,,,,,,,, 6 分因为直线l 与椭圆 C 有且只有一个公共点，y＝ kx＋ m，2故方程组x ＋ y2＝ 1 （ * ）有且只有一组解．由（ * ）得 (1＋ 4k2)x2＋ 8kmx＋ 4m2－ 4＝0．从而△＝ (8km)2－ 4(1＋ 4k2)( 4m2－ 4)＝ 0．化简，得 m2＝ 1＋4k2．①,,,,,,,,,,,,,,,,10 分因为直线 l 被圆 x2＋ y2＝ 5所截得的弦长为 22，所以圆心到直线l 的距离 d＝5－ 2＝ 3．即|m|＝ 3．②,,,,,,,,,,,,,,,14 分k2＋ 1由①②，解得 k2＝ 2， m2＝ 9．因为 m＞ 0，所以 m＝ 3．,,,,,,,,,,,,,,,16 分19．（本小题满分 16 分）解：（方法一）如图 1，以 A 为原点， AB 为 x 轴，建立平面直角坐标系． Ny因为tanα＝－ 2，故直线 AN 的方程是 y＝－ 2x．C设点 P(x0， y0)．P·因为点 P 到 AM 的距离为 3，故 y0＝ 3．由 P 到直线 AN 的距离为5，(A) OBx（第 19 题图 1）得∣ 2x0＋y0∣ ＝5，解得 x ＝ 1 或 x ＝－ 4(舍去 )，5所以点 P(1， 3)．,,,,,,,,,,,,4 分显然直线 BC 的斜率存在．设直线BC 的方程为y－ 3＝ k(x－ 1)，k∈ (－ 2， 0)．令 y＝ 0得 x ＝ 1－ 3．,,,,,,,,,,,,6 分Bk由 y－ 3＝k(x－1)，解得 y＝6－ 2k．,,,,,,,,,,,,8 分y＝－ 2xCk＋ 21－ k2＋ 6k－ 98k－ 9设△ ABC 的面积为 S，则S＝ 2 xB yC＝k2＋ 2k＝－ 1＋k2＋ 2k．,,,,,10 分－ 2(4k＋ 3)(k－ 3)＝ 0 得 k＝－ 3或 k＝3．由 S ＝2＋ 2k)24当－ 2＜ k＜－ 3时， S ＜ 0， S 单调递减；当－ 3＜k＜ 0 时， S ＞0， S 单调递增．,13 分443所以当 k＝－4时，即 AB＝5 时， S 取极小值，也为最小值15．答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分（方法二）如图 1，以 A 为原点， AB 为 x 轴，建立平面直角坐标系．因为tanα＝－ 2，故直线AN 的方程是 y＝－ 2x．设点 P(x0， y0)．因为点 P 到 AM 的距离为 3，故 y0＝ 3．由 P 到直线 AN 的距离为5，得∣ 2x0＋y0∣5，解得 x0＝ 1 或 x0＝－ 4(舍去 )，＝5所以点 P(1， 3)．显然直线BC 的斜率存在．设直线BC 的方程为令 y＝ 0 得 xB＝ 1－ k．y－ 3＝k(x－1)，解得 yC＝6－ 2k． y＝－ 2x＋ 2k,,,,,,,,,,,,y－ 3＝ k(x－ 1)，k∈ (－ 2， 0)． ,,,,,,,,,,,,,,,,,,,,,,,,分分分设△ ABC 的面积为 S，则 S＝ 1xB yC＝－ k2＋ 6k－ 98k2－ 9 ． ,,,,,2＝－ 1＋2k＋ 2kk ＋ 2kt＋ 9令 8k－ 9＝ t，则t∈ (－25，－ 9)，从而 k＝8 ．因此 S＝－ 1＋t＝－ 1＋ 264t＝－ 1＋64．,,,,t＋9 2t＋ 9＋ 34t＋225(＋2×t34＋ t＋2258)8t因为当t∈ (－ 25，－ 9)时， t＋225∈ (－ 34，－ 30] ， t分分当且仅当t＝－ 15 时，此时 AB＝ 5， 34＋ t＋225的最大值为4．从而 S 有最小值为 15．t答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分（方法三）如图 2，过点 P 作PE⊥AM ， PF ⊥ AN，垂足为E、 F ，连接 PA．设 AB ＝ x，AC ＝ y．因为 P 到 AM ， AN 的距离分别为3，5，NCP·FA EMPE＝ 3， PF ＝ 5．S△ABC ＝S△ ABP＋S△ APC ＝1112 x 3＋ 2 y5 ＝2(3x＋ 5y)．① ,,4 分因为 tan ＝－ 2，所以 sin＝ 2 ．5所以S△ABC ＝ 1 x y2 ．②,,,,,,,,,,,,,,,8 分25由①②可得1x y212＝ (3x＋ 5y)．52即 3 5x＋ 5y＝ 2xy．③,,,,,,,,,,,,,,,10 分因为 3 5x＋5y≥ 2155xy，所以2xy≥ 2 155xy．解得xy≥ 15 5．,,,,,,,,,,,,,,,13 分当且仅当 35x＝5y 取“＝”，结合③解得x＝5， y＝ 35．所以S△ABC ＝ 1 x y2 有最小值 15．25答：当 AB＝ 5km 时，该工业园区的面积最小，最小面积为15km 2．,,,,,,16 分20．（本小题满分16 分）解：（1）当 a＝－ 1，x∈[0 ，＋∞ )时， f(x) ＝－ x3＋ x＋ 1，从而 f ′(x)＝－ 3x2＋ 1．x＝ 1 时， f(1)＝ 1，f ′(1)＝－ 2，所以函数y＝f(x) (x∈ [0，＋∞ )) 的图象在 x＝ 1 处的切线方程为y－1＝－ 2(x－ 1)，即 2x＋ y－ 3＝ 0． ,,,,,,,,,,,,,,,,,,,3 分2） f(x)＝ g(x)即为 ax3＋ |x－ a|＝ x4．所以 x4－ ax3＝ |x－ a|，从而 x3(x－ a)＝ |x－ a|．此方程等价于x＝ a 或 x＞ a，或 x＜ a，,,,,,,,,,,,,,,,,6 分x＝ 1x＝－ 1．所以当a≥1 时，方程 f(x)＝g(x)有两个不同的解 a，－ 1；当－ 1＜ a＜1时，方程 f( x)＝ g(x)有三个不同的解 a，－ 1， 1；当a≤－ 1 时，方程 f(x)＝ g(x)有两个不同的解a， 1．,,,,,,,,,,,9 分3）当 a＞ 0，x∈ (a，＋∞ )时， f(x)＝ ax3＋ x－ a，f ′(x)＝ 3ax2＋ 1＞ 0，所以函数 f(x)在 (a，＋∞ )上是增函数，且 f(x) ＞f(a)＝ a4＞ 0．所以当x∈[a，a＋ 2]时，f(x)∈ [f(a)， f( a＋ 2)] ，1024∈ [1024， 1024f( x)f(a＋ 2)f(a) ] ，当x∈ [a＋ 2，＋∞ )时，f(x)∈ [ f(a＋ 2)，＋∞ )． ,,,,,,,,,,,,,, 11 分因为对任意的x1∈ [a， a＋ 2]，都存在x2∈ [a＋ 2，＋∞ )，使得 f(x1)f(x2)＝1024，所以 [1024，1024[ f(a＋2) ，＋∞ )．,,,,,,,,,,,,,,,,13 分f( a＋ 2)f(a) ]?从而1024 ≥ f(a＋ 2)．f(a＋ 2)所以 f 2(a＋2)≤ 1024 ，即 f(a＋2) ≤32，也即 a(a＋ 2)3＋2≤ 32．因为 a＞ 0，显然 a＝1 满足，而a≥ 2 时，均不满足．所以满足条件的正整数a 的取值的集合为 {1}．,,,,,,,,,,,,,,16 分20xx 届高三年级学情调研卷数学附加题参考答案及评分标准20xx.09说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 21．【选做题】在A 、 B、 C、 D 四小题中只能选做2 题，每小题 10 分，共计20 分．A．选修 4— 1：几何证明选讲证明：连接 AO．设圆 O 的半径为 r．A因为 PA 是圆 O 的切线， PBC 是圆 O 的割线，所以 PA2＝PC· PB．,,,,,,,,,,,,PCQOB3 分因为 PA＝ 4，PC＝ 2，所以 42＝2×(2＋ 2r)，解得 r ＝ 3．,,,,,,5 分（第 21 题 A 图）所以 PO＝PC＋ CO＝ 2＋ 3＝ 5， AO＝ r ＝ 3．由 PA 是圆 O 的切线得PA⊥ AO，故在Rt△ APO 中，因为AQ⊥PO，由面积法可知，1× AQ× PO＝1×AP ×AO ，22AP× AO 4× 312即 AQ＝PO5＝5 ．,,,,,,,,10 分B．选修 4— 2：矩阵与变换解：（1）因为矩阵 A＝2b113 属于特征值的一个特征向量为α＝－ 1，2b12－ b． ,,,,,,,,,3 分所以＝1 ，即＝13－ 1－ 1－2－ b＝，从而－ 2＝－．解得 b＝ 0，＝ 2．,,,,,,,,,,5 分（ 2）由（ 1）知， A＝20 ．13设曲线 C 上任一点 M(x， y)在矩阵 A 对应的变换作用后变为曲线 C 上一点 P(x0， y0 )，则x02x＝2x，＝3yx＋ 3y从而x0＝2x，,,,,,,,,,,,7 分y0＝ x＋ 3y．因为点 P 在曲线 C 上，所以 x02＋ 2y02＝ 2，即 (2x)2＋ 2(x＋3y)2＝ 2，从而 3x2＋ 6xy＋ 9y2＝ 1．所以曲线 C 的方程为3x2＋6xy＋ 9y2＝ 1．,,,,,,,,,,,,10 分C．选修 4— 4：坐标系与参数方程解：（方法一）直线 l 的普通方程为 x－3y＋3＝ 0．,,,,,,,,,,,,,,3 分因为点 P 在圆 C 上，故设 P(3＋cosθ，sinθ)，从而点 P 到直线 l 的距离π|2 3－2sin(θ－)|d＝| 3＋cosθ－3sinθ＋ 3|＝．,,,,,,,,7 分1222＋ (－ 3)所以 dmin＝ 3－ 1．即点 P 到直线 l 的距离的最小值为3－ 1．,,,,,,,,,,,,10 分( 方法二 )直线 l 的普通方程为x－ 3y＋3＝ 0．,,,,,,,,,,,,3 分圆 C 的圆心坐标为 (3，0) ，半径为 1．从而圆心 C 到直线 l 的距离为 d＝ | 3－ 0＋ 3| ＝ 3．,,,,,,,,,,6 分12＋( － 3)2所以点 P 到直线 l 的距离的最小值为 3－ 1．,,,,,,,,,,10 分D．选修 4— 5：不等式选讲证明：因为 a，b 是正数，且 a＋ b＝1，所以 (ax＋ by)(bx＋ ay)＝ abx2＋ ( a2 ＋ b2 )xy＋ aby2＝ ab(x2＋ y2)＋ (a2＋ b2)xy,,,,,,,,,,,3 分≥ ab 2xy＋ (a2＋ b2)xy,,,,,,,,,,,,8 分＝ (a＋ b)2xy＝ xy即 (ax＋ by)(bx＋ay)≥ xy 成立．,,,,,,,,,,,,10 分【必做题】第 22 题、第 23 题，每题10 分，共计20 分．22．解：（ 1）以 D 为原点， DA 为 x 轴， DC 为 y 轴， DD 1 为 z 轴，建立如图所示的空间直角坐标系．由题设，知 B(2， 3， 0)， A1(2， 0， 5)，C(0， 3，0) ，C1(0， 3，5)．z→→D 1C1因为 CE＝λCC1，所以 E(0， 3，5λ)．→A1B12 分从而 EB＝ (2， 0，－5λ)， EA1＝(2，－ 3， 5－5λ)．,, 当∠ BEA1 为钝角时，cos∠ BEA 1＜ 0，E→→DC y2× 2－5λ(5－5λ＜)0，所以EB · EA1＜0，即AB1＜λ＜ 4．x（第 22 题图）解得 5514,,,,,,,,,,,,,,5 分即实数λ的取值范围是 ( ， )．55→→（ 2）当λ＝时， EB ＝(2， 0，－ 2)， EA1＝ (2，－ 3， 3)． 5设平面 BEA1 的一个法向量为n1＝ (x，y， z)，→2x－ 2z＝ 0，由n1· EB ＝0，→得2x－ 3y＋ 3z＝ 0，n1· EA1＝ 05取 x＝ 1，得 y＝ 3， z＝ 1，所以平面 BEA1 的一个法向量为n1＝ (1，5， 1)．,,,,,,,,,,,,,7 分3易知，平面 BA1B1 的一个法向量为n2＝ (1， 0， 0)．因为 cos＝n1· n2 ＝143，| n1|· |n2|43439343,,,,,,,,,,,,,,10 分从而|cosθ|＝ 43 ．123．解：（ 1）因为 P(X＝ 10)＝ 12＝1C3＝ 3 ，， P(X＝ 5)＝ 2C510C51021C3＝ 3 ， P(X＝ 0)＝C3＝ 3 ，P(X＝ 2)＝ 2210C5C5所以 X 的概率分布表为： X1052P133310101010,,,,,,,,,,,4 分1333从而 E(X)＝10 10＋5 10＋210＋ 010＝ 3.1 元．,,,,,,,,,,,6 分（ 2）记该顾客一次摸球中奖为事件A，由（ 1）知， P(A)＝ 7 ，10291从而他两次摸球中至少有一次中奖的概率 P＝1－[1－ P(A)] ＝100．答：他两次摸球中至少有一次中奖的概率为 91 ．,,,,,,,,,,,10 分．100。

南京市2018届高三年级学情调研数学附加卷

南京市2018届高三年级学情调研卷数学附加题 2017.09 注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前，考生务必将自己的姓名、学校写在答题卡上．试题的答案写在答．题．卡．上对应题目的答案空格内．考试结束后，交回答题卡．21．【选做题】在A 、B 、C 、D 四小题中只能选做2题，每小题10分，共计20分．请在答．卷卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． A ．选修4—1：几何证明选讲如图，CD 是圆O 的切线，切点为D ，CA 是过圆心O 的割线且交圆O 于点B ， DA ＝DC ．求证： CA ＝3CB ．B ．选修4—2：矩阵与变换设二阶矩阵A ＝⎣⎡⎦⎤1234．（1）求A －1；（2）若曲线C 在矩阵A 对应的变换作用下得到曲线C '：6x 2－y 2＝1，求曲线C 的方程．C ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为⎩⎨⎧x ＝－1＋t ，y ＝t（t 为参数），圆C 的参数方程为⎩⎨⎧x ＝a ＋cos θ，y ＝2a ＋sin θ（θ为参数）．若直线l 与圆C 相切，求实数a 的值．（第21A 题）D ．选修4—5：不等式选讲解不等式：|x －2|＋|x ＋1|≥5．【必做题】第22题、第23题，每题10分，共计20分．请在答．卷卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）如图，在四棱锥P －ABCD 中，P A ⊥平面ABCD ，AB ⊥AD ，AD ∥BC ，AP ＝AB ＝AD ＝1．（1）若直线PB 与CD 所成角的大小为π3，求BC 的长；（2）求二面角B －PD －A 的余弦值．23．（本小题满分10分）袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有4个，分别编号为1，2，3，4．现从袋中随机取两个球．（1）若两个球颜色不同，求不同取法的种数；（2）在（1）的条件下，记两球编号的差的绝对值为随机变量X ，求随机变量X 的概率分布与数学期望． C D PB A （第22题）。

2018年高考南京市高三年级学情调研考试试卷(含答案)

南京市2018届高三年级学情调研考试英语2017.09本试卷分选择题和非选择题两部分。

满分120分，考试用时120分钟。

注意事项：答题前，务必将自己的学校、姓名、考试号写在答题纸上。

考试结束后，将答题纸交回。

第一部分听力（共两节，满分20分）做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题纸上。

第一节（共5小题；每小题1分，满分5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What are the speakers mainly talking about?A. A friend.B. A program.2.What time is it in New York?A.About 5 p.m.B. About 7 p.m.3.Why did the woman go to the city?A. To have a chat.B. To have dinner.4.How much will the woman pay if she buys two skirts?A. $38.B. $39.5.Where will the woman get the ticket?A. On the Internet.B. In the museum.第二节（共15小题：每小题1分，满分15分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听每段对话或独白前，你将有时间阅读各个小题, 每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6、7题。

6.What is the lost handbag like?A.It has a small button.B. It is a leather bag.C. It is an empty bag.7.What does the man ask the woman to do?A.To call the police.B. To search everywhere.C. To leave her information.听第7段材料，回答第8至10题。

2017-2018学年江苏省南京市高三(上)9月调研数学试卷

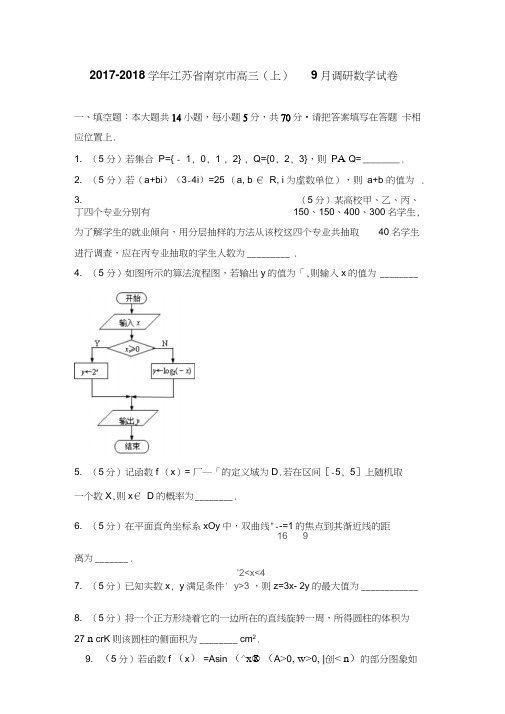
2017-2018学年江苏省南京市高三（上）9月调研数学试卷一、填空题：本大题共14小题，每小题5分，共70分•请把答案填写在答题卡相应位置上.1. （5 分）若集合P={ - 1, 0, 1 , 2} , Q={0, 2, 3}，则P A Q= _______ .2. （5 分）若（a+bi）（3-4i）=25 （a, b € R, i 为虚数单位），则a+b 的值为 .3. （5分）某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为_________ .4. （5 分）如图所示的算法流程图，若输出y的值为「,则输入x的值为________5. （5分）记函数f （x）= 厂―「的定义域为D.若在区间［-5, 5］上随机取一个数X,则x€ D的概率为________ .6. （5分）在平面直角坐标系xOy中，双曲线"--=1的焦点到其渐近线的距16 9离为_______ .'2<x<47. （5分）已知实数x, y满足条件' y>3 ，则z=3x- 2y的最大值为____________8. （5分）将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27 n crK则该圆柱的侧面积为________ cm2.9. （5分）若函数f （x）=Asin （^x® （A>0, w>0, |创< n）的部分图象如第1页（共24页）10. （5分）记等差数列｛a n｝前n项和为S n•若a m=10, S2m-1=110,贝U m的值为______ .11. _______________________________________________________________ （5分）已知函数f （x）是定义在R上的奇函数，且在（-X, 0］上为单调增函数•若f （- 1）=-2，则满足f （2x- 3）< 2的x的取值范围是 _________________ .12. （5分）在厶ABC 中，AB=3, AC=2, / BAC=120, BM= .若AM?EC=-竺,3 则实数入的值为_________ .13. （5分）在平面直角坐标系xOy中，若圆（x-2）2+ （y-2）2=1上存在点M , 使得点M关于x轴的对称点N在直线kx+y+3=0上，则实数k的最小值为________ .14（5分）已知函数f（x）= ……若存在唯一的整数x,使得|^-3 |x-l | + 3, （x>0）x>0成立，则实数a的取值范围为 ________ .二、解答题：本大题共6小题，共计90分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.15. （14分）在直三棱柱ABC- A1B1C1中，AB=AC E是BC的中点，求证：（I）平面ABE丄平面BBCC;（n）“c//平面ABE.第3页(共24页)第4页（共24页）416. （14分）在厶ABC 中，内角A , B, C 所对的边分别为a , b , c , cosB=.(I)若 c=2a,求二二L —的值；sinC(H) 若 c — B="，求 si nA 的值.417. (14分)某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置.设加工甲型装置的工人有x 人，他们加工完甲型装置所需时间为t 1小时，其余工人加工完乙型装置所需时间为t 2小时. 设 f (X )=t 1+t 2.(I)求f ( X )的解析式，并写出其定义域； (U)当x 等于多少时，f (x )取得最小值?2 218. (16分)如图，在平面直角坐标系 xOy 中，椭圆C : —=1 (a > b >0)a b的离心率为乎，且过点(1,爭).过椭圆C 的左顶点A 作直线交椭圆C 于另一点P ，交直线I : x=m (m >a )于点M .已知点B (1，0)，直线PB 交I 于点N .19. (16分)已知函数 f (x ) =2x 3— 3 (a+1) x 2+6ax ，a € R.(I)曲线y=f (x )在x=0处的切线的斜率为3,求a 的值；(U)若对于任意x €(0，+^)，f (x ) +f ( — x )> 12lnx 恒成立，求a 的取值范围；(I)求椭圆C 的方程;m 的值.(川)若a> 1,设函数f (x)在区间［1, 2］上的最大值、最小值分别为M (a)、m (a),记h (a) =M (a)—m (a),求h (a)的最小值.第5页(共24页)第6页（共24页）20. （16分）已知数列｛a n ｝的各项均为正数，记数列｛a n ｝的前n 项和为S ，数列｛a n 2｝的前 n 项和为 T n , 且 3T n =E 2+2S , n € N *.（I ）求a i 的值；（U ）求数列｛an ｝的通项公式；（川）若k , t € N *，且0, S k -3, S - S k 成等比数列，求k 和t 的值.【选做题】在21,22,23,24四小题中只能选做2题，每小题0分，共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. ［选修4-1:几何证明选讲］21. 如图，CD 是圆O 的切线，切点为D ，CA 是过圆心O 的割线且交圆O 于点B ， DA=DC 求证：CA=3CB［选修4-2:矩阵与变换］22 .设二阶矩阵A=P 2（I ）求 A -1;（U ）若曲线C 在矩阵A 对应的变换作用下得到曲线 C : 6X 2-『=1，求曲线C的方程.［选修4-4 :坐标系与参数方程］23 .在平面直角坐标系xOy 中，直线I 的参数方程为" （t 为参数），圆C［选修4-5:不等式选讲］ 24 .解不等式：|x -2|+| x+1| >5 .【必做题】第25题、第26题，每题10分，共计20分•请在答卷卡指定区域内作22 .设二阶矩阵A=（B 为参数）.若直线I 与圆C 相切，求实数a 的值.的参数方程为第7页(共24页)答•解答应写出文字说明、证明过程或演算步骤.25.如图，在四棱锥 P - ABCD 中，PA ±平面 ABCDAB 丄AD,AD// BC, AP=AB=AD=1(I)若直线PB 与CD 所成角的大小为一二，求BC 的长；26.袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有 4个，分别编号为1，2，3，4.现从袋中随机取两个球.(I)若两个球颜色不同，求不同取法的种数；(U)在(1)的条件下，记两球编号的差的绝对值为随机变量 X ,求随机变量X 的概率分布与数学期望.20仃-2018学年江苏省南京市高三（上）9月调研数学试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共70分•请把答案填写在答题卡相应位置上.1. （5 分）若集合P={ - 1, 0, 1 , 2} , Q={0, 2, 3}，则P A Q= {0, 2} . 【解答】解：集合P={ - 1 , 0, 1, 2},Q={0, 2, 3},则P A Q={ - 1 , 0, 1, 2} A {0, 2, 3}={0, 2}.故答案为：{0, 2}.2. （5 分）若（a+bi）（3-4i）=25 （a, b € R, i 为虚数单位），则a+b 的值为7.【解答】解：由题意得，（a+bi）（3-4i）=25,•••（3b- 4a）i+3a+4b=25,.f3b-4a=0l3a+4b=25--a=3 b=4,• a+b=7,故答案为：73. （5分）某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生，为了解学生的就业倾向，用分层抽样的方法从该校这四个专业共抽取40名学生进行调查，应在丙专业抽取的学生人数为16 .【解答】解：•••高校甲、乙、丙、丁四个专业分别有150、150、400、300名第8页（共24页）学生•本校共有学生150+150+400+300=1000,第9页(共24页)第10页（共24页）•••用分层抽样的方法从该校这四个专业共抽取 40名学生进行调查 •••每个个体被抽到的概率是•.•丙专业有400人， •要抽取400X 丄=1625 故答案为：164(5分)如图所示的算法流程图，若输出y 的值为丄，则输入x 的值为 -並2—【解答】解：根据流程图所示的顺序，可知：该程序的作用是计算分段函数y=''… .的函数值,［log 2Gx), x<0 当x >0时，y=2x =，解得x=- 1，不合条件，舍去；二当 xv 0 时，y=log2 (- x )=，，解得 x=- ■:;二综上，yJ 时，输入的x 值为-:. 故答案为：-15. (5分)记函数f (x ) = ： ,：「的定义域为D •若在区间［-5, 5］上随机取一个数x ,则x € D 的概率为_ 【解答】解：函数f (x )I ： = I| =则 4 —3x—x2> 0, 即卩/+3x— 4< 0, 解得-4W x< 1;••• f (x)的定义域为D=[ - 4, 1]; 在区间[-5, 5]上随机取一个数x, 则x€ D的概率为P= : J .5-(-5) 2故答案为：1 .26. （5分）在平面直角坐标系xOy中，双曲线厂—=1的焦点到其渐近线的距16 9离为3 .2 2【解答】解：双曲线二-—=1的焦点坐标为（土5,0）,渐近线的方程为x土二y=0,16 9 3双曲线二—_=1的焦点到渐近线的距离为：一口——=3,故答案为：3.7. （5分）已知实数x, y满足条件y>3 ，则z=3x- 2y的最大值为6 ^+y<8f2<x<4【解答】解：作出实数x, y满足条件、y>3，对应的平面区域如图：x+y<3L由z=3x- 2y 得y= x—,平移直线y= x—,经过点A时，直线丫= *的截距最小，此时z最大.2 2 2 2由（尸3,解得A （4, 3）,x=4L此时Z max=3X 4 -2X 3=6,故答案为：6.8. （5分）将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为 27 n er 3，，则该圆柱的侧面积为18n cm2.【解答】解：将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为 27 n cm,设正方形的边长为acm ,则V=nf ?a=27n 解得a=3cm ,•••该圆柱的侧面积为S=2冗X 3 X 3=18n crn . 故答案为：18 n9. （5分）若函数f （x ） =Asin （^x® （A >0, w>0, |创V n ）的部分图象如图所示，则f （ - n 的值为 -1.【解答】解：有函数的图象可得 A=2, 再根据］T=? 十_ ,求得3=. 由于点（n 2）在函数图象上, 可得: 2=2sin (=X n + ®),可得:3Xn +® =2kk €Z ,求得© =2k n k€ Z,又由于| ©| V n,可得：©=-=,6故函数的解析式为f (x) =2sin ( x-),3 6可得：f (—n) =2sin ( —Z n- —) = - 2si^^=—1.3 6 6故答案为：-1.10. (5分)记等差数列｛a n｝前n项和为S n.若a m=10, S m-1=110,则m的值为6 .【解答】解：由a m=10,--2a m =a1 +a2m -1 =20,c (血T) (a, +^兀_1 )二S2m-1= =10 (2m- 1) =110,解的m=6,故答案为：611. (5分)已知函数f (x)是定义在R上的奇函数，且在(-X, 0]上为单调增函数.若f (- 1) =-2,则满足f (2x-3)< 2的x的取值范围是 (-%, 2 .【解答】解：根据题意，函数f (x)是定义在R上的奇函数，且在(-X, 0]上为单调增函数，则在f (x)在[0, +X)上也是增函数，故函数f (x) R上也是增函数；又由 f (- 1) =-2,则 f (1) =-f (- 1) =2,则 f (2x- 3)< 2? 2x- 3< 1,解可得x<2,即不等式的解集为(-x, 2];故答案为：(-x, 2].12. (5分)在厶ABC中，AB=3, AC=2 / BAC=120,丽二蔽.若而?反=-则实数八的值为」—【解答】解：如图所示,△ ABC中，AB=3, AC=2 / BAC=120,r=x「=入(小)，—* —* —* —* —*• ••叶？：= (1+ !') ?:'=(AB + 入(AC - AB)) ? ( AC - AB)=[(i -八7S+蔽]?(疋-7S)=(1 - 2 八'?£'-( 1 - R ；.J. +X, ■=(1 - 2R X 3X 2 X cos120，( 1-R X 32+R ?217=19 X- 12=-三-解得X=.故答案为:13. (5分)在平面直角坐标系xOy中，若圆(x-2) 2+ (y-2) 2=1上存在点M , 使得点M关于x轴的对称点N在直线kx+y+3=0上，则实数k的最小值为 -；.【解答】解：根据题意，圆C: (x- 2) 2+ (y- 2) 2=1关于x轴的对称图形是：圆D: (x-2) 2+ (y+2) 2=1,则圆D上存在点N在直线kx+y+3=0 上,又直线kx+y+3=0过定点P (0,- 3),•••直线与圆D相切时，有d=r,解得k=-；或k=0,3•••实数k的最小值为-’.3故答案为：」.14. （5分）已知函数f（x）= … 」一若存在唯一的整数x,使得二互一| + 3f（x>0）x >0成立，则实数a的取值范围为[0, 2] U [3, 8]（【解答】解：作出f f x）的函数图象如图所示：•••存在唯一的整数x,使得二0成立,x••• a v f f x)只有1个整数解，又f (2) =0, ••• 0< av 3.(2)若x v 0,则f f x)> f f 0) =0,•••存在唯一的整数X,使得f > 0成立，X••• a>f (x)只有1 个整数解，又f (- 1) =2, f ( - 2) =8,2v a< 8.•••当O w a<2或3< a< 8时，「丄二->0只有1个整数解.x故答案为：[0, 2] U [3, 8].二、解答题：本大题共6小题，共计90分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤.15. (14分)在直三棱柱ABC- A1B1C1中，AB=AC E是BC的中点，求证：(I)平面ABE丄平面BBCC;(n) “c//平面ABE.【解答】(本小题满分14分)证明：(I)在直三棱柱ABC- A1B1C1中，CC丄平面ABC.••• AE?平面ABC, • CC丄AE.v AB=AC E为BC的中点，• AE丄BC. ••• BC?平面B1BCG, CC?平面B1BCC,且BC A CC=C,•AE丄平面B1BCC.••• AE?平面AB1E,：平面AB1E丄平面BBCC .(n)连接A1B,设A1B n AB1=F, 连接EF.在直三棱柱ABC- A1B1G中，四边形AA1B1B为平行四边形，• F为A1B的中点.••• E是BC的中点，所以EF/ A1C.••• EF?平面A0E, A1C?平面ARE,•A1C//平面ABiE.16. （14分）在厶ABC 中，内角A , B, C 所对的边分别为a , b , c , cosB=.5（I ）若c=2a,求二心的值;sinC（H ）若 C - B=，求 si nA 的值.4【解答】（本小题满分14分）解：（ 1）在厶ABC 中，因为cosB=:, 5所以：a 2 + c 2-b 2 42ac 5因为：c=2a, 所以： (f)2 + c 2-b 2 2=，即=■, 2cXf 5 £ 20由正弦定理得二二sinC c又 O v B v n,所以 sinB= '_ 一=，所以 sin2B=2sinBcosB=Z .1= 1 .5 55 25因为 C -B=_，即 C=B^ ,4 4 所以 A=n -( B+C ) =- 2B,4所以 sinA=sin (^^ - 2B ) =sin cos2B — cos sin2B=' )x4 4 4 225224 = 31 血 IF •.所以:sinC 10（U ）因为cosB=，所以 5cos2B =2coSB - i .尿 $所以:17. (14分)某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置.现将工人分成两组分别加工甲型和乙型装置. 设加工甲型装置的工人有x 人，他们加工完甲型装置所需时间为t 1小时，其余工人加工完乙型装置所需时间为t 2小时. 设 f ( X )=t 1+t 2.(I)求f ( X )的解析式，并写出其定义域; (U)当x 等于多少时，f (x )取得最小值?(10+x 100-x:')=10X( 10+6) =160. V x 100-x当且仅当x=75人时，函数f (x )取得最小值160小时.2 218. (16分)如图，在平面直角坐标系 xOy 中，椭圆C :+ =1 (a > b >0)己b的离心率为拳，且过点(1,半).过椭圆C 的左顶点A 作直线交椭圆C 于另一点P ，交直线I : x=m (m >a )于点M .已知点B (1，0)，直线PB 交I 于点N .(I)求椭圆C 的方程；(U)若MB 是线段PN 的垂直平分线，求实数 m 的值.【解答】解：(l )T t1=3 x••• f (x) =t1+t2=_ +' '■',工 100-x 5(II ) f ( x ) =1000 ： !t= Dr 112=・=航■.定义域为{x| K x < 99, x € N *}.X 100-M1) =10[x+ ( 100 - x ) ] (2 一i —) =10X 100-K> 10X( 10+2 ；川【解答】（本小题满分16分）解：（I ）因为椭圆C 的离心率为，, 所以 a 2=4b 2.又因为椭圆C 过点（1,二），3_所以亠T \-，a b 解得 a 2=4，b 2=1.2 “所以椭圆C 的方程为一.（U ）设 P （X o , y o ）, - 2v X o V 2, x o 工 1,2 则］—因为MB 是PN 的垂直平分线，所以P 关于B 的对称点N （2 - X o ,- y o ）,所以2 - X o =m. 由 A (-2, 0),P (xo , yo ),可得直线 AP 的方程为 y=r (X +2)，y D因为 PB 丄MB ,所以 k pB ?k MB = - 1，所以 k pB ?k MB = ?, = - 1,X Q -1m-1Yr* (nH-2)pn ________ ______________ _ - 1即：，i —「I = 1.所以因为 X o =2- m ,令 x=m ,得 y= .. (m+2),即 M (m ,屯+2(m+2)).2化简得3m2- 10m+4=0，解得m=3因为m>2,所以m=「319. (16分)已知函数f (x) =2x3- 3 (a+1) x2+6ax, a€ R.(I)曲线y=f (x)在x=0处的切线的斜率为3,求a的值；(U)若对于任意x€(0, +^) , f (x) +f (-x)> 121 nx恒成立，求a的取值范围；(川)若a> 1,设函数f (x)在区间［1, 2］上的最大值、最小值分别为M (a)、m (a),记h (a) =M (a)- m (a),求h (a)的最小值.【解答】解：(I) f'( x) =6x^- 6 (a+1) x+6a,故k=f'( 0) =6a,由6a=3,解得：a—;(n) f (x) +f (- x) =- 6 (a+1) x2> 12lnx对任意x€( 0, +x)恒成立，故-(a+1)》丁xg( x)豊,x> 0,则g( x 生警),令g' (x) =0,解得：x= ■■,故g (乂)在(0,二)递增，在(_, +x)递减，故g (x) max=g ( J =,e故-(a+1)》一，故a<- 1 - 一e e故a的范围是(-x,- 1-—］；(川)f'(x) =6x2- 6 (a+1) x+6a=6 (x- 1) (x- a),f (1) =3a- 1, f (2) =4,令f' (x) =0,解得：x=1 或x=a,①当1v a w「时，3x€( 1, a)时，f'(x)v0, f (乂)在(1, a)递减，x€(a, 2)时，f'(x)>0, f (幻在(a, 2)递增，I f (1)< f (2),故M (a) =f (2) =4, m (a) =f (a) =- a3+3a2,故h (a) =M (a)- m (a) =a3- 3a2+4,••• h' (a) =3a (a-2)v0,••• h (&)在(1,「］递减，3故a€( 1,吕］时，h (a)最小值=h (£)=［;②当.v a v 2时，3x€( 1, a)时，f'(x)v0, f (乂)在(1, a)递减，x€(a, 2)时，f'(x)>0, f (幻在(a, 2)递增，T f (1 )> f (2), • M (a) =f (1) =3a- 1, m (a) =f (a) =- a3+3a2, 故h (a) =M (a)- m (a) =a3- 3a2+3a - 1,T h' (a) =3 (a- 1) 2>0,故h (a)在(匚，2)递增，3故a€(「，2)时，h (a)> h (「)=［;③当a>2时，x€( 1, 2)时，f'( x)v 0, f (刈在(1, 2)递减，故M (a) =f (1) =3a- 1, m (a) =f (2) =4,故h (a) =M (a)- m (a) =3a- 5,故h (a)在［2, +x)上的最小值是h (2) =1,综上，h (a)最小值=三.M I20. (16分)已知数列｛a n｝的各项均为正数，记数列｛a n｝的前n项和为S，数列｛a n2｝的前n 项和为T n, 且3T n=E2+2S, n € N*.(I)求a1的值；(U)求数列｛an｝的通项公式；（川）若k, t € N*，且S, S k-S1, S - S k成等比数列，求k和t的值.【解答】解：（I）由3T n=S2+2S n, n €N*. n=1 时，3T i= -+2S,可得.... .工0，解得a i=1.（II）由3T n=S2+2S，n € N*. n >2 时，-- +2S n-1,相减可得：-「=S2Ji n-1 °n-l ^a n「+细,--3an=Si+Si T+2.• • 3a n+i=Si+i+Si+2，可得：3a n+i —3a n=a n+ 什a n,化为：a n+i=2a n. n=1 时，3E二蟲乜匕，可得3（1+£）二（1+ a»'+2（仔比），十 > 0,解得a2=2, 满足上式.•••数列｛a n｝是等比数列，首项为I,公比为2.二a n=2n—i.（III）由（ii）可得：sn=…「=2n—i.2-1由0, S k—0, S —S<成等比数列，•••.■-_ I •■.:,可得（2k- 2）2=2f-2k.化为：2f= （2k）2—3?2k+4，可得：2f —2= （2k—i）2—3?2k —i+i. （*）k=i时不满足题意，• k>2.k=2 时，2f=8,解得t=3.k>3时，t=2时，化为2k=3,不成立舍去.t > 3时，（*）左边为偶数，右边为奇数，不成立.综上可得：t=3, k=2.【选做题】在21,22,23,24四小题中只能选做2题，每小题0分，共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤. ［选修4-1:几何证明选讲］2i.如图，CD是圆O的切线，切点为D, CA是过圆心O的割线且交圆O于点B, DA=DC 求证：CA=3CB因为 DA=DC 所以/ DAO=Z C.在圆 O 中，AO=DO,所以/ DAO=Z ADO, 所以/ DOC=2/ DAO=2Z C . 因为CD 为圆O 的切线，所以/ ODC=9°,从而/ DOG / C=90,即 2/ C+/C=90, 故/ C=30,所以 OC=2OD=2OB 所以CB=OB 所以CA=3CB［选修4-2:矩阵与变换］ 22•设二阶矩阵A 』】'.13 4」(I)求 A";(n)若曲线C 在矩阵A 对应的变换作用下得到曲线 C : 6x 2- y 2=1，求曲线C的方程.(n)设曲线C 上任意一点P(x, y ),在矩阵A 对应的变换作用下得到点P (X’,y ),"detA =3 4 = " 2【解答】1 9解：(I厂A=34则［叮* 2］丹严八， _y ］ L3 dLyJ L3x+4y_.* =x+2yV =3x+4y•••(x ； y')在曲线 C 上，.6x 2-y'2=1,代入 6 (x+2y ) 2-( 3x+4y ) 2=1，化简得 8y 2 - 3^=1, .曲线C 的方程为8y 2-3x 2=1.［选修4-4 :坐标系与参数方程］23. 在平面直角坐标系xOy中，直线I 的参数方程为（尸T+t （ t 为参数），圆C【解答】解：由直线I 的参数方程为"'，得直线I 的普通方程为x -y+仁0.【尸t由圆C 的参数方程为（E+3 ，得圆C 的普通方程为（x -a ） 2+（y -2a ）2=1.Iy=2a+sin9因为直线I 与圆C 相切，所以二二-亠丨=1，V2 解得 a=1± ':. 所以实数a 的值为1 ±匚.［选修4-5:不等式选讲］ 24. 解不等式：|x -2|+| x+1| >5.【解答】解：（1）当X V- 1时，不等式可化为-x+2 - x- 1 >5,解得x <- 2; （2）当-Kx < 2时，不等式可化为-x+2+x+1 > 5,此时不等式无解；（3）当x >2时，不等式可化为x -2+x+1 >5,解得x >3; 所以原不等式的解集为（-X,-2］ U ［3, +x ）.【必做题】第25题、第26题，每题10分，共计20分.请在答卷卡指定区域内作答.解答应写出文字说明、证明过程或演算步骤.25. 如图，在四棱锥 P - ABCD 中，PA ±平面 ABCDAB 丄AD,AD// BC, AP=AB=AD=1I 尸t （B 为参数）.若直线I 与圆C 相切，求实数a 的值.的参数方程为， x^a^cos 0y^2a+sin 6（I）若直线PB与CD所成角的大小为二，求BC的长；【解答】解：(I)分别以AB AD 、AP 所在直线为x 、y 、z 轴建立如图所示的空间直角坐标系A - xyz.••• AP=AB=AD=1 ••• A (0 , 0, 0), B (1, 0, 0), D (0, 1, 0), P (0, 0, 1). 设 C (1, y , 0),则瓦=(1, 0, - 1), CD = (- 1,1- y , 0). ；直线P B 与CD 所成角大小为1即］J ，解得y=2或y=0 (舍)，V2x Vl+(l-y)2 2• C (1, 2, 0),则 BC 的长为 2;(U)设平面PBD 的一个法向量为■= (x , y , z ). •- 1= (1 , 0, - 1), 1= (0 , 1 , - 1),审 —*''''■ '■,令 x=1 ,则 y=1 , z=1 , = (1 , 1 , 1). PD "npy-z-0•••平面PAD 的一个法向量为 F (1 , 0 , 0), --cog 二|面角B - PD- A 的余弦值为 J .■C 1••• I cos v 〒: i'.l>1 =| (U)求二面角B - PD- A 的余弦值.26.袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有 4个，分别编号为1，2，3，4.现从袋中随机取两个球.（I ）若两个球颜色不同，求不同取法的种数；（U ）在（1）的条件下，记两球编号的差的绝对值为随机变量 X ,求随机变量X 的概率分布与数学期望.【解答】解：（1）两个球颜色不同的情况共有：？42=96 （种）.4（2）随机变量X 所有可能的值为0，1, 2，3.所以随机变量X 的概率分布列为:X12 3P13 ■g1 71所以 E ( =0X[+「+3 X-=.(X=0)96 4 (x=1)=二=■I，(X=2)=呻;=1 ■I -， (X=3)克!丄::.。

2018届高三9月调研测数学理试题含答案

2017-2018学年第一学期高三调研测试卷数学（理科）2017.9全卷满分：150分考试时间：120分钟第Ⅰ卷（共60分）一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）（）1．已知全集U=R ，集合A={x|lg(x-2)≥0}, B={x|x≥2}, 则(C U A)∩B= A ．{}13x x -<≤ B ．{}23x x ≤<C ．{}3x x ≤ D ．φ（）2．某居民小区为如图所示矩形ABCD ，A , C 两点处各有一个通信基站, 假设其信号覆盖范围分别是扇形区域ADE 和扇形区域CBF ，若在该小区内随机地选一地点, 则该地点无．信号的概率是 (注：该小区内无其他信号来源, 基站工作正常). A ．12π- B ．22π-C ．14π-D ．4π（）3．“0a ≤”是“复数1ai z i+=在复平面内对应的点在第三象限”的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件（）4．设{}n a 是等差数列，1359a a a ++=，69a =，则这个数列的前6项和等于 A ．12B ．24C ．36D ．48（）5．已知0.1 1.12log 0.1,2,0.2a b c ===，则,,a b c 的大小关系是A ．a b c <<B ．b c a <<C ．c a b <<D ．a cb <<（）6．把函数sin y x =（x R ∈）的图象上所有点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是A ．sin(2)3y x π=-，x R ∈B ．sin()26x y π=+，x R ∈ C ．sin(2)32y x π=+，x R ∈D ．sin(2)3y x π=+， x R ∈（）7．执行右图的程序框图，若输出的5n =，则输入整数p 的最大值是 A ．15 B ．14C ．7D ．6（）8．51(1)(1)x x++展开式中2x 的系数为A ．20B ．15C ．6D ．1（）9．设奇函数f (x )在(0，＋∞)上为单调递减函数，且f (1)＝0，则不等式()()20f x f x x-+≥的解集为A ．(－∞，－1]∪(0,1]B ．[－1,0]∪[1，＋∞)C ．(－∞，－1]∪[1，＋∞)D ．[－1,0)∪(0,1] （）10．一个四面体的三视图如图所示,则该四面体的表面积是A ．1+B ．1+2C ．2+D ．2（）11．设抛物线C ：y 2＝4x 的焦点为F ，直线l 过F 且与C 交于A ，B 两点．若 |AF |=2|BF |，则线段AB 的长为．A ．8B ．92C ．16D ．163 （）12．已知定义在),0[+∞上的函数)(x f 满足)2(2)(+=x f x f ，当)2,0[∈x 时，x x x f 42)(2+-=，设)(x f 在)2,22[n n -上的最大值为)(*N n a n ∈,且}{n a 的前n 项和为n S ，则n S =A ．1212--nB ．2214--n C ．n 212- D ．1214--n第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13．已知向量25,10),1,2(=+=⋅=→→→→→b a b a a ，则=→b .14．设y x ,满足约束条件⎪⎩⎪⎨⎧-≥≤+≤11y y x xy ，则y x z +=2的最大值为 .15．如图，已知双曲线2222:1x y C a b-=(0,0)a b >>的右顶点为,A O 为坐标原点，以A 为圆心的圆与双曲线C 的一条渐近线交于两点P ，Q ，若060PAQ ∠=，且3OQ OP =uuu r uu u r，则双曲线C 的离心率为.16．如图所示,ABCD 是边长为60 cm 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD 四个点重合于图中的点P, 正好形成一个正四棱柱形状的包装盒,若要包装盒容积V(cm 3)最大, 则EF 长为 cm ．三、解答题：（共70分。

2018届高三数学9月考题(含答案).docx

[X 2 + y 2 < 1 < x + y > — 111. 已知乂,丫满足1 yvO ，贝ijz = x-y 的取值范围是() A.[-返叮 B.[・ 1,1] C.[-返返] D. [ - 1,返] 12.已知定义在R 上的函数f (x)在(-8, -2)上是减函数，若g (x) =f (x - 2)是奇函数，且g (2)=0,则不等式xf (x) W0的解集是(A. ( - °°, - 2] U [2, +°°) C. ( - 8, - 4]U[ - 2, +8)二、填空题(20分)13. 已知f (x )= log 3(x 2-2x)?则函数f(x)的单调递减区间是 _____________ .14. 已知函数f(x) = x 3 + ax 2 + bx + a 2(a,b 6 R)且函数f(x)在x = 1处有极值10,则实数b 的值为15. _________ 已知f (x) = |e x -l|,又g(x) =f 2(x)-tf(x)(tG R),若满足g(x) = 一1的x 有三个，贝吐的取值范围是 ____________ •16. 设f(x)是定义在R 上的偶函数，且当x > 0时，f(x) = 2X ,若对任意的xG [a,a + 2],不等式 f(x + a) >『(x)恒成立，则实数a 的取值范围是 _____________ .=、解答题：木题共6道题，共70分.17. 锐角AABC 的内角A, B, C 的对边分别为a, b, c,己知AABC 的外接圆半径为R,旦满足R = t asinA (1) 求角A 的大小；(2)若a = 2,求AABC 周长的最大值.A. ( -- 3] B. [ - 3, +°°) C. ( - °°, VS] D. [V3, +8))B. [-4, -2]U[0, +°o) D. ( - °°, - 4] U [0, +8)2018届高三数学9月考题（含答案）2017-9-28一、选择题(60分)1. 若集合A={x|x> - 1},则( )A. OCAB. {0}cAC. {0}£AD. 0£A2. 设集合A = (X|X2-2X-3 < 0},B = {x|y = ln(2-x)},则A n B =()A. {x|-l < x < 3}B. {x|-l < x < 2}C. {x|-3 < x < 2}D. {x|l < x < 2}2 _3. 若复&z =屮i为虚数单位，^z=()A. 1 + iB. 1-iC. -1-iD. -1-i4. 已知命题p:Vx > 0,总有(x + l)e x > 1,则「p为()A. 3x o 三°，使得do + l)e X°三1B. 3x o > 0,使得do + l)e X°三1C. 3x o > °，使得(X。

高三数学-2018届江苏省南京市高三质量检测数学试卷精品

过 A 作 AN⊥ PD于 N，
∵ PD ＝（ a,2a,-2a） ,
设 PN =λPD ,
∴ AN = AP + PN =（λa,2 λa,2a-2λa）
∵ AN⊥ PD，
∴ AN ·PD =0．
∴ a·aλ+2a·2aλ-2a·（2a-2λa） =0．
解得 λ= 4 ． 9
∴ AN =（ 4 a， 8 a,
17．（本小题满分 12 分，第一小问满分 6 分，第二小问满分 6 分）
已知数列（ an ）是等差数列，（ bn ）是等比数列，且 a1=b1=2,b4=54,a1+a3=b2+b3．
（1）求数列 { b n }的通项公式
（2）求数列 { a n }的前 10 项和 S10 ．
18．（本小题满分 14 分，第一小问满分 6 分，第二小问满分 8 分）
在直角坐标系中， O 为坐标原点，设直线 l 经过点 P（ 3， 2 ），且与 x 轴交于点 F（ 2,0）．
（1）求直线 l 的方程；
（2）如果一个椭圆经过点 P，且以点 F 为它的一个焦点，求椭圆的标准方程；
（3）若在（Ⅰ）（Ⅱ）的情况下，设直线 l 与椭圆的另一个交点 Q，且 PM PQ ,当｜ OM ｜
∴ < ME , NA >=arccos= 10 ． 10
∴二面角 A-PD-E的大小为 arccos 10 ． 10
（ 3）解法一： ∵∠ EAB=∠ABC=∠ DEA=90°,
BC=DE=a,AB=AE=2a,
取 AE 中点 F，连 CF，
10 分
8分 10 分
∵ AF∥ =BC,
∴四边形 ABCF为平行四边形．

2018.9高三数学理科九月考试题答案

数学（理）答案2018.9一、选择题：本大题共12小题，每小题5分，共60分．二、填空题：本大题共4小题，每小题5分，共20分.请答案填在横线上. 13. 12e -14. 12- 15.1a ≥ 16.10,e ⎛⎫ ⎪⎝⎭三、解答题: 本大题共6小题,共70分.解答应写出文字说明, 演算步骤或证明过程.17. 解: （Ⅰ）f(x)＝2sinx(32sinx ＋12cosx)＝3×1－cos2x 2＋12sin2x ＝sin(2x －π3)＋32.函数f(x)的最小正周期为T ＝π由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，解得－π12＋k π≤x ≤5π12＋k π，k ∈Z ，所以函数f(x)的单调递增区间是[－π12＋k π，5π12＋k π]，k ∈Z .（Ⅱ）当x∈[0，π2]时，2x －π3∈[－π3，2π3]， sin(2x －π3)∈[－32，1]，f(x)∈[0，1＋32]．所以当x∈[0，π2]时，函数f(x)的值域为[0，1＋32]． 18. 解：（Ⅰ）由解得所以（Ⅱ）19. 解:（Ⅰ）正弦定理得又（Ⅱ）在，根据余弦定理得即又又 ,20.解:（Ⅰ）取BC 中点O ，连结AO ．∵△ABC 为正三角形，∴AO ⊥BC ． ∵在正三棱柱ABC －A 1B 1C 1中，平面ABC ⊥平面BCC 1B 1，∴AO ⊥平面BCC 1B 1．取B 1C 1中点O 1，以O 为原点，OB ，1OO ，OA 的方向为x ，y ，z 轴的正方向建立空间直角坐标系： O xyz -，如图所示，则B (1，0，0)，D (-1，1，0)， A 1(0，2，A (0，0，B 1(1，2，0)，∴(11,2,AB =，()2,1,0BD =-，(1BA =-． ∴10AB BD ⋅=，110AB BA ⋅=，∴1AB BD ⊥，11AB BA ⊥，∴AB 1⊥平面A 1BD ．（Ⅱ）设平面A 1AD 的法向量为(),,x y z =n ． 1,1,3()AD =--，1,2,0(0)AA =．∵AD ⊥n ，1AA ⊥n ，∴100AD AA ⋅=⋅⎧⎪⎪⎩=⎨n n，∴020x y y ⎧-+-==⎪⎨⎪⎩，0y x ==⎧⎪⎨⎪⎩，令1z =得(3,,1)0=n 为平面A 1AD 的一个法向量．由（1）知AB 1⊥平面A 1BD ，1AB 为平面A 1BD 的法向量，∴111cos AB AB AB ⋅-===⋅n n,n ． ∴锐二面角A －A 1D －B 的大小的余弦值为21. 解:（Ⅰ）证明：当1a =时，函数()2x f x e x =-．则()'2x f x e x =-，令()2x g x e x =-，则()'2x g x e =-，令()'0g x =，得l n 2x =．当()0,l n 2x ∈时，()'0g x <，当()ln2,x ∈+∞时，()'0g x >∴()f x 在[)0,+∞单调递增，∴()()01f x f ≥=．（Ⅱ）()f x 在()0,+∞有两个零点⇔方程2e 0x ax -=在()0,+∞有两个根，2x e a x ⇔=在()0,+∞有两个根，即函数y a =与()2xe G x x=的图像在()0,+∞有两个交点．()()3e 2'x x G x x -=，当()0,2x ∈时，()'0G x <，()G x 在()0,2递减当()2x ∈+∞,时，()'0G x >，()G x 在()2+∞,递增所以()G x 最小值为()2e 24G =，当0x →时，()G x →+∞，当x →+∞时，()G x →+∞，∴()f x 在()0,+∞有两个零点时，错误！未找到引用源。

江苏省南京市2018届高三第三次调研考试数学试卷(含答案和评分标准)

南京市2018届高三年级第三次模拟考试数学 2018．05一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．．．．．．．．．．） 1．集合A ＝{x|x 2＋x －6＝0}，B ＝{x|x 2－4＝0}，则A ∪B ＝．2．已知复数z 的共轭复数是－z ．若z (2－i )＝5，其中i 为虚数单位，则－z 的模为．3．某学校为了了解住校学生每天在校平均开销情况，随机抽取了500名学生，他们的每天在校平均开销都不低于20元且不超过60元，其频率分布直方图如图所示，则其中每天在校平均开销在[50，60]元的学生人数为．第3题第4题4．根据如图所示的伪代码，可知输出S 的值为．5．已知A ，B ，C 三人分别在连续三天中值班，每人值班一天，那么A 与B 在相邻两天值班的概率为．6．若实数x ，y 满足⎩⎪⎨⎪⎧x －y －3≤0，x ＋2y －5≥0，y －2≤0，则y x 的取值范围为． 7．已知α，β是两个不同的平面，l ，m 是两条不同的直线，有如下四个命题： ①若l ⊥α，l ⊥β，则α∥β； ②若l ⊥α，α⊥β，则l ∥β；③若l ∥α，l ⊥β，则α⊥β； ④若l ∥α，α⊥β，则l ⊥β．其中真命题为（填所有真命题的序号）．8．在平面直角坐标系xOy 中，若双曲线22221x y a b-=(a ＞0，b ＞0)的一个焦点到一条渐近线的距离为2a ，则该双曲线的离心率为．9．若等比数列{n a }的前n 项和为n S ，n ∈N *，且1a ＝1，6S ＝33S ，则n S 的值为．10．若()f x 是定义在R 上的周期为3的函数，且()fx ＝⎩⎪⎨⎪⎧ x 2＋x ＋a ，0≤x ≤2，－6x ＋18，2＜x ≤3，则(f a 1)+的值为．11．在平面直角坐标系xOy 中，圆M ：x 2＋y 2－6x －4y ＋8＝0与x 轴的两个交点分别为A ，B ，其中A 在B 的右侧，以AB 为直径的圆记为圆N ，过点A 作直线l 与圆M ，圆N 分别交于C ，D 两点．若D 为线段AC 的中点，则直线l 的方程为．12．在△ABC 中，AB ＝3，AC ＝2，D 为边BC 上一点．若AB →·AD →＝5，AC →·AD →＝﹣23，则AB →·AC →的值为．13．若正数a ，b ，c 成等差数列，则c 2a ＋b ＋b a ＋2c的最小值为． 14．已知a ，b ∈R ，e 为自然对数的底数．若存在b ∈[﹣3e ，﹣e 2]，使得函数()f x ＝e x ﹣ax－b 在[1，3]上存在零点，则a 的取值范围为．二、解答题（本大题共6小题，共计90分．请在答题纸指定区域．．．．．．．内作答，解答应写出文字说明，证明过程或演算步骤．）15．（本题满分14分）在平面直角坐标系xOy 中，锐角α，β的顶点为坐标原点O ，始边为x 轴的正半轴，终边与单位圆O 的交点分别为P ，Q ．已知点P 的横坐标为277，点Q 的纵坐标为3314．（1）求cos2α的值；（2）求2α﹣β的值．16．（本题满分14分）如图，在三棱锥P －ABC 中，PA ＝6，其余棱长均为2，M 是棱PC 上的一点，D ，E 分别为棱AB ，BC 的中点．（1）求证：平面PBC ⊥平面ABC ；（2）若PD ∥平面AEM ，求PM 的长．。

高三数学-【数学】江苏省南京市九校联合体2018届高三学情分析试卷精品

南京市九校联合体2018届高三数学学情分析试卷2018.12一、填空题（本题共14题，每题5分，共70分，请将正确答案填写在答题试卷上）1、复数ii4321+-在复平面上对应的点位于第象限． 2、已知集合{}11M =-，，11242x N x x +⎧⎫=<<∈⎨⎬⎩⎭Z ，，则M N = ．3、命题“0,x ∀>都有sin 1x ≥-”的否定：．４、已知,αβ是两个不同平面，,m n 是两条不同直线。

给出下列命题： ①若m ∥,,n m n αα⊥⊥则 ②若m ∥,,n m ααβ= 则∥n ③若,,m m αβα⊥⊥则∥β ④若,,m n m n α⊥⊥则∥α其中不正确的是．（填写你认为恰当的序号） 5、一个算法的流程图如右图所示，则输出S 的值为．6、设O OM ),1,0(),21,1(==为坐标原点，动点),(y x p 满足01,01OP OM OP ON ≤⋅≤≤⋅≤,则z y x =-的最小值是．7、函数1)1(log +-=x y a (01)a a >≠且，的图象恒过定点A ，若点A 在一次函数n mx y +=的图象上，其中0mn >，则12m n+的最小值为．8、设O 是△ABC 内部一点，且AOC AOB ∆∆-=+与则,2的面积之比为． 9、不等式322+-x x 122--≤a a 在R 上的解集是∅，则实数a 的取值范围是． 10、在样本的频率分布直方图中,共有4个小长方形,这4个小长方形的面积由小到大构成等比数列}{n a ,已知122a a =,且样本容量为300,则小长方形面积最大的一组的频数为．11、已知数列{n a }、{n b }都是等差数列，n n T S ,分别是它们的前n 项和，并且317++=n n T S nn ，则1612108221752b b b b a a a a ++++++= ． 12、实数,x y 满足tan ,tan x x y y ==，且x y ≠，则sin()sin()x y x y x y x y+--=+- ．13、已知04,k <<直线1:2280l kx y k --+=和直线222:2440l x k y k +--=与两坐标轴围成一个四边形，则使得这个四边形面积最小的k 值为．14、设)(x f 是定义在)1,0(上的函数，且满足：①对任意)1,0(∈x ，恒有)(x f >0；②对任意)1,0(,21∈x x ，恒有2)1()1()()(2121≤--+x f x f x f x f ,则关于函数)(x f 有①对任意)1,0(∈x ，都有()(1)f x f x >-；②对任意)1,0(∈x ，都有)1()(x f x f -=；③对任意)1,0(,21∈x x ，都有)()(21x f x f <；④对任意)1,0(,21∈x x ，都有)()(21x f x f =上述四个命题中正确的有．二、解答题：（本大题共6个小题，共90分．解答应写出文字说明，证明过程或演算步骤．） 15．（本小题满分12分）已知tan 2α=2，求：（1）tan()4πα+的值；（2） 6sin cos 3sin 2cos αααα+-的值．16．（本小题满分14分）某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验．(Ⅰ)求选取的2组数据恰好是相邻两个月的概率；(5分)(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y 关于x 的线性回归方程 y bx a =+；(6分)(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?(3分)(参考公式: 1122211()(),()n ni iiii i nniii i x y nx y x x y y b a y bx xnxx x ====---===---∑∑∑∑)17．（本小题满分15分）如图所示,在直四棱柱1111D C B A ABCD -中,BC DB =, DB AC ⊥,点M 是棱1BB 上一点． (Ⅰ)求证：//11D B 面BD A 1；(5分) (Ⅱ)求证：MD AC ⊥；(5分)(Ⅲ)试确定点M 的位置,使得平面1DMC⊥平面D D CC 11． (5分)MABCD A 1B 1C 1D 118．（本小题满分15分）已知圆O :222x y +=交x 轴于A ，B两点,曲线C 是以AB 为长轴,的椭圆,其左焦点为F ．若P 是圆O 上一点,连结PF ,过原点O 作直线PF 的垂线交椭圆C 的左准线于点Q ．(Ⅰ)求椭圆C 的标准方程；(5分)(Ⅱ)若点P 的坐标为(1,1),求证:直线PQ 与圆O 相切；(5分)(Ⅲ)试探究:当点P 在圆O 上运动时(不与A 、B 重合),直线PQ 与圆O 是否保持相切的位置关系?若是,请证明；若不是,请说明理由． (5分)19．（本小题满分18分）设数列{}n a 的前n 项和为n S ，且满足n S ＝2,1,2,3,n a n -=…。

南京市2018届高三数学9月调研试卷带答案

南京市2018届高三数学9月调研试卷（带答案）南京市2018届高三年级学情调研数学2017.09注意事项：1．本试卷共4页，包括填空题（第1题~第14题）、解答题（第15题~第20题）两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡上对应题目的答案空格内．考试结束后，交回答题卡．参考公式：柱体的体积公式：V＝Sh，其中S为柱体的底面积，h为柱体的高．一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上．1．若集合P＝{－1，0，1，2}，Q＝{0，2，3}，则P∩Q＝▲．2．若(a＋bi)(3－4i)＝25(a，b∈R，i为虚数单位)，则a＋b的值为▲．3．某高校甲、乙、丙、丁四个专业分别有150，150，400，300名学生．为了解学生的就业倾向，用分层抽样的方法从该校这四个专业中抽取40名学生进行调查，则应从丙专业抽取的学生人数为▲．4．如图所示的算法流程图，若输出y的值为12，则输入x的值为▲．5．记函数f(x)＝4－3x－x2的定义域为D．若在区间[－5，5]上随机取一个数x，则x∈D的概率为▲．6．在平面直角坐标系xOy中，双曲线x216－y29＝1的焦点到其渐近线的距离为▲．7．已知实数x，y满足条件2≤x≤4，y≥3，x＋y≤8，则z=3x－2y的最大值为▲．8．将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27πcm3，则该圆柱的侧面积为▲cm2.9．若函数f(x)＝Asin(x＋)(A＞0，＞0，||＜)的部分图象如图所示，则f(－)的值为▲．10．记等差数列前n项和为Sn．若am＝10，S2m－1＝110，则m的值为▲．11．已知函数f(x)是定义在R上的奇函数，且在(－∞，0]上为单调增函数．若f(－1)＝－2，则满足f(2x－3)≤2的x的取值范围是▲．12．在△ABC中，AB＝3，AC＝2，∠BAC＝120，→BM＝λ→BC．若→AM→BC＝－173，则实数λ的值为▲．13．在平面直角坐标系xOy中，若圆(x－2)2＋(y－2)2＝1上存在点M，使得点M关于x轴的对称点N在直线kx＋y＋3＝0上，则实数k的最小值为▲．14．已知函数f(x)＝2x2，x≤0，－3|x－1|＋3，x＞0．若存在唯一的整数x，使得f(x)－ax＞0成立，则实数a的取值范围为▲．二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（本小题满分14分）在直三棱柱ABC－A1B1C1中，AB＝AC，E是BC的中点，求证：（1）平面AB1E⊥平面B1BCC1；（2）A1C//平面AB1E．16．（本小题满分14分）在△ABC中，内角A，B，C所对的边分别为a，b，c，cosB＝45．（1）若c＝2a，求sinBsinC的值；（2）若C－B＝π4，求sinA的值．17．（本小题满分14分）某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成，每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为t1小时，其余工人加工完乙型装置所需时间为t2小时．设f(x)＝t1＋t2．（1）求f(x)的解析式，并写出其定义域；（2）当x等于多少时，f(x)取得最小值？18．（本小题满分16分）如图，在平面直角坐标系xOy中，椭圆C：x2a2＋y2b2＝1(a ＞b＞0)的离心率为32，且过点(1，32)．过椭圆C的左顶点A作直线交椭圆C于另一点P，交直线l：x＝m(m＞a)于点M．已知点B(1，0)，直线PB交l于点N．（1）求椭圆C的方程；（2）若MB是线段PN的垂直平分线，求实数m的值．19．（本小题满分16分）已知函数f(x)＝2x3－3(a+1)x2＋6ax，a∈R．（1）曲线y＝f(x)在x＝0处的切线的斜率为3，求a的值；（2）若对于任意x∈(0，+∞)，f(x)＋f(－x)≥12lnx恒成立，求a的取值范围；（3）若a＞1，设函数f(x)在区间[1，2]上的最大值、最小值分别为M(a)、m(a)，记h(a)＝M(a)－m(a)，求h(a)的最小值．20．(本小题满分16分)已知数列的各项均为正数，记数列的前n项和为Sn，数列的前n项和为Tn，且3Tn＝Sn2＋2Sn，n∈N*．（1）求a1的值；（2）求数列的通项公式；（3）若k，t∈N*，且S1，Sk－S1，St－Sk成等比数列，求k和t的值．南京市2018届高三年级学情调研卷数学附加题2017.09注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前，考生务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡上对应题目的答案空格内．考试结束后，交回答题卡．21．【选做题】在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．A．选修4—1：几何证明选讲如图，CD是圆O的切线，切点为D，CA是过圆心O的割线且交圆O于点B，DA＝DC．求证：CA＝3CB．B．选修4—2：矩阵与变换设二阶矩阵A＝1234．（1）求A－1；（2）若曲线C在矩阵A对应的变换作用下得到曲线C：6x2－y2＝1，求曲线C的方程．C．选修4—4：坐标系与参数方程在平面直角坐标系xOy中，直线l的参数方程为x＝－1＋t，y＝t（t为参数），圆C的参数方程为x＝a＋cos，y＝2a＋sin（θ为参数）．若直线l与圆C相切，求实数a的值．D．选修4—5：不等式选讲解不等式：|x－2|＋|x＋1|≥5．【必做题】第22题、第23题，每题10分，共计20分．请在答卷卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．22．（本小题满分10分）如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，AD∥BC，AP＝AB＝AD＝1．（1）若直线PB与CD所成角的大小为π3，求BC的长；（2）求二面角B－PD－A的余弦值．23．（本小题满分10分）袋中有形状和大小完全相同的四种不同颜色的小球，每种颜色的小球各有4个，分别编号为1，2，3，4．现从袋中随机取两个球．（1）若两个球颜色不同，求不同取法的种数；（2）在（1）的条件下，记两球编号的差的绝对值为随机变量X，求随机变量X的概率分布与数学期望．南京市2018届高三年级学情调研数学参考答案及评分标准说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数．4．只给整数分数，填空题不给中间分数．一、填空题（本大题共14小题，每小题5分，计70分.）1．{0，2}2．73．164．－25．126．37．68．189．－110．611．(－∞，2]12．1313．－4314．[0，2]∪[3，8]二、解答题（本大题共6小题，计90分．解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题卡的指定区域内）15．（本小题满分14分）证明：（1）在直三棱柱ABC－A1B1C1中，CC1平面ABC．因为AE平面ABC，所以CC1AE．……………2分因为AB＝AC，E为BC的中点，所以AEBC．因为BC平面B1BCC1，CC1平面B1BCC1，且BC∩CC1＝C，所以AE平面B1BCC1．………………5分因为AE平面AB1E，所以平面AB1E平面B1BCC1.……………………………7分（2）连接A1B，设A1B∩AB¬1＝F，连接EF．在直三棱柱ABC－A1B1C1中，四边形AA1B1B为平行四边形，所以F为A1B的中点．……………………………9分又因为E是BC的中点，所以EF∥A1C．……………………………11分因为EF平面AB1E，A1C平面AB1E，所以A1C∥平面AB1E.……………………………14分16．（本小题满分14分）解：（1）解法1在△ABC中，因为cosB＝45，所以a2＋c2－b22ac＝45．………………………2分因为c＝2a，所以(c2)2＋c2－b22c×c2＝45，即b2c2＝920，所以bc＝3510．……………………………4分又由正弦定理得sinBsinC＝bc，所以sinBsinC＝3510．……………………………6分解法2因为cosB＝45，B∈(0，)，所以sinB＝1－cos2B＝35．………………………2分因为c＝2a，由正弦定理得sinC＝2sinA，所以sinC＝2sin(B＋C)＝65cosC＋85sinC，即－sinC＝2cosC．………………………4分又因为sin2C＋cos2C＝1，sinC＞0，解得sinC＝255，所以sinBsinC＝3510．………………………6分（2）因为cosB＝45，所以cos2B＝2cos2B－1＝725．…………………………8分又0＜B＜π，所以sinB＝1－cos2B＝35，所以sin2B＝2sinBcosB＝2×35×45＝2425．…………………………10分因为C－B＝π4，即C＝B＋π4，所以A＝π－(B＋C)＝3π4－2B，所以sinA＝sin(3π4－2B)＝sin3π4cos2B－cos3π4sin2B………………………………12分＝22×725－(－22)×2425＝31250．…………………………………14分17．（本小题满分14分）解：（1）因为t1＝9000x，………………………2分t2＝30003(100－x)＝1000100－x， (4)分所以f(x)＝t1＋t2＝9000x＋1000100－x，………………………5分定义域为{x|1≤x≤99，x∈N*}．………………………6分（2）f(x)＝1000(9x＋1100－x)＝10[x＋(100－x)](9x＋1100－x)＝10[10＋9(100－x)x＋x100－x]． (10)分因为1≤x≤99，x∈N*，所以9(100－x)x＞0，x100－x＞0，所以9(100－x)x＋x100－x≥29(100－x)xx100－x＝6，…………………12分当且仅当9(100－x)x＝x100－x，即当x＝75时取等号．…………………13分答：当x＝75时，f(x)取得最小值． (14)分18．（本小题满分16分）解：（1）因为椭圆C的离心率为32，所以a2＝4b2．………………………2分又因为椭圆C过点(1，32)，所以1a2＋34b2＝1，………………………3分解得a2＝4，b2＝1．所以椭圆C的方程为x24＋y2＝1．………………………5分（2）解法1设P(x0，y0)，－2＜x0＜2，x0≠1，则x024＋y02＝1．因为MB是PN的垂直平分线，所以P关于B的对称点N(2－x0，－y0)，所以2－x0＝m．………………………7分由A(－2，0)，P(x0，y0)，可得直线AP的方程为y＝y0x0＋2(x＋2)，令x＝m，得y＝y0(m＋2)x0＋2，即M(m，y0(m＋2)x0＋2)．因为PB⊥MB，所以kPBkMB＝－1，所以kPBkMB＝y0x0－1y0(m＋2)x0＋2m－1＝－1，………………………10分即y02（m＋2）(x0－1)(x0＋2)(m－1)＝－1．因为x024＋y02＝1．所以(x0－2)(m＋2)4(x0－1)(m－1)＝1．………………………12分因为x0＝2－m，所以化简得3m2－10m＋4＝0，解得m＝5±133．………………………15分因为m＞2，所以m＝5＋133．………………………16分解法2①当AP的斜率不存在或为0时，不满足条件．………………………6分②设AP斜率为k，则AP：y＝k(x＋2)，联立x24＋y2＝1，y＝k(x＋2)，消去y得(4k2＋1)x2＋16k2x＋16k2－4＝0．因为xA＝－2，所以xP＝－8k2＋24k2＋1，所以yP＝4k4k2＋1，所以P(－8k2＋24k2＋1，4k4k2＋1)．………………………8分因为PN的中点为B，所以m＝2－－8k2＋24k2＋1＝16k24k2＋1．(*)……………………10分因为AP交直线l于点M，所以M(m，k(m＋2))，因为直线PB与x轴不垂直，所以－8k2＋24k2＋1≠1，即k2≠112，所以kPB＝4k4k2＋1－8k2＋24k2＋1－1＝－4k12k2－1，kMB＝k(m＋2)m－1．因为PB⊥MB，所以kPBkMB＝－1，所以－4k12k2－1k(m＋2)m－1＝－1．（**）………………………12分将(*)代入（**），化简得48k4－32k2＋1＝0，解得k2＝4±1312，所以m＝16k24k2＋1＝5±133．………………………15分又因为m＞2，所以m＝5＋133．………………………16分19．（本小题满分16分）解：（1）因为f(x)＝2x3－3(a＋1)x2＋6ax，所以f′(x)＝6x2－6(a＋1)x＋6a，所以曲线y＝f(x)在x＝0处的切线斜率k＝f′(0)＝6a，所以6a＝3，所以a＝12．………………………2分（2）f(x)＋f(－x)＝－6(a＋1)x2≥12lnx对任意x∈(0，+∞)恒成立，所以－(a＋1)≥2lnxx2．………………………4分令g(x)＝2lnxx2，x＞0，则g(x)＝2(1－2lnx)x3．令g(x)＝0，解得x＝e．当x∈(0，e)时，g(x)＞0，所以g(x)在(0，e)上单调递增；当x∈(e，＋∞)时，g(x)＜0，所以g(x)在(e，＋∞)上单调递减．所以g(x)max＝g(e)＝1e，………………………6分所以－(a＋1)≥1e，即a≤－1－1e，所以a的取值范围为(－∞，－1－1e]．………………………8分（3）因为f(x)＝2x3－3(a＋1)x2＋6ax，所以f′(x)＝6x2－6(a＋1)x＋6a＝6(x－1)(x－a)，f(1)＝3a－1，f(2)＝4．令f′(x)＝0，则x＝1或a．………………………10分f(1)＝3a－1，f(2)＝4．①当1＜a≤53时，当x∈(1，a)时，f(x)＜0，所以f(x)在(1，a)上单调递减；当x∈(a，2)时，f(x)＞0，所以f(x)在(a，2)上单调递增．又因为f(1)≤f(2)，所以M(a)＝f(2)＝4，m(a)＝f(a)＝－a3＋3a2，所以h(a)＝M(a)－m(a)＝4－(－a3＋3a2)＝a3－3a2＋4．因为h(a)＝3a2－6a＝3a(a－2)＜0，所以h(a)在(1，53]上单调递减，所以当a∈(1，53]时，h(a)最小值为h(53)＝827．………………………12分②当53＜a＜2时，当x∈(1，a)时，f(x)＜0，所以f(x)在(1，a)上单调递减；当x∈(a，2)时，f(x)＞0，所以f(x)在(a，2)上单调递增．又因为f(1)＞f(2)，所以M(a)＝f(1)＝3a－1，m(a)＝f(a)＝－a3＋3a2，所以h(a)＝M(a)－m(a)＝3a－1－(－a3＋3a2)＝a3－3a2＋3a－1．因为h(a)＝3a2－6a＋3＝3(a－1)2≥0．所以h(a)在(53，2)上单调递增，所以当a∈(53，2)时，h(a)＞h(53)＝827．………………………14分③当a≥2时，当x∈(1，2)时，f(x)＜0，所以f(x)在(1，2)上单调递减，所以M(a)＝f(1)＝3a－1，m(a)＝f(2)＝4，所以h(a)＝M(a)－m(a)＝3a－1－4＝3a－5，所以h(a)在[2，＋∞)上的最小值为h(2)＝1．综上，h(a)的最小值为827．………………………16分20．（本小题满分16分）解：（1）由3T1＝S12＋2S1，得3a12＝a12＋2a1，即a12－a1＝0．因为a1＞0，所以a1＝1．………………………2分（2）因为3Tn＝Sn2＋2Sn，①所以3Tn＋1＝Sn＋12＋2Sn＋1，②②－①，得3an＋12＝Sn＋12－Sn2＋2an＋1．因为an＋1＞0，所以3an＋1＝Sn＋1＋Sn＋2，③………………………5分所以3an＋2=Sn＋2＋Sn＋1＋2，④④－③，得3an＋2－3an＋1＝an＋2＋an＋1，即an＋2＝2an＋1，所以当n≥2时，an＋1an＝2．………………………8分又由3T2＝S22＋2S2，得3(1＋a22)＝(1＋a2)2＋2(1＋a2)，即a22－2a2＝0．因为a2＞0，所以a2＝2，所以a2a1＝2，所以对n∈N*，都有an＋1an＝2成立，所以数列的通项公式为an＝2n－1，n∈N*．………………………10分(3)由(2)可知S¬¬n＝2n－1．因为S1，Sk－S1，St－Sk成等比数列，所以(Sk－S1)2＝S1(St－Sk)，即(2k－2)2＝2t－2k，………………………12分所以2t＝(2k)2－32k＋4，即2t－2＝(2k－1)2－32k－2＋1(*)．由于Sk－S1≠0，所以k≠1，即k≥2．当k＝2时，2t＝8，得t＝3．………………………14分当k≥3时，由(*)，得(2k－1)2－32k－2＋1为奇数，所以t－2＝0，即t＝2，代入(*)得22k－2－32k －2＝0，即2k＝3，此时k无正整数解．综上，k＝2，t＝3．………………………16分南京市2018届高三年级学情调研数学附加题参考答案及评分标准21．【选做题】在A、B、C、D四小题中只能选做2题，每小题10分，共计20分．请在答题卡指定区域内作答．解答应写出文字说明、证明过程或演算步骤．A．选修4—1：几何证明选讲证明：连接OD，因为DA=DC，所以∠DAO=∠C．………………………2分在圆O中，AO=DO，所以∠DAO=∠ADO，所以∠DOC=2∠DAO=2∠C．………………………5分因为CD为圆O的切线，所以∠ODC=90°，从而DOC＋C＝90°，即2C＋C＝90°，故∠C＝30°，………………………7分所以OC＝2OD＝2OB，所以CB＝OB，所以CA＝3CB．………………………10分B．选修4—2：矩阵与变换解：（1）根据逆矩阵公式，可得A－1＝－2132－12．………………………4分（2）设曲线C上任意一点P(x，y)在矩阵A对应的变换作用下得到点P(x，y)，则xy＝1234xy＝x＋2y3x＋4y，所以x＝x＋2y，y＝3x＋4y．……………………8分因为(x，y)在曲线C上，所以6x2－y2＝1，代入6(x＋2y)2－(3x＋4y)2＝1，化简得8y2－3x2＝1，所以曲线C的方程为8y2－3x2＝1． (10)分C．选修4—4：坐标系与参数方程解：由直线l的参数方程为x＝－1＋t，y＝t，得直线l的普通方程为x－y＋1＝0．………………………2分由圆C的参数方程为x＝a＋cos，y＝2a＋sin，得圆C的普通方程为(x－a)2+(y－2a)2＝1．………………………4分因为直线l与圆C相切，所以∣a－2a＋1∣2＝1，………………………8分解得a＝1±2．所以实数a的值为1±2．………………………10分D．选修4—5：不等式选讲解：(1)当x＜－1时，不等式可化为－x＋2－x－1≥5，解得x≤－2；……………………2分(2)当－1≤x≤2时，不等式可化为－x＋2＋x＋1≥5，此时不等式无解；……………4分(3)当x＞2时，不等式可化为x－2＋x＋1≥5，解得x≥3；……………………6分所以原不等式的解集为(－∞，－2]∪[3，＋∞).…………………………10分【必做题】第22题、第23题，每题10分，共计20分．22．（本小题满分10分）解：（1）以{→AB，→AD，→AP}为单位正交基底，建立如图所示的空间直角坐标系A－xyz．因为AP＝AB＝AD＝1，所以A(0，0，0)，B(1，0，0)，D(0，1，0)，P(0，0，1)．设C(1，y，0)，则→PB＝(1，0，－1)，→CD＝(－1，1－y，0)．…………………………2分因为直线PB与CD所成角大小为π3，所以|cos＜→PB，→CD＞|＝|→PB→CD∣→PB∣∣→CD∣|＝12，即12×1＋(1－y)2＝12，解得y＝2或y＝0（舍），所以C(1，2，0)，所以BC的长为2．………………………5分（2）设平面PBD的一个法向量为n1＝(x，y，z)．因为→PB＝(1，0，－1)，→PD＝(0，1，－1)，则→PBn1＝0，→PDn1＝0，即x－z＝0，y－z＝0．令x＝1，则y＝1，z＝1，所以n1＝(1，1，1)．………………………7分因为平面PAD的一个法向量为n2＝(1，0，0)，所以cos＜n1，n2＞＝n1n2∣n1∣|n2∣＝33，所以，由图可知二面角B－PD－A的余弦值为33．………………………10分23．（本小题满分10分）解：（1）两个球颜色不同的情况共有C2442＝96(种).………………………3分（2）随机变量X所有可能的值为0，1，2，3．P(X＝0)＝4C2496＝14，………………………5分P(X＝1)＝3C14C1396＝38，P(X＝2)＝2C14C1396＝14，P(X＝3)＝C14C1396＝18．所以随机变量X的概率分布列为：………………………8分所以E(X)＝014＋138＋214＋318＝54．………………………10分。

高三数学-2018年江苏省南京市高三第一次调研测试数学试卷及答案精品

2018年江苏省南京市高三第一次调研测试数学 2018.03本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共150分．考试用时120分钟．注意事项：答题前，考生务必将学校、姓名、班级、学号写在答卷纸的密封线内．选择题答案按要求填涂在答卷纸上；非选择题的答案写在答卷纸上对应题目的答案空格内，答案不写在试卷上．考试结束，将答卷纸收回．参考公式：如果事件A 、B 互斥，那么P (A ＋B )＝P (A )＋P (B ) 如果事件A 、B 相互独立，那么P (A ·B )＝P (A )·P (B )如果事件A 在一次试验中发生的概率是P ，那么n 次独立重复试验中恰好发生k次的概率P n (k )＝C kn P k (1－P )n -k ．第Ⅰ卷(选择题共50分)一、选择题：本大题共10小题；每小题5分，共50分．在每小题给出的四个选项中，有且只有一项是符合题目要求的． 1．设集合A ，B 是全集U 的两个子集，则A ⊂≠B 是∁U B ⊂≠∁U A 的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2．已知过点A (－2，m )和B (m ，4)的直线与直线2x ＋y ＋1＝0平行，则m 的值为 A ．－8 B ．8 C ．0 D ．2 3．为了解一片经济林的生长情况，随机测量了其中100根据所得数据画出样本的频率分布直方图（如右），那么在这100株树木中，底部周长小于110cm 的株数是 A ．30 B ．60C ．70D ．804．若椭圆x 2a 2＋y 2＝1(a ＞0)的一条准线经过抛物线y 2＝－8x 的焦点，则该椭圆的离心率为A ．12B ．13C ． 32D ． 225．函数y ＝log 2x －1x(x ＞1)的反函数是周长(cm)A ．y ＝11－2x (x ＞0)B ．y ＝11－2x (x ＜0)C ．y ＝11＋2x (x ＞0)D ．y ＝11＋2x (x ＜0)6．设α，β为两个不重合的平面，l ，m ，n 为两两不重合的直线，给出下列四个命题：①若α∥β，l ⊂α，则l ∥β； ②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β； ③若l ∥α，l ⊥β，则α⊥β； ④若m 、n 是异面直线，m ∥α，n ∥α，且l ⊥m ，l ⊥n ，则l ⊥α. 其中真命题的序号是A ．①③④B ．①②③C ．①③D ．②④ 7．如果将函数y ＝sin2x ＋3cos2x 的图象按向量a 平移后所得的图象关于y 轴对称，那么向量a 可以是 A ．(π6，0) B ．(－π6，0) C ．(π12，0) D ．(－π12，0)8．若(1＋2x )n 展开式中x 3的系数等于x 2的系数的4倍，则n 等于A ．7B ．8C ．9D ．109．已知sin α＝55，sin(α－β)＝－1010，α，β 均为锐角，则β 等于 A ．5π12 B ．π3 C ．π4 D ．π610．将红、黑、白三个棋子放入如图所示的小方格内，每格只能放一个棋子，且3个棋子既不同行也不同列，则不同的放法有 A ．576种 B ．288种 C ．144种 D ．96种第Ⅱ卷(非选择题共100分)二、填空题：本大题共6小题；每小题5分，共30分．把答案填在题中横线上．11．在等差数列{a n }中，已知a 3＝8，a 6＝14，则数列{a n }的前8项的和S 8＝_____． 12．若关于x 的方程x 2＋1＝ax 有正实数根，则实数a 的取值范围是． 13．已知M (2，0)，N (0，2)，点P 满足−→MP ＝12−→MN ，O 为坐标原点，则−→OM ⋅−→OP ＝_______．14．已知函数y ＝f (x )的图象如图，则不等式f (2x ＋1x －)＞0的解集为__________．15．已知长方体ABCD —A 1B 1C 1D 1的顶点都在直径为3的球面上，AA 1=AB =2，点E 是DD 1的中点，则异面直线A 1E 与B 1D 所成角的大小为是__________． ▲ ▲ ▲ ▲ ▲16．在△ABC 中，已知tan C2＝sin(A ＋B )，给出以下四个论断：①tan A ⋅cot B ＝1 ②1＜sin A ＋sin B ≤ 2 ③sin 2A ＋cos 2B ＝1 ④sin 2A ＋sin 2B ＋sin 2C ＝2其中一定正确的是_______________（填上所有正确论断的序号）．三、解答题：本大题5小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17．(本小题满分12分，第一小问满分6分，第二小问满分6分) 在军训期间，某校学生进行实弹射击．（Ⅰ）通过抽签，将编号为1~6的六名同学排到1~6号靶位，试求恰有3名同学所抽靶位号与其编号相同的概率；（Ⅱ）此次军训实弹射击每人射击三次，总环数不少于28环的同学可获得射击标兵称号．已知某同学击中10环、9环、8环的概率分别为0.1、0.2、0.2，求该同学能获得射击标兵称号的概率．18．(本小题满分16分，第一小问满分5分，第二小问满分5分，第三小问满分6分) 如图，四边形ABCD 是正方形，PB ⊥平面ABCD ，MA ∥PB ，PB ＝AB ＝2MA ．（Ⅰ）证明：AC ∥平面PMD ；（Ⅱ）求直线BD 与平面PCD 所成的角的大小；（Ⅲ）求平面PMD 与平面ABCD 所成的二面角（锐角）的大小．19．(本小题满分14分，第一小问满分6分，第二小问满分8分)▲ A B C D P O M设不等式组⎩⎨⎧x ＋y >0，x －y >0表示的平面区域为D ．区域D 内的动点P 到直线x ＋y ＝0和直线x －y ＝0的距离之积为1．记点P 的轨迹为曲线C ．（Ⅰ）求曲线C 的方程；（Ⅱ）过点F (2，0)的直线与曲线C 交于A ，B 两点．若以线段AB 为直径的圆与y 轴相切，求线段AB 的长．20． (本小题满分14分，第一小问满分5分，第二小问满分9分) 已知函数f (x )＝x |x 2－a |，a ∈R ．（Ⅰ）当a ≤0时，求证函数f (x )在(－∞，＋∞)上是增函数；（Ⅱ）当a ＝3时，求函数f (x )在区间[0，b ]上的最大值．21．(本小题满分14分，第一小问满分6分，第二小问满分8分) 在数列{a n }中，已知a 1＝2，a n ＋1＝2a na n ＋1．（Ⅰ）证明数列{1a n－1}为等比数列，并求数列{a n }的通项公式；（Ⅱ）求证：∑ni=1a i (a i －1)＜3．2018年南京市高三数学第一次调研测试参考解答及评分标准2018.03说明：一、本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．二、对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．三、解答右端所注分数，表示考生正确做到这一步应得的累加分数．四、只给整数分数，选择题和填空题不给中间分数．11．88 12．[2，＋∞）13．2 14．（－2，1）15．45°16．②④．三、解答题17．解：（Ⅰ）设恰有3名同学所抽靶位号与其号码相同的事件为A，则事件A所包含的基本事件的种数为2C36，而六名同学通过抽签排到1~6号靶位的排法种数为A66．…3分由于每位同学通过抽签排到某个靶位是等可能的，所以P(A)＝2C36A66＝1 18．答：恰有3名同学所抽靶位号与其号码相同的概率为1 18．……………………………6分（Ⅱ）设该同学恰好击中28环、29环、30环的事件分别为B，C，D，他能获得射击标兵称号的事件为E，则事件B，C，D彼此互斥。

2018届江苏省南京市高三数学第二次调研测试题(word版)

南京市2018届高三第二次调研测试数学2018.04注意事项：1.本试卷共160分，考试时间120分钟2.答题前，考生务必将自己姓名，学校，班级，学号写在答题纸的密封线内，试题的答案写在答题纸．．．上对应题目的答案空格内，考试结束后，交回答题纸。

参考公式：设球的半径为R ，则球的体积公式为343V R π=一、填空题（本大题共14小题，每小题5分，共70分）1.已知全集{}2,1,0,1,2U =--，集合{}1,0,1A =-，{}2,1,0B =--，则_______________A B =U ð2.若将复数2(1)(12)i i -+∈表示为p+qi(p,q R,i 是序数单位)的形式，则p+q=3.已知向量,a b 满足||1,||3,,60____________a b a b a a b ==+=之间的夹角为度，则（）4.某学校为了解该校600名男生的百米成绩（单位：s ），随机选择了50名学生进行调查，右图是这50名学生百米成绩胡频率分布直方图。

根据样本的频率分布，估计这600名学生中成绩在[13,15]（单位：s ）内的人数大约是 .5.甲盒子里装有分别标有数字1.2,4,7的4张卡片，乙盒子里装有分别标有数字1,4的2张卡片，若从两个盒子中各随机地取出1张卡片，则2张卡片上的数字之和为奇数的概率是6.阅读左面的流程图，若输入a=6,b=1，则输出的结果是7.已知变量x,y 满足2,236y x x y z x y y x ≤⎧⎪+≥=+⎨⎪≥-⎩则的最大值是8.cos103sin10+=9.将边长为2的正方形ABCD 沿对角线BD 折成直二面角A-BD-C ，若点A 、B 、C 、D 都在一个以O 为球心的球面上，则球O 的体积为10.已知椭圆22221(0)x y a b a b+=>>的中心、右焦点、右顶点分别为O 、F 、A ，右准线与x 轴的交点为H ，则FA OH 的最大值为11.下列三个命题：①若函数()sin(2)f x x ϕ=+的图象关于y 轴对称，则2πϕ=；②若函数2()1ax f x x -=-的图象关于点（1，1）对称，则a=1； ③函数()|||2|f x x x =+-的图象关于直线x=1对称。

江苏省南京市2018届高三9月学情调研测试数学试卷(含答案)

江苏省南京市2018届高三9月学情调研测试数学试卷(含答案) 南京XXXX年级学习数学2017 .09参考公式:圆柱体体积公式:v = sh，其中s是圆柱体的底部面积，h是圆柱体的高度。

1，填空:这道大题有14项，每项5分。

总共70分。

请在答题纸上相应的位置填写答案。

1.如果集合p = {-1，0，1，2}，q = {0，2，3}，则p ∪; q =▲2。

如果(a+bi) (3-4i) = 25 (a，b∈R，I为虚数单位)，则A+B的值为▲ . 3。

一所大学的四个专业分别有150，150，400，300名学生。

为了了解学生的就业趋势，采用分层抽样的方法从该大学的四个专业中选取40名学生进行调查。

那么c专业的学生人数是▲14。

如算法流程图所示，如果输出y的值为，则输入2x的值为▲5。

记数函数f (x) = 4-3x-x2的定义域是D。

如果它在[-5区间内，则x ∈D的概率是▲x 26，如果一个数x是从[5]中随机取的。

在平面直角坐标系xOy中，从双曲线-= 1的焦点到169的渐近线的距离是▲ .？？2≤x≤4 x ≤ 4，7。

已知实数x，y满足条件？Y≥3，z = 3x-2y最大值？x+y≤8，？的值为▲8。

如果一个正方形绕其一边的直线旋转，并且圆柱体的体积为27πcm3，圆柱体的横向面积为▲ cm2.9。

如果函数f (x) = asin(？x+？)(A>0？> 0，|？| 10。

请注意，算术级数{an}的前N项之和是序号。

如果调幅= 10，S2M-1 = 110，则M值为▲11。

已知函数f(x)是定义在R上的奇函数，是(-∞，0)上的单调递增函数。

如果F (-1) =-2，则满足F (2x-3) ≤ 2的X的取值范围为▲20？4？X(问题9) 17 →→→→12。

在△ABC中，AB = 3，AC = 2，且BAC = 120？，BM = λ BC。

如果AM BC =-，实数λ3的值为▲13。

2021届江苏省南京市2018级高三上学期学情调研考试数学试卷及解析

2021届江苏省南京市2018级高三上学期学情调研考试数学试卷★祝考试顺利★(含答案)注意事项：1．本试卷共6页,包括单项选择题（第1题~第8题）、多项选择题（第9题~第12题）、填空题（第13题~第16题）、解答题（第17题~第22题）四部分．本试卷满分为150分,考试时间为120分钟．2．答卷前,考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置．3．作答选择题时,选出每小题的答案后,用2B 铅笔在答题卡上将对应题目选项的答案信息点涂黑；如需改动,用橡皮擦干净后,再选涂其他答案．答案不能答在试卷上．4．非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内,在其他位置作答一律无效．一、单项选择题：本大题共8小题,每小题5分,共40分．在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填涂在答题卡相应位置上．1．已知集合A ＝{x |x 2－x －2＜0},B ＝{x |1＜x ＜3 },则A ∩B ＝A ．{x |－1＜x ＜3}B ．{x |－1＜x ＜1}C ．{x |1＜x ＜2}D ．{x |2＜x ＜3}2．已知(3－4i)z ＝1＋i,其中i 为虚数单位,则在复平面内z 对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．已知向量a ,b 满足|a |＝1,|b |＝2,且|a ＋b |＝ 3,则a 与b 的夹角为A ．π6B ．π3C ．5π6D ．2π34．在平面直角坐标系xOy 中,若点P (43,0)到双曲线C ：x 2a 2－y 29＝1的一条渐近线的距离为6,则双曲线C 的离心率为A ．2B ．4C ． 2D ． 35．在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ．若2b cos C ≤2a －c ,则角B 的取值范围是A．(0,π3] B．(0,2π3] C．[π3,π) D．[2π3,π)6．设a＝log4 9,b＝2－1.2,c＝(827)－13,则A．a＞b＞c B．b＞a＞c C．a＞c＞b D．c＞a＞b7．在平面直角坐标系xOy中,已知圆A：(x－1)2＋y2＝1,点B(3,0),过动点P引圆A的切线,切点为T．若PT＝2PB,则动点P的轨迹方程为A．x2＋y2－14x＋18＝0 B．x2＋y2＋14x＋18＝0C．x2＋y2－10x＋18＝0 D．x2＋y2＋10x＋18＝08．已知奇函数f (x)的定义域为R,且f (1＋x)＝f (1－x)．若当x∈(0,1]时,f(x)＝log2(2x＋3),则f (932)的值是A．－3 B．－2 C．2 D．3二、多项选择题：本大题共4小题,每小题5分,共20分．在每小题给出的四个选项中,有多项符合题目要求,请把答案填涂在答题卡相应位置上．全部选对得5分,部分选对得3分,不选或有错选的得0分．9．5G时代已经到来,5G的发展将直接带动包括运营、制造、服务在内的通信行业整体的快速发展,进而对GDP增长产生直接贡献,并通过产业间的关联效应,间接带动国民经济各行业的发展,创造出更多的经济增加值．如图,某单位结合近年数据,对今后几年的5G经济产出做出预测．由上图提供的信息可知。

2018届高三南京市联合体学校调研测试数学试卷(理)

2018届高三南京市联合体学校调研测试数学试卷（理）满分：160分时间：120分钟一：填空题：（每题5分，共70分）1.已知集合{}1,3A =，{}23,log B m =，若{}1,2,3A B = ，则m =▲2.已知i 是虚数单位,若(1)2z i i -=,则=||z ▲3．为检验某校高一年级学生的身高情况，现采用先分层抽样后简单随机抽样的方法，抽取一个容量为210的样本，已知每个学生被抽取的概率为0.3，且男女生的比例是4:3，则该校高一年级女生的人数是▲4.欧阳修在《卖油翁》中写到：（翁）乃取一葫芦置于地，以钱覆其口，徐以杓酌油沥之，自钱孔入，而钱不湿，可见“行行出状元”，卖油翁的技艺让人叹为观止。

若铜钱是直径为 4cm 的圆，中间有边长为1cm 的正方形孔，若你随机地向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率是▲5. 运行如图所示的程序后，输出的结果为 ▲（第5题）6.双曲线221169x y -=的焦点到该双曲线渐近线距离为▲ 7.等差数列{}n a 中，首项12a =，且12334a a a +=-，则31a a =▲ 8. 函数()sinsin22xxf x π-=的最小正周期为____▲______．9.若不等式组02424x x y x y ≥⎧⎪+≤⎨⎪+≥⎩所表示的平面区域被直线4y kx =+分为面积相等的两部分，则k的值为▲10.已知函数12log ,2()23,2x x x f x a a x ≥⎧⎪=⎨⎪-<⎩（其中0a >且1)a ≠的值域为R ，则实数a 的取值范围为____▲__.11. 已知实数,x y ，0,0x y >>，且满足24xy x y ++=，则2x y +的最小值为__▲___ 12.已知,A B 为直线l ：y x =-上两动点，且4AB =，圆C ：226620x y x y +--+=,圆C 上存在点P ，使2210PA PB +=，则线段AB 中点M 的横坐标取值范围为▲13. 如图，,,A B C 是直线l 上的三点，P 是直线l 外一点，已知112AB BC ==，90CPB ∠= ，4tan 3APB ∠=．则PA PC ⋅ =__▲ ____14.已知点P 为曲线C ：212y x =上的一点，P 在第一象限，曲线C 在P 点处的切线为l ，过点P 垂直于l 的直线与曲线C 的另外一个交点为Q ，当P 点的横坐标为____▲____时，PQ 长度最小。

江苏省南京市届高三上学期学情调研(月)数学含答案

南京市2018届高三年级学情调研数学 2017 。

09注意事项:1．本试卷共4页，包括填空题（第1题~第14题)、解答题（第15题～第20题)两部分．本试卷满分为160分，考试时间为120分钟．2．答题前，请务必将自己的姓名、学校写在答题卡上．试题的答案写在答题卡．．．上对应题目的答案空格内．考试结束后，交回答题卡．参考公式:柱体的体积公式：V ＝Sh ，其中S 为柱体的底面积，h 为柱体的高．一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答．题卡．．相应位置．．．．上．1．若集合P ＝｛－1，0，1，2｝，Q ＝{0，2，3}，则P ∩Q ＝ ▲ ． 2．若(a ＋b i ）(3－4i ）＝25 （a ,b ∈R ，i 为虚数单位)，则a ＋b 的值为 ▲ ． 3．某高校甲、乙、丙、丁四个专业分别有150,150，400，300名学生．为了解学生的就业倾向，用分层抽样的方法从该校这四个Y（第4题）结束输入xx ≥0y ←2x输出yN开始 y ←log 2(－x )专业中抽取40名学生进行调查，则应从丙专业抽取的学生人数为 ▲ ．4．如图所示的算法流程图，若输出y 的值为错误!，则输入x 的值为 ▲ ．5．记函数f （x )＝错误! 的定义域为D ．若在区间［－5，5]上随机取一个数x ，则x ∈D 的概率为 ▲ ． 6．在平面直角坐标系xOy 中，双曲线错误!－错误!＝1的焦点到其渐近线的距离为 ▲ ．7．已知实数x ，y 满足条件错误!则z =3x －2y 的最大值为 ▲ ．8．将一个正方形绕着它的一边所在的直线旋转一周，所得圆柱的体积为27πcm 3，则该圆柱的侧面积为 ▲ cm 2。

9．若函数f (x ）＝A sin （x ＋)(A ＞0，＞0，||＜）的部分图象如图所示，则f (－）的值为 ▲ ．10．记等差数列{a n }前n 项和为S n ．若a m ＝10,S 2m －1＝110，则m 的值为 ▲ ．11．已知函数f (x ）是定义在R 上的奇函数,且在（－∞,0]上为单调增函数．若f (－1）＝－2,则满足f （2x －3)≤2的x 的取值范围是 ▲ ．12．在△ABC 中,AB ＝3,AC ＝2，∠BAC ＝120，错误!＝λ错误!．若xO y(第9题）42→AM ·错误!＝－错误!,则实数λ的值为 ▲ ．13．在平面直角坐标系xOy 中,若圆（x －2）2＋（y －2)2＝1上存在点M ,使得点M 关于x 轴的对称点N 在直线kx ＋y ＋3＝0上，则实数k 的最小值为 ▲ ． 14．已知函数f （x ）＝错误!若存在唯一的整数x ，使得错误!＞0成立，则实数a 的取值范围为 ▲ ．二、解答题：本大题共6小题，共计90分．请在答．题卡．．指定区域内．．．．．作答，解答时应写出文字说明、证明过程或演算步骤． 15．（本小题满分14分）在直三棱柱ABC －A 1B 1C 1中,AB ＝AC ,E 是BC 的中点，求证：（1）平面AB 1E ⊥平面B 1BCC 1；（2）A 1C //平面AB 1E ．16．（本小题满分14分）在△ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c ,cos B ＝45．（1）若c ＝2a ，求错误!的值；A 1B 1C 1ABCE(第15题）(2)若C－B＝错误!,求sin A的值．17．(本小题满分14分)某工厂有100名工人接受了生产1000台某产品的总任务，每台产品由9个甲型装置和3个乙型装置配套组成,每个工人每小时能加工完成1个甲型装置或3个乙型装置．现将工人分成两组分别加工甲型和乙型装置．设加工甲型装置的工人有x人，他们加工完甲型装置所需时间为t1小时，其余工人加工完乙型装置所需时间为t2小时．设f(x）＝t1＋t2．（1）求f（x）的解析式,并写出其定义域;（2)当x等于多少时，f（x)取得最小值？18．（本小题满分16分）如图，在平面直角坐标系xOy中，椭圆C：错误!＋错误!＝1（a＞b＞0)的离心率为错误!，且过点(1，错误!）．过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l：x＝m（m＞a）于点M．已知点B （1，0),直线PB交l于点N．(1)求椭圆C的方程；（2）若MB是线段PN的垂直平分线，求实数m的值．(第18题）19．(本小题满分16分）已知函数f（x）＝2x3－3(a+1)x2＋6ax，a∈R．(1）曲线y＝f(x)在x＝0处的切线的斜率为3，求a的值；（2）若对于任意x∈（0，+∞），f(x）＋f(－x）≥12ln x恒成立，求a的取值范围;（3）若a＞1，设函数f（x)在区间[1，2］上的最大值、最小值分别为M(a）、m（a），记h（a)＝M(a)－m（a)，求h(a）的最小值．20．（本小题满分16分）已知数列{a n}的各项均为正数，记数列｛a n}的前n项和为S n,数列｛a n2}的前n项和为T n，且3T n＝S n2＋2S n，n∈N*．（1）求a1的值；(2)求数列｛a n｝的通项公式；（3）若k，t∈N*，且S1，S k－S1,S t－S k成等比数列，求k和t的值．南京市2018届高三年级学情调研卷数学附加题2017.09注意事项：1．附加题供选修物理的考生使用．2．本试卷共40分，考试时间30分钟．3．答题前,考生务必将自己的姓名、学校写在答题卡上．试题的答案写在答．题．卡．上对应题目的答案空格内．考试结束后，交回答题卡．21．【选做题】在A 、B 、C 、D 四小题中只能选做2题,每小题10分，共计20分．请在答．卷卡指定区域内．．．．．．．作答．解答应写出文字说明、证明过程或演算步骤．A ．选修4-1:几何证明选讲如图,CD 是圆O 的切线，切点为D ，CA 是过圆心O 的割线且交圆O 于点B ，DA ＝DC ．求证： CA ＝3CB ．B ．选修4-2：矩阵与变换设二阶矩阵A ＝错误!．（1)求A －1；(2）若曲线C 在矩阵A 对应的变换作用下得到曲线C ：6x 2－y 2＝1，求曲线C 的方程．C ．选修4—4：坐标系与参数方程在平面直角坐标系xOy 中，直线l 的参数方程为错误!(t 为参数)，圆C 的参数方程为错误!（θ为参数）．若直线l 与圆C 相切，求实数a的值．DB CO （第21A 题）D ．选修4—5:不等式选讲解不等式：|x －2｜＋｜x ＋1｜≥5．【必做题】第22题、第23题，每题10分，共计20分．请在答．卷．卡指定区域内．．．．．．作答．解答应写出文字说明、证明过程或演算步骤． 22．（本小题满分10分）如图，在四棱锥P －ABCD 中，PA ⊥平面ABCD ，AB ⊥AD ，AD ∥BC ，AP ＝AB ＝AD＝1．（1）若直线PB 与CD 所成角的大小为错误!，求BC 的长; (2）求二面角B －PD －A 的余弦值．23．（本小题满分10分）袋中有形状和大小完全相同的四种不同颜色的小球,每种颜色的小球各有4个,分别编号为1，2，3，4．现从袋中随机取两个球．（1）若两个球颜色不同，求不同取法的种数；CDPBA（第22题）(2）在（1）的条件下，记两球编号的差的绝对值为随机变量X，求随机变量X的概率分布与数学期望．南京市2018届高三年级学情调研数学参考答案及评分标准说明：1．本解答给出的解法供参考．如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后续部分的解答未改变该题的内容和难度，可视影响的程度决定给分，但不得超过该部分正确解答应得分数的一半；如果后续部分的解答有较严重的错误，就不再给分．3．解答右端所注分数,表示考生正确做到这一步应得的累加分数．4．只给整数分数，填空题不给中间分数．一、填空题(本大题共14小题，每小题5分，计70分.）1．{0，2｝2．7 3．16 4．－错误! 5．错误!6．3 7． 6 8．189．－1 10．611．（－∞,2］ 12．错误! 13．－错误! 14．［0，2]∪［3，8]二、解答题（本大题共6小题,计90分．解答应写出必要的文字说明,证明过程或演算步骤,请把答案写在答题卡的指定区域内） 15．（本小题满分14分）证明:(1)在直三棱柱ABC －A 1B 1C 1中，CC 1平面ABC ．因为AE 平面ABC ，所以CC 1AE ． ……………2分因为AB ＝AC ，E 为BC 的中点,所以AEBC ．因为BC 平面B 1BCC 1，CC 1平面B 1BCC 1，且BC ∩CC 1＝C ,所以AE 平面B 1BCC 1． ………………5分因为AE 平面AB 1E ,所以平面AB 1E平面B 1BCC 1。