相交线平行线证明格式专题训练
相交线与平行线证明题专强化项训练
相交线与平行线证明题专强化项训练相交线与平行线证明题专项强化训练1如图，已知 A B// CD, /仁/ 3,试说明AC IIBD.2、如图，已知/ BAF = 50°,/ ACE = 140CD 丄CE ，能判断DC // AB 吗？为什么?3、如图，已知 CD 丄AD , DA 丄AB ,/ 1 = /2则DF 与AE 平行吗？为什么? C D4、如图，AB II CD,AD II BC, / A=3 / B.求/A 、 /B 、/C 、/D 的度数.B C5、如图，AB II CD,直线EF 交AB 、CD 于点G 、 H.如果，M 平分/ BGF,HN 平分/ CHE ,那么， 倉時、与H N 平行吗？为什么？F6、如图，/ 1 = / 2，AC平分/ DAB试说明: DC// AB.7、已知，如图15,/ ACB = 60°,/ ABC = 50°, BO、CO 分别平分/ ABC、/ ACB, EF是经过点O且平行于BC的直线，求/ BOC的度数。
&已知：如图2—99，AD II BC,/ 仁/2,/ 3= / 4. DE与CF平行吗？为什么?图 2 999、已知：如图AE//CD,EF交A B于G , 交CD于F, FH平分/ EFD，交AB于H，/ AGE=500求:E，BHF的度数。
A HB:C F D10、如图，直线AB、CD相交于点0, OA平分 /COE，/ COE:/ E0D=4 : 5,求/ BOD 的度数。
11、如图21, AB // DE，/ 1 = / ACB , / CAB = 2/ BAD,试说明AD // BC .闺2112、已知一个角的余角的补角比这个角的补角的 一半大90。
，则这个角的度数等于多少度？13、如图：已知AD// BE, /仁/2,请说明/ A= / E 的理由.14、已知，如图，BCE 、AFE 是直线，AB //CD ,15、已知如图，直线 AB 、CD 相交于O , 0E 平AD // BE E3A B求分/ BOD, OF 平分/ COB，/ 2 : / 1 = 4 ：1,求/ AOF的度数。
(完整版)相交线平行线专题证明
40、如图，已知AB∥CD，试再添上一个条 件，使∠1＝∠2成立。（要求给出两个以上 答案）
29、已知：如图，AD是一条直线，∠1=65°， ∠2=115°．求证：BE∥CF．
30、如图，CD∥AB，∠DCB=70°， ∠CBF=20°，∠EFB=130°，问直线EF与 AB有怎样的位置关系，为什么？
31、（1）已知AB∥CD，下列各图中的∠ABE、∠E、∠CDE 三个角之间各有什么关系？填入下列括号内，并选择一个 你自己喜欢的图加以证明。
3 F
C
6、已知，如图，AD∥BC，∠B＝70°，∠C ＝60°，求∠CAE的度数．（写理由）
、如图，已知，AC∥DE，DC∥FE，CD平 分∠ACB，求证：EF平分∠BED．
A
D
F
3
4 5
1 2
B
E
C
8、如图，∠AOB是∠BOC的补角，OD平分 ∠AOB、OE平分∠BOC，求∠DOE的度数。
37、经过平移，△ABC的边AB移到了EF， 作出平移后的三角形，你能给出两种作法 吗？请表述出来。
38、如图，AB∥CD，需增加什么条件才能使 ∠1=∠2成立？至少举出两种并证明。
39、（1）已知AB∥CD，EF∥MN，∠1＝115°， 求∠2和∠4的度数；
（2）本题隐含着一个规律，请你根据（1）的结 果进行归纳，试着用文字表述出来；
21、 如图，在△ABC中，CD⊥AB于点D， F G⊥AB 于点G， E D//BC。
试说明：∠EDC =∠B FG
22、已知：如图，AB∥CD，AP平分∠BAC， CP平分∠ACD，求∠APC的度数．
【原创】平行线与相交线必背20个证明题
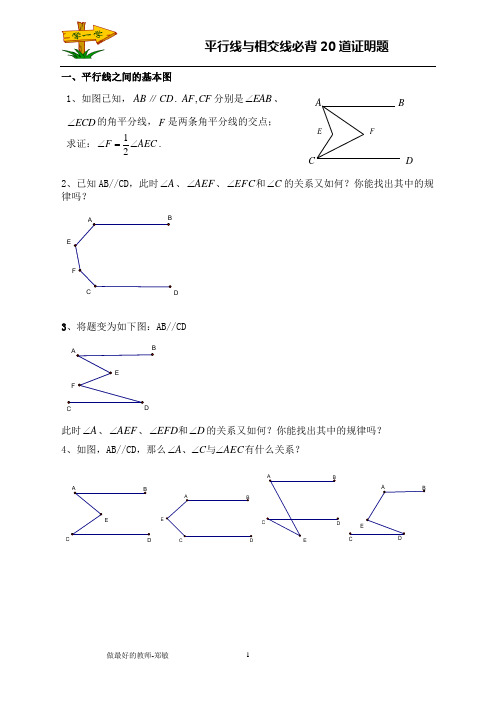
一、平行线之间的基本图1、如图已知，AB ∥CD .,AF CF 分别是EAB ∠、ECD ∠的角平分线，F 是两条角平分线的交点； 求证：12F AEC ∠=∠.2、已知AB//CD ，此时A ∠、AEF ∠、EFC ∠和C ∠的关系又如何？你能找出其中的规律吗？AEFD3、将题变为如下图：AB//CDABEFC此时A ∠、AEF ∠、EFD ∠和D ∠的关系又如何？你能找出其中的规律吗？ 4、如图，AB//CD ，那么AEC C A ∠∠∠与、有什么关系？ABDEABEABDEA BCEDB C AFE二、两组平行线的证明题【找出连接两组平行线的角】1.已知：如图，CD 平分∠ACB ，AC ∥DE ，∠DCE=∠FEB ，求证：EF 平分∠DEB ．3、已知：如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ，∠1=∠2,求证：DO ⊥AB.3、如图，已知EF ⊥AB ，∠3=∠B ，∠1=∠2，求证：CD ⊥AB 。
4、已知AD ⊥BC ，FG ⊥BC ，垂足分别为D 、G ，且∠1=∠2，猜想∠BDE 与∠C 有怎样的大小关系？试说明理由.三、两组平行线构造平行四边形1．已知：如图，AB 是一条直线，∠C = ∠1，∠2和∠D 互余，BE ⊥FD 于G ． 求证：AB ∥CD ．AD FBEC2、如图，E 点为DF 上的点，B 为AC 上的点，∠1=∠2，∠C =∠D ，求证DF ∥AC ．3、如图，M 、N 、T 和A 、B 、C 分别在同一直线上， 且∠1=∠3，∠P=∠T ，求证：∠M=∠R 。
四、证特殊角1、AB ∥CD ，∠BAC 的平分线和∠ACD 的平分线交于点E ，则∠AEC 的度数是 ．2、AB CD ∥，直线EF 与AB 、CD 分别相交于E 、F 两点，EP 平分∠AEF ，过点F 作PF EP 垂足为P ，若∠PEF ＝300，则∠PFC ＝_____．3、如图，已知：DE ∥AC ，CD 平分∠ACB ，EF 平分∠DEC ，∠1与∠2互余，求证：DG ∥EF.图7 图8AB CDEF1 423 (第22题)21GFEAMN A DBC b 21aE4．已知：如图，AB ∥DE ，CM 平分∠BCE ，CN ⊥CM ．求证：∠B ＝2∠DCN ．5.如图已知直线a ∥b ，AB 平分∠MAD ，AC 平分∠NAD ，DE ⊥AC 于E ，求证：∠1=∠2．4、求证：三角形内角之和等于180°．五、寻找角之间的关系1、如图2-97,已知：∠1=∠2，∠3=∠4，∠5=∠6.求证:AD ∥BC.2、已知，如图，BCE 、AFE 是直线，AB ∥CD ，∠1=∠2，∠3=∠4。
完整版相交线与平行线证明题专项训练
1如图，已知 AB // CD, /仁/3,试说明AC // BD.7、已知，如图15，/ ACB = 60°，/ ABC = 500，BO 、CO 分别平分/ ABC 、/ ACB ，EF 是经过点 0且平行于BC 的直 线，求/ BOC的度数。
8 已知：如图 2— 99，AD // BC ，/仁/2，Z 3= / 4 . DE 与CF 平行吗？为什么？相交线与平行线证明题专项训练 5、如图, 什么？AB // CD,直线EF 交AB 、CD 于点G 、H.如果GM 平分/ BGF,HN 平分/ CHE ，那么，GM 与HN 平行吗？为2、如图, 已知/ BAF = 50 °，/ ACE = 140°, CD 丄CE ，能判断DC // AB 吗？为什么？6、 女口图，/ 1 = Z 2，AC 平分/ DAB 试说明：DC//AB.BB4、如图, AB // CD,AD // BC, / A=3 / B.求/ A 、 / B 、/ C 、/ D 的度数.3、如图，已知 CD 丄AD ，DA 丄AB ，/ 1 = Z 2 则DF 与AE 平行吗？为什么？9、已知：如图AB/CD，EF交A求：/ BHF的度数。
B 于G,交CD 于F, FH 平分/ EFD，交AB 于H，/ AGE=50012、已知一个角的余角的补角比这个角的补角的一半大90°,则这个角的度数等于多少度?13、如图：已知AD// BE, /仁/ 2,请说明/ A=Z E的理由.14、已知，如图，BCE、AFE是直线, AB // CD , / 1 = / 2,/ 3=/ 4。
求证：AD //BE。
10、如图，直线AB、CD 相交于点O , OA 平分/ COE，/ COE : Z EOD=4 : 5,求/ BOD 的度数。
/ 1 =/ ACB，1/ CAB = 2 / BAD，试说明AD // BC .15、已知如图，直线AB、CD相交于B16、已知：如图/ 1= / 2，/ C=/D，O , OE 平分/ BOD , OF 平分/ COB，/ 2： / 1 = 4：1，求/ AOF 的度数。
相交线与平行线基础证明训练题
相交线与平行线基础证明训练题
1、根据题目所给条件，可以得出：∠2=∠3，XXX。
因此，根据平行线内错角相等的性质，可以得出____∥_____，
根据等角代换和平行线性质，可以得出____=______，进而得
出∠1=∠3.
2、根据题目所给条件，可以得出∠A=∠F，∠C=∠D。
因此，根据等角代换，可以得出AC∥DF，进而得出∠D=∠()。
又因为∠C=∠D，所以可以得出∠1=∠C。
因此，根据平行线
内错角相等的性质，可以得出BD∥CE。
3、根据题目所给条件，可以得出∠B+∠BCD=180°，
∠B=∠D。
因此，根据补角定理，可以得出AB∥CD。
又因为∠B=∠D，所以可以得出∠DCE=∠D。
因此，根据等角代换
和平行线性质，可以得出AD∥BE，进而得出∠E=∠DFE。
4、根据题目所给条件，可以得出∠1=∠2，DE∥FH。
因此，根据等角代换和平行线内错角相等的性质，可以得出
∠EDA=∠HFB。
又因为∠XXX∠XXX，且∠1=∠2，所以可以得出CD∥FG。
5、根据题目所给条件，可以得出AD⊥BC，EF⊥BC，∠1=∠2.因此，根据垂线与平行线性质和等角代换，可以得出EF∥AD，进而得出DG∥BA。
6、根据题目所给条件，可以得出AD⊥BC于D，
EF⊥BC于F，∠1=∠3.因此，根据等角代换和平行线性质，可以得出AD∥EF，进而得出AD平分∠BAC。
2023年七年级下册数学第五章相交线与平行线证明题阅读理解填理由专项训练(14道)
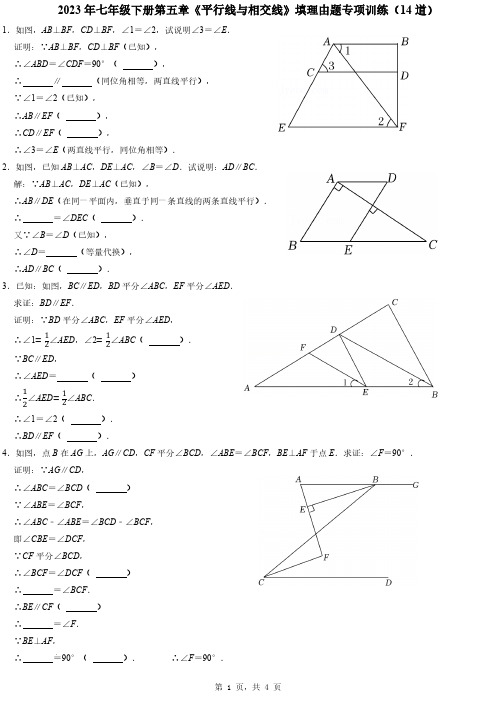
2023年七年级下册第五章《平行线与相交线》填理由题专项训练（14道）1．如图，AB⊥BF，CD⊥BF，∠1＝∠2，试说明∠3＝∠E．证明：∵AB⊥BF，CD⊥BF（已知），∴∠ABD＝∠CDF＝90°（），∴∥（同位角相等，两直线平行），∵∠1＝∠2（已知），∴AB∥EF（），∴CD∥EF（），∴∠3＝∠E（两直线平行，同位角相等）．2．如图，已知AB⊥AC，DE⊥AC，∠B＝∠D．试说明：AD∥BC．解：∵AB⊥AC，DE⊥AC（已知），∴AB∥DE（在同一平面内，垂直于同一条直线的两条直线平行）．∴＝∠DEC（）．又∵∠B＝∠D（已知），∴∠D＝（等量代换），∴AD∥BC（）．3．已知：如图，BC∥ED，BD平分∠ABC，EF平分∠AED．求证：BD∥EF．证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=12∠AED，∠2=12∠ABC（）．∵BC∥ED，∴∠AED＝（）∴12∠AED=12∠ABC．∴∠1＝∠2（）．∴BD∥EF（）．4．如图，点B在AG上，AG∥CD，CF平分∠BCD，∠ABE＝∠BCF，BE⊥AF于点E．求证：∠F＝90°．证明：∵AG∥CD，∴∠ABC＝∠BCD（）∵∠ABE＝∠BCF，∴∠ABC﹣∠ABE＝∠BCD﹣∠BCF，即∠CBE＝∠DCF，∵CF平分∠BCD，∴∠BCF＝∠DCF（）∴＝∠BCF．∴BE∥CF（）∴＝∠F．∵BE⊥AF，5．（2023秋•海口期末）如图，AB∥CD，∠1＝∠A．（1）试说明：AC∥ED；（2）若∠2＝∠3，FC与BD的位置关系如何？为什么？解：（1）∵AB∥CD，（已知）∴∠1＝∠BED，（）又∵∠1＝∠A，（已知）∴∠BED＝∠，（等量代换）∴∥．（）（2）FC与BD的位置关系是：．理由如下：∵AC∥ED，（已知）∴∠2＝∠．（）又∵∠2＝∠3，（已知）∴∠＝∠．（等量代换）∴∥．（）6．已知：如图，在△ABC中，FG∥CD，∠1＝∠3．求证：∠B+∠BDC＝180°．解：因为FG∥CD（已知），所以∠1＝．又因为∠1＝∠3（已知），所以∠2＝（等量代换）．所以BC∥（），所以∠B+∠BDE＝180°（）．7．如图，已知∠D＝108°，∠BAD＝72°，AC⊥BC于C，EF⊥BC于F．求证：∠1＝∠2．证明：∵∠D＝108°，∠BAD＝72°（已知）∴∠D+∠BAD＝180°∴AB∥CD（）∴∠1＝（）又∵AC⊥BC于C，EF⊥BC于F（已知）∴EF∥（）∴∠2＝（）∴∠1＝∠2（）8．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°．试说明：∠GDC＝∠B．解：∵AD⊥BC，EF⊥BC（已知）∴∠ADB＝∠EFB＝90°（）∴EF∥AD（）∴+∠2＝180°（）又∵∠2+∠3＝180°（已知）∴∠1＝（）∴∥（）9．（2023秋•丹江口市期末）如图，E、F分别在AB和CD上，∠1＝∠D，∠2与∠C互余，AF⊥CE于G，求证：AB∥CD．证明：∵AF⊥CE（已知），∴∠CGF＝90°（垂直的定义），∵∠1＝∠D（已知），∴AF∥（），∴∠4＝＝90°（），又∵∠2+∠3+∠4＝180°，∴∠2+∠3＝90°，∵∠2与∠C互余（已知），∴∠2+∠C＝90°，∴∠C＝，∴AB∥．（）10．（2023秋•青神县期末）如图，AB与EF交于点B，CD与EF交于点D，根据图形，请补全下面这道题的解答过程．（1）∵∠1＝∠2（已知）∴∥CD（）∴∠ABD+∠CDB＝（）（2）∵∠BAC＝65°，∠ACD＝115°，（已知）∴∠BAC+∠ACD＝180°（等式性质）∴AB∥CD（）（3）∵CD⊥AB于D，EF⊥AB于F，∠BAC＝55°，（已知）∴∠ABD＝∠CDF＝90°（垂直的定义）∴∥（同位角相等，两直线平行）又∵∠BAC＝55°，（已知）∴∠ACD＝．（）11．如图所示，已知∠1+∠2＝180°，∠3＝∠B，试判断∠AED与∠C的大小关系，并说明理由．证明：∵∠1+∠2＝180°（）∠1＝∠DFH（）∴（）∴EH∥AB（）∴∠3＝∠ADE（）∵∠3＝∠B∴∠B＝∠ADE（）∴DE∥BC∴∠AED＝∠C（）12．如图，已知AB∥CD，BE平分∠ABC，DB平分∠CDF，且∠ABC+∠CDF＝180°．求证：BE⊥DB．证明：∵AB∥CD∴∠ABC＝∠BCD（）∵∠ABC+∠CDF＝180°（）∴∠BCD+∠CDF＝180°（）∴BC∥DF（）于是∠DBC＝∠BDF（）∵BE平分∠ABC，DB平分∠CDF∴∠EBC=12∠ABC，∠BDF＝（）∵∠EBC+∠DBC＝∠EBC+∠BDF=12（∠ABC+∠CDF）即∠EBD＝∴BE⊥DB（）13．如图，EF⊥BC，∠1＝∠C，∠2+∠3＝180°，试说明∠ADC＝90°．请完善解答过程，并在括号内填写相应的理论依据．解：∵∠1＝∠C，（已知）∴GD∥．（）∴∠2＝∠DAC．（）∵∠2+∠3＝180°，（已知）∴∠DAC+∠3＝180°．（等量代换）∴AD∥EF．（）∴∠ADC＝∠．（）∵EF⊥BC，（已知）∴∠EFC＝90°．（）∴∠ADC＝90°．（等量代换）14．（2023秋•南关区期末）如图，已知AB∥DC，AC⊥BC，AC平分∠DAB，∠B＝50°，求∠D的大小．阅读下面的解答过程，并填括号里的空白（理由或数学式）．解：∵AB∥DC（），∴∠B+∠DCB＝180°（）．∵∠B＝（已知），∴∠DCB＝180°﹣∠B＝180°﹣50°＝130°．∵AC⊥BC（已知），∴∠ACB＝（垂直的定义）．∴∠2＝．∵AB∥DC（已知），∴∠1＝（）．∵AC平分∠DAB（已知），∴∠DAB＝2∠1＝（角平分线的定义）．∵AB∥DC（已知），∴+∠DAB＝180°（两条直线平行，同旁内角互补）．。
相交线与平行线基础证明训练题
相交线平行线证明题汇总1、如图，已知∠A=∠F，∠C=∠D，试说明BD∥CE.解：∵∠A=∠F(已知)∴AC∥DF()∴∠D=∠()又∵∠C=∠D(已知)∴∠1=∠C(等量代换)∴BD∥CE() 2、如图，已知∠B+∠BCD=180°，∠B=∠D.求证：∠E=∠DFE.证明：∵∠B+∠BCD=180°(已知)∴AB∥CD()∴∠B=∠DCE（）又∵∠B=∠D（已知）,∴∠DCE=∠D()∴AD∥BE()∴∠E=∠DFE（）3、如图，已知：∠1=∠2，当DE∥FH时，（1）证明：∠EDA=∠HFB（2）CD与FG有何关系?证明：（1）∵DE∥FH(已知)∴∠EDF=∠DFH()∴∠EDA=∠HFB()(2)∵∠EDF=∠DFH()且∠CDF=∠EDF-∠1,∠DFG=∠DFH-∠2又∵∠1=∠2（已知）∴CD∥FG()A BECGHF12DGHKF E DC B A 4、如右图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.证明：∵AD⊥BC,EF⊥BC()∴∠EFB=∠ADB=90°()∴EF∥AD()∴∠1=∠BAD ()又∵∠1=∠2()∴（等量代换）∴DG∥BA()5、如图：已知：AD⊥BC 于D，EF⊥BC 于F，∠1=∠3，求证：AD 平分∠BAC。
证明：∵AD⊥BCEG⊥BC 于F（已知）∴AD∥EF（）∴∠1＝∠E（）∠2＝∠3（）又∵∠3＝∠E（已知）∴∠1＝∠2（）∴AD 平分∠BAC（）6、如图所示,已知直线EF 和AB,CD 分别相交于K,H,且EG⊥AB,∠CHF=600,∠E=30°,试说明AB∥CD.证明：∵EG⊥AB（已知）∴∠EGK=90°()∴在ΔEGK 中∠E+∠EKG=90°（）又∵∠E=30°（）∴∠EKG=600又∵∠CHF=60∴∠EKG=∠CHF ∴AB∥CD （）7.如图：已知∠A＝∠F，∠C＝∠D，求证：BD∥CE 。
相交线与平行线证明题专项训练
321D CB A 相交线与平行线证明题专项训练1如图，已知A B ∥CD, ∠1=∠3, 试说明AC ∥BD.2、如图，已知∠BAF ＝50°，∠ACE ＝140°，CD ⊥CE ，能判断DC ∥AB 吗？为什么？3、如图，已知CD ⊥AD ，DA ⊥AB ，∠1＝∠2。
则DF 与AE 平行吗？为什么？4、如图，AB ∥CD,AD ∥BC,∠A=3∠B.求∠A 、∠B 、∠C 、∠D 的度数.5、如图，AB ∥CD,直线EF 交AB 、CD 于点G 、H.如果GM 平分∠BGF,HN 平分∠CHE ，那么，GM 与HN 平行吗？为什么？6、 如图，∠1=∠2，AC 平分∠DAB ，试说明：DC ∥AB.FE D C B AEFA B CD 12A D CB AB C D E F G H M N7、已知，如图15，∠ACB＝600，∠ABC＝500，BO、CO分别平分∠ABC 、∠ACB，EF是经过点O且平行于BC的直线，求∠BOC 的度数。
8、已知：如图2—99，AD∥BC，∠1=∠2，∠3=∠4．DE与CF平行吗?为什么?9、已知：如图ＡＢ∥ＣＤ，ＥＦ交ＡB于G，交CD于F，FH平分∠EFD，交AB于H ，∠AGE=500求：∠BHF的度数。
10、如图，直线AB、CD相交于点O，OA平分∠COE，∠COE：∠EOD=4：5，求∠BOD的度数。
∠CAB＝21∠BAD，试说明AD∥BC．11、如图21，AB∥DE，∠1＝∠ACB，12、已知一个角的余角的补角比这个角的补角的一半大90°，则这个角的度数等于多少度？13、如图：已知A D∥BE, ∠1=∠2, 请说明∠A=∠E的理由.HGFEDCBAFOECBA图15ECA BDO321EDCBA14、已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4。
求证：AD∥BE。
15、已知如图，直线AB、CD相交于O，OE平分∠BOD，OF平分∠COB，∠2∶∠1＝4∶1，求∠AOF的度数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 古符离初中七年级数学专题复习 相交线平行线证明格式专题训练 1．如图， （1）∵∠A= _________ （已知） ∴AC∥ED（ _________ ） （2）∵∠2= _________ （已知） ∴AC∥ED（ _________ ） （3）∵∠A+ _________ =180°（已知） ∴AB∥FD（ _________ ） （4）∵AB∥ _________ （已知） ∴∠2+∠AED=180°（ _________ ） （5）∵AC∥ _________ （已知） ∴∠C=∠1（ _________ ） 2．如图，已知AD∥BC，∠1=∠2，要证∠3+∠4=180°，请补充完整证明过程，并在括号内填上相应依据： ∵AD∥BC（已知）， ∴∠1=∠3（ _________ ）， ∵∠1=∠2（已知）， ∴∠2=∠3（ _________ ）， ∴BE∥DF（ _________ ）， ∴∠3+∠4=180°（ _________ ）． 3．完成下面推理过程： 如图，已知∠1=∠2，∠B=∠C，可推得AB∥CD．理由如下： ∵∠1=∠2（已知）， 且∠1=∠CGD（ _________ ）， ∴∠2=∠CGD（等量代换）． ∴CE∥BF（ _________ ）． ∴∠ _________ =∠C（ _________ ）． 又∵∠B=∠C（已知）， ∴∠ _________ =∠B（等量代换）． ∴AB∥CD（ _________ ）． 4．如图，点E在直线DF上，点B在直线AC上，若∠AGB=∠EHF，∠C=∠D． 则∠A=∠F，请说明理由． 解：∵∠AGB=∠EHF _________ ∠AGB= _________ （对顶角相等） ∴∠EHF=∠DGF ∴DB∥EC _________ ∴∠ _________ =∠DBA （ 两直线平行，同位角相等） 又∵∠C=∠D ∴∠DBA=∠D ∴DF∥ _________ （内错角相等，两直线平行） ∴∠A=∠F _________ ． 5．填空并完成以下证明： 已知，如图，∠1=∠ACB，∠2=∠3，求证：∠BDC+∠DGF=180°． 证明：∵∠1=∠ACB（已知） ∴DE∥BC （ _________ ） ∴∠2=∠DCF （ _________ ） ∵∠2=∠3（已知） ∴∠3=∠DCF （ _________ ） ∴CD∥FG（ _________ ） 2
∴∠BDC+∠DGF=180°（ _________ ）． 6．完成下列证明： 如图，已知AD⊥BC，EF⊥BC，∠1=∠2． 求证：DG∥BA． 证明：∵AD⊥BC，EF⊥BC（已知） ∴∠EFB=∠ADB=90°（ _________ ） ∴EF∥AD（ _________ ） ∴∠1=∠BAD（ _________ ） 又∵∠1=∠2（已知） ∴ _________ （等量代换） ∴DG∥BA．（ _________ ）
7．如图，BD是∠ABC的平分线，ED∥BC，∠FED=∠BDE，则EF也是∠AED的平分线．完成下列推理过程： 证明：∵BD是∠ABC的平分线（ _________ ） ∴∠ABD=∠DBC（ _________ ） ∵ED∥BC（ _________ ） ∴∠BDE=∠DBC（ _________ ） ∴ _________ （ _________ ） 又∵∠FED=∠BDE（ _________ ） ∴ _________ ∥ _________ （ _________ ） ∴∠AEF=∠ABD（ _________ ） ∴∠AEF=∠DEF（ _________ ） ∴EF是∠AED的平分线（ _________ ） 8．如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，那么DF∥AC，请完成它成立的理由． ∵∠1=∠2，∠2=∠3，∠1=∠4（ _________ ） ∴∠3=∠4（ _________ ） ∴ _________ ∥ _________ ，（ _________ ）， ∴∠C=∠ABD（ _________ ） ∵∠C=∠D（ _________ ） ∴∠D=∠ABD（ _________ ） ∴DF∥AC（ _________ ）． 9．学着说点理，填空： 如图，AD⊥BC于D，EG⊥BC于G，∠E=∠1，可得AD平分∠BAC． 理由如下： ∵AD⊥BC于D，EG⊥BC于G，（已知） ∴∠ADC=∠EGC=90°，（ _________ ） ∴AD∥EG，（ _________ ） ∴∠1=∠2，（ _________ ） ∠E=∠3，（两直线平行，同位角相等） 又∵∠E=∠1（已知） ∴ _________ = _________ （等量代换） ∴AD平分∠BAC（ _________ ） 10．推理填空： 已知，如图，BCE、AFE是直线，AB∥CD，∠1=∠2，∠3=∠4． 求证：AD∥BE． 证明：∵AB∥CD（已知） ∴∠4=∠ _________ （ _________ ） ∵∠3=∠4（已知） ∴∠3=∠ _________ （ _________ ） ∵∠1=∠2（已知） 3
B D
E 1
3 A
C F 2
∴∠1+∠CAF=∠2+∠CAF（等式的性质） 即∠BAF=∠ _________ ∴∠3=∠ _________ （ _________ ） ∴AD∥BE（ _________ ） 11．如图，EF∥AD，∠1=∠2，∠BAC=70°，将求∠AGD的过程填写完整，并在横线上填写理由： 因为EF∥AD（已知）， 所以∠2=∠3（两直线平行，同位角相等） 又因为∠1=∠2（已知）， 所以∠1= _________ （等量代换）， 所以AB∥ _________ （内错角相等，两直线平行）， 所以∠BAC+ _________ =180°（两直线平行，同旁内角互补）， 因为∠BAC=70°（已知）， 所以∠AGD= _________ （补角的定义） 12．如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整． 证明：∵∠1=∠2 （ 已知 ） ∴AE∥ _________ （ _________ ） ∴∠EAC=∠ _________ ，（ _________ ） 而AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴∠ _________ =∠EAC，∠4=∠ _________ （角平分线的定义） ∴∠ _________ =∠4（等量代换） ∴AB∥CD（ _________ ）． 13.完成推理填空：如图：直线AB、CD被EF所截，若已知AB//CD，求证：∠1 ＝ ∠2 。 证明：∵ AB//CD（已知）， ∴∠1 ＝ ∠（ ） 又∵∠2 ＝ ∠3， （ ） ∴∠1 ＝ ∠2（ ）。 14.完成推理填空：如图：已知∠A＝∠F，∠C＝∠D，求证：BD∥CE 。 证明：∵∠A＝∠F（ 已知 ） ∴AC∥DF （ ＿＿ ） ∴∠D＝∠ （ ＿＿ ） 又∵∠C＝∠D （ 已知 ）， ∴∠1＝∠C （ 等量代换 ） ∴BD∥CE（ ）。 15.如图：已知∠B＝∠BGD，∠DGF＝∠F，求证：∠B ＋ ∠F ＝180°。 证明：∵∠B＝∠BGD （___） ∴AB∥CD （ ＿＿＿＿ ） ∵∠DGF＝∠F；（ 已知 ） ∴CD∥EF （ ＿ ） ∵AB∥EF （ ＿＿ ） ∴∠B ＋ ∠F ＝180°（ ＿ ）。 16.已知，如图，∠1=∠ABC=∠ADC,∠3=∠5，∠2=∠4，∠ABC+∠BCD=180°． 证明：（1）∵∠1=∠ABC（已知）， ∴AD∥______ （2）∵∠3=∠5（已知）， ∴AB∥______, （___ __） （3）∵∠ABC+∠BCD=180°（已知）， ∴______∥_____,（__ __） 4
17.已知，如图11，∠BAE+∠AED=180°，∠M=∠N,试说明：∠1=∠2. 解：∵∠BAE+∠AED=180°（ 已知 ） ∴ ∥ （ ） ∴∠BAE= （ ） 又∵∠M=∠N（ 已知 ） ∴ ∥ （ ） ∴∠NAE=（ ） ∴∠BAE-∠NAE= - ∴即∠1=∠2 18.如图，EF∥AD，∠1 =∠2，∠BAC = 70°。将求∠AGD的过程填写完整。 解：∵EF∥AD（ ） ∴∠2 = （ ） ∵∠1 = ∠2（ ） ∴ ∠1 = ∠3。（ ） ∴ AB∥ 。（ ） ∴∠BAC + = 180°。（ ） ∵∠BAC = 70°，（ ） ∴∠AGD = 。 19.如图，∠5=∠CDA =∠ABC，∠1=∠4，∠2=∠3，∠BAD+∠CDA=180°，填空： 解：∵∠5=∠CDA（已知） ∴ // （ ） ∵∠5=∠ABC（已知） ∴ // （ ） ∵∠2=∠3（已知） ∴ // （ ） ∵∠BAD+∠CDA=180°（已知） ∴ // （ ） ∵∠5=∠CDA（已知），又∵∠5与∠BCD互补（ ） ∠CDA与互补（邻补角定义） ∴∠BCD=∠6（ ） ∴ // （ ）
20.如图，完成下列推理过程 已知：DE⊥AO于E， BO⊥AO，∠CFB=∠EDO 证明：CF∥DO 证明：∵DE⊥AO， BO⊥AO（已知） ∴∠DEA=∠BOA=900 （ ） ∵DE∥BO （ ） ∴∠EDO=∠DOF （ ） 又∵∠CFB=∠EDO（ ） ∴∠DOF=∠CFB（ ） ∴CF∥DO（ ）
C B
A
F E D O
GF
E
D
C
BA321