七数下期末复习题二
青岛版2020七年级数学下册期末综合复习基础训练题2(附答案)

青岛版2020七年级数学下册期末综合复习基础训练题2(附答案)1.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为扩大销售,尽快减少库存,商场决定釆取降价措施,调查发现,每件衬衫,每降价1元,平均每天可多销售2件,若商场每天要盈利1200元,每件衬衫应降价( )A .5元B .10元C .20元D .10元或20元2.如图,在△ABC 中,CD 平分∠ACB 交AB 于点D ,过点D 作DE ∥BC交AC 于点E,若∠A=54°,∠B=48°,则∠CDE 的大小为( )A .44°B .40°C .39°D .38°3.下列式子中,计算结果为2215x x +-的是( )A .(5)(3)x x +-B .(5)(3)x x -+C .(5)(3)x x ++D .(5)(3)x x -- 4.(2011•恩施州)下列运算正确的是( )A .a 6÷a 2=a 3B .a 5﹣a 3=a 2C .(3a 3)2=6a 9D .2(a 3b )2﹣3(a 3b )2=﹣a 6b 25.(x +3ab )(x -3ab )等于( )A .x 2 -9a 2b 2B .x 2 -9ab 2C .x 2 -ab 2D .x 2 -a 2b 26.下列说法正确的个数( )①线段有两个端点,直线有一个端点;②点A 到点B 的距离就是线段AB ;③两点之间线段最短;④ 若AB=BC ,则点B 为线段AC 的中点;⑤同角(或等角)的余角相等.A .4个B .3个C .2个D .1个7.平面直角坐标系内AB ∥y 轴,AB=5,点A 的坐标为(﹣5,3),则点B 的坐标为( )A .(﹣5,8)B .(0,3)C .(﹣5,8)或(﹣5,﹣2)D .(0,3)或(﹣10,3)8.如图,将一张正方形纸片剪出一个边长为m 的正方形之后,剩余部分可剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,另一边为23m +,则原正方形边长是 ( )A .6m +B .3m +C .23m +D .26m +9.若12512'∠=o ,225.12∠=o ,325.2∠=o ,则下列结论正确的是( )A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1=∠2=∠3 10.下列各方程组中,不是二元一次方程组的是()A.2583x yx y-=⎧⎨+=⎩B.113x zx y+=⎧⎪⎨=⎪⎩C.3225x yx y-=⎧⎨+=⎩D.1122311332x yx y⎧+=⎪⎪⎨⎪-=⎪⎩11.-0.000031用科学记数法表示为:__________________________12.钟面上8 点30 分时,时针与分针的夹角的度数是________ .13.已知一点到圆上的最短距离是2,最长距离是4,则圆的半径为____.14.已知4x=2x+3,则x=_________.32÷8n-1=2n,则n=_________.15.(x+2y-3)(x-2y-3)=_____-_____.16.有长为20m的铁栏杆,利用它和一面墙围成一个矩形花圃ABCD(如图),若花圃的面积为48m2,求AB的长.若设AB的长为xm,则可列方程为______.17.若2330x y++=,则927x y⋅=________.18.把多项式4m2﹣16n2分解因式的结果是_____.19.已知方程132x y-=,用含x的代数式表示y=_________________________。
七年级数学下学期期末复习试题4套

七年级数学下学期期末复习试题4套2019七年级数学下学期期末复习试题4套一、选择题(本大题共6题,每题2分,满分12分)1.下列说法正确的是(A)无限循环小数是无理数;(B)任何一个有理数都可以表示为分数的形式;(C)任何一个数的平方根有两个,它们互为相反数;(D)数轴上每一个点都可以表示唯一的一个有理数.2.在、0、3.14159、、、、0.1010010001、中,是无理数的个数为(A)1个; (B)2个; (C)3个; (D)4个.3.下列计算正确的是(A) ; (B) ;(C) ; (D) .4.已知:,那么实数a的取值范围是(A)a (B)a (C)a (D)a0.5.如图,(1)A与AEF是同旁内角;(2)BED与CFG是同位角;(3)AFE与BEF是内错角;(4)A与CFE是同位角.以上说法中,正确的个数为(A)1个; (B)2个;(C)3个; (D)4个.6.在平面直角坐标系中,a取任何实数,那么点M(a,a -1)17.如图,在△ABC中,B = 60,C = 40,AE平分BAC,ADBC,垂足为点D,那么DAE = 度.18.等腰三角形一腰上的高与另一腰的夹角为40,那么这个等腰三角形的顶角为度.三、(本大题共4小题,每题6分,满分24分)19.计算: .20.利用分数指数幂的运算性质进行计算: .21.已知:在△ABC中,A、B、C的外角的度数之比是3︰4︰5,求A的度数.22.如图,已知△ABC,根据下列要求作图并回答问题:(1)作边AB上的高CD;(2)过点D作直线BC的垂线,垂足为E;(3)点B到直线CD的距离是线段的长度.(不要求写画法,只需写出结论即可)四、(本大题共5题,每题8分,满分40分)23.如图,(1)写出点A、B、C的坐标:A ,B ,C ;(2)画出△ABC关于y轴的对称图形△A1B1C1;(3)联结BB1、AB1,求△ABB1的面积.24.如图,已知1 = 65,2 =3 = 115,那么AB与CD平行吗?EF 与GH平行吗?为什么?解:将1的邻补角记作4,则1 +4 = 180( ).因为 1 = 65,( ),所以 4 = 1801 = 180 - 65 = 115.因为 2 = 115( ),所以 2 =4 ( ).所以 ________ // _________( ).因为 4 = 115,3 = 115 ( ),所以 3 =4 ( ).所以 ________ // _________( ).25.如图,已知:B =C =AED = 90.(1)请你添加一个条件,使△ABE与△EC D全等,这个条件可以是 .(只需填写一个)(2)根据你所添加的条件,说明△ABE与△ECD全等的理由.26.如图,点D是等边△ABC中边AC上的任意一点,且△BDE 也是等边三角形,那么AE与BC一定平行吗?请说明理由.27.如图,在△ABC中,C = 90,CA = CB,AD平分BAC,BEAD 于点E。
2023—2024学年北师大版数学七年级下册期末复习题(含答案)

北师大版七年级数学下册期末复习测试题考试时间:120分钟满分150分一、单选题(本大题共10小题,每小题4分,总分40分)1.下列运算正确的是( )A.2a2+a2=3a4B.(﹣2a2)3=8a6C.a2÷a3=1aD.(a﹣b)2=a2﹣b22.不透明的袋子中装有红球2个、绿球3个,除颜色外红球和绿球无其他差别,从中随机摸出一个小球,那么摸到绿球的概率是( )A.23B.25C.32D.353.下列图案中,是轴对称图形的是( )A.B.C.D.4.如图,直线AB∥CD,直线l分别与直线AB,CD相交于点E,F,EG平分∠FEB交CD于点G.若∠CFE=50°,则∠FGE的度数为( )A.20°B.25°C.30°D.35°5.今年5月1日,我市某商场停车场的停车量为2000辆次,其中两轮电动车平均停车费为每辆1元一次,小汽车平均停车费为每辆5元一次,若两轮电动车停车辆数为x辆次,停车的总收入为y元,则y与x 的关系式为( )A.y=﹣4x+10000B.y=﹣3x+8000C.y=﹣2x+4000D.y=﹣4x+50006.将一副三角尺如图摆放,点D在AC上,延长EA交CB的延长线于点F,∠ABC=∠ADE=90°,∠C =30°,∠E=45°,则∠F的度数是( )A.10°B.15°C.20°D.25°7.现有如图所示的甲、乙、丙三种长方形或正方形纸片各15张,小明要用这些纸片中的若干张拼接(不重叠、无缝隙)一个长、宽分别为(5x+4y)和(3x+y)的长方形.下列判断正确的是( )A.甲种纸片剩余7张B.丙种纸片剩余10张C.乙种纸片缺少2张D.甲种和乙种纸片都不够用8.如图,已知长方形纸片ABCD,点E,F分别在边AD和BC上,且∠EFC=53°,H和G分别是边AD 和BC上的动点,现将点A,B沿EF向下折叠至点N,M处,将点C,D沿GH向上折叠至点P,K处,若MN∥PK,则∠KHD的度数为( )A.37°或143°B.74°或96°C.37°或105°D.74°或106°9.如图,在△ABC中,∠BAC=∠ABC=48°,过点C作CD⊥AB于点D,点E是CD上一点,将△ACE 沿着AE翻折得到△AFE,连接CF,若E,F,B三点恰好在同一条直线上,则∠CFA的度数是( )A.72°B.78°C.80°D.84°10.如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE 于点H,下面说法正确的是( )①△ABE的面积=△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.A.①②③④B.①②③C.②④D.①③二、填空题(本大题共5小题,每小题4分,总分20分)11.将数据0.000000023用科学记数法表示为 .12.某烤鸭店在确定烤鸭的烤制时间时,主要依据的是下表的数据:鸭的质量/千克1 1.52 2.53 3.54烤制时间/分6080100120140160180设鸭的质量为x千克,烤制时间为t,估计当x=6千克时,t的值为 分.13.如图,在四边形ABCD中,AB∥CD,∠BAD=90°,CE平分∠BCD,∠CBF=6∠EBF,AG∥CE,点H在直线CE上,满足∠FBH=∠DAG.若∠DAG=k∠EBH,则k的值是 .14.如图,已知D,E是△ABC边AB,AC上两点,沿线段DE折叠,使点A落在线段BC的点F处,若BD=DF,∠C=70°,则∠CEF= .15.如图,AB⊥CD于点E,且AB=CD=AC,若点I是△ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=135°;②BD=BI;③S△AIC=S△BID;④IF⊥AC.其中正确的是 (填序号).三、解答题(本大题共10小题,总分90分)16.(1)计算:−12024×4+(−13)−2+(π−5)0.(2)先化简,再求值:(a﹣1)(a+2)+(a+2)2﹣4a+1,其中a=−1 2.17.如图,AB∥CD,∠BAE=∠BCD,AE⊥DE,∠ABC=35°,求∠EDC的度数.18.5月是销售樱桃的季节,某樱桃种植园为了吸引顾客,推出入园采摘销售模式.已知采摘樱桃重量x (千克)与所需费用y(元)之间的关系可以用y=6x来表示.(1)上述关系中, 是自变量, 是因变量;(2)上述关系用表格表示如表,请补充填空:x/千克0.51 1.52 2.53…y/元361215…(3)48元能买多少千克樱桃?19.如图,在△ABC和△DEF中,B,E,C,F在同一条直线上,已知:AB=DE,AB//DE,BE=CF,试说明:∠A=∠D.20.如图,在△ABC中,BD平分∠ABC,DE⊥AB,AB=4,△ABD的面积为6,△BDC的面积为9,求BC的长.21.盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是38,写出表示x和y关系的表达式.(2)在(1)的条件下,往盒中再放进10枚黑棋,取得黑棋的概率变为12,求x和y的值.22.如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.(1)若∠BAE=40°,求∠C的度数;(2)若△ABC周长为14cm,AC=6cm,求DC长.23.我国著名数学家华罗庚曾说“数缺形时少直观,形少数时难入微”,数形结合的方法是我们解决数学问题常用到的思想方法.【方法生成】(1)通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,可得到我们学过的公式: .【拓展探究】(2)小圣得到启发,利用上面的方法得到一个新公式(如图2):(a+b+c)2= .【公式应用】根据小圣发现的新公式,解决下面的问题:(3)直接写出结果:(a﹣b﹣c)2= .(4)已知a+2=b+c,a2+b2+c2=85,求10bc﹣10a(b+c)的值.24.如图,CB为∠ACE的平分线,F是线段CB上一点,CA=CF,∠B=∠E,延长EF与线段AC相交于点D.(1)试说明:AB=FE;(2)若ED⊥AC,AB∥CE,求∠A的度数.25.如图,直线AB∥CD,直线EF与AB,CD分别交于点G,H,∠EHD=α(0°<α<90°).小明将一个含45°角的直角三角板PMN按如图①放置,使点N、M分别在直线AB,CD上,∠P=90°,∠PMN=45°.(1)填空:∠PNB+∠PMD ∠P(填“>”“<”或“=”);(2)若PN⊥EF,射线NO在∠MNG内交直线CD于点O,如图②.当N,M分别在点G,H的右侧,且∠GNO:∠MNO=3:2,PM∥NO时,求α的度数;(3)小明将三角板PMN沿直线AB左右移动,保持PM∥EF,射线NO平分∠MNG,点N,M分别在直线AB和直线CD上移动,请直接写出∠MON的度数(用含α的式子表示).北师大版七年级数学下册期末复习测试题参考答案一、单选题(本大题共10小题,每小题4分,总分40分)1-5.CDCBA 6-10 .BCDAB.二、填空题(本大题共5小题,每小题4分,总分20分)11.2.3×10﹣8.12.260.13.79或75.14.40°.15.①③④.三、解答题(本大题共10小题,总分90分)16.计算:−12024×4+(−13)−2+(π−5)0.解:(1)−12024×4+(−13)−2+(π−5)0=﹣1×4+9+1=6.(2)(a﹣1)(a+2)+(a+2)2﹣4a+1=a2+2a﹣a﹣2+a2+4a+4﹣4a+1=2a2+a+3,当a=−12时,原式=2×(−12)2+(−12)+3=2×14+(−12)+3=12−12+3=3.17.解:过E作EK∥CD,∵AB∥CD,∴EK∥AB,∴∠CDE+∠DEK=180°,∠BAE+∠AEK=180°,∠ABC+∠DCB=180°,∵∠BAE=∠BCD,∴∠AEK=∠ABC=35°,∵AE⊥DE,∴∠DEK=90°﹣35=55°,∴∠CDE=125°.18.解:(1)由题意得,x 是自变量,y 是因变量,故答案为:x ,y ;(2)由题意得,当x =1.5时,y =6×1.5=9;当x =3时,y =6×3=18,故答案为:9,18;(3)由题意得6x =48,解得x =8,∴48元能买8千克樱桃.19.解:∵BE =CF ,∴BE +EC =CF +EC ,即BC =EF ,∵AB //DE ,∴∠B =∠DEF ,在△ABC 和△DEF 中,AB =DE ,∠B =∠DEF ,BC =EF ,∴△ABC ≌△DEF (SAS ),∴∠A =∠D .20.解:如图所示,过点D 作DF ⊥BC 于F ,∵DE ⊥AB ,AB =4,△ABD 的面积为6,∴12AB ⋅DE =6,∴DE =3,∵BD平分∠ABC,DE⊥AB,DF⊥BC,∴DF=DE=3,∵△BDC的面积为9,∴12BC⋅DF=9,∴BC=6.21.解:(1)∵盒中有x枚黑棋和y枚白棋,∴袋中共有(x+y)个棋,∵黑棋的概率是3 8,∴可得关系式xx+y=38;(2)如果往口袋中再放进10个黑球,则取得黑棋的概率变为12,又可得x+10x+y+10=12;联立求解可得x=15,y=25.22.解:(1)∵AD垂直平分BE,EF垂直平分AC,∴AB=AE=EC,∴∠C=∠CAE,∵∠BAE=40°,∴∠AED=70°,∴∠C=12∠AED=35°;(2)∵△ABC周长14cm,AC=6cm,∴AB+BE+EC=8cm,即2DE+2EC=8cm,∴DE+EC=DC=4cm.23.解:(1)图中正方形面积(a+b)2,a2+2ab+b2,则(a+b)2=a2+2ab+b2,故答案为:(a+b)2=a2+2ab+b2;(2)a2+b2+c2+2ab+2ac+2bc,故答案为:a2+b2+c2+2ab+2ac+2bc;(3)由(2)得(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,∴(a﹣b﹣c)2=[a+(﹣b)+(﹣c)]2,=a2+(﹣b)2+(﹣c)2+2a(﹣b)+2a(﹣c)+2(﹣b)(﹣c),=a2+b2+c2﹣2ab﹣2ac+2bc,故答案为:a2+b2+c2﹣2ab﹣2ac+2bc;(4)∵a+2=b+c,∴a﹣b﹣c=﹣2,∴(a﹣b﹣c)2=4,∴a2+b2+c2﹣2ab﹣2ac+2bc=4,∵a2+b2+c2=85,∴bc−ab−ac=−81 2,∴10bc−10a(b+c)=10(bc−ab−ac)=10×(−812)=−405.24.解:(1)∵CB为∠ACE的角平分线,∴∠ACB=∠FCE,在△ABC与△FEC中,{∠B=∠E∠ACB=∠FCECA=CF,∴△ABC≌△FEC(AAS),∴AB=FE;(2)∵AB∥CE,∴∠B=∠FCE,∴∠E=∠B=∠FCE=∠ACB,∵ED⊥AC,即∠CDE=90°,∴∠E+∠FCE+∠ACB=90°,即3∠ACB=90°,∴∠ACB=30°,∴∠B=30°,∴∠A=180°﹣∠B﹣∠ACB=180°﹣30°﹣30°=120°.25.解:(1)过点P作直线JK∥AB,如图1,∵AB∥CD,∴AB∥JK∥CD,∴∠PNB=∠NPJ,∠PMD=∠JPM,∴∠PNB+∠PMD=∠NPJ+∠JPM=∠NPK=90°.故答案为:=.(2)延长PN交EF于点K,如图2,∵∠P=90°,∴PN⊥PM,∵PN⊥EF,∴EF∥PM,∵PM∥NO,∴EF∥PM∥NO,∴∠GHM=∠NOM,∠PMN=∠MNO,∵∠PMN=45°,∴∠PMN=∠MNO=45°,∵∠GNO:∠MNO=3:2,∴∠GNO=32∠MNO=32×45°=67.5°,∵AB∥CD,∴GNO=∠NOM,∴∠GHM=∠GNO=67.5°,∴α=67.5°.(3)①当N,M分别在点G,H的右侧,如图3,∵PM∥EF,∴∠EHM=∠PMD=α,∵∠PMN=45°,∴∠NMD=45°+α,∵AB∥CD,∴∠ANM=∠NMD=45°+α,∵射线NO平分∠MNG,∴∠ANO=∠MNO=12∠ANM=12(45°+α)=22.5°+12α;②当点N,M分别在点G,H的左侧,如图4,∵PM∥EF,∴∠EHD=∠PMD=α,∵∠PMN=45°,∴∠NMD=45°+α,∵AB∥CD,∴∠BNM+∠NMD=180°,∠BNO=∠MON,∵射线NO平分∠MNG,∴∠MNO=∠BNO=12∠MNB,∴∠MNB=180°﹣(45°+α),∴∠MNO=12∠MNB=∠MNB=12[180°−(45°+α)]=67.5°−12α,综上所述,∠MON=22.5°+12α或∠MON=67.5°−12α.。
湘教版七年级下数学期末复习试卷(二)整式的乘法

期末复习(二) 整式的乘法考点一幂的运算【例1】若a m+n·a m+1=a6,且m+2n=4,求m,n的值.【分析】已知m+2n=4,只要再找到一个关于m,n的二元一次方程即可组成方程组求解.可根据同底数幂的乘法法则,由等式左右两边a的指数相等得到.【解答】由已知得a2m+n+1=a6,于是有2m+n+1=6,即2m+n=5,又因为m+2n=4,所以m=2,n=1. 【方法归纳】对于乘方结果相等的两个数,如果底数相等,那么指数也相等.变式练习:1.下列计算正确的是( )A.a+2a=3a2B.(a2b)3=a6b3C.(a m)2=a m+2D.a3·a2=a62.若2x=3,4y=2,则2x+2y的值为__________.考点二多项式的乘法【例2】化简:2(x-1)(x+2)-3(3x-2)(2x-3).【分析】先按多项式乘法法则展开,再合并同类项.【解答】原式=2(x2+2x-x-2)-3(6x2-9x-4x+6)=-16x2+41x-22.【方法归纳】在计算多项式乘法时,要注意不漏项,不重项.多项式与多项式相乘,结果仍是多项式,在合并同类项之前,积的项数等于两个多项式项数的积.3.如果(x+m)与(x+1)的积中不含x项,那么m是( )A.-2B.-1C.1D.24.若2x3-ax2-5x+5=(2x2+ax-1)(x-b)+3,其中a、b为整数,则a+b的值为( )A.-4B.-2C.0D.4考点三乘法公式适用的多项式特点【例3】二次三项式x2-kx+9是一个完全平方式,则k的值是__________.【分析】先把x2-kx+9变形为x2-kx+32或x2-kx+(-3)2,根据两平方项确定中间项为±6x,即可确定k的值.【解答】±6【方法归纳】两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,即“首平方,尾平方,积的2倍在中央”.5.下列各式:①(a+b)(b+a);②(a-b)(a+b);③(-a+b)(a+b);④(-a+b)(-a-b),其中能用乘法公式计算的有( )A.1个B.2个C.3个D.4个考点四利用乘法公式计算【例4】先化简,再求值:(2a-b)(b+2a)-(a-2b)2+5b2.其中a=-1,b=2.【分析】把式子的前两部分分别运用平方差公式和完全平方公式化简.【解答】原式=(4a2-b2)-(a2-4ab+4b2)+5b2=3a2+4ab.当a=-1,b=2时,原式=3×(-1)2+4×(-1)×2=-5.【方法归纳】运用平方差公式时,要看清两个因式中的相同项和相反数项,其结果是相同项的平方减去相反数项的平方.6.下列等式成立的是( )A.(-a-b)2+(a-b)2=-4abB.(-a-b)2+(a-b)2=a2+b2C.(-a-b)(a-b)=(a-b)2D.(-a-b)(a-b)=b2-a27.若(a2+b2+1)(a2+b2-1)=15,那么a2+b2的值是__________.8.计算:(1)(a+b)2-(a-b)2-4ab; (2)[(x+2)(x-2)]2; (3)(a+3)(a-3)(a2-9).考点五乘法公式的几何背景【例5】(1)如图,请用两种不同的方式表示图中的大正方形的面积;(2)你根据上述结果可以得到一个什么公式?(3)利用这个公式计算:1022.【分析】根据图形可以得到:两个图形的面积有两种计算方法,一种是根据正方形的面积等于边长的平方计算;另一种方法是图形中两个长方形面积与两个正方形的面积的和,即可得到公式;然后利用公式计算即可.【解答】(1)方法一:(a+b)2.方法二:a2+2ab+b2.(2)(a+b)2=a2+2ab+b2.(3)1022=(100+2)2=1002+2×100×2+22=10 404.【方法归纳】根据同一个图形的面积的两种表示,所得到的代数式的值相等,由此可得到对应的代数恒等式.9.图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积是( )A.2ab B.(a+b)2 C.(a-b)2D.a2-b2复习测试:一、选择题(每小题3分,共24分)1.计算(-a2)3的结果是( )A.a5B.-a5C.a6D.-a62.下列运算正确的是( )A.x2+x3=x5B.(x-2)2=x2-4C.2x2·x3=2x5D.(x3)4=x73.下列各式中,与(1-a)(-a-1)相等的是( )A.a2-1B.a2-2a+1C.a2-2a-1D.a2+14.如果(x-2)(x+3)=x2+px+q,那么p、q的值为( )A.p=5,q=6 B.p=-1,q=6 C.p=1,q=-6 D.p=5,q=-65.若m的值使得x2+12x+m=(x+6)2-32成立,则m的值为( )A.2B.3C.4D.56.下列计算:①(a3)3=a6;②a2·a3=a6;③2m·3n=6m+n;④-a2·(-a)3=a5;⑤(a-b)3·(b-a)2=(a-b)5.其中错误的个数有( )A.1个B.2个C.3个D.4个7.一个长方体的长、宽、高分别是3a-4、2a、a,它的体积等于( )A.3a3-4a2B.a2C.6a3-8aD.6a3-8a28.请你计算:(1-x)(1+x),(1-x)(1+x+x2),…猜想(1-x)(1+x+x2+…+x n)的结果是( )A.1-x n+1B.1+x n+1C.1-x nD.1+x n二、填空题(每小题4分,共16分)9.计算:2m2·m8=__________.10.已知有理数a,b满足:a+b=2,a-b=5,则(a+b)3·(a-b)3的值是__________.11.卫星绕地球运动的速度是7.9×103米/秒,那么卫星绕地球运行3×106秒走过的路程是__________米.12.多项式4x2+1加上一个单项式后,使它能成为一个整式的完全平方,请写出所有可能的单项式为__________.三、解答题(共60分)13.(12分)计算:(1)(-2a2b)3+8(a2)2·(-a)2·(-b)3;(2)a(a+4b)-(a+2b)(a-2b)-4ab;(3)(2x-3y+1)(2x+3y-1).14.(10分)先化简,再求值:(1)(2019·河池)(x+2)2-(x+1)(x-1),其中x=1;(2)(2a+b)(3a-2b)-(a-2b)2,其中a=-2,b=1.15.(8分)已知a+b=1,ab=-6,求下列各式的值.(1)a2+b2; (2)a2-ab+b2.16.(10分)四个数a、b、c、d排成2行、2列,两边各加一条竖直线记成,定义=ad-bc,这个记号就叫做2阶行列式. 例如:=1×4-2×3=-2 . 若=10,求x的值.17.(10分)如图,某校有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划将阴影部分进行绿化,中间将修建一座雕像.(1)用含a、b的代数式表示绿化面积并化简;(2)求出当a=5米,b=2米时的绿化面积.18.(10分)如图a是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图b的形状,拼成一个正方形.(1)图b中的阴影部分面积为__________;(2)观察图b,请你写出三个代数式(m+n)2,(m-n)2,mn之间的等量关系是__________; (3)若x+y=-6,xy=2.75,利用(2)提供的等量关系计算x-y的值.参考答案变式练习1.B2.63.B4.D5.D6.D7.48.(1)原式=a2+2ab+b2-a2+2ab-b2-4ab=0.(2)原式=(x2-4)2=x4-8x2+16.(3)原式=(a2-9)(a2-9)=a4-18a2+81.9.C复习测试1.D2.C3.A4.C5.C6.C7.D8.A9.2m10 10.1 000 11.2.37×101012.±4x或4x413.(1)原式=-8a6b3-8a6b3=-16a6b3.(2)原式=a2+4ab-(a2-4b2)-4ab=a2+4ab-a2+4b2-4ab=4b2.(3)原式=[2x-(3y-1)][2x+(3y-1)]=4x2-(3y-1)2=4x2-(9y2-6y+1)=4x2-9y2+6y-1.14.(1)原式=x2+4x+4-(x2-1)=x2+4x+4-x2+1=4x+5.当x=1时,原式=4×1+5=9.(2)原式=6a2-ab-2b2-a2+4ab-4b2=5a2+3ab-6b2.当a=-2,b=1时,原式=5×(-2)2+3×(-2)×1-6×12=8.15.(1)a2+b2=(a+b)2-2ab=1+12=13.(2)a2-ab+b2=(a+b)2-3ab=12-3×(-6)=1+18=19.16.(x+1)2-(x-2)(x+2)=10,解得x=2.5.17.(1)S=(3a+b)(2a+b)-(a+b)2=6a2+3ab+2ab+b2-a2-2ab-b2=5a2+3ab(平方米).阴影(2)当a=5,b=2时,5a2+3ab=5×25+3×5×2=125+30=155(平方米).18.(1)m2-2mn+n2或(m-n)2.(2)(m+n)2=(m-n)2+4mn.(3)(x-y)2=(x+y)2-4xy=36-11=25,所以x-y的值是±5.。
人教版七年级数学下册期末测试题及复习资料详解共五套

李庄人教版七年级数学下学期末模拟试题(一)一、选择题:(本大题共10个小题,每小题3分,共30分) 1.若m >-1,则下列各式中错误的...是( ) A .6m >-6 B .-5m <-5 C .1>0 D .1-m <2 2.下列各式中,正确的是( )16±4 B.±164 C 327- 3 2(4)- 4 3.已知a >b >0,那么下列不等式组中无解..的是( ) A . B . C . D .4.一辆汽车在马路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为 ( )(A) 先右转50°,后右转40° (B) 先右转50°,后左转40° (C) 先右转50°,后左转130° (D) 先右转50°,后左转50° 5.解为的方程组是( ) A. B. C. D.6.如图,在△中,∠500,∠800,平分∠,平分∠,则∠的大小是( ) A .1000 B .1100 C .1150 D .1200PCBA 小刚小军小华(1) (2) (3)7.四条线段的长分别为3,4,5,7,则它们首尾相连可以组成不同的三角形的个数是( ) A .4 B .3 C .2 D .1 8.在各个内角都相等的多边形中,一个外角等于一个内角的12,则这个多边形的边数是( ) A .5 B .6 C .7 D .89.如图,△A 1B 1C 1是由△沿方向平移了长度的一半得到的,若△的面积为20 cm 2,则四边形A 11的面积为( )A .10 cm 2B .12 c m 2C .15 cm 2D .17 cm 210.课间操时,小华、小军、小刚的位置如图1,小华对小刚说,假如我的位置用(•0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成( )A.(5,4)B.(4,5)C.(3,4)D.(4,3)二、填空题:本大题共8个小题,每小题3分,共24分,把答案干脆填在答题卷的横线上. 11.49的平方根是,算术平方根是8的立方根是. 12.不等式59≤3(1)的解集是.13.假如点P(a,2)在第二象限,那么点Q(-3)在.14.如图3所示,在铁路旁边有一李庄,现要建一火车站,•为C 1A 1ABB 1CD了使李庄人乘火车最便利(即间隔 最近),请你在铁路旁选一点来建火车站(位置已选好),说明理由.15.从A 沿北偏东60°的方向行驶到B,再从B 沿南偏西20°的方向行驶到C,•则∠度.16.如图∥,∠100°平分∠,则∠.17.给出下列正多边形:① 正三角形;② 正方形;③ 正六边形;④ 正八边形.用上述正多边形中的一种可以辅满地面的是.(将全部答案的序号都填上) 18.若│x 2-25则.三、解答题:本大题共7个小题,共46分,解答题应写出文字说明、证明过程或演算步骤. 19.解不等式组:,并把解集在数轴上表示出来.20.解方程组:2313424()3(2)17x y x y x y ⎧-=⎪⎨⎪--+=⎩21.如图, ∥ , 平分∠,你能确定∠B 及∠C 的数量关系吗?请说明理由。
2022-2023学年北师大版数学七年级下册+第四章+三角形++期末复习题(2)
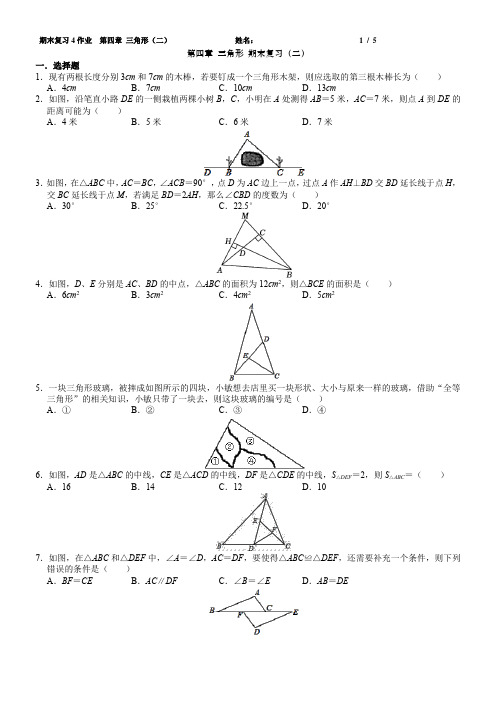
第四章三角形期末复习(二)一.选择题1.现有两根长度分别3cm和7cm的木棒,若要钉成一个三角形木架,则应选取的第三根木棒长为()A.4cm B.7cm C.10cm D.13cm2.如图,沿笔直小路DE的一侧栽植两棵小树B,C,小明在A处测得AB=5米,AC=7米,则点A到DE的距离可能为()A.4米B.5米C.6米D.7米3.如图,在△ABC中,AC=BC,∠ACB=90°,点D为AC边上一点,过点A作AH⊥BD交BD延长线于点H,交BC延长线于点M,若满足BD=2AH,那么∠CBD的度数为()A.30°B.25°C.22.5°D.20°4.如图,D、E分别是AC、BD的中点,△ABC的面积为12cm2,则△BCE的面积是()A.6cm2B.3cm2C.4cm2D.5cm25.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是()A.①B.②C.③D.④6.如图,AD是△ABC的中线,CE是△ACD的中线,DF是△CDE的中线,S△DEF=2,则S△ABC=()A.16B.14C.12D.107.如图,在△ABC和△DEF中,∠A=∠D,AC=DF,要使得△ABC≌△DEF,还需要补充一个条件,则下列错误的条件是()A.BF=CE B.AC∥DF C.∠B=∠E D.AB=DE8.下列长度的三条线段,能组成三角形的是()A.2,3,4B.2,3,5C.2,2,4D.2,2,59.如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为()A.12B.14C.16D.1810.若一个三角形的两边长分别为3cm、6cm,则它的第三边的长可能是()A.2cm B.3cm C.6cm D.9cm二、填空题36.如图,在△ABC中,AD平分∠BAC,∠BAC=80°,∠B=35°,则∠ADC的度数为°.13.如图,在△ABC中,AB=AC,BF=CD,BD=CE.若∠A=40°,则∠FDE=°.14.如图,在△ABC中,AB=AC,点D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=∠B =40°,DE交线段AC于点E.下列结论:①∠CDE=∠BAD;②BD=CE;③当D为BC中点时,DE⊥AC;④当△ADE为等腰三角形时,∠BAD=30°.其中正确的是(填序号).三、解答题15.已知:如图,AB∥CD,AB=CD,BF=CE.(1)求证:△ABF≌△DCE.(2)已知∠AFC=80°,求∠DEC的度数.16.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.17.如图,已知∠A=∠EDF,AD=BE,AC=DF.求证:BC∥EF.18.如图,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AD=AB.求证:AC=AE.19.如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.(1)求证:△ABD≌△ACE.(2)若∠ADE=2∠B,BD=2,求AE的长.20.本学期,我们学习了三角形相关知识,而四边形的学习,我们一般通过辅助线把四边形转化为三角形,通过三角形的基本性质和全等来解决一些问题.(1)如图1,在四边形ABCD中,AB=AD,∠B+∠D=180°,连接AC.①小明发现,此时AC平分∠BCD.他通过观察、实验,提出以下想法:延长CB到点E,使得BE=CD,连接AE,证明△ABE≌△ADC,从而利用全等和等腰三角形的性质可以证明AC平分∠BCD.请你参考小明的想法,写出完整的证明过程.②如图2,当∠BAD=90°时,请你判断线段AC,BC,CD之间的数量关系,并证明.(2)如图3,等腰△CDE、等腰△ABD的顶点分别为A、C,点B在线段CE上,且∠ABC+∠ADC=180°.请你判断∠DAE与∠DBE的数量关系,并证明.21.已知△ABC和△ADE都是等边三角形,点D在射线BF上,连接CE.(1)如图1,BD与CE是否相等?请说明理由;(2)如图1,求∠BCE的度数;(3)如图2,当D在BC延长线上时,连接BE,△ABE、△CDE与△ADE的面积有怎样的关系?并说明理由.22.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为一边且在AD的右侧作等腰直角三角形ADE,AD=AE,∠DAE=90°.解答下列问题.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,求证:BD=CE,BD⊥CE.②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,请说明理由.(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动.试探究:当△ABC满足一个什么条件时,CE⊥BD(点C、E重合除外).先画出相应图形,再说明理由.4 5 5。
2020-2021学年七年级数学苏科版下册期末复习综合提优2

苏科版七年级下期末复习综合提优2一、选择题:1纳米0.000000001=米,则2纳米用科学记数法表示为( ) A .9210-⨯B .9210-⨯C .8210-⨯D .8210-⨯2、甲种蔬菜保鲜适宜的温度是1℃~5℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是 ( )A .1℃~3℃B .3℃~5℃C .5℃~8℃D .1℃~8℃ 3、若||x +y +1与(x -y -2)2互为相反数,则(3x -y )3的值为 ( ) A .1 B .9 C .–9 D .274、命题“若∠1+∠2=90°,则∠1≠∠2”,能说明它是假命题的例子 ( )A .∠1=50°,∠2=40°B .∠1=50°,∠2=50°C .∠1=∠2=45°D .∠1=40°,∠2=40°5、若关于x 的不等式组⎩⎪⎨⎪⎧1+x >a ,2x -4≤0有解,则a 的取值范围是 ( )A .a ≤3B .a <3C .a <2D .a ≤26、已知命题:①相等两个数的平方相等;②若x >0,则||x =x ;③互为相反数的两个实数的商为-1;④异号两数相乘,积为负数.以上命题中为真命题的个数是 ( ) A .1个 B .2个 C .3个 D .4个7、已知3x =是关于x 的不等式22323ax xx +->的一个解,求a 的取值范围为( ) A .3a > B .3a < C .4a < D .4a >8、已知某三种图书的价格分别为10元,15元,20元.某学校计划恰好用500元购买上述图书30本,每种图书至少一本,则不同的购书方案有( )种.A .10B .9C .12D .11 9、如图,AD 是∠CAE 的平分线,∠B =35°,∠DAE =60°,则∠ACD =( ) A . 25° B .60° C .85° D .95°9题 10题10、已知关于x 的不等式23x m ->-的解集如图,则m 的值为( ) A .2 B .1 C .0 D .1-11、普通火车从绵阳至成都历时大约2小时,成绵城际快车开通后,时间大大缩短至几十分钟,现假定普通火车与城际快车两列对开的火车于同一时刻发车,其中普通火车由成都至绵阳,城际快车由绵阳至成都,这两车在途中相遇之后,各自用了80分钟和20分钟到达自己的终点绵阳、成都,则城际快车的平均速度是普通火车平均速度的()倍.A.2B.2.5C.3D.412、在中央电视台2套“开心辞典”节目中,有一期的某道题目是:如图所示,天平中放有苹果、香蕉、砝码,且两个天平都平衡,则一个苹果的重量是一个香蕉的重量的()A.43倍B.32倍C.2倍D.3倍12题13题13、如图,长方形ABCD被分成3个正方形和2个长方形后仍是中心对称图形,设长方形ABCD的周长为l,若图中3个正方形和2个长方形的周长和为l,则标号为①的正方形的边长为()A.l B.l C.l D.l14、某足球比赛小组赛的比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名(四队得分互不相等),且丙与其他球队均打平,则四个球队的得分之和可能为()A.13分或14分B.14分或15分C.15分或16分D.16分或17分15、已知n是正整数,若一个三角形的三边长分别是n+2、n+8、3n,则满足条件的n的值有()A.4个B.5个C.6个D.7个16、为了美化城市,经统一规划,将一正方形草坪的南北方向增加3m,东西方向缩短3m,则改造后的长方形草坪面积与原来正方形草坪面积相比( )A.减少9m2B.增加9m2C.保持不变D.增加6m217、若关于x,y的方程组的解满足x﹣y>﹣,则m的最小整数解为()A.﹣3B.﹣2C.﹣1D.018、若不等式组的解集为x<5,则m的取值范围为()A.m<4B.m≤4C.m≥4D.m>419、五张如图所示的长为a,宽为b(a>b)的小长方形纸片,按如图的方式不重叠地放在矩形ABCD中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足的关系式为()A.a=2b B.a=3b C.3a=2b D.2a=3b+119题20题20、利用两块完全一样的长方体木块测量一张桌子的高度,首先按图①所示的方式放置,再交换两木块的位置,按图②所示的方式放置.测量的数据如图,则桌子的高度等于()A.80cm B.75cm C.70cm D.65cm21、如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB=c,AC=b,则(m+n)与(b+c)的大小关系是()A.m+n>b+c B.m+n<b+c C.m+n=b+c D.无法确定21题二、填空题:1、一个多边形的内角和为900º,则这个多边形的边数是_____________.2、周长为24,各边长互不相等且都是整数的三角形共有个.3、已知a+a﹣1=4,则a4+a﹣4=.4、若实数a,b满足a﹣b=1,则代数式a2﹣b2﹣2b+5的值为.5、一个三角形的两边长分别为3 cm、5 cm,且第三边为偶数,则这个三角形的周长为______________ cm.6、已知10m=3,10n=5,则103m-n=_____________.7、分解因式:2x2+7xy﹣15y2﹣3x+11y﹣2=.8、△ABC的三边a,b,c为互不相同的整数,且abc+ab+ac+bc+a+b+c=119,则△ABC的周长为.9、若关于x ,y 的方程组⎩⎪⎨⎪⎧3x +y =1-a ,x +3y =3的解满足x +y <2,则a 的取值范围为_____________.10、如图,△ABC 沿AC 平移得到△A 'B 'C ',A 'B '交BC 于点D ,若AC =6,D 是BC 的中点,则C 'C = .10题 11题 12题11、如图,将分别含有30°、45°角的一副三角板重叠,使直角顶点重合,若两斜边相交构成的一个角为60°,则图中角α的度数为 度.12、如图,已知AE ∥BD ,∠1=130°,∠2=28°,则∠C 的度数为 .13、若x 2-2ax +16是完全平方式,则数a =_____________.14、如图,正八边形ABCDEFGH 中,延长对角线BF 与边DE 交于点M ,则∠M 的大小为 .14题 15题 16题 15、如图,∠A +∠B +∠C +∠D +∠E 的度数为 度.16、如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,…,依此递推,则第6层中含有正三角形个数是 ,第n 层中含有正三角形个数是 . 17、若不等式组的解集为﹣1<x <1,那么(a ﹣3)(b +3)的值等于 .18、已知关于x的不等式组只有2个整数解,则实数a的取值范围是19、《九章算术》是中国古代的数学专著,下面这道题是《九章算术》中第七章的一道题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”译文:“几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价格是多少?”设有x人,物品价格为y钱,可列方程组为.19题 22题 24题20、如果关于x的不等式组的整数解仅为1,2,3,那么适合这个不等式组的整数a,b组成的有序数对(a,b)个数为.21、某商场分别组装了甲、乙两种坚果营养袋,它们都由a、b、c三种坚果组成,甲种坚果营养袋每袋装有100克a坚果,300克b坚果,100克c坚果;乙种坚果营养袋每袋装有200克a坚果,100克b坚果,200克c坚果,甲、乙两种坚果营养袋每袋成本价均为袋中a、b、c三种坚果的成本价之和.已知b种坚果每100克的成本价为1元,乙种坚果营养袋每袋售价为5元,成本利润率为25%,甲种坚果营养袋每袋的成本利润率为,则这两种坚果营养袋的销售利润率为时,该商场销售甲、乙两种坚果营养袋的数量之比是.(已知:成本利润率=利润÷成本;销售利润率=利润÷售价)22、如图,周长为a的圆上有仅一点A在数轴上,点A所表示的数为1.该圆沿着数轴向右滚动一周后A对应的点为B,且滚动中恰好经过3个整数点(不包括A、B两点),则a的取值范围为______________.23、甲,乙,丙,丁,戊,六人,将在“学党史,讲党史”活动中进行演讲,要求每位演讲者只讲一次,并且在同一时间只有一位演讲者,三位演讲者在午餐前演讲,另三位演讲者在午餐后演讲,丙一定在午餐前演讲,仅有一位演讲者处在甲和乙之间,丁在第一位或在第三位发言.如果戊是第四位演讲者,那么第三位演讲者是.24、如图,∠MAB为锐角,AB=a,点B到射线AM的距离为d,点C在射线AM上,BC=x,若△ABC的形状、大小是唯一确定的,则x的取值范围是.25、因式分解:(a﹣2b)(a﹣2b﹣4)+4﹣c2=.26、已知:a>b>0,且a2+b2=ab,那么的值为.27、已知方程组的解是,老师让同学们解方程组,小聪先觉得这道题好象条件不够,后将方程组中的两个方程两边同除以5,整理得,运用换元思想,得,所以方程组的解为.现给出方程组的解是,请你写出方程组的解.三、解答题:1、(1)分解因式:y3-4y2+4y.(2)分解因式:x²(y²-1)+(1-y²)2、如图,BD是∠ABC的平分线,DE//CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.3、如图,AB∥CD,∠1=∠2,试说明∠E=∠FBC OPA3、已知,x ∶y ∶z =2∶3∶4,且xy +yz +xz =104,求2x 2+12y 2-9z 2的值.4、如图,O 为△ABC 中ABC ∠与ACB ∠的平分线的交点,分别过点B 、C 作BO PB ⊥,CO PC ⊥,若70=∠A °,你能够求出P ∠的度数吗?若能请写出解答过程。
【精品】07高等数学(下)期末复习题.doc

高等数学A C二丿期耒夏习題一.填空题1、 __________________________________________________________________________________ 设A = 2a + 3b,B = 3a-b, \a\ = 2,问= 4,(©%)=专,则A与直的夹角为____________________________ 。
2、过点(-1,4,3)H与直线兀-3 = * = 三平行的直线方程为________________________________ o3、方程兀2_4丁2+宓2=/儿当。
=0, b = 2;。
= 一4, & = -2;。
=0, b = 0时依次表示的曲面是__________________ ,________________ , __________________ O4、 ____________________________________________________ 设 /(%, y) = x + (y - l)arcsin ,则/Y(x,l)= , f y(0,1)=___________________________________________ 。
5、 _________________________________________________________________ 设u = x2 -xy + y2,花(1,1),I = (cos a, sin a),则%心= ____________________________________________ ,在 __________ 方向上,方向导数最大;在_____________ 方向上,方向导数有最小值;在______________ 方向上,方向导数为();grad M(/^)= _______________________ o6、 ____________________________________________________ 设x2 sin y-Jy\nz = 3,则乎= _ ,李=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学下册期末复习题二
班级: 姓名: 计分:
一、选择题(本题满分30分,共10小题,每小题3分)
1、下面有4个汽车标致图案,其中是轴对称图形的有( )
A .1个
B .2个
C .3个
D .4
2.已知1)2(3
2=+--y x a a 是一个二元一次方程,则a 的值为( ) A. 2± B. -2 C . 2 D. 无法确定 3.下列各式计算结果正确的是( )
A .2a a a =+
B .()2263a a =
C .()1122
+=+a a D .2a a a =⋅ 4.)()23)(23(=---b a b a
A .2269b ab a --
B .2296a ab b --
C .2249b a -
D .2294a b -
5.小亮解方程组 2212.x y x y +=⎧⎨-=⎩
●
的解为 5x y =⎧⎨=⎩,★,由于不小心滴上了两滴墨水,刚好遮住了两
个数●和★,则这两个数分别为( )
A .4和-6
B .-6和4
C .-2和8
D .8和-2 6.下面的多项式中,能因式分解的是( )
A .m 2+n
B .m 2-m +1
C .m 2-n
D .m 2-2m +1 7. ()a a m n 3·的计算结果是( ) A .a m n 3
+ B .a m n 3+ C .a m n 3()+ D .a mn 3 8.如图,下列条件中,不能判断直线l 1∥l 2的是( )
A.∠1=∠3
B.∠2=∠3
C.∠4=∠5
D.∠2+∠4=180°
9.如图,已知AB ∥CD ,直线l 分别交AB 、 CD 于点E 、F ,EG 平分∠BEF ,若∠EFG =40°,则∠EGF 的度数是( )
A .60°
B .70°
C .80°
D .90°
10.某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量如下表所示: 则这20户家庭该月用电量的众数和中位数分别是( )
A .180,160
B .160,180
C .160,160
D .180,180
二、 填空题(本题满分24分,共8小题,每小题3分) 11. 计算:8100×0.125100 =
12. 已知t 满足方程组323x t
y t
=-+⎧⎨=-⎩,则x 和y 之间满足的关系为 .
用电量
(千瓦·时
) 120
140
160 180 200 户数 2 3 6 7 2
13.分解因式:3a 2b +6ab 2= .
14.如图,两直线a 、b 被第三条直线c 所截,若∠1=50°,∠2=130°,则直线a 、b 的位置关 系是 .
15.如图,直线AB 、CD 相交于点O ,OE ⊥AB ,O 为垂足,如果∠EOD = 38°,则∠AOC = . 16.如图,AB ∥CD ,AC 与BD 相交于O 点,面积相等的两个三角形是 (
写一组就给满分).
(第14题图) (第15题图) (第16题图)
17.期中考试,小明语、数、英三科的平均分为85分,政、史、地三科的平均分为92分,生物99分,问七科的平均分是 .
18.有甲、乙、丙三种货物,若购甲3件,乙2件,丙1件,共需315元;若购甲4件,乙5件,丙6件,共需420元.问购甲、乙、丙各5件共需 元. 三.解答题(本题满分40分,共 5小题)
19.解方程组:(10分)
(1)⎩⎨⎧=+=-82332y x y x (2)⎪⎩
⎪⎨⎧=-+=+-=-+10
32425
2z y x z y x z y x
20.(8分)先化简再求值()()()()1x 3x 12x 12x 2x 2
-+-+--,其中x =-1.
21.(10分)分解因式:(1)2m ³n -8mn ³ (2)x 2-5x +6
3
2 1
c b
a
C
B
1
2
3
D G
A F
E
22.(6分)在网格上把三角形ABC向上平移8小格得到三角形A1B1C1,再作三角形A1B1C1关于直线MN的轴对称图形得到三角形A2B2C2。
并标明A1、B1、C1、和A2、B2、C2的位置.
23.(6分)如图所示,已知EF∥AD,∠1=∠2,∠BAC=68°,求∠AGD的度数。
请将括号内填上适当的条件。
解:因为EF∥AD ()
所以∠1=∠3 ()
又因为∠1=∠2 ()
所以∠2=∠3 ()
所以AB∥DG ()
所以∠BAC+∠AGD=180°()
又因为∠BAC=68°
所以∠AGD=112°
四、几何说理题(本题8分)
24.已知:如图,直线AB、CD被EF所截,若AB//CD,
试判断∠1与∠2的大小关系,并说明理由。
E
1
A B
3
C 2 D
F
五、应用题(本题8分)
25、如图所示的两架天平保持平衡,且每块巧克力的质量相等,•每个果冻的质量也相等,求一块巧克力的质量是多少克,一个果冻的质量是多少克?
六、综合题(本题10分)
26、本学期开学初,学校体育组对九年级某班50名学生进行了跳绳项目的测试,根据测试成绩制作了下面两个统计图。
根据统计图解答下列问题:
(1)本次测试的学生中,得4分的学生有多少人?
(2)本次测试的平均分是多少?
(3)通过一段时间的训练,体育组对该班学生的跳绳项目进行第二次测试,测得成绩的最低分为3分,且得4分和5分的人数共有45人,平均分比第一次提高了0.8分,问第二次测试中,得4分、5分的学生分别有多少人?。
