2020-2021初中数学二次函数经典测试题
2020-2021中考数学二次函数综合练习题及详细答案
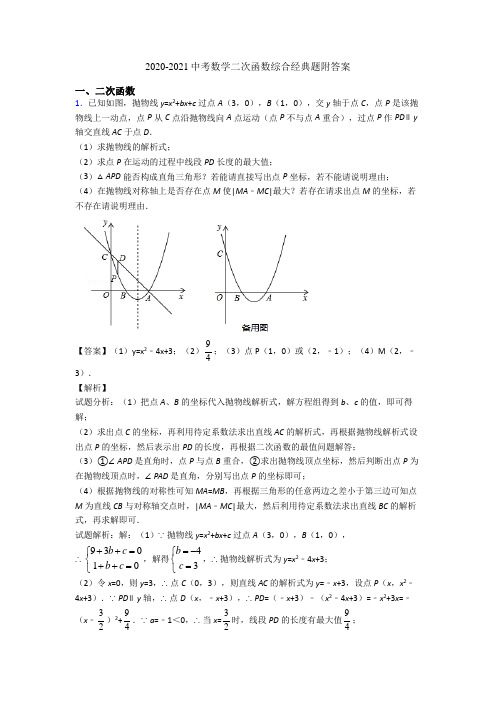
2020-2021中考数学二次函数综合练习题及详细答案一、二次函数1．新春佳节，电子鞭炮因其安全、无污染开始走俏．某商店经销一种电子鞭炮，已知这种电子鞭炮的成本价为每盒80元，市场调查发现，该种电子鞭炮每天的销售量y （盒）与销售单价x （元）有如下关系：y=﹣2x+320（80≤x≤160）．设这种电子鞭炮每天的销售利润为w 元．（1）求w 与x 之间的函数关系式；（2）该种电子鞭炮销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？ （3）该商店销售这种电子鞭炮要想每天获得2400元的销售利润，又想卖得快．那么销售单价应定为多少元？【答案】（1）w=﹣2x 2+480x ﹣25600；（2）销售单价定为120元时，每天销售利润最大，最大销售利润3200元（3）销售单价应定为100元 【解析】 【分析】 （1）用每件的利润()80x -乘以销售量即可得到每天的销售利润，即()()()80802320w x y x x =-=--+， 然后化为一般式即可；（2）把（1）中的解析式进行配方得到顶点式()221203200w x =--+，然后根据二次函数的最值问题求解；（3）求2400w =所对应的自变量的值，即解方程()2212032002400x --+=．然后检验即可. 【详解】（1）()()()80802320w x y x x =-=--+， 2248025600x x =-+-，w 与x 的函数关系式为：2248025600w x x =-+-； （2）()2224802560021203200w x x x =-+-=--+， 2080160x -<≤≤Q ，，∴当120x =时，w 有最大值．w 最大值为3200．答：销售单价定为120元时，每天销售利润最大，最大销售利润3200元． （3）当2400w =时，()2212032002400x --+=． 解得：12100140x x ，．== ∵想卖得快，2140x ∴=不符合题意，应舍去．答：销售单价应定为100元．2．某厂家生产一种新型电子产品，制造时每件的成本为40元，通过试销发现，销售量(y 万件)与销售单价(x 元)之间符合一次函数关系，其图象如图所示．()1求y 与x 的函数关系式；()2物价部门规定：这种电子产品销售单价不得超过每件80元，那么，当销售单价x 定为每件多少元时，厂家每月获得的利润()w 最大？最大利润是多少？【答案】（1）2280y x =-+；（2）当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元． 【解析】 【分析】()1根据函数图象经过点()40,200和点()60,160，利用待定系数法即可求出y 与x 的函数关系式；()2先根据利润=销售数量(⨯销售单价-成本)，由试销期间销售单价不低于成本单价，也不高于每千克80元，结合电子产品的成本价即可得出x 的取值范围，根据二次函数的增减性可得最值． 【详解】解：()1设y 与x 的函数关系式为()0y kx b k =+≠，Q 函数图象经过点()40,200和点()60,160，{4020060160k b k b +=∴+=，解得：{2280k b =-=，y ∴与x 的函数关系式为2280y x =-+．()2由题意得：()()224022802360112002(90)5000w x x x x x =--+=-+-=--+．Q 试销期间销售单价不低于成本单价，也不高于每千克80元，且电子产品的成本为每千克40元，∴自变量x 的取值范围是4080x ≤≤．20-<Q ，∴当90x <时，w 随x 的增大而增大， 80x ∴=时，w 有最大值，当80x =时，4800w =，答：当销售单价x 定为每件80元时，厂家每月获得的利润()w 最大，最大利润是4800元． 【点睛】本题考查了一次函数和二次函数的应用，根据点的坐标利用待定系数法求出函数关系式是解题的关键，并注意最值的求法．3．如图，直线y ＝-12x-3与x 轴，y 轴分别交于点A ，C ，经过点A ，C 的抛物线y ＝ax 2+bx ﹣3与x 轴的另一个交点为点B(2，0)，点D 是抛物线上一点，过点D 作DE ⊥x 轴于点E ，连接AD ，DC ．设点D 的横坐标为m ． (1)求抛物线的解析式；(2)当点D 在第三象限，设△DAC 的面积为S ，求S 与m 的函数关系式，并求出S 的最大值及此时点D 的坐标；(3)连接BC ，若∠EAD ＝∠OBC ，请直接写出此时点D 的坐标．【答案】(1)y ＝14x 2+x ﹣3；(2)S △ADC =﹣34(m+3)2+274；△ADC 的面积最大值为274；此时D(﹣3，﹣154)；(3)满足条件的点D 坐标为(﹣4，﹣3)或(8，21). 【解析】 【分析】（1）求出A 坐标，再用待定系数法求解析式；（2）设DE 与AC 的交点为点F.设点D 的坐标为：(m ，14m 2+m ﹣3)，则点F 的坐标为：(m ，﹣12m ﹣3)，根据S △ADC ＝S △ADF +S △DFC 求出解析式，再求最值；（3）①当点D 与点C 关于对称轴对称时，D(﹣4，﹣3)，根据对称性此时∠EAD ＝∠ABC ．②作点D(﹣4，﹣3)关于x 轴的对称点D′(﹣4，3)，直线AD′的解析式为y ＝32x+9，解方程组求出函数图像交点坐标. 【详解】解：(1)在y ＝﹣12x ﹣3中，当y ＝0时，x ＝﹣6， 即点A 的坐标为：(﹣6，0)，将A(﹣6，0)，B(2，0)代入y ＝ax 2+bx ﹣3得：366304230a b a b --=⎧⎨+-=⎩， 解得：141a b ⎧=⎪⎨⎪=⎩，∴抛物线的解析式为：y ＝14x 2+x ﹣3； (2)设点D 的坐标为：(m ，14m 2+m ﹣3)，则点F 的坐标为：(m ，﹣12m ﹣3)， 设DE 与AC 的交点为点F.∴DF ＝﹣12m ﹣3﹣(14m 2+m ﹣3)＝﹣14m 2﹣32m ， ∴S △ADC ＝S △ADF +S △DFC＝12DF•AE+12•DF•OE ＝12DF•OA ＝12×(﹣14m 2﹣32m)×6 ＝﹣34m 2﹣92m ＝﹣34(m+3)2+274，∵a ＝﹣34＜0， ∴抛物线开口向下，∴当m ＝﹣3时，S △ADC 存在最大值274， 又∵当m ＝﹣3时，14m 2+m ﹣3＝﹣154，∴存在点D(﹣3，﹣154)，使得△ADC 的面积最大，最大值为274； (3)①当点D 与点C 关于对称轴对称时，D(﹣4，﹣3)，根据对称性此时∠EAD ＝∠ABC ． ②作点D(﹣4，﹣3)关于x 轴的对称点D′(﹣4，3)，直线AD′的解析式为y＝3 2x+9，由2392134y xy x x⎧=+⎪⎪⎨⎪=+-⎪⎩，解得6xy=-⎧⎨=⎩或821xy=⎧⎨=⎩，此时直线AD′与抛物线交于D(8，21)，满足条件，综上所述，满足条件的点D坐标为(﹣4，﹣3)或(8，21)【点睛】本题属于二次函数综合题，考查了待定系数法，一次函数的应用，二次函数的性质等知识，解题的关键是学会构建二次函数解决最值问题，学会构建一次函数解决实际问题，属于中考压轴题．.4．如图，抛物线y＝﹣x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，3），点D是抛物线的顶点，过点D作x轴的垂线，垂足为E，连接DB．（1）求此抛物线的解析式及顶点D的坐标；（2）点M是抛物线上的动点，设点M的横坐标为m．①当∠MBA＝∠BDE时，求点M的坐标；②过点M作MN∥x轴，与抛物线交于点N，P为x轴上一点，连接PM，PN，将△PMN 沿着MN翻折，得△QMN，若四边形MPNQ恰好为正方形，直接写出m的值．【答案】（1）（1，4）（2）①点M坐标（﹣12，74）或（﹣32，﹣94）；②m的值为3172±或1172±【解析】【分析】（1）利用待定系数法即可解决问题；（2）①根据tan∠MBA=2233m mMGBG m-++=-，tan∠BDE=BEDE=12，由∠MBA=∠BDE，构建方程即可解决问题；②因为点M、N关于抛物线的对称轴对称，四边形MPNQ是正方形，推出点P是抛物线的对称轴与x轴的交点，即OP=1，易证GM=GP，即|-m2+2m+3|=|1-m|，解方程即可解决问题.【详解】（1）把点B（3，0），C（0，3）代入y=﹣x2+bx+c，得到930{3b cc-++==，解得2{3bc==，∴抛物线的解析式为y=﹣x2+2x+3，∵y=﹣x2+2x﹣1+1+3=﹣（x﹣1）2+4，∴顶点D坐标（1，4）；（2）①作MG⊥x轴于G，连接BM．则∠MGB=90°，设M（m，﹣m2+2m+3），∴MG=|﹣m2+2m+3|，BG=3﹣m，∴tan∠MBA=2233m mMGBG m-++=-，∵DE⊥x轴，D（1，4），∴∠DEB=90°，DE=4，OE=1，∵B（3，0），∴BE=2，∴tan∠BDE=BEDE =12，∵∠MBA=∠BDE，∴2233m mm-++-=12，当点M在x轴上方时，2233m mm-++-=12，解得m=﹣12或3（舍弃）， ∴M （﹣12，74）， 当点M 在x 轴下方时，2233m m m--- =12， 解得m=﹣32或m=3（舍弃）， ∴点M （﹣32，﹣94）， 综上所述，满足条件的点M 坐标（﹣12，74）或（﹣32，﹣94）； ②如图中，∵MN ∥x 轴，∴点M 、N 关于抛物线的对称轴对称， ∵四边形MPNQ 是正方形，∴点P 是抛物线的对称轴与x 轴的交点，即OP=1， 易证GM=GP ，即|﹣m 2+2m+3|=|1﹣m|， 当﹣m 2+2m+3=1﹣m 时，解得317±， 当﹣m 2+2m+3=m ﹣1时，解得117± ∴满足条件的m 317±或1172±. 【点睛】本题考查二次函数综合题、锐角三角函数、正方形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．5．如图1，已知抛物线y ＝ax 2+bx+3(a≠0)与x 轴交于点A(1，0)和点B(﹣3，0)，与y 轴交于点C ．(1)求抛物线的解析式；(2)设抛物线的对称轴与x 轴交于点M ，问在对称轴上是否存在点P ，使△CMP 为等腰三角形？若存在，请直接写出所有符合条件的点P 的坐标；若不存在，请说明理由．(3)在(1)中抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由．(4)如图2，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．【答案】（1）y＝﹣x2﹣2x+3；（2）存在符合条件的点P，其坐标为P（﹣1，10）或P（﹣1，﹣10）或P（﹣1，6）或P（﹣1，53）；（3）存在，Q（﹣1，2）；（4）63 8，315,24E⎛⎫-⎪⎝⎭.【解析】【分析】（1）已知抛物线过A、B两点，可将两点的坐标代入抛物线的解析式中，用待定系数法即可求出二次函数的解析式；（2）可根据（1）的函数解析式得出抛物线的对称轴，也就得出了M点的坐标，由于C是抛物线与y轴的交点，因此C的坐标为（0，3），根据M、C的坐标可求出CM的距离．然后分三种情况进行讨论：①当CP＝PM时，P位于CM的垂直平分线上．求P点坐标关键是求P的纵坐标，过P作PQ⊥y轴于Q，如果设PM＝CP＝x，那么直角三角形CPQ中CP＝x，OM的长，可根据M 的坐标得出，CQ＝3﹣x，因此可根据勾股定理求出x的值，P点的横坐标与M的横坐标相同，纵坐标为x，由此可得出P的坐标．②当CM＝MP时，根据CM的长即可求出P的纵坐标，也就得出了P的坐标（要注意分上下两点）．③当CM＝C P时，因为C的坐标为（0，3），那么直线y＝3必垂直平分PM，因此P的纵坐标是6，由此可得出P的坐标；（3）根据轴对称﹣最短路径问题解答；（4）由于四边形BOCE不是规则的四边形，因此可将四边形BOCE分割成规则的图形进行计算，过E作EF⊥x轴于F，S四边形BOCE＝S△BFE+S梯形FOCE．直角梯形FOCE中，FO为E的横坐标的绝对值，EF为E的纵坐标，已知C的纵坐标，就知道了OC的长．在△BFE中，BF＝BO﹣OF，因此可用E的横坐标表示出BF的长．如果根据抛物线设出E的坐标，然后代入上面的线段中，即可得出关于四边形BOCE的面积与E的横坐标的函数关系式，根据函数的性质即可求得四边形BOCE的最大值及对应的E的横坐标的值．即可求出此时E的坐标． 【详解】（1）∵抛物线y ＝ax 2+bx+3（a≠0）与x 轴交于点A （1，0）和点B （﹣3，0），∴309330a b a b ++=⎧⎨-+=⎩，解得：12a b =-⎧⎨=-⎩．∴所求抛物线解析式为：y ＝﹣x 2﹣2x+3； （2）如答图1，∵抛物线解析式为：y ＝﹣x 2﹣2x+3， ∴其对称轴为x ＝22-＝﹣1， ∴设P 点坐标为（﹣1，a ），当x ＝0时，y ＝3， ∴C （0，3），M （﹣1，0）∴当CP ＝PM 时，（﹣1）2+（3﹣a ）2＝a 2，解得a ＝53， ∴P 点坐标为：P 1（﹣1，53）； ∴当CM ＝PM 时，（﹣1）2+32＝a 2，解得a ＝±10， ∴P 点坐标为：P 2（﹣110）或P 3（﹣110）；∴当CM ＝CP 时，由勾股定理得：（﹣1）2+32＝（﹣1）2+（3﹣a ）2，解得a ＝6， ∴P 点坐标为：P 4（﹣1，6）．综上所述存在符合条件的点P ，其坐标为P （﹣110）或P （﹣110）或P （﹣1，6）或P （﹣1，53）； （3）存在，Q （﹣1，2），理由如下：如答图2，点C （0，3）关于对称轴x ＝﹣1的对称点C′的坐标是（﹣2，3），连接AC′，直线AC′与对称轴的交点即为点Q ．设直线AC′函数关系式为：y＝kx+t（k≠0）．将点A（1，0），C′（﹣2，3）代入，得23 k tk t+=⎧⎨-+=⎩，解得11kt=-⎧⎨=⎩，所以，直线AC′函数关系式为：y＝﹣x+1．将x＝﹣1代入，得y＝2，即：Q（﹣1，2）；（4）过点E作EF⊥x轴于点F，设E（a，﹣a2﹣2a+3）（﹣3＜a＜0）∴EF＝﹣a2﹣2a+3，BF＝a+3，OF＝﹣a∴S四边形BOCE＝12BF•EF+12（OC+EF）•OF＝12（a+3）•（﹣a2﹣2a+3）+12（﹣a2﹣2a+6）•（﹣a）＝﹣32a2﹣92a+92＝﹣32（a+32）2+638，∴当a＝﹣32时，S四边形BOCE最大，且最大值为638．此时，点E坐标为（﹣32，154）．【点睛】本题主要考查了二次函数的综合知识，要注意的是（2）中，不确定等腰三角形哪条边是底边的情况下，要分类进行求解，不要漏解．6．如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B．抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）如图1，设抛物线顶点为M，且M的坐标是（12，92），对称轴交AB于点N．①求抛物线的解析式；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由．【答案】（1）①y＝﹣2x2+2x+4；；②不存在点P，使四边形MNPD为菱形；；（2）存在，点D的坐标是（1，4）．【解析】【分析】（1）①由一次函数图象上点的坐标特征求得点B的坐标，设抛物线解析式为y＝a21922x⎛⎫-+⎪⎝⎭，把点B的坐标代入求得a的值即可；②不存在点P，使四边形MNPD为菱形．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），根据题意知PD∥MN，所以当PD＝MN时，四边形MNPD为平行四边形，根据该等量关系列出方程﹣2m2+4m＝32，通过解方程求得m的值，易得点N、P的坐标，然后推知PN＝MN是否成立即可；（2）设点D的坐标是（n，﹣2n2+2n+4），P（n，﹣2n+4）．根据S四边形BOAD＝S△BOA+S△ABD ＝4+S△ABD，则当S△ABD取最大值时，S四边形BOAD最大．根据三角形的面积公式得到函数S△ABD＝﹣2（n﹣1）2+2．由二次函数的性质求得最值．【详解】解：①如图1，∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭，∴设抛物线解析式为y＝21922a x⎛⎫-+⎪⎝⎭（a≠0）．∵直线y＝﹣2x+4交y轴于点B，∴点B的坐标是（0，4）．又∵点B在该抛物线上，∴21922a⎛⎫-+⎪⎝⎭＝4，解得a＝﹣2．故该抛物线的解析式为：y＝219222x⎛⎫--+⎪⎝⎭＝﹣2x2+2x+4；②不存在．理由如下：∵抛物线y＝219222x⎛⎫--+⎪⎝⎭的对称轴是直线x＝12，且该直线与直线AB交于点N，∴点N的坐标是1,32⎛⎫ ⎪⎝⎭．∴93322MN=-=．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），∴PD＝（﹣2m2+2m+4）﹣（﹣2m+4）＝﹣2m2+4m．∵PD∥MN．当PD＝MN时，四边形MNPD是平行四边形，即﹣2m2+4m＝32．解得 m1＝12（舍去），m2＝32．此时P（32，1）．∵PN∴PN≠MN，∴平行四边形MNPD不是菱形．∴不存在点P，使四边形MNPD为菱形；（2）存在，理由如下：设点D的坐标是（n，﹣2n2+2n+4），∵点P在线段AB上且直线PD⊥x轴，∴P（n，﹣2n+4）．由图可知S四边形BOAD＝S△BOA+S△ABD．其中S△BOA＝12OB•OA＝12×4×2＝4．则当S△ABD取最大值时，S四边形BOAD最大．S△ABD＝12（y D﹣y P）（x A﹣x B）＝y D﹣y P＝﹣2n2+2n+4﹣（﹣2n+4）＝﹣2n2+4n＝﹣2（n﹣1）2+2．当n＝1时，S△ABD取得最大值2，S四边形BOAD有最大值．此时点D的坐标是（1，4）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．7．如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．（1）求这个二次函数的解析式；（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P 的坐标，并求出△POB的面积；若不存在，请说明理由．【答案】（1）y=x2﹣3x。
2020-2021初中数学二次函数经典测试题附答案
其顶点坐标为（0，a2），与图
根据顶点坐标有a2=3，由抛
若二次函数的图形为第一个，则
若二次函数的图形为第二个，则
它们相矛盾；若二次函数的图形为第三个，把a=-1；若二次函数的图形为第四个，把（-2，0）
【详解】解：若二次函数的图形为第一个，对称轴为a2），而a2>0，所以二次函数的图形不能为第一个；若二次函数的图形为第二个，对称轴为y轴，则b=0，y=ax2+a2，a2=3，而当y=0时，x2=-a，所以- a=4，a=-4，所以二次函数的图形不能为第二个；若二次函数的图形为第三个，令x=-1，y=0，则a-b+a2+b=0，所以a=-1；若二次函数的图形为第四个，令x=0，y=0，则a2+b=0①；令x=-2，y=0，则4a-2b+a2+b=0② ，由①②得a=-2，这与图象开口向上不符合，所以二次函数的图形不能为第四个.
【答案】D
【解析】
【分析】
将二次函数解析式展开，结合二次函数的性质找出两二次函数的对称轴，二者做差后即可 得出平移方向及距离．
【详解】
解：∵y＝m（x＋3）（x＋9）＝mx2＋12 mx＋27m，y＝n（x－2）（x－6）＝nx2－8 nx＋12n，
∴二次函数y＝m（x＋3）（x＋9）的对称轴为直线x＝－6，二次函数y＝n（x－2）（x－6）的对称轴为直线x＝4，
2若该函数图象的对称轴为直线x x0，则必有0 x01；
3当x 时，y随x的增大而增大；
④若P 4,y1，Q 4 m,y2m 0是函数图象上的两点，如果y1y2总成立，则1
2020-2021中考数学二次函数综合经典题附答案解析
2020-2021中考数学二次函数综合经典题附答案解析一、二次函数1．已知二次函数223y ax ax =-+的最大值为4，且该抛物线与y 轴的交点为C ，顶点为D .（1）求该二次函数的解析式及点C ，D 的坐标；（2）点(,0)P t 是x 轴上的动点，①求PC PD -的最大值及对应的点P 的坐标；②设(0,2)Q t 是y 轴上的动点，若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点，求t 的取值范围.【答案】（1）2y x 2x 3=-++，C 点坐标为(0,3)，顶点D 的坐标为(1,4)；（2）①最，P 的坐标为(3,0)-，②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】（1）先利用对称轴公式x=2a 12a--=，计算对称轴，即顶点坐标为（1，4），再将两点代入列二元一次方程组求出解析式；（2）根据三角形的三边关系：可知P 、C 、D 三点共线时|PC-PD|取得最大值，求出直线CD 与x 轴的交点坐标，就是此时点P 的坐标；（3）先把函数中的绝对值化去，可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩，此函数是两个二次函数的一部分，分三种情况进行计算：①当线段PQ 过点（0，3），即点Q 与点C 重合时，两图象有一个公共点，当线段PQ 过点（3，0），即点P 与点（3，0）重合时，两函数有两个公共点，写出t 的取值；②线段PQ 与当函数y=a|x|2-2a|x|+c （x≥0）时有一个公共点时，求t 的值；③当线段PQ 过点（-3，0），即点P 与点（-3，0）重合时，线段PQ 与当函数y=a|x|2-2a|x|+c （x ＜0）时也有一个公共点，则当t≤-3时，都满足条件；综合以上结论，得出t 的取值．【详解】解：（1）∵2a x 12a-=-=， ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4，∴抛物线过点()1,4.得a 2a 34-+=，解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3，顶点D 的坐标为()1,4.（2）①∵PC PD CD -≤，∴当P,C,D 三点在一条直线上时，PC PD -取得最大值.连接DC 并延长交y 轴于点P ，PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入，得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+，将()P t,0，()Q 0,2t 的坐标代入，可得线段PQ 所在直线的方程为y 2x 2t =-+.（1）当线段PQ 过点()3,0-，即点P 与点()3,0-重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时t 3=-. ∴当t 3≤-时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （2）当线段PQ 过点()0,3，即点Q 与点C 重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时3t 2=. 当线段PQ 过点()3,0，即点P 与点()3,0重合时，t 3=，此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （3）将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥，并整理，得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=，解得7t 2=. ∴当7t 2=时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述，t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】 本题考查了二次函数的综合应用，先利用待定系数法求解析式，同时把最大值与三角形的三边关系联系在一起；同时对于二次函数利用动点求取值问题，从特殊点入手，把函数分成几部分考虑，按自变量从大到小的顺序或从小到大的顺序求解．2．如图，抛物线y ＝ax 2+bx +3（a ≠0）的对称轴为直线x ＝﹣1，抛物线交x 轴于A 、C 两点，与直线y ＝x ﹣1交于A 、B 两点，直线AB 与抛物线的对称轴交于点E ．（1）求抛物线的解析式．（2）点P 在直线AB 上方的抛物线上运动，若△ABP 的面积最大，求此时点P 的坐标． （3）在平面直角坐标系中，以点B 、E 、C 、D 为顶点的四边形是平行四边形，请直接写出符合条件点D 的坐标．【答案】(1)y ＝﹣x 2﹣2x+3；(2)点P(32-，154)；(3)符合条件的点D 的坐标为D 1(0，3)，D 2(﹣6，﹣3)，D 3(﹣2，﹣7)．【解析】【分析】 (1)令y ＝0，求出点A 的坐标，根据抛物线的对称轴是x ＝﹣1，求出点C 的坐标，再根据待定系数法求出抛物线的解析式即可；(2)设点P(m ，﹣m 2﹣2m+3)，利用抛物线与直线相交，求出点B 的坐标，过点P 作PF ∥y 轴交直线AB 于点F ，利用S △ABP ＝S △PBF +S △PFA ，用含m 的式子表示出△ABP 的面积，利用二次函数的最大值，即可求得点P 的坐标；(3)求出点E 的坐标，然后求出直线BC 、直线BE 、直线CE 的解析式，再根据以点B 、E 、C 、D 为顶点的四边形是平行四边形，得到直线D 1D 2、直线D 1D 3、直线D 2D 3的解析式，即可求出交点坐标．【详解】解：(1)令y ＝0，可得：x ﹣1＝0，解得：x ＝1，∴点A(1，0)，∵抛物线y ＝ax 2+bx+3(a≠0)的对称轴为直线x ＝﹣1，∴﹣1×2﹣1＝﹣3，即点C(﹣3，0)，∴309330a b a b ++⎧⎨-+⎩＝＝ ，解得：12a b -⎧⎨-⎩＝，＝∴抛物线的解析式为：y ＝﹣x 2﹣2x+3；(2)∵点P 在直线AB 上方的抛物线上运动，∴设点P(m ，﹣m 2﹣2m+3)，∵抛物线与直线y ＝x ﹣1交于A 、B 两点，∴2231y x x y x ⎧--+⎨-⎩＝＝ ，解得：1145x y -⎧⎨-⎩＝＝，2210x y ＝，＝⎧⎨⎩ ∴点B(﹣4，﹣5)，如图，过点P 作PF ∥y 轴交直线AB 于点F ， 则点F(m ，m ﹣1)，∴PF ＝﹣m 2﹣2m+3﹣m+1＝﹣m 2﹣3m+4，∴S △ABP ＝S △PBF +S △PFA ＝12(﹣m 2﹣3m+4)(m+4)+12(﹣m 2﹣3m+4)(1﹣m) ＝-52（m+32 ）2+ 1258， ∴当m ＝32-时，P 最大， ∴点P(32-，154). (3)当x ＝﹣1时，y ＝﹣1﹣1＝﹣2，∴点E(﹣1，﹣2)，如图，直线BC 的解析式为y ＝5x+15，直线BE 的解析式为y ＝x ﹣1，直线CE 的解析式为y ＝﹣x ﹣3，∵以点B 、C 、E 、D 为顶点的四边形是平行四边形，∴直线D 1D 3的解析式为y ＝5x+3，直线D 1D 2的解析式为y ＝x+3，直线D 2D 3的解析式为y ＝﹣x ﹣9，联立533y x y x +⎧⎨+⎩＝＝ 得D 1(0，3)， 同理可得D 2(﹣6，﹣3)，D 3(﹣2，﹣7)，综上所述，符合条件的点D 的坐标为D 1(0，3)，D 2(﹣6，﹣3)，D 3(﹣2，﹣7)．【点睛】本题考查二次函数的综合应用，解决第(2)小题中三角形面积的问题时，找到一条平行或垂直于坐标轴的边是关键；对于第(3)小题，要注意分类讨论、数形结合的运用，不要漏解．3．已知，点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，直线y＝mx+5分别交x轴正半轴，y轴于点A，B．（1）判断顶点M是否在直线y＝4x+1上，并说明理由．（2）如图1，若二次函数图象也经过点A，B，且mx+5＞﹣（x﹣b）2+4b+1，根据图象，写出x的取值范围．（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（14，y1），D（34，y2）都在二次函数图象上，试比较y1与y2的大小．【答案】（1）点M在直线y＝4x+1上；理由见解析；（2）x的取值范围是x＜0或x＞5；（3）①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【解析】【分析】（1）根据顶点式解析式，可得顶点坐标，根据点的坐标代入函数解析式检验，可得答案；（2）根据待定系数法，可得二次函数的解析式，根据函数图象与不等式的关系：图象在下方的函数值小，可得答案；（3）根据解方程组，可得顶点M的纵坐标的范围，根据二次函数的性质，可得答案．【详解】（1）点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，∴M的坐标是（b，4b+1），把x＝b代入y＝4x+1，得y＝4b+1，∴点M在直线y＝4x+1上；（2）如图1，直线y＝mx+5交y轴于点B，∴B点坐标为（0，5）又B在抛物线上，∴5＝﹣（0﹣b）2+4b+1＝5，解得b＝2，二次函数的解析是为y＝﹣（x﹣2）2+9，当y＝0时，﹣（x﹣2）2+9＝0，解得x1＝5，x2＝﹣1，∴A（5，0）．由图象，得当mx+5＞﹣（x﹣b）2+4b+1时，x的取值范围是x＜0或x＞5；（3）如图2，∵直线y＝4x+1与直线AB交于点E，与y轴交于F，A（5，0），B（0，5）得直线AB的解析式为y＝﹣x+5，联立EF，AB得方程组415 y xy x=+⎧⎨=-+⎩，解得45215xy⎧=⎪⎪⎨⎪=⎪⎩，∴点E（45，215），F（0，1）．点M在△AOB内，1＜4b+1＜215，∴0＜b＜45．当点C，D关于抛物线的对称轴对称时，b﹣14＝34﹣b，∴b＝12，且二次函数图象开口向下，顶点M在直线y＝4x+1上，综上：①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【点睛】本题考查了二次函数综合题，解（1）的关键是把点的坐标代入函数解析式检验；解（2）的关键是利用函数图不等式的关系：图象在上方的函数值大；解（3）的关键是解方程组得出顶点M的纵坐标的范围，又利用了二次函数的性质：a＜0时，点与对称轴的距离越小函数值越大．4．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x2+2x+3；直线AC的解析式为y=3x+3；（2）点M的坐标为（0，3）；（3）符合条件的点P的坐标为（73，209）或（103，﹣139），【解析】分析：（1）设交点式y=a（x+1）（x-3），展开得到-2a=2，然后求出a即可得到抛物线解析式；再确定C（0，3），然后利用待定系数法求直线AC的解析式；（2）利用二次函数的性质确定D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（-3，0），利用两点之间线段最短可判断此时MB+MD的值最小，则此时△BDM的周长最小，然后求出直线DB′的解析式即可得到点M的坐标；（3）过点C作AC的垂线交抛物线于另一点P，如图2，利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b，把C点坐标代入求出b得到直线PC的解析式为y=-13x+3，再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝得此时P点坐标；当过点A作AC的垂线交抛物线于另一点P时，利用同样的方法可求出此时P点坐标．详解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3；（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），∵MB=MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝，解得3xy=⎧⎨=⎩或73209xy⎧=⎪⎪⎨⎪=⎪⎩，则此时P点坐标为（73，209）；过点A作AC的垂线交抛物线于另一点P，直线PC的解析式可设为y=﹣x+b，把A（﹣1，0）代入得13+b=0，解得b=﹣13，∴直线PC的解析式为y=﹣13x﹣13，解方程组2231133y x xy x⎧-++⎪⎨--⎪⎩＝＝，解得1xy=-⎧⎨=⎩或103139xy⎧=⎪⎪⎨⎪=-⎪⎩，则此时P点坐标为（103，﹣139）.综上所述，符合条件的点P的坐标为（73，209）或（103，﹣139）.点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式，理解两直线垂直时一次项系数的关系，通过解方程组求把两函数的交点坐标；理解坐标与图形性质，会运用两点之间线段最短解决最短路径问题；会运用分类讨论的思想解决数学问题．5．如图，直线l：y＝﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y＝ax2﹣2ax+a+4（a＜0）经过点B，交x轴正半轴于点C．（1）求该抛物线的函数表达式；（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M 的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值及此时动点M的坐标；（3）将点A绕原点旋转得点A′，连接CA′、BA′，在旋转过程中，一动点M从点B出发，沿线段BA′以每秒3个单位的速度运动到A′，再沿线段A′C以每秒1个单位长度的速度运动到C后停止，求点M在整个运动过程中用时最少是多少？【答案】（1）y＝﹣x2+2x+3；（2）S与m的函数表达式是S＝252m m--，S的最大值是25 8，此时动点M的坐标是（52，74）；（3）点M在整个运动过程中用时最少是823秒．【解析】【分析】（1）首先求出B点的坐标，根据B点的坐标即可计算出二次函数的a值，进而即可计算出二次函数的解析式;（2）计算出C点的坐标，设出M点的坐标，再根据△ABM的面积为S＝S四边形OAMB﹣S△AOB ＝S△BOM+S△OAM﹣S△AOB，化简成二次函数，再根据二次函数求解最大值即可.（3）首先证明△OHA′∽△OA′B，再结合A′H+A′C≥HC即可计算出t的最小值.【详解】（1）将x＝0代入y＝﹣3x+3，得y＝3，∴点B的坐标为（0，3），∵抛物线y＝ax2﹣2ax+a+4（a＜0）经过点B，∴3＝a+4，得a＝﹣1，∴抛物线的解析式为：y＝﹣x2+2x+3；（2）将y＝0代入y＝﹣x2+2x+3，得x1＝﹣1，x2＝3，∴点C的坐标为（3，0），∵点M是抛物线上的一个动点，并且点M在第一象限内，点M的横坐标为m，∴0＜m ＜3，点M 的坐标为（m ，﹣m 2+2m +3）， 将y ＝0代入y ＝﹣3x +3，得x ＝1， ∴点A 的坐标（1，0）， ∵△ABM 的面积为S ，∴S ＝S 四边形OAMB ﹣S △AOB ＝S △BOM +S △OAM ﹣S △AOB ＝()2123313222m m m ⨯-++⨯⨯+-， 化简，得S ＝252m m --＝21525228m ⎛⎫--+ ⎪⎝⎭，∴当m ＝52时，S 取得最大值，此时S ＝258，此时点M 的坐标为（52，74）， 即S 与m 的函数表达式是S ＝252m m--，S 的最大值是258，此时动点M 的坐标是（52，74）； （3）如右图所示，取点H 的坐标为（0，13），连接HA ′、OA ′， ∵∠HOA ′＝∠A ′OB ，13OH OA '=，13OA OB '=， ∴△OHA ′∽△OA ′B ，∴3BA A H''=， 即3BA A H ''=，∵A ′H +A ′C ≥HC ＝22182333⎛⎫+= ⎪⎝⎭， ∴t ≥823， 即点M 在整个运动过程中用时最少是82秒．【点睛】本题主要考查抛物线的性质，关键在于设元，还有就是（3）中利用代替法计算t的取值范围，难度系数较大，是中考的压轴题.6．如图，抛物线y＝ax2＋bx（a≠0）过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C的坐标，并求出△ABC的面积；（3）点P是抛物线上一动点，且位于第四象限，是否存在这样的点P，使得△ABP的面积为△ABC面积的2倍？若存在，求出点P的坐标，若不存在，请说明理由；（4）若点M在直线BH上运动，点N在x轴正半轴上运动，当以点C，M，N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．【答案】（1）y＝－x2＋4x；（2）C（3，3），面积为3；（3）P的坐标为（5，－5）；（4）52或5．【解析】试题分析：（1）利用待定系数法进行求解即可；（2）先求出抛物线的对称轴，利用对称性即可写出点C的坐标，利用三角形面积公式即可求面积；（3）利用三角形的面积以及点P所处象限的特点即可求；（4）分情况进行讨论，确定点M、N，然后三角形的面积公式即可求.试题解析：（1）将A（4，0），B（1，3）代入到y＝ax2＋bx中，得16403a ba b+=⎧⎨+=⎩，解得14ab=-⎧⎨=⎩，∴抛物线的表达式为y＝－x2＋4x．（2）∵抛物线的表达式为y＝－x2＋4x，∴抛物线的对称轴为直线x＝2．又C，B关于对称轴对称，∴C（3，3）．∴BC＝2，∴S△ABC＝12×2×3＝3．（3）存在点P．作PQ⊥BH于点Q，设P（m，－m2＋4m）．∵S△ABP＝2S△ABC，S△ABC＝3，∴S△ABP＝6．∵S△ABP＋S△BPQ＝S△ABH＋S梯形AHQP∴6＋12×（m－1）×（3＋m2－4m）＝12×3×3＋12×（3＋m－1）（m2－4m）整理得m2－5m＝0，解得m1＝0（舍），m2＝5，∴点P的坐标为（5，－5）．（4）52或5．提示：①当以M为直角顶点，则S△CMN＝52；②当以N为直角顶点，S△CMN＝5；③当以C为直角顶点时，此种情况不存在．【点睛】本题是二次函数的综合题，主要考查待定系数法求解析式，三角形面积、直角三角形的判定等，能正确地根据题意确定图形，分情况进行讨论是解题的关键.7．如图甲，直线y=﹣x+3与x轴、y轴分别交于点B、点C，经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A，顶点为P．（1）求该抛物线的解析式；（2）在该抛物线的对称轴上是否存在点M，使以C，P，M为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M的坐标；若不存在，请说明理由；（3）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值（图乙、丙供画图探究）．【答案】（1）y=x2﹣4x+3；（2）（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）E点坐标为（，）时，△CBE的面积最大．【解析】试题分析：（1）由直线解析式可求得B、C坐标，利用待定系数法可求得抛物线解析式；（2）由抛物线解析式可求得P点坐标及对称轴，可设出M点坐标，表示出MC、MP和PC 的长，分MC=MP、MC=PC和MP=PC三种情况，可分别得到关于M点坐标的方程，可求得M点的坐标；（3）过E作EF⊥x轴，交直线BC于点F，交x轴于点D，可设出E点坐标，表示出F点的坐标，表示出EF的长，进一步可表示出△CBE的面积，利用二次函数的性质可求得其取得最大值时E点的坐标．试题解析：（1）∵直线y=﹣x+3与x轴、y轴分别交于点B、点C，∴B（3，0），C（0，3），把B、C坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=x2﹣4x+3；（2）∵y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线对称轴为x=2，P（2，﹣1），设M（2，t），且C（0，3），∴MC=，MP=|t+1|，PC=，∵△CPM为等腰三角形，∴有MC=MP、MC=PC和MP=PC三种情况，①当MC=MP时，则有=|t+1|，解得t=，此时M（2，）；②当MC=PC时，则有=2，解得t=﹣1（与P点重合，舍去）或t=7，此时M（2，7）；③当MP=PC时，则有|t+1|=2，解得t=﹣1+2或t=﹣1﹣2，此时M（2，﹣1+2）或（2，﹣1﹣2）；综上可知存在满足条件的点M，其坐标为（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）如图，过E作EF⊥x轴，交BC于点F，交x轴于点D，设E（x，x2﹣4x+3），则F（x，﹣x+3），∵0＜x＜3，∴EF=﹣x+3﹣（x2﹣4x+3）=﹣x2+3x，∴S△CBE=S△EFC+S△EFB=EF•OD+EF•BD=EF•OB=×3（﹣x2+3x）=﹣（x﹣）2+，∴当x=时，△CBE的面积最大，此时E点坐标为（，），即当E点坐标为（，）时，△CBE的面积最大．考点：二次函数综合题．8．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线对称轴DE交x轴于点E，连接BD．（1）求经过A，B，C三点的抛物线的函数表达式；（2）点P是线段BD上一点，当PE＝PC时，求点P的坐标．【答案】（1）y＝﹣x2+2x+3；（2）点P的坐标为（2，2）．【解析】【分析】（1）利用待定系数法求出过A，B，C三点的抛物线的函数表达式；（2）连接PC、PE，利用公式求出顶点D的坐标，利用待定系数法求出直线BD的解析式，设出点P的坐标为（x，﹣2x+6），利用勾股定理表示出PC2和PE2，根据题意列出方程，解方程求出x的值，计算求出点P的坐标．【详解】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，∴10930b cb c--+=⎧⎨-++=⎩，解得23bc=⎧⎨=⎩，∴所求的抛物线的函数表达式为y＝﹣x2+2x+3；（2）如图，连接PC，PE．抛物线的对称轴为x＝222(1)ba-=-⨯-＝1．当x＝1时，y＝4，∴点D的坐标为（1，4）．设直线BD的解析式为y＝kx+b，则430 k bk b+=⎧⎨+=⎩，解得26kb=-⎧⎨=⎩．∴直线BD的解析式为：y＝2x+6，设点P的坐标为（x，﹣2x+6），又C（0，3），E（1，0），则PC2＝x2+（3+2x﹣6）2，PE2＝（x﹣1）2+（﹣2x+6）2，∵PC＝PE，∴x2+（3+2x﹣6）2＝（x﹣1）2+（﹣2x+6）2，解得，x＝2，则y＝﹣2×2+6＝2，∴点P的坐标为（2，2）．【点睛】本题考查的是二次函数的图象和性质、待定系数法求函数解析式，掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键．9．如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B．抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）如图1，设抛物线顶点为M，且M的坐标是（12，92），对称轴交AB于点N．①求抛物线的解析式；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由．【答案】（1）①y＝﹣2x2+2x+4；；②不存在点P，使四边形MNPD为菱形；；（2）存在，点D的坐标是（1，4）．【解析】【分析】（1）①由一次函数图象上点的坐标特征求得点B的坐标，设抛物线解析式为y＝a21922x⎛⎫-+⎪⎝⎭，把点B的坐标代入求得a的值即可；②不存在点P，使四边形MNPD为菱形．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），根据题意知PD∥MN，所以当PD＝MN时，四边形MNPD为平行四边形，根据该等量关系列出方程﹣2m2+4m＝32，通过解方程求得m的值，易得点N、P的坐标，然后推知PN＝MN是否成立即可；（2）设点D的坐标是（n，﹣2n2+2n+4），P（n，﹣2n+4）．根据S四边形BOAD＝S△BOA+S△ABD ＝4+S△ABD，则当S△ABD取最大值时，S四边形BOAD最大．根据三角形的面积公式得到函数S△ABD＝﹣2（n﹣1）2+2．由二次函数的性质求得最值．【详解】解：①如图1，∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭，∴设抛物线解析式为y＝21922a x⎛⎫-+⎪⎝⎭（a≠0）．∵直线y＝﹣2x+4交y轴于点B，∴点B的坐标是（0，4）．又∵点B在该抛物线上，∴21922a⎛⎫-+⎪⎝⎭＝4，解得a＝﹣2．故该抛物线的解析式为：y＝219222x⎛⎫--+⎪⎝⎭＝﹣2x2+2x+4；②不存在．理由如下：∵抛物线y＝219222x⎛⎫--+⎪⎝⎭的对称轴是直线x＝12，且该直线与直线AB交于点N，∴点N的坐标是1,32⎛⎫ ⎪⎝⎭．∴93322MN=-=．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），∴PD＝（﹣2m2+2m+4）﹣（﹣2m+4）＝﹣2m2+4m．∵PD∥MN．当PD＝MN时，四边形MNPD是平行四边形，即﹣2m2+4m＝32．解得 m1＝12（舍去），m2＝32．此时P（32，1）．∵PN∴PN≠MN，∴平行四边形MNPD不是菱形．∴不存在点P，使四边形MNPD为菱形；（2）存在，理由如下：设点D的坐标是（n，﹣2n2+2n+4），∵点P在线段AB上且直线PD⊥x轴，∴P（n，﹣2n+4）．由图可知S四边形BOAD＝S△BOA+S△ABD．其中S△BOA＝12OB•OA＝12×4×2＝4．则当S△ABD取最大值时，S四边形BOAD最大．S△ABD＝12（y D﹣y P）（x A﹣x B）＝y D﹣y P＝﹣2n2+2n+4﹣（﹣2n+4）＝﹣2n2+4n＝﹣2（n﹣1）2+2．当n＝1时，S△ABD取得最大值2，S四边形BOAD有最大值．此时点D的坐标是（1，4）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．10．综合与探究如图，抛物线26y ax bx =++经过点A(-2,0)，B(4,0)两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为(14)m m <<.连接AC ，BC ，DB ，DC ． (1)求抛物线的函数表达式； (2)△BCD 的面积等于△AOC 的面积的34时，求m 的值； (3)在(2)的条件下，若点M 是x 轴上的一个动点，点N 是抛物线上一动点，试判断是否存在这样的点M,使得以点B ，D ，M ，N 为顶点的四边形是平行四边形，若存在，请直接写出点M 的坐标；若不存在，请说明理由.【答案】(1)233642y x x =-++；(2)3；(3)1234(8,0),(0,0),(14,0),(14,0)M M M M -. 【解析】 【分析】(1)利用待定系数法进行求解即可；(2)作直线DE ⊥x 轴于点E ，交BC 于点G ，作CF ⊥DE ，垂足为F ，先求出S △OAC =6，再根据S △BCD =34S △AOC ，得到S △BCD =92，然后求出BC 的解析式为362y x =-+，则可得点G 的坐标为3(,6)2m m -+，由此可得2334DG m m =-+，再根据S △BCD =S △CDG +S △BDG =12DG BO ⋅⋅，可得关于m 的方程，解方程即可求得答案；(3)存在，如下图所示，以BD 为边或者以BD 为对角线进行平行四边形的构图，以BD 为边时，有3种情况，由点D 的坐标可得点N 点纵坐标为±154，然后分点N 的纵坐标为154和点N 的纵坐标为154-两种情况分别求解；以BD 为对角线时，有1种情况，此时N 1点与N 2点重合，根据平行四边形的对边平行且相等可求得BM 1=N 1D=4，继而求得OM 1= 8，由此即可求得答案. 【详解】(1)抛物线2y ax bx c =++经过点A(-2,0)，B(4,0)，∴426016460a b a b -+=⎧⎨++=⎩， 解得3432a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线的函数表达式为233642y x x =-++； (2)作直线DE ⊥x 轴于点E ，交BC 于点G ，作CF ⊥DE ，垂足为F ， ∵点A 的坐标为(-2,0)，∴OA=2，由0x =，得6y =，∴点C 的坐标为(0,6)，∴OC=6，∴S △OAC =1126622OA OC ⋅⋅=⨯⨯=， ∵S △BCD =34S △AOC ， ∴S △BCD =39642⨯=， 设直线BC 的函数表达式为y kx n =+，由B ，C 两点的坐标得406k n n +=⎧⎨=⎩，解得326k n ⎧=-⎪⎨⎪=⎩， ∴直线BC 的函数表达式为362y x =-+， ∴点G 的坐标为3(,6)2m m -+， ∴2233336(6)34224DG m m m m m =-++--+=-+， ∵点B 的坐标为(4,0)，∴OB=4，∵S △BCD =S △CDG +S △BDG =1111()2222DG CF DG BE DG CF BE DG BO ⋅⋅+⋅⋅=⋅+=⋅⋅， ∴S △BCD =22133346242m m m m -+⨯=-+（）， ∴239622m m -+=， 解得11m =(舍)，23m =，∴m 的值为3；(3)存在，如下图所示，以BD 为边或者以BD 为对角线进行平行四边形的构图， 以BD 为边时，有3种情况，∵D 点坐标为15(3,)4，∴点N 点纵坐标为±154， 当点N 的纵坐标为154时，如点N 2，此时233156424x x -++=，解得：121,3x x =-=(舍)， ∴215(1,)4N -，∴2(0,0)M ； 当点N 的纵坐标为154-时，如点N 3，N 4， 此时233156424x x -++=-，解得：12114,114x x =-=+ ∴315(114,)4N +-，415(114,)4N --， ∴3(14,0)M ，4(14,0)M -；以BD 为对角线时，有1种情况，此时N 1点与N 2点重合，∵115(1,)4N -，D(3，154)， ∴N 1D=4，∴BM 1=N 1D=4，∴OM 1=OB+BM 1=8，∴M 1(8，0)， 综上，点M 的坐标为：1234(80)(00)(140)(140)M M M M -，，，，，，，.【点睛】本题考查的是二次函数的综合题，涉及了待定系数法、三角形的面积、解一元二次方程、平行四边形的性质等知识，运用了数形结合思想、分类讨论思想等数学思想，熟练掌握和灵活运用相关知识是解题的关键.11．某商场购进一批单价为4元的日用品．若按每件5元的价格销售，每月能卖出3万件；若按每件6元的价格销售，每月能卖出2万件，假定每月销售件数y （件）与价格x （元/件）之间满足一次函数关系．（1）试求y 与x 之间的函数关系式；（2）当销售价格定为多少时，才能使每月的利润最大？每月的最大利润是多少？【答案】（1）y10000x80000=-+（2）当销售价格定为6元时，每月的利润最大，每月的最大利润为40000元【解析】解：（1）由题意，可设y=kx+b，把（5，30000），（6，20000）代入得：5k b300006k b20000+=⎧⎨+=⎩，解得：k10000b80000=-⎧⎨=⎩。
2020-2021中考数学二次函数综合题含答案
2020-2021中考数学二次函数综合题含答案一、二次函数1．抛物线y ＝ax 2+bx ﹣3（a≠0）与直线y ＝kx+c （k≠0）相交于A （﹣1，0）、B （2，﹣3）两点，且抛物线与y 轴交于点C ． （1）求抛物线的解析式； （2）求出C 、D 两点的坐标（3）在第四象限抛物线上有一点P ，若△PCD 是以CD 为底边的等腰三角形，求出点P 的坐标．【答案】（1）y ＝x 2﹣2x ﹣3;（2）C （0，﹣3）,D （0，﹣1）;（3）P （2，﹣2）. 【解析】 【分析】（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得抛物线解析式． （2）当x ＝0时可求C 点坐标，求出直线AB 解析式，当x ＝0可求D 点坐标． （3）由题意可知P 点纵坐标为﹣2，代入抛物线解析式可求P 点横坐标． 【详解】解：（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入 y ＝ax 2+bx ﹣3可得 304233a b a b --=⎧⎨+-=-⎩解得12a b =⎧⎨=-⎩∴y ＝x 2﹣2x ﹣3（2）把x ＝0代入y ＝x 2﹣2x ﹣3中可得y ＝﹣3∴C （0，﹣3） 设y ＝kx+b ，把A （﹣1，0）、B （2，﹣3）两点坐标代入23k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩∴y ＝﹣x ﹣1 ∴D （0，﹣1）（3）由C （0，﹣3），D （0，﹣1）可知CD 的垂直平分线经过（0，﹣2） ∴P 点纵坐标为﹣2， ∴x 2﹣2x ﹣3＝﹣2解得：x ＝2∵x ＞0∴x ＝2．∴P （1+2，﹣2） 【点睛】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x ＝0代入二次函数解析式和一次函数解析式可求图象与y 轴交点坐标，知道点P 纵坐标带入抛物线解析式可求点P 的横坐标．2．如图，已知A （﹣2，0），B （4，0），抛物线y=ax 2+bx ﹣1过A 、B 两点，并与过A 点的直线y=﹣12x ﹣1交于点C ． （1）求抛物线解析式及对称轴；（2）在抛物线的对称轴上是否存在一点P ，使四边形ACPO 的周长最小？若存在，求出点P 的坐标，若不存在，请说明理由；（3）点M 为y 轴右侧抛物线上一点，过点M 作直线AC 的垂线，垂足为N ．问：是否存在这样的点N ，使以点M 、N 、C 为顶点的三角形与△AOC 相似，若存在，求出点N 的坐标，若不存在，请说明理由．【答案】（1）抛物线解析式为：y=211184x x --，抛物线对称轴为直线x=1；（2）存在P 点坐标为（1，﹣12）；（3）N 点坐标为（4，﹣3）或（2，﹣1） 【解析】分析：（1）由待定系数法求解即可；（2）将四边形周长最小转化为PC+PO 最小即可；（3）利用相似三角形对应点进行分类讨论，构造图形．设出点N 坐标，表示点M 坐标代入抛物线解析式即可．详解：（1）把A （-2，0），B （4，0）代入抛物线y=ax 2+bx-1，得042101641a b a b --⎧⎨+-⎩＝＝ 解得1814a b ⎧⎪⎪⎨⎪-⎪⎩＝＝∴抛物线解析式为：y=18x2−14x−1∴抛物线对称轴为直线x=-141228ba-=-⨯＝1（2）存在使四边形ACPO的周长最小，只需PC+PO最小∴取点C（0，-1）关于直线x=1的对称点C′（2，-1），连C′O与直线x=1的交点即为P 点．设过点C′、O直线解析式为：y=kx∴k=-12∴y=-12x则P点坐标为（1，-12）（3）当△AOC∽△MNC时，如图，延长MN交y轴于点D，过点N作NE⊥y轴于点E∵∠ACO=∠NCD，∠AOC=∠CND=90°∴∠CDN=∠CAO由相似，∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称，则N为DM中点设点N坐标为（a，-12a-1）由△EDN∽△OAC∴ED=2a∴点D 坐标为（0，-52a−1） ∵N 为DM 中点∴点M 坐标为（2a ，32a −1） 把M 代入y=18x 2−14x−1，解得 a=4则N 点坐标为（4，-3）当△AOC ∽△CNM 时，∠CAO=∠NCM∴CM ∥AB 则点C 关于直线x=1的对称点C′即为点N 由（2）N （2，-1）∴N 点坐标为（4，-3）或（2，-1）点睛：本题为代数几何综合题，考查了待定系数、两点之间线段最短的数学模型构造、三角形相似．解答时，应用了数形结合和分类讨论的数学思想．3．在平面直角坐标系中，O 为原点，抛物线2(0)2y ax x a =-≠经过点3)A -，对称轴为直线l ，点O 关于直线l 的对称点为点B .过点A 作直线//AC x 轴，交y 轴于点C .（Ⅰ）求该抛物线的解析式及对称轴；（Ⅱ）点P 在y 轴上，当PA PB +的值最小时，求点P 的坐标； （Ⅲ）抛物线上是否存在点Q ，使得13AOC AOQ S S ∆∆=，若存在，求出点Q 的坐标；若不存在，请说明理由.【答案】（Ⅰ）抛物线的解析式为212y x x =-;抛物线的对称轴为直线x =;（Ⅱ）P 点坐标为9(0,)4-;（Ⅲ）存在，Q 点坐标为或(-，理由见解析 【解析】 【分析】（Ⅰ）将3)A -点代入二次函数的解析式，即可求出a ，再根据对称轴的公式即可求解.（Ⅱ）先求出B 点胡坐标，要求PA PB +胡最小值，只需找到B 关于轴的对称点1B ，则直线A 1B 与y 轴的交点就是点P ，根据待定系数法求出AB 1的解析式，令y=0，即可求出P 点的坐标.（Ⅲ）设点Q 的坐标，并求出△AOQ 面积，从而得到△AOQ 面积，根据Q 点胡不同位置进行分类，用m 及割补法求出面积方程，即可求解.【详解】（Ⅰ）∵2(0) y ax x a=≠经过点3)A-，∴232a-=⨯-12a=，∴抛物线的解析式为2122y x x=-，∵212222bxa=-=-=⨯，∴抛物线的对称轴为直线x=（Ⅱ）∵点(0,0)O，对称轴为2x=，∴点O关于对称轴的对称点B点坐标为.作点B关于轴的对称点1B，得1(B-，设直线AB1的解析式为y kx b=+，把点3)A-，点1(B-代入得3bb⎧-=+⎪⎨=-+⎪⎩，解得94kb⎧=⎪⎪⎨⎪=-⎪⎩，∴944y x=--.∴直线94y x=-与y轴的交点即为P点.令0x=得9y4=-，∵P点坐标为9(0,)4-.（Ⅲ）∵3)A-，//AC x轴，∴AC=3OC=，∴113222AOCS OC AC∆=⋅=⋅=，又∵13AOC AOQS S∆∆=，∴3AOQ AOCS S∆∆==.设Q点坐标为21(,)2m m，如图情况一，作QR CA ⊥，交CA 延长线于点R ， ∵932AOQ AOC AQR OCRQ S S S S ∆∆∆=--=梯形， ∴()21133113333322222m m m m ⎛⎫⋅+-+-⋅⋅- ⎪ ⎪⎭-⎝2133933222m m ⎛⎫-+= ⎪ ⎪⎝⎭， 化简整理得23180m m --=， 解得133m =，223m =-.如图情况二，作QN AC ⊥，交AC 延长线于点N ，交x 轴于点M ， ∵93AOQ AQN QMO OMNA S S S S ∆∆∆=--=梯形， ∴2211331133(3m)3()222222m m m m m ⎛⎫⎛⎫--+--- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭393(3)22m m --+-=，化简整理得23180m m --=， 解得133m =，223m =-， ∴Q 点坐标为(33,0)或(23,15)-， ∴抛物线上存在点Q ，使得13AOC AOQ S S ∆∆=.【点睛】主要考查了二次函数的性质，以及求两边和的最小值，面积等常见的题型，计算量较大，但难度不是很大.4．在平面直角坐标系中，有两点(),A a b 、(),B c d ，若满足：当a b ≥时，c a =，2d b =-；当a b <时，c a <-，d b <，则称点为点的“友好点”.（1）点()4,1的“友好点”的坐标是_______.（2）点(),A a b 是直线2y x =-上的一点，点B 是点A 的“友好点”. ①当B 点与A 点重合时，求点A 的坐标.②当A 点与A 点不重合时，求线段AB 的长度随着a 的增大而减小时，a 的取值范围. 【答案】（1）()41-,；（2）①点A 的坐标是()2,0或()1,1-；②当1a <或322a ≤<时，AB 的长度随着a 的增大而减小； 【解析】 【分析】（1）直接利用“友好点”定义进行解题即可；（2）先利用 “友好点”定义求出B 点坐标，A 点又在直线2y x =-上，得到2b a =-；①当点A 和点B 重合，得2b b =-．解出即可，②当点A 和点B 不重合， 1a ≠且2a ≠．所以对a 分情况讨论，1°、当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭，所以当a ≤32时，AB 的长度随着a 的增大而减小，即取1a <．2°当12a <<时，()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭，当32a ≥时，AB 的长度随着a 的增大而减小，即取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【详解】（1）点()4,1，4＞1，根据“友好点”定义，得到点()4,1的“友好点”的坐标是()41-, （2）Q 点(),A a b 是直线2y x =-上的一点，∴2b a =-．Q 2a a >-，根据友好点的定义，点B 的坐标为()2,B a b -，①当点A 和点B 重合，∴2b b =-． 解得0b =或1b =-． 当0b =时，2a =；当1b =-时，1a =，∴点A 的坐标是()2,0或()1,1-．②当点A 和点B 不重合，1a ≠且2a ≠．当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭． ∴当a ≤32时，AB 的长度随着a 的增大而减小， ∴取1a <．当12a <<时， ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ ．∴当32a ≥时，AB 的长度随着a 的增大而减小， ∴取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【点睛】本题属于阅读理解题型，结合二次函数的基本性质进行解题，第二问的第二小问的关键是求出AB 的长用a 进行表示，然后利用二次函数基本性质进行分类讨论5．如图1，二次函数234y ax ax a =--的图像与x 轴交于,A B 两点(点A 在点B 的左侧)，与y 轴交于点()0,3C-.（1）求二次函数的表达式及点A 、点B 的坐标;（2）若点D 在二次函数图像上，且45DBC ABC S S =△△，求点D 的横坐标;（3）将直线BC 向下平移，与二次函数图像交于,M N 两点(M 在N 左侧)，如图2，过M 作ME y ∥轴，与直线BC 交于点E ，过N 作NF y ∥轴，与直线BC 交于点F ，当MN ME +的值最大时，求点M 的坐标.【答案】（1）y ＝239344x x --，A （﹣1，0），B （4，0）；（2）D 点的横坐标为22﹣2，2；（3）M （13，﹣113） 【解析】【分析】（1）求出a，即可求解；（2）求出直线BC的解析式，过点D作DH∥y轴，与直线BC交于点H，根据三角形面积的关系求解；（3）过点M作MG∥x轴，交FN的延长线于点G，设M（m，34m2﹣94m﹣3），N（n，34n2﹣94n﹣3），判断四边形MNFE是平行四边形，根据ME＝NF，求出m+n＝4，再确定ME+MN＝﹣34m2+3m+5﹣52m＝﹣34（m﹣13）2+6112，即可求M；【详解】（1）y＝ax2﹣3ax﹣4a与y轴交于点C（0，﹣3），∴a＝34，∴y＝34x2﹣94x﹣3，与x轴交点A（﹣1，0），B（4，0）；（2）设直线BC的解析式为y＝kx+b，∴403k bb+=⎧⎨=-⎩，∴343kb⎧=-⎪⎨⎪=-⎩，∴y＝34x﹣3；过点D作DH∥y轴，与直线BC交于点H，设H（x，34x﹣3），D（x，34x2﹣94x﹣3），∴DH＝|34x2﹣3x|，∵S△ABC＝1155323⨯⨯=，∴S△DBC＝41552⨯＝6，∴S△DBC＝2×|34x2﹣3x|＝6，∴x＝，x＝2﹣，x＝2；∴D点的横坐标为2﹣，2；（3）过点M作MG∥x轴，交FN的延长线于点G，设M（m，34m2﹣94m﹣3），N（n，34n2﹣94n﹣3），则E（m，34m﹣3），F（n，34n﹣3），∴ME＝﹣34m2+3m，NF＝﹣34n2+3n，∵EF∥MN，ME∥NF，∴四边形MNFE是平行四边形，∴ME＝NF，∴﹣34m2+3m＝﹣34n2+3n，∴m+n＝4，∴MG＝n﹣m＝4﹣2m，∴∠NMG＝∠OBC，∴cos∠NMG＝cos∠OBC＝MG OBMN BC,∵B（4，0），C（0，﹣3），∴OB＝4，OC＝3，在Rt△BOC中，BC＝5，∴MN＝54（n﹣m）＝54（4﹣2m）＝5﹣52m，∴ME+MN＝﹣34m2+3m+5﹣52m＝﹣34（m﹣13）2+6112，∵﹣34＜0，∴当m＝13时，ME+MN有最大值，∴M（13，﹣113）【点睛】本题考查二次函数图象及性质，一次函数图象及性质；熟练掌握待定系数法求函数解析式的方法，结合三角形的性质解题.6．二次函数y=x2-2mx+3（m＞）的图象与x轴交于点A（a，0）和点B（a+n，0）（n ＞0且n为整数），与y轴交于C点．（1）若a=1，①求二次函数关系式；②求△ABC的面积；（2）求证：a=m-；（3）线段AB（包括A、B）上有且只有三个点的横坐标是整数，求a的值．【答案】（1）y=x2-4x+3；3；（2）证明见解析；（3）a=1或a=−．【解析】试题分析：（1）①首先根据a=1求得A的坐标，然后代入二次函数的解析式，求得m的值即可确定二次函数的解析式；②根据解析式确定抛物线与坐标轴的交点坐标，从而确定三角形的面积；（2）将原二次函数配方后即可确定其对称轴为x=m，然后根据A、B两点关于x=m对称得到a+n-m=m-a，从而确定a、m、n之间的关系；（3）根据a=m-得到A（m-，0）代入y=（x-m）2-m2+3得0=（m--m）2-m2+3，求得m 的值即可确定a的值．试题解析：（1）①∵a=1，∴A（1，0），代入y=x2-2mx+3得1-2m+3=0，解得m=2，∴y=x2-4x+3；②在y=x2-4x+3中，当y=0时，有x2-4x+3=0可得x=1或x=3，∴A（1，0）、B（3，0），∴AB=2再根据解析式求出C点坐标为（0，3），∴OC=3，△ABC的面积=×2×3=3；（2）∵y=x2-2mx+3=（x-m）2-m2+3，∴对称轴为直线x=m，∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B∴点A和点B关于直线x=m对称，∴a+n-m=m-a，∴a=m-；（3）y=x2-2mx+3（m＞）化为顶点式为y=（x-m）2-m2+3（m＞）①当a为整数，因为n＞0且n为整数所以a+n是整数，∵线段AB（包括A、B）上有且只有三个点的横坐标是整数，∴n=2，∴a=m-1，∴A （m-1，0）代入y=（x-m ）2-m 2+3得（x-m ）2-m 2+3=0，∴m 2-4=0，∴m=2，m=-2（舍去），∴a=2-1=1，②当a 不是整数，因为n ＞0且n 为整数 所以a+n 不是整数，∵线段AB （包括A 、B ）上有且只有三个点的横坐标是整数，∴n=3，∴a=m-∴A （m-，0）代入y=（x-m ）2-m 2+3得0=（m--m ）2-m 2+3，∴m 2=， ∴m=，m=-（舍去）， ∴a=−，综上所述：a=1或a=−． 考点：二次函数综合题．7．如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上。
2020-2021中考数学二次函数综合经典题及答案解析
2020-2021中考数学二次函数综合经典题及答案解析一、二次函数1．如图，抛物线y=ax2+bx过点B（1，﹣3），对称轴是直线x=2，且抛物线与x轴的正半轴交于点A．（1）求抛物线的解析式，并根据图象直接写出当y≤0时，自变量x的取值范围；（2）在第二象限内的抛物线上有一点P，当PA⊥BA时，求△PAB的面积．【答案】（1）抛物线的解析式为y=x2﹣4x，自变量x的取值范图是0≤x≤4；（2）△PAB的面积=15．【解析】【分析】（1）将函数图象经过的点B坐标代入的函数的解析式中，再和对称轴方程联立求出待定系数a和b；（2）如图，过点B作BE⊥x轴，垂足为点E，过点P作PE⊥x轴，垂足为F，设P（x，x2-4x），证明△PFA∽△AEB,求出点P的坐标，将△PAB的面积构造成长方形去掉三个三角形的面积．【详解】（1）由题意得，322a bba+-⎧⎪⎨-⎪⎩＝＝，解得14 ab-⎧⎨⎩＝＝，∴抛物线的解析式为y=x2-4x，令y=0，得x2-2x=0，解得x=0或4，结合图象知，A的坐标为（4，0），根据图象开口向上，则y≤0时，自变量x的取值范围是0≤x≤4；（2）如图，过点B作BE⊥x轴，垂足为点E，过点P作PE⊥x轴，垂足为F，设P （x ，x 2-4x ）, ∵PA ⊥BA ∴∠PAF+∠BAE=90°, ∵∠PAF+∠FPA=90°, ∴∠FPA=∠BAE 又∠PFA=∠AEB=90° ∴△PFA ∽△AEB,∴PF AF AE BE =，即244213x x x--=-， 解得，x= −1，x=4（舍去） ∴x 2-4x=-5∴点P 的坐标为（-1，-5），又∵B 点坐标为（1，-3），易得到BP 直线为y=-4x+1 所以BP 与x 轴交点为（14，0） ∴S △PAB=115531524⨯⨯+= 【点睛】本题是二次函数综合题，求出函数解析式是解题的关键，特别是利用待定系数法将两条直线表达式解出，利用点的坐标求三角形的面积是关键．2．一座拱桥的轮廓是抛物线型(如图所示)，拱高6m ，跨度20m ，相邻两支柱间的距离均为5m.(1)将抛物线放在所给的直角坐标系中(如图所示)，其表达式是2y ax c =+的形式.请根据所给的数据求出a ，c 的值. (2)求支柱MN 的长度.(3)拱桥下地平面是双向行车道(正中间是一条宽2m 的隔离带)，其中的一条行车道能否并排行驶宽2m 、高3m 的三辆汽车(汽车间的间隔忽略不计)？请说说你的理由.【答案】（1）y=-350x 2+6；（2）5.5米；（3）一条行车道能并排行驶这样的三辆汽车． 【解析】试题分析：（1）根据题目可知A ．B ，C 的坐标，设出抛物线的解析式代入可求解． （2）设N 点的坐标为（5，y N ）可求出支柱MN 的长度．（3）设DN 是隔离带的宽，NG 是三辆车的宽度和．做GH 垂直AB 交抛物线于H 则可求解．试题解析： (1) 根据题目条件，A 、B 、C 的坐标分别是(-10,0)、(0,6)、(10,0).将B 、C 的坐标代入2y ax c =+，得 6,0100.c a c =⎧⎨=+⎩解得3,650a c =-=. ∴抛物线的表达式是23650y x =-+. (2) 可设N (5,N y )， 于是2356 4.550N y =-⨯+=. 从而支柱MN 的长度是10-4.5=5.5米.(3) 设DE 是隔离带的宽，EG 是三辆车的宽度和， 则G 点坐标是(7,0)(7=2÷2＋2×3).过G 点作GH 垂直AB 交抛物线于H ，则23176335050H y =-⨯+=+>. 根据抛物线的特点，可知一条行车道能并排行驶这样的三辆汽车.3．在平面直角坐标系xOy 中，抛物线y ＝x 2﹣2x +a ﹣3，当a ＝0时，抛物线与y 轴交于点A ，将点A 向右平移4个单位长度，得到点B ． （1）求点B 的坐标；（2）将抛物线在直线y ＝a 上方的部分沿直线y ＝a 翻折，图象的其他部分保持不变，得到一个新的图象，记为图形M ，若图形M 与线段AB 恰有两个公共点，结合函数的图象，求a 的取值范围．【答案】（1）A （0，﹣3），B （4，﹣3）；（2）﹣3＜a ≤0； 【解析】【分析】（1）由题意直接可求A，根据平移点的特点求B；（2）图形M与线段AB恰有两个公共点，y＝a要在AB线段的上方，当函数经过点A时，AB与函数两个交点的临界点；【详解】解：（1）A（0，﹣3），B（4，﹣3）；（2）当函数经过点A时，a＝0，∵图形M与线段AB恰有两个公共点，∴y＝a要在AB线段的上方，∴a＞﹣3∴﹣3＜a≤0；【点睛】本题二次函数的图象及性质；熟练掌握二次函数图象的特点，函数与线段相交的交点情况是解题的关键．4．如图，已知抛物线的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）。
2020-2021中考数学二次函数综合经典题附答案
2020-2021中考数学二次函数综合经典题附答案一、二次函数1．已知如图，抛物线y=x2+bx+c过点A（3，0），B（1，0），交y轴于点C，点P是该抛物线上一动点，点P从C点沿抛物线向A点运动（点P不与点A重合），过点P作PD∥y 轴交直线AC于点D．（1）求抛物线的解析式；（2）求点P在运动的过程中线段PD长度的最大值；（3）△APD能否构成直角三角形？若能请直接写出点P坐标，若不能请说明理由；（4）在抛物线对称轴上是否存在点M使|MA﹣MC|最大？若存在请求出点M的坐标，若不存在请说明理由．【答案】（1）y=x2﹣4x+3；（2）94；（3）点P（1，0）或（2，﹣1）；（4）M（2，﹣3）．【解析】试题分析：（1）把点A、B的坐标代入抛物线解析式，解方程组得到b、c的值，即可得解；（2）求出点C的坐标，再利用待定系数法求出直线AC的解析式，再根据抛物线解析式设出点P的坐标，然后表示出PD的长度，再根据二次函数的最值问题解答；（3）①∠APD是直角时，点P与点B重合，②求出抛物线顶点坐标，然后判断出点P为在抛物线顶点时，∠PAD是直角，分别写出点P的坐标即可；（4）根据抛物线的对称性可知MA=MB，再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时，|MA﹣MC|最大，然后利用待定系数法求出直线BC的解析式，再求解即可．试题解析：解：（1）∵抛物线y=x2+bx+c过点A（3，0），B（1，0），∴93010b cb c++=⎧⎨++=⎩，解得43bc=-⎧⎨=⎩，∴抛物线解析式为y=x2﹣4x+3；（2）令x=0，则y=3，∴点C（0，3），则直线AC的解析式为y=﹣x+3，设点P（x，x2﹣4x+3）．∵PD∥y轴，∴点D（x，﹣x+3），∴PD=（﹣x+3）﹣（x2﹣4x+3）=﹣x2+3x=﹣（x﹣32）2+94．∵a=﹣1＜0，∴当x=32时，线段PD的长度有最大值94；（3）①∠APD是直角时，点P与点B重合，此时，点P（1，0），②∵y=x2﹣4x+3=（x ﹣2）2﹣1，∴抛物线的顶点坐标为（2，﹣1）．∵A（3，0），∴点P为在抛物线顶点时，∠PAD=45°+45°=90°，此时，点P（2，﹣1）．综上所述：点P（1，0）或（2，﹣1）时，△APD能构成直角三角形；（4）由抛物线的对称性，对称轴垂直平分AB，∴MA=MB，由三角形的三边关系，|MA﹣MC|＜BC，∴当M、B、C三点共线时，|MA﹣MC|最大，为BC的长度，设直线BC的解析式为y=kx+b（k≠0），则3k bb+=⎧⎨=⎩，解得：33kb=-⎧⎨=⎩，∴直线BC的解析式为y=﹣3x+3．∵抛物线y=x2﹣4x+3的对称轴为直线x=2，∴当x=2时，y=﹣3×2+3=﹣3，∴点M （2，﹣3），即，抛物线对称轴上存在点M（2，﹣3），使|MA﹣MC|最大．点睛：本题是二次函数综合题，主要利用了待定系数法求二次函数解析式，二次函数的最值问题，二次函数的对称性以及顶点坐标的求解，（2）整理出PD的表达式是解题的关键，（3）关键在于利用点的坐标特征作出判断，（4）根据抛物线的对称性和三角形的三边关系判断出点M的位置是解题的关键．2．如图，关于x的二次函数y=x2+bx+c的图象与x轴交于点A（1，0）和点B与y轴交于点C（0，3），抛物线的对称轴与x轴交于点D．（1）求二次函数的表达式；（2）在y轴上是否存在一点P，使△PBC为等腰三角形？若存在．请求出点P的坐标；（3）有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N 从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积．【答案】（1）二次函数的表达式为：y=x2﹣4x+3；（2）点P的坐标为：（0，2（0，3﹣）或（0，-3）或（0，0）；（3）当点M 出发1秒到达D 点时，△MNB 面积最大，最大面积是1．此时点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处．【解析】【分析】（1）把A （1，0）和C （0，3）代入y=x 2+bx+c 得方程组，解方程组即可得二次函数的表达式；（2）先求出点B 的坐标，再根据勾股定理求得BC 的长，当△PBC 为等腰三角形时分三种情况进行讨论：①CP=CB ；②BP=BC ；③PB=PC ；分别根据这三种情况求出点P 的坐标； （3）设AM=t 则DN=2t ，由AB=2，得BM=2﹣t ，S △MNB=12×（2﹣t ）×2t=﹣t 2+2t ，把解析式化为顶点式，根据二次函数的性质即可得△MNB 最大面积；此时点M 在D 点，点N 在对称轴上x 轴上方2个单位处或点N 在对称轴上x 轴下方2个单位处．【详解】解：（1）把A （1，0）和C （0，3）代入y=x 2+bx+c ，103b c c ++=⎧⎨=⎩解得：b=﹣4，c=3，∴二次函数的表达式为：y=x 2﹣4x+3；（2）令y=0，则x 2﹣4x+3=0，解得：x=1或x=3，∴B （3，0），∴点P 在y 轴上，当△PBC 为等腰三角形时分三种情况进行讨论：如图1，①当CP=CB 时，，∴或OP=PC ﹣﹣3∴P1（0，P 2（0，3﹣②当PB=PC 时，OP=OB=3，∴P 3（0，-3）；③当BP=BC 时，∵OC=OB=3∴此时P 与O 重合，∴P 4（0，0）；综上所述，点P 的坐标为：（0，0，3﹣3，0）或（0，0）；（3）如图2，设AM=t，由AB=2，得BM=2﹣t，则DN=2t，∴S△MNB=1×（2﹣t）×2t=﹣t2+2t=﹣（t﹣1）2+1，2当点M出发1秒到达D点时，△MNB面积最大，最大面积是1．此时点N在对称轴上x 轴上方2个单位处或点N在对称轴上x轴下方2个单位处．3．已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c 的图象经过点A（m，0），B（0，n），如图所示．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，求出点C，D的坐标，并判断△BCD的形状；（3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P2个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．【答案】（1）223y x x =--；（2）C （3，0），D （1，﹣4），△BCD 是直角三角形；（3）2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩＜＜＜或＞ 【解析】试题分析：（1）先解一元二次方程，然后用待定系数法求出抛物线解析式；（2）先解方程求出抛物线与x 轴的交点，再判断出△BOC 和△BED 都是等腰直角三角形，从而得到结论；（3）先求出QF=1，再分两种情况，当点P 在点M 上方和下方，分别计算即可． 试题解析：解（1）∵2+430x x +=，∴11x =-，23x =-，∵m ，n 是一元二次方程2+430x x +=的两个实数根，且|m|＜|n|，∴m=﹣1，n=﹣3，∵抛物线223y x x =--的图象经过点A （m ，0），B （0，n ），∴10{3b c c -+==-，∴2{3b c =-=-，∴抛物线解析式为223y x x =--；（2）令y=0，则2230x x --=，∴11x =-，23x =，∴C （3，0），∵223y x x =--=2(1)4x --，∴顶点坐标D （1，﹣4），过点D 作DE ⊥y 轴，∵OB=OC=3，∴BE=DE=1，∴△BOC 和△BED 都是等腰直角三角形，∴∠OBC=∠DBE=45°，∴∠CBD=90°，∴△BCD 是直角三角形；（3）如图，∵B （0，﹣3），C （3，0），∴直线BC 解析式为y=x ﹣3，∵点P 的横坐标为t ，PM ⊥x 轴，∴点M 的横坐标为t ，∵点P 在直线BC 上，点M 在抛物线上，∴P （t ，t ﹣3），M （t ，223t t --），过点Q 作QF ⊥PM ，∴△PQF 是等腰直角三角形，∵2，∴QF=1．①当点P 在点M 上方时，即0＜t ＜3时，PM=t ﹣3﹣（223t t --）=23t t -+，∴S=12PM×QF=21(3)2t t -+=21322t t -+，②如图3，当点P 在点M 下方时，即t ＜0或t ＞3时，PM=223t t --﹣（t ﹣3）=23t t -，∴S=12PM×QF=12（23t t -）=21322t t -．综上所述，S=2213 (03)22{13 (03)22t t t t t t t 或-+<<-．考点：二次函数综合题；分类讨论．4．已知抛物线26y x x c =-++.（1）若该抛物线与x 轴有公共点，求c 的取值范围；（Ⅱ）设该抛物线与直线21y x =+交于M ，N 两点，若25MN =C 的值；（Ⅲ）点P ，点Q 是抛物线上位于第一象限的不同两点，,PA QB 都垂直于x 轴，垂足分别为A ，B ，若OPA OQB ∆≅∆，求c 的取值范围.【答案】（I ）9c -…；（Ⅱ）2c =-；（Ⅲ）c 的取值范围是2174c -<< 【解析】【分析】(1) 抛物线与x 轴有公共点，则判别式为非负数，列不等式求解即可;(2)求出二次函数与直线的交点，并根据勾股定理求出MN 的长度，列方程即可求解;(3)由OPA OQB ∆≅∆可知，P ,Q 两点的坐标特点，设坐标得到设点P 的坐标为(, )m n ，则点Q 的坐标为(,)n m ，代入二次函数，得到n,m 的关系，则只需保证该方程有正根即可求解.【详解】解：（I ）∵抛物线26y x x c =-++与x 轴有交点， ∴一元二次方程260x x c -++=有实根。
2020-2021初中数学二次函数经典测试题附答案
2020-2021初中数学二次函数经典测试题附答案一、选择题1．已知在平面直角坐标系中，有两个二次函数()()39m x x y =++及()()26y n x x =--图象，将二次函数()()39m x x y =++的图象按下列哪一种平移方式平移后，会使得此两个函数图象的对称轴重叠（ ） A ．向左平移2个单位长度 B ．向右平移2个单位长度C ．向左平移10个单位长度 D ．向右平移10个单位长度【答案】D 【解析】 【分析】将二次函数解析式展开，结合二次函数的性质找出两二次函数的对称轴，二者做差后即可得出平移方向及距离． 【详解】解：∵y ＝m （x ＋3）（x ＋9）＝mx 2＋12mx ＋27m ，y ＝n （x －2）（x －6）＝nx 2－8nx ＋12n ，∴二次函数y ＝m （x ＋3）（x ＋9）的对称轴为直线x ＝－6，二次函数y ＝n （x －2）（x －6）的对称轴为直线x ＝4， ∵4－（－6）＝10，∴将二次函数y ＝m （x ＋3）（x ＋9）的图形向右平移10个单位长度，两图象的对称轴重叠． 故选：D ． 【点睛】本题考查了二次函数图象与几何变换以及二次函数的性质，根据二次函数的性质找出两个二次函数的对称轴是解题的关键．2．对于二次函数()21202y ax a x a ⎛⎫=+-<⎪⎝⎭，下列说法正确的个数是（ ） ①对于任何满足条件的a ，该二次函数的图象都经过点()2,1和()0,0两点； ②若该函数图象的对称轴为直线0x x =，则必有001x <<； ③当0x ≥时，y 随x 的增大而增大；④若()14,P y ，()()24,0Q m y m +>是函数图象上的两点，如果12y y >总成立，则112a ≤-． A ．1个 B ．2个C ．3个D ．4个【答案】B 【解析】 【分析】根据二次函数的图象与性质（对称性、增减性）逐个判断即可． 【详解】对于()21202y ax a x a ⎛⎫=+-< ⎪⎝⎭当2x =时，142(2)12y a a =+-=，则二次函数的图象都经过点()2,1 当0x =时，0y =，则二次函数的图象都经过点()0,0 则说法①正确此二次函数的对称轴为1212124ax a a-=-=-+0a < 1114a∴-+> 01x ∴>，则说法②错误由二次函数的性质可知，抛物线的开口向下，当114x a<-+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小 因11104a-+>> 则当1014x a <-≤+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小 即说法③错误0m >44m ∴+>由12y y >总成立得，其对称轴1144x a=-+≤ 解得112a ≤-，则说法④正确 综上，说法正确的个数是2个 故选：B ． 【点睛】本题考查了二次函数的图象与性质（对称性、增减性），熟练掌握二次函数的图象与性质是解题关键．3．已知，二次函数y=ax 2+bx+a 2+b （a≠0）的图象为下列图象之一，则a 的值为（ ）A ．-1B ．1C ．-3D ．-4【答案】A 【解析】 【分析】分别对图形进行讨论：若二次函数的图形为第一个，则b=0，其顶点坐标为(0，a 2)，与图形中的顶点坐标不符；若二次函数的图形为第二个，则b=0，根据顶点坐标有a 2=3，由抛物线与x 的交点坐标得到x 2=-a ，所以a=-4，它们相矛盾；若二次函数的图形为第三个，把点(-1，0)代入解析式得到a-b+a 2+b=0，解得a=-1；若二次函数的图形为第四个，把(-2，0)和(0，0)分别代入解析式可计算出a 的值． 【详解】解：若二次函数的图形为第一个，对称轴为y 轴，则b=0，y=ax 2+a 2，其顶点坐标为(0，a 2)，而a 2>0，所以二次函数的图形不能为第一个；若二次函数的图形为第二个，对称轴为y 轴，则b=0，y=ax 2+a 2，a 2=3，而当y=0时，x 2=−a ，所以−a=4，a=−4，所以二次函数的图形不能为第二个；若二次函数的图形为第三个，令x=−1，y=0，则a−b+a 2+b=0，所以a=−1； 若二次函数的图形为第四个，令x=0，y=0，则a 2+b=0①；令x=−2，y=0，则4a−2b+a 2+b=0②，由①②得a=−2，这与图象开口向上不符合，所以二次函数的图形不能为第四个. 故选A. 【点睛】本题考查了二次函数y=ax 2+bx+c(a≠0)的图象与系数的关系：a ＞0，开口向上；a ＜0，开口向下；抛物线的对称轴为直线x=-；顶点坐标为(-，)；也考查了点在抛物线上则点的坐标满足抛物线的解析式.4．二次函数2(0)y ax bx c a =++≠的图象如图所示，下列结论①24b ac >，②0abc <，③20a b c +->，④0a b c ++<．其中正确的是（ ）A ．①④B ．②④C ．②③D ．①②③④【答案】A 【解析】 【分析】①抛物线与x 轴由两个交点，则240b ac ->，即24b ac >，所以①正确；②由二次函数图象可知，0a <，0b <，0c >，所以0abc >，故②错误； ③对称轴：直线12bx a=-=-，2b a =，所以24a b c a c +-=-，240a b c a c +-=-<，故③错误；④对称轴为直线1x =-，抛物线与x 轴一个交点132x -<<-，则抛物线与x 轴另一个交点201x <<，当1x =时，0y a b c =++<，故④正确． 【详解】解：①∵抛物线与x 轴由两个交点， ∴240b ac ->， 即24b ac >， 所以①正确；②由二次函数图象可知， 0a <，0b <，0c >，∴0abc >， 故②错误；③∵对称轴：直线12bx a=-=-， ∴2b a =，∴24a b c a c +-=-， ∵0a <，40a <，0c >，0a <，∴240a b c a c +-=-<，故③错误；④∵对称轴为直线1x =-，抛物线与x 轴一个交点132x -<<-， ∴抛物线与x 轴另一个交点201x <<，当1x =时，0y a b c =++<， 故④正确． 故选：A ． 【点睛】本题考查了二次函数图象与系数的关系，熟练掌握二次函数图象的性质是解题的关键．5．已知抛物线2:4W y x x c =-+，其顶点为A ，与y 轴交于点B ，将抛物线W 绕原点旋转180︒得到抛物线'W ，点,A B 的对应点分别为','A B ，若四边形''ABA B 为矩形，则c 的值为（ ）A ．BC ．32D ．52【答案】D 【解析】 【分析】先求出A(2，c-4)，B(0，c)，'(24),'(0)A c B c ---，，，，结合矩形的性质，列出关于c 的方程，即可求解． 【详解】∵抛物线2:4W y x x c =-+，其顶点为A ，与y 轴交于点B ，∴A(2，c-4)，B(0，c)，∵将抛物线W 绕原点旋转180︒得到抛物线'W ，点,A B 的对应点分别为','A B ，∴'(24),'(0)A c B c ---，，，， ∵四边形''ABA B 为矩形， ∴''AA BB =，∴[][]2222(2)(4)(4)(2)c c c --+---=，解得：52c =． 故选D ． 【点睛】本题主要考查二次函数图象的几何变换以及矩形的性质，掌握二次函数图象上点的坐标特征，关于原点中心对称的点的坐标特征以及矩形的对角线相等，是解题的关键．6．在抛物线y ＝a （x ﹣m ﹣1）2+c （a≠0）和直线y ＝﹣12x 的图象上有三点（x 1，m ）、（x 2，m ）、（x 3，m ），则x 1+x 2+x 3的结果是（ ）A ．3122m -+ B ．0 C ．1 D ．2【答案】D 【解析】 【分析】根据二次函数的对称性和一次函数图象上点的坐标特征即可求得结果． 【详解】解：如图，在抛物线y ＝a （x ﹣m ﹣1）2+c （a≠0）和直线y ＝﹣12x 的图象上有三点A （x 1，m ）、B （x 2，m ）、C （x 3，m ）， ∵y ＝a （x ﹣m ﹣1）2+c （a≠0） ∴抛物线的对称轴为直线x ＝m+1，∴232x x +＝m+1， ∴x 2+x 3＝2m+2，∵A （x 1，m ）在直线y ＝﹣12x 上， ∴m ＝﹣12x 1， ∴x 1＝﹣2m ，∴x 1+x 2+x 3＝﹣2m+2m+2＝2， 故选：D ．【点睛】本题考查了二次函数的对称性和一次函数图象上点的坐标特征，解题的关键是利用数形结合思想画出函数图形．7．二次函数2(,,y ax bx c a b c =++为常数，且0a ≠)中的x 与y 的部分对应值如表：x··· 1- 0 13 ··· y ···1-3 53···下列结论错误的是( ) A ．0ac < B ．3是关于x 的方程()210ax b x c +-+=的一个根；C ．当1x >时，y 的值随x 值的增大而减小；D ．当13x时，()210.ax b x c +-+>【答案】C 【解析】 【分析】根据函数中的x 与y 的部分对应值表，可以求得a 、b 、c 的值 然后在根据函数解析式及其图象即可对各个选项做出判断． 【详解】解：根据二次函数的x 与y 的部分对应值可知： 当1x =-时，1y =-，即1a b c -+=-， 当0x =时，3y =，即3c =， 当1x =时，5y =，即5a b c ++=，联立以上方程：135a b c c a b c -+=-⎧⎪=⎨⎪++=⎩，解得：133a b c =-⎧⎪=⎨⎪=⎩，∴233y x x =-++；A 、1330=-⨯=-<ac ，故本选项正确；B 、方程()210ax b x c +-+=可化为2230x x -++=，将3x =代入得：232339630-+⨯+=-++=，∴3是关于x 的方程()210ax b x c +-+=的一个根,故本选项正确；C 、233y x x =-++化为顶点式得：2321()24=--+y x ， ∵10a =-<，则抛物线的开口向下，∴当32x >时，y 的值随x 值的增大而减小；当32x <时，y 的值随x 值的增大而增大；故本选项错误；D 、不等式()210ax b x c +-+>可化为2230x x -++>，令2y x 2x 3=-++，由二次函数的图象可得：当0y >时，13x ，故本选项正确；故选：C ． 【点睛】本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数与不等式的关系，根据表中数据求出二次函数解析式是解题的关键．8．将抛物线y＝x2﹣4x+1向左平移至顶点落在y轴上，如图所示，则两条抛物线.直线y＝﹣3和x轴围成的图形的面积S（图中阴影部分）是（）A．5 B．6 C．7 D．8【答案】B【解析】【分析】B，C分别是顶点，A是抛物线与x轴的一个交点，连接OC，AB，阴影部分的面积就是平行四边形ABCO的面积.【详解】抛物线y＝x2﹣4x+1=(x-2)2-3的顶点坐标C(2.-3), 向左平移至顶点落在y轴上,此时顶点B(0,-3)，点A是抛物线与x轴的一个交点，连接OC，AB，如图，阴影部分的面积就是ABCO的面积，S=2×3=6；故选：B．【点睛】本题考查二次函数图象的性质，阴影部分的面积；能够将面积进行转化是解题的关键．9．足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线. 不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表：t01234567…h08141820201814…下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线92t ；③足球被踢出9s 时落地；④足球被踢出1.5s 时，距离地面的高度是11m. 其中正确结论的个数是（ ） A ．1 B ．2C ．3D ．4【答案】B 【解析】 【分析】 【详解】解：由题意，抛物线的解析式为y =ax （x ﹣9），把（1，8）代入可得a =﹣1， ∴y =﹣t 2+9t =﹣（t ﹣4.5）2+20.25，∴足球距离地面的最大高度为20.25m ，故①错误， ∴抛物线的对称轴t =4.5，故②正确，∵t =9时，y =0，∴足球被踢出9s 时落地，故③正确， ∵t =1.5时，y =11.25，故④错误，∴正确的有②③， 故选B ．10．已知二次函数223(0)y ax ax a a =--≠，关于此函数的图象及性质，下列结论中不一定成立的是( )A ．该图象的顶点坐标为()1,4a -B ．该图象与x 轴的交点为()()1,0,3,0-C ．若该图象经过点()2,5-，则一定经过点()4,5D ．当1x >时，y 随x 的增大而增大 【答案】D 【解析】 【分析】根据二次函数的图象与性质即可求出答案． 【详解】 解：y=a （x 2-2x-3） =a （x-3）（x+1） 令y=0， ∴x=3或x=-1，∴抛物线与x 轴的交点坐标为（3，0）与（-1，0），故B 成立； ∴抛物线的对称轴为：x=1， 令x=1代入y=ax 2-2ax-3a ， ∴y=a-2a-3a=-4a ，∴顶点坐标为（1，-4a ），故A 成立； 由于点（-2，5）与（4，5）关于直线x=1对称，∴若该图象经过点（-2，5），则一定经过点（4，5），故C 成立；当x ＞1，a ＞0时，y 随着x 的增大而增大，当x ＞1，a ＜0时，y 随着x 的增大而减少，故D 不一定成立；故选：D ． 【点睛】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于基础题型．11．如图，将一个小球从斜坡的点O 处抛出，小球的抛出路线可以用二次函数y ＝4x －12x 2刻画，斜坡可以用一次函数y ＝12x 刻画，下列结论错误的是( )A ．斜坡的坡度为1: 2B ．小球距O 点水平距离超过4米呈下降趋势C ．小球落地点距O 点水平距离为7米D ．当小球抛出高度达到7.5m 时，小球距O 点水平距离为3m 【答案】D 【解析】 【分析】求出抛物线与直线的交点，判断A 、C ；根据二次函数的性质求出对称轴，根据二次函数性质判断B ；求出当7.5y =时，x 的值，判定D ． 【详解】解：214212y x x y x ⎧=-+⎪⎪⎨⎪=⎪⎩，解得，1100x y =⎧⎨=⎩，22772x y =⎧⎪⎨=⎪⎩， 72∶7=1∶2，∴A 正确； 小球落地点距O 点水平距离为7米，C 正确；2142y x x =-21(4)82x =--+， 则抛物线的对称轴为4x =，∴当4x >时，y 随x 的增大而减小，即小球距O 点水平距离超过4米呈下降趋势，B 正确，当7.5y =时，217.542x x =-，整理得28150x x -+=， 解得，13x =，25x =，∴当小球抛出高度达到7.5m 时，小球水平距O 点水平距离为3m 或5m ，D 错误，符合题意； 故选：D 【点睛】本题考查的是解直角三角形的-坡度问题、二次函数的性质，掌握坡度的概念、二次函数的性质是解题的关键．12．二次函数2y ax bx c =++（,,a b c 是常数，0a ≠）的自变量x 与函数值y 的部分对应值如下表：且当12x =-时，与其对应的函数值0y >．有下列结论：①0abc >；②2-和3是关于x 的方程2ax bx c t ++=的两个根；③0m <203n +<．其中，正确结论的个数是（ ） A ．0 B ．1C ．2D ．3【答案】C 【解析】 【分析】首先确定对称轴，然后根据二次函数的图像和性质逐一进行分析即可求解． 【详解】∵由表格可知当x=0和x=1时的函数值相等都为-2 ∴抛物线的对称轴是：x=-2b a =12； ∴a 、b 异号，且b=-a ； ∵当x=0时y=c=-2 ∴c 0<∴abc >0，故①正确；∵根据抛物线的对称性可得当x=-2和x=3时的函数值相等都为t ∴2-和3是关于x 的方程2ax bx c t ++=的两个根；故②正确； ∵b=-a ，c=-2∴二次函数解析式：2-a -2=y ax x ∵当12x =-时，与其对应的函数值0y >．∴3204a ->，∴a 83>； ∵当x=-1和x=2时的函数值分别为m 和n ， ∴m=n=2a-2， ∴m+n=4a-4203>；故③错误 故选：C ． 【点睛】本题考查了二次函数的综合题型，主要利用了二次函数图象与系数的关系，二次函数的对称性，二次函数与一元二次方程等知识点，要会利用数形结合的思想，根据给定自变量x 与函数值y 的值结合二次函数的性质逐条分析给定的结论是关键．13．若用“*”表示一种运算规则，我们规定：a *b ＝ab ﹣a +b ，如：3*2＝3×2﹣3+2＝5．以下说法中错误的是（ ）A ．不等式（﹣2）*（3﹣x ）＜2的解集是x ＜3B ．函数y ＝（x +2）*x 的图象与x 轴有两个交点C ．在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数D ．方程（x ﹣2）*3＝5的解是x ＝5 【答案】D 【解析】 【分析】根据题目中所给的运算法则列出不等式，解不等式即可判定选项A ；根据题目中所给的运算法则求得函数解析式，由此即可判定选项B ；根据题目中所给的运算法则可得a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0，由此即可判定选项C ；根据题目中所给的运算法则列出方程，解方程即可判定选项D. 【详解】∵a *b ＝ab ﹣a +b ，∴（﹣2）*（3﹣x ）＝（﹣2）×（3﹣x ）﹣（﹣2）+（3﹣x ）＝x ﹣1， ∵（﹣2）*（3﹣x ）＜2，∴x ﹣1＜2，解得x ＜3，故选项A 正确；∵y ＝（x +2）*x ＝（x +2）x ﹣（x +2）+x ＝x 2+2x ﹣2，∴当y ＝0时，x 2+2x ﹣2＝0，解得，x 1＝﹣x 2＝﹣1B 正确； ∵a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0， ∴在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数，故选项C 正确；∵（x ﹣2）*3＝5，∴（x ﹣2）×3﹣（x ﹣2）+3＝5， 解得，x ＝3，故选项D 错误； 故选D ． 【点睛】本题是阅读理解题，根据题目中所给的运算法则得到相应的运算式子是解决问题的关键.14．二次函数y=﹣x 2+mx 的图象如图，对称轴为直线x=2，若关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解，则t 的取值范围是（ ）A ．t ＞﹣5B ．﹣5＜t ＜3C ．3＜t≤4D ．﹣5＜t≤4【答案】D 【解析】 【分析】先根据对称轴x=2求得m 的值，然后求得x=1和x=5时y 的值，最后根据图形的特点，得出直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4． 【详解】∵抛物线的对称轴为x ＝2， ∴22m-=-，m=4 如图，关于x 的一元二次方程﹣x 2+mx ﹣t=0的解就是抛物线y=﹣x 2+mx 与直线y=t 的交点的横坐标当x=1时，y=3， 当x=5时，y=﹣5，由图象可知关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解， 则直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4， ∴﹣5＜t≤4． 故选：D ．【点睛】本题考查二次函数与一元二次方程的关系，方程有解，反映在图象上即图象与x 轴(或某直线)有交点．15．已知抛物线y=x 2+2x 上三点A （﹣5，y 1），B （2.5，y 2），C （12，y 3），则y 1，y 2，y 3满足的关系式为（ ）A ．y 1＜y 2＜y 3B ．y 3＜y 2＜y 1C ．y 2＜y 1＜y 3D ．y 3＜y 1＜y 2 【答案】C 【解析】 【分析】首先求出抛物线y=x 2+2x 的对称轴，对称轴为直线x=-1；然后根据A 、B 、C 的横坐标与对称轴的位置，接着利用抛物线的增减性质即可求解；由B 离对称轴最近，A 次之，C 最远，则对应y 的值大小可确定. 【详解】 ∵抛物线y=x 2+2x ， ∴x=-1，而A （-5，y 1），B （2.5，y 2），C （12，y 3）， ∴B 离对称轴最近，A 次之，C 最远， ∴y 2＜y 1＜y 3． 故选:C ． 【点睛】本题考查了二次函数的图象和性质，二次函数图象上点的坐标特征等知识点，能熟记二次函数的性质是解此题的关键．16．已知抛物线y=x 2-2mx-4（m ＞0）的顶点M 关于坐标原点O 的对称点为M′，若点M′在这条抛物线上，则点M 的坐标为（ ） A ．（1，-5） B ．（3，-13） C ．（2，-8） D ．（4，-20）【答案】C 【解析】 【分析】 【详解】解：22224=()4y x mx x m m =-----，∴点M （m ，﹣m 2﹣4），∴点M′（﹣m ，m 2+4），∴m 2+2m 2﹣4=m 2+4．解得m=±2．∵m ＞0，∴m=2，∴M （2，﹣8）． 故选C ． 【点睛】本题考查二次函数的性质．17．在同一平面直角坐标系中，函数3y x a =+与2+3y ax x =的图象可能是（ ）A．B．C．D．【答案】C【解析】【分析】根据一次函数及二次函数的图像性质，逐一进行判断．【详解】解：A.由一次函数图像可知a＞0，因此二次函数图像开口向上，但对称轴32a-<应在y轴左侧，故此选项错误；B. 由一次函数图像可知a＜0，而由二次函数图像开口方向可知a＞0，故此选项错误；C. 由一次函数图像可知a＜0，因此二次函数图像开口向下，且对称轴32a->在y轴右侧，故此选项正确；D. 由一次函数图像可知a＞0，而由二次函数图像开口方向可知a＜0，故此选项错误；故选：C．【点睛】本题考查二次函数与一次函数图象的性质，解题的关键是利用数形结合思想分析图像，本题属于中等题型．18．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，分析下列四个结论：①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2，其中正确的结论有（）A．1个B．2个C．3个D．4个【答案】B 【解析】试题解析：①由开口向下，可得0,a < 又由抛物线与y 轴交于正半轴，可得0c >，再根据对称轴在y 轴左侧，得到b 与a 同号，则可得0,0b abc ， 故①错误；②由抛物线与x 轴有两个交点，可得240b ac ->， 故②正确； ③当2x =-时，0,y < 即420a b c -+< ……（1） 当1x =时，0y <,即0a b c ++< ……（2） （1）+（2）×2得，630a c +<， 即20a c +<， 又因为0,a <所以()230a a c a c ，++=+< 故③错误；④因为1x =时，0y a b c =++<，1x =-时，0y a b c =-+> 所以()()0a b c a b c ++-+<即()()22()0,a c b a c b a c b ⎡⎤⎡⎤+++-=+-<⎣⎦⎣⎦所以22().a c b +< 故④正确，综上可知，正确的结论有2个. 故选B ．19．在平面直角坐标系中，点P 的坐标为()1,2，将抛物线21322y x x =-+沿坐标轴平移一次，使其经过点P ，则平移的最短距离为（ ） A ．12B ．1C ．5D ．52【答案】B 【解析】 【分析】先求出平移后P 点对应点的坐标，求出平移距离，即可得出选项． 【详解】 解：21322y x x =-+=()215322x --， 当沿水平方向平移时，纵坐标和P 的纵坐标相同，把y=2代入得： 解得：x=0或6， 平移的最短距离为1-0=1；当沿竖直方向平移时，横坐标和P的横坐标相同，把x=1代入得：解得：y=12 -，平移的最短距离为152=22⎛⎫--⎪⎝⎭，即平移的最短距离是1，故选B.【点睛】本题考查了二次函数图象上点的坐标特征，能求出平移后对应的点的坐标是解此题的关键．20．平移抛物线y＝﹣（x﹣1）（x+3），下列哪种平移方法不能使平移后的抛物线经过原点（）A．向左平移1个单位B．向上平移3个单位C．向右平移3个单位D．向下平移3个单位【答案】B【解析】【分析】先将抛物线解析式转化为顶点式，然后根据顶点坐标的平移规律即可解答.【详解】解：y＝﹣（x﹣1）（x+3）=-（x+1）2+4A、向左平移1个单位后的解析式为：y＝-（x+2）2+4，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意；B、向上平移3个单位后的解析式为：y=-（x+1）2+7，当x=0时，y=3，即该抛物线不经过原点，故本选项符合题意；C、向右平移3个单位后的解析式为：y=-（x-2）2+4，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意.；D、向下平移3个单位后的解析式为：y=-（x+1）2+1，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意.【点睛】本题考查了二次函数图像的平移，函数图像平移规律：上移加，下移减，左移加，右移减.。
2020-2021中考数学专题《二次函数》综合检测试卷含答案解析
2020-2021中考数学专题《二次函数》综合检测试卷含答案解析一、二次函数1．在平面直角坐标系xOy中，已知抛物线的顶点坐标为（2，0），且经过点（4，1），如图，直线y=14x与抛物线交于A、B两点，直线l为y=﹣1．（1）求抛物线的解析式；（2）在l上是否存在一点P，使PA+PB取得最小值？若存在，求出点P的坐标；若不存在，请说明理由．（3）知F（x0，y0）为平面内一定点，M（m，n）为抛物线上一动点，且点M到直线l的距离与点M到点F的距离总是相等，求定点F的坐标．【答案】（1）抛物线的解析式为y=14x2﹣x+1．（2）点P的坐标为（2813，﹣1）．（3）定点F的坐标为（2，1）．【解析】分析：（1）由抛物线的顶点坐标为（2，0），可设抛物线的解析式为y=a（x-2）2，由抛物线过点（4，1），利用待定系数法即可求出抛物线的解析式；（2）联立直线AB与抛物线解析式成方程组，通过解方程组可求出点A、B的坐标，作点B关于直线l的对称点B′，连接AB′交直线l于点P，此时PA+PB取得最小值，根据点B的坐标可得出点B′的坐标，根据点A、B′的坐标利用待定系数法可求出直线AB′的解析式，再利用一次函数图象上点的坐标特征即可求出点P的坐标；（3）由点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征，即可得出（1-12-12y0）m2+（2-2x0+2y0）m+x02+y02-2y0-3=0，由m的任意性可得出关于x0、y0的方程组，解之即可求出顶点F的坐标．详解：（1）∵抛物线的顶点坐标为（2，0），设抛物线的解析式为y=a（x-2）2．∵该抛物线经过点（4，1），∴1=4a，解得：a=14，∴抛物线的解析式为y=14（x-2）2=14x2-x+1．（2）联立直线AB 与抛物线解析式成方程组，得：214114y x y x x ⎧⎪⎪⎨⎪-+⎪⎩＝＝，解得：11114x y ⎧⎪⎨⎪⎩＝＝，2241x y ⎧⎨⎩＝＝， ∴点A 的坐标为（1，14），点B 的坐标为（4，1）． 作点B 关于直线l 的对称点B′，连接AB′交直线l 于点P ，此时PA+PB 取得最小值（如图1所示）．∵点B （4，1），直线l 为y=-1，∴点B′的坐标为（4，-3）．设直线AB′的解析式为y=kx+b （k≠0），将A （1，14）、B′（4，-3）代入y=kx+b ，得： 1443k b k b ⎧+⎪⎨⎪+-⎩＝＝，解得：131243k b ⎧-⎪⎪⎨⎪⎪⎩＝＝， ∴直线AB′的解析式为y=-1312x+43， 当y=-1时，有-1312x+43=-1， 解得：x=2813， ∴点P 的坐标为（2813，-1）． （3）∵点M 到直线l 的距离与点M 到点F 的距离总是相等，∴（m-x 0）2+（n-y 0）2=（n+1）2，∴m 2-2x 0m+x 02-2y 0n+y 02=2n+1．∵M （m ，n ）为抛物线上一动点，∴n=14m2-m+1，∴m2-2x0m+x02-2y0（14m2-m+1）+y02=2（14m2-m+1）+1，整理得：（1-12-12y0）m2+（2-2x0+2y0）m+x02+y02-2y0-3=0．∵m为任意值，∴00220001110222220230yx yx y y⎧--⎪⎪-+⎨⎪+--⎪⎩＝＝＝，∴021xy⎧⎨⎩＝＝，∴定点F的坐标为（2，1）．点睛：本题考查了待定系数法求二次（一次）函数解析式、二次（一次）函数图象上点的坐标特征、轴对称中的最短路径问题以及解方程组，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用两点之间线段最短找出点P的位置；（3）根据点M到直线l的距离与点M到点F的距离总是相等结合二次函数图象上点的坐标特征，找出关于x0、y0的方程组．2．如图，抛物线y＝﹣x2﹣2x+3的图象与x轴交于A、B两点(点A在点B的左边)，与y轴交于点C，点D为抛物线的顶点．(1)求点A、B、C的坐标；(2)点M(m，0)为线段AB上一点(点M不与点A、B重合)，过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，可得矩形PQNM．如图，点P在点Q左边，试用含m的式子表示矩形PQNM的周长；(3)当矩形PQNM的周长最大时，m的值是多少？并求出此时的△AEM的面积；(4)在(3)的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G(点G在点F的上方)．若FG＝22DQ，求点F的坐标．【答案】(1)A(﹣3，0)，B(1，0)；C(0，3) ；(2)矩形PMNQ的周长＝﹣2m2﹣8m+2；(3) m＝﹣2；S＝12；(4)F(﹣4，﹣5)或(1，0)．【解析】【分析】（1）利用函数图象与坐标轴的交点的求法，求出点A，B，C的坐标；（2）先确定出抛物线对称轴，用m表示出PM，MN即可；（3）由（2）得到的结论判断出矩形周长最大时，确定出m，进而求出直线AC解析式，即可；（4）在（3）的基础上，判断出N应与原点重合，Q点与C点重合，求出DQ＝DC＝，再建立方程（n+3）﹣（﹣n2﹣2n+3）＝4即可．【详解】(1)由抛物线y＝﹣x2﹣2x+3可知，C(0，3)．令y＝0，则0＝﹣x2﹣2x+3，解得，x＝﹣3或x＝l，∴A(﹣3，0)，B(1，0)．(2)由抛物线y＝﹣x2﹣2x+3可知，对称轴为x＝﹣1．∵M(m，0)，∴PM＝﹣m2﹣2m+3，MN＝(﹣m﹣1)×2＝﹣2m﹣2，∴矩形PMNQ的周长＝2(PM+MN)＝(﹣m2﹣2m+3﹣2m﹣2)×2＝﹣2m2﹣8m+2．(3)∵﹣2m2﹣8m+2＝﹣2(m+2)2+10，∴矩形的周长最大时，m＝﹣2．∵A(﹣3，0)，C(0，3)，设直线AC的解析式y＝kx+b，∴303k bb-+=⎧⎨=⎩解得k＝l，b＝3，∴解析式y＝x+3，令x＝﹣2，则y＝1，∴E(﹣2，1)，∴EM＝1，AM＝1，∴S＝12AM×EM＝12．(4)∵M(﹣2，0)，抛物线的对称轴为x＝﹣l，∴N应与原点重合，Q点与C点重合，∴DQ＝DC，把x＝﹣1代入y＝﹣x2﹣2x+3，解得y＝4，∴D(﹣1，4)，∴DQ＝DC∵FG＝22DQ，∴FG＝4．设F(n，﹣n2﹣2n+3)，则G(n，n+3)，∵点G在点F的上方且FG＝4，∴(n+3)﹣(﹣n2﹣2n+3)＝4．解得n＝﹣4或n＝1，∴F(﹣4，﹣5)或(1，0)．【点睛】此题是二次函数综合题，主要考查了函数图象与坐标轴的交点的求法，待定系数法求函数解析式，函数极值的确定，解本题的关键是用m表示出矩形PMNQ的周长．3．已知，点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，直线y＝mx+5分别交x轴正半轴，y轴于点A，B．（1）判断顶点M是否在直线y＝4x+1上，并说明理由．（2）如图1，若二次函数图象也经过点A，B，且mx+5＞﹣（x﹣b）2+4b+1，根据图象，写出x的取值范围．（3）如图2，点A坐标为（5，0），点M在△AOB内，若点C（14，y1），D（34，y2）都在二次函数图象上，试比较y1与y2的大小．【答案】（1）点M在直线y＝4x+1上；理由见解析；（2）x的取值范围是x＜0或x＞5；（3）①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【解析】【分析】（1）根据顶点式解析式，可得顶点坐标，根据点的坐标代入函数解析式检验，可得答案；（2）根据待定系数法，可得二次函数的解析式，根据函数图象与不等式的关系：图象在下方的函数值小，可得答案；（3）根据解方程组，可得顶点M的纵坐标的范围，根据二次函数的性质，可得答案．【详解】（1）点M为二次函数y＝﹣（x﹣b）2+4b+1图象的顶点，∴M的坐标是（b，4b+1），把x＝b代入y＝4x+1，得y＝4b+1，∴点M在直线y＝4x+1上；（2）如图1，直线y＝mx+5交y轴于点B，∴B点坐标为（0，5）又B在抛物线上，∴5＝﹣（0﹣b）2+4b+1＝5，解得b＝2，二次函数的解析是为y＝﹣（x﹣2）2+9，当y＝0时，﹣（x﹣2）2+9＝0，解得x1＝5，x2＝﹣1，∴A（5，0）．由图象，得当mx+5＞﹣（x﹣b）2+4b+1时，x的取值范围是x＜0或x＞5；（3）如图2，∵直线y＝4x+1与直线AB交于点E，与y轴交于F，A（5，0），B（0，5）得直线AB的解析式为y＝﹣x+5，联立EF，AB得方程组415 y xy x=+⎧⎨=-+⎩，解得45215xy⎧=⎪⎪⎨⎪=⎪⎩，∴点E（45，215），F（0，1）．点M在△AOB内，1＜4b+1＜215，∴0＜b＜45．当点C，D关于抛物线的对称轴对称时，b﹣14＝34﹣b，∴b＝12，且二次函数图象开口向下，顶点M在直线y＝4x+1上，综上：①当0＜b＜12时，y1＞y2，②当b＝12时，y1＝y2，③当12＜b＜45时，y1＜y2．【点睛】本题考查了二次函数综合题，解（1）的关键是把点的坐标代入函数解析式检验；解（2）的关键是利用函数图不等式的关系：图象在上方的函数值大；解（3）的关键是解方程组得出顶点M 的纵坐标的范围，又利用了二次函数的性质：a ＜0时，点与对称轴的距离越小函数值越大．4．如图，已知A （﹣2，0），B （4，0），抛物线y=ax 2+bx ﹣1过A 、B 两点，并与过A 点的直线y=﹣12x ﹣1交于点C ． （1）求抛物线解析式及对称轴；（2）在抛物线的对称轴上是否存在一点P ，使四边形ACPO 的周长最小？若存在，求出点P 的坐标，若不存在，请说明理由；（3）点M 为y 轴右侧抛物线上一点，过点M 作直线AC 的垂线，垂足为N ．问：是否存在这样的点N ，使以点M 、N 、C 为顶点的三角形与△AOC 相似，若存在，求出点N 的坐标，若不存在，请说明理由．【答案】（1）抛物线解析式为：y=211184x x --，抛物线对称轴为直线x=1；（2）存在P 点坐标为（1，﹣12）；（3）N 点坐标为（4，﹣3）或（2，﹣1） 【解析】 分析：（1）由待定系数法求解即可；（2）将四边形周长最小转化为PC+PO 最小即可；（3）利用相似三角形对应点进行分类讨论，构造图形．设出点N 坐标，表示点M 坐标代入抛物线解析式即可．详解：（1）把A （-2，0），B （4，0）代入抛物线y=ax 2+bx-1，得042101641a b a b --⎧⎨+-⎩＝＝解得1814a b ⎧⎪⎪⎨⎪-⎪⎩＝＝ ∴抛物线解析式为：y=18x 2−14x−1 ∴抛物线对称轴为直线x=-141228b a -=-⨯＝1 （2）存在 使四边形ACPO 的周长最小，只需PC+PO 最小∴取点C （0，-1）关于直线x=1的对称点C′（2，-1），连C′O 与直线x=1的交点即为P 点．设过点C′、O 直线解析式为：y=kx∴k=-12∴y=-12x 则P 点坐标为（1，-12） （3）当△AOC ∽△MNC 时，如图，延长MN 交y 轴于点D ，过点N 作NE ⊥y 轴于点E∵∠ACO=∠NCD ，∠AOC=∠CND=90°∴∠CDN=∠CAO由相似，∠CAO=∠CMN∴∠CDN=∠CMN∵MN ⊥AC∴M 、D 关于AN 对称，则N 为DM 中点设点N 坐标为（a ，-12a-1） 由△EDN ∽△OAC∴ED=2a∴点D 坐标为（0，-52a−1） ∵N 为DM 中点∴点M 坐标为（2a ，32a−1） 把M 代入y=18x 2−14x−1，解得 a=4则N 点坐标为（4，-3）当△AOC ∽△CNM 时，∠CAO=∠NCM∴CM ∥AB 则点C 关于直线x=1的对称点C′即为点N由（2）N （2，-1）∴N 点坐标为（4，-3）或（2，-1）点睛：本题为代数几何综合题，考查了待定系数、两点之间线段最短的数学模型构造、三角形相似．解答时，应用了数形结合和分类讨论的数学思想．5．如图，抛物线21222y x x =-++与x 轴相交于A B ，两点，（点A 在B 点左侧）与y 轴交于点C.（Ⅰ）求A B ，两点坐标.（Ⅱ）连结AC ，若点P 在第一象限的抛物线上，P 的横坐标为t ，四边形ABPC 的面积为S.试用含t 的式子表示S ，并求t 为何值时，S 最大.（Ⅲ）在（Ⅱ）的基础上，若点,G H 分别为抛物线及其对称轴上的点，点G 的横坐标为m ，点H 的纵坐标为n ，且使得以,,,A G H P 四点构成的四边形为平行四边形，求满足条件的,m n 的值.【答案】（Ⅰ）(A B ；（Ⅱ）2(2S t t =--+<<,当t =时，S =最大；（Ⅲ）满足条件的点m n 、的值为：34m n ==，或1524m n ==-，或124m n =-= 【解析】【分析】（Ⅰ）令y=0，建立方程求解即可得出结论；（Ⅱ）设出点P 的坐标，利用S=S △AOC +S 梯形OCPQ +S △PQB ，即可得出结论；（Ⅲ）分三种情况，利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论．【详解】解：（Ⅰ）抛物线21222y x x =-++，令0y =，则212022x x -++=，解得：x =x =∴((,A B（Ⅱ）由抛物线21222y x x =-++，令0x =，∴2y =，∴()0,2C ， 如图1，点P 作PQ x ⊥轴于Q ，∵P 的横坐标为t ，∴设(),P t p ，∴212,,22p t PQ p BQ t OQ t =-++===，∴()()11122222AOC PQB OCPQ S S S S p t t p =++=++⨯+⨯⨯V V 梯形 1122t pt pt t =++-=++21222t t ⎫=-+++⎪⎪⎭2t t =+<<，∴当t =时，S =最大（Ⅲ）由（Ⅱ）知，2t =，∴)2,2P，∵抛物线212222y x x =-++的对称轴为22x =， ∴设2122,2,2G m m H n ⎛⎫⎫-++ ⎪⎪ ⎪⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形，()2,0A ， ①当AP 和HG 为对角线时，∴()2112111222,2022222222m m m n ⎛⎫⎛⎫=++=-+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴2324m n =-=， ②当AG 和PH 是对角线时，∴(()2112112122,2022222222m m m n ⎫⎛⎫=-+++=+⎪ ⎪⎪ ⎪⎭⎝⎭， ∴215,24m n ==-， ③AH 和PG 为对角线时，∴(()2121112122,2202222222m m m n ⎛⎫⎛⎫-=+-+++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴32124m n =-=， 即：满足条件的点m n 、的值为：234m n ==，或52154m n ==-，或3214m n == 【点睛】此题是二次函数综合题，主要考查了坐标轴上点的特点，三角形的面积公式，梯形的面积公式，平行四边形的性质，中点坐标公式，用方程的思想解决问题是解本题的关键．6．如图，抛物线y ＝ax 2+bx +4与x 轴交于点A （﹣1，0）、B （3，0），与y 轴交于点C ． （1）求抛物线的解析式；（2）如图1，D 为抛物线对称轴上一动点，求D 运动到什么位置时△DAC 的周长最小； （3）如图2，点E 在第一象限抛物线上，AE 与BC 交于点F ，若AF ：FE ＝2：1，求E 点坐标；（4）点M 、N 同时从B 点出发，分别沿BA 、BC 方向运动，它们的运动速度都是1个单位/秒，当点M 运动到点A 时，点N 停止运动，则当点N 停止运动后，在x 轴上是否存在点P ，使得△PBN 是等腰三角形？若存在，直接写出点P 的坐标；若不存在，请说明理由．【答案】（1）248433y x x =-++（2）81,3D ⎛⎫⎪⎝⎭（3）点P 的坐标P 1（﹣1，0）或P 2（7，0）或P 3（﹣95，0）或P 4（13，0）． 【解析】 【分析】（1）直接待定系数法代入求解即可 （2）找到D 点在对称轴时是△DAC 周长最小的点，先求出直线BC ，然后D 点横坐标是1，直接代入直线BC 求出纵坐标即可 （3）作EH ∥AB 交BC 于H ，则∠FAB ＝∠FEH ，∠FBA ＝∠FHE ，易证△ABF ∽△EHF ，得AB AF2EH EF==,得EH=2，设E （x ，248x x 433-++），则H （x ﹣2，420x 33-+），y E ＝y H ，解出方程x ＝1或x ＝2，得到E 点坐标 （4）△PBN 是等腰三角形，分成三种情况，①BP ＝BC 时，利用等腰三角性质直接得到P 1（﹣1，0）或P 2（7，0），②当NB ＝NP 时，作NH ⊥x 轴，易得△NHB ∽△COB ，利用比例式得到NH 、 BH 从而得到 PH ＝BH ，BP ，进而得到OP ，即得到P 点坐标，③当PN ＝PB 时，取NB 中点K ，作KP ⊥BN ，交x 轴于点P ，易得△NOB ∽△PKB ，利用比例式求出PB ，进而得到OP ，即求出P 点坐标 【详解】解：（1）将A （﹣1，0）、B （3，0）代入y ＝ax 2+bx+4，得 40930a b a b c -+=⎧⎨++=⎩解得a ＝43-，b ＝83， ∴抛物线的解析式248433y x x =-++； （2）22484164(1)3333=-++=--+y x x x ∴抛物线对称轴为直线x ＝1， ∴D 的横坐标为1，由（1）可得C （0，4）， ∵B （3，0）， ∴直线BC ：4y 43x =-+ ∵DA ＝DB ，△DAC 的周长＝AC+CD+AD ＝AC+CD+BD ， 连接BC ，与对称轴交于点D ，此时CD+BD 最小， ∵AC 为定值， ∴此时△DAC 的周长， 当x ＝1时，y ＝﹣43×1+4＝83， ∴D （1，83）； （3）作EH ∥AB 交BC 于H ，则∠FAB ＝∠FEH ，∠FBA ＝∠FHE ，∴△ABF ∽△EHF ， ∵AF ：FE ＝2：1，∴AB AF2EH EF ==， ∵AB ＝4， ∴EH ＝2，设E （x ，248x x 433-++），则H （x ﹣2，420x 33-+） ∵EH ∥AB ， ∴y E ＝y H ，∴248x x 433-++=420x 33-+ 解得x ＝1或x ＝2，y ＝163或4， ∴E （1，163）或（2，4）； （4）∵A （﹣1，0）、B （3，0），C （0，4） ∴AB ＝4，OC ＝4，点M 运动到点A 时，BM ＝AB ＝4， ∴BN ＝4，∵△PBN 是等腰三角形， ①BP ＝BC 时，若P 在点B 左侧，OP ＝PB ﹣OB ＝4﹣3＝1， ∴P 1（﹣1，0），若P 在点B 右侧，OP ＝OB+BP ＝4+3＝7， ∴P 2（7，0）；②当NB ＝NP 时，作NH ⊥x 轴， △NHB ∽△COB ，∴45NH BH BN OC OB BC === ∴NH ＝45OC ＝445⨯＝165，BH ＝45BC ＝125， ∴PH ＝BH ＝125， BP ＝245， ∴OP ＝BP ﹣OB ＝249355-=， ∴P 3（﹣95，0）； ③当PN ＝PB 时，取NB 中点K ，作KP ⊥BN ，交x 轴于点P ， ∴△NOB ∽△PKB ，∴PB BKBN OB= ∴PB ＝83，∴OP ＝OB ﹣PB ＝3﹣83＝13P 4（13，0） 综上，当△PBN 是等腰三角形时，点P 的坐标P 1（﹣1，0）或P 2（7，0）或P 3（﹣95，0）或P 4（13，0）． 【点睛】本题考查二次函数、平行线性质、相似三角形、等腰三角形性质及最短距离等知识点，综合程度比较高，对综合能力要求比较高. 第一问比较简单，考查待定系数法；第二问最短距离，找到D 点是解题关键；第三问证明出相似是关键；第四问能够分情况讨论是解题关键7．如图1，二次函数234y ax ax a =--的图像与x 轴交于,A B 两点(点A 在点B 的左侧)，与y 轴交于点()0,3C-.（1）求二次函数的表达式及点A 、点B 的坐标;（2）若点D 在二次函数图像上，且45DBC ABC S S =△△，求点D 的横坐标;（3）将直线BC 向下平移，与二次函数图像交于,M N 两点(M 在N 左侧)，如图2，过M 作ME y ∥轴，与直线BC 交于点E ，过N 作NF y ∥轴，与直线BC 交于点F ，当MN ME +的值最大时，求点M 的坐标.【答案】（1）y ＝239344x x --，A （﹣1，0），B （4，0）；（2）D 点的横坐标为22﹣2，2；（3）M （13，﹣113） 【解析】 【分析】（1）求出a ，即可求解；（2）求出直线BC 的解析式，过点D 作DH ∥y 轴，与直线BC 交于点H ，根据三角形面积的关系求解；（3）过点M 作MG ∥x 轴，交FN 的延长线于点G ，设M （m ，34m 2﹣94m ﹣3），N（n ，34n 2﹣94n ﹣3），判断四边形MNFE 是平行四边形，根据ME ＝NF ，求出m +n ＝4，再确定ME +MN ＝﹣34m 2+3m +5﹣52m ＝﹣34（m ﹣13）2+6112，即可求M ；【详解】（1）y ＝ax 2﹣3ax ﹣4a 与y 轴交于点C （0，﹣3），∴a ＝34，∴y＝34x2﹣94x﹣3，与x轴交点A（﹣1，0），B（4，0）；（2）设直线BC的解析式为y＝kx+b，∴403k bb+=⎧⎨=-⎩，∴343kb⎧=-⎪⎨⎪=-⎩，∴y＝34x﹣3；过点D作DH∥y轴，与直线BC交于点H，设H（x，34x﹣3），D（x，34x2﹣94x﹣3），∴DH＝|34x2﹣3x|，∵S△ABC＝1155323⨯⨯=，∴S△DBC＝41552⨯＝6，∴S△DBC＝2×|34x2﹣3x|＝6，∴x＝2+22，x＝2﹣22，x＝2；∴D点的横坐标为2+22，2﹣22，2；（3）过点M作MG∥x轴，交FN的延长线于点G，设M（m，34m2﹣94m﹣3），N（n，34n2﹣94n﹣3），则E（m，34m﹣3），F（n，34n﹣3），∴ME＝﹣34m2+3m，NF＝﹣34n2+3n，∵EF∥MN，ME∥NF，∴四边形MNFE 是平行四边形， ∴ME ＝NF ，∴﹣34m 2+3m ＝﹣34n 2+3n ， ∴m +n ＝4，∴MG ＝n ﹣m ＝4﹣2m ， ∴∠NMG ＝∠OBC ，∴cos ∠NMG ＝cos ∠OBC ＝MG OBMN BC=, ∵B （4，0），C （0，﹣3）， ∴OB ＝4，OC ＝3，在Rt △BOC 中，BC ＝5，∴MN ＝54（n ﹣m ）＝54（4﹣2m ）＝5﹣52m ， ∴ME +MN ＝﹣34m 2+3m +5﹣52m ＝﹣34（m ﹣13）2+6112，∵﹣34＜0， ∴当m ＝13时，ME +MN 有最大值，∴M （13，﹣113）【点睛】本题考查二次函数图象及性质，一次函数图象及性质；熟练掌握待定系数法求函数解析式的方法，结合三角形的性质解题.8．已知抛物线2y ax bx c =++上有两点M (m +1，a )、N (m ，b ). (1)当a ＝－1，m ＝1时，求抛物线2y ax bx c =++的解析式； (2)用含a 、m 的代数式表示b 和c ；(3)当a ＜0时，抛物线2y ax bx c =++满足24b ac a -=，2b c a +≥，34m ≤-， 求a 的取值范围.【答案】（1）11b c =⎧⎨=⎩；（2）b=-am ，c=-am ；（3）161393a -≤≤- 【解析】 【分析】（1）根据题意得到M (2，－1)、N (1，b )，代入抛物线解析式即可求出b 、c ；（2）将点M (m +1，a )、N (m ，b )代入抛物线2y ax bx c =++，可得22(1)(1)a m b m c a am bm c b⎧++++=⎨++=⎩，化简即可得出；（3）把b am =-，c am =-代入24b ac a -=可得214a m m=+，把b am =-，c am =-代入2b c a +≥可得1m ≥-，然后根据m 的取值范围可得a 的取值范围.【详解】解：(1)∵a ＝－1，m ＝1，∴M (2，－1)、N (1，b )由题意，得4211b c b c b -++=-⎧⎨-++=⎩，解，得11b c =⎧⎨=⎩(2) ∵点M (m +1，a )、N (m ，b )在抛物线2y ax bx c =++上22(1)(1)a m b m c a am bm c b ⎧++++=⎨++=⎩①②①－②得，2am b b +=-，∴b am =-把b am =-代入②，得c am =-(3)把b am =-，c am =-代入24b ac a -=得2224a m a m a +=0a <Q ，22141,4am am a m m∴+=∴=+ 把b am =-，c am =-代入2b c a +≥得22am a -≥，1m ∴≥-34m Q ≤-，314m ∴-≤≤-224(2)4m m m +=+-Q ，当2m >-时，24m m +随m 的增大而增大2393416m m ∴-≤+≤-216113943m m ∴-≤≤-+ 即161393a -≤≤- 【点睛】本题考查待定系数法求函数解析式以及二次函数的图像和性质，由函数图像上点的坐标特征求出b am =-，c am =-是解题关键.9．如图，抛物线y ＝﹣x 2+bx +c 经过A （﹣1，0），B （3，0）两点，且与y 轴交于点C ，点D 是抛物线的顶点，抛物线对称轴DE 交x 轴于点E ，连接BD ． （1）求经过A ，B ，C 三点的抛物线的函数表达式； （2）点P 是线段BD 上一点，当PE ＝PC 时，求点P 的坐标．【答案】（1）y＝﹣x2+2x+3；（2）点P的坐标为（2，2）．【解析】【分析】（1）利用待定系数法求出过A，B，C三点的抛物线的函数表达式；（2）连接PC、PE，利用公式求出顶点D的坐标，利用待定系数法求出直线BD的解析式，设出点P的坐标为（x，﹣2x+6），利用勾股定理表示出PC2和PE2，根据题意列出方程，解方程求出x的值，计算求出点P的坐标．【详解】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，∴10930b cb c--+=⎧⎨-++=⎩，解得23bc=⎧⎨=⎩，∴所求的抛物线的函数表达式为y＝﹣x2+2x+3；（2）如图，连接PC，PE．抛物线的对称轴为x＝222(1)ba-=-⨯-＝1．当x＝1时，y＝4，∴点D的坐标为（1，4）．设直线BD的解析式为y＝kx+b，则430 k bk b+=⎧⎨+=⎩，解得26kb=-⎧⎨=⎩．∴直线BD的解析式为：y＝2x+6，设点P的坐标为（x，﹣2x+6），又C（0，3），E（1，0），则PC2＝x2+（3+2x﹣6）2，PE2＝（x﹣1）2+（﹣2x+6）2，∵PC＝PE，∴x2+（3+2x﹣6）2＝（x﹣1）2+（﹣2x+6）2，解得，x＝2，则y＝﹣2×2+6＝2，∴点P的坐标为（2，2）．【点睛】本题考查的是二次函数的图象和性质、待定系数法求函数解析式，掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键．10．如图，在直角坐标系xOy中，二次函数y=x2+（2k﹣1）x+k+1的图象与x轴相交于O、A两点．（1）求这个二次函数的解析式；（2）在这条抛物线的对称轴右边的图象上有一点B，使△AOB的面积等于6，求点B的坐标；（3）对于（2）中的点B，在此抛物线上是否存在点P，使∠POB=90°？若存在，求出点P 的坐标，并求出△POB的面积；若不存在，请说明理由．【答案】（1）y=x2﹣3x。
2020-2021学年九年级上册数学第1章《二次函数》单元测试卷(有答案)
2020-2021学年九年级上册数学第 1章《二次函数》单元测试卷式是（）1. 卜列关于X 的函数一定为二次函数的是（ A . y=4xB , y= 5x2 - 3xC. y=ax 2+bx+cD , y=x 3-2x+12.将二次函数y= 2x 2+5的图象先向左平移 3个单位，再向下平移 1个单位，则平移后的函数关系A. y=2 (x+3) 2+6 B . y=2 (x+3) 2+4 C. y=2 (x- 3) 2+6D. y=2 (x-3) 2+43. 如图，某农场拟建一间矩形奶牛饲养室，打算一边利用房屋现有的墙（墙足够长） ,其余三边除大门外用栅栏围成，栅栏总长度为 50m,门宽为2m.若饲养室长为 xm,占地面积为ym 2,则关于x 的函数表达式为（:2+26x (2<x<52)B. C. -2 .y= - . x +50x (2w x< 52) y= - x 2+52x (2< x< 52) - 2 一 一 一 __________ y=一方x2+27x- 52 (2<x< 52)（aw0）在同一坐标系中的图象可能是（D .5.以下抛物线的顶点坐标为（2, 0）的是（10.如图，已知顶点为（-3, -6）的抛物线y=ax 2+bx+c 经过点（-1, -4）,则下列结论:-1;⑤若点（-2, m ） , （- 5, n ）在抛物线上，则 m>n,其中正确的个数共有（二.填空题⑥y= （ x+1 ） 2- x 2.这六个式子中，二次函数有12.把二次函数 y=x 2- 4x+5化为y=a （x —h ） 2+k 的形式，那么h+k=A . y= 3x 2+2B . y= 3x2 - 2C. y=3 (x — 2) 2D. y=3 (x+2) 26.二次函数y= ax 2+bx+c 的图象如图所示，其对称轴是x=-1, 卜列结论中正确的是（8.二次函数C. 2a+b=0D. a - b+c>2 (x-1) 2+b (aw0)的图象经过点(0, 2) a+b 的值是（ B. - 1C. 2D. 3 x 2- 2x+c 在-3< x< 2的范围内有最大值为一5, 则c 的值是（B. 3C. - 3D. - 69.二次函数 y=ax 2—2ax+b 中，当—1wxw 4 时，—2wyw3,贝U b — a 的值为( B. - 6或 7C. 3D. 3 或—2①b 2>4ac ；② ax 2+bx+c< - 6；③ 9a- 3b+c= - 6；④关于 x 的二次方程 ax 2+ bx+ c= - 4 的根为B. 2个C. 3个D. 4个11.观察：① y = 6x 2；② y=- 3x 2+5；③2 1y=200x 2+400x+200;④ y=x 3-2x;⑤ ¥二工 二.（只填序号）13. 一名男生参加抛实心球测试，已知球的高度 y （m ）与水平距离 x （m ）之间的关系是7.二次函数 y= a2B. 4ac< b -114 .已知抛物线的顶点坐标是(-2, 3),其图象是由抛物线 y=-8x 2+1平移得到的，则该抛物线的解析式为.15 .抛物线y=a (x- h) 2+k (a<0)经过(-1,3)、( 5, 3)两点，则关于 x 的不等式a (x- h -1) 2+k<3的解集为.16 .已知二次函数 y=ax 2+bx+c (aw0, a, b, c,为常数)，对称轴为直线 x=1,它的部分自变量x 与函数值y 的对应值如下表.请写出ax 2+bc+c= 0的一个正数解的近似值 (精确到0.1)x - 0.4 — 0.3 — 0.2 — 0.117 .若函数y=x 2+2x+m 的图象与x 轴没有交点，则 m 的取值范围是 .18 .已知二次函数 y=ax 2+ (a-1) x- 2a+1,当1vxv3时，y 随x 的增大而减小，则 a 的取值范围是.19 .如果二次函数y=a (x-1) 2(aw0)的图象在它的对称轴右侧部分是上升的，那么a 的取值范围是.20 .小甬是一个喜欢探究钻研的同学，他在和同学们一起研究某条抛物线y=-/父2的性质时，将一个直角三角板的直角顶点置于平面直角坐标系的原点 O,两直角边与该抛物线交于A, B 两点 (如图)，对该抛物线，小甬将三角板绕点 O 旋转任意角度时惊奇地发现，交点A, B 的连线段总经过一个固定的点，则该点的坐标是三.解答题21 .已知二次函数 y=2x 2+4x- 6,(1)将二次函数的解析式化为y= a (x-h) 2+k 的形式.(2)写出二次函数图象的开口方向、对称轴、顶点坐标. 22 .已知二次函数(k 为常数)，求k 的值.__ 1 2 产12工m,则这名男生抛实心球的成绩是3m.y= ax 2+ bx+c0.920.38—0.12—0.5823.在平面直角坐标系xOy中，抛物线y= ax2+4ax+4a-4 (aw0)的顶点为A.(1)求顶点A的坐标；(2)过点(0, 5)且平行于x轴的直线1,与抛物线y=ax2+4ax+4-4 (aw 0)交于B、C两点.①当a=1时，求线段BC的长；②当线段BC的长不小于8时，直接写出a的取值范围.532 -11— I I E II」] ■ I J 、-5 一4 4-2 口, 1 2 3 4 5x-2~-3-4-5 _____________24.已知二次函数的图象y=- x2+bx+c如图所示，它与轴的交点坐标为(- 1,0), (3, 0)(1)求b, c的值；(2)根据图象，直接写出函数值y<0时，自变量x的取值范围.25.二次函数y=ax2+bx+c (aw0)与一次函数y=x+k (kw0)的图象如图所示，根据图象解答下列问题：(1)写出方程ax2+bx+c=0的两个根；(2)写出不等式ax2+bx+c- x- k< 0的解集；(3)写出二次函数值y随x的增大而减小的自变量x的取值范围；(4)若方程ax2+bx+c= m有两个不等的实数根，求m的取值范围;26.如图，一段长为45m的篱笆围成一个一边靠墙的矩形花园，墙长为27m,设花园的面积为sm2,平行于墙的边为xm.若x不小于17m,(1)求出s关于x的函数关系式;(2)求s的最大值与最小值.花园27.在平面直角坐标系xOy中，二次函数y = x2-2mx+1图象与y轴的交点为A,将点A向右平移4个单位长度，向上平移1个单位长度得到点B.(1)直接写出点A的坐标为，点B的坐标为;(2)若函数y=x2-2mx+1的图象与线段AB恰有一个公共点，求m的取值范围.参考答案与试题解析・选择题1.解：A、是一次函数，故此选项不符合题意；B、是二次函数，故此选项符合题意；C、当a=0时不是二次函数，故此选项不符合题意；D、不是二次函数，故此选项不符合题意；故选：B.2.解：根据“左加右减，上加下减”的法则可知，将抛物线y= 2x2+5向左平移3个单位，再向下平移1个单位，那么所得到抛物线的函数关系式是y=2 (x+3) 2+4.故选：B.3.解：y关于x的函数表达式为：y=g (50+2-x) x b-l= ---- x+26x (2W x<52).故选：A.4,解：①当a>0时，二次函数y= ax2-a的图象开口向上、对称轴为y轴、顶点在y轴负半轴，一次函数y= ax - a (aw0)的图象经过第一、三、四象限，且两个函数的图象交于y轴同一点；②当a<0时，二次函数y= ax2-a的图象开口向下、对称轴为y轴、顶点在y轴正半轴，一次函数y=ax-a (aw0)的图象经过第一、二、四象限，且两个函数的图象交于y轴同一点.对照四个选项可知D正确.故选：D.5.解：抛物线y= 3x2+2的顶点为(0, 2);抛物线y= 3x2-2的顶点为(0, - 2);抛物线y=3 (x-2) 2的顶点为(2, 0);抛物线y=3 (x+2) 2的顶点为(-2, 0);故选：C.6.解：A、由抛物线的开口向下知a<0,对称轴在y轴的左侧，a、b同号，即b<0,与y轴的交点为在y轴的正半轴上，. 0,因此abc>0,故错误;B、抛物线与x轴有两个交点，b2 - 4ac>0,即4acv b2,故正确;C、对称轴为x= ----- --= - 1,得2a = b,23.2a- b= 0,故错误；D、•.当x= - 1 时，y>0• -a- b+c>0,故错误.故选：B.7.解：二.二次函数y=a (x- 1) 2+b (aw0)的图象经过点(0, 2),a+b = 2.故选：C.8.解：把二次函数y= - x2-2x+c转化成顶点坐标式为y= - (x+1) 2+c+l,又知二次函数的开口向下，对称轴为x=- 1,故当x= - 1时，二次函数有最大值为- 5,故-1+2+c= - 5,故c= - 6.故选：D.2 29.解：:抛物线y=ax — 2ax+b=a (x—1) +b- a,「•顶点(1, b - a)当a>0 时，当-1WxW4 时，—2WyW3,函数有最小值，b - a= - 2,当a<0 时，当—1wxw4 时，—2wyw3,函数有最大值，b - a= 3,故选：D.10.解：二•抛物线与x轴有2个交点，•・△= b2- 4ac>0,即b2>4ac,所以①正确；•.•抛物线的顶点坐标为(-3, - 6),即x= - 3时，函数有最小值，•.ax2+bx+c> - 6,所以②错误；•.•抛物线的顶点坐标为(-3, - 6),•••9a-3b+c= - 6,所以③正确；•••抛物线y= ax2+bx+c 经过点(-1, - 4),而抛物线的对称轴为直线x= - 3,.二点(-1, - 4)关于直线x= - 3的对称点(-5, - 4)在抛物线上，••・关于x的一元二次方程ax2+bx+c= - 4的两根为-5和-1 ,所以④错误；•••抛物线开口向上，对称轴为直线x= - 3,而点(-2, m) , ( - 5, n)在抛物线上，: - 3 - ( - 5) > - 2 - ( - 3),m<n,所以⑤错误.故选：B.二.填空题11.解：这六个式子中，二次函数有：①y=6x2；②y=- 3x2+5；③y= 200x2+400x+200;故答案为：①②③.12.解：y=x —4x+5= ( x _ 2) 2+1,. .h=2, k= 1,h+k=2+1= 3.故答案为：3.13.解：•••一名男生参加抛实心球测试，已知球的高度y (m)与水平距离x (m)之间的关系是7T小亭卷i 2: 1・・・当y=0,则0 = - y；5-x2+Vx+—, _L 乙O R-J解得：x1= 10, x2= - 2,，这名男生抛实心球的成绩为10m,故答案为：10.14.解：,•,该抛物线是由抛物线y= - 8x2+1平移得到的，a= - 8,又•••抛物线的顶点坐标是(- 2, 3),该抛物线的解析式为y=- 8 (x+2) 2+3.故答案为：y=- 8 (x+2) 2+3.15.解：二.抛物线y=a (x-h) 2+k (a>0)经过(-1, 3) , ( 5, 3)两点,，大致图象如图所示：•1-y= a (x- h- 1) 2+k (a>0)经过(0, 3) , (6, 3)两点则关于x的不等式a (x-h-1) 2+kW3的解集为：x< 0或x>6.故答案为：*^0或*>6.16.解：由表可知，当x= - 0.2时，y的值最接近0, 所以，方程ax2+bx+c= 0一个解的近似值为-0.2, 设正数解的近似值为a,.•.对称轴为直线x=1,一+(一。
2020-2021初中数学二次函数基础测试题及答案解析
2020-2021初中数学二次函数基础测试题及答案解析一、选择题1．若二次函数22y ax ax c =-+的图象经过点（﹣1，0），则方程220ax ax c -+=的解为（ ）A ．13x =-，21x =-B ．11x =，23x =C ．11x =-，23x =D ．13x =-，21x =【答案】C 【解析】 【分析】 【详解】∵二次函数22y ax ax c =-+的图象经过点（﹣1，0），∴方程220ax ax c -+=一定有一个解为：x=﹣1，∵抛物线的对称轴为：直线x=1，∴二次函数22y ax ax c =-+的图象与x 轴的另一个交点为：（3，0），∴方程220ax ax c -+=的解为：11x =-，23x =． 故选C ．考点：抛物线与x 轴的交点．2．如图，二次函数()200y ax bx c a =++=≠的图象与x 轴正半轴相交于A 、B 两点，与y 轴相交于点C ，对称轴为直线2x =，且OA OC =，则下列结论：①0abc >；②930a b c ++<；③1c >-；④关于x 的方程()200ax bx c a ++=≠有一个根为1a-，其中正确的结论个数有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】 【分析】由二次图像开口方向、对称轴与y 轴的交点可判断出a 、b 、c 的符号，从而可判断①；由图像可知当x ＝3时，y ＜0，可判断②；由OA ＝OC ，且OA ＜1，可判断③；把﹣1a代入方程整理得ac 2－bc ＋c ＝0，结合③可判断④；从而得出答案. 【详解】由图像开口向下，可知a ＜0，与y 轴的交点在x 轴的下方，可知c ＜0，又对称轴方程为x ＝2，∴﹣2ba＞0，∴b ＞0，∴abc ＞0，故①正确；由图像可知当x ＝3时，y ＞0，∴9a ＋3b ＋c ＞0，故②错误；由图像可知OA ＜1，∵OA ＝OC ，∴OC ＜1，即﹣c ＜1，故③正确；假设方程的一个根为x ＝﹣1a ，把﹣1a代入方程，整理得ac 2－bc ＋c ＝0， 即方程有一个根为x ＝﹣c ，由②知﹣c ＝OA ，而当x ＝OA 是方程的根，∴x ＝﹣c 是方程的根，即假设成立，故④正确.故选C. 【点睛】本题主要考查二次函数的图像与性质以及二次函数与一元二次方程的联系，熟练掌握二次函数的相关知识是解答此题的关键.3．对于二次函数()21202y ax a x a ⎛⎫=+-<⎪⎝⎭，下列说法正确的个数是（ ） ①对于任何满足条件的a ，该二次函数的图象都经过点()2,1和()0,0两点； ②若该函数图象的对称轴为直线0x x =，则必有001x <<； ③当0x ≥时，y 随x 的增大而增大；④若()14,P y ，()()24,0Q m y m +>是函数图象上的两点，如果12y y >总成立，则112a ≤-． A ．1个 B ．2个C ．3个D ．4个【答案】B 【解析】 【分析】根据二次函数的图象与性质（对称性、增减性）逐个判断即可． 【详解】对于()21202y ax a x a ⎛⎫=+-< ⎪⎝⎭当2x =时，142(2)12y a a =+-=，则二次函数的图象都经过点()2,1 当0x =时，0y =，则二次函数的图象都经过点()0,0 则说法①正确此二次函数的对称轴为1212124ax a a-=-=-+0a <Q 1114a∴-+> 01x ∴>，则说法②错误由二次函数的性质可知，抛物线的开口向下，当114x a<-+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小 因11104a-+>> 则当1014x a <-≤+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小 即说法③错误0m >Q44m ∴+>由12y y >总成立得，其对称轴1144x a=-+≤ 解得112a ≤-，则说法④正确 综上，说法正确的个数是2个 故选：B ． 【点睛】本题考查了二次函数的图象与性质（对称性、增减性），熟练掌握二次函数的图象与性质是解题关键．4．如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数by x=在同平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．【答案】D 【解析】 【分析】直接利用二次函数图象经过的象限得出a ，b ，c 的值取值范围，进而利用一次函数与反比例函数的性质得出答案． 【详解】∵二次函数y=ax 2+bx+c 的图象开口向下，∴a ＜0，∵二次函数y=ax 2+bx+c 的图象经过原点， ∴c=0，∵二次函数y=ax 2+bx+c 的图象对称轴在y 轴左侧， ∴a ，b 同号， ∴b ＜0，∴一次函数y=ax+c ，图象经过第二、四象限， 反比例函数y=bx图象分布在第二、四象限， 故选D ． 【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象，正确把握相关性质是解题关键．5．将抛物线243y x x =-+平移，使它平移后图象的顶点为()2,4-，则需将该抛物线（ ）A ．先向右平移4个单位，再向上平移5个单位B ．先向右平移4个单位，再向下平移5个单位C ．先向左平移4个单位，再向上平移5个单位D ．先向左平移4个单位，再向下平移5个单位 【答案】C 【解析】 【分析】 先把抛物线243y x x =-+化为顶点式，再根据函数图象平移的法则进行解答即可．【详解】 ∵抛物线243y x x =-+可化为()221y x =--∴其顶点坐标为：(2,−1)，∴若使其平移后的顶点为(−2,4)则先向左平移4个单位，再向上平移5个单位． 故选C. 【点睛】本题考查二次函数图像，熟练掌握平移是性质是解题关键.6．如图，二次函数y ＝ax 2+bx +c 的图象过点A （3，0），对称轴为直线x ＝1，给出以下结论：①abc ＜0；②3a +c ＝0；③ax 2+bx ≤a +b ；④若M （﹣0.5，y 1）、N （2.5，y 2）为函数图象上的两点，则y 1＜y 2．其中正确的是（ ）A ．①③④B ．①②3④C ．①②③D ．②③④【答案】C 【解析】 【分析】根据二次函数的图象与性质即可求出答案． 【详解】解：①由图象可知：a ＜0，c ＞0， 由对称轴可知：2ba-＞0， ∴b ＞0，∴abc ＜0，故①正确； ②由对称轴可知：2ba-＝1， ∴b ＝﹣2a ，∵抛物线过点（3，0）， ∴0＝9a+3b+c ， ∴9a ﹣6a+c ＝0， ∴3a+c ＝0，故②正确；③当x ＝1时，y 取最大值，y 的最大值为a+b+c ， 当x 取全体实数时，ax 2+bx+c≤a+b+c ， 即ax 2+bx≤a+b ，故③正确；④（﹣0.5，y 1）关于对称轴x ＝1的对称点为（2.5，y 1）： ∴y 1＝y 2，故④错误； 故选：C ． 【点睛】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于中等题型．7．二次函数y ＝x 2+bx 的对称轴为直线x ＝2，若关于x 的一元二次方程x 2+bx ﹣t ＝0（t 为实数）在﹣1＜x ＜4的范围内有解，则t 的取值范围是（ ） A ．0＜t ＜5 B ．﹣4≤t ＜5C ．﹣4≤t ＜0D ．t ≥﹣4【答案】B 【解析】 【分析】先求出b，确定二次函数解析式，关于x的一元二次方程x2+bx﹣t＝0的解可以看成二次函数y＝x2﹣4x与直线y＝t的交点，﹣1＜x＜4时﹣4≤y＜5，进而求解；【详解】解：∵对称轴为直线x＝2，∴b＝﹣4，∴y＝x2﹣4x，关于x的一元二次方程x2+bx﹣t＝0的解可以看成二次函数y＝x2﹣4x与直线y＝t的交点，∵﹣1＜x＜4，∴二次函数y的取值为﹣4≤y＜5，∴﹣4≤t＜5；故选：B．【点睛】本题考查二次函数图象的性质，一元二次方程的解；将一元二次方程的解转换为二次函数与直线交点问题，数形结合的解决问题是解题的关键．8．足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线. 不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表：下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线92t ；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m. 其中正确结论的个数是（）A．1 B．2 C．3 D．4【答案】B【解析】【分析】【详解】解：由题意，抛物线的解析式为y=ax（x﹣9），把（1，8）代入可得a=﹣1，∴y=﹣t2+9t=﹣（t﹣4.5）2+20.25，∴足球距离地面的最大高度为20.25m，故①错误，∴抛物线的对称轴t=4.5，故②正确，∵t=9时，y=0，∴足球被踢出9s时落地，故③正确，∵t=1.5时，y=11.25，故④错误，∴正确的有②③，故选B．9．如图，矩形ABCD 的周长是28cm ，且AB 比BC 长2cm ．若点P 从点A 出发，以1/cm s 的速度沿A D C →→方向匀速运动，同时点Q 从点A 出发，以2/cm s 的速度沿A B C →→方向匀速运动，当一个点到达点C 时，另一个点也随之停止运动．若设运动时间为()t s ，APQ V 的面积为()2cmS ，则()2cm S 与()t s 之间的函数图象大致是（ ）A ．B ．C ．D ．【答案】A 【解析】 【分析】先根据条件求出AB 、AD 的长，当0≤t≤4时，Q 在边AB 上，P 在边AD 上，如图1，计算S 与t 的关系式，分析图像可排除选项B 、C ；当4＜t≤6时，Q 在边BC 上，P 在边AD 上，如图2，计算S 与t 的关系式，分析图像即可排除选项D ，从而得结论． 【详解】解：由题意得2228AB BC +=，2AB BC =+， 可解得8AB =，6BC =，即6AD =，①当0≤t≤4时，Q 在边AB 上，P 在边AD 上，如图1，S △APQ =211222AP AQ t t t ==g g ， 图像是开口向上的抛物线，故选项B 、C 不正确； ②当4＜t≤6时，Q 在边BC 上，P 在边AD 上，如图2，S △APQ =118422AP AB t t =⨯=g ， 图像是一条线段，故选项D 不正确； 故选：A ． 【点睛】本题考查了动点问题的函数图象，根据动点P 和Q 的位置的不同确定三角形面积的不同，解决本题的关键是利用分类讨论的思想求出S 与t 的函数关系式．10．如图，ABC ∆为等边三角形，点P 从A 出发，沿A B C A →→→作匀速运动，则线段AP 的长度y 与运动时间x 之间的函数关系大致是（ ）A ．B ．C ．D ．【答案】B 【解析】 【分析】根据题意可知点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故可排除选项C 与D ；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值，故选项B 符合题意，选项A 不合题意． 【详解】根据题意得，点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故选项C 与选项D 不合题意；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值， ∴选项B 符合题意，选项A 不合题意． 故选B ． 【点睛】本题考查了动点问题的函数图象：通过分类讨论，利用三角形面积公式得到y 与x 的函数关系，然后根据二次函数和一次函数图象与性质解决问题．11．二次函数y=ax 2+bx+c （a≠0）的图象如图，给出下列四个结论：①4ac ﹣b 2＜0；②4a+c ＜2b ；③3b+2c ＜0；④m （am+b ）+b ＜a （m≠﹣1），其中正确结论的个数是（ ）A ．4个B ．3个C ．2个D ．1个【答案】B 【解析】 【分析】 【详解】解：∵抛物线和x 轴有两个交点， ∴b 2﹣4ac ＞0，∴4ac ﹣b 2＜0，∴①正确；∵对称轴是直线x ﹣1，和x 轴的一个交点在点（0，0）和点（1，0）之间， ∴抛物线和x 轴的另一个交点在（﹣3，0）和（﹣2，0）之间， ∴把（﹣2，0）代入抛物线得：y=4a ﹣2b+c ＞0， ∴4a+c ＞2b ，∴②错误；∵把（1，0）代入抛物线得：y=a+b+c ＜0， ∴2a+2b+2c ＜0， ∵b=2a ，∴3b ，2c ＜0，∴③正确； ∵抛物线的对称轴是直线x=﹣1， ∴y=a ﹣b+c 的值最大，即把（m ，0）（m≠0）代入得：y=am 2+bm+c ＜a ﹣b+c ， ∴am 2+bm+b ＜a ，即m （am+b ）+b ＜a ，∴④正确； 即正确的有3个， 故选B ．考点：二次函数图象与系数的关系12．如图，已知()4,1A --，线段AB 与x 轴平行，且2AB =，抛物线2y x mx n =-++经过点()0,3C 和()3,0D ，若线段AB 以每秒2个单位长度的速度向下平移，设平移的时间为t （秒）.若抛物线与线段AB 有公共点，则t 的取值范围是（ ）A ．010t ≤≤B ．210t ≤≤C ．28t ≤≤D ．210t <<【答案】B 【解析】 【分析】直接利用待定系数法求出二次函数，得出B 点坐标，分别得出当抛物线l 经过点B 时，当抛物线l 经过点A 时，求出y 的值，进而得出t 的取值范围； 【详解】解：（1）把点C （0，3）和D （3，0）的坐标代入y=-x 2+mx+n 中，得，23330n m n =⎧⎨-++=⎩解得32n m =⎧⎨=⎩∴抛物线l 解析式为y=-x 2+2x+3，设点B 的坐标为（-2，-1-2t ），点A 的坐标为（-4，-1-2t ）， 当抛物线l 经过点B 时，有y=-（-2）2+2×（-2）+3=-5， 当抛物线l 经过点A 时，有y=-（-4）2+2×（-4）+3=-21， 当抛物线l 与线段AB 总有公共点时，有-21≤-1-2t≤-5， 解得：2≤t≤10． 故应选B 【点睛】此题主要考查了二次函数综合以及不等式组的解法等知识，正确利用数形结合分析得出关于t 的不等式是解题关键．13．抛物线y=–x 2+bx+c 上部分点的横坐标x 、纵坐标y 的对应值如下表所示： x … –2 –1 0 1 2 … y…4664…从上表可知，下列说法错误的是A ．抛物线与x 轴的一个交点坐标为(–2，0)B ．抛物线与y 轴的交点坐标为(0，6)C ．抛物线的对称轴是直线x=0D ．抛物线在对称轴左侧部分是上升的【答案】C【解析】【分析】【详解】解：当x=-2时，y=0，∴抛物线过（-2，0），∴抛物线与x轴的一个交点坐标为（-2，0），故A正确；当x=0时，y=6，∴抛物线与y轴的交点坐标为（0，6），故B正确；当x=0和x=1时，y=6，∴对称轴为x=12，故C错误；当x＜12时，y随x的增大而增大，∴抛物线在对称轴左侧部分是上升的，故D正确；故选C．14．如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③13＜a＜23；④b＞c．其中含所有正确结论的选项是（）A．①②③B．①③④C．②③④D．①②④【答案】B【解析】【分析】根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号，从而判断①；根据对称性得到函数图象经过（3，0），则得②的判断；根据图象经过（-1，0）可得到a、b、c 之间的关系，从而对④作判断；从图象与y轴的交点B在（0，-2）和（0，-1）之间可以判断c的大小得出③的正误．【详解】①∵函数开口方向向上，∴a＞0；∵对称轴在y 轴右侧 ∴ab 异号，∵抛物线与y 轴交点在y 轴负半轴， ∴c ＜0， ∴abc ＞0， 故①正确；②∵图象与x 轴交于点A （-1，0），对称轴为直线x=1， ∴图象与x 轴的另一个交点为（3，0）， ∴当x=2时，y ＜0， ∴4a+2b+c ＜0， 故②错误；③∵图象与y 轴的交点B 在（0，-2）和（0，-1）之间， ∴-2＜c ＜-1∵-12ba ， ∴b=-2a ，∵函数图象经过（-1，0）， ∴a-b+c=0， ∴c=-3a ， ∴-2＜-3a ＜-1， ∴13＜a ＜23；故③正确 ④∵函数图象经过（-1，0）， ∴a-b+c=0， ∴b-c=a ， ∵a ＞0，∴b-c ＞0，即b ＞c ； 故④正确； 故选B ． 【点睛】主要考查图象与二次函数系数之间的关系．解题关键是注意掌握数形结合思想的应用．15．二次函数y ＝ax 2+bx +c （a ≠0）中的x 与y 的部分对应值如下表：给出以下结论：（1）二次函数y ＝ax 2+bx +c 有最小值，最小值为﹣3；（2）当﹣12＜x ＜2时，y ＜0；（3）已知点A （x 1，y 1）、B （x 2，y 2）在函数的图象上，则当﹣1＜x 1＜0，3＜x 2＜4时，y 1＞y 2．上述结论中正确的结论个数为（ ） A ．0 B ．1C ．2D ．3【答案】B 【解析】 【分析】根据表格的数据，以及二次函数的性质，即可对每个选项进行判断. 【详解】解：（1）函数的对称轴为：x ＝1，最小值为﹣4，故错误，不符合题意； （2）从表格可以看出，当﹣12＜x ＜2时，y ＜0，符合题意； （3）﹣1＜x 1＜0，3＜x 2＜4时，x 2离对称轴远，故错误，不符合题意； 故选择：B ． 【点睛】本题考查了二次函数的最值，抛物线与x 轴的交点，仔细分析表格数据，熟练掌握二次函数的性质是解题的关键．16．已知抛物线224y x x c =-+与直线2y =有两个不同的交点．下列结论：①4c <；②当1x =时，y 有最小值2c -；③方程22420x x c -+-=有两个不等实根；④若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形，则52c =；其中正确的结论的个数是（ ） A ．4 B ．3 C ．2D ．1【答案】B 【解析】 【分析】根据“抛物线224y x x c =-+与直线2y =有两个不同的交点”即可判断①③；根据抛物线的对称轴为直线x=1即可判断②；根据等腰直角三角形的性质，用c 表达出两个交点，代入抛物线解析式计算即可判断④． 【详解】解：∵抛物线224y x x c =-+与直线2y =有两个不同的交点，∴2242x x c -+=有两个不相等的实数根，即22420x x c -+-=有两个不相等的实数根，故③正确，∴1642(2)0c ∆=-⨯⨯->，解得：4c <，故①正确； ∵抛物线的对称轴为直线x=1，且抛物线开口向上， ∴当x=1时，2y c =-为最小值，故②正确；若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形， 则顶点（1，c-2）到直线y=2的距离等于两交点距离的一半，∵顶点（1，c-2）到直线y=2的距离为2-（c-2）=4-c ， ∴两交点的横坐标分别为1-（4-c ）=c-3与1+（4-c ）=5-c ∴两交点坐标为（c-3,2）与（5-c,2），将（c-3,2）代入224y x x c =-+中得：22(3)4(3)2c c c ---+=解得：72c =或4c = ∵4c <，∴72c =，故④错误， ∴正确的有①②③， 故选：B ． 【点睛】本题考查了二次函数与一元二次方程的关系以及二次函数的性质，解题的关键是熟练掌握函数与方程之间的联系．17．已知抛物线y=x 2+2x 上三点A （﹣5，y 1），B （2.5，y 2），C （12，y 3），则y 1，y 2，y 3满足的关系式为（ ）A ．y 1＜y 2＜y 3B ．y 3＜y 2＜y 1C ．y 2＜y 1＜y 3D ．y 3＜y 1＜y 2 【答案】C 【解析】 【分析】首先求出抛物线y=x 2+2x 的对称轴，对称轴为直线x=-1；然后根据A 、B 、C 的横坐标与对称轴的位置，接着利用抛物线的增减性质即可求解；由B 离对称轴最近，A 次之，C 最远，则对应y 的值大小可确定. 【详解】 ∵抛物线y=x 2+2x ， ∴x=-1，而A （-5，y 1），B （2.5，y 2），C （12，y 3）， ∴B 离对称轴最近，A 次之，C 最远， ∴y 2＜y 1＜y 3． 故选:C ． 【点睛】本题考查了二次函数的图象和性质，二次函数图象上点的坐标特征等知识点，能熟记二次函数的性质是解此题的关键．18．如图1，△ABC 中，∠A ＝30°，点P 从点A 出发以2cm /s 的速度沿折线A →C →B 运动，点Q 从点A 出发以vcm /s 的速度沿AB 运动，P ，Q 两点同时出发，当某一点运动到点B 时，两点同时停止运动．设运动时间为x （s ），△APQ 的面积为y （cm 2），y 关于x 的函数图象由C1，C2两段组成，如图2所示，有下列结论：①v＝1；②sin B＝13；③图象C2段的函数表达式为y＝﹣13x2+103x；④△APQ面积的最大值为8，其中正确有（）A．①②B．①②④C．①③④D．①②③④【答案】A【解析】【分析】①根据题意列出y＝12AP•AQ•sin A，即可解答②根据图像可知PQ同时到达B，则AB＝5，AC+CB＝10，再代入即可③把sin B＝13，代入解析式即可④根据题意可知当x＝﹣522ba时，y最大＝2512【详解】①当点P在AC上运动时，y＝12AP•AQ•sin A＝12×2x•vx＝vx2，当x＝1，y＝12时，得v＝1，故此选项正确；②由图象可知，PQ同时到达B，则AB＝5，AC+CB＝10，当P在BC上时y＝12•x•（10﹣2x）•sin B，当x＝4，y＝43时，代入解得sin B＝13，故此选项正确；③∵sin B＝13，∴当P在BC上时y＝12•x（10﹣2x）×13＝﹣13x2+53x，∴图象C2段的函数表达式为y＝﹣13x2+53x，故此选项不正确；④∵y ＝﹣13x 2+53x ， ∴当x ＝﹣522b a =时，y 最大＝2512， 故此选项不正确； 故选A ． 【点睛】此题考查了二次函数的运用，解题关键在于看图理解19．在同一直角坐标系中，反比例函数图像与二次函数图像的交点的个数至少有( ) A ．0 B ．1C ．2D ．3【答案】B 【解析】 【分析】根据二次函数和反比例函数的图象位置，画出图象，直接判断交点个数． 【详解】若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第一，三象限，故两个函数的交点只有一个，在第三象限．同理，若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第二，四象限，故两个函数的交点只有一个，在第四象限． 故答案为：B ．【点睛】本题考查了二次函数和反比例函数的图象问题，掌握二次函数和反比例函数的图象性质是解题的关键．20．在平面直角坐标系中，点P 的坐标为()1,2，将抛物线21322y x x =-+沿坐标轴平移一次，使其经过点P ，则平移的最短距离为（ ） A ．12B ．1C ．5D ．52【答案】B 【解析】 【分析】先求出平移后P 点对应点的坐标，求出平移距离，即可得出选项． 【详解】 解：21322y x x =-+=()215322x --， 当沿水平方向平移时，纵坐标和P 的纵坐标相同，把y=2代入得： 解得：x=0或6， 平移的最短距离为1-0=1；当沿竖直方向平移时，横坐标和P 的横坐标相同，把x=1代入得： 解得：y=12-， 平移的最短距离为152=22⎛⎫--⎪⎝⎭， 即平移的最短距离是1， 故选B. 【点睛】本题考查了二次函数图象上点的坐标特征，能求出平移后对应的点的坐标是解此题的关键．。
2020-2021初中数学二次函数基础测试题及解析
2020-2021初中数学二次函数基础测试题及解析一、选择题1．若二次函数22y ax ax c =-+的图象经过点（﹣1，0），则方程220ax ax c -+=的解为（ ）A ．13x =-，21x =-B ．11x =，23x =C ．11x =-，23x =D ．13x =-，21x =【答案】C【解析】【分析】【详解】∵二次函数22y ax ax c =-+的图象经过点（﹣1，0），∴方程220ax ax c -+=一定有一个解为：x=﹣1，∵抛物线的对称轴为：直线x=1，∴二次函数22y ax ax c =-+的图象与x 轴的另一个交点为：（3，0），∴方程220ax ax c -+=的解为：11x =-，23x =． 故选C ．考点：抛物线与x 轴的交点．2．如图，抛物线y=ax 2+bx+c （a≠0）过点（1，0）和点（0，﹣2），且顶点在第三象限，设P=a ﹣b+c ，则P 的取值范围是( )A ．﹣4＜P ＜0B ．﹣4＜P ＜﹣2C ．﹣2＜P ＜0D ．﹣1＜P ＜0【答案】A【解析】【分析】【详解】 解:∵二次函数的图象开口向上，∴a ＞0．∵对称轴在y 轴的左边，∴b 2a-＜0．∴b ＞0． ∵图象与y 轴的交点坐标是（0，﹣2），过（1，0）点，代入得：a+b ﹣2=0． ∴a=2﹣b ，b=2﹣a ．∴y=ax 2+（2﹣a ）x ﹣2．把x=﹣1代入得：y=a ﹣（2﹣a ）﹣2=2a ﹣4，∵b ＞0，∴b=2﹣a ＞0．∴a ＜2．∵a ＞0，∴0＜a ＜2．∴0＜2a ＜4．∴﹣4＜2a ﹣4＜0，即﹣4＜P ＜0．故选A ．【点睛】本题考查二次函数图象与系数的关系，利用数形结合思想解题是本题的解题关键．3．已知抛物线2y ax bx c =++与x 轴的一个交点坐标为(4,0)，其部分图象如图所示，下列结论：①抛物线一定过原点；②方程()200++=≠ax bx c a 的解为0x =或4；③0a b c -+<；④当04x <<时，20ax bx c ++<；⑤当2x <时，y 随x 增大而增大．其中结论正确的个数有（ ）A ．1B ．2C ．3D ．4【答案】D【解析】【分析】 根据题意，求得,,a b c ，根据二次函数的图像和性质，结合选项进行逐一分析，即可判断.【详解】 由题可知22b a-=，与x 轴的一个交点坐标为(4,0)，则另一个交点坐标为()0,0， 故可得1640a b c ++=，0c， 故可得4,0a b c -==①因为0c ，故①正确；②因为二次函数过点()()0,0,4,0，故②正确；③当1x =-时，函数值为0a b c -+<，故③正确；④由图可知，当04x <<时，0y <，故④正确；⑤由图可知，当2x <时，y 随x 增大而减小，故⑤错误；故选：D.【点睛】本题考查二次函数的图像和性质，涉及二次函数的增减性，属综合中档题.4．如图是抛物线y ＝ax 2+bx +c （a ≠0）的部分图象，其顶点坐标为（1，n ），且与x 轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①4a ﹣2b +c ＞0；②3a +b ＞0；③b 2＝4a （c ﹣n ）；④一元二次方程ax 2+bx +c ＝n ﹣1有两个互异实根．其中正确结论的个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】 根据二次函数图象和性质，开口向下，可得a<0，对称轴x=1，利用顶点坐标，图象与x 轴的交点情况，对照选项逐一分析即可．【详解】①∵抛物线与x 轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x ＝1，∴抛物线与x 轴的另一个交点在点（﹣2，0）和（﹣1，0）之间，∴当x ＝﹣2时，y ＜0，即4a ﹣2b +c ＜0，所以①不符合题意；②∵抛物线的对称轴为直线x ＝﹣2b a＝1，即b ＝﹣2a ， ∴3a +b ＝3a ﹣2a ＝a <0，所以②不符合题意；③∵抛物线的顶点坐标为（1，n ）， ∴244ac b a＝n ， ∴b 2＝4ac ﹣4an ＝4a （c ﹣n ），所以③符合题意；④∵抛物线与直线y ＝n 有一个公共点，∴抛物线与直线y ＝n ﹣1有2个公共点，∴一元二次方程ax 2+bx +c ＝n ﹣1有两个不相等的实数根，所以④符合题意．故选：B ．【点睛】本题考查了二次函数的图象和性质的应用，二次函数开口方向，对称轴，交点位置，二次函数与一次函数图象结合判定方程根的个数，掌握二次函数的图象和性质是解题的关键．5．将抛物线243y x x =-+平移，使它平移后图象的顶点为()2,4-，则需将该抛物线（ ） A ．先向右平移4个单位，再向上平移5个单位 B ．先向右平移4个单位，再向下平移5个单位C ．先向左平移4个单位，再向上平移5个单位D ．先向左平移4个单位，再向下平移5个单位【答案】C【解析】【分析】先把抛物线243y x x =-+化为顶点式，再根据函数图象平移的法则进行解答即可． 【详解】∵抛物线243y x x =-+可化为()221y x =--∴其顶点坐标为：(2,−1)，∴若使其平移后的顶点为(−2,4)则先向左平移4个单位，再向上平移5个单位． 故选C.【点睛】本题考查二次函数图像，熟练掌握平移是性质是解题关键.6．已知二次函数y =ax 2+bx +c 的图象如图所示，有以下结论：①a +b +c ＜0；②a ﹣b +c ＞1；③abc ＞0；④9a ﹣3b +c ＜0；⑤c ﹣a ＞1．其中所有正确结论的序号是( )A ．①②B ．①③④C ．①②③④D ．①②③④⑤【答案】D【解析】【分析】 根据抛物线的开口方向可得出a 的符号，再由抛物线与y 轴的交点可得出c 的值，然后进一步根据对称轴以及抛物线得出当x 1=、 x 1=-、x 3=-时的情况进一步综合判断即可．【详解】由图象可知，a ＜0，c=1，对称轴：x=b 12a-=-，∴b=2a，①由图可知：当x=1时，y＜0，∴a+b+c＜0，正确；②由图可知：当x=−1时，y＞1，∴a−b+c＞1，正确；③abc=2a2＞0，正确；④由图可知：当x=−3时，y＜0，∴9a−3b+c＜0，正确；⑤c−a=1−a＞1，正确；∴①②③④⑤正确．故选：D．【点睛】本题主要考查了抛物线的函数图像性质的综合运用，熟练掌握相关概念是解题关键．7．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＜0；（2）方程ax2+bx+c＝0两根都大于零；（3）y随x的增大而增大；（4）一次函数y＝x+bc 的图象一定不过第二象限．其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【解析】【分析】由图可知，x=2时函数值小于0，故（1）正确，函数与x轴的交点为x=1.x=3，都大于0，故（2）正确，由图像知（3）错误，由图象开口向上，a＞0，与y轴交于正半轴，c＞0，对称轴x=﹣＝1，故b＜0，bc＜0，即可判断一次函数y＝x+bc的图象.【详解】①由x＝2时，y＝4a+2b+c，由图象知：y＝4a+2b+c＜0，故正确；②方程ax2+bx+c＝0两根分别为1，3，都大于0，故正确；③当x＜2时，由图象知：y随x的增大而减小，故错误；④由图象开口向上，a＞0，与y轴交于正半轴，c＞0，x=﹣＝1＞0，∴b＜0，∴bc＜0，∴一次函数y＝x+bc的图象一定过第一、三、四象限，故正确；故正确的共有3个，故选：C．【点睛】此题主要考查二次函数的图像，解题的关键是熟知各系数所代表的含义.8．二次函数y＝x2+bx的对称轴为直线x＝2，若关于x的一元二次方程x2+bx﹣t＝0（t为实数）在﹣1＜x ＜4的范围内有解，则t 的取值范围是（ ）A ．0＜t ＜5B ．﹣4≤t ＜5C ．﹣4≤t ＜0D ．t ≥﹣4【答案】B【解析】【分析】先求出b ，确定二次函数解析式，关于x 的一元二次方程x 2+bx ﹣t ＝0的解可以看成二次函数y ＝x 2﹣4x 与直线y ＝t 的交点，﹣1＜x ＜4时﹣4≤y ＜5，进而求解；【详解】解：∵对称轴为直线x ＝2，∴b ＝﹣4，∴y ＝x 2﹣4x ，关于x 的一元二次方程x 2+bx ﹣t ＝0的解可以看成二次函数y ＝x 2﹣4x 与直线y ＝t 的交点， ∵﹣1＜x ＜4，∴二次函数y 的取值为﹣4≤y ＜5，∴﹣4≤t ＜5；故选：B ．【点睛】本题考查二次函数图象的性质，一元二次方程的解；将一元二次方程的解转换为二次函数与直线交点问题，数形结合的解决问题是解题的关键．9．已知在平面直角坐标系中，有两个二次函数()()39m x x y =++及()()26y n x x =--图象，将二次函数()()39m x x y =++的图象按下列哪一种平移方式平移后，会使得此两个函数图象的对称轴重叠（ ）A ．向左平移2个单位长度B ．向右平移2个单位长度C ．向左平移10个单位长度D ．向右平移10个单位长度【答案】D【解析】【分析】将二次函数解析式展开，结合二次函数的性质找出两二次函数的对称轴，二者做差后即可得出平移方向及距离．【详解】解：∵y ＝m （x ＋3）（x ＋9）＝mx 2＋12mx ＋27m ，y ＝n （x －2）（x －6）＝nx 2－8nx ＋12n ，∴二次函数y ＝m （x ＋3）（x ＋9）的对称轴为直线x ＝－6，二次函数y ＝n （x －2）（x －6）的对称轴为直线x ＝4，∵4－（－6）＝10，∴将二次函数y ＝m （x ＋3）（x ＋9）的图形向右平移10个单位长度，两图象的对称轴重叠．故选：D．【点睛】本题考查了二次函数图象与几何变换以及二次函数的性质，根据二次函数的性质找出两个二次函数的对称轴是解题的关键．10．若二次函数y＝ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，对于以下说法：①b2﹣4ac＞0②x＝x0是方程ax2+bx+c＝y0的解③x1＜x0＜x2④a（x0﹣x1）（x0﹣x2）＜0其中正确的是（）A．①③④B．①②④C．①②③D．②③【答案】B【解析】【分析】①根据二次函数图象与x轴有两个不同的交点，结合根的判别式即可得出△=b2-4ac＞0，①正确；②由点M（x0，y0）在二次函数图象上，利用二次函数图象上点的坐标特征即可得出x=x0是方程ax2+bx+c=y0的解，②正确；③分a＞0和a＜0考虑，当a＞0时得出x1＜x0＜x2；当a＜0时得出x0＜x1或x0＞x2，③错误；④将二次函数的解析式由一般式转化为交点式，再由点M（x0，y0）在x轴下方即可得出y0=a（x0-x1）（x0-x2）＜0，④正确．【详解】①∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，∴方程ax2+bx+c=0有两个不相等的实数根，∴△=b2-4ac＞0，①正确；②∵图象上有一点M（x0，y0），∴a+bx0+c=y0，∴x=x0是方程ax2+bx+c=y0的解，②正确；③当a＞0时，∵M（x0，y0）在x轴下方，∴x1＜x0＜x2；当a＜0时，∵M（x0，y0）在x轴下方，∴x0＜x1或x0＞x2，③错误；④∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），∴y=ax2+bx+c=a（x-x1）（x-x2），∵图象上有一点M（x0，y0）在x轴下方，∴y0=a（x0-x1）（x0-x2）＜0，④正确；故选B．【点睛】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及二次函数图象与系数的关系，根据二次函数的相关知识逐一分析四条结论的正误是解题的关键．11．抛物线y ＝ax 2+bx+c 的顶点为(﹣1，3)，与x 轴的交点A 在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中正确结论的个数为( )①若点P(﹣3，m)，Q(3，n)在抛物线上，则m ＜n ；②c ＝a+3；③a+b+c ＜0；④方程ax 2+bx+c ＝3有两个相等的实数根．A ．1个B ．2个C ．3个D ．4个【答案】C【解析】 试题分析：由抛物线与x 轴有两个交点，可知b 2-4ac ＞0，所以①错误；由抛物线的顶点为D （-1，2），可知抛物线的对称轴为直线x=-1，然后由抛物线与x 轴的一个交点A 在点（-3，0）和（-2，0）之间，可知抛物线与x 轴的另一个交点在点（0，0）和（1，0）之间，因此当x=1时，y ＜0，即a+b+c ＜0，所以②正确；由抛物线的顶点为D （-1，2），可知a-b+c=2，然后由抛物线的对称轴为直线x=2b a=-1，可得b=2a ，因此a-2a+c=2，即c-a=2，所以③正确；由于当x=-1时，二次函数有最大值为2，即只有x=-1时，ax 2+bx+c=2，因此方程ax2+bx+c-2=0有两个相等的实数根，所以④正确．故选C ．考点：二次函数的图像与性质12．二次函数y=ax 2+bx+c （a≠0）的图象如图，给出下列四个结论：①4ac ﹣b 2＜0；②4a+c ＜2b ；③3b+2c ＜0；④m （am+b ）+b ＜a （m≠﹣1），其中正确结论的个数是（ ）A ．4个B ．3个C ．2个D ．1个【答案】B【解析】【分析】【详解】解：∵抛物线和x轴有两个交点，∴b2﹣4ac＞0，∴4ac﹣b2＜0，∴①正确；∵对称轴是直线x﹣1，和x轴的一个交点在点（0，0）和点（1，0）之间，∴抛物线和x轴的另一个交点在（﹣3，0）和（﹣2，0）之间，∴把（﹣2，0）代入抛物线得：y=4a﹣2b+c＞0，∴4a+c＞2b，∴②错误；∵把（1，0）代入抛物线得：y=a+b+c＜0，∴2a+2b+2c＜0，∵b=2a，∴3b，2c＜0，∴③正确；∵抛物线的对称轴是直线x=﹣1，∴y=a﹣b+c的值最大，即把（m，0）（m≠0）代入得：y=am2+bm+c＜a﹣b+c，∴am2+bm+b＜a，即m（am+b）+b＜a，∴④正确；即正确的有3个，故选B．考点：二次函数图象与系数的关系13．如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③13＜a＜23；④b＞c．其中含所有正确结论的选项是（）A．①②③B．①③④C．②③④D．①②④【答案】B【解析】【分析】根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号，从而判断①；根据对称性得到函数图象经过（3，0），则得②的判断；根据图象经过（-1，0）可得到a 、b 、c 之间的关系，从而对④作判断；从图象与y 轴的交点B 在（0，-2）和（0，-1）之间可以判断c 的大小得出③的正误．【详解】①∵函数开口方向向上，∴a ＞0；∵对称轴在y 轴右侧∴ab 异号，∵抛物线与y 轴交点在y 轴负半轴，∴c ＜0，∴abc ＞0，故①正确；②∵图象与x 轴交于点A （-1，0），对称轴为直线x=1，∴图象与x 轴的另一个交点为（3，0），∴当x=2时，y ＜0，∴4a+2b+c ＜0，故②错误；③∵图象与y 轴的交点B 在（0，-2）和（0，-1）之间，∴-2＜c ＜-1∵-12b a， ∴b=-2a ， ∵函数图象经过（-1，0），∴a-b+c=0，∴c=-3a ，∴-2＜-3a ＜-1， ∴13＜a ＜23；故③正确 ④∵函数图象经过（-1，0），∴a-b+c=0，∴b-c=a ，∵a ＞0，∴b-c ＞0，即b ＞c ；故④正确；故选B ．【点睛】主要考查图象与二次函数系数之间的关系．解题关键是注意掌握数形结合思想的应用．14．一次函数y=ax+b 与反比例函数y=c x在同一平面直角坐标系中的图象如左图所示，则二次函数y=ax 2+bx+c 的图象可能是()A ．B ．C ．D ．【答案】B【解析】【分析】根据题中给出的函数图像结合一次函数性质得出a ＜0，b ＞0，再由反比例函数图像性质得出c ＜0，从而可判断二次函数图像开口向下，对称轴：2b x a =-＞0，即在y 轴的右边，与y 轴负半轴相交，从而可得答案.【详解】解：∵一次函数y=ax+b 图像过一、二、四，∴a ＜0，b ＞0，又∵反比例 函数y=c x 图像经过二、四象限， ∴c ＜0，∴二次函数对称轴：2b x a=-＞0， ∴二次函数y=ax 2+bx+c 图像开口向下，对称轴在y 轴的右边，与y 轴负半轴相交， 故答案为B.【点睛】本题考查了二次函数的图形，一次函数的图象，反比例函数的图象，熟练掌握二次函数的有关性质：开口方向、对称轴、与y 轴的交点坐标等确定出a 、b 、c 的情况是解题的关键．15．二次函数y=﹣x 2+mx 的图象如图，对称轴为直线x=2，若关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解，则t 的取值范围是（ ）A ．t ＞﹣5B ．﹣5＜t ＜3C ．3＜t≤4D ．﹣5＜t≤4【答案】D【解析】【分析】 先根据对称轴x=2求得m 的值，然后求得x=1和x=5时y 的值，最后根据图形的特点，得出直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4．【详解】∵抛物线的对称轴为x ＝2， ∴22m -=-，m=4 如图，关于x 的一元二次方程﹣x 2+mx ﹣t=0的解就是抛物线y=﹣x 2+mx 与直线y=t 的交点的横坐标当x=1时，y=3，当x=5时，y=﹣5，由图象可知关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解， 则直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4，∴﹣5＜t≤4．故选：D ．【点睛】本题考查二次函数与一元二次方程的关系，方程有解，反映在图象上即图象与x 轴(或某直线)有交点．16．函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是（ ）A ．B ．C ．D ．【答案】C【解析】【分析】根据a 、b 的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一排除．【详解】当a ＞0时，二次函数的图象开口向上，一次函数的图象经过一、三或一、二、三或一、三、四象限，故A 、D 不正确；由B 、C 中二次函数的图象可知，对称轴x=-2b a＞0，且a ＞0，则b ＜0， 但B 中，一次函数a ＞0，b ＞0，排除B ．故选C ．17．已知抛物线y ＝x 2+（2a +1）x +a 2﹣a ，则抛物线的顶点不可能在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】D【解析】【分析】求得顶点坐标，得出顶点的横坐标和纵坐标的关系式，即可求得．【详解】抛物线y ＝x 2+（2a +1）x +a 2﹣a 的顶点的横坐标为：x ＝﹣212a +＝﹣a ﹣12， 纵坐标为：y ＝()()224214a a a --+＝﹣2a ﹣14， ∴抛物线的顶点横坐标和纵坐标的关系式为：y ＝2x +34， ∴抛物线的顶点经过一二三象限，不经过第四象限，故选：D ．【点睛】 本题考查了二次函数的性质，得到顶点的横纵坐标的关系式是解题的关键．18．若二次函数y ＝x 2﹣2x+2在自变量x 满足m≤x≤m+1时的最小值为6，则m 的值为（ ）A ．5,5,15,12-+-B ．5,51-+C ．1D ．5,15--【答案】B【解析】【分析】 由抛物线解析式确定出其对称轴为x=1，分m ＞1或m+1＜1两种情况，分别确定出其最小值，由最小值为6，则可得到关于m 的方程，可求得m 的值．【详解】∵y ＝x 2﹣2x+2＝（x ﹣1）2+1，∴抛物线开口向上，对称轴为x ＝1，当m ＞1时，可知当自变量x 满足m≤x≤m+1时，y 随x 的增大而增大，∴当x ＝m 时，y 有最小值，∴m 2﹣2m+2＝6，解得m ＝1+5或m ＝1﹣5（舍去），当m+1＜1时，可知当自变量x 满足m≤x≤m+1时，y 随x 的增大而减小，∴当x ＝m+1时，y 有最小值，∴（m+1）2﹣2（m+1）+2＝6，解得m ＝5（舍去）或m ＝﹣5，综上可知m 的值为1+5或﹣5．故选B ．【点睛】本题主要考查二次函数的性质，用m 表示出其最小值是解题的关键．19．在同一平面直角坐标系中，函数3y x a =+与2+3y ax x =的图象可能是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】根据一次函数及二次函数的图像性质，逐一进行判断．【详解】解：A.由一次函数图像可知a＞0，因此二次函数图像开口向上，但对称轴32a-<应在y轴左侧，故此选项错误；B. 由一次函数图像可知a＜0，而由二次函数图像开口方向可知a＞0，故此选项错误；C. 由一次函数图像可知a＜0，因此二次函数图像开口向下，且对称轴32a->在y轴右侧，故此选项正确；D. 由一次函数图像可知a＞0，而由二次函数图像开口方向可知a＜0，故此选项错误；故选：C．【点睛】本题考查二次函数与一次函数图象的性质，解题的关键是利用数形结合思想分析图像，本题属于中等题型．20．如图抛物线交轴于和点，交轴负半轴于点，且.有下列结论：①；②；③.其中，正确结论的个数是（）A．B．C．D．【答案】C【解析】【分析】根据抛物线的开口方向，对称轴公式以及二次函数图象上点的坐标特征来判断a、b、c的符号以及它们之间的数量关系，即可得出结论．【详解】解：根据图象可知a＞0，c＜0，b＞0，∴, 故③错误；∵.∴B（-c，0）∴抛物线y=ax2+bx+c与x轴交于A（-2，0）和B（-c，0）两点，∴， ac2-bc+c=0∴，ac-b+1=0，∴，故②正确；∴，b=ac+1∴,∴2b-c=2，故①正确；故选：C．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a 决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）；常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．。
2020-2021初中数学二次函数基础测试题及答案
2020-2021初中数学二次函数基础测试题及答案一、选择题1．若用“*”表示一种运算规则，我们规定：a *b ＝ab ﹣a +b ，如：3*2＝3×2﹣3+2＝5．以下说法中错误的是（ ）A ．不等式（﹣2）*（3﹣x ）＜2的解集是x ＜3B ．函数y ＝（x +2）*x 的图象与x 轴有两个交点C ．在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数D ．方程（x ﹣2）*3＝5的解是x ＝5【答案】D【解析】【分析】根据题目中所给的运算法则列出不等式，解不等式即可判定选项A ；根据题目中所给的运算法则求得函数解析式，由此即可判定选项B ；根据题目中所给的运算法则可得a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0，由此即可判定选项C ；根据题目中所给的运算法则列出方程，解方程即可判定选项D.【详解】∵a *b ＝ab ﹣a +b ，∴（﹣2）*（3﹣x ）＝（﹣2）×（3﹣x ）﹣（﹣2）+（3﹣x ）＝x ﹣1，∵（﹣2）*（3﹣x ）＜2，∴x ﹣1＜2，解得x ＜3，故选项A 正确；∵y ＝（x +2）*x ＝（x +2）x ﹣（x +2）+x ＝x 2+2x ﹣2，∴当y ＝0时，x 2+2x ﹣2＝0，解得，x 1＝﹣x 2＝﹣1B 正确； ∵a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0， ∴在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数，故选项C 正确； ∵（x ﹣2）*3＝5，∴（x ﹣2）×3﹣（x ﹣2）+3＝5，解得，x ＝3，故选项D 错误；故选D ．【点睛】本题是阅读理解题，根据题目中所给的运算法则得到相应的运算式子是解决问题的关键.2．要将抛物线2y x =平移后得到抛物线223y x x =++，下列平移方法正确的是（ ） A ．向左平移1个单位，再向上平移2个单位 B ．向左平移1个单位，再向下平移2个单位 C ．向右平移1个单位，再向上平移2个单位 D ．向右平移1个单位，再向下平移2个单位【答案】A【解析】【分析】原抛物线顶点坐标为（0，0），平移后抛物线顶点坐标为（-1，2），由此确定平移办法．【详解】y=x 2+2x+3=（x+1）2+2，该抛物线的顶点坐标是（-1，2），抛物线y=x 2的顶点坐标是（0，0），则平移的方法可以是：将抛物线y=x 2向左平移1个单位长度，再向上平移2个单位长度． 故选：A ．【点睛】此题考查二次函数图象与几何变换．解题关键是将抛物线的平移问题转化为顶点的平移，寻找平移方法．3．如图,二次函数2y ax bx c =++的图象如图所示,则一次函数y ax c =+和反比例函数b y x=在同平面直角坐标系中的图象大致是（ ）A ．B ．C ．D ．【答案】D【解析】【分析】直接利用二次函数图象经过的象限得出a ，b ，c 的值取值范围，进而利用一次函数与反比例函数的性质得出答案．【详解】∵二次函数y=ax 2+bx+c 的图象开口向下，∴a ＜0，∵二次函数y=ax 2+bx+c 的图象经过原点，∴c=0，∵二次函数y=ax 2+bx+c 的图象对称轴在y 轴左侧，∴a ，b 同号，∴b ＜0，∴一次函数y=ax+c ，图象经过第二、四象限，反比例函数y=bx图象分布在第二、四象限，故选D．【点睛】此题主要考查了反比例函数、一次函数、二次函数的图象，正确把握相关性质是解题关键．4．如图，正方形ABCD中，AB＝4cm，点E、F同时从C点出发，以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动，到点A时停止运动．设运动时间为t（s），△AEF的面积为S （cm2），则S（cm2）与t（s）的函数关系可用图象表示为（）A．B．C．D．【答案】D【解析】试题分析：分类讨论：当0≤t≤4时，利用S=S正方形ABCD﹣S△ADF﹣S△ABE﹣S△CEF可得S=﹣t2+4t，配成顶点式得S=﹣（t﹣4）2+8，此时抛物线的开口向下，顶点坐标为（4，8）；当4＜t≤8时，直接根据三角形面积公式得到S=（8﹣t）2=（t﹣8）2，此时抛物线开口向上，顶点坐标为（8，0），于是根据这些特征可对四个选项进行判断．解：当0≤t≤4时，S=S正方形ABCD﹣S△ADF﹣S△ABE﹣S△CEF=4•4﹣•4•（4﹣t）﹣•4•（4﹣t）﹣•t•t=﹣t2+4t=﹣（t﹣4）2+8；当4＜t≤8时，S=•（8﹣t ）2=（t ﹣8）2．故选D ．考点：动点问题的函数图象．5．函数25y ax bx =++(0)a ≠，当1x =与7x =时函数值相等，则8x =时，函数值等于( )A ．5B ．52-C ．52D ．－5【答案】A【解析】【分析】根据二次函数的对称性，求得函数25y ax bx =++(0)a ≠的对称轴，进而判断与8x =的函数值相等时x 的值，由此可得结果．【详解】∵函数25y ax bx =++(0)a ≠，当1x =与7x =时函数值相等，∴函数25y ax bx =++(0)a ≠的对称轴为：1742x +==， ∴8x =与0x =的函数值相等，∴当8x =时，250055y ax bx a b =++=⨯+⨯+=，即8x =时，函数值等于5，故选：A ．【点睛】本题主要考查二次函数的图象和对称性．掌握二次函数的对称性和对称轴的求法，是解题的关键．6．二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，有下列结论：①abc ＞0；②a +b +c ＝2；③a 12>；④b ＞1，其中正确的结论个数是（ ）A ．1个B ．2 个C ．3 个D ．4 个【答案】C【解析】根据题意和函数图象，可以判断各个小题中的结论是否正确，本题得以解决．【详解】由图象可得，a ＞0，b ＞0，c ＜0，∴abc ＜0，故①错误，当x ＝1时，y ＝a +b +c ＝2，故②正确，当x ＝﹣1时，y ＝a ﹣b +c ＜0，由a +b +c ＝2得，a +c ＝2﹣b ，则a ﹣b +c ＝（a +c ）﹣b ＝2﹣b ﹣b ＜0，得b ＞1，故④正确， ∵12b a ->-，a ＞0，得122b a >>，故③正确， 故选C ．【点睛】 本题考查二次函数图象与系数的关系，解答本题的关键是明确题意，利用二次函数的性质和数形结合的思想解答．7．将抛物线y ＝x 2﹣4x +1向左平移至顶点落在y 轴上，如图所示，则两条抛物线.直线y ＝﹣3和x 轴围成的图形的面积S （图中阴影部分）是（ ）A ．5B ．6C ．7D ．8【答案】B 【解析】【分析】 B ，C 分别是顶点，A 是抛物线与x 轴的一个交点，连接OC ，AB ，阴影部分的面积就是平行四边形ABCO 的面积.【详解】抛物线y ＝x 2﹣4x +1=(x-2)2-3的顶点坐标C(2.-3), 向左平移至顶点落在y 轴上,此时顶点B(0,-3)，点A 是抛物线与x 轴的一个交点，连接OC ，AB ，如图，阴影部分的面积就是ABCO 的面积，S=2×3=6；故选：B ．本题考查二次函数图象的性质，阴影部分的面积；能够将面积进行转化是解题的关键．8．如图，抛物线y＝ax2+bx+c（a＞0）过原点O，与x轴另一交点为A，顶点为B，若△AOB为等边三角形，则b的值为（）A3B．﹣3C．﹣3D．﹣3【答案】B【解析】【分析】根据已知求出B（﹣2,24b ba a-），由△AOB为等边三角形，得到2b4a＝tan60°×（﹣2ba），即可求解；【详解】解：抛物线y＝ax2+bx+c（a＞0）过原点O，∴c＝0，B（﹣2,24b ba a-），∵△AOB为等边三角形，∴2b4a＝tan60°×（﹣2ba），∴b＝﹣3故选B．【点睛】本题考查二次函数图象及性质，等边三角形性质；能够将抛物线上点的关系转化为等边三角形的边关系是解题的关键．9．如图，抛物线2y ax bx c =++ 与x 轴交于点A （﹣1，0），顶点坐标（1，n ），与y 轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①abc ＞0；②3a +b ＜0；③﹣43≤a ≤﹣1；④a +b ≥am 2+bm （m 为任意实数）；⑤一元二次方程2ax bx c n ++= 有两个不相等的实数根，其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个【答案】B【解析】 解：∵抛物线开口向下，∴a ＜0，∵顶点坐标（1，n ），∴对称轴为直线x =1，∴2b a - =1，∴b =﹣2a ＞0，∵与y 轴的交点在（0，3），（0，4）之间（包含端点），∴3≤c ≤4，∴abc ＜0，故①错误；3a +b =3a +（﹣2a ）=a ＜0，故②正确；∵与x 轴交于点A （﹣1，0），∴a ﹣b +c =0，∴a ﹣（﹣2a ）+c =0，∴c =﹣3a ，∴3≤﹣3a ≤4，∴﹣43≤a ≤﹣1，故③正确； ∵顶点坐标为（1，n ），∴当x =1时，函数有最大值n ，∴a +b +c ≥am 2+bm +c ，∴a +b ≥am 2+bm ，故④正确；一元二次方程2ax bx c n ++=有两个相等的实数根x 1=x 2=1，故⑤错误．综上所述，结论正确的是②③④共3个．故选B ．点睛：本题考查了抛物线与x 轴的交点，二次函数的性质，主要利用了二次函数的开口方向，对称轴，最值问题，以及二次函数图象上点的坐标特征，关键在于根据顶点横坐标表示出a 、b 的关系．10．若A （－4，1y ），B （－3，2y ），C （1，3y ）为二次函数y =x 2+4x －m 的图象上的三点，则1y ，2y ，3y 的大小关系是（ ）A ．1y ＜2y ＜3yB ．3y ＜1y ＜2yC ．2y ＜1y ＜3yD ．1y ＜3y ＜2y【答案】C【解析】【分析】分别将点的坐标代入二次函数解析式，然后进行判断即可．【详解】解：y 1=（-4）2+4×（-4）m -=16-16m - =m -，y 2=（-3）2+4×（-3）m - =9-12m - =3m --，y 3=12+4×m - 1=1+4m - =5m -，∵-3m -＜m -＜5m -，∴y 2＜y 1＜y 3．故选：C.【点睛】本题考查了二次函数图象上点的坐标特征，解题的关键在于三个函数值的大小不受m 的影响．11．如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位长度的速度沿AB 向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC CD →方向运动，当P 运动到B 点时，P Q 、点同时停止运动．设P 点运动的时间为t 秒，APQ ∆的面积为S ，则表示S 与t 之间的函数关系的图象大致是（ ）A ．B ．C ．D ．【答案】D【解析】【分析】本题应分两段进行解答,①点P 在AB 上运动，点Q 在BC 上运动；②点P 在AB 上运动，点Q 在CD 上运动，依次得出S 与t 的关系式，即可判断得出答案．【详解】解：当点P 在AB 上运动，点Q 在BC 上运动时，此时，,2AP t BQ t ==2122APQ S t t t =⋅⋅=V ，函数图象为抛物线； 当点P 在AB 上运动，点Q 在BC 上运动时，此时，AP t =，APQ V 底边AP 上的高保持不变1422APQ S t t =⋅⋅=V ，函数图象为一次函数； 故选：D ．【点睛】本题考查的知识点是函数图象，理解题意，分段求出S 与t 之间的函数关系是解此题的关键．12．已知抛物线224y x x c =-+与直线2y =有两个不同的交点．下列结论：①4c <；②当1x =时，y 有最小值2c -；③方程22420x x c -+-=有两个不等实根；④若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形，则52c =；其中正确的结论的个数是（ ）A ．4B ．3C ．2D ．1 【答案】B【解析】【分析】根据“抛物线224y x x c =-+与直线2y =有两个不同的交点”即可判断①③；根据抛物线的对称轴为直线x=1即可判断②；根据等腰直角三角形的性质，用c 表达出两个交点，代入抛物线解析式计算即可判断④．【详解】解：∵抛物线224y x x c =-+与直线2y =有两个不同的交点，∴2242x x c -+=有两个不相等的实数根，即22420x x c -+-=有两个不相等的实数根，故③正确，∴1642(2)0c ∆=-⨯⨯->，解得：4c <，故①正确；∵抛物线的对称轴为直线x=1，且抛物线开口向上，∴当x=1时，2y c =-为最小值，故②正确；若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形，则顶点（1，c-2）到直线y=2的距离等于两交点距离的一半，∵顶点（1，c-2）到直线y=2的距离为2-（c-2）=4-c ，∴两交点的横坐标分别为1-（4-c ）=c-3与1+（4-c ）=5-c∴两交点坐标为（c-3,2）与（5-c,2），将（c-3,2）代入224y x x c =-+中得：22(3)4(3)2c c c ---+= 解得：72c =或4c = ∵4c <， ∴72c =，故④错误， ∴正确的有①②③，故选：B ．【点睛】 本题考查了二次函数与一元二次方程的关系以及二次函数的性质，解题的关键是熟练掌握函数与方程之间的联系．13．若二次函数y ＝ax 2+bx +c （a ≠0）的图象于x 轴的交点坐标分别为（x 1，0），（x 2，0），且x 1＜x 2，图象上有一点M （x 0，y 0）在x 轴下方，对于以下说法：①b 2﹣4ac ＞0②x ＝x 0是方程ax 2+bx +c ＝y 0的解③x 1＜x 0＜x 2④a （x 0﹣x 1）（x 0﹣x 2）＜0其中正确的是（ ）A ．①③④B ．①②④C ．①②③D ．②③ 【答案】B【解析】【分析】①根据二次函数图象与x 轴有两个不同的交点，结合根的判别式即可得出△=b 2-4ac ＞0，①正确；②由点M （x 0，y 0）在二次函数图象上，利用二次函数图象上点的坐标特征即可得出x=x 0是方程ax 2+bx+c=y 0的解，②正确；③分a ＞0和a ＜0考虑，当a ＞0时得出x 1＜x 0＜x 2；当a ＜0时得出x 0＜x 1或x 0＞x 2，③错误；④将二次函数的解析式由一般式转化为交点式，再由点M （x 0，y 0）在x 轴下方即可得出y 0=a （x 0-x 1）（x 0-x 2）＜0，④正确．【详解】①∵二次函数y=ax 2+bx+c （a≠0）的图象于x 轴的交点坐标分别为（x 1，0），（x 2，0），且x 1＜x 2，∴方程ax 2+bx+c=0有两个不相等的实数根，∴△=b 2-4ac ＞0，①正确；②∵图象上有一点M （x 0，y 0），∴a +bx 0+c=y 0，∴x=x 0是方程ax 2+bx+c=y 0的解，②正确；③当a ＞0时，∵M （x 0，y 0）在x 轴下方，∴x 1＜x 0＜x 2；当a ＜0时，∵M （x 0，y 0）在x 轴下方，∴x 0＜x 1或x 0＞x 2，③错误；④∵二次函数y=ax 2+bx+c （a≠0）的图象于x 轴的交点坐标分别为（x 1，0），（x 2，0），∴y=ax2+bx+c=a（x-x1）（x-x2），∵图象上有一点M（x0，y0）在x轴下方，∴y0=a（x0-x1）（x0-x2）＜0，④正确；故选B．【点睛】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及二次函数图象与系数的关系，根据二次函数的相关知识逐一分析四条结论的正误是解题的关键．14．已知二次函数y＝ax2＋bx＋c的图像如图所示，则下列结论正确的个数有（）①c＞0；②b2－4ac＜0；③ a－b＋c＞0；④当x＞－1时，y随x的增大而减小．A．4个B．3个C．2个D．1个【答案】C【解析】【分析】由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据抛物线与x轴交点及x=-1时二次函数的值的情况进行推理，进而对所得结论进行判断．【详解】解：由图象可知，a＜0，c＞0，故①正确；抛物线与x轴有两个交点，则b²-4ac>0,故②错误;∵当x=-1时，y>0,即a-b+c>0，故③正确;由图象可知，图象开口向下，对称轴x＞-1，在对称轴右侧， y随x的增大而减小，而在对称轴左侧和-1之间，是y随x的增大而减小，故④错误．故选：C．【点睛】本题考查了二次函数图象与系数的关系：二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a 共同决定对称轴的位置：当a与b同号时，对称轴在y轴左；当a与b异号时，对称轴在y轴右．常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）．抛物线与x轴交点个数由判别式确定：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b2-4ac＜0时，抛物线与x轴没有交点．15．已知二次函数y＝ax2+bx+c(a＞0)经过点M(﹣1，2)和点N(1，﹣2)，则下列说法错误的是( )A ．a +c ＝0B ．无论a 取何值，此二次函数图象与x 轴必有两个交点，且函数图象截x 轴所得的线段长度必大于2C ．当函数在x ＜110时，y 随x 的增大而减小 D ．当﹣1＜m ＜n ＜0时，m +n ＜2a 【答案】C【解析】【分析】根据二次函数的图象和性质对各项进行判断即可．【详解】解：∵函数经过点M (﹣1，2)和点N (1，﹣2)，∴a ﹣b +c ＝2，a +b +c ＝﹣2，∴a +c ＝0，b ＝﹣2，∴A 正确；∵c ＝﹣a ，b ＝﹣2，∴y ＝ax 2﹣2x ﹣a ，∴△＝4+4a 2＞0，∴无论a 为何值，函数图象与x 轴必有两个交点，∵x 1+x 2＝2a，x 1x 2＝﹣1，∴|x 1﹣x 2|＝＞2， ∴B 正确；二次函数y ＝ax 2+bx +c (a ＞0)的对称轴x ＝﹣2b a ＝1a ， 当a ＞0时，不能判定x ＜110时，y 随x 的增大而减小； ∴C 错误；∵﹣1＜m ＜n ＜0，a ＞0，∴m +n ＜0，2a ＞0， ∴m +n ＜2a； ∴D 正确，故选：C ．【点睛】本题考查了二次函数的问题，掌握二次函数的图象和性质是解题的关键．16．在同一平面直角坐标系中，函数3y x a =+与2+3y ax x =的图象可能是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】根据一次函数及二次函数的图像性质，逐一进行判断．【详解】解：A.由一次函数图像可知a ＞0，因此二次函数图像开口向上，但对称轴302a -<应在y 轴左侧，故此选项错误；B. 由一次函数图像可知a ＜0，而由二次函数图像开口方向可知a ＞0，故此选项错误；C. 由一次函数图像可知a ＜0，因此二次函数图像开口向下，且对称轴302a->在y 轴右侧，故此选项正确；D. 由一次函数图像可知a ＞0，而由二次函数图像开口方向可知a ＜0，故此选项错误； 故选：C ．【点睛】本题考查二次函数与一次函数图象的性质，解题的关键是利用数形结合思想分析图像，本题属于中等题型．17．平移抛物线2:L y x =得到抛物线L '，使得抛物线L '的顶点关于原点对称的点仍在抛物线L '上，下列的平移中，不能得到满足条件的抛物线L '的是（ ）A ．向右平移1个单位，再向下平移2个单位B ．向左平移1个单位，再向下平移2个单位C ．向左平移32个单位，再向下平移92个单位D ．向左平移3个单位，再向下平移9个单位【答案】D【解析】【分析】通过各个选项的平移分别得到相应的函数关系式，再判断原点是否在该抛物线上即可．【详解】解：由A 选项可得L '为：2(1)2y x =--，则顶点为（1，-2），顶点（1，-2）关于原点的对称点为（-1，2），当x ＝-1时，y ＝2，则对称点在该函数图像上，故A 选项不符合题意；由B 选项可得L '为：2(1)2y x =+-，则顶点为（-1，-2），顶点（-1，-2）关于原点的对称点为（1，2），当x ＝1时，y ＝2，则对称点在该函数图像上，故B 选项不符合题意；由C 选项可得L '为：239()22y x =+-， 则顶点为（-32，-92），顶点（-32，-92）关于原点的对称点为（32，92）， 当x ＝32时，y ＝92，则对称点在该函数图像上，故C 选项不符合题意； 由D 选项可得L '为：2(3)9y x =+-，则顶点为（-3，-9），顶点（-3，-9）关于原点的对称点为（3，9），当x ＝3时，y ＝27≠9，则对称点不在该函数图像上，故D 选项符合题意；故选：D ．【点睛】本题考查了二次函数图像的平移，熟练掌握平移的规律“左加右减，上加下减”是解决本题的关键．18．如图1，在△ABC 中，∠B ＝90°，∠C ＝30°，动点P 从点B 开始沿边BA 、AC 向点C 以恒定的速度移动，动点Q 从点B 开始沿边BC 向点C 以恒定的速度移动，两点同时到达点C ，设△BPQ 的面积为y （cm 2）．运动时间为x （s ），y 与x 之间关系如图2所示，当点P 恰好为AC 的中点时，PQ 的长为（ ）A ．2B ．4C ．3D ．3【答案】C【分析】点P、Q的速度比为3：3，根据x＝2，y＝63，确定P、Q运动的速度，即可求解．【详解】解：设AB＝a，∠C＝30°，则AC＝2a，BC＝3a，设P、Q同时到达的时间为T，则点P的速度为3aT，点Q的速度为3aT，故点P、Q的速度比为3：3，故设点P、Q的速度分别为：3v、3v，由图2知，当x＝2时，y＝63，此时点P到达点A的位置，即AB＝2×3v＝6v，BQ＝2×3v＝23v，y＝12⨯AB×BQ＝12⨯6v×23v＝63，解得：v＝1，故点P、Q的速度分别为：3，3，AB＝6v＝6＝a，则AC＝12，BC＝63，如图当点P在AC的中点时，PC＝6，此时点P运动的距离为AB+AP＝12，需要的时间为12÷3＝4，则BQ＝3x＝43，CQ＝BC﹣BQ＝63﹣43＝23，过点P作PH⊥BC于点H，PC＝6，则PH＝PC sin C＝6×12＝3，同理CH＝33，则HQ＝CH﹣CQ＝33﹣23＝3，PQ＝22PH HQ+＝39+＝23，故选：C．【点睛】本题考查的是动点图象问题，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．19．如图抛物线交轴于和点，交轴负半轴于点，且.有下列结论：①；②；③.其中，正确结论的个数是A．B．C．D．【答案】C【解析】【分析】根据抛物线的开口方向，对称轴公式以及二次函数图象上点的坐标特征来判断a、b、c的符号以及它们之间的数量关系，即可得出结论．【详解】解：根据图象可知a＞0，c＜0，b＞0，∴, 故③错误；∵.∴B（-c，0）∴抛物线y=ax2+bx+c与x轴交于A（-2，0）和B（-c，0）两点，∴， ac2-bc+c=0∴，ac-b+1=0，∴，故②正确；∴，b=ac+1∴,∴2b-c=2，故①正确；故选：C．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax2+bx+c（a≠0），二次项系数a 决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）；常数项c决定抛物线与y轴交点：抛物线与y轴交于（0，c）；抛物线与x轴交点个数由△决定：△=b2-4ac＞0时，抛物线与x轴有2个交点；△=b2-4ac=0时，抛物线与x轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点．20．已知二次函数y ＝ax 2+bx+c 的图象如图所示，下列结i 论：①abc ＞0；②b 2﹣4ac ＞0；③2a+b ＝0；④a ﹣b+c ＜0．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】【分析】 首先根据开口方向确定a 的取值范围，根据对称轴的位置确定b 的取值范围，根据抛物线与y 轴的交点确定c 的取值范围，根据抛物线与x 轴是否有交点确定b 2﹣4ac 的取值范围，根据x ＝﹣1函数值可以判断．【详解】解：Q 抛物线开口向下，0a ∴<，Q 对称轴12b x a=-=， 0b ∴>，Q 抛物线与y 轴的交点在x 轴的上方，0c ∴>，0abc ∴<，故①错误；Q 抛物线与x 轴有两个交点，240b ac ∴->，故②正确；Q 对称轴12b x a=-=， 2a b ∴=-， 20a b ∴+=，故③正确；根据图象可知，当1x =-时，0y a b c =-+<，故④正确；故选：C ．【点睛】此题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用是解题关键．。
2020-2021中考数学二次函数综合经典题含详细答案
2020-2021中考数学二次函数综合经典题含详细答案一、二次函数1．如图，对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点，其中A 点的坐标为（－3，0）．（1）求点B 的坐标；（2）已知a 1=，C 为抛物线与y 轴的交点．①若点P 在抛物线上，且POC BOC S 4S ∆∆=，求点P 的坐标；②设点Q 是线段AC 上的动点，作QD ⊥x 轴交抛物线于点D ，求线段QD 长度的最大值．【答案】（1）点B 的坐标为（1，0）.（2）①点P 的坐标为（4，21）或（－4，5）.②线段QD 长度的最大值为94. 【解析】【分析】（1）由抛物线的对称性直接得点B 的坐标．（2）①用待定系数法求出抛物线的解析式，从而可得点C 的坐标，得到BOC S ∆，设出点P 的坐标，根据POC BOC S 4S ∆∆=列式求解即可求得点P 的坐标．②用待定系数法求出直线AC 的解析式，由点Q 在线段AC 上，可设点Q 的坐标为(q,-q-3)，从而由QD ⊥x 轴交抛物线于点D ，得点D 的坐标为(q,q 2+2q-3)，从而线段QD 等于两点纵坐标之差，列出函数关系式应用二次函数最值原理求解.【详解】解：（1）∵A 、B 两点关于对称轴x 1=-对称 ，且A 点的坐标为（－3，0）， ∴点B 的坐标为（1，0）.（2）①∵抛物线a 1=，对称轴为x 1=-，经过点A （－3，0）， ∴2a 1b 12a 9a 3b c 0=⎧⎪⎪-=-⎨⎪-+=⎪⎩，解得a 1b 2c 3=⎧⎪=⎨⎪=-⎩.∴抛物线的解析式为2y x 2x 3=+-.∴B 点的坐标为（0，－3）.∴OB=1，OC=3.∴BOC 13S 1322∆=⨯⨯=. 设点P 的坐标为(p,p 2+2p-3)，则POC 13S 3p p 22∆=⨯⨯=. ∵POC BOC S 4S ∆∆=，∴3p 62=，解得p 4=±. 当p 4=时2p 2p 321+-=；当p 4=-时，2p 2p 35+-=，∴点P 的坐标为（4，21）或（－4，5）.②设直线AC 的解析式为y kx b =+，将点A ，C 的坐标代入，得：3k b 0b 3-+=⎧⎨=-⎩，解得：k 1b 3=-⎧⎨=-⎩. ∴直线AC 的解析式为y x 3=--.∵点Q 在线段AC 上，∴设点Q 的坐标为(q,-q-3).又∵QD ⊥x 轴交抛物线于点D ，∴点D 的坐标为(q,q 2+2q-3).∴()22239QD q 3q 2q 3q 3q q 24⎛⎫=---+-=--=-++ ⎪⎝⎭. ∵a 10<=-，-3302<<-∴线段QD 长度的最大值为94.2．如图，抛物线y ＝x 2﹣mx ﹣（m +1）与x 轴负半轴交于点A （x 1，0），与x 轴正半轴交于点B （x 2，0）（OA ＜OB ），与y 轴交于点C ，且满足x 12+x 22﹣x 1x 2＝13．（1）求抛物线的解析式；（2）以点B 为直角顶点，BC 为直角边作Rt △BCD ，CD 交抛物线于第四象限的点E ，若EC ＝ED ，求点E 的坐标；（3）在抛物线上是否存在点Q ，使得S △ACQ ＝2S △AOC ？若存在，求出点Q 的坐标；若不存在，说明理由．【答案】（1）y ＝x 2﹣2x ﹣3；（2）E 点坐标为（1132+，﹣1132）；（3）点Q 的坐标为（﹣3，12）或（2，﹣3）．理由见解析.【解析】【分析】（1）由根与系数的关系可得x1+x2＝m，x1•x2＝﹣（m+1），代入x12+x22﹣x1x2＝13，求出m1＝2，m2＝﹣5．根据OA＜OB，得出抛物线的对称轴在y轴右侧，那么m＝2，即可确定抛物线的解析式；（2）连接BE、OE．根据直角三角形斜边上的中线等于斜边的一半得出BE＝12CD＝CE．利用SSS证明△OBE≌△OCE，得出∠BOE＝∠COE，即点E在第四象限的角平分线上，设E点坐标为（m，﹣m），代入y＝x2﹣2x﹣3，求出m的值，即可得到E点坐标；（3）过点Q作AC的平行线交x轴于点F，连接CF，根据三角形的面积公式可得S△ACQ＝S△ACF．由S△ACQ＝2S△AOC，得出S△ACF＝2S△AOC，那么AF＝2OA＝2，F（1，0）．利用待定系数法求出直线AC的解析式为y＝﹣3x﹣3．根据AC∥FQ，可设直线FQ的解析式为y＝﹣3x+b，将F（1，0）代入，利用待定系数法求出直线FQ的解析式为y＝﹣3x+3，把它与抛物线的解析式联立，得出方程组22333y x xy x⎧=--⎨=-+⎩，求解即可得出点Q的坐标．【详解】（1）∵抛物线y＝x2﹣mx﹣（m+1）与x轴负半轴交于点A（x1，0），与x轴正半轴交于点B（x2，0），∴x1+x2＝m，x1•x2＝﹣（m+1），∵x12+x22﹣x1x2＝13，∴（x1+x2）2﹣3x1x2＝13，∴m2+3（m+1）＝13，即m2+3m﹣10＝0，解得m1＝2，m2＝﹣5．∵OA＜OB，∴抛物线的对称轴在y轴右侧，∴m＝2，∴抛物线的解析式为y＝x2﹣2x﹣3；（2）连接BE、OE．∵在Rt△BCD中，∠CBD＝90°，EC＝ED，∴BE ＝12CD ＝CE ． 令y ＝x 2﹣2x ﹣3＝0，解得x 1＝﹣1，x 2＝3，∴A （﹣1，0），B （3，0），∵C （0，﹣3），∴OB ＝OC ，又∵BE ＝CE ，OE ＝OE ，∴△OBE ≌△OCE （SSS ），∴∠BOE ＝∠COE ，∴点E 在第四象限的角平分线上，设E 点坐标为（m ，﹣m ），将E （m ，﹣m ）代入y ＝x 2﹣2x ﹣3，得m ＝m 2﹣2m ﹣3，解得m ＝1132±， ∵点E 在第四象限，∴E 点坐标为（113+，﹣113+）； （3）过点Q 作AC 的平行线交x 轴于点F ，连接CF ，则S △ACQ ＝S △ACF ．∵S △ACQ ＝2S △AOC ，∴S △ACF ＝2S △AOC ，∴AF ＝2OA ＝2，∴F （1，0）．∵A （﹣1，0），C （0，﹣3），∴直线AC 的解析式为y ＝﹣3x ﹣3．∵AC ∥FQ ，∴设直线FQ 的解析式为y ＝﹣3x +b ，将F （1，0）代入，得0＝﹣3+b ，解得b ＝3，∴直线FQ 的解析式为y ＝﹣3x +3．联立22333y x x y x ⎧=--⎨=-+⎩，解得113 12x y =-⎧⎨=⎩，2223xy=⎧⎨=-⎩，∴点Q的坐标为（﹣3，12）或（2，﹣3）．【点睛】本题是二次函数综合题，其中涉及到一元二次方程根与系数的关系，求二次函数的解析式，直角三角形的性质，全等三角形的判定与性质，二次函数图象上点的坐标特征，三角形的面积，一次函数图象与几何变换，待定系数法求直线的解析式，抛物线与直线交点坐标的求法，综合性较强，难度适中．利用数形结合与方程思想是解题的关键．3．如图1，抛物线C1：y=ax2﹣2ax+c（a＜0）与x轴交于A、B两点，与y轴交于点C．已知点A的坐标为（﹣1，0），点O为坐标原点，OC=3OA，抛物线C1的顶点为G．（1）求出抛物线C1的解析式，并写出点G的坐标；（2）如图2，将抛物线C1向下平移k（k＞0）个单位，得到抛物线C2，设C2与x轴的交点为A′、B′，顶点为G′，当△A′B′G′是等边三角形时，求k的值：（3）在（2）的条件下，如图3，设点M为x轴正半轴上一动点，过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点，试探究在直线y=﹣1上是否存在点N，使得以P、Q、N 为顶点的三角形与△AOQ全等，若存在，直接写出点M，N的坐标：若不存在，请说明理由．【答案】（1）抛物线C1的解析式为y=﹣x2+2x+3，点G的坐标为（1，4）；（2）k=1；（3）M1113+0）、N1131）；M2113+，0）、N2（1，﹣1）；M3（4，0）、N3（10，﹣1）；M4（4，0）、N4（﹣2，﹣1）．【解析】【分析】（1）由点A的坐标及OC=3OA得点C坐标，将A、C坐标代入解析式求解可得；（2）设抛物线C2的解析式为y=﹣x2+2x+3﹣k，即y=﹣（x﹣1）2+4﹣k，′作G′D⊥x轴于点D，设BD′=m，由等边三角形性质知点B′的坐标为（m+1，0），点G′的坐标为（1，3m），代入所设解析式求解可得；（3）设M（x，0），则P（x，﹣x2+2x+3）、Q（x，﹣x2+2x+2），根据PQ=OA=1且∠AOQ、∠PQN均为钝角知△AOQ≌△PQN，延长PQ交直线y=﹣1于点H，证△OQM≌△QNH，根据对应边相等建立关于x的方程，解之求得x的值从而进一步求解即可．【详解】（1）∵点A 的坐标为（﹣1，0），∴OA=1，∴OC=3OA ，∴点C 的坐标为（0，3），将A 、C 坐标代入y=ax 2﹣2ax+c ，得：203a a c c ++=⎧⎨=⎩， 解得：13a c =-⎧⎨=⎩， ∴抛物线C 1的解析式为y=﹣x 2+2x+3=﹣（x ﹣1）2+4，所以点G 的坐标为（1，4）；（2）设抛物线C 2的解析式为y=﹣x 2+2x+3﹣k ，即y=﹣（x ﹣1）2+4﹣k ，过点G′作G′D ⊥x 轴于点D ，设BD′=m ，∵△A′B′G′为等边三角形，∴33，则点B′的坐标为（m+1，0），点G′的坐标为（13），将点B′、G′的坐标代入y=﹣（x ﹣1）2+4﹣k ，得：24043m k k m⎧-+-=⎪⎨-=⎪⎩， 解得：1104m k =⎧⎨=⎩（舍），2231m k ⎧=⎪⎨=⎪⎩， ∴k=1；（3）设M （x ，0），则P （x ，﹣x 2+2x+3）、Q （x ，﹣x 2+2x+2），∴PQ=OA=1，∵∠AOQ 、∠PQN 均为钝角，∴△AOQ ≌△PQN ，如图2，延长PQ 交直线y=﹣1于点H ，则∠QHN=∠OMQ=90°，又∵△AOQ ≌△PQN ，∴OQ=QN ，∠AOQ=∠PQN ，∴∠MOQ=∠HQN ，∴△OQM ≌△QNH （AAS ），∴OM=QH ，即x=﹣x 2+2x+2+1，解得：x=113±（负值舍去）， 当x=1132+时，HN=QM=﹣x 2+2x+2=1312-，点M （1132+，0），∴点N 坐标为（113++131-，﹣1），即（13，﹣1）；或（113+﹣131-，﹣1），即（1，﹣1）；如图3，同理可得△OQM ≌△PNH ，∴OM=PH ，即x=﹣（﹣x 2+2x+2）﹣1，解得：x=﹣1（舍）或x=4，当x=4时，点M 的坐标为（4，0），HN=QM=﹣（﹣x 2+2x+2）=6，∴点N 的坐标为（4+6，﹣1）即（10，﹣1），或（4﹣6，﹣1）即（﹣2，﹣1）；综上点M1（1132+，0）、N1（13，﹣1）；M2（1132+，0）、N2（1，﹣1）；M3（4，0）、N3（10，﹣1）；M4（4，0）、N4（﹣2，﹣1）．【点睛】本题考查的是二次函数的综合题，涉及到的知识有待定系数法、等边三角形的性质、全等三角形的判定与性质等，熟练掌握待定系数法求函数解析式、等边三角形的性质、全等三角形的判定与性质、运用分类讨论思想是解题的关键.4．如图，抛物线y＝ax2＋bx（a≠0）过A（4，0），B（1，3）两点，点C、B关于抛物线的对称轴对称，过点B作直线BH⊥x轴，交x轴于点H．（1）求抛物线的表达式；（2）直接写出点C的坐标，并求出△ABC的面积；（3）点P是抛物线上一动点，且位于第四象限，是否存在这样的点P，使得△ABP的面积为△ABC面积的2倍？若存在，求出点P的坐标，若不存在，请说明理由；（4）若点M在直线BH上运动，点N在x轴正半轴上运动，当以点C，M，N为顶点的三角形为等腰直角三角形时，请直接写出此时△CMN的面积．【答案】（1）y＝－x2＋4x；（2）C（3，3），面积为3；（3）P的坐标为（5，－5）；（4）52或5．【解析】试题分析：（1）利用待定系数法进行求解即可；（2）先求出抛物线的对称轴，利用对称性即可写出点C的坐标，利用三角形面积公式即可求面积；（3）利用三角形的面积以及点P所处象限的特点即可求；（4）分情况进行讨论，确定点M、N，然后三角形的面积公式即可求.试题解析：（1）将A（4，0），B（1，3）代入到y＝ax2＋bx中，得16403a ba b+=⎧⎨+=⎩，解得14ab=-⎧⎨=⎩，∴抛物线的表达式为y＝－x2＋4x．（2）∵抛物线的表达式为y＝－x2＋4x，∴抛物线的对称轴为直线x＝2．又C，B关于对称轴对称，∴C（3，3）．∴BC＝2，∴S△ABC＝12×2×3＝3．（3）存在点P．作PQ⊥BH于点Q，设P（m，－m2＋4m）．∵S△ABP＝2S△ABC，S△ABC＝3，∴S△ABP＝6．∵S△ABP＋S△BPQ＝S△ABH＋S梯形AHQP∴6＋12×（m－1）×（3＋m2－4m）＝12×3×3＋12×（3＋m－1）（m2－4m）整理得m2－5m＝0，解得m1＝0（舍），m2＝5，∴点P的坐标为（5，－5）．（4）52或5．提示：①当以M为直角顶点，则S△CMN＝52；②当以N为直角顶点，S△CMN＝5；③当以C为直角顶点时，此种情况不存在．【点睛】本题是二次函数的综合题，主要考查待定系数法求解析式，三角形面积、直角三角形的判定等，能正确地根据题意确定图形，分情况进行讨论是解题的关键.5．已知，抛物线y＝﹣x2+bx+c经过点A（﹣1，0）和C（0，3）．（1）求抛物线的解析式；（2）在抛物线的对称轴上，是否存在点P，使PA+PC的值最小？如果存在，请求出点P的坐标，如果不存在，请说明理由；（3）设点M在抛物线的对称轴上，当△MAC是直角三角形时，求点M的坐标．【答案】（1）223y x x =-++；（2）当PA PC +的值最小时，点P 的坐标为()1,2；（3）点M 的坐标为()1,1、()1,2、81,3⎛⎫ ⎪⎝⎭或21,3⎛⎫-⎪⎝⎭. 【解析】【分析】 ()1由点A 、C 的坐标，利用待定系数法即可求出抛物线的解析式；()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，利用二次函数图象上点的坐标特征可求出点B 的坐标，由点B 、C 的坐标利用待定系数法即可求出直线BC 的解析式，利用配方法可求出抛物线的对称轴，再利用一次函数图象上点的坐标特征即可求出点P 的坐标；()3设点M 的坐标为()1,m ，则22CM (10)(m 3)=-+-，()22AC [01](30)10=--+-=，()22AM [11](m 0)=--+-，分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况，利用勾股定理可得出关于m 的一元二次方程或一元一次方程，解之可得出m 的值，进而即可得出点M 的坐标．【详解】解：()1将()1,0A -、()0,3C 代入2y x bx c =-++中， 得：{103b c c --+==，解得：{23b c ==， ∴抛物线的解析式为223y x x =-++．()2连接BC 交抛物线对称轴于点P ，此时PA PC +取最小值，如图1所示．当0y =时，有2230x x -++=，解得：11x =-，23x =，∴点B 的坐标为()3,0．Q 抛物线的解析式为2223(1)4y x x x =-++=--+，∴抛物线的对称轴为直线1x =．设直线BC 的解析式为()0y kx d k =+≠，将()3,0B 、()0,3C 代入y kx d =+中，得：{303k d d +==，解得：{13k d =-=，∴直线BC 的解析式为3y x =-+．Q 当1x =时，32y x =-+=，∴当PA PC +的值最小时，点P 的坐标为()1,2．()3设点M 的坐标为()1,m ，则22(10)(3)CM m =-+-，()22[01](30)10AC =--+-=，()22[11](0)AM m =--+-．分三种情况考虑：①当90AMC ∠=o 时，有222AC AM CM =+，即22101(3)4m m =+-++，解得：11m =，22m =，∴点M 的坐标为()1,1或()1,2；②当90ACM ∠=o 时，有222AM AC CM =+，即224101(3)m m +=++-，解得：83m =， ∴点M 的坐标为81,3⎛⎫⎪⎝⎭；③当90CAM ∠=o 时，有222CM AM AC =+，即221(3)410m m +-=++，解得：23m =-， ∴点M 的坐标为21,.3⎛⎫- ⎪⎝⎭综上所述：当MAC V 是直角三角形时，点M 的坐标为()1,1、()1,2、81,3⎛⎫⎪⎝⎭或21,.3⎛⎫- ⎪⎝⎭【点睛】本题考查待定系数法求二次(一次)函数解析式、二次(一次)函数图象的点的坐标特征、轴对称中的最短路径问题以及勾股定理，解题的关键是：()1由点的坐标，利用待定系数法求出抛物线解析式；()2由两点之间线段最短结合抛物线的对称性找出点P 的位置；()3分AMC 90∠=o 、ACM 90∠=o 和CAM 90∠=o 三种情况，列出关于m 的方程．6．如图甲，直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ，经过B 、C 两点的抛物线y=x 2+bx+c 与x 轴的另一个交点为A ，顶点为P ． （1）求该抛物线的解析式；（2）在该抛物线的对称轴上是否存在点M ，使以C ，P ，M 为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M 的坐标；若不存在，请说明理由； （3）当0＜x ＜3时，在抛物线上求一点E ，使△CBE 的面积有最大值（图乙、丙供画图探究）．【答案】（1）y=x 2﹣4x+3；（2）（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）E 点坐标为（，）时，△CBE 的面积最大．【解析】试题分析：（1）由直线解析式可求得B 、C 坐标，利用待定系数法可求得抛物线解析式； （2）由抛物线解析式可求得P 点坐标及对称轴，可设出M 点坐标，表示出MC 、MP 和PC 的长，分MC=MP 、MC=PC 和MP=PC 三种情况，可分别得到关于M 点坐标的方程，可求得M 点的坐标；（3）过E 作EF ⊥x 轴，交直线BC 于点F ，交x 轴于点D ，可设出E 点坐标，表示出F 点的坐标，表示出EF 的长，进一步可表示出△CBE 的面积，利用二次函数的性质可求得其取得最大值时E 点的坐标．试题解析：（1）∵直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ， ∴B （3，0），C （0，3）， 把B 、C 坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=x 2﹣4x+3； （2）∵y=x 2﹣4x+3=（x ﹣2）2﹣1， ∴抛物线对称轴为x=2，P （2，﹣1）， 设M （2，t ），且C （0，3）， ∴MC=，MP=|t+1|，PC=，∵△CPM 为等腰三角形，∴有MC=MP 、MC=PC 和MP=PC 三种情况，①当MC=MP 时，则有=|t+1|，解得t=，此时M （2，）；②当MC=PC 时，则有=2，解得t=﹣1（与P 点重合，舍去）或t=7，此时M （2，7）；③当MP=PC 时，则有|t+1|=2，解得t=﹣1+2或t=﹣1﹣2，此时M （2，﹣1+2）或（2，﹣1﹣2）； 综上可知存在满足条件的点M ，其坐标为（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）如图，过E 作EF ⊥x 轴，交BC 于点F ，交x 轴于点D ，设E （x ，x 2﹣4x+3），则F （x ，﹣x+3）， ∵0＜x ＜3，∴EF=﹣x+3﹣（x 2﹣4x+3）=﹣x 2+3x ， ∴S △CBE =S △EFC +S △EFB =EF•OD+EF•BD=EF•OB=×3（﹣x 2+3x ）=﹣（x ﹣）2+，∴当x=时，△CBE 的面积最大，此时E 点坐标为（，），即当E 点坐标为（，）时，△CBE 的面积最大．考点：二次函数综合题．7．综合与探究如图，抛物线26y ax bx =++经过点A(-2,0)，B(4,0)两点，与y 轴交于点C ，点D 是抛物线上一个动点，设点D 的横坐标为(14)m m <<.连接AC ，BC ，DB ，DC ． (1)求抛物线的函数表达式； (2)△BCD 的面积等于△AOC 的面积的34时，求m 的值； (3)在(2)的条件下，若点M 是x 轴上的一个动点，点N 是抛物线上一动点，试判断是否存在这样的点M,使得以点B ，D ，M ，N 为顶点的四边形是平行四边形，若存在，请直接写出点M 的坐标；若不存在，请说明理由.【答案】(1)233642y x x =-++；(2)3；(3)1234(8,0),(0,0),(14,0),(14,0)M M M M -. 【解析】 【分析】(1)利用待定系数法进行求解即可；(2)作直线DE ⊥x 轴于点E ，交BC 于点G ，作CF ⊥DE ，垂足为F ，先求出S △OAC =6，再根据S △BCD =34S △AOC ，得到S △BCD =92，然后求出BC 的解析式为362y x =-+，则可得点G 的坐标为3(,6)2m m -+，由此可得2334DG m m =-+，再根据S △BCD =S △CDG +S △BDG =12DG BO ⋅⋅，可得关于m 的方程，解方程即可求得答案；(3)存在，如下图所示，以BD 为边或者以BD 为对角线进行平行四边形的构图，以BD 为边时，有3种情况，由点D 的坐标可得点N 点纵坐标为±154，然后分点N 的纵坐标为154和点N 的纵坐标为154-两种情况分别求解；以BD 为对角线时，有1种情况，此时N 1点与N 2点重合，根据平行四边形的对边平行且相等可求得BM 1=N 1D=4，继而求得OM 1= 8，由此即可求得答案. 【详解】(1)抛物线2y ax bx c =++经过点A(-2,0)，B(4,0)，∴426016460a b a b -+=⎧⎨++=⎩， 解得3432a b ⎧=-⎪⎪⎨⎪=⎪⎩，∴抛物线的函数表达式为233642y x x =-++； (2)作直线DE ⊥x 轴于点E ，交BC 于点G ，作CF ⊥DE ，垂足为F ， ∵点A 的坐标为(-2,0)，∴OA=2，由0x =，得6y =，∴点C 的坐标为(0,6)，∴OC=6， ∴S △OAC =1126622OA OC ⋅⋅=⨯⨯=， ∵S △BCD =34S △AOC ， ∴S △BCD =39642⨯=，设直线BC 的函数表达式为y kx n =+，由B ，C 两点的坐标得406k n n +=⎧⎨=⎩，解得326k n ⎧=-⎪⎨⎪=⎩，∴直线BC 的函数表达式为362y x =-+， ∴点G 的坐标为3(,6)2m m -+， ∴2233336(6)34224DG m m m m m =-++--+=-+， ∵点B 的坐标为(4,0)，∴OB=4，∵S △BCD =S △CDG +S △BDG =1111()2222DG CF DG BE DG CF BE DG BO ⋅⋅+⋅⋅=⋅+=⋅⋅， ∴S △BCD =22133346242m m m m -+⨯=-+（）， ∴239622m m -+=， 解得11m =(舍)，23m =， ∴m 的值为3；(3)存在，如下图所示，以BD 为边或者以BD 为对角线进行平行四边形的构图， 以BD 为边时，有3种情况， ∵D 点坐标为15(3,)4，∴点N 点纵坐标为±154，当点N 的纵坐标为154时，如点N 2，此时233156424x x -++=，解得：121,3x x =-=(舍)， ∴215(1,)4N -，∴2(0,0)M ； 当点N 的纵坐标为154-时，如点N 3，N 4， 此时233156424x x -++=-，解得：12114,114x x =-=+ ∴315(114,)4N +-，415(114,)4N --， ∴3(14,0)M ，4(14,0)M -；以BD 为对角线时，有1种情况，此时N 1点与N 2点重合，∵115(1,)4N -，D(3，154)，∴N 1D=4， ∴BM 1=N 1D=4， ∴OM 1=OB+BM 1=8， ∴M 1(8，0)，综上，点M 的坐标为：1234(80)(00)(140)(140)M M M M -，，，，，，，.【点睛】本题考查的是二次函数的综合题，涉及了待定系数法、三角形的面积、解一元二次方程、平行四边形的性质等知识，运用了数形结合思想、分类讨论思想等数学思想，熟练掌握和灵活运用相关知识是解题的关键.8．某商场销售一种商品的进价为每件30元，销售过程中发现月销售量y （件）与销售单价x （元）之间的关系如图所示．（1）根据图象直接写出y 与x 之间的函数关系式．（2）设这种商品月利润为W （元），求W 与x 之间的函数关系式． （3）这种商品的销售单价定为多少元时，月利润最大？最大月利润是多少？ 【答案】（1）y ＝180(4060)3300(6090)x x x x -+≤≤⎧⎨-+<≤⎩；（2）W ＝222105400(4060)33909000(6090)x x x x x x ⎧-+-≤≤⎨-+-<≤⎩;（3）这种商品的销售单价定为65元时，月利润最大，最大月利润是3675． 【解析】 【分析】（1）当40≤x≤60时，设y 与x 之间的函数关系式为y=kx+b ，当60＜x≤90时，设y 与x 之间的函数关系式为y=mx+n ，解方程组即可得到结论；（2）当40≤x≤60时，当60＜x≤90时，根据题意即可得到函数解析式；（3）当40≤x≤60时，W=-x 2+210x-5400，得到当x=60时，W 最大=-602+210×60-5400=3600，当60＜x≤90时，W=-3x 2+390x-9000，得到当x=65时，W 最大=-3×652+390×65-9000=3675，于是得到结论． 【详解】解：（1）当40≤x ≤60时，设y 与x 之间的函数关系式为y ＝kx +b ， 将（40，140），（60，120）代入得4014060120k b k b +=⎧⎨+=⎩，解得：1180k b =-⎧⎨=⎩，∴y 与x 之间的函数关系式为y ＝﹣x +180；当60＜x ≤90时，设y 与x 之间的函数关系式为y ＝mx +n ，将（90，30），（60，120）代入得903060120m n m n +=⎧⎨+=⎩，解得：3300m n =-⎧⎨=⎩，∴y ＝﹣3x +300；综上所述，y ＝180(4060)3300(6090)x x x x -+≤≤⎧⎨-+<≤⎩；（2）当40≤x ≤60时，W ＝（x ﹣30）y ＝（x ﹣30）（﹣x +180）＝﹣x 2+210x ﹣5400， 当60＜x ≤90时，W ＝（x ﹣30）（﹣3x +300）＝﹣3x 2+390x ﹣9000，综上所述，W ＝222105400(4060)33909000(6090)x x x x x x ⎧-+-≤≤⎨-+-<≤⎩； （3）当40≤x ≤60时，W ＝﹣x 2+210x ﹣5400，∵﹣1＜0，对称轴x ＝2102--＝105，∴当40≤x ≤60时，W 随x 的增大而增大，∴当x ＝60时，W 最大＝﹣602+210×60﹣5400＝3600， 当60＜x ≤90时，W ＝﹣3x 2+390x ﹣9000，∵﹣3＜0，对称轴x ＝3906--＝65，∵60＜x ≤90，∴当x ＝65时，W 最大＝﹣3×652+390×65﹣9000＝3675， ∵3675＞3600，∴当x ＝65时，W 最大＝3675，答：这种商品的销售单价定为65元时，月利润最大，最大月利润是3675． 【点睛】本题考查了把实际问题转化为二次函数，再利用二次函数的性质进行实际应用．根据题意分情况建立二次函数的模型是解题的关键．9．已知：如图，抛物线y ＝ax 2+bx +3与坐标轴分别交于点A ，B （﹣3，0），C （1，0），点P 是线段AB 上方抛物线上的一个动点． （1）求抛物线解析式；（2）当点P 运动到什么位置时，△PAB 的面积最大？（3）过点P 作x 轴的垂线，交线段AB 于点D ，再过点P 作PE ∥x 轴交抛物线于点E ，连接DE ，请问是否存在点P 使△PDE 为等腰直角三角形？若存在，求点P 的坐标；若不存在，说明理由．【答案】（1）y ＝﹣x 2﹣2x +3 （2）（﹣32，154） （3）存在，P （﹣2，3）或P（52-+，52-+）【解析】 【分析】（1）用待定系数法求解；（2）过点P 作PH ⊥x 轴于点H ，交AB 于点F ，直线AB 解析式为y ＝x +3，设P （t ，﹣t 2﹣2t +3）（﹣3＜t ＜0），则F （t ，t +3），则PF ＝﹣t 2﹣2t +3﹣（t +3）＝﹣t 2﹣3t ，根据S △PAB ＝S △PAF +S △PBF 写出解析式，再求函数最大值；（3）设P （t ，﹣t 2﹣2t +3）（﹣3＜t ＜0），则D （t ，t +3），PD ＝﹣t 2﹣3t ，由抛物线y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4，由对称轴为直线x ＝﹣1，PE ∥x 轴交抛物线于点E ，得y E ＝y P ，即点E 、P 关于对称轴对称，所以2E Px x +＝﹣1，得x E ＝﹣2﹣x P ＝﹣2﹣t ，故PE ＝|x E ﹣x P |＝|﹣2﹣2t |，由△PDE 为等腰直角三角形，∠DPE ＝90°，得PD ＝PE ，再分情况讨论：①当﹣3＜t≤﹣1时，PE ＝﹣2﹣2t ；②当﹣1＜t ＜0时，PE ＝2+2t 【详解】解：（1）∵抛物线y ＝ax 2+bx +3过点B （﹣3，0），C （1，0） ∴933030a b a b -+=⎧⎨++=⎩ 解得：12a b =-⎧⎨=-⎩∴抛物线解析式为y ＝﹣x 2﹣2x +3（2）过点P 作PH ⊥x 轴于点H ，交AB 于点F ∵x ＝0时，y ＝﹣x 2﹣2x +3＝3 ∴A （0，3）∴直线AB 解析式为y ＝x +3 ∵点P 在线段AB 上方抛物线上 ∴设P （t ，﹣t 2﹣2t +3）（﹣3＜t ＜0） ∴F （t ，t +3）∴PF ＝﹣t 2﹣2t +3﹣（t +3）＝﹣t 2﹣3t ∴S △PAB ＝S △PAF +S △PBF ＝12PF •OH +12PF •BH ＝12PF •OB ＝32（﹣t 2﹣3t ）＝﹣32（t +32）2+278∴点P 运动到坐标为（﹣32，154），△PAB 面积最大 （3）存在点P 使△PDE 为等腰直角三角形设P （t ，﹣t 2﹣2t +3）（﹣3＜t ＜0），则D （t ，t +3） ∴PD ＝﹣t 2﹣2t +3﹣（t +3）＝﹣t 2﹣3t ∵抛物线y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4 ∴对称轴为直线x ＝﹣1∵PE ∥x 轴交抛物线于点E∴y E ＝y P ，即点E 、P 关于对称轴对称 ∴2E Px x +＝﹣1 ∴x E ＝﹣2﹣x P ＝﹣2﹣t ∴PE ＝|x E ﹣x P |＝|﹣2﹣2t |∵△PDE 为等腰直角三角形，∠DPE ＝90° ∴PD ＝PE①当﹣3＜t ≤﹣1时，PE ＝﹣2﹣2t ∴﹣t 2﹣3t ＝﹣2﹣2t 解得：t 1＝1（舍去），t 2＝﹣2 ∴P （﹣2，3）②当﹣1＜t ＜0时，PE ＝2+2t ∴﹣t 2﹣3t ＝2+2t 解得：t 1＝517-+，t 2＝517--（舍去） ∴P （517-+，5317-+）综上所述，点P 坐标为（﹣2，3）或（517-+，5317-+）时使△PDE 为等腰直角三角形．【点睛】考核知识点：二次函数的综合.数形结合分析问题，运用轴对称性质和等腰三角形性质分析问题是关键.10．（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m ，宽是4 m ．按照图中所示的直角坐标系，抛物线可以用y=16-x 2+bx+c 表示，且抛物线上的点C 到OB 的水平距离为3 m ，到地面OA 的距离为172m.（1）求抛物线的函数关系式，并计算出拱顶D 到地面OA 的距离；（2）一辆货运汽车载一长方体集装箱后高为6m ，宽为4m ，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m ，那么两排灯的水平距离最小是多少米？【答案】（1）抛物线的函数关系式为y=16-x 2+2x+4，拱顶D 到地面OA 的距离为10 m ；(2)两排灯的水平距离最小是3． 【解析】 【详解】试题分析：根据点B 和点C 在函数图象上，利用待定系数法求出b 和c 的值，从而得出函数解析式，根据解析式求出顶点坐标，得出最大值；根据题意得出车最外侧与地面OA 的交点为（2,0）（或（10,0）），然后求出当x=2或x=10时y 的值，与6进行比较大小，比6大就可以通过，比6小就不能通过；将y=8代入函数，得出x 的值，然后进行做差得出最小值．试题解析：（1）由题知点17(0,4),3,2B C ⎛⎫⎪⎝⎭在抛物线上 所以41719326c b c =⎧⎪⎨=-⨯++⎪⎩，解得24b c =⎧⎨=⎩，所以21246y x x =-++ 所以，当62bx a=-=时，10t y =≦ 答：21246y x x =-++，拱顶D 到地面OA 的距离为10米 （2）由题知车最外侧与地面OA 的交点为（2,0）（或（10,0）） 当x=2或x=10时，2263y =>，所以可以通过 （3）令8y =，即212486x x -++=，可得212240x x -+=，解得12623,623x x =+=- 1243x x -=答：两排灯的水平距离最小是43 考点：二次函数的实际应用．11．如图，抛物线y=﹣（x ﹣1）2+c 与x 轴交于A ，B （A ，B 分别在y 轴的左右两侧）两点，与y 轴的正半轴交于点C ，顶点为D ，已知A （﹣1，0）．（1）求点B ，C 的坐标；（2）判断△CDB 的形状并说明理由；（3）将△COB 沿x 轴向右平移t 个单位长度（0＜t ＜3）得到△QPE ．△QPE 与△CDB 重叠部分（如图中阴影部分）面积为S ，求S 与t 的函数关系式，并写出自变量t 的取值范围． 【答案】(Ⅰ)B(3，0)；C(0，3)；(Ⅱ)CDB ∆为直角三角形；(Ⅲ)22333(0)221933(3)222t t t S t t t ⎧-+<≤⎪⎪=⎨⎪=-+<<⎪⎩.【解析】 【分析】（1）首先用待定系数法求出抛物线的解析式，然后进一步确定点B ，C 的坐标． （2）分别求出△CDB 三边的长度，利用勾股定理的逆定理判定△CDB 为直角三角形． （3）△COB 沿x 轴向右平移过程中，分两个阶段： ①当0＜t≤32时，如答图2所示，此时重叠部分为一个四边形； ②当32＜t ＜3时，如答图3所示，此时重叠部分为一个三角形． 【详解】解：(Ⅰ)∵点()1,0A -在抛物线()21y x c =--+上，∴()2011c =---+，得4c =∴抛物线解析式为：()214y x =--+，令0x =，得3y =，∴()0,3C ； 令0y =，得1x =-或3x =，∴()3,0B . (Ⅱ)CDB ∆为直角三角形.理由如下： 由抛物线解析式，得顶点D 的坐标为()1,4. 如答图1所示，过点D 作DM x ⊥轴于点M ， 则1OM =，4DM =，2BM OB OM =-=.过点C 作CN DM ⊥于点N ，则1CN =，1DN DM MN DM OC =-=-=. 在Rt OBC ∆中，由勾股定理得：22223332BC OB OC =+=+=； 在Rt CND ∆中，由勾股定理得：2222112CD CN DN =+=+=； 在Rt BMD ∆中，由勾股定理得：22222425BD BM DM =+=+=.∵222BC CD BD +=， ∴CDB ∆为直角三角形.(Ⅲ)设直线BC 的解析式为y kx b =+， ∵()()3,0,0,3B C ，∴303k b b +=⎧⎨=⎩，解得1,3k b =-=，∴3y x =-+，直线QE 是直线BC 向右平移t 个单位得到，∴直线QE 的解析式为：()33y x t x t =--+=-++； 设直线BD 的解析式为y mx n =+， ∵()()3,0,1,4B D ， ∴304m n m n +=⎧⎨+=⎩，解得：2,6m n =-=，∴26y x =-+.连续CQ 并延长，射线CQ 交BD 交于G ，则3,32G ⎛⎫ ⎪⎝⎭. 在COB ∆向右平移的过程中： (1)当302t <≤时，如答图2所示：设PQ 与BC 交于点K ，可得QK CQ t ==，3PB PK t ==-.设QE 与BD 的交点为F ，则：263y x y x t =-+⎧⎨=-++⎩. 解得32x t y t =-⎧⎨=⎩，∴()3,2F t t -.111222QPE PBK FBE F S S S S PE PQ PB PK BE y ∆∆∆=--=⋅-⋅-⋅ ()221113333232222t t t t t =⨯⨯---⋅=-+. (2)当332t <<时，如答图3所示：设PQ 分别与BC BD 、交于点K 、点J . ∵CQ t =，∴KQ t =，3PK PB t ==-.直线BD 解析式为26y x =-+，令x t =，得62y t =-， ∴(),62J t t -.1122PBJ PBK S S S PB PJ PB PK ∆∆=-=⋅-⋅ ()()()211362322t t t =---- 219322t t =-+. 综上所述，S 与t 的函数关系式为：2233302219333222t t t S t t t ⎧⎛⎫-+<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-+<< ⎪⎪⎝⎭⎩.12．已知函数()()22,1,222x nx n x n y n nx x x n ⎧-++≥⎪=⎨-++<⎪⎩（n 为常数） （1）当5n =，①点()4,P b 在此函数图象上，求b 的值； ②求此函数的最大值．（2）已知线段AB 的两个端点坐标分别为()()2,24,2A B 、，当此函数的图象与线段AB 只有一个交点时，直接写出n 的取值范围．（3）当此函数图象上有4个点到x 轴的距离等于4，求n 的取值范围．【答案】（1）①92b =②458；（2）1845n <≤，823n ≤<时，图象与线段AB 只有一个交点；（3）函数图象上有4个点到x 轴的距离等于4时，8n >或3142n ≤<． 【解析】 【分析】（1）①将()4,P b 代入2155222y x x =-++；②当5x ≥时，当5x =时有最大值为5；当5x <时，当52x =时有最大值为458；故函数的最大值为458； （2）将点()4,2代入2y x nx n =-++中，得到185n =，所以1845n <≤时，图象与线段AB 只有一个交点；将点()2,2）代入2y x nx n =-++和21222n n y x x =-++中，得到82,3n n ==， 所以823n ≤<时图象与线段AB 只有一个交点； （3）当xn =时，42n >，得到8n >；当2n x =时，1482n +≤，得到312n ≥，当x n=时，22y n n n n =-++=，4n <． 【详解】解：（1）当5n =时，()()225551555222x x x y x x x ⎧-++≥⎪=⎨-++<⎪⎩， ①将()4,P b 代入2155222y x x =-++， ∴92b =； ②当5x ≥时，当5x =时有最大值为5； 当5x <时，当52x =时有最大值为458； ∴函数的最大值为458； （2）将点()4,2代入2y x nx n =-++中，∴185n =， ∴1845n <≤时，图象与线段AB 只有一个交点； 将点()2,2代入2y x nx n =-++中， ∴2n =， 将点()2,2代入21222n ny x x =-++中， ∴83n =， ∴823n ≤<时图象与线段AB 只有一个交点； 综上所述：1845n <≤，823n ≤<时，图象与线段AB 只有一个交点； （3）当xn =时，22112222n n y n n =-++=，42n>，∴8n >； 当2n x =时，182n y =+， 1482n +≤，∴312n ≥， 当xn =时，22y n n n n =-++=，4n <；∴函数图象上有4个点到x 轴的距离等于4时，8n >或3142n ≤<． 【点睛】考核知识点：二次函数综合.数形结合分析问题是关键.13．如图1，抛物线经过平行四边形的顶点、、，抛物线与轴的另一交点为.经过点的直线将平行四边形分割为面积相等的两部分，与抛物线交于另一点.点为直线上方抛物线上一动点，设点的横坐标为.（1）求抛物线的解析式； （2）当何值时，的面积最大?并求最大值的立方根；（3）是否存在点使为直角三角形?若存在，求出的值；若不存在，说明理由.【答案】（1）抛物线解析式为y=﹣x 2+2x+3；（2）当t=时，△PEF 的面积最大，其最大值为×，最大值的立方根为=；（3）存在满足条件的点P ，t 的值为1或【解析】试题分析：（1）由A 、B 、C 三点的坐标，利用待定系数法可求得抛物线解析式； （2）由A 、C 坐标可求得平行四边形的中心的坐标，由抛物线的对称性可求得E 点坐标，从而可求得直线EF 的解析式，作PH ⊥x 轴，交直线l 于点M ，作FN ⊥PH ，则可用t 表示出PM 的长，从而可表示出△PEF 的面积，再利用二次函数的性质可求得其最大值，再求其最大值的立方根即可；（3）由题意可知有∠PAE=90°或∠APE=90°两种情况，当∠PAE=90°时，作PG⊥y轴，利用等腰直角三角形的性质可得到关于t的方程，可求得t的值；当∠APE=90°时，作PK⊥x 轴，AQ⊥PK，则可证得△PKE∽△AQP，利用相似三角形的性质可得到关于t的方程，可求得t的值．试题解析：（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+2x+3；（2）∵A（0，3），D（2，3），∴BC=AD=2，∵B（﹣1，0），∴C（1，0），∴线段AC的中点为（，），∵直线l将平行四边形ABCD分割为面积相等两部分，∴直线l过平行四边形的对称中心，∵A、D关于对称轴对称，∴抛物线对称轴为x=1，∴E（3，0），设直线l的解析式为y=kx+m，把E点和对称中心坐标代入可得，解得，∴直线l的解析式为y=﹣x+，联立直线l和抛物线解析式可得，解得或，∴F（﹣，），如图1，作PH⊥x轴，交l于点M，作FN⊥PH，∵P点横坐标为t，∴P（t，﹣t2+2t+3），M（t，﹣t+），∴PM=﹣t2+2t+3﹣（﹣t+）=﹣t2+t+，∴S△PEF=S△PFM+S△PEM=PM•FN+PM•EH=PM•（FN+EH）=（﹣t2+t+）（3+）=﹣（t﹣）+×，∴当t=时，△PEF的面积最大，其最大值为×，∴最大值的立方根为=；（3）由图可知∠PEA≠90°，∴只能有∠PAE=90°或∠APE=90°，①当∠PAE=90°时，如图2，作PG⊥y轴，∵OA=OE，∴∠OAE=∠OEA=45°，∴∠PAG=∠APG=45°，∴PG=AG，∴t=﹣t2+2t+3﹣3，即﹣t2+t=0，解得t=1或t=0（舍去），②当∠APE=90°时，如图3，作PK⊥x轴，AQ⊥PK，则PK=﹣t2+2t+3，AQ=t，KE=3﹣t，PQ=﹣t2+2t+3﹣3=﹣t2+2t，∵∠APQ+∠KPE=∠APQ+∠PAQ=90°，∴∠PAQ=∠KPE，且∠PKE=∠PQA，∴△PKE∽△AQP，∴，即，即t2﹣t﹣1=0，解得t=或t=＜﹣（舍去），综上可知存在满足条件的点P，t的值为1或．考点：二次函数综合题14．如图，在平面直角坐标系中，抛物线y=ax2+bx+c交x轴于A、B两点，交y轴于点C（0，﹣43），OA=1，OB=4，直线l过点A，交y轴于点D，交抛物线于点E，且满足tan∠OAD=34．（1）求抛物线的解析式；（2）动点P从点B出发，沿x轴正方形以每秒2个单位长度的速度向点A运动，动点Q 从点A出发，沿射线AE以每秒1个单位长度的速度向点E运动，当点P运动到点A时，点Q也停止运动，设运动时间为t秒．①在P、Q的运动过程中，是否存在某一时刻t，使得△ADC与△PQA相似，若存在，求出t的值；若不存在，请说明理由．②在P、Q的运动过程中，是否存在某一时刻t，使得△APQ与△CAQ的面积之和最大？若存在，求出t的值；若不存在，请说明理由．【答案】（1）抛物线的解析式为y=21433x x +-；（2）①存在t=10047或t=3534，使得△ADC 与△PQA 相似；②当t=139时，△APQ 与△CAQ 的面积之和最大. 【解析】 分析：（1）应用待定系数法求解析式（2）①分别用t 表示△ADC 、△PQA 各边，应用分类讨论相似三角形比例式，求t 值； ②分别用t 表示△APQ 与△CAQ 的面积之和，讨论最大值．详解：（1）∵OA=1，OB=4，∴A （1，0），B （﹣4，0），设抛物线的解析式为y=a （x+4）（x ﹣1），∵点C （0，﹣43）在抛物线上， ∴﹣4=4(1)3a ⨯⨯-， 解得a=13. ∴抛物线的解析式为y=2114(4)(1)333x x x x +-=+-. （2）存在t ，使得△ADC 与△PQA 相似． 理由：①在Rt △AOC 中，OA=1，OC=43， 则tan ∠ACO=34OA OC =， ∵tan ∠OAD=34， ∴∠OAD=∠ACO ， ∵直线l 的解析式为y=3(1)4x -， ∴D （0，﹣34）， ∵点C （0，﹣43）， ∴CD=4373412-=， 由AC 2=OC 2+OA 2，得AC=53， 在△AQP 中，AP=AB ﹣PB=5﹣2t ，AQ=t ，由∠PAQ=∠ACD ，要使△ADC 与△PQA 相似，只需AP CDAQ AC=或AP ACAQ CD=，则有7521253tt-=或5523712tt-=，解得t1=10047，t2=3534，∵t1＜2.5，t2＜2.5，∴存在t=10047或t=3534，使得△ADC与△PQA相似；②存在t，使得△APQ与△CAQ的面积之和最大，理由：作PF⊥AQ于点F，CN⊥AQ于N，在△APF中，PF=AP•sin∠PAF=352)5t-（，在△AOD中，由AD2=OD2+OA2，得AD=54，在△ADC中，由S△ADC=11··22AD CN CD OA=，∴CN=71·7125154CD OAAD⨯==，∴S△AQP+S△AQC=21137313169()[(52)]()2251559135AQ PF CN t t t+=--+=--+，∴当t=139时，△APQ与△CAQ的面积之和最大.点睛：本题为代数、几何综合题，考查待定系数法、相似三角形判定、二次函数最值，应用了分类讨论和数形结合思想．15．某大学生利用暑假40天社会实践参与了一家网店经营，了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示．。
2020-2021中考数学二次函数的综合题试题含详细答案
2020-2021中考数学二次函数的综合题试题含详细答案一、二次函数1．如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上。
（1）求抛物线的解析式；（2）在（1）中抛物线的第二象限图象上是否存在一点P ，使△POB 与△POC 全等？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若点Q 是y 轴上一点，且△ABQ 为直角三角形，求点Q 的坐标。
【答案】解：（1）2y x 2x 3=--；（2）存在，P （1-132，13-12）；（3）Q 点坐标为（0，-72）或（0，32）或（0，－1）或（0，－3）. 【解析】【分析】 （1）已知点A 坐标可确定直线AB 的解析式，进一步能求出点B 的坐标．点A 是抛物线的顶点，那么可以将抛物线的解析式设为顶点式，再代入点B 的坐标，依据待定系数法可解. （2）首先由抛物线的解析式求出点C 的坐标，在△POB 和△POC 中，已知的条件是公共边OP ，若OB 与OC 不相等，那么这两个三角形不能构成全等三角形；若OB 等于OC ，那么还要满足的条件为：∠POC=∠POB ，各自去掉一个直角后容易发现，点P 正好在第二象限的角平分线上，联立直线y=-x 与抛物线的解析式，直接求交点坐标即可，同时还要注意点P 在第二象限的限定条件.（3）分别以A 、B 、Q 为直角顶点，分类进行讨论，找出相关的相似三角形，依据对应线段成比例进行求解即可.【详解】解：（1）把A （1，﹣4）代入y ＝kx ﹣6，得k ＝2，∴y ＝2x ﹣6，令y ＝0，解得：x ＝3，∴B 的坐标是（3，0）．∵A 为顶点，∴设抛物线的解析为y ＝a （x ﹣1）2﹣4，把B（3，0）代入得：4a﹣4＝0，解得a＝1，∴y＝（x﹣1）2﹣4＝x2﹣2x﹣3．（2）存在．∵OB＝OC＝3，OP＝OP，∴当∠POB＝∠POC时，△POB≌△POC，此时PO平分第二象限，即PO的解析式为y＝﹣x．设P（m，﹣m），则﹣m＝m2﹣2m﹣3，解得m＝1-132（m＝1+132＞0，舍），∴P（1-13，13-1）．（3）①如图，当∠Q1AB＝90°时，△DAQ1∽△DOB，∴1DQADOD DB=，即56=135，∴DQ1＝52，∴OQ1＝72，即Q1（0，-72）；②如图，当∠Q2BA＝90°时，△BOQ2∽△DOB，∴2OQOBOD OB=，即2363OQ=，∴OQ2＝32，即Q2（0，32）；③如图，当∠AQ3B＝90°时，作AE⊥y轴于E，则△BOQ3∽△Q3EA，∴33OQOBQ E AE=，即33341OQOQ=-∴OQ32﹣4OQ3+3＝0，∴OQ3＝1或3，即Q3（0，﹣1），Q4（0，﹣3）．综上，Q点坐标为（0，-72）或（0，32）或（0，﹣1）或（0，﹣3）．2．如图，已知抛物线2y ax bx c =++经过A （－3，0），B （1，0），C （0，3）三点，其顶点为D ，对称轴是直线l ，l 与x 轴交于点H ．（1）求该抛物线的解析式；（2）若点P 是该抛物线对称轴l 上的一个动点，求△PBC 周长的最小值；（3）如图（2），若E 是线段AD 上的一个动点（ E 与A 、D 不重合），过E 点作平行于y 轴的直线交抛物线于点F ，交x 轴于点G ，设点E 的横坐标为m ，△ADF 的面积为S ． ①求S 与m 的函数关系式；②S 是否存在最大值？若存在，求出最大值及此时点E 的坐标； 若不存在，请说明理由．【答案】（1）2y x 2x 3=--+.（2）3210.（3）①2S m 4m 3=---.②当m=﹣2时，S 最大，最大值为1，此时点E 的坐标为（﹣2，2）.【解析】【分析】（1）根据函数图象经过的三点，用待定系数法确定二次函数的解析式即可.（2）根据BC 是定值，得到当PB+PC 最小时，△PBC 的周长最小，根据点的坐标求得相应线段的长即可.（3）设点E 的横坐标为m ，表示出E （m ，2m+6），F （m ，2m 2m 3--+），最后表示出EF 的长，从而表示出S 于m 的函数关系，然后求二次函数的最值即可.【详解】解：（1）∵抛物线2y ax bx c =++经过A （－3，0），B （1，0），∴可设抛物线交点式为()()y a x 3x 1=+-.又∵抛物线2y ax bx c =++经过C （0，3），∴a 1=-.∴抛物线的解析式为：()()y x 3x 1=-+-，即2y x 2x 3=--+.（2）∵△PBC 的周长为：PB+PC+BC ，且BC 是定值.∴当PB+PC 最小时，△PBC 的周长最小.∵点A 、点B 关于对称轴I 对称，∴连接AC 交l 于点P ，即点P 为所求的点.∵AP=BP ，∴△PBC 的周长最小是：PB+PC+BC=AC+BC.∵A （－3，0），B （1，0），C （0，3），∴AC=32，BC=10.∴△PBC 的周长最小是：3210+.（3）①∵抛物线2y x 2x 3=--+顶点D 的坐标为（﹣1，4），A （﹣3，0），∴直线AD 的解析式为y=2x+6∵点E 的横坐标为m ，∴E （m ，2m+6），F （m ，2m 2m 3--+）∴()22EF m 2m 32m 6m 4m 3=--+-+=---. ∴()22DEF AEF 1111S S S EF GH EF AG EF AH m 4m 32m 4m 32222∆∆=+=⋅⋅+⋅⋅=⋅⋅=⋅---⋅=---.∴S 与m 的函数关系式为2S m 4m 3=---.②()22S m 4m 3m 21=---=-++，∴当m=﹣2时，S 最大，最大值为1，此时点E 的坐标为（﹣2，2）.3．如图，已知A （﹣2，0），B （4，0），抛物线y=ax 2+bx ﹣1过A 、B 两点，并与过A 点的直线y=﹣12x ﹣1交于点C ． （1）求抛物线解析式及对称轴；（2）在抛物线的对称轴上是否存在一点P ，使四边形ACPO 的周长最小？若存在，求出点P 的坐标，若不存在，请说明理由；（3）点M 为y 轴右侧抛物线上一点，过点M 作直线AC 的垂线，垂足为N ．问：是否存在这样的点N ，使以点M 、N 、C 为顶点的三角形与△AOC 相似，若存在，求出点N 的坐标，若不存在，请说明理由．【答案】（1）抛物线解析式为：y=211184x x --，抛物线对称轴为直线x=1；（2）存在P 点坐标为（1，﹣12）；（3）N 点坐标为（4，﹣3）或（2，﹣1） 【解析】 分析：（1）由待定系数法求解即可；（2）将四边形周长最小转化为PC+PO 最小即可；（3）利用相似三角形对应点进行分类讨论，构造图形．设出点N 坐标，表示点M 坐标代入抛物线解析式即可．详解：（1）把A （-2，0），B （4，0）代入抛物线y=ax 2+bx-1，得042101641a b a b --⎧⎨+-⎩＝＝ 解得1814a b ⎧⎪⎪⎨⎪-⎪⎩＝＝ ∴抛物线解析式为：y=18x 2−14x−1 ∴抛物线对称轴为直线x=-141228b a -=-⨯＝1 （2）存在 使四边形ACPO 的周长最小，只需PC+PO 最小∴取点C （0，-1）关于直线x=1的对称点C′（2，-1），连C′O 与直线x=1的交点即为P 点．设过点C′、O 直线解析式为：y=kx∴k=-12∴y=-12x 则P 点坐标为（1，-12） （3）当△AOC ∽△MNC 时，如图，延长MN 交y 轴于点D ，过点N 作NE ⊥y 轴于点E∵∠ACO=∠NCD，∠AOC=∠CND=90°∴∠CDN=∠CAO由相似，∠CAO=∠CMN∴∠CDN=∠CMN∵MN⊥AC∴M、D关于AN对称，则N为DM中点设点N坐标为（a，-12a-1）由△EDN∽△OAC ∴ED=2a∴点D坐标为（0，-52a−1）∵N为DM中点∴点M坐标为（2a，32a−1）把M代入y=18x2−14x−1，解得a=4则N点坐标为（4，-3）当△AOC∽△CNM时，∠CAO=∠NCM∴CM∥AB则点C关于直线x=1的对称点C′即为点N由（2）N（2，-1）∴N点坐标为（4，-3）或（2，-1）点睛：本题为代数几何综合题，考查了待定系数、两点之间线段最短的数学模型构造、三角形相似．解答时，应用了数形结合和分类讨论的数学思想．4．已知，抛物线y=x2+2mx(m为常数且m≠0）．（1）判断该抛物线与x轴的交点个数，并说明理由．（2）若点A（-n+5，0），B(n-1，0)在该抛物线上，点M为抛物线的顶点，求△ABM的面积．（3）若点（2，p)，（3，g ），（4，r)均在该抛物线上，且p<g<r ，求m 的取值范围．【答案】（1）抛物线与x 轴有2个交点，理由见解析；（2）△ABM 的面积为8；（3）m 的取值范围m>-2.5【解析】【分析】（1）首先算出根的判别式b 2-4ac 的值，根据偶数次幂的非负性，判断该值一定大于0，从而根据抛物线与x 轴交点个数与根的判别式的关系即可得出结论；（2）根据抛物线的对称性及A,B 两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程，求解算出m 的值，进而求出抛物线的解析式，得出A,B,M 三点的坐标，根据三角形的面积计算方法，即可算出答案；（3）方法一（图象法）：根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时，显然不符合题目条件；当对称轴在直线x=2的左边时，显然符合题目条件（如图2），从而列出不等式得出m 的取值范围；当对称轴在直线x=2和x=3之间时，满足3-（-m)>-m-2即可（如图3），再列出不等式得出m 的取值范围，综上所述，求出m 的取值范围；方法二（代数法）：将三点的横坐标分贝代入抛物线的解析式，用含m 的式子表示出p,g,r ，再代入 p<g<r 即可列出关于m 的不等式组，求解即可。
2020-2021初中数学二次函数经典测试题附解析
2020-2021初中数学二次函数经典测试题附解析一、选择题1．如图，已知()4,1A --，线段AB 与x 轴平行，且2AB =，抛物线2y x mx n =-++经过点()0,3C 和()3,0D ，若线段AB 以每秒2个单位长度的速度向下平移，设平移的时间为t （秒）.若抛物线与线段AB 有公共点，则t 的取值范围是（ ）A ．010t ≤≤B ．210t ≤≤C ．28t ≤≤D ．210t <<【答案】B【解析】【分析】 直接利用待定系数法求出二次函数，得出B 点坐标，分别得出当抛物线l 经过点B 时，当抛物线l 经过点A 时，求出y 的值，进而得出t 的取值范围；【详解】解：（1）把点C （0，3）和D （3，0）的坐标代入y=-x 2+mx+n 中，得，23330n m n =⎧⎨-++=⎩解得32n m =⎧⎨=⎩∴抛物线l 解析式为y=-x 2+2x+3，设点B 的坐标为（-2，-1-2t ），点A 的坐标为（-4，-1-2t ），当抛物线l 经过点B 时，有y=-（-2）2+2×（-2）+3=-5，当抛物线l 经过点A 时，有y=-（-4）2+2×（-4）+3=-21，当抛物线l 与线段AB 总有公共点时，有-21≤-1-2t≤-5，解得：2≤t≤10．故应选B【点睛】此题主要考查了二次函数综合以及不等式组的解法等知识，正确利用数形结合分析得出关于t 的不等式是解题关键．2．已知，二次函数y=ax 2+bx+a 2+b （a≠0）的图象为下列图象之一，则a 的值为（ ）A．-1 B．1 C．-3 D．-4【答案】A【解析】【分析】分别对图形进行讨论：若二次函数的图形为第一个，则b=0，其顶点坐标为(0，a2)，与图形中的顶点坐标不符；若二次函数的图形为第二个，则b=0，根据顶点坐标有a2=3，由抛物线与x的交点坐标得到x2=-a，所以a=-4，它们相矛盾；若二次函数的图形为第三个，把点(-1，0)代入解析式得到a-b+a2+b=0，解得a=-1；若二次函数的图形为第四个，把(-2，0)和(0，0)分别代入解析式可计算出a的值．【详解】解：若二次函数的图形为第一个，对称轴为y轴，则b=0，y=ax2+a2，其顶点坐标为(0，a2)，而a2>0，所以二次函数的图形不能为第一个；若二次函数的图形为第二个，对称轴为y轴，则b=0，y=ax2+a2，a2=3，而当y=0时，x2=−a，所以−a=4，a=−4，所以二次函数的图形不能为第二个；若二次函数的图形为第三个，令x=−1，y=0，则a−b+a2+b=0，所以a=−1；若二次函数的图形为第四个，令x=0，y=0，则a2+b=0①；令x=−2，y=0，则4a−2b+a2+b=0②，由①②得a=−2，这与图象开口向上不符合，所以二次函数的图形不能为第四个.故选A.【点睛】本题考查了二次函数y=ax2+bx+c(a≠0)的图象与系数的关系：a＞0，开口向上；a＜0，开口向下；抛物线的对称轴为直线x=-；顶点坐标为(-，)；也考查了点在抛物线上则点的坐标满足抛物线的解析式.3．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）4a+2b+c＜0；（2）方程ax2+bx+c＝0两根都大于零；（3）y随x的增大而增大；（4）一次函数y＝x+bc 的图象一定不过第二象限．其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】C【解析】【分析】由图可知，x=2时函数值小于0，故（1）正确，函数与x轴的交点为x=1.x=3，都大于0，故（2）正确，由图像知（3）错误，由图象开口向上，a＞0，与y轴交于正半轴，c＞0，对称轴x=﹣＝1，故b＜0，bc＜0，即可判断一次函数y＝x+bc的图象.【详解】①由x＝2时，y＝4a+2b+c，由图象知：y＝4a+2b+c＜0，故正确；②方程ax2+bx+c＝0两根分别为1，3，都大于0，故正确；③当x＜2时，由图象知：y随x的增大而减小，故错误；④由图象开口向上，a＞0，与y轴交于正半轴，c＞0，x=﹣＝1＞0，∴b＜0，∴bc＜0，∴一次函数y＝x+bc的图象一定过第一、三、四象限，故正确；故正确的共有3个，故选：C．【点睛】此题主要考查二次函数的图像，解题的关键是熟知各系数所代表的含义.4．如图，坐标平面上，二次函数y＝﹣x2+4x﹣k的图形与x轴交于A、B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k值为何？( )A．1 B．12C．43D．45【答案】D【解析】【分析】求出顶点和C的坐标，由三角形的面积关系得出关于k的方程，解方程即可．【详解】解：∵y＝﹣x2+4x﹣k＝﹣(x﹣2)2+4﹣k，∴顶点D(2，4﹣k)，C(0，﹣k)，∴OC＝k，∵△ABC的面积＝12AB•OC＝12AB•k，△ABD的面积＝12AB(4﹣k)，△ABC与△ABD的面积比为1：4，∴k ＝14(4﹣k)， 解得：k ＝45． 故选：D ．【点睛】 本题考查了抛物线与x 轴的交点、抛物线的顶点式；根据三角形的面积关系得出方程是解决问题的关键．5．四位同学在研究函数2y x bx c =++（,b c 是常数）时，甲发现当1x =时，函数有最小值；乙发现1-是方程20x bx c ++=的一个根；丙发现函数的最小值为3；丁发现当2x =时，4y =，已知这四位同学中只有一位发现的结论是错误的，则该同学是（ ） A ．甲B ．乙C ．丙D ．丁【答案】B【解析】【分析】利用假设法逐一分析，分别求出二次函数的解析式，再判断与假设是否矛盾即可得出结论．【详解】解：A ．假设甲同学的结论错误，则乙、丙、丁的结论都正确由乙、丁同学的结论可得 01442b c b c =-+⎧⎨=++⎩解得：1323b c ⎧=⎪⎪⎨⎪=-⎪⎩∴二次函数的解析式为：221212533636⎛⎫=+-=+ ⎪⎝⎭-y x x x ∴当x=16-时，y 的最小值为2536-，与丙的结论矛盾，故假设不成立，故本选项不符合题意；B ．假设乙同学的结论错误，则甲、丙、丁的结论都正确由甲、丙的结论可得二次函数解析式为()213y x =-+当x=2时，解得y=4，当x=-1时，y=7≠0∴此时符合假设条件，故本选项符合题意；C ． 假设丙同学的结论错误，则甲、乙、丁的结论都正确由甲乙的结论可得1201b b c⎧-=⎪⎨⎪=-+⎩ 解得：23b c =-⎧⎨=-⎩∴223y x x =--当x=2时，解得：y=-3，与丁的结论矛盾，故假设不成立，故本选项不符合题意； D ． 假设丁同学的结论错误，则甲、乙、丙的结论都正确由甲、丙的结论可得二次函数解析式为()213y x =-+当x=-1时，解得y=7≠0，与乙的结论矛盾，故假设不成立，故本选项不符合题意． 故选B ．【点睛】此题考查的是利用待定系数法求二次函数解析式，利用假设法求出b 、c 的值是解决此题的关键．6．已知二次函数223(0)y ax ax a a =--≠，关于此函数的图象及性质，下列结论中不一定成立的是( )A ．该图象的顶点坐标为()1,4a -B ．该图象与x 轴的交点为()()1,0,3,0-C ．若该图象经过点()2,5-，则一定经过点()4,5D ．当1x >时，y 随x 的增大而增大【答案】D【解析】【分析】根据二次函数的图象与性质即可求出答案．【详解】解：y=a （x 2-2x-3）=a （x-3）（x+1）令y=0，∴x=3或x=-1，∴抛物线与x 轴的交点坐标为（3，0）与（-1，0），故B 成立；∴抛物线的对称轴为：x=1，令x=1代入y=ax 2-2ax-3a ，∴y=a-2a-3a=-4a ，∴顶点坐标为（1，-4a ），故A 成立；由于点（-2，5）与（4，5）关于直线x=1对称，∴若该图象经过点（-2，5），则一定经过点（4，5），故C 成立；当x ＞1，a ＞0时，y 随着x 的增大而增大，当x ＞1，a ＜0时，y 随着x 的增大而减少，故D不一定成立；故选：D．【点睛】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于基础题型．7．在平面直角坐标系内，已知点A（﹣1，0），点B（1，1）都在直线1122y x=+上，若抛物线y＝ax2﹣x+1（a≠0）与线段AB有两个不同的交点，则a的取值范围是（）A．a≤﹣2 B．a＜98C．1≤a＜98或a≤﹣2 D．﹣2≤a＜98【答案】C【解析】【分析】分a＞0，a＜0两种情况讨论，根据题意列出不等式组，可求a的取值范围．【详解】∵抛物线y＝ax2﹣x+1（a≠0）与线段AB有两个不同的交点，∴令1122x+＝ax2﹣x+1，则2ax2﹣3x+1＝0∴△＝9﹣8a＞0∴a＜9 8①当a＜0时，110111 aa++≤⎧⎨-+≤⎩解得：a≤﹣2∴a≤﹣2②当a＞0时，110111 aa++≥⎧⎨-+≥⎩解得：a≥1∴1≤a＜9 8综上所述：1≤a＜98或a≤﹣2故选：C．【点睛】本题考查二次函数图象与系数的关系，一次函数图象上点的坐标特征，二次函数图象点的坐标特征，利用分类讨论思想解决问题是本题的关键．8．若二次函数y＝ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，对于以下说法：①b2﹣4ac＞0②x＝x0是方程ax2+bx+c＝y0的解③x1＜x0＜x2④a（x0﹣x1）（x0﹣x2）＜0其中正确的是（）A．①③④B．①②④C．①②③D．②③【答案】B【解析】【分析】①根据二次函数图象与x轴有两个不同的交点，结合根的判别式即可得出△=b2-4ac＞0，①正确；②由点M（x0，y0）在二次函数图象上，利用二次函数图象上点的坐标特征即可得出x=x0是方程ax2+bx+c=y0的解，②正确；③分a＞0和a＜0考虑，当a＞0时得出x1＜x0＜x2；当a＜0时得出x0＜x1或x0＞x2，③错误；④将二次函数的解析式由一般式转化为交点式，再由点M（x0，y0）在x轴下方即可得出y0=a（x0-x1）（x0-x2）＜0，④正确．【详解】①∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，∴方程ax2+bx+c=0有两个不相等的实数根，∴△=b2-4ac＞0，①正确；②∵图象上有一点M（x0，y0），∴a+bx0+c=y0，∴x=x0是方程ax2+bx+c=y0的解，②正确；③当a＞0时，∵M（x0，y0）在x轴下方，∴x1＜x0＜x2；当a＜0时，∵M（x0，y0）在x轴下方，∴x0＜x1或x0＞x2，③错误；④∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），∴y=ax2+bx+c=a（x-x1）（x-x2），∵图象上有一点M（x0，y0）在x轴下方，∴y0=a（x0-x1）（x0-x2）＜0，④正确；故选B．【点睛】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及二次函数图象与系数的关系，根据二次函数的相关知识逐一分析四条结论的正误是解题的关键．9．如图，已知将抛物线21y x =-沿x 轴向上翻折与所得抛物线围成一个封闭区域（包括边界），在这个区域内有5个整点（点M 满足横、纵坐标都为整数，则把点M 叫做“整点”）.现将抛物线()()2120y a x a =++<沿x 轴向下翻折，所得抛物线与原抛物线所围成的封闭区域内（包括边界）恰有11个整点，则a 的取值范围是（ ）A ．1a ≤-B ．12a ≤-C ．112a -<≤D ．112a -≤<- 【答案】D【解析】【分析】 画出图象，利用图象可得m 的取值范围【详解】解：∵ ()()2120y a x a =++<∴该抛物线开口向下，顶点(-1，2)，对称轴是直线x=-1.∴点(-1,2)、点(-1，1)、点(-1, 0)、点(-1,-1)、点(-1，-2)符合题意，此时x 轴.上的点(-2, 0)、(0, 0)也符合题意，将(0，1)代入()()2120y a x a =++<得到1=a+2.解得a=-1.将(1, 0)代入()()2120y a x a =++<得到0= 4a+2.解得a=1-2∵有11个整点， ∴点(0，-1)、点(-2, -1)、点(-2,1)、点(0，1)也必须符合题意.综上可知:当1-1a<-2≤ 时，点(-1，2)、点(-1，1)、点(-1, 0)、点(-1，-1)、点(-1，-2)、点(-2, 0)、(0，0)、点(0，-1)、点(-2，-1)、点(-2，1)、点(0, 1)，共有11个整点符合题意, 故选: D.【点睛】 本题考查了二次函数图象与系数的关系，抛物线与x 轴的交点的求法，利用图象解决问题是本题的关键.10．若用“*”表示一种运算规则，我们规定：a *b ＝ab ﹣a +b ，如：3*2＝3×2﹣3+2＝5．以下说法中错误的是（ ）A ．不等式（﹣2）*（3﹣x ）＜2的解集是x ＜3B ．函数y ＝（x +2）*x 的图象与x 轴有两个交点C ．在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数D ．方程（x ﹣2）*3＝5的解是x ＝5【答案】D【解析】【分析】根据题目中所给的运算法则列出不等式，解不等式即可判定选项A ；根据题目中所给的运算法则求得函数解析式，由此即可判定选项B ；根据题目中所给的运算法则可得a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0，由此即可判定选项C ；根据题目中所给的运算法则列出方程，解方程即可判定选项D.【详解】∵a *b ＝ab ﹣a +b ，∴（﹣2）*（3﹣x ）＝（﹣2）×（3﹣x ）﹣（﹣2）+（3﹣x ）＝x ﹣1，∵（﹣2）*（3﹣x ）＜2，∴x ﹣1＜2，解得x ＜3，故选项A 正确；∵y ＝（x +2）*x ＝（x +2）x ﹣（x +2）+x ＝x 2+2x ﹣2，∴当y ＝0时，x 2+2x ﹣2＝0，解得，x 1＝﹣x 2＝﹣1B 正确； ∵a *（a +1）＝a （a +1）﹣a +（a +1）＝a 2+a +1＝（a +12）2+34＞0， ∴在实数范围内，无论a 取何值，代数式a *（a +1）的值总为正数，故选项C 正确； ∵（x ﹣2）*3＝5，∴（x ﹣2）×3﹣（x ﹣2）+3＝5，解得，x ＝3，故选项D 错误；故选D．【点睛】本题是阅读理解题，根据题目中所给的运算法则得到相应的运算式子是解决问题的关键.11．如图，已知二次函数y=ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x=1．下列结论：①abc＞0；②4a+2b+c＞0；③13＜a＜23；④b＞c．其中含所有正确结论的选项是（）A．①②③B．①③④C．②③④D．①②④【答案】B【解析】【分析】根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号，从而判断①；根据对称性得到函数图象经过（3，0），则得②的判断；根据图象经过（-1，0）可得到a、b、c 之间的关系，从而对④作判断；从图象与y轴的交点B在（0，-2）和（0，-1）之间可以判断c的大小得出③的正误．【详解】①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（-1，0），对称轴为直线x=1，∴图象与x轴的另一个交点为（3，0），∴当x=2时，y＜0，∴4a+2b+c＜0，故②错误；③∵图象与y轴的交点B在（0，-2）和（0，-1）之间，∴-2＜c ＜-1 ∵-12b a=， ∴b=-2a ， ∵函数图象经过（-1，0），∴a-b+c=0，∴c=-3a ，∴-2＜-3a ＜-1，∴13＜a ＜23；故③正确 ④∵函数图象经过（-1，0），∴a-b+c=0，∴b-c=a ，∵a ＞0，∴b-c ＞0，即b ＞c ；故④正确；故选B ．【点睛】主要考查图象与二次函数系数之间的关系．解题关键是注意掌握数形结合思想的应用．12．二次函数y=﹣x 2+mx 的图象如图，对称轴为直线x=2，若关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解，则t 的取值范围是（ ）A ．t ＞﹣5B ．﹣5＜t ＜3C ．3＜t≤4D ．﹣5＜t≤4【答案】D【解析】【分析】 先根据对称轴x=2求得m 的值，然后求得x=1和x=5时y 的值，最后根据图形的特点，得出直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4．【详解】∵抛物线的对称轴为x ＝2，∴22m -=-，m=4 如图，关于x 的一元二次方程﹣x 2+mx ﹣t=0的解就是抛物线y=﹣x 2+mx 与直线y=t 的交点的横坐标当x=1时，y=3，当x=5时，y=﹣5，由图象可知关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解， 则直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4，∴﹣5＜t≤4．故选：D ．【点睛】本题考查二次函数与一元二次方程的关系，方程有解，反映在图象上即图象与x 轴(或某直线)有交点．13．在同一平面直角坐标系中，函数y=ax 2+bx 与y=bx+a 的图象可能是（ ）A ．B ．C ．D ．【答案】C【解析】试题解析：A 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，对称轴x=﹣2b a＜0，应在y 轴的左侧，故不合题意，图形错误． B 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＜0；而对于抛物线y=ax 2+bx 来说，图象应开口向下，故不合题意，图形错误．C 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，对称轴x=﹣2b a位于y 轴的右侧，故符合题意，D 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，a ＜0，故不合题意，图形错误．故选C ．考点：二次函数的图象；一次函数的图象．14．函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是（ ） A ． B ． C ． D ．【答案】C【解析】【分析】根据a 、b 的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一排除．【详解】当a ＞0时，二次函数的图象开口向上，一次函数的图象经过一、三或一、二、三或一、三、四象限，故A 、D 不正确；由B 、C 中二次函数的图象可知，对称轴x=-2b a＞0，且a ＞0，则b ＜0， 但B 中，一次函数a ＞0，b ＞0，排除B ．故选C ．15．已知抛物线y ＝x 2+（2a +1）x +a 2﹣a ，则抛物线的顶点不可能在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】D【解析】【分析】求得顶点坐标，得出顶点的横坐标和纵坐标的关系式，即可求得．【详解】抛物线y ＝x 2+（2a +1）x +a 2﹣a 的顶点的横坐标为：x ＝﹣212a +＝﹣a ﹣12， 纵坐标为：y ＝()()224214a a a --+＝﹣2a ﹣14， ∴抛物线的顶点横坐标和纵坐标的关系式为：y ＝2x +34，∴抛物线的顶点经过一二三象限，不经过第四象限，故选：D ．【点睛】本题考查了二次函数的性质，得到顶点的横纵坐标的关系式是解题的关键．16．已知抛物线224y x x c =-+与直线2y =有两个不同的交点．下列结论：①4c <；②当1x =时，y 有最小值2c -；③方程22420x x c -+-=有两个不等实根；④若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形，则52c =；其中正确的结论的个数是（ ）A ．4B ．3C ．2D ．1 【答案】B【解析】【分析】根据“抛物线224y x x c =-+与直线2y =有两个不同的交点”即可判断①③；根据抛物线的对称轴为直线x=1即可判断②；根据等腰直角三角形的性质，用c 表达出两个交点，代入抛物线解析式计算即可判断④．【详解】解：∵抛物线224y x x c =-+与直线2y =有两个不同的交点，∴2242x x c -+=有两个不相等的实数根，即22420x x c -+-=有两个不相等的实数根，故③正确，∴1642(2)0c ∆=-⨯⨯->，解得：4c <，故①正确；∵抛物线的对称轴为直线x=1，且抛物线开口向上，∴当x=1时，2y c =-为最小值，故②正确；若连接这两个交点与抛物线的顶点，恰好是一个等腰直角三角形，则顶点（1，c-2）到直线y=2的距离等于两交点距离的一半，∵顶点（1，c-2）到直线y=2的距离为2-（c-2）=4-c ，∴两交点的横坐标分别为1-（4-c ）=c-3与1+（4-c ）=5-c∴两交点坐标为（c-3,2）与（5-c,2），将（c-3,2）代入224y x x c =-+中得：22(3)4(3)2c c c ---+= 解得：72c =或4c = ∵4c <， ∴72c =，故④错误， ∴正确的有①②③，故选：B ．【点睛】本题考查了二次函数与一元二次方程的关系以及二次函数的性质，解题的关键是熟练掌握函数与方程之间的联系．17．已知抛物线y ＝x 2+2x ﹣m ﹣1与x 轴没有交点，则函数y ＝的大致图象是（ ） A ． B ．C ．D ．【答案】B【解析】【分析】由题意可求m ＜﹣2，即可求解．【详解】∵抛物线y ＝x 2+2x ﹣m ﹣1与x 轴没有交点，∴△＝4﹣4（﹣m ﹣1）＜0∴m ＜﹣2∴函数y ＝的图象在第二、第四象限，故选B ．【点睛】本题考查了反比例函数的图象，二次函数性质，求m 的取值范围是本题的关键．18．已知二次函数2()y x h =-- (h 为常数),当自变量x 的值满足25x ≤≤时,与其对应的函数值y 的最大值为-1,则h 的值为( )A ．3或6B ．1或6C ．1或3D ．4或6【答案】B【解析】分析：分h ＜2、2≤h≤5和h ＞5三种情况考虑：当h ＜2时，根据二次函数的性质可得出关于h 的一元二次方程，解之即可得出结论；当2≤h≤5时，由此时函数的最大值为0与题意不符，可得出该情况不存在；当h ＞5时，根据二次函数的性质可得出关于h 的一元二次方程，解之即可得出结论．综上即可得出结论．详解：如图，当h ＜2时，有-（2-h ）2=-1，解得：h 1=1，h 2=3（舍去）；当2≤h≤5时，y=-（x-h ）2的最大值为0，不符合题意；当h ＞5时，有-（5-h ）2=-1，解得：h 3=4（舍去），h 4=6．综上所述：h 的值为1或6．故选B ．点睛：本题考查了二次函数的最值以及二次函数的性质，分h ＜2、2≤h≤5和h ＞5三种情况求出h 值是解题的关键．19．已知抛物线y=x 2-2mx-4（m ＞0）的顶点M 关于坐标原点O 的对称点为M′，若点M′在这条抛物线上，则点M 的坐标为（ ）A ．（1，-5）B ．（3，-13）C ．（2，-8）D ．（4，-20）【答案】C【解析】【分析】【详解】解：22224=()4y x mx x m m =-----，∴点M （m ，﹣m 2﹣4），∴点M′（﹣m ，m 2+4），∴m 2+2m 2﹣4=m 2+4．解得m=±2．∵m ＞0，∴m=2，∴M （2，﹣8）． 故选C ．【点睛】本题考查二次函数的性质．20．平移抛物线2:L y x =得到抛物线L '，使得抛物线L '的顶点关于原点对称的点仍在抛物线L '上，下列的平移中，不能得到满足条件的抛物线L '的是（ ）A ．向右平移1个单位，再向下平移2个单位B ．向左平移1个单位，再向下平移2个单位C ．向左平移32个单位，再向下平移92个单位 D ．向左平移3个单位，再向下平移9个单位【答案】D【解析】【分析】通过各个选项的平移分别得到相应的函数关系式，再判断原点是否在该抛物线上即可．【详解】解：由A 选项可得L '为：2(1)2y x =--，则顶点为（1，-2），顶点（1，-2）关于原点的对称点为（-1，2），当x ＝-1时，y ＝2，则对称点在该函数图像上，故A 选项不符合题意；由B 选项可得L '为：2(1)2y x =+-，则顶点为（-1，-2），顶点（-1，-2）关于原点的对称点为（1，2），当x ＝1时，y ＝2，则对称点在该函数图像上，故B 选项不符合题意；由C 选项可得L '为：239()22y x =+-， 则顶点为（-32，-92），顶点（-32，-92）关于原点的对称点为（32，92）， 当x ＝32时，y ＝92，则对称点在该函数图像上，故C 选项不符合题意； 由D 选项可得L '为：2(3)9y x =+-，则顶点为（-3，-9），顶点（-3，-9）关于原点的对称点为（3，9），当x ＝3时，y ＝27≠9，则对称点不在该函数图像上，故D 选项符合题意；故选：D ．【点睛】本题考查了二次函数图像的平移，熟练掌握平移的规律“左加右减，上加下减”是解决本题的关键．。
2020-2021中考数学二次函数综合经典题
2020-2021中考数学二次函数综合经典题一、二次函数1．在平面直角坐标系中，点O为坐标原点，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），B（3，0），与y轴交于点C（0，3），顶点为G．（1）求抛物线和直线AC的解析式；（2）如图，设E（m，0）为x轴上一动点，若△CGE和△CGO的面积满足S△CGE＝S△CGO，求点E的坐标；（3）如图，设点P从点A出发，以每秒1个单位长度的速度沿x轴向右运动，运动时间为ts，点M为射线AC上一动点，过点M作MN∥x轴交抛物线对称轴右侧部分于点N．试探究点P在运动过程中，是否存在以P，M，N为顶点的三角形为等腰直角三角形？若存在，求出t的值；若不存在，请说明理由．【答案】（1）抛物线解析式为：y＝﹣x2+2x+3；直线AC解析式为：y＝3x+3；（2）点E 坐标为（1，0）或（﹣7，0）；（3）存在以P，M，N为顶点的三角形为等腰直角三角形，t的值为或或．【解析】【分析】（1）用待定系数法即能求出抛物线和直线AC解析式．（2）△CGE与△CGO虽然有公共底边CG，但高不好求，故把△CGE构造在比较好求的三角形内计算．延长GC交x轴于点F，则△FGE与△FCE的差即为△CGE．（3）设M的坐标（e，3e+3），分别以M、N、P为直角顶点作分类讨论，利用等腰直角三角形的特殊线段长度关系，用e表示相关线段并列方程求解，再根据e与AP的关系求t 的值．【详解】（1）∵抛物线y=ax2+bx+c过点A（-1，0），B（3，0），C（0，3），, 解得：，∴抛物线解析式为：y=-x2+2x+3，设直线AC解析式为y=kx+3，∴-k+3=0，得：k=3，∴直线AC解析式为：y=3x+3.（2）延长GC交x轴于点F，过G作GH⊥x轴于点H，∵y=-x2+2x+3=-（x-1）2+4，∴G（1，4），GH=4，∴S△CGO=OC•x G=×3×1=，∴S△CGE=S△CGO=×=2，①若点E在x轴正半轴上，设直线CG：y=k1x+3，∴k1+3=4 得：k1=1，∴直线CG解析式：y=x+3，∴F（-3，0），∵E（m，0），∴EF=m-（-3）=m+3，∴S△CGE=S△FGE-S△FCE=EF•GH-EF•OC=EF•（GH-OC）=（m+3）•（4-3）=，∴=2，解得：m=1，∴E的坐标为（1，0）.②若点E在x轴负半轴上，则点E到直线CG的距离与点（1，0）到直线CG距离相等，即点E到F的距离等于点（1，0）到F的距离，∴EF=-3-m=1-（-3）=4，解得：m=-7 即E（-7，0），综上所述，点E坐标为（1，0）或（-7，0）.（3）存在以P，M，N为顶点的三角形为等腰直角三角形，设M（e，3e+3），则y N=y M=3e+3，①若∠MPN=90°，PM=PN，如图2，过点M作MQ⊥x轴于点Q，过点N作NR⊥x轴于点R，∵MN∥x轴，∴MQ=NR=3e+3，∴Rt△MQP≌Rt△NRP（HL），∴PQ=PR，∠MPQ=∠NPR=45°，∴MQ=PQ=PR=NR=3e+3，∴x N=x M+3e+3+3e+3=7e+6，即N（7e+6，3e+3），∵N在抛物线上，∴-（7e+6）2+2（7e+6）+3=3e+3，解得：e1=-1（舍去），e2=−，∵AP=t，OP=t-1，OP+OQ=PQ，∴t-1-e=3e+3，∴t=4e+4=，②若∠PMN=90°，PM=MN，如图3，∴MN=PM=3e+3，∴x N=x M+3e+3=4e+3，即N（4e+3，3e+3），∴-（4e+3）2+2（4e+3）+3=3e+3，解得：e1=-1（舍去），e2=−，∴t=AP=e-（-1）=−+1＝，③若∠PNM=90°，PN=MN，如图4，∴MN=PN=3e+3，N（4e+3，3e+3），解得：e=−，∴t=AP=OA+OP=1+4e+3=，综上所述，存在以P，M，N为顶点的三角形为等腰直角三角形，t的值为或或．【点睛】本题考查了待定系数法求函数解析式，坐标系中三角形面积计算，等腰直角三角形的性质，解一元二次方程，考查了分类讨论和方程思想．第（3）题根据等腰直角三角形的性质找到相关线段长的关系是解题关键，灵活运用因式分解法解一元二次方程能简便运算．2．如图1，对称轴为直线x=1的抛物线y=12x2+bx+c，与x轴交于A、B两点（点A在点B的左侧），且点A坐标为(-1，0).又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与抛物线对称轴交于点E，点C与坐标原点O关于该对称轴成轴对称.（1）求点B 的坐标和抛物线的表达式；（2）当AE：EP=1：4 时，求点E 的坐标；（3）如图 2，在（2）的条件下，将线段 OC 绕点 O 逆时针旋转得到OC ′，旋转角为α(0°＜α＜90°)，连接C ′D、C′B，求C ′B+ 23C′D 的最小值．【答案】（1）B（3，0）；抛物线的表达式为：y=12x2-x-32；（2）E(1，6)；（3）C′B＋2 3C′D【解析】试题分析：（1）由抛物线的对称轴和过点A，即可得到抛物线的解析式，令y=0，解方程可得B的坐标；（2）过点P作PF⊥x轴，垂足为F．由平行线分线段弄成比例定理可得AE AP =AGAF=EGPF=15，从而求出E的坐标；（3）由E（1，6）、A（-1，0）可得AP的函数表达式为y=3x+3，得到D（0，3）．如图，取点M（0，43），连接MC′、BM．则可求出OM，BM的长，得到△MOC′∽△C′OD．进而得到MC′＝23C′D，由C′B＋23C′D＝C′B＋MC′≥BF可得到结论．试题解析：解：（1）∵抛物线y=12x2+bx+c的对称轴为直线x=1，∴-122b⨯=1，∴b=-1．∵抛物线过点A（-1，0），∴12-b+c=0，解得：c=-32，即：抛物线的表达式为：y=12x2-x-32．令y=0，则12x2-x-32=0，解得：x1=-1，x2=3，即B（3，0）；（2）过点P作PF⊥x轴，垂足为F．∵EG∥PF，AE：EP=1：4，∴AEAP =AGAF=EGPF=15．又∵AG=2，∴AF=10，∴F（9，0）．当x=9时，y=30，即P（9，30），PF=30，∴EG=6，∴E（1，6）．（3）由E（1，6）、A（-1，0）可得AP的函数表达式为y=3x+3，则D（0，3）．∵原点O与点C关于该对称轴成轴对称，∴EG=6，∴C（2，0），∴OC′＝OC＝2．如图，取点M（0，43），连接MC′、BM．则OM＝43，BM．∵423'23OMOC==，'23OCOD=，且∠DOC′＝∠C′OD，∴△MOC′∽△C′OD．∴'2'3MCC D=，∴MC′＝23C′D，∴C′B＋23C′D＝C′B＋MC′≥BM，∴C′B＋23C′D的最小值为点睛：本题是二次函数的综合题，解答本题主要应用了待定系数法求二次函数的解析式，相似三角形的性质和判定，求得AF 的长是解答问题（2）的关键；和差倍分的转化是解答问题（3）的关键．3．如图，直线AB 和抛物线的交点是A （0，﹣3），B （5，9），已知抛物线的顶点D 的横坐标是2．（1）求抛物线的解析式及顶点坐标；（2）在x 轴上是否存在一点C ，与A ，B 组成等腰三角形？若存在，求出点C 的坐标，若不在，请说明理由；（3）在直线AB 的下方抛物线上找一点P ，连接PA ，PB 使得△PAB 的面积最大，并求出这个最大值．【答案】（1）21248355y x x =--，顶点D （2，635-）；（2）C （10±0）或（5222±0）或（9710，0）；（3）752【解析】 【分析】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入函数表达式，即可求解； （2）分AB =AC 、AB =BC 、AC =BC ，三种情况求解即可；（3）由S △PAB 12=•PH •x B ，即可求解． 【详解】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2①，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入上式得：9=25a +5b ﹣3②，联立①、②解得：a 125=，b 485=-，c =﹣3，∴抛物线的解析式为：y 125=x 2485-x ﹣3． 当x =2时，y 635=-，即顶点D 的坐标为（2，635-）； （2）A （0，﹣3），B （5，9），则AB =13，设点C 坐标（m ，0），分三种情况讨论：①当AB =AC 时，则：（m ）2+（﹣3）2=132，解得：m ，即点C 坐标为：（，0）或（﹣，0）；②当AB =BC 时，则：（5﹣m ）2+92=132，解得：m =5±，即：点C 坐标为（5+，0）或（5﹣0）；③当AC =BC 时，则：5﹣m ）2+92=（m ）2+（﹣3）2，解得：m =9710，则点C 坐标为（9710，0）．综上所述：存在，点C 的坐标为：（，0）或（5±0）或（9710，0）； （3）过点P 作y 轴的平行线交AB 于点H ．设直线AB 的表达式为y =kx ﹣3，把点B 坐标代入上式，9=5k ﹣3，则k 125=，故函数的表达式为：y 125=x ﹣3，设点P 坐标为（m ，125m 2485-m ﹣3），则点H 坐标为（m ，125m ﹣3），S △PAB 12=•PH •x B 52=（125-m 2+12m ）=－6m 2+30m =25756()22m --+，当m =52时，S △PAB 取得最大值为：752． 答：△PAB 的面积最大值为752．【点睛】本题是二次函数综合题．主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．4．函数()2110,>02y x mx x m =-++≥的图象记为1C ，函数()2110,>02y x mx x m =---<的图象记为2C ，其中m 为常数，1C 与2C 合起来的图象记为C .（Ⅰ）若1C 过点()1,1时，求m 的值； （Ⅱ）若2C 的顶点在直线1y =上，求m 的值； （Ⅲ）设C 在42x -≤≤上最高点的纵坐标为0y ，当0392y ≤≤时，求m 的取值范围. 【答案】（Ⅰ）12m =；（Ⅱ）2m =；（Ⅲ）912m ≤≤. 【解析】 【分析】（Ⅰ）将点C 的坐标代入1C 的解析式即可求出m 的值；（Ⅱ）先求出抛物线2C 的顶点坐标，再根据顶点在直线y 1=上得出关于m 的方程，解之即可（Ⅲ）先求出抛物线1C 的顶点坐标，结合（Ⅱ）抛物线2C 的顶点坐标，和x 的取值范围，分三种情形讨论求解即可； 【详解】解：（Ⅰ）将点()1,1代入1C 的解析式，解得1m .2=（Ⅱ）抛物线2C 的顶点坐标为2m m,12⎛⎫-- ⎪⎝⎭， 令2m 112-=，得m 2,=± ∵m>0，∴m 2.=（Ⅲ）∵抛物线1C 的顶点2m P m,12⎛⎫+ ⎪⎝⎭，抛物线2C 的顶点2m Q m,12⎛⎫-- ⎪⎝⎭， 当0m 2<≤时，最高点是抛物线G 1的顶点∴203m y 1922≤=+≤，解得1m 2.≤≤ 当2m 4<≤时，G 1中（2，2m-1）是最高点，0y =2m-1 ∴32≤2m-19≤，解得2m 4.<≤ 当m>4时，G 2中（-4，4m-9）是最高点，0y =4m-9． ∴32≤4m-99≤，解得94m 2<≤. 综上所述，91m 2≤≤即为所求. 【点睛】本题考查二次函数综合题，待定系数法、不等式组等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，利用数形结合的思想解决问题，属于中考压轴题．5．如图所示，已知平面直角坐标系xOy ，抛物线过点A(4,0)、B(1,3)(1)求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；(2)记该抛物线的对称轴为直线l ，设抛物线上的点P(m,n)在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值.【答案】(1)y=-224(2)4y x x x =-+=--+，对称轴为：x=2，顶点坐标为：（2，4）(2)m 、n 的值分别为 5，-5 【解析】（1） 将点A(4,0)、B(1,3) 的坐标分别代入y ＝－x 2＋bx ＋c ，得： 4b+c-16=0，b+c-1="3" ，解得：b="4" ， c=0．所以抛物线的表达式为：24y x x =-+． y=-224(2)4y x x x =-+=--+，所以 抛物线的对称轴为：x=2，顶点坐标为：（2，4）． （2） 由题可知，E 、F 点坐标分别为（4-m ，n ），（m-4，n ）． 三角形POF 的面积为：1/2×4×|n|= 2|n|， 三角形AOP 的面积为：1/2×4×|n|= 2|n|，四边形OAPF 的面积= 三角形POF 的面积+三角形AOP 的面积=20， 所以 4|n|=20， n=-5．（因为点P(m,n)在第四象限，所以n<0） 又n=-2m +4m ，所以2m -4m-5=0，m=5．（因为点P(m,n)在第四象限，所以m>0) 故所求m 、n 的值分别为 5，-5．6．在平面直角坐标系中，有两点(),A a b 、(),B c d ，若满足：当a b ≥时，c a =，2d b =-；当a b <时，c a <-，d b <，则称点为点的“友好点”.（1）点()4,1的“友好点”的坐标是_______.（2）点(),A a b 是直线2y x =-上的一点，点B 是点A 的“友好点”. ①当B 点与A 点重合时，求点A 的坐标.②当A 点与A 点不重合时，求线段AB 的长度随着a 的增大而减小时，a 的取值范围. 【答案】（1）()41-,；（2）①点A 的坐标是()2,0或()1,1-；②当1a <或322a ≤<时，AB 的长度随着a 的增大而减小； 【解析】 【分析】（1）直接利用“友好点”定义进行解题即可；（2）先利用 “友好点”定义求出B 点坐标，A 点又在直线2y x =-上，得到2b a =-；①当点A 和点B 重合，得2b b =-．解出即可，②当点A 和点B 不重合， 1a ≠且2a ≠．所以对a 分情况讨论，1°、当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭，所以当a ≤32时，AB 的长度随着a 的增大而减小，即取1a <．2°当12a <<时，()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭，当32a ≥时，AB 的长度随着a 的增大而减小，即取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【详解】（1）点()4,1，4＞1，根据“友好点”定义，得到点()4,1的“友好点”的坐标是()41-,（2）Q 点(),A a b 是直线2y x =-上的一点，∴2b a =-．Q 2a a >-，根据友好点的定义，点B 的坐标为()2,B a b -，①当点A 和点B 重合，∴2b b =-． 解得0b =或1b =-． 当0b =时，2a =；当1b =-时，1a =，∴点A 的坐标是()2,0或()1,1-．②当点A 和点B 不重合，1a ≠且2a ≠．当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭． ∴当a ≤32时，AB 的长度随着a 的增大而减小， ∴取1a <．当12a <<时， ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ ．∴当32a ≥时，AB 的长度随着a 的增大而减小， ∴取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【点睛】本题属于阅读理解题型，结合二次函数的基本性质进行解题，第二问的第二小问的关键是求出AB 的长用a 进行表示，然后利用二次函数基本性质进行分类讨论7．如图，已知二次函数的图象过点O （0，0）．A （8，4），与x 轴交于另一点B ，且对称轴是直线x ＝3．（1）求该二次函数的解析式；（2）若M 是OB 上的一点，作MN ∥AB 交OA 于N ，当△ANM 面积最大时，求M 的坐标；（3）P 是x 轴上的点，过P 作PQ ⊥x 轴与抛物线交于Q ．过A 作AC ⊥x 轴于C ，当以O ，P ，Q 为顶点的三角形与以O ，A ，C 为顶点的三角形相似时，求P 点的坐标．【答案】（1）21342y x x =-；（2）当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）；（3）P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）． 【解析】 【分析】（1）先利用抛物线的对称性确定B （6，0），然后设交点式求抛物线解析式；（2）设M （t ，0），先其求出直线OA 的解析式为12y x =直线AB 的解析式为y=2x-12，直线MN 的解析式为y=2x-2t ，再通过解方程组1222y x y x t⎧=⎪⎨⎪=-⎩得N （42t,t 33），接着利用三角形面积公式，利用S △AMN =S △AOM -S △NOM 得到AMN 112S 4t t t 223∆=⋅⋅-⋅⋅然后根据二次函数的性质解决问题； （3）设Q 213m,m m 42⎛⎫- ⎪⎝⎭，根据相似三角形的判定方法，当PQ PO OC AC=时，△PQO ∽△COA ，则213m m 2|m |42-=；当PQ POAC OC=时，△PQO ∽△CAO ，则2131m m m 422-=，然后分别解关于m 的绝对值方程可得到对应的P 点坐标． 【详解】解：（1）∵抛物线过原点，对称轴是直线x ＝3， ∴B 点坐标为（6，0），设抛物线解析式为y ＝ax （x ﹣6）， 把A （8，4）代入得a•8•2＝4，解得a ＝14， ∴抛物线解析式为y ＝14x （x ﹣6），即y ＝14x 2﹣32x ； （2）设M （t ，0），易得直线OA 的解析式为y ＝12x ， 设直线AB 的解析式为y ＝kx+b ，把B （6，0），A （8，4）代入得6084k b k b +=⎧⎨+=⎩，解得k 2b 12=⎧⎨=-⎩，∴直线AB 的解析式为y ＝2x ﹣12， ∵MN ∥AB ，∴设直线MN 的解析式为y ＝2x+n ， 把M （t ，0）代入得2t+n ＝0，解得n ＝﹣2t ， ∴直线MN 的解析式为y ＝2x ﹣2t ，解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得4323x t y t ⎧=⎪⎪⎨⎪=⎪⎩，则42N t,t 33⎛⎫ ⎪⎝⎭， ∴S △AMN ＝S △AOM ﹣S △NOM1124t t t 223=⋅⋅-⋅⋅ 21t 2t 3=-+21(t 3)33=--+，当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）； （3）设213m,m m 42⎛⎫- ⎪⎝⎭， ∵∠OPQ ＝∠ACO ， ∴当PQ PO OC AC =时，△PQO ∽△COA ，即PQ PO 84=， ∴PQ ＝2PO ，即213m m 2|m |42-=， 解方程213m m 2m 42-=得m 1＝0（舍去），m 2＝14，此时P 点坐标为（14，0）； 解方程213m m 2m 42-=-得m 1＝0（舍去），m 2＝﹣2，此时P 点坐标为（﹣2，0）； ∴当PQ PO AC OC =时，△PQO ∽△CAO ，即PQ PO 48=， ∴PQ ＝12PO ，即2131m m m 422-=，解方程2131m m m 422=-=得m 1＝0（舍去），m 2＝8，此时P 点坐标为（8，0）；解方程2131m m m 422=-=-得m 1＝0（舍去），m 2＝4，此时P 点坐标为（4，0）； 综上所述，P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）． 【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；灵活运用相似比表示线段之间的关系；会运用分类讨论的思想解决数学问题．8．如图，对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点，其中A 点的坐标为（－3，0）．（1）求点B 的坐标；（2）已知a 1=，C 为抛物线与y 轴的交点．①若点P 在抛物线上，且POC BOC S 4S ∆∆=，求点P 的坐标；②设点Q 是线段AC 上的动点，作QD ⊥x 轴交抛物线于点D ，求线段QD 长度的最大值． 【答案】（1）点B 的坐标为（1，0）. （2）①点P 的坐标为（4，21）或（－4，5）. ②线段QD 长度的最大值为94. 【解析】 【分析】（1）由抛物线的对称性直接得点B 的坐标．（2）①用待定系数法求出抛物线的解析式，从而可得点C 的坐标，得到BOC S ∆，设出点P 的坐标，根据POC BOC S 4S ∆∆=列式求解即可求得点P 的坐标．②用待定系数法求出直线AC 的解析式，由点Q 在线段AC 上，可设点Q 的坐标为(q,-q-3)，从而由QD ⊥x 轴交抛物线于点D ，得点D 的坐标为(q,q 2+2q-3)，从而线段QD 等于两点纵坐标之差，列出函数关系式应用二次函数最值原理求解. 【详解】解：（1）∵A 、B 两点关于对称轴x 1=-对称 ，且A 点的坐标为（－3，0）， ∴点B 的坐标为（1，0）.（2）①∵抛物线a 1=，对称轴为x 1=-，经过点A （－3，0），∴2a 1b12a 9a 3b c 0=⎧⎪⎪-=-⎨⎪-+=⎪⎩，解得a 1b 2c 3=⎧⎪=⎨⎪=-⎩. ∴抛物线的解析式为2y x 2x 3=+-.∴B 点的坐标为（0，－3）.∴OB=1，OC=3.∴BOC 13S 1322∆=⨯⨯=. 设点P 的坐标为(p,p 2+2p-3)，则POC 13S 3p p 22∆=⨯⨯=. ∵POC BOC S 4S ∆∆=，∴3p 62=，解得p 4=±. 当p 4=时2p 2p 321+-=；当p 4=-时，2p 2p 35+-=， ∴点P 的坐标为（4，21）或（－4，5）.②设直线AC 的解析式为y kx b =+，将点A ，C 的坐标代入，得：3k b 0b 3-+=⎧⎨=-⎩，解得：k 1b 3=-⎧⎨=-⎩. ∴直线AC 的解析式为y x 3=--.∵点Q 在线段AC 上，∴设点Q 的坐标为(q,-q-3). 又∵QD ⊥x 轴交抛物线于点D ，∴点D 的坐标为(q,q 2+2q-3).∴()22239QD q 3q 2q 3q 3q q 24⎛⎫=---+-=--=-++ ⎪⎝⎭.∵a 10<=-，-3302<<- ∴线段QD 长度的最大值为94.9．如图，已知二次函数y=ax 2+bx+c 的图象与x 轴相交于A （﹣1，0），B （3，0）两点，与y 轴相交于点C （0，﹣3）． （1）求这个二次函数的表达式；（2）若P 是第四象限内这个二次函数的图象上任意一点，PH ⊥x 轴于点H ，与BC 交于点M ，连接PC ．①求线段PM 的最大值；②当△PCM 是以PM 为一腰的等腰三角形时，求点P 的坐标．【答案】（1）二次函数的表达式y=x 2﹣2x ﹣3；（2）①PM 最大=94；②P （2，﹣3）或（22﹣2）． 【解析】 【分析】（1）根据待定系数法，可得答案；（2）①根据平行于y 轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；②根据等腰三角形的定义，可得方程，根据解方程，可得答案． 【详解】（1）将A ，B ，C 代入函数解析式，得09303a b c a b c c -+=⎧⎪++=⎨⎪=-⎩，解得123a b c =⎧⎪=-⎨⎪=-⎩，这个二次函数的表达式y=x 2﹣2x ﹣3； （2）设BC 的解析式为y=kx+b ， 将B ，C 的坐标代入函数解析式，得303k b b +=⎧⎨=-⎩，解得13k b =⎧⎨=-⎩， BC 的解析式为y=x ﹣3，设M （n ，n ﹣3），P （n ，n 2﹣2n ﹣3）， PM=（n ﹣3）﹣（n 2﹣2n ﹣3）=﹣n 2+3n=﹣（n ﹣32）2+94， 当n=32时，PM 最大=94； ②当PM=PC 时，（﹣n 2+3n ）2=n 2+（n 2﹣2n ﹣3+3）2， 解得n 1=0（不符合题意，舍），n 2=2， n 2﹣2n ﹣3=-3， P （2，-3）；当PM=MC 时，（﹣n 2+3n ）2=n 2+（n ﹣3+3）2，解得n 1=0（不符合题意，舍），n 2=3+2（不符合题意，舍），n 3=3-2， n 2﹣2n ﹣3=2-42， P （3-2，2-42）；综上所述：P （2，﹣3）或（3-2，2﹣42）． 【点睛】本题考查了二次函数的综合题，涉及到待定系数法、二次函数的最值、等腰三角形等知识，综合性较强，解题的关键是认真分析，弄清解题的思路有方法.10． 阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”．例如，点M （1，3）的特征线有：x =1，y =3，y =x +2，y =﹣x +4．问题与探究：如图，在平面直角坐标系中有正方形OABC ，点B 在第一象限，A 、C 分别在x 轴和y 轴上，抛物线21()4y x m n =-+经过B 、C 两点，顶点D 在正方形内部． （1）直接写出点D （m ，n ）所有的特征线；（2）若点D 有一条特征线是y =x +1，求此抛物线的解析式；（3）点P 是AB 边上除点A 外的任意一点，连接OP ，将△OAP 沿着OP 折叠，点A 落在点A ′的位置，当点A ′在平行于坐标轴的D 点的特征线上时，满足（2）中条件的抛物线向下平移多少距离，其顶点落在OP 上？【答案】（1）x =m ，y =n ，y =x +n ﹣m ，y =﹣x +m+n ；（2）21(2)34y x =-+；（3）抛物923-2312距离，其顶点落在OP 上． 【解析】试题分析：（1）根据特征线直接求出点D 的特征线；（2）由点D 的一条特征线和正方形的性质求出点D 的坐标，从而求出抛物线解析式； （2）分平行于x 轴和y 轴两种情况，由折叠的性质计算即可．试题解析：解：（1）∵点D （m ，n ），∴点D （m ，n ）的特征线是x =m ，y =n ，y =x +n ﹣m ，y =﹣x +m +n ；（2）点D 有一条特征线是y =x +1，∴n ﹣m =1，∴n =m +1．∵抛物线解析式为21()4y x m n =-+，∴21()14y x m m =-++，∵四边形OABC 是正方形，且D 点为正方形的对称轴，D （m ，n ），∴B （2m ，2m ），∴21(2)24y m m n m =-+=，将n =m +1带入得到m =2，n =3；∴D （2，3），∴抛物线解析式为21(2)34y x =-+． （3）①如图，当点A ′在平行于y 轴的D 点的特征线时：根据题意可得，D （2，3），∴OA ′=OA =4，OM =2，∴∠A ′OM =60°，∴∠A ′OP =∠AOP =30°，∴MN =3=23，∴抛物线需要向下平移的距离=233-=923-．②如图，当点A ′在平行于x 轴的D 点的特征线时，设A ′（p ，3），则OA ′=OA =4，OE =3，EA ′=2243-=7，∴A ′F =4﹣7，设P （4，c ）（c ＞0），，在Rt △A ′FP 中，（4﹣7）2+（3﹣c ）2=c 2，∴c =1647-，∴P （4，1647-），∴直线OP 解析式为y =47-x ，∴N （2，827-），∴抛物线需要向下平移的距离=3﹣8273-=1273+． 综上所述：抛物线向下平移923-或127+距离，其顶点落在OP 上．点睛：此题是二次函数综合题，主要考查了折叠的性质，正方形的性质，解答本题的关键是用正方形的性质求出点D 的坐标．11．在直角坐标系中，我们不妨将横坐标，纵坐标均为整数的点称之为“中国结”。
2020-2021初中数学二次函数专项训练及解析答案(1)
2020-2021初中数学二次函数专项训练及解析答案(1)一、选择题1．如图是二次函数2y ax bx c =++的图象，其对称轴为1x =.下列结论：①0abc >；②20a b +=；③930a b c ++<；④若12310,,,23y y ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭是抛物线上两点，则12y y >.其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】 由抛物线开口方向得到a ＜0，根据对称轴得到b=-2a ＞0，由抛物线与y 轴的交点位置得到c ＞0，则可对①进行判断；由b=-2a 可对②进行判断；利用抛物线的对称性可得到抛物线与x 轴的另一个交点为（3，0），则可判断当x=3时，y=0，于是可对③进行判断；通过二次函数的增减性可对④进行判断．【详解】解：∵抛物线开口向下，∴a ＜0，∵抛物线的对称轴为直线12b x a=-= ，∴b=-2a ＞0， ∵抛物线与y 轴的交点在x 轴上方， ∴c ＞0，∴abc ＜0，所以①错误；∵b=-2a ，∴2a+b=0，所以②正确；∵抛物线与x 轴的一个交点为（-1，0），抛物线的对称轴为直线x=1，∴抛物线与x 轴的另一个交点为（3，0），∴当x=3时，y=0，∴930a b c ++=，所以③错误；∵抛物线的对称轴为直线x=1，且抛物线开口向下，∴当x 1<时，y 随x 的增大而增大∵103132-<-<点13,2y ⎛⎫-⎪⎝⎭到对称轴的距离比点210,3y ⎛⎫- ⎪⎝⎭对称轴的距离近， ∴y 1>y 2，所以④正确． 故选B ．【点睛】 本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a≠0），二次项系数a 决定抛物线的开口方向和大小，当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左； 当a 与b 异号时（即ab ＜0），对称轴在y 轴右；常数项c 决定抛物线与y 轴交点：抛物线与y 轴交于（0，c ）；抛物线与x 轴交点个数由△决定：△=b 2-4ac ＞0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点．2．函数25y ax bx =++(0)a ≠，当1x =与7x =时函数值相等，则8x =时，函数值等于( )A ．5B ．52-C ．52D ．－5【答案】A【解析】【分析】根据二次函数的对称性，求得函数25y ax bx =++(0)a ≠的对称轴，进而判断与8x =的函数值相等时x 的值，由此可得结果．【详解】∵函数25y ax bx =++(0)a ≠，当1x =与7x =时函数值相等，∴函数25y ax bx =++(0)a ≠的对称轴为：1742x +==， ∴8x =与0x =的函数值相等，∴当8x =时，250055y ax bx a b =++=⨯+⨯+=，即8x =时，函数值等于5，故选：A ．【点睛】本题主要考查二次函数的图象和对称性．掌握二次函数的对称性和对称轴的求法，是解题的关键．3．如图是二次函数2y ax bx c =++的图象，有下面四个结论：0abc >①；0a b c ②-+>； 230a b +>③；40c b ->④，其中正确的结论是( )A ．①②B ．①②③C ． ①③④D ． ①②④【答案】D【解析】【分析】 根据抛物线开口方向得到a 0>，根据对称轴02b x a =->得到b 0<，根据抛物线与y 轴的交点在x 轴下方得到c 0<，所以0abc >；1x =-时，由图像可知此时0y >，所以0a b c -+>；由对称轴123b x a =-=，可得230a b +=；当2x =时，由图像可知此时0y >，即420a bc ++>，将23a b =-代入可得40c b ->.【详解】①根据抛物线开口方向得到0a >，根据对称轴02b x a=->得到b 0<，根据抛物线与y 轴的交点在x 轴下方得到c 0<，所以0abc >，故①正确.②1x =-时，由图像可知此时0y >，即0a b c -+>，故②正确.③由对称轴123b x a =-=，可得230a b +=，所以230a b +>错误，故③错误； ④当2x =时，由图像可知此时0y >，即420a bc ++>，将③中230a b +=变形为23a b =-，代入可得40c b ->，故④正确.故答案选D.【点睛】本题考查了二次函数的图像与系数的关系，注意用数形结合的思想解决问题。
2020-2021中考数学 二次函数综合试题及详细答案
2020-2021中考数学 二次函数综合试题及详细答案一、二次函数1．如图，在平面直角坐标系中有一直角三角形AOB ，O 为坐标原点，OA ＝1，tan ∠BAO ＝3，将此三角形绕原点O 逆时针旋转90°，得到△DOC ，抛物线y ＝ax 2+bx +c 经过点A 、B 、C ．（1）求抛物线的解析式；（2）若点P 是第二象限内抛物线上的动点，其横坐标为t ，设抛物线对称轴l 与x 轴交于一点E ，连接PE ，交CD 于F ，求以C 、E 、F 为顶点三角形与△COD 相似时点P 的坐标． 【答案】（1）抛物线的解析式为y=﹣x 2﹣2x+3；（2）当△CEF 与△COD 相似时，P 点的坐标为（﹣1，4）或（﹣2，3）． 【解析】 【分析】（1）根据正切函数，可得OB ，根据旋转的性质，可得△DOC ≌△AOB ，根据待定系数法，可得函数解析式；（2）分两种情况讨论：①当∠CEF ＝90°时，△CEF ∽△COD ，此时点P 在对称轴上，即点P 为抛物线的顶点；②当∠CFE ＝90°时，△CFE ∽△COD ，过点P 作PM ⊥x 轴于M 点，得到△EFC ∽△EMP ，根据相似三角形的性质，可得PM 与ME 的关系，解方程，可得t 的值，根据自变量与函数值的对应关系，可得答案． 【详解】（1）在Rt △AOB 中，OA ＝1，tan ∠BAO OBOA==3，∴OB ＝3OA ＝3． ∵△DOC 是由△AOB 绕点O 逆时针旋转90°而得到的，∴△DOC ≌△AOB ，∴OC ＝OB ＝3，OD ＝OA ＝1，∴A ，B ，C 的坐标分别为（1，0），（0，3），（﹣3，0），代入解析式为09303a b c a b c c ++=⎧⎪-+=⎨⎪=⎩，解得：123a b c =-⎧⎪=-⎨⎪=⎩，抛物线的解析式为y ＝﹣x 2﹣2x +3； （2）∵抛物线的解析式为y ＝﹣x 2﹣2x +3，∴对称轴为l 2ba=-=-1，∴E 点坐标为（﹣1，0），如图，分两种情况讨论：①当∠CEF ＝90°时，△CEF ∽△COD ，此时点P 在对称轴上，即点P 为抛物线的顶点，P（﹣1，4）；②当∠CFE ＝90°时，△CFE ∽△COD ，过点P 作PM ⊥x 轴于M 点，∵∠CFE=∠PME=90°，∠CEF=∠PEM ，∴△EFC ∽△EMP ，∴13EM EF OD MP CF CO ===，∴MP ＝3ME ． ∵点P 的横坐标为t ，∴P （t ，﹣t 2﹣2t +3）．∵P 在第二象限，∴PM ＝﹣t 2﹣2t +3，ME ＝﹣1﹣t ，t ＜0，∴﹣t 2﹣2t +3＝3（﹣1﹣t ），解得：t 1＝﹣2，t 2＝3（与t ＜0矛盾，舍去）．当t ＝﹣2时，y ＝﹣（﹣2）2﹣2×（﹣2）+3＝3，∴P （﹣2，3）．综上所述：当△CEF 与△COD 相似时，P 点的坐标为（﹣1，4）或（﹣2，3）． 【点睛】本题是二次函数综合题．解（1）的关键是利用旋转的性质得出OC ，OD 的长，又利用了待定系数法；解（2）的关键是利用相似三角形的性质得出MP ＝3ME ．2．如图，在平面直角坐标系中，抛物线y=ax 2+bx+c 的顶点坐标为P （2，9），与x 轴交于点A ，B ，与y 轴交于点C （0，5）． （Ⅰ）求二次函数的解析式及点A ，B 的坐标；（Ⅱ）设点Q 在第一象限的抛物线上，若其关于原点的对称点Q′也在抛物线上，求点Q 的坐标；（Ⅲ）若点M 在抛物线上，点N 在抛物线的对称轴上，使得以A ，C ，M ，N 为顶点的四边形是平行四边形，且AC 为其一边，求点M ，N 的坐标．【答案】（1）y=﹣x 2+4x+5，A （﹣1，0），B （5，0）；（2）Q 553）M （1，8），N （2，13）或M′（3，8），N′（2，3）． 【解析】 【分析】(1)设顶点式，再代入C点坐标即可求解解析式，再令y=0可求解A和B点坐标；(2)设点Q（m，﹣m2+4m+5），则其关于原点的对称点Q′（﹣m，m2﹣4m﹣5），再将Q′坐标代入抛物线解析式即可求解m的值，同时注意题干条件“Q在第一象限的抛物线上”；(3)利用平移AC的思路，作MK⊥对称轴x=2于K，使MK=OC，分M点在对称轴左边和右边两种情况分类讨论即可.【详解】（Ⅰ）设二次函数的解析式为y=a（x﹣2）2+9，把C（0，5）代入得到a=﹣1，∴y=﹣（x﹣2）2+9，即y=﹣x2+4x+5，令y=0，得到：x2﹣4x﹣5=0，解得x=﹣1或5，∴A（﹣1，0），B（5，0）．（Ⅱ）设点Q（m，﹣m2+4m+5），则Q′（﹣m，m2﹣4m﹣5）．把点Q′坐标代入y=﹣x2+4x+5，得到：m2﹣4m﹣5=﹣m2﹣4m+5，∴m=5或5（舍弃），∴Q（5，45）．（Ⅲ）如图，作MK⊥对称轴x=2于K．①当MK=OA，NK=OC=5时，四边形ACNM是平行四边形．∵此时点M的横坐标为1，∴y=8，∴M（1，8），N（2，13），②当M′K=OA=1，KN′=OC=5时，四边形ACM′N′是平行四边形，此时M′的横坐标为3，可得M′（3，8），N′（2，3）．【点睛】本题主要考查了二次函数的应用，第3问中理解通过平移AC可应用“一组对边平行且相等”得到平行四边形.3．抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C 、D 两点的坐标（3）在第四象限抛物线上有一点P ，若△PCD 是以CD 为底边的等腰三角形，求出点P 的坐标．【答案】（1）y ＝x 2﹣2x ﹣3;（2）C （0，﹣3）,D （0，﹣1）;（3）P （2，﹣2）. 【解析】 【分析】（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得抛物线解析式． （2）当x ＝0时可求C 点坐标，求出直线AB 解析式，当x ＝0可求D 点坐标． （3）由题意可知P 点纵坐标为﹣2，代入抛物线解析式可求P 点横坐标． 【详解】解：（1）把A （﹣1，0）、B （2，﹣3）两点坐标代入y ＝ax 2+bx ﹣3可得 304233a b a b --=⎧⎨+-=-⎩解得12a b =⎧⎨=-⎩∴y ＝x 2﹣2x ﹣3（2）把x ＝0代入y ＝x 2﹣2x ﹣3中可得y ＝﹣3∴C （0，﹣3） 设y ＝kx+b ，把A （﹣1，0）、B （2，﹣3）两点坐标代入23k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩∴y ＝﹣x ﹣1 ∴D （0，﹣1）（3）由C （0，﹣3），D （0，﹣1）可知CD 的垂直平分线经过（0，﹣2） ∴P 点纵坐标为﹣2， ∴x 2﹣2x ﹣3＝﹣2解得：x ＝2∵x ＞0∴x ＝2． ∴P （2，﹣2） 【点睛】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x ＝0代入二次函数解析式和一次函数解析式可求图象与y 轴交点坐标，知道点P 纵坐标带入抛物线解析式可求点P 的横坐标．4．如图，在平面直角坐标系中，抛物线y=ax2+2x+c与x轴交于A（﹣1，0）B（3，0）两点，与y轴交于点C，点D是该抛物线的顶点．（1）求抛物线的解析式和直线AC的解析式；（2）请在y轴上找一点M，使△BDM的周长最小，求出点M的坐标；（3）试探究：在拋物线上是否存在点P，使以点A，P，C为顶点，AC为直角边的三角形是直角三角形？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）抛物线解析式为y=﹣x2+2x+3；直线AC的解析式为y=3x+3；（2）点M的坐标为（0，3）；（3）符合条件的点P的坐标为（73，209）或（103，﹣139），【解析】分析：（1）设交点式y=a（x+1）（x-3），展开得到-2a=2，然后求出a即可得到抛物线解析式；再确定C（0，3），然后利用待定系数法求直线AC的解析式；（2）利用二次函数的性质确定D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（-3，0），利用两点之间线段最短可判断此时MB+MD的值最小，则此时△BDM的周长最小，然后求出直线DB′的解析式即可得到点M的坐标；（3）过点C作AC的垂线交抛物线于另一点P，如图2，利用两直线垂直一次项系数互为负倒数设直线PC的解析式为y=-13x+b，把C点坐标代入求出b得到直线PC的解析式为y=-13x+3，再解方程组223133y x xy x⎧-++⎪⎨-+⎪⎩＝＝得此时P点坐标；当过点A作AC的垂线交抛物线于另一点P时，利用同样的方法可求出此时P点坐标．详解：（1）设抛物线解析式为y=a（x+1）（x﹣3），即y=ax2﹣2ax﹣3a，∴﹣2a=2，解得a=﹣1，∴抛物线解析式为y=﹣x2+2x+3；当x=0时，y=﹣x2+2x+3=3，则C（0，3），设直线AC的解析式为y=px+q，把A（﹣1，0），C（0，3）代入得3p qq-+=⎧⎨=⎩，解得33pq=⎧⎨=⎩，∴直线AC的解析式为y=3x+3；（2）∵y=﹣x2+2x+3=﹣（x﹣1）2+4，∴顶点D的坐标为（1，4），作B点关于y轴的对称点B′，连接DB′交y轴于M，如图1，则B′（﹣3，0），∵MB=MB′，∴MB+MD=MB′+MD=DB′，此时MB+MD的值最小，而BD的值不变，∴此时△BDM的周长最小，易得直线DB′的解析式为y=x+3，当x=0时，y=x+3=3，∴点M的坐标为（0，3）；（3）存在．过点C作AC的垂线交抛物线于另一点P，如图2，∵直线AC的解析式为y=3x+3，∴直线PC的解析式可设为y=﹣13x+b，把C（0，3）代入得b=3，∴直线PC的解析式为y=﹣13x+3，解方程组223133y x x y x ⎧-++⎪⎨-+⎪⎩＝＝，解得03x y =⎧⎨=⎩或73209x y ⎧=⎪⎪⎨⎪=⎪⎩，则此时P 点坐标为（73，209）； 过点A 作AC 的垂线交抛物线于另一点P ，直线PC 的解析式可设为y=﹣x+b ， 把A （﹣1，0）代入得13+b=0，解得b=﹣13， ∴直线PC 的解析式为y=﹣13x ﹣13， 解方程组2231133y x x y x ⎧-++⎪⎨--⎪⎩＝＝，解得10x y =-⎧⎨=⎩或103139x y ⎧=⎪⎪⎨⎪=-⎪⎩，则此时P 点坐标为（103，﹣139）. 综上所述，符合条件的点P 的坐标为（73，209）或（103，﹣139）. 点睛：本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式，理解两直线垂直时一次项系数的关系，通过解方程组求把两函数的交点坐标；理解坐标与图形性质，会运用两点之间线段最短解决最短路径问题；会运用分类讨论的思想解决数学问题．5．在平面直角坐标系中，有两点(),A a b 、(),B c d ，若满足：当a b ≥时，c a =，2d b =-；当a b <时，c a <-，d b <，则称点为点的“友好点”.（1）点()4,1的“友好点”的坐标是_______.（2）点(),A a b 是直线2y x =-上的一点，点B 是点A 的“友好点”. ①当B 点与A 点重合时，求点A 的坐标.②当A 点与A 点不重合时，求线段AB 的长度随着a 的增大而减小时，a 的取值范围. 【答案】（1）()41-,；（2）①点A 的坐标是()2,0或()1,1-；②当1a <或322a ≤<时，AB 的长度随着a 的增大而减小； 【解析】 【分析】（1）直接利用“友好点”定义进行解题即可；（2）先利用 “友好点”定义求出B 点坐标，A 点又在直线2y x =-上，得到2b a =-；①当点A 和点B 重合，得2b b =-．解出即可，②当点A 和点B 不重合， 1a ≠且2a ≠．所以对a 分情况讨论，1°、当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭，所以当a ≤32时，AB 的长度随着a 的增大而减小，即取1a <．2°当12a <<时，()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭，当32a ≥时，AB 的长度随着a 的增大而减小，即取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【详解】（1）点()4,1，4＞1，根据“友好点”定义，得到点()4,1的“友好点”的坐标是()41-, （2）Q 点(),A a b 是直线2y x =-上的一点，∴2b a =-．Q 2a a >-，根据友好点的定义，点B 的坐标为()2,B a b -，①当点A 和点B 重合，∴2b b =-． 解得0b =或1b =-． 当0b =时，2a =；当1b =-时，1a =，∴点A 的坐标是()2,0或()1,1-．②当点A 和点B 不重合，1a ≠且2a ≠．当1a <或2a >时，()222313224AB b b a a a ⎛⎫=--=-+=-- ⎪⎝⎭． ∴当a ≤32时，AB 的长度随着a 的增大而减小， ∴取1a <．当12a <<时， ()22231+3224AB b b a a a ⎛⎫=--=--=--+ ⎪⎝⎭ ．∴当32a ≥时，AB 的长度随着a 的增大而减小， ∴取322a ≤<． 综上，当1a <或322a ≤<时，AB 的长度随着a 的增大而减小． 【点睛】本题属于阅读理解题型，结合二次函数的基本性质进行解题，第二问的第二小问的关键是求出AB 的长用a 进行表示，然后利用二次函数基本性质进行分类讨论6．如图1，抛物线经过平行四边形的顶点、、，抛物线与轴的另一交点为.经过点的直线将平行四边形分割为面积相等的两部分，与抛物线交于另一点.点为直线上方抛物线上一动点，设点的横坐标为.（1）求抛物线的解析式；（2）当何值时，的面积最大?并求最大值的立方根；（3）是否存在点使为直角三角形?若存在，求出的值；若不存在，说明理由.【答案】（1）抛物线解析式为y=﹣x2+2x+3；（2）当t=时，△PEF的面积最大，其最大值为×，最大值的立方根为=；（3）存在满足条件的点P，t的值为1或【解析】试题分析：（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）由A、C坐标可求得平行四边形的中心的坐标，由抛物线的对称性可求得E点坐标，从而可求得直线EF的解析式，作PH⊥x轴，交直线l于点M，作FN⊥PH，则可用t表示出PM的长，从而可表示出△PEF的面积，再利用二次函数的性质可求得其最大值，再求其最大值的立方根即可；（3）由题意可知有∠PAE=90°或∠APE=90°两种情况，当∠PAE=90°时，作PG⊥y轴，利用等腰直角三角形的性质可得到关于t的方程，可求得t的值；当∠APE=90°时，作PK⊥x 轴，AQ⊥PK，则可证得△PKE∽△AQP，利用相似三角形的性质可得到关于t的方程，可求得t的值．试题解析：（1）由题意可得，解得，∴抛物线解析式为y=﹣x2+2x+3；（2）∵A（0，3），D（2，3），∴BC=AD=2，∵B（﹣1，0），∴C（1，0），∴线段AC的中点为（，），∵直线l将平行四边形ABCD分割为面积相等两部分，∴直线l过平行四边形的对称中心，∵A、D关于对称轴对称，∴抛物线对称轴为x=1，∴E（3，0），设直线l的解析式为y=kx+m，把E点和对称中心坐标代入可得，解得，∴直线l的解析式为y=﹣x+，联立直线l和抛物线解析式可得，解得或，∴F（﹣，），如图1，作PH⊥x轴，交l于点M，作FN⊥PH，∵P点横坐标为t，∴P（t，﹣t2+2t+3），M（t，﹣t+），∴PM=﹣t2+2t+3﹣（﹣t+）=﹣t2+t+，∴S△PEF=S△PFM+S△PEM=PM•FN+PM•EH=PM•（FN+EH）=（﹣t2+t+）（3+）=﹣（t﹣）+×，∴当t=时，△PEF的面积最大，其最大值为×，∴最大值的立方根为=；（3）由图可知∠PEA≠90°，∴只能有∠PAE=90°或∠APE=90°，①当∠PAE=90°时，如图2，作PG⊥y轴，∵OA=OE，∴∠OAE=∠OEA=45°，∴∠PAG=∠APG=45°，∴PG=AG，∴t=﹣t2+2t+3﹣3，即﹣t2+t=0，解得t=1或t=0（舍去），②当∠APE=90°时，如图3，作PK⊥x轴，AQ⊥PK，则PK=﹣t2+2t+3，AQ=t，KE=3﹣t，PQ=﹣t2+2t+3﹣3=﹣t2+2t，∵∠APQ+∠KPE=∠APQ+∠PAQ=90°，∴∠PAQ=∠KPE，且∠PKE=∠PQA，∴△PKE∽△AQP，∴，即，即t2﹣t﹣1=0，解得t=或t=＜﹣（舍去），综上可知存在满足条件的点P，t的值为1或．考点：二次函数综合题7．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，且与y轴交于点C，点D是抛物线的顶点，抛物线对称轴DE交x轴于点E，连接BD．（1）求经过A，B，C三点的抛物线的函数表达式；（2）点P是线段BD上一点，当PE＝PC时，求点P的坐标．【答案】（1）y＝﹣x2+2x+3；（2）点P的坐标为（2，2）．【解析】【分析】（1）利用待定系数法求出过A，B，C三点的抛物线的函数表达式；（2）连接PC、PE，利用公式求出顶点D的坐标，利用待定系数法求出直线BD的解析式，设出点P的坐标为（x，﹣2x+6），利用勾股定理表示出PC2和PE2，根据题意列出方程，解方程求出x的值，计算求出点P的坐标．【详解】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（3，0）两点，∴10930b cb c--+=⎧⎨-++=⎩，解得23bc=⎧⎨=⎩，∴所求的抛物线的函数表达式为y＝﹣x2+2x+3；（2）如图，连接PC，PE．抛物线的对称轴为x＝222(1)ba-=-⨯-＝1．当x＝1时，y＝4，∴点D的坐标为（1，4）．设直线BD的解析式为y＝kx+b，则430 k bk b+=⎧⎨+=⎩，解得26kb=-⎧⎨=⎩．∴直线BD的解析式为：y＝2x+6，设点P的坐标为（x，﹣2x+6），又C（0，3），E（1，0），则PC2＝x2+（3+2x﹣6）2，PE2＝（x﹣1）2+（﹣2x+6）2，∵PC＝PE，∴x2+（3+2x﹣6）2＝（x﹣1）2+（﹣2x+6）2，解得，x ＝2，则y ＝﹣2×2+6＝2，∴点P 的坐标为（2，2）．【点睛】本题考查的是二次函数的图象和性质、待定系数法求函数解析式，掌握二次函数的图象和性质、灵活运用待定系数法是解题的关键．8．（2017南宁，第26题，10分）如图，已知抛物线2239y ax ax a =--与坐标轴交于A ，B ，C 三点，其中C （0，3），∠BAC 的平分线AE 交y 轴于点D ，交BC 于点E ，过点D 的直线l 与射线AC ，AB 分别交于点M ，N ．（1）直接写出a 的值、点A 的坐标及抛物线的对称轴；（2）点P 为抛物线的对称轴上一动点，若△PAD 为等腰三角形，求出点P 的坐标； （3）证明：当直线l 绕点D 旋转时，11AM AN+均为定值，并求出该定值．【答案】（1）a =13-，A 30），抛物线的对称轴为x 32）点P 的坐标为3034）；（3）32． 【解析】试题分析：（1）由点C 的坐标为（0，3），可知﹣9a =3，故此可求得a 的值，然后令y =0得到关于x 的方程，解关于x 的方程可得到点A 和点B 的坐标，最后利用抛物线的对称性可确定出抛物线的对称轴；（2）利用特殊锐角三角函数值可求得∠CAO =60°，依据AE 为∠BAC 的角平分线可求得∠DAO =30°，然后利用特殊锐角三角函数值可求得OD =1，则可得到点D 的坐标．设点P 的坐标为（3，a ）．依据两点的距离公式可求得AD 、AP 、DP 的长，然后分为AD =PA 、AD =DP 、AP =DP 三种情况列方程求解即可； （3）设直线MN 的解析式为y =kx +1，接下来求得点M 和点N 的横坐标，于是可得到AN 的长，然后利用特殊锐角三角函数值可求得AM 的长，最后将AM 和AN 的长代入化简即可．试题解析：（1）∵C （0，3），∴﹣9a =3，解得：a =13-．令y =0得：22390ax ax a --=，∵a ≠0，∴22390x x --=，解得：x =﹣3或x =33，∴点A 的坐标为（﹣3，0），B （33，0），∴抛物线的对称轴为x =3．（2）∵OA =3，OC =3，∴tan ∠CAO =3，∴∠CAO =60°． ∵AE 为∠BAC 的平分线，∴∠DAO =30°，∴DO =33AO =1，∴点D 的坐标为（0，1）． 设点P 的坐标为（3，a ）．依据两点间的距离公式可知：AD 2=4，AP 2=12+a 2，DP 2=3+（a ﹣1）2．当AD =PA 时，4=12+a 2，方程无解．当AD =DP 时，4=3+（a ﹣1）2，解得a =0或a =2（舍去），∴点P 的坐标为（3，0）． 当AP =DP 时，12+a 2=3+（a ﹣1）2，解得a =﹣4，∴点P 的坐标为（3，﹣4）． 综上所述，点P 的坐标为（3，0）或（3，﹣4）．（3）设直线AC 的解析式为y =mx +3，将点A 的坐标代入得：330m -+=，解得：m =3，∴直线AC 的解析式为33y x =+．设直线MN 的解析式为y =kx +1．把y =0代入y =kx +1得：kx +1=0，解得：x =1k -，∴点N 的坐标为（1k -，0），∴AN =13k-+=31k -． 将33y x =+与y =kx +1联立解得：x =3k -，∴点M 的横坐标为3k -．过点M 作MG ⊥x 轴，垂足为G ．则AG =33k +-．∵∠MAG =60°，∠AGM =90°，∴AM =2AG 233k -233k k -，∴11AM AN +=323231k k k -+-- =33232k k --=3(31)2(31)k k -- =32． 点睛：本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数、二次函数的解析式，分类讨论是解答问题（2）的关键，求得点M 的坐标和点N 的坐标是解答问题（3）的关键．9．在平面直角坐标系xOy 中(如图)，已知抛物线y ＝x 2－2x ，其顶点为A ．(1)写出这条抛物线的开口方向、顶点A 的坐标，并说明它的变化情况；(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点”①试求抛物线y ＝x 2－2x 的“不动点”的坐标；②平移抛物线y ＝x 2－2x ，使所得新抛物线的顶点B 是该抛物线的“不动点”，其对称轴与x 轴交于点C ，且四边形OABC 是梯形，求新抛物线的表达式.【答案】(l)抛物线y ＝x 2－2x 的开口向上，顶点A 的坐标是(1，－1)，抛物线的变化情况是：抛物线在对称轴左侧的部分是下降的，右侧的部分是上升的；(2)①(0，0)、(3，3)； ②新抛物线的表达式是y ＝(x ＋1)2－1.【解析】【分析】（1）Q 10a =>，故该抛物线开口向上，顶点A 的坐标为()1,1-；（2）①设抛物线“不动点”坐标为(),t t ，则22t t t =-，即可求解；②新抛物线顶点B 为“不动点”，则设点(),B m m ，则新抛物线的对称轴为：x m =，与x 轴的交点(),0C m ，四边形OABC 是梯形，则直线x m =在y 轴左侧，而点()1,1A -，点(),B m m ，则1m =-，即可求解.【详解】(l)Q 10a =>，抛物线y ＝x 2－2x 的开口向上，顶点A 的坐标是(1，－1)，抛物线的变化情况是：抛物线在对称轴左侧的部分是下降的，右侧的部分是上升的.(2)①设抛物线y ＝x 2－2x 的“不动点”坐标为(t ，t).则t ＝t 2－2t ，解得t 1＝0，t 2＝3.所以，抛物线y ＝x 2－2x 的“不动点”的坐标是(0，0)、(3，3).②∵新抛物线的顶点B 是其“不动点”，∴设点B 的坐标为(m ，m)∴新抛物线的对称轴为直线x ＝m ，与x 轴的交点为C(m ，0)∵四边形OABC 是梯形，∴直线x ＝m 在y 轴左侧.∵BC 与OA 不平行∴OC ∥AB.又∵点A 的坐标为(1，一1)，点B 的坐标为(m ，m)，∴m ＝－1.∴新抛物线是由抛物线y ＝x 2－2x 向左平移2个单位得到的，∴新抛物线的表达式是y ＝(x ＋1)2－1.【点睛】本题为二次函数综合运用题，涉及到二次函数基本知识、梯形基本性质，此类新定义题目，通常按照题设顺序，逐次求解即可.10．如图，抛物线25(0)y ax bx a =+-≠经过x 轴上的点A （1，0）和点B 及y 轴上的点C ，经过B 、C 两点的直线为y x n =+．①求抛物线的解析式．②点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t 为何值时，△PBE 的面积最大并求出最大值．③过点A 作AM BC ⊥于点M ，过抛物线上一动点N （不与点B 、C 重合）作直线AM 的平行线交直线BC 于点Q ．若点A 、M 、N 、Q 为顶点的四边形是平行四边形，求点N 的横坐标．【答案】①265y x x =-+-；②当2t =时，△PBE 的面积最大，最大值为22③点N 的横坐标为：4或5412+或5412． 【解析】【分析】 ①点B 、C 在直线为y x n =+上，则B （﹣n ，0）、C （0，n ），点A （1，0）在抛物线上，所以250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩，解得1a =-，6b =，因此抛物线解析式：265y x x =-+-；②先求出点P 到BC 的高h为sin 45)BP t ︒=-，于是211(4)2(2)2222PBE S BE h t t t ∆=⋅=⨯-⨯=-+2t =时，△PBE 的面积最大，最大值为③由①知，BC 所在直线为：5y x =-，所以点A 到直线BC的距离d =N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN为等腰直角三角形，即NQ PQ ==4PN =，Ⅰ．4NH HP +=，所以265(5)4m m m -+---=解得11m =（舍去），24m =，Ⅱ．4NH HP +=，()25654m m m ---+-=解得152m =，252m =（舍去），Ⅲ．4NH HP -=，()265[(5)]4m m m --+----=，解得152m =（舍去），2m =【详解】解：①∵点B 、C 在直线为y x n =+上，∴B （﹣n ，0）、C （0，n ），∵点A （1，0）在抛物线上， ∴250505a b an bn n +-=⎧⎪+-=⎨⎪=-⎩，∴1a =-，6b =，∴抛物线解析式：265y x x =-+-；②由题意，得，4PB t =-，2BE t =，由①知，45OBC ︒∠=，∴点P 到BC 的高h为sin 45)BP t ︒=-，∴211(4)2(2)2222PBE S BE h t t t ∆=⋅=⨯-⨯=-+当2t =时，△PBE 的面积最大，最大值为③由①知，BC 所在直线为：5y x =-，∴点A 到直线BC 的距离d =过点N 作x 轴的垂线交直线BC 于点P ，交x 轴于点H ．设()2,65N m m m -+-，则(,0)H m 、(,5)P m m -，易证△PQN 为等腰直角三角形，即NQ PQ ==∴4PN =，Ⅰ．4NH HP +=，∴265(5)4m m m -+---=解得11m =，24m =，∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，∴4m =；Ⅱ．4NH HP +=，∴()25654m m m ---+-=解得152m =，252m =， ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，5m >，∴52m =， Ⅲ．4NH HP -=， ∴()265[(5)]4m m m --+----=，解得152m =，252m =， ∵点A 、M 、N 、Q 为顶点的四边形是平行四边形，0m <，∴m =， 综上所述，若点A 、M 、N 、Q 为顶点的四边形是平行四边形，点N 的横坐标为：4或52+或52． 【点睛】本题考查了二次函数，熟练掌握二次函数的性质、平行四边形的判定与性质是解题的关键．11．如图①，抛物线2(1)y x a x a =-++-与x 轴交于A 、B 两点(点A 位于点B 的左侧)，与y 轴交于点C ，已知ABC ∆的面积为6.(1)求a 的值；(2)求ABC ∆外接圆圆心的坐标；(3)如图②，P 是抛物线上一点，点Q 为射线CA 上一点，且P 、Q 两点均在第三象限内，Q 、A 是位于直线BP 同侧的不同两点，若点P 到x 轴的距离为d ，QPB ∆的面积为2d ，且PAQ AQB ∠=∠，求点Q 的坐标.【答案】(1)-3；(2)坐标(-1，1)；(3)Q ()4,1-.【解析】【分析】（1）利用抛物线解析式得到A 、B 、C 三点坐标，然后利用三角形面积公式列出方程解出a ；（2）利用第一问得到A 、B 、C 三点坐标，求出AC 解析式，找到AC 垂直平分线的解析式，与AB 垂直平分线解析式联立，解出x 、y 即为圆心坐标；（3）过点P 做PD ⊥x 轴，PD =d ，发现△ABP 与△QBP 的面积相等，得到A 、D 两点到PB 得距离相等，可得AQ PB ∥，求出PB 解析式，与二次函数解析式联立得到P 点坐标，又易证ABQ QPA ∆∆≌，得到BQ =AP 26Q 点坐标，点与点的距离列出方程，解出Q 点坐标即可【详解】(1)解：由题意得()()1y x x a =---由图知：0a ＜所以A (,0a )，()10B ,,()0,C a - ()()112ABC S a a ∆=-⋅-=6 34()a a =-=或舍∴3a =-(2)由(1)得A (-3,0)，()10B ,,()0,3C ∴直线AC 得解析式为：3y x =+AC 中点坐标为33,22⎛⎫-⎪⎝⎭∴AC 的垂直平分线为：y x =-又∵AB 的垂直平分线为：1x =-∴1y x x =-⎧⎨=-⎩ 得11x y =-⎧⎨=⎩ ABC ∆外接圆圆心的坐标(-1，1).(3)解：过点P 做PD ⊥x 轴由题意得：PD =d ，∴12ABP S PD AB ∆=⋅ =2d∵QPB ∆的面积为2d∴ABP BPQ S S ∆∆=，即A 、D 两点到PB 得距离相等∴AQ PB ∥设PB 直线解析式为;y x b =+过点(1,0)B∴1y x =-∴2123y x y x x =-⎧⎨=--+⎩易得45x y =-⎧⎨=⎩ 1()0x y =⎧⎨=⎩舍 所以P (-4,-5),由题意及PAQ AQB ∠=∠易得：ABQ QPA ∆∆≌∴BQ =AP 26设Q (m ，-1)(0m ＜)∴()221126m -+= 4m =-∴Q ()4,1-.【点睛】本题考查二次函数综合性问题，涉及到一次函数、三角形外接圆圆心、全等三角形等知识点，第一问关键在于用a 表示出A 、B 、C 三点坐标；第二问关键在于找到AC 垂直平分线的解析式，与AB 垂直平分线解析式；第三问关键在于能够求出PB 的解析式12．已知矩形ABCD 中，AB =5cm ，点P 为对角线AC 上的一点，且AP =25cm .如图①，动点M 从点A 出发，在矩形边上沿着A B C →→的方向匀速运动(不包含点C ).设动点M 的运动时间为t (s )，APM ∆的面积为S (cm ²)，S 与t 的函数关系如图②所示： (1)直接写出动点M 的运动速度为 /cm s ，BC 的长度为 cm ;(2)如图③，动点M 重新从点A 出发，在矩形边上，按原来的速度和方向匀速运动.同时，另一个动点N 从点D 出发，在矩形边上沿着D C B →→的方向匀速运动，设动点N 的运动速度为()/v cm s .已知两动点M 、N 经过时间()x s 在线段BC 上相遇(不包含点C )，动点M 、N 相遇后立即停止运动，记此时APM DPN ∆∆与的面积为()()2212,S cm S cm . ①求动点N 运动速度()/v cm s 的取值范围;②试探究12S S ⋅是否存在最大值.若存在，求出12S S ⋅的最大值并确定运动速度时间x 的值；若不存在，请说明理由.【答案】(1)2，10；(2)①2/6/3cm s v cm s ≤＜；②当154x =时，12S S ⋅取最大值2254. 【解析】 【分析】（1）由题意可知图像中0~2.5s 时，M 在AB 上运动，求出速度，2.5~7.5s 时，M 在BC 上运动，求出BC 长度；（2）①分别求出在C 点相遇和在B 点相遇时的速度，取中间速度，注意C 点相遇时的速度不能取等于；②过M 点做MH ⊥AC ，则125MH CM ==得到S 1，同时利用12()PAD CDM ABM N ABCD S S S S S S ∆∆∆+=---（N ）矩形=15，得到S 2，再得到12S S ⋅关于x 的二次函数，利用二次函数性质求得最大值 【详解】(1)5÷2.5=2/cm s ；（7.5-2.5）×2=10cm (2)①解：在C 点相遇得到方程57.5v= 在B 点相遇得到方程152.5v=∴5=7.515=2.5 vv⎧⎪⎪⎨⎪⎪⎩解得23=5vv⎧=⎪⎨⎪⎩∵在边BC上相遇，且不包含C点∴2/6/3cm s v cm s≤＜②如下图12()PAD CDM ABM NABCDS S S S S S∆∆∆+=---（N）矩形()()5152525751022x x⨯-⨯-=---=15过M点做MH⊥AC，则125MH CM==∴112152S MH AP x=⋅=-+∴22S x=()122152S S x x⋅=-+⋅=2430x x-+=215225444x⎛⎫--+⎪⎝⎭因为152.57.54＜＜，所以当154x=时，12S S⋅取最大值2254.【点睛】本题重点考查动点问题，二次函数的应用，求不规则图形的面积等知识点，第一问关键能够从图像中得到信息，第二问第一小问关键在理清楚运动过程，第二小问关键在能够用x 表示出S1和S213．复习课中，教师给出关于x的函数（k是实数）.教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上.学生思考后，黑板上出现了一些结论.教师作为活动一员，又补充一些结论，并从中选择如下四条：①存在函数，其图像经过（1,0）点；②函数图像与坐标轴总有三个不同的交点；③当时，不是y随x的增大而增大就是y随x的增大而减小；④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数；教师：请你分别判断四条结论的真假，并给出理由，最后简单写出解决问题时所用的数学方法.【答案】①真，②假，③假，④真，理由和所用的数学方法见解析.【解析】试题分析：根据方程思想，特殊与一般思想，反证思想，分类思想对各结论进行判断.试题解析：①真，②假，③假，④真.理由如下：①将（1,0）代入，得，解得.∴存在函数，其图像经过（1,0）点.∴结论①为真.②举反例如，当时，函数的图象与坐标轴只有两个不同的交点.∴结论②为假.③∵当时，二次函数（k是实数）的对称轴为，∴可举反例如，当时，二次函数为，当时，y随x的增大而减小；当时，y随x的增大而增大.∴结论③为假.④∵当时，二次函数的最值为，∴当时，有最小值，最小值为负；当时，有最大值，最大值为正.∴结论④为真.解决问题时所用的数学方法有方程思想，特殊与一般思想，反证思想，分类思想考点：1.曲线上点的坐标与方程的关系；2.二次函数的性质；3.方程思想、特殊元素法、反证思想和分类思想的应用.14．如图，已知二次函数y=ax2+bx+3 的图象与x轴分别交于A(1,0)，B(3,0)两点，与y轴交于点C（1）求此二次函数解析式；（2）点D 为抛物线的顶点，试判断△BCD 的形状，并说明理由；（3）将直线BC 向上平移t(t>0)个单位，平移后的直线与抛物线交于M ，N 两点（点M 在y 轴的右侧），当△AMN 为直角三角形时，求t 的值． 【答案】（1）243y x x =-+；（2）△BCD 为直角三角形，理由见解析；（3）当△AMN为直角三角形时，t 的值为1或4．【解析】 【分析】（1）根据点A 、B 的坐标，利用待定系数法即可求出二次函数解析式；（2）利用配方法及二次函数图象上点的坐标特征，可求出点C 、D 的坐标，利用两点间的距离公式可求出CD 、BD 、BC 的长，由勾股定理的逆定理可证出△BCD 为直角三角形； （3）根据点B 、C 的坐标，利用待定系数法可求出直线BC 的解析式，进而可找出平移后直线的解析式，联立两函数解析式成方程组，通过解方程组可找出点M 、N 的坐标，利用两点间的距离公式可求出AM 2、AN 2、MN 2的值，分别令三个角为直角，利用勾股定理可得出关于t 的无理方程，解之即可得出结论． 【详解】（1）将()1,0A 、()3,0B 代入23y ax bx =++，得：309330a b a b ++=⎧⎨++=⎩，解得：14a b =⎧⎨=-⎩， ∴此二次函数解析式为243y x x =-+．（2）BCD ∆为直角三角形，理由如下：()224321y x x x Q =-+=--， ∴顶点D 的坐标为()2,1-．当0x =时，2433y x x =-+=，∴点C 的坐标为()0,3．Q 点B 的坐标为()3,0，()()22300332BC ∴=-+-=，BD ==，CD ==22220BC BD CD +==Q ，90CBD ∴∠=︒，BCD ∴∆为直角三角形．（3）设直线BC 的解析式为()0y kx c k =+≠， 将()3,0B ，()0,3C 代入y kx c =+，得：303k c c +=⎧⎨=⎩，解得：13k c =-⎧⎨=⎩， ∴直线BC 的解析式为3y x =-+，∴将直线BC 向上平移t 个单位得到的直线的解析式为3y x t =-++．联立新直线与抛物线的解析式成方程组，得：2343y x ty x x =-++⎧⎨=-+⎩，解得：11x y ⎧=⎪⎪⎨⎪=⎪⎩22x y ⎧=⎪⎪⎨⎪=⎪⎩∴点M 的坐标为，点N 的坐标为，32)2t ++．Q 点A 的坐标为()1,0，(22223321057122t AM t t t ⎛⎫⎛⎫+-∴=-+-=++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭(22223321057122t AN t t t ⎛⎫⎛⎫-++=-+-=++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，2223332321882222t t MN t ⎛⎛-+++=-+-=+ ⎝⎭⎝⎭． AMN ∆Q 为直角三角形， ∴分三种情况考虑：①当90MAN ∠=︒时，有222AM AN MN +=，即((22571571188t t t t t t t ++-+++++=+，整理，得：220t t +-=，解得：11t =，22t =-（不合题意，舍去）； ②当90AMN ∠=︒时，有222AM MN AN +=，即()()225719418857194t t t t t t t t t ++-++++=+++++，整理，得：2280t t --=，解得：14t =，22t =-（不合题意，舍去）； ③当90ANM ∠=︒时，有222AN MN AN +=，即()()225719418857194t t t t t t t t t +++++++=++-++，整理，得：()941940t t t ++++=．0t >Q ，∴该方程无解（或解均为增解）．综上所述：当AMN ∆为直角三角形时，t 的值为1或4． 【点睛】本题考查了待定系数法求二次函数解析式、待定系数法求一次函数解析式、二次函数图象上点的坐标特征、勾股定理以及勾股定理的逆定理，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数解析式；（2）利用两点间的距离公式结合勾股定理的逆定理找出BC 2+BD 2=CD 2；（3）分∠MAN =90°、∠AMN =90°及∠ANM =90°三种情况考虑．15．如图，△ABC 的顶点坐标分别为A （﹣6，0），B （4，0），C （0，8），把△ABC 沿直线BC 翻折，点A 的对应点为D ，抛物线y=ax 2﹣10ax+c 经过点C ，顶点M 在直线BC 上．（1）证明四边形ABCD 是菱形，并求点D 的坐标； （2）求抛物线的对称轴和函数表达式；（3）在抛物线上是否存在点P ，使得△PBD 与△PCD 的面积相等？若存在，直接写出点P 的坐标；若不存在，请说明理由． 【答案】（1）详见解析。
2020-2021中考数学 二次函数综合试题及答案
2020-2021中考数学二次函数综合试题及答案一、二次函数1．如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（1，0）、C（﹣2，3）两点，与y 轴交于点N，其顶点为D．（1）求抛物线及直线AC的函数关系式；（2）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值及此时点P 的坐标；（3）在对称轴上是否存在一点M，使△ANM的周长最小．若存在，请求出M点的坐标和△ANM周长的最小值；若不存在，请说明理由．【答案】（1）y＝﹣x2﹣2x+3；y＝﹣x+1；（2）当x＝﹣12时，△APC的面积取最大值，最大值为278，此时点P的坐标为（﹣12，154）；（3）在对称轴上存在一点M（﹣1，2），使△ANM的周长最小，△ANM周长的最小值为102【解析】【分析】（1）根据点A，C的坐标，利用待定系数法即可求出抛物线及直线AC的函数关系式；（2）过点P作PE∥y轴交x轴于点E，交直线AC于点F，过点C作CQ∥y轴交x轴于点Q，设点P的坐标为（x，﹣x2﹣2x+3）（﹣2＜x＜1），则点E的坐标为（x，0），点F的坐标为（x，﹣x+1），进而可得出PF的值，由点C的坐标可得出点Q的坐标，进而可得出AQ的值，利用三角形的面积公式可得出S△APC＝﹣32x2﹣32x+3，再利用二次函数的性质，即可解决最值问题；（3）利用二次函数图象上点的坐标特征可得出点N的坐标，利用配方法可找出抛物线的对称轴，由点C，N的坐标可得出点C，N关于抛物线的对称轴对称，令直线AC与抛物线的对称轴的交点为点M，则此时△ANM周长取最小值，再利用一次函数图象上点的坐标特征求出点M的坐标，以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论．【详解】（1）将A（1，0），C（﹣2，3）代入y＝﹣x2+bx+c，得：10423b c b c -++=⎧⎨--+=⎩，解得：23b c =-⎧⎨=⎩， ∴抛物线的函数关系式为y ＝﹣x 2﹣2x +3； 设直线AC 的函数关系式为y ＝mx +n （m ≠0）， 将A （1，0），C （﹣2，3）代入y ＝mx +n ，得：023m n m n +=⎧⎨-+=⎩，解得：11m n =-⎧⎨=⎩， ∴直线AC 的函数关系式为y ＝﹣x +1．（2）过点P 作PE ∥y 轴交x 轴于点E ，交直线AC 于点F ，过点C 作CQ ∥y 轴交x 轴于点Q ，如图1所示．设点P 的坐标为（x ，﹣x 2﹣2x +3）（﹣2＜x ＜1），则点E 的坐标为（x ，0），点F 的坐标为（x ，﹣x +1），∴PE ＝﹣x 2﹣2x +3，EF ＝﹣x +1，EF ＝PE ﹣EF ＝﹣x 2﹣2x +3﹣（﹣x +1）＝﹣x 2﹣x +2． ∵点C 的坐标为（﹣2，3）， ∴点Q 的坐标为（﹣2，0）， ∴AQ ＝1﹣（﹣2）＝3， ∴S △APC ＝12AQ •PF ＝﹣32x 2﹣32x +3＝﹣32（x +12）2+278． ∵﹣32＜0， ∴当x ＝﹣12时，△APC 的面积取最大值，最大值为278，此时点P 的坐标为（﹣12，154）． （3）当x ＝0时，y ＝﹣x 2﹣2x +3＝3， ∴点N 的坐标为（0，3）． ∵y ＝﹣x 2﹣2x +3＝﹣（x +1）2+4， ∴抛物线的对称轴为直线x ＝﹣1． ∵点C 的坐标为（﹣2，3）， ∴点C ，N 关于抛物线的对称轴对称．令直线AC 与抛物线的对称轴的交点为点M ，如图2所示． ∵点C ，N 关于抛物线的对称轴对称， ∴MN ＝CM ，∴AM +MN ＝AM +MC ＝AC ， ∴此时△ANM 周长取最小值． 当x ＝﹣1时，y ＝﹣x +1＝2， ∴此时点M 的坐标为（﹣1，2）．∵点A 的坐标为（1，0），点C 的坐标为（﹣2，3），点N 的坐标为（0，3），∴AC＝，AN ，∴C△ANM＝AM+MN+AN＝AC+AN＝32+10．∴在对称轴上存在一点M（﹣1，2），使△ANM的周长最小，△ANM周长的最小值为32+10．【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长，解题的关键是：（1）根据点的坐标，利用待定系数法求出抛物线及直线AC的函数关系式；（2）利用三角形的面积公式找出S△APC＝﹣32x2﹣32x+3的最值；（3）利用二次函数图象的对称性结合两点之间线段最短找出点M的位置．2．如图，在平面直角坐标系中，点O为坐标原点，直线y=﹣x+n与x轴、y轴分别交于B、C两点，抛物线y=ax2+bx+3(a≠0)过C、B两点，交x轴于另一点A，连接AC，且tan∠CAO=3．(1)求抛物线的解析式；(2)若点P是射线CB上一点，过点P作x轴的垂线，垂足为H，交抛物线于Q，设P点横坐标为t，线段PQ的长为d，求出d与t之间的函数关系式，并写出相应的自变量t的取值范围；(3)在(2)的条件下，当点P在线段BC上时，设PH=e，已知d，e是以y为未知数的一元二次方程：y2－(m+3)y+14(5m2－2m+13)="0" (m为常数)的两个实数根，点M在抛物线上，连接MQ、MH、PM，且．MP平分∠QMH，求出t值及点M的坐标．【答案】(1) y=-x 2+2x+3；(2)223(03){3(3)d t t t d t t t =-+<<=->；（3）t=1，2，2)和(12，2). 【解析】 【分析】（1）当x=0时代入抛物线y=ax 2+bx+3（a≠0）就可以求出y=3而得出C 的坐标，就可以得出直线的解析式，就可以求出B 的坐标，在直角三角形AOC 中，由三角形函数值就可以求出OA 的值，得出A 的坐标，再由待定系数法建立二元一次方程组求出其解就可以得出结论；（2）分两种情况讨论，当点P 在线段CB 上时，和如图3点P 在射线BN 上时，就有P 点的坐标为（t ，-t+3），Q 点的坐标为（t ，-t 2+2t+3），就可以得出d 与t 之间的函数关系式而得出结论；（3）根据根的判别式就可以求出m 的值，就可以求出方程的解而求得PQ 和PH 的值，延长MP 至L ，使LP=MP ，连接LQ 、LH ，如图2，延长MP 至L ，使LP=MP ，连接LQ 、LH ，就可以得出四边形LQMH 是平行四边形，进而得出四边形LQMH 是菱形，由菱形的性质就可以求出结论． 【详解】（1）当x=0，则y=-x+n=0+n=n ，y=ax 2+bx+3=3， ∴OC=3=n ． 当y=0，∴-x+3=0，x=3=OB ， ∴B （3，0）．在△AOC 中，∠AOC ＝90°，tan ∠CAO=33OC OA OA==， ∴OA=1， ∴A （-1，0）．将A （-1，0），B （3，0）代入y=ax2+bx+3， 得9330{30a b a b ++=-+=，解得：1 {2 ab=-=∴抛物线的解析式：y=-x2+2x+3；(2) 如图1，∵P点的横坐标为t 且PQ垂直于x轴∴P点的坐标为(t，－t+3)，Q点的坐标为(t，－t2+2t+3).∴PQ=|(－t+3)－(－t2+2t+3)|="|" t2－3t |∴223(03) {3(3)d t t td t t t=-+<<=->；∵d，e是y2－(m+3)y+14(5m2－2m+13)=0（m为常数）的两个实数根，∴△≥0，即△=(m+3)2－4×14(5m2－2m+13)≥0整理得：△= －4(m－1)2≥0，∵－4(m－1)2≤0，∴△=0，m=1，∴ PQ与PH是y2－4y+4=0的两个实数根，解得y1=y2=2∴ PQ=PH=2，∴－t+3=2，∴t="1,"∴此时Q是抛物线的顶点，延长MP至L，使LP=MP，连接LQ、LH，如图2，∵LP=MP，PQ=PH，∴四边形LQMH是平行四边形，∴LH∥QM，∴∠1=∠3，∵∠1=∠2，∴∠2=∠3，∴LH=MH，∴平行四边形LQMH是菱形，∴PM⊥QH，∴点M的纵坐标与P点纵坐标相同，都是2，∴在y=－x2+2x+3令y=2，得x 2－2x －1=0，∴x 1，x 2=1综上：t 值为1，M 点坐标为，2)和(1，2).3．对于二次函数 y=ax 2+（b+1）x+（b ﹣1），若存在实数 x 0，使得当 x=x 0，函数 y=x 0，则称x 0 为该函数的“不变值”.（1）当 a=1，b=﹣2 时，求该函数的“不变值”；（2）对任意实数 b ，函数 y 恒有两个相异的“不变值”，求 a 的取值范围；（3）在（2）的条件下，若该图象上 A 、B 两点的横坐标是该函数的“不变值”，且 A 、B 两点关于直线 y=kx-2a+3 对称，求 b 的最小值. 【答案】（1）－1，3；（2）0<a<1；（3）－98【解析】 【分析】（1）先确定二次函数解析式为y=x 2-x-3，根据x o 是函数y 的一个不动点的定义，把（x o ，x o ）代入得x 02-x 0-3=x o ，然后解此一元二次方程即可；（2）根据x o 是函数y 的一个不动点的定义得到ax o 2+（b+1）x o +（b-1）=x o ，整理得ax 02+bx o +（b-1）=0，则根据判别式的意义得到△=b 2-4a （b-1）>0，即b 2-4ab+4a>0，把b 2-4ab+4a 看作b 的二次函数，由于对任意实数b ，b 2-4ab+4a>0成立，则（4a ）2-4.4a<0，然后解此不等式即可.（3）（利用两点关于直线对称的两个结论，一是中点在已知直线上，二是两点连线和已知直线垂直.找到a ，b 之间的关系式，整理后在利用基本不等式求解可得. 【详解】解：（1）当a=1，b=-2时，二次函数解析式为y=x 2-x-3，把（x o ，x o ）代入得x 02-x 0-3=x o ，解得x o =-1或x o =3，所以函数y 的不动点为-1和3；（2）因为y=x o ，所以ax o 2+（b+1）x o +（b-1）=x o ，即ax 02+bx o +（b-1）=0，因为函数y 恒有两个相异的不动点，所以此方程有两个不相等的实数解，所以△=b 2-4a （b-1）>0，即b 2-4ab+4a>0，而对任意实数b ，b 2-4ab+4a>0成立，所以（4a ）2-4.4a<0，解得0<a<1.（3）设A （x 1，x 1），B （x 2，x 2），则x 1+x 2b a=- A ，B 的中点的坐标为（1212,22x x x x ++ ），即M （,22b ba a-- ） A 、B 两点关于直线y=kx-2a+3对称， 又∵A ，B 在直线y=x 上，∴k=-1，A ，B 的中点M 在直线y=kx-2a+3上.∴b a -=ba-2a+3 得：b=2a 2-3a 所以当且仅当a=34 时，b 有最小值－98【点睛】本题是在新定义下对函数知识的综合考查，是一道好题.关于两点关于直线对称的问题，有两个结论同时存在，一是中点在已知直线上，二是两点连线和已知直线垂直.4．如图，抛物线212222y x x =-++与x 轴相交于A B ，两点，（点A 在B 点左侧）与y 轴交于点C.（Ⅰ）求A B ，两点坐标.（Ⅱ）连结AC ，若点P 在第一象限的抛物线上，P 的横坐标为t ，四边形ABPC 的面积为S.试用含t 的式子表示S ，并求t 为何值时，S 最大.（Ⅲ）在（Ⅱ）的基础上，若点,G H 分别为抛物线及其对称轴上的点，点G 的横坐标为m ，点H 的纵坐标为n ，且使得以,,,A G H P 四点构成的四边形为平行四边形，求满足条件的,m n 的值.【答案】（Ⅰ）(2,0),2,0)A B ；（Ⅱ）222)42(022)S t t =-+<<,当2t =时，42S =最大；（Ⅲ）满足条件的点m n 、的值为：2324m n =-=，或521524m n ==-，或32124m n =-= 【解析】 【分析】（Ⅰ）令y=0，建立方程求解即可得出结论；（Ⅱ）设出点P 的坐标，利用S=S △AOC +S 梯形OCPQ +S △PQB ，即可得出结论；（Ⅲ）分三种情况，利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论． 【详解】解：（Ⅰ）抛物线21222y x x =-++， 令0y =，则212202x x -++=， 解得：2x =-22x =∴()()2,0,22,0A B - （Ⅱ）由抛物线21222y x x =-++，令0x =，∴2y =，∴()0,2C ， 如图1，点P 作PQ x ⊥轴于Q ， ∵P 的横坐标为t ，∴设(),P t p ， ∴2122,22,2p t t PQ p BQ t OQ t =-++==-=， ∴()()11122222222AOC PQB OCPQ S S S S p t t p =++=⨯⨯++⨯+⨯-⨯V V 梯形 11222222t pt p pt p t =+++-=++ 21222222t t t ⎛⎫=-++++ ⎪ ⎪⎭()22242(022)2t t =--+<<，∴当2t =时，42S =最大；（Ⅲ）由（Ⅱ）知，2t =，∴)2,2P，∵抛物线21222y x x =-++的对称轴为2x =∴设2122,2,222G m m m H n ⎛⎫⎛⎫-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形，()2,0A ， ①当AP 和HG 为对角线时，∴()2112111222,2022222222m m m n ⎛⎫⎛⎫=++=-+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，∴23,24m n =-=， ②当AG 和PH 是对角线时， ∴()()2112112122,2022222222m m m n ⎛⎫⎛⎫-=+-+++=+ ⎪ ⎪ ⎪ ⎪⎭⎝⎭， ∴5215,24m n ==-， ③AH 和PG 为对角线时，∴()()2121112122,22022222m m m n ⎛⎫⎛⎫-+=+-+++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭， ∴321,24m n =-=， 即：满足条件的点m n 、的值为：23,24m n =-=，或5215,24m n ==-，或321,24m n =-= 【点睛】此题是二次函数综合题，主要考查了坐标轴上点的特点，三角形的面积公式，梯形的面积公式，平行四边形的性质，中点坐标公式，用方程的思想解决问题是解本题的关键．5．如图，已知二次函数的图象过点O （0，0）．A （8，4），与x 轴交于另一点B ，且对称轴是直线x ＝3．（1）求该二次函数的解析式；（2）若M 是OB 上的一点，作MN ∥AB 交OA 于N ，当△ANM 面积最大时，求M 的坐标；（3）P 是x 轴上的点，过P 作PQ ⊥x 轴与抛物线交于Q ．过A 作AC ⊥x 轴于C ，当以O ，P ，Q 为顶点的三角形与以O ，A ，C 为顶点的三角形相似时，求P 点的坐标．【答案】（1）21342y x x =-；（2）当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）；（3）P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）． 【解析】 【分析】（1）先利用抛物线的对称性确定B （6，0），然后设交点式求抛物线解析式； （2）设M （t ，0），先其求出直线OA 的解析式为12y x =直线AB 的解析式为y=2x-12，直线MN 的解析式为y=2x-2t ，再通过解方程组1222y xy x t⎧=⎪⎨⎪=-⎩得N （42t,t 33），接着利用三角形面积公式，利用S △AMN =S △AOM -S △NOM 得到AMN 112S 4t t t 223∆=⋅⋅-⋅⋅然后根据二次函数的性质解决问题； （3）设Q 213m,m m 42⎛⎫- ⎪⎝⎭，根据相似三角形的判定方法，当PQ PO OC AC=时，△PQO ∽△COA ，则213m m 2|m |42-=；当PQ POAC OC=时，△PQO ∽△CAO ，则2131m m m 422-=，然后分别解关于m 的绝对值方程可得到对应的P 点坐标． 【详解】解：（1）∵抛物线过原点，对称轴是直线x ＝3， ∴B 点坐标为（6，0），设抛物线解析式为y ＝ax （x ﹣6）， 把A （8，4）代入得a•8•2＝4，解得a ＝14， ∴抛物线解析式为y ＝14x （x ﹣6），即y ＝14x 2﹣32x ； （2）设M （t ，0），易得直线OA 的解析式为y ＝12x ， 设直线AB 的解析式为y ＝kx+b ，把B （6，0），A （8，4）代入得6084k b k b +=⎧⎨+=⎩，解得k 2b 12=⎧⎨=-⎩，∴直线AB 的解析式为y ＝2x ﹣12， ∵MN ∥AB ，∴设直线MN 的解析式为y ＝2x+n ， 把M （t ，0）代入得2t+n ＝0，解得n ＝﹣2t ， ∴直线MN 的解析式为y ＝2x ﹣2t ，解方程组1222y x y x t ⎧=⎪⎨⎪=-⎩得4323x t y t ⎧=⎪⎪⎨⎪=⎪⎩，则42N t,t 33⎛⎫ ⎪⎝⎭， ∴S △AMN ＝S △AOM ﹣S △NOM1124t t t 223=⋅⋅-⋅⋅ 21t 2t 3=-+ 21(t 3)33=--+， 当t ＝3时，S △AMN 有最大值3，此时M 点坐标为（3，0）；（3）设213m,m m 42⎛⎫- ⎪⎝⎭， ∵∠OPQ ＝∠ACO ，∴当PQ PO OC AC =时，△PQO ∽△COA ，即PQ PO 84=， ∴PQ ＝2PO ，即213m m 2|m |42-=， 解方程213m m 2m 42-=得m 1＝0（舍去），m 2＝14，此时P 点坐标为（14，0）； 解方程213m m 2m 42-=-得m 1＝0（舍去），m 2＝﹣2，此时P 点坐标为（﹣2，0）； ∴当PQ PO AC OC =时，△PQO ∽△CAO ，即PQ PO 48=， ∴PQ ＝12PO ，即2131m m m 422-=， 解方程2131m m m 422=-=得m 1＝0（舍去），m 2＝8，此时P 点坐标为（8，0）； 解方程2131m m m 422=-=-得m 1＝0（舍去），m 2＝4，此时P 点坐标为（4，0）； 综上所述，P 点坐标为（14，0）或（﹣2，0）或（4，0）或（8，0）．【点睛】本题考查了二次函数的综合题：熟练掌握二次函数图象上点的坐标特征和二次函数的性质；会利用待定系数法求函数解析式；理解坐标与图形性质；灵活运用相似比表示线段之间的关系；会运用分类讨论的思想解决数学问题．6．已知抛物线2(5)6y x m x m =-+-+-.（1）求证：该抛物线与x 轴总有交点；（2）若该抛物线与x 轴有一个交点的横坐标大于3且小于5，求m 的取值范围；（3）设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ，若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ，求m 的值.【答案】（1）证明见解析；（2）1?<?m?3<；（3）56m m ==或【解析】【分析】（1）本题需先根据判别式解出无论m 为任何实数都不小于零，再判断出物线与x 轴总有交点．（2）根据公式法解方程，利用已有的条件，就能确定出m 的取值范围，即可得到结果． （3）根据抛物线y=-x 2+（5-m ）x+6-m ，求出与y 轴的交点M 的坐标，再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标，列方程可得结论．【详解】（1）证明：∵()()()222454670b ac m m m ∆=-=-+-=-≥∴抛物线与x 轴总有交点.（2）解：由（1）()27m ∆=-，根据求根公式可知，方程的两根为：x = 即1216x x m =-=-+， 由题意，有 3<-m 6<5+1<?m 3∴<(3)解：令 x = 0， y =6m -+∴ M （0，6m -+）由（2）可知抛物线与x 轴的交点为（-1，0）和（6m -+，0），它们关于直线y x =-的对称点分别为（0 ， 1）和（0， 6m -），由题意，可得：6166m m m 或-+=-+=-56m m ∴==或【点睛】本题考查对抛物线与x 轴的交点，解一元一次方程，解一元一次不等式，根的判别式，对称等，解题关键是熟练理解和掌握以上性质，并能综合运用这些性质进行计算．7．如图1，在平面直角坐标系中，直线AB ：y ＝kx +b （k ＜0，b ＞0），与x 轴交于点A 、与y 轴交于点B ，直线CD 与x 轴交于点C 、与y 轴交于点D ．若直线CD 的解析式为y ＝﹣1k（x +b ），则称直线CD 为直线AB 的”姊线”，经过点A 、B 、C 的抛物线称为直线AB 的“母线”．（1）若直线AB 的解析式为：y ＝﹣3x +6，求AB 的”姊线”CD 的解析式为： （直接填空）；（2）若直线AB 的”母线”解析式为：2142y x x =-+，求AB 的”姊线”CD 的解析式； （3）如图2，在（2）的条件下，点P 为第二象限”母线”上的动点，连接OP ，交”姊线”CD 于点Q ，设点P 的横坐标为m ，PQ 与OQ 的比值为y ，求y 与m 的函数关系式，并求y 的最大值；（4）如图3，若AB 的解析式为：y ＝mx +3（m ＜0），AB 的“姊线”为CD ，点G 为AB 的中点，点H 为CD 的中点，连接OH ，若GH ＝5，请直接写出AB 的”母线”的函数解析式．【答案】（1）1(6)3y x =+；（2）（2，0）、（0，4）、（﹣4，0）；（3）当m ＝﹣32，y 最大值为338；（4）y ＝x 2﹣2x ﹣3． 【解析】【分析】（1）由k ，b 的值以及”姊线”的定义即可求解；（2）令x ＝0，得y 值，令y ＝0，得x 值，即可求得点A 、B 、C 的坐标，从而求得直线CD 的表达式；（3）设点P 的横坐标为m ，则点P （m ，n ），n ＝﹣12m 2﹣m+4， 从而求得直线OP 的表达式，将直线OP 和CD 表达式联立并解得点Q 坐标，由此求得P Q y y ，从而求得y ＝﹣12m 2﹣32m+3，故当m ＝﹣32，y 最大值为338； （4）由直线AB 的解析式可得AB 的“姊线”CD 的表达式y ＝﹣1m（x+3），令x ＝0，得 y 值，令y ＝0，得x 值，可得点C 、D 的坐标，由此可得点H 坐标，同理可得点G 坐标， 由勾股定理得：m 值，即可求得点A 、B 、C 的坐标，从而得到 “母线”函数的表达式．【详解】（1）由题意得：k ＝﹣3，b ＝6， 则答案为：y ＝13（x+6）； （2）令x ＝0，则y ＝4，令y ＝0，则x ＝2或﹣4，点A 、B 、C 的坐标分别为（2，0）、（0，4）、（﹣4，0），则直线CD 的表达式为：y ＝12（x+4）＝12x+2； （3）设点P 的横坐标为m ，则点P （m ，n ），n ＝﹣12m 2﹣m+4， 则直线OP 的表达式为：y ＝n mx ， 将直线OP 和CD 表达式联立得122n y x m y x ⎧=⎪⎪⎨⎪=+⎪⎩， 解得：点Q （2438m m m --+，222838m m m m +-+-） 则P Q y y ＝﹣12m 2﹣32m+4， y ＝1P Q P Q Q y y y PQ OQ y y -==-＝﹣12m 2﹣32m+3， 当m ＝﹣32，y 最大值为338； （4）直线CD 的表达式为：y ＝﹣1m （x+3）， 令x ＝0，则y ＝﹣3m，令y ＝0，则x ＝﹣3， 故点C 、D 的坐标为（﹣3，0）、（0，﹣3m ），则点H （﹣32，﹣32m ）， 同理可得：点G （﹣32m ，32）， 则GH 2＝（32+32m ）2+（32﹣32m）2＝（5）2， 解得：m ＝﹣3（正值已舍去），则点A 、B 、C 的坐标分别为（1，0）、（0，3）、（﹣3，0），则“母线”函数的表达式为：y ＝a （x ﹣1）（x+3）＝a （x 2﹣2x ﹣3），即：﹣3a ＝﹣3，解得：a ＝1，故：“母线”函数的表达式为：y ＝x 2﹣2x ﹣3．【点睛】此题是二次函数综合题目，考查了“姊线”的定义，待定系数法求二次函数解析式，二次函数的最值问题，掌握二次函数的有关性质是解答此题的关键.8．二次函数y=x 2-2mx+3（m ＞）的图象与x 轴交于点A （a ，0）和点B （a+n ，0）（n＞0且n为整数），与y轴交于C点．（1）若a=1，①求二次函数关系式；②求△ABC的面积；（2）求证：a=m-；（3）线段AB（包括A、B）上有且只有三个点的横坐标是整数，求a的值．【答案】（1）y=x2-4x+3；3；（2）证明见解析；（3）a=1或a=−．【解析】试题分析：（1）①首先根据a=1求得A的坐标，然后代入二次函数的解析式，求得m的值即可确定二次函数的解析式；②根据解析式确定抛物线与坐标轴的交点坐标，从而确定三角形的面积；（2）将原二次函数配方后即可确定其对称轴为x=m，然后根据A、B两点关于x=m对称得到a+n-m=m-a，从而确定a、m、n之间的关系；（3）根据a=m-得到A（m-，0）代入y=（x-m）2-m2+3得0=（m--m）2-m2+3，求得m 的值即可确定a的值．试题解析：（1）①∵a=1，∴A（1，0），代入y=x2-2mx+3得1-2m+3=0，解得m=2，∴y=x2-4x+3；②在y=x2-4x+3中，当y=0时，有x2-4x+3=0可得x=1或x=3，∴A（1，0）、B（3，0），∴AB=2再根据解析式求出C点坐标为（0，3），∴OC=3，△ABC的面积=×2×3=3；（2）∵y=x2-2mx+3=（x-m）2-m2+3，∴对称轴为直线x=m，∵二次函数y=x2-2mx+3的图象与x轴交于点A和点B∴点A和点B关于直线x=m对称，∴a+n-m=m-a，∴a=m-；（3）y=x2-2mx+3（m＞）化为顶点式为y=（x-m）2-m2+3（m＞）①当a为整数，因为n＞0且n为整数所以a+n是整数，∵线段AB（包括A、B）上有且只有三个点的横坐标是整数，∴n=2，∴a=m-1，∴A（m-1，0）代入y=（x-m）2-m2+3得（x-m）2-m2+3=0，∴m2-4=0，∴m=2，m=-2（舍去），∴a=2-1=1，②当a不是整数，因为n＞0且n为整数所以a+n不是整数，∵线段AB（包括A、B）上有且只有三个点的横坐标是整数，∴n=3，∴a=m-∴A（m-，0）代入y=（x-m）2-m2+3得0=（m--m）2-m2+3，∴m2=，∴m=，m=-（舍去），∴a=−，综上所述：a=1或a=−．考点：二次函数综合题．9．如图，已知直线y＝﹣2x+4分别交x轴、y轴于点A、B．抛物线过A、B两点，点P是线段AB上一动点，过点P作PC⊥x轴于点C，交抛物线于点D．（1）如图1，设抛物线顶点为M，且M的坐标是（12，92），对称轴交AB于点N．①求抛物线的解析式；②是否存在点P，使四边形MNPD为菱形？并说明理由；（2）是否存在这样的点D，使得四边形BOAD的面积最大？若存在，求出此时点D的坐标；若不存在，请说明理由．【答案】（1）①y＝﹣2x2+2x+4；；②不存在点P，使四边形MNPD为菱形；；（2）存在，点D的坐标是（1，4）．【解析】【分析】（1）①由一次函数图象上点的坐标特征求得点B的坐标，设抛物线解析式为y＝a21922x⎛⎫-+⎪⎝⎭，把点B的坐标代入求得a的值即可；②不存在点P，使四边形MNPD为菱形．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），根据题意知PD∥MN，所以当PD＝MN时，四边形MNPD为平行四边形，根据该等量关系列出方程﹣2m2+4m＝32，通过解方程求得m的值，易得点N、P的坐标，然后推知PN＝MN是否成立即可；（2）设点D的坐标是（n，﹣2n2+2n+4），P（n，﹣2n+4）．根据S四边形BOAD＝S△BOA+S△ABD ＝4+S△ABD，则当S△ABD取最大值时，S四边形BOAD最大．根据三角形的面积公式得到函数S△ABD＝﹣2（n﹣1）2+2．由二次函数的性质求得最值．【详解】解：①如图1，∵顶点M的坐标是19,22⎛⎫ ⎪⎝⎭，∴设抛物线解析式为y＝21922a x⎛⎫-+⎪⎝⎭（a≠0）．∵直线y＝﹣2x+4交y轴于点B，∴点B的坐标是（0，4）．又∵点B在该抛物线上，∴21922a⎛⎫-+⎪⎝⎭＝4，解得a＝﹣2．故该抛物线的解析式为：y＝219222x⎛⎫--+⎪⎝⎭＝﹣2x2+2x+4；②不存在．理由如下：∵抛物线y＝219222x⎛⎫--+⎪⎝⎭的对称轴是直线x＝12，且该直线与直线AB交于点N，∴点N的坐标是1,32⎛⎫ ⎪⎝⎭．∴93322MN=-=．设点P的坐标是（m，﹣2m+4），则D（m，﹣2m2+2m+4），∴PD＝（﹣2m2+2m+4）﹣（﹣2m+4）＝﹣2m2+4m．∵PD∥MN．当PD＝MN时，四边形MNPD是平行四边形，即﹣2m2+4m＝32．解得 m1＝12（舍去），m2＝32．此时P（32，1）．∵PN＝5，∴PN≠MN，∴平行四边形MNPD不是菱形．∴不存在点P，使四边形MNPD为菱形；（2）存在，理由如下：设点D的坐标是（n，﹣2n2+2n+4），∵点P在线段AB上且直线PD⊥x轴，∴P（n，﹣2n+4）．由图可知S四边形BOAD＝S△BOA+S△ABD．其中S△BOA＝12OB•OA＝12×4×2＝4．则当S△ABD取最大值时，S四边形BOAD最大．S△ABD＝12（y D﹣y P）（x A﹣x B）＝y D﹣y P＝﹣2n2+2n+4﹣（﹣2n+4）＝﹣2n2+4n＝﹣2（n﹣1）2+2．当n＝1时，S△ABD取得最大值2，S四边形BOAD有最大值．此时点D的坐标是（1，4）．【点睛】主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．10．如图①,已知抛物线y=ax2+bx+c的图像经过点A（0，3)、B（1，0），其对称轴为直线l：x=2，过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点，设其横坐标为m.（1）求抛物线的解析式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当m为何值时，四边形AOPE 面积最大，并求出其最大值；（3）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由.【答案】（1）y=x2-4x+3.（2）当m=52时，四边形AOPE面积最大，最大值为758.（3）P点的坐标为：P1（3+5，15-），P2（35-，1+5），P3（5+5，1+5），P4（552-，152-）.【解析】分析：（1）利用对称性可得点D的坐标，利用交点式可得抛物线的解析式；（2）设P（m，m2-4m+3），根据OE的解析式表示点G的坐标，表示PG的长，根据面积和可得四边形AOPE的面积，利用配方法可得其最大值；（3）存在四种情况：如图3，作辅助线，构建全等三角形，证明△OMP≌△PNF，根据OM=PN列方程可得点P 的坐标；同理可得其他图形中点P的坐标．详解：（1）如图1，设抛物线与x轴的另一个交点为D，由对称性得：D（3，0），设抛物线的解析式为：y=a（x-1）（x-3），把A（0，3）代入得：3=3a，a=1，∴抛物线的解析式；y=x2-4x+3；（2）如图2，设P（m，m2-4m+3），∵OE平分∠AOB，∠AOB=90°，∴∠AOE=45°，∴△AOE是等腰直角三角形，∴AE=OA=3，∴E（3，3），易得OE的解析式为：y=x，过P作PG∥y轴，交OE于点G，∴G（m，m），∴PG=m-（m2-4m+3）=-m2+5m-3，∴S四边形AOPE=S△AOE+S△POE，=12×3×3+12PG•AE，=92+12×3×（-m2+5m-3），=-32m2+152m，=32（m-52）2+758，∵-32＜0，∴当m=52时，S有最大值是758；（3）如图3，过P作MN⊥y轴，交y轴于M，交l于N，∵△OPF是等腰直角三角形，且OP=PF，易得△OMP≌△PNF，∴OM=PN，∵P（m，m2-4m+3），则-m2+4m-3=2-m，解得：5+555-∴P的坐标为（52，1+52）或（552-152）；如图4，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN=FM，则-m2+4m-3=m-2，解得：x=3+5或35-；P的坐标为（3+5，15-）或（35-，1+5）；综上所述，点P的坐标是：（5+52，1+52）或（552-，152-）或（3+5，15-）或（35-，1+5）．点睛：本题属于二次函数综合题，主要考查了二次函数的综合应用，相似三角形的判定与性质以及解一元二次方程的方法，解第（2）问时需要运用配方法，解第（3）问时需要运用分类讨论思想和方程的思想解决问题．11．如图①，在平面直角坐标系xOy 中，抛物线y=ax2+bx+3经过点A(-1，0) 、B(3，0) 两点，且与y轴交于点C.（1）求抛物线的表达式；（2）如图②，用宽为4个单位长度的直尺垂直于x轴，并沿x轴左右平移，直尺的左右两边所在的直线与抛物线相交于P、 Q两点（点P在点Q的左侧），连接PQ，在线段PQ上方抛物线上有一动点D ，连接DP 、DQ. ①若点P 的横坐标为12-，求△DPQ 面积的最大值，并求此时点D 的坐标； ②直尺在平移过程中，△DPQ 面积是否有最大值？若有，求出面积的最大值；若没有，请说明理由.【答案】（1）抛物线y=-x 2+2x+3；（2）①点D （ 31524，）；②△PQD 面积的最大值为8 【解析】分析：（1）根据点A 、B 的坐标，利用待定系数法即可求出抛物线的表达式；（2）（I ）由点P 的横坐标可得出点P 、Q 的坐标，利用待定系数法可求出直线PQ 的表达式，过点D 作DE ∥y 轴交直线PQ 于点E ，设点D 的坐标为（x ，-x 2+2x+3），则点E 的坐标为（x ，-x+54），进而即可得出DE 的长度，利用三角形的面积公式可得出S △DPQ =-2x 2+6x+72，再利用二次函数的性质即可解决最值问题； （II ）假设存在，设点P 的横坐标为t ，则点Q 的横坐标为4+t ，进而可得出点P 、Q 的坐标，利用待定系数法可求出直线PQ 的表达式，设点D 的坐标为（x ，-x 2+2x+3），则点E 的坐标为（x ，-2（t+1）x+t 2+4t+3），进而即可得出DE 的长度，利用三角形的面积公式可得出S △DPQ =-2x 2+4（t+2）x-2t 2-8t ，再利用二次函数的性质即可解决最值问题． 详解：（1）将A （-1，0）、B （3，0）代入y=ax 2+bx+3，得：309330a b a b -+⎧⎨++⎩＝＝，解得：12a b -⎧⎨⎩＝＝， ∴抛物线的表达式为y=-x 2+2x+3． （2）（I ）当点P 的横坐标为-12时，点Q 的横坐标为72，∴此时点P 的坐标为（-12，74），点Q 的坐标为（72，-94）．设直线PQ 的表达式为y=mx+n ，将P （-12，74）、Q （72，-94）代入y=mx+n ，得：17247924m n m n ⎧-+⎪⎪⎨⎪+-⎪⎩＝＝，解得：154m n -⎧⎪⎨⎪⎩＝＝，∴直线PQ 的表达式为y=-x+54． 如图②，过点D 作DE ∥y 轴交直线PQ 于点E ，设点D的坐标为（x，-x2+2x+3），则点E的坐标为（x，-x+54），∴DE=-x2+2x+3-（-x+54）=-x2+3x+74，∴S△DPQ=12DE•（x Q-x P）=-2x2+6x+72=-2（x-32）2+8．∵-2＜0，∴当x=32时，△DPQ的面积取最大值，最大值为8，此时点D的坐标为（32，154）．（II）假设存在，设点P的横坐标为t，则点Q的横坐标为4+t，∴点P的坐标为（t，-t2+2t+3），点Q的坐标为（4+t，-（4+t）2+2（4+t）+3），利用待定系数法易知，直线PQ的表达式为y=-2（t+1）x+t2+4t+3．设点D的坐标为（x，-x2+2x+3），则点E的坐标为（x，-2（t+1）x+t2+4t+3），∴DE=-x2+2x+3-[-2（t+1）x+t2+4t+3]=-x2+2（t+2）x-t2-4t，∴S△DPQ=12DE•（x Q-x P）=-2x2+4（t+2）x-2t2-8t=-2[x-（t+2）]2+8．∵-2＜0，∴当x=t+2时，△DPQ的面积取最大值，最大值为8．∴假设成立，即直尺在平移过程中，△DPQ面积有最大值，面积的最大值为8．点睛：本题考查了待定系数法求二次（一次）函数解析式、二次（一次）函数图象上点的坐标特征、三角形的面积以及二次函数的最值，解题的关键是：（1）根据点的坐标，利用待定系数法求出二次函数表达式；（2）（I）利用三角形的面积公式找出S△DPQ=-2x2+6x+72；（II）利用三角形的面积公式找出S△DPQ=-2x2+4（t+2）x-2t2-8t．12．如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=12．（1）求抛物线的解析式；（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q 的坐标；若不存在，请说明理由．【答案】（1）y=12x2+32x﹣2；（2）9；（3）点Q的坐标为（﹣2，4）或（﹣2，﹣1）．【解析】（1）如答图1所示，利用已知条件求出点B的坐标，然后用待定系数法求出抛物线的解析式．（2）如答图1所示，首先求出四边形BMCA面积的表达式，然后利用二次函数的性质求出其最大值．（3）如答图2所示，首先求出直线AC与直线x=2的交点F的坐标，从而确定了Rt△AGF 的各个边长；然后证明Rt△AGF∽Rt△QEF，利用相似线段比例关系列出方程，求出点Q的坐标．考点：二次函数综合题，曲线上点的坐标与方程的关系，锐角三角函数定义，由实际问题列函数关系式，二次函数最值，勾股定理，相似三角形的判定和性质，圆的切线性质．13．（本小题满分12分）如图，在平面直角坐标系xOy中，抛物线（）与x轴交于A，B两点（点A在点B的左侧），经过点A的直线l：与y轴负半轴交于点C，与抛物线的另一个交点为D，且CD=4AC．（1）直接写出点A的坐标，并求直线l的函数表达式（其中k，b用含a的式子表示）；（2）点E是直线l上方的抛物线上的动点，若△ACE的面积的最大值为，求a的值；（3）设P是抛物线的对称轴上的一点，点Q在抛物线上，以点A，D，P，Q为顶点的四边形能否成为矩形？若能，求出点P的坐标；若不能，请说明理由．【答案】（1）A（－1，0），；（2）；（3）P的坐标为（1，）或（1，－4）．【解析】试题分析：（1）在中，令y=0，得到，，得到A（－1，0），B（3，0），由直线l经过点A，得到，故，令，即，由于CD＝4AC，故点D的横坐标为4，即有，得到，从而得出直线l的函数表达式；（2）过点E作EF∥y轴，交直线l于点F，设E（，），则F（，），EF＝=，S△ACE＝S△AFE－S△CFE＝＝，故△ACE的面积的最大值为，而△ACE的面积的最大值为，所以，解得；（3）令，即，解得，，得到D （4，5a），因为抛物线的对称轴为，设P（1，m），然后分两种情况讨论：①若AD是矩形的一条边，②若AD是矩形的一条对角线．试题解析：（1）∵=，令y=0，得到，，∴A（－1，0），B（3，0），∵直线l经过点A，∴，，∴，令，即，∵CD＝4AC，∴点D的横坐标为4，∴，∴，∴直线l的函数表达式为；（2）过点E作EF∥y轴，交直线l于点F，设E（，），则F（，），EF＝=，S△ACE＝S△AFE－S△CFE＝＝＝，∴△ACE的面积的最大值为，∵△ACE的面积的最大值为，∴，解得；（3）令，即，解得，，∴D（4，5a），∵，∴抛物线的对称轴为，设P（1，m），①若AD是矩形的一条边，则Q（－4，21a），m＝21a＋5a＝26a，则P（1，26a），∵四边形ADPQ为矩形，∴∠ADP＝90°，∴，∴，即，∵，∴，∴P1（1，）；②若AD是矩形的一条对角线，则线段AD的中点坐标为（，），Q（2，），m ＝，则P（1，8a），∵四边形APDQ为矩形，∴∠APD＝90°，∴，∴，即，∵，∴，∴P2（1，－4）．综上所述，以点A、D、P、Q为顶点的四边形能成为矩形，点P的坐标为（1，）或（1，－4）．考点：二次函数综合题．14．已知抛物线27y x3x4=--的顶点为点D，并与x轴相交于A、B两点（点A在点B 的左侧），与y轴相交于点C．（1）求点A、B、C、D的坐标；（2）在y轴的正半轴上是否存在点P，使以点P、O、A为顶点的三角形与△AOC相似？若存在，求出点P的坐标；若不存在，请说明理由；（3）取点E（34，0）和点F（0，），直线l经过E、F两点，点G是线段BD的中点．①点G是否在直线l上，请说明理由；②在抛物线上是否存在点M，使点M关于直线l的对称点在x轴上？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】解：（1） D（32，﹣4）（2） P（0，74）或（0，17）（3）详见解析【解析】【分析】（1）令y=0，解关于x的一元二次方程求出A、B的坐标，令x=0求出点C的坐标，再根据顶点坐标公式计算即可求出顶点D的坐标．（2）根据点A、C的坐标求出OA、OC的长，再分OA和OA是对应边，OA和OC是对应边两种情况，利用相似三角形对应边成比例列式求出OP的长，从而得解．（3）①设直线l的解析式为y=kx+b（k≠0），利用待定系数法求一次函数解析式求出直线l的解析式，再利用中点公式求出点G的坐标，然后根据直线上点的坐标特征验证即可．②设抛物线的对称轴与x轴交点为H，求出OE、OF、HD、HB的长，然后求出△OEF和△HDB相似，根据相似三角形对应角相等求出∠OFE=∠HBD，然后求出EG⊥BD，从而得到直线l是线段BD的垂直平分线，根据线段垂直平分线的性质点D关于直线l的对称点就是B，从而判断出点M就是直线DE与抛物线的交点．再设直线DE的解析式为y=mx+n，利用待定系数法求一次函数解析求出直线DE的解析式，然后与抛物线解析式联立求解即可得到符合条件的点M．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2020-2021初中数学二次函数经典测试题一、选择题1．已知二次函数y ＝ax 2+bx +c (a ＞0)经过点M (﹣1，2)和点N (1，﹣2)，则下列说法错误的是( )A ．a +c ＝0B ．无论a 取何值，此二次函数图象与x 轴必有两个交点，且函数图象截x 轴所得的线段长度必大于2C ．当函数在x ＜110时，y 随x 的增大而减小 D ．当﹣1＜m ＜n ＜0时，m +n ＜2a 【答案】C【解析】【分析】根据二次函数的图象和性质对各项进行判断即可．【详解】解：∵函数经过点M (﹣1，2)和点N (1，﹣2)，∴a ﹣b +c ＝2，a +b +c ＝﹣2，∴a +c ＝0，b ＝﹣2，∴A 正确；∵c ＝﹣a ，b ＝﹣2，∴y ＝ax 2﹣2x ﹣a ，∴△＝4+4a 2＞0，∴无论a 为何值，函数图象与x 轴必有两个交点，∵x 1+x 2＝2a，x 1x 2＝﹣1，∴|x 1﹣x 2|＝＞2， ∴B 正确；二次函数y ＝ax 2+bx +c (a ＞0)的对称轴x ＝﹣2b a ＝1a ， 当a ＞0时，不能判定x ＜110时，y 随x 的增大而减小； ∴C 错误；∵﹣1＜m ＜n ＜0，a ＞0，∴m +n ＜0，2a ＞0， ∴m +n ＜2a；∴D正确，故选：C．【点睛】本题考查了二次函数的问题，掌握二次函数的图象和性质是解题的关键．2．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，则下列4个结论：①abc＜0；②2a+b ＝0；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论的个数是（）A．1 B．2 C．3 D．4【答案】D【解析】【分析】根据二次函数y＝ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定解答．【详解】①由抛物线的对称轴可知：﹣＞0，∴ab＜0，∵抛物线与y轴的交点在正半轴上，∴c＞0，∴abc＜0，故①正确；②∵﹣＝1，∴b＝﹣2a，∴2a+b＝0，故②正确．③∵（0，c）关于直线x＝1的对称点为（2，c），而x＝0时，y＝c＞0，∴x＝2时，y＝c＞0，∴y＝4a+2b+c＞0，故③正确；④由图象可知：△＞0，∴b2﹣4ac＞0，故②正确；故选：D．【点睛】本题考查二次函数的图象与系数的关系，解题的关键是熟练运用二次函数的图象与性质，属于中考常考题型．3．如图，抛物线2119y x =-与x 轴交于A B ，两点，D 是以点()0,4C 为圆心，1为半径的圆上的动点，E 是线段AD 的中点，连接,OE BD ，则线段OE 的最小值是（ ）A ．2B ．322C ．52D ．3【答案】A【解析】【分析】 根据抛物线解析式即可得出A 点与B 点坐标，结合题意进一步可以得出BC 长为5，利用三角形中位线性质可知OE=12BD ，而BD 最小值即为BC 长减去圆的半径，据此进一步求解即可.【详解】∵2119y x =-， ∴当0y =时，21019x =-， 解得：=3x ±，∴A 点与B 点坐标分别为：(3-，0)，(3，0)，即：AO=BO=3，∴O 点为AB 的中点，又∵圆心C 坐标为(0，4)，∴OC=4，∴BC 长度2205OB C +=，∵O 点为AB 的中点，E 点为AD 的中点，∴OE 为△ABD 的中位线，即：OE=12BD ， ∵D 点是圆上的动点，由图可知，BD 最小值即为BC 长减去圆的半径，∴BD 的最小值为4，∴OE=12BD=2， 即OE 的最小值为2，故选：A.【点睛】本题主要考查了抛物线性质与三角形中位线性质的综合运用，熟练掌握相关概念是解题关键.4．方程2x 3x 10+-=的根可视为函数3y x =+的图象与函数1y x =的图象交点的横坐标，则方程3x 2x 10+-=的实根x 0所在的范围是（ ）A ．010<x <4 B ．011<x <43 C ．011<x <32 D ．01<x <12 【答案】C【解析】【分析】首先根据题意推断方程x 3+2x-1=0的实根是函数y=x 2+2与1y x=的图象交点的横坐标，再根据四个选项中x 的取值代入两函数解析式，找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x 3+2x-1=0的实根x 所在范围．【详解】解：依题意得方程3x 2x 10+-=的实根是函数2y x 2=+与1y x=的图象交点的横坐标，这两个函数的图象如图所示，它们的交点在第一象限．当x=14时，21y x 2216=+=，1y 4x ==，此时抛物线的图象在反比例函数下方； 当x=13时，21229y x =+=，1y 3x ==，此时抛物线的图象在反比例函数下方； 当x=12时，21224y x =+=，1y 2x==，此时抛物线的图象在反比例函数上方；当x=1时，2y x 23=+=，1y 1x==，此时抛物线的图象在反比例函数上方． ∴方程3x 2x 10+-=的实根x 0所在范围为：011<x <32． 故选C ．【点睛】此题考查了学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．5．一列自然数0，1，2，3，…，100．依次将该列数中的每一个数平方后除以100，得到一列新数．则下列结论正确的是（ ）A ．原数与对应新数的差不可能等于零B ．原数与对应新数的差，随着原数的增大而增大C ．当原数与对应新数的差等于21时，原数等于30D ．当原数取50时，原数与对应新数的差最大【答案】D【解析】【分析】设出原数，表示出新数，利用解方程和函数性质即可求解．【详解】解：设原数为m ，则新数为21100m ， 设新数与原数的差为y 则2211100100y m m m m =-=-+， 易得，当m ＝0时，y ＝0，则A 错误 ∵10100-< 当1m 50122100b a ﹣﹣﹣===⎛⎫⨯ ⎪⎝⎭时，y 有最大值．则B 错误，D 正确． 当y ＝21时，21100m m -+＝21 解得1m ＝30，2m ＝70，则C 错误．故答案选：D ．【点睛】本题以规律探究为背景，综合考查二次函数性质和解一元二次方程，解题时要注意将数字规律转化为数学符号．6．已知二次函数y =ax 2+bx +c 的图象如图所示，有以下结论：①a +b +c ＜0；②a ﹣b +c ＞1；③abc ＞0；④9a ﹣3b +c ＜0；⑤c ﹣a ＞1．其中所有正确结论的序号是( )A ．①②B ．①③④C ．①②③④D ．①②③④⑤【答案】D【解析】【分析】 根据抛物线的开口方向可得出a 的符号，再由抛物线与y 轴的交点可得出c 的值，然后进一步根据对称轴以及抛物线得出当x 1=、 x 1=-、x 3=-时的情况进一步综合判断即可．【详解】由图象可知，a ＜0，c=1，对称轴：x=b12a-=-， ∴b=2a ， ①由图可知：当x=1时，y ＜0，∴a+b+c ＜0，正确；②由图可知：当x=−1时，y ＞1，∴a −b+c ＞1，正确；③a bc=2a 2＞0，正确；④由图可知：当x=−3时，y ＜0，∴9a −3b+c ＜0，正确；⑤c−a=1−a ＞1，正确；∴①②③④⑤正确．故选：D ．【点睛】本题主要考查了抛物线的函数图像性质的综合运用，熟练掌握相关概念是解题关键．7．如图，抛物线2y ax bx c =++ 与x 轴交于点A （﹣1，0），顶点坐标（1，n ），与y 轴的交点在（0，3），（0，4）之间（包含端点），则下列结论：①abc ＞0；②3a +b ＜0；③﹣43≤a ≤﹣1；④a +b ≥am 2+bm （m 为任意实数）；⑤一元二次方程2ax bx c n ++= 有两个不相等的实数根，其中正确的有（ ）A ．2个B ．3个C ．4个D ．5个【答案】B【解析】 解：∵抛物线开口向下，∴a ＜0，∵顶点坐标（1，n ），∴对称轴为直线x =1，∴2b a - =1，∴b =﹣2a ＞0，∵与y 轴的交点在（0，3），（0，4）之间（包含端点），∴3≤c ≤4，∴abc ＜0，故①错误；3a +b =3a +（﹣2a ）=a ＜0，故②正确；∵与x 轴交于点A （﹣1，0），∴a ﹣b +c =0，∴a ﹣（﹣2a ）+c =0，∴c =﹣3a ，∴3≤﹣3a ≤4，∴﹣43≤a ≤﹣1，故③正确； ∵顶点坐标为（1，n ），∴当x =1时，函数有最大值n ，∴a +b +c ≥am 2+bm +c ，∴a +b ≥am 2+bm ，故④正确；一元二次方程2ax bx c n ++=有两个相等的实数根x 1=x 2=1，故⑤错误．综上所述，结论正确的是②③④共3个．故选B ．点睛：本题考查了抛物线与x 轴的交点，二次函数的性质，主要利用了二次函数的开口方向，对称轴，最值问题，以及二次函数图象上点的坐标特征，关键在于根据顶点横坐标表示出a 、b 的关系．8．如图，ABC ∆为等边三角形，点P 从A 出发，沿A B C A →→→作匀速运动，则线段AP 的长度y 与运动时间x 之间的函数关系大致是（ ）A ．B ．C ．D ．【答案】B【分析】根据题意可知点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故可排除选项C 与D ；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值，故选项B 符合题意，选项A 不合题意．【详解】根据题意得，点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故选项C 与选项D 不合题意；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值，∴选项B 符合题意，选项A 不合题意．故选B ．【点睛】本题考查了动点问题的函数图象：通过分类讨论，利用三角形面积公式得到y 与x 的函数关系，然后根据二次函数和一次函数图象与性质解决问题．9．抛物线y ＝ax 2+bx+c 的顶点为(﹣1，3)，与x 轴的交点A 在点(﹣3，0)和(﹣2，0)之间，其部分图象如图，则以下结论，其中正确结论的个数为( )①若点P(﹣3，m)，Q(3，n)在抛物线上，则m ＜n ；②c ＝a+3；③a+b+c ＜0；④方程ax 2+bx+c ＝3有两个相等的实数根．A ．1个B ．2个C ．3个D ．4个【答案】C【解析】 试题分析：由抛物线与x 轴有两个交点，可知b 2-4ac ＞0，所以①错误；由抛物线的顶点为D （-1，2），可知抛物线的对称轴为直线x=-1，然后由抛物线与x 轴的一个交点A 在点（-3，0）和（-2，0）之间，可知抛物线与x 轴的另一个交点在点（0，0）和（1，0）之间，因此当x=1时，y ＜0，即a+b+c ＜0，所以②正确；由抛物线的顶点为D （-1，2），可知a-b+c=2，然后由抛物线的对称轴为直线x=2b a=-1，可得b=2a ，因此a-2a+c=2，即c-a=2，所以③正确；由于当x=-1时，二次函数有最大值为2，即只有x=-1时，ax 2+bx+c=2，因此方程ax2+bx+c-2=0有两个相等的实数根，所以④正确．考点：二次函数的图像与性质10．如图是二次函数2y ax bx c =++的图象，其对称轴为1x =.下列结论：①0abc >；②20a b +=；③930a b c ++<；④若12310,,,23y y ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭是抛物线上两点，则12y y >.其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】B【解析】【分析】 由抛物线开口方向得到a ＜0，根据对称轴得到b=-2a ＞0，由抛物线与y 轴的交点位置得到c ＞0，则可对①进行判断；由b=-2a 可对②进行判断；利用抛物线的对称性可得到抛物线与x 轴的另一个交点为（3，0），则可判断当x=3时，y=0，于是可对③进行判断；通过二次函数的增减性可对④进行判断．【详解】解：∵抛物线开口向下，∴a ＜0，∵抛物线的对称轴为直线12b x a=-= ，∴b=-2a ＞0， ∵抛物线与y 轴的交点在x 轴上方， ∴c ＞0，∴abc ＜0，所以①错误；∵b=-2a ，∴2a+b=0，所以②正确；∵抛物线与x 轴的一个交点为（-1，0），抛物线的对称轴为直线x=1，∴抛物线与x 轴的另一个交点为（3，0），∴当x=3时，y=0，∴930a b c ++=，所以③错误；∵抛物线的对称轴为直线x=1，且抛物线开口向下，∴当x 1<时，y 随x 的增大而增大∵103132-<-< 点13,2y ⎛⎫-⎪⎝⎭到对称轴的距离比点210,3y ⎛⎫- ⎪⎝⎭ 对称轴的距离近， ∴y 1>y 2，所以④正确． 故选B ．【点睛】本题考查了二次函数图象与系数的关系：对于二次函数y=ax 2+bx+c （a≠0），二次项系数a 决定抛物线的开口方向和大小，当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时（即ab ＞0），对称轴在y 轴左； 当a 与b 异号时（即ab ＜0），对称轴在y 轴右；常数项c 决定抛物线与y 轴交点：抛物线与y 轴交于（0，c ）；抛物线与x 轴交点个数由△决定：△=b 2-4ac ＞0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点．11．在同一平面直角坐标系中，函数y=ax 2+bx 与y=bx+a 的图象可能是（ ）A ．B ．C ．D ．【答案】C【解析】试题解析：A 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，对称轴x=﹣2b a＜0，应在y 轴的左侧，故不合题意，图形错误． B 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＜0；而对于抛物线y=ax 2+bx 来说，图象应开口向下，故不合题意，图形错误．C 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，对称轴x=﹣2b a位于y 轴的右侧，故符合题意， D 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，a ＜0，故不合题意，图形错误．故选C．考点：二次函数的图象；一次函数的图象．12．若二次函数y＝ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M（x0，y0）在x轴下方，对于以下说法：①b2﹣4ac＞0②x＝x0是方程ax2+bx+c＝y0的解③x1＜x0＜x2④a（x0﹣x1）（x0﹣x2）＜0其中正确的是（）A．①③④B．①②④C．①②③D．②③【答案】B【解析】【分析】①根据二次函数图象与x轴有两个不同的交点，结合根的判别式即可得出△=b2-4ac＞0，①正确；②由点M（x0，y0）在二次函数图象上，利用二次函数图象上点的坐标特征即可得出x=x0是方程ax2+bx+c=y0的解，②正确；③分a＞0和a＜0考虑，当a＞0时得出x1＜x0＜x2；当a＜0时得出x0＜x1或x0＞x2，③错误；④将二次函数的解析式由一般式转化为交点式，再由点M（x0，y0）在x轴下方即可得出y0=a（x0-x1）（x0-x2）＜0，④正确．【详解】①∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），且x1＜x2，∴方程ax2+bx+c=0有两个不相等的实数根，∴△=b2-4ac＞0，①正确；②∵图象上有一点M（x0，y0），∴a+bx0+c=y0，∴x=x0是方程ax2+bx+c=y0的解，②正确；③当a＞0时，∵M（x0，y0）在x轴下方，∴x1＜x0＜x2；当a＜0时，∵M（x0，y0）在x轴下方，∴x0＜x1或x0＞x2，③错误；④∵二次函数y=ax2+bx+c（a≠0）的图象于x轴的交点坐标分别为（x1，0），（x2，0），∴y=ax2+bx+c=a（x-x1）（x-x2），∵图象上有一点M（x0，y0）在x轴下方，∴y0=a（x0-x1）（x0-x2）＜0，④正确；故选B．【点睛】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及二次函数图象与系数的关系，根据二次函数的相关知识逐一分析四条结论的正误是解题的关键．13．已知二次函数y＝ax2＋bx＋c的图像如图所示，则下列结论正确的个数有（）①c ＞0；②b 2－4ac ＜0；③ a －b ＋c ＞0；④当x ＞－1时，y 随x 的增大而减小．A ．4个B ．3个C ．2个D ．1个【答案】C【解析】【分析】 由抛物线的开口方向判断a 与0的关系，由抛物线与y 轴的交点判断c 与0的关系，然后根据抛物线与x 轴交点及x=-1时二次函数的值的情况进行推理，进而对所得结论进行判断．【详解】解：由图象可知，a ＜0，c ＞0，故①正确；抛物线与x 轴有两个交点，则b²-4ac>0,故②错误;∵当x=-1时，y>0,即a-b+c>0， 故③正确;由图象可知，图象开口向下，对称轴x ＞-1，在对称轴右侧， y 随x 的增大而减小，而在对称轴左侧和-1之间，是y 随x 的增大而减小，故④错误．故选：C ．【点睛】本题考查了二次函数图象与系数的关系：二次项系数a 决定抛物线的开口方向和大小．当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置：当a 与b 同号时，对称轴在y 轴左； 当a 与b 异号时，对称轴在y 轴右．常数项c 决定抛物线与y 轴交点：抛物线与y 轴交于（0，c ）．抛物线与x 轴交点个数由判别式确定：△=b 2-4ac ＞0时，抛物线与x 轴有2个交点；△=b 2-4ac=0时，抛物线与x 轴有1个交点；△=b 2-4ac ＜0时，抛物线与x 轴没有交点．14．二次函数2(,,y ax bx c a b c =++为常数，且0a ≠)中的x 与y 的部分对应值如表： x ···1- 0 1 3 ··· y··· 1- 3 53 ··· 下列结论错误的是( )A ．0ac <B ．3是关于x 的方程()210ax b x c +-+=的一个根；C ．当1x >时，y 的值随x 值的增大而减小；D ．当13x -<<时，()210.ax b x c +-+>【答案】C【解析】【分析】根据函数中的x 与y 的部分对应值表，可以求得a 、b 、c 的值 然后在根据函数解析式及其图象即可对各个选项做出判断．【详解】解：根据二次函数的x 与y 的部分对应值可知：当1x =-时，1y =-，即1a b c -+=-，当0x =时，3y =，即3c =，当1x =时，5y =，即5a b c ++=，联立以上方程：135a b c c a b c -+=-⎧⎪=⎨⎪++=⎩，解得：133a b c =-⎧⎪=⎨⎪=⎩，∴233y x x =-++；A 、1330=-⨯=-<ac ，故本选项正确；B 、方程()210ax b x c +-+=可化为2230x x -++=， 将3x =代入得：232339630-+⨯+=-++=，∴3是关于x 的方程()210ax b x c +-+=的一个根,故本选项正确； C 、233y x x =-++化为顶点式得：2321()24=--+y x ， ∵10a =-<，则抛物线的开口向下， ∴当32x >时，y 的值随x 值的增大而减小；当32x <时，y 的值随x 值的增大而增大；故本选项错误； D 、不等式()210ax b x c +-+>可化为2230x x -++>，令2y x 2x 3=-++， 由二次函数的图象可得：当0y >时，13x -<<，故本选项正确；故选：C ．【点睛】本题考查了待定系数法求二次函数解析式、二次函数的性质、二次函数与不等式的关系，根据表中数据求出二次函数解析式是解题的关键．15．已知二次函数2()y x h =-- (h 为常数),当自变量x 的值满足25x ≤≤时,与其对应的函数值y的最大值为-1,则h的值为( )A．3或6 B．1或6 C．1或3 D．4或6【答案】B【解析】分析：分h＜2、2≤h≤5和h＞5三种情况考虑：当h＜2时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论；当2≤h≤5时，由此时函数的最大值为0与题意不符，可得出该情况不存在；当h＞5时，根据二次函数的性质可得出关于h的一元二次方程，解之即可得出结论．综上即可得出结论．详解：如图，当h＜2时，有-（2-h）2=-1，解得：h1=1，h2=3（舍去）；当2≤h≤5时，y=-（x-h）2的最大值为0，不符合题意；当h＞5时，有-（5-h）2=-1，解得：h3=4（舍去），h4=6．综上所述：h的值为1或6．故选B．点睛：本题考查了二次函数的最值以及二次函数的性质，分h＜2、2≤h≤5和h＞5三种情况求出h值是解题的关键．16．如图1，△ABC中，∠A＝30°，点P从点A出发以2cm/s的速度沿折线A→C→B运动，点Q从点A出发以vcm/s的速度沿AB运动，P，Q两点同时出发，当某一点运动到点B 时，两点同时停止运动．设运动时间为x（s），△APQ的面积为y（cm2），y关于x的函数图象由C1，C2两段组成，如图2所示，有下列结论：①v＝1；②sin B＝13；③图象C2段的函数表达式为y＝﹣13x2+103x；④△APQ面积的最大值为8，其中正确有（）A．①②B．①②④C．①③④D．①②③④【答案】A【解析】【分析】①根据题意列出y＝12AP•AQ•sin A，即可解答②根据图像可知PQ同时到达B，则AB＝5，AC+CB＝10，再代入即可③把sin B＝13，代入解析式即可④根据题意可知当x＝﹣522ba=时，y最大＝2512【详解】①当点P在AC上运动时，y＝12AP•AQ•sin A＝12×2x•vx＝vx2，当x＝1，y＝12时，得v＝1，故此选项正确；②由图象可知，PQ同时到达B，则AB＝5，AC+CB＝10，当P在BC上时y＝12•x•（10﹣2x）•sin B，当x＝4，y＝43时，代入解得sin B＝13，故此选项正确；③∵sin B＝13，∴当P在BC上时y＝12•x（10﹣2x）×13＝﹣13x2+53x，∴图象C2段的函数表达式为y＝﹣13x2+53x，故此选项不正确；④∵y＝﹣13x2+53x，∴当x＝﹣522ba=时，y最大＝2512，故此选项不正确；故选A．【点睛】此题考查了二次函数的运用，解题关键在于看图理解17．已知抛物线y=x2-2mx-4（m＞0）的顶点M关于坐标原点O的对称点为M′，若点M′在这条抛物线上，则点M的坐标为（）A ．（1，-5）B ．（3，-13）C ．（2，-8）D ．（4，-20）【答案】C【解析】【分析】【详解】 解：22224=()4y x mx x m m =-----，∴点M （m ，﹣m 2﹣4），∴点M′（﹣m ，m 2+4），∴m 2+2m 2﹣4=m 2+4．解得m=±2．∵m ＞0，∴m=2，∴M （2，﹣8）． 故选C ．【点睛】本题考查二次函数的性质．18．在函数2y x=，3y x =+，2y x =的图象中，是中心对称图形，且对称中心是原点的图象共有（ ）A ．0个B ．1个C ．2个D ．3个【答案】B【解析】【分析】根据中心对称图形的定义与函数的图象即可求解．【详解】 y=x+3的图象是中心对称图形，但对称中心不是原点；y=x 2图象不是中心对称图形；只有函数2y x=符合条件． 故选：B ．【点睛】 本题考查函数的图象性质与中心对称图形的性质，熟练掌握相关知识是解题的关键．19．如图，抛物线y =ax 2+bx +c （a ≠0）与x 轴交于（-1，0），（3，0）两点，则下列说法：①abc ＜0；②a -b +c =0；③2a +b =0；④2a +c ＞0；⑤若A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）为抛物线上三点，且-1＜x 1＜x 2＜1，x 3＞3，则y 2＜y 1＜y 3，其中正确的结论是（ ）A ．①⑤B ．②④C ．②③④D ．②③⑤【答案】D【解析】【分析】①abc ＜0，由图象知c ＜0，a 、b 异号，所以，①错误；②a -b+c=0，当x=-1时，y=a-b+c=0，正确；③2a+b=0，函数对称轴x=-2b a=1，故正确；④2a+c ＞0，由②、③知：3a+c=0，而-a ＜0，∴2a+c ＜0，故错误；⑤若A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）为抛物线上三点，且-1＜x 1＜x 2＜1，x 3＞3，则y 2＜y 1＜y 3，把A 、B 、C 坐标大致在图上标出，可知正确．【详解】解：①abc ＜0，由图象知c ＜0，a 、b 异号，所以，①错误；②a -b+c=0，当x=-1时，y=a-b+c=0，正确；③2a+b=0，函数对称轴x=-2b a=1，故正确； ④2a+c ＞0，由②、③知：3a+c=0，而-a ＜0，∴2a+c ＜0，故错误；⑤若A （x 1，y 1），B （x 2，y 2），C （x 3，y 3）为抛物线上三点，且-1＜x 1＜x 2＜1，x 3＞3，则y 2＜y 1＜y 3，把A 、B 、C 坐标大致在图上标出，可知正确；故选D ．【点睛】考查图象与二次函数系数之间的关系，要会求对称轴、x=±1等特殊点y 的值．20．已知二次函数y ＝ax 2+bx+c 的图象如图所示，下列结i 论：①abc ＞0；②b 2﹣4ac ＞0；③2a+b ＝0；④a ﹣b+c ＜0．其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C【解析】【分析】 首先根据开口方向确定a 的取值范围，根据对称轴的位置确定b 的取值范围，根据抛物线与y 轴的交点确定c 的取值范围，根据抛物线与x 轴是否有交点确定b 2﹣4ac 的取值范围，根据x ＝﹣1函数值可以判断．【详解】解：Q 抛物线开口向下，0a ∴<，Q 对称轴12b x a=-=， 0b ∴>，Q 抛物线与y 轴的交点在x 轴的上方，0c ∴>，0abc ∴<，故①错误；Q 抛物线与x 轴有两个交点，240b ac ∴->，故②正确；Q 对称轴12b x a=-=， 2a b ∴=-， 20a b ∴+=，故③正确；根据图象可知，当1x =-时，0y a b c =-+<，故④正确；故选：C ．【点睛】此题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用是解题关键．。