2011年宁波大学考博真题 随机过程
宁波大学3812光通信理论与技术2010--2013,2015--2019年考博初试专业课真题
宁波大学2019年博士研究生招生考试初试试题(A卷)
(答案必须写在考点提供的答题纸上)
科目代码：3812总分值：100科目名称：光通信理论与技术
一、计算题(共70分)
1．（15分）设想一根30km长的光纤，在波长1300nm处的衰减为0.8dB/km，如果我们从一端注入功率为200μW的光信号，求其输出功率P out。
2．（15分）一峰值发光波长在800nm的GaAs激光器，其谐振腔长400μm，且材料折射率为n=3.6，如果增益g为750nm<λ<850nm的范围内都大于总损耗系数αt，试求此激光器中能存在多少个模式？
3．（15分）一段12km长的光纤线路，其损耗为1.5dB/km：
a)如果在接收端保持0.3μW的接收光功率，则发送端的功率至少为多少？
b)如果光纤的损耗变为2.5dB/km，则所需的输入光功率又为多少？
4．（15分）有一长距离单模光纤传输系统，工作波长为1300nm，其它参数如下：
LD光源平均入纤功率：0dBm；光缆损耗：0.5dB/km；熔接头损耗：0.1dB/km；
活动连接器损耗（2个）：0.5dB/个；APD接收机灵敏度：-55dBm(BER=10-9)；
系统富余度：12dB。
试求损耗限制传输的距离。
5．（10分）计算n1=1.48及n2=1.46的阶跃折射率光纤的数值孔径。
如果光纤端面外介质折射率n=1.00，则允许的最大入射角θmax为多少？
二、简答题（共30分）
1．（15分）简述引起单模光纤色散的原因，在光通信系统中如何克服这些色散对带宽带来的影响。
2．（15分）简述模间色散的时域测量方法及工作原理，并画出该方法的原理框图。
第1页共1页。
宁波大学3802机械振动2009,2011,2014,2016--2018年考博初试专业课真题
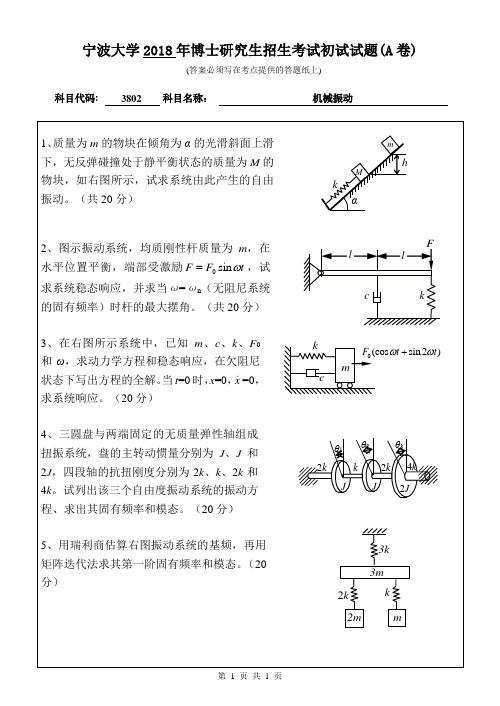
波形，可表示为 y Y sin 2 x ，其中 Y=4cm，L=10m，如右 L
图所示，求小车在以水平速度 v=36km/h 行驶时，车身上下振 动的振幅。（18 分）
4、在右图所示系统中，质量受到一常值力 F0 的作用，试用杜 哈梅积分求出零初值条件下的运动规律。（12 分）
F
l
l
c
k
k
F0 (cost sin 2t)
m c
θ1 θ2
θ3
2k
k 2k 4k
J
J 2J
3k
3m
2k
k
2m
m
第1页共1页
考试科目: 适用专业:
宁波大学 2014 年攻读博士学位研究生
入 学 考 试 试 题(A 卷) (答案必须写在答题纸上)
机械振动 工程力学
科目代码： 3802
1、如右图所示 4 个系统，已知弹簧的刚度、轴 的抗扭刚度、悬臂梁端的等效弹簧刚度、圆盘的 转动惯量、物块质量等，分别写出其动力学方程， 并求其固有频率。（每个 5 分，共 20 分）
分）
θ1
θ2
k
k
J
4J 7k
6、用矩阵迭代法计算右图所示系统的基频和第 一阶振型。（18 分）
k
2k
3k
k
m
2m
3m
第1页共1页
宁波大学 2017 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码 : 3802 科目名称：
机械振动
1、右图所示单摆，摆杆质量忽略不计。求系统微幅 振动的动力学方程和通解；设摆杆初始偏角为θ0， 初速度为零，求系统的振动。（16 分）
（完整版）随机过程习题答案
（完整版）随机过程习题答案随机过程部分习题答案习题22.1 设随机过程b t b Vt t X ),,0(,)(+∞∈+=为常数，)1,0(~N V ，求)(t X 的⼀维概率密度、均值和相关函数。
解因)1,0(~N V，所以1,0==DV EV ，b Vt t X +=)(也服从正态分布，b b tEV b Vt E t X E =+=+=][)]([ 22][)]([t DV t b Vt D t X D ==+=所以),(~)(2t b N t X ，)(t X 的⼀维概率密度为),(,21);(222)(+∞-∞∈=--x ett x f t b x π，),0(+∞∈t均值函数 b t X E t m X ==)]([)(相关函数)])([()]()([),(b Vt b Vs E t X s X E t s R X ++==][22b btV bsV stV E +++=2b st +=2.2 设随机变量Y 具有概率密度)(y f ，令Yt e t X -=)(，0,0>>Y t ，求随机过程)(t X 的⼀维概率密度及),(),(21t t R t EX X 。
解对于任意0>t，Yt e t X -=)(是随机变量Y 的函数是随机变量，根据随机变量函数的分布的求法，}ln {}{})({);(x Yt P x e P x t X P t x F t Y ≤-=≤=≤=-)ln (1}ln {1}ln {tx F t x Y P t x Y P Y --=-≤-=-≥= 对x 求导得)(t X 的⼀维概率密度xtt x f t x f Y 1)ln ();(-=，0>t)(][)]([)(dy y f e eE t X E t m yt tY X相关函数+∞+-+---====0)()(2121)(][][)]()([),(212121dy y f e e E e e E t X t X E t t R t t y t t Y t Y t Y X 2.3 若从0=t 开始每隔21秒抛掷⼀枚均匀的硬币做实验，定义随机过程=时刻抛得反⾯时刻抛得正⾯t t t t t X ,2),cos()(π试求：（1）)(t X 的⼀维分布函数),1(),21(x F x F 和；（2）)(t X 的⼆维分布函数),;1,21(21x x F ；（3）)(t X 的均值)1(),(X X m t m ，⽅差 )1(),(22X Xt σσ。
宁波大学随机过程2009--2020年考博初试真题
之间的关系是______________________，高斯随机过程通过线性系统后是否还是高斯随机过 程？
4. 若平稳随机过程 X(t) 的自相关函数为 Rx ( ) _________________。
a2 cos 3
，则其平均功率 1 2
Sx ( )d ＝
第1页共3页
宁波大学 2020 年博士研究生招生考试初试试题(B 卷)
3． 假 设 两 个 相 互 独 立 的 随 机 变 量 X 、Y 服 从 正 态 分 布 N (m1, s12) 和 N (m2, s22) ， 则 随 机 变 量 Z = X + 2Y 服从_________分布。若令W [X,Y ]T ，则W 的协方差矩阵为_________。
j
=
2
sin
q
+ 2
j·cos
q
2
j
cos
q
+
cos
j
=
2
cos
+ 2
j·cos
q
2
j
一、概念题（每题 4 分，共 40 分）
sin a sin b
=
-
1 2
cos (a
+
b)-
cos (a
- b)
cos a cos b
=
1 2
cos (a
+
b) +
cos (a
- b)
sin
q
-
sin
j
=
2
cos
宁波大学 2020 年博士研究生招生考试初试试题(B 卷)
(答案必须写在考点提供的答题纸上)
科目代码： 2603 总分值： 100 科目名称：
随机过程习题解答第1,2章
习题11. 令X(t)为二阶矩存在的随机过程，试证它是宽平稳的当且仅当EX(s)与E[X(s)X(s+t)]都不依赖s.证明：充分性：若X(t)为宽平稳的，则由定义知EX(t)=μ， EX(s)X(s+t)=r(t) 均与s 无关必要性：若EX(s)与EX(s)X(s+t)都与s 无关，说明EX(t)=常数， EX(s)X(s+t)为t 的函数2. 记1U ，．．．，n U 为在（０,１）中均匀分布的独立随机变量，对0 < t , x < 1定义I( t , x)=⎩⎨⎧>≤，，，，t x t x 01并记X(t)=),(11∑=nk k U t I n ，10≤≤t ，这是1U ，．．．，n U 的经验分布函数。
试求过程X （t ）的均值和协方差函数。
解： EI ()k U t ,= P ()t U k ≤= t ， D()),(k U t I = EI ()k U t ,－()2),(kU t EI= t －2t = t(1－t)j k ≠， cov ()),(),(j k U s I U t I ，=EI(t,k U )I(s,j U )－EI(t, k U )EI(s, j U ) = st －st=0k = j ， cov ()),(),(j k U s I U t I ，= EI(t,k U )I(s,j U )－st = min(t,s)－stEX(t)=),(11∑=n k k U t EI n =∑=nk tn 11= tcov ())(),(s X t X =()()),(),,(cov 1),(),,(cov 1212j kjk nk k k U s I Ut I n U s I U t I n ∑∑≠=+=[]∑=nk st t s n12),min(1－=()st t s n－),min(13.令1Z ，2Z 为独立的正态分布随机变量，均值为0，方差为2σ，λ为实数，定义过程()t Sin Z t Cos Z t X λλ21+=.试求()t X 的均值函数和协方差函数，它是宽平稳的吗？Solution: ()221,0~,σN Z Z . 02221==EZ EZ .()()221σ==Z D Z D ，()0,21=Z Z Cov ,()0=t EX ，()()()()()[]s Sin Z s Cos Z t Sin Z t Cos Z E s X t X Cov λλλλ2121,+⋅+=[]t C o s S i n Z Z s t S i n C o s Z Z s t S i n S i n Z t C o s C o s Z E λλλλλλλλ12212221+++=()02++=s t S i n S i n s t C o s C o s λλλλσ =()[]λσs t Cos -2(){}t X 为宽平稳过程.4.Poisson 过程()0,≥t t X 满足（i ）()00=X ；(ii)对s t >，()()s X t X -服从均值为()s t -λ的Poisson 分布；（iii ）过程是有独立增量的.试求其均值函数和协方差函数.它是宽平稳的吗？Solution ()()()()t X t X E t EX λ=-=0，()()t t X D λ= ()()()()()s t s X t EX s X t X Cov λλ⋅-=,()()()()()ts s EX s X s X t X E 22λ-+-= ()()()()ts s EX s X D 220λ-++=()ts s s 22λλλ-+=()t s s λλλ-+=1 显然()t X 不是宽平稳的.5. ()t X 为第4题中的Poisson 过程，记()()()t X t X t y -+=1，试求过程()t y 的均值函数和协方差函数，并研究其平稳性. Solution ()λλ=⋅=1t Ey , ()()λ=t y DCov(y(t),y(s))=Ey(t)y(s)-Ey(t)y(s)=E(x(t+1)-x(t))(x(s+1)-x(s))-λ2(1)若s+1<t, 即s≤t-1，则Cov(y(t),y(s))=0-λ2=-λ2(2)若t<s+1≤t+1, 即t>s>t-1, 则Cov(y(t),y(s))=E[x(t+1)-x(s+1)+x(s+1)-x(t)][x(s+1)-x(t)+x(t)-x(s)] -λ2=E(x(t+1)-x(s+1))(x(s+1)-x(t))+E(x(t+1)-x(s+1))(x(t)-x(s))+E(x(s+1)-x(t))+E(x(s+1)-x(t))(x(t)-x(s))- λ2=λ(s+1-t)= λ-λ(t-s)- λ2(3) 若t<s<t+1Cov(y(t),y(s))= E [x(t+1)-x(s)+x(s)-x(t)] [x(s+1)-x(t+1)+x(t+1)-x(s)]- λ2 =(x(t+1)-x(s))(x(s+1)-x(t+1))+E(x(t+1)-x(s))(x(t+1)-x(s))+E(x(s)-x(t))(x(s+1)-x(t+1))+E(x(s)-x(t))(x(t+1)-x(s))- λ2=0+λ(t+1-s)+0-λ2=λ+λ(t-s)- λ2(4) 若s>t+1 Cov(y(t),y(s))=0-λ2=-λ2由此知，故方差只与t-s有关，与t,s无关故此过程为宽平稳的。
宁波大学概率论与数理统计2015--2020年考博初试真题
8. 随机地从一批零件中抽取 16 个，测得长度 为：2.14，2.10，2.13，2.15，2.13，2.12，2.13，
2.10，2.15，2.12，2.14，2.10，2.13，2.11，2.14，2.11，设零件长度分布为正态分布，若 0.01， 试求总体 的 90％的置信区间。已知： z0.05 1.645 （10 分）
4. (15 分) 设(X,Y)的概率密度是:
f
(x,
y)
Ay(1
x),
0 x 1, 0 y x
0,
其它
求f x y
5. (15 分)
设 X 的概率密度为
f (x)
1 e x 2
,
x ,，求随机变量 X 的数学 X~N(22.40,0.032),气缸的直径 Y~N（22.50，0.042），X，Y 相互独立， 任取一个活塞，任取一只气缸，求活塞能装入气缸的概率。Ф(2)=0.9772.
6. 在总体 X~N(52,6.32)中抽取容量为 36 的样本，求样本均值落在 50.8 至 53.8 之间的的概 率。（计算结果以标准正态分布函数表示即可）（12 分）
7. 随机地取某零件 6 只，测得它们的直径（mm）为：9.01, 9.03,9.00, 8.98, 8.96, 9.02。试求 μ 和 σ2 的矩估计值。 （15 分）
（1）这两颗花籽都发芽的概率
（5 分）
（2）至少有一颗能发芽的概率
（5 分）
（3）恰有一颗能发芽的概率
（5 分）
2. (15 分)
设
X 的概率密度为
f
X
(
x)
x
/
8, 0,
0 x 其它
4
宁波大学2019(信息学院)博士研究生入学考试2603随机过程初试试卷(B卷)
(答案必须写在考点提供的答题纸上)科目代码：2603总分值：100科目名称：随机过程本试题可能用到的公式：积化和差：()()1sin cos sin sin 2a b a b a b =++-()()1sin sin cos cos 2a b a b a b =-+--()()1cos sin sin sin 2a b a b a b =+--()()1cos cos cos cos 2a b a b a b =++-和差化积：sin sin 2sin cos 22q j q j q j +-+=·sin sin 2cos sin 22q j q j q j +--=·cos cos 2cos cos 22q j q j q j +-+=·cos cos 2sin sin 22q j q j q j +--=-·一、概念题（每题4分，共40分）1．随机过程的样本函数是____。
a.随机函数 b.确定的时间函数 c.随机变量的函数。
2．设随机变量X 的均值为3，方差为2。
现定义新的随机变量为622Y X =-+，则[]E XY =____________；X 与Y 相关还是不相关_________。
3．假设两个相互独立的随机变量X 、Y 服从正态分布211(,)N m s 和222(,)N m s ，则随机变量=+2Z X Y 服从_________分布。
若令=[,]T W X Y ，则W 的协方差矩阵为_________。
4．若线性系统的输入为平稳随机过程，则输出随机过程是否平稳？____________；若输入与输出过程分别为()X t 和()Y t ，系统相应为()h t .写出输出过程自相关函数与输入过程自相关函数之间的关系。
________________________5．各态历经过程是平稳随机过程，对吗？__________________。
各态历经过程的两个条件分别是_________________________和_________________________。
宁波大学2605光电子学2011--2013,2015--2019年考博初试专业课真题
(答案必须写在考点提供的答题纸上)
科目代码： 2605 总分值： 100 科目名称：
一、选择题（30 分 每题 3 分）
光电子学
1. 下列各种特性中哪个特性可以概括激光的本质特性（ ）
A. 单色性 B. 相干性 C. 高光子简并度 D. 方向性
请计算如下参数：
（1）该激光器可能输出的纵模有多少个？
（2）中心频率 v0 对应的纵模序数 q 值分别是多少？
（3）为了获得单纵模输出，腔长最长为多少？
四、 设计题（20 分）
试分析光电鼠标的工作原理和主要模块功能，要求：画出光电鼠标的工作原理图或框图，并 说明每一部分的主要工作原理；白色光电鼠标点与黑色光电鼠标垫在光电鼠标使用效果上是否有 区别？为什么？如何才能有效的提高光电鼠标的灵敏度和精确度？
二、 计算题：(共 30 分)
1. 已知三能级激光系统(如下图)，其能级间各跃迁的几率分别为：无辐射跃迁 S32=5×106s-1， S21≈0；自发发射 A31=3×106s-1， A21=3×102s-1。激光上下能级的统计权重均为3，腔内只存在一个 振荡模，不计光的各种损耗。（12分） (1) 说明闪光灯泵浦情况下该激光器的激光形成过程；(2分) (2) 请列出完整的速率方程组；(5分) (3) 稳态情况下，如果介质激光上下能级粒子数相等，则 W13 应为多少？(5 分)
C. 2> 3>1
D. 3> 2>1
E
n3，3
n2，2
n1，1
n0 n
5. 关于高斯光束的说法，不正确的是（ ）
A. 束腰处的等相位面是平面
B. 无穷处的等相位面是平面
宁波大学信息功能材料2013,2015--2020年考博初试真题
二、判断题：本大题共 10 小题，每小题 2 分，共 20 分，对的打√，错的打。
1. 电子和空穴的移动都能形成电流。（ ） 2. 金属与半导体导电机制的区别在于：金属由自由电子导电，半导体由非平衡载流子导电。（ ） 3. 费米能级物理意义是指：该能级上的一个状态被电子占据的几率是 1/2。（ ） 4. 四能级固体激光器比三能级或准三能级激光器容易产生振荡发射。（ ） 5. 掺铒碲化物光纤放大器具有超宽的增益带宽特性，其增益带宽可达 80nm，特别适合于 DWDM
三、简答计算题：共 50 分，第 1 题 15 分，第 2 题 20 分，第 3 题 15 分。
1. 平衡 p-n 结的空间电荷区示意图如下，画出空间电荷区中载流子漂移运动和扩散运动的方向（在下图 右侧直线上添加箭头），并说明扩散电流和漂移电流之间的关系。
2. 光纤按照制作材料、折射率分布形式以及光波模式的不同来划分，各分为哪些类型? 一阶跃光纤 n1 ＝1.5，n2＝1.498，工作波长 1.32m，试求： (1)单模传输时光纤的纤芯半径是多少? (2)此光纤的数值孔径是多大?
（A）辐射跃迁；（B）非辐射跃迁；（C）受激辐射；（D）自发辐射
2. 在绝对零度下，可以被电子填满的最高能带为（ ） （A）导带；（B）价带；（C）禁带；（D）带隙
3. 激光晶体 YAG 是指（ ）。 （A）蓝宝石；（B）钇铝石榴石；（C）钇镓石榴石；（D）钆镓石榴石
4. 目前，通信用光纤的纤芯和包层构成的材料绝大多数是（ ）。 （A）多成分玻璃；（B）石英和塑料；（C）石英；（D）塑料
（D）灵敏度比致冷型高很多
研究生《随机过程》考试题
随机过程考试题（2009）一，（12分）已知12,X X 为独立同指数分布(1)EXP 的随机变量。
（1） 证明12X X +与112X X X +独立；（2） 令112212,Y X X Y X X =+=-,求12,Y Y 的联合概率密度. 二，（10分）设随机变量X 的分布律为{}11,0,1,2,.2x P X x x +=== 令 (){}min ,,0,1,2,.X n X n n ==求随机过程(){},0X X n n =≥的一维分布律及均值函数. 三，（12分）设(){},0N N t t =≥的强度为0λ>的Possion 过程， （1） 证明：若0,1s t n <<≥，则()(){}1kn kk n s s P N s k N t n C t t -⎛⎫⎛⎫===- ⎪⎪⎝⎭⎝⎭（2） 设随机变量T 与N 相互独立，且{},0.tP T t et μ->=>证明：(){},0,1,2,.kP N t k k μμλμλμ⎛⎫===⎪++⎝⎭四，（12分）设Markov 链的状态空间{}1,2,3S =，初始分布(){}014,12,14π=，一步转移概率矩阵为11124411022010⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭P 求：（1） 二步转移概率矩阵()2P（2） ()(){}22,42;P X X == （3） ()()321.E X X ⎡⎤=⎣⎦设Markov 链的状态空间{}1,2,3,4,5S =,一步转移概率矩阵为113001312140140000100010000001⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭P（1） 画出状态转移图；（2） 指出哪些是非常返态？哪些是常返态？ （3） 求常返态的周期及平均回转时间； （4） 给出状态空间S 的分解。
六（12分）设(){},X t t -∞<<+∞是均方可导的平稳过程，其自相关函数为{}.X R τ令 ()(),dX t Y t t dt=-∞<<+∞（1） 求()Y t 的自相关函数（2） 问(){},Y t t -∞<<+∞是否为平稳过程？为什么？ 七，（12分）已知下列平稳过程X 的相关函数为{}.X R τ（相应地，谱密度()X S ω），求X 的谱密度（相应地，相关函数）： （1）{}()()4cos 3X R ecos ττπττ-=+（2）()()651,15150,15X S ωδωωωω⎧⎛⎫+-≤⎪ ⎪=⎨⎝⎭⎪>⎩（已知：()()()()11000cos ;12;fff f ωτπδωωδωωπδω---++⎡⎤⎣⎦ ()()()()10222200cos 0.f a f aaea aaτωτωωωω--+>-+++ ）八，（8分）设有二阶矩随机变量X 及普通实函数()()f t t -∞<<+∞，证明：若f 在0t t =点可导， 则()()00t t Xf t Xf t ='=⎡⎤⎣⎦设有如图所示的交通网络，流入的为图示强度的Possion 过程（假定各过程独立），而在交会处车辆按图示的概率选择行走方向（假定方向的选择也相互独立）.描述三个出口处的交通的情况.随即过程试题（2006）1， 已知()()123123123,06,,,0x x x x x x e f x x x others -++⎧<<<⎪=⎨⎪⎩112213323,22,y x y x x y x x ==-=-求： （1）123,,y y y 的概率密度（2）1Ey ,1Dy2，设X 的均值函数为()X m t ，自相关函数为()12,X R t t ，用()X m t 和()12,X R t t 来表示()()(),,X X X D t C t t ϕ3，,X Y 两个随机变量均值函数和方差分别为,,,X Y X Y m m δδ,相关系数为ρ，设Z X t Y =+,求()(),Z Z m t R t4，一强度为λ的Passion 过程，求： （1）()(){}P x t m x j n ==（2）若(){}110P N e -==,求()()23E N N ⎡⎤⎣⎦（3或者5）5，设()h x 为平方可积函数。
宁波大学数学物理方程2009--2020年考博初试真题
宁波大学2020年博士研究生招生考试初试试题(A卷)(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)第1页共2页科目代码：2601总分值：100科目名称：数学物理方程计算题（共5题，共100分）1.(20分)一均匀，各向同性的弹性圆膜，四周固定。
只考虑膜的横振动，试给出该定解问题。
（如果将膜割开，则割缝两侧的相互牵引力的线集度称为膜的张力，单位为N/m；本问题中，膜内任一位置其张力被认为相同）。
2.(20分)用分离变量方法解下面定解问题。
(,)(,),0,0(0,)0,(,)0(,0)t xx x u x t u x t x t u t u t u x x ππ=<<>⎧⎪==⎨⎪=⎩3.(20分)利用行波法解定解问题：4.(20分)求解非齐次方程定解问题。
220220(),0,0(0,)(,)(,0)()u u u u x l t t x u t u l t u u x f x αβ⎧∂∂=--<<>⎪∂∂⎪==⎨⎪=⎪⎩上面0,,u βα均为常数，)(x f 为已知函数。
[提示：作变量代换.),(0t e t x v u u β-+=]200000,0cos ,sin 0tt xx t t t x x u a u x t u x u xu ===⎧-=<<∞<<∞⎪⎪==⎨⎪=⎪⎩(答案必须写在考点提供的答题纸上)第2页共2页科目代码：2601总分值：100科目名称：数学物理方程5.(20分)利用Laplace 变换求解下面定解问题分别讨论()1,()cos f t f t t ω==两种情况。
附：2()(0,0)(,0)0,(,0)0,(0,)(),lim (,)0,tt xx t x x u a u f t x t u x u x u t f t u x t →∞⎧=+<<∞>⎪⎪==⎨⎪==⎪⎩科目代码:2601 科目名称： 数学物理方程第 1 页 共 2 页1. (20分) 均匀等截面弹性直杆在一维纵振动时，受摩擦阻力的作用，设杆中单位质量所受的摩阻力与质点的速度大小成正比( 比例系数为β)，试导出其由位移表示的动力学微分方程。
宁波大学细胞生物学2009--2020年考博初试真题
宁波大学2020年博士研究生招生考试初试试题(B卷)(答案必须写在考点提供的答题纸上)(答案必须写在考点提供的答题纸上)科目代码：3816总分值：100科目名称：细胞生物学一、名词解释（每题3分，共30分）1.核仁2.细胞通讯3.脂质体4.细胞培养5.细胞自噬6.信号肽7.端粒8.凋亡小体9.Hayflick界限10.分子开关二、问答题（共55分）1.Na+-K+泵工作原理及生理学意义（8分）2.列举可用于细胞形态结构观察5种显微镜类型及其特定功能。
（7分）3.模式生物的特点是什么？请列举说明模式生物的使用在细胞生物学研究中的作用（7分）4.请简述肌肉收缩原理。
（8分）5.请简述依赖于甘露糖-6-磷酸（M6P）分选途径的溶酶体酶的合成、加工和分选过程。
（10分）6.请简述细胞细胞骨架的类型、功能。
（6分）7.请简述细胞凋亡与坏死的区别是什么?有什么常用方法鉴定细胞凋亡？（9分）三、论述题（共15分）1．简述受体酪氨酸蛋白激酶介导的RTKs-Ras信号通路组成及其功能。
20世纪90年代末，克林顿实验室的一名研究生发现了一种特殊形式的HER2蛋白。
该蛋白与HER2胞外域的一小部分类似，但没有位于细胞和细胞膜内的部分。
因其抗癌作用原理，将之命名为戴默赛特(Dimercept)。
请根据前面所述原理以及下图说明戴默塞特这个抗肿瘤药物作用原理。
（7分）第1页共2页(答案必须写在考点提供的答题纸上)科目代码：3816总分值：100科目名称：细胞生物学2、将鸡红细胞放入数种等渗溶液（0.17mol/L氯化钠、0.17mol/L氯化铵、0.17mol/L硝酸钠、0.12mol/L硫酸钠、0.17mol/L醋酸胺、0.12mol/L草酸铵、0.32mol/L葡萄糖、0.32mol/L乙醇）中，请根据溶血情况，将等渗溶液分组并说明理由。
（8分）第2页共2页宁波大学2018年博士研究生招生考试初试试题(B卷)(答案必须写在考点提供的答题纸上)科目代码: 3816 科目名称：细胞生物学第 1 页共1 页入学考试试题(B卷)(答案必须写在答题纸上)考试科目:细胞生物学科目代码：3816适用专业:水产养殖、渔业资源一、名词解释（每个3分，共30分）1.亲核蛋白（karyophilic protein）2.管家基因(house-keeping genes)3.端粒(telomere)4.接触抑制（contact inhibition）5.分子伴侣（molecular chaperon）6.脂质体（liposome）7.内膜系统(endomembrane system)8.流动镶嵌模型（fluid mosail model）9.原代细胞（primary culture cell）10.细胞连接（cell junction）二、简答题（每个10分，共70分）1.请举出5种用于细胞形态结构观察的研究工具，并指明它们的主要用途。
2013-2015年宁波大学考博真题3809智能系统 A
5. 对 5 个不同省份的发展情况进行调查统计后，得到 以下每个省份 两两间 的距离矩阵： 4 6 1 6 0 0 9 7 3 4 D 6 9 0 10 5 10 0 8 1 7 6 3 5 8 0 试用类平均法 ( 均值 ) 对其进行聚类， 分别给出聚成 2 类和 3 类的结果。 (12%) 6. 对于下图所示的Boltzmann机,假设每个结点的阈值都为0，连接权值如图所示， 如何采用模拟退火(Simulated Annealing)技术,使网络尽快达到系统平衡态? 如 果达到了平衡态，请计算系统处在状态{S1=1,S2=1,S3=1,S4=1}的概率是多少？ 要求给出具体的计算过程。 （13%）
宁波大学 2014 年攻读博士学位研究生 入 学 考 试 试 题(B 卷) (答案必须写在答题纸上)
考试科目: 适用专业: 智能系统 移动计算与人机交互 科目代码： 3809
1. 试设计一个感知器， 将下图中带黑点标志的输入 （001, 101, 110, 111） 与其它输入(000, 010, 011, 100) 区分开来，要求给出详细的感知器结构和具体权值，单元个数尽可能的少。 (10%)
k k
请详细解释这二个计算公式的含义。
第 1 页， 共 3
(12%)
页
宁波大学 2015 年攻读博士学位研究生 入 学 考 试 试 题 (A 卷)
考试科目: 适用专业: 智能系统 (A)
(答案必须写在答题纸上)
科目代码：
3809
移动计算与人机交互
4. 如图所示的特征脸（Eigenfaces）是机器视觉领域中用于人脸图像分析的一组特征 向量，通过主元分析（PCA）得到。请问： （a）进行 PCA 的主要步骤有哪些？ （b）试给出运用 PCA 进行特征脸分析的详细过程，并指出如何进行高维人脸数 据降维。 （14%）