吉林省吉林市朝鲜族中学2014高中数学 3.1.3 概率的基本性质(第1课时)学案
合集下载
3.1.3概率的基本性质

预习导学 课堂讲义 当堂检测
课堂讲义
3.1.3 概率的基本性质
(3)不是互斥事件,当然不可能是对立事件. 理由是:从40张扑克牌中任意抽取1张,“抽出的牌点数为5 的倍数”与“抽出的牌点数大于9”这两个事件可能同时发 生,如抽得牌点数为10,因此,二者不是互斥事件,当然不 可能是对立事件.
预习导学 课堂讲义 当堂检测
()
A.A⊆B
B.A=B
C.A+B表示向上的点数是1或2或3
D.AB表示向上的点数是1或2或3
答案 C
解析 设A={1,2},B={2,3},A∩B={1},A∪B={1,
2,3},∴A+B表示向上的点数为1或2或3.
预习导学 课堂讲义 当堂检测
当堂检测
3.1.3 概率的基本性质
3.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设
A={两次都击中飞机},B={两次都没击中飞机},C={恰
有一弹击中飞机},D={至少有一弹击中飞机},下列关系
不正确的是
()
A.A⊆D
B.B∩D=∅
C.A∪C=D
D.A∪B=B∪D
答案 D
解析 “恰有一弹击中飞机”指第一枚击中第二枚没中或
第一枚没中第二枚击中,“至少有一弹击中”包含两种情
况:一种是恰有一弹击中,一种是两弹都击中,
3.1.3 概率的基本性质
规律方法 1.互斥事件的概率的加法公式P(A∪B)=P(A)+ P(B). 2.对于一个较复杂的事件,一般将其分解成几个简单的 事件,当这些事件彼此互斥时,原事件的概率就是这些简 单事件的概率的和. 3.当求解的问题中有“至多”、“至少”、“最少”等 关键词语时,常常考虑其反面,通过求其反面,然后转化 为所求问题.
高中数学新人教版A版精品教案《3.1.3 概率的基本性质》
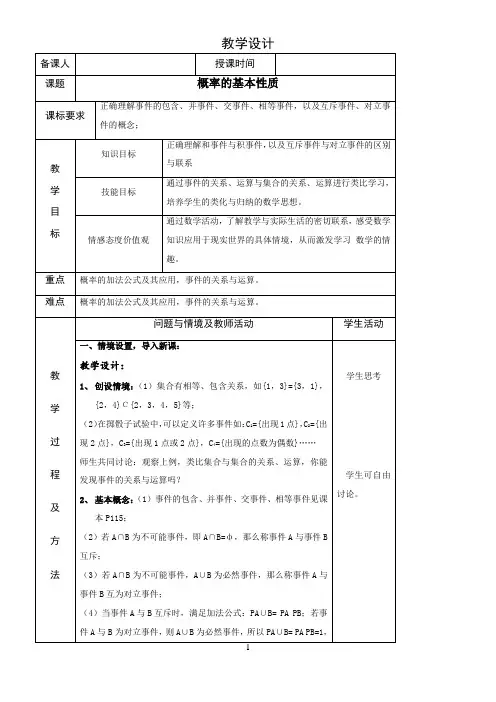
(3)若A∩B为不可能事件,A∪B为必然事件,那么称事件A与事件B互为对立事件;
(4)当事件A与B互斥时,满足加法公式:PA∪B= PA PB;若事件A与B为对立事件,则A∪B为必然事件,所以PA∪B= PA PB=1,于是有PA=1—PB.
3、例题分析:
例1一个射手进行一次射击,试判断下列事件哪些是互斥事件哪些是对立事件
教
学
小
结
课后
反思
3
(2)在掷骰子试验中,可以定义许多事件如:C1={出现1点},C2={出现2点},C3={出现1点或2点},C4={出现的点数为偶数}……
师生共同讨论:观察上例,类比集合与集合的关系、运算,你能发现事件的关系与运算吗?
2、基本概念:(1)事件的包含、并事件、交事件、相等事件见课本P115;
(2)若A∩B为不可能事件,即A∩B=ф,那么称事件A与事件B互斥;
解:记“出现奇数点或偶数点”为事件C,则C=A∪B,因为A、B是互斥事件,所以PC=PA PB= =1
答:出现奇数点或偶数点的概率为1
例3如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:
(1)取到红色牌(率是多少?
通过数学活动,了解教学与实际生活的密切联系,感受数学知识应用于现实世界的具体情境,从而激发学习数学的情趣。
重点
概率的加法公式及其应用,事件的关系与运算。
难点
概率的加法公式及其应用,事件的关系与运算。
教
学
过
程
及
方
法
问题与情境及教师活动
学生活动
一、情境设置,导入新课:
教学设计:
1、创设情境:(1)集合有相等、包含关系,如{1,3}={3,1},{2,4}С{2,3,4,5}等;
(4)当事件A与B互斥时,满足加法公式:PA∪B= PA PB;若事件A与B为对立事件,则A∪B为必然事件,所以PA∪B= PA PB=1,于是有PA=1—PB.
3、例题分析:
例1一个射手进行一次射击,试判断下列事件哪些是互斥事件哪些是对立事件
教
学
小
结
课后
反思
3
(2)在掷骰子试验中,可以定义许多事件如:C1={出现1点},C2={出现2点},C3={出现1点或2点},C4={出现的点数为偶数}……
师生共同讨论:观察上例,类比集合与集合的关系、运算,你能发现事件的关系与运算吗?
2、基本概念:(1)事件的包含、并事件、交事件、相等事件见课本P115;
(2)若A∩B为不可能事件,即A∩B=ф,那么称事件A与事件B互斥;
解:记“出现奇数点或偶数点”为事件C,则C=A∪B,因为A、B是互斥事件,所以PC=PA PB= =1
答:出现奇数点或偶数点的概率为1
例3如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:
(1)取到红色牌(率是多少?
通过数学活动,了解教学与实际生活的密切联系,感受数学知识应用于现实世界的具体情境,从而激发学习数学的情趣。
重点
概率的加法公式及其应用,事件的关系与运算。
难点
概率的加法公式及其应用,事件的关系与运算。
教
学
过
程
及
方
法
问题与情境及教师活动
学生活动
一、情境设置,导入新课:
教学设计:
1、创设情境:(1)集合有相等、包含关系,如{1,3}={3,1},{2,4}С{2,3,4,5}等;
吉林省伊通满族自治县第三中学校高中数学必修三课件:3-1-3概率的基本性质(第一课时)

但精通赌博的梅尔认为他赢的可能性大,所以他应 该得全部赌金,于是,他们请求数学家帕斯卡评判。 帕斯卡得到答案后,又求教于数学家费尔马。他 们的一致裁决是:保罗应分3枚金币,梅尔应分9枚 金币。 帕斯卡是这样解决的:如果再玩一局,或是梅尔胜, 或是保罗胜。如梅尔胜,那么他可以得到全部金币 (记为1);如果保罗胜,那么两人各胜两局,应各得金 币的一半(记为1/2)。由于这一局中两人获胜的可 能性相等,因此梅尔得金币的可能性应是两种可能 性大小的一半,另一半为保罗所有,即梅尔为 (1+1/2)/2=3/4,保罗为(0+1/2)/2=1/4。所以他们各 得9枚和3枚金币。
注:不可能事件记作 ,任何事件都包括不可能事件。
事件的关系和运算: (2)相等关系
一般地,对事件A与事件B若 B A且A B , 那么称事件A与事件B相等,记作A=B 。
BA
例. 事件 C1 ={ 出现1 点 }发生,则事件 D1 ={出现的 点数不大于 1 }就一定会发生,反过来也一样,所以 C1=D1。
一.事件的关系与运算
在掷骰子的试验中,我们可以定义许多事件,如: C1 ={ 出现 1 点 };C2 ={出现 2 点};C3 ={ 出现 3 点 }; C4 ={ 出现 4 点 };C5 ={出现 5 点};C6 ={ 出现 6 点 }; D1 ={ 出现的点数不大于 1 };D2 ={ 出现的点数大于 3 }; D3 ={ 出现的点数小于 5 }; E ={ 出现的点数小于 7 }; F ={ 出现的点数大于 6 }; G ={ 出现的点数为偶数 }; H ={ 出现的点数为奇数 }; …… 思考: 1. 上述事件中有必然事件或不可能事件吗?有的话,哪 些是?
A,B的并事件
事件的关系 (2)并事件(和事件)
高中数学知识素材3.1.3 概率的基本性质

A∪B(或 A+B)
A∩B(或 AB)
图示
若A∩B为不可能事件, A∪B为必然事件,那么 称事件A与事件B互为对 立事件
若A∩B=Ø, 且A∪B=U, 则A与B对 立
图示
定义
表示法
事 并事件 件 的 运 算 交事件
若某事件发生当且仅当事件 A发生或事件B发生,则称此 事件为事件A与事件B的并事 件(或和事件)
若某事件发生当且仅当事 件A发生且事件B发生,则 称此事件为事件A与事件B 的交事件(或积事件)
2.事件的关系与运算
定义表示法Fra bibliotek包含 关系
事 件 的 互斥 关 事件 系
对立 事件
一般地,对于事件A与事件B, 如果事件A发生,则事件B一定 B A(或 发生,这时称事件B包含事件 A B) A(或称事件A包含于事件B)
若A∩B为不可能事件, 则称事件A与事件B互 斥
若A∩B=Ø, 则A与B互 斥
3.1.3 2.概率的基本性质 (1)0≤P(A)≤1; (2)当事件A,B互斥时, P(A∪B)=P(A)+P(B); (3)当事件A,B对立时, P(A∪B)=P(A)+P(B)=1 或P(A)=1-P(B).
2. 一人在打靶中,连续射击两次,事件“至少有一 次中靶”的对立事件是(D ) A.至多有一次中靶 B.两次都中靶 C.只有一次中靶 D.两次都不中靶
高中数学优质课件 3.1.3概率的基本性质

事件A与事件B互为对立事件的含义是:这两个 事件在任何一次试验中有且仅有一个发生。
例如:
M={出现的点数为偶数} N={出现的点数为奇数}
A
B
则有:M与N互为对立事件
概念探究
事件的关系与运算
互斥事件:不可能同时发生的两个事件叫做互斥事件.如
C 1 {出现1点};C 2 {出现2点};C 3 {出现3点} C 4 {出现4点};C 5 {出现5点};C 6 {出现6点}
分析:要判断所给事件是对立还是互斥,首先将两个概念的
联系与区别弄清楚,互斥事件是指不可能同时发生的两事件,
而对立事件是建立在互斥事件的基础上,两个事件中一个不发 生,另一个必发生。
解:A与C互斥(不可能同时发生),B与C互斥,C与D互斥, C与D是对立事件(至少一个发生).
概念探究
事件的关系与运算
若B A,且A B,则称事件A与事件B相等。
例如:
G={出现的点数不大于1}
A={出现1点}
所以有G=A 注:两个事件相等也就是说这两个事件是同一个事件。
概念探究
事件的关系与运算
(3)若某事件发生当且仅当事件发生A或事件B发生, 则称此事件为事件A与事件B的
并事件(或和事件)。记A B(或A+B)
则有:H ∩J=D
概念探究
事件的关系与运算
(4)若A B为不可能事件(A B=),
那么称事件A与事件B互斥。
例如:
A
B
D={出现4点} F={出现6点}
M={出现的点数为偶数} N={出现的点数为奇数}
则有:事件D与事件F互斥
事件M与事件N互斥
概念探究
事件的关系与运算
(5)若A B为不可能事件,A B为必然事件, 那么称事件A与事件B互为对立事件。
高中数学人教版必修三《3.1.3概率的基本性质》课件

3.1.3
概率的基本 性质
数学人教版 高中数学
学习目标
1.正确理解事件的包含、并事件、交事件、相等事件,以及互斥事件、 对峙事件的概念; 2.理解并熟记概率的基本性质; 3.会用概率的性质求某些事件的概率.
摸索 一粒骰子掷一次,记事件A={显现的点数大于4},事件B={显现的 点数为5},则事件B产生时,事件A一定产生吗? 答案 由于5>4,故B产生时A一定产生. 一样地,对于事件A与事件B,如果事件 A 产生,则事件 B 一定产生,这时 称事件B包含事件A(或称事件A包含于事件B),记作 B⊇A (或A⊆B).不可能 事件记为∅,任何事件都包含不可能事件.如果事件A产生,则事件B一定 产生,反之也成立,(若 B⊇A ,且 A⊆B),我们说这两个事件相等,即A =B.
12
例3 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为 0.3,0.2,0.1,0.4. (1)求他乘火车或乘飞机去的概率; 解 记“他乘火车”为事件A,“他乘轮船”为事件B,“他乘汽车”为事件C, “他乘飞机”为事件D. 这四个事件两两不可能同时产生,
故它们彼此互斥,
所以P(A∪D)=P(A)+P(D)=0.3+0.4=0.7. 即他乘火车或乘飞机去的概率为0.7.
3.求复杂事件的概率通常有两种方法: (1)将所求事件转化成彼此互斥事件的并事件; (2)先求其对峙事件的概率,再求所求事件的概率.
谢谢大家
类型一 事件的关系与运算
例1 判定下列各对事件是不是互斥事件,并说明理由. 某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中: (1)“恰有1名男生”和“恰有2名男生”; 解 是互斥事件. 理由是:在所选的2名同学中,“恰有1名男生”实质是选出的是“1名男生和 1名女生”,它与“恰有2名男生”不可能同时产生,所以是一对互斥事件.
概率的基本 性质
数学人教版 高中数学
学习目标
1.正确理解事件的包含、并事件、交事件、相等事件,以及互斥事件、 对峙事件的概念; 2.理解并熟记概率的基本性质; 3.会用概率的性质求某些事件的概率.
摸索 一粒骰子掷一次,记事件A={显现的点数大于4},事件B={显现的 点数为5},则事件B产生时,事件A一定产生吗? 答案 由于5>4,故B产生时A一定产生. 一样地,对于事件A与事件B,如果事件 A 产生,则事件 B 一定产生,这时 称事件B包含事件A(或称事件A包含于事件B),记作 B⊇A (或A⊆B).不可能 事件记为∅,任何事件都包含不可能事件.如果事件A产生,则事件B一定 产生,反之也成立,(若 B⊇A ,且 A⊆B),我们说这两个事件相等,即A =B.
12
例3 某公务员去开会,他乘火车、轮船、汽车、飞机去的概率分别为 0.3,0.2,0.1,0.4. (1)求他乘火车或乘飞机去的概率; 解 记“他乘火车”为事件A,“他乘轮船”为事件B,“他乘汽车”为事件C, “他乘飞机”为事件D. 这四个事件两两不可能同时产生,
故它们彼此互斥,
所以P(A∪D)=P(A)+P(D)=0.3+0.4=0.7. 即他乘火车或乘飞机去的概率为0.7.
3.求复杂事件的概率通常有两种方法: (1)将所求事件转化成彼此互斥事件的并事件; (2)先求其对峙事件的概率,再求所求事件的概率.
谢谢大家
类型一 事件的关系与运算
例1 判定下列各对事件是不是互斥事件,并说明理由. 某小组有3名男生和2名女生,从中任选2名同学去参加演讲比赛,其中: (1)“恰有1名男生”和“恰有2名男生”; 解 是互斥事件. 理由是:在所选的2名同学中,“恰有1名男生”实质是选出的是“1名男生和 1名女生”,它与“恰有2名男生”不可能同时产生,所以是一对互斥事件.
人教A版高中数学必修三3.1.3概率的基本性质
[ 典例 3] 某射击运动员在一次射击中射中 10 环、9 环、8 环、7 环、7 环以下的概率分别为 0.1,0.2,0.3,0.3,0.1. 计算这个运动员在一次射击中:
(1)射中 10 环或 9 环的概率; (2)至少射中 7 环的概率.
[解] 设“射中 10 环”、“射中 9 环”、“射中 8 环”、 “射中 7 环”、“射中 7 环以下”的事件分别为 A,B,C, D,E,则
A
B
例.因为事件C1={出现1点}与事件C2={出现2点}不可能 同时发生,故这两个事件互斥。
事件的关系和运算:
(6)互为对立事件
若A B 为不可能事件,A B为必然事件,那么称事
件A与事件B互为对立事件,其含义是:事件A与事件B在 任何一次试验中有且仅有一个发生。
如图:
A
B
例. 事件G ={出现的点数为偶数}与事件H ={出现的点 数为奇数} 即为互为对立事件。
举一反三
从 40 张扑克牌(红桃、黑桃、方块、梅花点数从 1~10 各 10 张)中任抽取 1 张,判断下列给出的每对事件是否为互斥事件, 是否为对立事件,并说明理由. (1)“抽出红桃”与“抽出黑桃”; (2)“抽出红色牌”与“抽出黑色牌”; (3)“抽出牌的点数为 5 的倍数”与“抽出牌的点数大于 9”. 解:(1)是互斥事件,不是对立事件.理由是:从 40 张扑克牌 中任意抽取 1 张,“抽出红桃”和“抽出黑桃”是不可能同 时发生的,所以是互斥事件.同时,不能保证其中必有一个 发生,这是由于还可能抽出“方块”或者“梅花”,因此二 者不是对立事件.
P(A∪B)=P(A)+P(B) (3)特别地,当事件A与事件B互为对立事件时,
有 P(A)=1- P(B)
3.1.3 概率的基本性质
3.1.3 概率的基本性质
探究:
在掷骰子实验中,可以定义许多事件,
D 1 {出现的点数不大于1};D 2 { 出现的点数大于3}; D 3 {出现的点数小于3}; E {出现的点数小于7};F {出现的点数大于6};; G {出现的点数为偶数};H {出现的点数为奇数};
互斥事件,
所以 P(A)=P(A0)+P(A1)+P(A2)=0.1+0.16+0.3=0.56。
不是互斥事件,也不是对立事件
事件的关系和运算
事件 关系 事件 运算
3.事件的并 (或和)
1.包含关系 2.等价关系
4.事件的交 (或积) 5.事件的互斥 (或互不相容) 6.对立事件 (逆事件)
思考:你能说说互斥事件和对立事件的区别吗?
2.互斥事件与对立事件的区别与联系: 互斥事件是指事件A与事件B在一次试验中 不会同时发生,其具体包括三种不同的情形: (1)事件A发生且事件B不发生;(2)事件A不 发生且事件B发生;(3)事件A与事件B同时不 发生. 对立事件是指事件A与事件B有且仅有一个 发生,其包括两种情形;(1)事件A发生且B不 发生;(2)事件B发生事件A不发生. 对立事件是互斥事件的特殊情形。
解法2: “甲不输”看作是“乙胜”的对立事件, P(A)=1-P(C)=1-0.3=0.7
练习:
1.如果某士兵射击一次,未中靶的概率为0.05,求中 靶概率。 解:设该士兵射击一次,“中靶”为事件A,“未中靶” 为事件B, 则A与B互为对立事件, 故P(A)=1-P(B)=1-0.05=0.95。
如在掷骰子实验中,事件.
P(G) = 1- 1/2 = 1/2
A B
G { 出现的点数为偶数}; H { 出现的点数为奇数};
探究:
在掷骰子实验中,可以定义许多事件,
D 1 {出现的点数不大于1};D 2 { 出现的点数大于3}; D 3 {出现的点数小于3}; E {出现的点数小于7};F {出现的点数大于6};; G {出现的点数为偶数};H {出现的点数为奇数};
互斥事件,
所以 P(A)=P(A0)+P(A1)+P(A2)=0.1+0.16+0.3=0.56。
不是互斥事件,也不是对立事件
事件的关系和运算
事件 关系 事件 运算
3.事件的并 (或和)
1.包含关系 2.等价关系
4.事件的交 (或积) 5.事件的互斥 (或互不相容) 6.对立事件 (逆事件)
思考:你能说说互斥事件和对立事件的区别吗?
2.互斥事件与对立事件的区别与联系: 互斥事件是指事件A与事件B在一次试验中 不会同时发生,其具体包括三种不同的情形: (1)事件A发生且事件B不发生;(2)事件A不 发生且事件B发生;(3)事件A与事件B同时不 发生. 对立事件是指事件A与事件B有且仅有一个 发生,其包括两种情形;(1)事件A发生且B不 发生;(2)事件B发生事件A不发生. 对立事件是互斥事件的特殊情形。
解法2: “甲不输”看作是“乙胜”的对立事件, P(A)=1-P(C)=1-0.3=0.7
练习:
1.如果某士兵射击一次,未中靶的概率为0.05,求中 靶概率。 解:设该士兵射击一次,“中靶”为事件A,“未中靶” 为事件B, 则A与B互为对立事件, 故P(A)=1-P(B)=1-0.05=0.95。
如在掷骰子实验中,事件.
P(G) = 1- 1/2 = 1/2
A B
G { 出现的点数为偶数}; H { 出现的点数为奇数};
课件4:3.1.3 概率的基本性质
(2)①P(A)=1 0100, P(B)=1 10000=1010, P(C)=1 50000=210. 故事件 A,B,C 的概率分别为1 0100,1100,210. ②1 张奖券中奖包含中特等奖、一等奖、二等奖.设“1 张奖券 中奖”这个事件为 M,则 M=A∪B∪C. 因为 A、B、C 两两互斥,
解:由本例的解答可知 C=A∪B∪E;C∩F=A∪B.
(1)事件间的运算:
(2)进行事件的运算时,一是要紧扣运算的定义,二是要全面考 察同一条件下的试验可能出现的全部结果,必要时可利用 Venn 图或列出全部的试验结果进行分析.
2.(1)下列结论:①A、B 为两个事件,则 P(A∪B)
=P(A)+P(B);②若事件 A、B、C 两两互斥,则 P(A)+P(B)
1.事件的关系 (1)包含关系 一般地,对于事件 A 与事件 B,如果事件 A__发__生_,则事件 B 一定发生,这时称事件 B 包含事件 A(或称事件 A 包含于事件 B),记作_B_⊇__A_ (或 A⊆B).不可能事件记作∅,任何事件都包含 不可能事件.
类比集合,事件 B 包含事件 A 用图
转化与化归思想的核心是把陌生问题转化为熟悉的问题,事实 上解题过程就是一个缩小已知与求解的差异的过程,是求解系 统趋近于目标系统的过程.在本节中运用加法公式及对立思想 把复杂概率分解为易求解的概率问题.当一个事件的概率较难 求解,而对立事件易求时,应用对立事件公式转化成求对立事 件的概率,或是转化成几个易求解的互斥事件的和事件去求解.
解:(1)设“排队人数为 0”“排队人数为 1”“排队人数为 2”“排队人数为 3”“排队人数为 4”“排队人数为 4 人以上” 为事件 A,B,C,D,E,F,它们两两互斥. ①“至多 2 个人排队”的概率为 P(A∪B∪C)=P(A)+P(B)+P(C) =0.1+0.16+0.3=0.56. ②“至少 2 个人排队”的概率为 1-P(A∪B)=1-P(A)-P(B) =1-0.1-0.16=0.74.
3.1 3.1.3 概率的基本性质
2.事件的运算 (1)并事件:若某事件 C 发生当且仅当事件 A 发生或 事件 B 发生,则称此事件 C 为事件 A 与事件 B 的并事件 (或和事件), 记作 C=A∪B(或 C=A+B). (2)交事件:若某事件 C 发生当且仅当事件 A 发生 且 事件 B 发生,则称此事件 C 为事件 A 与事件 B 的交事件(或积事件), 记作 C=A∩B (或 C=AB).
(1)P(射中 10 环或 9 环)=P(A∪B)=P(A)+ P(B)=0.24+0.28=0.52,所以射中 10 环或 9 环的 概率为 0.52.
(2)事件“至少射中 7 环”与事件 E“射中 7 环 以下”是对立事件,则 P(至少射中 7 环)=1-P(E) =1-0.13=0.87.
所以至少射中 7 环的概率为 0.87.
3.概率的性质 (1)范围:任何事件的概率 P(A)∈[0,1] . (2)必然事件的概率:必然事件的概率 P(A)=1 . (3)不可能事件的概率:不可能事件的概率 P(A)= 0 . (4)概率加法公式:如果事件 A 与事件 B 互斥,则有 P(A∪B)= P(A)+P(B) . (5)对立事件的概率:若事件 A 与事件 B 互为对立事 件,那么 A∪B 为必然事件,则有 P(A∪B)= P(A)+ P(B)= 1,即 P(A)= 1-P(B) .
问(1)事件 D 与 A、B 是什么样的运算关系? (2)事件 C 与 A 的交事件是什么事件?
解:(1)对于事件 D,可能的结果为 1 个红球 2 个 白球,或 2 个红球 1 个白球,故 D=A∪B.
(2)对于事件 C,可能的结果为 1 个红球 2 个白球, 2 个红球 1 个白球,三个均为红球,故 C∩A=A.
(4)事件 D2 与 G 及事件 C2 间有什么关系? 提示:D2∩G=C2. (5)事件 C1 与事件 C2 间有什么关系? 提示:这两个事件为互斥事件.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)取出1球是红球或黑球的概率;
(2)取出的1球是红球、黑球或白球的概率.
三.当堂练习
1.一个人打靶时连续射击两次事件“至少有一次中靶”的互斥事件是()
A.至多有一次中靶B.两次都中靶C.只有一次中靶D.两次都不中靶
2.把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁四人,每人分得一张,那么事件“甲得红牌”与事件“乙分得红牌”是( )
A.对立事件B.互斥但不对立事件 C.必然事件D.不可能事件
3.从一堆产品(其中正品与次品都 多于2件)中任取2件,观察正品件数与次品件数,判断下列每件事件是不是互斥事件,如果是,再判断它们是 不是对立事件。
(1)恰好有1件次品恰好有2件次品;
(2)至少有1件次品和全是次品;
(3)至少有1件正品和至少有1件次品;
吉林省吉林市朝鲜族中学2014高中数学3.1.3概率的基本性质(第1课时)学案(无答案)新人教A版必修3
学习目标
1.正确理解事件的包含、并和、交积、相等,及互斥事件和对立事件的概念;
2.掌握概率的几个基本性质;正确理解和事件与积事件,以及互斥事件与对立事件的区别与联系.
学习重点
概率的几个基本性质
学习难点
概率的加法公式及其应用
学习内容
学法指导
一.知识点
1.事件的关系与运算
(1) 包含事件:
(2)相等事件:
(3)和事件:
(4)积事件:
(5)互斥事件:
(6)对立事件:
2.概率的基本性质
(1)任何事件的概率ຫໍສະໝຸດ P(A),则P(A)的取 值范围是___________
(2)事件的概率为1
(3)记不 可 能事件为F,P(F)=
(4)当A与B互斥时,A∪B发生的频数等于A发生的频数加上B发生的频数,所以 =;所以P(A∪B)=
(5)特别地,若A与B为对立事件,则A∪B为必然事件,
P(A∪B)==P(A)+P(B) P(A)=
二.典型例题
例1:一个射手进行一 次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;事件B:命中环数为10环;
(4)至少有1件次品和全是正品;
4.某射手在一次射击训练中,射中10环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一 次射击中:
(1)射中10环或9环 的概率;(2)少于7环的概率。
阅读教材
自主填写
注意互斥事件与对立事件的区别与联系
事件关系的判断
事件的运算
检测
事件C:命中环数小于6环;事件D:命中环数为6、7、8、9、10环.
例2:如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
例3:一盒中装有各色球12只,其中5只红球、4只黑球、2只白球、1只绿球.从中随机取 出1球,求:
(2)取出的1球是红球、黑球或白球的概率.
三.当堂练习
1.一个人打靶时连续射击两次事件“至少有一次中靶”的互斥事件是()
A.至多有一次中靶B.两次都中靶C.只有一次中靶D.两次都不中靶
2.把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁四人,每人分得一张,那么事件“甲得红牌”与事件“乙分得红牌”是( )
A.对立事件B.互斥但不对立事件 C.必然事件D.不可能事件
3.从一堆产品(其中正品与次品都 多于2件)中任取2件,观察正品件数与次品件数,判断下列每件事件是不是互斥事件,如果是,再判断它们是 不是对立事件。
(1)恰好有1件次品恰好有2件次品;
(2)至少有1件次品和全是次品;
(3)至少有1件正品和至少有1件次品;
吉林省吉林市朝鲜族中学2014高中数学3.1.3概率的基本性质(第1课时)学案(无答案)新人教A版必修3
学习目标
1.正确理解事件的包含、并和、交积、相等,及互斥事件和对立事件的概念;
2.掌握概率的几个基本性质;正确理解和事件与积事件,以及互斥事件与对立事件的区别与联系.
学习重点
概率的几个基本性质
学习难点
概率的加法公式及其应用
学习内容
学法指导
一.知识点
1.事件的关系与运算
(1) 包含事件:
(2)相等事件:
(3)和事件:
(4)积事件:
(5)互斥事件:
(6)对立事件:
2.概率的基本性质
(1)任何事件的概率ຫໍສະໝຸດ P(A),则P(A)的取 值范围是___________
(2)事件的概率为1
(3)记不 可 能事件为F,P(F)=
(4)当A与B互斥时,A∪B发生的频数等于A发生的频数加上B发生的频数,所以 =;所以P(A∪B)=
(5)特别地,若A与B为对立事件,则A∪B为必然事件,
P(A∪B)==P(A)+P(B) P(A)=
二.典型例题
例1:一个射手进行一 次射击,试判断下列事件哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;事件B:命中环数为10环;
(4)至少有1件次品和全是正品;
4.某射手在一次射击训练中,射中10环、8环、7环的概率分别为0.21,0.23,0.25,0.28,计算该射手在一 次射击中:
(1)射中10环或9环 的概率;(2)少于7环的概率。
阅读教材
自主填写
注意互斥事件与对立事件的区别与联系
事件关系的判断
事件的运算
检测
事件C:命中环数小于6环;事件D:命中环数为6、7、8、9、10环.
例2:如果从不包括大小王的52张扑克牌中随机抽取一张,那么取到红心(事件A)的概率是 ,取到方块(事件B)的概率是 ,问:
(1)取到红色牌(事件C)的概率是多少?
(2)取到黑色牌(事件D)的概率是多少?
例3:一盒中装有各色球12只,其中5只红球、4只黑球、2只白球、1只绿球.从中随机取 出1球,求:
