带p-laplacian算子四阶四点边值问题的迭代解
含有p-Laplacian算子n阶多点边值问题在共振条件下非负解的存在性

曲 阜 师 范 大 学
Junl o Q f N r l ora f uu oma
V0 _ 8 No. l3 1
Jn 0 2 a .2 1
含有 PL pai -a l a c n算子 n阶 多点 边值 问题在共振 条件下非 负解的存在性
1 引
言
对 于二 阶线 性 常微分 方程 多点边 值 问题可解 性 的研 究是 由 It l n和 Mo ev首先 开 始 的 ,见 文献 [.] ie s 1 . 2
此后 , 便有了诸多关于非线性有限多点边值 问题的研究 . 。 但是在共振条件下 , 含有 pLp c n -al i 算子 n aa 阶奇异多点边值 问题却很 少有人研究 , 本文主要运用推广到算子 . Ⅳ在锥上的零点指数 , 讨论 了含 有 P .
_÷ Ke rL.
定义 2 3 设 力为 中的有界开集 , . 若有 Q ) l中的有界集 , Ⅳ( 为 , 且 ( 一 ) ) , Q ( 为 中的紧集 , 则 称 Ⅳ在 上为 一 紧的. H= j i 则 H. n L y 令 L+ - P, , C d o 为线性双射 , 且有有界逆算子满足
m一 2
(. ) 1 1
() ” ) 0 = ( =… = 0
’ )= ,()=∑ o ( , ( 0 “1 0 / ) i “
(2 1) .
其 ( = Iu > = ,+ = f0 ]R R 续R= ,) ∈(,, 中 M l- Pl 古 寺 1:, ד 连 , [∞; c0) ) 2 ; u ; P ,[ 1 一 + 0 。 (1
孟 令 君 , 刘 立 山
( 曲阜师范大学数学科学学院 , 7 15 山东省 曲阜市 ) 2 36 ,
laplacian算子matlab程序

laplacian算子matlab程序Laplacian算子是常用的图像处理算法之一,它可以用于边缘检测、图像增强等应用。
在Matlab中,我们可以使用Laplacian算子对图像进行处理并得到边缘信息。
本文将介绍如何使用Matlab编写Laplacian算子的程序,并展示算法在图像处理中的实际应用。
Laplacian算子的定义如下:L(x, y) = ∂²I(x, y)/∂x² + ∂²I(x, y)/∂y²其中,L(x, y)是Laplacian算子的输出,I(x, y)是输入图像,∂²I(x, y)/∂x²和∂²I(x, y)/∂y²分别是图像在水平和竖直方向上的二阶导数。
在Matlab中,我们可以使用内置的函数`fspecial`和`imfilter`实现Laplacian算子。
具体步骤如下:步骤1:读取图像首先,我们需要读取一幅图像作为输入。
可以使用`imread`函数读取图像,并使用`imshow`函数显示图像。
```matlabimage = imread('input.jpg');imshow(image);```步骤2:构造Laplacian算子的卷积核在Matlab中,我们可以使用`fspecial`函数构造一个Laplacian算子的卷积核。
Laplacian算子的卷积核通常取如下形式:```0 -1 0-1 4 -10 -1 0```可以使用`fspecial('laplacian')`函数生成Laplacian算子的卷积核。
为了增强边缘效果,我们可以对卷积核进行归一化处理,使其元素之和为1。
```matlablaplacian = fspecial('laplacian');laplacian = laplacian / sum(abs(laplacian(:)));```步骤3:应用Laplacian算子使用`imfilter`函数将Laplacian算子应用到图像上。
laplacian算子

laplacian算子
Laplacian算子的概念可以追溯到17,18世纪时期的拉普拉斯,他是贝尔定理的发现者。
它是一种线性微分运算符,可以在几何物理学和数学中被广泛的应用。
在数学领域,它的作用是函数本身的二阶微分的求取,也就是函数的梯度及曲率的求取。
在图像处理中,Laplacian算子可以用来检测边缘和角点,所以在应用上非常广泛。
对拉普拉斯算子来说,它的应用主要有三个方面:边缘检测、受激响应和角点检测。
首先,它可用来检测图像边缘,即在连续的图像域中,其像素值发生了重大变化,这种变化称为边缘。
通过拉普拉斯算子,可以得到图像中存在的边界,这种算法在现实世界中也被广泛使用,比如在自动驾驶领域中就经常使用拉普拉斯算子来检测路径的边缘,以便更好的控制行驶方向。
此外,拉普拉斯算子也可以用来检测受激响应,它可以通过响应的极大值检测来检测图像的受激响应,使用Laplacian算子可以找到极大值位置,从而判断出图像中存在的灰度特征点,这样就可以将不同图像生成一张总图,便于研究不同图像之间的关系。
最后,Laplacian算子可以用来检测角点,这种技术相当普遍,利用Laplace拉普拉斯算子可以检测出图像中的角点。
当选择的模板大小和阈值较小时,仅有非常强烈的角点会被检测到,而其他稍弱的角点会被忽略;当选择的模板大小和阈值较大时,会检测到更多的角点,但也增加了误报率。
Laplacian算子是一个非常重要的工具,在计算机视觉中得到了
广泛的应用。
它可以用来检测图像中的边缘,受激响应和角点。
它的本质是一个二阶梯度,具有十分重要的特性,如果能够准确的检测到这些边缘甚至角点,将会大大的提升我们的图像识别能力。
带p-Laplacian算子的分数阶微分方程边值问题在无穷区间中解的存在性

o n a n u n b o u n d e d d o ma i n a r e o b t a i n e d . Ke y wo r d s f r a c t i o n l a d i f e r e n t i a l e q u a t i o n;b o u n d a r y v lu a e p ob r l e m ;i n i f n i t e i n t e r v l ;f a i x e d p o i n t t h e o r e m
近年来 , 分数阶微分方程在国内外引起 了极大 的研究兴趣 , 特别是边值 问题解 的存在性 4 。 . 据作者所
知, 目 前很少有学者研究带 p - L a p l a c i a n 算子的分数阶微分方程边值问题解 的存在性 剖, 尤其是无穷区间中
解 的存在性研究甚少 . 无穷区间上的边值问题在物理学 、 自然科学等领域中有很多实际应用 , 如不稳定的气体通过半无穷带气 孔媒介问题 , 孤立中子的电势问题等 - l 0 ] . 因此 , 对它的研究具有重要的意义. 受以上文献的启发 , 本文主要利用 S c h a u d e r 不动点定理研究如下一类带 P — L a p l a c i a n 算子的分数阶微分 方程边值问题在无穷 区间中解 的存在性 : 『 +咖 ( + ( t ) ); t , u ( t ) , : ( t ) ) , t E( 0 ,+O 0) ,
2 . C o l l e g e o f ci S e n c e s . C h i n a U n i v e si r t y o f Mi n i n g a n d T e c h n o l o g y , X u z h o u 2 2 1 1 1 6, C h i n a )
一类p—laplace方程边值问题解的存在性

一类p—laplace方程边值问题解的存在性理解一类p-Laplace方程边值问题解的存在性:1. p—Laplace方程简介p—Laplace方程是一种常见的椭圆型偏微分方程,它在空间变换、热传导中也有广泛的应用。
它的解由p—Laplace方程决定:∂u/∂x+∂v/∂y=u^(p-2)f,其中p是大于等于1的任意常数,u,v是满足边界条件的函数,x,y是定义域内的坐标,f是常函数。
2. 一类p—Laplace方程边值问题的存在性一类p—Laplace方程的边值问题的存在性取决于其常数p的大小。
如果p大于1,那么该方程有唯一解;如果p小于1,那么该方程可能有无穷多解;如果p=1,则该方程常有唯一解,又有可能出现无穷多解。
3. p—Laplace方程边值问题解的存在性判定判定一类p—Laplace方程边值问题解的存在性,要仔细检查边界条件是否符合两个条件:(1)任意的边界函数都必须满足给定边界条件;(2)边界条件必须对所有满足方程组调和函数,如成反馈函数、空间变换函数等来施加有效制约。
缺一不可,边值问题解才能有存在性。
4. p>1时一类p—Laplace方程边值问题解的存在性当p大于1时,p—Laplace方程边值问题解有唯一解。
这是因为二阶偏微分方程组只能有一个解, p大于1时,椭圆型经ene变换可以转化为二阶偏微分方程组,根据拓扑的余定理,二阶偏微分方程组必有唯一解,故这时候方程解有存在性。
5. p<1时一类p-Laplace方程边值问题解的存在性当p小于1时,p—Laplace方程边值问题解可能有无穷多解。
这是因为当p<1时,椭圆型经ene变换不能转化为二阶偏微分方程组,根据拓扑的余定理,任一条件的任何解,如满足给定的边界条件,都是经en变换回解法所得,因此这种情况下该方程解有无穷多解的存在性。
6. p=1时一类p—Laplace方程边值问题解的存在性当p等于1时,p—Laplace方程边值问题解存在性有两种情形:(1)如果边界条件符合两个条件(前面讲到),有唯一解;(2)另一种情形是,如果边界条件不完全符合两个条件,则可能出现无穷多解。
具p-Laplacian算子时滞微分方程边值问题解的存在唯一性

>o 使得 任意 的 ∈U,>T, 有 I f一l , t j 都 () i s I 。 E 为定 义在 ( 一ro )R) m ()<£令 [ ,o , 上的 所有 函数 z的集
合 , 且 z在 [ ,。 上连 续 可微 且 导数 连 续 有界 。E 是 一个 B n c 并 0。 ) a a h空 间 , 定义 其 范 数 l・l 为 I 一 I l £ I z
ma m x I () , pI f 1, x{ a z £ Is () )z∈E。 u z
一 r O : 手
引理 1 设 z ∈c( 一, c ) R) O o ) 的连续可 微 函数 , z是边值 问题 ( ) ( ) E ,o 上 的 [ . o , 为[ ,o 上 , 则 1~ 3在 0o )
一
个解 , 当且仅 当
f f, ()
一
一r f O, ≤ ≤
1翰。 ) f 。 ( ff t。 , ) ≥ d o
() 5
定理 1 假设
I t zI f(, ) ≤F(, l I ,f 2 ∈E ,o xc( 一r 0 , xR, , t I ,2I (, ) o o ) ) , [ , ] R)
J n 2 1 u . 02
具 一 a lc n算 子 时滞 微分 方 程 边 值 问题 L pai a 解 的存在 唯一 性
韦 煜明 , 王 勇 , 艳秋 , 唐 范江 华
( 广西 师 范 大 学 数学 科学 学 院 , 西 桂 林 5 1 0 ) 广 4 0 4
摘
要 : 文 主 要研 究 无 穷 区 间上 具有 户 L pai 本 一al a c n算 子 的 时滞 微分 方 程 边 值 问题 解 的 存 在 性 和 唯 一 性 , 利用
laplace积分的几种计算方法

laplace 积分的几种计算方法Laplace 积分是一种数学技巧,用于解决带有指数或高阶微分项的微分方程。
它通常用于求解线性高阶常微分方程的解析解。
Laplace 积分的几种计算方法包括:初值问题法:这种方法的基本思想是将Laplace 积分表示为初值问题的形式,然后使用常规的数值求解方法求解。
公式如下:{y (n )+a 1y (n−1)+a 2y (n−2)+⋯+a n−1y ′+a n y =g (t )y (t 0)=y 0y (1)(t 0)=y 1⋯y (n−1)(t 0)=y n−1 反演积分法:这种方法的基本思想是通过反演积分将Laplace 积分转化为函数值的形式,然后再使用常规的数值求解方法求解。
公式如下:L −1[F (s )]=12πi ∫e st F (s )ds c+i ∞c−i ∞其中,L −1[F (s )] 表示 Laplace 反演,c 是极点的实部,i 是虚数单位。
分段线性插值法:这种方法的基本思想是将 Laplace 积分分成若干个子区间,然后在每个子区间内使用线性插值法求解。
公式如下:L −1[F (s )]≈∑t i −t i−12ni=1[f (t i−1)+f (t i )]+O (ℎ2)其中,t i 是分段点,ℎ 是分段间隔。
牛顿迭代法:这种方法的基本思想是使用牛顿迭代法对 Laplace 积分进行近似求解。
公式如下:x k+1=x k −F (x k )F ′(x k )其中,x k 是迭代变量,F (x ) 是待求解的 Laplace 积分函数。
分数阶差分格式:这种方法的基本思想是使用分数阶差分格式对 Laplace 积分进行近似求解。
公式如下:1ℎα∑(−1)i−1i!ni=1(αi)(x−t i)α−i f(t i)+O(ℎα+1)其中,ℎ是分段间隔,α是差分阶数,t i是分段点,f(t i)是待求解的Laplace 积分函数。
这些方法均可用于求解Laplace 积分,但其适用范围和精度有所不同,应根据具体问题选择适当的方法。
【国家自然科学基金】_p-laplacian边值问题_基金支持热词逐年推荐_【万方软件创新助手】_20140803
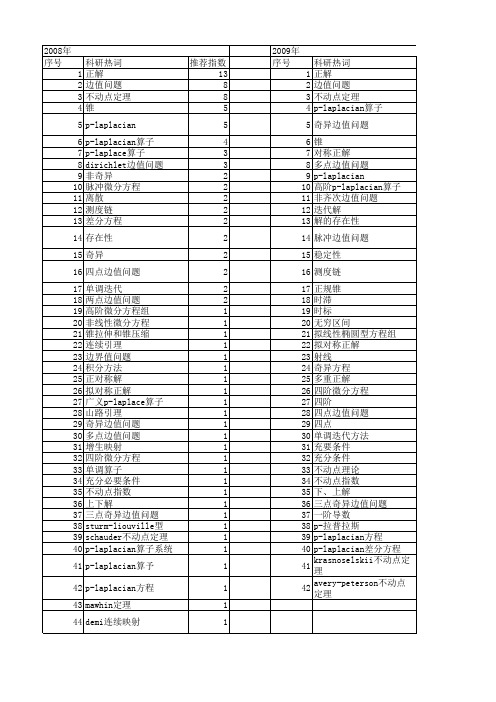
推荐指数 10 6 4 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
科研热词 正解 边值问题 不动点定理 p-laplacian算子 奇异边值问题 锥 对称正解 多点边值问题 p-laplacian 高阶p-laplacian算子 非齐次边值问题 迭代解 解的存在性 脉冲边值问题 稳定性 测度链 正规锥 时滞 时标 无穷区间 拟线性椭圆型方程组 拟对称正解 射线 奇异方程 多重正解 四阶微分方程 四阶 四点边值问题 四点 单调迭代方法 充要条件 充分条件 不动点理论 不动点指数 下、上解 三点奇异边值问题 一阶导数 p-拉普拉斯 p-laplacian方程 p-laplacian差分方程 krasnoselskii不动点定理 avery-peterson不动点定理
推荐指数 13 8 8 5 5 4 3 3 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
科研热词 推荐指数 正解 6 边值问题 5 不动点定理 5 p-laplacian方程 3 迭代解 2 奇异脉冲方程 2 p-laplacian算子 2 p-laplacian 2 高阶导数 1 锥 1 连续引理 1 脉冲 1 测度链 1 正解的存在性 1 时滞 1 时标 1 拟线性化 1 拟对称正解 1 拟对称 1 广义p-laplace算子 1 山路引理 1 山路定理 1 存在 1 奇异混合单调算子 1 多点边值问题 1 多个正解 1 增生映射 1 四点边值问题 1 单调迭代 1 单调算子 1 半直线 1 全连续 1 不动点 1 上下解 1 三点边值问题 1 一阶导数 1 一维p-laplacian算子 1 p-拉普拉斯算子 1 p-laplacian边值问题 1 p-laplace算子 1 p-laplace 1 p-lapace差分方程边值问题 1 leray-schauder度 1 leray-schauder不动点定理 1 dirichlet边值问题 1 demi连续映射 1 banach空间 1 avery-peterson不动点定理 1 (ps)条件 1 (c)条件 1
