最新习题二(答案)
西方经济学课后练习题答案 (2)

习题二1.简释下列概念:需求答:是指在某一特定时期内,对应于某一商品的各种价格,人们愿意而且能够购买的数量。
需求规律答:一种普遍经济现象的经验总结,指在影响需求的其他因素既定的条件下,商品的需求量与其价格之间存在着反向的依存关系,即商品价格上升,需求量减少;商品价格下降,需求量增加.需求的变动答:指当商品本身的价格不变时,由于其他因素的变动引起的需求数量的变化。
供给答:是指生产者(厂商)在一定时期和一定价格水平下愿意而且能够提供的某种商品的数量。
供给规律答:一种普遍经济现象的经验总结,指:在影响供给的其他因素既定的条件下,商品的供给量与其价格之间存在着正向的依存关系,即商品价格上升,供给量增加;商品价格下降,供给量减少.供给的变动答:指当商品本身的价格既定时,由于其他因素的变动引起的供给数量的变化。
需求的价格弹性答:是指一种商品的需求量对其价格变动的反应程度,其弹性系数等于需求量变动的百分比除以价格变动的百分比.通常简称为需求弹性。
需求的收入弹性答:是指一种商品的需求量对消费者收入变动的反应程度,其弹性系数等于需求量变动的百分比与收入变动的百分比之比。
需求的交叉弹性答:是需求的交叉价格弹性的简称,指一种商品的需求量对另一种商品的价格变动的反应程度,其弹性系数等于一种商品需求量变动的百分比与另一种商品价格变动的百分比之比。
供给弹性答:是一种商品的供给量对其价格变动的反应程度,其弹性系数等于供给量变动的百分比与价格变动的百分比之比。
均衡价格答:是指消费者对某种商品的需求量等于生产者所提供的该商品的供给量时的市场价格。
供求规律答:指均衡价格和均衡产量与需求均呈同方向变动,均衡价格与供给呈反方向变动,而均衡产量与供给呈同方向变动。
2.下列情况发生时,某种蘑菇的需求曲线如何移动?⑴卫生组织发布一份报告,称食用这种蘑菇会致癌;⑵另一种蘑菇价格上涨了;⑶消费者收入增加了;⑷培育蘑菇的工人工资增加了。
答:⑴对此蘑菇的需求曲线会向左移。
普通高等学校招生全国统一考试(新课标Ⅱ卷)文数答案解析(正式版)(解析版).docx

一、选择题:本大题共12道小题,每小题5分,共60分.1.已知集合{}|12A x x =-<<,{}|03B x x =<<,则A B =U ( ) A .()1,3- B .()1,0- C .()0,2 D .()2,3 【答案】A考点:集合运算. 2. 若为a 实数,且2i3i 1ia +=++,则a =( ) A .4- B .3- C .3 D .4 【答案】D 【解析】试题分析:由题意可得()()2i 1i 3i 24i 4a a +=++=+⇒= ,故选D. 考点:复数运算.3. 根据下面给出的2004年至2013年我国二氧化碳年排放量(单位:万吨)柱形图,以下结论中不正确的是( )A .逐年比较,2008年减少二氧化碳排放量的效果最显著B .2007年我国治理二氧化碳排放显现成效C .2006年以来我国二氧化碳年排放量呈减少趋势D .2006年以来我国二氧化碳年排放量与年份正相关 【答案】 D考点:柱形图4. 已知()1,1=-a ,()1,2=-b ,则(2)+⋅=a b a ( ) A .1- B .0 C .1 D .2 【答案】C 【解析】试题分析:由题意可得22=a ,3,⋅=-a b 所以()222431+⋅=+⋅=-=a b a a a b .故选C.考点:向量数量积.5. 设n S 是等差数列{}n a 的前n 项和,若1353a a a ++=,则5S =( ) A .5 B .7 C .9 D .11 【答案】A 【解析】试题解析:13533331a a a a a ++==⇒=,()15535552a a S a +===.故选A. 考点:等差数列6. 一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )1A.8 1B.7 1C.6 1D.5【答案】D 【解析】试题分析:截去部分是正方体的一个角,其体积是正方体体积的16,所以截去部分体积与剩余部分体积的比值为15,故选D.考点:三视图7. 已知三点(1,0),(0,3),(2,3)A B C,则△ABC外接圆的圆心到原点的距离为()5 A. 321B.25C.4D.3【答案】B考点:直线与圆的方程.8. 右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的,a b分别为14,18,则输出的a为()A.0B.2C.4D.14【答案】B 【解析】试题分析:由题意输出的a 是18,14的最大公约数2,故选B. 考点:1. 更相减损术;2.程序框图. 9.已知等比数列{}n a 满足114a =,()35441a a a =-,则2a =( )A.2B.1 1C.2 1D.8【答案】C 【解析】试题分析:由题意可得()235444412a a a a a ==-⇒=,所以34182a q q a ==⇒= ,故2112a a q ==,选C.考点:等比数列.10. 已知B A ,是球O 的球面上两点,︒=∠90AOB ,C 为该球面上的动点.若三棱锥ABC O -体积的最大值为36,则球O 的表面积为( )A.π36B. π64C.π144D. π256 【答案】C考点:球与几何体的切接.11. 如图,长方形的边AB =2,BC =1,O 是AB 的中点,点P 沿着边BC ,CD 与DA 运动,记BOP x ∠= ,将动点P 到A ,B 两点距离之和表示为x 的函数()f x ,则的图像大致为( )A .B .C .D .【答案】B考点:函数图像12. 设函数21()ln(1||)1f x x x=+-+,则使得()(21)f x f x >-成立的x 的取值范围是( ) A .1,13⎛⎫ ⎪⎝⎭ B .()1,1,3⎛⎫-∞+∞ ⎪⎝⎭U C .11,33⎛⎫- ⎪⎝⎭D .11,,33⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭U 【答案】A 【解析】试题分析:由21()ln(1||)1f x x x =+-+可知()f x 是偶函数,且在[)0,+∞是增函数,所以 ()()()()121212113f x f x f x f x x x x >-⇔>-⇔>-⇔<< .故选A.考点:函数性质二、填空题:本大题共4小题,每小题5分,共20分13. 已知函数()32f x ax x =-的图像过点(-1,4),则a = .【答案】-2 【解析】试题分析:由()32f x ax x =-可得()1242f a a -=-+=⇒=- .考点:函数解析式14. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 .【答案】8考点:线性规划15. 已知双曲线过点()4,3,且渐近线方程为12y x =±,则该双曲线的标准方程为 . 【答案】2214x y -=考点:双曲线几何性质16. 已知曲线ln y x x =+在点()1,1 处的切线与曲线()221y ax a x =+++ 相切,则a = .【答案】8【解析】试题分析:由11y x'=+可得曲线ln y x x =+在点()1,1处的切线斜率为2,故切线方程为21y x =-,与 ()221y ax a x =+++ 联立得220ax ax ++=,显然0a ≠,所以由 2808a a a ∆=-=⇒=.考点:导数的几何意义. 三、解答题17(本小题满分12分)△ABC 中D 是BC 上的点,AD 平分∠BAC ,BD =2DC . (I )求sin sin BC∠∠ ;(II )若60BAC ∠=o ,求B ∠. 【答案】(I )12;30o .考点:解三角形试题解析:(I )由正弦定理得,,sin sin sin sin AD BD AD DCB BADC CAD==∠∠∠∠ 因为AD 平分∠BAC ,BD =2DC ,所以sin 1.sin 2B DC C BD ∠==∠.(II )因为()180,60,C BAC B BAC ∠=-∠+∠∠=oo所以()31sin sin sin .2C BAC B B B ∠=∠+∠=∠+∠ 由(I )知2sin sin B C ∠=∠, 所以3tan 30.3B B ∠=∠=o考点:解三角形18. (本小题满分12分)某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度.(不要求计算出具体值,给出结论即可)B地区用户满意度评分的频率分布直方图(II)根据用户满意度评分,将用户的满意度评分分为三个等级:估计那个地区的用户的满意度等级为不满意的概率大,说明理由.【答案】(I)见试题解析(II)A地区的用户的满意度等级为不满意的概率大.考点:1.频率分布直方图;2.概率估计.19. (本小题满分12分)如图,长方体1111ABCD A B C D -中AB =16,BC =10,18AA =,点E ,F 分别在1111,A B D C 上,11 4.A E D F ==过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(I )在图中画出这个正方形(不必说明画法与理由); (II )求平面α把该长方体分成的两部分体积的比值. 【答案】(I )见试题解析(II )97 或79考点:1.几何体中的截面问题;2.几何体的体积20. (本小题满分12分)已知椭圆()2222:10x y C a b a b+=>> 的离心率为22,点(2在C 上.(I )求C 的方程;(II )直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明:直线OM 的斜率与直线l 的斜率乘积为定值.【答案】(I )2222184x y +=(II )见试题解析考点:直线与椭圆21. (本小题满分12分)已知()()ln 1f x x a x =+-.(I )讨论()f x 的单调性;(II )当()f x 有最大值,且最大值大于22a -时,求a 的取值范围.【答案】(I )0a ≤,()f x 在()0,+∞是单调递增;0a >,()f x 在10,a ⎛⎫ ⎪⎝⎭单调递增,在1,a ⎛⎫+∞ ⎪⎝⎭单调递减;(II )()0,1.【解析】考点:导数的应用.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号22. (本小题满分10分)选修4-1:几何证明选讲如图O是等腰三角形AB C内一点,圆O与△ABC的底边BC交于M,N两点,与底边上的高交于点G,且与AB,AC 分别相切于E,F两点.(I )证明EF BC P ;(II )若AG 等于圆O 半径,且23AE MN == ,求四边形EBCF 的面积.【答案】(I )见试题解析;(II )1633考点:1.几何证明;2.四边形面积的计算.23. (本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线1cos ,:sin ,x t C y t αα=⎧⎨=⎩ (t 为参数,且0t ≠ ),其中0απ≤<,在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线23:2sin ,:23cos .C C ρθρθ==(I )求2C 与3C 交点的直角坐标;(II )若1C 与 2C 相交于点A ,1C 与3C 相交于点B ,求AB 最大值.【答案】(I )()330,0,2⎫⎪⎪⎝⎭;(II )4.【解析】试题分析:(I )把2C 与3C 的方程化为直角坐标方程分别为2220x y y +-=,2230x y x +-=,联立解考点:参数方程、直角坐标及极坐标方程的互化.24. (本小题满分10分)选修4-5:不等式证明选讲设,,,a b c d 均为正数,且a b c d +=+.证明:(I )若ab cd > ,a b c d >(II a b c d >a b c d -<-的充要条件. 【答案】【解析】试题分析:(I )由a b c d +=+及ab cd >,可证明22a b c d >,开方即得a b c d >(II )本小题可借助第一问的结论来证明,但要分必要性与充分性来证明.试题解析:解:(I )因为22,,a b a b ab c d c d cd =++=++考点:不等式证明.。
高中音乐学业水平考试练习题二(含答案)

高中音乐学业水平考试练习题(二)学校:姓名:准考证号:桌号:考生须知:1.本次考试满分为60分,时间为30分钟;2.请务必在试卷上相应位置填写学校、姓名、准考证号和考试桌号;3.根据题目要求用2B铅笔将答案涂写在答题卡上的相应位置处;4.本次考试,单项选择题共45题,判断题共15题。
每题分值均为1分。
一、单项选择题(本大题共45小题,每小题1分,共45分。
每题只有一个答案符合题目要求,请将正确答案填涂在答题卡上。
其中1—35题为听力题,听完每段音乐后,你都有5秒钟的时间答题和阅读下一小题,每段音乐仅听一遍。
)1.聆听音乐片段,选择该片段曲名( B )A.《1812序曲》B.《彩云追月》C.《月光奏鸣曲》2.聆听音乐片段,选择该片段曲名( A )A.《国际歌》B.《祖国颂》C.《大进行曲》3.聆听音乐片段,选择该片段曲名( A )A.《祝酒歌》B.《松花江上》C.《这一仗打得真漂亮》4.聆听音乐片段,选择该片段曲名( A )A.《辽阔的草原》B.《纺织谣》C.《酒歌》5.聆听音乐片段,选择该片段曲名( C )A.《赶牲灵》B.《下四川》C.《过滩号子》6.聆听音乐片段,选择该片段曲名( B )A.《小河淌水》B.《无锡景》C.《铜钱歌》7.聆听音乐片段,选择该片段曲名( B )A.《索兰调》B.《樱花》C.《星星索》8.聆听音乐片段,选择该片段曲名( A )A.《阳关三叠》B.《春江花月夜》C.《彩云追月》9.聆听音乐片段,选择该片段曲名( C )A.《黄河》B.《卖布谣》C.《开路先锋》10.聆听音乐片段,选择该片段曲名( C )A.《全世界人民心一条》B.《我们走在大路上》C.《在希望的田野上》11.聆听音乐片段,选择该片段主奏乐器( B )A.单簧管B.钢琴C.大提琴12.聆听音乐片段,选择该片段主奏乐器( A )A.竹笛B.扬琴C.箜篌13.聆听音乐片段,选择该片段主奏乐器( A )A.二胡B.小提琴C.古筝14.聆听音乐片段,选择该片段主奏乐器( B )A.云锣B.马头琴C.手鼓15.聆听音乐片段,选择该片段主奏乐器( A )A.古琴B.编钟C.埙16.聆听音乐片段,选择该片段主奏乐器( C )A.笙B.箫C.唢呐17.聆听音乐片段,选择该片段主奏乐器( B )A.琵琶B.古筝C.葫芦丝 18.聆听音乐片段,选择该片段演唱形式( B )A.童声合唱B.混声合唱C.男声合唱 19.聆听音乐片段,选择该片段演唱形式( A )A.轮唱B.独唱C.重唱20.聆听音乐片段,选择该片段演奏形式( B )A.西洋管弦乐合奏B.民族管弦乐合奏C.室内乐21.聆听音乐片段,选择该片段演奏形式( B )A.协奏B.独奏C.重奏22.聆听音乐片段,选择下列民歌流行的地区( C )A.蒙古B.西藏C.新疆23.聆听音乐片段,选择该片段歌曲所属民族( A )A.藏族B.维吾尔族C.彝族24.聆听音乐片段,选择出该片段曲名及所属地区( C )A.陕北《赶牲灵》B.云南《小河淌水》C.湖南《铜钱歌》 25.聆听音乐片段,选择出该片段的体裁( B )A.山歌B.号子C.小调26.聆听音乐片段,选择出该片段所属国家( A )A.日本B.朝鲜C.加拿大 27.聆听音乐片段,选择出该片段所属剧种( A )A.京剧B.扬剧C.黄梅戏28.聆听音乐片段,选择出该唱段的曲名( A )A.《海岛冰轮初转腾》B.《迎来春色换人间》C.《路遇》29.聆听音乐片段,选择出该片段所属曲艺种类( B )A.京韵大鼓B.苏州弹词C.常德丝弦 30.聆听音乐片段,选择出该音乐主题所出自的影片( C )A.《冰山上的来客》B.《辛德勒的名单》C.《红楼梦》 31.聆听音乐片段,选择出该片段所属地区( B )A.江苏无锡B.江苏扬州C.浙江乐清 32.聆听音乐片段,选择出该片段的曲作者( A )A.冼星海B.三宝C.施光南 33.聆听音乐片段,选择出该片段的曲作者( B )A.莫扎特B.贝多芬C.海顿34.聆听音乐片段,选择出该片段的曲作者( A )A.肖邦B.斯特拉文斯基C.巴赫35.聆听音乐片段,选择能表达你对音乐情绪感受最恰当的词( B ) A.庄严 B.喜悦 C.悲伤36.我国古代文人音乐的代表性乐器是( C )A.古筝B.琵琶C.古琴37.非洲音乐的灵魂是( A )A.鼓B.小提琴C.钢琴38.不属于我国民族乐器的是( C )A.三弦B.二胡C.风笛39.不属于西洋木管乐器组的是( B )A.长笛B.大提琴C.单簧管40.被誉为“钢琴诗人”的作曲家是( C )A.贝多芬B.莫扎特C.肖邦41.通俗歌曲《天堂》的创作中采用的民族风格是( A )A.蒙古族B.哈萨克族C.藏族42.被称为“国粹”的是( B )A.越剧B.京剧C.评剧43.苏州弹词使用的主要乐器是( B )A.二胡大鼓B.琵琶三弦C.渔鼓笛子44.以舞蹈为主要表现手段,综合音乐、美术、文学的艺术形式是( A )A.舞剧B.歌剧C.戏曲45.《斗牛士之歌》选自法国作曲家比才的歌剧( B )A.《图兰朵》B.《卡门》C.《党的女儿》二、判断题(本大题共15小题,每小题1分,共15分。
精益六西格玛管理绿带练习题二(含答案)

单项选择1.下列哪一选项陈述是实施流程改进的第一步:A.识别顾客的需求B.识别非增值的流程C.确定流程的负责人D.识别增值的流程2.战略是指组织为适应未来环境的变化,追求长期生存和发展而进行的整体谋划和决策。
战略制定的步骤包括:①评价组织治理:评价组织高层领导的绩效。
②分析内部环境:寻找决定优势(S)与劣势(W)的战略因素。
③确定战略目标。
④进行SWOT战略因素综合分析,形成和确定战略方案。
⑤分析外部环境:寻找显示出机会(O)和威胁(T)的战略因素。
⑥评估当前绩效。
则以下关于步骤的排序正确的是:A.⑥→①→②→⑤→③→④B.⑥→①→⑤→②→③→④C.①→⑥→②→⑤→③→④D.①→⑥→⑤→②→③→④3.精益生产聚焦于消除浪费和过程非增值。
按照精益生产的基本原则,以下哪些属于增值活动:A.将物料运输到作业现场B.将工件切削到要求的规格C.检测产品确保合格D.修整工件表面的毛刺4.下列关于精益价值流图(VSM)的描述,不正确的是()A.通常包含物料流和信息流B.流描述的是端到端的活动C.仅指创造价值的活动D.包括顾客需求信息5.新产品开发三阶段设计思想:系统设计、参数设计、容差设计是由以下哪位质量管理专家提出来的:A.田口玄一B.戴明C.朱兰D.石川馨6.对精益思想的五项原则正确的表述顺序是:A.识别价值流-确定价值-流动-拉动-尽善尽美B.确定价值-识别价值流-拉动-流动-尽善尽美C.流动-拉动-确定价值-识别价值流-尽善尽美D.确定价值-识别价值流-流动-拉动-尽善尽美7.一般在六西格玛项目中,会有高阶流程图和详细流程图,下述那个工具可以用来描述高阶流程图:A.跨职能流程图B.SIPOCC.泳道图D.意大利面条图8.某项目团队采用头脑风暴法分析了雨伞的顾客声音(VOC),包括能方便的将伞收起来、伞柄方便抓握、伞面雨水快速滑落、携带雨伞很方便、容易折叠、能承受较大的风、能够持久的挡雨、能承受较大强度的雨等。
结构力学(二)习题及答案
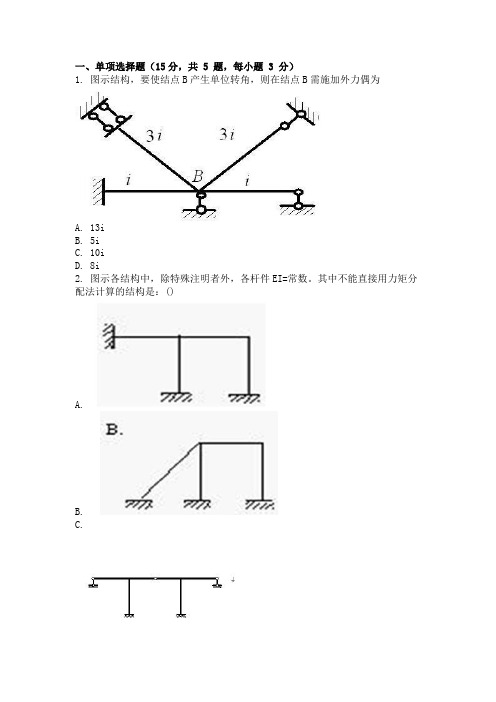
一、单项选择题(15分,共 5 题,每小题 3 分)1. 图示结构,要使结点B产生单位转角,则在结点B需施加外力偶为A. 13iB. 5iC. 10iD. 8i2. 图示各结构中,除特殊注明者外,各杆件EI=常数。
其中不能直接用力矩分配法计算的结构是:()A.B.C.D.3. 图示两个结构的关系是()。
A. 内力相同,变形也相同B. 内力相同,变形不相同C. 内力不相同,变形相同D. 内力不相同,变形不相同4. 图示刚架中杆长l,EI相同,A点的水平位移为:()l2/3EI(→)A. 2MB. Ml2/3EI(→)l2/3EI(←)C. 2MD. Ml2/3EI(←)的值为()5. 图示结构MCBA. 0.5 FLB. FLC. 1.5 FLD. 2 FL二、判断题(30分,共 10 题,每小题 3 分)1. 图示结构横梁无弯曲变形,故其上无弯矩()2. 静定结构的支反力一定可以只凭平衡方程求解得到()3. 在荷载作用下,超静定结构的内力与EI的绝对值大小有关。
()4. 力法方程的物理意义是表示变形条件。
()5. 计算超静定结构位移时,单位力只能加在原超静定结构上。
()6. 位移法仅适用于解超静定结构,不适用于解静定结构。
()7. 图示梁AB在所示荷载作用下的M图面积为:gl3/38. 单独使用力矩分配法,只能解算连续梁及无侧移刚架。
()9. 功的互等定理仅适用于线性弹性体系,不适用于非线性非弹性体系()10. 对于某结构,在1、2截面分别作用P1与P2,当P1=1,P2=0,时,1点的挠度为a1,2点挠度为a2。
当P1=0,P2=1,时,则1点的挠度为(a1+a2)。
()三、填空题(30分,共 10 题,每小题 3 分)1.位移法方程中的系数是由______互等定理得到的结果。
2. 对图示结构作内力分析时,应先计算 ______ 部分,再计算 ______ 部分3.图示结构K截面的弯矩M K=_____。
2023年试验检测师之道路工程练习题(二)及答案

2023年试验检测师之道路工程练习题(二)及答案单选题(共30题)1、良好的级配应使集料满足如下()要求。
A.总表面积小,空隙率大B.总表面积小,空隙率小C.总表面积大,空隙率大D.总表面积大,空隙率小【答案】 B2、在沥青混合料中起填充作用的,粒径小于()的矿物质粉末,称为填料。
A.1.18mmB.0.6mmC.0.3mmD.0.075mm【答案】 D3、标准套筛的筛孔粒径是按()递减的方式设置的。
A.1/2B.1/3C.1/4D.1/5【答案】 A4、某新建高速公路交工验收,沥青混凝土路面采用横向力系数测试车检测,己知该路面的抗滑设计标准SFC=49.测值:45、55、53、42、49、50、61、56、50、52。
针对本项目回答以下问题。
(己知保证率95%时,t0.95/√10=0.580)2)本路段交工验收的评价结果为()。
(2017真题)(2017检师真题)A.优B.良C.合格D.不合格【答案】 D5、采用相对用量表示法表示水泥混凝土的配合比,如1:2.34:3.76:0.52,其中1为()的比值。
A.细集料B.粗集料C.水D.水泥【答案】 D6、细集料砂当量试验中,砂当量结果描述正确的是()。
A.砂当量值越高,表示集料越洁净B.砂当量值越低,表示集料越洁净C.砂当量值与集料清洁度无关D.砂当量值越高,表示集料越粗【答案】 A7、二级公路土方路基路床压实度规定值为()。
A.≥96%B.≥95%C.≥94%D.≥93%【答案】 B8、用贝克曼梁法测定高速公路土基回弹弯沉时,加载车的后轴轴载一般为()。
A.60kNB.80kNC.100kND.120kN【答案】 C9、某水泥抗弯拉强度试验结果分别为:4.4MPa,3.6MPa,3.8MPa,则其抗折强度为()A.3.6MPaB.3.7MPaC.3.8MPaD.3.9MPa【答案】 B10、以下关于热沥青取样的描述不正确的是()。
A.有搅拌设备的储罐中取样时,先将经加热已经变成流体的黏稠沥青充分搅拌后,用取样器从沥青层的中部取规定数量样品B.从沥青罐车中取样,当仅有放料阀时,待放出全部沥青的1/2时取样;若从顶盖处取样时,可用取样器从中部取样C.当沥青罐车卸料过程中取样时,按时间间隔均匀地取至少3个规定数量沥青,然后将这些沥青充分混合后取规定数量样品D.沥青样品可存放在密封带盖的金属容器中,或灌入塑料桶等密闭容器中存放。
《微积分》(中国商业出版社 经管类)课后习题答案二

《微积分》(中国商业出版社 经管类)课后习题答案习 题 二1.列数列}{n x 当∞→n 时的变化趋势,判定它们是否收敛,在收敛时指出它们的极限: (1); )1(1>=a ax nn (2); 3)1(nn x -= (3); 11ng x n = (4); )11()1(nx n n +-= (5); 1)1(3n x n n -+= (6); 1sec nx n =(7); 2642)12(531limn n n ++++-++++∞→ (8). 2121121211lim )1(22-∞→++++++n n解:1)收敛.因为当∞→n 时,; )1(>∞→a a n 所以; 0→n x 所以. 01lim lim ==∞→∞→nx n x ax2)因为⎪⎩⎪⎨⎧==为奇数为偶数n n x x n n 313 所以n x 是发散的;3)发散的.因为当∞→n 时,01→n ;所以-∞→=ng x n 11; 4)因为⎩⎨⎧-=为奇数为偶数n n x n 1 1 所以n x 是发散的;5)收敛的.因为当∞→n 时, 01→n ;所以31)1(3→-+=n x n n ;即∞→x lim 3=n x ; 6)收敛的.当∞→n 时,01→n ;11sec →n ;即∞→x lim 1=n x ; 7)因为nn n n n n n n +=+-+=++++-+++12)22(2)121(2642)12(531 ;所以∞→x lim11=+nn; 所以是收敛的;8)因为23211)21(1212112121121211121)1(221=----=++++++----n n n n1211-+n所以2321123lim 1=+-∞→n x ; 所以是收敛的;2.据我国古书记载,公元前三世纪战国时代的思想家庄子在其著作中提出“一尺之棰,日取其半,万世不竭”的朴素极限思想,将一尺长的木棒,“日取其半”,每日剩下的部分表示成数列,并考察其极限.解:数列为; 21 , , 21 , 21,11-n 2所以通项为; 211-=n n a 所以∞→x lim 0=n a ;3.由函数图形判别函数极限是否存在,如存在则求出其值:(1); )0(lim 0>→μμx x (2); )0(lim <∞→μμx x(3); 1) , 0(lim 0≠>→a a x x (4); 1) , 0(lim ≠>∞→a a x x(5); 1) , 0(log lim 1≠>→a x a x (6); arccos lim 1x x -→(7); arctan lim 1x x → (8). cos lim x x ∞→解:1)当0x →时,∞→x lim ; 0)0(=>u x u2)∞→x lim ∞→=<x u u x lim)0(; 0)0u (1=<-ux3)∞→x lim 1)1 , 0(=≠>a a a x4) 0; 1<a∞→x lim ⎩⎨⎧><=≠>.1 1.1 0)1 , 0(a a a a a x 所1 ; 1>a 5)0)1 , 0(log lim 1=≠>-→a a a x x6)π=-→x arccos lim 1x 所以; 1cos -=π7). 4x arctan lim 1π=-→x8)x cos lim ∞→x 的极限不存在4.求下列函数在指定点处的左、右极限,并判定函数在该点的极限是否存在:(1); 0 , )(==x xx x f (2); 0 ,3)( 1==xx f x(3); 0 ,1arctan )(==x x x f(4). 1 , 21 , )1arcsin(1 , )1(11)(=⎪⎩⎪⎨⎧≤≤-<+=x x x x x g x f解:1)10lim -→x +→≠-=0lim 1)x (f x ; 1)(f =x 所以该点的极限不存在2)10lim -→x ≠=0)x (f +→0lim x ; )x (f ∞=所以该点的极限不存在3)10lim -→x ; 2f(x)lim 2-f(x)0ππ=≠=+→x 所以该点的极限不存在4) ; 0)x (f lim 211)x (f lim 11=≠=+-→→x x g 所以该点的极限不存在5.用δε-或N -ε的方法陈述下列极限:(1); )(lim A x f ax =+→ (2); )(lim A x f ax =-→(3); )(lim A x f x =+∞→ (4). )(lim A x f x =-∞→解:1)当δ<-<a x 0时 ξ<-A x f )(2)当δ<<x -a 0时 ξ<-A x f )( 3)当M x >时 ξ<-A x f )( 4)当-M x <时 ξ<-A x f )(6.用极限的严格定义(即δε-或N -ε的方法)证明下列极限: (1); 01lim4=∞→nn (2); 31135lim22-=+-∞→n n n(3); 01lim 1=++-→x x (4). 010lim =-∞→x x解:1)对于任意给定的ξ,要使δψξ成立,只要使ξ14>n 即1n ξ>成立所以对于任意给定的ξ,存在41N ξ=当N n >时恒有ξ<-014n成立,故01lim4=∞→n x2)对于任意给定的ξ,要使ξ<++-3113522n n 成立即29316 )(1lim ξξ->+∞=→n x f o x x 成立所以对于正数ξ,存在293-16N ξξ=成立当N n >时恒有ξ<++-3113522n n 成立 所以31135lim22-=+-∞→n n x 3)由于10)(+=-x x f 所以对于任意给定的0>ξ,存在2ξδ=当δ<+<10x 时 恒有ξ<-0)(x f 成立 故01lim 1=++-→x x4)对于任意给定的正数ξ要使ξ<-010x 成立即ξ1g x >成立 所以存在. 1g X ξ=当X x >时恒有ξ1g x >成立 即. 010lim =∞→x x7.求下列极限:(1); )(lim 330hx h x h -+→ (2); 11lim 1--→x x n x(3);)2(arctan lim1x x x ++∞→ (4); 11lim 21⎪⎪⎭⎫⎝⎛---→x x x xx (5); 11lim220xx x +-→ (6); 231lim3xx x +--∞→(7); 22312lim 4---+→x x x (8). )31(lim 22---++∞→x x x x x解:1)22203322303303)33(lim 33lim )(lim x h xh x hx h xh h x x h h h x h h h =++=-+++=-+→→→2)n x x n x =--→11lim 1 3)12)1(arctan lim 2arctan lim 1+=+=⎪⎪⎪⎭⎫⎝⎛++∞→+∞→πx x x x x 4)x x x x x x xx x x x x x 1lim)1()1)(1(lim )11(lim 1121+=-+-=---→→→ 5)2)11(lim )11(lim11lim20222022-=++-=-++=+-→→→x xx x x x x x x6))31)(2(91231lim33+-+--=+---∞→x x x xx x)31)(2()42)(2(33323+-++-+=x x x x x2-= 7))312)(22()312)(312(lim22312lim44++--++-+=---+→→x x x x x x x x)312)(22()4(2lim 4++---=→x x x x)312()22(2lim 4+++-=→x x x322=8))31(lim 22---++∞→x x x x x)3142(lim 22--++++=∞→x x x x x x1)31111142(lim 2=--++++=∞→xx x x xx8.求. 3545lim 1-∞→+-n n n解:51)53(95)54(411lim3545lim211=+-=+-∞→++-∞→n nn n n n nn9.下列数列}{n x ,当∞→n 时是否是无穷小量? (1); 31050nn x =(2)[]; 1)1(1n x nn -+=(3). n n n x =解:1)是无穷小量 因为0lim =∞→n n x2)是,因为0lim =∞→n n x (n 为奇数或者偶数)3)不是.10.当0→x 时下列变量中哪些是无穷小量?哪些是无穷大量?(1);100 3x y = (2); 1012100x y =(3); )1(log 2x y += (4); 4cot x y =(5); 2sec ⎪⎭⎫⎝⎛-=x y π(6). 1sin 1xx y =解:1)是无穷小,因为0lim 0=→y x2)是无穷大量,因为+∞=→y x 0lim3)是无穷小量,因为0lim 0=→y x4)是无穷大量,因为+∞=→y x 0lim5)是无穷大量,因为+∞=→y x 0lim6)非大非小11.已知)()(lim 0x g x f x x →存在,而0)(lim 0=→x g x x ,证明. 0)(lim 0=→x f x x解:因为, 5252lim 5arctan 2lim00==→→x x x x x x)(lim )(lim )()(lim 00x g x f x g x f x x x x x x →→→=存在 而0)(lim 0=→x g x x所以; 0)(lim 0=→x f x x12.设31lim 21=-++→x bax x x ,求a ,b .解:因为3lim 1lim 121=+=-++→→y x x b ax x x x所以1)2)(1(12---=-++x x x x b ax x 所以1a =,2b -=13.设011lim 2=⎪⎪⎭⎫⎝⎛--++∞→b ax x x x ,求a ,. b解:011lim )11(lim 222=+----+=--++∞→∞→x bbx ax ax x b ax x x x x所以即b bx ax ax x ----+221为一常数 所以-1b 1a ==14.当0→x 时,下列变量中与423x x +相比为同阶无穷小的是(B ).A .xB .2xC .3xD .4x解:B . 因为3131lim3lim 204220=+=+→→x x x x x x15.求. 28159lim 4823+--∞→n n n n n解:3281591lim281593lim4835482=+--=+--∞→∞→nn n n n nn n n16.设a x →时∞→)(x f ,∞→)(x g ,则下列各式中成立的是(D ).A .∞→+)()(x g x fB .0)()(→-x g x fC .0)()(1→+x g x f D .0)(1→x f解:D.因为a x →时∞→f(x),∞→g(x),所以0)(1→x f ,0)(1→x g .17.求下列极限 (1); )72()43()12(lim 510--+∞→x x x x (2). )cos 100(1lim 32x xx x x +++∞→解:1)=--+∞→510)72()43()12(limx x x x 32243232)72()43()12(lim15510151515510==--+∞→x x x x x x 2)x)105100(1111lim)105100(1lim 232+++=+++∞→∞→xx x x x x x x x18.求下列极限:(1); 3sin 2sin lim0x x x → (2); sin sin lim 0xx xx x +-→(3); 5arctan 2lim0x x x → (4); sin lim ⎪⎭⎫ ⎝⎛∞→n n n π(5); sin lim x x x -→ππ (6); cos 1lim 0xxx -+→(7); cos 1cos 1lim20x x x --→ (8); sin tan lim 0xxx x -→(9); sin tan cos lim 0x x x x x x --→ (10). 65)1sin(lim 21-+-→x x x x解:1)3232lim 3sin 2sin lim00==→→x x x x x x2)0sin 1sin 1lim sin sin lim00=+-=+-→→xx x xx x x x x x 3)5252lim 5arctan 2lim00==→→x x x x x x4)ππππ===∞→∞→∞→nn nn nn n n n 1lim 1sin lim)sin (lim5)11cos lim ' )()(sin lim sin lim'=-=-=-→→→xx x x x x x x πππππ 6)2)'2sin 2()'(lim2sin2limcos 1lim 000===-+++→→→xx xx xx x x x7)2 8)0)cos cos 1(lim ')'sin (tan lim sin tan lim 2000=-=-=-→→→x x x x x x x x x x x9)1cos lim )cos (sin )cos 1(lim sin tan cos lim0==-=--→→→x xx x x x x x x x x x10)7111lim )6)(1(1lim65)1sin(lim 1121=+=+--=-+-→→→x x x x x x x x x x19.设3)1sin(lim 221=-++→x b ax x x ,求a ,. b解:因为3)1)(1(lim)1sin(lim21221=+-++=-++→→x x bax x x b ax x x x所以)5)(1(2+-=++x x b ax x所以-5b . 4==a20.设nn n n x n ++++++=22212111 ,用极限存在的夹逼准则求. lim n n x ∞→解:因为nn nx n nn +≤≤+22111而111lim 2=+∞→n nn ,11lim 2=+∞→nn nn所以1lim =∞→n n x21.求下列极限:(1); 31lim 3xx x ⎪⎭⎫ ⎝⎛+∞→ (2); )21(lim 13+∞→-xx x(3); 21lim 30x x x +→ (4); )tan 1(lim cot 210x x x -→+(5); 1232lim 1+∞→⎪⎭⎫⎝⎛++x x x x (6). 1312lim 10xx x x ⎪⎭⎫ ⎝⎛--→解:1). ])31[(lim )31(lim 9933e xx xx x x =+=+∞→∞→2). )21(*])21[(lim )21(lim 3232213---∞→+∞→=--=-e xx x xx xx3). 323221030])21[(lim 21lime x x x x xx =+=+→→4). e x)tan 1(*]x)tan 1[(lim x)tan 1(lim 2-2tanx 12cotx -10=+++-→=→x x5). 1x)1221(lim )1232(lim 212121x e x x x x x x =+++=++++∞→+∞→6)xx x x x x x x 1010)131(lim )1312(lim --=--→→ =331)311(lim +-→-+x x x=. e22.设xx x k x x xx 2sinlim lim 2∞→-∞→=⎪⎭⎫⎝⎛-,求. k解:因为.222sin 2lim 2sinlim ==∞→∞→xx x x x x所以. 2)1(lim )(lim 22*2==-=--∞→-∞→k kk xx x x e xk x k x 所以. n2121k =23.判定下列函数在定义域上是否连续(说明理由):(1)⎪⎩⎪⎨⎧=≠=; 0 , 0,0 , 1sin )(2x x x x x f (2)⎪⎩⎪⎨⎧=≠=. 0 , 1, 0 , sin )(x x xx x f解:1)因为0x)(f lim 0=→x ,而0f(0)=.所以f(x)在定义域上是连续的。
基础会计学书本习题答案(最新)

《基础会计学》课后习题参考答案第一章一、单选1、C2、A3、C4、A5、A6、C7、B8、B9、D 10、 C二、多选1、AC2、ACD3、BD4、BCD5、ABCD6、AB7、ABC8、ABC9、ABCD 10、ABC三、判断1、√2、√3、√4、√5、√6、√7、√8、√9、√ 10、×11、√ 12、× 13、× 14、× 15、×第二章一、单选1、C2、C3、D4、B5、B6、D7、B8、A9、C 10、B二、多选1、ABC2、ABC3、CD4、ACD5、BD6、ABC7、ABCD8、ABD9、ABC 10、ABCD三、判断1、×2、×3、×4、×5、×6、√7、√8、√9、√ 10、√四、简答略五、业务题习题一解答:习题二[作业题2-5-2]解答:经济业务对会计要素的影响7月31日:资产总额:510000元;负债总额:160000元;所有者权益总额:350000元第三章一、单选1、A2、C3、D4、A5、B6、C7、A8、D9、B 10、B二、多选1、ABCD2、ABCD3、AB4、ABCD5、BD6、ABD7、ABCD8、ABC9、BC 10、AB三、判断1、×2、√3、×4、√5、√6、√7、√8、√9、√ 10、×四、简答略五、业务题习题一:习题二:习题三:根据8月份发生的每笔经济业务的类型,编制会计分录习题四:(注意:请将第8笔业务金额110 000改为10 000元)3、根据1、2步的资料,开设有关账户,登记期初、本期数额,结出本期发生额和期末余额库存现金银行存款应收账款期初: 2000 期初:15000 期初:83000③50000 ②80000 ③ 50000 ④ 70000 ⑥ 20000⑥20000 ⑤5000合: 50000 ⑦20000 合: 70000 合: 20000余: 52000 ⑧10000余: 133000合:100000 合:85000余:30000原材料库存商品期初:270000 期初:240000① 50000⑤5000 合: 0合: 5 5 000 余:240000余: 325000固定资产短期借款应付账款期初:270000 期初:110000 期初:20000⑧ 10000 ⑦20000 ① 50000 余: 270000 合: 10000 合: 20000 合: 50000余: 100000 余: 50000实收资本主营业务收入期初:750000 ② 80000④70000余: 750000合: 1500004、编制试算平衡表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习 题 二
1 2-1 某双层介质绝缘结构,第一、二层介质的电容、电阻分别为:C 1=4200PF 、
2 R 1=1400M Ω;C 2=3000PF ,R 2=2100M Ω.施加40kV 直流电压时,试求:
3 (1)t=0合闸瞬间,C 1、C 2上各有多少电荷?
4 (2)到达稳态后,C 1、C 2上各有多少电荷?,绝缘中的电导电流为多大?
5
解: (1) t=0时 u u u C C u u =+=2112
2
1 ;
6 可得:
c
u C Q c u C Q kv
u kv u 1070 10703.23 ;7.166
222611121--⨯==⨯====
7
(2) t=∞时 u u u R R u u =+=2121
2
1 ;
8 可得:
A
R R u
I c
u C Q c u C Q kv u kv u μ 43.11 1072 102.6724 ;162
162226
11121=+=⨯==⨯====--
9
10
11
2-2 某设备的对地电容C=3200PF ,工频下的tan δ=0.01,如果施加32kV (有12 效值)工频电压,求:
13 (1)设备绝缘所吸收的无功功率和所消耗的有功功率。
14 (2)若将该绝缘用并联等值电路来表示,其中电阻值R P 为多少? 15 (3)若将该绝缘用串联等值电路来表示,其中电阻r s 和电容C S 值各为多少?
16
解:(1)
乏 1030 19.10tan 22=====c u uI Q W
c u p C ϖδϖ
17
18 (2)
Ω
==∴=
M c
R cR P p
5.99tan 1
1
tan δϖϖδ并联等值电路下:
19
20 (3) Ω==
∴=k c
R cR P s
95.9tan
tan ϖδ
ϖδ串联等值电路下:
21
2-3 充有变压器油的均匀电场间隙极间距离d=30mm ,极间施加施加工频电22 压u=300kV (有效值)。
若在极间放置一屏障,设油εr1=2,极间障εr2=4,求:
23 (1)极间障厚度为3mm 时,极间障和油中的电场强度各为多少?油中的电24 场强度比没有极间障时提高了多少倍?
25
(2)极间障厚度为10mm 时,极间障和油中的电场强度各为多少?油中的26 电场强度比没有极间障时提高了多少倍?
27
mm
kV E mm kV E d d d d d u E d E d E E /10 ; /5.10 27 ;3 ;30 4 2 ; 212122r 1r 22112211===-======+=得:代入;;将:εεεε 28
29 mm
kV E mm kV E d d d d d u E d E d E E /6 ; /12 20 ;10 ;30 4 2 ; 212122r 1r 22112211===-======+=得:代入;;将:εεεε
30
2-4 一根额定电压为220kV (有效值)的单芯电力电缆,芯线外半径31 r 0=20.5mm ,油纸绝缘层厚度d=18mm,分阶为两层,分阶半径r 2=30mm 内层绝缘ε
32 r1
=4.3,外层绝缘εr2=3.5,试求在额定电压下:
33 (1)内层绝缘最大工作场强和利用系数 34 (2)外层绝缘最大工作场强和利用系数 35 2-5 电介质的绝缘电阻和导体的电阻有何不同?
36 2-6 气体、液体、固体电介质的击穿过程有何异同,试比较之。
37
解:(1)
(2)
38
2-7 影响液体电介质击穿的主要因素有哪些?
39
2-8 固体电介质的电击穿和热击穿有何区别?。
