第二章 流体的P-V-T关系讲解
合集下载
化工热力学第二章 流体的pVT关系

南阳理工学院
生化学院
化工热力学
第二章
流体的PVT关系 关系 流体的
(3)理想气体状态方程的变型
G G pV = RT ........... n = M M
气体密度:ρ = G = pM .......... ( Kg / m3 ) 气体密度:
V RT
p1V1 p2V2 = = nR T1 T2
( ∂ P ∂V )T=T = 0 C 2 (∂ P ∂V2 )T=TC = 0
化工热力学
第二章
流体的PVT关系 关系 流体的
∂V = βV ∂T p
∂V = − κV ∂p T
dV = β dT − κdp V
对于液体,由于其具有不可压缩性,体积膨胀系数和等温 对于液体,由于其具有不可压缩性, 压缩系数是温度和压力的弱函数, 压缩系数是温度和压力的弱函数,其数值可以从文献或工具书 中查到。因此,在液体的温度和压力变化不大时, 中查到。因此,在液体的温度和压力变化不大时,可以将体积 膨胀系数和等温压缩系数当作常数,则 膨胀系数和等温压缩系数当作常数,
南阳理工学院
生化学院
化工热力学
第二章
流体的PVT关系 关系 流体的
2.1 纯物质的 纯物质的p-V-T关系 关系
流体的PVT数据是化工生产﹑工程设计和科学 数据是化工生产﹑ 流体的 数据是化工生产 研究最为基本的数据, 研究最为基本的数据,它们是化工热力学的基础 数据。这些数据是可以直接测量的, 数据。这些数据是可以直接测量的,也可以通过 关联计算得到。要进行关联计算,首先,我们就 关联计算得到。要进行关联计算,首先, 要搞清楚纯物质PVT之间有何种数学关系。 之间有何种数学关系。 要搞清楚纯物质 之间有何种数学关系 三维立体图2-1是典型的纯物质的 关系图。 三维立体图 是典型的纯物质的PVT关系图。 是典型的纯物质的 关系图
化工热力学-流体的 p-V-T 关系

Z
Z
Z
1
q
Z
或
Z
0.026196
Z
Z
0.026196
1.026196 Z 6.6060 0.026196
将 Z= 代入上式右边,迭代计算后得到收敛值Z=0.04331。
V l ZRT 0.043318.314350 133.3 cm3mol1
p
0.9457
为了比较计算结果,在例2/5-1的情况下,运用四种立方型状态 方程所计算得到的V v及V l 值列表如下:
第二章 流体的 p-V-T 关系
(一)纯流体的三维相图
自由度与相律
(二)纯流体的二维相图
异戊烷的p-V图
p-T相图
T-V图
(三)纯流体 pVT 行为的模型化
→ 什么是状态方程?
f p,V,T 0
dV
V T
p
dT
V p
T
dp
V=V(T,p)
p=p(T,V )
(四)理想气体
只有在Zc相等的条件下,对比态原理才能成立
以ω为第三参数的对应状态原理
Z f pr ,Tr ,
偏心因子
Pitzer: 物质对比饱和蒸汽压的对数,与对比温度的倒数呈 下列线性关系
log
prS
a 1
1 Tr
prS
pS pc
球形分子虽然临界参数相差很大,但在Tr=0.7时,对比蒸气压 logprS = -1 。
ZC 3/8 1/3 1/3 0.30740
临界压缩因子Zc
VDW: 3/8 RK/SRK: 1/3 PR: 0.3047
立方型状态方程的数值求解
p
RT
V b
V
第二章流体的P-V-T关系2[1].3_2.4
![第二章流体的P-V-T关系2[1].3_2.4](https://img.taocdn.com/s3/m/5ce631a4d1f34693daef3e13.png)
BP Z 1 RT
例:二元混合物
Bm yi y j Bij (2 58)
i j
Bm yi y j Bij
i 1 j 1
2
2
二次型混合规则
y1 y1B11 y1 y2 B12 y2 y1B21 y2 y2 B22
3
例2-3
4.6 10 pr Z 0.214pr (1) 6 21.4910
6
Z Z Z (2)
0 1
3、计算步骤 设初值 Z0 (1) Pr
查图 +Tr
Z0
,Z1
(2)
Z1
| Z0 - Z1 | < ε
?
至| Zn-1 - Zn | < ε ………..
误差为1.216%!
3) 普遍化关联法 误差仅为0.53%!!! 精度:普遍化关联法 > RK方程 > 理想气体 例2-4,2-5
总结: 对比态原理— 计算压缩因子Z
查阅有关文 献的两参数 压缩因子图 (Z c=0.27)
附表三
研究对应态原理的意义
符合对应态关系的不仅有 Z ,还有其它流体的多 种基础物性。如:热容、逸度、蒸气压,但 Z 是 最基本的,因为状态方程是推算其它性质最重要 的模型。 使流体性质在对比状态下便于比较。当已知一种 物质的某种性质时,往往可以用这个原理来确定 另一结构与之相近的物质的性质。
1. 不含有物性常数,以对比参数作为独立
变量;
2. 可用于任何流体的任一条件下的PTV性
质计算。
三、对比态原理——两参数压缩因子(P17)
P T V Pr , Tr ,Vr Pc Tc Vc
PV PcVc PrVr PrVr Z ZC RT RTc Tr Tr
化工热力学_02流体的 p-V-T关系讲解

21
证明Zc = 0.375
p RT a V b V2
p ( V )T TC 0
RTc (Vc b)2
2a Vc3
0
a 9RTcVc ; 8
2 p ( V 2 )T TC 0
2RTc (Vc b)3
6a Vc 4
0
b Vc 3
9RTCVC
pC
RTC a VC b VC 2
pC
第二章 流体的p-V-T关系
学时: 8 ( 共 4 讲,第 2-5 讲 )
目的要求:
(1) 熟悉纯物质的p-V -T图及相图上的重要概念(重点)。 (2) 应用R-K方程、两相维里方程计算单组分气体的p-VT关系。 (3) 正确、熟练地应用三参数普遍化方法计算单组分气 体的p-V-T关系。 (4) 理解对比态原理及三参数对比态原理计算物性的方 法,了解偏心因子对比态原理(重点) 。
11
b: 低压下的气体(特别是难液化的N2、H2、CO、CH4等), 在工程设计中,在几个大气压下,仍可按照理想气体状态
方程计算P、V、T;而较易液化的气体,如NH3,CO2,C2H4 等,在较低的压力下,也不能用理想气体状态方程计算。 c: 应用时注意 R 当 T(K), P(Pa), V(m3/mol)时,R=8.314J/mol.K 当 T(K), P(Pa), V(m3/kmol)时,R=8.314×103 J / kmol.K
1
第一节 纯物质的p-V-T性质 (第1讲,重点)
物质的状态及性质的变化是由于温度、压力变化引起的, 因此流体的p-V-T数据是化工生产、工程设计和科学研究最 为基本的数据,是化工热力学的基础。
(1)可以通过p-V-T关系实现流体的P、V、T三者之间的互算
证明Zc = 0.375
p RT a V b V2
p ( V )T TC 0
RTc (Vc b)2
2a Vc3
0
a 9RTcVc ; 8
2 p ( V 2 )T TC 0
2RTc (Vc b)3
6a Vc 4
0
b Vc 3
9RTCVC
pC
RTC a VC b VC 2
pC
第二章 流体的p-V-T关系
学时: 8 ( 共 4 讲,第 2-5 讲 )
目的要求:
(1) 熟悉纯物质的p-V -T图及相图上的重要概念(重点)。 (2) 应用R-K方程、两相维里方程计算单组分气体的p-VT关系。 (3) 正确、熟练地应用三参数普遍化方法计算单组分气 体的p-V-T关系。 (4) 理解对比态原理及三参数对比态原理计算物性的方 法,了解偏心因子对比态原理(重点) 。
11
b: 低压下的气体(特别是难液化的N2、H2、CO、CH4等), 在工程设计中,在几个大气压下,仍可按照理想气体状态
方程计算P、V、T;而较易液化的气体,如NH3,CO2,C2H4 等,在较低的压力下,也不能用理想气体状态方程计算。 c: 应用时注意 R 当 T(K), P(Pa), V(m3/mol)时,R=8.314J/mol.K 当 T(K), P(Pa), V(m3/kmol)时,R=8.314×103 J / kmol.K
1
第一节 纯物质的p-V-T性质 (第1讲,重点)
物质的状态及性质的变化是由于温度、压力变化引起的, 因此流体的p-V-T数据是化工生产、工程设计和科学研究最 为基本的数据,是化工热力学的基础。
(1)可以通过p-V-T关系实现流体的P、V、T三者之间的互算
第二章流体的P-V-T关系与状态方程

2.2.3 立方型状态方程
2.2.3.1 Van der Waals (vdW)范德华方程
RT a pVbV2
体积修正项, b为有效分子体 积,斥力参数
压力修正项, a为引力参数
vdW方程的优点:
1)1873年范德华在其著名的论文“关于气态和液态的连 续性”中提出,是第一个有实用意义的状态方程。1910年 曾获诺贝尔奖。
方程两边乘以 (V b ) P
得:
RT a(Vb)
VbPP1 T/2VVb
V k 1R P TbPa 1T /2 V V k k V b kb
初值取
1.875107
理想气体EOS只适合压力非常低的气体, 不适合真实气体。
2.2.2 气体的非理想性
真实气体分子有大小、分子间有相互作用力是造成气体非理 想性的原因。 真实气体对理想气体的偏离程度可以用压缩因子Z来表达:
Z PV V RT Vig
分子间吸引力促使Z<1; 分子间排斥力使Z>1; 吸引力和排斥力的平衡暗指Z=1。
方程在P →0 时,应变为:PV = RT
2. 低压下的气体(特别是难液化的N2,H2,CO,CH4,…), 在工程设计中,在几十个大气压(几个MPa)下,仍可按 理想气体状态方程计算P、V、T: 而对较易液化的气体,如NH3,CO2,C2H4(乙炔)等,在 较低压力下,也不能用理想气体状态方程计算。
对方程的引力项进行修正,以使计算的V减小, 提高计算的准确性,是真正实用的EOS。
R-K 方程中的常数a,b 的求取
•用同于vdW方程的方法得到常数a,b值, •即临界等温线在临界点的条件得到:
a 0 .42748
R
2T
2.5 c
化工热力学第2章流体的PVT关系
时,这种流体就处于对比状态。
例如:H2 和N2这两种流体
对于H2
状态点记为1,P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2,P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ,Pr1=Pr2 时,此时就称这两种流体处
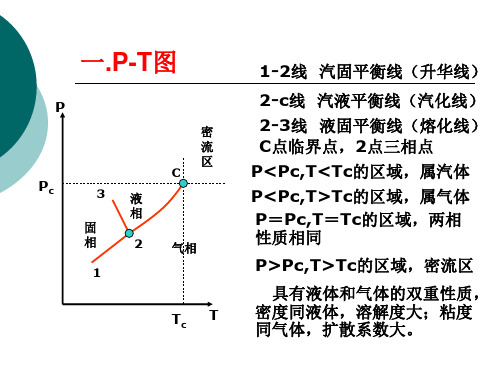
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线(升华线)
2-c线 汽液平衡线(汽化线) 2-3线 液固平衡线(熔化线) C点临界点,2点三相点 P<Pc,T<Tc的区域,属汽体 P<Pc,T>Tc的区域,属气体 P=Pc,T=Tc的区域,两相 性质相同
P>Pc,T>Tc的区域,密流区
压缩因 子,方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年,Redlich and Kwong)
(1) R-K Eq的一般形式:
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值, 不能将二者混淆。 在范德华方程中,修正项为a/V2,没有考虑温度的影响 在R-K方程中,修正项为,考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数,具有单位。
为表征物质分子的偏心度,既非球型分子偏离球对称的 程度,简单流体为0
R-K Eq经过修改后,应用范围扩宽。 SRK Eq:可用于两相PVT性质的计算,对烃类计算,其 精确度很高。
例如:H2 和N2这两种流体
对于H2
状态点记为1,P1 V1 T1
Tr1 =T1/TcH2
Pr1=P1/PcH2
对于N2
状态点记为2,P2 V2 T2
Tr2 =T2/TcN2
Pr2=P2/PcN2
当Tr1=Tr2 ,Pr1=Pr2 时,此时就称这两种流体处
一.P-T图
P
Pc
3液
相
固
相
2
1
密 流 区 C
气相
Tc T
1-2线 汽固平衡线(升华线)
2-c线 汽液平衡线(汽化线) 2-3线 液固平衡线(熔化线) C点临界点,2点三相点 P<Pc,T<Tc的区域,属汽体 P<Pc,T>Tc的区域,属气体 P=Pc,T=Tc的区域,两相 性质相同
P>Pc,T>Tc的区域,密流区
压缩因 子,方 程的计 算值和 实测值 的符合 程度是 判断方 程的优 劣标志 之一。
2. R-K Equation (1949年,Redlich and Kwong)
(1) R-K Eq的一般形式:
P
RT V-b
-
a T0.5V(V
b)
(2-11)
① R-K Equation中常数值不同于范德华方程中的a、b值, 不能将二者混淆。 在范德华方程中,修正项为a/V2,没有考虑温度的影响 在R-K方程中,修正项为,考虑了温度的影响。 ② R-K Equation中常数a、b值是物性常数,具有单位。
为表征物质分子的偏心度,既非球型分子偏离球对称的 程度,简单流体为0
R-K Eq经过修改后,应用范围扩宽。 SRK Eq:可用于两相PVT性质的计算,对烃类计算,其 精确度很高。
化工热力学第二章-----流体的PVT关系 [兼容模式]
![化工热力学第二章-----流体的PVT关系 [兼容模式]](https://img.taocdn.com/s3/m/83ffab71a26925c52cc5bf48.png)
24
MH方程
方程情况 ( 1 ) MH 方程是 1955 年 Martin 教授和我国学者候虞钧 教授提出的。首次发表在杂志AIChE J(美国化学工程 师会刊)上。有9个参数。 (2)为了提高该方程在高密度区的精确度,Martin于 1959年对该方程进一步改进。 (3)1981年候虞钧教授等又将该方程的适用范围扩展 到液相区,改进后的方程称为MH-81型方程。
0.5 r 2
k 0.3746 1.54226 0.26992 2
a( T )=a( T )=f (Tc,pc, Tr ,ω)
15
P-R方程
方程使用情况: (1)RK方程和SRK方程在计算临界压缩因子Zc和液 体密度时都会出现较大的偏差,PR方程弥补这 一明显的不足; (2)它在计算饱和蒸气压、饱和液体密度等方面有更 好的准确度; (3)是工程相平衡计算中最常用的方程之一。
8
van der Waals方程
1873年van der Waals(范德华) 首次提出了能表达从气态 到液态连续性的状态方程 :
•参数: (1)a/V2—分子引力修正项。 由于分子相互吸引力存在,分子撞击器壁的力减小,造成压力 减小。 (2)b —分子本身体积的校正项。 分子本身占有体积,分子自由活动空间减小,由V变成V-b。 分子自由活动空间的减小造成分子撞击器壁的力增大。b增大, 造成压力增大。
2
一、纯物质的P-T关系
1-2线 汽固平衡线(升华线)
P
A
Pc
C
超临 界流 体区
2-c线 汽液平衡线(汽化线) 2-3线 液固平衡线(熔化线) C点临界点,2点三相点 P<Pc, T<Tc的区域,属汽体 P<Pc, T>Tc的区域,属气体
化工热力学第二章 流体的pVT关系

化工热力学
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式: p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数,在SRK 方程中,a 不仅是物性的函数,而且还是温度的函数,只有在特 定的温度下,对于某一物质而言, a 才能为定值。
方程常数:
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求:
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法, 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体,由于其具有不可压缩性,体积膨胀系数和等温 压缩系数是温度和压力的弱函数,其数值可以从文献或工具书 中查到。因此,在液体的温度和压力变化不大时,可以将体积 膨胀系数和等温压缩系数当作常数,则
第二章 流体的PVT关系
第2章 流体的p-V-T关系
流体指除固体以外的流动相的总称。均 匀流体一般分为液体和气体两类。
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
重点内容
纯物质的p-V-T关系
状态方程 立方型状态方程 多参数状态方程 对应态原理及其应用 流体的蒸气压、蒸发焓和蒸发熵
方程形式: p RT a(T )
V b V (V b)
Soave 是把R-K 方程中的常数a 看作是温度的函数,在SRK 方程中,a 不仅是物性的函数,而且还是温度的函数,只有在特 定的温度下,对于某一物质而言, a 才能为定值。
方程常数:
a(T
)
ac
(Tr
,)
0.42748
混合规则与混合物的p-V-T关系 液体的p-V-T关系
南阳理工学院 生化学院
化工热力学
第二章 流体的PVT关系
本章要求:
1.了解纯物质的P-T图和P-V图 2.正确、熟练地应用R-K方程、两项维里方程计 算单组分气体的P-V-T关系 3.正确、熟练地应用三参数普遍化方法计算单组 分气体的P-V-T关系 4.了解计算真实气体混合物P-V-T关系的方法, 并会进行计算。
化工热力学
第二章 流体的PVT关系
V T
p
V
V V p T
dV dT dp V
对于液体,由于其具有不可压缩性,体积膨胀系数和等温 压缩系数是温度和压力的弱函数,其数值可以从文献或工具书 中查到。因此,在液体的温度和压力变化不大时,可以将体积 膨胀系数和等温压缩系数当作常数,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
RT
V V2 V3
B B RT
C C B2 R2T 2
D D 3BC 2B3 R3T 3
微观上, Virial 系数反映了分子间的相互 作用 ,如第二 Virial 系数( B 或 B´ )反映了两 分子间的相互作用,第三 Virial 系数( C 或 C´ ) 反映了三分子间的相
2 用状态方程可计算不能直接从实验测定的 其它热力学性质。
3 用状态方程可进行相平衡和化学反应平衡计 算。
2.2.1 理想气体方程
PV RT Z PV 1
RT
P为气体压力;V为摩尔体积; T为绝对温度;R为通用气体常数。
理想气体方程的应用
1 在较低压力和较高温度下可用理想气体 方程进行计算。
2.2.3 立方型状态方程
立方型状态方程可以展开成为 V 的三次方 形式。 van der Waals 方程是第一个适用真实 气体的立方型方程,其形式为:
RT a P V b V2
(2–5)
a
27
R
T2 2 C
64PC
b RTC 8PC
1 Redlich - Kwong ( RK )方程
互作用等等。
宏观上, Virial 系数仅是温度的函数。
舍项Virial 方程
Z 1 BP RT BC
Z 1 V V2
P < 1.5 Mpa P < 5.0 MPa
Virial 系数的获取
( 1 ) 由统计力学进行理论计算 目前应用很少
( 2 ) 由实验测定或者由文献查得 精度较高
( 3 ) 用普遍化关联式计算 方便,但精度不如实验测定的数据
2 为真实气体状态方程计算提供初始值。
3 判断真实气体状态方程的极限情况的正
确程度,当 P 0 或者 V 时,任何
的状态方程都还原为理想气体方程。
2.2.2 Virial方程
Virial方程的两种形式
Z PV 1 B P C P2 DP3 RT
Z PV 1 B C D
A ap 0.42748 Pr T
R2T 2
T2 r
B bP 0.08664 Pr
RT
Tr
SRK方程可以表示成压缩因子Z的三次方表达式:
Z 3 Z 2 A B B2 Z AB 0
3 Peng - Robinson ( PR )方程
P
RT V b
T 2.5 r
B bP 0.08664 Pr
RT
Tr
Tr
T Tc
Pr
P Pc
RK方程可以表示成压缩因子Z的三次方表达式:
Z 3 Z 2 A B B2 Z AB 0 Z PV
RT
2 Soave - Redlich - Kwong ( SRK )方程
P
RT V b
V
V
a
b
bV
b
2 10
a
ac
T
0.45724
R
T2 2 0.07780 RTc Pc
T
1
0.37464
1.54226
0.26992
2
1
T 0.5 r
2
PR方程预测液体摩尔体积的准确度较SRK有明 显的改善。
A ap 0.45724 Pr T
R2T 2
T2 r
B bP 0.07780 Pr
RT
Tr
PR方程可以表示成压缩因子Z的三次方表达式:
Z 3 1 BZ 2 A 2B 3B2 Z AB B2 B3 0
4 立方型状态方程的根及其求解方法
给定T和V,由立方型状 态方程可直接求得P 。但大 多数情况是由T和P求 V 。
2 流体的 P-V-T关系
2.1 纯物质的P-V-T关系 2.2 气体的状态方程 2.3 对比态原理及其应用 2.4 液体的P-V-T性质 2.5 真实气体混合物的P-V-T关系
2.1 纯物质的P-V-T关系
液
固 液
临界点
固
固液
气
临界点 气
汽
汽
凝固时收缩
凝固时膨胀
图2-1 纯物质的P-V-T相图
图2-2 P-V-T相图的投影图
2P V2
T
,c
0
2.2 状态方程 equation of state
纯流体的状态方程(EOS) 是描述流体P-V-T性质的 关系式。
f( P, T, V ) = 0
混合物的状态方程中还包括混合物的组成(通 常是摩尔分数)。
状态方程的应用
1 用一个状态方程即可精确地代表相当广泛 范围内的P、V、T实验数据,借此可精确地计算 所需的P、V、T数据。
当T > Tc 时,立方型状 态方程有一个实根,它是气 体容积。
当T<Tc时,高压下立 方型状态方程有一个实根, 它是液体容积。低压存在三 个不同实根,最大的V值是蒸 气容积,最小的V值是液体容 积,中间的根无物理意义。
立方型状态方程的求根方法: (1)三次方程求根公式; (2)迭代法。
简单迭代法求立方型状态方程的根( 以RK 方程为例说明,其它立方型状态方程求解根方 法类似。)
( 1 )蒸汽的摩尔体积
P
RT V b
在常压下加热水
液体水
带有活塞的汽缸保 持恒压
T
2
3
1
5 4
v
临界点
气体
液体
液体和蒸汽
饱和液相线 (泡点线)
饱和汽相线 (露点线)
图 2-3 纯物质的P-T图
PC
气 液 液/汽
汽 饱和汽相线
饱和汽相线
VC
纯物质的P-V图
在临界点 C :
P V
T ,c
0
RT
a
P V b T1/2V V b
a
0.42768
R T2 2.5 c
Pc
b 0.08664 RTc Pc
RK方程能较成功地用于气相P-V-T的计算,但 液相的效果较差,也不能预测纯流体的蒸汽压(即汽 液平衡)。
定义参数A和B:
A ap 0.42748 Pr
R T2 2.5
V
a
V
b
2 8
a
ac
T
0.42748
R 2Tc2 Pc
T
b 0.08664 RTc Pc
T
1
0.48
1.574
0.176
2
1
T 0.5 r
2
与RK方程相比,SRK方程大大提高了表达纯物质 汽液平衡的能力,使之能用于混合物的汽液平衡计算, 故在工业上获得了广泛的应用。
